Multispectral UAV-Based Monitoring of Leek Dry-Biomass and Nitrogen Uptake across Multiple Sites and Growing Seasons
Abstract
1. Introduction
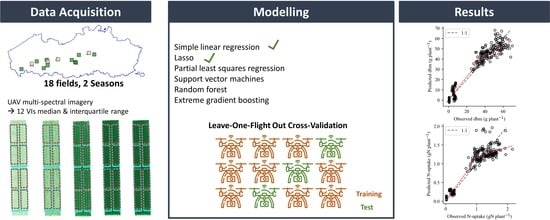
2. Materials and Methods
2.1. Data Acquisition
2.1.1. Site Description and Agricultural Management
2.1.2. Plant Samples
2.1.3. UAV Monitoring
2.2. Image Processing and Feature Extraction
2.3. Statistical Analysis
2.3.1. Modelling Approaches
2.3.2. Model Training and Hyperparameter Optimization
2.3.3. Model Selection and Validation
3. Results
3.1. UAV Flights and Plant Samples
3.2. Regression Analysis and Model Selection
3.2.1. SLR Models
3.2.2. Model Selection for DBM Prediction
3.2.3. Model Selection for N-Uptake Prediction
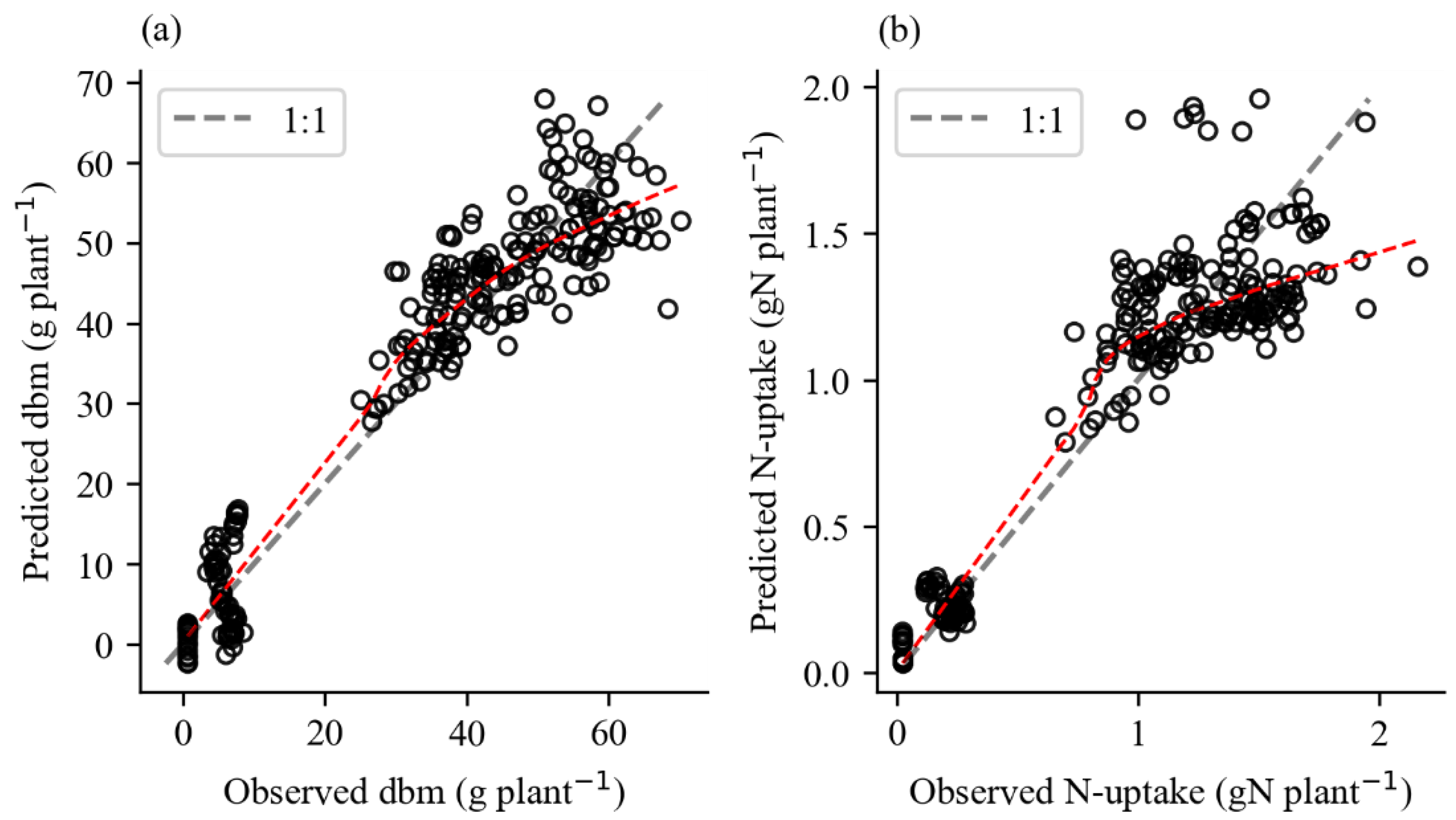
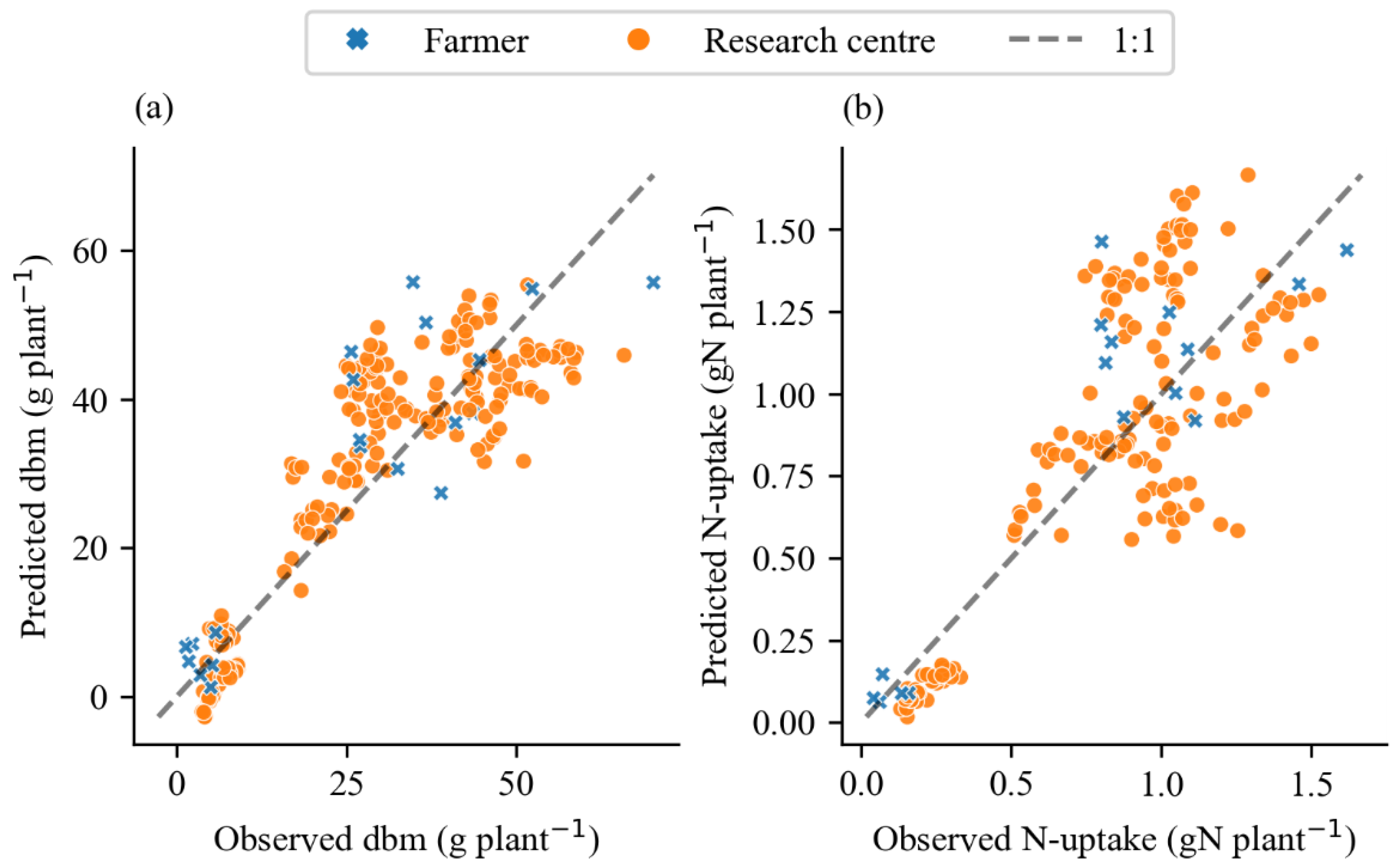
3.3. Model Validation
3.3.1. Pluston Variety
3.3.2. Model Transfer to Other Varieties
4. Discussion
4.1. Model Selection and Validation
4.2. Model Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| SLR | Lasso | PLSR | SVR | RFR | xGBR | |
|---|---|---|---|---|---|---|
| (g plant−1) | 8.15 | 4.49 | 5.07 | 3.58 | 1.7 | 1.96 |
| (g plant−1) | 8.17 | 4.88 | 5.32 | 4.36 | 4.18 | 4.35 |
| RMSEct (g plant−1) | 8.19 | 4.47 | 5.38 | 4.31 | 4.20 | 4.52 |
| rRMSEct (%) | 38.74 | 23.05 | 25.47 | 20.0 | 19.89 | 21.38 |
| Biasct (g plant−1) | 0.01 | 0.00 | 0.10 | −0.05 | −0.20 | −0.63 |
| R2 | 0.85 | 0.95 | 0.94 | 0.96 | 0.96 | 0.96 |
| SLR | Lasso | PLSR | SVR | RFR | xGBR | |
|---|---|---|---|---|---|---|
| (g plant−1) | 0.21 | 0.15 | 0.14 | 0.08 | 0.06 | 0.14 |
| (g plant−1) | 0.21 | 0.16 | 0.16 | 0.16 | 0.14 | 0.15 |
| RMSEct (g plant−1) | 0.21 | 0.16 | 0.16 | 0.17 | 0.14 | 0.16 |
| rRMSEct (%) | 36.44 | 28.36 | 27.19 | 29.23 | 24.35 | 27.83 |
| Biasct (g plant−1) | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 |
| R2 | 0.87 | 0.92 | 0.93 | 0.91 | 0.94 | 0.93 |
References
- Zhang, X.; Davidson, E.A.; Mauzerall, D.L.; Searchinger, T.D.; Dumas, P.; Shen, Y. Managing Nitrogen for Sustainable Development. Nature 2015, 528, 51–59. [Google Scholar] [CrossRef]
- Thompson, R.B.; Tremblay, N.; Fink, M.; Gallardo, M.; Padilla, F.M. Tools and Strategies for Sustainable Nitrogen Fertilisation of Vegetable Crops; Springer: Cham, Switzerland, 2017; pp. 11–63. [Google Scholar]
- Groenten Openlucht|Landbouw & Visserij. Available online: https://landbouwcijfers.vlaanderen.be/landbouw/groenten-openlucht (accessed on 31 August 2022).
- FAO Crops and Livestock Products. Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 31 August 2022).
- Thompson, R.B.; Voogt, W.; Incrocci, L.; Fink, M.; de Neve, S. Strategies for Optimal Fertiliser Management of Vegetable Crops in Europe. Acta Hortic. 2018, 1192, 129–140. [Google Scholar] [CrossRef]
- Tei, F.; de Neve, S.; de Haan, J.; Kristensen, H.L. Nitrogen Management of Vegetable Crops. Agric. Water Manag. 2020, 240, 106316. [Google Scholar]
- Padilla, F.M.; Gallardo, M.; Peña-Fleitas, M.T.; de Souza, R.; Thompson, R.B. Proximal Optical Sensors for Nitrogen Management of Vegetable Crops: A Review. Sensors 2018, 18, 2083. [Google Scholar] [CrossRef] [PubMed]
- Ulissi, V.; Antonucci, F.; Benincasa, P.; Farneselli, M.; Tosti, G.; Guiducci, M.; Tei, F.; Costa, C.; Pallottino, F.; Pari, L.; et al. Nitrogen Concentration Estimation in Tomato Leaves by VIS-NIR Non-Destructive Spectroscopy. Sensors 2011, 11, 6411–6424. [Google Scholar] [CrossRef]
- de Souza, R.; Peña-Fleitas, M.T.; Thompson, R.B.; Gallardo, M.; Grasso, R.; Padilla, F.M. The Use of Chlorophyll Meters to Assess Crop N Status and Derivation of Sufficiency Values for Sweet Pepper. Sensors 2019, 19, 2949. [Google Scholar] [CrossRef] [PubMed]
- de Souza, R.; Grasso, R.; Teresa Peña-Fleitas, M.; Gallardo, M.; Thompson, R.B.; Padilla, F.M. Effect of Cultivar on Chlorophyll Meter and Canopy Reflectance Measurements in Cucumber. Sensors 2020, 20, 509. [Google Scholar] [CrossRef]
- Corti, M.; Marino Gallina, P.; Cavalli, D.; Cabassi, G. Hyperspectral Imaging of Spinach Canopy under Combined Water and Nitrogen Stress to Estimate Biomass, Water, and Nitrogen Content. Biosyst. Eng. 2017, 158, 38–50. [Google Scholar] [CrossRef]
- Marino, S.; Alvino, A. Hyperspectral Vegetation Indices for Predicting Onion (Allium cepa L.) Yield Spatial Variability. Comput. Electron. Agric. 2015, 116, 109–117. [Google Scholar] [CrossRef]
- Suarez, L.A.; Robson, A.; McPhee, J.; O’Halloran, J.; van Sprang, C. Accuracy of Carrot Yield Forecasting Using Proximal Hyperspectral and Satellite Multispectral Data. Precis. Agric. 2020, 21, 1304–1326. [Google Scholar] [CrossRef]
- Marino, S.; Basso, B.; Leone, A.P.; Alvino, A. Agronomic Traits and Vegetation Indices of Two Onion Hybrids. Sci. Hortic. 2013, 155, 56–64. [Google Scholar] [CrossRef]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A Review on UAV-Based Applications for Precision Agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef]
- Wittstruck, L.; Kühling, I.; Trautz, D.; Kohlbrecher, M.; Jarmer, T. UAV-Based RGB Imagery for Hokkaido Pumpkin (Cucurbita Max.) Detection and Yield Estimation. Sensors 2021, 21, 118. [Google Scholar] [CrossRef] [PubMed]
- Ballesteros, R.; Ortega, J.F.; Hernandez, D.; Moreno, M.A. Onion Biomass Monitoring Using UAV-Based RGB Imaging. Precis. Agric. 2018, 19, 840–857. [Google Scholar] [CrossRef]
- Moeckel, T.; Dayananda, S.; Nidamanuri, R.R.; Nautiyal, S.; Hanumaiah, N.; Buerkert, A.; Wachendorf, M. Estimation of Vegetable Crop Parameter by Multi-Temporal UAV-Borne Images. Remote Sens. 2018, 10, 805. [Google Scholar] [CrossRef]
- Kim, D.-W.; Yun, H.; Jeong, S.-J.; Kwon, Y.-S.; Kim, S.-G.; Lee, W.; Kim, H.-J. Modeling and Testing of Growth Status for Chinese Cabbage and White Radish with UAV-Based RGB Imagery. Remote Sens. 2018, 10, 563. [Google Scholar] [CrossRef]
- Astor, T.; Dayananda, S.; Nautiyal, S.; Wachendorf, M. Vegetable Crop Biomass Estimation Using Hyperspectral and RGB 3D UAV Data. Agronomy 2020, 10, 1600. [Google Scholar] [CrossRef]
- Xie, C.; Yang, C. A Review on Plant High-Throughput Phenotyping Traits Using UAV-Based Sensors. Comput. Electron. Agric. 2020, 178, 105731. [Google Scholar] [CrossRef]
- Panday, U.S.; Pratihast, A.K.; Aryal, J.; Kayastha, R.B. A Review on Drone-Based Data Solutions for Cereal Crops. Drones 2020, 4, 41. [Google Scholar] [CrossRef]
- Johansen, K.; Morton, M.J.L.; Malbeteau, Y.; Aragon, B.; Al-Mashharawi, S.; Ziliani, M.G.; Angel, Y.; Fiene, G.; Negrão, S.; Mousa, M.A.A.; et al. Predicting Biomass and Yield in a Tomato Phenotyping Experiment Using UAV Imagery and Random Forest. Front. Artif. Intell. 2020, 3, 28. [Google Scholar] [CrossRef]
- de Nies, J.; Verhaeghe, M. Het Documenteren en Milieukundig Bijstellen van Het KNS en Andere Bemestingsadviessystemen in de Tuinbouw met het Oog op Een Ruimere Toepassing in de Tuinbouw Zoals Voorzien in het Actieprogramma 2011–2014. Available online: http://www.vlm.be/nl//SiteCollectionDocuments/Mestbank/Studies/Bemestingsadviessystementuinbouw/20141114eindrapportVlaamsKNS.pdf (accessed on 23 January 2020).
- Lorenz, H.P.; Schlaghecken, J.; Engel, G.; Maync, A.; Ziegler, J.; Strohmeyer, K. Ordnungsgemaesse Stickstoff-Versorgung im Freiland-Gemuesebau nach dem, Kulturbegleitenden-Nmin-Sollwerte-(KNS)-System; Ministerium fuer Landwirtschaft, Weinbau und Forsten Rheinland-Pfalz: Mainz, Germany, 1989; 85p. (In German) [Google Scholar]
- Mihaljev, Ž.A.; Jakšić, S.M.; Prica, N.B.; Ćupić, Ž.N.; Živkov-Baloš, M.M. Comparison of the Kjeldahl Method, Dumas Method and NIR Method for Total Nitrogen Determination in Meat and Meat Products. J. Agroaliment. Process. Technol. 2015, 21, 365–370. [Google Scholar]
- Gillies, S.; Ward, B.; Petersen, A.S. Others Rasterio: Geospatial Raster I/O for Python Programmers. 2013. Available online: https://github.com/rasterio/rasterio (accessed on 7 October 2022).
- Haumont, J.; Lootens, P.; Cool, S.; van Beek, J.; Raymaekers, D.; Ampe, E.M.; de Cuypere, T.; Bes, O.; Bodyn, J.; Saeys, W. 60. Leek Growth Monitoring Using Multispectral UAV Imagery; Wageningen Academic Publishers: Wageningen, The Netherlands, 2021; pp. 501–507. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts; NASA Special Publication: Washington, DC, USA, 1974; Volume 351, p. 309. [Google Scholar]
- Gitelson, A.; Merzlyak, M.N. Quantitative Estimation of Chlorophyll-a Using Reflectance Spectra: Experiments with Autumn Chestnut and Maple Leaves. J. Photochem. Photobiol. B 1994, 22, 247–252. [Google Scholar] [CrossRef]
- Gitelson, A.; Kaufman, Y.; Merzlyak, M. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Bradford, J.M.; Murden, D. Airborne Hyperspectral Imagery and Yield Monitor Data for Mapping Cotton Yield Variability. Precis. Agric. 2004, 5, 445–461. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Dash, J.; Curran, P.J. The MERIS Terrestrial Chlorophyll Index. Int. J. Remote Sens. 2010, 25, 5403–5413. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Barnes, E.M.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident Detection of Crop Water Stress, Nitrogen Status and Canopy Density Using Ground Based Multispectral Data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000; Volume 1619, p. 6. [Google Scholar]
- Gitelson, A.; Gritz, Y.; Merzlyak, M. Relationships between Leaf Chlorophyll Content and Spectral Reflectance and Algorithms for Non-Destructive Chlorophyll Assessment in Higher Plant Leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial Least-Squares Regression: A Tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. {XGBoost}: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association of Computer Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in {P}ython. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Saeys, W.; Nguyen Do Trong, N.; Van Beers, R.; Nicolaï, B.M. Multivariate Calibration of Spectroscopic Sensors for Postharvest Quality Evaluation: A Review. Postharvest Biol. Technol. 2019, 158, 110981. [Google Scholar] [CrossRef]
- Kemps, B.J.; Saeys, W.; Mertens, K.; Darius, P.; de Baerdemaeker, J.G.; de Ketelaere, B. The Importance of Choosing the Right Validation Strategy in Inverse Modelling. J. Near Infrared Spectrosc. 2010, 18, 231–237. [Google Scholar] [CrossRef]
- Luo, S.; Jiang, X.; He, Y.; Li, J.; Jiao, W.; Zhang, S.; Xu, F.; Han, Z.; Sun, J.; Yang, J.; et al. Multi-Dimensional Variables and Feature Parameter Selection for Aboveground Biomass Estimation of Potato Based on UAV Multispectral Imagery. Front. Plant Sci. 2022, 13, 2673. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-Based Plant Height from Crop Surface Models, Visible, and near Infrared Vegetation Indices for Biomass Monitoring in Barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Pranga, J.; Borra-Serrano, I.; Aper, J.; de Swaef, T.; Ghesquiere, A.; Quataert, P.; Roldán-Ruiz, I.; Janssens, I.A.; Ruysschaert, G.; Lootens, P. Improving Accuracy of Herbage Yield Predictions in Perennial Ryegrass with UAV-Based Structural and Spectral Data Fusion and Machine Learning. Remote Sens. 2021, 13, 3459. [Google Scholar] [CrossRef]
- Viljanen, N.; Honkavaara, E.; Näsi, R.; Hakala, T.; Niemeläinen, O.; Kaivosoja, J. A Novel Machine Learning Method for Estimating Biomass of Grass Swards Using a Photogrammetric Canopy Height Model, Images and Vegetation Indices Captured by a Drone. Agriculture 2018, 8, 70. [Google Scholar] [CrossRef]
- Näsi, R.; Viljanen, N.; Kaivosoja, J.; Alhonoja, K.; Hakala, T.; Markelin, L.; Honkavaara, E. Estimating Biomass and Nitrogen Amount of Barley and Grass Using UAV and Aircraft Based Spectral and Photogrammetric 3D Features. Remote Sens. 2018, 10, 1082. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
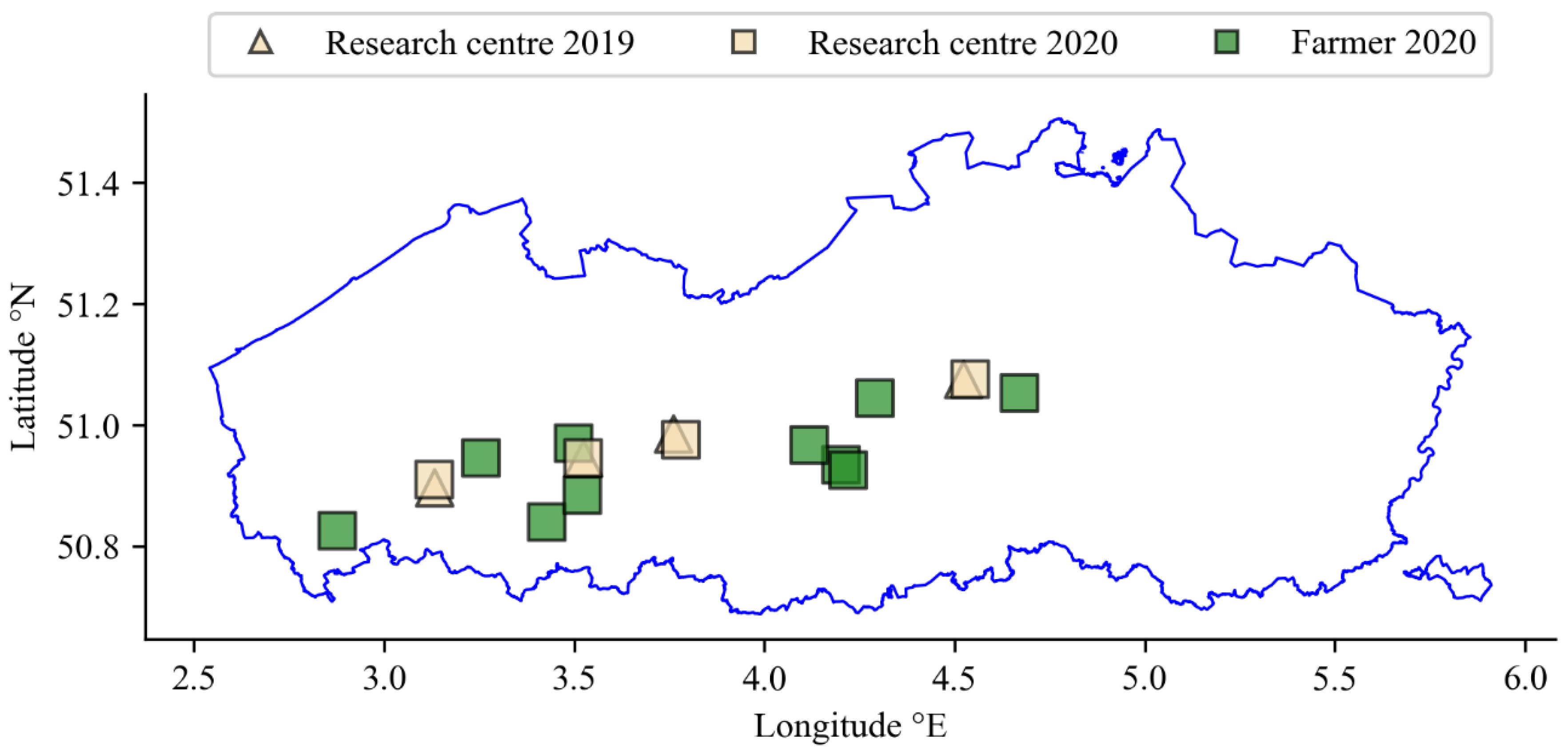

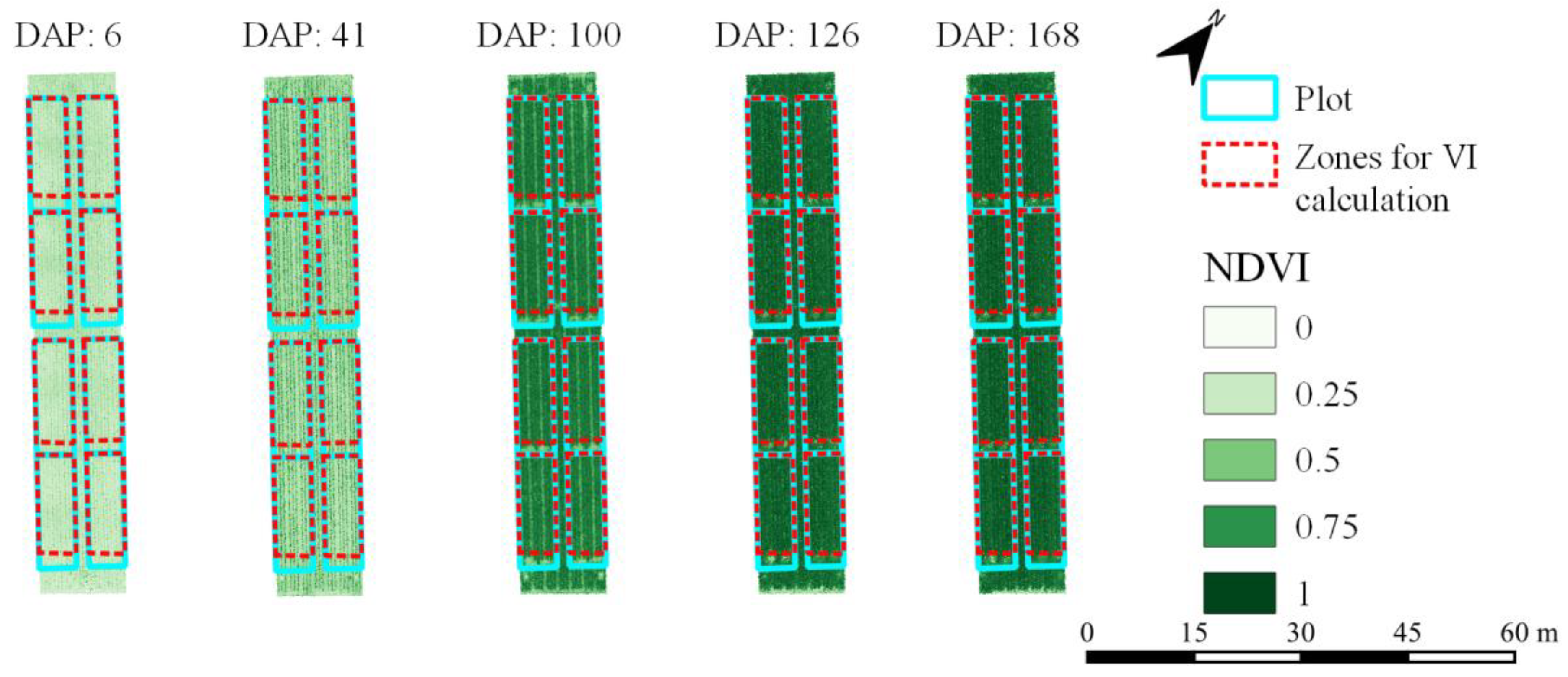


| Season | Type | Location | Area (ha) | Variety | Fertilizer | Plant Density (ha−1) | nplots | nflights | nobs | DAP |
|---|---|---|---|---|---|---|---|---|---|---|
| 2019 | Research Centre | ILVO 1 | 0.89 | Pluston | CAN | 153 846 | 12 | 3 | 40 | 41, 99, 125 |
| Inagro 2 | 0.53 | Pluston | CAN | 153 846 | 24 | 5 | 120 | 41, 101, 132, 176, 216 | ||
| PCG 2 | 0.14 | Pluston | CAN | 153 846 | 12 | 4 | 48 | 3, 41, 100, 129 | ||
| PSKW 1 | 0.09 | Pluston | CAN | 178 571 | 8 | 5 | 40 | 6, 41, 100, 126, 168 | ||
| 2020 | Research Centre | ILVO 1 | 0.48 | Pluston | CAN | 153 846 | 16 | 4 | 64 | 44, 83, 136, 251 |
| Inagro 2 | 0.32 | Pluston | CAN | 153 846 | 16 | 4 | 64 | 49, 91, 135, 210 | ||
| PCG 2 | 0.18 | Pluston | CAN | 153 846 | 4 | 3 | 12 | 42, 84, 129 | ||
| PSKW 1 | 0.28 | Pluston | CAN | 178 571 | 16 | 4 (1) * | 64 (16) * | 36, 77, 105, 149 * | ||
| Farmer | F1 2 | 3.51 | Vitaton | PS + Urean | 185 185 | 3 | 3 | 9 | 43, 124, 257 | |
| F2 1 | 2.97 | Chiefton | CM + CAN | 185 185 | 2 | 2 | 4 | 43, 134 | ||
| Pluston | CM + CAN | 185 185 | 1 | 2 | 2 | 38, 129 | ||||
| F3 2 | 1.45 | Pluston | CS + CAN | 161 943 | 3 | 3 | 9 | 36, 118, 183 | ||
| F4 2 | 3.09 | Krypton | N.A. § | 161 943 | 2 | 2 | 4 | 54, 243 | ||
| F5 1 | 2.14 | Harston | PS + CAN | 170 940 | 2 | 3 (1) * | 6 (2) * | 44, 100, 266 * | ||
| F6 2 | 1.88 | Vitaton | CS + CAN | 151 515 | 2 | 1 | 2 | 204 | ||
| F7 2 | 1.21 | Pluston | PS + CAN | 175 439 | 1 | 3 | 3 | 40, 122, 176 | ||
| Poulton | PS + CAN | 175 439 | 2 | 3 | 6 | 56, 138, 187 | ||||
| F8 2 | 0.79 | Harston | CM + APP | 208 333 | 2 | 2 | 4 | 47, 263 | ||
| F9 1 | 1.95 | Pluston | Novatec | 227 273 | 2 | 3 (1) * | 6 (2) * | 37, 106, 150 * | ||
| F10 1 | 0.66 | Poulton | RM + CAN | 170 940 | 2 | 2 (0) * | 4 (0) * | 43, 134 | ||
| Total 2019 | 56 | 17 | 248 | |||||||
| Total 2020 | 76 | 44 (32) * | 263 (203) * | |||||||
| Total | 132 | 61 | 511 (451) * |
| VI | Formula | References |
|---|---|---|
| NDVI | (nir − red)/(nir + red) | [29] |
| NDRE | (nir − rededge)/(nir + rededge) | [30] |
| GNDVI | (nir − green)/(nir + green) | [31] |
| BNDVI | (nir − blue)/(nir + blue) | [32] |
| RWDRVI | (0.1 × nir − red)/(0.1× nir + red) | [33] |
| BWDRVI | (0.1 × nir − blue)/(0.1× nir + blue) | [33] |
| MTCI | (nir − rededge)/(rededge − red) | [34] |
| MCARI | (rededge − red) − 0.2(rededge − green)(rededge/red) | [35] |
| CCCI | [(nir + red)(nir − rededge)]/[(nir − red)(nir + rededge)] | [36] |
| CI-green | nir/green − 1 | [37] |
| CI-rededge | nir/rededge − 1 | [37] |
| SAVI | [(1 + 0.5) × (nir − rededge)]/(nir + red + 0.5) | [38] |
| SLR | Lasso | PLSR | SVR | RFR | xGBR | |
|---|---|---|---|---|---|---|
| (g plant−1) | 8.11 | 5.00 | 5.26 | 3.59 | 3.30 | 1.97 |
| (g plant−1) | 6.34 | 7.22 | 7.58 | 11.15 | 6.37 | 6.31 |
| RMSEct (g plant−1) | 9.08 | 6.60 | 7.90 | 10.92 | 6.35 | 6.72 |
| rRMSEct (%) | 42.97 | 31.21 | 37.36 | 51.67 | 30.03 | 31.80 |
| Biasct (g plant−1) | −0.02 | 0.59 | 0.70 | −0.07 | −0.43 | −0.89 |
| R2 | 0.81 | 0.90 | 0.87 | 0.73 | 0.91 | 0.90 |
| SLR | Lasso | PLSR | SVR | RFR | xGBR | |
|---|---|---|---|---|---|---|
| (g plant−1) | 0.21 | 0.20 | 0.16 | 0.08 | 0.11 | 0.15 |
| (g plant−1) | 0.20 | 0.25 | 0.23 | 0.32 | 0.19 | 0.18 |
| RMSEct (g plant−1) | 0.22 | 0.29 | 0.26 | 0.30 | 0.21 | 0.23 |
| rRMSEct (%) | 39.08 | 51.35 | 44.89 | 52.49 | 36.78 | 40.11 |
| Biasct (g plant−1) | 0.00 | 0.05 | 0.01 | 0.14 | 0.03 | −0.05 |
| R2 | 0.85 | 0.75 | 0.82 | 0.78 | 0.87 | 0.87 |
| Field Type | All | Research Centre | Farmer | |
|---|---|---|---|---|
| Variety | Pluston | Pluston | Pluston | |
| DBM | ||||
| nobs | 224 | 204 | 20 | |
| RMSEP | 8.50 | 8.37 | 9.79 | |
| rRMSEP | 49.98 | 49.96 | 50.62 | |
| Bias | 1.28 | 1.10 | 3.11 | |
| R2 | 0.77 | 0.77 | 0.78 | |
| N-uptake | ||||
| nobs | 172 | 156 | 16 | |
| RMSEP | 0.27 | 0.28 | 0.24 | |
| rRMSEP | 69.77 | 72.76 | 49.51 | |
| Bias | 0.03 | 0.02 | 0.09 | |
| R2 | 0.68 | 0.67 | 0.82 |
| Variety | Chiefton | Harston | Krypton | Poulton | Vitaton | |
|---|---|---|---|---|---|---|
| DBM | ||||||
| nobs | 4 | 10 | 4 | 10 | 11 | |
| RMSEP | 6.19 | 21.68 | 9.20 | 13.32 | 11.59 | |
| Bias | 1.03 | 3.89 | 3.94 | 9.83 | 0.23 | |
| R2 | 1.00 | 0.59 | 0.86 | 0.71 | 0.70 | |
| N-uptake | ||||||
| nobs | 4 | 6 | 4 | 6 | 11 | |
| RMSEP | 0.27 | 0.26 | 0.26 | 0.30 | 0.44 | |
| Bias | 0.24 | −0.01 | 0.04 | 0.23 | 0.29 | |
| R2 | 0.96 | 0.73 | 0.77 | 0.96 | 0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haumont, J.; Lootens, P.; Cool, S.; Van Beek, J.; Raymaekers, D.; Ampe, E.; De Cuypere, T.; Bes, O.; Bodyn, J.; Saeys, W. Multispectral UAV-Based Monitoring of Leek Dry-Biomass and Nitrogen Uptake across Multiple Sites and Growing Seasons. Remote Sens. 2022, 14, 6211. https://doi.org/10.3390/rs14246211
Haumont J, Lootens P, Cool S, Van Beek J, Raymaekers D, Ampe E, De Cuypere T, Bes O, Bodyn J, Saeys W. Multispectral UAV-Based Monitoring of Leek Dry-Biomass and Nitrogen Uptake across Multiple Sites and Growing Seasons. Remote Sensing. 2022; 14(24):6211. https://doi.org/10.3390/rs14246211
Chicago/Turabian StyleHaumont, Jérémie, Peter Lootens, Simon Cool, Jonathan Van Beek, Dries Raymaekers, Eva Ampe, Tim De Cuypere, Onno Bes, Jonas Bodyn, and Wouter Saeys. 2022. "Multispectral UAV-Based Monitoring of Leek Dry-Biomass and Nitrogen Uptake across Multiple Sites and Growing Seasons" Remote Sensing 14, no. 24: 6211. https://doi.org/10.3390/rs14246211
APA StyleHaumont, J., Lootens, P., Cool, S., Van Beek, J., Raymaekers, D., Ampe, E., De Cuypere, T., Bes, O., Bodyn, J., & Saeys, W. (2022). Multispectral UAV-Based Monitoring of Leek Dry-Biomass and Nitrogen Uptake across Multiple Sites and Growing Seasons. Remote Sensing, 14(24), 6211. https://doi.org/10.3390/rs14246211