Using Deep Learning to Model Elevation Differences between Radar and Laser Altimetry
Abstract
1. Introduction
2. Data
3. Method
3.1. Data Filtering and Preparation
3.1.1. CryoSat-2 Data
3.1.2. ICESat-2 Data
3.1.3. ArcticDEM Data
3.1.4. Spatio-Temporal Join
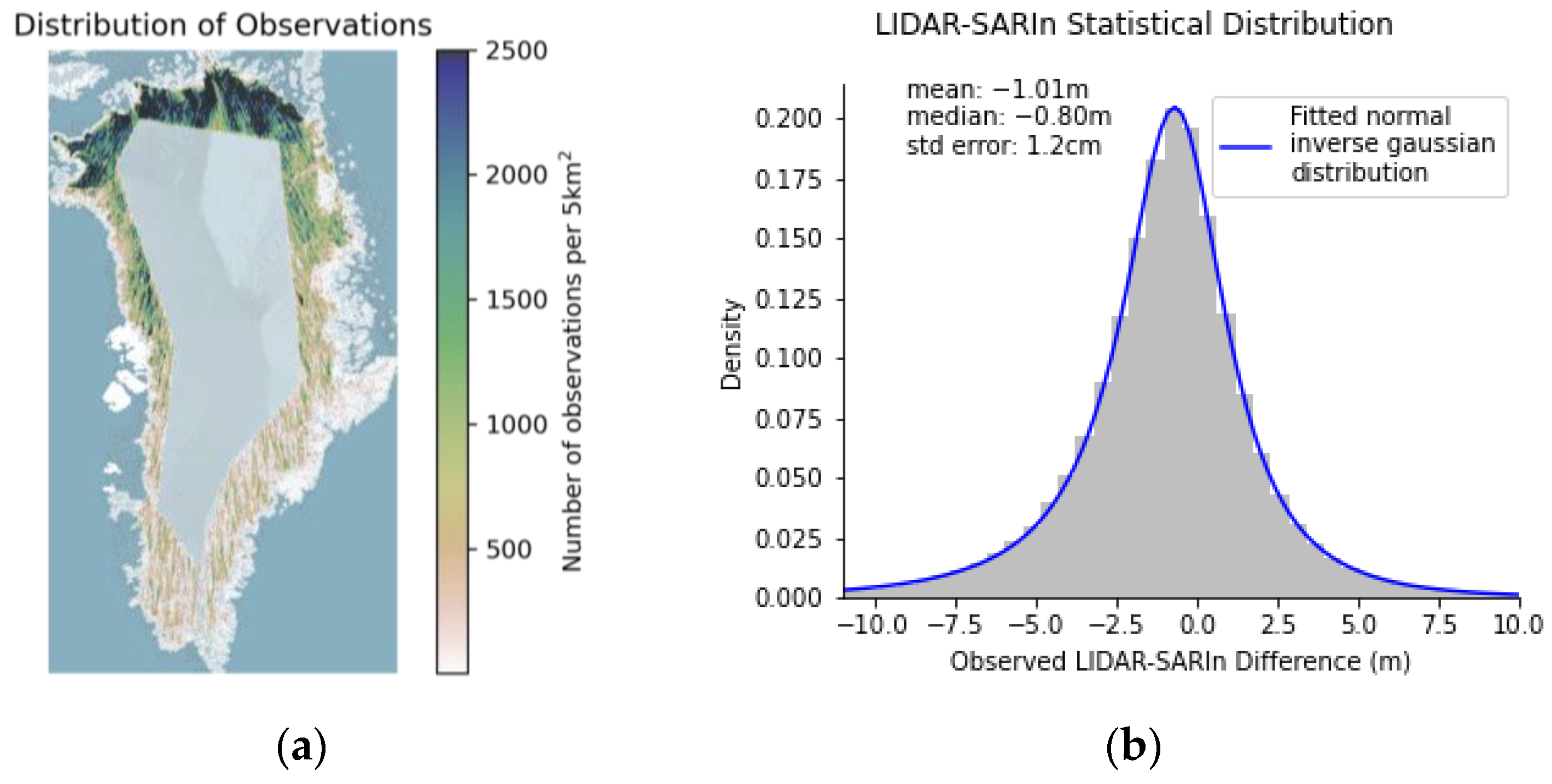
3.2. Statistical Assumptions
3.3. CryoSat-2 SARIn vs. ICESat-2 LIDAR Maps
3.4. Models
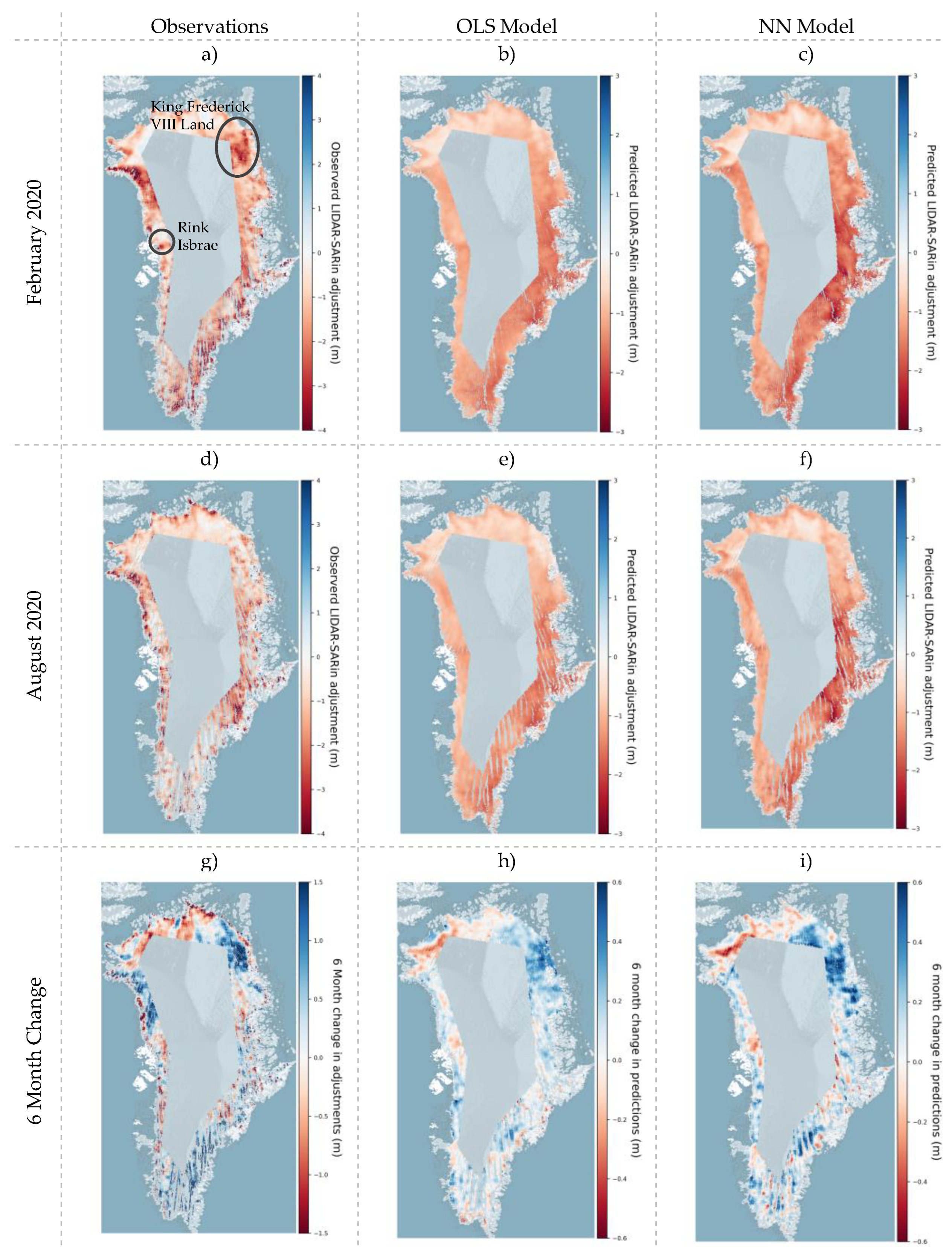
4. Results
5. Discussion
5.1. Observations
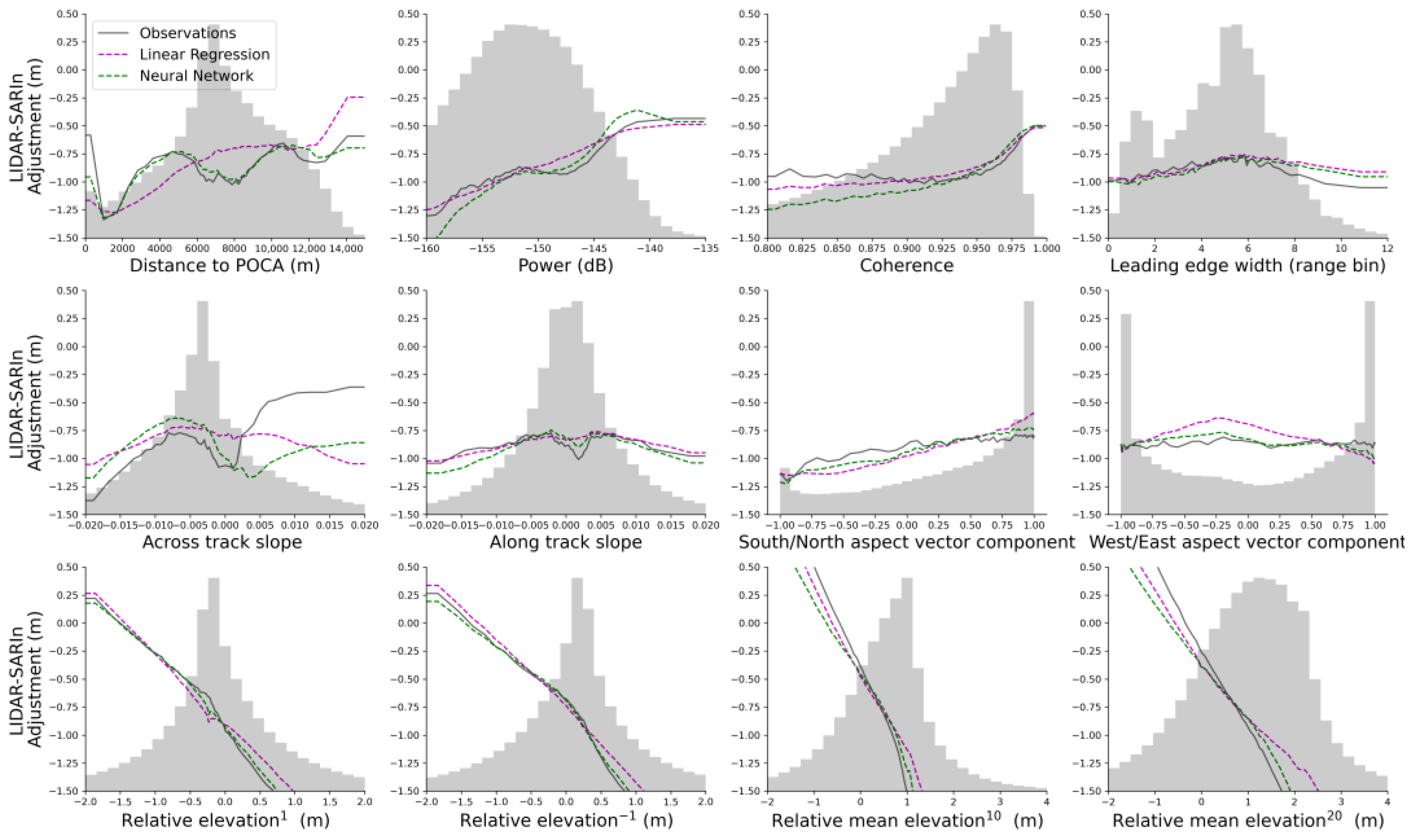
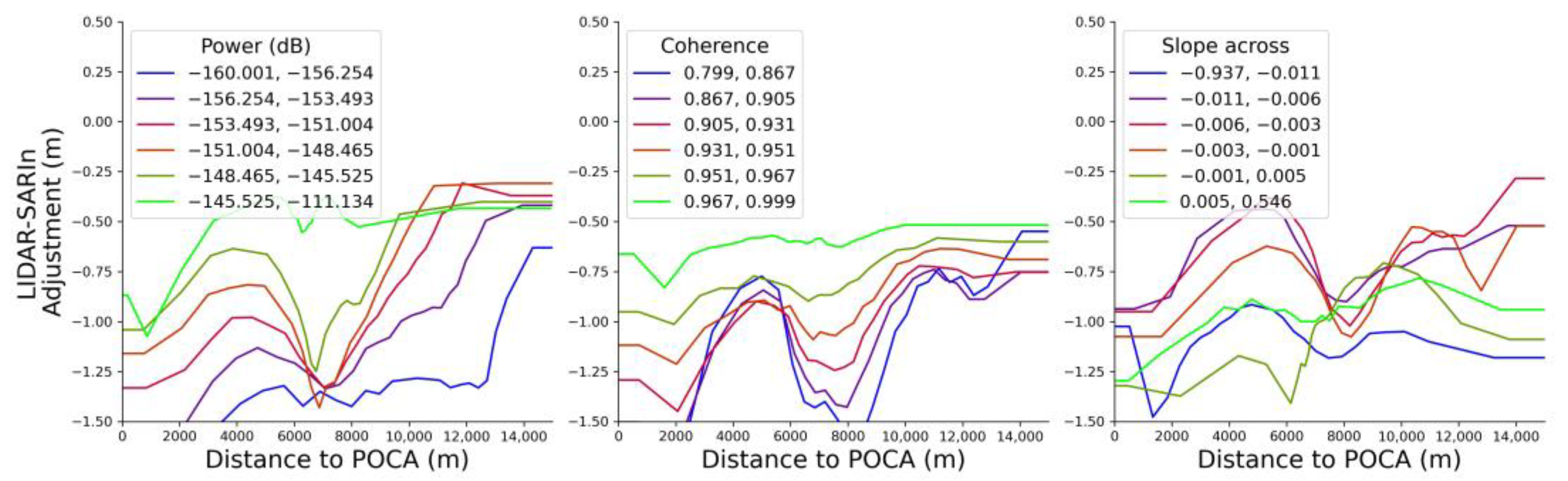
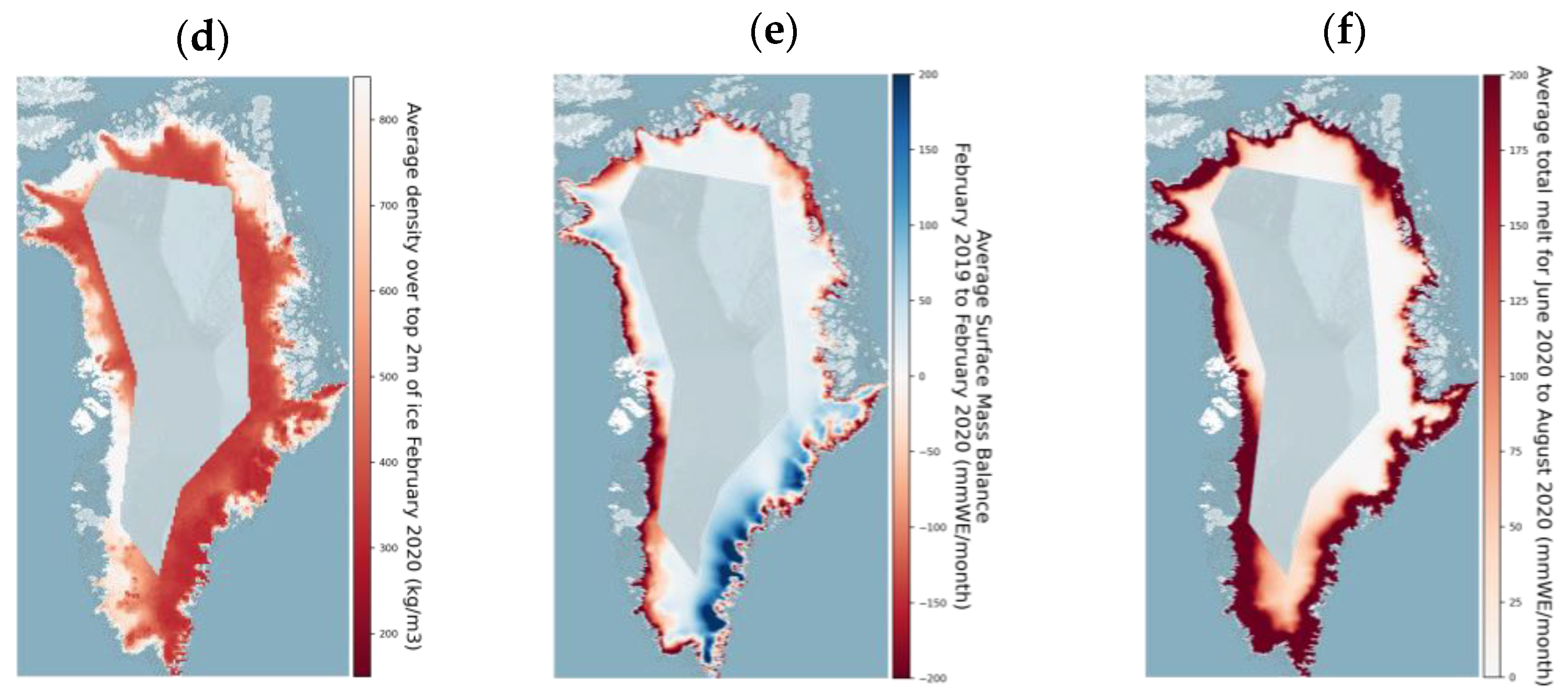
5.1.1. LIDAR-SARIn Differences-Observed Contribution Drivers
5.1.2. LIDAR-SARIn Differences–Spatial and Temporal Trends
5.2. OLS and NN Models-Strengths
5.3. OLS and NN Models-Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zwally, H.J.; Bindschadler, R.A.; Brenner, A.C.; Major, J.A.; Marsh, J.G. Growth of Greenland Ice Sheet: Measurement. Science 1989, 246, 1587–1589. [Google Scholar] [CrossRef] [PubMed]
- Wingham, D.J.; Ridout, A.J.; Scharroo, R.; Arthern, R.J.; Shum, C.K. Antarctic Elevation Change from 1992 to 1996. Science 1998, 282, 456–458. [Google Scholar] [CrossRef]
- Shepherd, A.; Wingham, D.; Payne, T.; Skvarca, P. Larsen Ice Shelf Has Progressively Thinned. Science 2003, 302, 856–859. [Google Scholar] [CrossRef]
- Shepherd, A.; Wingham, D.J.; Mansley, J.A.D.; Corr, H.F.J. Inland Thinning of Pine Island Glacier, West Antarctica. Science 2001, 291, 862–864. [Google Scholar] [CrossRef]
- Zwally, H.J.; Giovinetto, M.B.; Li, J.; Cornejo, H.G.; Beckley, M.A.; Brenner, A.C.; Saba, J.L.; Yi, D. Mass Changes of the Greenland and Antarctic Ice Sheets and Shelves and Contributions to Sea-Level Rise: 1992–2002. J. Glaciol. 2005, 51, 509–527. [Google Scholar] [CrossRef]
- Wingham, D.J.; Shepherd, A.; Muir, A.; Marshall, G.J. Mass Balance of the Antarctic Ice Sheet. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2006, 364, 1627–1635. [Google Scholar] [CrossRef]
- Fricker, H.A.; Scambos, T.; Bindschadler, R.; Padman, L. An Active Subglacial Water System in West Antarctica Mapped from Space. Science 2007, 315, 1544–1548. [Google Scholar] [CrossRef]
- Pritchard, H.D.; Arthern, R.J.; Vaughan, D.G.; Edwards, L.A. Extensive Dynamic Thinning on the Margins of the Greenland and Antarctic Ice Sheets. Nature 2009, 461, 971–975. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting Patterns of Early Twenty-First-Century Glacier Mass Change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef]
- Bamber, J.L.; Griggs, J.A.; Hurkmans, R.T.W.L.; Dowdeswell, J.A.; Gogineni, S.P.; Howat, I.; Mouginot, J.; Paden, J.; Palmer, S.; Rignot, E.; et al. A New Bed Elevation Dataset for Greenland. Cryosphere 2013, 7, 499–510. [Google Scholar] [CrossRef]
- McMillan, M.; Shepherd, A.; Sundal, A.; Briggs, K.; Muir, A.; Ridout, A.; Hogg, A.; Wingham, D. Increased Ice Losses from Antarctica Detected by CryoSat-2. Geophys. Res. Lett. 2014, 41, 3899–3905. [Google Scholar] [CrossRef]
- Gourmelen, N.; Goldberg, D.N.; Snow, K.; Henley, S.F.; Bingham, R.G.; Kimura, S.; Hogg, A.E.; Shepherd, A.; Mouginot, J.; Lenaerts, J.T.M.; et al. Channelized Melting Drives Thinning under a Rapidly Melting Antarctic Ice Shelf. Geophys. Res. Lett. 2017, 44, 9796–9804. [Google Scholar] [CrossRef]
- Gourmelen, N.; Escorihuela, M.J.; Shepherd, A.; Foresta, L.; Muir, A.; Garcia-Mondéjar, A.; Roca, M.; Baker, S.G.; Drinkwater, M.R. CryoSat-2 Swath Interferometric Altimetry for Mapping Ice Elevation and Elevation Change. Adv. Space Res. 2018, 62, 1226–1242. [Google Scholar] [CrossRef]
- Rémy, F.; Parouty, S. Antarctic Ice Sheet and Radar Altimetry: A Review. Remote Sens. 2009, 1, 1212–1239. [Google Scholar] [CrossRef]
- Nilsson, J.; Vallelonga, P.; Simonsen, S.B.; Sørensen, L.S.; Forsberg, R.; Dahl-Jensen, D.; Hirabayashi, M.; Goto-Azuma, K.; Hvidberg, C.S.; Kjær, H.A.; et al. Greenland 2012 Melt Event Effects on CryoSat-2 Radar Altimetry. Geophys. Res. Lett. 2015, 42, 3919–3926. [Google Scholar] [CrossRef]
- Slater, T.; Shepherd, A.; Mcmillan, M.; Armitage, T.W.K.; Otosaka, I.; Arthern, R.J. Compensating Changes in the Penetration Depth of Pulse-Limited Radar Altimetry over the Greenland Ice Sheet. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9633–9642. [Google Scholar] [CrossRef]
- Gray, L. Brief Communication: Glacier Run-off Estimation Using Altimetry-Derived Basin Volume Change: Case Study at Humboldt Glacier, Northwest Greenland. Cryosphere 2021, 15, 1005–1014. [Google Scholar] [CrossRef]
- Slater, T.; Shepherd, A.; McMillan, M.; Leeson, A.; Gilbert, L.; Muir, A.; Munneke, P.K.; Noël, B.; Fettweis, X.; van den Broeke, M.; et al. Increased Variability in Greenland Ice Sheet Runoff from Satellite Observations. Nat. Commun. 2021, 12, 6069. [Google Scholar] [CrossRef] [PubMed]
- Arthern, R.J.; Wingham, D.J.; Ridout, A.L. Controls on ERS Altimeter Measurements over Ice Sheets: Footprint-Scale Topography, Backscatter Fluctuations, and the Dependence of Microwave Penetration Depth on Satellite Orientation. J. Geophys. Res. Atmos. 2001, 106, 33471–33484. [Google Scholar] [CrossRef]
- Gray, L.; Burgess, D.; Copland, L.; Langley, K.; Gogineni, P.; Paden, J.; Leuschen, C.; van As, D.; Fausto, R.; Joughin, I.; et al. Measuring Height Change around the Periphery of the Greenland Ice Sheet with Radar Altimetry. Front. Earth Sci. 2019, 7, 146. [Google Scholar] [CrossRef]
- Recchia, L.; Scagliola, M.; Giudici, D.; Kuschnerus, M. An Accurate Semianalytical Waveform Model for Mispointed SAR Interferometric Altimeters. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1537–1541. [Google Scholar] [CrossRef]
- Snauffer, A.M.; Hsieh, W.W.; Cannon, A.J.; Schnorbus, M.A. Improving Gridded Snow Water Equivalent Products in British Columbia, Canada: Multi-Source Data Fusion by Neural Network Models. Cryosphere 2018, 12, 891–905. [Google Scholar] [CrossRef]
- Tollenaar, V.; Zekollari, H.; Lhermitte, S.; Tax, D.M.J.; Debaille, V.; Goderis, S.; Claeys, P.; Pattyn, F. Unexplored Antarctic Meteorite Collection Sites Revealed through Machine Learning. Sci. Adv. 2022, 8, eabj8138. [Google Scholar] [CrossRef] [PubMed]
- Braakmann-Folgmann, A.; Donlon, C. Estimating Snow Depth on Arctic Sea Ice Using Satellite Microwave Radiometry and a Neural Network. Cryosphere 2019, 13, 2421–2438. [Google Scholar] [CrossRef]
- Memarian Sorkhabi, O.; Asgari, J.; Amiri-Simkooei, A. Wavelet Decomposition and Deep Learning of Altimetry Waveform Retracking for Lake Urmia Water Level Survey. Mar. Georesources Geotechnol. 2022, 40, 361–369. [Google Scholar] [CrossRef]
- Gray, L.; Burgess, D.; Copland, L.; Cullen, R.; Galin, N.; Hawley, R.; Helm, V. Interferometric Swath Processing of Cryosat Data for Glacial Ice Topography. Cryosphere 2013, 7, 1857–1867. [Google Scholar] [CrossRef]
- Hawley, R.L.; Shepherd, A.; Cullen, R.; Helm, V.; Wingham, D.J. Ice-Sheet Elevations from across-Track Processing of Airborne Interferometric Radar Altimetry. Geophys. Res. Lett. 2009, 36, L22501. [Google Scholar] [CrossRef]
- Krabill, W. IceBridge ATM L2 Icessn Elevation, Slope, and Roughness, Version 2; NASA Distribution Active Archive Center, National Snow Ice Data Center: Boulder, CO, USA, 2014.
- Smith, B. ATLAS/ICESat-2 L3A Land Ice Height, Version 3; National Snow and Ice Data Center: Boulder, CO, USA, 2020. [Google Scholar]
- Porter, C.; Morin, P.; Howat, I.; Noh, M.-J.; Bates, B.; Peterman, K.; Keesey, S.; Schlenk, M.; Gardiner, J.; Tomko, K.; et al. ArcticDEM, Version 3. 2019. Available online: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/OHHUKH (accessed on 20 February 2022).
- Legrésy, B.; Rémy, F. Altimetric Observations of Surface Characteristics of the Antarctic Ice Sheet. J. Glaciol. 1997, 43, 265–275. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- McNabb, R.; Nuth, C.; Kääb, A.; Girod, L. Sensitivity of Glacier Volume Change Estimation to DEM Void Interpolation. Cryosphere 2019, 13, 895–910. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: Nice, France, 2019; pp. 8024–8035. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. Proc. Icml. 2013, 30, 3. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-Normalizing Neural Networks. arXiv 2017, arXiv:1706.02515. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning; Bach, F., Blei, D., Eds.; PMLR: Lille, France, 2015; Volume 37, pp. 448–456. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the Importance of Initialization and Momentum in Deep Learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Dasgupta, S., McAllester, D., Eds.; PMLR: Atlanta, GA, USA, 2013; Volume 28, pp. 1139–1147. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Earthwave. The University of Edinburgh. isardSAT CryoTEMPO-EOLIS—Elevation over Land Ice from Swath—Product Handbook. 2020. Available online: https://Earth.Esa.Int/Eogateway/Documents/20142/37627/CryoTEMPO-Thematic-Product-Handbook.Pdf (accessed on 20 February 2022).
- Gray, L.; Burgess, D.; Copland, L.; Dunse, T.; Langley, K.; Moholdt, G. A Revised Calibration of the Interferometric Mode of the CryoSat-2 Radar Altimeter Improves Ice Height and Height Change Measurements in Western Greenland. Cryosphere 2017, 11, 1041–1058. [Google Scholar] [CrossRef]
- Davis, C.H.; Moore, R.K. A Combined Surface-and Volume-Scattering Model for Ice-Sheet Radar Altimetry. J. Glaciol. 1993, 39, 675–686. [Google Scholar] [CrossRef]
- Ridley, J.K.; Partington, K.C. A Model of Satellite Radar Altimeter Return from Ice Sheets. Int. J. Remote Sens. 1988, 9, 601–624. [Google Scholar] [CrossRef]
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A Mission to Determine the Fluctuations in Earth’s Land and Marine Ice Fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Krabill, W. Greenland Ice Sheet: Increased Coastal Thinning. Geophys. Res. Lett. 2004, 31, L24402. [Google Scholar] [CrossRef]
- Bingham, A.W.; Drinkwater, M.R. Recent Changes in the Microwave Scattering Properties of the Antarctic Ice Sheet. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1810–1820. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Smith, B.E. Assessment of ICESat-2 Ice Sheet Surface Heights, Based on Comparisons over the Interior of the Antarctic Ice Sheet. Geophys. Res. Lett. 2019, 46, 13072–13078. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Thomas, T.C.; Pennington, T.A.; Rebold, T.W.; Nicholas, J.B.; Rowlands, D.D.; Gardner, A.S.; Bae, S. ICESat-2 Pointing Calibration and Geolocation Performance. Earth Space Sci. 2021, 8, e2020EA001494. [Google Scholar] [CrossRef]
- Fettweis, X.; Hofer, S.; Krebs-Kanzow, U.; Amory, C.; Aoki, T.; Berends, C.J.; Born, A.; Box, J.E.; Delhasse, A.; Fujita, K.; et al. GrSMBMIP: Intercomparison of the Modelled 1980–2012 Surface Mass Balance over the Greenland Ice Sheet. Cryosphere 2020, 14, 3935–3958. [Google Scholar] [CrossRef]
- Kern, M.; Cullen, R.; Berruti, B.; Bouffard, J.; Casal, T.; Drinkwater, M.R.; Gabriele, A.; Lecuyot, A.; Ludwig, M.; Midthassel, R.; et al. The Copernicus Polar Ice and Snow Topography Altimeter (CRISTAL) High-Priority Candidate Mission. Cryosphere 2020, 14, 2235–2251. [Google Scholar] [CrossRef]

| Model Input Parameters | Source |
|---|---|
| Distance to POCA | CryoSat2-SARIn |
| Power | CryoSat2-SARIn |
| Coherence | CryoSat2-SARIn |
| Leading Edge Width | CryoSat2-SARIn |
| Relative Elevationi (i = {−3, −2, −1, 1, 2, 3}) | CryoSat2-SARIn |
| Relative Elevation Meanj (j = {10, 20}) | CryoSat2-SARIn |
| Across Track Slope | ArcticDEM |
| Along Track Slope | ArcticDEM |
| South/North Aspect Vector Component | ArcticDEM |
| West/East Aspect Vector Component | ArcticDEM |
| Model | Mean (m) | Standard Error (m) | Median (m) | RMSE (m) | MAD (m) | r |
|---|---|---|---|---|---|---|
| Ordinary Least Squares (OLS) | −0.175 | 0.020 | −0.105 | 3.183 | 1.102 | 0.372 |
| Neural Network (NN) | −0.048 | 0.019 | −0.053 | 2.958 | 0.987 | 0.500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horton, A.; Ewart, M.; Gourmelen, N.; Fettweis, X.; Storkey, A. Using Deep Learning to Model Elevation Differences between Radar and Laser Altimetry. Remote Sens. 2022, 14, 6210. https://doi.org/10.3390/rs14246210
Horton A, Ewart M, Gourmelen N, Fettweis X, Storkey A. Using Deep Learning to Model Elevation Differences between Radar and Laser Altimetry. Remote Sensing. 2022; 14(24):6210. https://doi.org/10.3390/rs14246210
Chicago/Turabian StyleHorton, Alex, Martin Ewart, Noel Gourmelen, Xavier Fettweis, and Amos Storkey. 2022. "Using Deep Learning to Model Elevation Differences between Radar and Laser Altimetry" Remote Sensing 14, no. 24: 6210. https://doi.org/10.3390/rs14246210
APA StyleHorton, A., Ewart, M., Gourmelen, N., Fettweis, X., & Storkey, A. (2022). Using Deep Learning to Model Elevation Differences between Radar and Laser Altimetry. Remote Sensing, 14(24), 6210. https://doi.org/10.3390/rs14246210





