Review of Ground Penetrating Radar Applications for Water Dynamics Studies in Unsaturated Zone
Abstract
1. Introduction
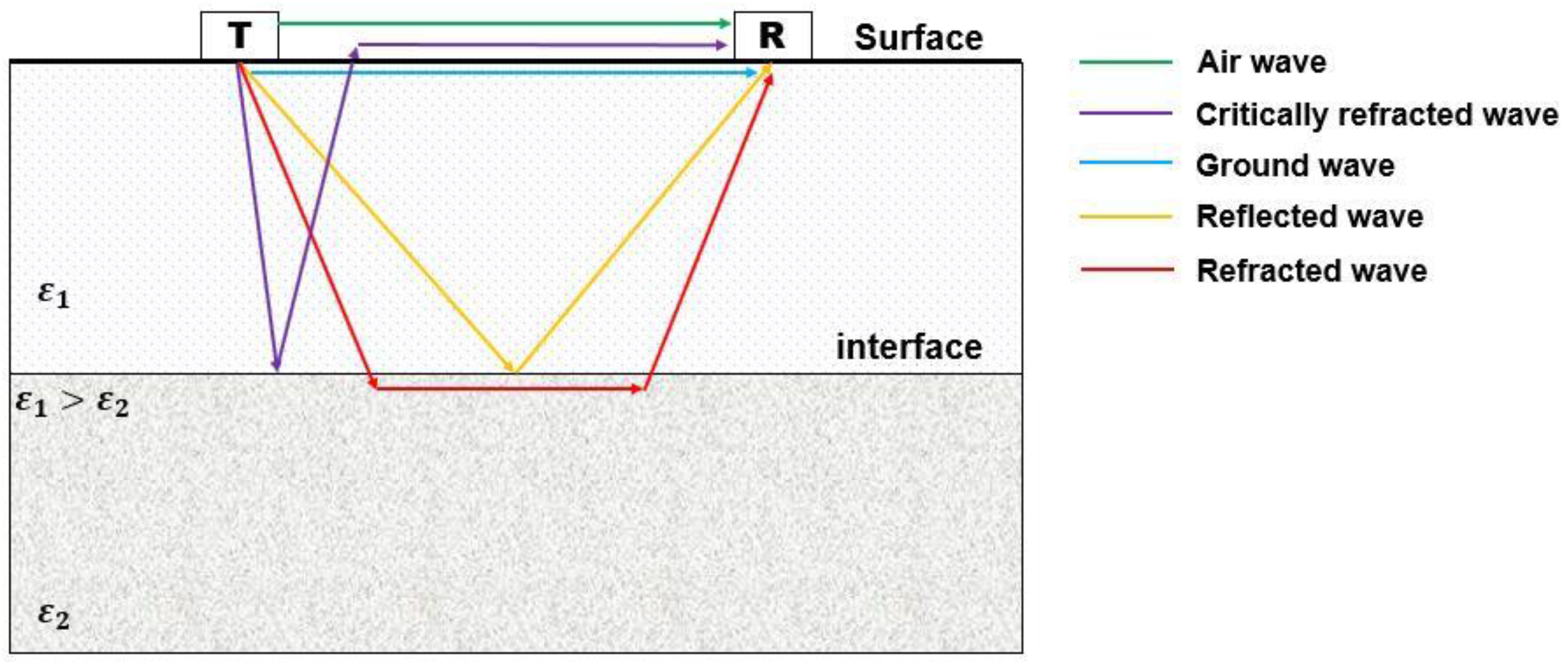
Principle of GPR Method
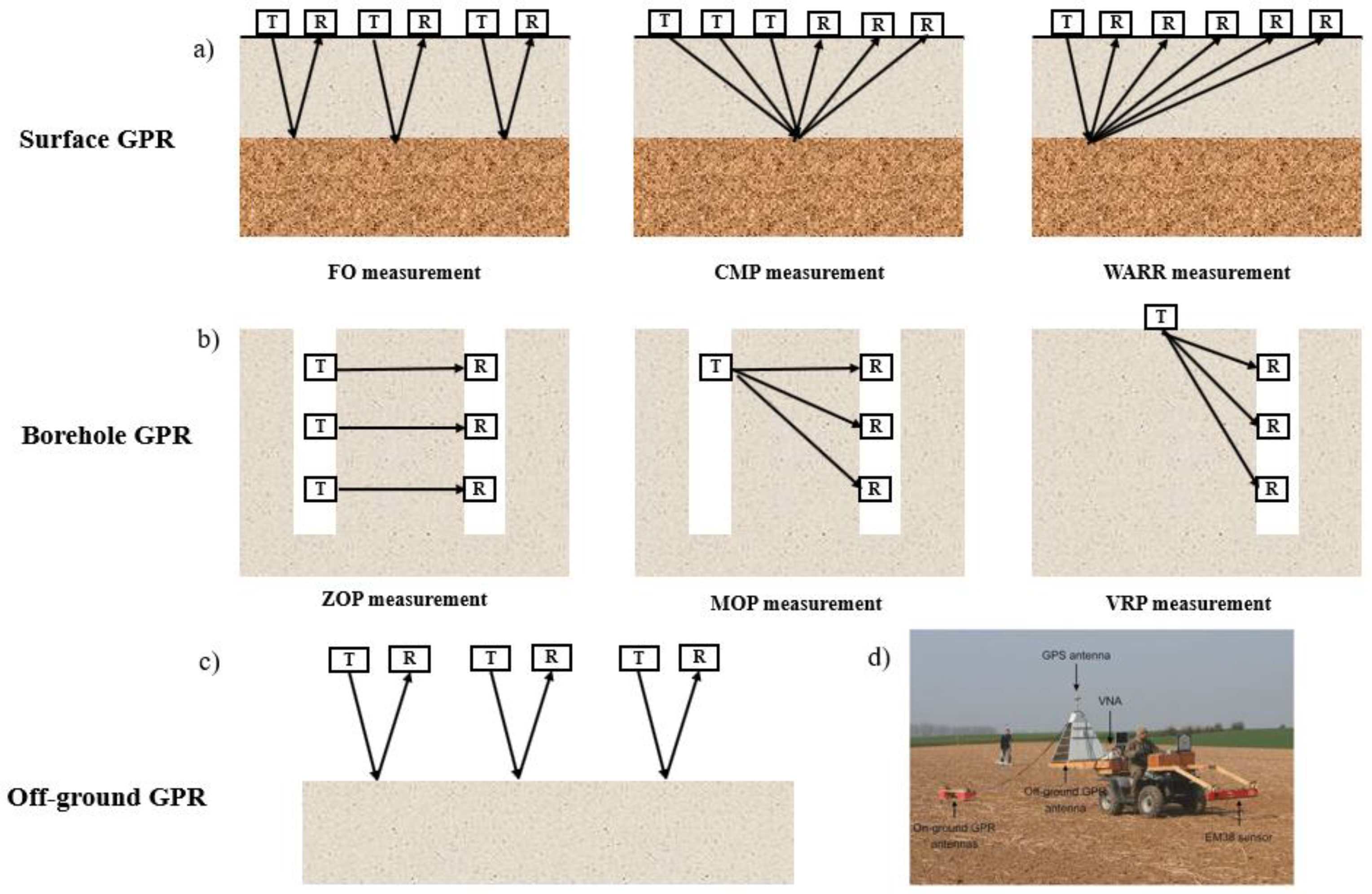
2. Techniques for SWC Measurements
2.1. Surface GPR for SWC Measurements
2.1.1. Single Offset Surface GPR for SWC Measurements
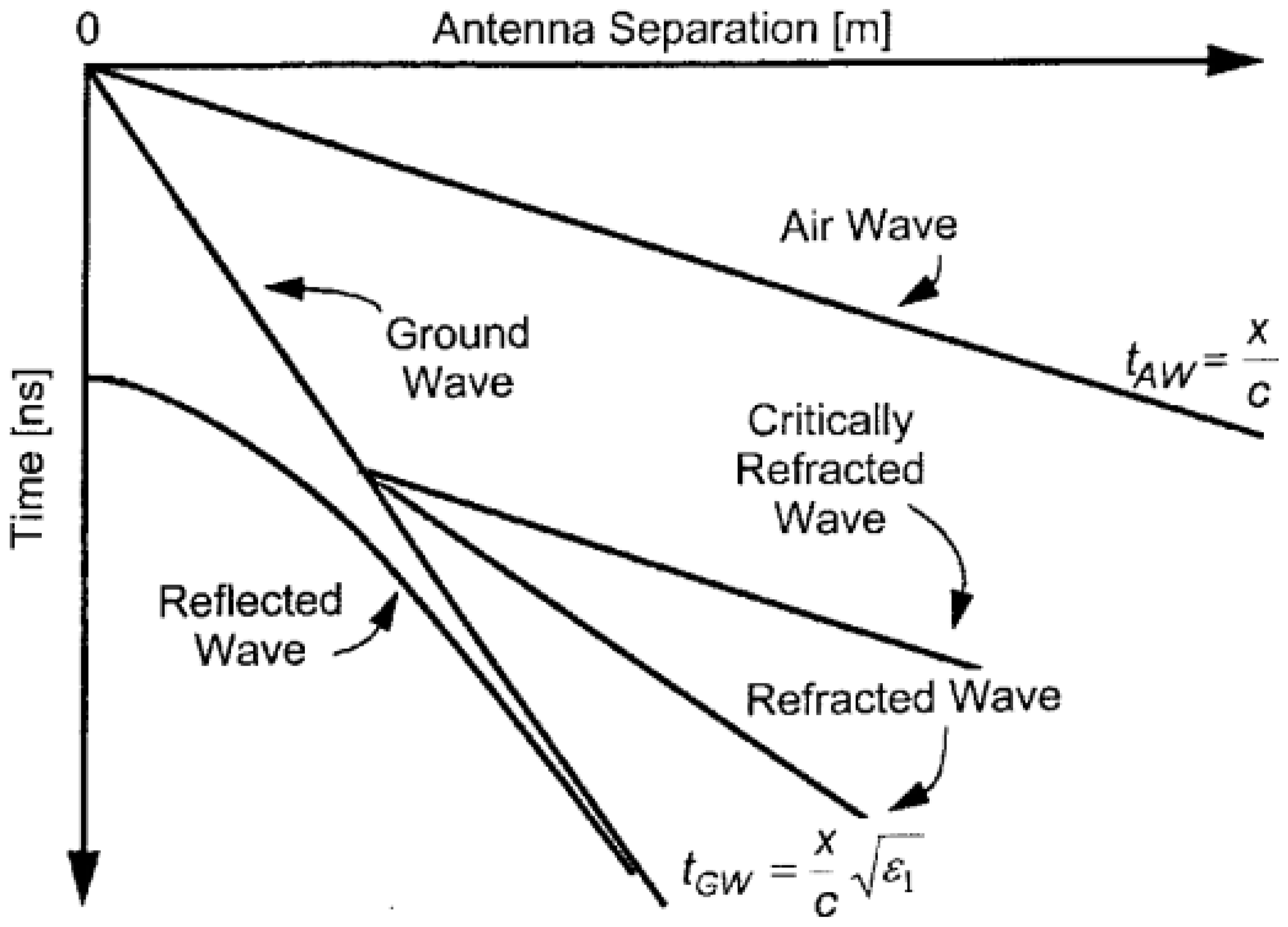
2.1.2. Multi-Offset Surface GPR for SWC Measurements
2.2. Borehole GPR for SWC Measurements
2.2.1. ZOP Borehole GPR for SWC Measurements
2.2.2. MOP Borehole GPR for SWC Measurements
2.2.3. VRP Borehole GPR for SWC Measurements
2.3. Off-Ground GPR for SWC Measurements
2.4. Other Advanced Methods for SWC Measurements
2.4.1. Full Waveform Inversion (FWI)
2.4.2. Average Envelope Amplitude (AEA) Method
2.4.3. Frequency Shift Method
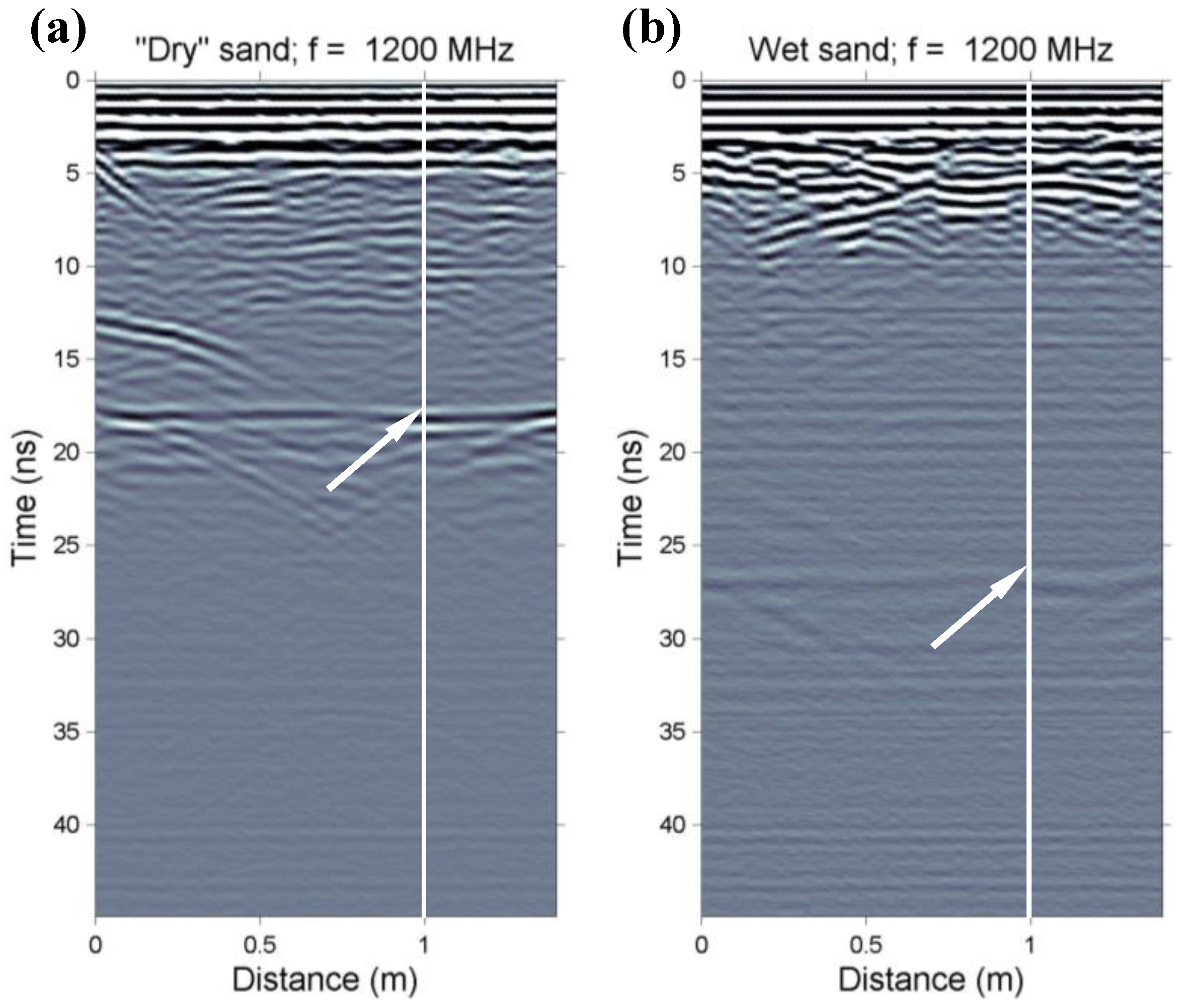
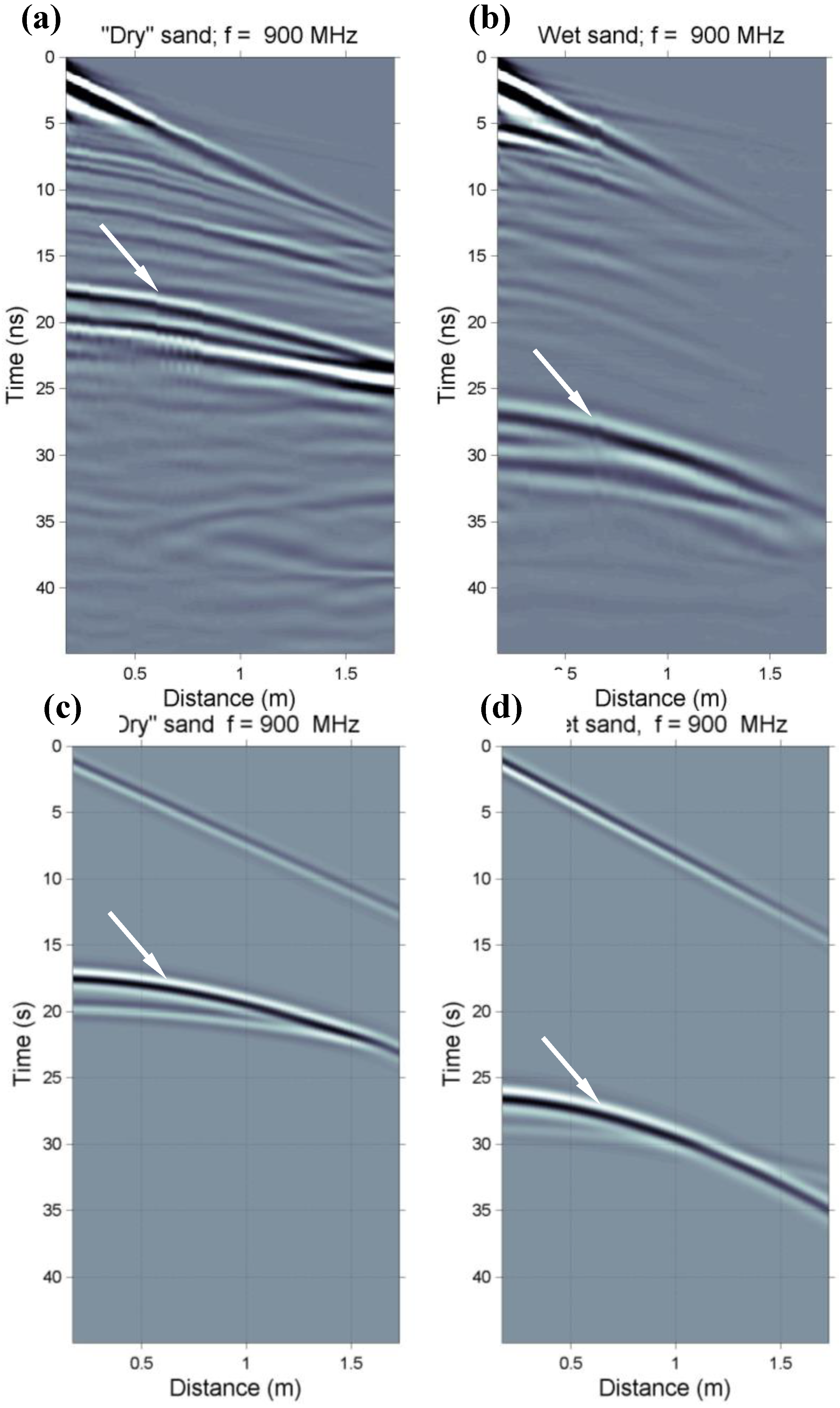
2.5. Experiments of SWC Detection with GPR
2.5.1. GPR Data from a Sand Box Experiment
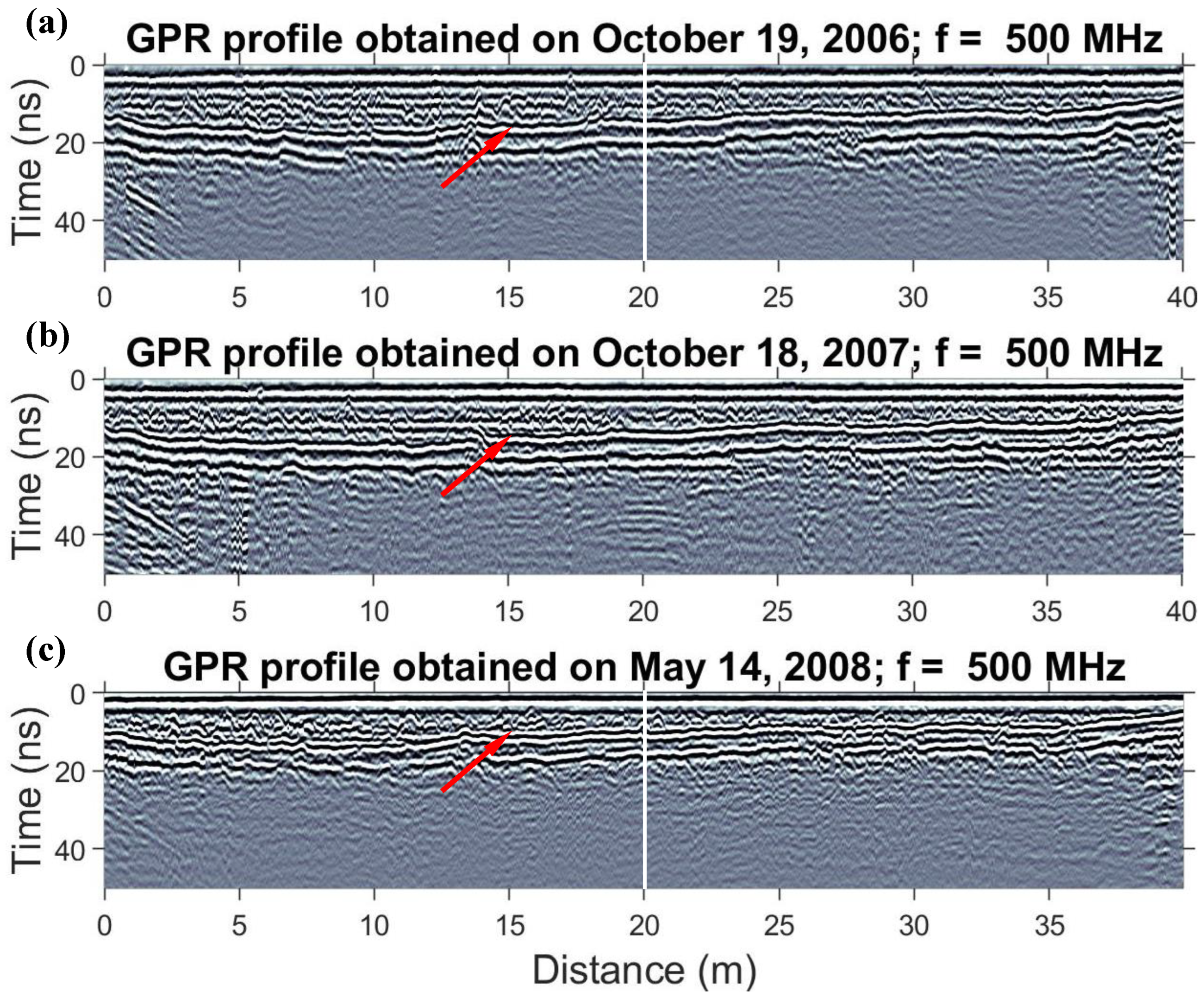
2.5.2. GPR Measurements on Moist Soils
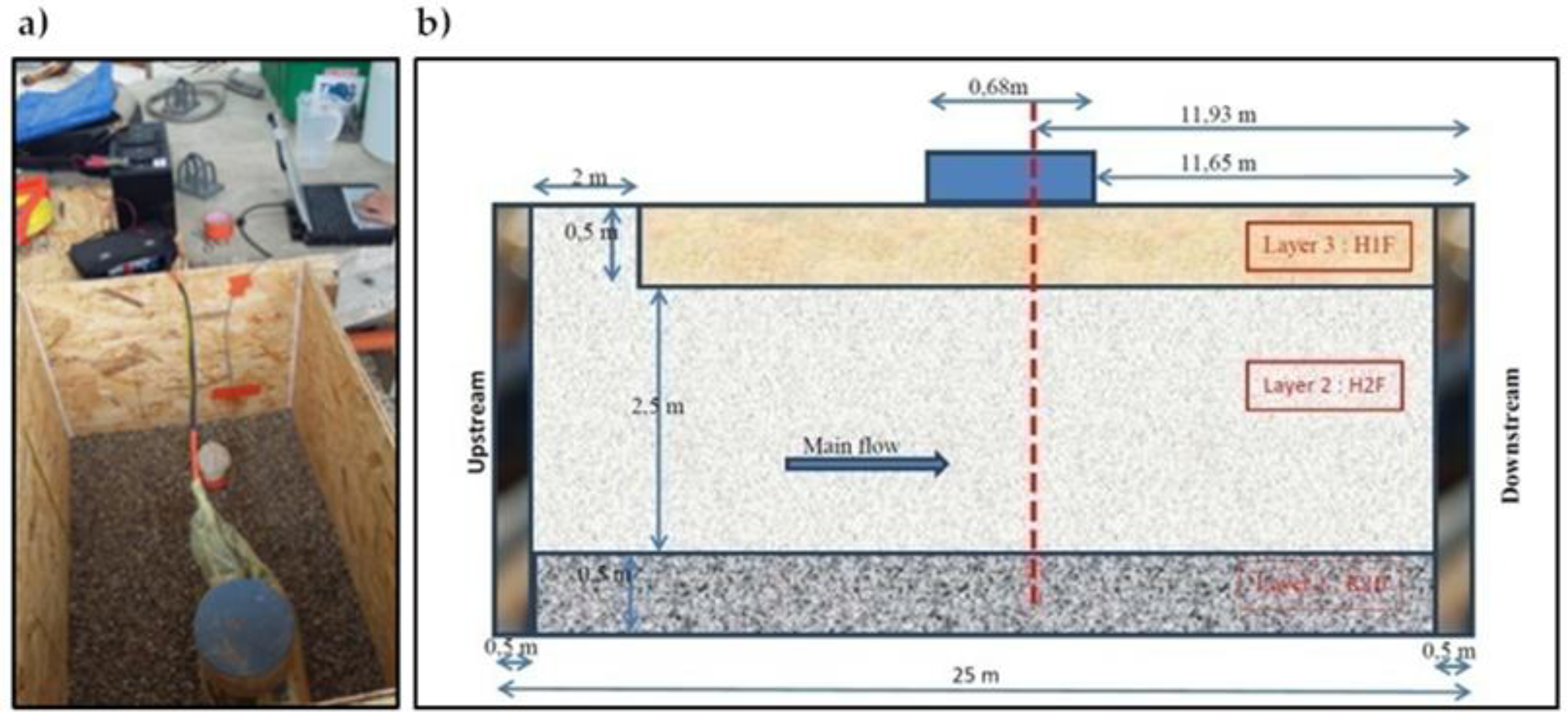
2.5.3. GPR Measurements during an Infiltration Experiment on an Unsaturated Sandy Soil
The Evolution of the Water Front
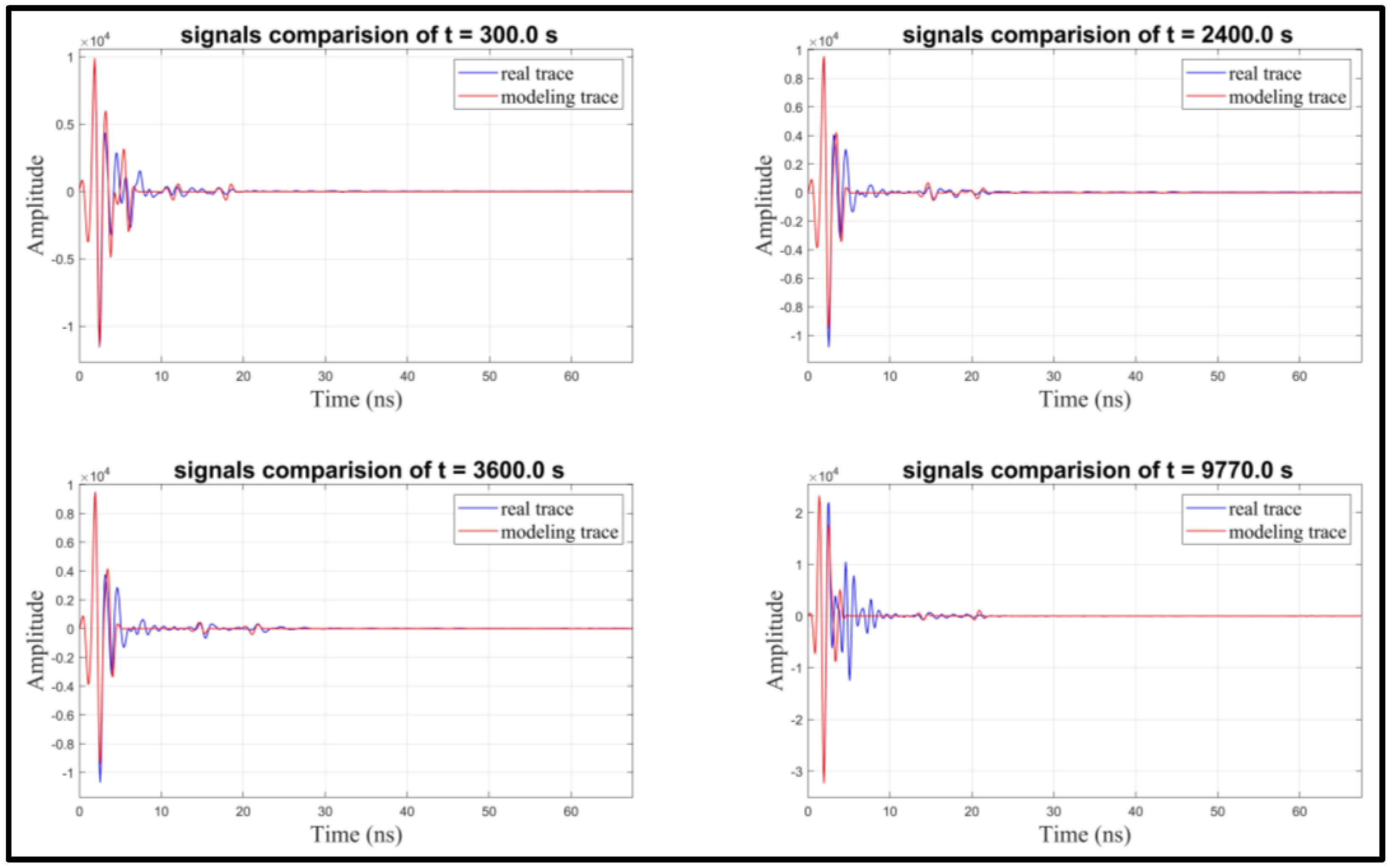
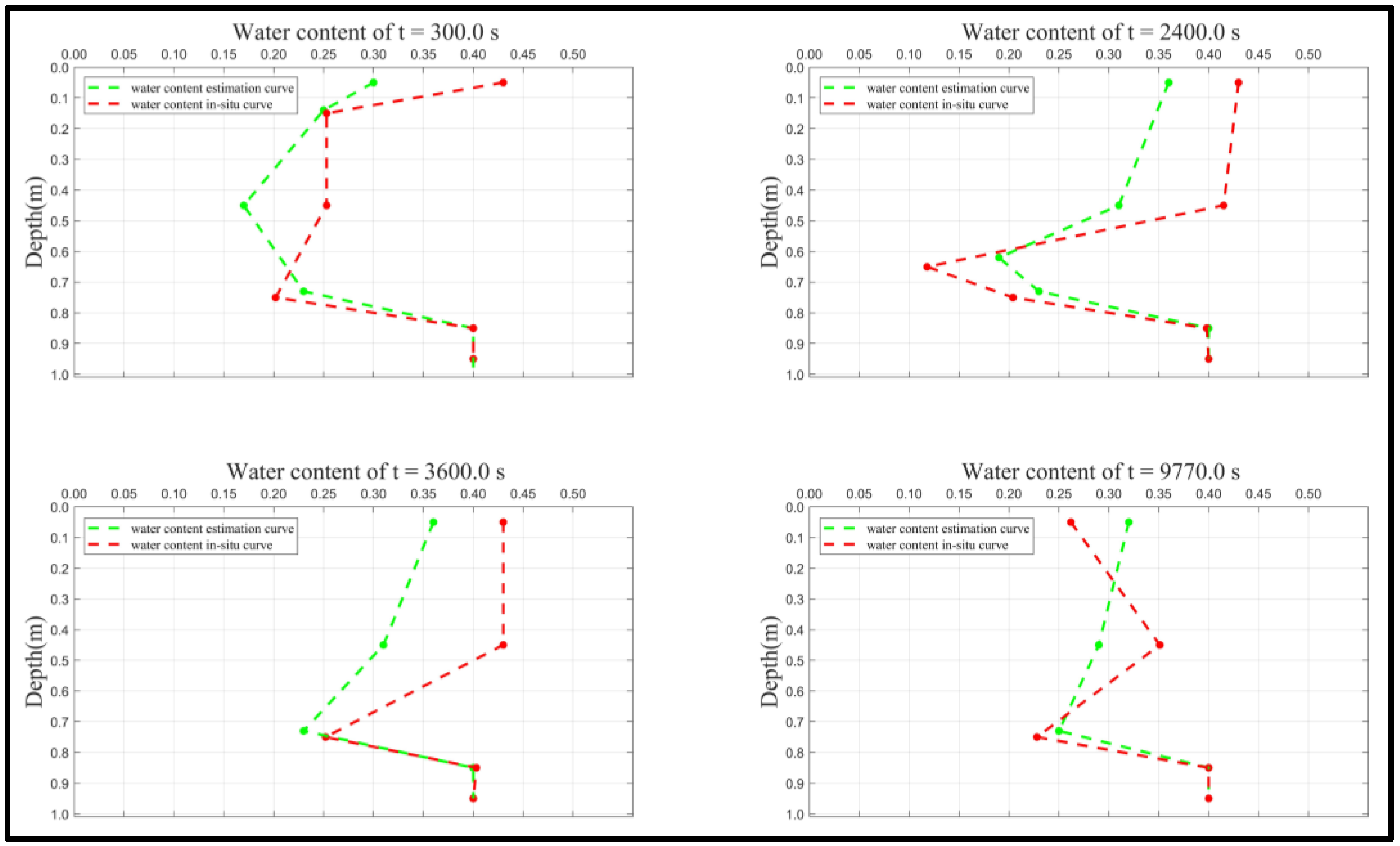
The Estimation of SWC by GPR
3. Techniques for SHP Estimation
3.1. Estimating Hydraulic Properties Based on Travel Time
3.2. Estimating Hydraulic Properties Based on FWI
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
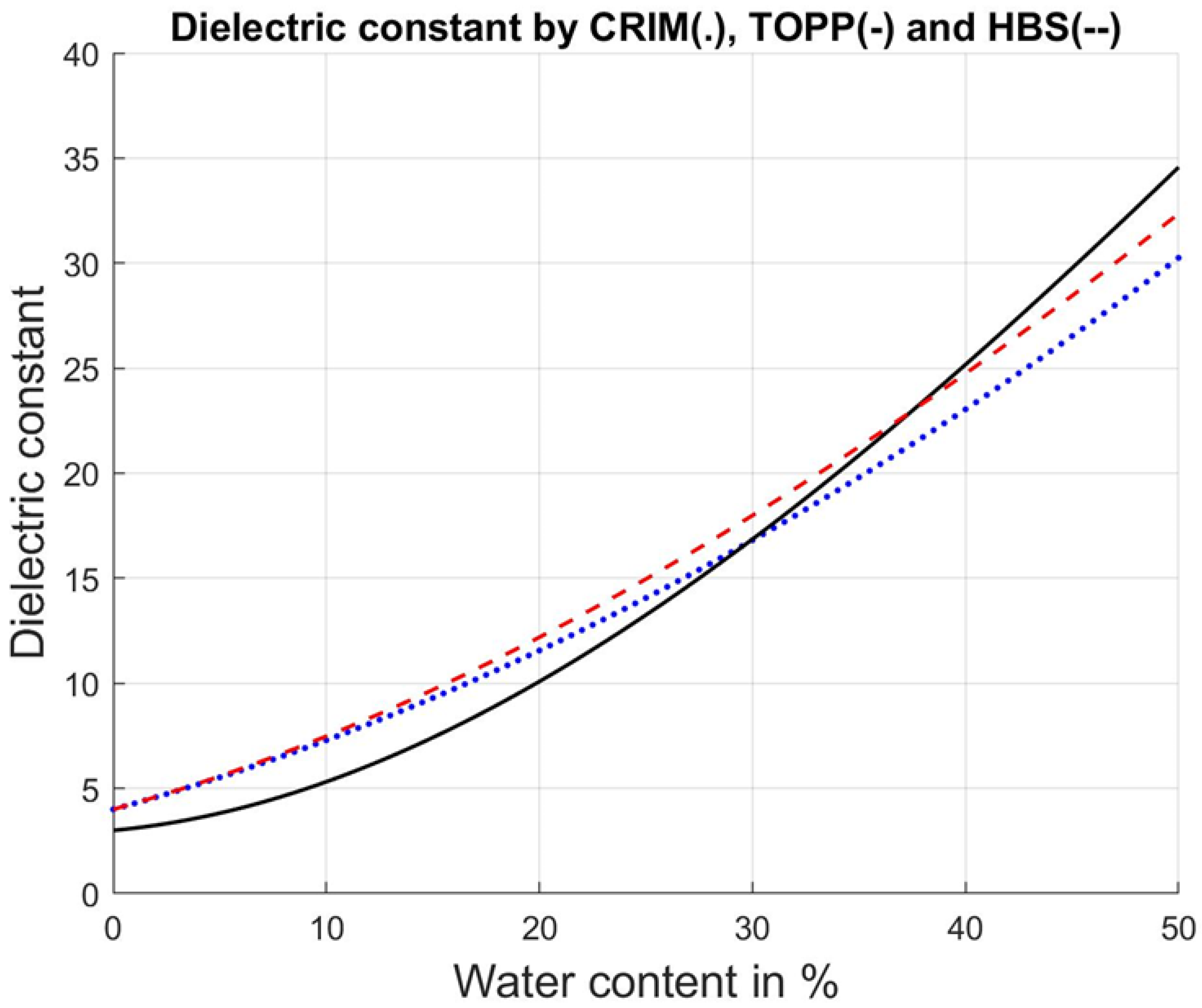
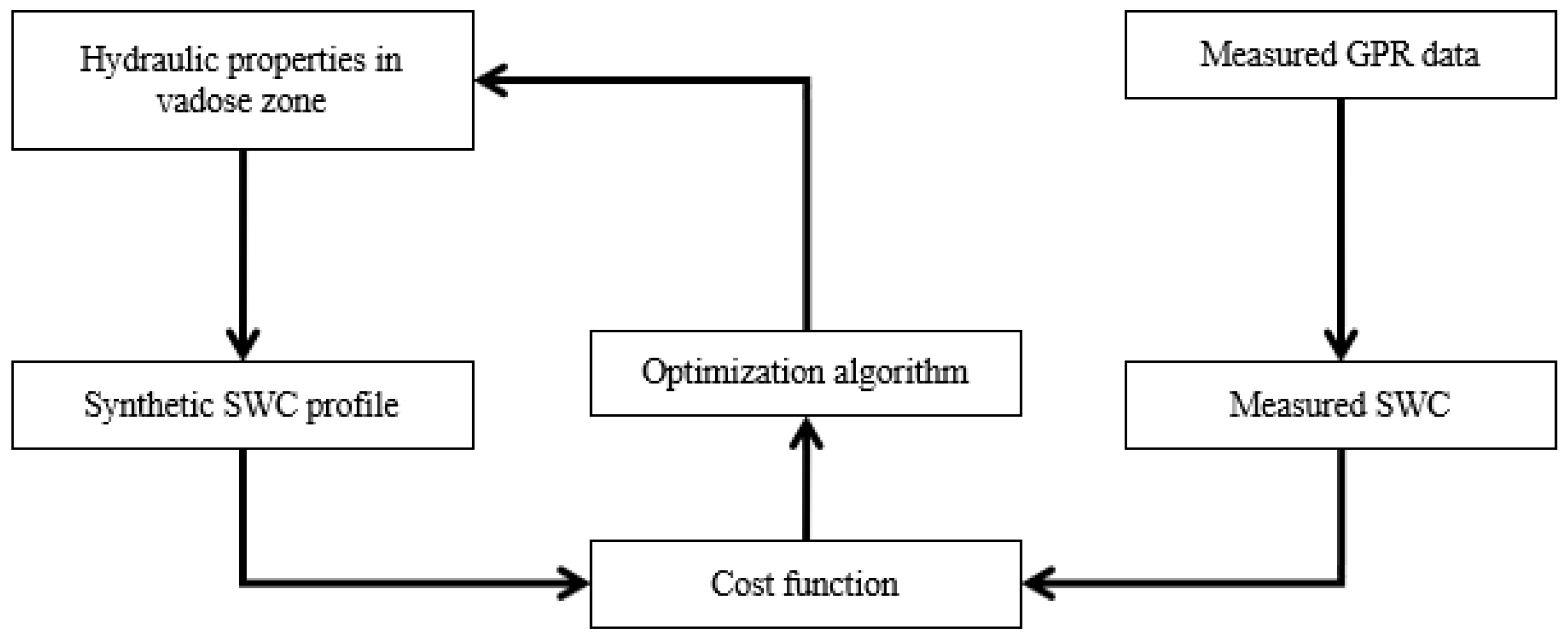
Appendix B
Appendix C
Appendix D
Appendix E
References
- Field, J.P.; Breshears, D.D.; Law, D.J.; Villegas, J.C.; López-Hoffman, L.; Brooks, P.D.; Chorover, J.; Barron-Gafford, G.A.; Gallery, R.E.; Litvak, M.E.; et al. Critical Zone Services: Expanding Context, Constraints, and Currency beyond Ecosystem Services. Vadose Zone J. 2015, 14, vzj2014.2010.0142. [Google Scholar] [CrossRef]
- Council, N.R. Basic Research Opportunities in Earth Science; The National Academies Press: Washington, DC, USA, 2001; p. 168. [Google Scholar]
- Xu, X.; Liu, W. The global distribution of Earth’s critical zone and its controlling factors. Geophys. Res. Lett. 2017, 44, 3201–3208. [Google Scholar] [CrossRef]
- Chorover, J.; Kretzschmar, R.; Garcia-Pichel, F.; Sparks, D.L. Soil Biogeochemical Processes within the Critical Zone. Elements 2007, 3, 321–326. [Google Scholar] [CrossRef]
- Ferraro, J.V.; Hoggarth, J.A.; Zori, D.; Binetti, K.M.; Stinchcomb, G. Integrating Human Activities, Archeology, and the Paleo-Critical Zone Paradigm. Front. Earth Sci. 2018, 6, 84. [Google Scholar] [CrossRef]
- Cui, F.; Bao, J.; Cao, Z.; Li, L.; Zheng, Q. Soil hydraulic parameters estimation using ground penetrating radar data via ensemble smoother with multiple data assimilation. J. Hydrol. 2020, 583, 124552. [Google Scholar] [CrossRef]
- Léger, E.; Saintenoy, A.; Coquet, Y. Hydrodynamic parameters of a sandy soil determined by ground-penetrating radar inside a single ring infiltrometer. Water Resour. Res. 2014, 50, 5459–5474. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil Moisture Measurement for Ecological and Hydrological Watershed-Scale Observatories: A Review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Chanasyk, D.S.; Naeth, M.A. Field measurement of soil moisture using neutron probes. Can. J. Soil Sci. 1996, 76, 317–323. [Google Scholar] [CrossRef]
- Brosten, T.R.; Day-Lewis, F.D.; Schultz, G.M.; Curtis, G.P.; Lane, J.W. Inversion of multi-frequency electromagnetic induction data for 3D characterization of hydraulic conductivity. J. Appl. Geophys. 2011, 73, 323–335. [Google Scholar] [CrossRef]
- Moghadas, D.; Jadoon, K.Z.; McCabe, M.F. Spatiotemporal monitoring of soil water content profiles in an irrigated field using probabilistic inversion of time-lapse EMI data. Adv. Water Resour. 2017, 110, 238–248. [Google Scholar] [CrossRef]
- Huisman, J.A.; Rings, J.; Vrugt, J.A.; Sorg, J.; Vereecken, H. Hydraulic properties of a model dike from coupled Bayesian and multi-criteria hydrogeophysical inversion. J. Hydrol. 2010, 380, 62–73. [Google Scholar] [CrossRef]
- Manoli, G.; Rossi, M.; Pasetto, D.; Deiana, R.; Ferraris, S.; Cassiani, G.; Putti, M. An iterative particle filter approach for coupled hydro-geophysical inversion of a controlled infiltration experiment. J. Comput. Phys. 2015, 283, 37–51. [Google Scholar] [CrossRef]
- Brunet, P.; Clément, R.; Bouvier, C. Monitoring soil water content and deficit using Electrical Resistivity Tomography (ERT)—A case study in the Cevennes area, France. J. Hydrol. 2010, 380, 146–153. [Google Scholar] [CrossRef]
- Mboh, C.M.; Huisman, J.A.; Van Gaelen, N.; Rings, J.; Vereecken, H. Coupled hydrogeophysical inversion of electrical resistances and inflow measurements for topsoil hydraulic properties under constant head infiltration. Near Surf. Geophys. 2012, 10, 413–426. [Google Scholar] [CrossRef]
- Hubbard, S.S.; Rubin, Y. Hydrogeological parameter estimation using geophysical data: A review of selected techniques. J. Contam. Hydrol. 2000, 45, 3–34. [Google Scholar] [CrossRef]
- Klotzsche, A.; Jonard, F.; Looms, M.C.; van der Kruk, J.; Huisman, J.A. Measuring Soil Water Content with Ground Penetrating Radar: A Decade of Progress. Vadose Zone J. 2018, 17, 180052. [Google Scholar] [CrossRef]
- Yu, Y.; Weihermüller, L.; Klotzsche, A.; Lärm, L.; Vereecken, H.; Huisman, J.A. Sequential and coupled inversion of horizontal borehole ground penetrating radar data to estimate soil hydraulic properties at the field scale. J. Hydrol. 2021, 596, 126010. [Google Scholar] [CrossRef]
- Jaumann, S.; Roth, K. Soil hydraulic material properties and layered architecture from time-lapse GPR. Hydrol. Earth Syst. Sci. 2018, 22, 2551–2573. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, J.; Huang, P.; Roth, K. Estimating field-scale soil water dynamics at a heterogeneous site using multi-channel GPR. Hydrol. Earth Syst. Sci. 2012, 16, 4361–4372. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring Soil Water Content with Ground Penetrating Radar: A Review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Cui, X.; Liu, Q.; Cao, X.; Chen, X. Measurement of soil water content using ground-penetrating radar: A review of current methods. Int. J. Digit. Earth 2019, 12, 95–118. [Google Scholar] [CrossRef]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy1. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Greaves, R.J.; Lesmes, D.P.; Lee, J.M.; Toksoz, M.N. Velocity variations and water content estimated from multi-offset, ground-penetrating radar. Geophysics 1996, 61, 683–695. [Google Scholar] [CrossRef]
- Bano, M.; Tsend-Ayush, N.; Schlupp, A.; Munkhuu, U. Ground-Penetrating Radar Imaging of Near-Surface Deformation along the Songino Active Fault in the Vicinity of Ulaanbaatar, Mongolia. Appl. Sci. 2021, 11, 8242. [Google Scholar] [CrossRef]
- Xuan, F.; Motoyuki, S. Pre-stack migration applied to GPR for landmine detection. Inverse Probl. 2004, 20, S99. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, X.; Ding, C.; Dong, Z.; Liu, C.; Liang, W. Heterogeneous Weathering Process of Lunar Regolith Revealed by Polarimetric Attributes Analysis of Chang’E-4 Lunar Penetrating Radar Data Acquired During the Yutu-2 Turnings. Geophys. Res. Lett. 2022, 49, e2022GL099207. [Google Scholar] [CrossRef]
- Vellidis, G.; Smith, C.M.; Thomas, L.D.; Asmussen, E.L. Detecting wetting front movement in a sandy soil with ground-penetrating radar. Trans. ASAE 1990, 33, 1867–1874. [Google Scholar] [CrossRef]
- Hagrey, A.; Müller. GPR study of pore water content and salinity in sand. Geophys. Prospect. 2000, 48, 63–85. [Google Scholar] [CrossRef]
- Birken, R.; Versteeg, R. Use of four-dimensional ground penetrating radar and advanced visualization methods to determine subsurface fluid migration. J. Appl. Geophys. 2000, 43, 215–226. [Google Scholar] [CrossRef]
- Grote, K.; Hubbard, S.; Rubin, Y. GPR monitoring of volumetric water content in soils applied to highway construction and maintenance. Lead. Edge 2002, 21, 482–504. [Google Scholar] [CrossRef][Green Version]
- Gish, T.J.; Dulaney, W.P.; Kung, K.J.S.; Daughtry, C.S.T.; Doolittle, J.A.; Miller, P.T. Evaluating Use of Ground-Penetrating Radar for Identifying Subsurface Flow Pathways. Soil Sci. Soc. Am. J. 2002, 66, 1620–1629. [Google Scholar] [CrossRef]
- Schmalz, B.; Lennartz, B. Analyses of soil water content variations and GPR attribute distributions. J. Hydrol. 2002, 267, 217–226. [Google Scholar] [CrossRef]
- Stoffregen, H.; Zenker, T.; Wessolek, G. Accuracy of soil water content measurements using ground penetrating radar: Comparison of ground penetrating radar and lysimeter data. J. Hydrol. 2002, 267, 201–206. [Google Scholar] [CrossRef]
- Loeffler, O.; Bano, M. Ground Penetrating Radar Measurements in a Controlled Vadose Zone: Influence of the Water Content. Vadose Zone J. 2004, 3, 1082–1092. [Google Scholar] [CrossRef]
- Makkawi, M.H. Integrating GPR and geostatistical techniques to map the spatial extent of a shallow groundwater system. J. Geophys. Eng. 2004, 1, 56–62. [Google Scholar] [CrossRef]
- Wollschläger, U.; Roth, K. Estimation of Temporal Changes of Volumetric Soil Water Content from Ground-Penetrating Radar Reflections. Subsurf. Sens. Technol. Appl. 2005, 6, 207–218. [Google Scholar] [CrossRef]
- Lunt, I.A.; Hubbard, S.S.; Rubin, Y. Soil moisture content estimation using ground-penetrating radar reflection data. J. Hydrol. 2005, 307, 254–269. [Google Scholar] [CrossRef]
- Turesson, A. Water content and porosity estimated from ground-penetrating radar and resistivity. J. Appl. Geophys. 2006, 58, 99–111. [Google Scholar] [CrossRef]
- Saintenoy, A.; Schneider, S.; Tucholka, P. Evaluating Ground Penetrating Radar Use for Water Infiltration Monitoring. Vadose Zone J. 2008, 7, 208–214. [Google Scholar] [CrossRef]
- Irving, J.; Knight, R.; Holliger, K. Estimation of the lateral correlation structure of subsurface water content from surface-based ground-penetrating radar reflection images. Water Resour. Res. 2009, 45, W12404. [Google Scholar] [CrossRef]
- Haarder, E.B.; Looms, M.C.; Jensen, K.H.; Nielsen, L. Visualizing Unsaturated Flow Phenomena Using High-Resolution Reflection Ground Penetrating Radar. Vadose Zone J. 2011, 10, 84–97. [Google Scholar] [CrossRef]
- Klenk, P.; Jaumann, S.; Roth, K. Quantitative high-resolution observations of soil water dynamics in a complicated architecture using time-lapse ground-penetrating radar. Hydrol. Earth Syst. Sci. 2015, 19, 1125–1139. [Google Scholar] [CrossRef]
- Schmelzbach, C.; Tronicke, J.; Dietrich, P. High-resolution water content estimation from surface-based ground-penetrating radar reflection data by impedance inversion. Water Resour. Res. 2012, 48, W08505. [Google Scholar] [CrossRef]
- Guo, L.; Chen, J.; Lin, H. Subsurface lateral preferential flow network revealed by time-lapse ground-penetrating radar in a hillslope. Water Resour. Res. 2014, 50, 9127–9147. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, H.; Doolittle, J. Soil layering and preferential flow impacts on seasonal changes of GPR signals in two contrasting soils. Geoderma 2014, 213, 560–569. [Google Scholar] [CrossRef]
- Yu, Z.; Dylan, B.; Dryver, H.; Tian, X. Sand moisture assessment using instantaneous phase information in ground penetrating radar data. In Proceedings of the Structural Health Monitoring and Inspection of Advanced Materials, Aerospace, and Civil Infrastructure, San Diego, CA, USA, 8–12 March 2015; p. 943726. [Google Scholar]
- Shamir, O.; Goldshleger, N.; Basson, U.; Reshef, M. Mapping Spatial Moisture Content of Unsaturated Agricultural Soils With Ground-Penetrating Radar. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B8, 1279–1285. [Google Scholar] [CrossRef]
- Shamir, O.; Goldshleger, N.; Basson, U.; Reshef, M. Laboratory Measurements of Subsurface Spatial Moisture Content by Ground-Penetrating Radar (GPR) Diffraction and Reflection Imaging of Agricultural Soils. Remote Sens. 2018, 10, 1667. [Google Scholar] [CrossRef]
- Ercoli, M.; Di Matteo, L.; Pauselli, C.; Mancinelli, P.; Frapiccini, S.; Talegalli, L.; Cannata, A. Integrated GPR and laboratory water content measures of sandy soils: From laboratory to field scale. Constr. Build. Mater. 2018, 159, 734–744. [Google Scholar] [CrossRef]
- Nyquist, J.E.; Toran, L.; Pitman, L.; Guo, L.; Lin, H. Testing the Fill-and-Spill Model of Subsurface Lateral Flow Using Ground-Penetrating Radar and Dye Tracing. Vadose Zone J. 2018, 17, 170142. [Google Scholar] [CrossRef]
- Di Prima, S.; Winiarski, T.; Angulo-Jaramillo, R.; Stewart, R.D.; Castellini, M.; Abou Najm, M.R.; Ventrella, D.; Pirastru, M.; Giadrossich, F.; Capello, G.; et al. Detecting infiltrated water and preferential flow pathways through time-lapse ground-penetrating radar surveys. Sci. Total Environ. 2020, 726, 138511. [Google Scholar] [CrossRef] [PubMed]
- Mangel, A.R.; Moysey, S.M.J.; Bradford, J. Reflection tomography of time-lapse GPR data for studying dynamic unsaturated flow phenomena. Hydrol. Earth Syst. Sci. 2020, 24, 159–167. [Google Scholar] [CrossRef]
- Zhang, M.H.; Bano, M.; Feng, X.; Lesparre, N.; Girard, J.F.; Razakarisoa, O.; Belfort, B.; Lehmann, F.; Friedmann, P. Estimating water content of unsaturated sandy soils by GPR during a drainage experiment. IOP Conf. Ser. Earth Environ. Sci. 2021, 660, 012018. [Google Scholar] [CrossRef]
- Zhang, M.; Bano, M.; Feng, X. Estimating Water Content of Unsaturated Sandy Soils by Ground-Penetrating Radar During an Infiltration Experiment. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bordeaux, France, 29 August–2 September 2021; Volume 2021, pp. 1–5. [Google Scholar] [CrossRef]
- van Overmeeren, R.A.; Sariowan, S.V.; Gehrels, J.C. Ground penetrating radar for determining volumetric soil water content; results of comparative measurements at two test sites. J. Hydrol. 1997, 197, 316–338. [Google Scholar] [CrossRef]
- Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Monitoring Temporal Development of Spatial Soil Water Content Variation: Comparison of Ground Penetrating Radar and Time Domain Reflectometry. Vadose Zone J. 2003, 2, 519–529. [Google Scholar] [CrossRef]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D. Measuring and Modeling of Direct Ground Wave Depth Penetration Under Transient Soil Moisture Conditions. Subsurf. Sens. Technol. Appl. 2005, 6, 193–205. [Google Scholar] [CrossRef]
- Grote, K.; Hubbard, S.; Rubin, Y. Field-scale estimation of volumetric water content using ground-penetrating radar ground wave techniques. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Klenk, P.; Buchner, J.S.; Roth, K.; Wollschläger, U.; Qin, Y.; Zhou, K. On the reliability of current GPR ground wave methods for determining near-surface water contents. In Proceedings of the 2011 6th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Aachen, Germany, 22–24 June 2011; pp. 1–5. [Google Scholar]
- Qin, Y.; Chen, X.; Zhou, K.; Klenk, P.; Roth, K.; Sun, L. Ground-penetrating radar for monitoring the distribution of near-surface soil water content in the Gurbantünggüt Desert. Environ. Earth Sci. 2013, 70, 2883–2893. [Google Scholar] [CrossRef]
- Mahmoudzadeh Ardekani, M.R. Off- and on-ground GPR techniques for field-scale soil moisture mapping. Geoderma 2013, 200–201, 55–66. [Google Scholar] [CrossRef]
- Thitimakorn, T.; Kummode, S.; Kupongsak, S. Determination of Spatial and Temporal Variations of Volumetric Soil Water Content Using Ground Penetrating Radar: A Case Study in Thailand. Appl. Environ. Res. 2016, 38, 33–46. [Google Scholar] [CrossRef]
- Pettinelli, E.; Vannaroni, G.; Di Pasquo, B.; Mattei, E.; Di Matteo, A.; De Santis, A.; Annan, P.A. Correlation between near-surface electromagnetic soil parameters and early-time GPR signals: An experimental study. Geophysics 2007, 72, A25–A28. [Google Scholar] [CrossRef]
- Pettinelli, E.; Di Matteo, A.; Beaubien, S.E.; Mattei, E.; Lauro, S.E.; Galli, A.; Vannaroni, G. A controlled experiment to investigate the correlation between early-time signal attributes of ground-coupled radar and soil dielectric properties. J. Appl. Geophys. 2014, 101, 68–76. [Google Scholar] [CrossRef]
- Ferrara, C.; Barone, P.M.; Steelman, C.M.; Pettinelli, E.; Endres, A.L. Monitoring Shallow Soil Water Content Under Natural Field Conditions Using the Early-Time GPR Signal Technique. Vadose Zone J. 2013, 12, vzj2012.0202. [Google Scholar] [CrossRef]
- Algeo, J.; Van Dam, R.L.; Slater, L. Early-Time GPR: A Method to Monitor Spatial Variations in Soil Water Content during Irrigation in Clay Soils. Vadose Zone J. 2016, 15, vzj2016.2003.0026. [Google Scholar] [CrossRef]
- Benedetto, A. Water content evaluation in unsaturated soil using GPR signal analysis in the frequency domain. J. Appl. Geophys. 2010, 71, 26–35. [Google Scholar] [CrossRef]
- Benedetto, A.; Benedetto, F. Remote Sensing of Soil Moisture Content by GPR Signal Processing in the Frequency Domain. IEEE Sens. J. 2011, 11, 2432–2441. [Google Scholar] [CrossRef]
- Benedetto, A.; Tosti, F.; Ortuani, B.; Giudici, M.; Mele, M. Soil moisture mapping using GPR for pavement applications. In Proceedings of the 2013 7th International Workshop on Advanced Ground Penetrating Radar, Nantes, France, 2–5 July 2013; pp. 1–5. [Google Scholar]
- Weiler, K.W.; Steenhuis, T.S.; Boll, J.; Kung, K.J.S. Comparison of Ground Penetrating Radar and Time-Domain Reflectometry as Soil Water Sensors. Soil Sci. Soc. Am. J. 1998, 62, 1237–1239. [Google Scholar] [CrossRef]
- Huisman, J.A.; Sperl, C.; Bouten, W.; Verstraten, J.M. Soil water content measurements at different scales: Accuracy of time domain reflectometry and ground-penetrating radar. J. Hydrol. 2001, 245, 48–58. [Google Scholar] [CrossRef]
- Garambois, S.; Sénéchal, P.; Perroud, H. On the use of combined geophysical methods to assess water content and water conductivity of near-surface formations. J. Hydrol. 2002, 259, 32–48. [Google Scholar] [CrossRef]
- Strobbia, C.; Cassiani, G. Multilayer ground-penetrating radar guided waves in shallow soil layers for estimating soil water content. Geophysics 2007, 72, J17–J29. [Google Scholar] [CrossRef]
- Bradford, J.H. Measuring Water Content Heterogeneity Using Multifold GPR with Reflection Tomography. Vadose Zone J. 2008, 7, 184–193. [Google Scholar] [CrossRef]
- Gerhards, H.; Wollschläger, U.; Yu, Q.; Schiwek, P.; Pan, X.; Roth, K. Continuous and simultaneous measurement of reflector depth and average soil-water content with multichannel ground-penetrating radar. Geophysics 2008, 73, J15–J23. [Google Scholar] [CrossRef]
- Buchner, J.S.; Kühne, A.; Antz, B.; Roth, K.; Wollschläger, U. Observation of volumetric water content and reflector depth with multichannel ground-penetrating radar in an artificial sand volume. In Proceedings of the 2011 6th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Aachen, Germany, 22–24 June 2011; pp. 1–5. [Google Scholar]
- Buchner, J.S.; Wollschläger, U.; Roth, K. Inverting surface GPR data using FDTD simulation and automatic detection of reflections to estimate subsurface water content and geometry. Geophysics 2012, 77, H45–H55. [Google Scholar] [CrossRef]
- Steelman, C.M.; Endres, A.L. Assessing vertical soil moisture dynamics using multi-frequency GPR common-midpoint soundings. J. Hydrol. 2012, 436–437, 51–66. [Google Scholar] [CrossRef]
- Steelman, C.M.; Endres, A.L.; Jones, J.P. High-resolution ground-penetrating radar monitoring of soil moisture dynamics: Field results, interpretation, and comparison with unsaturated flow model. Water Resour. Res. 2012, 48, W09538. [Google Scholar] [CrossRef]
- Mangel, A.R.; Moysey, S.M.J.; Ryan, J.C.; Tarbutton, J.A. Multi-offset ground-penetrating radar imaging of a lab-scale infiltration test. Hydrol. Earth Syst. Sci. 2012, 16, 4009–4022. [Google Scholar] [CrossRef]
- Mangel, A.R.; Lytle, B.A.; Moysey, S.M.J. Automated high-resolution GPR data collection for monitoring dynamic hydrologic processes in two and three dimensions. Lead. Edge 2015, 34, 190–196. [Google Scholar] [CrossRef]
- Allroggen, N.; van Schaik, N.L.M.B.; Tronicke, J. 4D ground-penetrating radar during a plot scale dye tracer experiment. J. Appl. Geophys. 2015, 118, 139–144. [Google Scholar] [CrossRef]
- Iwasaki, T.; Kuroda, S.; Saito, H.; Tobe, Y.; Suzuki, K.; Fujimaki, H.; Inoue, M. Monitoring Infiltration Process Seamlessly Using Array Ground Penetrating Radar. Agric. Environ. Lett. 2016, 1, 160002. [Google Scholar] [CrossRef]
- Kaufmann, M.S.; Klotzsche, A.; Vereecken, H.; van der Kruk, J. Simultaneous multichannel multi-offset ground-penetrating radar measurements for soil characterization. Vadose Zone J. 2020, 19, e20017. [Google Scholar] [CrossRef]
- Yu, Y.; Klotzsche, A.; Weihermüller, L.; Huisman, J.A.; Vanderborght, J.; Vereecken, H.; van der Kruk, J. Measuring vertical soil water content profiles by combining horizontal borehole and dispersive surface ground penetrating radar data. Near Surf. Geophys. 2020, 18, 275–294. [Google Scholar] [CrossRef]
- Saito, H.; Kuroda, S.; Iwasaki, T.; Sala, J.; Fujimaki, H. Estimating infiltration front depth using time-lapse multioffset gathers obtained from ground-penetrating-radar antenna array. Geophysics 2021, 86, WB51–WB59. [Google Scholar] [CrossRef]
- Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Mapping spatial variation in surface soil water content: Comparison of ground-penetrating radar and time domain reflectometry. J. Hydrol. 2002, 269, 194–207. [Google Scholar] [CrossRef]
- Hubbard, S.; Grote, K.; Rubin, Y. Mapping the volumetric soil water content of a California vineyard using high-frequency GPR ground wave data. Lead. Edge 2002, 21, 552–559. [Google Scholar] [CrossRef]
- Grote, K.; Anger, C.; Kelly, B.; Hubbard, S.; Rubin, Y. Characterization of Soil Water Content Variability and Soil Texture using GPR Groundwave Techniques. J. Environ. Eng. Geophys. 2010, 15, 93–110. [Google Scholar] [CrossRef]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D. An analysis of the ground-penetrating radar direct ground wave method for soil water content measurement. Hydrol. Processes 2003, 17, 3615–3628. [Google Scholar] [CrossRef]
- Galagedara, L.W.; Redman, J.D.; Parkin, G.W.; Annan, A.P.; Endres, A.L. Numerical Modeling of GPR to Determine the Direct Ground Wave Sampling Depth. Vadose Zone J. 2005, 4, 1096–1106. [Google Scholar] [CrossRef]
- Weihermüller, L.; Huisman, J.A.; Lambot, S.; Herbst, M.; Vereecken, H. Mapping the spatial variation of soil water content at the field scale with different ground penetrating radar techniques. J. Hydrol. 2007, 340, 205–216. [Google Scholar] [CrossRef]
- Steelman, C.M.; Endres, A.L. An examination of direct ground wave soil moisture monitoring over an annual cycle of soil conditions. Water Resour. Res. 2010, 46, W11533. [Google Scholar] [CrossRef]
- Cao, Q.; Song, X.; Wu, H.; Gao, L.; Liu, F.; Yang, S.; Zhang, G. Mapping the response of volumetric soil water content to an intense rainfall event at the field scale using GPR. J. Hydrol. 2020, 583, 124605. [Google Scholar] [CrossRef]
- Knoll, M.D.; Clement, W.P. Vertical Radar Profiling to Determine Dielectric Constant, Water Content and Porosity Values at Well Locations. In Symposium on the Application of Geophysics to Engineering and Environmental Problems 1999; Symposium on the Application of Geophysics to Engineering and Environmental Problems Proceedings; Environment and Engineering Geophysical Society: Oakland, CA, USA, 1999; pp. 821–830. [Google Scholar]
- Alumbaugh, D.; Paprocki, L.; Brainard, J.; Rautman, C. Monitoring Infiltration within the Vadose Zone Using Cross Borehole Ground Penetrating Radar. In Symposium on the Application of Geophysics to Engineering and Environmental Problems 2000; Symposium on the Application of Geophysics to Engineering and Environmental Problems Proceedings; Environment and Engineering Geophysical Society: Arlington, VA, USA, 2000; pp. 273–281. [Google Scholar]
- Parkin, G.; Redman, D.; von Bertoldi, P.; Zhang, Z. Measurement of soil water content below a wastewater trench using ground-penetrating radar. Water Resour. Res. 2000, 36, 2147–2154. [Google Scholar] [CrossRef]
- Binley, A.; Winship, P.; Middleton, R.; Pokar, M.; West, J. High-resolution characterization of vadose zone dynamics using cross-borehole radar. Water Resour. Res. 2001, 37, 2639–2652. [Google Scholar] [CrossRef]
- Binley, A.; Cassiani, G.; Middleton, R.; Winship, P. Vadose zone flow model parameterisation using cross-borehole radar and resistivity imaging. J. Hydrol. 2002, 267, 147–159. [Google Scholar] [CrossRef]
- Binley, A.; Winship, P.; West, L.J.; Pokar, M.; Middleton, R. Seasonal variation of moisture content in unsaturated sandstone inferred from borehole radar and resistivity profiles. J. Hydrol. 2002, 267, 160–172. [Google Scholar] [CrossRef]
- Galagedara, L.W.; Gary, W.P.; Redman, J.D.; Endres, A.L. Temporal and spatial variation of soil water content measured by borehole GPR under irrigation and drainage. In Proceedings of the Ninth International Conference on Ground Penetrating Radar, Santa Barbara, CA, USA, 29 April–2 May 2002; pp. 180–185. [Google Scholar]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D.; Endres, A.L. Assessment of Soil Moisture Content Measured by Borehole GPR and TDR Under Transient Irrigation and Drainage. J. Environ. Eng. Geophys. 2003, 8, 77–86. [Google Scholar] [CrossRef]
- Rucker, D.F.; Ferré, T.P.A. Near-Surface Water Content Estimation with Borehole Ground Penetrating Radar Using Critically Refracted Waves. Vadose Zone J. 2003, 2, 247–252. [Google Scholar] [CrossRef]
- Rucker, D.F.; Ferré, T.P.A. Correcting Water Content Measurement Errors Associated with Critically Refracted First Arrivals on Zero Offset Profiling Borehole Ground Penetrating Radar Profiles. Vadose Zone J. 2004, 3, 278–287. [Google Scholar] [CrossRef]
- Rucker, D.F.; Ferré, T.P.A. Automated water content reconstruction of zero-offset borehole ground penetrating radar data using simulated annealing. J. Hydrol. 2005, 309, 1–16. [Google Scholar] [CrossRef]
- Ferré, T.P.A.; von Glinski, G.; Ferré, L.A. Monitoring the Maximum Depth of Drainage in Response to Pumping Using Borehole Ground Penetrating Radar. Vadose Zone J. 2003, 2, 511–518. [Google Scholar] [CrossRef]
- Kowalsky, M.B.; Finsterle, S.; Rubin, Y. Estimating flow parameter distributions using ground-penetrating radar and hydrological measurements during transient flow in the vadose zone. Adv. Water Resour. 2004, 27, 583–599. [Google Scholar] [CrossRef]
- Looms, M.C.; Jensen, K.H.; Binley, A.; Nielsen, L. Monitoring Unsaturated Flow and Transport Using Cross-Borehole Geophysical Methods. Vadose Zone J. 2008, 7, 227–237. [Google Scholar] [CrossRef]
- Kuroda, S.; Jang, H.; Kim, H.J. Time-lapse borehole radar monitoring of an infiltration experiment in the vadose zone. J. Appl. Geophys. 2009, 67, 361–366. [Google Scholar] [CrossRef]
- Wijewardana, Y.G.N.S.; Galagedara, L.W. Estimation of spatio-temporal variability of soil water content in agricultural fields with ground penetrating radar. J. Hydrol. 2010, 391, 24–33. [Google Scholar] [CrossRef]
- Haarder, E.B.; Binley, A.; Looms, M.C.; Doetsch, J.; Nielsen, L.; Jensen, K.H. Comparing Plume Characteristics Inferred from Cross-Borehole Geophysical Data. Vadose Zone J. 2012, 11, vzj2012.0031. [Google Scholar] [CrossRef]
- Klotzsche, A.; Lärm, L.; Vanderborght, J.; Cai, G.; Morandage, S.; Zörner, M.; Vereecken, H.; van der Kruk, J. Monitoring Soil Water Content Using Time-Lapse Horizontal Borehole GPR Data at the Field-Plot Scale. Vadose Zone J. 2019, 18, 190044. [Google Scholar] [CrossRef]
- Hubbard, S.S.; Peterson, J.E.; Majer, E.L.; Zawislanski, P.T.; Williams, K.H.; Roberts, J.; Wobber, F. Estimation of permeable pathways and water content using tomographic radar data. Lead. Edge 1997, 16, 1623–1630. [Google Scholar] [CrossRef]
- Eppstein, M.J.; Dougherty, D.E. Efficient three-dimensional data inversion: Soil characterization and moisture Monitoring from cross-well ground-penetrating radar at a Vermont Test Site. Water Resour. Res. 1998, 34, 1889–1900. [Google Scholar] [CrossRef]
- Alumbaugh, D.; Chang, P.Y.; Paprocki, L.; Brainard, J.R.; Glass, R.J.; Rautman, C.A. Estimating moisture contents in the vadose zone using cross-borehole ground penetrating radar: A study of accuracy and repeatability. Water Resour. Res. 2002, 38, 45-1–45-12. [Google Scholar] [CrossRef]
- Chang, P.-Y.; Alumbaugh, D.; Brainard, J.; Hall, L. The application of ground penetrating radar attenuation tomography in a vadose zone infiltration experiment. J. Contam. Hydrol. 2004, 71, 67–87. [Google Scholar] [CrossRef]
- Deiana, R.; Cassiani, G.; Kemna, A.; Villa, A.; Bruno, V.; Bagliani, A. An experiment of non-invasive characterization of the vadose zone via water injection and cross-hole time-lapse geophysical monitoring. Near Surf. Geophys. 2007, 5, 183–194. [Google Scholar] [CrossRef]
- Dafflon, B.; Irving, J.; Barrash, W. Inversion of multiple intersecting high-resolution crosshole GPR profiles for hydrological characterization at the Boise Hydrogeophysical Research Site. J. Appl. Geophys. 2011, 73, 305–314. [Google Scholar] [CrossRef]
- Cassiani, G.; Strobbia, C.; Gallotti, L. Vertical Radar Profiles for the Characterization of Deep Vadose Zones. Vadose Zone J. 2004, 3, 1093–1105. [Google Scholar] [CrossRef]
- Strobach, E.; Harris, B.D.; Dupuis, J.C.; Kepic, A.W. Time-lapse borehole radar for monitoring rainfall infiltration through podosol horizons in a sandy vadose zone. Water Resour. Res. 2014, 50, 2140–2163. [Google Scholar] [CrossRef]
- Chanzy, A.; Tarussov, A.; Bonn, F.; Judge, A. Soil Water Content Determination Using a Digital Ground-Penetrating Radar. Soil Sci. Soc. Am. J. 1996, 60, 1318–1326. [Google Scholar] [CrossRef]
- Redman, J.D.; Davis, J.L.; Galagedara, L.W.; Gary, W.P. Field studies of GPR air launched surface reflectivity measurements of soil water content. In Proceedings of the Ninth International Conference on Ground Penetrating Radar, Santa Barbara, CA, USA, 29 April–2 May 2002; pp. 156–161. [Google Scholar]
- Redman, D.; Galagedara, L.; Parkin, G. Measuring Soil Water Content with the Ground Penetrating Radar Surface Reflectivity Method: Effects of Spatial Variability. In Proceedings of the 2003 ASAE Annual Meeting, St. Joseph, MI, USA, 27–30 July 2003. [Google Scholar]
- Serbin, G.; Or, D. Ground-penetrating radar measurement of soil water content dynamics using a suspended horn antenna. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1695–1705. [Google Scholar] [CrossRef]
- Serbin, G.; Or, D. Ground-penetrating radar measurement of crop and surface water content dynamics. Remote Sens. Environ. 2005, 96, 119–134. [Google Scholar] [CrossRef]
- Lambot, S.; Rhebergen, J.; van den Bosch, I.; Slob, E.C.; Vanclooster, M. Measuring the Soil Water Content Profile of a Sandy Soil with an Off-Ground Monostatic Ground Penetrating Radar. Vadose Zone J. 2004, 3, 1063–1071. [Google Scholar] [CrossRef]
- Lambot, S.; Weihermüller, L.; Huisman, J.A.; Vereecken, H.; Vanclooster, M.; Slob, E.C. Analysis of air-launched ground-penetrating radar techniques to measure the soil surface water content. Water Resour. Res. 2006, 42, W11403. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.; Chavarro, D.; Lubczynski, M.; Vereecken, H. Measuring soil surface water content in irrigated areas of southern Tunisia using full-waveform inversion of proximal GPR data. Near Surf. Geophys. 2008, 6, 403–410. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Lambot, S.; Scharnagl, B.; van der Kruk, J.; Slob, E.; Vereecken, H. Quantifying field-scale surface soil water content from proximal GPR signal inversion in the time domain. Near Surf. Geophys. 2010, 8, 483–491. [Google Scholar] [CrossRef]
- Minet, J.; Lambot, S.; Slob, E.C.; Vanclooster, M. Soil Surface Water Content Estimation by Full-Waveform GPR Signal Inversion in the Presence of Thin Layers. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1138–1150. [Google Scholar] [CrossRef]
- Minet, J.; Bogaert, P.; Vanclooster, M.; Lambot, S. Validation of ground penetrating radar full-waveform inversion for field scale soil moisture mapping. J. Hydrol. 2012, 424–425, 112–123. [Google Scholar] [CrossRef]
- Jonard, F.; Weihermuller, L.; Jadoon, K.Z.; Schwank, M.; Vereecken, H.; Lambot, S. Mapping Field-Scale Soil Moisture With L-Band Radiometer and Ground-Penetrating Radar Over Bare Soil. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2863–2875. [Google Scholar] [CrossRef]
- Jonard, F.; Weihermüller, L.; Vereecken, H.; Lambot, S. Accounting for soil surface roughness in the inversion of ultrawideband off-ground GPR signal for soil moisture retrieval. Geophysics 2012, 77, H1–H7. [Google Scholar] [CrossRef]
- Jonard, F.; Mahmoudzadeh, M.; Roisin, C.; Weihermüller, L.; André, F.; Minet, J.; Vereecken, H.; Lambot, S. Characterization of tillage effects on the spatial variation of soil properties using ground-penetrating radar and electromagnetic induction. Geoderma 2013, 207–208, 310–322. [Google Scholar] [CrossRef]
- Tran, A.P.; Ardekani, M.R.M.; Lambot, S. Coupling of dielectric mixing models with full-wave ground-penetrating radar signal inversion for sandy-soil-moisture estimation. Geophysics 2012, 77, H33–H44. [Google Scholar] [CrossRef]
- Tran, A.P.; Bogaert, P.; Wiaux, F.; Vanclooster, M.; Lambot, S. High-resolution space–time quantification of soil moisture along a hillslope using joint analysis of ground penetrating radar and frequency domain reflectometry data. J. Hydrol. 2015, 523, 252–261. [Google Scholar] [CrossRef]
- Moghadas, D.; Jadoon, K.Z.; Vanderborght, J.; Lambot, S.; Vereecken, H. Estimation of the near surface soil water content during evaporation using air-launched ground-penetrating radar. Near Surf. Geophys. 2014, 12, 623–634. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.C.; Bosch, I.v.d.; Stockbroeckx, B.; Vanclooster, M. Modeling of ground-penetrating Radar for accurate characterization of subsurface electric properties. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2555–2568. [Google Scholar] [CrossRef]
- Busch, S.; van der Kruk, J.; Bikowski, J.; Vereecken, H. Quantitative conductivity and permittivity estimation using full-waveform inversion of on-ground GPR data. Geophysics 2012, 77, H79–H91. [Google Scholar] [CrossRef]
- Lavoué, F.; Brossier, R.; Métivier, L.; Garambois, S.; Virieux, J. Two-dimensional permittivity and conductivity imaging by full waveform inversion of multioffset GPR data: A frequency-domain quasi-Newton approach. Geophys. J. Int. 2014, 197, 248–268. [Google Scholar] [CrossRef]
- Feng, X.; Ren, Q.; Liu, C.; Zhang, X. Joint acoustic full-waveform inversion of crosshole seismic and ground-penetrating radar data in the frequency domain. Geophysics 2017, 82, H41–H56. [Google Scholar] [CrossRef]
- Nilot, E.; Feng, X.; Zhang, Y.; Zhang, M.; Dong, Z.; Zhou, H.; Zhang, X. Multiparameter Full-waveform inversion of on-ground GPR using Memoryless quasi-Newton (MLQN) method. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–4. [Google Scholar]
- Lambot, S.; André, F. Full-Wave Modeling of Near-Field Radar Data for Planar Layered Media Reconstruction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2295–2303. [Google Scholar] [CrossRef]
- Zajícová, K.; Chuman, T. Application of ground penetrating radar methods in soil studies: A review. Geoderma 2019, 343, 116–129. [Google Scholar] [CrossRef]
- Bano, M.; Loeffler, O.; Girard, J.-F. Ground penetrating radar imaging and time-domain modelling of the infiltration of diesel fuel in a sandbox experiment. Comptes Rendus Geosci. 2009, 341, 846–858. [Google Scholar] [CrossRef]
- Bano, M. Modelling of GPR waves for lossy media obeying a complex power law of frequency for dielectric permittivity. Geophys. Prospect. 2004, 52, 11–26. [Google Scholar] [CrossRef]
- Bano, M. Modeling GPR data in the fourier domain: Choice of the radar source. In Proceedings of the 2016 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016; pp. 1–6. [Google Scholar]
- Wagner, B.J. Simultaneous parameter estimation and contaminant source characterization for coupled groundwater flow and contaminant transport modelling. J. Hydrol. 1992, 135, 275–303. [Google Scholar] [CrossRef]
- Vereecken, H.; Kasteel, R.; Vanderborght, J.; Harter, T. Upscaling Hydraulic Properties and Soil Water Flow Processes in Heterogeneous Soils: A Review. Vadose Zone J. 2007, 6, 1–28. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Chen, J.; Hubbard, S.; Rubin, Y. Estimating the hydraulic conductivity at the south oyster site from geophysical tomographic data using Bayesian Techniques based on the normal linear regression model. Water Resour. Res. 2001, 37, 1603–1613. [Google Scholar] [CrossRef]
- Cassiani, G.; Binley, A. Modeling unsaturated flow in a layered formation under quasi-steady state conditions using geophysical data constraints. Adv. Water Resour. 2005, 28, 467–477. [Google Scholar] [CrossRef]
- Rossi, M.; Manoli, G.; Pasetto, D.; Deiana, R.; Ferraris, S.; Strobbia, C.; Putti, M.; Cassiani, G. Coupled inverse modeling of a controlled irrigation experiment using multiple hydro-geophysical data. Adv. Water Resour. 2015, 82, 150–165. [Google Scholar] [CrossRef]
- Kowalsky, M.B.; Finsterle, S.; Peterson, J.; Hubbard, S.; Rubin, Y.; Majer, E.; Ward, A.; Gee, G. Estimation of field-scale soil hydraulic and dielectric parameters through joint inversion of GPR and hydrological data. Water Resour. Res. 2005, 41, W11425. [Google Scholar] [CrossRef]
- Looms, M.C.; Binley, A.; Jensen, K.H.; Nielsen, L.; Hansen, T.M. Identifying Unsaturated Hydraulic Parameters Using an Integrated Data Fusion Approach on Cross-Borehole Geophysical Data. Vadose Zone J. 2008, 7, 238–248. [Google Scholar] [CrossRef]
- Linde, N.; Finsterle, S.; Hubbard, S. Inversion of tracer test data using tomographic constraints. Water Resour. Res. 2006, 42, W04410. [Google Scholar] [CrossRef]
- Moysey, S.M. Hydrologic trajectories in transient ground-penetrating-radar reflection data. Geophysics 2010, 75, WA211–WA219. [Google Scholar] [CrossRef]
- Saintenoy, A.; Hopmans, J.W. Ground Penetrating Radar: Water Table Detection Sensitivity to Soil Water Retention Properties. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 748–753. [Google Scholar] [CrossRef]
- Scholer, M.; Irving, J.; Binley, A.; Holliger, K. Estimating vadose zone hydraulic properties using ground penetrating radar: The impact of prior information. Water Resour. Res. 2011, 47, W10512. [Google Scholar] [CrossRef]
- Scholer, M.; Irving, J.; Looms, M.C.; Nielsen, L.; Holliger, K. Bayesian Markov-Chain-Monte-Carlo Inversion of Time-Lapse Crosshole GPR Data to Characterize the Vadose Zone at the Arrenaes Site, Denmark. Vadose Zone J. 2012, 11, vzj2011.0153. [Google Scholar] [CrossRef]
- Busch, S.; Weihermüller, L.; Huisman, J.A.; Steelman, C.M.; Endres, A.L.; Vereecken, H.; van der Kruk, J. Coupled hydrogeophysical inversion of time-lapse surface GPR data to estimate hydraulic properties of a layered subsurface. Water Resour. Res. 2013, 49, 8480–8494. [Google Scholar] [CrossRef]
- Bradford, J.; Thoma, M.; Barrash, W. Estimating hydrologic parameters from water table dynamics using coupled hydrologic and ground-penetrating radar inversion. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 232–237. [Google Scholar]
- Leger, E.; Saintenoy, A.; Coquet, Y. Estimating saturated hydraulic conductivity from ground-based GPR monitoring Porchet infiltration in sandy soil. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 124–130. [Google Scholar]
- Léger, E.; Saintenoy, A.; Tucholka, P.; Coquet, Y. Hydrodynamic Parameters of a Sandy Soil Determined by Ground-Penetrating Radar Monitoring of Porchet Infiltrations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 188–200. [Google Scholar] [CrossRef]
- Léger, E.; Saintenoy, A.; Coquet, Y.; Tucholka, P.; Zeyen, H. Evaluating hydrodynamic parameters accounting for water retention hysteresis in a large sand column using surface GPR. J. Appl. Geophys. 2020, 182, 104176. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.C.; Vanclooster, M.; Vereecken, H. Closed loop GPR data inversion for soil hydraulic and electric property determination. Geophys. Res. Lett. 2006, 33, L21405. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Slob, E.; Vanclooster, M.; Vereecken, H.; Lambot, S. Uniqueness and stability analysis of hydrogeophysical inversion for time-lapse ground-penetrating radar estimates of shallow soil hydraulic properties. Water Resour. Res. 2008, 44, W09421. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.; Rhebergen, J.; Lopera, O.; Jadoon, K.Z.; Vereecken, H. Remote Estimation of the Hydraulic Properties of a Sand Using Full-Waveform Integrated Hydrogeophysical Inversion of Time-Lapse, Off-Ground GPR Data. Vadose Zone J. 2009, 8, 743–754. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Weihermüller, L.; Scharnagl, B.; Kowalsky, M.B.; Bechtold, M.; Hubbard, S.S.; Vereecken, H.; Lambot, S. Estimation of Soil Hydraulic Parameters in the Field by Integrated Hydrogeophysical Inversion of Time-Lapse Ground-Penetrating Radar Data. Vadose Zone J. 2012, 11, vzj2011.0177. [Google Scholar] [CrossRef]
- Jonard, F.; Weihermüller, L.; Schwank, M.; Jadoon, K.Z.; Vereecken, H.; Lambot, S. Estimation of Hydraulic Properties of a Sandy Soil Using Ground-Based Active and Passive Microwave Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3095–3109. [Google Scholar] [CrossRef]
- Tran, A.P.; Vanclooster, M.; Zupanski, M.; Lambot, S. Joint estimation of soil moisture profile and hydraulic parameters by ground-penetrating radar data assimilation with maximum likelihood ensemble filter. Water Resour. Res. 2014, 50, 3131–3146. [Google Scholar] [CrossRef]
- Dagenbach, A.; Buchner, J.S.; Klenk, P.; Roth, K. Identifying a parameterisation of the soil water retention curve from on-ground GPR measurements. Hydrol. Earth Syst. Sci. 2013, 17, 611–618. [Google Scholar] [CrossRef]
- Yu, Y.; Huisman, J.A.; Klotzsche, A.; Vereecken, H.; Weihermüller, L. Coupled full-waveform inversion of horizontal borehole ground penetrating radar data to estimate soil hydraulic parameters: A synthetic study. J. Hydrol. 2022, 610, 127817. [Google Scholar] [CrossRef]
- Roth, K.; Schulin, R.; Flühler, H.; Attinger, W. Calibration of time domain reflectometry for water content measurement using a composite dielectric approach. Water Resour. Res. 1990, 26, 2267–2273. [Google Scholar] [CrossRef]
- Sen, P.N.; Scala, C.; Cohen, M.H. A self-similar model for sedimentary rocks with application to the dielectric constant of fused glass beads. Geophysics 1981, 46, 781–795. [Google Scholar] [CrossRef]
- Johnson, R.H.; Poeter, E.P. Iterative use of the Bruggeman-Hanai-Sen mixing model to determine water saturations in sand. Geophysics 2005, 70, K33–K38. [Google Scholar] [CrossRef]
- Lambot, S.; Antoine, M.; van den Bosch, I.; Slob, E.C.; Vanclooster, M. Electromagnetic Inversion of GPR Signals and Subsequent Hydrodynamic Inversion to Estimate Effective Vadose Zone Hydraulic Properties. Vadose Zone J. 2004, 3, 1072–1081. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Tillard, S.; Dubois, J.-C. Analysis of GPR data: Wave propagation velocity determination. J. Appl. Geophys. 1995, 33, 77–91. [Google Scholar] [CrossRef]




| Configurations of Radar System | Measured Modes | Methods | Related References |
|---|---|---|---|
| Surface GPR | Single Offset | Reflected Wave | Vellidis et al., 1990 [29]; Al and Müller, 2000 [30]; Birken and Versteeg, 2000 [31]; Grote et al., 2002 [32]; Gish et al., 2002 [33]; Schmalz and Lennartz, 2002 [34]; Stoffregen et al., 2002 [35]; Loeffler and Bano, 2004 [36]; Makkawi, 2004 [37]; Wollschläger and Roth, 2005 [38]; Lunt et al., 2005 [39]; Turesson, 2006 [40]; Saintenoy et al., 2008 [41]; Irving et al., 2009 [42]; Haarder et al., 2011 [43]; Klenk et al., 2015 [44]; Schmelzbach et al., 2012 [45]; Guo et al., 2014 [46]; Zhang et al., 2014 [47]; Yu et al., 2015 [48]; Shamir et al., 2016, 2018 [49,50]; Ercoli et al., 2018 [51]; Nyquist et al., 2018 [52]; Di Prima et al., 2020 [53]; Mangel et al., 2020 [54]; Zhang et al., 2021a, 2021b [55,56] |
| Ground Wave | van Overmeeren et al., 1997 [57]; Huisman et al., 2003b [58]; Galagedara et al., 2005b [59]; Grote et al., 2003 [60]; Klenk et al., 2011 [61]; Pan et al., 2012a [20]; Qin et al., 2013 [62]; Ardekani, 2013 [63]; Thitimakorn et al., 2016 [64] | ||
| AEA | Pettinelli et al., 2007, 2014 [65,66]; Ferrara et al., 2013 [67]; Algeo et al., 2016 [68] | ||
| Frequency Shift | Benedetto, 2010 [69]; Benedetto and Benedetto, 2011 [70]; Benedetto et al., 2013 [71] | ||
| Multi-Offset | Reflected Wave | Greaves et al., 1996 [25]; Weiler et al., 1998 [72]; Huisman et al., 2001 [73]; Garambois et al., 2002 [74]; Turesson, 2006 [40]; Strobbia and Cassiani, 2007 [75]; Bradford, 2008 [76]; Gerhards et al., 2008 [77]; Buchner et al., 2011, 2012 [78,79]; Steelman et al., 2012a, 2012b [80,81]; Mangel et al., 2012, 2015 [82,83]; Allroggen et al., 2015 [84]; Iwasaki et al., 2016 [85]; Kaufmann et al., 2020 [86]; Yu et al., 2020 [87]; Saito et al., 2021 [88] | |
| Ground Wave | Huisman et al., 2001, 2002, 2003a, 2003b [22,58,73,89]; Hubbard et al., 2002 [90]; Grote et al., 2003, 2010 [60,91]; Galagedara et al., 2003a, 2005a, 2005b [59,92,93]; Weihermüller et al., 2007 [94]; Steelman et al., 2010, 2012b [81,95]; Thitimakorn et al., 2016 [64]; Cao et al., 2020 [96] | ||
| Borehole GPR | Zero Offset | Knoll and Clement, 1999 [97]; Alumbaugh et al., 2000 [98]; Parkin et al., 2000 [99]; Binley et al., 2001, 2002a, 2002b [100,101,102]; Galagedara et al., 2002, 2003b [103,104]; Rucker and Ferré, 2003, 2004, 2005 [105,106,107]; Ferré et al., 2003 [108]; Kowalsky et al., 2004 [109]; Looms et al., 2008a [110]; Kuroda et al., 2009 [111]; Wijewardana and Galagedara, 2010 [112]; Haarder et al., 2012 [113]; Klotzsche et al., 2019 [114]; Yu et al., 2020 [87] | |
| Multi-Offset | Hubbard et al., 1997 [115]; Eppstein and Dougherty, 1998 [116]; Parkin et al., 2000 [99]; Binley et al., 2001, 2002a [100,101]; Galagedara et al., 2002, 2003b [103,104]; Alumbaugh et al., 2002 [117]; Chang et al., 2004 [118]; Deiana et al., 2007 [119]; Looms et al., 2008a [110]; Wijewardana and Galagedara, 2010 [112]; Dafflon et al., 2011 [120]; Haarder et al., 2012 [113] | ||
| Vertical Radar | Knoll and Clement, 1999 [97]; Cassiani et al., 2004 [121]; Dafflon et al., 2011 [120]; Strobach et al., 2014 [122] | ||
| Off-ground GPR | Surface Reflections | Chanzy et al., 1996 [123]; Redman, 2002 [124,125]; Serbin and Or, 2004, 2005 [126,127]; Lambot et al., 2004a [128,129,130]; Weihermüller et al., 2007 [94]; Jadoon et al., 2010 [131]; Minet et al., 2010, 2012 [132,133]; Jonard et al., 2011, 2012, 2013 [134,135,136]; Tran et al., 2012 [137,138]; Ardekani, 2013 [63]; Moghadas et al., 2014 [139]; Mangel et al., 2015 [83] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Feng, X.; Bano, M.; Xing, H.; Wang, T.; Liang, W.; Zhou, H.; Dong, Z.; An, Y.; Zhang, Y. Review of Ground Penetrating Radar Applications for Water Dynamics Studies in Unsaturated Zone. Remote Sens. 2022, 14, 5993. https://doi.org/10.3390/rs14235993
Zhang M, Feng X, Bano M, Xing H, Wang T, Liang W, Zhou H, Dong Z, An Y, Zhang Y. Review of Ground Penetrating Radar Applications for Water Dynamics Studies in Unsaturated Zone. Remote Sensing. 2022; 14(23):5993. https://doi.org/10.3390/rs14235993
Chicago/Turabian StyleZhang, Minghe, Xuan Feng, Maksim Bano, Huiting Xing, Taihan Wang, Wenjing Liang, Haoqiu Zhou, Zejun Dong, Yafei An, and Yinghao Zhang. 2022. "Review of Ground Penetrating Radar Applications for Water Dynamics Studies in Unsaturated Zone" Remote Sensing 14, no. 23: 5993. https://doi.org/10.3390/rs14235993
APA StyleZhang, M., Feng, X., Bano, M., Xing, H., Wang, T., Liang, W., Zhou, H., Dong, Z., An, Y., & Zhang, Y. (2022). Review of Ground Penetrating Radar Applications for Water Dynamics Studies in Unsaturated Zone. Remote Sensing, 14(23), 5993. https://doi.org/10.3390/rs14235993