Ground-Penetrating Radar Full-Wave Inversion for Soil Moisture Mapping in Trench-Hill Potato Fields for Precise Irrigation

Abstract

In this paper, we analysed the effect of trench-hill soil surface on ground-penetrating radar (GPR) full-wave inversion for soil moisture measurement. We conducted numerical experiments by modelling the trench-hill surface using finite-difference time–domain (FDTD) simulations. The FDTD simulations were carried out with the open-source software gprMax, using different centre frequencies, namely, 150 MHz, 250 MHz and 450 MHz. The gprMax source/receiver for each centre frequency was calibrated, respectively, to transform the FDTD radar signal to normalized Green’s functions for wave propagation in multilayered media. The radar signals and inversion results of the three different frequency ranges are compared. The FDTD Green’s functions of the trench-hill surface with a flat surface are also compared. The results show that the trench-hill surface only slightly affects the inversion when frequency is lower than 190 MHz, which agrees with Rayleigh’s criterion. Field measurements were performed as well, using a prototype radar mounted on an irrigation robot. The low-frequency antenna was calibrated over a large water plane. The optimal operating frequency range was set to 130–190 MHz. TDR measurements were performed as well for comparison. The results demonstrated promising perspectives for automated and real-time determination of the root–zone soil moisture in potato fields, and thereby for precise and automatic irrigation.

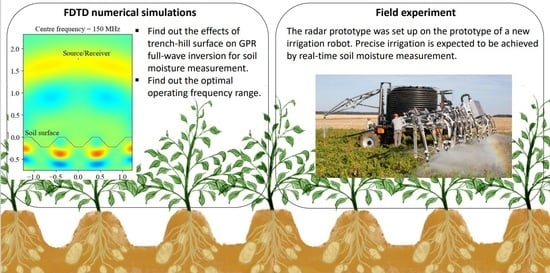
1. Introduction

For potato crop, a hilling planting approach is commonly used to increase both yield and quality as it improves fertilizer and water use efficiency, protects plants from frost, etc. [1,2,3]. In addition, it is well recognized that keeping high soil moisture (e.g., above 50% available moisture) is also necessary [4,5]. Moisture measurement for hill shape soil is therefore an important need in agriculture, especially when considering the evolution of regulations on water use.

Various methods have been developed for soil surface water content observation, including ground, proximal, and remote sensing. Ground-based sensors such as time-domain reflectometry (TDR) and capacitive sensors are invasive and only provide local measurements that do not capture the inherent field variability. Satellite sensing is used for large- and global-scale observations and provides only shallow soil information (<5 cm) [6].

GPR has been considered for soil moisture measurement for more than three decades [7,8,9,10]. Recent reviews are given [11,12,13]. Most GPR data processing techniques used for soil moisture retrieval have been based on the straight-ray or one-dimensional wave propagation approximation. The soil dielectric permittivity is retrieved from either the soil surface reflexion coefficient or the propagation velocity derived from the propagation time along the considered propagation path. For instance, the common midpoint (CMP) and wide angle reflexion and refraction (WARR) provide electromagnetic (EM) wave velocity information [8,9,14,15,16]. The average envelope amplitude (AEA) method or early-time signal analysis focuses on changes of the first arrival signals in terms of amplitude, shape and duration, resulting from variations of soil properties such as dielectric permittivity and electrical conductivity [17,18,19,20,21]. The full-wave inversion method has been widely considered to be promising since it is conducted by minimizing the misfit between observed and modelled data. Full-wave modelling and inversion methods with different hypotheses or resolution methods have also been proposed for soil dielectric permittivity retrieval. With the finite-difference time-domain (FDTD) method, the full-wave inversion method has been applied to the multi-offset or crosshole GPR data [22,23,24]. However, with these methods, the EM source and antennas are not accounted for. Although these methods are relatively simple to implement and have demonstrated their potential, they suffer from inherent estimation errors originating from the underlying simplifying model assumptions and, moreover, they are quite cumbersome to apply in real application contexts. They are also difficult to automatize and, therefore, they require some user expertise. As a result, their application has mostly remained in the scientific community. Frequency-domain GPR can be operated with a single antenna acting as the transmitter and receiver at the same time, which makes the radar system and measurement configuration much simpler. In 2004, Lambot et al. introduced a far-field full-wave radar equation accounting for the radar source, antennas, antenna–medium interactions and three-dimensional wave propagation in planar layered media using Green’s functions [25]. Once the radar is calibrated, i.e., the antenna characteristic functions have been determined, soil dielectric permittivity and correlated moisture can be automatically retrieved using full-wave inversion, namely, by fitting the radar model to the measured data. The model was later generalized to near-field conditions [26]. The model was successfully applied in a series of hydrogeophysical applications [27,28,29,30], including high-resolution soil moisture mapping [31] and, more recently, drone-borne GPR [32].

In the remote sensing community or others, scattering by rough surfaces has been investigated for decades. Empirical and physical models can be applied to determine the wind speed and direction which causes ring-waves over the water surface. EM scattering can be included in Maxwell’s equations to be determined, and there are various methods to solve it, e.g., the separation of variables method, the FDTD, the finite element method (FEM) and Green’s function formulation, etc. [33,34,35]. Scattering from periodic surfaces was proposed to be addressed by applying boundary conditions [36,37]. Craeye et al. analysed and observed scattering rain- and wind-roughened water surface using video camera and very high frequency radar with specific pointing, e.g., 13.5 GHz and 30${}^{\circ }$ [38,39]. Plenty of studies have been performed to model the layered rough medium surface scattering. Lemaire et al. analysed ring-wave spectra to give the model for radar response simulation and inversion [40]. It is necessary to take into account the surface roughness in remote or proximal sensing data, as it would be affected by diffuse scattering in addition to the specular scattering. Most of the studies considered the soil roughness in the forward and inverse models. For off-ground radar and remote sensing measurements, surface roughness is usually mathematically assumed to be stationary with random Gaussian height distribution, and described by the mean, variance, correlation length of the surface height, etc. [41,42,43,44,45,46]. Jonard et al. considered random rough layers based on the scalar Kirchhoff-tangent plane approximation model and developed a closed-form asymptotic EM model [47]. There are two ways to keep the inversion results as accurate as possible: (1) Accounting for the soil surface roughness as pre-estimated information in the inverse model, but it makes inversion more complex and may lead to non-uniqueness inversion issues, especially in real-field conditions, and (2) using the right frequency range in the inversion process, which allows for neglecting the roughness effects [44]. In addition, according to Rayleigh’s criterion, the roughness amplitude should be smaller than one-eighth of the minimal wavelength. However, those simulations are for small and random protuberances, but for the potato crop, the soil is regularly shaped with the protuberance around 0.2 m. There is still a need to investigate its feasibility, and also to find out the proper operating frequencies.

As a first approximation, neglecting vertical variability in the medium, the hilling system for the potato crop can be seen as a semi-infinite homogeneous medium with a very rough, structured surface. On this consideration, the objective then goes back to the investigation of the effect of soil roughness on moisture measurement. In this paper, we conducted numerical experiments and field measurements to investigate the effect of the potato hilling system on the full-wave inversion method for soil moisture measurements. The numerical experiments were conducted using the FDTD simulations carried out with the open-source software gprMax of Giannopoulos [48] and Warren et al. [49], which modelled the 3D hill-shape soil. In addition, 2D simulations were conducted as well to observe the EM wave propagation. The centre frequencies were set to 150, 250 and 450 MHz, respectively. For the numerical data pre-processing, a radar equation originating from the one proposed by Lambot et al. [25,26] was applied to calculate the transfer functions of the gprMax Hertzian dipole antenna, or the source/receiver, which was then used to transform the FDTD radar signal to the multilayered Green’s functions. We compared the radar signals of the three centre frequencies, and compared the Green’s functions of the trench-hill and flat surface. We also investigated the effects of the trench-hill structure on the full-wave inversion results for the different frequency ranges. Finally, a radar system operating in the less affected range was used in real field conditions to measure soil moisture, within the frame of the EU agROBOfood MIRAGE project. For the field measurement, we used a log-periodic antenna and calibrated it over a large river. TDR measurements were also conducted for comparison.

2. Methodology

2.1. Full-Wave Inversion to Retrieve Soil Moisture

The radar system used in this study is based on vector network analyser (VNA) technology combined with a monostatic log-periodic antenna. Hence, a radar measurement consists of the frequency-dependent, complex-valued $S_{11}\left(\omega \right)$ quantity, representing the ratio between the received signal and the transmitted signal, $\omega$ being the angular frequency. The radar measurements are described using the radar equation of Lambot et al. [25], Lambot and André [26], which accounts for the radar-antenna system and wave propagation in three-dimensional planar multilayered media. For far-field conditions, the radar equation is expressed as follows:

$$S_{11}\left(\omega \right)=\frac{B\left(\omega \right)}{A\left(\omega \right)}=R_i\left(\omega \right)+\frac{T\left(\omega \right)G_{xx}\left(\omega \right)}{1-G_{xx}\left(\omega \right)R_s\left(\omega \right)}$$

(1)

where $A\left(\omega \right)$ and $B\left(\omega \right)$ are the received and emitted signals at the VNA reference plane, respectively. $G_{xx}\left(\omega \right)$ is the Green’s function defined as the x-component of the backscattered electric field for a unit, x-directed electric source for wave propagation in 3D planar layered media [25,50,51]. $R_i\left(\omega \right)$ is the global reflexion coefficient of the antenna for fields incident from the radar reference plane onto the source point. $T\left(\omega \right)$ is the antenna transmitting-receiving response function. $R_s\left(\omega \right)$ is the global reflexion coefficient of the antenna for fields incident from the antenna phase centre (backscattered field) onto the radar reference plane. For the same antenna setup, the calibration is needed only once, i.e., the determination of the antenna characteristic functions $R_i$, T, and $R_s$. The calibration was conducted through several measurements over a known reference plane, and solving a matrix equation as expressed from Equation (1). The reference plane should be large enough for a given antenna and operating frequency range (e.g., ideally larger than 5–10 times the maximal wavelength).

The inverse problem is defined using the least-squares formulation. Inversion is conducted in the time-domain, and the objective function is expressed as:

$$\varphi \left(\mathbf{b}\right)={\left({\mathbf{g}}_{xx}^{*}\left(t\right)-{\mathbf{g}}_{xx}(\mathbf{b},t)\right)}^{⊺}\left({\mathbf{g}}_{xx}^{*}\left(t\right)-{\mathbf{g}}_{xx}(\mathbf{b},t)\right)$$

(2)

where ${\mathbf{g}}_{xx}^{*}\left(t\right)$ and ${\mathbf{g}}_{xx}(\mathbf{b},t)$ are, respectively, the measured (or simulated) and modelled Green’s function vectors, and obtained by inverse Fourier transform of $G_{xx}\left(\omega \right)$, so t denotes time. Performing inversion in the time domain allows for focusing on a time window, e.g., corresponding to the surface reflection only. Later reflexions can then be disregarded and the subsurface model thereby approximates better to a half-space medium. $\mathbf{b}$ is the parameter vector [$h,{\mathsf{\epsilon }}_r$], where h is the distance between the antenna phase centre and the medium surface, and ${\mathsf{\epsilon }}_r$ is the relative permittivity of the medium. A look-up table (LUT) is used for robust and fast inversion. Indeed, as there are two unknowns only, the objective function can be calculated in the full parameter space and finding the minimum becomes therefore straightforward. The LUT includes the ${\mathbf{g}}_{xx}(\mathbf{b},t)$ for the whole parameter space.

In this study, we used the petrophysical relation of Topp [52] to estimate the volumetric soil moisture $\theta$ from the GPR-derived dielectric permittivity ${\epsilon }_r$:

$$\theta =-5.3\times {10}^{-2}+2.92\times {10}^{-2}{\epsilon }_r-5.5\times {10}^{-4}{\epsilon }_r^2+4.3\times {10}^{-6}{\epsilon }_r^3$$

(3)

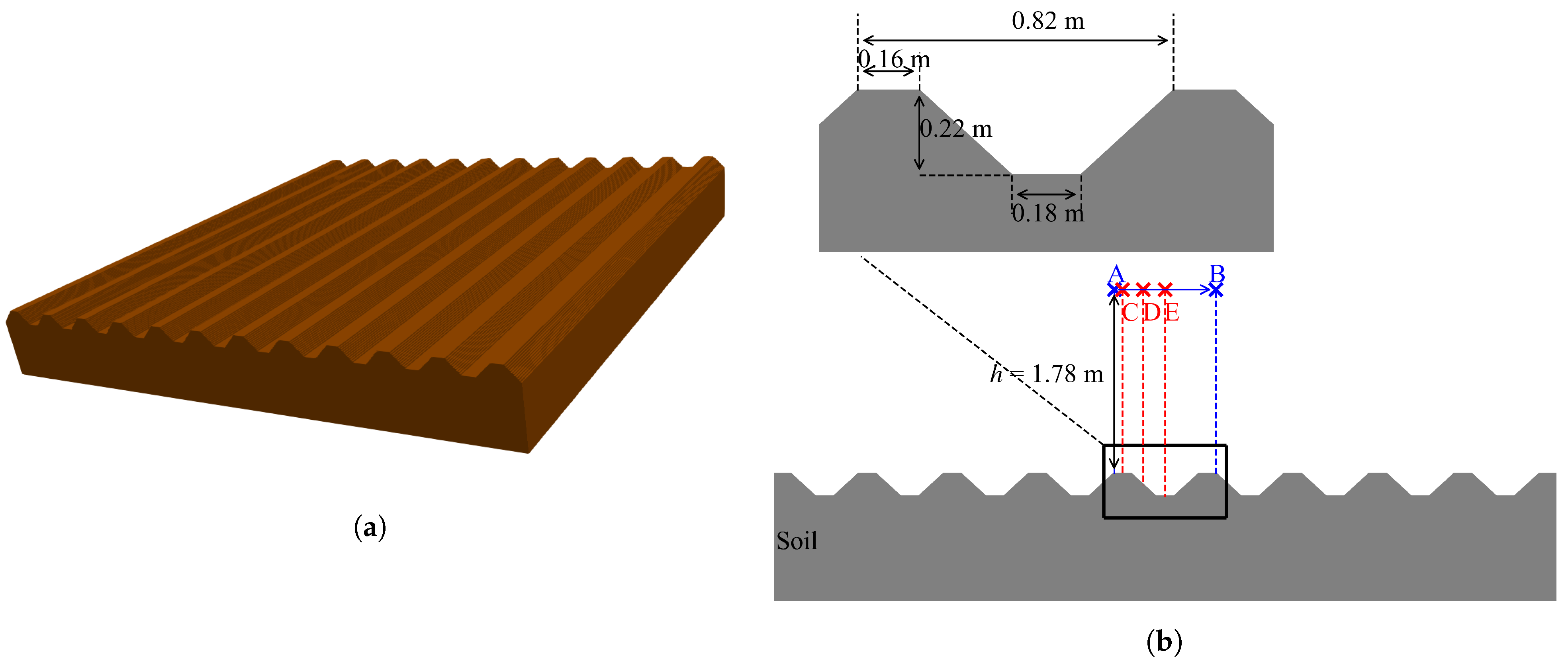
2.2. FDTD Numerical Simulation and Calibration

We used gprMax3D to model the trench-hill soil surface. GprMax is an open-source software that simulates EM wave propagation, solving Maxwell’s equations with the FDTD method and Yee’s algorithm [49,53].

For the inversion, the FDTD simulated data needed to be transformed into multilayered media Green’s functions as in Equation (1). We define $a\left(t\right)$ as the gprMax electric source signal in the time domain and $b\left(t\right)$ as the simulated backscattered electric field, respectively. $A\left(\omega \right)$ and $B\left(\omega \right)$ are their frequency–domain counterparts. Therefore, Equation (1) becomes [47]:

$$B\left(\omega \right)=H_i\left(\omega \right)+H\left(\omega \right)G_{xx}\left(\omega \right)$$

(4)

where $H_i\left(\omega \right)=A\left(\omega \right)R_i\left(\omega \right)$ and $H\left(\omega \right)=A\left(\omega \right)T\left(\omega \right)$. In gprMax, the antenna reduces to point sources and receivers, so $R_s\left(\omega \right)=0$. Indeed, in that case, there is no physical antenna described and, hence, no variation of impedance within the antenna (the antenna does not act as a reflector). $H_i\left(\omega \right)$ represents the direct transmission between the transmitter and the receiver, and $H\left(\omega \right)$ permits field normalization, including deconvolution of the source waveform.

To calculate $H_i\left(\omega \right)$ and $H\left(\omega \right)$ (i.e., to calibrate the virtual antenna), simulations with two configurations are needed using gprMax. A source/receiver situates at the free space, where $G_{xx}=0$, so $H_i\left(\omega \right)=B\left(\omega \right)$. Then, another configuration involves the source/receiver to be situated over a perfect electrical conductor (PEC). Electrical properties of the PEC are known for the Green’s function $G_{xx}\left(\omega \right)$, from which $H\left(\omega \right)$ is calculated. Once $H_i\left(\omega \right)$ and $H\left(\omega \right)$ are known, the FDTD Green’s function is obtained in the frequency domain as:

$$G_{xx}\left(\omega \right)=\frac{B\left(\omega \right)-H_i\left(\omega \right)}{H\left(\omega \right)}$$

(5)

3. Numerical Experiments

The soil surface geometrical model is shown in Figure 1. The simulations were conducted in 3D and 2D with different centre frequencies. The 3D model was carried out for data inversion, and the 2D is to observe the EM wave propagation. The mound dimensions (in Figure 1b) for the simulations are typical values for potato crops [54,55]. We do not consider the effect of crops in this study as during all the growing periods, and the height and coverage density of the crops can be neglected [56,57].

We considered two configurations in the numerical experiments. In configuration i, the relative permittivity ${\epsilon }_r$ of the soil was set to 10, and the distance h between the source/receiver and the top of the surface was set to 1.78 m. This height was chosen as a realistic far-field antenna configuration for real field applications considering the lowest frequency range. Three sources with different centre frequencies were used, respectively, i.e., 150 MHz, 250 MHz and 450 MHz. The source/receiver, namely, the virtual antenna, moved from point A to B as in Figure 1b, thereby covering a full surface period, with a step of 0.02 m, resulting in 50 measurements for each centre frequency. To avoid the boundary noise problem in the FDTD model, the domain sizes were set relatively large as $14\times 13\times 14$ m, $10\times 6\times 10$ m and $6\times 5\times 6$ m, for the simulations with the centre frequencies of 150 MHz, 250 MHz and 450 MHz, respectively. All the measurements were collected at the centre of the domain. To keep a reasonable physical phase–velocity error, the spatial discretisations of the simulation domain were set to 0.02 m, 0.02 m and 0.01 m, respectively. In configuration ii, ${\epsilon }_r$ varied from 5 to 22, representing a realistic range of possible soil moisture as encountered in agricultural fields. One source/receiver with centre frequency of 150 MHz was used, and measurements were performed at three positions (the top, slope and bottom of the soil surface). The source/receiver is situated at the same height as in configuration i, i.e., 1.78 m above the top of the surface.

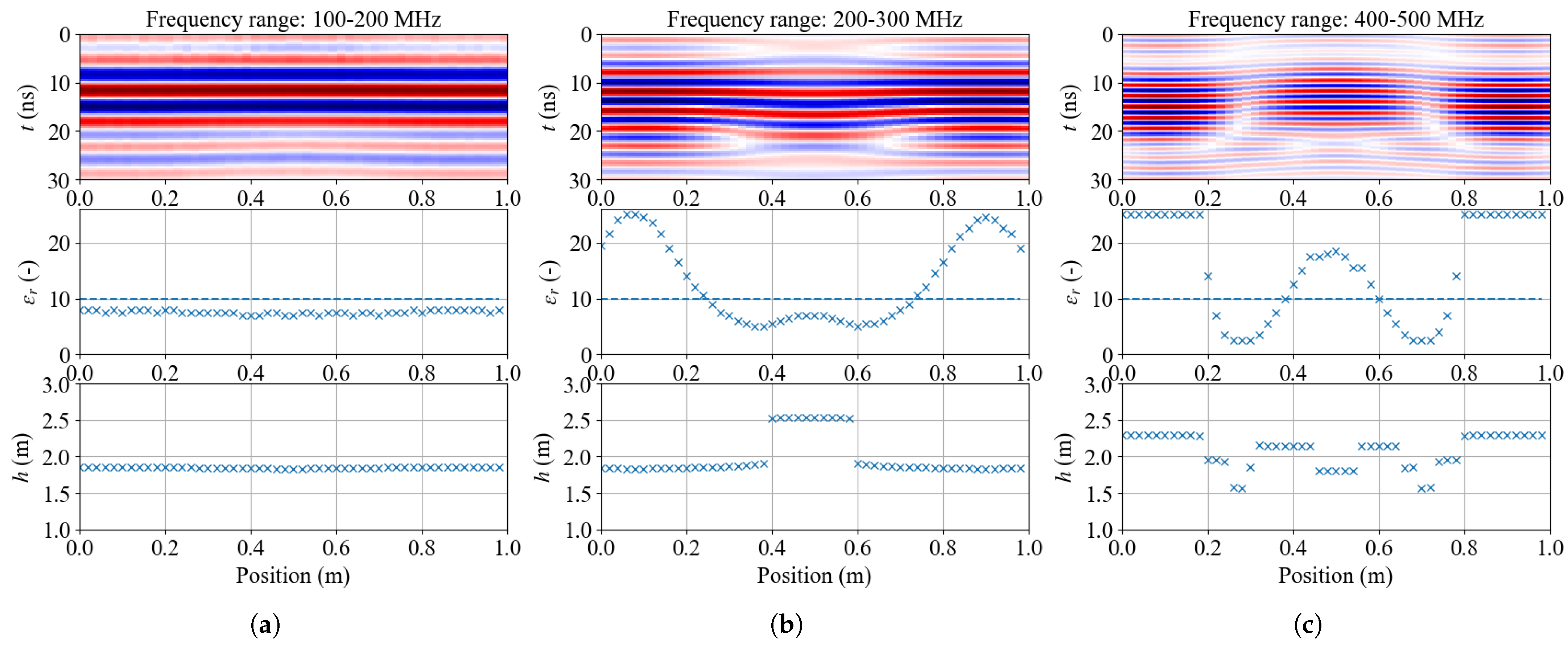
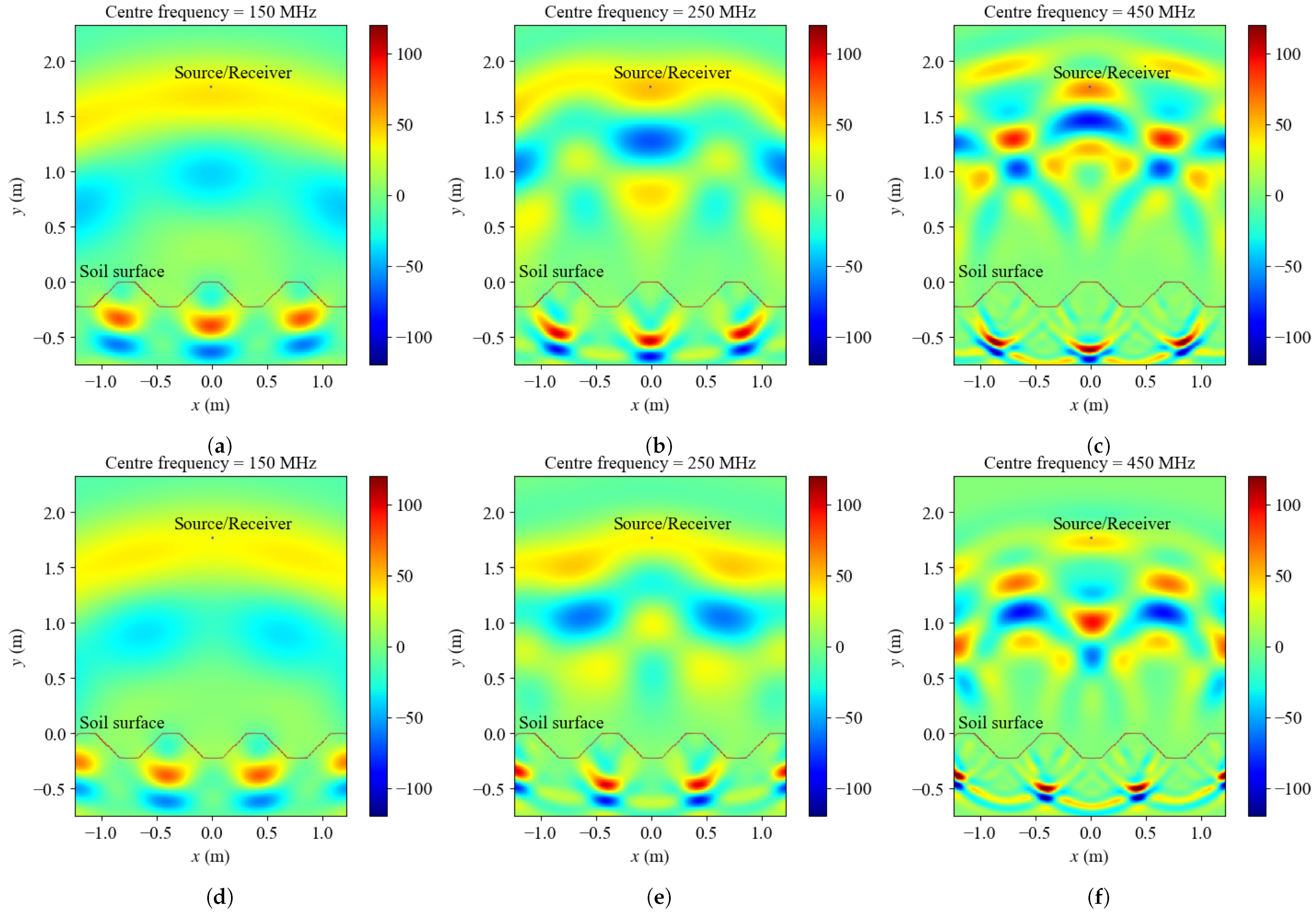
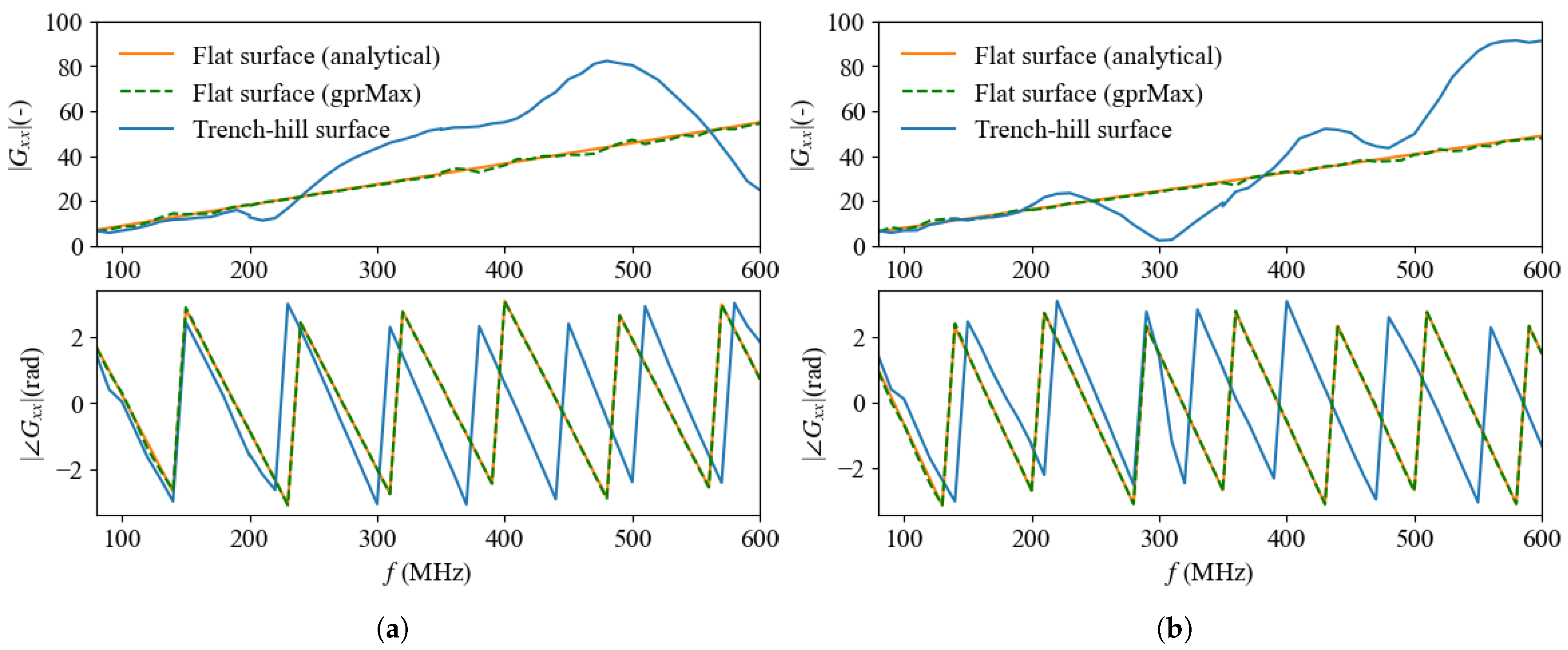
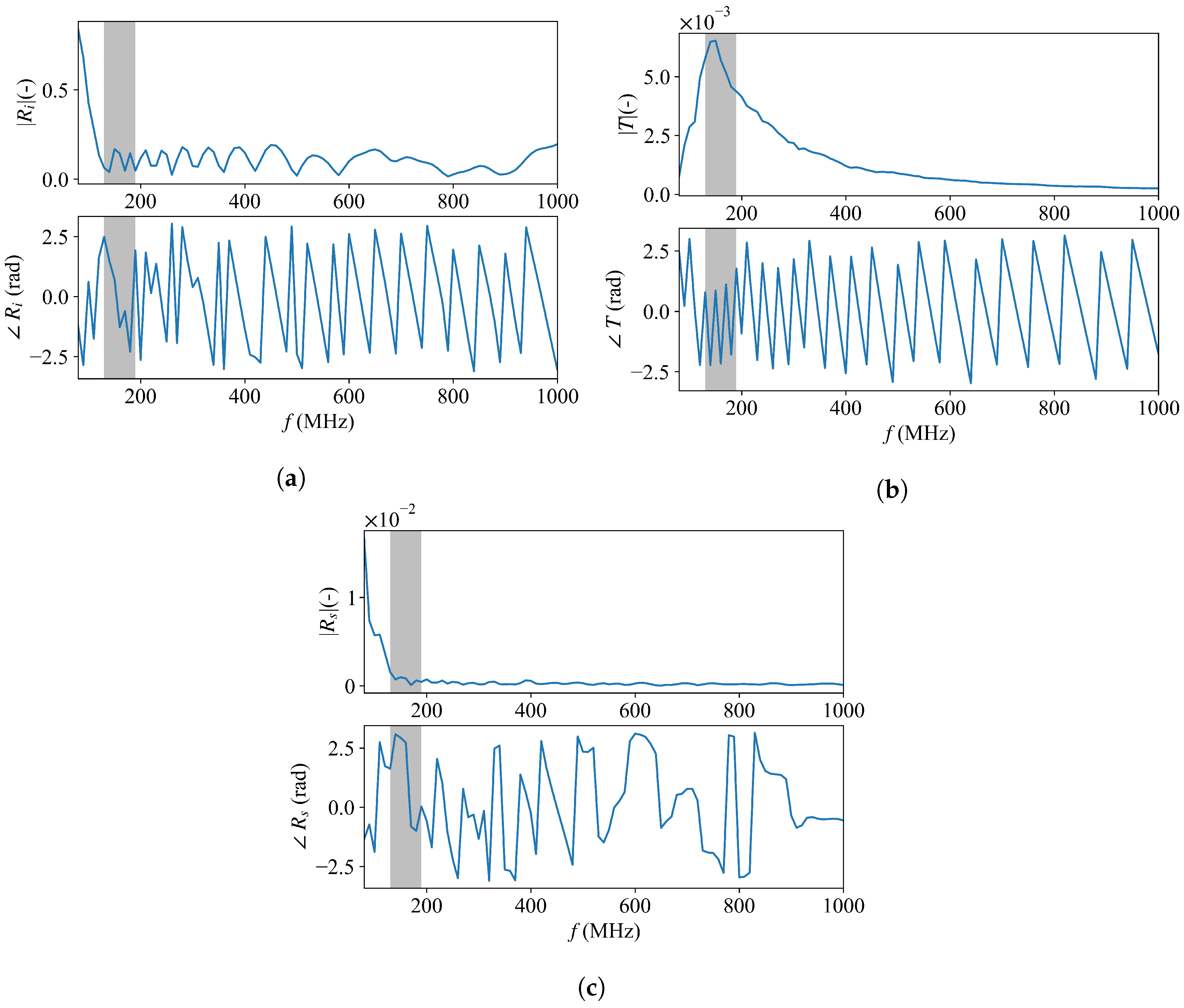
3.1. Configuration 1: 3 Sources with Different Centre Frequencies

In this configuration, there are 50 measurements for each centre frequency, i.e., 150 MHz, 250 MHz and 450 MHz. For the source/receiver of each centre frequency, the corresponding virtual antenna transfer functions $H_i\left(\omega \right)$ and $H\left(\omega \right)$ were used to obtain the corresponding FDTD Green’s functions. The calibrations and calculations of the Green’s functions were all conducted within the frequency range 80–600 MHz. To keep a good signal-to-noise ratio (SNR) with respect to FDTD numerical errors for the imaging and inversion, we considered only the frequency ranges that were not far from the operating centre frequencies, i.e., 100–200 MHz for the centre frequency of 150 MHz, 200–300 MHz for the centre frequency of 250 MHz, and 400–500 MHz for the centre frequency of 450 MHz. For the inversions, the parameter vectors were defined as $\mathbf{h}=\left[13\right]$ m with intervals of 0.01 m and ${\epsilon }_{\mathbf{r}}=\left[225\right]$ with intervals of 0.5, resulting in 9447 parameter pairs and 9447 corresponding Green’s functions building the LUT for each frequency range.

Figure 2 presents the FDTD Green’s functions and the inversion results for the three frequency ranges. From Figure 2a, the reflections with the frequency range 100–200 MHz seem constant, as well as the inversion results for ${\epsilon }_r$ and h. We do not observe any significant difference between the top, hill and bottom. However, ${\epsilon }_r$ was sightly underestimated (the estimated ${\epsilon }_r$ ranges from about 7.5 to 8, but the true value is 10). Estimated h is also constant at around 1.84 m, which is between the minimal and maximal of the true value range (1.78 m and 2 m). With the operating frequency range increasing, the effect of the trench-hill structure becomes well visible. Accordingly, the inversion results become subject to significant errors. In particular, when the frequency range is 400–500 MHz (Figure 2c), destructive and constructive interferences occur, which results, respectively, in under- and over-estimations of the relative permittivity. We also present the magnitude of the electric field in Figure 3. It was obtained with gprMax 2D, using the three centre frequencies 150 MHz, 250 MHz and 450 MHz. The virtual antenna was situated above the centre of the top (Figure 3a–c) and above the centre of the bottom (Figure 3d–f) of the central trench-hill period of the geometry. We present the propagation time for which the receiver receives the peak of the signal, which is seen as the reflection of the soil surface. Please note that the peaks do not correspond to the FDTD Green’s function in Figure 2 but to $b\left(t\right)-h_i\left(t\right)$ where $h_i\left(t\right)$ is $H_i\left(\omega \right)$ in the time domain. When the centre frequency is 150 MHz, the electric field, in terms of arrival time and amplitude, seems only slightly affected when the source/receiver is situated at different positions. With the centre frequency increasing, the difference becomes significant. The 450 MHz centre frequency produces higher magnitude especially when the source/receiver was situated above the top (Figure 3c).

To learn more about the effect of the trench-hill surface on the surface reflection, we compared the frequency–domain Green’s functions of trench-hill with those for the flat surface. We also compared the Green’s functions of the flat surface obtained by the analytical solution and gprMax. Two virtual antenna positions were considered. For Figure 4a, the source/receiver was above the centre of the top, so the flat surface reflection was obtained with h = 1.78 m, and ${\epsilon }_r=10$. For Figure 4b, the source/receiver was above the centre of the bottom, hence h = 2 m, and ${\epsilon }_r=10$. A combination of different frequency ranges was carried out for all the FDTD Green’s functions to cover the full 80–600 MHz bandwidth of analysis. The combination is necessary because it helps to keep the valuable information (high SNR) for each centre frequency, i.e., 80–200 MHz for centre frequency 150 MHz, 200–350 MHz for 250 MHz and 350–600 MHz for 450 MHz, with a step of 10 MHz.

From Figure 4, we firstly observe the good agreement between both analytical and FDTD Green’s functions for the flat surface, as for the homogenous half-space, the frequency–domain Green’s function amplitude in linearly increasing with frequency. The FDTD Green’s functions (for both trench-hill and flat surfaces) are well continuous between the three centre frequency simulations. The trench-hill surface curves follow well the flat surface curves below about 190 MHz, although the amplitude is slightly lower. It corresponds to the inversion results shown in Figure 2a, where ${\epsilon }_r$ is indeed underestimated. The slight phase shift observed between 80 and 100 MHz is due to the fact that the effective observed reflection occurs between the top and the bottom of the trench-hill surface. In Figure 4a, the shift is to the left because the effective value is larger than 1.78 m. In Figure 4b, the shift of the blue curve is to the right because the effective value is smaller than 2.00 m. The wavelength decreasing with increasing frequency, the shift becomes larger. When the frequency is higher than 190 MHz, the Green’s function for the trench-hill surface and the flat surface start to be rapidly quite different. The behaviour is also different when the antenna is above the trench or the hill. It is concluded that the trench-hill surface does not significantly affect the inversion when the frequency is lower than 190 MHz. This conclusion agrees with the soil roughness analysis conducted by Lambot et al. [44] and Rayleigh’s criterion, namely, the radar signal is not affected by the soil roughness if the protuberances are smaller than one eighth the wavelength. In our case, the protuberance is 0.22 m, corresponding to an acceptable highest frequency around 170 MHz. Obviously, considering even lower frequencies would be even more advantageous regarding trench-hill effects on the surface reflection, but in that case, the effect of the soil electrical conductivity would then become significant, making the inverse problem ill-posed [58].

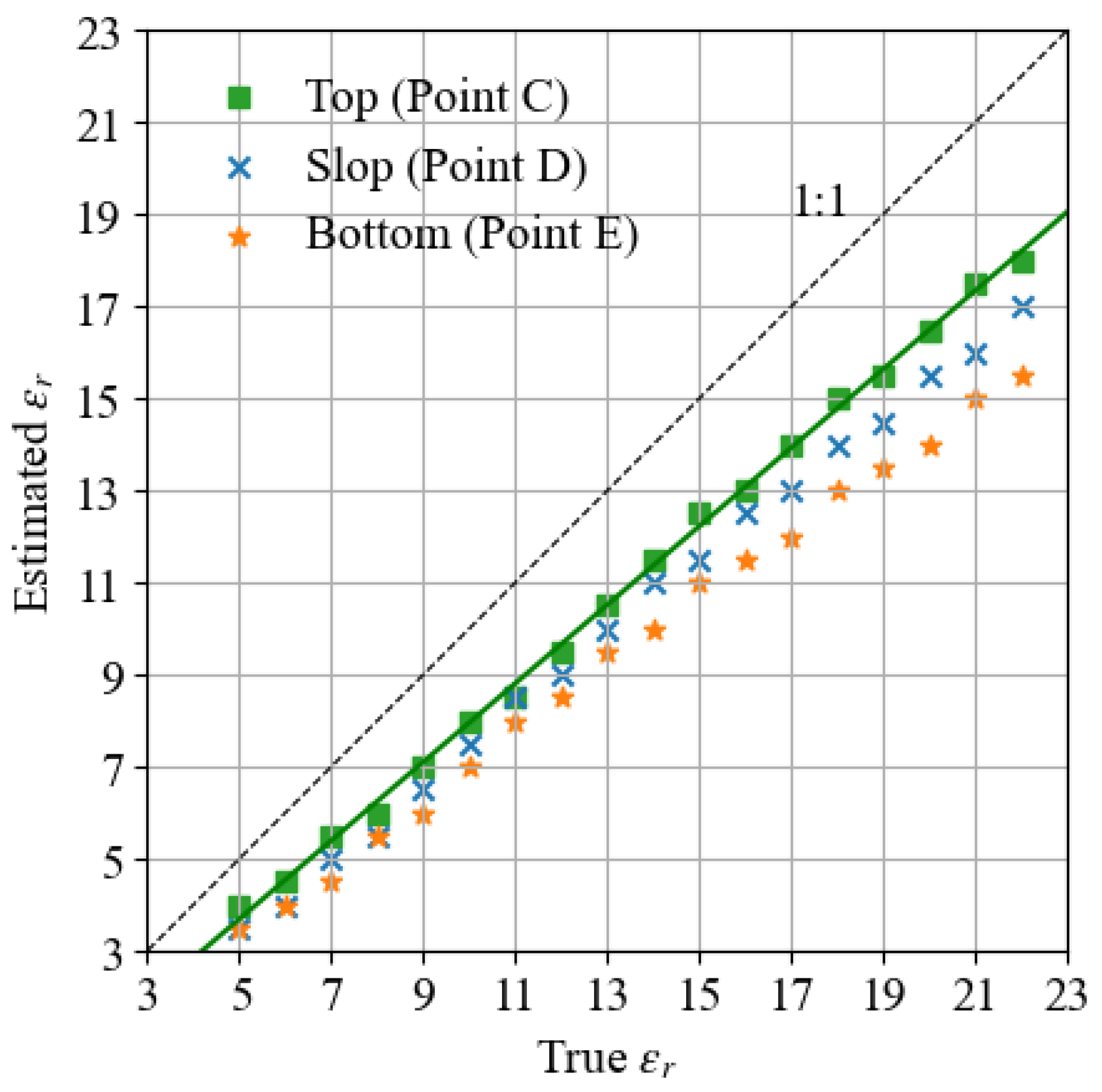
3.2. Configuration 2: 150 MHz Source over the Soil Surface with Different Positions and Soil Properties

Given the results above, we conducted numerical simulations with the virtual antenna located above the centre of the top, slope and bottom of the trench-hill structure, respectively, shown as point C, point D and point E in Figure 1b. The centre frequency was 150 MHz. ${\epsilon }_r$ ranged from 5 to 22 with a step of 1. The frequency range is 100–190 MHz for the inversion. The result is presented in Figure 5. The estimated relative permittivity values are lower than the true values, but linearly increase with the true values increasing. The measurements over the top of the hill contain less errors compared to the two other positions (the green square markers). Nevertheless, the linear structure of the error enables the use of a linear correction function to project the inversely estimated permittivity to the true ones. For the source/receiver above the hill configuration, we found the following relationship:

$${\epsilon }_{r,true}=0.85\times {\epsilon }_{r,estimated}-0.58.$$

(6)

4. Field Experiments

4.1. Ground-Penetrating Radar

The radar system consists of a lightweight vector network analyser (Planar R60, Copper Mountain Technologies, Indianapolis, IN, USA), an Intel computer stick, a power bank and a smartphone. An ultrawide band log-periodic antenna (model VULP 9118 C, Schwarzbeck Mess-Elektronik, Schönau, Germany) was used as a transmitter and receiver. The radar prototype was set up in the frame of the EU agROBOfood MIRAGE project. The measurements and full-wave inversions were performed in real-time using a prototype of the gprSense software (Sensar Consulting, Chaumont-Gistoux, Belgium). The radar measurements were performed in the 130–190 MHz frequency range. The higher frequency was chosen to minimize trench-hill effects and the lower cut off frequency was chosen to maximize SNR (see antenna calibration results below), minimize soil electrical conductivity effects and ensure a reasonable size for the field set up. In particular, the lower the frequency, the larger the distance between the radar and the support to avoid interferences.

Given the operating frequencies and the requirement of a calibrating surface larger than 5–10 times the largest wavelength, we calibrated the antenna over a river. Indeed, for a frequency of 100 MHz, the free-space wavelength is 3 m and, hence, the calibrating surface should be larger than 15–30 m. Using a perfect electrical conductor such as a copper plane of that size would require expensive infrastructures. For the calibration, an 8 m long rope was used to hang the antenna over the water surface from a high bridge to avoid unwanted reflections from the bridge structure (shown in Figure 6). In that respect, the high-directivity of the log-periodic antenna is particularly suitable (relatively small back lobes). Several measurements were performed with different distances between the antenna and the water surface. The antenna characteristic functions are presented in Figure 7. The functions were determined in the range 80–1000 MHz. The grey bar indicates the frequency range 130–190 MHz. Within this frequency range, the magnitude of return loss $R_i$ is lower than 0.168 (VSWR < 1.4), and feedback loss $R_s$ is accordingly also relatively low. The antenna can be qualified as excellent in that frequency range. The transmitting-receiving response T is relatively high, corresponding to a high antenna gain [59].

The radar prototype was set up on the prototype of a new irrigation robot (named Oscar), which is also developed in the frame of the EU MIRAGE project (Osiris Agriculture, Illies, France). Oscar is able to irrigate the field with a speed between 0.3 km/h and 1 km/h, spreading water 20 h per day and 15-m wide without any need from human action. In particular, it uses water energy to generate its own electricity to power all its equipment. The radar was mounted on Oscar through a plastic support, which was specifically designed for the application. The radar was fixed at about 3 m in front of the robot and was positioned above the central hill (see Figure 8). Oscar navigates through a differential GPS with a horizontal positioning error lower than 3 cm. In that way, it can handle automatically a localization error lower than 3 cm for every types of field, to handle automatically the water supply pipe and to module water doses on a per nozzle basis. The precise irrigation is expected to be achieved by real-time soil moisture measurement. The irrigation robot Oscar is designed to irrigate automatically when the soil moisture value is relatively low. The field measurements were conducted on 9 August 2022, over a potato field in the Vallée Jean Réaux Sains-Morainvillers, France.

4.2. Time–Domain Reflectometry

For comparison, we did TDR measurements using the TEROS 12 sensor (meter group, Pullman, WA, USA). It measures soil moisture, temperature and electrical conductivity with three stainless steel needles. The length of each needle is 5.5 cm. The distance between the two needles for soil moisture is only 3 cm. It measures the dielectric permittivity of the surrounding medium using an EM field. A 70-MHz oscillating wave is supplied to the sensor needles. The TEROS 12 microprocessor measures the charge time and outputs a raw value based on the substrate dielectric permittivity. Then, the raw value is transformed into relative dielectric permittivity ${\epsilon }_r$, which hereby is used to calculate volumetric water content through Topp’s equation as Equation (3).

The TDR measurement was conducted following two of the GPR acquisition lines (a short profile length: 25 m, shown as area B in Figure 9a, and a long profile length: 540 m, shown as area A in Figure 9a). The short soil profile was subject to irrigation the day before and, hence, was relatively wet. The second profile (area A) did not receive any irrigation. For the short profile, the TDR measurements were conducted around every 3 m along the profile, and we averaged two successive values. We averaged GPR measurements of every 6.5 m successive values to compare with the TDR. For the long profile, the TDR measurements were conducted every 10 m, and we averaged three successive values, and we averaged GPR measurements of every 30 m successive values to compare with the TDR. We used the root mean square error (RMSE) and mean absolute error (MAE) to quantitatively compare GPR and TDR results as follows:

$$\mathrm{RMSE}=\sqrt{\sum _{n=1}^N{\displaystyle \frac{{({\theta }_{n,\mathrm{TDR}}-{\theta }_{n,\mathrm{GPR}})}^2}{N-1}}}$$

(7)

and

$$\mathrm{MAE}={\displaystyle \frac{{\sum }_{n=1}^N|{\theta }_{n,\mathrm{TDR}}-{\theta }_{n,\mathrm{GPR}}|}{N}}$$

(8)

where N is the number of TDR measurements, and in this study $\mathit{N}=20$ for each measurement depth.

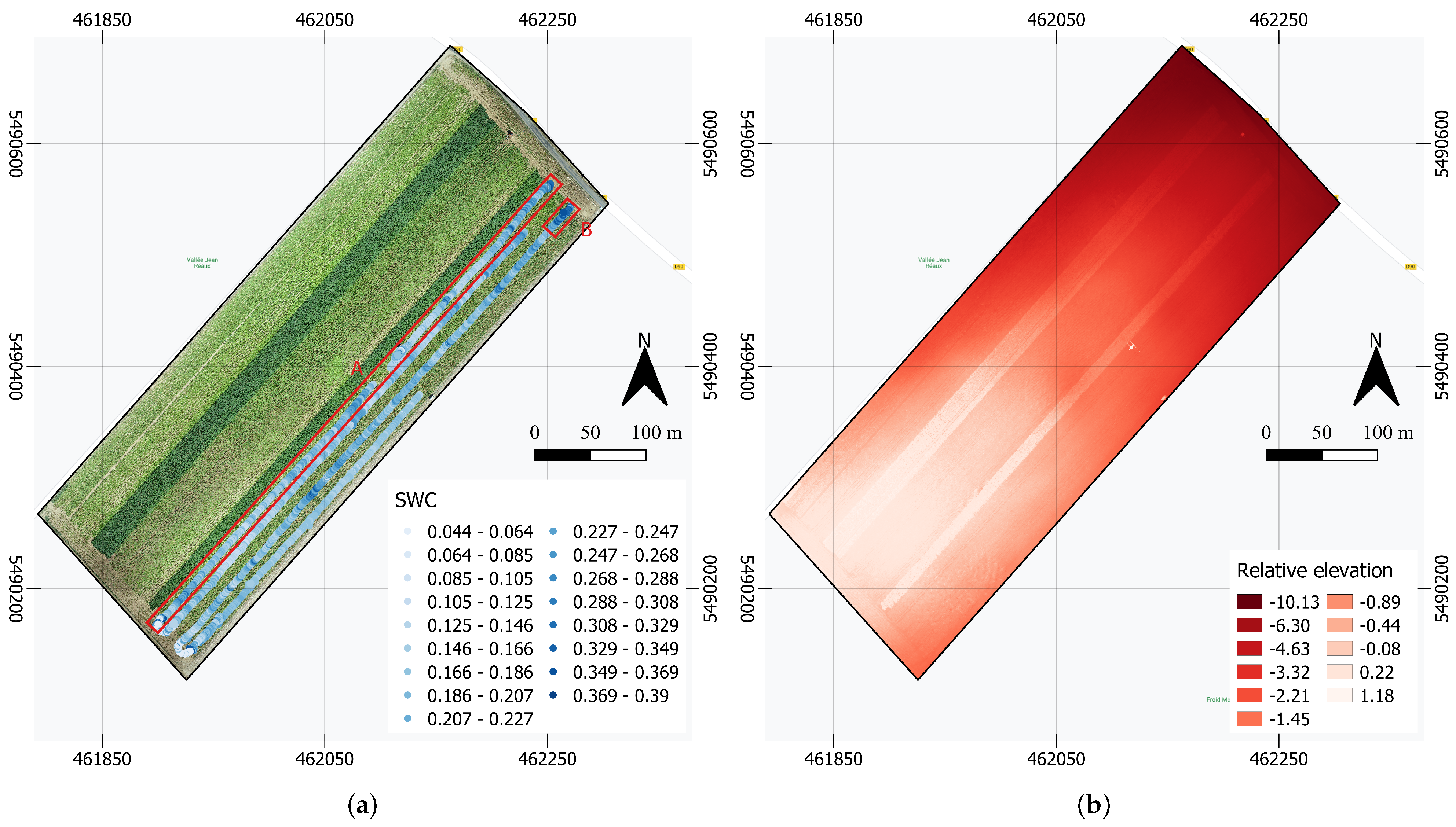
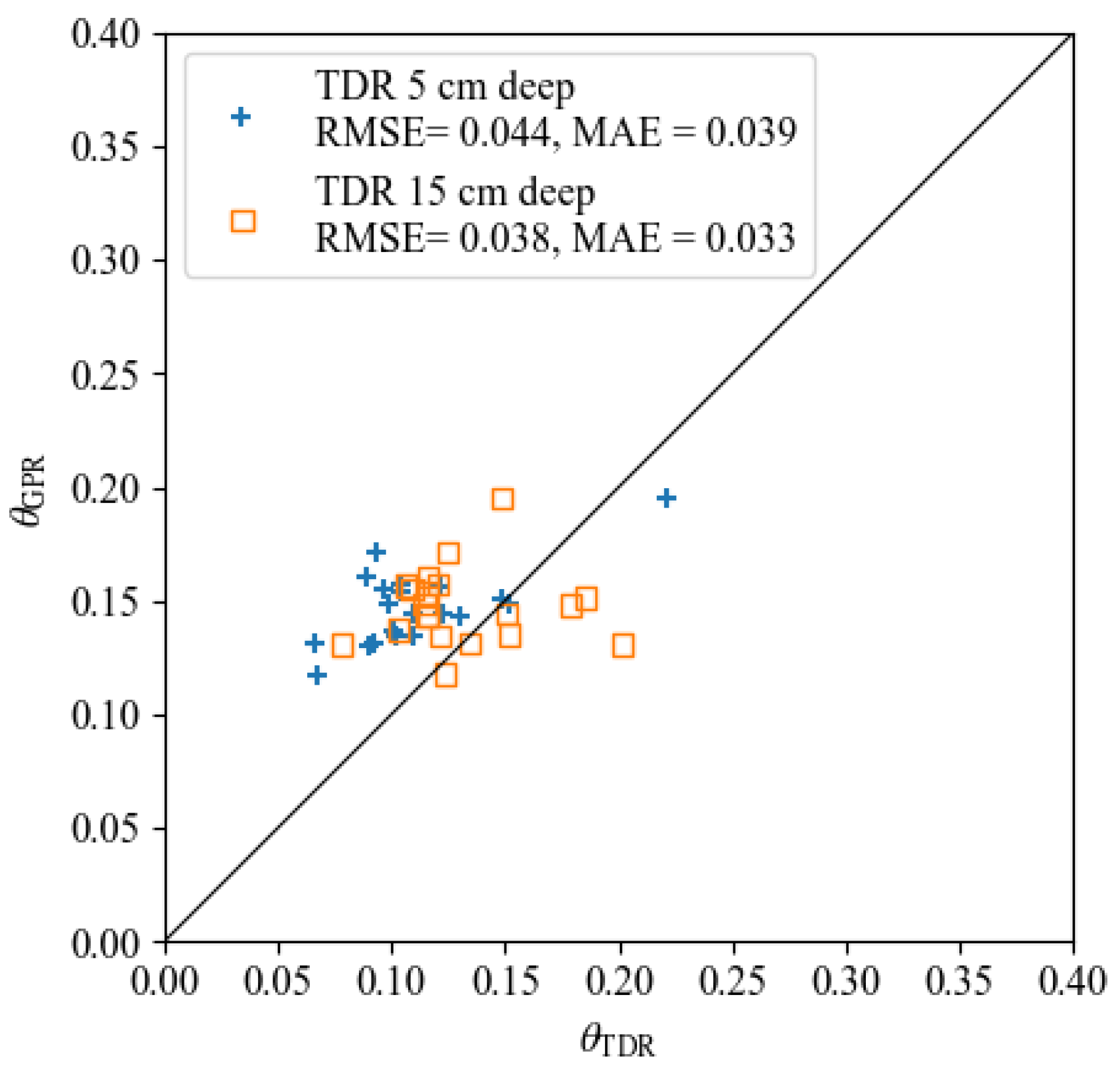
4.3. Results and Discussion

The GPR results are shown in Figure 9a, with the corresponding orthophoto as the background. The observed soil moisture values highlight the inherent soil variability and also show some spatial correlation. From the southwest to the northeast, the water content is getting higher, since the elevation is getting lower from the southwest to the northeast (see Figure 9b). The relative elevation map was obtained from aerial drone photographies using photogrammetry, whose processing was performed using the Agisoft Metashape software. The DJI Phantom 4Pro was used for the image acquisitions.

For comparison, we plot the GPR and TDR results in Figure 10. TDR measurement at 5 cm depth is generally lower than the GPR. GPR result is closer to TDR measurements at 15 cm depth with an RMSE of 0.038 and MAE of 0.033. The 5 cm depth is drier because it is near the surface (dry summer conditions), where the soil is also much less dense. Following the analyses of Lambot et al. [27] and Wu and Lambot [58], we estimate that the GPR characterization depth in the 130–190 MHz frequency range is about 40 cm, depending on the soil properties themselves. This explains the lower values observed for TDR at 5 and 15 cm depth. However, the GPR characterization depth is of interest as it does correspond to a major part of the root zone as well as to the zone of interest for managing irrigation. The observed differences between GPR and TDR are also to be attributed to the different characterization scales and the inherent variability of soil moisture, even at the dm scale.

5. Conclusions and Perspectives

In this study, we analysed GPR full-wave inversion for soil moisture measurement in trench-hill potato fields. To understand the trench-hill surface effects on the full-wave inversion, we conducted 2D and 3D FDTD simulations using gprMax. The 2D simulations were used for observing the EM wave propagation, and the 3D were used for full-wave inversion. Three different centre frequencies were considered, i.e., 150 MHz, 250 MHz and 450 MHz, respectively. To obtain the 3D FDTD Green’s function, the virtual antenna (the source/receiver) of each centre frequency was calibrated, using two other simulations with the source/receiver situated in the free space and over a PEC. We related the FDTD Green’s functions with the inversion results. We found that the radar signal is not significantly affected by the trench-hill structure in the 100–200 MHz frequency range. The FDTD Green’s function of the trench-hill surface stays almost the same as the flat surface when frequency is lower than 190 MHz. However, it still leads to a slight underestimation of the permittivity after inversion. This bias can be corrected for using a linear regression. The most accurate results are obtained when the source/receiver is above the hill. The higher frequency ranges are strongly affected by the trench-hill structure, and the results are quite different depending on the position of the source/receiver over the trench or the hill. This makes it difficult to account for in the electromagnetic model.

Field measurements were performed over a potato field. A log-periodic antenna was used and calibrated over a large water body, i.e., a river with a relatively smooth surface. The optimal 130–190 MHz frequency range was used for inversion, and the bias correction was applied on the inversion results. For comparison, several TDR measurements were also conducted. The soil volumetric water content was calculated using Topp’s equation [52] for ${\epsilon }_r$ obtained both from GPR and TDR, as expressed in Equation (3). The results are consistent from the soil map for both soil moisture values and the variation. The observed differences were attributed to the different characterization scales of both instrument and soil moisture variability (different soil volumes are characterized by both techniques). The GPR characterization depth in the 130–190 MHz frequency range is estimated to be around 0.40 m, corresponding to a key part of the root–zone. In addition, within the chosen frequency range, the roughness and crop effects can be ignored, so it makes the forward model simpler, and together with the LUT, it greatly reduces the processing time to achieve real-time determination and irrigation.

The results of this study suggest new lines of research regarding modelling of electromagnetic scattering by structured surfaces. It also opens promising perspectives to support precision irrigation in a real application context.