A New Spatiotemporal Estimator to Downscale GRACE Gravity Models for Terrestrial and Groundwater Storage Variations Estimation
Abstract
1. Introduction
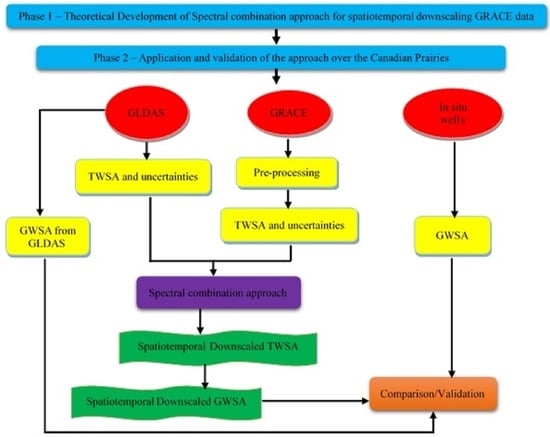
2. Materials and Methods
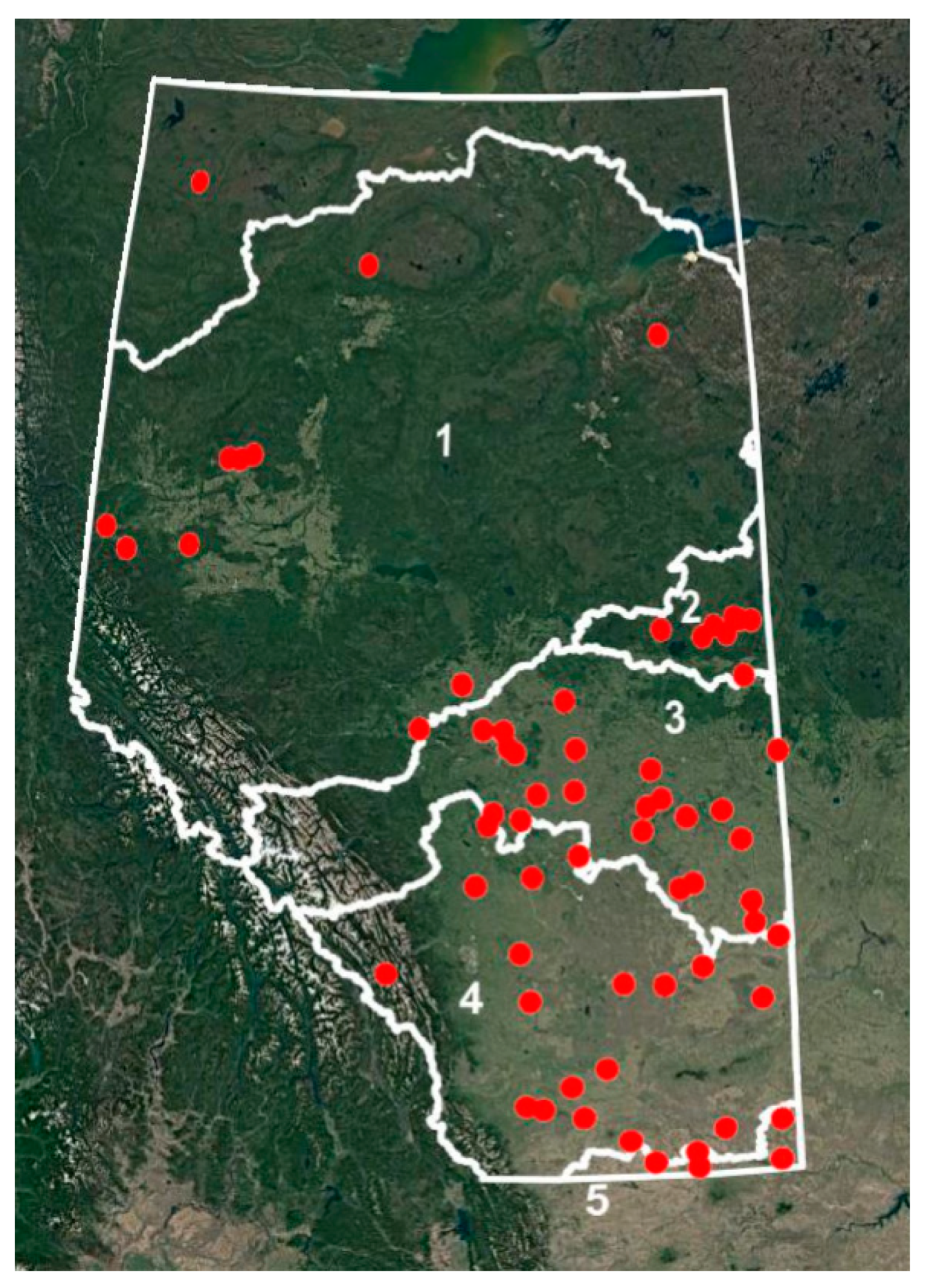
2.1. Materials
2.2. Methodology
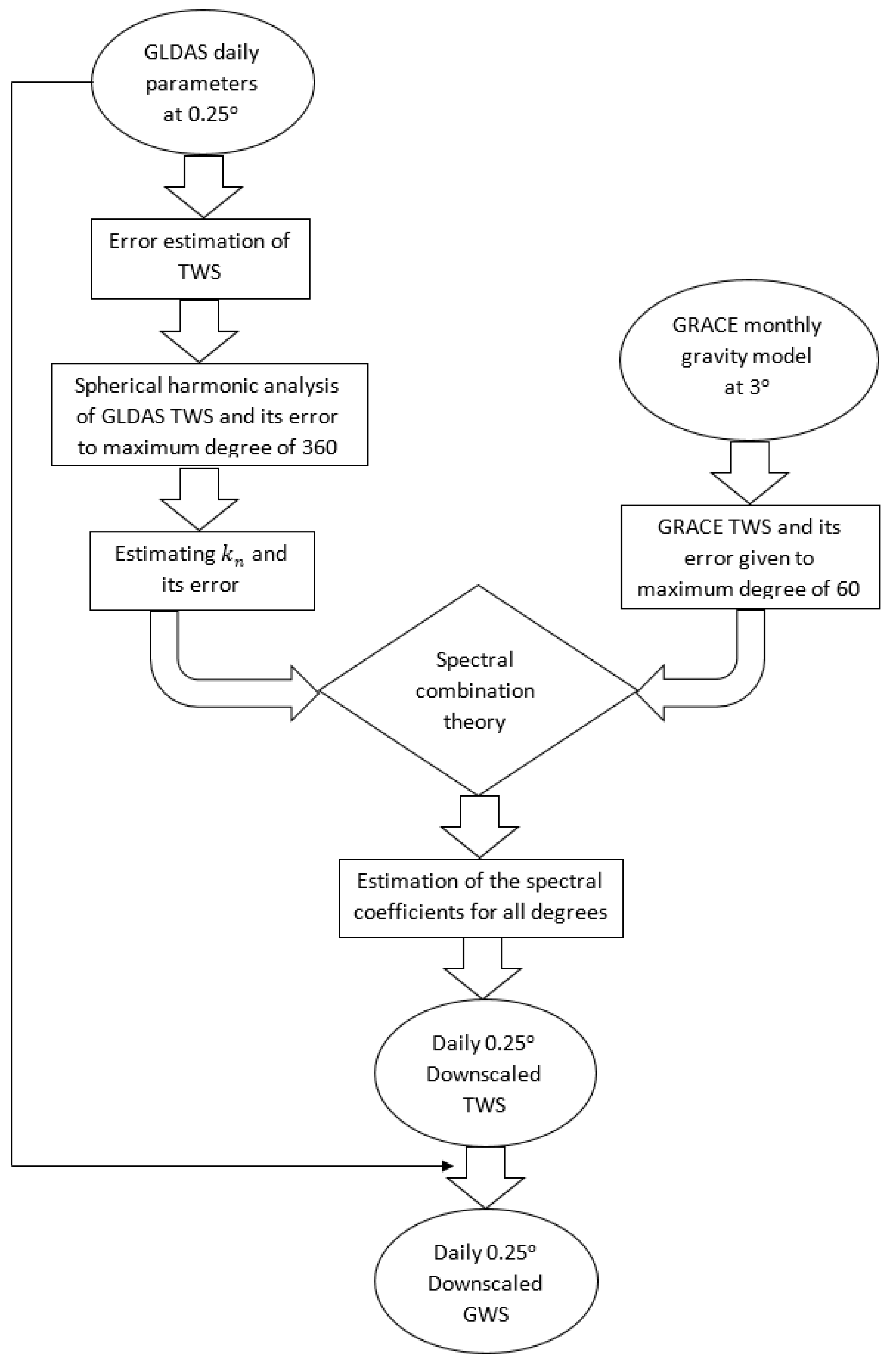
2.2.1. Spectral Combination Theory for Spatiotemporal Downscaling
2.2.2. Validation of the Approach
3. Results
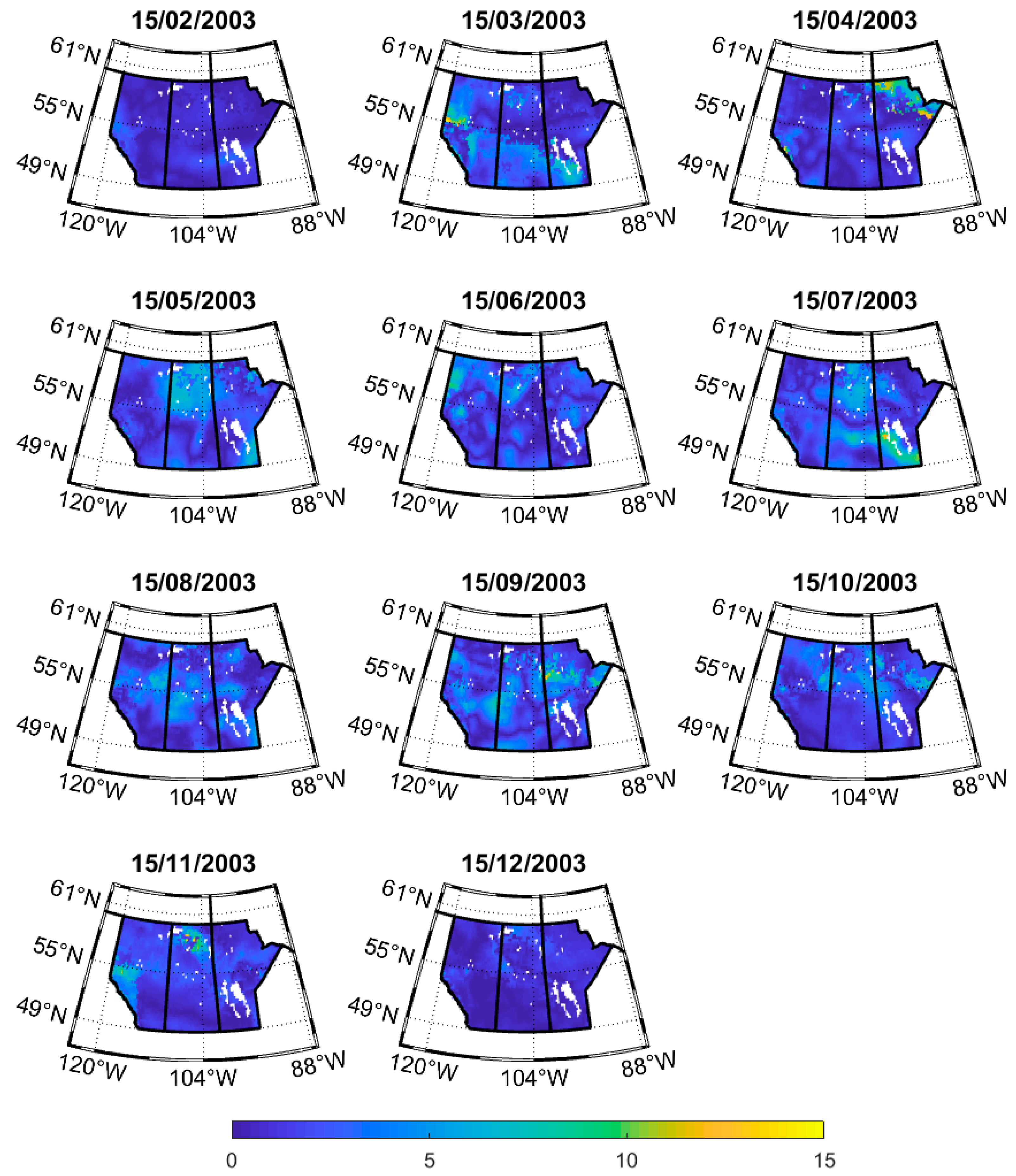
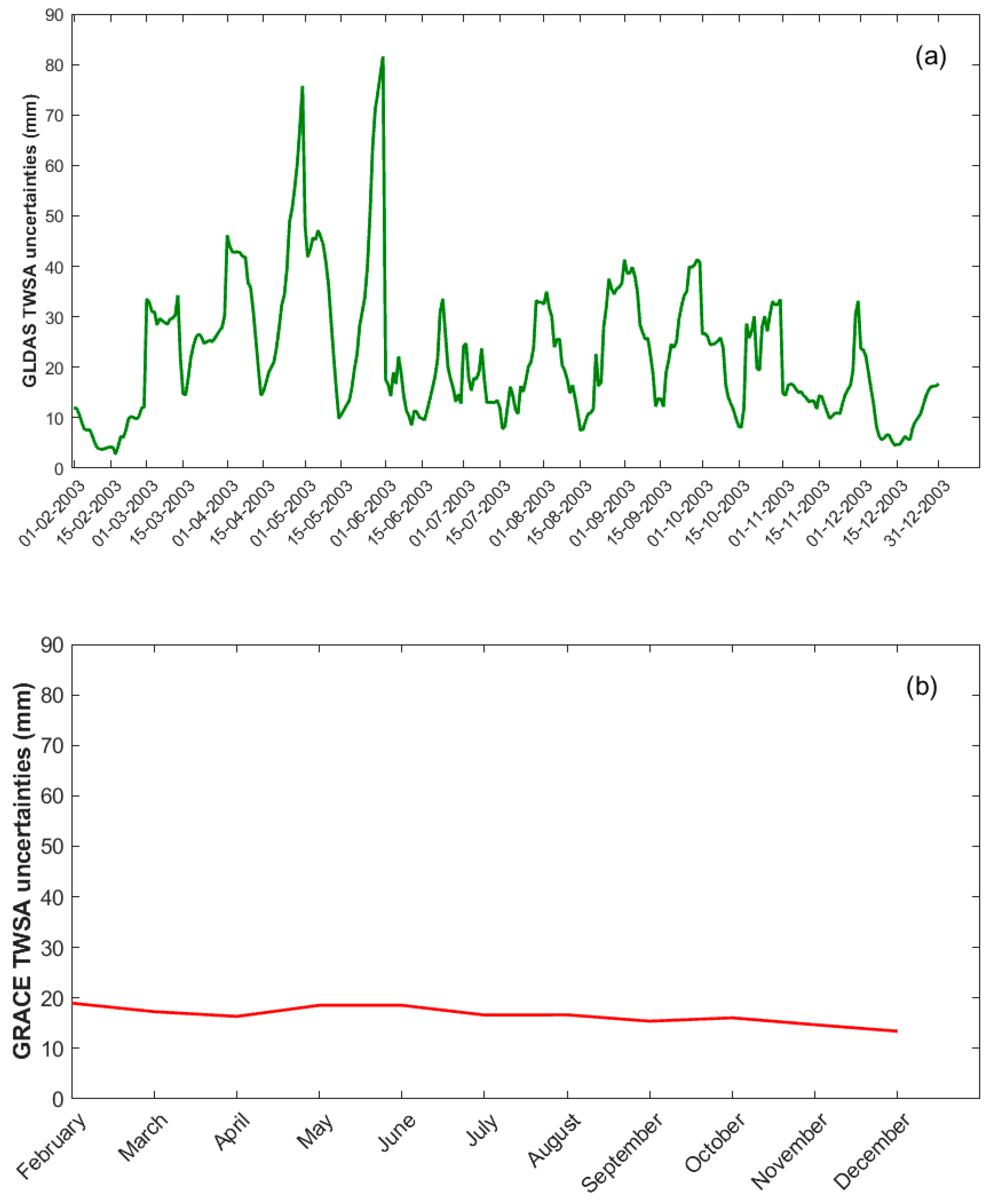
3.1. Uncertainty Results of GLDAS and GRACE TWS Anomalies
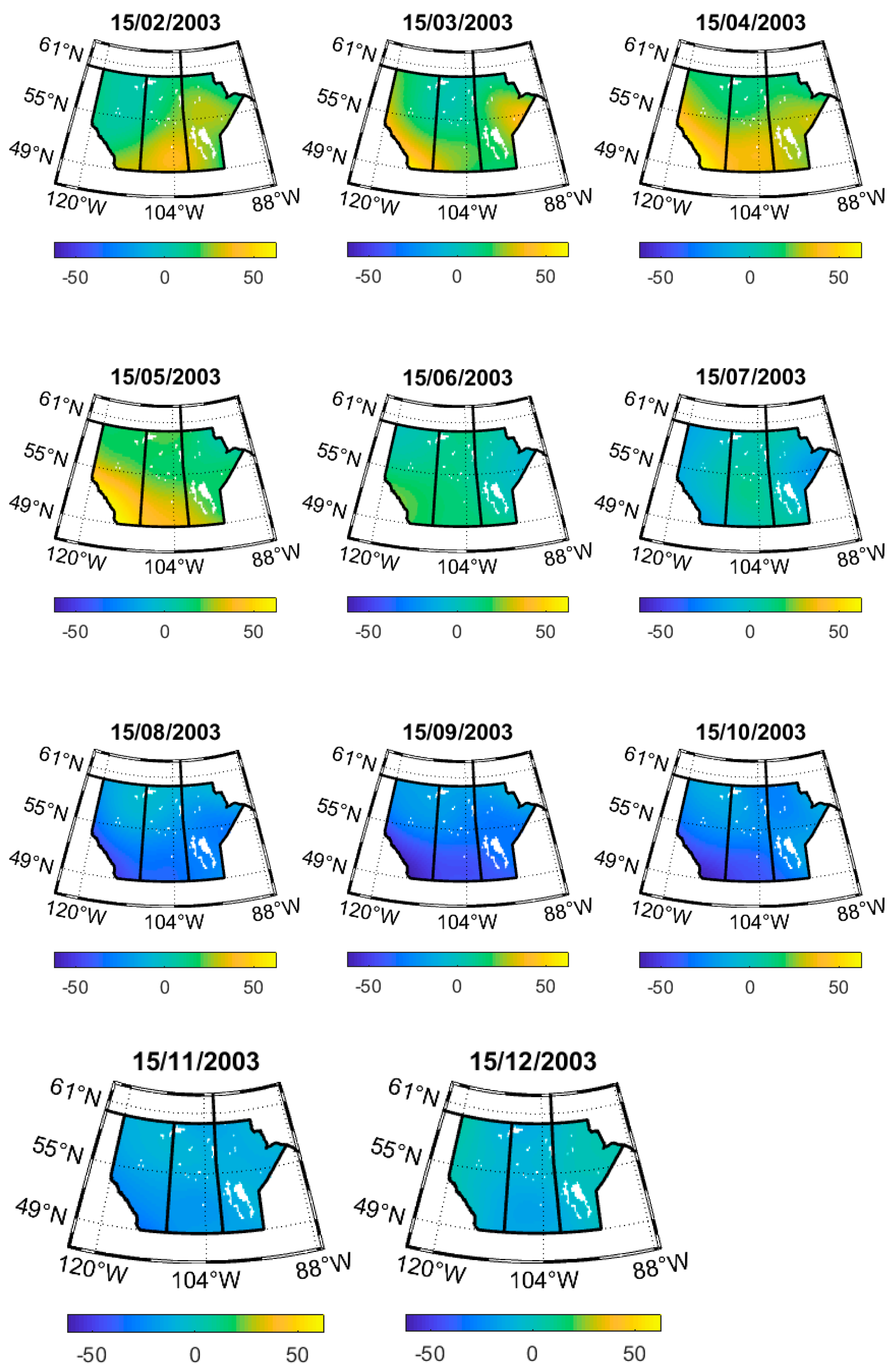
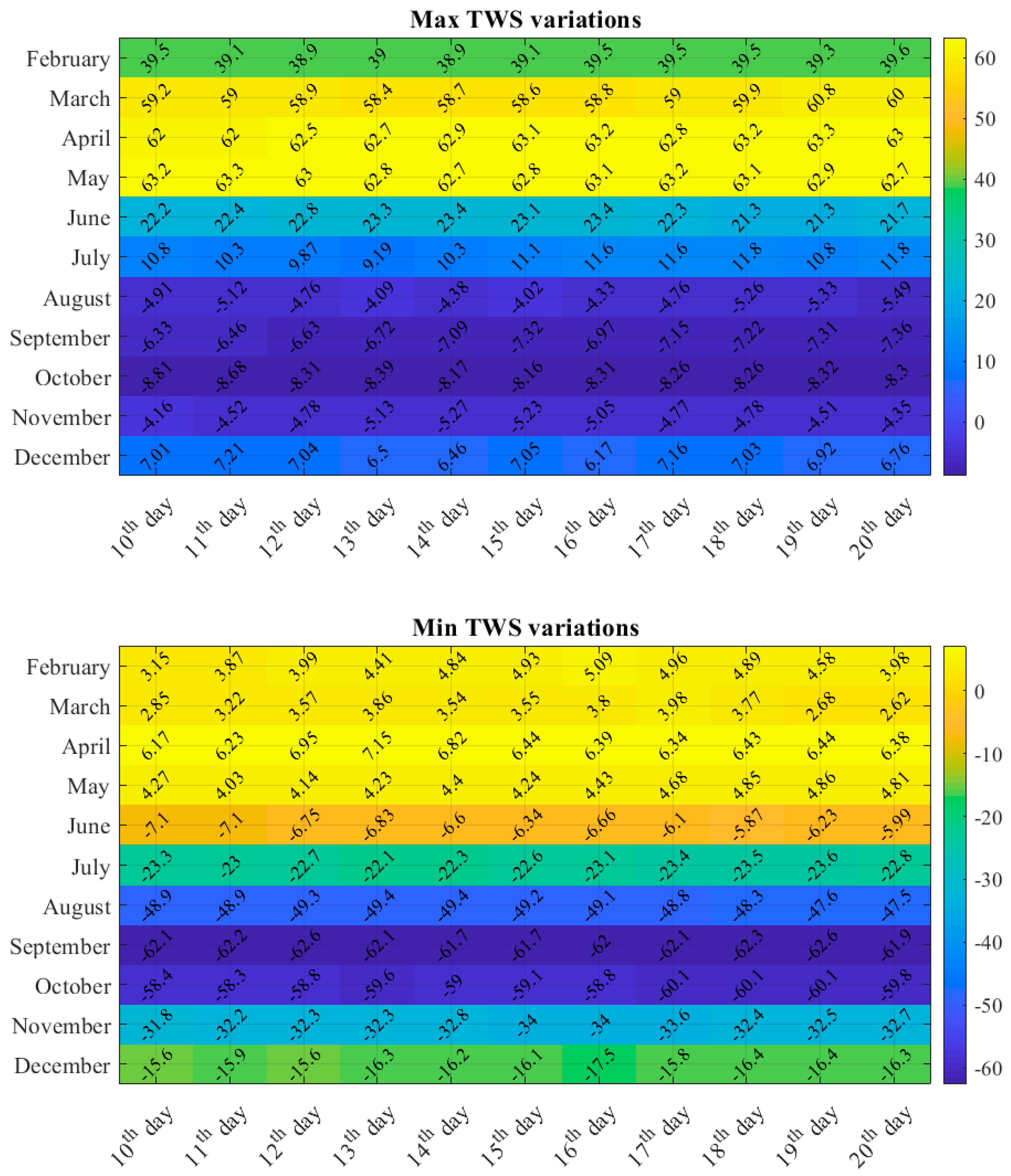
3.2. Daily Downscaled GRACE TWSA at 0.25°
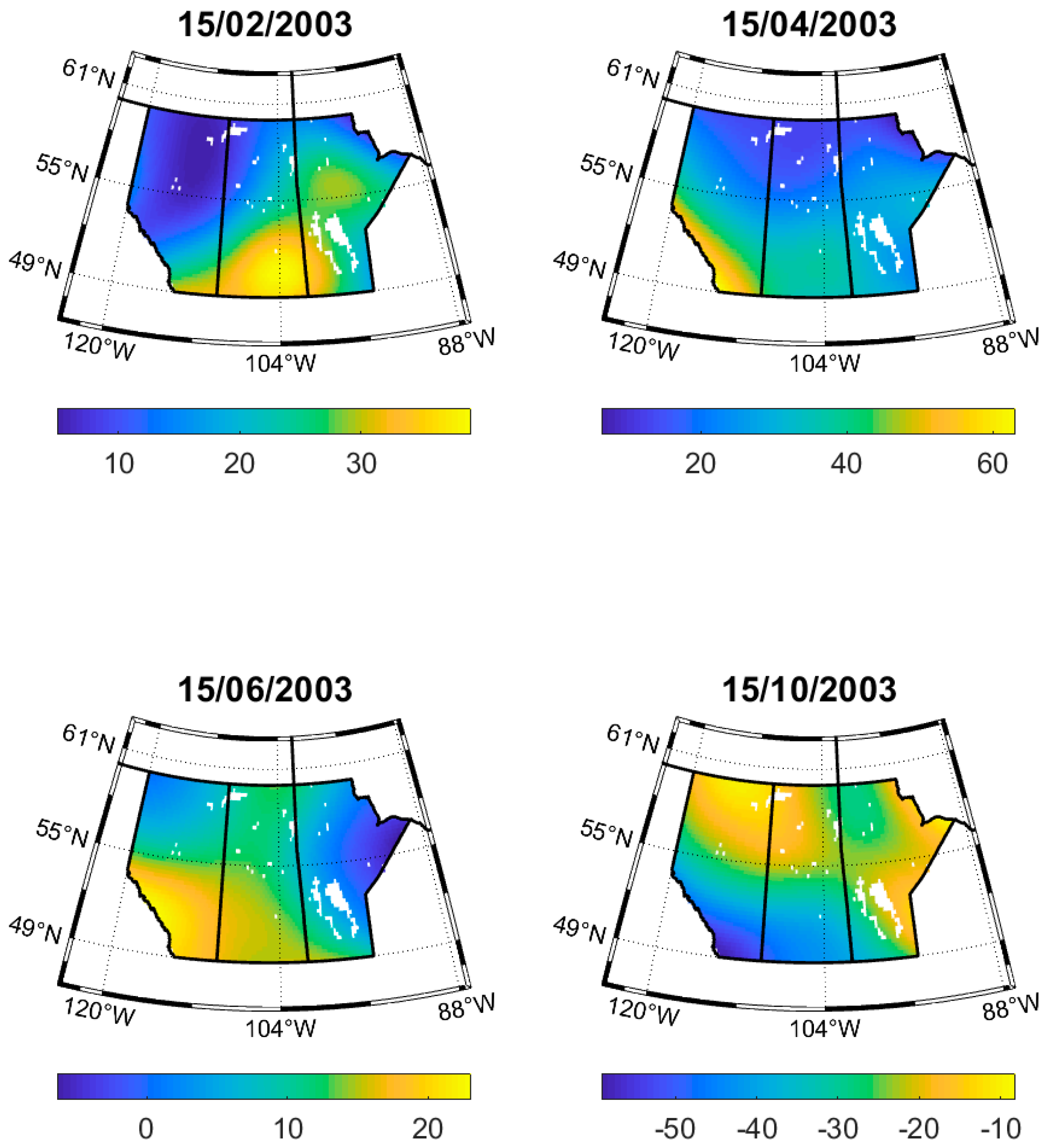
3.3. Daily Downscaled GRACE GWSA at 0.25°
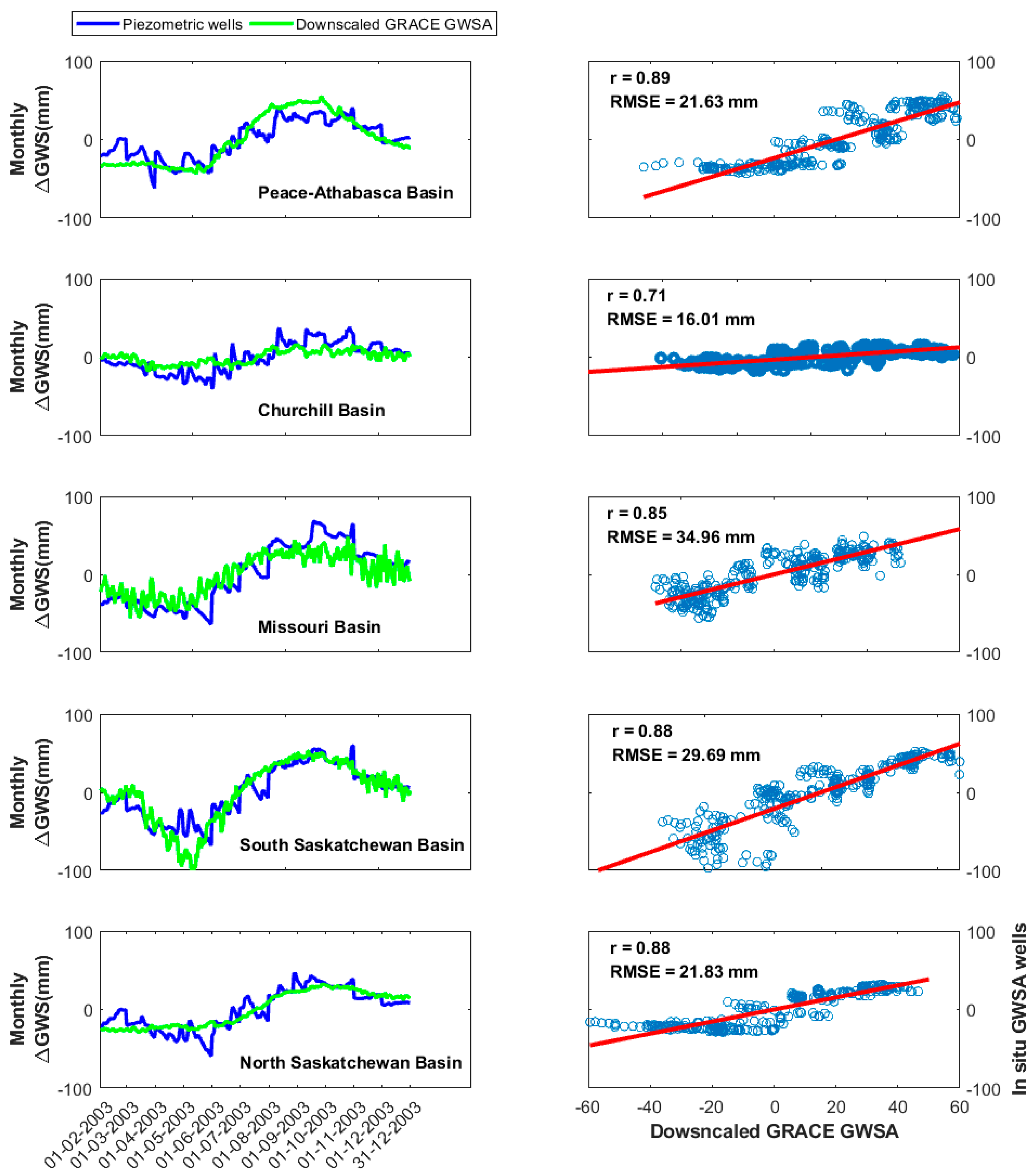
3.4. Validation of the Results with In Situ Wells
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Halloran, L.J.S. Improving groundwater storage change estimates using time-lapse gravimetry with Gravi4GW. Environ. Model. Softw. 2022, 150, 105340. [Google Scholar] [CrossRef]
- Liard, J.; Huang, J.; Silliker, J.; Jobin, D.; Wang, S.; Doherty, A. Detecting groundwater storage change using micro-gravity survey in Waterloo Moraine. In Proceedings of the Geohydro 2011, Quebec City, QC, Canada, 28–31 August 2011. [Google Scholar]
- Castellazzi, P.; Longuevergne, L.; Martel, R.; Rivera, A.; Brouard, C.; Chaussard, E. Quantitative mapping of groundwater depletion at the water management scale using a combined GRACE/InSAR approach. Remote Sens. Environ. 2018, 205, 408–418. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Michel, C.; Russell, H.A. Surface deformation observed by InSAR shows connections with water storage change in Southern Ontario. J. Hydrol. Reg. Stud. 2020, 2020, 27. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Güntner, A. Improvement of Global Hydrological Models Using GRACE Data. Surv. Geophys. 2008, 29, 375–397. [Google Scholar] [CrossRef]
- Wang, S.; Huang, J.; Li, J.; Rivera, A.; McKenney, D.W.; Sheffield, J. Assessment of water budget for sixteen large drainage basins in Canada. J. Hydrol. 2014, 512, 1–15. [Google Scholar] [CrossRef]
- Wang, S.; Li, J. Terrestrial water storage climatology for Canada from GRACE satellite observations in 2002–2014. Can. J. Remote Sens. 2016, 42, 190–202. [Google Scholar] [CrossRef]
- Chen, J.; Cazenave, A.; Dahle, C.; Llovel, W.; Panet, I.; Pfeffer, J.; Moreira, L. Applications and Challenges of GRACE and GRACE Follow-On Satellite Gravimetry. Surv. Geophys. 2022, 43, 305–345. [Google Scholar] [CrossRef]
- Seyoum, W.; Kwon, D.; Milewski, A. Downscaling GRACE TWSA data into high-resolution groundwater level anomaly using machine learning-based models in a glacial aquifer system. Remote Sens. 2019, 11, 824. [Google Scholar] [CrossRef]
- Milewski, A.M.; Thomas, M.B.; Seyoum, W.M.; Rasmussen, T.C. Spatial downscaling of GRACE TWSA data to identify spatiotemporal groundwater level trends in the Upper Floridan Aquifer, Georgia, USA. Remote Sens. 2019, 11, 2756. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.M.; Pham, Q.B.; Rahaman, M.d.M.; Dang, T.D.; Anh, D.T. Improving the resolution of GRACE data for spatio-temporal groundwater storage assessment. Remote Sens. 2021, 13, 3513. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, W.; Yin, W.; Li, X.; Zhang, G.; Zhang, J. Improving the spatial resolution of GRACE-derived terrestrial water storage changes in small areas using the Machine Learning Spatial Downscaling Method. Remote Sens. 2021, 13, 4760. [Google Scholar] [CrossRef]
- He, H.; Yang, K.; Wang, S.; Petrosians, H.A.; Liu, M.; Li, J.; Marcato, J.J.; Goncalves, W.N.; Wang, L.; Li, J. Deep learning approaches to spatial downscaling of GRACE Terrestrial Water Storage Products using EALCO Model over Canada. Can. J. Remote Sens. 2021, 47, 657–675. [Google Scholar] [CrossRef]
- Chen, L.; He, Q.; Liu, K.; Li, J.; Jing, C. Downscaling of GRACE-derived groundwater storage based on the Random Forest model. Remote Sens. 2019, 11, 2979. [Google Scholar] [CrossRef]
- Zuo, J.; Xu, J.; Chen, Y.; Li, W. Downscaling simulation of groundwater storage in the Tarim River Basin in Northwest China based on GRACE data. Phys. Chem. Earth 2021, 123, 103042. [Google Scholar] [CrossRef]
- Lavado, C.J.; Maneta, M.; Schnabel, S. Prediction of near-surface soil moisture at large scale by digital terrain modeling and neural networks. Environ. Monit. Assess. 2006, 121, 213–232. [Google Scholar] [CrossRef]
- Seyoum, W.M.; Milewski, A.M. Improved methods for estimating local terrestrial water dynamics from GRACE in the Northern High Plains. Adv. Water Resour. 2017, 110, 279–290. [Google Scholar] [CrossRef]
- Miro, M.; Famiglietti, J. Downscaling GRACE remote sensing datasets to high-resolution groundwater storage change maps of California’s Central Valley. Remote Sens. 2018, 10, 143. [Google Scholar] [CrossRef]
- Shang, Q.; Liu, X.; Deng, X.; Zhang, B. Downscaling of GRACE datasets based on relevance vector machine using InSAR time series to generate maps of groundwater storage changes at local scale. J. Appl. Remote Sens. 2019, 13, 048503. [Google Scholar] [CrossRef]
- Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.A.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T.M. Statistical applications to downscale GRACE-derived terrestrial water storage data and to fill temporal gaps. Remote Sens. 2020, 12, 533. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, S.; Li, J. Spatiotemporal downscaling of GRACE Total Water Storage using Land Surface Model outputs. Remote Sens. 2021, 13, 900. [Google Scholar] [CrossRef]
- Wilby, R.L.; Charles, S.P.; Zorita, E.; Timbal, B.; Whetton, P.; Mearns, L.O. Guidelines for Use of Climate Scenarios Developed from Statistical Downscaling Methods. Task Group of Data and Scenario Support for Impacts and Climate Analysis (TGICA). Intergovernmental Panel on Climate Change. 2004. Available online: http://www.ipcc-data.org/guidelines/dgm_no1_v1_10-2003.pdf (accessed on 20 August 2017).
- Fatolazadeh, F.; Eshagh, M.; Goïta, K. New spectro-spatial downscaling of terrestrial and groundwater storage variations estimated by GRACE models. J. Hydrol. 2022, 615, 128635. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Least squares combination of satellite harmonics and integral formulas in physical geodesy. Gerlands Beitr Geophys. 1980, 89, 371–377. [Google Scholar]
- Sjöberg, L.E. Least squares combination of satellite and terrestrial data in physical geodesy. Ann. Geophys. 1981, 37, 25–30. [Google Scholar]
- Wenzel, H.G. Geoid computation by least squares spectral combination using integral kernels. In Proceedings of the International Association of Geodesy (IAG), Tokyo, Japan, 7–20 May 1982; pp. 438–453. [Google Scholar]
- Eshagh, M. Spectral combination of spherical gradiometric boundary-value problems: A theoretical study. Pure Appl. Geophys. 2012, 169, 2201–2215. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 2011, 116, B01409. [Google Scholar] [CrossRef]
- Fatolazadeh, F.; Goïta, K. Reconstructing groundwater storage variations from GRACE observations using a new Gaussian-Han-Fan (GHF) smoothing approach. J. Hydrol. 2022, 604, 127234. [Google Scholar] [CrossRef]
- Kromm, D.E. Water conservation in the irrigated prairies of Canada and the United States. Can. Water Resour. J. 1993, 18, 451–458. [Google Scholar] [CrossRef]
- Gan, T.Y. Reducing vulnerability of water resources of Canadian Prairies to potential droughts and possible climatic warming. Water Resour. Manag. 2000, 14, 111–135. [Google Scholar] [CrossRef]
- Larocque, M.; Broda, S. Groundwater-surface water interactions in Canada. Can. Water Resour. J. 2016, 41, 451–454. [Google Scholar] [CrossRef]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Save, H. GRACE satellite monitoring of large depletion in water storage in response to the 2011 drought in Texas. Geophys. Res. Lett. 2013, 40, 3395–3401. [Google Scholar] [CrossRef]
- Singh, A.K.; Jasrotia, A.S.; Taloor, A.K.; Kotlia, B.S.; Kumar, V.; Roy, S.; Ray, P.K.C.; Singh, K.K.; Singh, A.K.A.; Sharma, A.K. Estimation of quantitative measures of total water storage variation from GRACE and GLDAS-NOAH satellites using geospatial technology. Quat. Int. 2017, 444, 191–200. [Google Scholar] [CrossRef]
- Bhanja, S.N.; Zhang, X.; Wang, J. Estimating long-term groundwater storage and its controlling factors in Alberta, Canada. Hydrol. Earth Syst. Sci. 2018, 22, 6241–6255. [Google Scholar] [CrossRef]
- Feng, W.; Shum, C.; Zhong, M.; Pan, Y. Groundwater storage changes in China from satellite gravity: An overview. Remote Sens. 2018, 10, 674. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, W.; Nie, N.; Guo, Y. Long-term groundwater storage variations estimated in the Songhua River Basin by using GRACE products, Land Surface Models, and in-situ observations. Sci. Total Environ. 2019, 649, 372–387. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Güntner, A.; Tomasella, J.; Pfeffer, J.; Ramillien, G.; Emilio, T.; Schietti, J.; Seoane, L.; da Silva Carvalho, J.; et al. The spatio-temporal variability of groundwater storage in the Amazon River Basin. Adv. Water Resour. 2019, 124, 41–52. [Google Scholar] [CrossRef]
- Rateb, A.; Scanlon, B.R.; Pool, D.R.; Sun, A.; Zhang, Z.; Chen, J.; Clark, B.; Faunt, C.C.; Haugh, C.J.; Hill, M.; et al. Comparison of groundwater storage changes from GRACE satellites with monitoring and modeling of major U.S. aquifers. Water Resour. Res. 2020, 56, e27556. [Google Scholar] [CrossRef]
- Wang, S.; Liu, H.; Yu, Y.; Zhao, W.; Yang, Q.; Liu, J. Evaluation of groundwater sustainability in the arid Hexi Corridor of Northwestern China, using GRACE, GLDAS and measured groundwater data products. Sci. Total Environ. 2020, 705, 135829. [Google Scholar] [CrossRef]
- Field, A.P. Kendall’s Coefficient of Concordance. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Lu, Y.; Hsu, H.T.; Jiang, F.Z. The regional geopotential model to degree and order 720 in China. In Geodesy Beyond 2000; Schwarz, K.P., Ed.; International Association of Geodesy Symposia, 121; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Gruber, A.; De Lannoy, G.; Albergel, C.; Al-Yaari, A.; Brocca, L.; Calvet, J.-C.; Colliander, A.; Cosh, M.; Crow, W.; Dorigo, W.; et al. Validation practices for satellite soil moisture retrievals: What are (the) errors? Remote Sens. Environ. 2020, 244, 111806. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Yang, H.; Zhu, X.; Tian, Y.; Jiang, X.; Huang, X.; Feng, L. Large uncertainties in runoff estimations of GLDAS versions 2.0 and 2.1 in China. Earth Space Sci. 2020, 7, e2019EA000829. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Y.; Luo, Y.; Rivera, A. Spatial and seasonal variations in evapotranspiration over Canada’s landmass. Hydrol. Earth Syst. Sci. 2013, 17, 3561–3575. [Google Scholar] [CrossRef]
- Fatolazadeh, F.; Goïta, K. Mapping terrestrial water storage changes in Canada using GRACE and GRACE-FO. Sci. Total Environ. 2021, 779, 146435. [Google Scholar] [CrossRef] [PubMed]
- Vincent, L.A.; Zhang, X.; Mekis, É.; Wan, H.; Bush, E.J. Changes in Canada’s climate: Trends in indices based on daily temperature and precipitation data. Atmos.-Ocean 2018, 56, 332–349. [Google Scholar] [CrossRef]
- Bahrami, A.; Goïta, K.; Magagi, R. Analysing the contribution of snow water equivalent to the terrestrial water storage over Canada. Hydrol. Process. 2020, 34, 175–188. [Google Scholar] [CrossRef]
- Li, Z.; Wang, S. Water yield variability and response to climate change across Canada. Hydrol. Sci. J. 2021, 66, 1169–1184. [Google Scholar] [CrossRef]
- Whitfield, P.H.; Cannon, A.J. Recent Variations in Climate and Hydrology in Canada. Can. Water Resour. J. 2000, 25, 19–65. [Google Scholar] [CrossRef]
- Ireson, A.; Barr, A.; Johnstone, J.; Mamet, S.; van der Kamp, G.; Whitfield, C.; Michel, N.L.; North, R.L.; Westbrook, C.J.; DeBeer, C. The changing water cycle: The Boreal Plains ecozone of Western Canada. Wiley Interdiscip. Rev. Water 2015, 2, 505–521. [Google Scholar] [CrossRef]
- Jiang, Z.S.; Hsu, Y.J.; Yuan, L.G.; Huang, D.F. Monitoring time-varying terrestrial water storage changes using daily GNSS measurements in Yunnan, southwest China. Remote Sens. Environ. 2021, 254, 112249. [Google Scholar] [CrossRef]
- Liu, B.; Yu, W.; Dai, W.; Xing, X.; Kuang, C. Estimation of Terrestrial Water Storage Variations in Sichuan-Yunnan Region from GPS Observations Using Independent Component Analysis. Remote Sens. 2022, 14, 282. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Kalicz, P.; Kucsara, M. Streamflow characteristics of two forested catchments in Sopron Hills. Acta Silv. Lignaria Hung. 2006, 2, 81–92. [Google Scholar]
- Gribovszki, Z.; Kalicz, P.; Szilágyi, J.; Kucsara, M. Riparian zone evapotranspiration estimation from diurnal groundwater level fluctuations. J. Hydrol. 2008, 349, 6–17. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Szilágyi, J.; Kalicz, P. Diurnal fluctuations in shallow groundwater levels and streamflow rates and their interpretation—A review. J. Hydrol. 2010, 385, 371–383. [Google Scholar] [CrossRef]
- Wu, L.; Gomez-Velez, J.D.; Krause, S.; Wörman, A.; Singh, T.; Nützmann, G.; Lewandowski, J. How daily groundwater table drawdown affects the diel rhythm of hyporheic exchange. Hydrol. Earth Syst. Sci. 2021, 25, 1905–1921. [Google Scholar] [CrossRef]
- Nagy, V.I. Hidrológia (Hydrology); Tankönyvkiadó: Budapest, Hungary, 1965. [Google Scholar]
- Juhász, J. Hidrogeológia (Hydrogeology); Akadémiai kiadó: Budapest, Hungary, 2002. (In Hungarian) [Google Scholar]
- Bi, H.; Ma, J. Evaluation of simulated soil moisture in GLDAS using in-situ measurements over the Tibetan Plateau. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4825–4828. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, X.; Chen, X. Evaluation of GLDAS-1 and GLDAS-2 forcing data and Noah model simulations over China at the monthly scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]

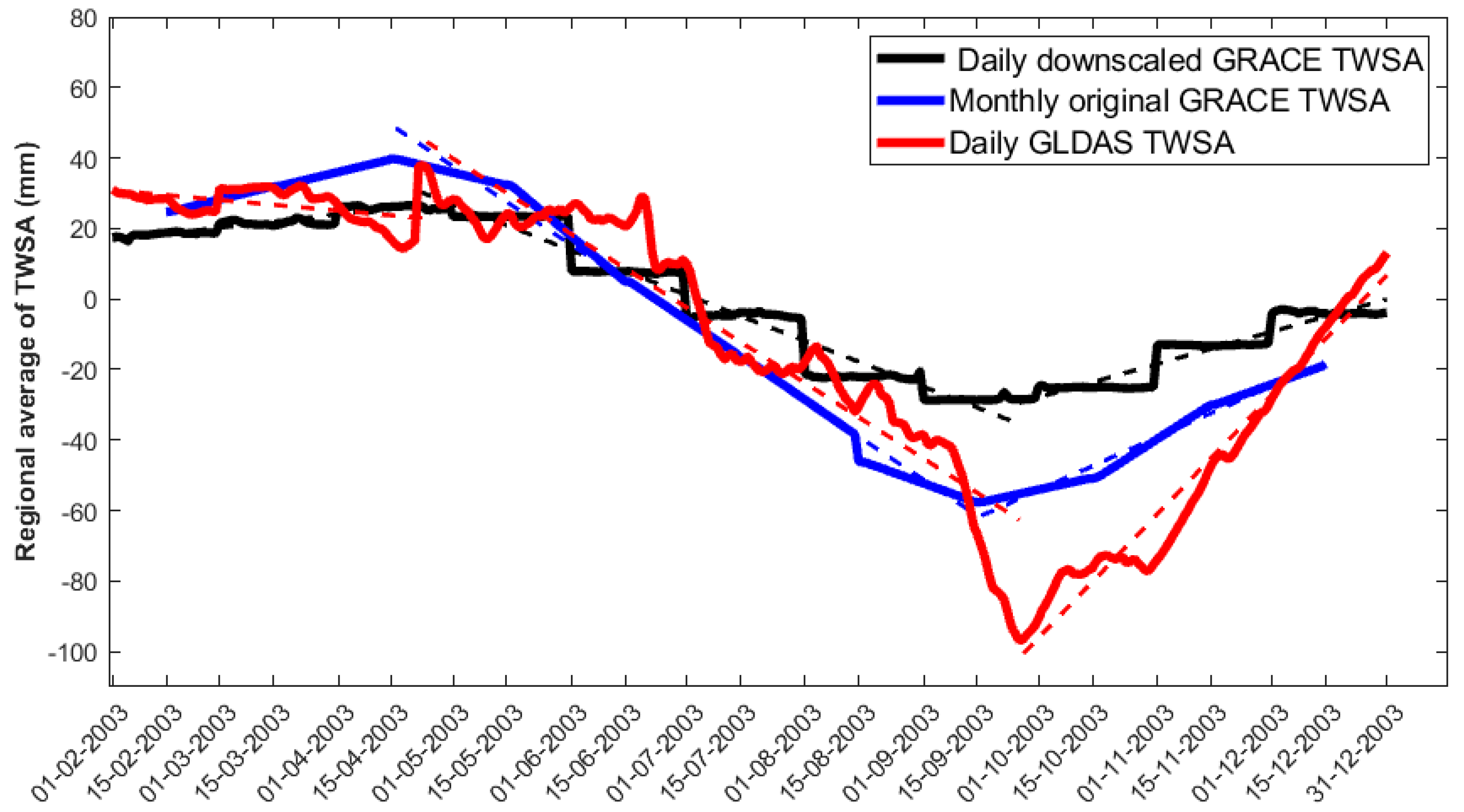

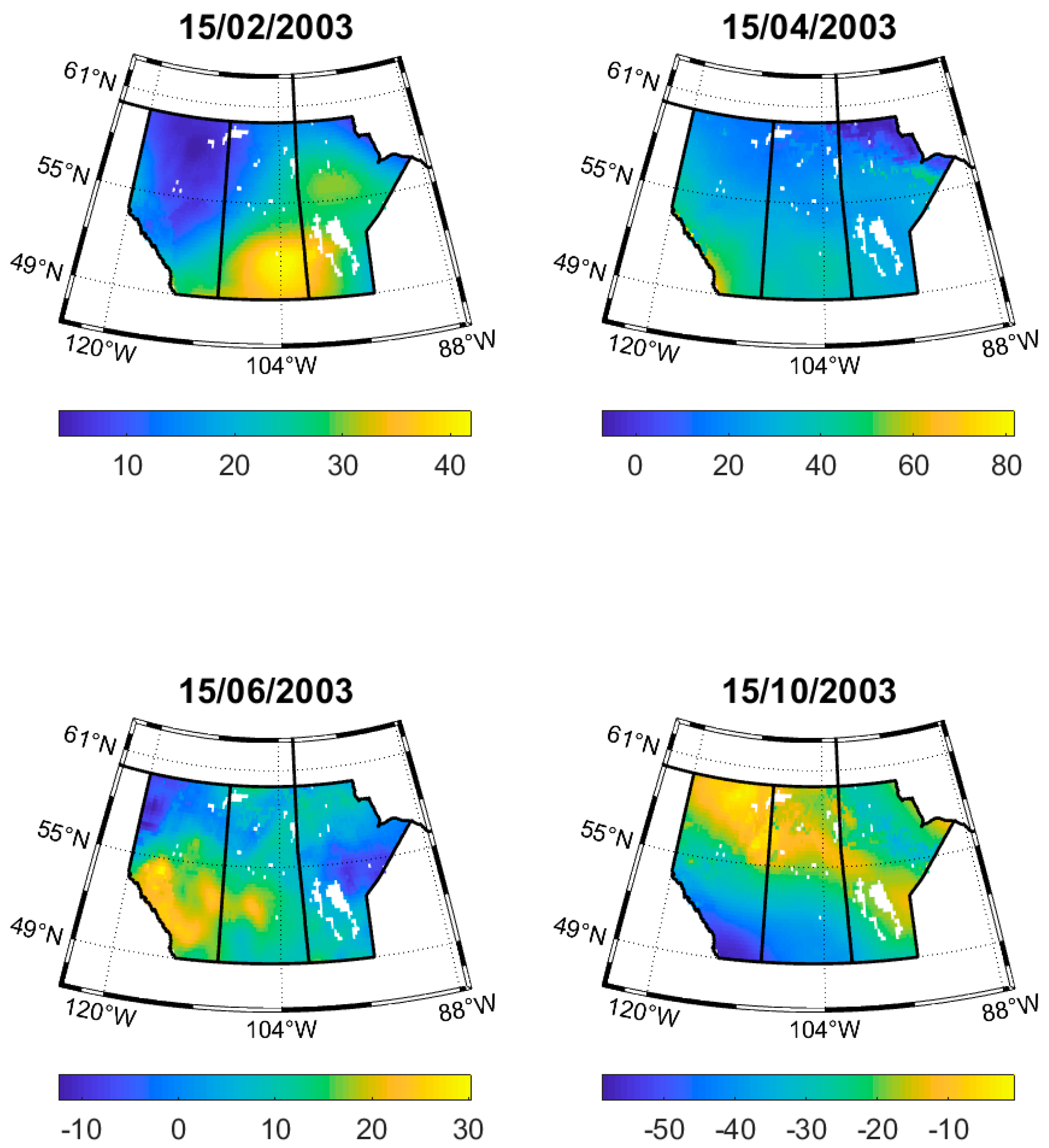
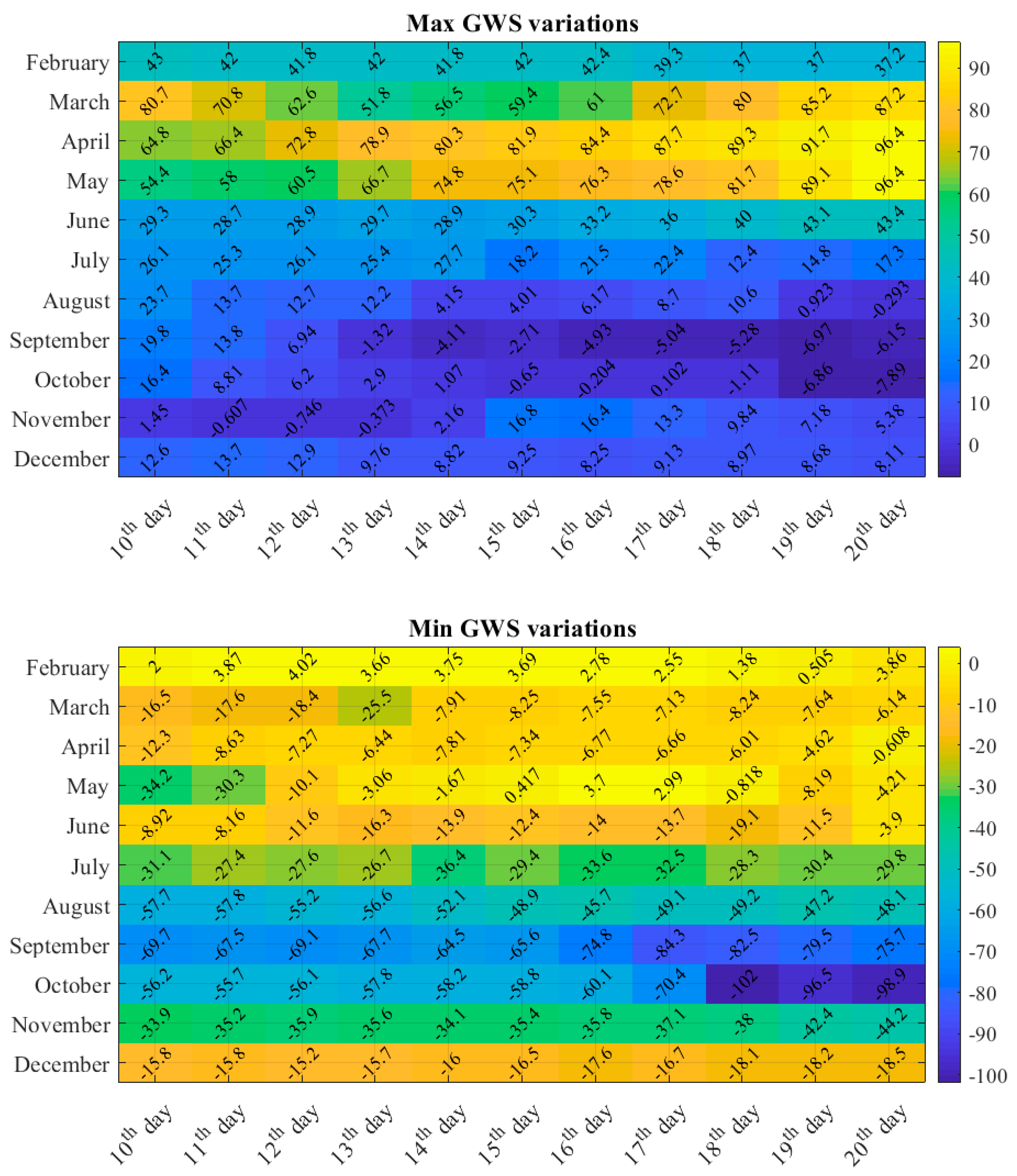
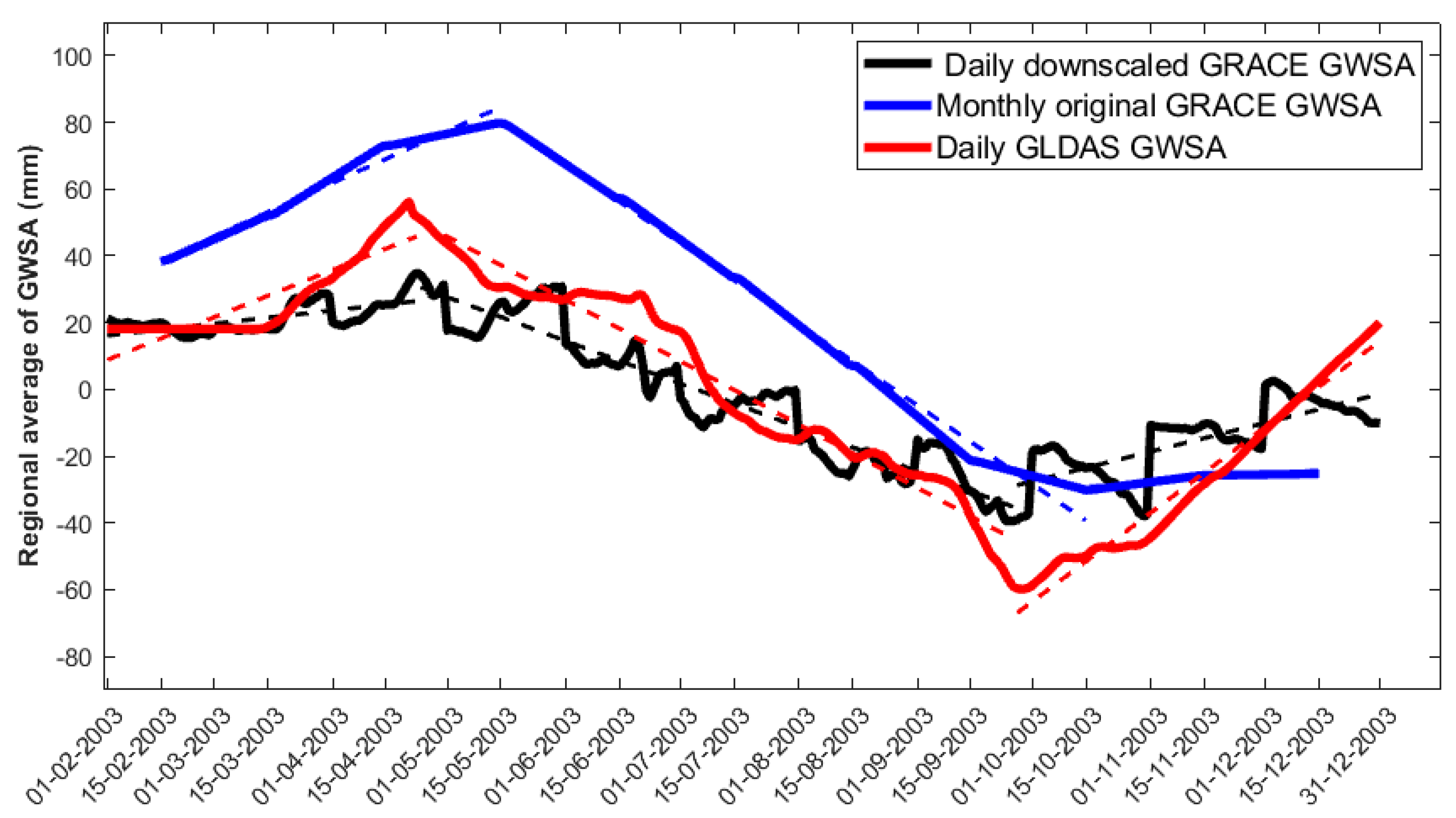
| Well Latitude (degree) | Well Longitude (degree) | r with Our GWSA | RMSE with Our GWSA | Well Latitude (degree) | Well Longitude (degree) | r with Our GWSA | RMSE with Our GWSA |
|---|---|---|---|---|---|---|---|
| 57.5193 | −111.404 | 0.52 | 10.58 | 49.3784 | −112.203 | 0.57 | 38.72 |
| 53.5889 | −114.996 | 0.75 | 23.30 | 49.0787 | −111.333 | 0.82 | 37.70 |
| 52.6254 | −114.053 | 0.73 | 27.16 | 49.5236 | −110.218 | 0.81 | 32.81 |
| 53.5836 | −114.108 | 0.84 | 22.16 | 49.2376 | −111.351 | 0.86 | 37.72 |
| 52.0061 | −111.268 | 0.88 | 25.91 | 49.4722 | −110.968 | 0.81 | 35.47 |
| 52.0117 | −114.215 | 0.88 | 29.69 | 49.1039 | −110.251 | 0.85 | 34.96 |
| 52.8649 | −111.647 | 0.55 | 23.14 | 56.1892 | −117.999 | 0.77 | 17.67 |
| 52.5503 | −111.915 | 0.83 | 24.23 | 56.1891 | −117.821 | 0.85 | 17.66 |
| 52.6753 | −111.322 | 0.79 | 24.18 | 56.2466 | −117.636 | 0.82 | 17.60 |
| 52.7874 | −111.857 | 0.61 | 23.17 | 55.1961 | −119.397 | 0.72 | 24.28 |
| 53.2870 | −110.017 | 0.63 | 20.10 | 55.3961 | −119.737 | 0.86 | 23.60 |
| 54.5596 | −111.589 | 0.71 | 16.01 | 55.2935 | −118.461 | 0.89 | 21.63 |
| 52.4212 | −110.607 | 0.82 | 24.29 | 54.6465 | −110.509 | 0.71 | 15.28 |
| 53.1611 | −111.789 | 0.73 | 22.10 | 54.0609 | −110.408 | 0.84 | 17.08 |
| 52.7257 | −110.848 | 0.74 | 23.62 | 54.4728 | −110.984 | 0.64 | 16.02 |
| 51.1073 | −115.366 | 0.43 | 36.72 | 54.4857 | −110.625 | 0.72 | 15.80 |
| 50.8446 | −113.466 | 0.79 | 34.62 | 54.6062 | −110.252 | 0.81 | 15.17 |
| 50.1354 | −112.494 | 0.61 | 36.00 | 54.6209 | −110.431 | 0.81 | 15.13 |
| 51.0085 | −112.237 | 0.76 | 31.07 | 54.5759 | −110.811 | 0.62 | 15.39 |
| 51.3319 | −113.614 | 0.84 | 32.69 | 53.8759 | −112.975 | 0.61 | 19.32 |
| 51.1566 | −111.190 | 0.75 | 29.51 | 52.9683 | −112.854 | 0.89 | 24.10 |
| 50.7972 | −110.418 | 0.91 | 29.31 | 52.7451 | −113.972 | 0.43 | 25.42 |
| 50.9797 | −111.700 | 0.58 | 31.24 | 53.3552 | −113.664 | 0.81 | 22.90 |
| 51.9536 | −111.445 | 0.51 | 26.76 | 53.4102 | −113.762 | 0.84 | 23.09 |
| 51.7889 | −110.504 | 0.92 | 26.12 | 52.1027 | −113.444 | 0.67 | 28.40 |
| 51.4146 | −110.168 | 0.59 | 27.32 | 52.6834 | −113.595 | 0.75 | 27.24 |
| 51.5718 | −110.474 | 0.85 | 26.73 | 52.3175 | −112.802 | 0.61 | 26.49 |
| 49.9583 | −112.939 | 0.77 | 38.32 | 53.5689 | −113.828 | 0.57 | 21.60 |
| 49.6351 | −112.786 | 0.59 | 39.54 | 52.9381 | −113.365 | 0.89 | 24.88 |
| 49.1437 | −111.890 | 0.48 | 39.06 | 58.9796 | −118.915 | 0.54 | 14.31 |
| 49.7570 | −113.510 | 0.53 | 40.43 | 58.2244 | −116.018 | 0.74 | 12.78 |
| 49.7278 | −113.298 | 0.63 | 41.77 | 54.0359 | −114.397 | 0.81 | 19.99 |
| 53.3876 | −112.829 | 0.88 | 21.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatolazadeh, F.; Eshagh, M.; Goïta, K.; Wang, S. A New Spatiotemporal Estimator to Downscale GRACE Gravity Models for Terrestrial and Groundwater Storage Variations Estimation. Remote Sens. 2022, 14, 5991. https://doi.org/10.3390/rs14235991
Fatolazadeh F, Eshagh M, Goïta K, Wang S. A New Spatiotemporal Estimator to Downscale GRACE Gravity Models for Terrestrial and Groundwater Storage Variations Estimation. Remote Sensing. 2022; 14(23):5991. https://doi.org/10.3390/rs14235991
Chicago/Turabian StyleFatolazadeh, Farzam, Mehdi Eshagh, Kalifa Goïta, and Shusen Wang. 2022. "A New Spatiotemporal Estimator to Downscale GRACE Gravity Models for Terrestrial and Groundwater Storage Variations Estimation" Remote Sensing 14, no. 23: 5991. https://doi.org/10.3390/rs14235991
APA StyleFatolazadeh, F., Eshagh, M., Goïta, K., & Wang, S. (2022). A New Spatiotemporal Estimator to Downscale GRACE Gravity Models for Terrestrial and Groundwater Storage Variations Estimation. Remote Sensing, 14(23), 5991. https://doi.org/10.3390/rs14235991