GNSS RTK/UWB/DBA Fusion Positioning Method and Its Performance Evaluation
Abstract
1. Introduction
2. Relevant Principles and Mathematical Models
2.1. GNSS RTK Mathematical Models
2.2. UWB Location Principles and Mathematical Models
2.3. DBA Basic Principles and Mathematical Models
3. GNSS RTK/UWB/DBA Fusion Positioning Model
3.1. Functional and Stochastic Model
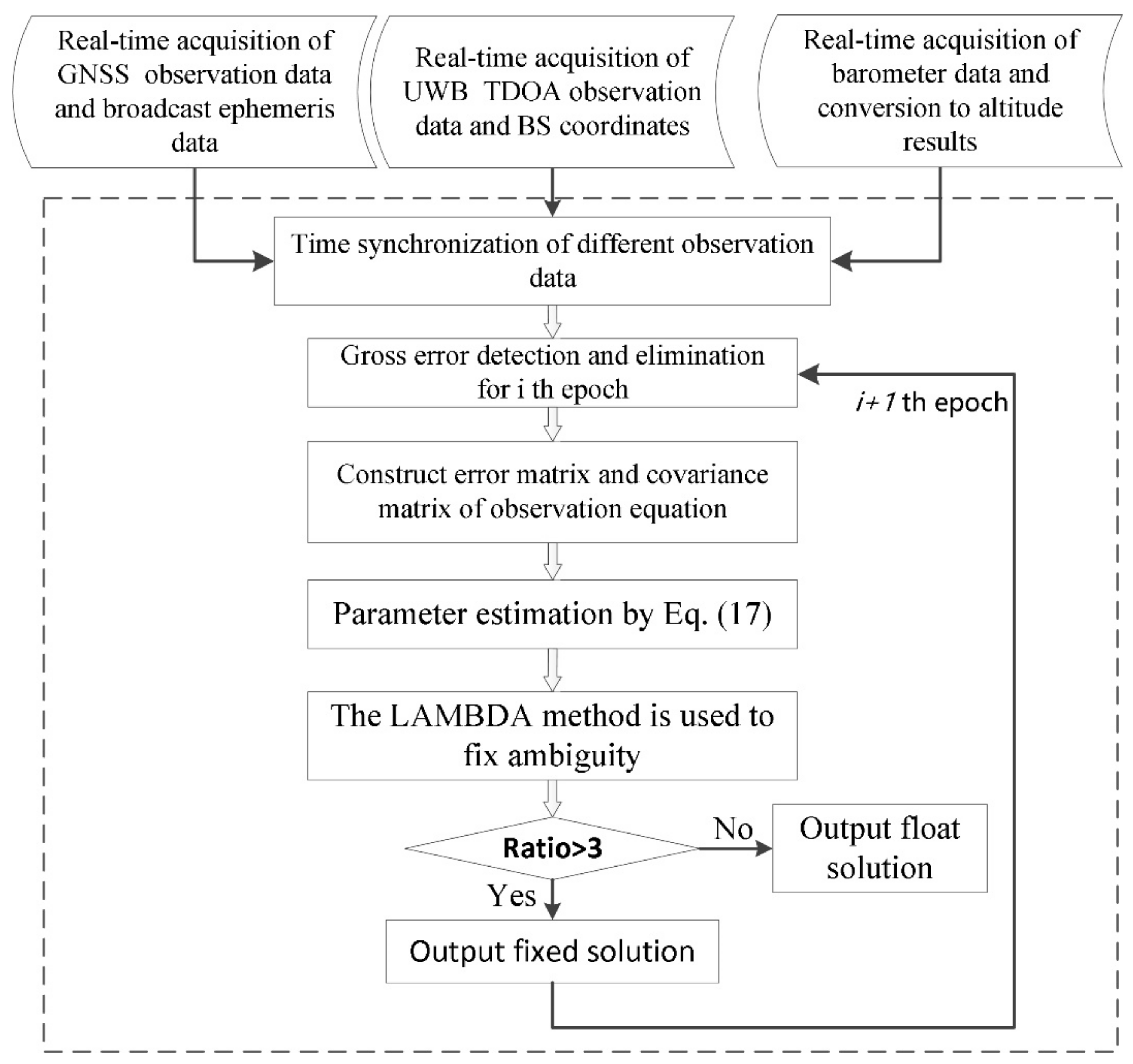
3.2. Parameter Estimation Processes and Flowchart
4. Experimental and Results Analysis
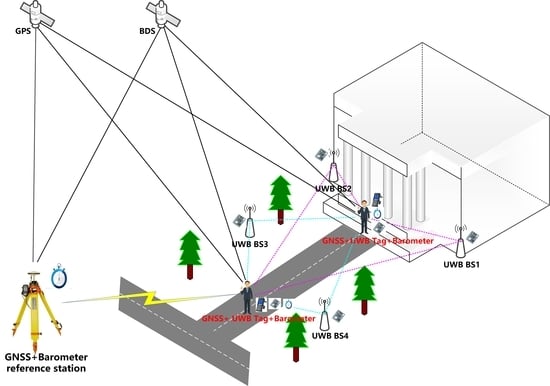
4.1. Experimental Data
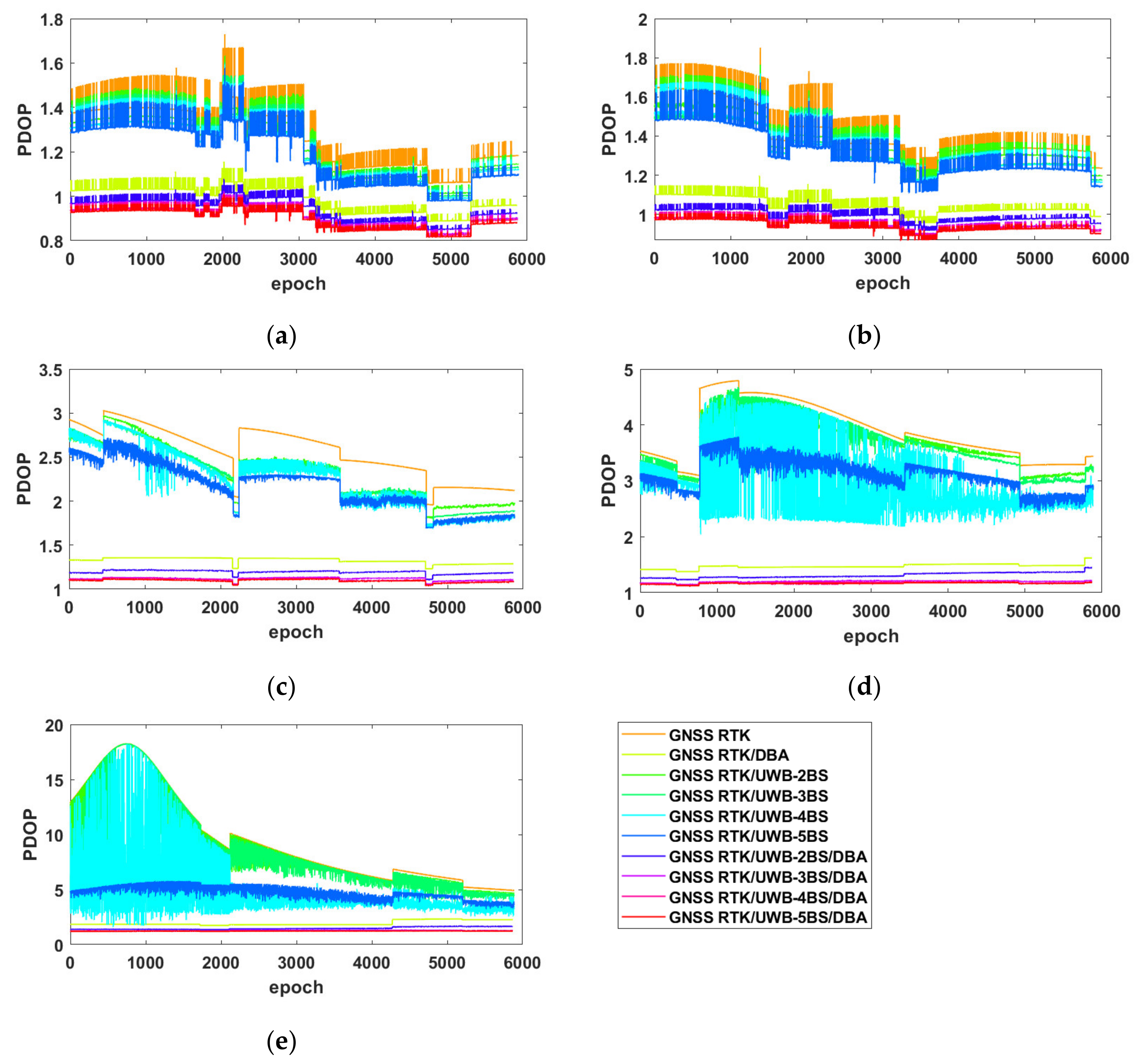
4.2. Static Experimental Results and Analysis
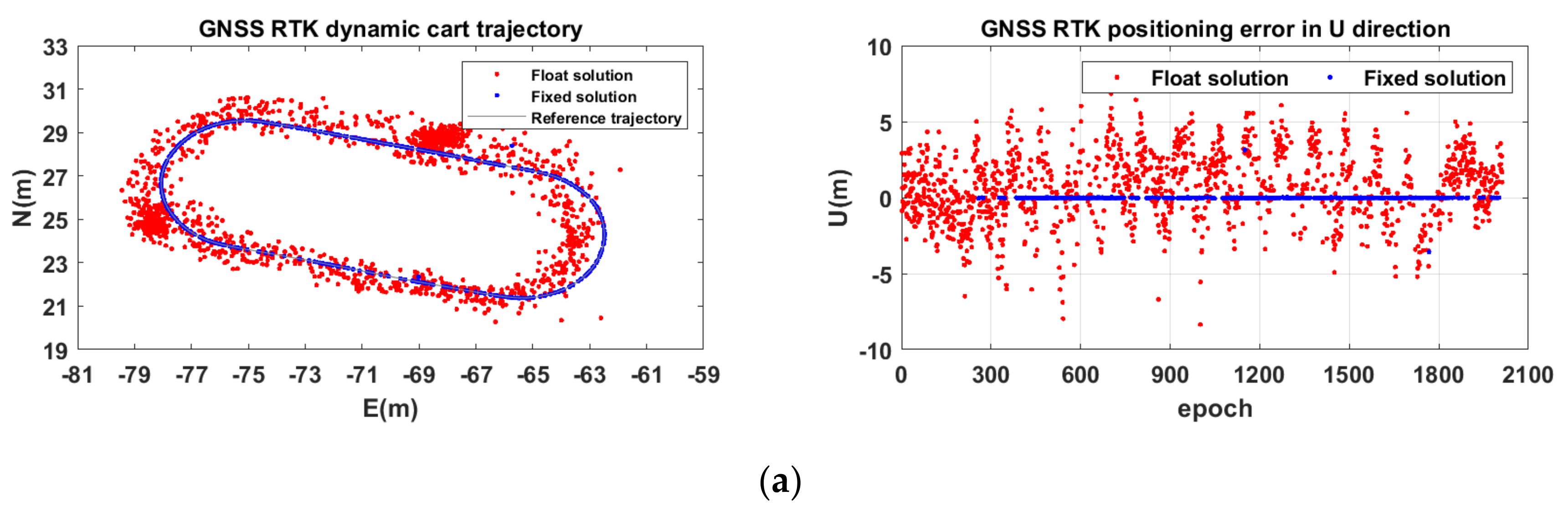
4.3. Dynamic Cart Experimental Results and Analysis
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, H.; Wang, J.; Wang, J.; Tan, X. Performance Analysis on Carrier Phase-Based Tightly-Coupled GPS/BDS/INS Integration in GNSS Degraded and Denied Environments. Sensors 2015, 15, 8685–8711. [Google Scholar] [CrossRef]
- Cristodaro, C.; Dovis, F.; Falco, G.; Pini, M. GNSS Receiver Performance in Urban Environment: Challenges and Test Approaches for Automotive Applications. In Proceedings of the International Conference of Electrical & Electronic Technologies for Automotive, Turin, Italy, 15–16 June 2017. [Google Scholar]
- Wang, C.; Xu, A.; Sui, X.; Hao, Y.; Shi, Z.; Chen, Z. A Seamless Navigation System and Applications for Autonomous Vehicles Using a Tightly Coupled GNSS/UWB/INS/Map Integration Scheme. Remote Sens. 2022, 14, 27. [Google Scholar] [CrossRef]
- Zirari, S.; Canalda, P.; Spies, F. WiFi GPS based combined positioning algorithm. In Proceedings of the 2010 IEEE International Conference on Wireless Communications, Networking and Information Security, Beijing, China, 25–27 June 2010; pp. 684–688. [Google Scholar]
- Wang, J.; Tsujii, T.; Rizos, C.; Dai, L.; Moore, M.J.G.R.A. GPS and pseudo-satellites integration for precise positioning. Geomat. Res. Australas. 2001, 74, 103–117. [Google Scholar]
- Tobie, A.-M.; Garcia-Pena, A.; Thevenon, P.; Vezinet, J.; Aubault, M. Hybrid navigation filters performances between GPS, Galileo and 5G TOA measurements in multipath environment. In Proceedings of the Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online, 22–25 September 2020; pp. 2107–2140. [Google Scholar]
- Sahinoglu, Z.; Gezici, S.; Guvenc, I. Ultra-Wideband Positioning Systems (Theoretical Limits, Ranging Algorithms, and Protocols); Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Bastida-Castillo, A.; Gómez-Carmona, C.D.; De La Cruz Sánchez, E.; Pino-Ortega, J. Comparing accuracy between global positioning systems and ultra-wideband-based position tracking systems used for tactical analyses in soccer. Eur. J. Sport Sci. 2019, 19, 1157–1165. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A Novel NLOS Mitigation Algorithm for UWB Localization in Harsh Indoor Environments. IEEE Trans. Veh. Technol. 2018, 68, 686–699. [Google Scholar] [CrossRef]
- Opshaug, G.R.; Enge, P. Integrated GPS and UWB Navigation System: (Motivates the Necessity of Non-Interference). In Proceedings of the IEEE Conference on Ultra Wideband Systems & Technologies, Baltimore, MD, USA, 21–23 May 2002. [Google Scholar]
- Tan, K.M.; Law, C.L. GPS and UWB Integration for indoor positioning. In Proceedings of the International Conference on Information, Singapore, 10–13 December 2007. [Google Scholar]
- Gonzalez, J.; Blanco, J.L.; Galindo, C.; Ortiz-De-Galisteo, A.; Fernandez-Madrigal, J.A.; Moreno, F.A.; Martinez, J.L. Combination of UWB and GPS for indoor-outdoor vehicle localization. In Proceedings of the 2007 IEEE International Symposium on Intelligent Signal Processing, Alcala de Henares, Spain, 3–5 October 2007; pp. 885–890. [Google Scholar] [CrossRef]
- Chiu, D.S.; Macgougan, G.; O’Keefe, K. UWB Assisted GPS RTK in Hostile Environments. In Proceedings of the ION GNSS 2008, The Satellite Division of the Institute of Navigation 20th International Technical Meeting, Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Chiu, S.T. Ultra Wideband Augmented GPS; University of Calgary: Calgary, AB, Canada, 2008. [Google Scholar]
- MacGougan, G.D. Real-Time Kinematic Surveying Using Tightly-Coupled GPS and Ultra-Wideband Ranging; University of Calgary: Calgary, AB, Canada, 2009. [Google Scholar]
- MacGougan, G.D.; O’Keefe, K. Real Time UWB Error Estimation in a Tightly Coupled GPS/UWB Positioning System. In Proceedings of the Institute of Navigation 2009 International Technical Meeting, Anaheim, CA, USA, 26–28 January 2009. [Google Scholar]
- MacGougan, G.D.; O’Keefe, K.; Klukas, R. Accuracy and reliability of tightly coupled GPS/ultra-wideband positioning for surveying in urban environments. GPS Solut. 2010, 14, 351–364. [Google Scholar] [CrossRef]
- Jiang, Y. Integration of UWB Ranging and GPS for Improved Relative Vehicle Positioning and Ambiguity Resolution; University of Calgary: Calgary, AB, Canada, 2012. [Google Scholar]
- O’Keefe, K.; Jiang, Y.; Petovello, M. An Investigation of tightly-coupled UWB/low-cost GPS for vehicle-to-infrastructure relative positioning. In Proceedings of the Radar Conference, Cincinnati, OH, USA, 19–23 May 2014. [Google Scholar]
- Liu, F. Research on High Precision Seamless Positioning Model and Method Based on Multi-Sensor Fusion; China University of Mining and Technology: Xuzhou, China, 2020. [Google Scholar]
- Wang, N. The Key Modals and System of GNSS/UWB Network Positioning; Beijing University of Civil Engineering and Architecture: Beijing, China, 2020. [Google Scholar]
- Abolfathi, E.A.; O’Keefe, K. Integrating Vision Derived Bearing Measurements with Differential GPS and UWB Ranges for Vehicle-to-vehicle Relative Navigation. In Proceedings of the 26th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2013), Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Li, Z.; Zheng, N.; Wang, J.; Gao, J. Performance Comparison among Different Precise Satellite Ephemeris and Clock Products for PPP/INS/UWB Tightly Coupled Positioning. J. Navig. 2017, 71, 585–606. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, C.; Zhou, Q.; Wang, H.; Gao, Q.; Chen, Y. A combined GPS UWB and MARG locationing algorithm for indoor and outdoor mixed scenario. Clust. Comput. 2018, 22, 5965–5974. [Google Scholar] [CrossRef]
- Wang, N.; Li, R.; Han, Z.; Qiu, W.; Wang, Z. Research on relative navigation algorithm of small UAV based on inertial/GNSS/UWB. Electron. Meas. Technol. 2019, 42, 94–100. [Google Scholar]
- Guo, R.; Su, R.R.; Liu, L.; Hu, G.M.; Chang, Z.Q. COMPASS RDSS Positioning Accuracy Analysis. In Proceedings of the 5th China Satellite Navigation Conference (CSNC), Nanjing, China, 21–23 May 2014; pp. 219–228. [Google Scholar]
- Abdalati, W.; Zwally, H.J.; Bindschadler, R.; Csatho, B.; Farrell, S.L.; Fricker, H.A.; Harding, D.; Kwok, R.; Lefsky, M.; Markus, T. The ICESat-2 laser altimetry mission. Proc. IEEE 2010, 98, 735–751. [Google Scholar] [CrossRef]
- Jao, C.-S.; Wang, Y.; Lin, Y.-W.; Shkel, A.M. A hybrid barometric/ultrasonic altimeter for aiding ZUPT-based inertial pedestrian navigation systems. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online, 22–25 September 2020; pp. 2500–2517. [Google Scholar]
- Hu, Z.Q.; Zhang, L.R.; Ji, Y.F. Applications of differential barometric altimeter in ground cellular communication positioning network. IET Sci. Meas. Technol. 2020, 14, 322–331. [Google Scholar] [CrossRef]
- Wang, S.; Dong, X.; Liu, G.; Gao, M.; Zhao, W.; Lv, D.; Cao, S. Low-Cost Single-Frequency DGNSS/DBA Combined Positioning Research and Performance Evaluation. Remote Sens. 2022, 14, 586. [Google Scholar] [CrossRef]
- Guoxiang, A.I.; Sheng, P.X.; Jinlin, D.U.; Zheng, Y.G.; Cai, X.D.; Haitao, W.U.; Yonghui, H.U.; Hua, Y.A. Barometric altimetry system as virtual constellation applied in CAPS. Sci. China Ser. G–Phys. Mech. Astron. 2009, 38, 1702–1710. [Google Scholar]
- Shi, H.; Pei, J. The solutions of navigation observation equations for CAPS. Sci. China Ser. G–Phys. Mech. Astron. 2009, 52, 434–444. [Google Scholar] [CrossRef]
- Ji, Y.F.; Sun, X.Y. Analysis on the positioning precision of CAPS. Sci. China Ser. G–Phys. Mech. Astron. 2009, 52, 328–332. [Google Scholar] [CrossRef]
- Sabatini, A.M.; Genovese, V. A Sensor Fusion Method for Tracking Vertical Velocity and Height Based on Inertial and Barometric Altimeter Measurements. Sensors 2014, 14, 13324–13347. [Google Scholar] [CrossRef]
- Wang, H.; Wen, Y.; Zhao, D. Differential barometric-based positioning technique for indoor elevation measurement in IoT medical applications. Technol. Health Care Off. J. Eur. Soc. Eng. 2017, 25, S295–S304. [Google Scholar] [CrossRef]
- Masse, F.; Bourke, A.K.; Chardonnens, J.; Paraschiv-Ionescu, A.; Aminian, K. Suitability of commercial barometric pressure sensors to distinguish sitting and standing activities for wearable monitoring. Med. Eng. Phys. 2014, 36, 739–744. [Google Scholar] [CrossRef]
- Seok, H.W.; Ansari, K.; Panachai, C.; Jamjareegulgarn, P. Individual performance of multi-GNSS signals in the determination of STEC over Thailand with the applicability of Klobuchar model. Adv. Space Res. 2022, 69, 1301–1318. [Google Scholar] [CrossRef]
- Xu, G.; Xu, Y. GPS Theory, Algorithms and Applications, 3rd ed.; Science Press: Beijing, China, 2017. [Google Scholar]
- Bolanakis, D.E.; Laopoulos, T.; Kotsis, K.T. A Prototype Wireless Sensor Network System for a Comparative Evaluation of Differential and Absolute Barometric Altimetry. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 20–28. [Google Scholar] [CrossRef]
- Hu, Z. Study on Key Technologies in Integration System of Navigation Based on Multi-Sensor Information such as Differential Barometric Altimetry; University of Chinese Academy of Sciences: Beijing, China, 2014. [Google Scholar]
- Shi, H.-L.; Sun, X.; Li, Z. Principle of Forwarding Satellite Navigation; Science Press: Beijing, China, 2009. [Google Scholar]
- King, B.; Bock, Y. Documentation for the GAMIT GPS Analysis Software; Massachusetts Institute of Technology: Cambridge, MA, USA, 1999. [Google Scholar]
- Li, Z.; Hunag, J. GPS Surveying and Data Processing; Wuhan University Press: Wuhan, China, 2013. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Chang, X.W.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Li, W.; Li, W.; Cui, X.; Zhao, S.; Lu, M. A Tightly Coupled RTK/INS Algorithm with Ambiguity Resolution in the Position Domain for Ground Vehicles in Harsh Urban Environments. Sensors 2018, 18, 2160. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Liu, G.; Wang, S.; Xiao, G.; Zhao, W.; Lv, D. Research on Tightly Coupled Multi-Antenna GNSS/MEMS Single-Frequency Single-Epoch Attitude Determination in Urban Environment. Remote Sens. 2021, 13, 2710. [Google Scholar] [CrossRef]










| Parameter Type | Processing Strategy |
|---|---|
| GNSS receiver | u-blox NEO-M8T |
| UWB system and range | TracTech, from 50 to 100 m |
| BMP280 barometer resolution | 0.01 mbar (0.1 m) |
| Position parameters | Single epoch mode |
| Atmospheric delays | Ignored in short baseline length |
| Ambiguity parameters | Single epoch mode and LAMBDA method resolution |
| Ratio threshold value | 3.0 |
| DBA altitude | Simplified DBA formula |
| UWB BS number | From 2 to 5 |
| Combination Mode | UWB BS | Elevation Mask Angles (Degrees) | ||||
|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | ||
| GNSS RTK | - | 1.28 | 1.42 | 2.56 | 3.87 | 9.57 |
| GNSS RTK/DBA | - | 0.98 | 1.04 | 1.32 | 1.47 | 1.94 |
| GNSS RTK/UWB | 2 | 1.23 | 1.38 | 2.33 | 3.65 | 9.12 |
| 3 | 1.21 | 1.34 | 2.30 | 3.65 | 8.43 | |
| 4 | 1.20 | 1.33 | 2.26 | 2.94 | 4.78 | |
| 5 | 1.18 | 1.31 | 2.17 | 3.12 | 4.72 | |
| GNSS RTK/UWB/DBA | 2 | 0.94 | 0.99 | 1.19 | 1.31 | 1.47 |
| 3 | 0.90 | 0.95 | 1.11 | 1.19 | 1.27 | |
| 4 | 0.90 | 0.94 | 1.10 | 1.17 | 1.23 | |
| 5 | 0.89 | 0.94 | 1.09 | 1.16 | 1.22 | |
| Combination Mode | UWB BS | Elevation Mask Angles (Degrees) | ||||
|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | ||
| GNSS RTK | - | 89.90% | 96.27% | 90.02% | 82.76% | 19.15% |
| GNSS RTK/DBA | - | 90.73% | 97.19% | 93.68% | 91.62% | 43.06% |
| GNSS RTK/UWB | 2 | 88.58% | 97.21% | 93.45% | 85.43% | 39.91% |
| 3 | 88.87% | 98.36% | 97.89% | 94.00% | 57.50% | |
| 4 | 88.61% | 98.47% | 98.91% | 97.07% | 65.86% | |
| 5 | 87.40% | 98.28% | 98.53% | 96.63% | 76.04% | |
| GNSS RTK/UWB/DBA | 2 | 89.22% | 97.68% | 96.25% | 94.17% | 64.79% |
| 3 | 89.33% | 98.48% | 98.96% | 97.07% | 80.55% | |
| 4 | 89.08% | 98.56% | 99.06% | 97.29% | 81.40% | |
| 5 | 87.39% | 98.36% | 98.80% | 96.83% | 79.08% | |
| Combination Mode | UWB BS | <1 cm | <5 cm | ||||
|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | ||
| GNSS RTK | - | 83.41% | 90.14% | 49.97% | 90.46% | 90.68% | 90.19% |
| GNSS RTK/DBA | - | 84.17% | 93.78% | 49.84% | 93.97% | 94.29% | 94.09% |
| GNSS RTK/UWB | 3 | 86.35% | 97.89% | 53.81% | 98.01% | 97.96% | 97.90% |
| 5 | 86.96% | 98.58% | 54.10% | 98.55% | 98.82% | 98.52% | |
| GNSS RTK/UWB/DBA | 3 | 86.99% | 98.96% | 53.85% | 98.96% | 99.03% | 98.93% |
| 5 | 86.99% | 98.84% | 54.19% | 98.82% | 98.98% | 98.88% | |
| Combination Mode | UWB BS | <1 cm | <5 cm | ||||
|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | ||
| GNSS RTK | - | 18.27% | 18.78% | 7.50% | 18.71% | 21.59% | 18.54% |
| GNSS RTK/DBA | - | 41.72% | 43.10% | 16.39% | 43.25% | 45.81% | 43.17% |
| GNSS RTK/UWB | 3 | 51.19% | 53.89% | 20.71% | 56.49% | 56.78% | 49.01% |
| 5 | 68.22% | 75.22% | 25.50% | 76.17% | 80.37% | 64.65% | |
| GNSS RTK/UWB/DBA | 3 | 73.77% | 79.55% | 29.14% | 80.57% | 83.94% | 70.08% |
| 5 | 70.52% | 77.81% | 26.77% | 79.17% | 83.00% | 67.08% | |
| Combination Mode | UWB BS | Elevation Mask Angles (Degrees) | ||||
|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | ||
| GNSS RTK | - | 1.30 | 1.71 | 2.24 | 3.32 | 5.34 |
| GNSS RTK/DBA | - | 1.01 | 1.12 | 1.25 | 1.42 | 1.79 |
| GNSS RTK/UWB | 2 | 1.30 | 1.70 | 2.22 | 3.30 | 3.28 |
| 3 | 1.26 | 1.66 | 2.19 | 3.29 | 3.02 | |
| 4 | 1.17 | 1.55 | 2.03 | 3.17 | 2.56 | |
| 5 | 1.17 | 1.53 | 2.00 | 2.98 | 2.33 | |
| GNSS RTK/UWB/DBA | 2 | 1.01 | 1.11 | 1.24 | 1.41 | 1.60 |
| 3 | 0.98 | 1.09 | 1.22 | 1.40 | 1.53 | |
| 4 | 0.94 | 1.04 | 1.17 | 1.35 | 1.36 | |
| 5 | 0.93 | 1.03 | 1.15 | 1.31 | 1.23 | |
| Combination Mode | UWB BS | Elevation Mask Angles (Degrees) | ||||
|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | ||
| GNSS RTK | - | 83.50% | 89.81% | 92.94% | 88.17% | 32.80% |
| GNSS RTK/DBA | - | 83.85% | 90.26% | 94.48% | 91.15% | 49.90% |
| GNSS RTK/UWB | 2 | 84.29% | 91.75% | 95.58% | 89.66% | 57.06% |
| 3 | 84.89% | 92.25% | 94.78% | 90.71% | 71.27% | |
| 4 | 85.14% | 92.64% | 97.61% | 97.17% | 84.94% | |
| 5 | 85.04% | 92.79% | 98.16% | 98.16% | 88.77% | |
| GNSS RTK/UWB/DBA | 2 | 84.84% | 91.70% | 96.27% | 95.43% | 67.15% |
| 3 | 85.14% | 92.35% | 97.12% | 96.22% | 79.82% | |
| 4 | 85.09% | 92.69% | 97.96% | 97.61% | 86.93% | |
| 5 | 85.04% | 92.79% | 98.21% | 98.16% | 89.51% | |
| Combination Mode | UWB BS | <1 cm | <5 cm | ||||
|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | ||
| GNSS RTK | - | 92.84% | 89.91% | 70.87% | 93.04% | 93.89% | 93.04% |
| GNSS RTK/DBA | - | 94.33% | 91.25% | 71.57% | 94.58% | 95.28% | 94.88% |
| GNSS RTK/UWB | 3 | 94.09% | 90.06% | 70.68% | 95.33% | 95.58% | 94.83% |
| 5 | 97.37% | 91.55% | 66.60% | 98.71% | 98.81% | 98.21% | |
| GNSS RTK/UWB/DBA | 3 | 96.42% | 91.85% | 72.42% | 97.71% | 97.86% | 97.27% |
| 5 | 97.42% | 91.40% | 66.00% | 98.71% | 98.86% | 98.41% | |
| Combination Mode | UWB BS | <1 cm | <5 cm | ||||
|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | ||
| GNSS RTK | - | 32.95% | 33.35% | 9.69% | 34.94% | 37.18% | 33.85% |
| GNSS RTK/DBA | - | 50.05% | 50.30% | 14.21% | 51.74% | 53.18% | 53.23% |
| GNSS RTK/UWB | 3 | 70.68% | 70.97% | 14.36% | 73.01% | 74.35% | 70.18% |
| 5 | 88.72% | 88.42% | 19.53% | 93.84% | 90.90% | 88.02% | |
| GNSS RTK/UWB/DBA | 3 | 80.77% | 79.87% | 17.99% | 85.69% | 82.41% | 80.02% |
| 5 | 89.02% | 89.02% | 19.63% | 93.99% | 91.40% | 88.97% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Dong, X.; Liu, G.; Gao, M.; Xiao, G.; Zhao, W.; Lv, D. GNSS RTK/UWB/DBA Fusion Positioning Method and Its Performance Evaluation. Remote Sens. 2022, 14, 5928. https://doi.org/10.3390/rs14235928
Wang S, Dong X, Liu G, Gao M, Xiao G, Zhao W, Lv D. GNSS RTK/UWB/DBA Fusion Positioning Method and Its Performance Evaluation. Remote Sensing. 2022; 14(23):5928. https://doi.org/10.3390/rs14235928
Chicago/Turabian StyleWang, Shengliang, Xianshu Dong, Genyou Liu, Ming Gao, Gongwei Xiao, Wenhao Zhao, and Dong Lv. 2022. "GNSS RTK/UWB/DBA Fusion Positioning Method and Its Performance Evaluation" Remote Sensing 14, no. 23: 5928. https://doi.org/10.3390/rs14235928
APA StyleWang, S., Dong, X., Liu, G., Gao, M., Xiao, G., Zhao, W., & Lv, D. (2022). GNSS RTK/UWB/DBA Fusion Positioning Method and Its Performance Evaluation. Remote Sensing, 14(23), 5928. https://doi.org/10.3390/rs14235928