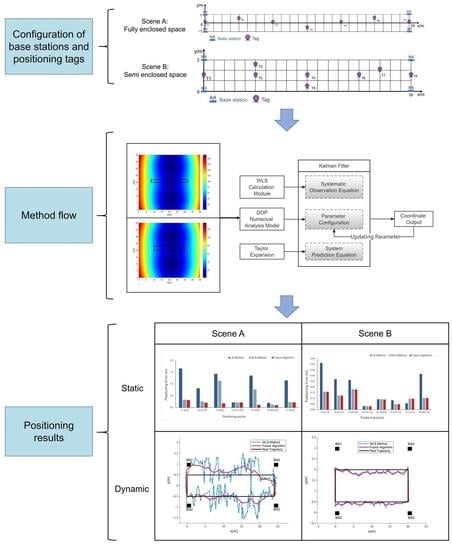
Combining Dilution of Precision and Kalman Filtering for UWB Positioning in a Narrow Space
Abstract
1. Introduction
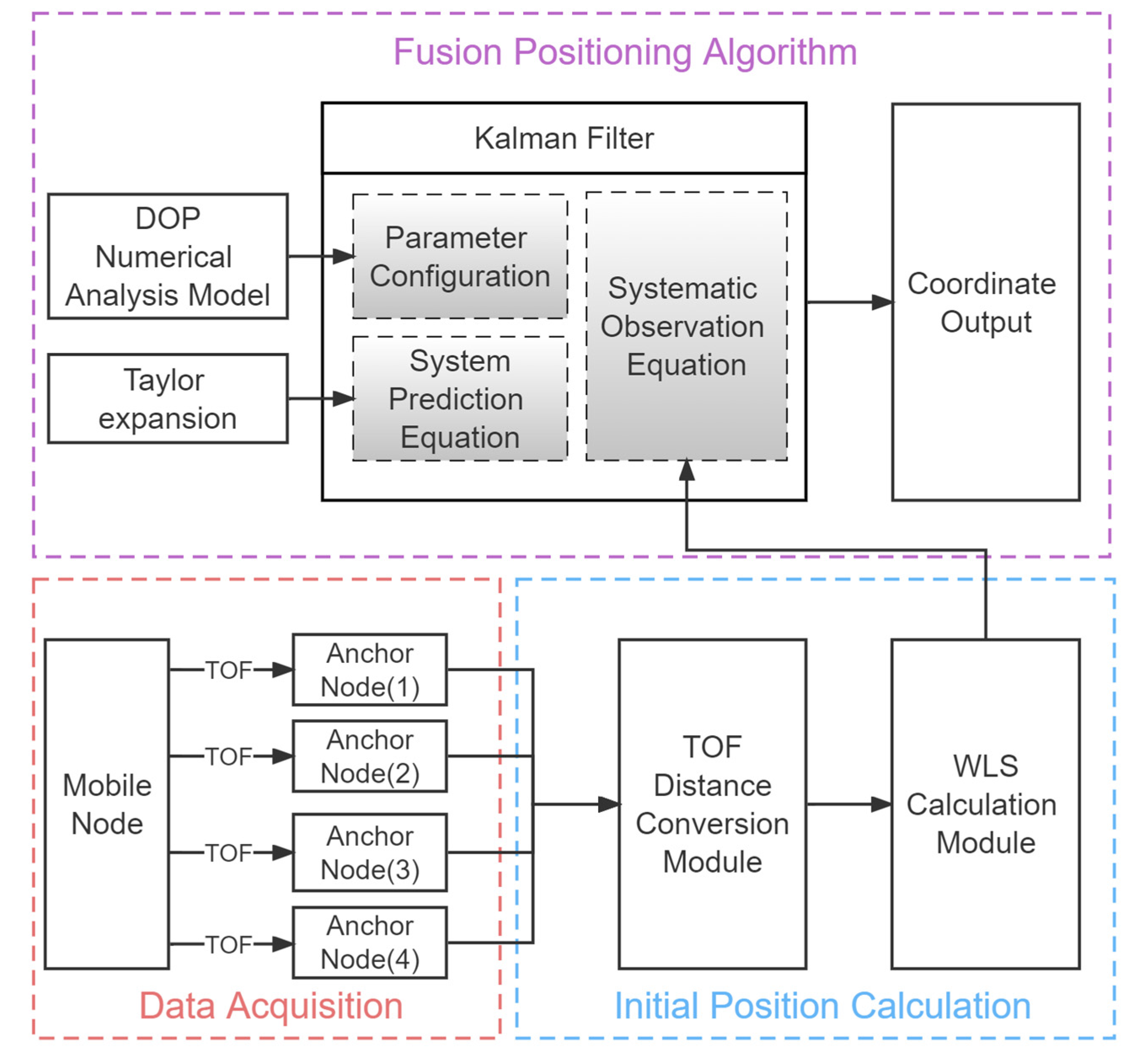
2. Methods
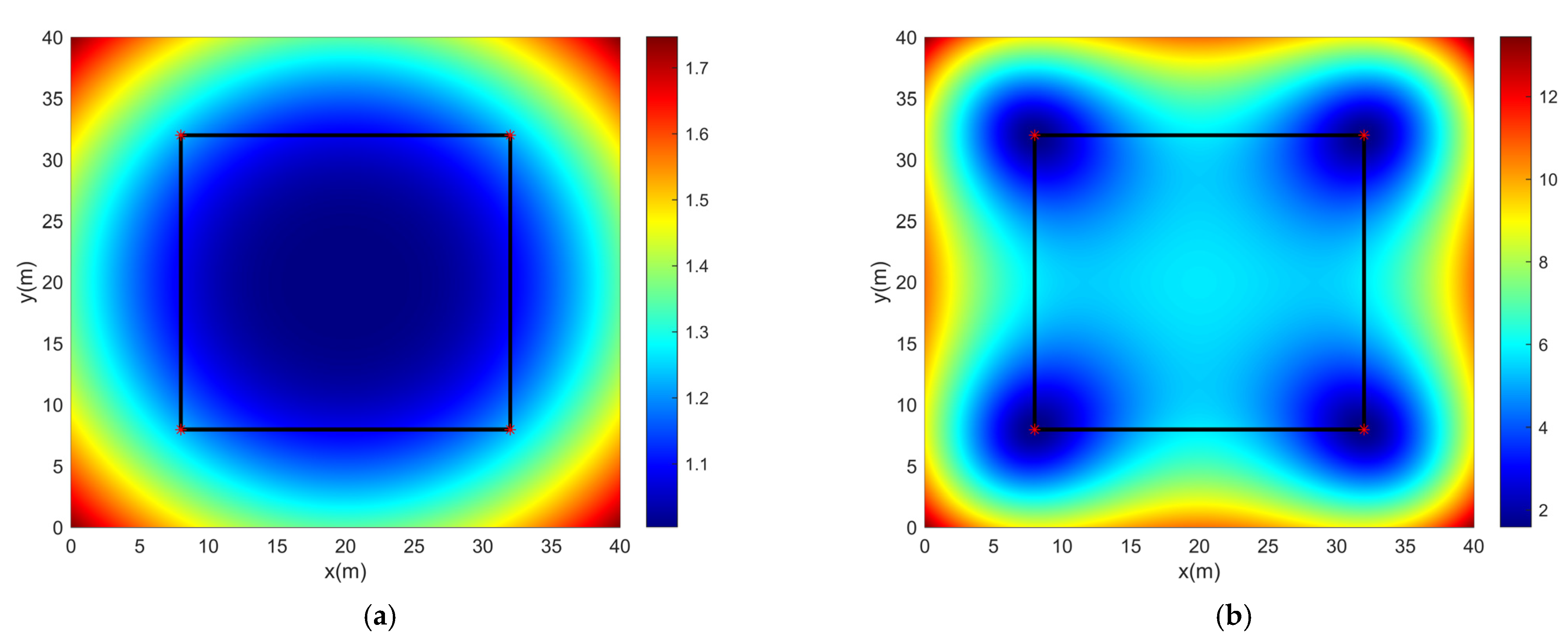
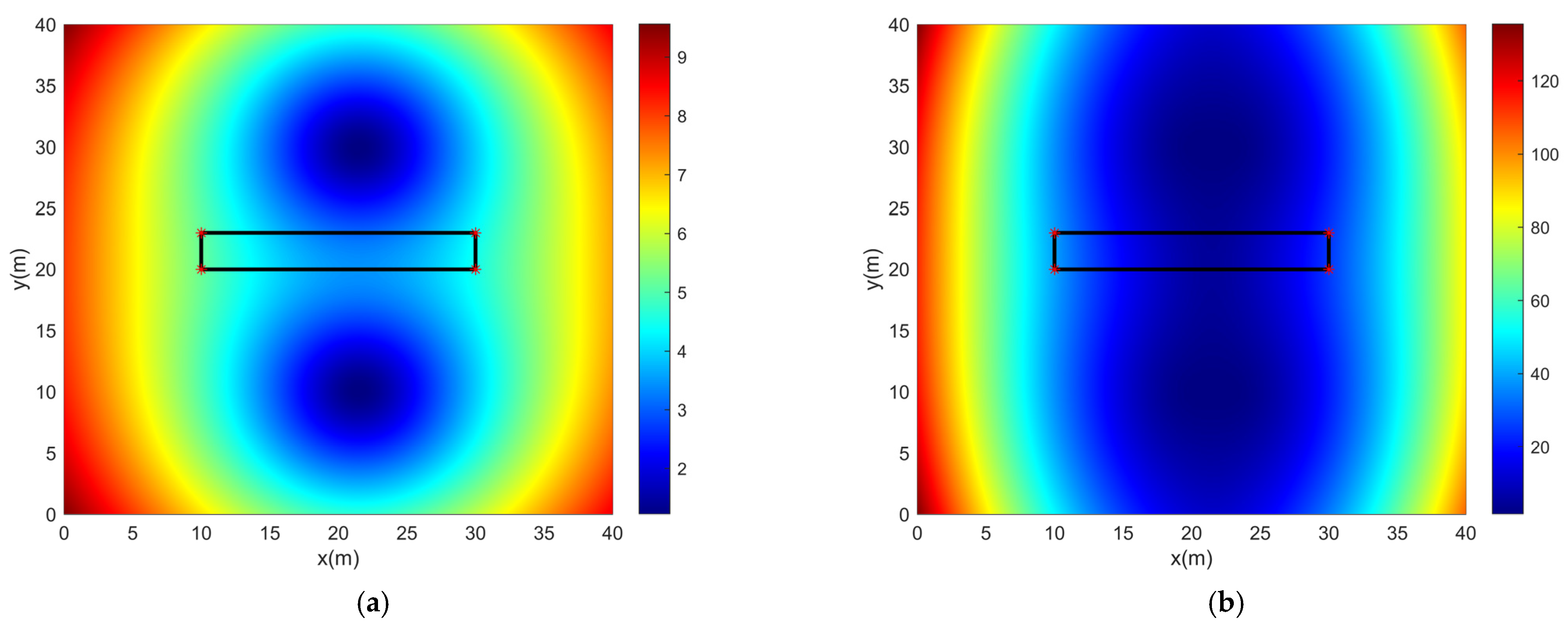
2.1. Positioning Algorithm and DOP Numerical Distribution Model
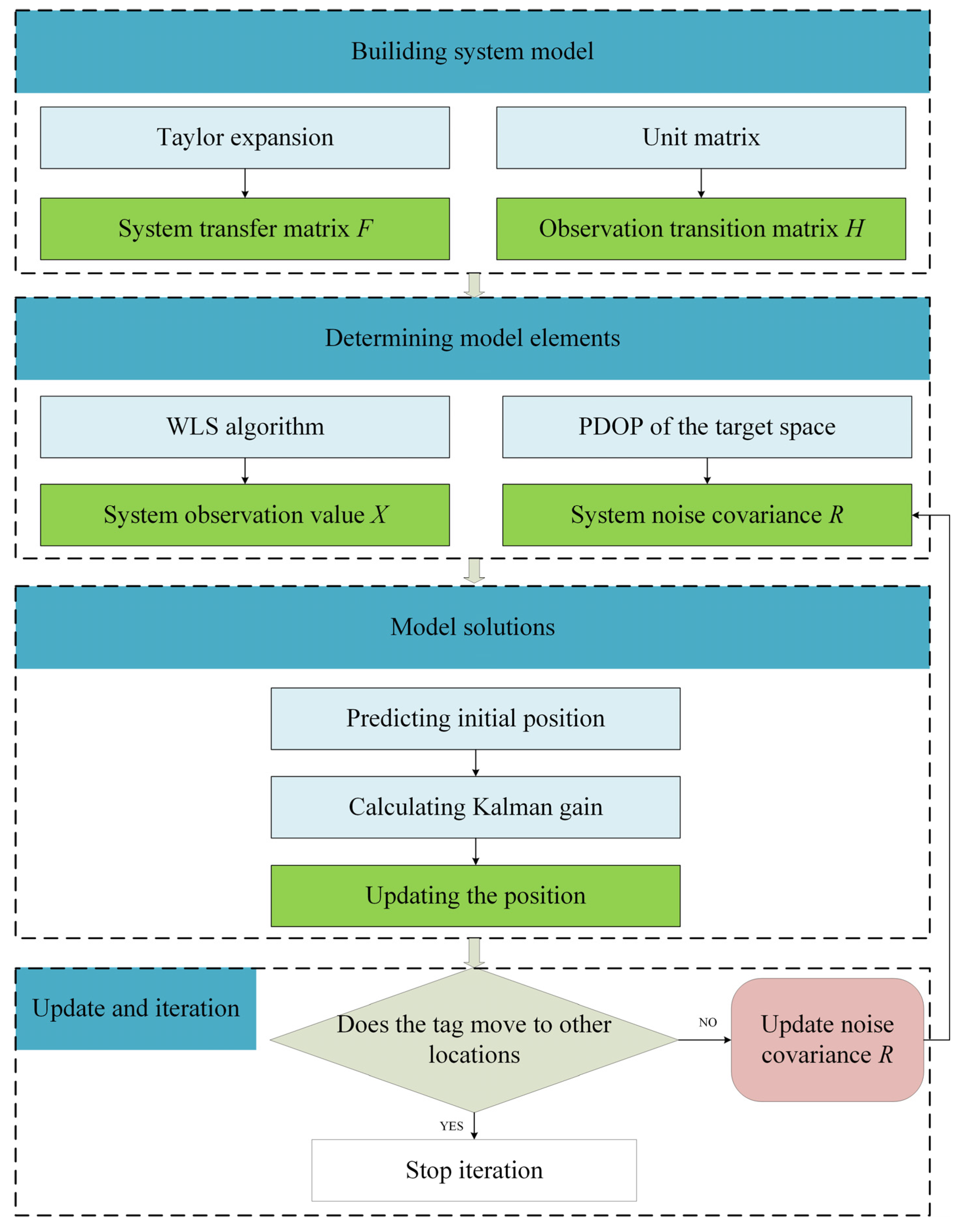
2.2. Optimized Kalman Filter Parameter Configuration Based on DOP Values
- (1)
- Prediction steps:
- (2)
- Supplementary Kalman gain:
- (3)
- Update steps:
2.3. Fusion Positioning Algorithm
- Building the system model:
- 2.
- Measuring system observation value X:
- 3.
- Calculating system noise covariance R:
- 4.
- Calculating the Kalman gain K:
- 5.
- Predicting the position coordinate:
- 6.
- Updating measurement noise covariance R:
3. Experiments and Results
3.1. Experimental Protocol
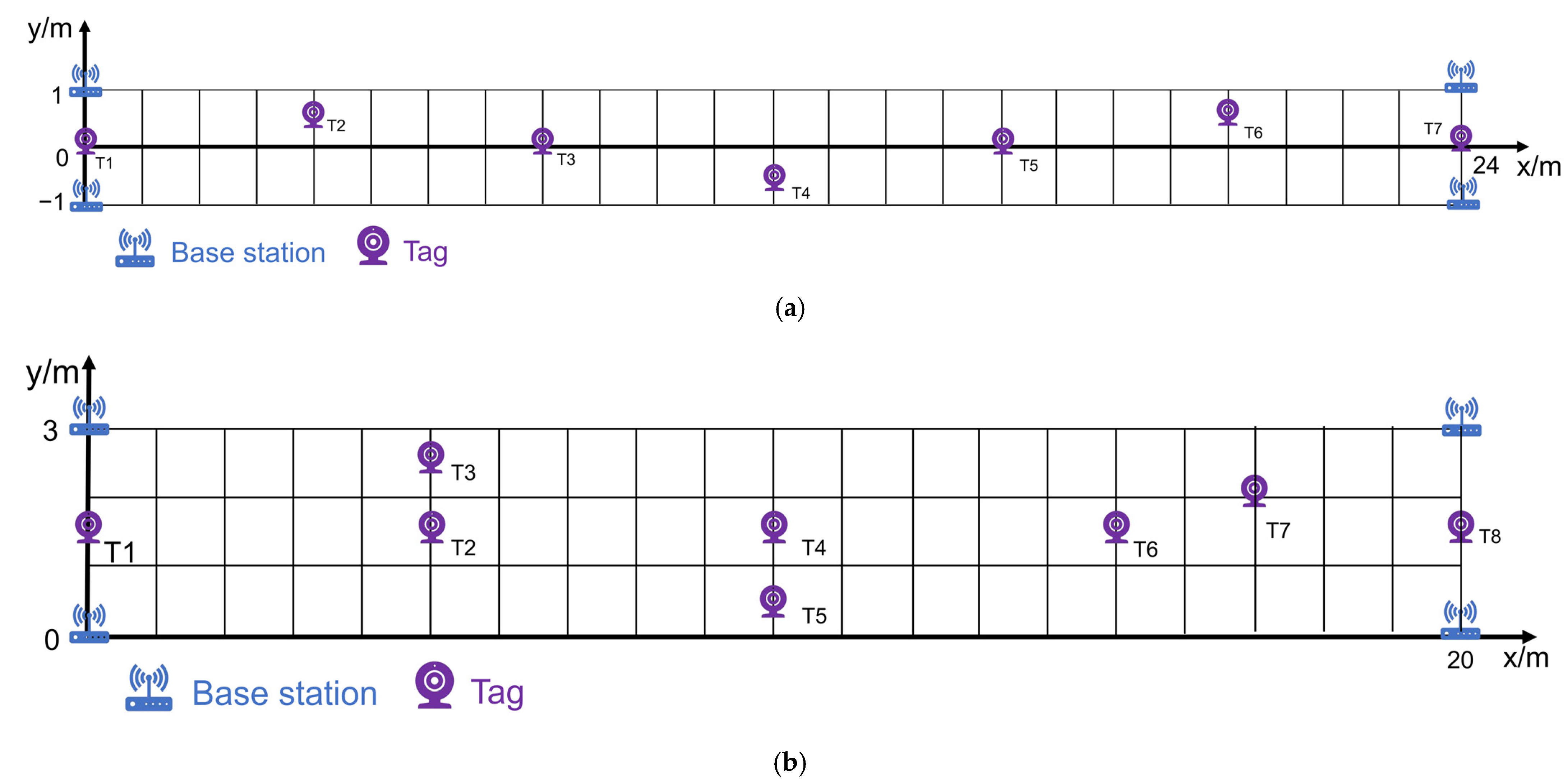
3.1.1. Experimental Scene
3.1.2. Experimental Hardware
3.1.3. Experimental Scheme
3.2. Experimental Results of the DOP Numerical Analysis Model
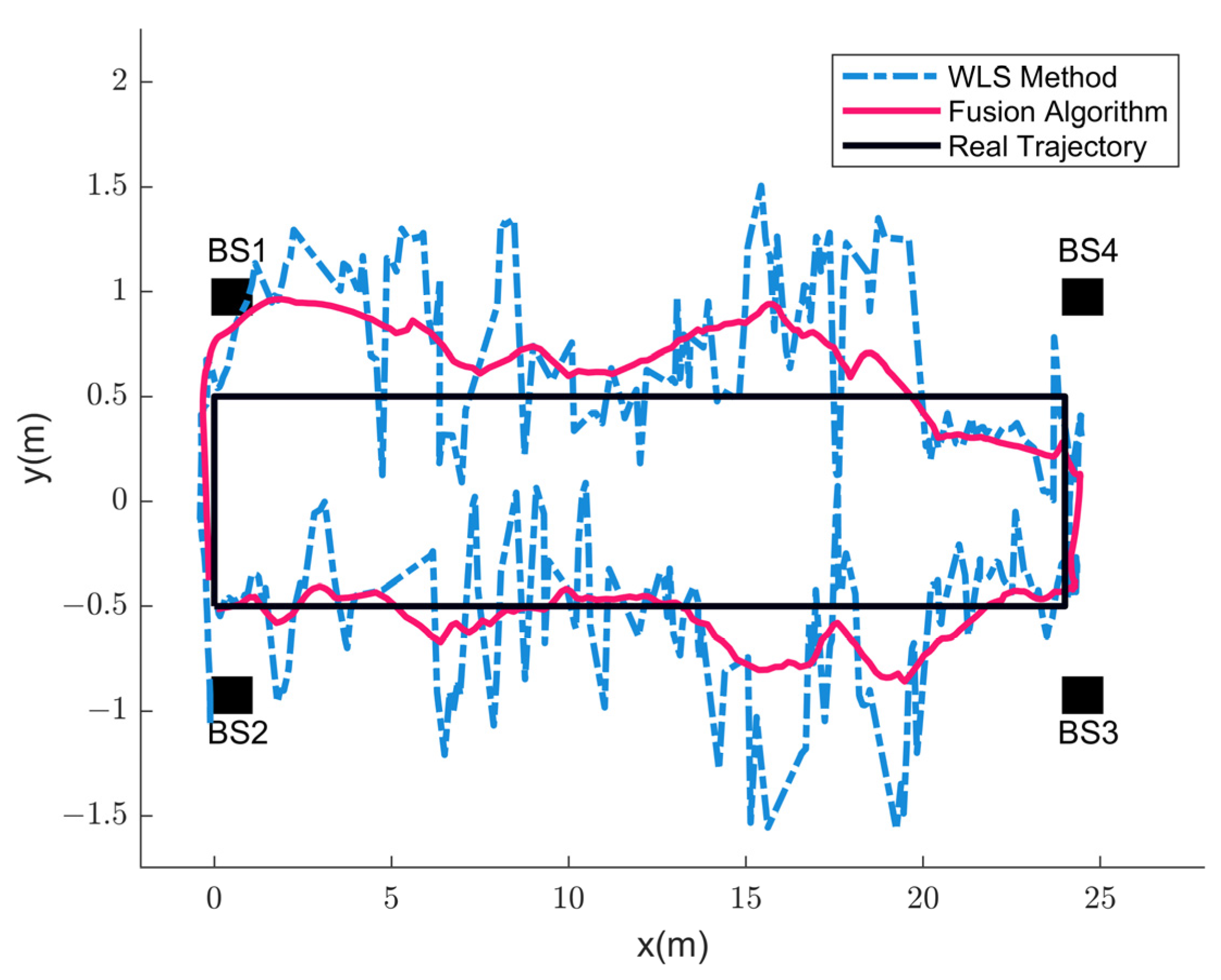
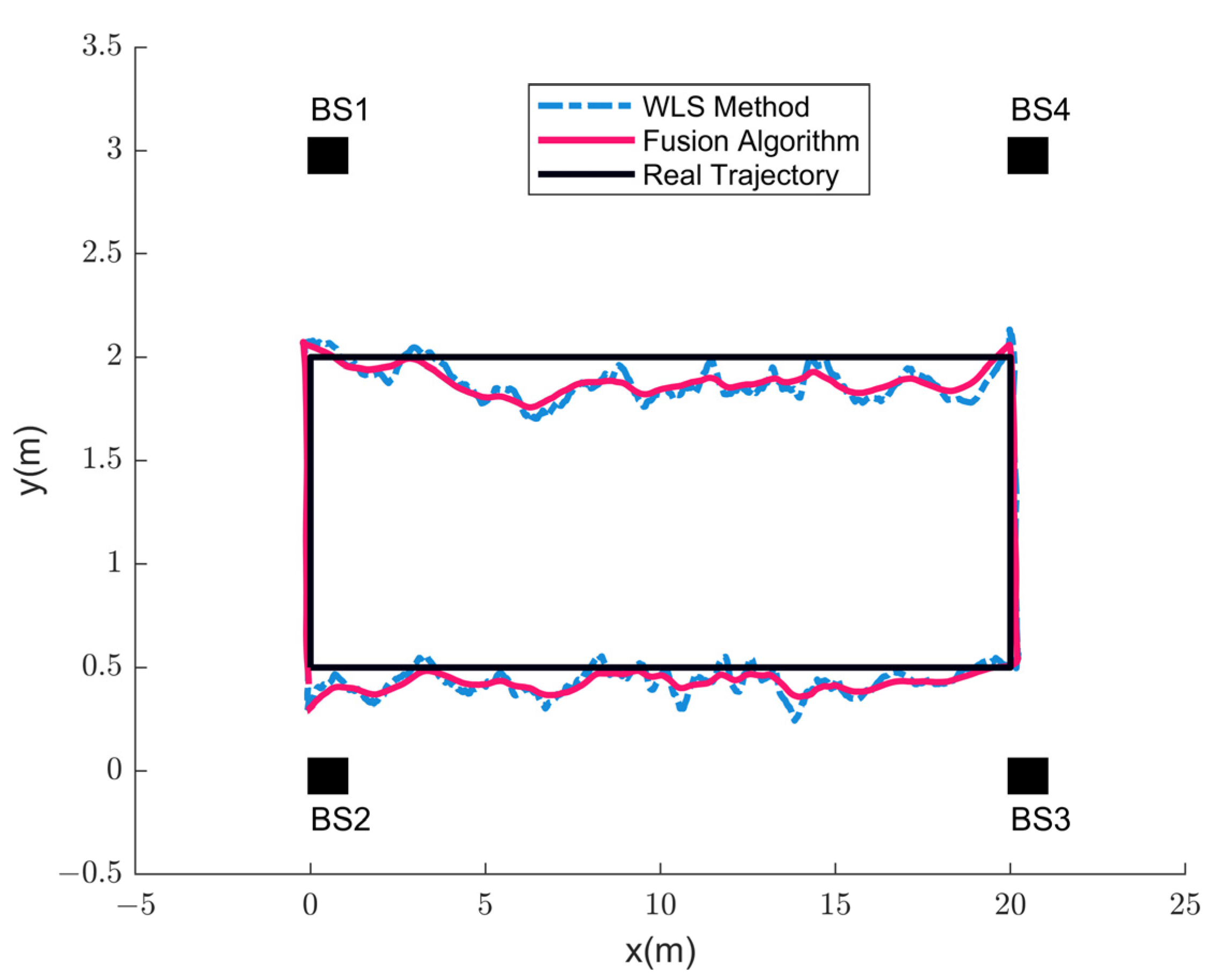
3.3. Experimental Results of Positioning
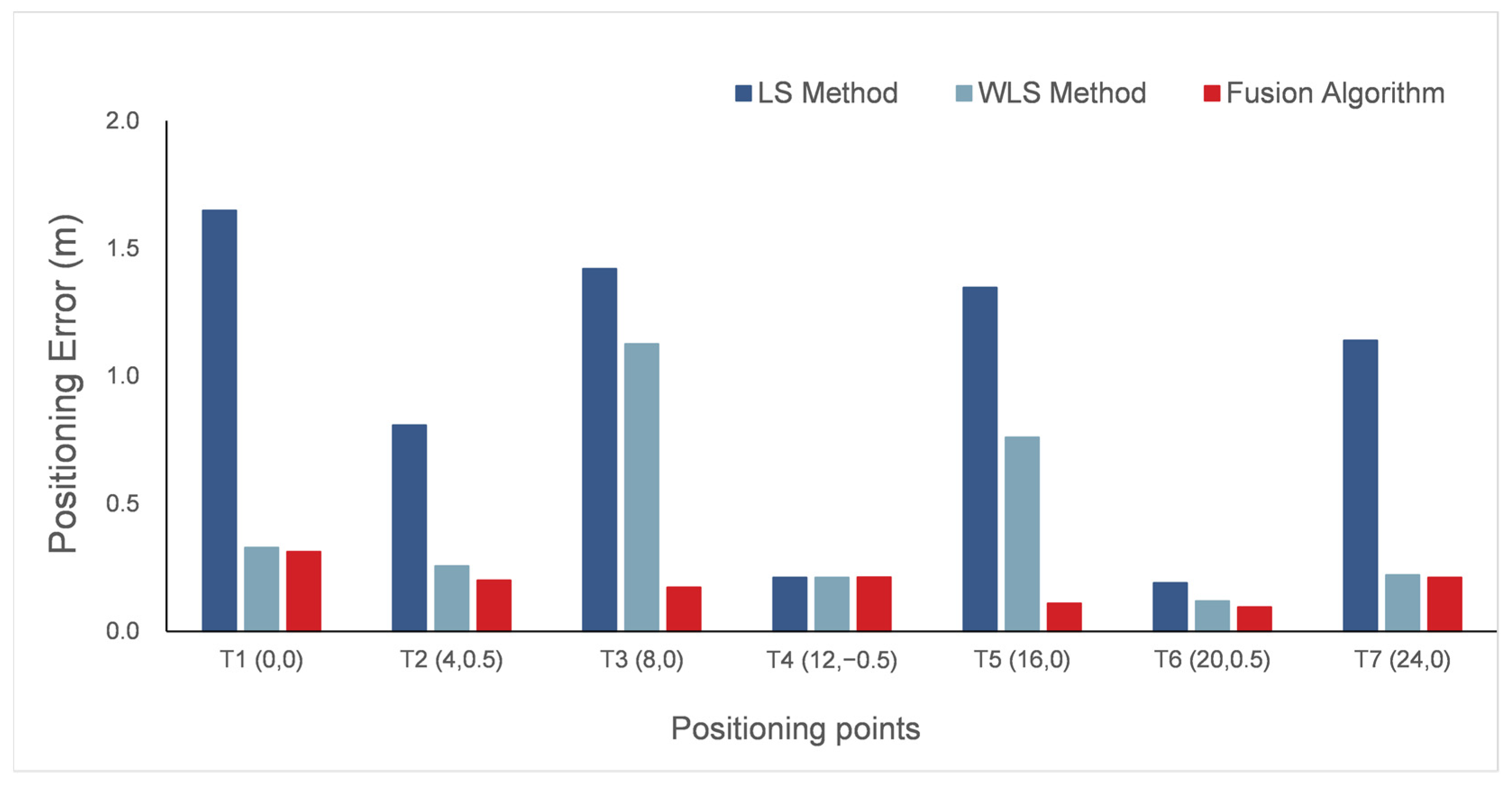
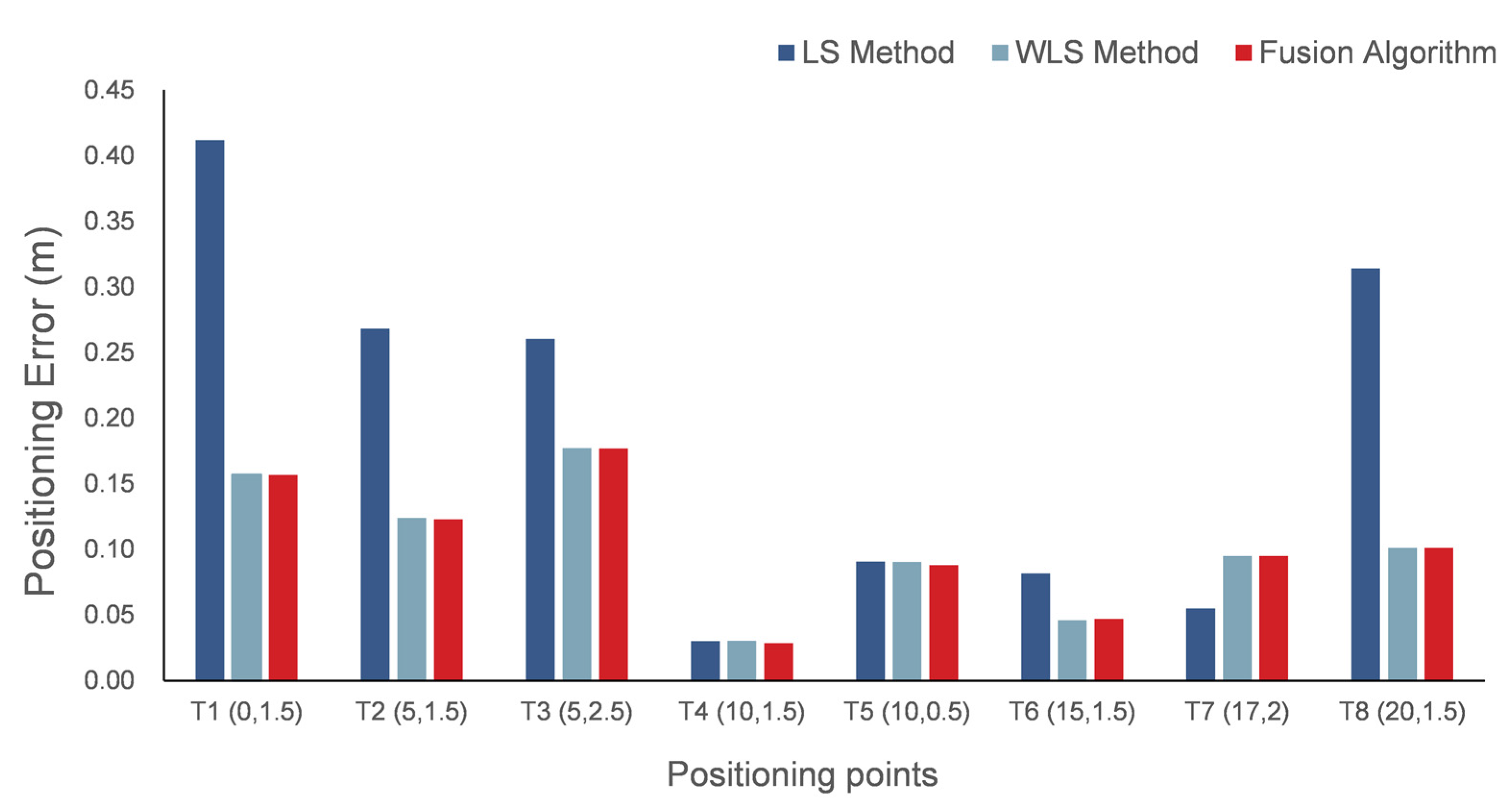
3.3.1. Static Positioning
3.3.2. Dynamic Positioning
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oguntala, G.; Abd-Alhameed, R.; Jones, S.; Noras, J.; Patwary, M.; Rodriguez, J. Indoor Location Identification Technologies for Real-Time IoT-Based Applications: An Inclusive Survey. Comput. Sci. Rev. 2018, 30, 55–79. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Asaad, S.M.; Maghdid, H.S. A Comprehensive Review of Indoor/Outdoor Localization Solutions in IoT Era: Research Challenges and Future Perspectives. Comput. Netw. 2022, 212, 109041. [Google Scholar] [CrossRef]
- Zhuang, Y.; Wang, Q.; Shi, M.; Cao, P.; Qi, L.; Yang, J. Low-Power Centimeter-Level Localization for Indoor Mobile Robots Based on Ensemble Kalman Smoother Using Received Signal Strength. IEEE Internet Things J. 2019, 6, 6513–6522. [Google Scholar] [CrossRef]
- Otero, R.; Lagüela, S.; Garrido, I.; Arias, P. Mobile Indoor Mapping Technologies: A Review. Autom. Constr. 2020, 120, 103399. [Google Scholar] [CrossRef]
- Maranò, S.; Gifford, W.M.; Wymeersch, H.; Win, M.Z. NLOS Identification and Mitigation for Localization Based on UWB Experimental Data. IEEE J. Sel. Areas Commun. 2010, 28, 1026–1035. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef]
- Chandra, A.; Prokeš, A.; Mikulášek, T.; Blumenstein, J.; Kukolev, P.; Zemen, T.; Mecklenbräuker, C.F. Frequency-Domain In-Vehicle UWB Channel Modeling. IEEE Trans. Veh. Technol. 2016, 65, 3929–3940. [Google Scholar] [CrossRef]
- Wang, S.; Mao, G.; Zhang, J.A. Joint Time-of-Arrival Estimation for Coherent UWB Ranging in Multipath Environment with Multi-User Interference. IEEE Trans. Signal Process. 2019, 67, 3743–3755. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, M. The LOS/NLOS Classification Method Based on Deep Learning for the UWB Localization System in Coal Mines. Appl. Sci. 2022, 12, 6484. [Google Scholar] [CrossRef]
- Yu, B.; Fan, G.; Luo, Y.; Sheng, C.; Gan, X.; Huang, L.; Rong, Q. Multi-Source Fusion Positioning Algorithm Based on Pseudo-Satellite for Indoor Narrow and Long Areas. Adv. Space Res. 2021, 68, 4456–4469. [Google Scholar] [CrossRef]
- Zhao, W.; Zong, R.; Yao, B.; Gao, J.; Liao, G. Analysis of Influencing Factors on Flashover in the Long-Narrow Confined Space. Procedia Eng. 2013, 62, 250–257. [Google Scholar] [CrossRef]
- Sadeghi, S.; Soltanmohammadlou, N.; Nasirzadeh, F. Applications of Wireless Sensor Networks to Improve Occupational Safety and Health in Underground Mines. J. Safety Res. 2022, in press. [Google Scholar] [CrossRef]
- Ranjan, A.; Sahu, H.B.; Misra, P. Modeling and Measurements for Wireless Communication Networks in Underground Mine Environments. Measurement 2020, 149, 106980. [Google Scholar] [CrossRef]
- Sharp, I.; Yu, K.; Hedley, M. On the GDOP and Accuracy for Indoor Positioning. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2032–2051. [Google Scholar] [CrossRef]
- Jian, S.; Yongling, F.; Lin, T.; Shengguang, L. A Survey and Application of Indoor Positioning Based on Scene Classification Optimization. In Proceedings of the 2015 IEEE 12th Intl Conf on Ubiquitous Intelligence and Computing and 2015 IEEE 12th Intl Conf on Autonomic and Trusted Computing and 2015 IEEE 15th Intl Conf on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom), Beijing, China, 10–14 August 2015; pp. 1558–1562. [Google Scholar]
- Wang, H.; Zhan, X.; Zhang, Y. Geometric Dilution of Precision for GPS Single-Point Positioning Based on Four Satellites. J. Syst. Eng. Electron. 2008, 19, 1058–1063. [Google Scholar] [CrossRef]
- Li, C.; Teng, Y.; Kang, R. Some Remarks on Geometric Dilution of Precision (GDOP) at User Level in Multi-GNSS Positioning. Adv. Space Res. 2018, 62, 3048–3052. [Google Scholar] [CrossRef]
- Feng, G.; Shen, C.; Long, C.; Dong, F. GDOP Index in UWB Indoor Location System Experiment. In Proceedings of the 2015 IEEE Sensors, Valencia, Spain, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Wang, M.; Chen, Z.; Zhou, Z.; Fu, J.; Qiu, H. Analysis of the Applicability of Dilution of Precision in the Base Station Configuration Optimization of Ultrawideband Indoor TDOA Positioning System. IEEE Access 2020, 8, 225076–225087. [Google Scholar] [CrossRef]
- Bais, A.; Kiwan, H.; Morgan, Y. On Optimal Placement of Short Range Base Stations for Indoor Position Estimation. J. Appl. Res. Technol. 2014, 12, 886–897. [Google Scholar] [CrossRef]
- Syafrudin, M.; Walter, C.; Schweinzer, H. Robust Locating Using LPS LOSNUS under NLOS Conditions. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; pp. 582–590. [Google Scholar]
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial Applications of the Kalman Filter: A Review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef]
- Basar, T. A New Approach to Linear Filtering and Prediction Problems. In Control Theory: Twenty-Five Seminal Papers (1932–1981); IEEE: Piscataway, NJ, USA, 2001; pp. 167–179. ISBN 978-0-470-54433-4. [Google Scholar]
- Janjanam, L.; Saha, S.K.; Kar, R.; Mandal, D. Improving the Modelling Efficiency of Hammerstein System Using Kalman Filter and Its Parameters Optimised Using Social Mimic Algorithm: Application to Heating and Cascade Water Tanks. J. Frankl. Inst. 2022, 359, 1239–1273. [Google Scholar] [CrossRef]
- Li, Q.; Li, R.; Ji, K.; Dai, W. Kalman Filter and Its Application. In Proceedings of the 2015 8th International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Tianjin, China, 1–3 November 2015; pp. 74–77. [Google Scholar]
- Li, M. The Simulation Research of Multi-Model Adaptive KF and Target Tracking. In Proceedings of the 2021 Chinese Intelligent Systems Conference; Jia, Y., Zhang, W., Fu, Y., Yu, Z., Zheng, S., Eds.; Springer: Singapore, 2022; pp. 11–18. [Google Scholar]
- Li, D.; Wang, X.; Chen, D.; Zhang, Q.; Yang, Y. A Precise Ultra-Wideband Ranging Method Using Pre-Corrected Strategy and Particle Swarm Optimization Algorithm. Measurement 2022, 194, 110966. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, R.; Wang, J.; Yu, T.; Su, A. Nonlinear State Estimation with Delayed Measurements Using Data Fusion Technique and Cubature Kalman Filter for Chemical Processes. Chem. Eng. Res. Des. 2019, 141, 502–515. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Y.; Sun, X.; Sang, H. A New Multi-Sensor Hierarchical Data Fusion Algorithm Based on Unscented Kalman Filter for the Attitude Observation of the Wave Glider. Appl. Ocean Res. 2021, 109, 102562. [Google Scholar] [CrossRef]
- Cheng, J.H.; Yu, P.P.; Huang, Y.R. Application of Improved Kalman Filter in Under-Ground Positioning System of Coal Mine. IEEE Trans. Appl. Supercond. 2021, 31, 0603904. [Google Scholar] [CrossRef]
- Feng, D.; Wang, C.; He, C.; Zhuang, Y.; Xia, X.-G. Kalman-Filter-Based Integration of IMU and UWB for High-Accuracy Indoor Positioning and Navigation. IEEE Internet Things J. 2020, 7, 3133–3146. [Google Scholar] [CrossRef]
- Ananthasayanam, M.R.; Mohan, M.S.; Naik, N.; Gemson, R.M.O. A Heuristic Reference Recursive Recipe for Adaptively Tuning the Kalman Filter Statistics Part-1: Formulation and Simulation Studies. Sādhanā 2016, 41, 1473–1490. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Xu, L.; Yang, E. Highly Computationally Efficient State Filter Based on the Delta Operator. Int. J. Adapt. Control Signal Process. 2019, 33, 875–889. [Google Scholar] [CrossRef]
- Tabacek, J.; Havlena, V. Reduction of Prediction Error Sensitivity to Parameters in Kalman Filter. J. Frankl. Inst. 2022, 359, 1303–1326. [Google Scholar] [CrossRef]
- Herrera, L.; Rodríguez-Liñán, M.C.; Clemente, E.; Meza-Sánchez, M.; Monay-Arredondo, L. Evolved Extended Kalman Filter for First-Order Dynamical Systems with Unknown Measurements Noise Covariance. Appl. Soft Comput. 2022, 115, 108174. [Google Scholar] [CrossRef]
- Wang, J.; Ying, J.; Jiang, S. UWB Base Station Layout Optimization in Underground Parking Lots. J. Highw. Transp. Res. Dev. Engl. Ed. 2021, 15, 82–87. [Google Scholar] [CrossRef]
- Xiaolin, N.; Yuqing, Y.; Mingzhen, G.; Weiren, W.; Jiancheng, F.; Gang, L. Pulsar Navigation Using Time of Arrival (TOA) and Time Differential TOA (TDTOA). Acta Astronaut. 2018, 142, 57–63. [Google Scholar] [CrossRef]
- Zhang, Y.; Chu, Y.; Fu, Y.; Li, Z.; Song, Y. UWB Positioning Analysis and Algorithm Research. Procedia Comput. Sci. 2022, 198, 466–471. [Google Scholar] [CrossRef]
- Xu, P. Improving the Weighted Least Squares Estimation of Parameters in Errors-in-Variables Models. J. Frankl. Inst. 2019, 356, 8785–8802. [Google Scholar] [CrossRef]
- Svecova, M.; Kocur, D.; Zetik, R. Object Localization Using Round Trip Propagation Time Measurements. In Proceedings of the 2008 18th International Conference Radioelektronika, Prague, Czech Republic, 24–25 April 2008; pp. 1–4. [Google Scholar]
- Biswas, S.K.; Qiao, L.; Dempster, A.G. Effect of PDOP on Performance of Kalman Filters for GNSS-Based Space Vehicle Position Estimation. GPS Solut. 2017, 21, 1379–1387. [Google Scholar] [CrossRef]
- Navon, E.; Bobrovsky, B.Z. An Efficient Outlier Rejection Technique for Kalman Filters. Signal Process. 2021, 188, 108164. [Google Scholar] [CrossRef]
- Wang, G.; Chen, B.; Yang, X.; Peng, B.; Feng, Z. Numerically Stable Minimum Error Entropy Kalman Filter. Signal Process. 2021, 181, 107914. [Google Scholar] [CrossRef]
- Liu, T.; Cheng, S.; Wei, Y.; Li, A.; Wang, Y. Fractional Central Difference Kalman Filter with Unknown Prior Information. Signal Process. 2019, 154, 294–303. [Google Scholar] [CrossRef]
- Qiu, F.; Zhang, W. Position Error vs. Signal Measurements: An Analysis towards Lower Error Bound in Sensor Network. Digit. Signal Process. 2022, 129, 103637. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, H.; Yang, J.; Chen, Y.; Martin, R.P.; Li, X. A Study of Localization Accuracy Using Multiple Frequencies and Powers. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1955–1965. [Google Scholar] [CrossRef]
- Sharma, R.; Badarla, V. Geometrical Optimization of A Novel Beacon Placement Strategy for 3D Indoor Localization. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018; pp. 1–6. [Google Scholar]
- Pan, H.; Qi, X.; Liu, M.; Liu, L. Indoor Scenario-Based UWB Anchor Placement Optimization Method for Indoor Localization. Expert Syst. Appl. 2022, 205, 117723. [Google Scholar] [CrossRef]
- Specht, M. Experimental Studies on the Relationship between HDOP and Position Error in the GPS System. Metrol. Meas. Syst. 2022, 29, 17–36. [Google Scholar]
- Li, Y.; Zhang, Z.; He, X.; Wen, Y.; Cao, X. Realistic Stochastic Modeling Considering the PDOP and Its Application in Real-Time GNSS Point Positioning under Challenging Environments. Measurement 2022, 197, 111342. [Google Scholar] [CrossRef]
- Djosic, S.; Stojanovic, I.; Jovanovic, M.; Djordjevic, G.L. Multi-Algorithm UWB-Based Localization Method for Mixed LOS/NLOS Environments. Comput. Commun. 2022, 181, 365–373. [Google Scholar] [CrossRef]
- Li, C.T.; Cheng, J.C.P.; Chen, K. Top 10 Technologies for Indoor Positioning on Construction Sites. Autom. Constr. 2020, 118, 103309. [Google Scholar] [CrossRef]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A Novel NLOS Mitigation Algorithm for UWB Localization in Harsh Indoor Environments. IEEE Trans. Veh. Technol. 2019, 68, 686–699. [Google Scholar] [CrossRef]



| A0 | A1 | A2 | A3 | |
|---|---|---|---|---|
| X/m | 8 | 32 | 32 | 8 |
| Y/m | 8 | 8 | 32 | 32 |
| Z/m | 3 | 3 | 3 | 3 |
| A0 | A1 | A2 | A3 | |
|---|---|---|---|---|
| X/m | 8 | 32 | 32 | 8 |
| Y/m | 20 | 20 | 22 | 22 |
| Z/m | 3 | 3 | 3 | 3 |
| A0 | A1 | A2 | A3 | |
|---|---|---|---|---|
| X/m | 10 | 30 | 30 | 10 |
| Y/m | 20 | 20 | 23 | 23 |
| Z/m | 3 | 3 | 3 | 3 |
| Tag Number | Scene A | Scene B | ||||
|---|---|---|---|---|---|---|
| LS (m) | WLS (m) | Fusion (m) | LS (m) | WLS (m) | Fusion (m) | |
| T1 | 1.648 | 0.328 | 0.311 | 0.412 | 0.157 | 0.157 |
| T2 | 0.807 | 0.256 | 0.199 | 0.268 | 0.124 | 0.123 |
| T3 | 1.420 | 1.125 | 0.171 | 0.260 | 0.177 | 0.177 |
| T4 | 0.211 | 0.210 | 0.212 | 0.030 | 0.030 | 0.028 |
| T5 | 1.347 | 0.759 | 0.110 | 0.090 | 0.090 | 0.088 |
| T6 | 0.189 | 0.118 | 0.095 | 0.082 | 0.046 | 0.047 |
| T7 | 1.139 | 0.221 | 0.210 | 0.055 | 0.095 | 0.095 |
| T8 | null | null | null | 0.314 | 0.101 | 0.101 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Li, W.; Yang, G.; Jiao, Z.; Yan, J. Combining Dilution of Precision and Kalman Filtering for UWB Positioning in a Narrow Space. Remote Sens. 2022, 14, 5409. https://doi.org/10.3390/rs14215409
Guo Y, Li W, Yang G, Jiao Z, Yan J. Combining Dilution of Precision and Kalman Filtering for UWB Positioning in a Narrow Space. Remote Sensing. 2022; 14(21):5409. https://doi.org/10.3390/rs14215409
Chicago/Turabian StyleGuo, Yunjian, Weihong Li, Guang Yang, Zhenhang Jiao, and Jiachen Yan. 2022. "Combining Dilution of Precision and Kalman Filtering for UWB Positioning in a Narrow Space" Remote Sensing 14, no. 21: 5409. https://doi.org/10.3390/rs14215409
APA StyleGuo, Y., Li, W., Yang, G., Jiao, Z., & Yan, J. (2022). Combining Dilution of Precision and Kalman Filtering for UWB Positioning in a Narrow Space. Remote Sensing, 14(21), 5409. https://doi.org/10.3390/rs14215409