Quantifying the Effect of River Ice Surface Roughness on Sentinel-1 SAR Backscatter

Abstract

Satellite-based C-band synthetic aperture radar (SAR) imagery is an effective tool to map and monitor river ice on regional scales because the SAR backscatter is affected by various physical properties of the ice, including roughness, thickness, and structure. Validation of SAR-based river ice classification maps is typically performed using expert interpretation of aerial or ground reference images of the river ice surface, using visually apparent changes in surface roughness to delineate different ice classes. Although many studies achieve high classification accuracies using this qualitative technique, it is not possible to determine if the river ice information contained within the SAR backscatter data originates from the changes in surface roughness used to create the validation data, or from some other ice property that may be more relevant for ice jam forecasting. In this study, we present the first systematic, quantitative investigation of the effect of river ice surface roughness on C-band Sentinel-1 backscatter. We use uncrewed aerial vehicle-based Structure from Motion photogrammetry to generate high-resolution (0.03 m) digital elevation models of river ice surfaces, from which we derive measurements of surface roughness. We employ Random Forest models first to repeat previous ice classification studies, and then as regression models to explore quantitative relationships between ice surface roughness and Sentinel-1 backscatter. Classification accuracies are similar to those reported in previous studies (77–96%) but poor regression performance for many surface roughness metrics (5–113% mean absolute percentage errors) indicates a weak relationship between river ice surface roughness and Sentinel-1 backscatter. Additional work is necessary to determine which physical ice properties are strong controls on C-band SAR backscatter.

1. Introduction

Seasonal ice cover on high latitude rivers affects the ecology [1], morphology [2], sediment transport [3], and hydraulics [4] of river systems. Perhaps the most consequential aspects of river ice for human society are ice jams and associated flooding. Many types of ice jams and jamming mechanics are well-described [5], and rapid-onset, damaging ice jam floods are often associated with mechanical spring breakup [6]. This scenario occurs at the end of the ice season when a sudden increase in river discharge (e.g., from a rain-on-snow event) causes ice to release from the river channel before significant thermal deterioration of the ice has taken place. As the broken ice pieces run downstream, they may jam in a bend, constrict, or reach with stronger ice cover and cause backwater flooding. Later, the sudden release of the blocked ice sends an ice jam wave (“jave”) of ice and water downstream which can cause rapid flooding. The April 2020 mechanical breakup of ice on the Athabasca River in Alberta, Canada resulted in an ice jam more than 20 km in length that formed near the town of Fort McMurray and caused an estimated C $1.1 billion in flooding damages, the evacuation of more than 13,000 residents, and one death [7]. These events are difficult to forecast due to the dynamic interactions between many hydrological, meteorological, and geomorphological factors [8]. Ice jam flood forecasts combine meteorological forecasts and hydrological conditions with the seasonal history and current state of river ice, including information about ice extent, type, and strength [4].

Satellite remote sensing has been used in previous studies to obtain river ice information at regional scales. In particular, synthetic aperture radar (SAR) has proven useful for classifying ice types and tracking ice evolution because microwave scattering is strongly affected by the physical properties of river ice, including surface roughness, thickness, and the presence of impurities (e.g., air inclusions or silt) within ice layers [9,10]. Figure 1 illustrates this effect. Previous studies that have created ice classification maps using fully polarimetric RADARSAT-2 data (e.g., [11,12,13,14,15]) conclude that the highest classification accuracies are achieved when HH polarized data are included in the classification model. For a comprehensive overview of SAR-based river ice studies, see van der Sanden et al. [16].

The roughness of the ice cover at the air-ice interface is the most easily observable among the scattering-relevant properties. Accordingly, ground photos or airplane surveys of frozen rivers have been used as validation data for regional SAR-based ice cover classification [17,18,19,20]. Various ice types are delineated via expert interpretation of the photos, typically using visually-apparent changes in surface roughness to distinguish between different types [14,16,21]. The boundaries of the ice classes are digitized and used as labels for training and validation data, then compared to SAR data using supervised and unsupervised classification algorithms. Some studies that use this validation technique have reported global classification accuracies above 90% for some model configurations [12] with accuracies reaching as high as 99% for individual classes [21]. Such robust classification results show that SAR backscatter data contain information derived from the physical properties of river ice. However, this inherently subjective validation method results in ambiguity when interpreting ice maps: it is impossible to quantify the degree to which changes in SAR backscatter are related to surface roughness (visible at the surface) compared to other scattering-relevant properties (changes in ice thickness or structure not visible at the surface). This ambiguity is further complicated by the fact that changes in scattering-relevant properties are not always spatially correlated. For example, field measurements show that the thickness and roughness of ice jams are related linearly on average, but thickness can also vary significantly over small (~m) spatial scales due to the dynamic processes involved in river ice formation [22]. Ambiguity in the interpretation of ice maps with respect to the true ice conditions could lead to inaccurate ice jam forecasts.

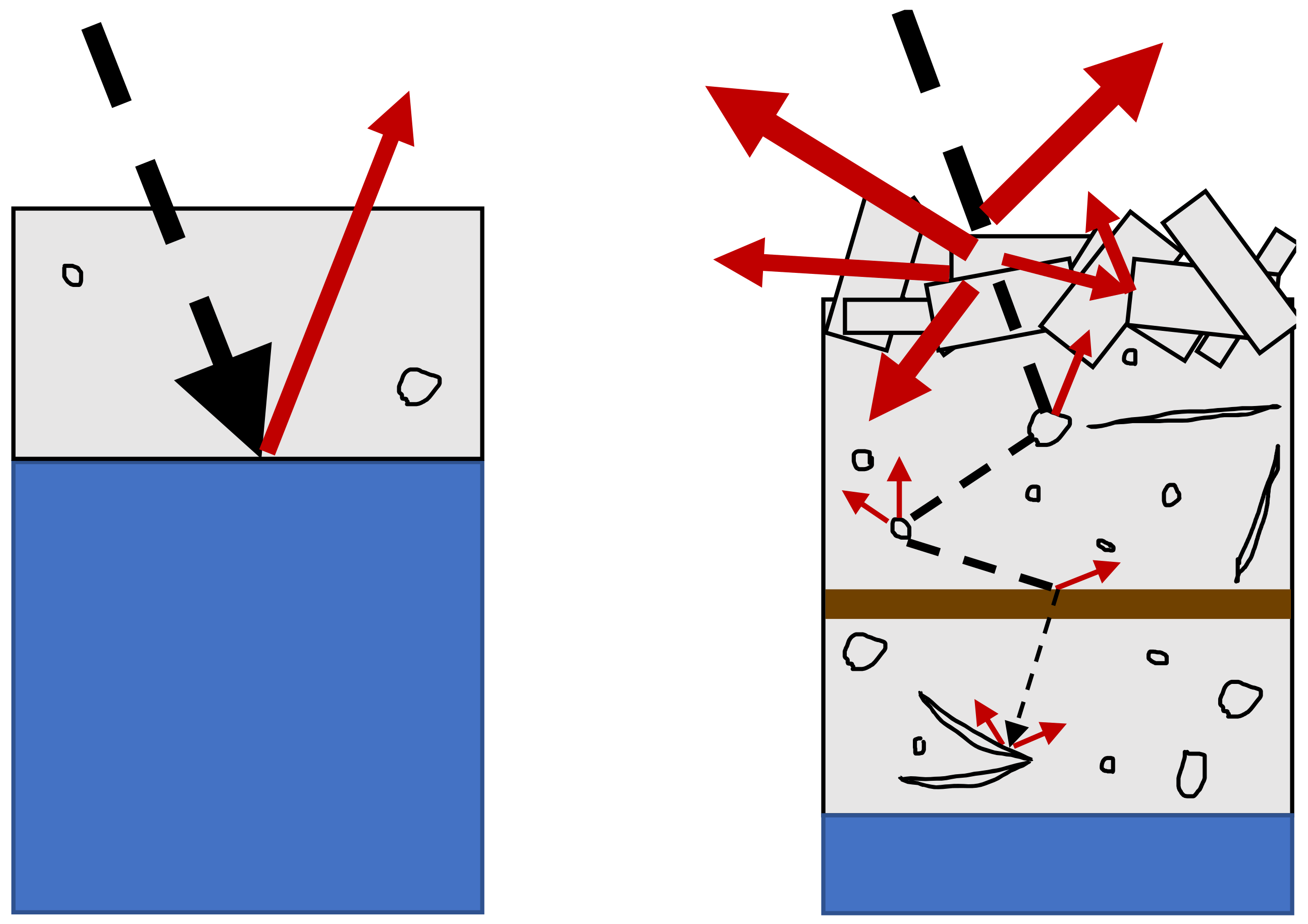
With respect to microwave scattering, classification of the roughness of any surface (i.e., smooth vs. rough) depends on the wavelength $\lambda$ and incidence angle $\theta$ of the incident radiation [23]. The roughness of a surface determines the type of scattering, with smooth surfaces resulting primarily in specular reflection away from the sensor and rough surfaces resulting in isotropic scattering, leading to increased backscatter [24]. Surface roughness is typically quantified by calculating the standard deviation h of heights of individual features of a surface. As a general rule of thumb, the features used to calculate h should have a horizontal spacing no greater than $\lambda /10$ [25]. Based on equations given by Sabins [26], van der Sanden and Drouin [23] calculate that for C-band SAR with $\lambda =0.055$ m and $\theta ={35}^{°}$ (representative of RADARSAT-2 data), the ice surface at the air-ice interface is considered radiometrically smooth when $h<0.0027$ m and rough when $h>0.0154$ m for surface features separated by distances less than 0.0056 m. These microscale roughness features that affect SAR backscatter behavior are orders of magnitude smaller than the decimeter-scale and larger ice pieces that are physically relevant for ice jam formation. However, validation of SAR-derived river ice products has typically been approached from the perspective of traditional river ice science, which relies on visible changes in surface roughness (thereby emphasizing large roughness features) to denote rough and smooth surfaces [14,20,21]. For SAR-based products to be incorporated into operational ice jam forecasting, this disconnect between radiometrically- and physically-relevant roughness scales must be addressed to reduce uncertainty when interpreting ice cover maps.

In this study, we present the first systematic, quantitative investigation of the effect of river ice surface roughness on the European Space Agency’s Sentinel-1 SAR backscatter. The Sentinel-1 platform utilizes the same C-band ($\lambda =0.055$ m) SAR wavelength as RADARSAT-2, but over land surfaces (i.e., frozen rivers of interest) typically operates in dual-polarized VV and VH mode. Even without the information-rich HH band, Sentinel-1 imagery has been used successfully to derive qualitative river ice information at regional scales [27,28,29]. Sentinel-1 imagery is also freely available through the Copernicus Open Access Hub whereas there are non-trivial costs associated with acquiring RADARSAT-2 imagery, especially on an operational basis. For ground validation data we use an uncrewed aerial vehicle (UAV)-based Structure from Motion (SfM) photogrammetry [30] to generate high-resolution (0.03 m) digital elevation models (DEMs) of a river ice surface, from which we derive measurements of surface roughness. UAVs have been employed in previous river ice literature to generate training photosets for ice classifiers [31,32,33], and UAV-SfM has been used to calculate ice surface area and channel-wide fractional ice coverage [34] and to measure ice thickness and volume [35,36,37,38]. Importantly, Rødtang et al. [38] established that UAV-SfM accuracy remained consistent across ice-free, freezeup, and midwinter ice conditions, demonstrating that this technique is suitable as a general method to measure all types of river ice. The UAV-based method also improves upon the limitations of traditional river ice photography methods. Ground-based photos provide a limited extent of the frozen river surface at very low viewing angles, which may complicate the interpretation of the image. Airplane-based surveys provide high-quality images over greater extents but come with high operational costs.

We note that the 0.03 m resolution of our UAV-based measurements does not meet the threshold criteria of 0.0056 m (i.e., $\lambda /10$) necessary for separating radiometrically smooth and rough surfaces with respect to C-band Sentinel-1 measurements. However, the two-order of magnitude difference in spatial resolutions between the UAV and satellite datasets allows for an in-depth examination of surface roughness features that are contained within, but not explicitly resolved by, a 10 m Sentinel-1 pixel. Hence, this paper serves as an attempt to quantify the information contained in river ice surface roughness which has been used by expert visual interpreters in previous studies. We employ Random Forest (RF) regression models for this purpose. We approach this exploration with the following hypotheses:

• RF regression models for river ice surface roughness prediction are not location- or condition-specific; model performance will improve for models trained with data from multiple aerial surveys compared to models trained with a single survey.
• Regression model performance will be affected by the spatial scale at which river ice surface roughness elements are quantified. Finer spatial scales will provide more detailed information content and result in better model performance while coarser spatial scales with less detailed information content will result in worse model performance.
• Regardless of the spatial scale or method used to quantify river ice surface roughness, the roughness will show, at best, a moderately strong correlation with Sentinel-1 backscatter because other physical properties related to ice structure that affect the backscatter signal are not measured by the UAV-SfM method, and therefore not accounted for in the models.

Exploring these hypotheses can enhance ice jam forecasts by improving our understanding of the river ice information contained in SAR imagery. If SAR backscatter is strongly controlled by ice roughness, traditional visually-based validation can still be utilized for ice classification maps and ice jam forecasters can incorporate roughness information into their forecast models. Finding a weak relationship between SAR backscatter and ice roughness could help guide future field campaigns to target measurements of ice properties that are more relevant with respect to SAR imagery, for both current and future sensor platforms. The remainder of the paper is organized as follows: Section 2 details our methodology for UAV aerial surveys, surface roughness measurements, and RF analysis; Section 3 contains results, which are discussed in Section 4; finally, we conclude the study briefly in Section 5.

2. Methods

Our measurements of river ice surface roughness are derived from high-resolution, SfM-based DEMs generated from UAV aerial surveys. Before we investigate quantitative relationships with Random Forest (RF) regression models, we must first verify that RF models in general are appropriate to use with our novel dataset. Without this verification it would be difficult to interpret poor regression performance: are the poor results because the observed surface roughness values have little influence on the SAR backscatter, or are they due to a poorly-chosen model for the dataset?

For this reason, we begin our analysis with RF classification, a supervised technique which has been used successfully to classify river ice using Sentinel-1 imagery [29]. Demonstrating that RFs can classify our novel dataset with acceptable accuracy provides a straightforward interpretation of RF regression results. We create various quantitative metrics with UAV-derived surface roughness measurements to describe the roughness characteristics within the Sentinel-1 pixels in different ways. We also investigate the effect of summarizing the UAV-derived roughness information at different spatial scales, and explore how these different expressions affect RF regression performance.

2.1. Study Site and Ice Conditions

Our study site was a short reach (~0.25 km${}^2$) of the Yellowstone River near Glendive, Montana, USA (Figure 2). The Yellowstone is the longest uncontrolled river in the continental United States (1114 km) and drains approximately 100,000 km${}^2$ of the land area into the upper Missouri River. The channel at our site is approximately 200 m wide and features a large bend. The site has straightforward river access, a multi-decadal history of ice jam formation, and lies in the imaging path of the Sentinel-1B satellite. Strong, gusty winds (>10 m s${}^{-1}$) are typical of the winter months and impede regular UAV operations in the area. Flight dates were planned around Sentinel-1B flyovers that also aligned with fair weather and less windy conditions. We completed two aerial surveys of the site on 19 February and 4 March 2021 before Sentinel-1B went offline in December 2021.

The 19 February aerial survey captured typical midwinter ice conditions. Trace amounts of snow were recorded on 17 and 18 February at the nearby Dawson Community Airport weather station and air temperatures remained at or below freezing during those days. On 19 February a thin (~0.05 m) layer of dry snow was present on top of the river ice at the study site. During the ~2 h aerial survey on 19 February, air temperature ranged from approximately −20 to −16 ${}^{°}$C, and wind speeds increased from calm to approximately 8 m s${}^{-1}$ with stronger gusts, which terminated operations before the entire survey could be completed.

Conditions during the 4 March aerial survey were more representative of the spring transitional period. From 1–3 March daytime high temperatures were above freezing for several hours, with overnight lows dropping back below freezing. It is assumed that the top of the ice surface exhibited diurnal changes during this period, with liquid water appearing during the day and refreezing overnight. The dry snow layer present on the ice during the 19 February survey had either melted or metamorphosed into patchy, wet snow cover by the time we conducted the 4 March survey. Air temperatures increased from below to above freezing and winds remained calm during this full survey.

2.2. UAV Surveys, SfM Processing, and Surface Roughness Calculations

We designed aerial surveys for our study so that the final SfM products would achieve <0.1 m spatial resolution, two orders of magnitude finer than Sentinel-1 backscatter data. We used a commercially-available Vision Aerial Switchblade-Elite tricopter UAV with an integrated Real Time Kinematics (RTK) GPS unit and a Sony $\alpha 6000$ 24.3-megapixel camera payload. We flew pre-planned gridded flight paths at 80 m above ground level with 70% front and side image overlap. The planned survey resulted in 1251 overlapping photos geotagged with latitude, longitude, and altitude information. The 19 February photoset contains only 985 photos because inclement weather prevented us from surveying the entire site. The 4 March photoset contains all 1251 photos. On each field date, we also surveyed at least 6 ground control points on riverbanks and other ice-free areas using Emlid Reach RS2 RTK GNSS receivers to further reduce the georeferencing error.

SfM processing was completed using Agisoft Metashape Professional v1.6.2 [39]. We followed the procedure and suggested processing parameters detailed by Over et al. [40]. The final root-mean-square reprojection error was 0.135 m and 0.131 m for the point clouds used to generate the 19 February and 4 March products, respectively. The SfM-derived products used for further analysis were an orthomosaic photo and a DEM of the study site from each flight date. The native resolution of the DEMs were 0.028 and 0.030 m for the 19 February and 4 March surveys, respectively. Both DEMs were aligned and exported at 0.03 m resolution for further analysis.

Within the river channel portion of the DEMs, we calculated surface roughness at every pixel as the standard deviation of elevation within a 3 × 3 moving pixel window. We chose the smallest window size possible to minimize artificial smoothing of the finely-detailed information present in the DEM. The use of a moving window resulted in surface roughness data at the same 0.03 m spatial resolution as the raw elevation data.

2.3. Sentinel-1 Imagery

Our field site was imaged by the Sentinel-1B platform on 18 February and 2 March at around 18:00 local time (MDT). The two satellite images were acquired approximately 12 h and 36 h before our aerial surveys on 19 February and 4 March, respectively. We downloaded the Ground Range Detected (GRD) products for both images from the Alaska Satellite Facility Vertex Distributed Active Archive Center. We preprocessed the GRD images by applying an orbit file, radiometric calibration, radiometric terrain flattening, and range-doppler terrain correction to obtain VV and VH backscatter intensity in terms of ${\gamma }_0$ with units of dB. ${\gamma }_0$ has been used in previous river ice SAR studies [16,29] because it is less sensitive to changes in radar incidence angle than other measures of backscatter [41]. All image pre-processing was completed using the ESA SNAP software v8.0 [42]. 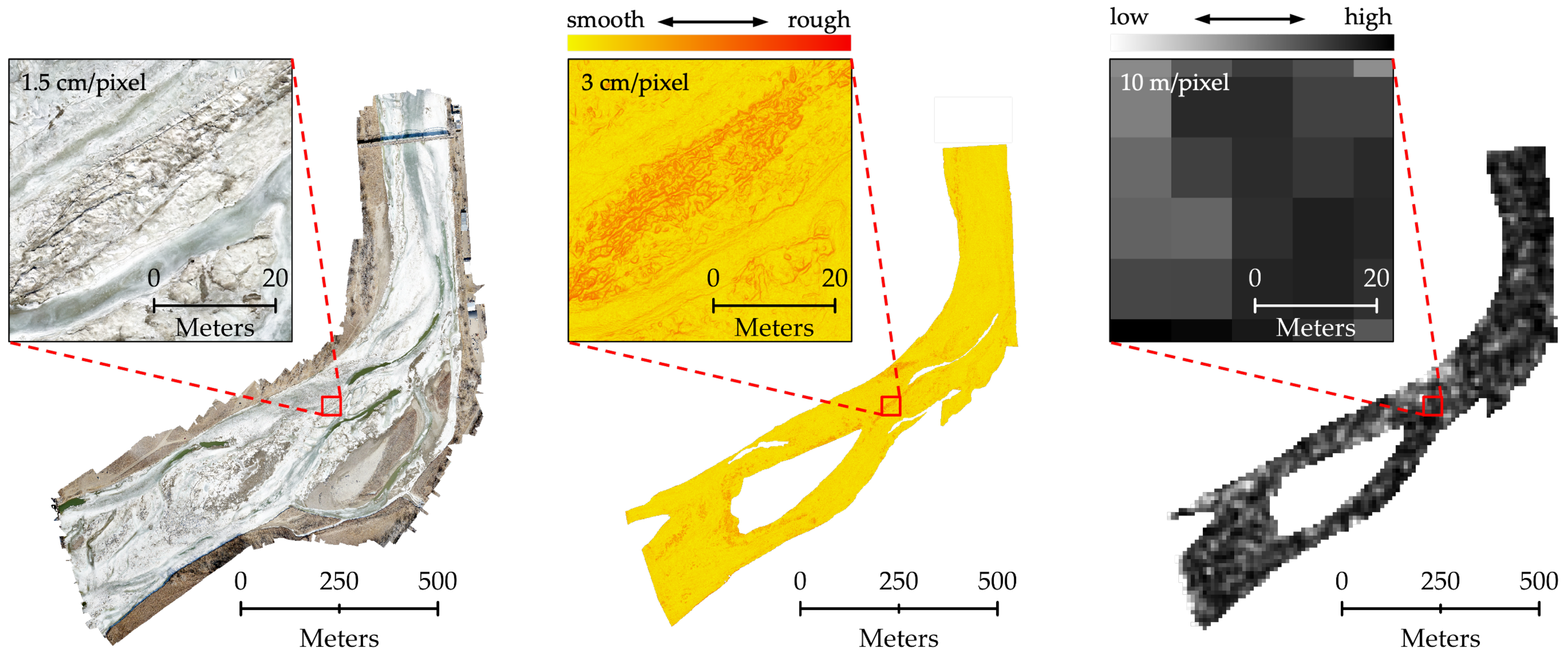Figure 3 shows a comparison of Sentinel-1 VH backscatter alongside UAV orthoimagery and surface roughness measurements.

For the purposes of using Sentinel-1 data as predictor variables, we created additional derived products from the VV and VH bands: the inverse and square of each band, and the product and ratios of both bands, for a total of eight predictors (

Table 1. Sentinel-1 predictor variables used in Random Forest classification and regression models.

Type	Name	Formula
Raw	VV	—
	VH	—
Derived	VV inverse	1/VV
	VH inverse	1/VH
	VV square	VV${}^2$
	VH square	VH${}^2$
	Ratio 1	VV/VH
	Ratio 2	VH/VV
	Product	VV · VH

). This type of feature engineering is a common step in machine learning studies [43]. These eight predictors comprise the Sentinel-1 data used to predict ice type in RF classification experiments and measured surface roughness in RF regression experiments.

2.4. Random Forest Classification

Here we adopt the typical validation strategy of visual interpretation of the UAV-derived orthoimagery. Following de Roda Husman et al. [29] and van der Sanden et al. [16], we initially selected rubble ice (relatively rough), sheet ice (relatively smooth), and open water as the three target classes. We created polygons in ArcGIS Pro marking areas of the three classes in the SfM-derived orthophotos, then overlaid the Sentinel-1 imagery. We discarded any Sentinel-1 pixels that imaged areas outside the boundaries of the frozen river channel to remove backscatter measurements affected by vegetation, bare ground, and built structures. We classified the remaining pixels using an area thresholding technique, where a class label was assigned to a pixel if the label comprised a larger percentage of the pixel’s area than the threshold value (e.g., 50%). This threshold value potentially has a large effect on classification performance: higher values result in more distinct groups, but come at the expense of smaller datasets available to train and test the models. We optimized classification accuracy by experimenting with a range of area threshold values from 50% to 100%. We also note that individual pixels in an input dataset with the same class label are not necessarily spatially adjacent.

Ice conditions at the study site featured very few open water leads and even with the lowest area threshold value of 50%, only 14 Sentinel-1 pixels were classified as open water between both survey dates. This proved to be an insufficient number of samples to generate reasonable classification results and so the open water class was dropped from consideration. To test the general applicability of the classification model on the two remaining classes (sheet ice and rubble ice) we conducted three model runs trained using different datasets: samples from the two survey dates individually, and a third dataset combining the samples from both dates. The individual-date models were not exposed to samples from the other date during either the training or testing phases. We ran each of the three model configurations 100 times, where the input datasets were randomly divided into a 70%/30% train/test data split during each run. Classification accuracy in Section 3 is calculated using the combined output from all 100 model runs.

We implement the RF algorithm using scikit-learn [44], a Python machine learning package. Like most machine learning algorithms, RFs contain a number of hyperparameters that provide the modeler control over the architecture of the algorithm and the computing resources required to train the model. Hyperparameter values are user-specified prior to running the model (i.e., not derived from the input dataset) and can affect model accuracy and other performance measures. Two RF hyperparameters that should be adjusted are the number of decision trees in the forest (’n_estimators’ parameter in the scikit-learn implementation) and the number of predictor variables that should be considered at each split in each tree (’mtry’ parameter) [45]. The default ’mtry’ value in scikit-learn is set as the square root of the number of predictor variables, and several studies have concluded that this is generally a reasonable value [46]. After an extensive review of the literature, Belgiu and Drăguţ [47] suggest a value of 500 trees when using RF classification with remotely sensed data. Our specific model architecture (along with all code and data necessary to repeat the model) can be found in the GitHub repository for this project [48].

2.5. Random Forest Regression

The input dataset for RF regression consists of all available river ice surface roughness measurements and is not based on subjective visual interpretation of ice classes. To compile the dataset we began by selecting only Sentinel-1 pixels from both survey dates that imaged an area 100% covered by ice. This removed backscatter measurements affected by vegetation, bare ground, and built structures. We additionally masked pixels that covered the small areas of open water or bright, homogeneous snow cover. The SfM algorithm cannot locate tie points within these surface types and the resulting DEM contains erroneous elevation values. After clipping and masking we retained 1371 Sentinel-1 pixels that aligned with ice in the 19 February aerial survey and 2320 pixels for the 4 March survey, for a total of 3691 pixels.

Each 10 m Sentinel-1 pixel contains more than 100,000 UAV surface roughness measurements at the 0.03 m spatial scale. However, RF regression models require training data in the form of one-to-one mapping between the target (surface roughness) and predictor variables (Sentinel-1 products). For our study, this requires that within each Sentinel-1 pixel we transform the 100,000 UAV measurements into metrics that represent the fine-scale surface roughness information as a single numerical value. Many transformations are possible and we create two broad suites of surface roughness metrics. Metrics in the first suite can be described as either spatially-based or distribution-based. For the single spatially-based metric, we calculated Moran’s I statistic [49], a measure of spatial autocorrelation, for the UAV measurements inside each Sentinel-1 pixel using ArcGIS Pro. In the distribution-based approach, we fit a log-normal curve to a 100-bin histogram of the UAV measurements contained within each Sentinel-1 pixel. We extracted the means and standard deviations of the estimated distributions as roughness metrics to be used for regression targets.

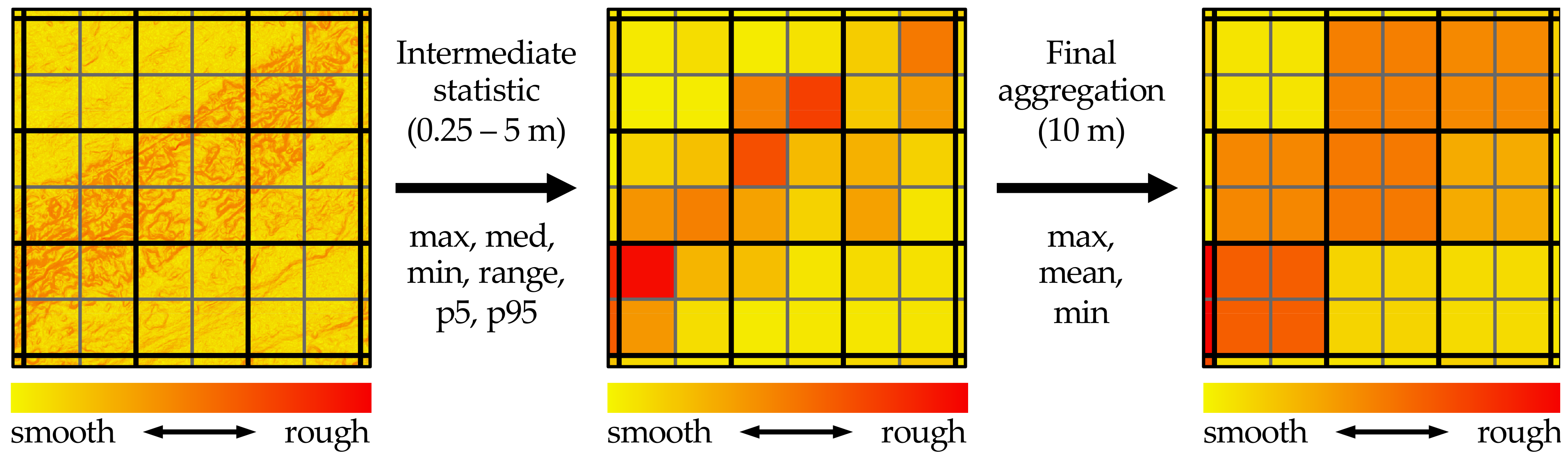
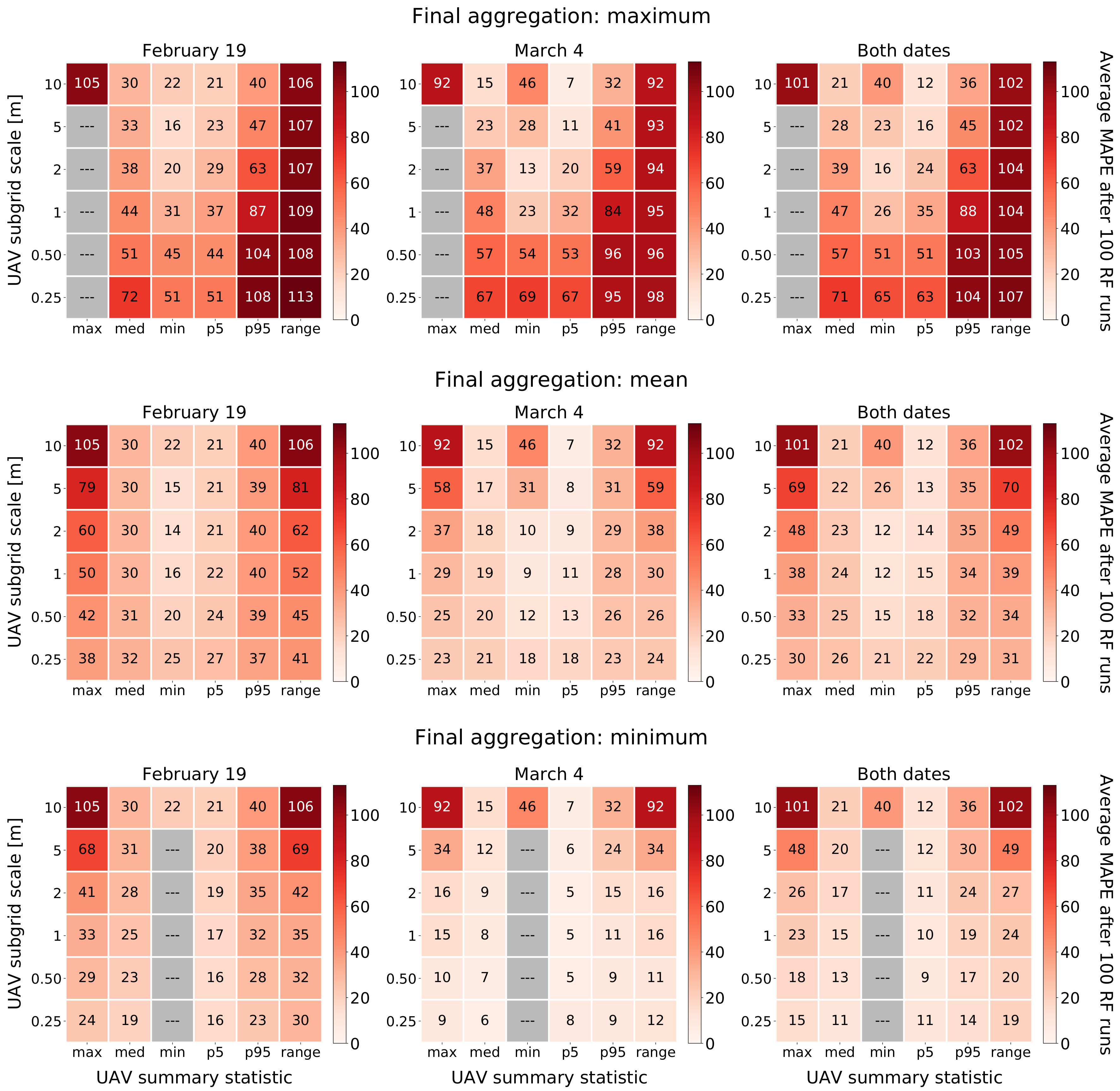
The second suite of metrics was developed to explore the effects of downsampling the UAV roughness measurements at different subgrid spatial scales with respect to the 10 m Sentinel-1 pixels. Figure 4 illustrates the process of deriving these subgrid-statistic roughness metrics. First, we create a new raster grid at an intermediate spatial scale (0.25, 0.5, 1, 2, or 5 m) overlaid on the 10 m Sentinel-1 grid. We resample the 0.03 m UAV measurements to the intermediate grid using a variety of statistics (maximum, median, minimum, range, 5th percentile, and 95th percentile) to emphasize different aspects of the roughness features. Finally, we downsample the intermediate roughness values to a single value in the native 10 m Sentinel-1 resolution using a final aggregation operation (maximum, minimum, and mean). For completeness we also calculate the maximum, median, minimum, range, 5th percentile, and 95th percentile roughness at 10 m resolution directly from the UAV data, skipping the intermediate subgrid step and removing the need to apply a second aggregation operation.

As in the RF classification, we tested the general applicability of the regression models by training/testing models using roughness metrics from the two survey dates individually, plus a third dataset combining metrics from both dates. We ran each of the three model configurations 100 times, where the input datasets were randomly divided into a 70%/30% train/test data split during each run. We increased the number of trees in the forest (’n_estimators’ parameter) to 2000 for regression models, above which the reduction in regression error is negligible [50].

3. Results

3.1. Surface Roughness Measurements

Figure 5 shows the observed probability density functions (PDF) and cumulative density functions (CDF) for UAV-derived river ice surface roughness measurements on the 19 February and 4 March, displayed on a logarithmic x-axis. The density functions were computed using every UAV measurement contained within the 3691 Sentinel-1 retained for the regression models (approximately 410 million observations). For both survey dates, surface roughness measurements vary over several orders of magnitude from fractions of a millimeter to a few centimeters. While these measurements seem relatively small, it is important to remember that they represent the standard deviation of elevation in a 0.09 × 0.09 m area on the ice. Roughness measurements from both survey dates appear to approximate log-normal distributions. The 19 February PDF is centered at approximately 0.0019 m and has a larger standard deviation (i.e., the curve appears wider) than the 4 March PDF, which is centered at approximately 0.0011 m. This indicates a greater range of river ice surface roughness, and also rougher ice on average, on 19 February than on 4 March. Hence when these measurements are the basis for regression targets, models trained with the 19 February data will be exposed to a wider dataset domain than models trained only with the 4 March data.

3.2. Random Forest Classification

Figure 6 shows the observed PDFs and CDFs of surface roughness measurements for the sheet ice and rubble ice class samples selected from the two aerial survey dates with an area threshold value of 50%. Roughness PDFs for sheet ice and rubble ice overlap on both dates, but there is a larger separation between the classes in the 19 February samples (Figure 6, top row) than in the 4 March samples (Figure 6, bottom row). This result is not surprising given the relative shapes of the density functions containing all roughness measurements on the two survey dates (Figure 5).

Figure 7 shows RF classification accuracies using a variety of training datasets and classification area threshold values. Fewer samples are available to include in the training datasets as the class area threshold increases. 80 samples of sheet ice and rubble ice (160 samples total) were selected from each date with an area threshold of 50%, down to 24 samples of both classes (48 samples total) with a threshold of 100%. Note that samples from both dates are merged for the combined-date model, so the training datasets are twice as large as compared to those for the single-date models. For the 19 February model, accuracy generally increases as the threshold increases, but the 4 March model has a peak at 70%. This indicates that increasing the area threshold creates more separation between samples in the two classes, and therefore it is easier for the model to classify correctly. However, with our relatively small dataset there is a point where the total sample size becomes too small to properly train the classifier. The optimum threshold value for our dataset appears to be 70%, where the 19 February model achieves 96% and 94% accuracy for sheet ice and rubble ice, the 4 March model achieves 78% and 87% accuracy, and the combined model achieves 83% and 77% accuracy.

3.3. Random Forest Regression

Figure 8 shows RF regression results for Moran’s I statistic, estimated log-normal mean, and estimated log-normal standard deviation for models trained/tested on surface roughness measurements from 19 February only (left column), 4 March only (middle column), and both dates combined (right column). Red dashed lines in each figure are 1-1 lines representing perfect regression accuracy. Noted at the top of each figure are the mean absolute percentage error (MAPE) and $R^2$ values for the model configurations. Similar to classification results, reported MAPE values are calculated as the average MAPE after 100 RF model runs, where the input dataset is randomly divided into a 70%/30% train/test data split during each run. All regression targets for all model configurations exhibit a considerable amount of spread. MAPE values range from 9–29% and the error values for the combined-date models are approximately the average of the error values for the two individual-date models. Overall errors for a single target are lowest for the estimated log-normal standard deviation but highest for the estimated log-normal mean.

We prefer to use MAPE as our model assessment metric in this context because it enables an intuitive comparison of the relative error between the many different regression targets. We include $R^2$ values in these regression figures to demonstrate that this metric is misleading and inappropriate for our results. For all targets, the $R^2$ value for the combined-date regression model is higher than either of the individual-date models. This is not because the combined-date model performs better, but because a larger training dataset results in a larger number of points used to compute the metric for this model configuration. We suggest that future studies consider this possibility and choose a more appropriate metric such as MAPE to assess regression performance.

Figure 9 shows RF regression results for a single subgrid-statistic roughness metric. The first step in the derivation of this metric was calculated as the median surface roughness at a 0.25 m subgrid resolution (i.e., moving from the left panel to the middle panel in Figure 4). The three rows of plots in Figure 9 represent regression results for these intermediate measurements aggregated using the three different aggregation operations (i.e., moving from the middle panel to the right panel in Figure 4 using maximum, mean, and minimum aggregation operations). Note that the three rows have different y-axis limits, which altogether span two orders of magnitude. The columns in Figure 9 again represent RF models trained with input data sets from 19 February only (left column), 4 March only (middle column), and both dates combined (right column). Although significant spread is present in the regression results of all nine model configurations, the 4 March data are more tightly clustered than the 19 February data for all aggregation operations. This is an intuitive result when considering the density functions for surface roughness measurements from the two survey dates (Figure 5). Data outliers are largest for the datasets derived using maximum final aggregation (top row) and smallest for datasets derived using minimum final aggregation (bottom row), which correspond to the highest and lowest MAPE values, respectively. Figures similar to Figure 9 for all subgrid-statistic regression targets can be found in the Supplemental Data. Although MAPE values change slightly for other subgrid-statistic targets, regression model performance for all targets follows the general patterns discussed above.

Figure 10 shows a summary of MAPE values for RF regression models trained to predict all subgrid-statistic targets. The nine scatter plots shown in Figure 9 correspond to a single colored cell in each of the nine grids in Figure 10 (’med’ summary statistic on the x-axes and 0.25 m subgrid scale on the y-axes). The other colored cells in the nine grids represent MAPE values calculated for other subgrid-statistic roughness metrics, for which detailed scatter plots are available in the Supplementary Data. Rows of grids again separate targets by the final aggregation operation and columns of grids again separate models trained with samples from 19 February only (left column), 4 March only (middle column), and both survey dates combined (right column). Errors are generally higher for the 19 February models compared to the 4 March models, and errors for the combined model are approximately the average between the two individual-date models. The models tend to perform better (i.e., errors decrease) when trained on targets that emphasize the left tail of surface roughness distributions. This pattern is evident at the level of the target metrics (errors are lower for minimum and 5th percentile targets than maximum and 95th percentile targets) and at the level of final aggregation (errors are lower when aggregating by minimum subgrid roughness than by maximum subgrid roughness). For targets with mean and minimum operations for final aggregation, model performance generally improves as the subgrid spatial scale becomes finer. The opposite trend is apparent for targets aggregated by maximum roughness, where MAPE values increase as the subgrid-scale becomes finer. Note that for target metrics originally calculated at 10 m spatial resolution (the top row of cells in each larger grid), model performance does not change with the final aggregation statistic because no operation is required to aggregate the data to the Sentinel-1 grid. Grey cells that do not contain MAPE values represent redundant model runs: for example, calculating the maximum of 1 m subgrid cells and then aggregating to 10 m by again applying the maximum is equivalent to simply calculating the maximum of the original 10 m cell. This type of redundant model run was not conducted and is excluded from analysis.

4. Discussion

The goal of our analysis is to quantify the effect of river ice surface roughness on Sentinel-1 backscatter. We conducted aerial surveys at a site on the Yellowstone River on 19 February and 4 March 2021, representing midwinter and early spring ice conditions, respectively. To demonstrate that our dataset could successfully train an RF model, we hand-labeled areas of rubble (rough) ice and sheet (smooth) ice in orthomosaic photos of the surveyed area and trained an RF classifier to predict ice classes using Sentinel-1 backscatter data. Next, we measured surface roughness using DEMs of the surveyed area and used the measurements to create various roughness metrics, which we used as RF regression targets.

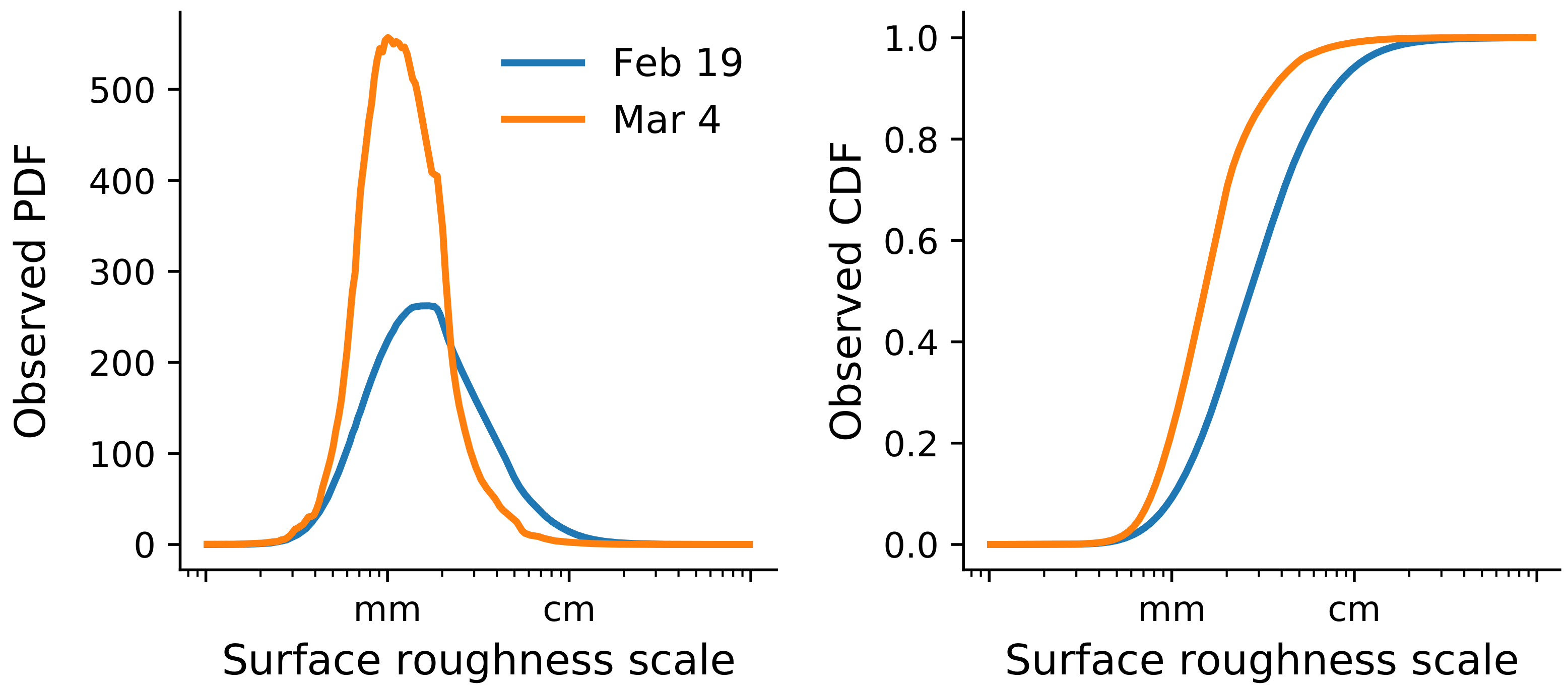
Observed density functions of surface roughness measurements from the two survey dates (Figure 5) show that the 19 February ice surface was rougher on average and spanned a wider range of roughness values than the 4 March ice surface. This was a surprising result based on our experience of hand-delineating polygons representing rubble ice and sheet ice areas in the orthomosaic photos from the two dates. Many locations in the scene that were covered with a thin layer of bright white snow in the 19 February orthophoto appeared darker in color and more textured in the 4 March orthophoto. The overall effect of the thin snow cover was that the 19 February surface appeared visually smoother than the 4 March surface. However, the SfM algorithm was able to detect ice pieces and other roughness elements in many snow-covered areas of the 19 February that were not visually apparent, but would still affect SAR backscatter. Previous ice classification studies that use a visual interpretation of aerial photos as validation data have not had the benefit of fine-scale roughness measurements to use for this type of comparison (Figure 6). If we had difficulty detecting roughness features in 0.03 m UAV orthophotos, it stands to reason that this issue may have been amplified in previous studies with lower-resolution imagery.

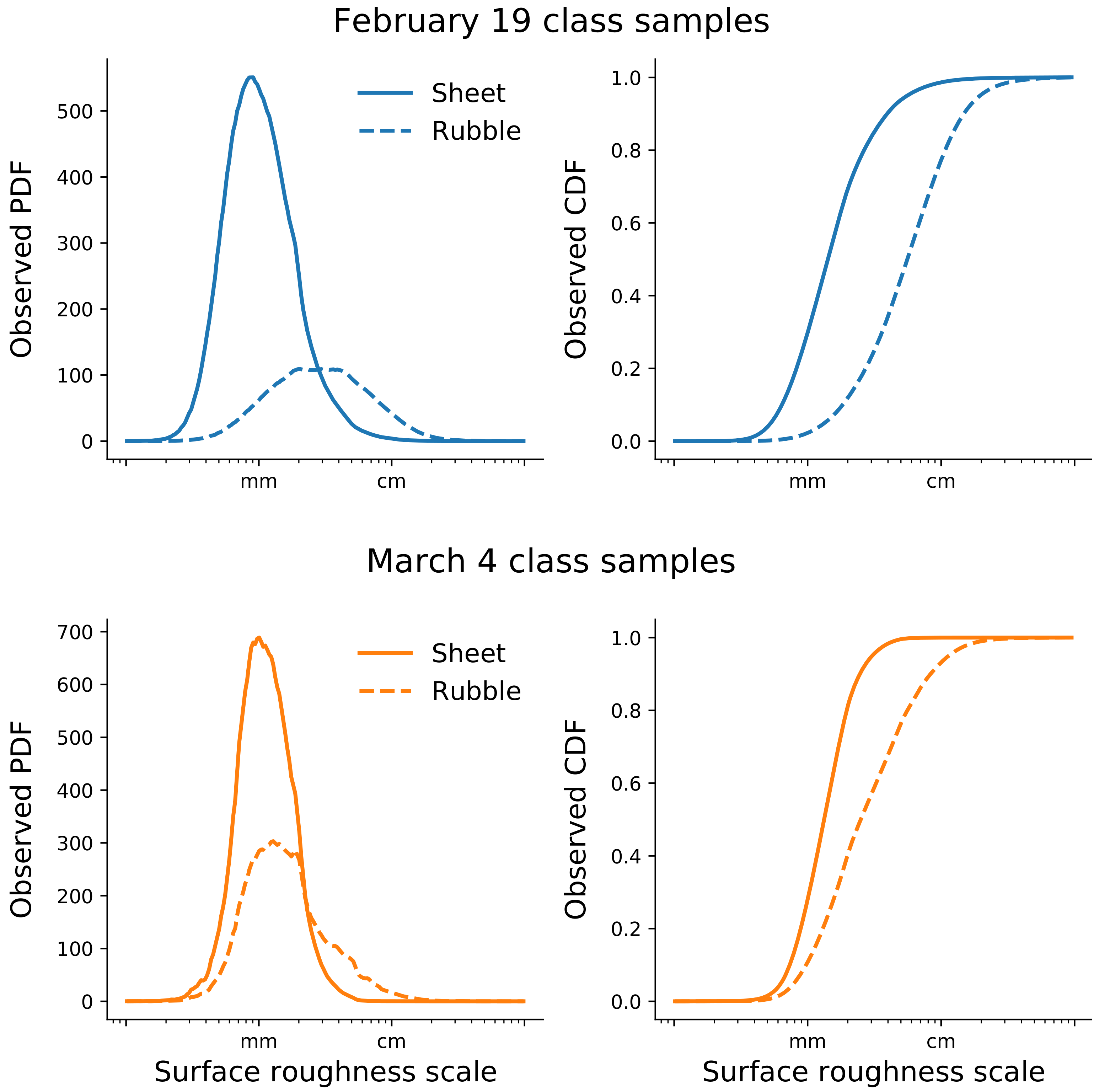
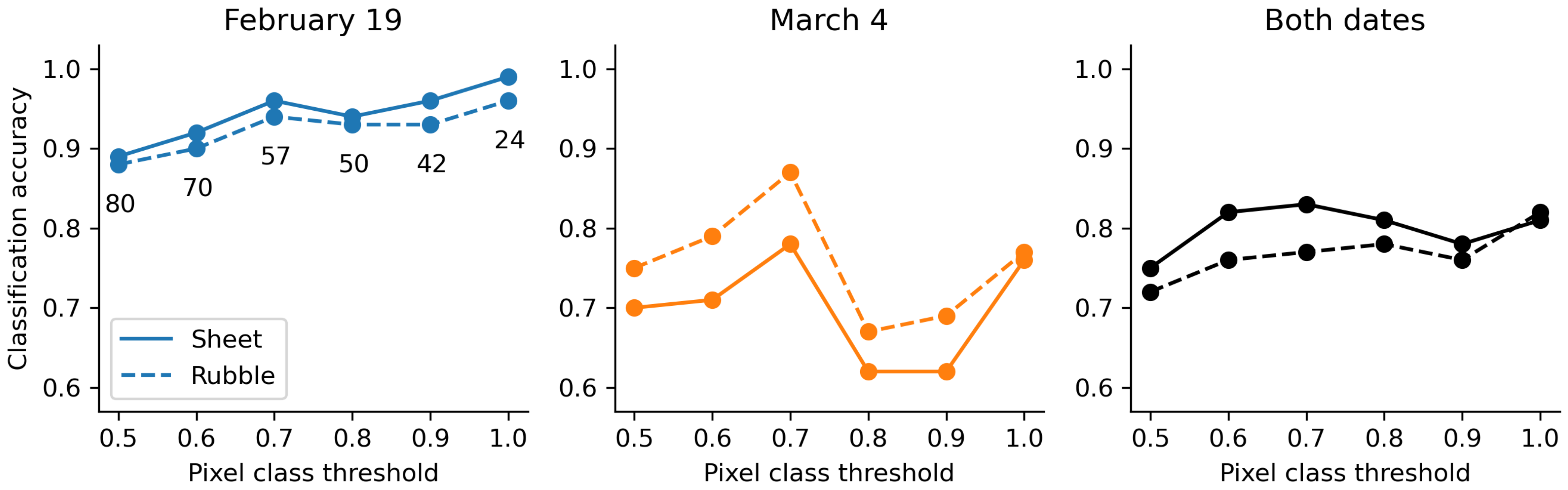
Figure 6 shows that the distributions of measured surface roughness within sheet ice and rubble ice samples were different between the 19 February and 4 March models. Significant overlap in measured surface roughness for sheet ice and rubble ice in the 4 March model resulted in lower classification accuracy (Figure 7). We note that increasing the area threshold value used to classify pixels increased the separation between the distributions of rubble ice and sheet ice on both dates, which should generally improve classification performance. However, for our small dataset, threshold values above 70% resulted in too few observations for the 4 March training datasets and actually reduced classification accuracy. We expect that the optimum value of this threshold parameter would change for different UAV-based datasets. Future studies using our methodology should consider adjusting this threshold value accordingly. The different roughness distributions were also consequential for regression results. The smaller range of observed roughness on 4 March translates to less spread in the 4 March regression training dataset, and therefore improved MAPE values for regression models (Figure 8 and Figure 9).

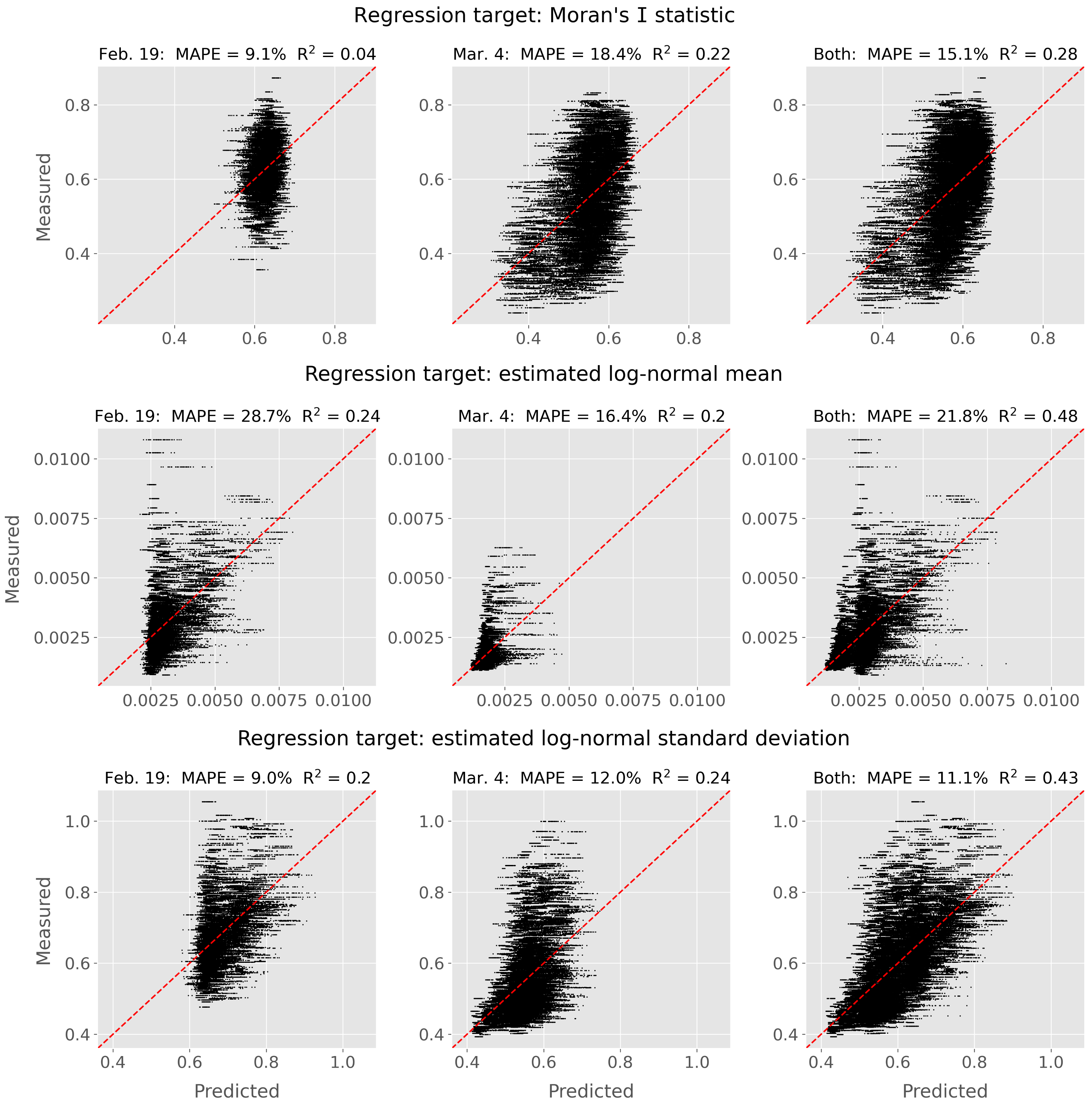
MAPE values for spatially-based and distribution-based RF regression targets (Figure 8) suggest that Sentinel-1 backscatter may contain some information about the standard deviation of surface roughness elements within each pixel, but contains less information about the average roughness. However, a considerable spread is present in the regression results of all three variables in Figure 8. Even though MAPE values are lowest for the estimated log-normal standard deviation, the predictions for this target are so varied that they are of questionable utility. Efforts to predict spatial autocorrelation using Moran’s I statistic as the regression target similarly did not produce quality results. Future studies could consider different spatial statistics, including local indicators of spatial autocorrelations [51], but any such indicators calculated at a subgrid-scale with respect to satellite SAR data should be treated with careful consideration when aggregating to a scale of the backscatter measurements.

For subgrid-statistic targets (Figure 9, plus additional figures in Supplementary Data), the wider data spread in the 19 February models (left column) compared to the 4 March models (middle column) is likely due to the different ice conditions on the two dates. Consistently cold temperatures leading up to the 18 February 18:00 MDT Sentinel-1 image collection ensured that the thin layer of snow overlaying the ice was dry, and liquid water was not present anywhere on the ice surface. Under these conditions the bulk dielectric constant of the river ice is relatively low (i.e., permittivity is relatively high) and incident Sentinel-1 microwaves penetrate into the ice cover and are affected by the structural properties of the ice. Temperatures leading up to the 2 March 18:00 MDT Sentinel-1 image were above freezing for 12 h and hit a daytime high of 15 °C at approximately 16:00. It is very likely that liquid water was present on some areas of the ice surface at the time the 2 March image was captured. Under these wet conditions, permittivity decreases sharply and surface roughness is the dominant microwave scattering mechanism [16]. These different ice conditions could account for part of the difference in the amount of spread between the 19 February and 4 March regression models, and consequently the difference in MAPE. We note again here that the time between Sentinel-1 image collection and UAV aerial surveys was approximately 12 h for the February datasets and 36 h for the March datasets. This difference, especially during the freeze-thaw cycle of the spring transition period, is a source of error in our regression models that is difficult to quantify.

Regression models in this study performed best on targets that emphasized the minimum roughness measured within a pixel, whether that emphasis was derived from the subgrid statistic (minimum, 5th percentile) or the minimum aggregation operation. A comparison of the performance of all model configurations for a single target (Figure 9) shows that the three aggregation operations (the three rows in Figure 9) have similar amounts of relative spread in the predictions, even though the data range compresses by two orders of magnitude between the maximum and minimum aggregation operations. This is an indication that Sentinel-1 backscatter measurements may contain some information related to the minimum river ice surface roughness, which could be related to the type of microwave interactions on the ice surface (specular reflection vs. surface scattering).

We reiterate that our 0.03 m UAV surface roughness measurements do not meet the threshold criteria of 0.0056 m (i.e., $\lambda /10$) necessary to conclusively delineate radiometrically smooth and rough surfaces with respect to Sentinel-1 microwave scattering behavior. However, the upcoming NASA-ISRO NISAR satellite mission will collect L-band ($\lambda =0.24$ m) SAR measurements on a 12-day global repeat cycle [52]. Our UAV methodology generates surface roughness measurements at the threshold 0.024 m spatial resolution simply by flying at a slightly lower altitude than the 80 m flown for this study. Using the method and calculations provided by van der Sanden and Drouin [23] and Sabins [26], and assuming an average incidence angle of 41 degrees [52] we calculate that $h<0.0127$ m indicates a radiometrically smooth surface at the air-ice interface, $h>0.0723$ m indicates a radiometrically rough surface, with intermediate roughness between these values. Most ice surfaces in the dataset we collected for this study would be classified as radiometrically smooth with respect to NISAR, but some rubble ice in the 19 February model would be in the intermediate roughness class. We suspect that radiometrically rough surfaces may be found in large ice jams, though that conjecture will have to be addressed by future research. We also note that our methodology is not limited to river ice and could be used to measure the roughness of any surface of interest.

5. Conclusions

We presented the first systematic, quantitative investigation of the effect of river ice surface roughness on Sentinel-1 C-band SAR backscatter. Measurements of surface roughness were derived from aerial surveys at a site on the Yellowstone River on 19 February and 4 March 2021, representing midwinter and early spring ice conditions, respectively. Our UAV-based methodology improves upon the limitations of traditional ground-based or airplane-based river ice photography, and can be used to measure ice roughness on frozen rivers globally. Poor numerical regression results (5–113% MAPE) coupled with reasonable visually-based classification results (77–96%) suggest that Sentinel-1 backscatter data contain information derived from river ice, but that information is not strongly related to ice surface roughness. Although the results of our study are not perfectly conclusive, they suggest several relevant paths forward for future SAR-based river ice studies, which we discuss below in the context of our original hypotheses.

Our first hypothesis was that RF regression models relating river ice surface roughness to SAR backscatter are not location- or condition-specific, and that model performance will improve for models trained with data from multiple surveys. Our results based on individual-date and combined-date regression models suggest the opposite: regression error is affected by ice conditions which in turn affect Sentinel-1 backscatter, and regression models based only on surface roughness appear to work better in wet-ice conditions. However, our analysis is based on two aerial surveys which only represent a small subset of possible ice conditions on global rivers. Future work should attempt to incorporate additional survey dates to generate a larger dataset that spans a wider range of ice conditions and geographic locations. We also recommend conducting aerial surveys as close as possible to the time of satellite flyover, as permitted by weather conditions and other logistical considerations.

Our second hypothesis was that regression model performance will be affected by the spatial scale at which river ice surface roughness elements are quantified, with finer spatial scales resulting in lower regression errors. Our regression results suggest that, while model performance does generally improve for subgrid-statistic roughness targets as spatial resolution becomes finer, model performance is more strongly controlled by which tail of the distribution is emphasized by the regression target. RF regression models perform better on targets that emphasize the left tail of the distribution (minimum or 5th percentile roughness, or aggregating by minimum roughness) compared to targets that emphasize the right tail (maximum or 95th percentile roughness, or aggregating by maximum roughness). Future studies may be able to examine these patterns in more detail by incorporating fully-polarimetric SAR imagery (e.g., from RADARSAT-2) or SAR imagery at different wavelengths (e.g., L-band NISAR measurements). Adding SAR-based predictor variables derived from HH-polarized backscatter, as well as H-A-$\alpha$ and other polarimetric decomposition products, could improve upon results reported here and detect new trends.

Our final hypothesis was that river ice surface roughness will have at best a moderately strong correlation with Sentinel-1 backscatter because other physical ice properties are not accounted for in the regression models. Regression results using surface roughness measurements were not particularly strong, but ice classification using the traditional visually-based validation method achieved accuracies similar to those published in previous studies. This is an indication that Sentinel-1 SAR backscatter data contain information derived from the river ice, but that information is not strongly related to ice surface roughness. We suggest that the most impactful future work would include field campaigns to measure other ice properties simultaneously with surface roughness. For example, a UAV-based ground penetrating radar [53] could potentially retrieve ice thickness and structure measurements, which could be used alongside surface roughness in regression models. Spatially distributed ice core samples [23,54] could enable comparison of the relative effects of surface roughness and vertical ice structure on SAR backscatter.