A Comprehensive Study on Factors Affecting the Calibration of Potential Evapotranspiration Derived from the Thornthwaite Model
Abstract
:1. Introduction
2. Data Acquisition
2.1. Selection of Study Region and Period
2.2. Retrieval of GNSS-ZTD
2.3. Meteorological and Time-Varying Variables
3. Methodology
3.1. Estimation of PET
3.1.1. Thornthwaite Equations
3.1.2. Penman–Monteith Equations
3.2. Calibration of PET
- Calculation of PET differences between PM-PET and TH-PET estimates:
- 2.
- Calibration of TH-PET estimates using GNSS and meteorological variables:
- 3.
- Calculation of a new set of TH-PET values over the whole period:
4. Investigation of Factors Affecting the Calibration Performance of PET Estimates
4.1. Selection of Variables for Calibration
4.2. Comparison of Seasonal Calibration Effects
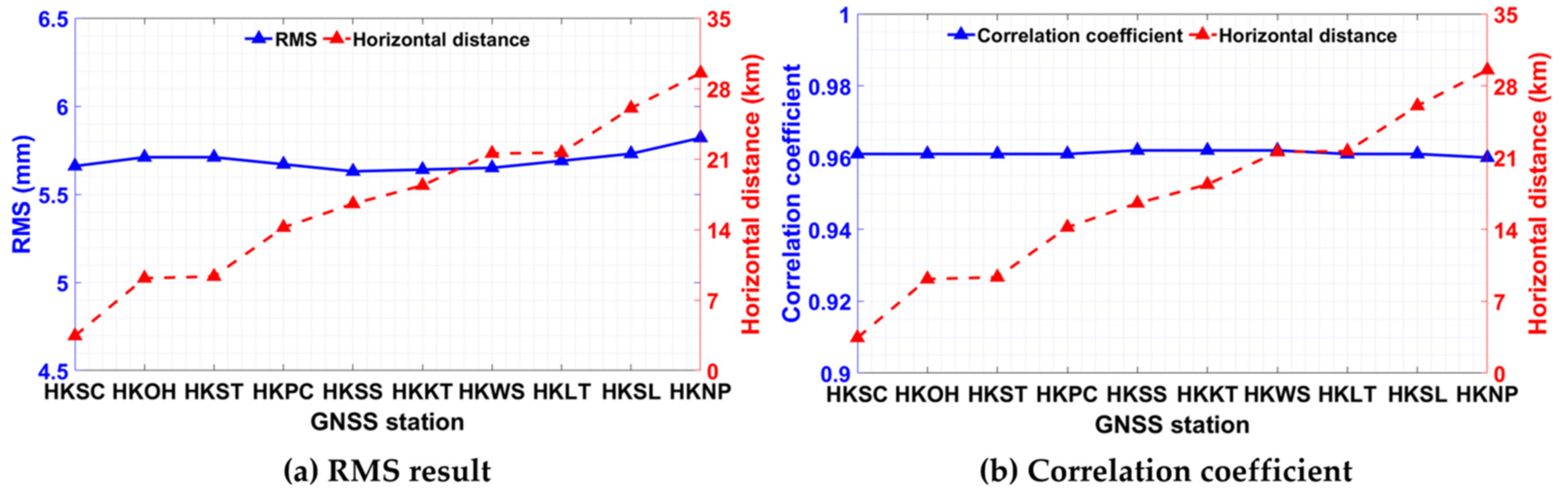
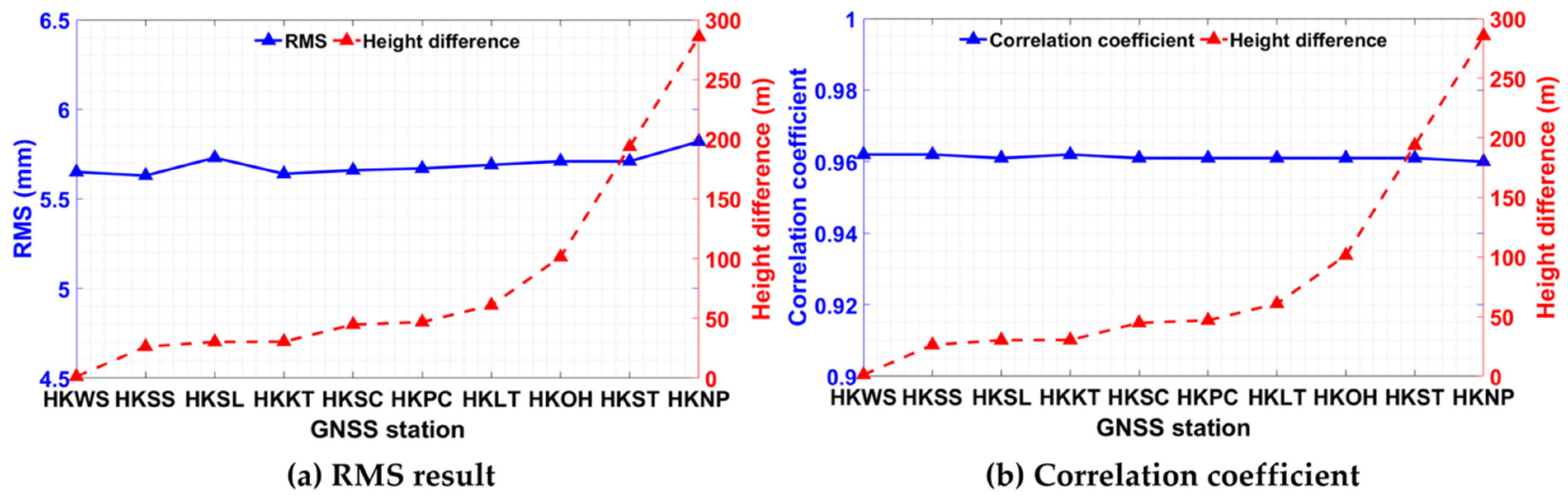
4.3. Spatial Distribution of GNSS and Weather Stations
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McKenney, M.S.; Rosenberg, N.J. Sensitivity of some potential evapotranspiration estimation methods to climate change. Agric. Forest Meteorol. 1993, 64, 81–110. [Google Scholar] [CrossRef]
- Fisher, J.B.; Whittaker, R.J.; Malhi, Y. ET come home: Potential evapotranspiration in geographical ecology. Glob. Ecol. Biogeog. 2011, 20, 1–18. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Guidelines for computing crop water requirements. Irrig. Drain. Pap. 1998, 56, 300. [Google Scholar]
- Valipour, M.; Sefidkouhi, M.A.G.; Raeini, M. Selecting the best model to estimate potential evapotranspiration with respect to climate change and magnitudes of extreme events. Agr. Water Manag. 2017, 180, 50–60. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Park, H.E.; Roh, K.M.; Yoo, S.M.; Choi, B.K.; Chung, J.K.; Cho, J. Quality assessment of tropospheric delay estimated by precise point positioning in the Korean peninsula. J. Position Nav. Timing 2014, 3, 131–141. [Google Scholar] [CrossRef]
- Song, L.; Zhuang, Q.; Yin, Y.; Wu, S.; Zhu, X. Intercomparison of Model-Estimated Potential Evapotranspiration on the Tibetan Plateau during 1981–2010. Earth Interact. 2017, 21, 1–22. [Google Scholar] [CrossRef]
- Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
- Rezaei, M.; Valipour, M.; Valipour, M. Modelling evapotranspiration to increase the accuracy of the estimations based on the climatic parameters. Water Conserv. Sci. Eng. 2016, 1, 197–207. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N. Evaluation of Variable Infiltration Capacity model and MODIS-Terra satellite-derived grid-scale evapotranspiration. J. Irrig. Drain Eng. 2017, 143, 1. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Yuan, S.; Quiring, S.M. Drought in the US Great Plains (1980–2012): A sensitivity study using different methods for estimating potential evapotranspiration in the Palmer Drought Severity Index. J. Geophys. Res. Atmos. 2014, 119, 10996–11010. [Google Scholar] [CrossRef]
- Almorox, J.; Quej, V.H.; Martí, P. Global performance ranking of temperature-based approaches for evapotranspiration estimation considering Köppen climate classes. J. Hydrol. 2021, 528, 514–522. [Google Scholar] [CrossRef]
- Donohue, R.J.; McVicar, T.R.; Roderick, M.L. Assessing the ability of potential evaporation formulations to capture the dynamics in evaporative demand within a changing climate. J. Hydrol. 2010, 386, 186–197. [Google Scholar] [CrossRef]
- Van der Schrier, G.; Jones, P.D.; Briffa, K.R. The sensitivity of the PDSI to the Thornthwaite and Penman-Monteith parameterizations for potential evapotranspiration. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef]
- Karunarathne, A.M.A.N.; Gad, E.F.; Disfani, M.M.; Sivanerupan, S.; Wilson, J.L. Review of calculation procedures of Thornthwaite Moisture Index and its impact on footing design. Aust. Geomech. J. 2016, 51, 85–95. [Google Scholar]
- Ma, X.; Zhao, Q.; Yao, Y.; Yao, W. A novel method of retrieving potential ET in China. J. Hydrol. 2021, 598, 126271. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, Y.; Li, Z.; Yao, Y. Retrieval of a High-Precision Drought Monitoring Index by Using GNSS-Derived ZTD and Temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8730–8743. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Du, Z.; Yang, P.; Yao, Y. Improved drought monitoring index using GNSS-derived precipitable water vapor over the loess plateau area. Sensors 2019, 19, 5566. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Yao, Y.; Zhao, Q. Regional GNSS-Derived SPCI: Verification and Improvement in Yunnan, China. Remote Sens. 2021, 13, 1918. [Google Scholar] [CrossRef]
- Elgered, G.; Davis, J.L.; Herring, T.A.; Shapiro, I. Geodesy by radio interferometry: Water vapor radiometry for estimation of the wet delay. J. Geophys. Res. Sol. Earth 1991, 96, 6541–6555. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.; Ware, R. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.; Anthes, R.; Rocken, C.; Ware, R. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Rocken, C.; Ware, R.; Van Hove, T.; Solheim, F.; Alber, C.; Johnson, J.; Bevis, M.; Businger, S. Sensing atmospheric water vapor with the Global Positioning System. Geophys. Res. Lett. 1993, 20, 2631–2634. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; He, C.; Cheng, Y.; Li, X. Determination of zenith hydrostatic delay and its impact on GNSS-derived integrated water vapor. Atmos. Meas. Tech. 2017, 10, 2807–2820. [Google Scholar] [CrossRef]
- Ma, X.; Yao, Y.; Zhang, B.; He, C. Retrieval of high spatial resolution precipitable water vapor maps using heterogeneous earth observation data. Remote Sens. Environ. 2022, 278, 113100. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Yao, W.; Yao, Y. Hourly Rainfall Forecast Model Using Supervised Learning Algorithm. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4100509. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Li, Z.; Cheng, Y.; Li, L.; Yuan, H. The correlation between GNSS-derived precipitable water vapor and sea surface temperature and its responses to El Niño–Southern Oscillation. Remote Sens. Environ. 2018, 216, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Qiu, C.; Zhang, S.; Zhang, J.; Xie, M.; Li, L. Development of an improved model for prediction of short-term heavy precipitation based on GNSS-derived PWV. Remote Sens. 2020, 12, 4101. [Google Scholar] [CrossRef]
- Yao, Y.; Shan, L.; Zhao, Q. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application. Sci. Rep. 2017, 7, 12465. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Zhang, J.; Qiu, C.; Zhang, S.; Li, L. An Improved Model for Detecting Heavy Precipitation Using GNSS-derived Zenith Total Delay Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5392–5405. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Li, Z. Real-time precise point positioning based zenith tropospheric delay for precipitation forecasting. Sci. Rep. 2018, 8, 7939. [Google Scholar] [CrossRef]
- Manandhar, S.; Dev, S.; Lee, Y.H.; Meng, Y.S.; Winkler, S. A data-driven approach for accurate rainfall prediction. IEEE Trans. Geosci. Rem. Sens. 2019, 57, 9323–9331. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Q.; Yao, W.; Ma, X.; Yao, Y.; Liu, L. Short-term rainfall forecast model based on the improved Bp–nn algorithm. Sci. Rep. 2019, 9, 19751. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Zhang, K.; Wu, S.; Xu, Y.; Liu, Y.; Qiu, C.; Zhang, J.; Fu, E.; Li, L. A Neural Network-based Approach for the Detection of Heavy Precipitation Using GNSS Observations and Surface Meteorological Data. J. Atmos. Sol.-Terr. Phys. 2021, 225, 105763. [Google Scholar] [CrossRef]
- Li, P.W.; Wong, W.K.; Cheung, P.; Yeung, H.Y. An overview of nowcasting development, applications, and services in the Hong Kong Observatory. J. Meteorol. Res. 2014, 28, 859–876. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z.; Wong, W.K.; Woo, W.C. Detecting water vapor variability during heavy precipitation events in Hong Kong using the GPS tomographic technique. J. Atmos. Ocean. Tech. 2017, 34, 1001–1019. [Google Scholar] [CrossRef]
- Hartley, K.; Tortajada, C.; Biswas, A.K. Political dynamics and water supply in Hong Kong. Environ. Dev. 2018, 27, 107–117. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Choy, S.; Wu, S.; Jiang, C.; Zhang, J.; Qiu, C.; Li, L. A new cumulative anomaly-based model for the detection of heavy precipitation using GNSS-derived tropospheric products. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4105718. [Google Scholar] [CrossRef]
- Hong Kong Observatory. Climate of Hong Kong. Available online: https://www.hko.gov.hk/en/cis/climahk.htm (accessed on 15 July 2022).
- Arias, P.; Bellouin, N.; Coppola, E.; Jones, R.; Krinner, G.; Marotzke, J.; Naik, V.; Palmer, M.; Plattner, G.-K.; Rogelj, J.; et al. Climate Change 2021: The Physical Science Basis. Contribution of Working Group14 I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Summary; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software, Version 5.2; Astronomical Institute, University of Bern: Berne, Switzerland, 2015. [Google Scholar]
- Kouba, J. A guide to using International GNSS Service (IGS) products. 2009. Available online: http://acc.igs.org/UsingIGSProductsVer21.pdf (accessed on 11 July 2022).
- Griffiths, J. Combined orbits and clocks from IGS second reprocessing. J. Geod. 2019, 93, 177–195. [Google Scholar] [CrossRef] [PubMed]
- Byram, S.; Hackman, C.; Tracey, J. Computation of a high-precision GPS-based troposphere product by the USNO. In Proceedings of the 24th international technical meeting of the satellite division of the institute of navigation (ION GNSS 2011), Portland, OR, USA, 19–23 September 2011; pp. 572–578. [Google Scholar]
- Douša, J. Towards an operational near real-time precipitable water vapor estimation. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 189–194. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions 2010 (IERS Technical Note; 36); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; 179p, ISBN 3-89888-989-6. [Google Scholar]
- Haase, J.; Ge, M.; Vedel, H.; Calais, E. Accuracy and variability of GPS tropospheric delay measurements of water vapor in the western Mediterranean. J. Appl. Meteorol. 2003, 42, 1547–1568. [Google Scholar] [CrossRef]
- Stępniak, K.; Bock, O.; Bosser, P.; Wielgosz, P. Outliers and uncertainties in GNSS ZTD estimates from double-difference processing and precise point positioning. GPS Solut. 2022, 26, 74. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, B.; Chan, S.; Cao, Y.; Gao, Y.; Zhang, K.; Nichol, J. Analysis and modelling of water vapour and temperature changes in Hong Kong using a 40-year radiosonde record: 1973–2012. Int. J. Clim. 2014, 35, 462–474. [Google Scholar] [CrossRef]
- Westerhoff, R.S. Using uncertainty of Penman and Penman–Monteith methods in combined satellite and ground-based evapotranspiration estimates. Remote Sens. Environ. 2015, 169, 102–112. [Google Scholar] [CrossRef]
- GB/T 20481-2017; Grades of Meteorological Drought. China Meteorological Administration: Beijing, China, 2017.
- Funk, C.; Shukla, S. Drought Early Warning and Forecasting: Theory and Practice; Elsevier: Oxford, UK, 2020. [Google Scholar]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd international conference on Machine learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 161–168. [Google Scholar]
- Gupta, H.V.; Kling, H. On typical range, sensitivity, and normalization of Mean Squared Error and Nash-Sutcliffe Efficiency type metrics. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Zeybek, M. Nash-sutcliffe efficiency approach for quality improvement. J. Appl. Math. Comp. 2018, 2, 496–503. [Google Scholar] [CrossRef]
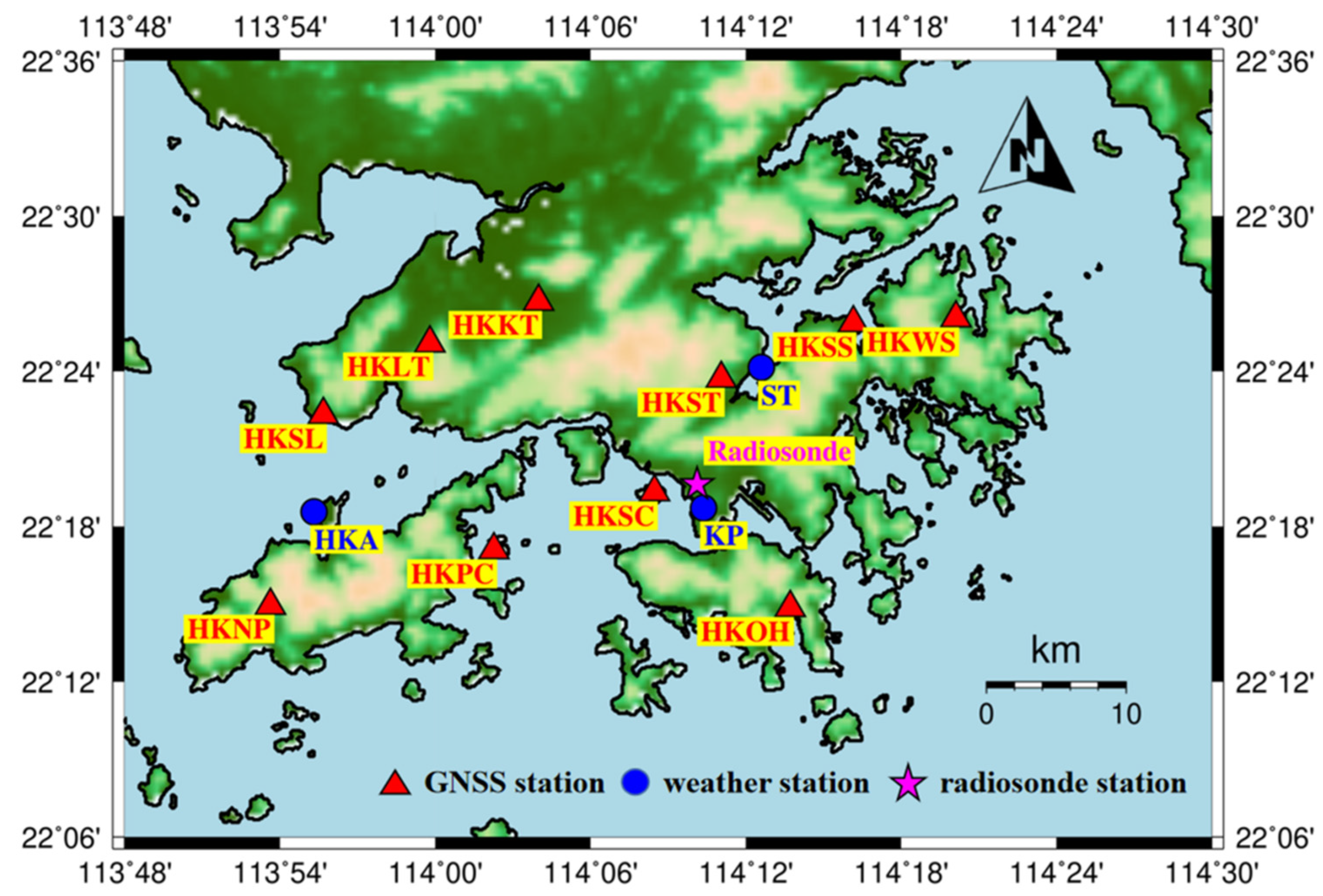

| Station ID | Latitude (°) | Longitude (°) | Height (m) | |
|---|---|---|---|---|
| GNSS station | HKKT | 22.45 | 114.07 | 34.54 |
| HKLT | 22.42 | 114.00 | 125.90 | |
| HKNP | 22.25 | 113.89 | 350.67 | |
| HKOH | 22.25 | 114.23 | 166.38 | |
| HKPC | 22.29 | 114.04 | 18.09 | |
| HKSC | 22.32 | 114.14 | 20.20 | |
| HKSL | 22.37 | 113.93 | 95.27 | |
| HKSS | 22.43 | 114.27 | 38.68 | |
| HKST | 22.40 | 114.18 | 258.69 | |
| HKWS | 22.43 | 114.34 | 63.76 | |
| Weather station | HKA | 22.31 | 113.92 | 6.00 |
| KP | 22.31 | 114.17 | 65.00 | |
| ST | 22.40 | 114.21 | 6.00 | |
| Scheme No. | Variables | No. of Variables |
|---|---|---|
| 1 | T, P | 2 |
| 2 | T, ZTD | 2 |
| 3 | P, ZTD | 2 |
| 4 | T, P, ZTD | 3 |
| 5 | T, P, MJD | 3 |
| 6 | T, ZTD, MJD | 3 |
| 7 | P, ZTD, MJD | 3 |
| 8 | T, P, ZTD, MJD | 4 |
| Scheme No. | Calibration Variable | Fitting Results (2008–2019) | Verification Results (2020–2021) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias (mm) | RMS (mm) | r | NSE | Bias (mm) | RMS (mm) | r | NSE | ||
| 1 | T P | 0 | 8.03 | 0.919 | 0.852 | 1.98 | 10.40 | 0.919 | 0.723 |
| 2 | T ZTD | 0 | 7.51 | 0.938 | 0.881 | 2.35 | 8.63 | 0.937 | 0.802 |
| 3 | P ZTD | 0 | 7.82 | 0.938 | 0.875 | 0.07 | 8.85 | 0.936 | 0.798 |
| 4 | T P ZTD | 0 | 7.33 | 0.947 | 0.897 | 1.92 | 8.30 | 0.938 | 0.814 |
| 5 | T P MJD | 0 | 7.86 | 0.923 | 0.855 | 1.61 | 10.05 | 0.923 | 0.731 |
| 6 | T ZTD MJD | 0 | 7.34 | 0.944 | 0.891 | 2.13 | 8.39 | 0.939 | 0.806 |
| 7 | P ZTD MJD | 0 | 7.44 | 0.946 | 0.890 | 0.03 | 8.56 | 0.938 | 0.808 |
| 8 | T P ZTD MJD | 0 | 6.95 | 0.952 | 0.904 | 1.35 | 8.13 | 0.940 | 0.824 |
| 9 | None | 2.59 | 34.42 | 0.919 | −0.512 | 4.07 | 39.23 | 0.902 | −1.432 |
| Season | With Calibration (Scheme 8 in Table 3) | Without Calibration | Improvement Rate of RMS Result (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias (mm) | RMS (mm) | r | NSE | Bias (mm) | RMS (mm) | r | NSE | ||
| Spring | 9.49 | 9.34 | 0.935 | 0.596 | 12.84 | 27.10 | 0.778 | −1.198 | 65.54 |
| Summer | −2.06 | 5.48 | 0.856 | 0.668 | −36.72 | 37.85 | 0.759 | −6.704 | 85.52 |
| Autumn | −2.68 | 6.24 | 0.933 | 0.824 | −7.00 | 25.50 | 0.839 | −0.582 | 75.52 |
| Winter | −5.30 | 6.20 | 0.769 | 0.387 | 40.98 | 43.10 | 0.230 | −14.874 | 85.61 |
| HKA Station | KP Station | ST Station | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GNSS | Horizontal Distance (km) | RMS (mm) | r | GNSS | Horizontal Distance (km) | RMS (mm) | r | GNSS | Horizontal Distance (km) | RMS (mm) | r |
| HKSL | 6.984 | 8.52 | 0.941 | HKSC | 3.443 | 5.66 | 0.961 | HKST | 2.771 | 6.66 | 0.955 |
| HKNP | 7.304 | 8.69 | 0.938 | HKOH | 9.166 | 5.71 | 0.961 | HKSS | 6.875 | 6.55 | 0.957 |
| HKPC | 12.228 | 8.49 | 0.941 | HKST | 9.343 | 5.71 | 0.961 | HKSC | 11.392 | 6.63 | 0.956 |
| HKLT | 14.315 | 8.48 | 0.941 | HKPC | 14.208 | 5.67 | 0.961 | HKWS | 13.366 | 6.57 | 0.956 |
| HKKT | 21.168 | 8.40 | 0.942 | HKSS | 16.555 | 5.63 | 0.962 | HKKT | 15.475 | 6.55 | 0.957 |
| HKSC | 22.599 | 8.48 | 0.941 | HKKT | 18.378 | 5.64 | 0.962 | HKOH | 17.319 | 6.65 | 0.955 |
| HKST | 28.610 | 8.54 | 0.940 | HKWS | 21.557 | 5.65 | 0.962 | HKLT | 22.005 | 6.62 | 0.956 |
| HKOH | 32.291 | 8.56 | 0.940 | HKLT | 21.623 | 5.69 | 0.961 | HKPC | 22.015 | 6.61 | 0.956 |
| HKSS | 38.193 | 8.42 | 0.942 | HKSL | 26.046 | 5.73 | 0.961 | HKSL | 29.191 | 6.63 | 0.956 |
| HKWS | 44.723 | 8.44 | 0.942 | HKNP | 29.533 | 5.82 | 0.960 | HKNP | 36.717 | 6.76 | 0.954 |
| HKA Station | KP Station | ST Station | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GNSS | Height Difference (m) | RMS (mm) | r | GNSS | Height Difference (m) | RMS (mm) | r | GNSS | Height Difference (m) | RMS (mm) | r |
| HKPC | 12.094 | 8.49 | 0.941 | HKWS | 1.239 | 5.65 | 0.962 | HKPC | 12.094 | 6.61 | 0.956 |
| HKSC | 14.204 | 8.48 | 0.941 | HKSS | 26.316 | 5.63 | 0.962 | HKSC | 14.204 | 6.63 | 0.956 |
| HKKT | 28.542 | 8.40 | 0.942 | HKSL | 30.267 | 5.73 | 0.961 | HKKT | 28.542 | 6.55 | 0.957 |
| HKSS | 32.684 | 8.42 | 0.942 | HKKT | 30.459 | 5.64 | 0.962 | HKSS | 32.684 | 6.55 | 0.957 |
| HKWS | 57.761 | 8.44 | 0.942 | HKSC | 44.796 | 5.66 | 0.961 | HKWS | 57.761 | 6.57 | 0.956 |
| HKSL | 89.267 | 8.52 | 0.941 | HKPC | 46.906 | 5.67 | 0.961 | HKSL | 89.267 | 6.63 | 0.956 |
| HKLT | 119.897 | 8.48 | 0.941 | HKLT | 60.897 | 5.69 | 0.961 | HKLT | 119.897 | 6.62 | 0.956 |
| HKOH | 160.376 | 8.56 | 0.940 | HKOH | 101.376 | 5.71 | 0.961 | HKOH | 160.376 | 6.65 | 0.955 |
| HKST | 252.690 | 8.54 | 0.940 | HKST | 193.690 | 5.71 | 0.961 | HKST | 252.690 | 6.66 | 0.955 |
| HKNP | 344.665 | 8.69 | 0.938 | HKNP | 285.665 | 5.82 | 0.960 | HKNP | 344.665 | 6.76 | 0.954 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jiang, C.; Choy, S.; Wang, X.; Zhang, K.; Zhu, D. A Comprehensive Study on Factors Affecting the Calibration of Potential Evapotranspiration Derived from the Thornthwaite Model. Remote Sens. 2022, 14, 4644. https://doi.org/10.3390/rs14184644
Li H, Jiang C, Choy S, Wang X, Zhang K, Zhu D. A Comprehensive Study on Factors Affecting the Calibration of Potential Evapotranspiration Derived from the Thornthwaite Model. Remote Sensing. 2022; 14(18):4644. https://doi.org/10.3390/rs14184644
Chicago/Turabian StyleLi, Haobo, Chenhui Jiang, Suelynn Choy, Xiaoming Wang, Kefei Zhang, and Dejun Zhu. 2022. "A Comprehensive Study on Factors Affecting the Calibration of Potential Evapotranspiration Derived from the Thornthwaite Model" Remote Sensing 14, no. 18: 4644. https://doi.org/10.3390/rs14184644
APA StyleLi, H., Jiang, C., Choy, S., Wang, X., Zhang, K., & Zhu, D. (2022). A Comprehensive Study on Factors Affecting the Calibration of Potential Evapotranspiration Derived from the Thornthwaite Model. Remote Sensing, 14(18), 4644. https://doi.org/10.3390/rs14184644








