Abstract
Water vapor is a dominant greenhouse gas. It significantly impacts the atmosphere by trapping heat and infrared radiation. The greenhouse effect is essential for life on Earth but can also be harmful. Although the amount of water vapor in the atmosphere is not much during the water cycle, it is the most active element in rapid changes in both spatial and temporal domains. GNSS tomography’s ability to model the high-resolution 3D distribution of water vapor is a promising means of measuring and monitoring the spatial-temporal variation of water vapor. This study developed and tested a new GNSS tomographic model using adaptive voxel parameterization. It uses a 3D traversal algorithm to dynamically determine the position of voxels at each tomographic sampling epoch. It means that the new algorithm can exclude the voxels that no GNSS signals pass through, reducing the influence of such voxels in the construction of the tomographic model. This study provides a new approach to investigating the inversion of atmospheric water vapor. The experiment used one-month data from the Hong Kong network in September 2020, and the results were compared with the general system. The local radiosonde data is a reference for verification of the two approaches. The mean root-mean-square error (RMSE) and IQR of the water vapor profiles derived from AAR are decreased by 55% and 48% with respect to the GFR results, respectively. The results show that the accuracy of the new method outperforms the general approach in the result statistics. The successful implementation of the research has significant potential to drive the development of GNSS tomography in the study of weather and climate change.
1. Introduction
Water vapor, as a standard component of the atmosphere, makes a large contribution to driving the weather and climate [1,2]. It is also a potent greenhouse gas which is continuously generated by evaporation. The commonly used technique for water vapor sounding is the radiosonde—a telemetry instrument which transmits atmospheric parameters (e.g., humidity, pressure, temperature, and wind) from the atmosphere to the ground receiver by the weather balloon. However, because of the poor performance of the radiosonde in horizontal and temporary resolution, it is not enough to meet the rapid development of remote sensing technology in monitoring atmospheric water vapor. To overcome this problem, the use of global navigation satellite systems (GNSS) for retrieving the atmospheric water vapor is a promising approach, since they are all-weather, have a high spatial-temporal resolution, and operate round the clock. Based on the processing of the signals between ground GNSS stations and a constellation of satellites, GNSS tomography can obtain the three-dimensional distribution of the water vapor in the troposphere with a high spatial-temporal resolution. GNSS tomography also has potential value in severe weather research and short-term weather forecasting [3].
Reference [4] proposed the initial GNSS tomographic model in three main steps: (1) discretization of the region over the GNSS network into the tomographic voxels—water vapor parameters on cuboid in three-dimensional space; (2) construction of the tomographic and constraint equations; (3) calculation of the pre-set water vapor parameters by the method of solving tomographic equations. Currently, most research about GNSS tomography also focuses on the three steps above. Reference [5] presented an approach based on the Kalman Filter (KF) technique—Wet Refractivity Kalman Filter (WeRKaF)—which designs the tomographic covariance matrix used in the implementation of the tomographic inversion. Reference [6] combined the framework of discrete inverse theory and the prior information to obtain the reconstructed field of water vapor. Reference [7] achieved a high accuracy result of tomography by using the inter-voxel constraints and a priori refractivity information. Reference [8] focused on the inversion of the equations system and used the Moore–Penrose pseudo-inverse method to obtain the minimum constraints solution with no additional assumptions. Reference [9] presented new parameterized approaches—the parameterization of voxels by trilinear and spline functions, which minimizes the discretization effects of the tomographic model. Reference [10] optimized the layer spacing and the optimal results showed that the exponential height spacing method outperforms the constant method. For the horizontal boundary optimization, Reference [11] moved the voxel along the latitude and longitude to achieve the optimal scheme of rays passing through voxels. Reference [12] developed a near real-time 4D water vapor tomographic system through the sliding time window strategy and double-difference network solution. Reference [13] developed the GNSS tomography model TOMO2 to construct the correlation between voxels by introducing a robust Kalman filter. Reference [14] investigated a Gaussian exponential vertical interpolation method, which conforms to the vertical variation characteristic of water vapor. Based on the method of the Eikonal equation and the least-squares QR regularization method, Reference [15] proposed a robust 3D ray tracing technique, which has no limitation of the certain azimuthally fixed vertical plane for the GNSS tomographic modeling. Reference [16] developed a method for the adaptive tomographic region to adjust the node parameterization positions dynamically. Reference [17] proposed an improved pixel-based water vapor tomography model to reflect the variations in voxels and the continuity of the troposphere. As in the earlier study, various simulations [18,19,20] also have been conducted for the study of the key factors of the GNSS tomography (e.g., elevation cutoff angles, reference station vertical geometries, network size, the observation noise, the available navigation satellites, and the boundary layer). Although many research studies have improved the tomographic model, there are relatively few studies that focuses on the smallest parameterized unit—voxel.
GNSS signals propagating through the troposphere would be delayed by the water vapor. This delay, often called wet delay, is an important observation for the tomographic inversion. Nowadays, most of the methods for building the tomographic region only depend on the distribution of the GNSS signals in the top boundary, in which the water vapor density is roughly equal to zero. This type of tomographic region covers the GNSS signals by a cuboid—the length and the width of which only best fits the GNSS signals in the top boundary. However, the real distribution of the GNSS signals roughly covers a shape of an upside-down blunt cone instead of a cuboid. In addition, the uniform size of voxels often is used together with the regular tomographic region (i.e., cuboid-shaped tomographic region). It results in three problems: (1) the GNSS signals cannot completely cross all of the voxels in the cuboid-shaped tomographic region; (2) redundant voxels/space (i.e., voxels/space are not crossed by the signals) of the tomographic region also increase the calculation burden and degrade the solution quality; (3) the uniform spatial resolution (i.e., uniform size of voxels) of GNSS tomography is unreasonable—since the GNSS signals are spread rapidly from the ground to the sky, the spatial resolution of GNSS tomography decreases with the increase in height. However, few studies have focused on the elimination of redundant voxels (i.e., tracing rays through the voxel). Reference [21] proposed an improved tomographic method based on optimized voxels, which only considers the voxels passed by GNSS rays, which use water vapor information to find the null-ray-passed voxels. Since this approach is essentially to solve problems through tomographic equations, it cannot study tomographic modeling method through visualization. Reference [22] proposed another approach to trace rays through a fast voxel traversal algorithm during the tomography process, which only provides a uniform layering method. It is important to note that both of these approaches theoretically have a 100 percent detection accuracy.
To overcome the above problems, we propose a new adaptive voxel parameterization method, which can effectively search the voxels traversed by signals in each epoch and adapt the density of the signals in each tomographic layer. The new approach can effectively avoid the problem of empirical assignment for no-signal voxels on the ground and the strong constraint problem of water vapor tomographic inversion. The GNSS network distribution will no longer limit the construction of the tomographic region, only the distribution of the GNSS signals need to be considered. Moreover, the thickness of each layer of voxels can be adjusted according to the actual distribution of atmospheric water vapor. This new approach excludes the redundant voxels by the 3D traversal algorithm, which is used with different sizes of voxels to adapt the variable distribution of the GNSS signals in different tomographic layers. This algorithm is introduced in Section 2 below.
2. GNSS Tomographic Modeling
2.1. GNSS Tomographic Observation
GNSS tomographic observation represents a water vapor value on a GNSS signal in three-dimensional space. GNSS signals suffer the bend and delay when it crosses the troposphere. Due to the bend of the GNSS signals being ignored; the curving signal is replaced by the straight line. The tropospheric delay includes two components: the atmospheric dry delay and the atmospheric wet delay. The wet delay is the observation of the GNSS tomography, which can be calculated by
where SWD is the slant wet delay; mw(e) is the wet mapping function; ZWD is the zenith wet delay; mg(e) is the gradient mapping function; and are the wet gradients in the north–south and east–west directions, respectively, which is separated from the gradients (i.e., the wet gradients plus the dry gradients); and R is the cleaning post-fit residuals [23,24]. It is noted that the dry gradients are removed with an assumption that the dry gradient is constant over periods of 12 h, and it can be removed by averaging the gradient solution over that period [25].
In this study, the SWD is converted to slant water vapor (SWV) by multiplying the conversion factor [26]. The SWV is the GNSS tomographic observation, which relates to the solution of the water vapor parameters in g m−3. The new approach to adaptive voxel parameterization is in the next section, and the quantitative relationship between the observed values and water vapor parameters was established.
2.2. Adaptive Voxel Parameterization
Adaptive voxel parameterization is a process to establish the function relation between the tomographic observations and the water vapor parameters, which is needed for the solution of the tomographic equations. The process of realization of the adaptive voxel parameterization mainly includes two components: (1) determination and discretization of the tomographic region by the 3D traversal algorithm; (2) based on the first step, establishment of the tomographic observation equations between the tomographic observations and the water vapor parameters. Its procedure is elaborated in the next subsection. It is noted that since some constraints are necessary for the tomographic equations, the tomographic observation equations are part of the tomographic equations.
2.2.1. Determination and Discretization of the Tomographic Region
The 3D traversal algorithm is proposed to model the tomographic region and at the same time to discretize this region through the following two steps: (1) determination of the pixels which are crossed by the projection of GNSS signals in the three projection planes (i.e., xy-plane, xz-plane and yz-plane); (2) determination of the voxels which are crossed by the GNSS signals through the three-plane projection of the voxels (i.e., pixels in the three projection planes). Both steps are elaborated on in the following passages.
- (1)
- Determination of the pixels crossed by the projection of GNSS signals
The 2D traversal algorithm is firstly introduced to obtain the pixels crossed by the projection of GNSS signals in the projection plane, which can be extended to the three dimensions. For instance, the 2D traversal algorithm to determine the pixels, which are crossed by the projection of GNSS signals in the xy-plane, is illustrated in this section.
As shown in Figure 1, the projection of the GNSS signal in the xy-plane is expressed as the line AB or LAB. The pixels crossed by the LAB are defined by the 2D traversal algorithm. The 2D traversal algorithm consists of two phases—initialization and incremental traversal. The initialization traversal begins by identifying the pixel where the beginning point (i.e., point A) is located. The integer variables X and Y are initialized to the starting pixel coordinates (i.e., pixel index number). For the incremental traversal, the size of the pixel (i.e., the width (Xs) and the height (Ys) of a pixel) and the components of the coordinate difference between A and B (i.e., x1 − x2 and y1 − y2) determine whether X and Y are incremented (+1) or decremented (−1) as the LAB crosses pixel boundaries.
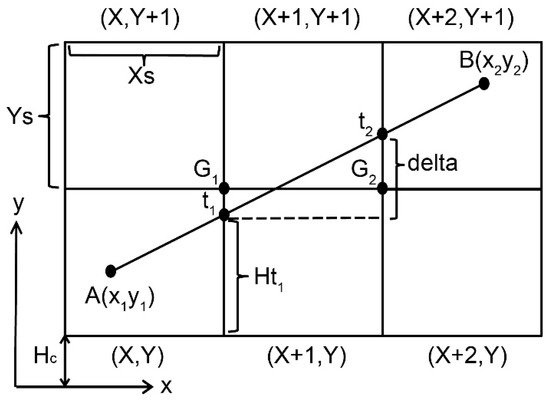
Figure 1.
GNSS signal through the pixel in xy-plane; Xs and Ys are the sizes of the pixels; variables X and Y with integers define the position of the pixel; two points A (x1, y1) and B (x2, y2) define the line AB in the xy-coordinate plane.
Figure 1 shows one of the cases—(1) x-axis is the principal axis and the y-axis is the sub-axis. It can be expressed as Ys/Xs is larger than |y1 − y2|/|x1 − x2|; (2) the X variables increase along the positive direction of the x-axis (i.e., x1 − x2 < 0), and the Y variables increase along the positive direction of the y-axis (i.e., y1 − y2 < 0). As shown in Table 1, LAB can be classified into eight types according to compare Ys/Xs and |y1 − y2|/|x1 − x2|, and to judge the plus-minus sign of the x1 − x2 and y1 − y2. It is important to note that each of these types is similar to the following case, so we will not repeat them again in this paper.

Table 1.
The different types of LAB.
In this case (i.e., No. 1 in Table 1), the beginning point A in the pixel (X, Y) and the position of G1 is set to the upper-right corner of the initial pixel (i.e., pixel (X, Y)). LAB is below G1 (the upper-right corner of pixel (X, Y)) by comparison of the height of t1 and G1, which indicates that LAB crosses the neighboring pixel (X + 1, Y). When the pixels traversed by LAB are determined by the comparison of G1 and t1, the last pixel (i.e., (X + 1, Y)) will be the initial pixel for the next step, and the upper-right corner of the initial pixel is the next G2. It should be noted that the height of t1 is the perpendicular distance from t1 to the principal axis (a similar way to define the height of G1). Repeating the above procedures from pixel (X + 1, Y), LAB is above G2 (the upper-right corner of pixel (X + 1, Y)), which means that LAB crosses the pixels: (X + 1, Y + 1) and (X + 2, Y + 1). Since endpoint B is in the pixel (X + 2, Y + 1), the traversal algorithm is finished.
After removing the perpendicular distance (i.e., Hc) from the bottom of the pixel to the principal axis (i.e., x-axis), the height of the Gi is an integral multiple of Ys and the height of ti can be expressed by
where Hti is the height of ti; Ht1 is the height of t1; the delta represents the increments (in Figure 1), which is a constant. Through Equation (2), the height of the ti is compared to the height of the Gi iteratively to define the pixels crossed by the 2D line (e.g., LAB).
- (2)
- Determination of the voxels crossed by the GNSS signals
Based on the 2D traversal algorithm introduced in the last section, the pixels crossed by the projections of GNSS signal (red lines) in the three projection planes (i.e., XY plane, XZ plane, and YZ plane) can be determined, as shown in Figure 2. Further, taking advantage of the 3D traversal algorithm, the voxels crossed by the GNSS signal (top-left panel) can be defined by the pixels which are crossed by the projection of GNSS signals in the three projection planes. For example, the GNSS signal from A to B (top-left panel) must cross the three voxels—(X Y Z), (X Y + 1 Z + 1) and (X + 1 Y + 1 Z + 1)—according to the XY plane and XZ plane (top-right panel and bottom-left panel in Figure 2). However, there exist two kinds of paths from (X Y Z) to (X + 1 Y + 1 Z + 1), i.e., path 1—from (X Y Z) to (X Y + 1 Z) to (X Y + 1 Z + 1) to (X + 1 Y + 1 Z + 1), and path 2— from (X Y Z) to (X Y Z + 1) to (X Y + 1 Z + 1) to (X + 1 Y + 1 Z + 1), but only one of the paths is correct. To address the above issues, two controversial voxels (X Y + 1 Z) and (X Y Z + 1) in path 1 and path 2, respectively, are projected onto the YZ plane to compare with the corresponding pixel (i.e., (Y + 1 Z)) in the bottom-right panel. It is easy to find that path 1 is the correct path.
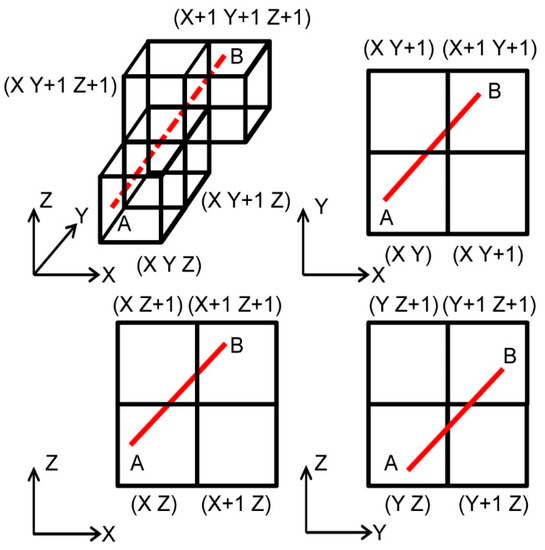
Figure 2.
Determination of the voxels crossed by the GNSS signals according to the 3D traversal algorithm: red dashed line is the part of the GNSS signal inside the voxels, and all the red lines are the projection of the GNSS signal in three different planes.
Based on the 3D traversal algorithm introduced above, each of the GNSS signals used for building a tomographic model can achieve voxelization (i.e., the discretization of GNSS signals by the voxels). Figure 3 shows that the voxels (blue cubes) only crossed by the signal (red line) are lit blue. It means that no extra voxels are introduced in the tomographic model. The 3D traversal algorithm is used to find all the “pierced voxel s” (blue cubes) passed by the signals, which finally established the tomographic region without the redundant voxels. The tomographic region according to the 3D traversal algorithm shows not only its ability to achieve an accurate region that is crossed by signals but also its great potential in adaptive building the tomographic region in different GNSS networks.
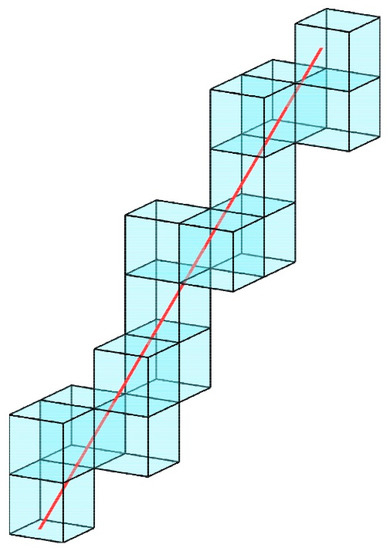
Figure 3.
The 3D traversal algorithm is used to define the voxels (blue cubes) through the signal (red line).
The performance of the GNSS tomography mainly depends on the quality and distribution of the tomographic observations (i.e., GNSS signals with information about the atmospheric water vapor), which is extremely limited by the distribution of the satellite constellation during the tomographic observing period. At present, the common tomographic region is often cuboid shaped, which results in quite a few voxels not being traversed by any rays, due to the actual integral distribution forms of the GNSS signals close to an inverted conical shape rather than a cuboid shape. In this study, the tomographic region is dynamically determined according to the 3D traversal algorithm at each tomographic epoch. As shown in Figure 4a, the traditional method for tomographic region partitioning is to divide the cube region into multiple voxels. This method is rough and contains many voxels that are not passed by GNSS signals (i.e., the hollow cubes in Figure 4a), so the region partitioning cannot be adjusted adaptively according to the distribution of GNSS signals. In Figure 4b, the 3D traversal algorithm determines all of the voxels through the GNSS signals (i.e., all of the detected voxels intersect the rays). These voxels are used for the tomographic modeling without redundancy. Redundancy results in the increase in horizontal constraints for smoothing the empty voxels, which remarkably reduces the accuracy of the tomographic results. Since this new method adaptively detects the voxels (blue cubes) that the signals pass through at the different epochs rather than dividing a rough area in Figure 4a, the adaptive tomographic region in Figure 4b is determined by the actual signal distribution of the GNSS network, which is more reasonable.
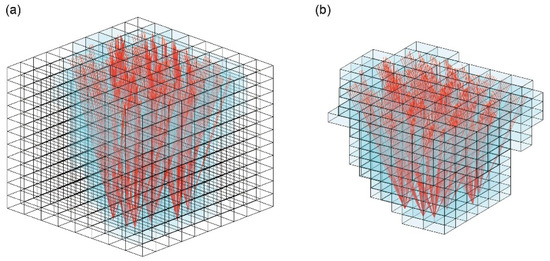
Figure 4.
The tomographic region defined by (a) the traditional method and (b) the 3D traversal algorithm.
2.2.2. Construction of Tomographic Equations
The 3D traversal algorithm belongs to one algorithm for ray tracing [27,28]. We classified the type of line for ray tracing. It results that each iteration can determine one or two passing voxels. Classification of lines in advance is beneficial to the later multi-step calculation, especially if more voxels need to be determined in the later stage. In our study, the 3D traversal algorithm results are obtained by using the 2D traversal algorithm. The 3D traversal algorithm is applied to the modeling and optimization of the tomographic region and then the construction of tomographic equations by computing the distances traveled by the GNSS signal in each voxel of the tomographic model. For each SWV observation, described in Section 2.1, the above distances are used for constructing systems of a tomographic observation equation, which has the ability to estimate the water vapor parameters by the following system of linear Equations:
where Avoxel is a matrix that includes the information about the distances traveled by the signals; BSWV is the vector of SWV observations, and X is the vector of the unknown atmospheric water vapor density values in all voxels.
The GNSS tomographic observations are inadequate to obtain the result of the tomographic inversion, especially compared to the huge tomographic region. To address this problem, prior information (constraints) containing horizontal and vertical directions are added to the tomographic equations. It should be noted that the horizontal constraints are only for the “pierced voxel”. Due to the empty voxels being removed from the tomographic model, the horizontal constraints for those voxels (i.e., not be crossed by any GNSS signals) are not taken into account during the process of tomographic inversion.
3. Experiments and Results
3.1. Tomographic Region and Strategy
Hong Kong Satellite Positioning Reference Station Network (SatRef) is the most important experimental data in this study. Therefore, all of the data used were collected and built closely around SatRef. Each of the positions of the GNSS station that belong to SatRef is marked out with a red triangle in detail in Figure 5, which also shows the horizontal tomographic area. In addition, the vertical area is from the surface to 11,000 m in the air. GAMIT/GLOBK (v.10.7) was utilized to process the GNSS data with the 30 s sampling rate. For atmospheric delay models of GAMIT, the Saastamoinen model was set as the expressions for the dry zenith delay, and VMF1 mapping function was used for both the hydrostatic and wet delay. In the processing, the three International GNSS Service (IGS) stations (CHAN station, BJFS station and USUD station) were introduced to obtain the accurate tomographic parameters. The radiosonde data from the Meteorological Station (Hong Kong King’s Park, HKKP) were used as a reference and compared with the moisture profile obtained by tomographic imaging. Because September 2020 was much hotter, cloudier, and wetter than usual, which more suitable for the tomographic experiment, the experimental data were collected from September 2020 (day of year (DOY) 245–274) for the validation of the tomographic approaches. All of the above data were used for two experimental schemes and the performance of the 3D water vapor inversion was compared. The performances of the general voxel method for tomographic modeling and that of the adaptive voxel parameterization method proposed are quantified for non-uniform vertical tomographic modeling in the following two cases:
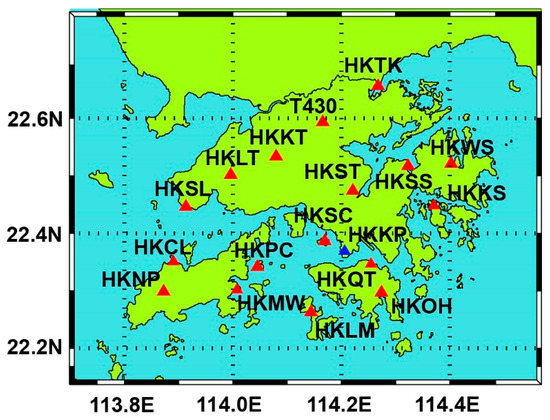
Figure 5.
Horizontal distribution of the SatRef and meteorological station (HKKP).
- (1)
- GFR: general voxel approach with a fixed cuboid tomographic region;
- (2)
- AAR: adaptive voxel parameterization with an accurate tomographic region.
It is noted that the above two schemes further convert the wet refractivity into water vapor density.
3.2. Results
To compare the precision of GFR and AAR results, tomographic solutions at UTC 0 and UTC 12 on DOY 245 and 259 (the former for a sunny day and the latter for a rainy day) were compared with the HKKP data (as a reference). The resultant water vapor profiles are shown in Figure 6. It can be seen that the AAR reconstructed water vapor profiles (red line) are almost consistent with the radiosonde data, except for the water vapor profile of the bottom part at UTC 12 on DOY 245. However, GNSS tomographic results based on GFR have poor performance compared with that of AAR.
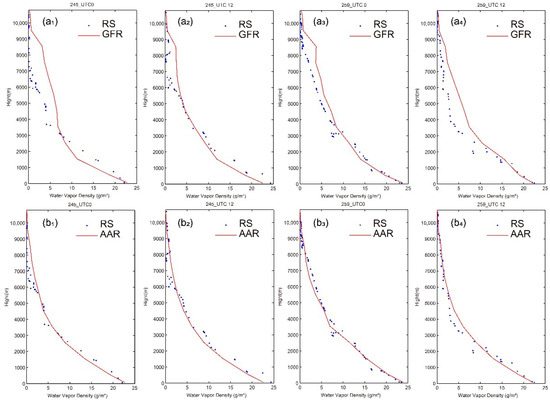
Figure 6.
Tomographic water vapor profiles (red lines) at UTC 0 and UTC 12 on DOY 245 and DOY 259 in 2020 were compared with the sounding data from HKKP (blue dots). (a1–a4) GFR reconstructs water vapor profiles. (b1–b4) AAR reconstructs water vapor profiles.
As can be seen in Table 2, it is more obvious which scheme is most suitable for GNSS tomography. AAR gives more accurate results than GFR regarding root-mean-square error (RMSE). Similarly, in comparison to results, AAR generally has small biases, especially that of DOY 245 at UTC 12 in Figure 6b2. The interquartile range (IQR) as a robust statistic provides a more accurate reflection of the central tendency of datasets. The IQR values show that the tomographic solutions obtained by the AAR algorithm are more concentrated than those obtained by the GFR algorithm.

Table 2.
The statistical results for each subfigure in Figure 6.
In this section, statistical characteristics of results throughout September 2020 (day of year (DOY) 245–274) are presented in Table 3 with statistical arguments which are used in the single-day analysis. Combining with scatter plots of water vapor density in Figure 7a,b, the following conclusion could be obtained: compared with GFR, AAR has high precision and robustness. Box plots in Figure 7c also present the differences between GFR and AAR. The box plots, to some extent, reflect the discreteness of datasets. The errors, the radiosonde data as a reference, produced by the GFR are significantly more dispersed than that of the AAR.

Table 3.
Statistics show the difference in water vapor estimations between GFR and AAR throughout September 2020.
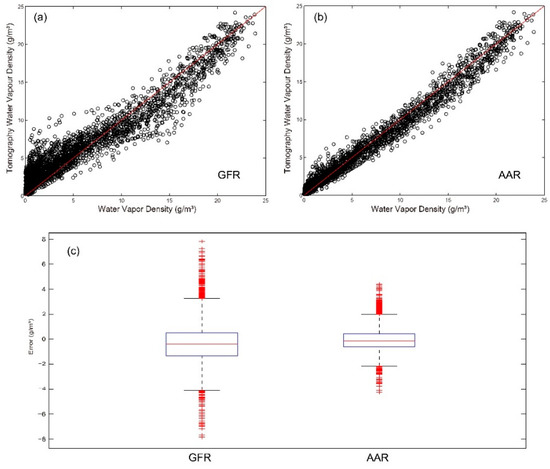
Figure 7.
Graphs showed the statistical results of water vapor tomography for GFR and AAR in September 2020: (a) and (b) are the comparison of radiosonde data with two schemes (GFR and AAR) by the scatter plots, and (c) is the comparison of error in tomographic results by box plots.
4. Conclusions
In this paper, a new GNSS tomography approach based on adaptive voxel parameterization is proposed. This approach constructs an adaptive model by using a 3D traversal algorithm, which dynamically models the tomographic region and, at the same time, discretizes this region. In the traditional tomographic model, a fixed tomographic region is preset for each tomographic epoch. The preset fixed tomographic region takes into account the range where most of the GNSS signals are located but does not consider that there are voxels in the region that no signal passes through. As a result, the voxels model used in the tomography parameterization contains many redundant voxels, which need to be estimated by unnecessary horizontal constraints. However, these additional constraints will reduce the quality of the water vapor tomography results. In this study, a new GNSS tomography approach based on adaptive voxel parameterization is proposed. This approach constructs an adaptive model by using a 3D traversal algorithm, which dynamically models the tomographic region and at the same time to discretize this region.
Using GNSS data (SatRef) through September 2020, the new method (AAR) proved its capacity to retrieve 3D water vapor by comparing it with the general method (GFR). Based on the atmospheric water vapor data, as reference values, provided by the Hong Kong sounding station (HKKP), the water vapor tomography of the two methods is statistically analyzed in this study. The results of the GNSS water vapor tomography experiment in Hong Kong show the following: (1) based on monthly statistics, the adaptive voxel-based model for the dynamic determination of the tomographic region (i.e., AAR scheme) exceeds the general voxel approach with a fixed cuboid tomographic region (i.e., GFR scheme); (2) although GFR and AAR have an approximate trend in the change in water vapor with height, AAR is more in line with the actual change in water vapor, which is obviously reflected in different heights.
Our future work will be focusing on the determination of the reasonable size of the voxels in each layer, which will give full play to the advantages of the new approach (AAR).
Author Contributions
Data curation, N.D., X.T. and Y.W.; formal analysis, N.D. and X.T.; funding acquisition, N.D., S.Z., Z.H. and K.Z.; investigation, S.Z. and K.Z.; methodology, N.D., Y.W. and X.L.; project administration, N.D., S.Z. and K.Z.; resources, X.T. and Z.H.; software, Y.W. and Y.Z.; supervision, S.Z. and K.Z.; validation, X.T. and K.Z.; visualization, N.D. and X.L.; writing—original draft, N.D., X.T. and L.H.; writing—review and editing, N.D., Y.Z. and L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This study is funded by the National Natural Science Foundation of China (No. 42204013, No. 42101256, and No. 41904013), the China Natural Science Funds under Grants (No.41904033), CAS Pioneer Hundred Talents Program, Foundation of Jiangsu Normal University (No.19XSRS010), the Natural Science Foundation of Jiangsu Province (No. BK20221146), the Project funded by the China Postdoctoral Science Foundation (No. 2021M703496), and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the Survey and Mapping Office (SMO) of Lands Department, Hong Kong for the provision of GNSS data from the Hong Kong Satellite Positioning Reference Station Network (SatRef). We also thank King’s Park Observatory for the provision of radiosonde data, and the Department of Earth Atmospheric and Planetary Sciences, MIT for the GAMIT/GLOBK software. The editor and reviewer team are also highly appreciated for their valuable comments, which makes great improvements in the quality of the paper. GNSS data in the RINEX format used for this study can be downloaded from the website (http://www.geodetic.gov.hk/smo/gsi/programs/en/GSS/satref/satref.htm, accessed on 15 September 2022). Radiosonde data of King’s Park Meteorological Station can be downloaded from the website (http://weather.uwyo.edu/upperair/sounding.html, accessed on 15 September 2022). The authors do not have any possible conflicts of interest.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, B.; Liu, Z. Global water vapor variability and trend from the latest 36 year (1979 to 2014) data of ECMWF and NCEP reanalyses, radiosonde, GPS, and microwave satellite. J. Geophys. Res. -Atmos. 2016, 121, 11,442–11,462. [Google Scholar] [CrossRef]
- Ye, H.; Fetzer, E.J.; Wong, S.; Behrangi, A.; Yang, D.; Lambrigtson, B.H. Increasing atmospheric water vapor and higher daily precipitation intensity over northern Eurasia. Geophys. Res. Lett. 2016, 42, 9404–9410. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z.; Wong, W.; Woo, W. Detecting Water Vapor Variability during Heavy Precipitation Events in Hong Kong Using the GPS Tomographic Technique. J. Atmos. Ocean. Tech. 2017, 34, 1001–1019. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Gradinarsky, L.P. Sensing Atmospheric Water Vapor Using Radio Waves. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2002. [Google Scholar]
- Champollion, C.; Masson, F.; Bouin, M.N.; Walpersdorf, A.; Doerflinger, E.; Bock, O.; Van Baelen, J. GPS water vapour tomography: Preliminary results from the ESCOMPTE field experiment. Atmos. Res. 2005, 74, 253–274. [Google Scholar] [CrossRef]
- Troller, M.; Geiger, A.; Brockmann, E.; Bettems, J.M.; Burki, B.; Kahle, H.G. Tomographic determination of the spatial distribution of water vapor using GPS observations. ASR 2006, 37, 2211–2217. [Google Scholar] [CrossRef]
- Rohm, W.; Bosy, J. Local tomography troposphere model over mountains area. Atmos. Res. 2009, 93, 777–783. [Google Scholar] [CrossRef]
- Perler, D.; Geiger, A.; Hurter, F. 4D GPS water vapor tomography: New parameterized approaches. J. Geod. 2011, 85, 539–550. [Google Scholar] [CrossRef]
- Manning, T. Sensing the Dynamics of Severe Weather Using 4D GPS Tomography in the Australian Region. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2013. [Google Scholar]
- Chen, B.; Liu, Z. Voxel-optimized regional water vapor tomography and comparison with radiosonde and numerical weather model. J. Geodesy. 2014, 88, 691–703. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.R.; Liu, Y.Y.; Zhang, J.J.; Xia, P.F. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Ann. Geophys. -Ger. 2014, 32, 911–923. [Google Scholar] [CrossRef]
- Rohm, W.; Zhang, K.; Bosy, J. Limited constraint, robust Kalman filtering for GNSS troposphere tomography. Atmos. Meas. Tech. 2014, 7, 1475–1486. [Google Scholar] [CrossRef]
- Ye, S.; Xia, P.; Cai, C. Optimization of GPS water vapor tomography technique with radiosonde and COSMIC historical data. Ann. Geophys. 2016, 34, 789–799. [Google Scholar] [CrossRef]
- Haji Aghajany, S.; Amerian, Y. Three dimensional ray tracing technique for tropospheric water vapor tomography using GPS measurements. J. Atmos. SolL-Terr. Phy. 2017, 164, 81–88. [Google Scholar] [CrossRef]
- Ding, N.; Zhang, S.B.; Wu, S.Q.; Wang, X.M.; Zhang, K.F. Adaptive Node Parameterization for Dynamic Determination of Boundaries and Nodes of GNSS Tomographic Models. J. Geophys. Res. Atmos. 2018, 123, 1990–2003. [Google Scholar] [CrossRef]
- Yao, Y.; Xin, L.; Zhao, Q. An improved pixel-based water vapor tomography model. Ann. Geophys. 2019, 37, 89–100. [Google Scholar] [CrossRef]
- Rohm, W.; Bosy, J. The verification of GNSS tropospheric tomography model in a mountainous area. Adv. Space. Res. 2011, 47, 1721–1730. [Google Scholar] [CrossRef]
- Nilsson, T.; Gradinarsky, L. Water vapor tomography using GPS phase observations: Simulation results. IEEE. T Geosci. Remote. 2006, 44, 2927–2941. [Google Scholar] [CrossRef]
- Sudhir, M.S. Investigations into the Estimation of Tropospheric Delay and Wet Refractivity Using GPS Measurements. Ph.D. Thesis, Department of Geomatics Engineering, University of Calgary, Calgary, AB, Canada, 2003. [Google Scholar]
- Yao, Y.; Liu, C.; Xu, C. A New GNSS-Derived Water Vapor Tomography Method Based on Optimized Voxel for Large GNSS Network. Remote Sens. 2020, 12, 2306. [Google Scholar] [CrossRef]
- Hu, H.; Liu, M.; Zhong, J.; Deng, X.; Cao, Y.; Fang, P. A Case Study of the 3D Water Vapor Tomography Model Based on a Fast Voxel Traversal Algorithm for Ray Tracing. Remote Sens. 2021, 13, 2422. [Google Scholar] [CrossRef]
- Shoji, Y.; Nakamura, H.; Iwabuchi, T.; Aonashi, K.; Seko, H.; Mishima, K.; Itagaki, A.; Ichikawa, R.; Ohtani, R. Tsukuba GPS dense net campaign observation: Improvement in GPS analysis of slant path delay by stacking one-way postfit phase residuals. J. Meteorol. Soc. Japan. 2004, 82, 301–314. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res.-Sol. Ea. 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl Met. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Kui, Y.L. An All-integer Algorithm for Drawing Anti-aliased Straight Lines. Comput. Graph. Forum. 1994, 13, 219–221. [Google Scholar] [CrossRef]
- Amanatides, J.; Woo, A. A Fast Voxel Traversal Algorithm for Ray Tracing. Eurographics 1987, 87, 3–10. Available online: https://www.cse.chalmers.se/edu/year/2012/course/_courses_2011/TDA361/grid.pdf (accessed on 10 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).