Enhancing Aboveground Biomass Estimation for Three Pinus Forests in Yunnan, SW China, Using Landsat 8
Abstract
:1. Introduction
- (1)
- Do estimation models have an impact on the AGB estimation for pine forests?
- (2)
- Is it possible to estimate the AGB for the three pine forests using the habitat dataset?
- (3)
- Does the employment of a habitat dataset reduce the probability of overestimation and underestimation of the AGB estimation?
2. Materials and Methods
2.1. Study Area
2.2. Sample Plot Data and Forest AGB
2.3. Acquisition of Remote-Sensing Datasets
2.4. Acquisition of Habitat Datasets
2.5. Acquisition of Combined Datasets
2.6. AGB Modeling Algorithms
2.6.1. Stepwise Linear Regression (SLR)
2.6.2. Random Forest (RF)
2.6.3. Support Vector Machine (SVM)
2.7. Model Evaluation
3. Results
3.1. Model Performance
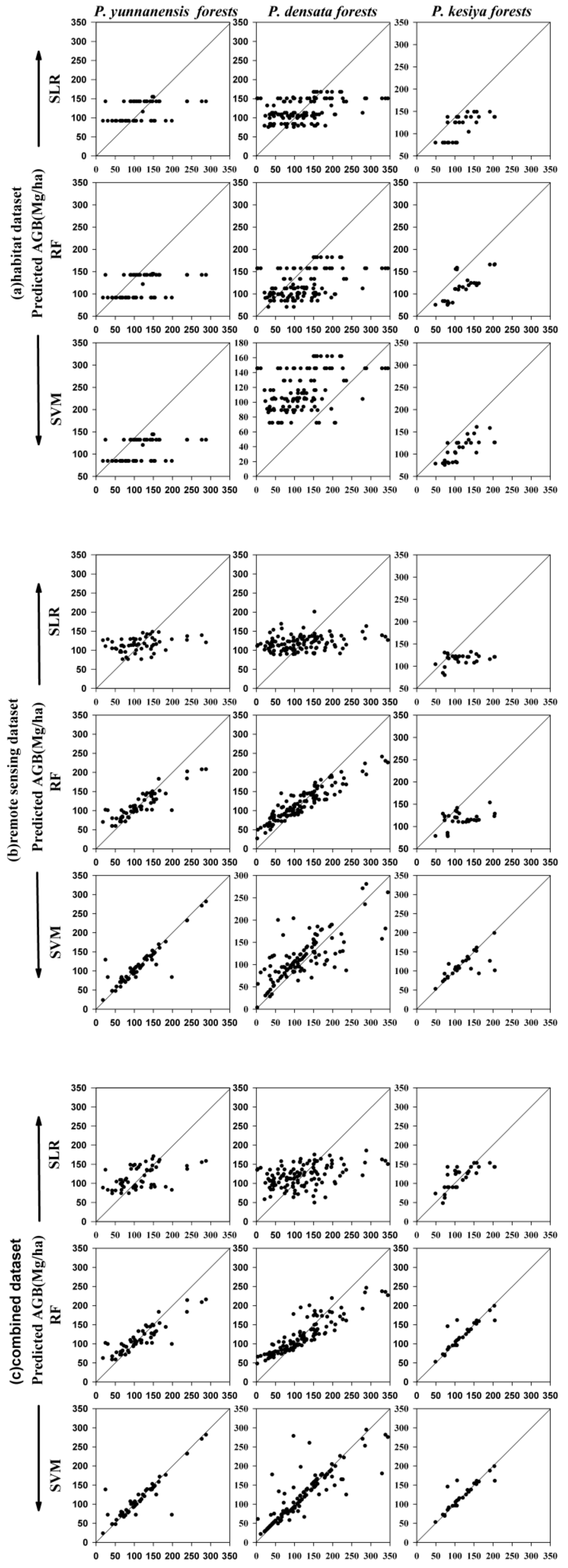
3.2. AGB Estimation Based on Different Datasets
4. Discussion
4.1. The Selection of Modeling Algorithms
4.2. Selection of Suitable Variables for AGB Modeling
4.3. AGB Estimation by Incorporating the Habitat Dataset into the Models
4.4. Comparison and Implication of Similar Studies
4.5. Limitation and Future Research
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ou, G.; Lv, Y.; Xu, H.; Wang, G. Improving Forest Aboveground Biomass Estimation of Pinus densata Forest in Yunnan of Southwest China by Spatial Regression using Landsat 8 Images. Remote Sens. 2019, 11, 2750. [Google Scholar] [CrossRef]
- Kramer, P.J. Carbon Dioxide Concentration, Photosynthesis, and Dry Matter Production. BioScience 1981, 31, 29–33. [Google Scholar] [CrossRef]
- Olson, J.S.; Watts, J.A.; Allison, L.J. Carbon in Live Vegetation of Major World Ecosystems; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1983. [Google Scholar]
- Woodwell, G.M.; Whittaker, R.; Reiners, W.; Likens, G.E.; Delwiche, C.; Botkin, D. The Biota and the World Carbon Budget: The terrestrial biomass appears to be a net source of carbon dioxide for the atmosphere. Science 1978, 199, 141–146. [Google Scholar] [CrossRef]
- Xu, W.; Jin, X.; Yang, X.; Wang, Z.; Liu, J.; Wang, D.; Shan, W.; Zhou, Y. The estimation of forest vegetation biomass in China in spatial grid. J. Nat. Resour. 2018, 33, 1725–1741. [Google Scholar]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Cairns, M.A.; Brown, S.; Helmer, E.H.; Baumgardner, G.A. Root biomass allocation in the world’s upland forests. Oecologia 1997, 111, 1–11. [Google Scholar] [CrossRef]
- Yang, S.; Feng, Q.; Liang, T.; Liu, B.; Zhang, W.; Xie, H. Modeling grassland above-ground biomass based on artificial neural network and remote sensing in the Three-River Headwaters Region. Remote Sens. Environ. 2018, 204, 448–455. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote sensing of above-ground biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Calvao, T.; Palmeirim, J. Mapping Mediterranean scrub with satellite imagery: Biomass estimation and spectral behaviour. Int. J. Remote Sens. 2004, 25, 3113–3126. [Google Scholar] [CrossRef]
- Li, M.; Tan, Y.; Pan, J.; Peng, S. Modeling forest aboveground biomass by combining spectrum, textures and topographic features. Front. For. China 2008, 3, 10–15. [Google Scholar] [CrossRef]
- Rahman, M.; Csaplovics, E.; Koch, B. An efficient regression strategy for extracting forest biomass information from satellite sensor data. Int. J. Remote Sens. 2005, 26, 1511–1519. [Google Scholar] [CrossRef]
- Zheng, D.; Rademacher, J.; Chen, J.; Crow, T.; Bresee, M.; Le Moine, J.; Ryu, S.-R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ. 2004, 93, 402–411. [Google Scholar] [CrossRef]
- Buckley, J.R.; Smith, A.M. Monitoring grasslands with RADARSAT 2 quad-pol imagery. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, Hawaii, USA, 25–30 July 2010; pp. 3090–3093. [Google Scholar]
- Le Toan, T.; Quegan, S.; Davidson, M.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Pandey, U.; Kushwaha, S.; Kachhwaha, T.; Kunwar, P.; Dadhwal, V. Potential of Envisat ASAR data for woody biomass assessment. Trop. Ecol. 2010, 51, 117. [Google Scholar]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Saremi, H.; Kumar, L.; Stone, C.; Melville, G.; Turner, R. Sub-compartment variation in tree height, stem diameter and stocking in a Pinus radiata D. Don plantation examined using airborne LiDAR data. Remote Sens. 2014, 6, 7592–7609. [Google Scholar] [CrossRef]
- Saremi, H.; Kumar, L.; Turner, R.; Stone, C. Airborne LiDAR derived canopy height model reveals a significant difference in radiata pine (Pinus radiata D. Don) heights based on slope and aspect of sites. Trees 2014, 28, 733–744. [Google Scholar] [CrossRef]
- Sarker, M.L.R.; Nichol, J.; Iz, H.B.; Ahmad, B.B.; Rahman, A.A. Forest biomass estimation using texture measurements of high-resolution dual-polarization C-band SAR data. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3371–3384. [Google Scholar] [CrossRef]
- Wempen, J.M.; McCarter, M.K. Comparison of L-band and X-band differential interferometric synthetic aperture radar for mine subsidence monitoring in central Utah. Int. J. Min. Sci. Technol. 2017, 27, 159–163. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Qian, B.; He, L.; Liu, J.; Wang, R.; Jing, Q.; Champagne, C.; McNairn, H.; Powers, J. Estimating crop biomass using leaf area index derived from Landsat 8 and Sentinel-2 data. ISPRS J. Photogramm. Remote Sens. 2020, 168, 236–250. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef] [PubMed]
- López-Serrano, P.M.; Cardenas Dominguez, J.L.; Corral-Rivas, J.J.; Jiménez, E.; López-Sánchez, C.A.; Vega-Nieva, D.J. Modeling of aboveground biomass with Landsat 8 OLI and machine learning in temperate forests. Forests 2019, 11, 11. [Google Scholar] [CrossRef] [Green Version]
- Otgonbayar, M.; Atzberger, C.; Chambers, J.; Damdinsuren, A. Mapping pasture biomass in Mongolia using partial least squares, random forest regression and Landsat 8 imagery. Int. J. Remote Sens. 2019, 40, 3204–3226. [Google Scholar] [CrossRef]
- Duncanson, L.; Niemann, K.; Wulder, M. Integration of GLAS and Landsat TM data for aboveground biomass estimation. Can. J. Remote Sens. 2010, 36, 129–141. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Z.; Liu, L.; Li, C.; Peng, D.; Xiao, P. Improving Estimation of Woody Aboveground Biomass of Sparse Mixed Forest over Dryland Ecosystem by Combining Landsat-8, GaoFen-2, and UAV Imagery. Remote Sens. 2021, 13, 4859. [Google Scholar] [CrossRef]
- Meng, S.; Pang, Y.; Zhang, Z.; Jia, W.; Li, Z. Mapping aboveground biomass using texture indices from aerial photos in a temperate forest of Northeastern China. Remote Sens. 2016, 8, 230. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Gregoire, T.G.; Ståhl, G. Model-assisted estimation of change in forest biomass over an 11 year period in a sample survey supported by airborne LiDAR: A case study with post-stratification to provide “activity data”. Remote Sens. Environ. 2013, 128, 299–314. [Google Scholar] [CrossRef]
- Ou, G.; Li, C.; Lv, Y.; Wei, A.; Xiong, H.; Xu, H.; Wang, G. Improving aboveground biomass estimation of Pinus densata forests in Yunnan using Landsat 8 imagery by incorporating age dummy variable and method comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef]
- Puliti, S.; Hauglin, M.; Breidenbach, J.; Montesano, P.; Neigh, C.; Rahlf, J.; Solberg, S.; Klingenberg, T.; Astrup, R. Modelling above-ground biomass stock over Norway using national forest inventory data with ArcticDEM and Sentinel-2 data. Remote Sens. Environ. 2020, 236, 111501. [Google Scholar] [CrossRef]
- Ene, L.T.; Næsset, E.; Gobakken, T.; Bollandsås, O.M.; Mauya, E.W.; Zahabu, E. Large-scale estimation of change in aboveground biomass in miombo woodlands using airborne laser scanning and national forest inventory data. Remote Sens. Environ. 2017, 188, 106–117. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, C.; Xu, H.; Wang, G. Estimating aboveground biomass of Pinus densata-dominated forests using Landsat time series and permanent sample plot data. J. For. Res. 2018, 30, 1689–1706. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Castillo-Santiago, M.Á.; Mas, J.F.; Wheeler, C.E.; Andres-Mauricio, J.; Tun-Dzul, F.; George-Chacón, S.P.; Reyes-Palomeque, G.; Castellanos-Basto, B.; Vaca, R. Improving aboveground biomass maps of tropical dry forests by integrating LiDAR, ALOS PALSAR, climate and field data. Carbon Balance Manag. 2020, 15, 15. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-Q.; Ali, A. Climate regulates the functional traits–aboveground biomass relationships at a community-level in forests: A global meta-analysis. Sci. Total Environ. 2021, 761, 143238. [Google Scholar] [CrossRef] [PubMed]
- Schucknecht, A.; Meroni, M.; Kayitakire, F.; Boureima, A. Phenology-based biomass estimation to support rangeland management in semi-arid environments. Remote Sens. 2017, 9, 463. [Google Scholar] [CrossRef]
- Liu, N.; Harper, R.J.; Handcock, R.N.; Evans, B.; Sochacki, S.J.; Dell, B.; Walden, L.L.; Liu, S. Seasonal timing for estimating carbon mitigation in revegetation of abandoned agricultural land with high spatial resolution remote sensing. Remote Sens. 2017, 9, 545. [Google Scholar] [CrossRef]
- Lumbierres, M.; Méndez, P.F.; Bustamante, J.; Soriguer, R.; Santamaría, L. Modeling biomass production in seasonal wetlands using MODIS NDVI land surface phenology. Remote Sens. 2017, 9, 392. [Google Scholar] [CrossRef]
- Yan, Z.; Chen, Y. Habitat Selection in Animals. Chin. J. Ecol. 1998, 17, 43–49. [Google Scholar]
- Sillero, N.; Arenas-Castro, S.; Enriquez-Urzelai, U.; Vale, C.G.; Sousa-Guedes, D.; Martínez-Freiría, F.; Real, R.; Barbosa, A.M. Want to model a species niche? A step-by-step guideline on correlative ecological niche modelling. Ecol. Model. 2021, 456, 109671. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, H.; Zhou, X.; Yin, B.; Zhou, D.; Tao, Y. Biomass allocation patterns of an ephemeral species (Erodium oxyrhinchum) in different habitats and germination types in the Gurbantunggut Desert, China. Arid. Zone Res. 2022, 39, 541–550. [Google Scholar] [CrossRef]
- Qiu, X.; Xu, Z.; Tu, Y.; Luo, J. Module biomass and allocation characteristics of invasive plant Tagetes minuta population modules in different habitats. Guihaia 2021, 41, 447–455. [Google Scholar] [CrossRef]
- Hao, J.; Yao, X.; Huang, Y.; Yao, J.; Chen, Y.; Xie, H.; Chen, R. Effect of Different Habitats on the Species Diversity of Communities and Modular Biomass of Riparian Vegetation in the Wenjiang Section of the Jinma Rive. Acta Bot. Boreal.-Occident. Sin. 2016, 36, 1864–1871. [Google Scholar] [CrossRef]
- Zhou, X.; Zuo, X.; Zhao, X.; Wang, S.; Luo, Y.; Yue, X.; Zhang, L. Effect of change in semiarid sand dune habitat on aboveground plant biomass, carbon and nitrogen. Acta Pratacult. Sin. 2014, 23, 36–44. [Google Scholar] [CrossRef]
- He, Z. Soil microbial biomass and Its significance in nutrient cycling and environmental quality assessment. Soils 1997, 29, 61–69. [Google Scholar]
- Chen, I.-C.; Hill, J.K.; Ohlemüller, R.; Roy, D.B.; Thomas, C.D. Rapid range shifts of species associated with high levels of climate warming. Science 2011, 333, 1024–1026. [Google Scholar] [CrossRef]
- Gontier, M.; Balfors, B.; Mörtberg, U. Biodiversity in environmental assessment—Current practice and tools for prediction. Environ. Impact Assess. Rev. 2006, 26, 268–286. [Google Scholar] [CrossRef]
- Steiner, N.C.; Köhler, W. Effects of landscape patterns on species richness—A modelling approach. Agric. Ecosyst. Environ. 2003, 98, 353–361. [Google Scholar] [CrossRef]
- Hansen, A.J.; McComb, W.C.; Vega, R.; Raphael, M.G.; Hunter, M. Bird habitat relationships in natural and managed forests in the west Cascades of Oregon. Ecol. Appl. 1995, 5, 555–569. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Sisk, T.D.; Milne, A.; Morgan, G.; Orr, T. Remotely sensed indicators of habitat heterogeneity: Use of synthetic aperture radar in mapping vegetation structure and bird habitat. Remote Sens. Environ. 1997, 60, 217–227. [Google Scholar] [CrossRef]
- Duro, D.C.; Coops, N.C.; Wulder, M.A.; Han, T. Development of a large area biodiversity monitoring system driven by remote sensing. Prog. Phys. Geogr. 2007, 31, 235–260. [Google Scholar] [CrossRef]
- He, K.S.; Bradley, B.A.; Cord, A.F.; Rocchini, D.; Tuanmu, M.N.; Schmidtlein, S.; Turner, W.; Wegmann, M.; Pettorelli, N. Will remote sensing shape the next generation of species distribution models? Remote Sens. Ecol. Conserv. 2015, 1, 4–18. [Google Scholar] [CrossRef]
- Chapman, D.S. Weak climatic associations among British plant distributions. Glob. Ecol. Biogeogr. 2010, 19, 831–841. [Google Scholar] [CrossRef]
- Beale, C.M.; Lennon, J.J.; Gimona, A. Opening the climate envelope reveals no macroscale associations with climate in European birds. Proc. Natl. Acad. Sci. USA 2008, 105, 14908–14912. [Google Scholar] [CrossRef] [PubMed]
- Loiselle, B.A.; Jørgensen, P.M.; Consiglio, T.; Jiménez, I.; Blake, J.G.; Lohmann, L.G.; Montiel, O.M. Predicting species distributions from herbarium collections: Does climate bias in collection sampling influence model outcomes? J. Biogeogr. 2008, 35, 105–116. [Google Scholar] [CrossRef]
- Li, X.; Mao, F.; Du, H.; Zhou, G.; Xing, L.; Liu, T.; Han, N.; Liu, Y.; Zheng, J.; Dong, L. Spatiotemporal evolution and impacts of climate change on bamboo distribution in China. J. Environ. Manag. 2019, 248, 109265. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, H.; Wang, H. Potential geographical distribution of populus euphratica in China under future climate change scenarios based on Maxent model. Acta Ecol. Sin. 2020, 40, 6552–6563. [Google Scholar] [CrossRef]
- Hu, W.; Zhao, B.; Wang, Y.; Dong, P.; Zhang, D.; Yu, W.; Chen, G.; Chen, B. Assessing the potential distributions of mangrove forests in Fujian Province using MaxEnt model. China Environ. Sci. 2020, 40, 4029–4038. [Google Scholar]
- Bahn, V.; McGill, B.J. Can niche-based distribution models outperform spatial interpolation? Glob. Ecol. Biogeogr. 2007, 16, 733–742. [Google Scholar] [CrossRef]
- Yang, X.-Q.; Kushwaha, S.; Saran, S.; Xu, J.; Roy, P. Maxent modeling for predicting the potential distribution of medicinal plant, Justicia adhatoda L. in Lesser Himalayan foothills. Ecol. Eng. 2013, 51, 83–87. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Fleming, A.L.; Wang, G.; McRoberts, R.E. Comparison of methods toward multi-scale forest carbon mapping and spatial uncertainty analysis: Combining national forest inventory plot data and Landsat TM images. Eur. J. For. Res. 2015, 134, 125–137. [Google Scholar] [CrossRef]
- Yan, W.; Zong, S.; Luo, Y.; Cao, C.; Li, Z.; Guo, Q. Application of stepwise regression model in predicting the movement of Artemisia ordosica boring insects. J. Beijing For. Univ. 2009, 31, 140–144. [Google Scholar]
- Wang, J.; Shen, W.; Li, W.; Li, M.; Zhen, G. Performances Comparison of Multiple Non-linear Models for Estimating Plantations’ Biomass Based on RapidEye Imagery. J. Northwest For. Univ. 2015, 30, 196–202. [Google Scholar] [CrossRef]
- Liu, L. Model regression analysis of Pinus yunnanensis biomass in northwest Yunnan. J. Shandong For. Sci. Technol. 2015, 5–9, 34. [Google Scholar]
- Chen, Q.; Zheng, Z.; Feng, Z.; Ma, Y.; Sha, L.; Xu, H. Biomass and carbon storage of Pinus kesiya var. langbianensis in Puer’Yunnan. J. Yunnan Univ Nat. Sci. 2014, 36, 439–445. [Google Scholar]
- Ou, G.; Wang, J.; Xu, H.; Chen, K.; Zheng, H.; Zhang, B.; Sun, X.; Xu, T.; Xiao, Y. Incorporating topographic factors in nonlinear mixed-effects models for aboveground biomass of natural Simao pine in Yunnan, China. J. For. Res. 2015, 27, 119–131. [Google Scholar] [CrossRef]
- Galidaki, G.; Zianis, D.; Gitas, I.; Radoglou, K.; Karathanassi, V.; Tsakiri–Strati, M.; Woodhouse, I.; Mallinis, G. Vegetation biomass estimation with remote sensing: Focus on forest and other wooded land over the Mediterranean ecosystem. Int. J. Remote Sens. 2017, 38, 1940–1966. [Google Scholar] [CrossRef]
- Li, P.; Meng, G.; Wang, Y.; Li, G.; Li, G.; Cai, Y.; Wang, Q. Analysis of Growth Process Pinus yunnanensis Natural Secondary Forests in Yongren County of Yunnan Province. J. West China For. Sci. 2012, 41, 47–52. [Google Scholar]
- Sun, X.; Xiong, X.; Xu, H.; Wei, A.; Li, C.; Lv, Y.; Zhang, B.; Ou, G. Modelling of Individual Tree Biomass Factors for Natural Pinus densata Forest. For. Resour. Manag. 2016, 49–53, 60. [Google Scholar] [CrossRef]
- Shen, C.; Yue, C.; Mei, H. Dynamic Monitoring of Puer Land Use Change Based on Landsat Data. For. Inventory Plan. 2016, 41, 72. [Google Scholar] [CrossRef]
- Fourcade, Y.; Besnard, A.G.; Secondi, J. Paintings predict the distribution of species, or the challenge of selecting environmental predictors and evaluation statistics. Glob. Ecol. Biogeogr. 2018, 27, 245–256. [Google Scholar] [CrossRef]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Bourque, C.P.-A. Relating modelled habitat suitability for Abies balsamea to on-the-ground species structural characteristics in naturally growing forests. Ecol. Indic. 2020, 111, 105981. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, Z.; Sun, H.; Wang, G. Mapping forest ecosystem biomass density for Xiangjiang River Basin by combining plot and remote sensing data and comparing spatial extrapolation methods. Remote Sens. 2017, 9, 241. [Google Scholar] [CrossRef]
- Huang, J.; Hou, Y.; Su, W.; Liu, J.; Zhu, D. Mapping corn and soybean cropped area with GF-1 WFV data. Trans. Chin. Soc. Agric. Eng. 2017, 33, 164–170. [Google Scholar] [CrossRef]
- Zhang, X.; Li, F.; Zhen, Z.; Zhao, Y. Forest Vegetation Classification of Landsat8 Remote Sensing Image Based on Random Forests Model. J. Northeast. For. Univ. 2016, 44, 53–57. [Google Scholar] [CrossRef]
- Wang, L.; Ma, C.; Zhou, X.; Zi, Y.; Zhu, X.; Guo, W. Estimation of Wheat Leaf SPAD Value Using RF Algorithmic Model and Remote Sensing Data. Trans. Chin. Soc. Agric. Mach. 2015, 46, 259–265. [Google Scholar] [CrossRef]
- Guo, P.; Li, M.; Luo, W.; Lin, Q.; Tang, Q.; Liu, Z. Prediction of soil total nitrogen for rubber plantation at regional scale based on environmental variables and random forest approach. Trans. Chin. Soc. Agric. Eng. 2015, 31, 194–202. [Google Scholar] [CrossRef]
- Lin, Z.; Wu, C.; Hong, W.; Hong, T. Yield model of Cunninghamia lanceolata plantation based on back propagation neural network and support vector machine. J. Beijing For. Univ. 2015, 37, 42–47. [Google Scholar] [CrossRef]
- Ding, S.; Qi, B.; Tan, H. An Overview on Theory and Algorithm of Support Vector Machines. J. Univ. Electron. Sci. Technol. China 2011, 40, 1–10. [Google Scholar] [CrossRef]
- Xie, S.; Shen, F.; Qiu, X. Face Recognition Method Based on Support Vector Machine. Comput. Eng. 2009, 35, 186–188. [Google Scholar] [CrossRef]
- Gao, W.; Wang, N. Prediction of Shallow-water Reverberation Time Series Using Support Vector Machine. Comput. Eng. 2008, 34, 25–27. [Google Scholar] [CrossRef]
- Feng, Y.; Lu, D.; Chen, Q.; Keller, M.; Moran, E.; dos-Santos, M.N.; Bolfe, E.L.; Batistella, M. Examining effective use of data sources and modeling algorithms for improving biomass estimation in a moist tropical forest of the Brazilian Amazon. Int. J. Digit. Earth 2017, 10, 996–1016. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Li, M. An evaluation of eight machine learning regression algorithms for forest aboveground biomass estimation from multiple satellite data products. Remote Sens. 2020, 12, 4015. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and evaluation of three methods for estimating forest above ground biomass using TM and GLAS data. Remote Sens. 2017, 9, 341. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of northeastern China using GLAS and MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 140–152. [Google Scholar] [CrossRef]
- Ali, I.; Cawkwell, F.; Dwyer, E.; Barrett, B.; Green, S. Satellite remote sensing of grasslands: From observation to management. J. Plant Ecol. 2016, 9, 649–671. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Y.; Chen, B. Estimating Spartina alterniflora fractional vegetation cover and aboveground biomass in a coastal wetland using SPOT6 satellite and UAV data. Aquat. Bot. 2018, 144, 38–45. [Google Scholar] [CrossRef]
- Phinn, S.; Franklin, J.; Hope, A.; Stow, D.; Huenneke, L. Biomass distribution mapping using airborne digital video imagery and spatial statistics in a semi-arid environment. J. Environ. Manag. 1996, 47, 139–164. [Google Scholar] [CrossRef]
- Yuan, Z.; Gazol, A.; Wang, X.; Lin, F.; Ye, J.; Zhang, Z.; Suo, Y.; Kuang, X.; Wang, Y.; Jia, S. Pattern and dynamics of biomass stock in old growth forests: The role of habitat and tree size. Acta Oecologica 2016, 75, 15–23. [Google Scholar] [CrossRef]
- Lanham, B.S.; Gribben, P.E.; Poore, A.G. Beyond the border: Effects of an expanding algal habitat on the fauna of neighbouring habitats. Mar. Environ. Res. 2015, 106, 10–18. [Google Scholar] [CrossRef]
- Cutler, M.; Boyd, D.; Foody, G.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data: An assessment of predictions between regions. ISPRS J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef]
- Sarr, D.A.; Hibbs, D.E.; Huston, M.A. A hierarchical perspective of plant diversity. Q. Rev. Biol. 2005, 80, 187–212. [Google Scholar] [CrossRef] [PubMed]
- Rosenzweig, M.L. Species Diversity in Space and Time; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Huy, B.; Kralicek, K.; Poudel, K.P.; Phuong, V.T.; Van Khoa, P.; Hung, N.D.; Temesgen, H. Allometric equations for estimating tree aboveground biomass in evergreen broadleaf forests of Viet Nam. For. Ecol. Manag. 2016, 382, 193–205. [Google Scholar] [CrossRef]
- Salum, R.B.; Souza-Filho, P.W.M.; Simard, M.; Silva, C.A.; Fernandes, M.E.; Cougo, M.F.; do Nascimento Junior, W.; Rogers, K. Improving mangrove above-ground biomass estimates using LiDAR. Estuar. Coast. Shelf Sci. 2020, 236, 106585. [Google Scholar] [CrossRef]


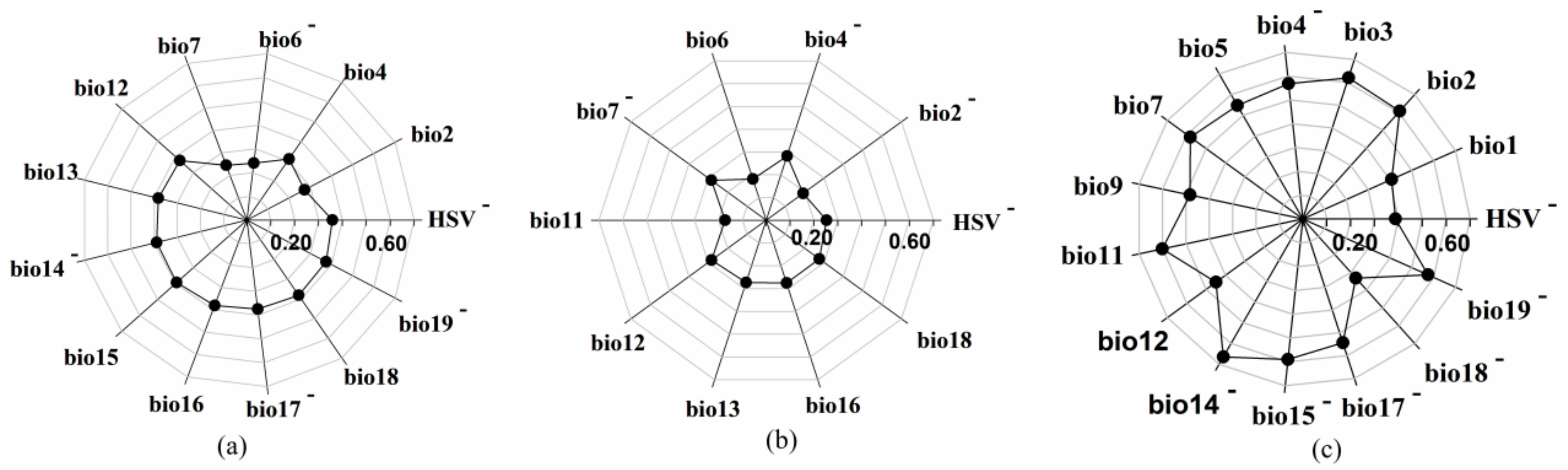
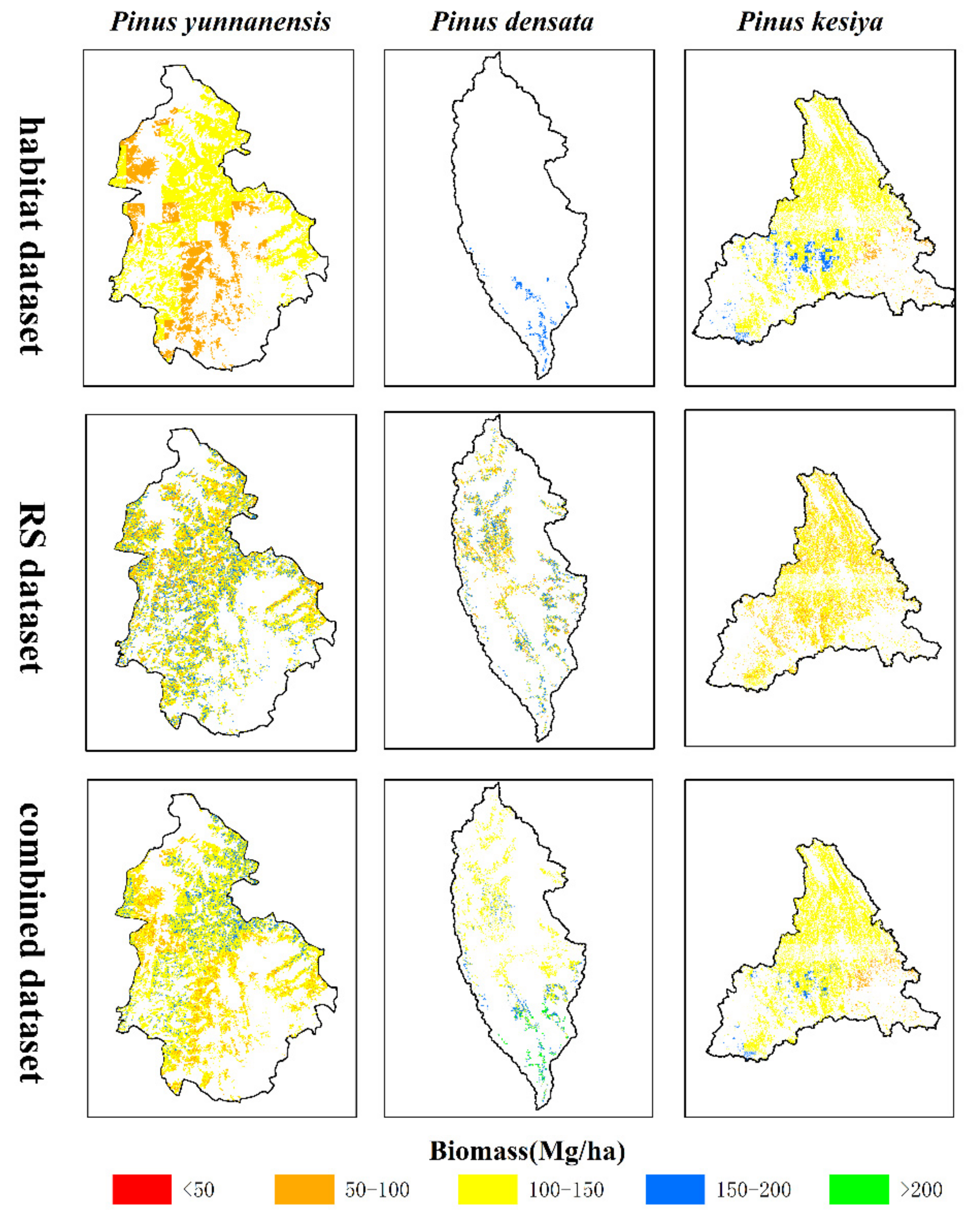

| Species | Number of Plots | Statistical Indicators | AGB (Mg/ha) |
|---|---|---|---|
| Pinus yunnanensis | 87 | Min. | 17.901 |
| Max. | 287.679 | ||
| Mean | 114.868 | ||
| Pinus densata | 147 | Min. | 2.114 |
| Max. | 344.382 | ||
| Mean | 121.474 | ||
| Pinus kesiya | 45 | Min. | 49.063 |
| Max. | 204.448 | ||
| Mean | 116.432 |
| Study Area | Image ID | Average Cloud Cover (%) | Start Time |
|---|---|---|---|
| Yongren | LC81300422016030LGN00 | 0.00 | 30 January 2016 |
| Shangri-la | LC81310412016325LGN00 | 0.40 | 20 November 2016 |
| LC81320402016348LGN00 | 0.73 | 13 December 2016 | |
| LC81320412016348LGN00 | 0.76 | 13 December 2016 | |
| Pu’er | LC81290442015052LGN00 | 0.08 | 21 February 2015 |
| LC81290452015052LGN00 | 1.87 | 21 February 2015 | |
| LC81310432015066LGN00 | 0.00 | 7 March 2015 | |
| LC81310442015066LGN00 | 0.00 | 7 March 2015 | |
| LC81300432015075LGN00 | 0.18 | 16 March 2015 | |
| LC81300442016046LGN00 | 0.00 | 15 February 2016 | |
| LC81300452016046LGN00 | 0.01 | 15 February 2016 | |
| LC81310452016069LGN00 | 0.41 | 9 March 2016 |
| Variable Code | Variable Description | Variable Code | Variable Description |
|---|---|---|---|
| Bio1 | Annual mean temperature | Bio2 | Mean diurnal range |
| Bio3 | Isothermality | Bio4 | Temperature seasonality |
| Bio5 | Max temperature of the warmest month | Bio6 | Min temperature of the coldest month |
| Bio7 | Range of annual temperature | Bio8 | Mean temperature of the wettest quarter |
| Bio9 | Mean temperature of the driest quarter | Bio10 | Mean temperature of the warmest quarter |
| Bio11 | Mean temperature of the coldest quarter | Bio12 | Annual average precipitation |
| Bio13 | Precipitation of the wettest month | Bio14 | Precipitation of the driest month |
| Bio15 | Precipitation seasonality | Bio16 | Precipitation of the wettest quarter |
| Bio17 | Precipitation of the driest quarter | Bio18 | Precipitation of the warmest quarter |
| Bio19 | Precipitation of the coldest quarter |
| Fitting | Testing | |||||||
|---|---|---|---|---|---|---|---|---|
| Species | Number | AGB Range (Mg/ha) | AGB Mean (Mg/ha) | AGB Std. Dev. (Mg/ha) | Number | AGB Range (Mg/ha) | AGB Mean (Mg/ha) | AGB Std. Dev. (Mg/ha) |
| Pinus yunnanensis | 57 | 17.9–287.7 | 115.1 | 56.9 | 30 | 40.6–270.2 | 114.4 | 53.1 |
| Pinus densata | 117 | 2.1–344.4 | 119.3 | 70.6 | 30 | 11.1–344.4 | 107.6 | 76.3 |
| Pinus kesiya | 30 | 49.1–204.4 | 116.2 | 40 | 15 | 70.1–192.2 | 116.8 | 33.6 |
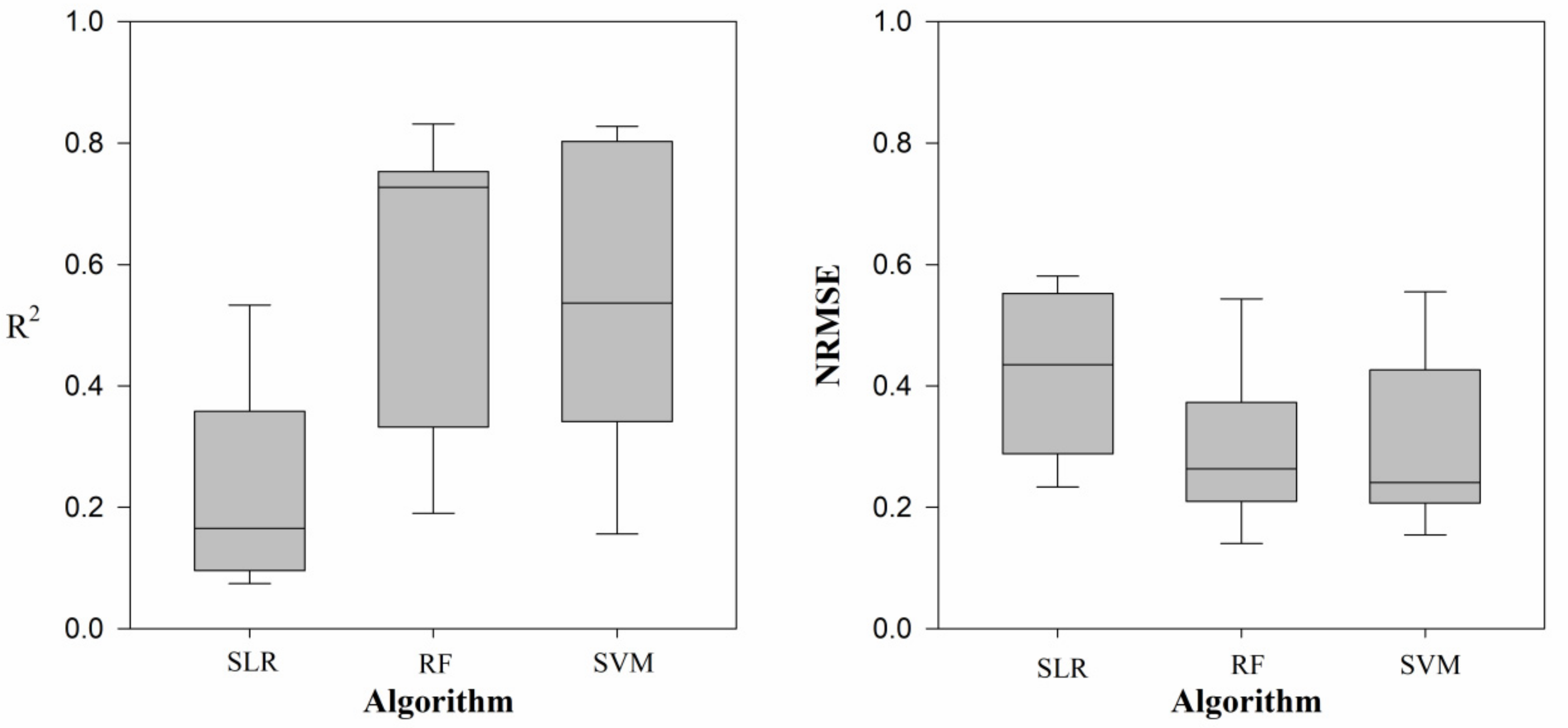
| Model | Fitting | Testing | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE (Mg/ha) | NRMSE | ME (Mg/ha) | MRE (%) | MARE (%) | |
| SLR | 0.3165 | 47.1631 | 0.4035 | −3.0224 | 3.2818 | 39.8129 |
| RF | 0.7698 | 27.1188 | 0.2320 | −1.8477 | −1.8103 | 30.5218 |
| SVM | 0.7840 | 26.1543 | 0.2238 | −4.5969 | −3.9566 | 35.5108 |
| Species | Dataset | Fitting | Testing | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | ME (Mg/ha) | MRE (%) | MARE (%) | ||
| Pinus yunnanensis | Habitat | 0.2028 | 50.8261 | 0.4416 | 4.65 | 4.0639 | 38.2588 |
| RS | 0.7074 | 30.7922 | 0.2675 | −0.3226 | −0.2819 | 34.8031 | |
| Combined | 0.7268 | 29.7535 | 0.2585 | 0.0963 | 0.0842 | 35.682 | |
| Pinus densata | Habitat | 0.1903 | 63.5056 | 0.5322 | −13.776 | −12.797 | 45.9524 |
| RS | 0.7511 | 35.2124 | 0.2951 | −9.4358 | −8.7654 | 30.5785 | |
| Combined | 0.7343 | 36.3738 | 0.3048 | −5.7433 | −5.3352 | 28.1384 | |
| Pinus kesiya | Habitat | 0.7553 | 19.7669 | 0.1701 | 4.6127 | 3.9489 | 25.6779 |
| RS | 0.4617 | 29.3169 | 0.2522 | 3.9373 | 3.3708 | 23.7645 | |
| Combined | 0.8316 | 16.3906 | 0.1410 | 3.7964 | 3.2502 | 25.3048 | |
| Species | Dataset | <50 (Mg/ha) | 50–100 (Mg/ha) | 100–150 (Mg/ha) | 150–200 (Mg/ha) | >200 (Mg/ha) | Overall | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | ||
| Pinus yunnanensis | habitat | 51.08 | --- | 34.29 | 19.46 | −13.41 | 31.10 | −49.54 | 12.97 | −128.17 | 0.67 | −4.65 | 50.52 |
| RS | 43.89 | --- | 41.74 | 30.38 | −10.79 | 25.18 | −39.83 | 29.24 | −128.59 | 27.03 | 0.32 | 53.68 | |
| combined | 40.67 | --- | 40.00 | 28.85 | −10.07 | 30.36 | −41.96 | 19.46 | −122.51 | 2.59 | −0.11 | 51.86 | |
| Pinus densata | habitat | 70.84 | 38.02 | 46.59 | 33.09 | −33.36 | 15.85 | 1.08 | 27.10 | −158.37 | 36.04 | 13.78 | 73.88 |
| RS | 50.37 | 32.01 | 26.42 | 28.24 | −13.86 | 19.58 | −17.81 | 36.80 | −86.73 | 37.73 | 9.44 | 48.52 | |
| combined | 34.57 | 13.82 | 26.42 | 34.54 | −21.11 | 13.18 | −7.61 | 31.36 | −92.04 | 25.92 | 5.74 | 47.23 | |
| Pinus kesiya | habitat | --- | --- | 11.71 | 11.99 | −2.33 | 32.63 | −61.54 | 6.84 | --- | --- | −4.61 | 33.19 |
| RS | --- | --- | 26.34 | 15.86 | −14.74 | 16.23 | −56.95 | 20.45 | --- | --- | −3.94 | 32.79 | |
| combined | --- | --- | 12.65 | 12.25 | −3.68 | 34.32 | −53.54 | 9.46 | --- | --- | −3.80 | 32.56 | |
| Species | Variables | R2 |
|---|---|---|
| Pinus yunnanensis | B6_homo, B4_entro, B7_homo, SIPI, B4_semo, B7_diss | 0.7268 |
| Pinus densata | ARVI, SRI, EVI, bio4, bio7, bio12 | 0.7343 |
| Pinus kesiya | B4_mean, bio4, bio14, bio17, bio19, HSV | 0.8316 |
| Species | Model | Important Variables |
|---|---|---|
| P. yunnanensis | SLR | B7_homo |
| RF | B6_homo, B4_entro, B7_homo | |
| P. densata | SLR | SRI |
| RF | ARVI, SRI, EVI | |
| P. kesiya | SLR | B4_mean |
| RF | B4_mean, B2_corr, B2_con |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Liu, Y.; Li, L.; Liu, Y.; Wu, Y.; Xu, H.; Ou, G. Enhancing Aboveground Biomass Estimation for Three Pinus Forests in Yunnan, SW China, Using Landsat 8. Remote Sens. 2022, 14, 4589. https://doi.org/10.3390/rs14184589
Tang J, Liu Y, Li L, Liu Y, Wu Y, Xu H, Ou G. Enhancing Aboveground Biomass Estimation for Three Pinus Forests in Yunnan, SW China, Using Landsat 8. Remote Sensing. 2022; 14(18):4589. https://doi.org/10.3390/rs14184589
Chicago/Turabian StyleTang, Jing, Ying Liu, Lu Li, Yanfeng Liu, Yong Wu, Hui Xu, and Guanglong Ou. 2022. "Enhancing Aboveground Biomass Estimation for Three Pinus Forests in Yunnan, SW China, Using Landsat 8" Remote Sensing 14, no. 18: 4589. https://doi.org/10.3390/rs14184589
APA StyleTang, J., Liu, Y., Li, L., Liu, Y., Wu, Y., Xu, H., & Ou, G. (2022). Enhancing Aboveground Biomass Estimation for Three Pinus Forests in Yunnan, SW China, Using Landsat 8. Remote Sensing, 14(18), 4589. https://doi.org/10.3390/rs14184589








