Abstract
The bottom depth of coastal benthic habitats plays a vital role in the coastal ecological environment and navigation. In optically shallow waters (OSWs), seafloor reflectance has an impact on the remotely sensed data, and thus, water depth can be retrieved from the remote sensing reflectance () values provided by satellite imagery. Empirical methods for depth estimation are mainly limited by field measurements coverage. In addition, owing to the diverse range of water bio-optical properties in coastal regions, the high-precision models that could be applied to all OSWs are insufficient. In this study, we developed a novel bottom-depth retrieval method based on Hydrolight simulated datasets, in which were generated from radiative transfer theory instead of actual satellite data. Additionally, this method takes into consideration the variable conditions of water depth, chlorophyll concentrations, and bottom reflectance. The bottom depth can be derived from using a data-driven machine learning method based on the random forest (RF) model. The determination coefficient (R2) was greater than 0.98, and the root mean squared error () was less than 0.4 m for the training and validation datasets. This model shows promise for use in different coastal regions while also broadening the applications that utilize satellite data. Specifically, we derived the bottom depth in three areas in the South China Sea, i.e., the coastal regions of Wenchang city, Xincun Bay, and Huaguang Reef, based on Sentinel-2 imagery. The derived depths were validated by the bathymetric data acquired by spaceborne photon-counting lidar ICESat-2, which was able to penetrate clean shallow waters for sufficient bottom detection. The predicted bottom depth showed good agreement with the true depth, and large-scale mapping compensated for the limitations resulting from along-track ICESat-2 data. Under a variety of circumstances, this general-purpose depth retrieval model can be effectively applied to high spatial resolution imagery (such as that from Sentinel-2) for bottom depth mapping in optically shallow waters.
1. Introduction
Coastal benthic habitats (such as seagrass and coral reefs) play a significant role in the flow of nutrients and energy, the global environment, and the carbon balance [1]. In the context of global climate change, these vulnerable ecosystems are under pressure and are susceptible to degradation. They are increasingly threatened by human activities, including the impact of terrestrial nutrients and sediment loading [2,3]. Bottom depth measurements of these dynamic ecosystems are required for the mapping and monitoring of their health status and are critical for nautical navigation and transportation [4,5]. Although the bathymetric data for these regions are important, traditional field measurements, such as shipborne sounding or airborne lidar, are frequently insufficient for determining accurate depths [6]. In addition, field-based bathymetric survey operations are time-consuming, labor-intensive, and potentially hazardous in some areas, making them unsuitable and impractical for large-scale bathymetric analysis.
Remote sensing is becoming an increasingly important method for estimating coastal shallow water depths due to its extensive spatial coverage, high spatial resolution, and high temporal resolution. For optically shallow waters (OSWs), the bottom signals can be reflected in the water-leaving radiance and remote sensing reflectance () signatures. For clean waters, waters may be optically shallow to depths <20 m, but in turbid coastal waters, OSW depth might mean 1–3 m [7]. Due to the optical signatures reflected by the bottom substratum and water column properties that can be captured by satellite imagery, many satellite-derived bathymetry (SDB) approaches have been widely adopted, which are cost-effective for rapidly mapping depth in a large region. The accuracy of SDB has advanced to the stage where it is now utilized in the current generation of nautical charts [7]. The two main types of depth retrieval methods are the empirical and semianalytical methods. Empirical methods, such as single- and multiband linear models [8] and log-transformed band ratio models [9], are widely used for multiple spatial and spectral resolution imagery due to their simplicity [10,11]. However, these methods are mostly limited by geolocation and water types since they rely on in situ measurements to calibrate the model parameters. The semianalytical techniques, which are based on the radiative transfer process, have been proven to be more accurate than the empirical approach [12]. Lee et al., proposed a nonlinear spectral optimization approach to obtain the shallow water depth and water column properties using hyperspectral data [13,14,15]. Mobley et al., proposed a different method that relied on spectrum matching and look-up-table (LUT) [16]. Prior depth measurements are not required for these physics-based methodologies, but they are highly dependent on the spectral information, knowledge of water optical properties, and assumptions regarding benthic spectral shape [17].
In recent years, as bottom depth has been shown to strongly correlate with multiple optical signatures, data-driven machine learning (ML) methods have offered new insights for bathymetry estimation due to their ability to solve nonlinear problems. Different models have been utilized, such as the backpropagation neural network (BPNN) [18], multilayer perceptron (MLP) [19], and random forest [20]. Among these ML models, random forest [21] has been confirmed as a more flexible model for depth retrieval compared to earlier empirical or semianalytical models [22,23]. However, most ML models for depth retrieval are still based on actual field data. In addition, if the training datasets are regional or do not consider as many substratum types as possible, these methods are limited and not portable for other shallow regions. Coastal areas are highly variable, which makes it difficult to establish a general bottom depth retrieval model. Thus, efforts have been made to obtain sufficient depth measurements to feed the ML model.
With the advancement of spaceborne lidar, the recently launched Ice, Cloud, and land Elevation Satellite-2 (ICESat-2) provides accurate along-track bottom depths for optically shallow waters when the light penetration is satisfactory. The depth measurements from ICESat-2 address the lack of reference “seed depths” and have the potential for global science applications [24]. However, the high-accuracy water depths obtained from ICESat-2 remain insufficient for large-scale mapping due to their low temporal resolution and the fact that observations are only made along-track. Some studies applied the depths from ICESat-2 and spectral data from satellite images to obtain the SDB through empirical regression [25,26]. Nevertheless, this approach may introduce some spatial uncertainties due to the linear format.
Consequently, the purpose of this study is to utilize a multitude of simulated datasets, including bathymetry data of optically shallow waters and the corresponding remote sensing reflectance, to develop a bottom depth retrieval model that may subsequently be easily adapted for OSW bottom depth mapping using high-spatial resolution satellite imagery. Specifically, the simulated datasets are generated by considering various and sufficient benthic type conditions and water column properties by Hydrolight simulations [27,28], which is a radiative transfer numerical model for calculating the underwater light field in OSWs. Then, we used the random forest model for the bottom depth retrieval with the spectral indices of remote sensing reflectance as the predictor variables. The accurate ICESat-2-derived bottom depth [29,30] served as the validation for the satellite-derived bottom depths. Without relying on any in situ measurements and prior knowledge, the established bottom depth retrieval model can be extensively applied to coastal optical shallow waters for a broad range of bottom depth mapping.
2. Materials and Methods
2.1. ICESat-2 Data
On 15 September 2018, the spaceborne laser altimeter ICESat-2 was launched carrying the Advanced Topographic Laser Altimeter System (ATLAS) [31]. The photon-counting ATLAS transmits a green (532 nm) laser pulse every 0.7 m along its track (10,000 laser pulses per second) and has a ~13 m diameter footprint size. It has three pairs of laser beams separated by 3.3 km across the track. Each beam is divided into strong and weak subbeams, with an energy ratio of approximately 4:1 [32].
Level-2 Global Geolocated Photon Data (ATL03) (https://nsidc.org/data/atl03, accessed on 18 May 2022), which provide time, latitude, longitude, and WGS-84-based ellipsoidal heights for each photon event with a temporal resolution of 91 days, were used in this study for bathymetry extraction in optically shallow waters. Geophysical phenomena (e.g., effects of the atmosphere and solid earth deformation) were corrected, and the WGS-84 ellipsoidal heights were converted to orthometric heights utilizing the open-source software Photon Research and Engineering Analysis Library (PhoREAL) (https://github.com/icesat-2UT/PhoREAL, accessed on 5 June 2022). In addition, the photons were classified as either signal or background, with confidence levels ranging from 0 to 4 [32]. For the extraction of the corrected bottom depth from ATL03 products, the following processes were introduced:
2.1.1. Identification of Water Surface and Bottom Signals
The higher the confidence level, the more likely the photon is a valid signal [33]. However, confidence assessments are not stable for the removal of noise due to the different distribution of signal and noise in the water column, which is influenced by strong absorption, attenuation, and scattering [25]. Some noises (confidence equal to 0) could be useful signals, while some signals (confidence of 4) could be noise. Thus, we employed the density-based spatial clustering of applications with noise method (DBSCAN) [34] to detect sea surface signals and seafloor signals as well as noise removal which has been widely used for surface and bottom photon classification [19,25,35]. The radius of a neighborhood (Eps) and the minimum number of points (MinPts) are the two critical parameters, with the adaptive value indicating the optimal cluster result.
2.1.2. Bathymetric Correction
We eliminated the background signal, set the surface height to 0 m, and then applied the bathymetric correction method based on the seafloor and sea surface photons categorized by DBSCAN clustering. The correction proposed by Ma et al. [25] was applied; this approach considers the refraction effect in the air-water interface, the fluctuation effect on the water surface, and the refraction error on the sloping water surface. This bathymetric correction method is more appropriate for rough sea surfaces and has been shown to perform well with less than or close to 10% of the maximum depth [25].
2.2. Sentinel-2 Satellite Imagery
The ESA launched Sentinel-2A and Sentinel-2B on 23 June 2015, and 7 March 2017, respectively. The Multispectral Instrument (MSI) onboard the twin satellites has 13 spectral bands, a 290 km swath width, high spatial resolution (10 m), and frequent revisit capability (5-day revisit period), providing a new perspective of the coastal and ocean ecological environment [36]. The band information is listed in Table 1. The spatial resolution of Sentinel-2 can capture the detailed and small-scaled features caused by bottom depth variations, tidal differences, and steep slopes, which is beneficial for bottom depth estimation.

Table 1.
Band Information of the Sentinel-2 Multispectral Instrument.
In this study, Level-1C products were obtained from the Copernicus Open Access Hub (https://scihub.copernicus.eu/dhus/#/home, accessed on 18 May 2022). The ACOLITE processor, which was developed and is widely used for inland and coastal waters, was utilized for atmospheric correction (AC) [10,37,38].
Considering the variable tidal height due to the different observation times between high spatial resolution imagery and spaceborne lidar, tidal correction is crucial for accurate bathymetry retrieval, especially in shallow water. In accordance with the tidal height data from the nearby tide gauge stations provided by the National Marine Data Center (http://mds.nmdis.org.cn/pages/tidalCurrent.html, accessed on 26 May 2022), we can obtain the tidal heights of ICESat-2 and Sentinel-2 during the observation times. The tidal height difference between these two satellites was then estimated. Consequently, we converted the ICESat-2 observed depth to the instantaneous water depth corresponding to the observation time of Sentinel-2 by combining the ICESat-2 estimated water depth and the tidal height difference between these two satellites.
2.3. Extraction of Optically Shallow Waters
The classical band ratio model [9] has been widely used in satellite-based depth retrieval. It uses the log-transformed ratio relationship of the reflectance of two bands. By setting the optimal threshold, this format can be adapted to extract optically shallow waters, since water depth is sensitive to the log-ratio values of remote sensing reflectance [39]. The ratio of the two near-infrared (NIR) bands, 750 nm and 900 nm, has proven to be a reliable and robust index for detecting OSWs. Additionally, it is insensitive to water constituent concentrations [40]. Due to its strong absorption, pure seawater has a relatively low reflectance in the NIR bands, while various types of substrates have comparatively higher reflectance. As a result, it makes sense to extract OSWs using the two NIR bands that correspond to the Sentinel-2 bands, specifically 705 nm and 783 nm, with the log-ratio format (Equation (1)), and the value of increasing with decreasing shallow water depth.
2.4. Radiative Transfer Simulations by the Hydrolight
Hydrolight (HE5) is a numerical radiative transfer model for natural light in water [41] that calculates the radiance distributions within and leaving water bodies [27,28]. In this study, we used HE5 to generate sufficient datasets of under various water conditions, including the inherent optical properties (IOPs), bottom types, and water depth.
3. Development of the Bottom Depth Retrieval Model
3.1. Generation of Simulated Datasets
Hydrolight radiative transfer simulation is a valuable method for deriving shallow water bathymetry, benthic types, and water optical properties [12,14,15,16]. The “New Case-1” model with finite depth embedded in HE5, in which all IOPs are determined by the chlorophyll concentration (), can be assumed to be applicable for clean optical shallow waters for the generation of simulated datasets [27]. The bottom signal, water depth (), and water column IOPs for typical Case-1 OSWs all affect the remote sensing reflectance (), which can be simplified as follows:
We can therefore establish a depth retrieval model with broad applicability without any in situ knowledge if we have a sufficient dataset of known and depths under various situations of water optical properties and bottom types. This is achieved by considering that can be easily obtained from satellite imagery.
According to HE5, which is depicted in Figure 1, different bottom reflectances of various benthic types are provided, and the bottom is considered to be an opaque, Lambertian reflecting surface. We utilized the wavelength range from 400 nm to 800 nm, since the spectra from HE5 may be unrealistic in the 300–350 and 800–1000 nm ranges, which were extrapolated by splines. Due to the complicated benthic types covered by each pixel, we obtained more bottom reflectance by the linear combination of two benthic types as follows:
where and are the proportions of benthic types and , respectively, and and represent the reflectance of these two benthic types. The proportion was given in 20% steps, including 20%, 40%, 60%, and 80%; for example, 20% clean seagrass and 80% coral, 40% clean seagrass and 60% coral. Clean seagrass, seagrass, and coral were chosen as the major substrates, and additional substrates were included. The combination of clean seagrass and other sediments from HE5 is demonstrated in Figure 2 as an example. As a result, there were 145 types of input bottom reflectance comprising 13 different types of sediment and 132 mixed endmembers.
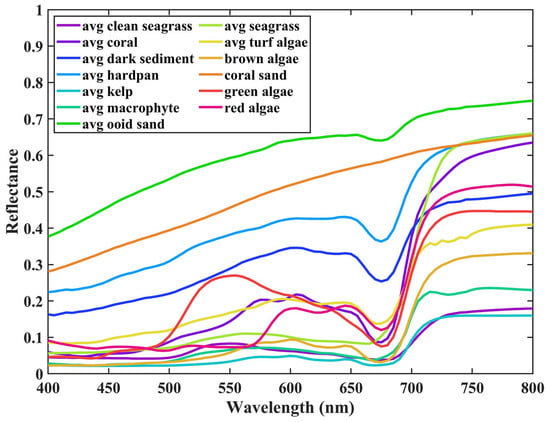
Figure 1.
Bottom reflectance of various sediments provided by HE5, covering from 400 nm to 800 nm.
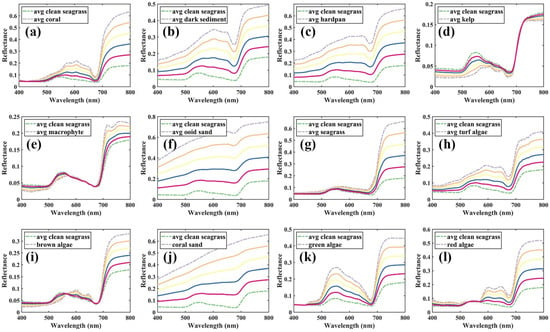
Figure 2.
An example of the mixture of two bottom types with 20%, 40%, 60%, and 80% fractions. One of the bottom types is the clean seagrass (green dashed line), and the other one is the rest of the sediment from HE5 (purple dashed line), (a) coral, (b) dark sediment, (c) hardpan, (d) kelp, (e) macrophyte, (f) ooid sand, (g) seagrass, (h) turf algae, (i) brown algae, (j) coral sand, (k) green algae, (l) red algae. The solid lines from top to bottom represent the mixed endmembers with the proportion of clean seagrass from 20% to 80% with 20% steps.
In addition, the water depth was set to vary from 0.01 m to 10 m with a linear random distribution, the chlorophyll concentration was set to range from 0.01 mg/m3 to 5 mg/m3 with a logarithmic random distribution, and the 145 bottom types were randomly distributed with a total of 40,000 groups, as shown in Figure 3. The solar zenith angles were set to be evenly distributed at 15°, 30°, 45°, and 60°. The simulated wavelength was determined by the central wavelength of the visible and near-infrared bands of Sentinel-2, together with the wavelength range of the HE5 bottom spectra. The bioluminescence and inelastic scatter were ignored, and other detailed HE5 setups are given in Table 2.
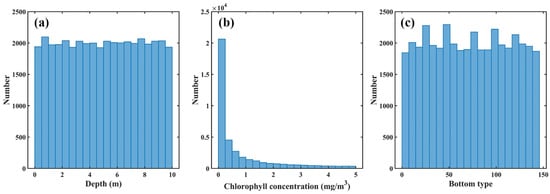
Figure 3.
The distribution histogram of (a) depth; (b) chlorophyll concentration; (c) bottom type.

Table 2.
Detailed Setups for the Hydrolight Simulation.
3.2. Model Training and Evaluation
The goal of this study was to establish a depth retrieval model based on simulated remote sensing reflectance and corresponding depth. Based on the HE5 setups, we generated 40,000 remote sensing reflectance values for optical shallow water. Figure 4 displays the distribution histogram of for each band. The shallower the water depth, the more significant the contribution of bottom reflectance to becomes, while the deeper the water depth, the more significant the contribution of the water column. Compared to the visible bands, the value of from the red band to the NIR band was relatively low due to the strong absorption of water. Since multiple-predictor models exhibited greater robustness for bathymetry [42], appropriate predictors were determined first by a correlation analysis of different spectral indices rather than depending on a single predictor. As a result of the set wavelength range of bottom reflectance and simulated wavelength, we mainly applied the six wavelengths from the visible band to the red edge band (b1–b6). As shown in Figure 5, the correlation coefficient (R) between spectral indices and depth was computed, including single-band reflectance, band ratio, and band difference. The band difference (BD) is determined in the following manner, where and are the reflectances of two different bands:
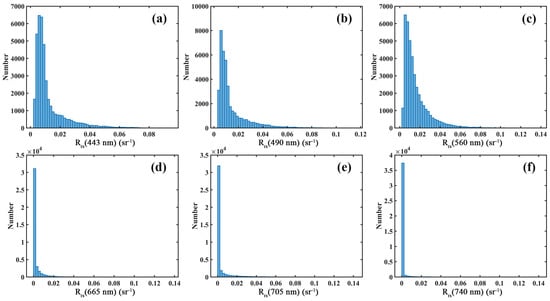
Figure 4.
The distribution histogram of the generated () for each wavelength from 443 nm to 740 nm, (a) 443 nm; (b) 490 nm; (c) 560 nm; (d) 665 nm; (e) 705 nm; (f) 740 nm.
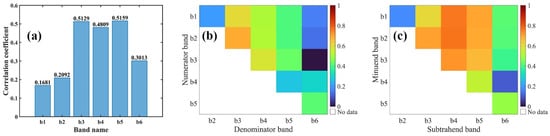
Figure 5.
The correlation coefficient between water depth and (a) single band value from b1 to b6; (b) band ratio, where the vertical coordinate is the numerator band and the horizontal coordinate is the denominator band; (c) band difference, where the vertical coordinate is the minuend band and the horizontal coordinate is the subtrahend band.
The strongest correlation coefficient of all ratio formats is b2 to b3, which corresponds to the blue band to green band ratio, as stated in and supported by Stumpf et al. [9]. Compared to most single band and band ratio formats, the BD format has a substantially more significant R value. There are thus 36 spectral features altogether. However, using all features for model training might result in overfitting, i.e., certain predictors could be redundant or irrelevant, which could reduce the regression model’s accuracy [43]. Therefore, before model training, feature selection is crucial. We proceeded by choosing indices that have high R values (R > 0.5). The classical max-relevance and min-redundancy (mRMR) approach [44], which selects valuable features based on mutual information, was then employed in this study. As shown in Figure 6a, the 16 significant features with correlation coefficients larger than 0.5 are arranged by the mRMR approach.
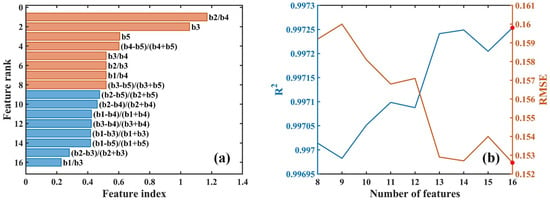
Figure 6.
(a) The rank of 16 features with a high R-value (R > 0.5) by using the mRMR approach; (b) R2 and of the depth retrieval model under the different numbers of features.
Since bathymetry has a complicated relationship with due to the impact of bottom reflectance, water IOPs, and water depth, the conventional statistical model has trouble tackling this complex nonlinear problem. Random forest is an ensemble machine learning model that combines a large set of regression trees [21]. It is capable of determining variable importance and performing powerful regression and classification with high accuracy. In recent years, the random forest has gained popularity in place of linear regression for satellite-derived bathymetry due to its greater performance [22,23]. We utilized the RF regression model to estimate water depth, with water depth as the object variable and spectral features of as independent variables. The simulated dataset was randomly divided into training datasets (80%) and validation datasets (20%) for accuracy evaluation.
The 16 spectral features were sorted by using the mRMR method, and then we determined the optimal feature numbers for the RF regression model by comparing the determination coefficient (R2) and root mean squared error () between the true depth () and the RF model predicted depth (). The calculation equation of is defined as follows:
Since the first eight variables are of greater significance (Figure 6a), we examined the number of variables from feature 8 to 16 by the statistical metrics R2 and . As illustrated in Figure 6b, it is evident that an increasing number of input variables did not linearly increase the accuracy of the model. However, it seems that using 16 variables, which have the highest R2 and lowest , will yield the best performance for estimating the water depth.
Based on the determined input variables, we conducted the RF model training with the optimal number of grown trees. The variable importance ranking is shown in Figure 7a. The greater the importance of a feature, the greater its contributions to the model. Consequently, this provided the most critical spectral index of , followed by and . In addition, the feature has the least impact on the accuracy of the model. As shown in Figure 7b,c, the depth retrieval model exhibited great performance, with R2 values between the true depth and predicted depth above 0.98 for both the training and validation datasets. The value for the training dataset was 0.1524 m, and the for the validation dataset was 0.3471 m. The values of R2 and for the validation dataset were slightly lower and larger than those of the training dataset, respectively, but still reasonable. The error increases as the water depths increase, and the predicted water depth is somewhat underestimated compared to the true depth, especially under deep water depth conditions.
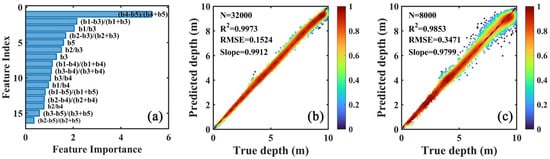
Figure 7.
(a) Importance ranking of selected spectra indices; (b) Density scatter plots between true depth and model predicted depth for training; (c) Density scatter plots between true depth and model predicted depth for independent validation. The dotted line is the 1:1 line, and the color of the dots represents the density.
Figure 8 illustrates the flowchart depicting the process of deriving bottom depth from satellite observations. Specifically, the model was established using the random forest model and trained by the simulated dataset. Based on the established model, we can apply it to the high spatial resolution imagery after atmospheric correction to obtain bottom depth maps. Additionally, the along-track ICESat-2 data provide a potent tool for validation in optically shallow waters, where field investigation data are relatively sparse. In brief, this model uses simulated datasets to provide valuable directions for the general-purpose bathymetry retrieval model, which can be employed across a broad range of conditions.
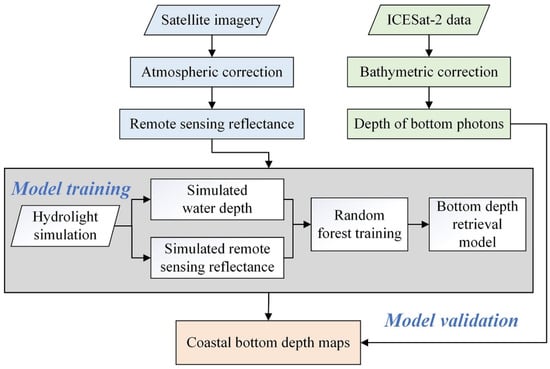
Figure 8.
Flowchart of the satellite-based bottom depth retrieval process based on the established model built upon the simulation datasets. The ICESat-2 data can be further applied for model validation.
4. Results
4.1. Validation Sites
To evaluate the accuracy and portability of the OSW bottom depth retrieval model to actual satellite data, which are not included in our training data, we selected three regions with various benthic habitats in the South China Sea (Figure 9a). The selection of sites considers a variety of bottom types (e.g., sand, coral, and seagrass), the water quality is clean and can be assumed to be Case-1 water, and the acquisition times of ICESat-2 data and cloud-free Sentinel-2 imagery are similar.
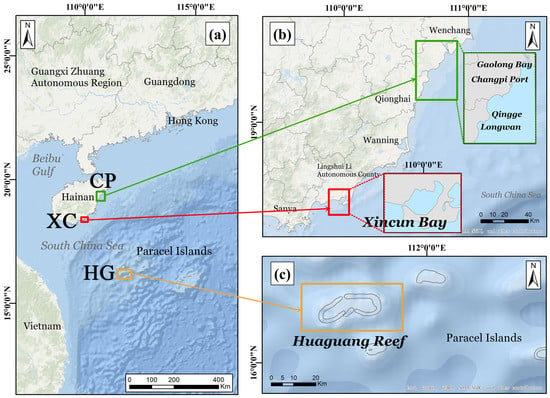
Figure 9.
The locations of three regions, with the green box for Changpi Port (CP), red box for Xincun Bay (XC), and yellow box for Huaguang Reef (HG). The base map is obtained from the World Ocean Base from Esri. (a) is the location for the three regions, (b) is the enlarged location for CP and XC, and (c) is the enlarged location for HG.
The first study site (green box in Figure 9b) is located in eastern Hainan Province, where there is a large amount of seagrass along the coast, primarily distributed along Gaolong Bay and Changpi Port in Wenchang city, and Qingge and Longwan in Qionghai city. Here, we abbreviate this region as CP (19°12′N–19°33′N, 110°35′E–110°51′E). Additionally, seagrass can also be found in Xincun Bay (XC) in Lingshui Li Autonomous County (18°23′N–18°27′N, 109°57′E–110°02′E), which is in southeastern Hainan Province (red box in Figure 9b). This bay is a nearly completely enclosed lagoon with only one channel flowing to the ocean, and no large rivers provide terrestrial input. In Xincun Bay, seagrass is mainly distributed on the south and east coasts, with the south coast having a relatively higher density than the east coast [45]. We selected this region as the second study site. The third study site is the Huaguang Reef (HG) (16°09′N–16°17′N, 111°34′E–111°49′E) (Figure 9c). One of the large atolls in the Paracel Islands, Huaguang Reef is relatively well developed and has reef gates on its northern and southern sides. Although direct observations of water depth have accumulated through single and multibeam echo-sounders, Electronic Navigation Charts (ENC), lidar sensors, seismic methods, and other methods, there are still few field measurements from coastal regions, particularly in optically shallow waters where it is challenging to perform field surveys. Thus, satellite measurements are urgently required to compensate for the absence of bathymetry in nearshore OSWs.
4.2. Bottom Depth Derived from Sentinel-2 Imagery
We employed 10-m spatial resolution Sentinel-2 satellite imagery, which is favorable for OSW bottom depth estimation. The acquisition times of the three regions are given in Table 3. Due to the Sentinel-2 imagery acquired in summer being more susceptible to the sun glint and to mixing with the reflectance of the strong reflectivity substratum, we chose the imagery collected in winter or spring, which were less affected by clouds and shadows. The L1C products were first atmospherically corrected by the ACOLITE processor to obtain the remote sensing reflectance . Based on the established depth retrieval model, we calculated all feature indices of each pixel of the satellite imagery and then input them into the model. Accordingly, the predicted depth was then generated. It should be noted that for large water depths, the bottom signal is unable to return to the water surface and is therefore not captured by satellite sensors. Thus, there is no detectable substratum signal in optically deep waters. Therefore, the estimated depth of optically deep waters is inaccurate and unreliable and is beyond the detectable range of the bottom depth retrieval model. Consequently, we masked the predicted depth of optically deep waters (ODWs) by setting the optimal thresholds of the index. The pixel values of that are larger than the set threshold can be assumed to be the optical shallow waters, and conversely, pixel values smaller than the threshold were masked. We exhibited the extraction result of the optically shallow waters in Xincun Bay for an illustration, as shown in Figure 10. Specifically, we firstly obtained the atmospherically corrected Sentinel-2 imagery (Figure 10a). Then, we calculated the values of for the whole imagery (Figure 10b) with the brighter the gray color, the higher the values. The map of showed contrast difference between shallow and deep areas, and the histogram of the values also existed a valley, the optimal threshold for the extraction of OSWs. Finally, the regions with values larger than the optimal threshold are classified as the OSWs. Similarly, we could obtain the OSWs for CP and HG.

Table 3.
The Acquisition Time of Sentinel-2 and ICESat-2 and the Accuracy Assessment for Three Regions.

Figure 10.
The process of extraction of optically shallow waters in Xincun Bay. (a) The atmospherically corrected Sentinel-2 imagery. (b) The for the whole imagery and the corresponding data value histogram for choosing the optimal threshold. (c) The extraction result of OSWs for Xincun Bay with red regions highlighted.
Figure 11 illustrates the retrieved depth of optically shallow waters based on the bottom depth retrieval model for the three regions where the optically deep waters were masked. It should be noted that the retrieved depth is instantaneous and is affected by the tide level. In the direction from each coastal area to the open ocean, all bottom depths exhibited similar geographic patterns from shallow to deep. The bottom depth along Changpi Port to Longwan was within 2.5 m, and the benthic types of these regions are mainly seagrass, sand, and sporadic coral reef. The shallow areas of Changpi Port were mostly found at a distance of ~3 km from land, whereas the shallow regions of Qingge and Longwan were mostly found within ~2 km. This result also indicated that the shallow benthic distribution area of Changpi Port might be larger than that of the other two areas. In addition, the retrieved bottom depth in Xincun Bay was <2 m in OSWs. This result agrees with the result of Wang et al. [46], who found that the seagrass region in Xincun Bay had water depths of less than 2 m and that different species had varying depth distributions. Additionally, as shown in Figure 11c, the bottom depth of Huaguang Reef is less than 5 m. The benthic types in HG are mainly sand, coral, rock, and rubble. The geomorphic class of OSWs in HG was mainly composed of shallow lagoons, reef flats, and reef crests that were generally shallow and located in less than 5 m of water [47], which is consistent with our model result. Overall, the satellite-based bottom depth provides practical proof of the trend and pattern of water depth change. The model can act as a foundation for the future identification and classification of benthic habitats due to the general pattern of geomorphological features it reflects, such as discontinuous or spotty patches.
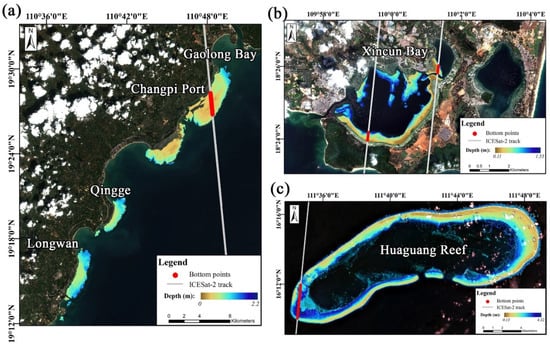
Figure 11.
The retrieved depth from the developed model for OSWs of (a) Changpi Port and the surrounding shallow waters; (b) Xincun Bay; (c) Huaguang reef. The gray lines represent the ICESat-2 track, which just passes through the corresponding region, and the bottom points are highlighted with red dots.
4.3. Bottom Depth Validation Based on ICESat-2 Along-Track Data
The ICESat-2 lidar provides a new perspective for bathymetry in relatively clean and shallow water. Therefore, to evaluate the Sentinel-2 retrieved bottom depth, we used the ICESat-2 ATL03 product to extract the along-track bottom depth and assumed that the bathymetrically corrected depth values of ICESat-2 photons could be regarded as the true depths. In addition, we assumed that changes in bottom depth over a short temporal period were minimal. Thus, the matchup of lidar data and satellite imagery within ±2 weeks is reasonable [48].
For the three study sites, we matched the suitable tracks that passed through the corresponding OSWs (gray lines in Figure 11) within ±1 week between ICESat-2 data and Sentinel-2 imagery. The corresponding acquisition dates for bottom depth validation of two spaceborne satellites are shown in Table 3. The distribution of obvious bottom signals in the red parts of these tracks (red dots in Figure 11) is illustrated in subgraph (a) in Figure 12A–D. The WGS-84 ellipsoidal heights were converted to orthometric heights (mean sea level height). The bottom signals were evident and beneficial for the subsequent identification of sea surface signals, bottom signals, and background signals. The classification of these three main classes, as shown in subgraph (b) in Figure 12A–D, was conducted based on the DBSCAN method instead of the official confidence measurements. The blue dots are the sea surface signals, the green dots are the bottom signals, and the black dots are the background signals. Then, to obtain the absolute value of water depth, we removed the background signals and set the sea surface photons to 0 m (subgraph (c) in Figure 12A–D). In addition, we corrected bottom depth errors arising from the refraction effect in the air-water interface, the fluctuation effect on the water surface, and the refraction error on the sloping water surface, as shown in subgraph (d) in Figure 12A–D, and then obtained the bathymetric corrected bottom depth along the ground track (red dots). The bathymetric correction process for CP is depicted in Figure 12A, for XC in Figure 12B,C with two tracks passing through the seagrass regions on the same day, and for HG in Figure 12D.
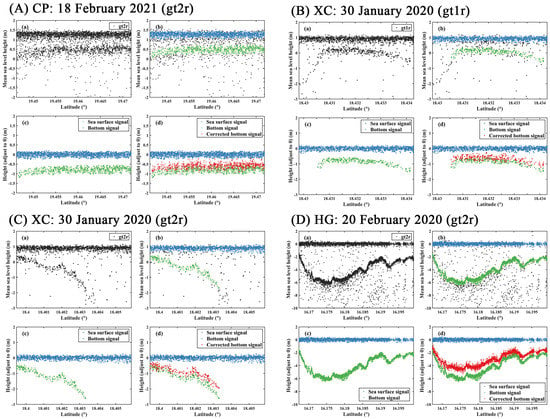
Figure 12.
The bathymetric correction process for the three regions: (A) CP; (B,C) XC; (D) HG. For each graph, (a) is the photon orthometric height from ATL03 products, and the corresponding track is shown in the legend; (b) is the clustering result for all photons based on the DBSCAN method; (c) is the distribution of sea surface signals (blue dots) and the bottom signals (green dots) after DBSCAN clustering, noise removal, and sea surface adjustment to 0 m; and (d) is the corrected depth of bottom signals (red dots).
Since the separation between the adjacent laser pulses for ICESat-2 is approximately 0.7 m in the along-track direction [31], while Sentinel-2 has a spatial resolution of 10 m, there could be multiple bottom photons within one pixel of Sentinel-2 imagery. As a result, the ICESat-2 bottom depths inside each pixel had to be averaged to match the Sentinel-2-derived bottom depths for the corresponding pixel. However, due to the nonlinear impact, the bottom depth calculated from low-resolution data is not just an average of bottom depths calculated from the corresponding high-resolution data [49]. The computation was simplified based on the assumption that the bottom albedo is homogeneous, as follows:
where n is the number of ICESat-2 points contained within a single Sentinel-2 pixel, is the bottom depth of ICESat-2 photons, and is the weighted average bottom depth [19]. Furthermore, the ICESat-2 measured depth should be converted to the instantaneous depth of the corresponding Sentinel-2 imagery observation time by taking into account the different tidal heights [35]. The bottom depth measured from ICESat-2 has already been converted to the absolute depth. Therefore, we obtained the tidal difference relative to the tidal level datum during the observation time of Sentinel-2 at the nearby tide gauge station, and then the instantaneous true bottom depth was obtained by adding the tidal difference. Overall, we obtained the instantaneous water depth by combining the tidal difference between lidar and satellite observation times, which can be assumed to be the true bottom depth.
As illustrated in Figure 13, we compared the predicted depth from our bottom depth retrieval model and the ICESat-2 derived depth by the density scatter plots for the three regions. The predicted depth is roughly consistent with the ICESat-2 derived depth, particularly in HG. The bottom depth of HG mainly ranged from 0 to 5 m, and the value of mean absolute percentage error (MAPE) was smaller than 15%. In CP, the bottom depth range was much smaller than that in HG, with all within 1 m. This depth range was often neglected in previous studies. However, the statistical results, with MAPE < 30% and = 0.1743 m, show great potential for shallow bottom depth estimation. In addition, due to fewer data matchups (a total of 91) in XC, the statistics were not as great as those in CP and HG. The bottom depth range was from 0 to 2 m, which is consistent with the main distribution range of seagrass in Xincun Bay. The value of MAPE is 38.06%, and is 0.3172 m. Furthermore, because the bottom depth from ICESat-2 was averaged, and the spatial variations of depth and bottom types may be substantial within a single pixel, there may have been errors and inaccuracies in the model results. The uncertainties of atmospheric correction in coastal regions also lead to the error of the model input, , and the uncertainties of tidal correction have a significant impact on these relatively shallow waters. Additionally, for the extremely shallow areas (water depth of less than 2 m) in the three regions, the underestimation and overestimation trends were not the same. For CP and XC, the model underestimated the water depths compared to the ICESat-2 derived depths, while it overestimated them for HG. The underestimation for larger depths in HG may have been caused by the error from the proposed model, in which the predicted water depth was somewhat underestimated compared to the true depth under deep water depth conditions during model development and validation. However, for shallow waters, this underestimation may have resulted from the atmospheric correction error in extremely shallow waters. It should also be noted that CP, XC, and the deep regions of HG are mostly covered by sand, which has high bottom reflectance and might result in the underestimation of water depth. In contrast, the shallow regions of HG are mostly covered by rock, rubble, and microalgal mats (obtained from https://allencoralatlas.org/, accessed on 5 June 2022). These benthic types have lower reflectance than the sand, which might result in the overestimation of water depth. As a result, the error of the model result may have a relationship with the benthic types to some extent. Nevertheless, the total performance in independent validation datasets of our bottom depth retrieval model has proven to be effective and has potential for the depth estimation of OSWs when data from field surveys is unavailable.
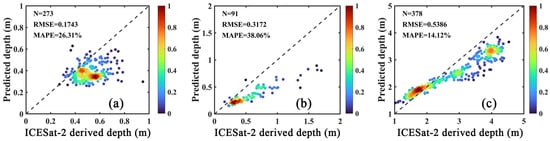
Figure 13.
The density scatter plots between the ICESat-2 derived depth and the predicted depth from our depth retrieval model for three regions: (a) CP; (b) XC; (c) HG. The dotted line is the 1:1 line, and the color of the dots represents the density.
5. Discussion
In this study, we developed a novel bottom depth retrieval model for optically shallow waters utilizing Hydrolight simulated datasets, providing an alternative method that compensates for scarce coastal bathymetric field data. The remote sensing reflectance for OSWs, as measured by satellite sensors, is influenced by the signal from the seafloor. Therefore, with the advantages of large spatial coverage and information from multiple spectra, satellite-based bathymetry is bestowed with several merits. The simulated were generated under different water depths, bottom reflectance, and chlorophyll concentrations by HE5, and then the nonlinear relationship between water depth and was successfully trained based on the nonlinear resolving ability of the random forest machine learning method. To examine the applicability and accuracy of the developed model, we applied the model to Sentinel-2 imageries with high spatial resolution in three typical regions in the South China Sea to retrieve the bottom depth of OSWs. The reference water depths of these regions were obtained by the spaceborne photon counting lidar ICESat-2, which has been extensively applied for the estimation of along-track bottom depth and can be considered the true depth after bathymetry correction and tidal correction. Validation results by the simulated datasets and the comparison between Sentinel-2 retrieved depth and ICESat-2 depth indicated that the established model can provide accurate bottom depths in coastal optically shallow waters and that it exhibits extensive advantages in OSW bottom depth mapping without the requirement of field investigations or prior knowledge. Furthermore, as bottom depth is important for bottom type identification and bottom reflectance retrieval, this approach may be applied to the high spatial resolution detection of coastal benthic features.
Traditional SDB methods usually rely on regional field water depth and then determine the relationship between spectral information and depth [9,10,50]. Such methods can achieve great performance and high accuracy but may not be applicable in other regions. This poses challenges for the robust and consistent coastal bottom depth mapping scheme, since coastal areas are complex and vary widely, both in the inherent optical properties of the water column and benthic types. The remote sensing reflectance produced from the radiative transfer simulations can take various and comprehensive IOPs and bottom types into consideration while reducing the environmental interference on input accuracy. Combining the benefits of the data-driven ML method, using only spectral information, , and no demand for parameters of water column IOPs, the bottom depth retrieval model provides strong applicability and operability potential. The values of were above 0.98 for both the training and validation datasets, the for the training dataset was 0.1524 m, and the for the validation dataset was 0.3471 m. The range of applicability of the proposed technique was mainly limited by the settings of simulated datasets. As the simulation was based on the assumption of clean Case 1 OSWs, the depth ranged from 0.01 m to 10 m, and the chlorophyll concentration ranged from 0.01 to 5 mg/m3, our proposed technique could be applied in satellite imageries for clean shallow waters based on the range of model training data (depth from 0.01 m to 10 m and chlorophyll concentration from 0.01 to 5 mg/m3). In addition, the independent validation of three regions in the South China Sea demonstrated the potential of the model under different water bio-optical conditions, such as different bottom types (e.g., sand, seagrass, and coral reef), different degrees of water clarity (e.g., the degree of transparency in HG is obviously higher than that in CP and XC), and different bottom depth ranges, including extremely shallow water. The values of for these regions are less than 0.6 m, and the values of MAPE are less than 39%.
The accuracy of the input of could significantly impact the performance of our model. Currently, accurate atmospheric correction in coastal regions is still a challenge, although AC over the open sea has been adequately performed [51,52]. Thus, the uncertainties in AC lead to errors in the retrieved bottom depth. In addition, because the pixel size of Sentinel-2 is 10 m and the true depth of each pixel is calculated from the average of several ICESat-2 bottom points within a single pixel, the bottom depth may vary substantially within one pixel. This is particularly the case in regions with different benthic habitats, which introduce inaccuracies into the model result. The uncertainty of tidal data could also create additional errors in optically shallow waters.
6. Conclusions
In this study, a novel bottom depth retrieval method based on Hydrolight simulated datasets was proposed, which considered the variable conditions of water depth, chlorophyll concentrations, and bottom reflectance. The performance of the bottom depth retrieval model is generally good in both simulated datasets and across three different validation sites. The model opens up the possibility of using simulated datasets in bottom-depth retrieval studies. Although the simulated central spectral bands were identical to those of Sentinel-2 in this study, the central wavelength can also be set according to other high-spatial resolution and multispectral or hyperspectral satellites for broader applications. Additionally, we can consider other conditions of benthic reflectance and water IOPs to improve the model accuracy, including terrestrial impacts, such as the colored dissolved organic matter and suspended particulate matter in some coastal regions. In comparison to high-accuracy bathymetry data from soundings or airborne lidar, the proposed cost-effective model emphasizes the applicable in coastal optically shallow waters without any in situ measurements and offers the ability to express spatial patterns influenced by benthic habitats while compensating for the absence of bathymetry data in coastal shallow waters or remote areas.
Author Contributions
Conceptualization, Y.W. and X.H.; data curation, Y.W. and D.W.; investigation, Y.W., X.H. and D.W.; methodology, Y.W., X.H. and Y.B.; project administration, X.H. and Y.B.; software, Q.Z.; supervision, X.H. and Y.B.; validation, F.G.; visualization, Y.W. and T.L.; writing—original draft, Y.W.; writing—review & editing, X.H. and Y.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grants #41825014 and #42176177) and the Key Special Project for Introduced Talents Team of the Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou) (GML2019ZD0602).
Data Availability Statement
The Sentinel-2 data were provided by the European Space Agency (ESA) Copernicus Open Access Hub (https://scihub.copernicus.eu/dhus/#/home, accessed on 18 May 2022). ICESat-2 data were obtained from the NASA Goddard Space Flight Center (GSFC) (https://nsidc.org/data/atl03, accessed on 18 May 2022).
Acknowledgments
We gratefully acknowledge the European Space Agency (ESA) Copernicus Open Access Hub for offering the Sentinel-2 data from https://scihub.copernicus.eu/dhus/#/home and the NASA Goddard Space Flight Center (GSFC) for delivering the ICESat-2 data from https://nsidc.org/data/atl03 used in this study. We are also grateful for the help with data collection and processing provided by the SOED/SIO/MNR satellite ground station, satellite data processing, and sharing facility, and marine satellite data online analysis platform (SatCO2).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eyre, B.D.; Ferguson, A.J.P.; Webb, A.; Maher, D.; Oakes, J.M. Metabolism of Different Benthic Habitats and Their Contribution to the Carbon Budget of a Shallow Oligotrophic Sub-Tropical Coastal System (Southern Moreton Bay, Australia). Biogeochemistry 2011, 102, 87–110. [Google Scholar] [CrossRef]
- Waycott, M.; Duarte, C.M.; Carruthers, T.J.B.; Orth, R.J.; Dennison, W.C.; Olyarnik, S.; Calladine, A.; Fourqurean, J.W.; Heck, K.L.; Hughes, A.R.; et al. Accelerating Loss of Seagrasses across the Globe Threatens Coastal Ecosystems. Proc. Natl. Acad. Sci. USA 2009, 106, 12377–12381. [Google Scholar] [CrossRef] [PubMed]
- Newton, A.; Icely, J.; Cristina, S.; Brito, A.; Cardoso, A.C.; Colijn, F.; Riva, S.D.; Gertz, F.; Hansen, J.W.; Holmer, M.; et al. An Overview of Ecological Status, Vulnerability and Future Perspectives of European Large Shallow, Semi-Enclosed Coastal Systems, Lagoons and Transitional Waters. Estuar. Coast. Shelf Sci. 2014, 140, 95–122. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral Bathymetry Using a Simple Physically Based Algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.J.; Barrilero, O.; Laporte, J.; Koetz, B. Coral Reef Applications of Sentinel-2: Coverage, Characteristics, Bathymetry and Benthic Mapping with Comparison to Landsat 8. Remote Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Li, J.; Knapp, D.E.; Schill, S.R.; Roelfsema, C.; Phinn, S.; Silman, M.; Mascaro, J.; Asner, G.P. Adaptive Bathymetry Estimation for Shallow Coastal Waters Using Planet Dove Satellites. Remote Sens. Environ. 2019, 232, 111302. [Google Scholar] [CrossRef]
- Kutser, T. Remote Sensing of Shallow Waters—A 50 Year Retrospective and Future Directions. Remote Sens. Environ. 2020, 18, 111619. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive Remote Sensing Techniques for Mapping Water Depth and Bottom Features. Appl. Opt. 1978, 17, 379. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of Water Depth with High-Resolution Satellite Imagery over Variable Bottom Types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Retrieval of Nearshore Bathymetry from Sentinel-2A and 2B Satellites in South Florida Coastal Waters. Estuar. Coast. Shelf Sci. 2019, 226, 106277. [Google Scholar] [CrossRef]
- Cahalane, C.; Magee, A.; Monteys, X.; Casal, G.; Hanafin, J.; Harris, P. A Comparison of Landsat 8, RapidEye and Pleiades Products for Improving Empirical Predictions of Satellite-Derived Bathymetry. Remote Sens. Environ. 2019, 233, 111414. [Google Scholar] [CrossRef] [PubMed]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of Shallow Water Bathymetry, Hydro-Optics, and Benthos Mapping Techniques in Australian and Caribbean Coastal Environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral Remote Sensing for Shallow Waters I A Semianalytical Model. Appl. Opt. 1998, 37, 6329. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral Remote Sensing for Shallow Waters: 2 Deriving Bottom Depths and Water Properties by Optimization. Appl. Opt. 1999, 38, 3831. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Chen, R.F.; Peacock, T.G. Properties of the Water Column and Bottom Derived from Airborne Visible Infrared Imaging Spectrometer (AVIRIS) Data. J. Geophys. Res. Oceans 2001, 106, 11639–11651. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bissett, W.P.; Kohler, D.D.R.; Reid, R.P.; et al. Interpretation of Hyperspectral Remote-Sensing Imagery by Spectrum Matching and Look-up Tables. Appl. Opt. 2005, 44, 3576. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Z.; Liu, Z.; Hu, C.; He, M.-X. Mapping Bottom Depth and Albedo in Coastal Waters of the South China Sea Islands and Reefs Using Landsat TM and ETM+ Data. Int. J. Remote Sens. 2014, 35, 4156–4172. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Liu, H.; Su, H.; Li, X.; Zheng, W. Deriving Bathymetry from Optical Images with a Localized Neural Network Algorithm. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5334–5342. [Google Scholar] [CrossRef]
- Lai, W.; Lee, Z.; Wang, J.; Wang, Y.; Garcia, R.; Zhang, H. A Portable Algorithm to Retrieve Bottom Depth of Optically Shallow Waters from Top-of-Atmosphere Measurements. J. Remote Sens. 2022, 2022, 9831947. [Google Scholar] [CrossRef]
- Manessa, M.D.M.; Setiawan, K.T.; Haidar, M.; Supriatna, S.; Pataropura, A.; Supardjo, A.H. Optimization of the Random Forest Algorithm for Multispectral Derived Bathymetry. Int. J. Geoinf. 2020, 16, 1–6. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Manessa, M.D.M.; Kanno, A.; Sekine, M.; Haidar, M.; Yamamoto, K.; Imai, T.; Higuchi, T. Satellite-Derived Bathymetry Using Random Forest Algorithm and Worldview-2 Imagery. J. Geomat. Plan. 2016, 3, 10. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite Derived Bathymetry Using Machine Learning and Multi-Temporal Satellite Images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef]
- Babbel, B.J.; Parrish, C.E.; Magruder, L.A. ICESat-2 Elevation Retrievals in Support of Satellite-Derived Bathymetry for Global Science Applications. Geophys. Res. Lett. 2021, 48, e2020GL090629. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-Derived Bathymetry Using the ICESat-2 Lidar and Sentinel-2 Imagery Datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Thomas, N.; Pertiwi, A.P.; Traganos, D.; Lagomasino, D.; Poursanidis, D.; Moreno, S.; Fatoyinbo, L. Space-Borne Cloud-Native Satellite-Derived Bathymetry (SDB) Models Using ICESat-2 And Sentinel-2. Geophys. Res. Lett. 2021, 48, e2020GL092170. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K. Hydrolight 5 Ecolight 5 Technical Documentation; Sequoia Scientific, Inc.: Bellevue, WA, USA, 2008; p. 100. [Google Scholar]
- Mobley, C.D.; Sundman, L.K. Hydrolight 5 Ecolight 5 Users Guide; Sequoia Scientific, Inc.: Bellevue, WA, USA, 2008; p. 104. [Google Scholar]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Coveney, S.; Monteys, X.; Hedley, J.D.; Castillo-Campo, Y.; Kelleher, B. ICESat-2 Marine Bathymetry: Extraction, Refraction Adjustment and Vertical Accuracy as a Function of Depth in Mid-Latitude Temperate Contexts. Remote Sens. 2021, 13, 4352. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.; Rebold, T. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 5; NASA: Boulder, CO, USA, 2021. [Google Scholar] [CrossRef]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.; Rebold, T. ICE, CLOUD, and Land Elevation Satellite—2 (ICESat-2) Project Algorithm Theoretical Basis Document (ATBD) for Global Geolocated Photons ATL03; Goddard Space Flight Cent: Greenbelt, MD, USA, 2021. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the KDD-96, Portland, OR, USA, 2–4 August 1996; AAAI Press: Menlo Park, CA, USA, 1996; Volume 96, pp. 226–231. [Google Scholar]
- Wang, Y.; He, X.; Bai, Y.; Wang, D.; Zhu, Q.; Gong, F.; Yang, D.; Li, T. Satellite Retrieval of Benthic Reflectance by Combining Lidar and Passive High-Resolution Imagery: Case-I Water. Remote Sens. Environ. 2022, 272, 112955. [Google Scholar] [CrossRef]
- Delwart, S. Sentinel-2 User Handbook; ESA Standard Document; ESA: Paris, France, 2015; Volume 1, pp. 1–64. [Google Scholar]
- Vanhellemont, Q.; Ruddick, K. Acolite for Sentinel-2: Aquatic Applications of MSI Imagery. In Proceedings of the ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; pp. 9–13. [Google Scholar]
- Vanhellemont, Q. Adaptation of the Dark Spectrum Fitting Atmospheric Correction for Aquatic Applications of the Landsat and Sentinel-2 Archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, J.; Deng, R.; Liang, Y.; Gao, Y.; Chen, Q.; Xiong, L.; Liu, Y.; Tang, Y.; Tang, D. A Downscaled Bathymetric Mapping Approach Combining Multitemporal Landsat-8 and High Spatial Resolution Imagery: Demonstrations from Clear to Turbid Waters. ISPRS J. Photogramm. Remote Sens. 2021, 180, 65–81. [Google Scholar] [CrossRef]
- Arabi, B.; Salama, M.S.; van der Wal, D.; Pitarch, J.; Verhoef, W. The Impact of Sea Bottom Effects on the Retrieval of Water Constituent Concentrations from MERIS and OLCI Images in Shallow Tidal Waters Supported by Radiative Transfer Modeling. Remote Sens. Environ. 2020, 237, 111596. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Niroumand-Jadidi, M.; Vitti, A.; Lyzenga, D.R. Multiple Optimal Depth Predictors Analysis (MODPA) for River Bathymetry: Findings from Spectroradiometry, Simulations, and Satellite Imagery. Remote Sens. Environ. 2018, 218, 132–147. [Google Scholar] [CrossRef]
- Howley, T.; Madden, M.G.; O’Connell, M.-L.; Ryder, A.G. The Effect of Principal Component Analysis on Machine Learning Accuracy with High-Dimensional Spectral Data. Knowl.-Based Syst. 2006, 19, 363–370. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature Selection Based on Mutual Information Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Yang, D.; Yang, C. Detection of Seagrass Distribution Changes from 1991 to 2006 in Xincun Bay, Hainan, with Satellite Remote Sensing. Sensors 2009, 9, 830–844. [Google Scholar] [CrossRef]
- Wang, D.; Wu, R.; Li, Y.; Wu, Z. Tropical Typical Marine Ecosystem Research; China Ocean Press: Beijing, China, 2013; ISBN 978-7-5027-8611-3. [Google Scholar]
- Kennedy, E.; Roelfsema, C.; Lyons, M.; Kovacs, E.; Borrego-Acevedo, R.; Roe, M.; Phinn, S.; Larsen, K.; Murray, N.; Yuwono, D.; et al. Reef Cover: A Coral Reef Classification to Guide Global Habitat Mapping from Remote Sensing; Systems Biology. Sci. Data 2021, 8, 196. [Google Scholar] [CrossRef]
- Lee, Z.; Shangguan, M.; Garcia, R.A.; Lai, W.; Lu, X.; Wang, J.; Yan, X. Confidence Measure of the Shallow-Water Bathymetry Map Obtained through the Fusion of Lidar and Multiband Image Data. J. Remote Sens. 2021, 2021, 9841804. [Google Scholar] [CrossRef]
- Lee, Z.; Hu, C.; Arnone, R.; Liu, Z. Impact of Sub-Pixel Variations on Ocean Color Remote Sensing Products. Opt. Express 2012, 20, 20844–20854. [Google Scholar] [CrossRef]
- Casal, G.; Harris, P.; Monteys, X.; Hedley, J.; Cahalane, C.; McCarthy, T. Understanding Satellite-Derived Bathymetry Using Sentinel 2 Imagery and Spatial Prediction Models. GIScience Remote Sens. 2020, 57, 271–286. [Google Scholar] [CrossRef]
- Wang, M.; IOCCG. Atmospheric Correction for Remotely-Sensed Ocean-Colour; International Ocean Colour Coordinating Group (IOCCG): Monterey, CA, USA, 2010. [Google Scholar]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A Global Assessment of Atmospheric Correction Methods for Landsat-8 and Sentinel-2 over Lakes, Rivers, and Coastal Waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).