Forest Height Mapping Using Feature Selection and Machine Learning by Integrating Multi-Source Satellite Data in Baoding City, North China
Abstract
:1. Introduction
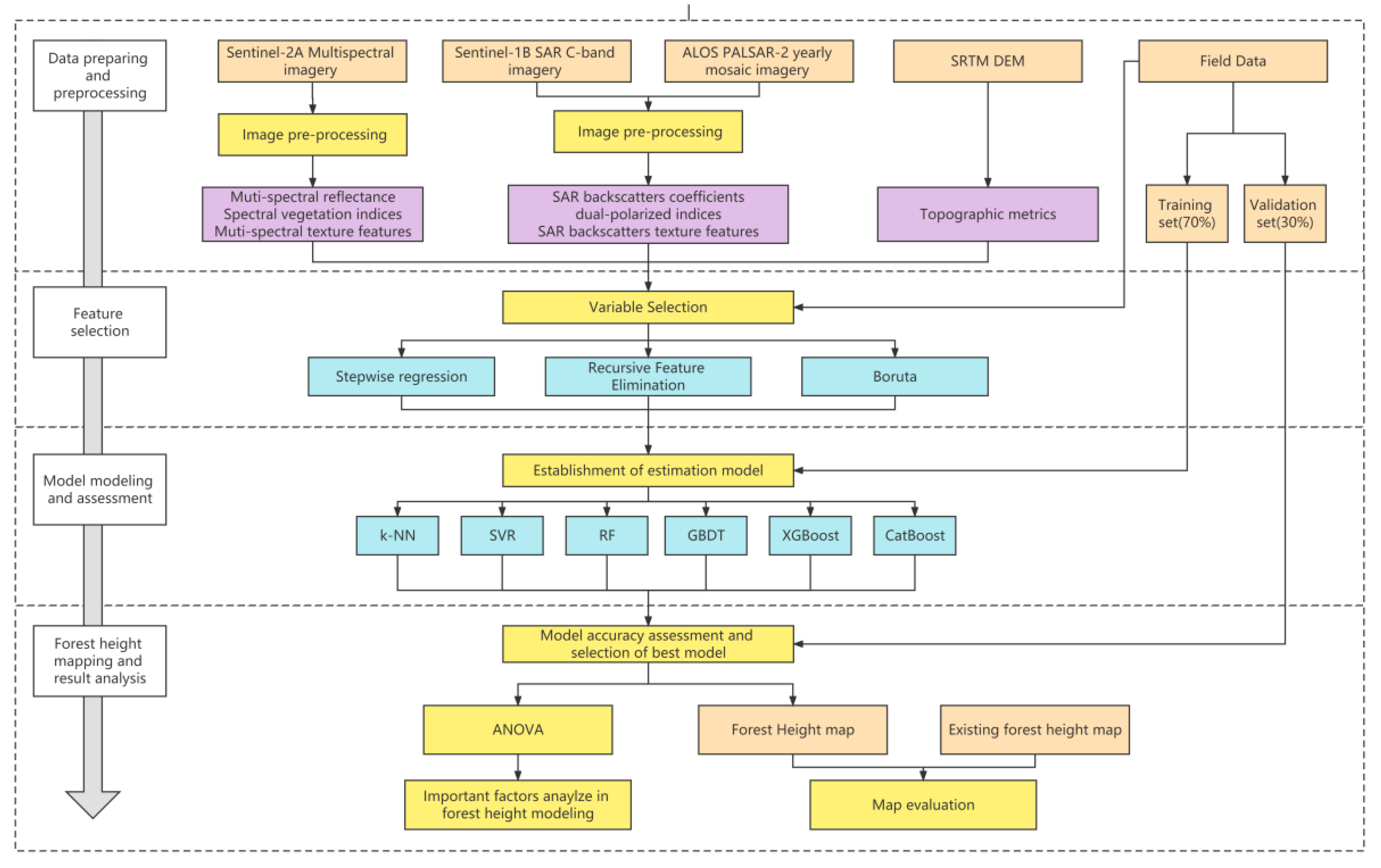
2. Materials and Methods
2.1. Study Area
2.2. Methodological Framework of This Study
2.3. Data Source and Preprocessing
2.3.1. Field Data Collection
2.3.2. Sentinel-2 Multispectral Imagery and Preprocessing
2.3.3. Synthetic Aperture Radar (SAR) Data and Preprocessing
2.3.4. Topographic and Ancillary Data
2.4. Feature Variable Extraction
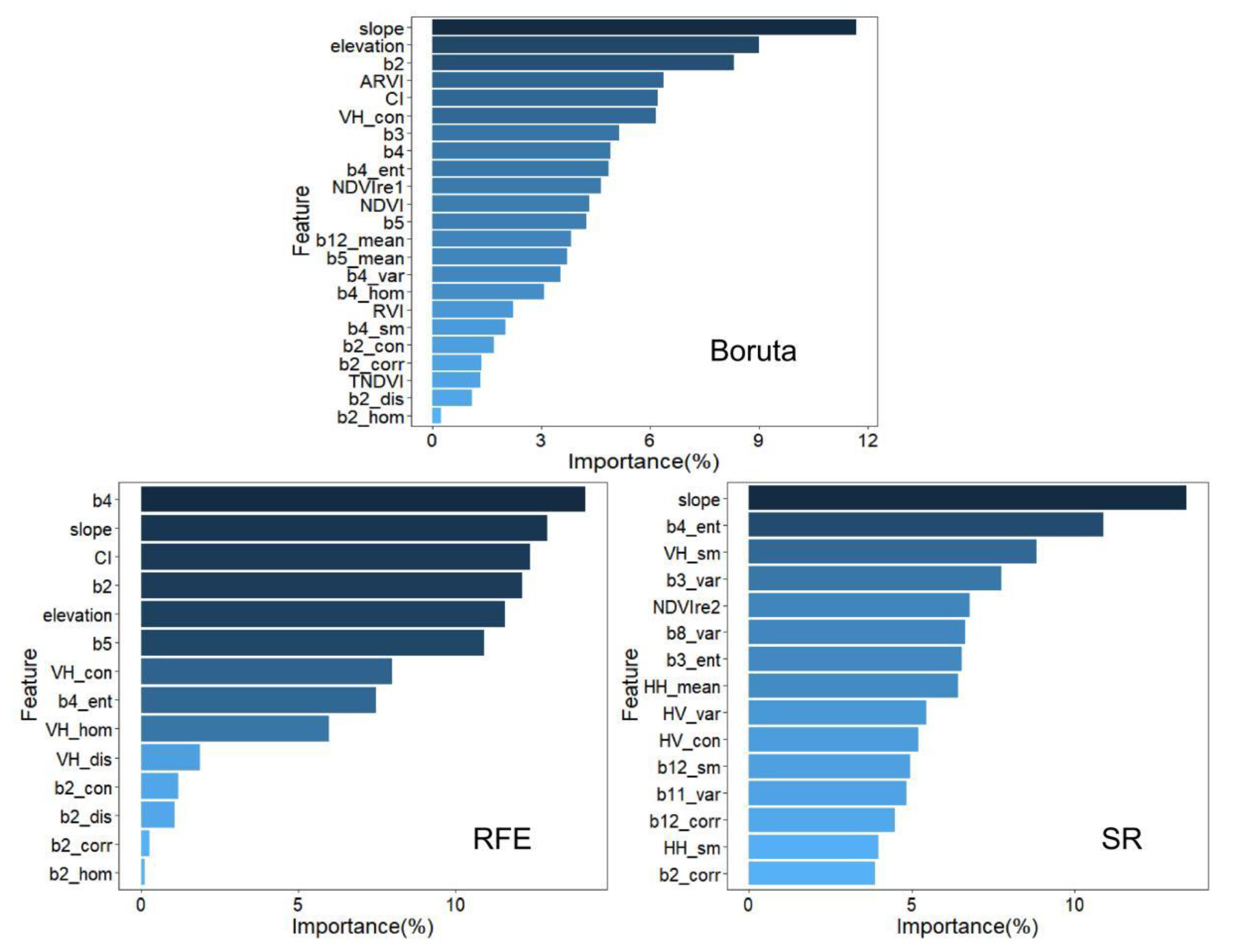
2.5. Feature Variable Selection
2.5.1. Stepwise Regression Analysis
2.5.2. Recursive Feature Elimination
2.5.3. Boruta
2.6. Machine Learning Algorithms
2.6.1. K-Nearest Neighbor
2.6.2. Support Vector Machine Regression
2.6.3. Random Forest
2.6.4. Gradient Boosting Decision Tree
2.6.5. Extreme Gradient Boosting
2.6.6. Categorical Boosting
2.6.7. Tuning the Hyperparameters for the Machine Learning Algorithms
2.7. Model Evaluation
2.8. ANOVA Analysis
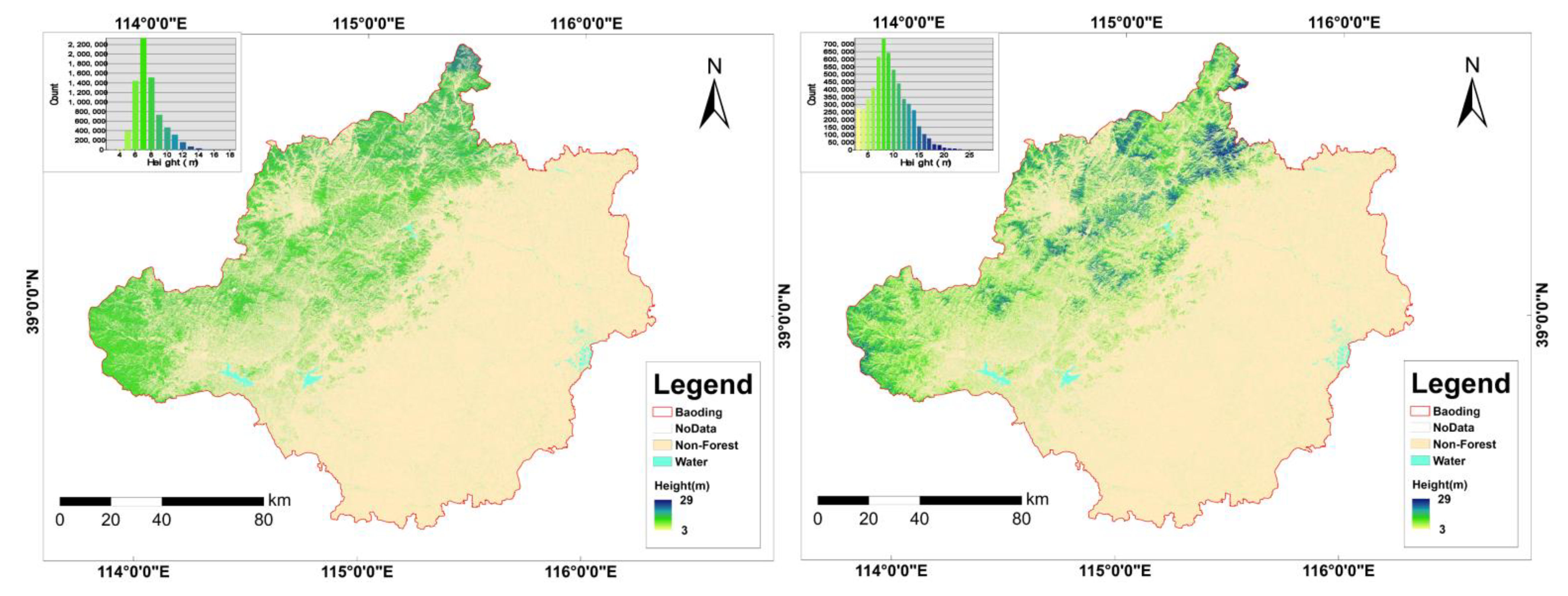
2.9. Forest Height Mapping and Product Evaluation
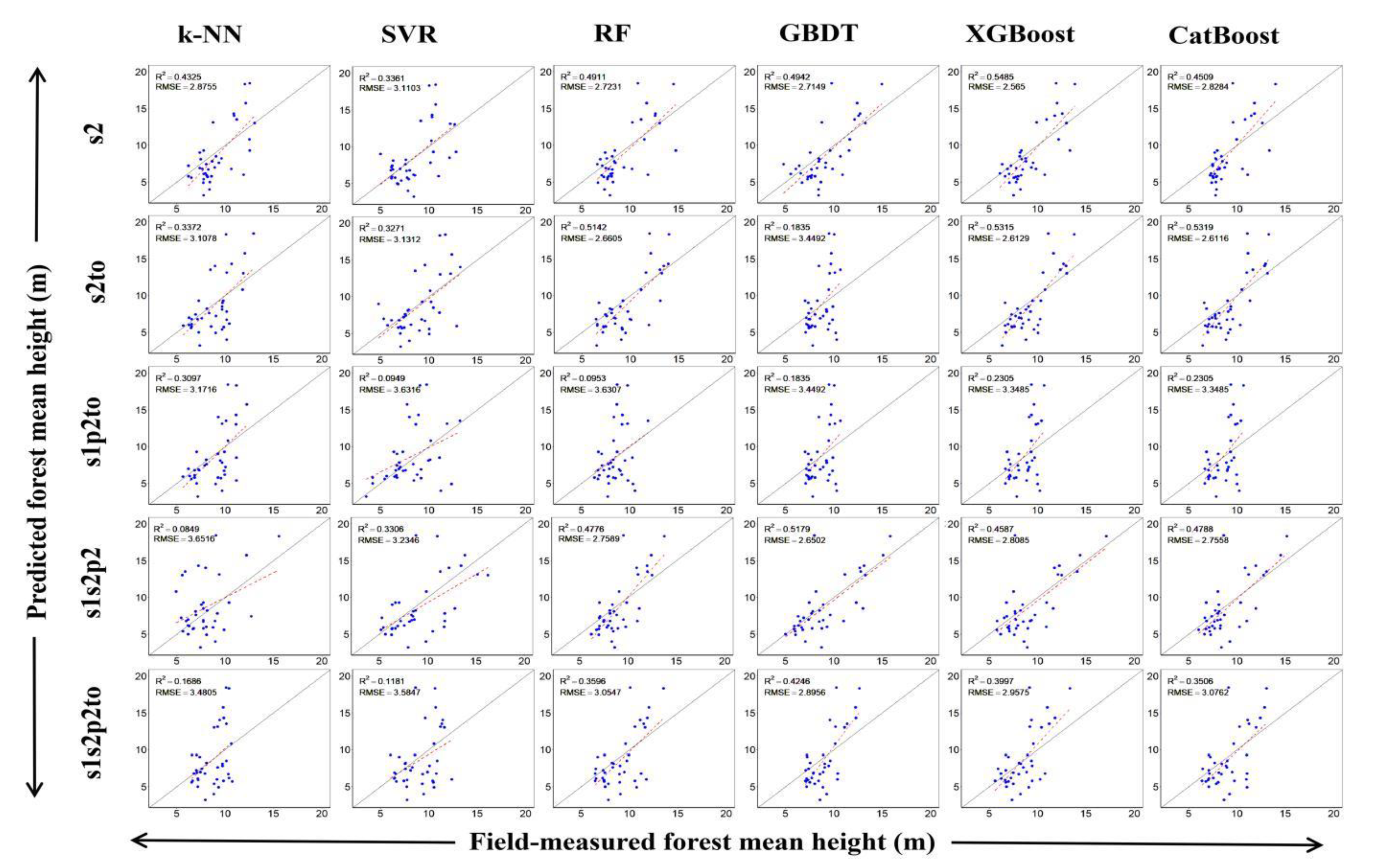
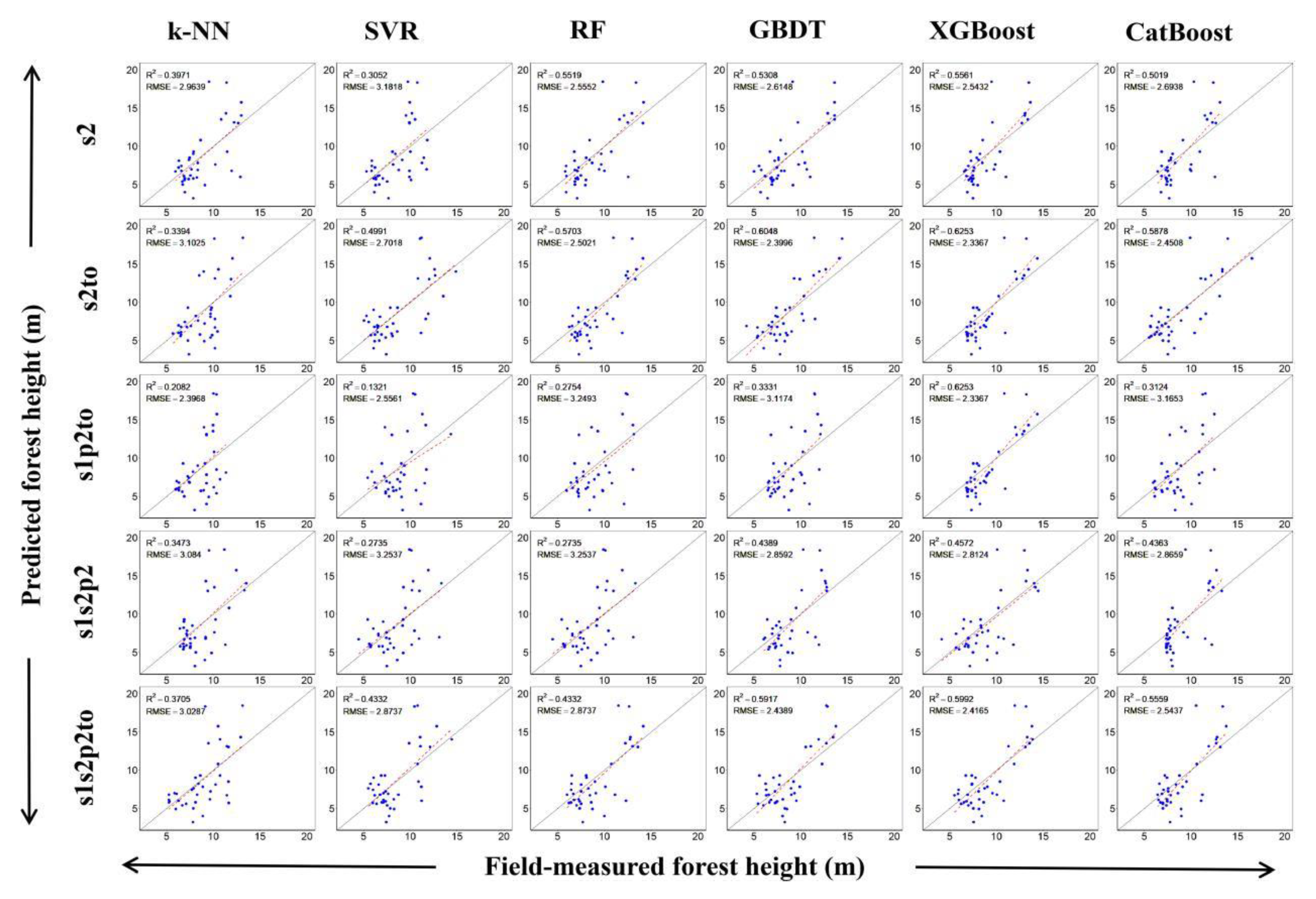
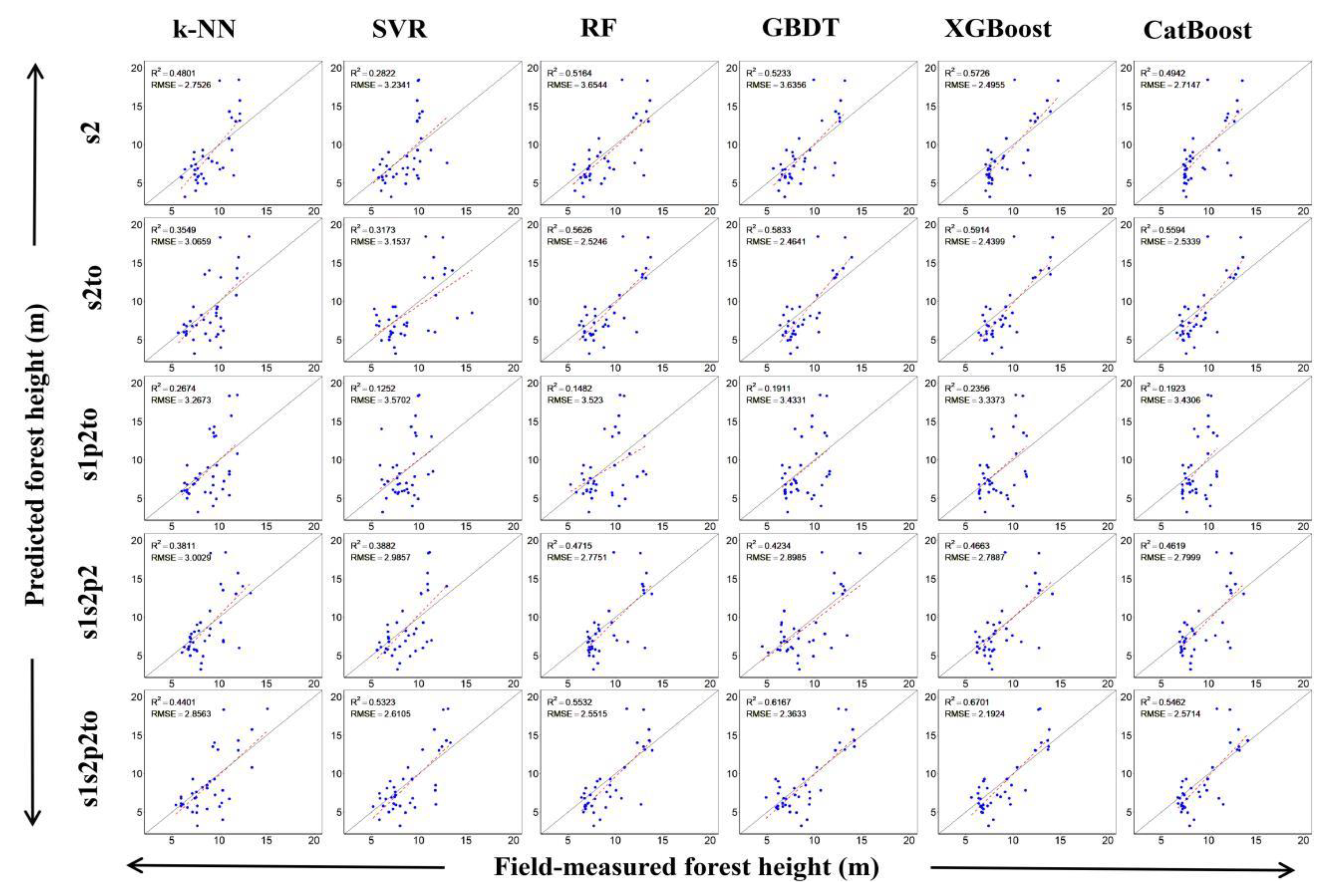
3. Results
3.1. Feature Variable Selected for Forest Height Modeling
3.2. Forest Height Modeling Results
3.3. Variable Importance Analysis
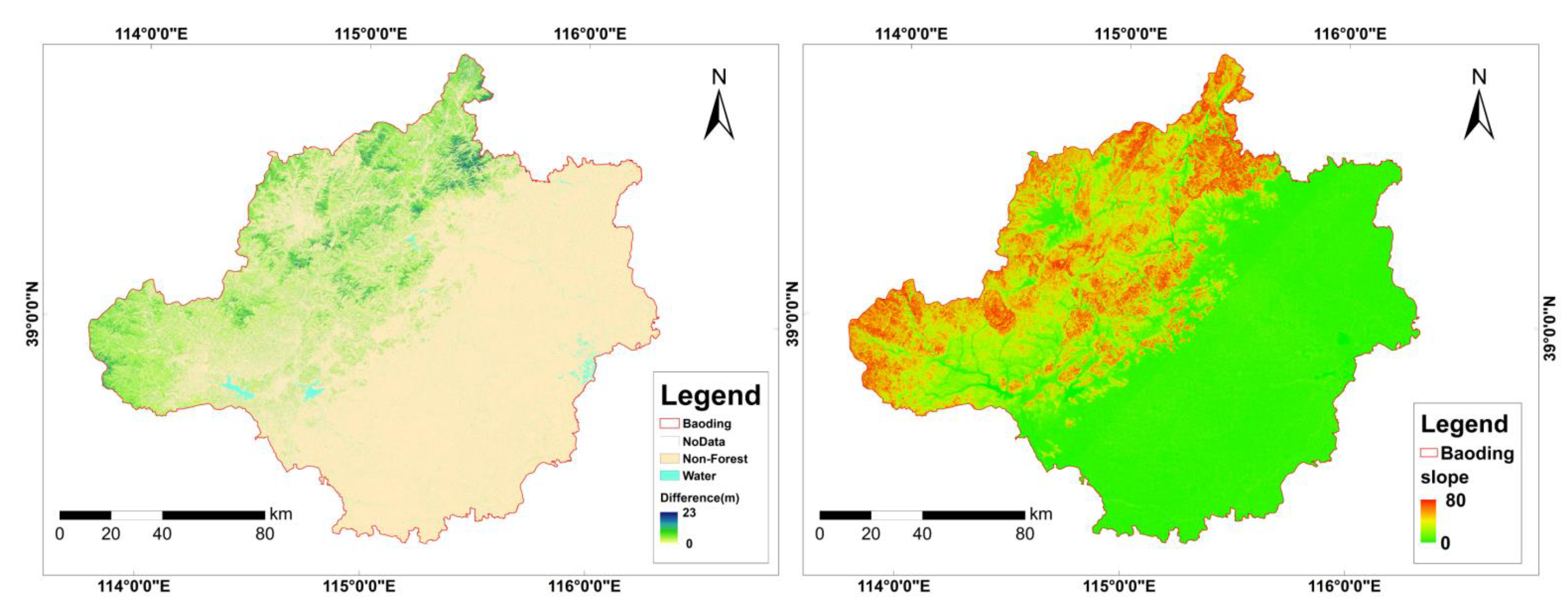
3.4. Forest Height Mapping and Comparison to Existing Product
4. Discussion
4.1. Performance of Multi-Source Satellite Metrics for Forest Height Estimation
4.2. Performance of Different Feature Variable Selection Methods
4.3. Performance of Different Machine Learning Algorithms
4.4. Important Factors Analyze in Forest Height Estimation
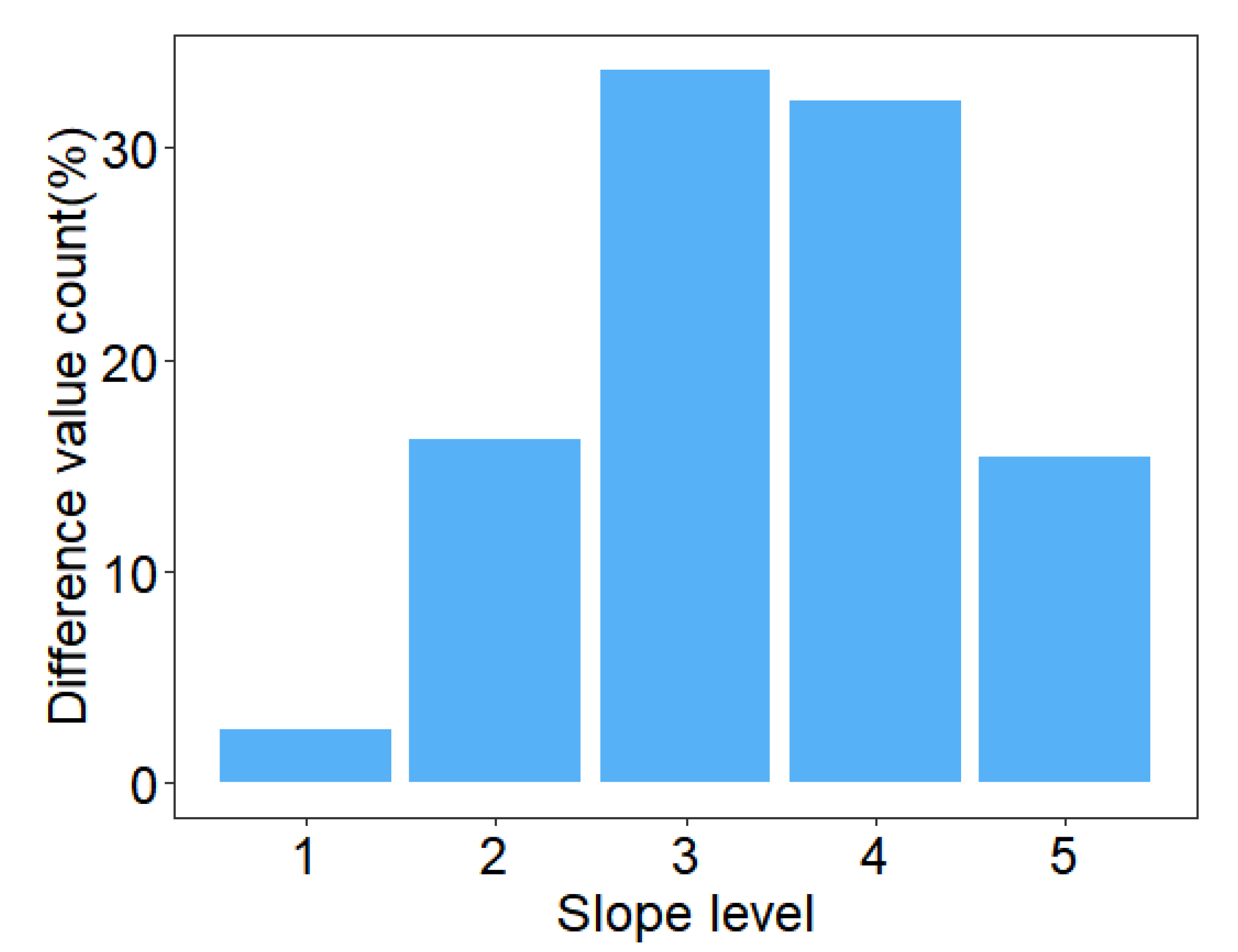
4.5. Map Product Comparison
4.6. Recent Related Works Comparison
4.7. Limitations and Prospects
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Achard, F.; Eva, H.; Stibig, H.; Mayaux, P.; Gallego, J.; Richards, T.; Malingreau, J. Determination of Deforestation Rates of the World’s Humid Tropical Forests. Science 2002, 297, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Kaufmann, R.; Myneni, R.; Tucker, C.; Kauppi, P.; Liski, J.; Buermann, W.; Alexeyev, V.; Hughes, M. Remote sensing estimates of boreal and temperate forest woody biomass: Carbon pools, sources, and sinks. Remote Sens. Environ. 2003, 84, 393–410. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Zhou, X.; Gong, P. Integration of multi-resource remotely sensed data and allometric models for forest aboveground biomass estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Hurtt, G.; Zhao, M.; Sahajpal, R.; Armstrong, A.; Birdsey, R.; Campbell, E.; Dolan, K.; Dubayah, R.; Fisk, J.; Flanagan, S.; et al. Beyond MRV: High-resolution forest carbon modeling for climate mitigation planning over Maryland, USA. Environ. Res. Lett. 2019, 14, 045013. [Google Scholar] [CrossRef]
- Herold, M.; Carter, S.; Avitabile, V.; Espejo, A.; Jonckheere, I.; Lucas, R.; McRoberts, R.; Næsset, E.; Nightingale, J.; Petersen, R.; et al. The Role and Need for Space-Based Forest Biomass-Related Measurements in Environmental Management and Policy. Surv. Geophys. 2019, 40, 757–778. [Google Scholar] [CrossRef]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; Crowther, T.; et al. The Importance of Consistent Global Forest Aboveground Biomass Product Validation. Surv. Geophys. 2019, 40, 979–999. [Google Scholar] [CrossRef]
- Wulder, M.; White, J.; Nelson, R.; Næsset, E.; Ørka, H.; Coops, N.; Hilker, T.; Bater, C.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Hansen, M.; Potapov, P.; Goetz, S.; Turubanova, S.; Tyukavina, A.; Krylov, A.; Kommareddy, A.; Egorov, A. Mapping tree height distributions in Sub-Saharan Africa using Landsat 7 and 8 data. Remote Sens. Environ. 2016, 185, 221–232. [Google Scholar] [CrossRef]
- Wolter, P.; Townsend, P.; Sturtevant, B. Estimation of forest structural parameters using 5 and 10 meter SPOT-5 satellite data. Remote Sens. Environ. 2009, 113, 2019–2036. [Google Scholar] [CrossRef]
- Potapov, P.; Tyukavina, A.; Turubanova, S.; Talero, Y.; Hernandez-Serna, A.; Hansen, M.; Saah, D.; Tenneson, K.; Poortinga, A.; Aekakkararungroj, A.; et al. Annual continuous fields of woody vegetation structure in the Lower Mekong region from 2000–2017 Landsat time-series. Remote Sens. Environ. 2019, 232, 111278. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011, 116, 4021. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Alexander, C.; Korstjens, A.; Hill, R. Influence of micro-topography and crown characteristics on tree height estimations in tropical forests based on LiDAR canopy height models. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 105–113. [Google Scholar] [CrossRef]
- Almeida, D.; Broadbent, E.; Zambrano, A.; Wilkinson, B.; Ferreira, M.; Chazdon, R.; Meli, P.; Gorgens, E.; Silva, C.; Stark, S.; et al. Monitoring the structure of forest restoration plantations with a drone-lidar system. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 192–198. [Google Scholar] [CrossRef]
- Zhang, Z.; Ni, W.; Sun, G.; Huang, W.; Ranson, K.J.; Cook, B.D.; Guo, Z. Biomass retrieval from L-band Polarimetric UAVSAR Backscatter and prism stereo imagery. Remote Sens. Environ. 2017, 194, 331–346. [Google Scholar] [CrossRef]
- Qi, W.; Lee, S.-K.; Hancock, S.; Luthcke, S.; Tang, H.; Armston, J.; Dubayah, R. Improved Forest height estimation by fusion of simulated GEDI LIDAR data and TanDEM-X Insar Data. Remote Sens. Environ. 2019, 221, 621–634. [Google Scholar] [CrossRef]
- Li, C.; Song, J.; Wang, J. New approach to calculating tree height at the regional scale. For. Ecosyst. 2021, 8, 24. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Lang, N.; Schindler, K.; Wegner, J.D. Country-wide high-resolution vegetation height mapping with sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Multibaseline Polarimetric Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1086–1104. [Google Scholar] [CrossRef] [Green Version]
- López-Serrano, P.M.; López-Sánchez, C.A.; Álvarez-González, J.G.; García-Gutiérrez, J. A Comparison of Machine Learning Techniques Applied to Landsat-5 TM Spectral Data for Biomass Estimation. Can. J. Remote Sens. 2016, 42, 690–705. [Google Scholar] [CrossRef]
- Huang, W.; Min, W.; Ding, J.; Liu, Y.; Hu, Y.; Ni, W.; Shen, H. Forest height mapping using inventory and multi-source satellite data over Hunan Province in southern China. For. Ecosyst. 2022, 9, 100006. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in northeast China using SAR Sentinel-1B, multispectral sentinel-2a, and DEM imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Amini, J.; Sumantyo, J.T.S. Employing a Method on SAR and Optical Images for Forest Biomass Estimation. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4020–4026. [Google Scholar] [CrossRef]
- Forkuor, G.; Benewinde Zoungrana, J.-B.; Dimobe, K.; Ouattara, B.; Vadrevu, K.P.; Tondoh, J.E. Above-ground biomass mapping in West African dryland forest using Sentinel-1 and 2 datasets—A case study. Remote Sens. Environ. 2020, 236, e111496. [Google Scholar] [CrossRef]
- Li, H.; Kato, T.; Hayashi, M.; Wu, L. Estimation of forest aboveground biomass of two major conifers in Ibaraki Prefecture, Japan, from palsar-2 and sentinel-2 data. Remote Sens. 2022, 14, 468. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Li, G.; Moran, E. A survey of remote sensing-basedd aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth. 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Li, X.; Lin, H.; Long, J.; Xu, X. Mapping the growing stem volume of the coniferous plantations in north China using multispectral data from integrated GF-2 and sentinel-2 images and an optimized feature variable selection method. Remote Sens. 2021, 13, 2740. [Google Scholar] [CrossRef]
- Li, G.; Xie, Z.; Jiang, X.; Lu, D.; Chen, E. Integration of ZiYuan-3 Multispectral and Stereo Data for Modeling Aboveground Biomass of Larch Plantations in North China. Remote Sens. 2019, 11, 2328. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Lv, G.; Xu, J.; Cui, G. Integrating multi-source remote sensing to assess forest aboveground biomass in the Khingan mountains of north-eastern China using machine-learning algorithms. Remote Sens. 2022, 14, 1039. [Google Scholar] [CrossRef]
- Purohit, S.; Aggarwal, S.P.; Patel, N.R. Estimation of forest aboveground biomass using combination of Landsat 8 and sentinel-1a data with random forest regression algorithm in Himalayan foothills. Trop. Ecol. 2021, 62, 288–300. [Google Scholar] [CrossRef]
- Peng, X.; Zhao, A.; Chen, Y.; Chen, Q.; Liu, H.; Wang, J.; Li, H. Comparison of modeling algorithms for Forest Canopy Structures based on UAV-LIDAR: A case study in tropical China. Forests 2020, 11, 1324. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, S.; Zhao, F.; Tian, L.; Zhao, Z. Comparison of machine learning algorithms for Forest parameter estimations and application for Forest Quality Assessments. For. Ecol. Manag. 2019, 434, 224–234. [Google Scholar] [CrossRef]
- Chen, M.; Qiu, X.; Zeng, W.; Peng, D. Combining sample plot stratification and machine learning algorithms to improve forest aboveground carbon density estimation in northeast China using Airborne Lidar Data. Remote Sens. 2022, 14, 1477. [Google Scholar] [CrossRef]
- Yu, G.; Lu, Z.; Lai, Y. Comparative Study on Variable Selection Approaches in Establishment of Remote Sens. Model for Forest Biomass Estimation. Remote Sens. 2019, 11, 1437. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of feature selection and CatBoost for prediction: The first application to the estimation of aboveground biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Extending airborne lidar-derived estimates of forest canopy cover and height over large areas using KNN with Landsat Time Series Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3489–3496. [Google Scholar] [CrossRef]
- Özçelik, R.; Diamantopoulou, M.J.; Crecente-Campo, F.; Eler, U. Estimating crimean juniper tree height using nonlinear regression and artificial neural network models. For. Ecol. Manag. 2013, 306, 52–60. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of Gedi and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Wang, M.; Sun, R.; Xiao, Z. Estimation of forest canopy height and aboveground biomass from Spaceborne Lidar and landsat imageries in Maryland. Remote Sens. 2018, 10, 344. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Ding, J.; Guo, Z.; Tang, S.; Wang, C.; Huang, Q.; Liu, R.; Chen, J.M. A combined glas and Modis estimation of the global distribution of mean forest canopy height. Remote Sens. Environ. 2016, 174, 24–43. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Xia, J.; Ha, N.T.; Le, N.N.; Nguyen, T.T.T.; Dao, T.H.; Vu, T.T.P.; Pham, T.D.; Takeuchi, W. Comparison of Machine Learning Methods for Estimating Mangrove Above-Ground Biomass Using Multiple Source Remote Sens. Data in the Red River Delta Biosphere Reserve, Vietnam. Remote Sens. 2020, 12, 1334. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Liu, J. A stacking ensemble algorithm for improving the biases of forest aboveground biomass estimations from multiple remotely sensed datasets. GIsci. Remote Sens. 2022, 59, 234–249. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Mullissa, A.; Vollrath, A.; Odongo-Braun, C.; Slagter, B.; Balling, J.; Gou, Y.; Gorelick, N.; Reiche, J. Sentinel-1 SAR Backscatter Analysis Ready Data Preparation in Google Earth Engine. Remote Sens. 2021, 13, 1954. [Google Scholar] [CrossRef]
- The Japan Aerospace Exploration Agency(JAXA). Global 25m Resolution PALSAR-2/PALSAR Mosaic and Forest/Non-Forest Map (FNF) Dataset Description; JAXA: Tsukuba, Japan, 2019. [Google Scholar]
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y.; et al. Stable classification with limited sample: Transferring a 30-M resolution sample set collected in 2015 to mapping 10-M resolution global land cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, X.; Wu, F.; Sun, Z.; Xia, H.; Meng, Q.; Huang, W.; Zhou, H.; Gao, J.; Li, W.; et al. Estimating Forest Stock Volume in Hunan Province, China, by integrating in situ plot data, sentinel-2 images, and linear and machine learning regression models. Remote Sens. 2020, 12, 186. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Pirotti, F.; Callegari, M.; Chen, Q.; Cuozzo, G.; Lingua, E.; Notarnicola, C.; Papale, D. Potential of ALOS2 and NDVI to Estimate Forest Above-Ground Biomass, and Comparison with Lidar-Derived Estimates. Remote Sens. 2017, 9, 18. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of northeastern China using GLAS and MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 140–152. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National forest aboveground biomass mapping from ICESat/GLAS data and MODIS imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef]
- Whittingham, M.J.; Stephens, P.A.; Bradbury, R.B.; Freckleton, R.P. Why do we still use stepwise modelling in ecology and behaviour? J. Anim. Ecol. 2006, 75, 1182–1189. [Google Scholar] [CrossRef]
- Adame-Campos, R.L.; Ghilardi, A.; Gao, Y.; Paneque-Gálvez, J.; Mas, J. Variables Selection for Aboveground Biomass Estimations Using Satellite Data: A Comparison between Relative Importance Approach and Stepwise Akaike’s Information Criterion. ISPRS Int. J. Geo-Inf. 2019, 8, 245. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D.; Venables, W.N. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
- Pullanagari, R.; Kereszturi, G.; Yule, I. Integrating airborne hyperspectral, topographic, and soil data for estimating pasture quality using recursive feature elimination with random forest regression. Remote Sens. 2018, 10, 1117. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, H.; Zhou, Q.; Yang, F.; Luo, L. Structure damage detection based on random forest recursive feature elimination. Mech. Syst. Signal Process. 2014, 46, 82–90. [Google Scholar] [CrossRef]
- Granitto, P.M.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive feature elimination with random forest for ptr-ms analysis of agroindustrial products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Chirici, G.; Barbati, A.; Corona, P.; Marchetti, M.; Travaglini, D.; Maselli, F.; Bertini, R. Non-parametric and parametric methods using satellite images for estimating growing stock volume in Alpine and mediterranean forest ecosystems. Remote Sens. Environ. 2008, 112, 2686–2700. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the K-nearest neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in remote sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.; Tien Bui, D. Improving accuracy estimation of forest aboveground biomass based on incorporation of Alos-2 palsar-2 and sentinel-2a imagery and Machine Learning: A case study of the hyrcanian forest area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Deb, D.; Deb, S.; Chakraborty, D.; Singh, J.P.; Singh, A.K.; Dutta, P.; Choudhury, A. Aboveground biomass estimation of an agro-pastoral ecology in semi-arid Bundelkhand region of India from Landsat Data: A comparison of support vector machine and traditional regression models. Geocarto. Int. 2020, 37, 1043–1058. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S.; Fang, J. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Li, M. An evaluation of eight machine learning regression algorithms for forest aboveground biomass estimation from multiple satellite data products. Remote Sens. 2020, 12, 4015. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal Combination of Predictors and Algorithms for Forest Above-Ground Biomass Mapping from Sentinel and SRTM Data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Yang, L.; Liang, S.; Zhang, Y. A New Method for Generating a Global Forest Aboveground Biomass Map From Multiple High-Level Satellite Products and Ancillary Information. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2587–2597. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Yu, J.-W.; Yoon, Y.-W.; Baek, W.-K.; Jung, H.-S. Forest vertical structure mapping using two-seasonal optic images and LIDAR DSM acquired from UAV platform through Random Forest, XGBoost, and support vector machine approaches. Remote Sens. 2021, 13, 4282. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and sentinel-1a data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef] [PubMed]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Sun, H.; He, J.; Chen, Y.; Zhao, B. Space-Time Sea Surface PCO2 Estimation in the North Atlantic Based on CatBoost. Remote Sens. 2021, 13, 2805. [Google Scholar] [CrossRef]
- Ahirwal, J.; Nath, A.; Brahma, B.; Deb, S.; Sahoo, U.K.; Nath, A.J. Patterns and Driving Factors of Biomass Carbon and Soil Organic Carbon Stock in the Indian Himalayan Region. Sci. Total Environ. 2021, 770, 145292. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling icesat-2 lidar with sentinel-1, sentinel-2 and landsat-8 data. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X. Constructing a finer-resolution forest height in China using icesat/glas, landsat and Alos Palsar data and height patterns of natural forests and plantations. Remote Sens. 2019, 11, 1740. [Google Scholar] [CrossRef]
- Xi, Z.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest canopy height mapping by synergizing icesat-2, sentinel-1, sentinel-2 and topographic information based on machine learning methods. Remote Sens. 2022, 14, 364. [Google Scholar] [CrossRef]
- Agjee, N.H.; Ismail, R.; Mutanga, O. Identifying relevant hyperspectral bands using Boruta: A temporal analysis of water hyacinth biocontrol. J. Appl. Remote Sens. 2016, 10, 042002. [Google Scholar] [CrossRef]
- Arjasakusuma, S.; Swahyu Kusuma, S.; Phinn, S. Evaluating variable selection and machine learning algorithms for Estimating Forest Heights by combining Lidar and Hyperspectral Data. ISPRS Int. J. Geo-Inf. 2020, 9, 507. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Alcarde Alvares, C.; Stape, J.L.; Bailly, J.S.; Scolforo, H.F.; Cegatta, I.R.; Zribi, M.; Le Maire, G. Terrain Slope effect on forest height and wood volume estimation from Gedi Data. Remote Sens. 2021, 13, 2136. [Google Scholar] [CrossRef]
- Xing, Y.; de Gier, A.; Zhang, J.; Wang, L. An Improved Method for Estimating Forest Canopy Height Using ICESat-GLAS Full Waveform Data over Sloping Terrain: A Case Study in Changbai Mountains, China. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 385–392. [Google Scholar] [CrossRef]
- Pourshamsi, M.; Xia, J.; Yokoya, N.; Garcia, M.; Lavalle, M.; Pottier, E.; Balzter, H. Tropical Forest Canopy Height Estimation from combined polarimetric SAR and Lidar using machine-learning. ISPRS J. Photogramm. Remote Sens. 2021, 172, 79–94. [Google Scholar] [CrossRef]


| Dataset | Sample Size | Min (m) | Max (m) | Mean (m) | Median (m) | Std (m) |
|---|---|---|---|---|---|---|
| Training | 91 | 3.00 | 24.50 | 8.57 | 7.50 | 3.92 |
| Validation | 37 | 3.20 | 18.40 | 8.58 | 7.20 | 3.87 |
| Total | 128 | 3.00 | 24.50 | 8.57 | 7.30 | 3.89 |
| Source | Feature Variables | Description | |
|---|---|---|---|
| Sentinel-2 multispectral data | Multispectral bands (10) | b2 | Blue, 490 nm |
| b3 | Green, 560 nm | ||
| b4 | Red, 665 nm | ||
| b5 | Red edge, 705 nm | ||
| b6 | Red edge, 749 nm | ||
| b7 | Red edge, 783 nm | ||
| b8 | Near-infrared, 842 nm | ||
| b8a | Near-infrared, 865 nm | ||
| b11 | Short-wave infrared, 1610 nm | ||
| b12 | Short-wave infrared, 2190 nm | ||
| Vegetation indices (20) | SAVI | Soil adjusted vegetation index, 1.5 × (B8−B4)/(B8 + B4 + 0.5) | |
| NDVI | Normalized difference vegetation index, (B8 − B4)/(B8 + B4) | ||
| MSAVI2 | Second modified soil adjusted vegetation index, 0.5 × [2 × (B8 + 1) − sqrt[(2 × B8 + 1) × (2 × B8 + 1) – 8 × (B8 − B4)]] | ||
| RVI | Ratio vegetation index, B8/B4 | ||
| PVI | Perpendicular vegetation index, sin(a) × B8 − cos(a) × B4(a = 45°) | ||
| IPVI | Infrared percentage vegetation index, B8/(B8 + B4) | ||
| WDVI | Weighted difference vegetation index, B8 − 0.5 × B4 | ||
| TNDVI | Transformed normalized difference vegetation index, sqrt[(B8 − B4)/(B8 + B4) + 0.5] | ||
| GNDVI | Green normalized difference vegetation index, (B8 − B3)/(B8 + B3) | ||
| CI | Color index, (B4 − B3)/(B4 + B3) | ||
| ARVI | Atmospherically resistant vegetation index, (B8 – 2 × B4 + B2)/(B8 + 2 × B4 − B2) | ||
| MCARI | Modified chlorophyll absorption ratio index, [(B5 − B4) − 0.2 × B5 − B3)] × (B5 − B4) | ||
| MTCI | Meris terrestrial chlorophyll index, (B6 − B5)/(B5 − B4) | ||
| EVI | Enhanced vegetation index, 2.5 × [(B8 − B4)/(B8 + 6 × B4 − 7.5 × B2 + 1)] | ||
| EVI2 | Enhanced vegetation index2, 2.5 × [(B8 − B4)/(B8 + 2.4 × B4 + 1)] | ||
| NDVIre1 | Normalized Difference Vegetation Index red-edge1,(B8 − B5)/(B8 + B5) | ||
| NDVIre2 | Normalized Difference Vegetation Index red-edge1, (B8cB6)/(B8 + B6) | ||
| mNDVI | Modified normalized difference vegetation index, (B8 − B4)/(B8 + B4 − 2 × B2) | ||
| mNDVIre | Modified red edge normalized difference vegetation index, (B8 − B5)/(B8 + B5 − 2 × B2) | ||
| NDII | normalized difference infrared index, (B8 − B11)/(B8 + B11) | ||
| SAVI | Soil adjusted vegetation index, 1.5 × (B8 − B4/(B8 + B4 + 0.5) | ||
| NDVI | Normalized difference vegetation index, (B8 − B4)/(B8 + B4) | ||
| MSAVI2 | Second modified soil adjusted vegetation index, 0.5 × [2 × (B8 + 1) − sqrt[(2 × B8 + 1) × (2 × B8 + 1) − 8 × (B8 − B4)]] | ||
| RVI | Ratio vegetation index, B8/B4 | ||
| PVI | Perpendicular vegetation index, sin(a) × B8 − cos(a) × B4, (a = 45°) | ||
| IPVI | Infrared percentage vegetation index, B8/(B8 + B4) | ||
| Texture (80) | b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_con | Contrast | |
| b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_corr | Correlation | ||
| b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_dis | Dissimilarity | ||
| b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_ent | Entropy | ||
| b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_hom | Homogeneity | ||
| b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_mean | Mean | ||
| b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_sm | Angular second moment | ||
| b2/b3/b4/b5/b6/b7/b8/b8a/b11/b12_var | Variance | ||
| Sentinel-1 and PALSAR-2 mosaic | Polarization (8) | VV | Vertical transmit-vertical channel backscattering coefficients, dB |
| VH | Vertical transmit-horizontal channel backscattering coefficients, dB | ||
| HH | Horizontal transmit- horizontal channel backscattering coefficients, dB | ||
| HV | Horizontal transmit-vertical channel backscattering coefficients, dB | ||
| V/H | VV/VH | ||
| s1npdi | (VV − VH)/(VV + VH) | ||
| H/V | HH/HV | ||
| p2npdi | (HH − HV)/(HH + HV) | ||
| Texture (32) | VV/VH/HH/HV_con | Contrast | |
| VV/VH/HH/HV_corr | Correlation | ||
| VV/VH/HH/HV_dis | Dissimilarity | ||
| VV/VH/HH/HV_ent | Entropy | ||
| VV/VH/HH/HV_hom | Homogeneity | ||
| VV/VH/HH/HV_mean | Mean | ||
| VV/VH/HH/HV_sm | Angular second moment | ||
| VV/VH/HH/HV_var | Variance | ||
| SRTM DEM | (3) | elevation | elevation |
| slope | slope | ||
| aspect | aspect |
| Scenario ID | Variable Combination | Short Name |
|---|---|---|
| 1 | Sentinel-2 | s2 |
| 2 | Sentinel-2, SRTM DEM | s2to |
| 3 | Senitnel-1, Sentinel-2, PALSAR-2 mosaic | s1s2p2 |
| 4 | Sentinel-1, PALSAR-2 mosaic, SRTM DEM | s1p2to |
| 5 | Sentinel-1, Sentinel-2, PALSAR-2 mosaic, SRTM DEM | s1s2p2to |
| Algorithm | Hyperparameter | Description | Hyperparameter Configurations |
|---|---|---|---|
| k-NN | k | the number of neighbors considered. | (1–10) at intervals of 1 |
| SVR | C | the cost of constraints violation | (1–10) at intervals of 1 |
| gamma | the parameter needed for all kernels except linear | (0–0.2) at intervals of 0.01 | |
| RF | mtry | the number of predictor variables randomly sampled at each split | (1–10) at intervals of 1 |
| ntree | the number of trees | (100–1000) at intervals of 100 | |
| GBDT | ntree | the number of trees | (100–1000) at intervals of 100 |
| maxdepth | the depth of the tree | (1–10) at intervals of 1 | |
| shrinkage | the learning rate | (0.01–0.1) at intervals of 0.01 | |
| min terminal node | the minimum samples required in a terminal node. | (1–10) at intervals of 1 | |
| XGBoost | max_depth | the depth of the tree | (1–10) at intervals of 1 |
| eta | the learning rate | (0.01–0.1) at intervals of 0.01 | |
| gamma | minimum loss reduction of the tree | (0–1) at intervals of 0.1 | |
| colsample_bytree | the number of predictor variables supplied to a tree | (0–1) at intervals of 0.1 | |
| min_child_weight | minimum number of instances | (1–10) at intervals of 1 | |
| subsample | the number of observations supplied to a tree | (0–1) at intervals of 0.1 | |
| CatBoost | depth | the depth of the tree | |
| learning_rate | the learning rate | (0.01–0.1) at intervals of 0.01 | |
| l2_leaf_reg | the coefficient at the L2 regularization term of the cost function | (1–10) at intervals of 1 | |
| rsm | the percentage of features to use at each split selection | (0–1) at intervals of 0.1 |
| Scenario Name | Feature Selection Method | Number of Selected Variables | Name of Selected Variables |
|---|---|---|---|
| s2 | Stepwise regression analysis | 9 | b11, NDVIre2, b2_hom, b3_ent, b3_var, b4_ent, b4_var, b5_hom, b11_mean; |
| Recursive feature elimination | 10 | b2, b4, b5, CI, b2_con, b2_corr, b2_hom, b2_dis, b4_ent, b4_sm; | |
| Boruta | 16 | b2, b3, b4, b5, CI, b2_con, b2_corr, b2_dis, b2_hom, b3_mean, b4_dis, b4_ent, b4_hom, b4_mean, b4_sm, b12_mean; | |
| s2to | Stepwise regression analysis | 14 | b3, NDVIre2, b2_corr, b2_sm, b3_mean, b4_ent, b4_sm, b5_mean, b8_dis, b8_var, b11_var, b12_corr, b12_var, elevation; |
| Recursive feature elimination | 10 | b2, b5, CI, b2_con, b2_corr, b2_dis, b2_hom, b4_ent, elevation, slope; | |
| Boruta | 18 | b2, b4, b5, CI, NDVI, b2_con, b2_corr, b2_dis, b2_hom, b3_mean, b4_ent, b4_hom, b4_mean, b4_sm, b4_var, b5_ent, elevation, slope; | |
| s1s2p2 | Stepwise regression analysis | 8 | NDVIre2, b2_hom, b4_ent, b5_sm, VV_dis, HH_con, HH_mean, HV_var; |
| Recursive feature elimination | 12 | b2, b4, b5, b2_corr, CI, b2_con, b2_dis, b2_hom, b4_ent, VH_con, VH_dis, VH_hom; | |
| Boruta | 21 | b2, b4, b5, ARVI, CI, NDVI, b2_con, b2_corr, b2_dis, b2_hom, b2_mean, b2_sm, b3_mean, b4_ent, b4_hom, b4_sm, b4_var, b5_mean, VH_con, VH_dis, VH_hom; | |
| s1p2to | Stepwise regression analysis | 6 | HH_mean, HV_con, HV_ent, HV_sm, HV_var, elevation; |
| Recursive feature elimination | 3 | HH_con, elevation, slope; | |
| Boruta | 3 | VV_var, elevation, slope; | |
| s1s2p2to | Stepwise regression analysis | 15 | NDVIre2, b2_corr, b3_ent, b3_var, b4_ent, b8_var, b11_var, b12_corr, b12_sm, VH_sm, HH_mean, HH_sm, HV_con, HV_var, slope; |
| Recursive feature elimination | 14 | b2, b4, b5, CI, b2_con, b2_corr, b2_dis, b2_hom, b4_ent, VH_con, VH_dis, VH_hom, elevation, slope; | |
| Boruta | 23 | b2, b3, b4, b5, ARVI, CI, NDVI, NDVIre1, RVI, TNDVI, b2_con, b2_corr, b2_dis, b2_hom, b4_ent, b4_hom, b4_sm, b4_var, b5_mean, b12_mean, VH_con, elevation, slope. |
| Data Scenario | Regression Method | Feature Selection Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SR | RFE | Boruta | ||||||||
| R2 | RMSE (m) | rRMSE (%) | R2 | RMSE (m) | rRMSE (%) | R2 | RMSE (m) | rRMSE (%) | ||
| s2 | k-NN | 0.43 | 2.9 | 33.53 | 0.40 | 3.0 | 34.56 | 0.48 | 2.8 | 32.11 |
| s2 | SVR | 0.33 | 3.1 | 36.27 | 0.31 | 3.2 | 37.10 | 0.28 | 3.2 | 37.71 |
| s2 | RF | 0.49 | 2.7 | 31.75 | 0.55 | 2.6 | 29.80 | 0.52 | 2.7 | 30.95 |
| s2 | GBDT | 0.49 | 2.7 | 31.66 | 0.53 | 2.6 | 30.49 | 0.52 | 2.6 | 30.73 |
| s2 | XgBoost | 0.55 | 2.6 | 29.91 | 0.56 | 2.5 | 29.66 | 0.57 | 2.5 | 29.10 |
| s2 | CatBoost | 0.45 | 2.8 | 32.98 | 0.50 | 2.7 | 31.41 | 0.49 | 2.7 | 31.66 |
| s1s2p2 | k-NN | 0.08 | 3.7 | 42.58 | 0.35 | 3.1 | 35.96 | 0.38 | 3.0 | 35.02 |
| s1s2p2 | SVR | 0.33 | 3.2 | 37.72 | 0.27 | 3.3 | 37.94 | 0.39 | 3.0 | 34.82 |
| s1s2p2 | RF | 0.48 | 2.8 | 32.17 | 0.46 | 2.8 | 32.83 | 0.47 | 2.8 | 32.36 |
| s1s2p2 | GBDT | 0.52 | 2.7 | 30.90 | 0.44 | 2.9 | 33.34 | 0.42 | 2.9 | 33.80 |
| s1s2p2 | XgBoost | 0.46 | 2.8 | 32.75 | 0.46 | 2.8 | 32.80 | 0.47 | 2.8 | 32.52 |
| s1s2p2 | CatBoost | 0.48 | 2.8 | 32.14 | 0.44 | 2.9 | 33.42 | 0.46 | 2.8 | 32.65 |
| s2to | k-NN | 0.34 | 3.1 | 36.24 | 0.34 | 3.1 | 36.18 | 0.35 | 3.1 | 35.75 |
| s2to | SVR | 0.33 | 3.1 | 36.51 | 0.50 | 2.7 | 31.51 | 0.32 | 3.2 | 36.77 |
| s2to | RF | 0.51 | 2.7 | 31.02 | 0.57 | 2.5 | 29.18 | 0.56 | 2.5 | 29.44 |
| s2to | GBDT | 0.53 | 2.6 | 30.54 | 0.60 | 2.4 | 27.98 | 0.58 | 2.5 | 28.73 |
| s2to | XgBoost | 0.53 | 2.6 | 30.47 | 0.63 | 2.3 | 27.25 | 0.59 | 2.4 | 28.45 |
| s2to | CatBoost | 0.53 | 2.6 | 30.45 | 0.59 | 2.5 | 28.58 | 0.56 | 2.5 | 29.55 |
| s1p2to | k-NN | 0.31 | 3.2 | 36.98 | 0.21 | 3.4 | 39.61 | 0.27 | 3.3 | 38.10 |
| s1p2to | SVR | 0.09 | 3.6 | 42.35 | 0.13 | 3.6 | 41.47 | 0.13 | 3.6 | 41.63 |
| s1p2to | RF | 0.10 | 3.6 | 42.34 | 0.28 | 3.2 | 37.89 | 0.15 | 3.5 | 41.08 |
| s1p2to | GBDT | 0.18 | 3.5 | 40.22 | 0.33 | 3.1 | 36.35 | 0.19 | 3.4 | 40.03 |
| s1p2to | XgBoost | 0.23 | 3.3 | 39.05 | 0.37 | 3.0 | 35.38 | 0.24 | 3.3 | 38.92 |
| s1p2to | CatBoost | 0.24 | 3.3 | 38.88 | 0.31 | 3.2 | 36.91 | 0.19 | 3.4 | 40.00 |
| s1s2p2to | k-NN | 0.17 | 3.5 | 40.59 | 0.37 | 3.0 | 35.32 | 0.44 | 2.9 | 33.31 |
| s1s2p2to | SVR | 0.12 | 3.6 | 41.80 | 0.43 | 2.9 | 33.51 | 0.53 | 2.6 | 30.44 |
| s1s2p2to | RF | 0.36 | 3.1 | 35.62 | 0.50 | 2.7 | 31.49 | 0.55 | 2.6 | 29.75 |
| s1s2p2to | GBDT | 0.42 | 2.9 | 33.77 | 0.59 | 2.4 | 28.44 | 0.62 | 2.4 | 27.56 |
| s1s2p2to | XgBoost | 0.40 | 3.0 | 34.49 | 0.60 | 2.4 | 28.18 | 0.67 | 2.2 | 25.57 |
| s1s2p2to | CatBoost | 0.35 | 3.1 | 35.87 | 0.56 | 2.5 | 29.66 | 0.55 | 2.6 | 29.98 |
| Product | Nominal Year | Data Source | Nominal Resolution | Algorithm | Forest Height (m) | |||
|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean. | Std. | |||||
| Map of Potapov | 2019 | Landsat, GEDI, SRTM | 30 m | Regression tree | 3.00 | 29.00 | 9.15 | 3.62 |
| Map of this study | 2016 | Sentinel-1, Sentinel-2, SRTM | 25 m | XGBoost | 2.97 | 17.91 | 7.64 | 1.70 |
| Method | RMSE | rRMSE | Average Running Time (s) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean. | Std. | Min. | Max. | Mean. | Std. | Min. | Max. | Mean. | Std. | ||
| SR | 0.08 | 0.55 | 0.36 | 0.15 | 2.6 | 3.7 | 3.0 | 0.4 | 29.91 | 42.58 | 35.38 | 4.09 | 3.68 |
| RFE | 0.13 | 0.63 | 0.44 | 0.13 | 2.2 | 3.6 | 2.8 | 0.3 | 25.57 | 41.46 | 33.13 | 3.81 | 3343.77 |
| Boruta | 0.13 | 0.67 | 0.43 | 0.15 | 2.3 | 3.6 | 2.9 | 0.4 | 27.25 | 41.63 | 33.28 | 4.36 | 17.75 |
| Factor | Df | R2 | RMSE | rRMSE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SumSq | η2 | Pr (>F) | SumSq | η2 | Pr (>F) | SumSq | η2 | Pr (>F) | ||
| Data source | 4 | 0.90 | 0.47 | <2.2 × 10−16 *** | 5.30 | 0.46 | 2.571 × 10−07 *** | 720.87 | 0.46 | 2.571 × 10−07 *** |
| Feature selection method | 2 | 0.11 | 0.06 | 2.147 × 10−06 *** | 0.70 | 0.06 | <2.2 × 10−16 *** | 95.02 | 0.06 | <2.2 × 10−16 *** |
| Regression algorithm | 5 | 0.45 | 0.24 | 1.345 × 10−12 *** | 2.86 | 0.25 | 4.992 × 10−14 *** | 389.54 | 0.25 | 4.992 × 10−14 *** |
| Data source Feature selection method | 8 | 0.16 | 0.08 | 1.412 × 10−05 *** | 1.00 | 0.09 | 1.860 × 10−06 *** | 136.25 | 0.09 | 1.860 × 10−06 *** |
| Data source Regression algorithm | 20 | 0.14 | 0.07 | 0.01107 * | 0.85 | 0.07 | 0.003017 ** | 115.79 | 0.07 | 0.003017 ** |
| Feature selection method Regression algorithm | 10 | 0.02 | 0.01 | 0.84356 | 0.09 | 0.01 | 0.826854 | 11.96 | 0.01 | 0.826854 |
| Residuals | 40 | 0.12 | 0.62 | 83.68 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Chen, M.; Yang, F.; Yang, C.; Yang, P.; Gao, Y.; Shang, Y.; Peng, D. Forest Height Mapping Using Feature Selection and Machine Learning by Integrating Multi-Source Satellite Data in Baoding City, North China. Remote Sens. 2022, 14, 4434. https://doi.org/10.3390/rs14184434
Zhang N, Chen M, Yang F, Yang C, Yang P, Gao Y, Shang Y, Peng D. Forest Height Mapping Using Feature Selection and Machine Learning by Integrating Multi-Source Satellite Data in Baoding City, North China. Remote Sensing. 2022; 14(18):4434. https://doi.org/10.3390/rs14184434
Chicago/Turabian StyleZhang, Nan, Mingjie Chen, Fan Yang, Cancan Yang, Penghui Yang, Yushan Gao, Yue Shang, and Daoli Peng. 2022. "Forest Height Mapping Using Feature Selection and Machine Learning by Integrating Multi-Source Satellite Data in Baoding City, North China" Remote Sensing 14, no. 18: 4434. https://doi.org/10.3390/rs14184434
APA StyleZhang, N., Chen, M., Yang, F., Yang, C., Yang, P., Gao, Y., Shang, Y., & Peng, D. (2022). Forest Height Mapping Using Feature Selection and Machine Learning by Integrating Multi-Source Satellite Data in Baoding City, North China. Remote Sensing, 14(18), 4434. https://doi.org/10.3390/rs14184434








