Abstract
In order to effectively improve the dim and small target detection ability of photoelectric detection system to solve the high false rate issue under complex clouds scene in background modeling, a novelty Hessian matrix and F-norm collaborative filtering is proposed in this paper. Considering the influence of edge noise, we propose an improved Hessian matrix background modeling (IHMM) algorithm, where a local saliency function for adaptive representation of the local gradient difference between the target and background region is constructed to suppress the background and preserve the target. Because the target energy is still weak after the background modeling, a new local multi-scale gradient maximum (LMGM) energy-enhancement model is constructed to enhance the target signal, and with the help of LMGM, the target’s energy significant growth and the target’s recognition are clearer. Thus, based on the above preprocessing, using the motion correlation of the target between frames, this paper proposes an innovative collaborative filtering model combining F-norm and Pasteur coefficient (FNPC) to obtain the real target in sequence images. In this paper, we selected six scenes of the target size of 2 × 2 to 3 × 3 and with complex clouds and ground edge contour to finish experimental verification. By comparing with 10 algorithms, the background modeling indicators SSIM, SNR, and IC of the IHMM model are greater than 0.9999, 47.4750 dB, and 12.1008 dB, respectively. In addition, the target energy-enhancement effect of LMGM model reaches 17.9850 dB in six scenes, and when the false alarm rate is 0.01%, the detection rate of the FNPC model reaches 100% in all scenes. It shows that the algorithm proposed in this paper has excellent performance in dim and small target detection.
1. Introduction
Dim and small target detection is commonly used in space monitoring, infrared early warning, and space debris detection, and is a topic of broad concern [1]. According to the definition of international society of optical engineering, the local signal-to-noise ratio of weak and small targets is less than 5 dB, and the target size in the image is 2 × 2 to 9 × 9, which occupies an image size of 256 × 0.12% of 256 [2]. However, due to the long imaging distance of small targets, the targets are often affected by dense clouds and system noise, all resulting in ineffective target energy, lack of shape and texture, and extremely low imaging contrast, seriously affecting the detection and extraction of targets by the imaging system [3]. Hence, it is very important to carry out research on the signal detection of targets. For example, Liu et al. proposed the one-step symmetric GLRT for the subspace signals processing method [4], and designed the generalized likelihood ratio using the generalized symmetric structure to verify and compare the unknown matrix to realize the detection of target signals. On the basis of PCA principal component model analysis, Hua et al. developed a new learning discriminant matrix information geometry (MIG) detector in unsupervised scenes [5], and applied it to signal detection in a non-uniform environment, laying a foundation for the detection of weak and small targets. In the process of actual detection research, how to highlight the target signal while suppressing the image background information to the greatest extent has become the focus of dim signal detection research. With the passage of time, the detection of small targets in long-distance space is mainly divided into three categories: detection based on the traditional spatiotemporal filtering model, detection based on the low-rank sparse recovery theory, and the detection model based on neural network deep learning. All of them use different information to model the background of the image to obtain the difference image and the background image.
Among the traditional spatiotemporal filtering models, the morphological filtering model [6,7], spatial gradient model [8,9], and anisotropic filtering model [10,11] have achieved acceptable detection results. In morphological filtering, Wang et al. improved top hat filtering according to the direction of target motion and proposed non-concentric multi-directional ring structural elements to suppress the background of the image [12]. The model distinguishes the background from the target according to the differences in the structural elements in each direction, and better suppresses the undulating background in the image. However, traditional spatiotemporal information processing will destroy the inherent low-rank characteristics of the image, resulting in a high false alarm rate of model detection. Therefore, the combination of spatiotemporal domain and low-rank characteristics for background prediction is proposed. For example, the low-rank tensor dim small target detection model based on top hat regularization [13], projected by Hu et al., which uses the sensitivity of top hat structural elements to image features to suppress the image background, improves the operation efficiency of the model and solves the defects of the traditional model and low-rank theory in detection to a certain extent. Due to the close relationship between morphological filtering and filtering structural elements, the filtering organizational elements in different scenes are quite different, resulting in the low adaptability of target detection in different scenes. Nevertheless, morphological filtering is closely related to filter structural elements, and the filtering structural elements in different scenes are quite disparate, resulting in the low adaptability of target detection in different scenes. Therefore, during the development of target detection, research on local information to complete target detection has achieved significant results. For example, Bhattacharya et al. proposed an adaptive general four-component scattering power decomposition method (AG4U) [14] to complete the monitoring and extraction of ground information in San Francisco and California. In this method, the image is analyzed by two 3 × 3 complex special unitary transformation matrices to select the corresponding component decomposition mode to adaptively complete the information extraction. Muhuri et al. analyzed and described the snow cover distribution in the Himalayas of India by using the polarization fraction variation with the temporal RADARSAT-2 C-band method [15]. This method also used the constructed 3 × 3 matrix for local analysis to obtain the detailed information of the image, and achieved excellent verification results. Touzi et al. used the RCM (Radarsat Constellation Mission) model [16] to detect ships on the sea in long-distance satellite imaging, and analyzed the whole image through a 5 × 5 matrix sliding window to extract weak signals of ships and enhance their contrast in the image. This method has important practical application contribution to actual ship detection and classification. All of the above methods show that the method of target detection based on local information analysis is progressive, and can be applied to the detection of small and weak targets, which provides a good theoretical support for the development of infrared small and weak target detection. In the detection of dim and small targets by analyzing the local information of the matrix, the gradient analysis of local region pixels is used to suppress the background and then enhance the target energy, which can better solve the detection problem caused by the lack of target texture information [17]. For example, Chen et al. proposed the dim small target detection method (LCM) based on local contrast [1], which selects candidate targets by analyzing the local contrast difference between the target region and the surrounding neighborhood. Then, the DK model is combined with the characteristics of multi-frame correlation to extract the real target, with fairly sound effects. On this basis, researchers have proposed many target detection models for local information processing, such as the RLCM model [18] proposed by Han et al., the HB-MLCM model [19] proposed by Shi et al., and the MLCM-LEF model [20] proposed by Xia et al., all of which analyze the local information of the image to realize background suppression and then enhance the energy of the target. Such algorithms greatly improve the contrast of the image and ensure that the target can be satisfactorily detected. Nonetheless, the model based on regional gradient analysis is used for target detection in complex scenes, where strong noise is retained and the target features are not obvious. Lin et al. proposed an improved anisotropic filter for target detection [10]. The model analyzes the pixel gradient by constructing a new diffusion function so as to meet the purpose of background suppression and deliver better results in scenes with a flat background. However, the gradient operation of a single pixel makes the model retain more edge contours in the face of complex scenes with cloud layers, and the false alarm detection rate of the algorithm is high.
In the low-rank sparse theory, the method of target detection combined with sparse dictionary has also attained great background modeling performance. These methods mainly use the low-rank characteristics of the background and the sparse characteristics of the target to inverse decompose the image and finish background suppression. The RPCA model [21,22], PSTNN model [23], MPCM model [24], FKRW model [25], LRT-THR model [13], ASTTV model [26], etc., have remarkable expression in single-frame target detection. Zhang et al. combined a new non-convex low-rank constraint function with the IPT model [27] to construct a tensor kernel norm to form a PSTNN model, which can suppress the background while retaining the signal of the target, enhance the robustness of the model, and meet the requirements of image background prediction. The IPI detection model [28] proposed by Gao et al. also obtained outstanding performance, and can better reverse the background information of an image so that the energy of the target can be better preserved, while in the face of complex cloud scenes with multiple changing edge contours, the low-rank recovery effect is unsatisfactory, and the detection result underperforms.
Dim and small target detection of deep learning mainly uses the pretraining mode to complete the target detection; examples include the RISTD network model [29], SSD network model [30,31], GAN model [32], CNN network model [33], RCNN model [34], Fast RCNN model [35,36], etc. The SSD-ST model proposed by Ding et al. [30] constructs the detection layer and information layer with different resolutions through the pyramid structure of SSD multi-scale features. In the training process in this method, after classifying the information of the image, the energy of the low-resolution layer is suppressed, and part of the energy of the high-resolution layer is enhanced to accomplish the background modeling processing and realize the target detection. Nevertheless, because neural network training requires a large number of training samples to consolidate the detection rate of the network, it takes a long time to apply it in different scenes, and with the passage of time, the dynamic background in the target scene leads to the decline in the adaptability of training parameters, and the effect of target detection is unexpected.
In sum, the above algorithms have certain limitations in the detection of dim and small targets, and their detection results are poor in the face of complex and cloudy dynamic scenes. Consequently, Refs. [37,38] used the Hessian matrix to highlight the local difference information between the target and the background, and the effect is ideal. In this paper, the Hessian matrix is improved to realize the background modeling of the image. The research shows that even after the background modeling, the target signal is still faint, which is not conducive to target detection. Therefore, on this basis, we researched target signal enhancement. Relevant researchers have carried out corresponding research on target energy-enhancement methods, such as high-order correlation [39,40], the multi-scale approximation enhancement method [41], etc. These enhancement algorithms provide reference ideas for the enhancement of dim and small signals. To further increase the discrimination between the target and a small part of noise, researchers have proposed multi-frame detection methods using the multi-frame motion correlation information, such as Zhao et al., who proposed mobile pipeline filtering [42], and Liu et al., who proposed mobile weighted pipeline filtering [43]. The collaborative filtering algorithm based on the Pasteur correlation coefficient and the Jaccard coefficient proposed by Yang et al. [44] and the collaborative filtering algorithm based on the improved similarity of the Pasteur correlation coefficient proposed by Wu et al. [45] have achieved ideal results. However, in the face of complex motion scenes, these algorithms will cause detection loss when the target motion speed is faster and exceeds the detection pipe diameter or when there is little difference between the target and the background. Accordingly, we use the motion correlation and similarity of the target between frames to propose a collaborative filtering detection model combining F-norm and Pasteur correlation to complete the multi-frame detection of the target.
In view of the shortcomings of the above related algorithms, the corresponding work and contributions of this paper in the research of dim and small target detection can be summarized as follows:
(1) An improved Hessian matrix mode (IHMM) algorithm is proposed. Here, a local saliency function is constructed to adaptively describe the local gradient difference, and then the eigenvalue of the Hessian matrix is solved through the local gradient difference characteristic, so as to highlight the gradient difference between the background and the target to achieve background suppression. After experimental verification, the structural similarity SSIM, signal-to-noise ratio (SNR), and image contrast gain IC of the proposed IHMM model after background suppression are 0.9999, 47.4750 dB, and 12.1008 dB, on average, in six scenes. (2) An energy-enhancement method for target detection based on local multi-scale gradient maximum (LMGM) is proposed to enhance the energy of the difference image after background modeling, and the average value of the enhanced signal-to-noise ratio of the first frame of six scenes is 17.9850 dB. (3) A collaborative filtering detection model combining F-norm and Pasteur correlation (FNPC) is proposed by using the interframe correlation characteristics of sequence images to realize sequence target detection, and when the false alarm rate is 0.01%, the detection rate in six scenarios is 100%.
2. Materials and Methods
In the imaging mechanism of remote detection of dim and small targets, there is low compatibility between the target and the background, resulting in a large gray pixel difference between the target and the neighborhood background, which provides support for the background modeling algorithm proposed in this paper. This section mainly introduces the improved Hessian matrix background modeling algorithm and the related principles of the gradient significance function described by local information. The detailed principles are as follows.
2.1. Improve the Background Modeling Principle of Hessian Matrix
Taking advantage of the large gray difference between the target and the background, the gradient significance function model is mainly used to adaptively calculate and enlarge the local gradient difference information to highlight the target. First, a 3 × 3 local region block is constructed with a single pixel as the central pixel in the figure, and the gradient of the central pixel of the region block is compared with its surrounding pixels to carry out local gradient adaptive calculation and analysis to highlight the target. The operation is as follows (Figure 1):
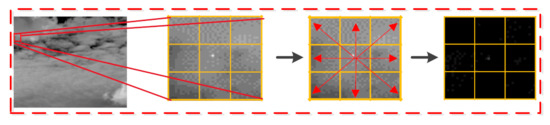
Figure 1.
Details of the constructed local gradient model.
As shown in the figure, in the constructed 3 × 3 local area block, the gradient value between pixels in the background area is not significantly different, but the gray pixel difference between the target and the background is large. Therefore, according to this characteristic, the significance analysis effect shown in the figure on the right is obtained after the gradient study of local pixels. The corresponding model construction is as follows:
where D is the image processed by the local gradient saliency function, Z is a defining constant, and M and X are the adaptive parameters of the local gradient saliency function in gradient analysis, which obtain the corresponding values through the local gradient analysis judgment model; the specific model is as follows:
where is the coordinate position of the current pixel, r is the selected radius of the local area block, and the value in the text is 1. F is the original input image, is the selected local area block, is the gradient difference between the central pixel and the adjacent pixel in the local area, is the coordinate position of the pixel in the local area , and is the central pixel value of the local area . Considering that the gradient operation in the local region includes intermediate pixels, when , the control coefficient X is equal to the minimum gradient value, and M is a defining constant. When , the control coefficient X is equal to the current local gradient, and M takes the minimum value of all gradients.
When the above model is applied to image background modeling, the model not only improves the significance of the target, but also improves the significance of more noise, and the recognition degree of the target is low. Therefore, similar to the method of extracting feature points by combining Gaussian filtering and Hessian matrix, after the local gradient saliency function suppresses most of the noise and edge contour, we use the determinant value of the Hessian matrix to better reflect the characteristics of the local gradient structure information of the image, and apply the Hessian matrix to background modeling to suppress the background of the image further. Firstly, the Hessian matrix filter template d = ([−1 0 1])⁄2, = [1 −2 1] is defined in combination with the selected 3 × 3 region block, and the corresponding Hessian matrix is defined as follows [38]:
where D is the image processed by Formula (1); is the coordinate position of the Hessian matrix pixel in the image; and ) are the second-order derivatives of image pixels in the lower , and directions, respectively. According to the definition of image pixels, we calculate the first-order derivatives [46]. The second-order derivatives of pixels in each direction are as follows:
In practical application, in order to improve the operation efficiency, the convolution operation form is adopted when calculating the second derivative of image pixel. Therefore, after Hessian matrix is combined with filter templates D and D2, Formula (3) can be simplified as
In the formula, , respectively, represent the results of convolution operation with the filter template in the , and directions in the processed image D, represents convolution operation in the x direction, represents convolution operation in the y direction, and represents convolution operation in the direction. According to the calculation principle of Hessian matrix, the operation formula for completing image background modeling is as follows:
where represents an empty matrix of the same size as the input image f, which is used to output the final difference result.
According to the above related principles, the overall process of background suppression of the improved Hessian matrix background modeling algorithm proposed in this paper is as follows:
As shown in the figure, after passing through the local gradient significance function, there is still more noise interference in the image, and the target recognition degree is not high. However, after passing through the Hessian matrix, the target in the figure is highly significant, which can clearly identify the location of the target and achieve the purpose of background suppression and target preservation.
2.2. Energy-Enhancement Principle Based on Local Multi-Scale Gradient Maxima
In target detection, the energy intensity of the target after background modeling has a direct impact on target detection. Enhancing the target energy is a common processing method in target detection, such as in the high-order correlation model [39,40], multi-directional gradient [47], and multi-scale gradient [48], which are all models to enhance the energy, and that have achieved good suitable results. After the improved Hessian matrix background suppression shown in Figure 2, the target is significantly highlighted, but the signal energy is weak, which is not conducive to target detection and extraction. In this paper, we consider that the multi-scale gradient enhancement algorithm can effectively distinguish the difference between the target point and the noise point, but it is found that while the model enhances the energy of the difference map, the energy of some noise points is also increased, resulting in image confusion. Therefore, in this paper we improve the multi-scale gradient model, combine the multi-scale gradient model with the local maximum segmentation in the literature [49], and construct the maximum energy-enhancement detection model of the local multi-scale gradient, which greatly improves the contrast of the target in the image. The specific multi-scale gradient model is as follows [50]:
where P is the image after the background modeling is completed by the improved Hessian matrix, and represent the multi-scale gradient values of the current pixel in the upper, lower, left, and right directions, respectively. represents the center pixel of the image, and l and represent the radius of the region that controls the multi-scale gradient enhancement energy, which is a predetermined constant. Basis on multi-scale gradient, the overall pseudocode of the enhancement model is as follows:

Figure 2.
Flow chart of Hessian matrix background suppression model with local gradient significance.
According to the K in Formula (9) and the result of Table 1, K enhanced the regions’ result . Intending to magnify the target in the multi-scale direction, the K locals’ results were used to make the operation produce the preliminary enhancement result , and then, combining with difference diagram P, to produce the final enhanced result . The specific formula is as follows:

Table 1.
Pseudo code for target signal enhancement.
2.3. Detection Model of F-Norm and Pasteur Coefficient Collaborative Filtering
In the remote photoelectric imaging weak and small target detection system, it is of practical significance to realize the multi-frame detection of sequence targets. In the sequence of multi-frame images, the target motion characteristics are not obvious, and there is a notable correlation between the front and back frames. Considering the uneven energy distribution during target imaging, the phenomenon of missing frames in target detection occurs frequently when multiple frames are detected. Hence, we use the characteristics of F-norm, which is region computing, to detect the highlighted candidate regions and fuse the energy in the regions to improve the identification of real targets. Then, we combine the F-norm with the Pasteur correlation coefficient to determine the real target through the similarity correlation between frames, and we complete the target detection of multiple frames. The detailed model construction is as follows:
(1) To highlight the gradient difference between the target neighborhood and the background neighborhood, we construct a local region filling model of F-norm to highlight the candidate target and calculate the F-norm of the upper, lower, left, and right regions of the pixel. The specific definitions are as follows:
where represent the F norm of the center, upper, lower, left, and right blocks when L is 3; represents the current pixel coordinates; represents the variables that control the pixel coordinate position in the region; and k represents the moving steps of the central pixel up, down, left, and right, and takes a constant. is the image after the above enhanced target energy. When the F norm of the middle region block is the maximum, we fill the region with the gray pixel mean value and assign a value of 0 to the surrounding neighborhood block. The specific F-norm candidate target enhancement model is as follows:
where S represents the F-norm set of the neighborhood block of the central pixel, represents the target after energy enhancement, k is defined as above, and represents the image that has completed the filling process; if the F-norm of the middle region block reaches the maximum, this indicates that the region block contains candidate targets after energy enhancement, and all pixels in the region block are assigned the value of the region block pixel mean processing. On the contrary, it indicates that there is no candidate target after energy enhancement in the selected block, and the selected block is assigned a value of 0.
(2) On the basis of F-norm highlighting, we use the motion characteristics of the target between frames to construct the distance constraint, and Pasteur similarity constraint collaborative filtering model of the target motion to realize the multi-frame detection of the target. The specific model is as follows:
where dis is the distance between the real target at time t and the candidate target at time , is the image whose real target coordinates are known to be at time t, is the image whose candidate target coordinates are , and when dis is less than the set threshold , the coordinates of the candidate targets are output . u and v represent the local area in the two frames at time t and time t + 1, respectively; and are the mean values of the two regions; represents the Pasteur similarity of two local regions; and and represent the pixel values in the two local areas, respectively. The larger the Pasteur correlation of the two frames, the better the correlation of the image.
(3) Combined with the above distance constraint and similarity constraint model, we construct a multi-frame correlation target discrimination model to finally determine the real target location and realize the multi-frame detection of the target. When the constraint distance dis meets the constraint condition and reaches , the candidate target coordinates in time t + 1 are updated to the real target coordinates , and we assign the energy of the target neighborhood to the maximum gray value in the figure, which is specifically defined as follows:
where represents the real coordinates of the target at the finally determined time, and indicates that the target detection has been completed at time .
2.4. Summary of the Overall Process of the Algorithm
According to the construction of the above model, the overall process of weak and small target detection in this paper can be summarized as follows Figure 3:

Figure 3.
Overall flow chart of detection model.
As shown in the Figure 3, we first use the improved Hessian matrix to model the background of the image, restore the image background, and output the image difference image. Then, in order to improve the target signal, an energy-enhancement model of local multi-scale gradient maximum is constructed to enhance the signal of the difference image. Finally, using the interframe correlation characteristics of the target, a detection model of F-norm and Pasteur coefficient collaborative filtering is constructed to realize the detection of sequence targets. The overall algorithm pseudocode is shown in the following table (Table 2):

Table 2.
Pseudocode of the overall flow of the algorithm.
2.5. Technical Evaluation Index
To reflect the effect of this algorithm on background suppression, target energy signal retention, and target signal enhancement, we cite structural similarity , image signal-to-noise ratio , and contrast gain as the evaluation indicators of this model. The specific evaluation model is as follows [51,52]:
where and are the mean and standard deviation of the input image, respectively; is the covariance between the input image and the background image; and and are constants. and represent the mean value of the target area and the background area, respectively; is the standard deviation of the background area. In Formula (15), , and , represent the mean value of different pixel matrices divided by the input image and the output image with the target as the center, respectively; indicates the location of the target; l and refer to different division radii, with values of 1 and 4, respectively, and refer to the contrast gain ratio of the input image and the output image at the target; and refers to the ratio of the signal gain ratio of the input image and the output image, which is an important indicator of the signal enhancement or attenuation of the target before and after the algorithm.
2.6. Experimental Setup
In order to reflect the applicability of the algorithm in the scene, we improve the detection rate of the algorithm in complex scenes and reduce the detection false alarm rate. According to the definition of dim and small targets, this paper selects six scenes to participate in the algorithm test. The target size is between 2 × 2 and 3 × 3, the target signal-to-noise is less than 5 dB, and there is more edge contour interference. Scenario A is the outfield data taken by our team, and scenario B is the dataset in Ref. [53] (A dataset for infrared image dim-small aircraft target detection and tracking under ground/air background (scidb.cn)) (accessed on 28 October 2019). Scenarios C and D are the publicly available video data on Git-Hub (daxj-uanxiong/infrared-small-target-images: infrared small target images (github.com)) (accessed on 3 Feburary 2020). Scenarios E and F are datasets from Ref. [54] (https://www.scidb.cn/en/detail?dataSetId=808025946870251520) (accessed on 8 Feburary 2022). Details of the relevant scenes and the original background and 3D information are as follows:
As shown in the figure, the six scenes selected have low signal-to-noise ratio and complex backgrounds, which can better test the model.
3. Results
With the Table 3 and the Figure 4, this section describes the relevant experiments and experimental results analysis on the model in terms of image background suppression, energy enhancement, and sequence target detection. First, the algorithm proposed in this paper is used for background modeling in six sequence scenes. The top hat filtering model [55], anisotropic model (ANI) [56], PSTNN model [23], ASTTV model [26], NTFRA model [57], GST model [58], NRAM model [59], HB-MLCM model [37], and the ADMD model [60] and UCTransNet model [61] are compared and analyzed with the proposed model with the step in Figure 3. Then, the proposed local gradient multi-scale maximum energy-enhancement model is used to enhance the target signal, and it is used as the final background modeling effect. Finally, on the basis of comparing the algorithms, this algorithm is compared with other detection models for sequential multi-frame detection to complete the target detection.

Table 3.
Sequence scene-related information.
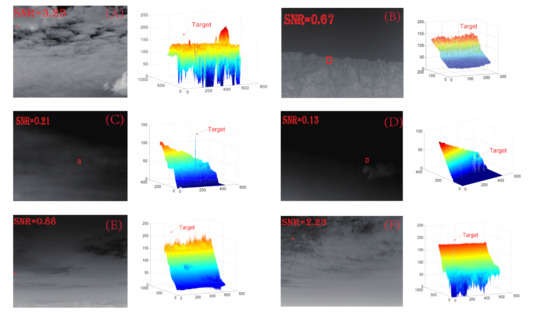
Figure 4.
Sequence scene original, original 3D.
3.1. Comparison and Analysis of IHMM Model Background Modeling Results
The background suppression effects in the six scenes selected by each detection model and the detection model in this paper are shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. From Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, it can be seen that the top hat filter, which relies on filter structure elements for background suppression, has poor background suppression in the six scenes, and there is more edge noise in the corresponding 3D images, indicating that the fixed filter structure elements of the model impose a greater limitation on the algorithm in the face of scenes with more complex backgrounds. In the anisotropic filtering results in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the background suppression in scenes A, B, E, and F with more clouds and more complex backgrounds is not satisfactory, and the interference information is clearly characterized in the difference images. This indicates that the background suppression using gradient calculation of the image with individual image elements is less effective in suppressing the background with strong contours. The PSTNN model, ASTTV model, GST model, NTFRA model, NRAM model, HBMLCM model, and ADMD model in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 all utilize the low-rank theory background modeling; e.g., the PSTNN model, which utilizes the combination of local tensor and weight parametrization, can effectively preserve the target signal while performing background suppression. The model utilizes the singularity property of the target in the image to preserve the pixel points with a relatively large weight share, which is effective, as shown in the detection effect in scenes C and D. However, in the face of scenes with long edge contours, the detection model still retains some contour information, such as in the detection of scenes A, B, E, and F, all of which have some false alarms present. The grinding edge detection method of non-convex tensor low-rank approximation with adaptively assigned weights is proposed in the ASTTV model, which can adaptively come up with different suppression strengths for different image element values and can better restore the background details while preserving the target, such as the background modeling effect in scenes A, B, C, and D, with less redundant information in the difference image. The GST detection model is an earlier tensor model applied in target detection, which combines two-dimensional Gaussian and second-order conjugate symmetric derivatives to form a background suppression model, and achieves good background suppression in scenes B, C, D, E, and F, indicating that the model has suitable robustness and adaptability. The background suppression results of the NTFRA model are represented in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, combining the LogTFNN model, the local tensor model, and the HTV model to propose the NTFRA model after improving the IPT model. From the above figure, it can be seen that the detection of the target is achieved in all scenes, but according to the scene of differential 3D images, the model also has a high false alarm and the background suppression is less satisfactory. Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show the background suppression results of the NRAM model, which incorporates one or two parameters proposing a non-convex, more convergent rank agent-weighted parametric background suppression model, which solves the problem of not accurately recovering the image background and target using only one parameter. Its detection results are better in all six scenes, and it maintains a low false alarm rate overall. In the HBMLCM detection model, firstly, the improved IHBF model is proposed to enhance the energy of the target based on the model of HBF. Then, the LCM model is improved, and the adaptable MLCM model is proposed to combine with IHBF before composing the HBMLCM model, which makes the target’s energy stronger when background suppression processing is performed. As can be seen in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the target energy detected by the HBMLCM model is generally stronger than that of the rest of the algorithm models, but the background suppression effect is poor in the face of scenes where the image contains more complex information, such as in the three scenes of A, B, and E, where more interference remains in the difference image. Based on the AAGD detection model, the detection model ADMD with absolute directional mean difference is proposed mainly to increase the saliency of the target, using the saliency of the target to construct a local inner and outer window discrimination mechanism of a single image element to carry out the energy enhancement of the target, solving the problem that AAGD cannot detect the target in the strong low-contrast edge. As shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the ADMD model can effectively enhance the target signal and perform target detection, but it is less effective in detection in scenes containing more contour clouds, such as scenes A, B, E, and F. The differential images of scenes A, B, E, and F also retain a high level of false alarms. The background modeling algorithm of the improved Hessian matrix is found to maintain a low false alarm rate while achieving target detection, which indicates that the model constructed in this paper has a better background suppression performance and achieves the purpose of background modeling. However, it is found that the target energy retained by the proposed model is weak through the corresponding differential 3D image, which is not conducive to the subsequent detection of the target, so the energy-enhancement model of local multi-scale gradient maximization is proposed to enhance the energy of the target and improve the contrast of the image by using the locally significant characteristics of the target; the specific experimental results are detailed in the following section.

Figure 5.
(a–j): Top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method’s difference diagram and three-dimensional diagram in scene A, respectively.

Figure 6.
(a–j): Top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method’s difference diagram and three-dimensional diagram in scene B, respectively.

Figure 7.
(a–j): Top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method’s difference diagram and three-dimensional diagram in scene C, respectively.

Figure 8.
(a–j): Top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method’s difference diagram and three-dimensional diagram in scene D, respectively.

Figure 9.
(a–j): Top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method’s difference diagram and three-dimensional diagram in scene E, respectively.

Figure 10.
(a–j): Top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method’s difference diagram and three-dimensional diagram in scene F, respectively.
3.2. Result Analysis of Target Detection Energy-Enhancement Model Based on Local Multi-Scale Gradient Maxima
To reflect the effect of the proposed model on target signal enhancement after background modeling, we analyze the signal-to-noise ratio before and after applying the proposed maximum energy-enhancement model of local multi-scale gradient. The specific experimental results are shown in the following figure:
As shown in the above Figure 11, after applying the maximum energy-enhancement model of local multi-scale gradient, the target signal and signal-to-noise ratio of each scene were significantly enhanced, indicating that the proposed improved Hessian matrix background suppression model can enhance the target signal after combining with the energy-enhancement model, and thus improve the robustness and adaptability of the model.
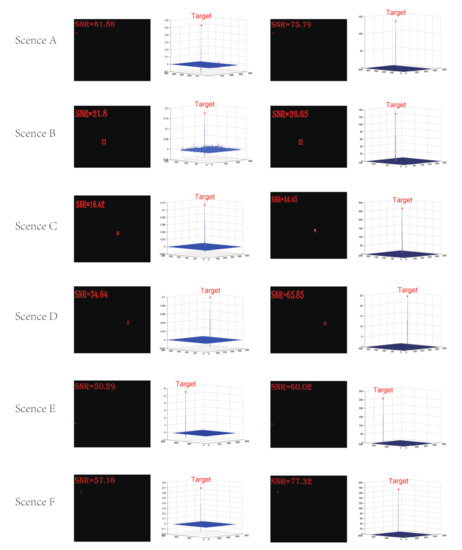
Figure 11.
Comparison diagram of energy-enhancement model of local multi-scale gradient maximum before and after energy enhancement for 6 scenes.
3.3. Analysis of Indicators of Model Background Suppression Results
After the background suppression comparison of the above algorithm models, in order to reflect the feasibility and innovation of the model constructed in this paper from the perspective of data, we employ structural similarity (SSIM), signal-to-noise ratio (SNR), and contrast gain (IC) to evaluate the algorithm results of the above models. The relevant parameters applied by the algorithms of the above models are shown in the following table (Table 4):

Table 4.
Relevant computational parameters for each model.
According to the calculation parameters of each model set in the Table 4, the background suppression effects of Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 are obtained after the background suppression of the selected six scenes. Then, according to the above evaluation indicators of SSIM, SNR, and IC, the background suppression detection model proposed in this paper is compared with the above models for the calculation of relevant indicators, and the feasibility of this algorithm is reflected through the comparison of actual data. The specific index data are shown in Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 below:

Table 5.
Calculation of indicators in scenario A of each model.

Table 6.
Calculation of indicators in scenario B of each model.

Table 7.
Calculation of indicators in scenario C of each model.

Table 8.
Calculation of indicators in scenario D of each model.

Table 9.
Calculation of indicators in scenario E of each model.

Table 10.
Calculation of indicators in scenario F of each model.
From Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 above, it can be observed that the algorithm proposed in this paper has adequate structural similarity, signal-to-noise ratio, and contrast gain in background modeling. It can restore the detailed information to the background, retain the signal of the target, increase the signal-to-noise ratio and contrast of the differential image, and lay a foundation for target detection. Considering that the target often changes with the dynamic scene in the process of moving, and that there are differences in the energy contained in the target at each time, it is still limited to directly carry out sequential multi-frame target detection on the difference map with low signal after background suppression on the original image. Therefore, based on the above model, using the interframe characteristics of the target in the sequence, we propose a detection model of F-norm and Pasteur correlation coefficient collaborative filtering to realize the multi-frame detection of the target and output the corresponding target motion trajectory. The specific experimental results are described in the next section.
3.4. Analysis of Multi-Frame Target Detection Results
In terms of the effect of the detection model proposed in this paper on the detection of sequential multi-frame targets, this section compares the results of the proposed detection model with those of the above models. The specific effects are as follows (Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17).

Figure 12.
Panels (a1–j1) shows the detection results of sequence A of top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method.

Figure 13.
Panels (a1–j1) shows the detection results of sequence B of top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method.

Figure 14.
Panels (a1–j1) shows the detection results of sequence C of top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method.
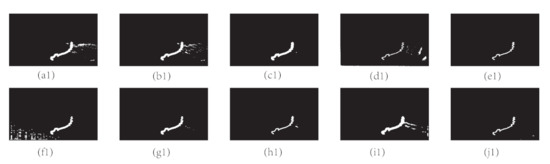
Figure 15.
Panels (a1–j1) shows the detection results of sequence D of top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method.

Figure 16.
Panels (a1–j1) shows the detection results of sequence E of top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method.

Figure 17.
Panels (a1–j1) shows the detection results of sequence F of top hat, ANI, PSTNN, ASTTV, GST, NTFRA, NRAM, HB-MLCM, ADMD, and the proposed method.
As shown in the figure above, the proposed algorithm can detect multiple frames of targets and output the trajectories of targets, and the content of false alarm targets in the trajectories is the least among the six scenes, indicating that the algorithm achieved suitable results in background modeling and can suppress the edge background contour in the figure. However, when the figure contains other interfering targets, the algorithm will also detect and output them, causing trouble with the detection of real targets. Therefore, based on the local characteristics of the target imaging in the image and the correlation between frames of the sequence image, we propose a detection model of F-norm and Barker coefficient collaborative filtering to detect and extract the multi-frame target and improve the target recognition. The specific test results are shown in the following figure:
As shown in the Figure 18, to avoid the influence of partial noise on the target detection of sequence multiple frames, the detection model of F-parametric and baroclinic coefficient co-filtering proposed in this paper using the interframe correlation property of sequence images can achieve the target detection and output the motion trajectory of the target in different sequences, which shows the feasibility and innovation of the algorithm.

Figure 18.
Detection results of the FNPC detection model.
3.5. Analysis of ROC Indicators
To further reflect the feasibility of the proposed model in weak target detection, the detection effect of the above model on targets in each scenario is evaluated by the detection rate and false alarm rate , and the specific evaluation model is defined as follows:
where and denote the detection rate and false alarm rate of the target, respectively, and the feasibility of the proposed model is demonstrated by plotting the detection rate and false alarm rate curves of each model, as shown in the following figure (Figure 9):
As shown in the above Figure 19, the detection model constructed in this paper achieves a detection rate of 100% in all the six selected sequence scenarios, and the false alarm rate does not exceed 0.01%. In scenario A, the NRAM model, ASTTV model, and the proposed detection model perform better, maintaining a 100% detection rate, while the false alarm rate does not exceed 0.01%, followed by the UCTransNet network which gradually rises and reaches detection rate of 98%. The last are the top hat filtering model, ANI model, and PSTNN detection model. In scenario B, because the scene belongs to half-space and half-ground attributes, the image contains more detailed information, which causes some trouble in the detection of each model, but it can be observed from the figure that the detection model proposed in this paper can maintain a low false alarm rate while the detection rate is 100%, which indicates that the model has certain scene adaptability and can achieve the purpose of target detection. In this scene, the ADMD model, ANI model, and GST model have better effects, and the detection rate reaches 100%, followed by the UCTransNet network detection model which reaches a detection rate of 97%. Meanwhile, the NRAM model has a poorer detection effect, and the detection rate is only 11% under the same segmentation threshold. Scenarios C and D have smoother backgrounds and obvious target features, and the target detection effect is better for more models, but the ASTTV model in scenario C has a poor effect, and the detection rate Pd is only 81%; similarly, the NTFRA model in scenario D has a poor effect, and the detection rate is only 83%. The UCTransNet model reaches detection rate 99% and 98% in scenes C and D, respectively. In scenario E, the detection rate of the proposed model constructed is maintained at 100% under the same conditions and the false alarm rate Pf is 0%, followed by the UCTransNet model, ASTTV model, GST model, and top hat filtering, which all achieve a 100% detection rate. In scenario F, the detection effect is obviously stratified, the detection effects of the ADMD model, ANI model, and NTFRA model are poor, and the detection rate of other models is better, which indicates that the three models cannot achieve the detection of the target under this limited threshold condition. In summary, our proposed detection model can achieve the detection of the target in six different backgrounds and has merits compared with other advanced detection models, reflecting the feasibility, innovation, and adaptability of the model.

Figure 19.
Schematic of ROC curves for 10 model detection models in 6 sequence scenarios.
3.6. Comparison of Computational Model Complexity
To sum up, the method proposed in this paper achieved certain results in the detection of infrared weak and small targets. In order to fit the actual application, this section compares the background modeling complexity of the above comparison algorithm and the algorithm proposed in this paper, and reflects the operation complexity of each operation model in the background modeling through the background modeling operation time of different scenes. Specific data are shown in the following table:
As shown in Table 11, the background modeling algorithm of the improved Hessian matrix proposed in this paper has different operation time in different scenarios. Among them, the GST model, PSTNN model, ANI model, top hat filter model, HBMLCM filter model, and ADMD filter model have less operation time. The ASTTV model, NTFRA model, and NRAM model have a long operation time. The operation time of the algorithm proposed in this paper is moderate, and the average operation time in all the selected scenes is 4.1890 frames per second. This shows that the background modeling model proposed in this paper needs to be further optimized to meet the requirements of weak small target detection in the field.

Table 11.
Calculation of background modeling complexity in different scenarios of each model (unit: frames/second).
4. Discussion
From the comparison and verification of the above experiments, it can be seen that the existing weak and small target detection methods cannot suppress the complex background when modeling the background in the scene where the image signal-to-noise ratio is low, the edge contour is prominent, and part of the ground information is covered, resulting in target detection failure and high false alarm rate. For example, top hat filtering, using fixed filter structure elements for background modeling, brings great limitations to the algorithm. The background suppression effect of the six scenes is poor, and there are many edge noise points in the corresponding three-dimensional image. Anisotropic filtering (ANI) often appears in the detection of weak and small targets. This model uses the characteristic that the energy of the target is diffused from point to point, and often combines with the kernel diffusion function to conduct background modeling. However, due to the fixed gradient analysis property of the kernel diffusion function, the anisotropic filtering model often retains more edge contours and noise points in the background modeling of complex scenes, and the target discrimination is low. The GST detection model is a tensor model applied in earliertarget detection. The overall operation speed of the model is fast, and the background suppression effect is excellent for scenes with stable background and few contours. However, since the model combines two-dimensional Gauss and second-order conjugate symmetric derivatives to form a background suppression model, the conjugate operation is not adaptable to scenes with strong edge contours, resulting in the retention of contours and strong noise points in the scene. The PSTNN model proposed by Zhang et al. can effectively retain the target signal while suppressing the background by using the background modeling method combining local tensor and weight norm, but when facing the scene with long edge contour, the detection model will still retain some contour information. However, this method uses tensors in background suppression and provides a research idea for low rank sparse background restoration. For example, the ASTTV model in this paper proposes an edge grinding detection method of low rank approximation of non-convex tensors with adaptive weight assignment, which can adapt to different suppression intensities for different pixel values in the image and retain the target signal; however, in the above ASTTV background suppression difference map and three-dimensional map, it can be observed that the target signal is excessively suppressed and the target signal is not obvious. The HBMLCM detection model is quite different from the traditional background modeling algorithm. This model firstly enhances the energy of the original image in local prefetching to highlight the target, and then carries out background modeling to detect the target. The model ensures that the target can be detected to a certain extent; however, in the above experiments, it can be seen that the research idea of enhancing first and then detecting is not effective in the background suppression when facing the scene with sharp ground contours and some contour information of the ground is still retained in the scene. In the same way, using local information processing, the ADMD model is improved on the detection model of AAGDto enhance the target signal. From the experimental results, it can be seen that its background modeling effect is prominent in stable scenes, but its background suppression effect is poor in strong edge contour ground scenes. However, when the deep learning of UCTransNet is used for background modeling, the real target points need to be segmented after the overall training of the sequence scene, and the target detection is not required after the background modeling. Therefore, the index analysis after the background modeling is not carried out in this paper, which simplifies the detection process of weak and small targets to a certain extent and has a high accuracy. However, the training takes a long time and the adaptability is poor, and the detection model based on neural network has great limitations in the detection of dynamic dim and small targets. In addition, from the data in Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, it can be clearly observed that the existing algorithms have large differences in background modeling and low stability when facing different scenes, which leads to low adaptability of the corresponding algorithms. The method in this paper made corresponding work for the defects of the above algorithms. After relevant theoretical research and scientific verification, it is found that the background modeling of the algorithm proposed in this paper is stable in different scenes, and the dynamic background suppression and target signal retention are prominent, so as to achieve the goal of target detection. For the subsequent scenes with more edge contour clouds, the next step may consider adding low rank tensor theory to distinguish the difference between edge information, target information, and corner points, so as to highlight the target signal and reduce the false alarm rate.
5. Conclusions
Considering that in long-range imaging, the target in the image conforms to the distribution characteristics of point spread function, and its energy is diffused from the center to the surrounding, based on the gray difference between the target point and the adjacent background, an adaptive gradient saliency function model is constructed to highlight the target signal while suppressing most of the background. However, after relevant research and experimental verification, it is concluded that the target energy is always weakened after background modeling, which brings difficulties to target detection. According to the gradient difference between the target point and the noise point in different directions, a local multi-scale gradient maximum energy-enhancement detection model is constructed, which greatly improves the contrast of the target in the image. Finally, according to the mutual correlation of target motion on continuous multi-frame images and the random appearance of noise, a detection model of F-norm and Pasteur coefficient collaborative filtering is proposed to realize the detection of the final target point. According to the above experiments and relevant data, the summary is as follows:
- (1)
- The proposed IHMM detection model can retain the target signal when performing background suppression in the complex scenes. Compared with traditional methods, the SSIM, SRN, and IC indexes are greater than 0.9999, 47.4750 dB, and 12.1008 dB, respectively.
- (2)
- The proposed LMGM model can significantly improve the signal-to-noise ratio of the target in the difference image, and the target energy-enhancement effect of the LMGM model reached 17.9850 dB in six scenes.
- (3)
- The FNPC model proposed in this paper can maintain a high detection rate when the false alarm rate is low, and when the false alarm rate is 0.01%, the detection rate of the FNPC model reaches 100% in all scenes.
Author Contributions
Conceptualization, X.F. and J.L.; methodology, J.L., X.F., H.C., L.M. and F.L.; software, J.L., X.F., H.C., L.M. and F.L.; validation, J.L., X.F., H.C., L.M. and F.L.; formal analysis, J.L., X.F., H.C., L.M. and F.L.; investigation, J.L., X.F., H.C., L.M. and F.L.; resources, J.L., X.F., H.C., L.M. and F.L.; data curation, J.L., X.F., H.C., L.M. and F.L.; writing—original draft preparation, J.L.; writing—review and editing, J.L., X.F., H.C., L.M. and F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China under Grant (62001129), Guangxi Natural Science Foundation (2021GXNSFBA075029).
Data Availability Statement
Not applicable.
Acknowledgments
We thank the raw data support the findings of this study are openly available in (A dataset for infrared image dim-small aircraft target detection and tracking under ground/air background (scidb.cn)) (accessed on 28 October 2019). Scenarios (daxj-uanxiong/infrared-small-target-images: infrared small target images (github.com)), (accessed on 3 Feburary 2020). The datasets from (https://www.scidb.cn/en/detail?dataSetId=808025946870251520)(accessed on 8 Feburary 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The abbreviations used in this manuscript are as follows:
| IHMM | Improved Hessian matrix background modeling |
| LMGM | Local multi-scale gradient maxima |
| FNPC | F-norm and Pasteur correlation |
| ANI | Anisotropy |
| PSTNN | Partial sum of tensor nuclear norm |
| ASTTV | Asymmetric spatial–temporal total variation |
| GST | Generalized structure tensor |
| NTFRA | Non-convex tensor fibered rank approximation |
| NRAM | Non-convex rank approximation minimization |
| HB-MLCM | High-boost-based multi-scale local contrast measure |
| ADMD | Absolute directional mean difference |
| SSIM | Structural similarity image |
| SNR | Signal-to-noise ratio |
| IC | Contrast gain |
References
- Chen, C.L.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A Local Contrast Method for Small Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 574–581. [Google Scholar] [CrossRef]
- Tang, Z.Y. Research on Infrared Small Target Detection and Tracking Algorithm Based on Image Sparse Representation; Shanghai Jiaotong University: Shanghai, China, 2012; pp. 1–16. [Google Scholar]
- Yang, X.; Zhou, Y.; Zhou, D.; Yang, R.; Hu, Y. A new infrared small and dim target detection algorithm based on multi-directional composite window. Infrared Phys. Technol. 2015, 71, 402–407. [Google Scholar] [CrossRef]
- Hua, X.; Ono, Y.; Peng, L.; Xu, Y. Unsupervised Learning Discriminative MIG Detectors in Nonhomogeneous Clutter. IEEE Trans. Commun. 2022, 70, 4107–4120. [Google Scholar] [CrossRef]
- Liu, J.; Sun, S.Y.; Liu, W.J. One-step persymmetric GLRT for subspace signals. IEEE Trans. Signal Process. 2019, 67, 3639–3648. [Google Scholar] [CrossRef]
- Deng, L.Z.; Zhang, J.K.; Xu, G.X.; Zhu, H. Infrared small target detection via adaptive M-estimator ring top-hat transformation. Pattern Recognit. 2021, 112, 1–9. [Google Scholar] [CrossRef]
- Lu, F.X.; Li, J.Y.; Chen, Q.; Chen, G.L.; Rao, P. PM model dim small target detection based on Top-Hat transform. Syst. Eng. Electron. 2018, 7, 1417–1421. [Google Scholar]
- Peng, S. Research on Infrared Dim Small Target Detection Algorithm Based on Space-Time Filtering; University of Electronic Science and Technology: Chengdu, China, 2020. [Google Scholar]
- Chen, Y.; Hao, Y.G.; Wang, H.Y.; Wang, K. Dynamic Programming Track-Before-Detect Algorithm Based on Local Gradient and Intensity Map. Comput. Sci. 2021, 1433, 1–12. [Google Scholar]
- Lin, Q.; Huang, S.C.; Wu, X.; Zhong, Y. Infrared small target detection based on nuclear anisotropic diffusion. Intense Excit. Part. Beams 2015, 27, 0110141–0110144. [Google Scholar]
- Wang, Y.H.; Liu, W.N. Dim Target Enhancement Algorithm for Low-contrast Image based on Anisotropic Diffusion. Opto-Electron. Eng. 2008, 35, 15–19. [Google Scholar]
- Wang, C.; Wang, L. Multidirectional Ring Top-Hat Transformation for Infrared Small Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8077–8088. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, S.; Deng, L.; Li, Y.; Xiao, F. Infrared Small Target Detection via Low-Rank Tensor Completion With Top-Hat Regularization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1004–1016. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Singh, G.; Manickam, S.; Yamaguchi, Y. An adaptive general four-component scattering power decomposition with unitary transformation of coherency matrix (AG4U). IEEE GRSL 2015, 12, 2110–2115. [Google Scholar] [CrossRef]
- Muhuri, A.; Manickam, S.; Bhattacharya, A. Snow cover mapping using polarization fraction variation with temporal RADARSAT-2 C-band full-polarimetric SAR data over the Indian Himalayas. IEEE JSTARS 2018, 11, 2192–2209. [Google Scholar] [CrossRef]
- Touzi, R.; Vachon, P.W. RCM polarimetric SAR for enhanced ship detection and classification. Can. J. Remote Sens. 2015, 41, 473–484. [Google Scholar] [CrossRef]
- Liu, J.; He, Z.; Chen, Z.; Shao, L. Tiny and Dim Infrared Target Detection Based on Weighted Local Contrast. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1780–1784. [Google Scholar] [CrossRef]
- Xia, C.Q.; Li, X.R.; Zhao, L.Y.; Shu, R. Infrared Small Target Detection Based on Multiscale Local Contrast Measure Using Local Energy Factor. IEEE Geosci. Remote Sens. Lett. 2020, 17, 157–161. [Google Scholar] [CrossRef]
- Shi, Y.F.; Wei, Y.T.; Yao, H.; Pan, D.H.; Xiao, G.R. High-Boost-Based Multiscale Local Contrast Measure for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2018, 15, 33–37. [Google Scholar] [CrossRef]
- Liu, Z.X.; H, W.L.; He, C.M. Sparse reconstruction algorithm based on new Hessian approximation matrix. Math. Pract. Theory 2019, 49, 167–177. [Google Scholar]
- Candes, E.J.; Li, X.D.; Yi, M.; John, W. Robust principal component analysis Recovering low-rank matrices from sparse errors. IEEE Sens. Array Multichannel Signal Process. Workshop 2010, 4, 201–204. [Google Scholar]
- Lin, Z.C.; Chen, M.M.; Yi, M. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. arXiv 2013, arXiv:1009.5055. [Google Scholar]
- Zhang, L.D.; Peng, Z.M. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Wei, Y.T.; You, X.G.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Qin, Y.; Bruzzone, L.; Gao, C.Q.; Li, B. Infrared Small Target Detection Based on Facet Kernel and Random Walker. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7104–7118. [Google Scholar] [CrossRef]
- Liu, T.; Yang, J.G.; Li, B.Y.; Xiao, C. Non-Convex Tensor Low-Rank Approximation for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar]
- Dai, Y.M.; Wu, Y.Q. Reweighted Infrared Patch-Tensor Model With Both Nonlocal and Local Priors for Single-Frame Small Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5000. [Google Scholar] [CrossRef]
- Hou, Q.Y.; Wang, Z.P.; Tan, F.J.; Zhao, Y.; Zheng, H.L.; Zhang, W. RISTDnet: Robust Infrared Small Target Detection Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ding, L.H.; Xu, X.; Cao, Y.; Zhai, G.T.; Yang, F.; Qian, L. Detection and tracking of infrared small target by jointly using SSD and pipeline filter. Digit. Signal Process. 2021, 110, 102949. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C. SSD: Single Shot MultiBox Detector; Springer International Publishing AG: Dordrecht, The Netherlands, 2016; Volume ECVV 2016, pp. 21–27. [Google Scholar]
- Zhao, D.; Zhou, H.X.; Rong, S.H. An Adaptation of Cnn for Small Target Detection in the Infrared. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Zhao, B.; Wang, C.P.; Fu, Q.; Han, Z.S. A Novel Pattern for Infrared Small Target Detection With Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4481–4492. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Girshick, R. Fast R-CNN. In In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; 1504, pp. 1440–1448. [Google Scholar]
- Ren, S.Q.; He, K.M.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Bao, Q.; Li, F. A method of fringe center extraction based on Hessian matrix and gradient variance. Comput. Digit. Eng. 2020, 48, 1–6. [Google Scholar]
- Zhang, N.N. Multiscale Solar Chromosphere Fiber Recognition Algorithm Based on Bilateral Filtering and Hessian Matrix; Kunming University of Technology: Kunming, China, 2021. [Google Scholar]
- Ren, L.J.; Mahmood, R. Dim Target Detection and Clutter Rejection Using Modified High Order Correlation. IEEE Int. Jt. Conf. Neural Netw. 1992, 4, 289–294. [Google Scholar]
- Nanbara, J.H.; Mahmood, R. Target Detection Utilizing Neural Nteworks and Modified High-order Correlation Method. SPIE 1995, 2496, 687–697. [Google Scholar]
- Tzannes, A.P.; Brooks, D.H. Detecting Small Moving Objects Using Temporal Hypothesis Testing. IEEE Trans. Aerosp. Electron. Syst. 2001, 38, 570–584. [Google Scholar] [CrossRef]
- Zhao, X.M.; Yuan, S.C.; Ma, Q.L.; Qi, L.L. Research on infrared small target detection method based on mobile pipeline filter. Infrared Phys. Technol. 2009, 31, 295–297. [Google Scholar]
- Liu, J.; Ji, H.B. Infrared weak target detection based on moving weighted pipe filtering. J. Xidian Univ. 2007, 34, 743–745. [Google Scholar]
- Yang, J.H.; Liu, F.A. Collaborative filtering algorithm based on Bhattacharyya coefficient and Jaccard coefficient. J. Comput. Appl. 2016, 36, 2007–2010. [Google Scholar]
- Wu, W.Q.; Wang, J.F.; Zhang, P.F.; Liu, Y.L. A collaborative filtering algorithm based on improved similarity of Pasteur correlation coefficient. Comput. Appl. Softw. 2017, 34, 265–275. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Procrssing, 3rd ed.; Pearson International Editio: Bengaluru, India, 2007; Chapter 10; pp. 711–715. [Google Scholar]
- Zong, S.G.; Wang, J.A.; Ma, Z.G. A new dual band target detection algorithm in strong clutter. Infrared Technol. 2005, 1, 57–61. [Google Scholar]
- Abdelkawy, E.; Mcgaughy, D. Small IR Target Detection using Fast Orthogonal Search. SPIE 2005, 5807, 67–76. [Google Scholar]
- Zhang, Q.; Cai, J.J.; Zhang, Q.H.; Zhao, R.J. Small Dim Infrared Targets Segmentation Method Based on Local Maximum. Infrared Technol. 2011, 33, 41–45. [Google Scholar]
- Yang, Y. Research on Small Target Detection and Recognition Technology; Institute of Optoelectronics Technology, Chinese Academy of Sciences: Beijing, China, 2005. [Google Scholar]
- Zhang, M.; Dong, L.; Zheng, H.; Xu, W. Infrared maritime small target detection based on edge and local intensity features. Infrared Phys. Technol. 2021, 119, 103940. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Hui, B.W.; Song, Z.Y.; Fan, H.Q.; Zhong, P.; Hu, W.D.; Zhang, X.F. Ground_ Infrared image dim small aircraft target detection and tracking data set in empty background. China Sci. Data 2020, 5, 1–12. [Google Scholar]
- Sun, X.L.; Guo, L.C.; Zhang, W.L.; Wang, Z.; Hou, Y.J. Infrared dim moving target detection data set in complex background. China Sci. Data 2020, 10, 1–19. [Google Scholar]
- Li, D.W. Infrared Dim Small Target Detection in Complex Background; Harbin Institute of Technology: Harbin, China, 2013. [Google Scholar]
- Li, J.L.; Fan, X.S.; Chen, H.J.; Li, B.; Min, L.; Xu, Z.Y. Dim and Small Target Detection Based on Improved Spatiotemporal Filtering. IEEE Photonics J. 2022, 14, 1–11. [Google Scholar]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Gao, C.Q.; Tian, J.W.; Wang, P. Generalised-structure-tensor-based infrared small target detection. Electron. Lett. 2008, 44, 1349–1351. [Google Scholar] [CrossRef]
- Zhang, L.D.; Peng, L.B.; Zhang, T.F.; Cao, S.Y.; Peng, Z.M. Infrared Small Target Detection via Non-Convex Rank Approximation Minimization Joint l2,1 Norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Moradi, S.; Moallem, P.; Sabahi, M.F. Fast and robust small infrared target detection using absolute directional mean difference algorithm. Signal Process. 2020, 177, 107727. [Google Scholar] [CrossRef]
- Wang, H.N.; Cao, P.; Wang, J.Q.; Zaiane, O.R. UCTransNet: Rethinking the Skip Connections in U-Net from a Channel-wise Perspective with Transformer. In Proceedings of the Thirty-Sixth AAAI Conference on Artificial Intelligence (AAAI-22), Virtual, 22 February–1 March 2022; Volume 36, pp. 2441–2449. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).