Abstract
Cadastral marks constitute a dense source of information for topographical surveys required to update cadastral maps. Historically, in Italy, cadastral marks have been the cartographic network for the implementation of mapping updates. Different sources of cadastral marks can be used by cadastral surveyors. In recent years, the cadastre is moving toward a digital world, and with the advancement of surveying technology, GNSS CORS technology has emerged in the positioning of cadastral marks. An analysis of congruence among cadastral marks using GNSS CORS and official maps is missing. Thus, this work aims to analyze the positional accuracy of some cadastral marks, located in Palermo, Italy, with regard to the official maps produced by the cadastral bureau, the local cartography, and Google Earth maps. A survey of 60 cadastral marks was carried out by conventional GNSS NRTK procedures, with the lateral offset method due to their materialization (mostly building edges), which is not always directly detectable. The cadastral marks’ positioning was obtained from different maps: cadastral maps and related monographic files, numerical technical maps, and Google Earth maps, to check their coordinate congruence. A statistical approach was performed to check whether the distribution frequencies of the coordinate’s differences belonged to the bivariate normal distribution for the planimetric coordinates and the univariate normal distribution for the altimetric component. The results show that the hypothesis of a normal distribution is confirmed in most of the pairs, and specifically, most of the analyses indicate that the highest congruencies seem to characterize the coordinates determined by using the GNSS and with those that can be deduced by the numerical technical maps. The results obtained experimentally show centimetric accuracies obtained by the GNSS NRTK survey, in both the planimetric and altimetric components, while the accuracies obtained from the georeferencing of the cadastral maps show differences in the order of 0.4–0.8 m. Meanwhile, the differences resulting from comparing the technical cartography produced by the local authority and Google Earth maps show greater criticalities, with a metric order of magnitude.
1. Introduction
With the introduction of a new cadastral regulation in Italy, for about 20 years, a newfangled standard for updating cadastral surveys has been established through the use of the Global Navigation Satellite System (GNSS). This regulation has integrated various circulars that have succeeded over time. Among these, the Circular No. 2/1987 established the cadastral mark points (Punti fiduciali, PFs). At present, there are about 1.6 million PFs in the national territory characterized by an average relative distance of 250–300 m. The PFs consist of permanent and accessible artefacts. Monographic information and relative distances are made available for most of them free of charge [1], with the Italian Revenue Agency (Agenzia delle Entrate, AE) keeping the history of their updates [2].
The coordinates of the PFs in the Cassini–Soldner system were determined by the AE and are published in the monograph; please see Figure 1 on the left-hand side (in Italian). In agreement with Circular No. 3 of 16/10/2009 [3], AE implements an archive of points known as coordinates, including fiducial points, in the European Terrestrial Reference Frame 2000 (ETRF2000). The implementation of this archive allows the AE to pursue the objective of transforming cadastral maps into the ETRF2000 frame, as required by the INSPIRE (Infrastructure for Spatial Information in Europe) directive [4] besides a note for the management and processing of geographic data in Geographic Information Systems (GIS), delivered by the geodetic directorate of the main cartographic authority of the Italian state, the Military Geographic Institute (Istituto Geografico Militare, IGM) [5].

Figure 1.
An example of AE monographs with PF coordinates georeferenced in the Cassini-Solder system (in Italian).
It should be noted that such information, stored and managed by the AE, has been produced by thousands of technicians to update cadastral documents. Cadastral documents should be updated by binding the territory artefact to PFs. However, this last prescription is often disregarded due to the practical difficulty of finding marks. PSs are often not characterized by an appropriate distribution, often not only within a single map sheet, while new PFs are not designed to be established. In addition, marks are not always inspected on-site. Reference to a network of PFs is made, directly or indirectly, for each topographical survey for cadastral updating.
The role of these marks is twofold: to reconstruct the object of the survey on the strength of the measurements and to allow it to be included in the cadastral mapping regardless of its coordinates. Work on the network has begun in areas most subjected to cadastral updates (i.e., evolving urban areas), while areas where updates are more sporadic, such as historic centers or mountain areas, have been left to the last.
In recent years, several studies have discoursed the methodologies of data software, acquisition, and processing of PFs. Among these, Hope et el. proved a least-squares-based adjustment to be a versatile addition to GIS for incorporating boundary line collinearities [6], while [7] demonstrated that when digitized cadastral maps are characterized by significant systematic errors, it is possible to improve the accuracies of the coordinates by incorporating scale parameters in the least-squares-based adjustment.
Janssen et al. [8] used traditional Global Positioning System (GPS) observations in real-time kinematic (RTK) to improve the existing cadastral survey in New South Wales, Australia. It is shown that accuracies, evaluated in terms of root mean square (RMS), were about 11 mm in the horizontal and 34 mm in the vertical components. Calculated bearings agree very well with the official values derived from the state’s survey control database.
Dabove tested both single-base RTK and Virtual Reference Station (VRS) near real-time kinematic (NRTK) methodologies using single-frequency GPS/GNSS mass-market receivers. The author reported differences between the reference coordinates and the estimated ones of a few centimeters if the distance between the master and the rover was lower than a few kilometers. In particular, the difference was about a couple of centimeters for the East and North components and about 5 cm for the Up component [9]. Cina et al. [10] proposed a new redefinition of cadastral boundaries using GNSS and ‘original’ cadastral maps (‘originali di impianto’ in Italian) of the Italian Land Cadastre.
Charoenkalunyuta et al. [11] investigated the horizontal accuracy of GNSS cadastral surveying using the Thai-NRTK GNSS Continuously Operating Reference Station (CORS) VRS network in Thailand. After investigating about 2100 marks, a maximum distance from CORS of 50 km was recommended to obtain reliable positioning for cadastral surveying. Housarová et al. and Yuwono et al. [12,13] tested the unmanned aerial vehicle (UAV) photogrammetry for cadastral purposes, respectively, in the Czech Republic and Indonesia. The differences in the resulting coordinates and the internal accuracy of the UAV method are discussed. Results show centimetric accuracy using GNSS positioning.
Bramanto et al. [14] introduced a modified LAMBDA ambiguity resolution and Kalman filtering to improve the accuracy of RTK GNSS positioning. Due to unresolved distortions, the resulting accuracy on a single baseline ranged from several centimeters to decimeters, which were considered compatible with cadastral applications.
Gill et al. [15] explored the potential need for the legal traceability of GNSS measurements, with particular reference to the CORS Malaysia network (MyRTKnet), to obtain standard regulations and guidelines for the cadastral survey (i.e., Cadastral Survey Regulations 2009) to enclose GNSS measurements in NRTK mode. Erenoglu [16] evaluated the most commonly used GPS/GNSS methods for cadastral surveying in Turkey, highlighting the benefits of the NRTK method.
Lauterbach and Timo de Vries [17] evaluated different surveying methods for cadastral mapping in Namibia, including orthophoto-based boundary demarcation, mobile mapping applications, handheld GPS, low-cost GNSS with a u-blox receiver, and GNSS RTK based on Namibian CORS; all methods were reported to be appropriate for Namibia except for the handheld GPS method.
Melnikov et al. [18] tested a web service for online processing of GNSS observation for geodetic support to cadastral work, namely, the Canadian CSRS-PPP web service. The web service has shown a high level of convergence of the solutions.
Beinat and Crosilla [19] reported a system of updating Italian cadastral maps, an analytical method performing the general adjustment of the network of PFs and the insertion of the surveyed cadastral parcels in an existing digital map. By analyzing the AE survey archives, including the distances between pairs of PF, the procedure based on the least-squares method mutually adjusts the fiducial polygons as unitary parts of the PF network. The procedure employs similarity adjustment transformation models computed by generalized procrustean algorithms and preserves the geometric shape of the survey.
The reported state of the art does not claim to be exhaustive; however, in the authors’ opinion, it highlights many studies on methods, performance, and accuracy of GNSS positioning. None of these, however, assesses the congruence of GNSS positioning and other sources of coordinates of cadastral marks.
The current paper, indeed, presents an experience carried out throughout the city area of Palermo, northwestern Sicily (Italy), in an urban area of approximately 16 km2. Through an NRTK GNSS survey, the coordinates of 60 cadastral marks were determined and compared with cadastral data, local maps, and Google Earth satellite images.
The cadastral survey was carried out through a GNSS receiver, in agreement with instruction no. 3 of 11/12/2003 [20], which established a traditional RTK survey. Indeed, initially, GNSS surveys were carried out in RTK mode (i.e., with two master and rover receivers).
Starting from 2009 (Circular No. 3 of 16/10/2009), [3] the use of NRTK (network real-time kinematic) CORS (Continuously Operating Reference Stations) has been regulated, and the protocols standardized, allowing the use of the differential corrections, including the VRS (Virtual Reference Station), FKP (FlächenKorrektur Parameter), and MRS (Multireference Station).
This manuscript aims to evaluate the congruence of different positioning methodologies of cadastral marks. Pullar and Donaldson [21] reported that errors in observation measurements are normally distributed by analyzing some accuracy issues for the spatial update of digital cadastral maps. Within our research, the position of the marks is also analyzed to remove the outliers under the hypostasis that measurement errors are normally distributed. Planimetric differences in the positions were considered multivariate normally distributed, while altimetric differences were considered univariate normally distributed.
The paper is organized as follows: the description of the materials and methods is discussed in Section 2, including the description of the UNIPA GNSS CORS network employed in the acquisition and study area, the design of the topographic and expeditious surveys, the description of the cadastral map and related monographic file, the description of the numerical technical maps, the characteristics of the Google Earth maps, and the statistical approach employed to analyze the data, while the results and discussion of the analyses are presented in Section 3, including some multivariate normality analyses of the planimetric differences ΔE and ΔN and univariate normality analyses of the altimetric differences Δh. Finally, some conclusive remarks and planned developments of the research study are reported in Section 4.
2. Materials and Methods
2.1. UNIPA GNSS CORS Network and Study Area
The UNIPA GNSS CORS network was materialized in 2006 for scientific purposes by researchers of the Department of Engineering, University of Palermo [22]. It is made up of eight CORSs located in western Sicily, in the provinces of Palermo, Trapani, Agrigento, and Caltanissetta. All CORSs were equipped with Topcon NET G-3 GPS and GLONASS-enabled receivers. Up to 2012, the control center (CC) was at the Department of Engineering of the University of Palermo, and the GNSS State Monitoring and Representation Technique (GNSMART) software by Geo++ was used to manage the CORS network and to produce the NRTK corrections. Since 2013, all reference stations were included in the NetGEO GNSS CORS network, managed by Topcon Italy. The network provides daily RINEX data (30″), hourly raw data (1″), and real-time GNSS data stream code (nearest station, VRS, and FKP). Preliminarily, the coordinates of the reference stations were established in ITRF05 and ETRF89 (epoch 1989.0) frames. For about 10 years, six CORSs have been included in the Italian GNSS national dynamic network (Rete Dinamica Nazionale (RDN)), which is a regional reference frame subcommission for Europe (EUREF), a European subnetwork, aiming to monitor the reference system variations, according to Maseroli [23]. The RDN network is computed in the ETRF2000 reference frame (epoch 2008.0) using the Bernese 5.0 software; thus, the coordinates of the UNIPA GNSS CORS network were also calculated in this frame. Data from the UNIPA GNSS CORS network were also included within a European regional integration of long-term national dense network solutions for the positions and velocities of more than 3000 stations, as shown in Kenyeres et al. [24].
In Dardanelli et al. [22], all the details concerning the design, data availability, preliminary studies and analysis involving the GNSS CORS network, geodetic framework used, time series of coordinates and displacements retrieved in time, and statistical analysis with the cumulative distribution function (CDF) are shown.
Over the last 15 years, the UNIPA GNSS CORS network has been used in many papers in different fields for technical and scientific applications, in particular concerning positional accuracy. In recent years, Dardanelli et al. [25] compared different GNSS survey methods (NRTK, PPP, and static modes) in pairs by applying statistical tests to analyze the positioning congruence obtained with different approaches. Meanwhile, Dardanelli and Pipitone [26] evaluated the effects of a GNSS CORS network geometry and differential corrections on the solutions, with an analysis carried out using 10 different network configurations, with different stations’ interdistances.
As already mentioned, in the present research study, the study area was specifically selected within the city of Palermo (Italy), where the PFs face critical issues related to the presence of urban canyons for the satellite geometric configuration (GDOP and PDOP). The distance between the selected PFs and the CORS station located in Palermo ranged between 1300 and 5550 m.
Since the survey was carried out in the urban environment. The coordinates of 60 cadastral reference points were positioned with GNSS using an NRTK GNSS correction and an electronic distance meter. Then, the coordinates were compared with those of cadastral data, local maps, and Google Earth (Figure 2).

Figure 2.
The location of Sicily (red rectangle, Frame A) within the Italian territory (light green, Geocentric CRS RDN2008-EPSG: 6706). CORS permanent stations in Sicily (Frame B, black dots, Projected CRS ETRF2000-RDN2008 UTM zone 33N-EPSG: 6708) overimposed the delimitation of the municipality of Palermo (red line). Cadastral marks in Palermo (red dots, Frame C, EPSG: 6708).
2.2. Topographic and Expeditious Surveys
PFs should allow generating a mesh of triangles having sides between 250 and 300 m in length. In Palermo, the average distance between the two closest PFs is 467 m, while the first, second, and third quartiles are 282, 355, and 523 m, respectively (PF update of 27 July 2022). In the present dataset, the average distance between the two closest PFs was 296 m, while the first, second, and third quartiles were 256, 265 and 294 m.
Since the cadastral marks were originally established by the AE in buildings corners, the positions of the PFs were suitable for surveying with classical topographic instrumentation, such as total stations.
Concerning the NRTK GNSS positioning, it was decided to survey the neighborhood of the PFs, with three independent substations, measured with a lateral offset below 5 m, using an electronic distance meter, Leica Disto A5. The receiver was connected with an aluminum pole, and the external antenna was installed around it; to achieve the highest precision in measuring the position of the substations, it was mounted a topographic bipod to support the equipment. A Topcon GRS-1 receiver was used for the survey, with an occupation time of 15′, while the rate was 1 s and the cut-off angle was fixed to 10 degrees to reduce PDOP in urban receiving environments. The GNSS Topcon GRS-1 (Geodetic Rover System) is a fully integrated dual constellation GPS+GLONASS 72-channel rover system, which is a complete system, which includes a handheld GNSS receiver and controller with a high-performance processor, built-in camera, electronic compass, and barcode reader, as well as an SD memory slot, internal GSM modem, and wireless connectivity with WiFi and Bluetooth® technology. By adding the PG-A1 external antenna and connection to UNIPA GNSS CORS via the nearest correction, it becomes a dual-frequency, dual constellation, centimeter precision GNSS RTK receiver. The electronic distance meter Leica Disto A5, on the other hand, has an accuracy of ±1.5 mm and ranges from 0 to 200 m. On board the receiver GRS-1 is installed Mercurio software developed by GeoPro (Topcon Corporation, Ancona, Italy), allowing the acquisition, tracking, and management of survey data. It combines positioning solutions with computer-aided design (CAD) software for user-friendly graphical data management. It can process data acquired by both total stations and GNSS receivers in different modes. Once the survey was completed, data processing was outsourced to Meridiana ver. 2020 software (by GeoPro, Topcon Corporation, Ancona, Italy) to check for outliers with regard to set tolerances.
2.3. Cadastral Map at a Scale of 1:2000 and Monographic File
Italian cadastral survey and geographical survey systems are based on a different ‘geodetic coordinate system’. The Cassini-Soldner projection was adopted in the Italian cadastral system as follows:
- Coordinates were referred to a reference center (the cadastral origin);
- For most of the Italian territory, the cadastral coordinates have as origin 1 of 31 different vertices (named major origins), which therefore give rise to many different coordinate systems;
- A transverse cylinder tangent along the meridian at the reference center was adopted as a projection surface.
At the beginning of the unification process of the Italian state, the different cadastral systems could not be completed or unified due to the different pre-existing systems; a total of 849 origins were adopted to cover the national territory: 31 with large surface extents and 818 with small extents, initially also with different coordinate calculation systems.
In particular, in the case study, the surveyed area belongs to a small extended cadastral origin.
The former was made by the old geodetic system, but later by a ‘World Geodetic Coordinates System’. The above-mentioned information systems cannot be reprojected on each other, resulting in different coordinate estimations, even in the same area. Therefore, the datum was changed from the local geodetic system to the world geodetic system.
The coordinates of the PFs were referenced to the AE monographs (Figure 2); these coordinates are expressed in Italy, including in Sicily, in the Cassini–Soldner reference system [22]. The Cassini–Soldner reference system has been used for the production of the majority of the cadastral maps (approximately 80% of the whole cartographic assets). This representation was adopted for the first time in 1709, to produce a map of France (scale: 1:86,400) initiated by Cesare Cassini, continued by his son Giacomo, and completed by his grandson Domenico. A century later, in 1810, Johann von Soldner introduced this representation for the survey of the ‘new Bavarian cadastre’, a choice that was soon followed by other German countries.
As widely accepted [27,28], given the Cassini–Soldner and WGS84 geodetic coordinates of the cadastral origins, the seven parameters of the Burša-Wolf transformation [28,29,30] and the three abridging Molodensky parameters [31] between the two data allowed for obtaining a fine horizontal accuracy [32].
The representation consists in projecting along with the generators of a cylinder tangent to the ellipsoid along a central meridian of the area. The map is obtained by unfolding the cylinder on a plane, using as the x-axis the tangent to the central meridian and as the y-axis the perpendicular line through the central point of the area, with their intersection defining the origin of the system. This transverse cylindrical projection maintains a scale along the central meridian and all lines parallel to it and is neither conformal nor equal area.
In the above-reported example (Figure 2), the PF is located in the corner of a building (see the section ‘fotografia o schizzo prospettico’) (photograph or perspective sketch section), while its planimetric position is shown in the section ‘estratto di mappa’ (map extract section). Finally, the planimetric and altimetric reliabilities of the fiducial points are represented by numerical codes (see ‘attendibilità’ in the section ‘coordinate e quote’, the reliability in the planimetric coordinates and altitudes section). For instance, in the above-reported example, the planimetric reliability 12 indicates a point defining the boundary of three properties or building edges positioned by external technicians, while the altimetric reliability 04 indicates a PF for the cadastre update.
Coordinates are converted in two steps from Cassini–Soldner to ETRF2000 (1.2008). First, the formulae of Antongiovanni and Ghetti [33] were applied (in Italian). These equations involve the transformation first from Cassini–Soldner coordinates to Gauss Boaga coordinates (GB-1940), in the old Italian datum Roma 40, valid in Italy until 2011. Regarding the geodetic datum, the province of Palermo belongs to the areas of ‘small extension’ of which the definition of the cadastral development center is uncertain.
The computation involves establishing the rototranslation coefficients and the deviations that result from the linear transformations; then the polynomial coefficients are calculated as a function of which the deviations can be determined, and finally, the coordinates of all points are transformed.
The conversion formulae to calculate the geographic coordinates (the latitude and longitude and , in radian) as a function of the cadastral coordinates X and Y are Equations (1)–(3):
where
- –
- and represent the latitude and longitude of the projection centre;
- –
- represent the meridian curvature radius and the maximum radius of curvature of the surface (gran normale, simply referred to as ‘auxiliary quantities’ in [34]) at ;
- –
- and represent the meridian curvature radius and the maximum radius of curvature of the surface at .
As given by Equations (4) and (5), respectively:
and Equations (6) and (7)
being the major and minor semiaxes of the Bessel ellipsoid a = 6,377,397.15 m and b = 6,356,078.96 m.
Once the GB-1940 coordinates of the PFs were obtained, they were transformed into ETRF2000 (1.2008) via Verto 3K software [35], delivered by the main cartographic authority of the Italian state, the Italian Military Geographic Institute (Istituto Geografico Militare, IGMI). After the ETRF2000 (1.2008) coordinates of the PFs were determined, the original maps in Cassini–Soldner were georeferenced based on the 2008 Operational Regulations drawn up by the AE [36]. To georeference the digitized map (200 dpi), at least nine reference points are required; then a rototranslation transformation needs to be applied. A tolerable error <0.25 mm at the graphical scale is required; also, a difference between the denominator of the nominal scale of the map and the actual nominal scale obtained with the georeferencing process is prescribed, divided by the nominal scale in an absolute value <5‰.
2.4. Numerical Technical Map at a Scale of 1:2000
In 2003, the Department of Urban Planning of the Regional Department of Territory and Environment (Dipartimento di Urbanistica dell’Assessorato Territorio e Ambiente della Regione Sicilia) within the framework of Measure 5.05 of the P.O.R. Sicily 2000–2006 started the realization of the digital cartography at a scale 1:2000.
A Geographic Information System (GIS) vector format was used to produce the coverage of the regional urban centers at a scale of 1:2000. The production was referred to as CART2000 [37].
The realization of the numerical technical maps was subdivided into four cartographic lots. The numerical technical map (Carta Tecnica Numerica, CTN) was represented in Gauss projection and framed in the regional technical map (Carta Tecnica Regionale, CTR) at a scale of 1:10.000; therefore, each CTN covers the 25th part of a CTR.
Planimetric and altimetric tolerances are the following:
The tolerable deviation (tolerance) of a planimetric position (t) is t = 0.80 m, while the tolerance of the distance between two points (td) is td = 0.60 + D/1000 m, where D is the topographic distance between the points, if D ≤ 600 m, td = 1.20 m if D > 600 m. The tolerance of the elevation (th) is th = 0.60 m, while the tolerance of the height difference between two points (tq) is tq = 0.60 + D/1000 m, where D ≤ 300 m., tq = 0.90 m if D > 300 m. The tolerance of the height of a point belonging to a contour line (tcl) is tcl = 0.90 m. For contour lines of the terrain covered by dense perennial vegetation, the tolerance of the height of a point belonging to the contour line (th) is half the average height of the vegetation.
Each CTN map is identified by a number and a name, where the number is codified through seven digits (XXXYYZZ), where the first three digits identify the sheet (scale: 1:50,000), the fourth and fifth digits identify the corresponding CTR section (1:10,000), and the sixth and seventh identify the CTN sheet (1:2000), while the name refers to the main municipality covered by the CTN, with subtitles indicating the surveyed area (neighborhood, hamlet, residential zone, etc.). As the a priori accuracy of a map is conventionally considered equal to 2 × ±0.02 mm at the scale of the map, for the CTN (1:2000), a value of 0.80 m is accepted.
2.5. Google Earth Map
Google Earth (GE) is a free software (https://www.google.it/intl/it/earth/, last accessed on 3 August 2022) that allows one to freely explore remotely sensed images of the surface of the earth [38]. It has been easily the most successful geo-browser since it is fast and its markup language allows displaying the geospatial data on a high-resolution satellite image, thus, to a certain extent, fulfilling the concept of Digital Earth [39,40].
More precisely, the GE geo-browser allows visualizing and querying coordinates and distances using satellite images, aerial photographs, and topographical data through a GIS platform. Specifically, GE can be explored by providing geographical coordinates, or addresses, or by navigating the planet with the mouse. Most cities are available in high spatial resolution so that the streets and buildings can be seen. The level of resolution depends on the importance of the location, indeed urban centers are covered by high-resolution satellite images, up to 15 centimeters in specific areas, such as Google’s headquarters. Since GE is often used to visualize urban areas, the high-resolution GE imageries are composed in true color. Visualized images derive from the superimposition of static images taken from different sources. Different areas of the world show images with different details and at different times.
Many studies have been conducted on the positional accuracy of maps obtained from GE. Concerning Italy, the following are noteworthy: Pulighe et al. [41] tested the horizontal accuracy of very high-resolution GE images in the city of Rome over different years (2007, 2011, and 2013). The authors, similar to the present study, used both Global Positioning System ground truth data and cadastral photogrammetric marks. The authors showed that GE’s very high-resolution imageries over Rome have an overall positional accuracy close to 1 m, sufficient for deriving ground-truth samples, measurements, and large-scale planimetric maps [28].
The georeferencing of GE images is easily checked [42]. Indeed, errors in image alignment are apparent as disjointed linear features, such as roads and coastlines at the boundary between two adjacent images.
The positional accuracy of GE is not fixed; instead, it varies in time with the process of updating GE by replacing older images with more recent images with a finer resolution [43]. The authors report a horizontal accuracy of GE images in Sudan of about 1.80 m. Guo et al. [44] tested the horizontal accuracy of GE images in Australia. The authors reported an overall accuracy in the western coastal areas ranging between 0.7 and 1.4 m; the accuracy resulting in the central desert ranged between 1.4 and 2.2 m, while the images acquired over the western mountains and hills resulted in the lowest accuracy (14.5 and 17.1 m). Farah and Algarni [45] assessed the positional accuracy of GE images in South Arabia using differential static GPS. The authors reported an average horizontal error of 6.84 m (with an RMSE of 2.18 m), while the average vertical error was 0.30 m (with an RMSE of 1.51 m). Adam and Abdulrahman [46] implemented a semiautomated method for assessing the horizontal positional accuracy of GE imagery with reference to the real-time kinematic (RTK) positioning. The authors reported a mean horizontal error of 1.23 m (with an RMSE of 1.53 m).
In Figure 3, an example of coordinate determination of PFs by monographs (a), cadastral map (b), municipal technical map (c), and Google Earth map was reported.

Figure 3.
Example of coordinate determination: (a) fiducial marks image, (b) cadastral map, (c) numerical technical map, (d) Google Earth map.
2.6. Data Analysis
This work aims to evaluate the congruence of different positioning methodologies (Google Earth map (GE), numerical technical map (CTN), cadastral map (MC), Global Navigation Satellite System positioning (GNSS)). The solutions’ congruence was assessed by statistically analyzing the coordinate’s differences on selected marks. The analysis was performed by considering the difference along with each coordinate component (North, N; East, E; and Ellipsoidal Height, h), as well as the planimetric difference and the tridimensional distance. Coherent with the approach of Dardanelli et al. [20], six different comparisons were carried out for the planimetric components (Figure 4, left panel): GE vs. CTN, MC vs. CTN, GNSS vs. CTN, MC vs. GE, GNSS vs. GE, GNSS vs. MC, while three different comparisons were carried out for the altimetric components (right panel): GE vs. CTN, GNSS vs. CTN, GNSS vs. GE, since the altimetric component was not available for MC (thus, pairs were not reported in Figure 4, right panel).

Figure 4.
Conceptual scheme of comparisons: (a) planimetric component; (b) altimetric component.
Three times the standard deviation can be considered a maximum deviation from the mean. Thus, the lower and upper tolerance limits were calculated to identify candidates’ outliers, assuming that the distribution is normal.
Thus, we examined the consistency of the empirical distribution of the pairs ΔE–ΔN with the theoretical multivariate normal distribution. Among these tests, we applied the multivariate normality testing (Mardia) for skewness and kurtosis [47]. Indeed, skewness and kurtosis can provide a straight measure of departure from normality. Mardia’s multivariate skewness and kurtosis statistics and their corresponding p-value result in multivariate normality if the p-values of skewness and kurtosis statistics are greater than a threshold.
To strengthen the results, Royston’s multivariate normality test [48,49,50,51] was applied as well. It combines the Shapiro–Wilk statistics for the separate variables and compares the result to a chi-square distribution.
Additionally, the Doornik–Hansen omnibus test for multivariate normality was used [52], which measures the skewness and kurtosis of multivariate data being transformed to ensure independence.
While it is plausible to consider the multivariability of the pairs ΔE–ΔN, given the GNSS principle of operation, it is reasonable to consider the univariability of Δh. Again, to strengthen the results, different tests were applied.
The agreement of the empirical distribution of the pairs Δh with the theoretical univariate normal distribution is tested through the Shapiro–Wilk test [53,54] especially valid for small samples, and the D’Agostino–Pearson test [55,56] consisting of the integration of skewness and kurtosis tests. In this case, the sum of the squares of the statistics, that is the skewness divided by the standard error and the kurtosis divided by the standard error, is tested to follow a chi-square distribution with 2 degrees of freedom.
Simple statistics were then applied to the planimetric and altimetric difference dataset’s antecedent and subsequent removal of the outliers.
The mean values, μ, and the standard deviations, σ, of the differences in the coordinates, ΔN, ΔE, and Δh, were compared with the corresponding value before removing the outliers. The sample skewness, S, and the kurtosis index, Κ, evaluated before and after removing the outliers, allowed for assessing whether and how much the empirical frequency distribution has more symmetricity and mesokurticity. The interquartile range, IQR, defined as the difference between the 75th and 25th percentiles of the data, was used to measure the statistical dispersion of the data [57].
Finally, regarding the planimetric differences, the confidence ellipse, an isocontour of the bivariate normal distribution was represented. In particular, a 95% confidence ellipse was calculated to define the region, including 95% of ΔE, ΔN pairs.
Meanwhile, regarding the altimetric differences, the empirical distribution frequency of Δh was graphically compared with a best-fitting univariate normal distribution and was plotted on a normal quantile–quantile plot (Q–Q plot) to visualize whether the empirical distribution agreed with the theoretical normal distribution.
3. Results and Discussion
This section provides a concise description and interpretation of the multivariate analysis of the ΔE–ΔN pairs and the univariate analysis of Δh. Then, the congruence of the positions of the cadastral marks was assessed on the official maps produced by the cadastral bureau, the local cartography, and Google Earth maps or positioned via GNSS and electronic distance meters.
3.1. Descriptive Statistics
Since GNSS acquisitions were carried out in an urban environment, it is helpful to report precisions and standard deviations of the GNSS solutions (Figure 5).
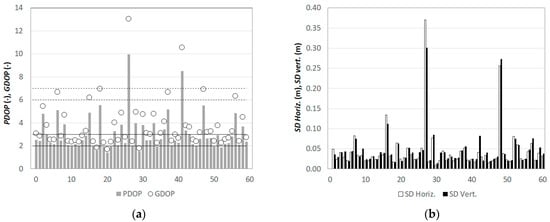
Figure 5.
Precision and standard deviation of the GNSS solutions: (a) positional dilution of precision (PDOP, grey bars) and geometric dilution of precision (GDOP, empty dots). Overimposed the maximum suitable values for the PDOP (2–3, continuous lines) and the GDOP (6–7, dashed lines). (b) Standard deviation (SD) (m) of the planimetric components (SD Horiz., white bars) and the vertical component (SD Vert., black bars).
In 30% of the acquisitions (18 of 60), PDOP values were higher than the acceptable threshold (2–3) (Figure 5, panel a). These are due to urban canyons with narrow roads and tall buildings. However, GDOP values were higher than the acceptable threshold (6–7) only in two cases (GDOP = 13.1 and 10.6), according to the instructions for the Italian cadastral update. Additionally, two acquisitions were characterized by high standard deviations, both horizontal and vertical (panel b). However, the two points did not exhibit any abnormal behavior in subsequent analyses; thus, they were kept in the dataset.
Mean, median, standard deviation, kurtosis, skewness, and interquartile range were calculated to describe ΔE; ΔN of the pairs GE–CTN, MC–CTN, GNSS–CTN, MC–GE, GNSS–GE, and GNSS–MC (Table 1); and Δh of the pairs GE–CTN, GNSS–CTN, and GNSS–GE (Table 2).

Table 1.
Descriptive statistics of ΔE: mean, median, standard deviation, kurtosis, skewness, and IQR.

Table 2.
Descriptive statistics of Δh: mean, median, standard deviation, kurtosis, skewness, and IQR.
The mean, median, and standard deviation of ΔE closer to the null value are those characterizing the GNSS–CTN pairs (−0.05, −0.10, and 0.66, respectively), while kurtosis and skewness are smaller for the MC–GE pairs (−0.08 and 0.04, respectively). Finally, the lowest IQR characterizes the GNSS–CTN pairs (0.52).
Coherent with ΔE, the mean, median, and standard deviation of ΔN closer to the null value are those characterizing the GNSS–CTN pairs (−0.22, −0.16, and 0.75, respectively). Different from ΔE, kurtosis and skewness for ΔN are smaller for the GE–CTN pairs (0.31 and 0.62, respectively). Again, coherent with ΔE, the lowest IQR of ΔN characterizes the GNSS–CTN pairs (0.69).
The mean, median, and standard deviation of Δh closer to the null value are those characterizing the GNSS–CTN pairs (0.05, 0.03, and 0.30, respectively), while kurtosis and skewness are smaller for the pairs GE–CTN (0.49 and 0.51, respectively) and GNSS–GE (0.39 and −0.55, respectively). Finally, the lowest IQR characterizes the GNSS–CTN pairs (0.30).
3.2. Multivariate Normality Analyses
The bivariate normal distribution of the planimetric components was tested. To strengthen the results, the multivariate normality testing (Mardia) for skewness and kurtosis (Table 3 and Table 4, respectively), Royston’s multivariate normality test (Table 5), and the Doornik-Hansen omnibus test (Table 6) were applied. A graphical representation of the confidence ellipse of the planimetric differences (ΔE, ΔN) was used for assessing multivariate normality.

Table 3.
Multivariate normality testing (Mardia) for skewness of the pairs ΔE–ΔN. The degree of freedom (df) = 4. Values after outliers’ removal are reported between parentheses. * p-Values < 0.02 are omitted. The skewness and chi-square (chi-sq) values are also reported. The resulting bivariate normal distributions are highlighted in bold.

Table 4.
Multivariate normality testing (Mardia) for kurtosis of the pairs ΔE–ΔN. The degree of freedom (df) = 4. Values after outliers’ removal are reported between parentheses. p-Values < 0.02 are omitted. The kurtosis and the test statistic z-stat are also reported. The resulting bivariate normal distributions are highlighted in bold.

Table 5.
Royston’s multivariate normality test of the pairs ΔE–ΔN. The equivalent degree of freedom (df) = 2. Values after outliers’ removal are reported between parentheses. p-Values < 0.02 are omitted. The resulting bivariate normal distributions are highlighted in bold.

Table 6.
Doornik–Hansen omnibus test for multivariate normality of the pairs ΔE–ΔN. The degree of freedom (df) = 4. Values after outliers’ removal are reported between parentheses. p-Values < 0.02 are omitted. The resulting bivariate normal distributions are highlighted in bold.
Testing Bivariate Normal Distribution ΔE ΔN
Regarding the skewness test, we highlighted in bold the p-values and the p-values using the correction factor for small samples (p-value*) when larger than = 0.02. In these cases, we retained the null hypothesis and considered the samples as coming from a normal distribution. For the pairs GNSS–CTN, this occurred after the removal of the outliers (p-value = 0.87) with skewness and chi-sq equal to 0.13 and 1.26, while for the GNSS–GE pair, it occurred both before and after the removal of the outliers (0.07 and 0.09, respectively) with skewness and chi-sq equal to 0.87 and 8.66 before outliers’ removal, reduced to 0.85 and 8.17 after outliers’ removal.
As regards the kurtosis test, we highlighted in bold the p-values when larger than = 0.02. In these cases, we retained the null hypothesis and considered the samples as coming from a normal distribution. This occurred for the pairs GE–CTN, GNSS–CTN, GNSS–GE, and GNSS–MS only after the removal of the outliers (p-value = 0.07, 0.06, 0.06, and 0.52, respectively, and z-stat = 1.83, 1.88, 1.88, and 0.64, respectively) with kurtosis equal to 9.92, 10.00, 9.97, and 8.69, respectively.
Royston’s multivariate normality test returned a normal distribution for GNSS–CTN, MC–GE, GNSS–GE, and GNSS–MS after outliers’ removal (p-value = 0.07, 0.12, 0.05, and 0.06, respectively), while none of the datasets were marked as normally distributed before outliers’ removal.
On the other hand, in the Doornik–Hansen omnibus test, we highlighted in bold the p-values when larger than = 0.02. In these cases, we retained the null hypothesis and considered the samples as coming from a normal distribution. The multivariate test returned a normal distribution for the pairs GE–CTN, GNSS–GE, and GNSS–MS after the removal of the outliers (p-value = 0.17, 0.07, and 0.10, respectively).
The univariate test for ΔE returned a normal distribution for all the pairs after the removal of the outliers (p-value = 0.17, 0.07, and 0.10, respectively). The univariate test for ΔN returned a normal distribution for GE–CTN, MC–CTN, GNSS–CTN, GNSS–GE, and GNSS–MS after outliers’ removal (p-value = 0.16, 0.07, 0.13, 0.15, and 0.21, respectively).
The confidence ellipse was used for visually checking the normality of the planimetric components ΔE and ΔN (Figure 6).

Figure 6.
Graphical verification of the bivariate normal distribution: confidence ellipses pre- and after outliers’ removal (dashed red line and continuous red line, respectively). The confidence level for the confidence envelope is set to 0.95. Pairs (before outliers’ removal) are represented with white dots, while pairs after outliers’ removal are overimposed with black dots.
The magnitudes of the ellipse axes depend on the variance of the ΔE and ΔN. The confidence ellipses, of course, become smaller after removing the outliers. Additionally, it is clear that the correlation between ΔE and ΔN diminishes (e.g., GE–CTN, MC–CTN, and GNSS–CTN). The range of variability of all the graphs is −15–15 m, except for the pairs GNSS–CTN, which is characterized by an order of magnitude smaller variability (−3–3 m). For the latter, the lengths of the two axes of the ellipse are 2.41 and 1.48 m (before outliers’ removal) and 1.70 and 1.50 m (after outliers’ removal), while the angles (in radians) that the ellipse makes with the x-axis are 2.21 and 1.95 rad (before and after outliers’ removal, respectively).
The angle of the ellipse is determined by the covariance of ΔE and ΔN. When the covariance is high, such that the data are correlated, it results in an ellipse not aligned to the x- or y-axis, such as the ΔN of the pairs GE–CTN and GNSS–CTN for the raw data (before outliers’ removal), although these pairs lost correlation after removing the outliers. Meanwhile, the pairs GNSS–GE are correlated for both raw and filtered data (before and after outliers’ removal).
3.3. Univariate Normality Analyses
The univariate normal distribution of the altimetric difference Δh was tested to find out any possible outlier. To strengthen the results, Shapiro–Wilk and D’Agostino–Pearson (Table 7) were applied. The Q–Q plot was used for graphically checking the normality of Δh, before and after outliers’ removal.

Table 7.
Shapiro–Wilk and D’Agostino–Pearson tests of the pairs Δh: p-values < 0.02 are omitted, while the resulting univariate normal distributions are highlighted in bold.
Normal Distribution Test Δh
The results of D’Agostino–Pearson are coherent with those of Shapiro–Wilk. While the pairs GE–CTN and GNSS–GE follow a normal distribution both before and after outliers’ removal, the GNSS–CTN pairs do not follow a normal distribution before outliers’ removal. Indeed, the Shapiro–Wilk test and the D’Agostino–Pearson test return a normal distribution of Δh for all the pairs (GE–CTN, GNSS–CTN, and GNSS–GE) after outliers’ removal (p-value = 0.20, 0.62, and 0.25, and p-value = 0.19, 0.59, and 0.20 for the Shapiro–Wilk and the D’Agostino–Pearson tests, respectively), while only the pairs GE–CTN and GNSS–GE return a normal distribution before outliers’ removal.
The empirical distribution agrees with the theoretical one since after linearly transforming the Δh pairs, the Q–Q plot follows a line (Figure 7, panels a–c). However, the two distributions being compared are not identical (the quantiles do not follow the bisector line).

Figure 7.
Q–Q plots for the (a) GE-CTN, (b) GNSS-CTN, and (c) GNSS-GE Δh pairs: before outliers’ removal (white dot) and after outliers’ removal (red dots overimposed). The trend lines before and after candidate outliers’ removal are represented with dashed and continuous lines, respectively.
From this point of view, GNSS–CTN gave the best result. Outliers are reported with empty circles. Before and after removing the outliers, the interpolating line did not visually change, except for GNSS–CTN. Additionally, the upper end of the Q–Q plot for the GNSS–CTN pairs deviated from the straight line as the empirical distribution before outliers’ removal was right-skewed (or positively skewed).
3.4. Coordinate Difference Analyses
Coordinate differences (Figure 8) refer to the mean value, first and third quartiles of the data after the removal of the outliers.

Figure 8.
I quartile, average, and III quartiles of the coordinate difference (P025, μ, and P025, respectively) of the components: (a) ΔN, (b) ΔE, and (c) Δh, and of the planimetric and plano-altimetric differences: (d) D2D and (e) D3D, respectively). Values are evaluated after outliers’ removal.
The range of variability of ΔN and ΔE (−2.5–2.5 m) is smaller than the range of variability of Δh (−12–12 m). Lower differences characterize the GNSS–CTN pairs for the differences ΔN (P0.25 = −0.39, μ = 0.12, and P0.75 = −0.09), ΔE (P0.25 = −0.47, μ = −0.13, and P0.75 = 0.17), and Δh (P0.25 = −0–09, μ = 0.03, and P0.75 = 0.19).
The range of variability of D2D (0–5 m) is, consequently, smaller than the range of variability of D3D (0–12 m). Lower differences characterize again the GNSS–CTN differences: P0.25 = 0.33, μ = 0.68, and P0.75 = 0.96 for the planimetric composition, and P0.25 = 0.45, μ = 0.74, and P0.75 = 1.03 for the plano-altimetric composition (Figure 8).
4. Conclusions
As a result of this work, the congruence of some cadastral marks was assessed on the official maps produced by the cadastral bureau, the local cartography, and Google Earth maps. Of course, results refer to only one cadastral system used in a particular country (Italy). However, the experimental results show centimetric accuracies achievable with the GNSS NRTK methodology, in both the planimetric and altimetric components, which is in agreement with [58], which found planimetric errors in the range of 0.03–0.08 m using the NRTK VRS observation technique at selected Cadastral Reference Mark points. Meanwhile, the accuracies obtained from the georeferencing of the cadastral maps show differences in the order of 0.4–0.8 m, always adhering to the planimetric accuracy of the maps under investigation.
In particular, the descriptive statistics of the coordinate differences of both planimetric components, ΔE and ΔN, show the smallest mean, median, standard deviation, and IQR for the GNSS–CTN pairs (<0.75 m), while kurtosis and skewness are smaller for the pairs MC–GE (ΔE component) and GE–CTN (ΔN component).
Based on the Mardia multivariate normality analyses for skewness and kurtosis of the pairs ΔE–ΔN, the pairs GNSS–CTN and GNSS–GE show a normal distribution after outliers’ removal (p-value = 0.13 and 0.06, respectively, for GNSS–CTN, and p-value = 0.07 and 0.06, respectively, for GNSS–GE).
On the other hand, in Royston’s multivariate normality and the Doornik–Hansen omnibus tests of the pairs ΔE–ΔN, the pairs GNSS–GE and GNSS–MS follow a normal distribution after outliers’ removal (p-value = 0.05 and 0.06, respectively, for Royston’s multivariate normality test, and p-value = 0.07 and 0.10, respectively, for the Doornik–Hansen omnibus test. The pairs GNSS–CTN, MC–GE, and GE–CTN return a multivariate normal distribution in only one of the tests.
The graphical verification of the bivariate normal distribution through the representation of the confidence ellipse clearly shows that the pairs GNSS–CTN are characterized by a range of variability one-fifth smaller than all the other pairs.
Regarding the altimetric differences Δh, results are shown on the pairs GE–CTN, GNSS–CTN, and GNSS–GE, since the altimetric positions of MC are not available. The Q–Q plot is represented to graphically verify the univariate normal distribution of ΔH. The GNSS–CTN pairs show the closest quantiles to the bisector line, indicating that the empirical distribution is more similar to the theoretical one. Regarding the Shapiro–Wilk and D’Agostino–Pearson tests of the pairs Δh after outliers’ removal, both tests return a normal distribution for all the pairs (GE–CTN, GNSS–CTN, and GNSS–GE) (p-value = 0.20, 0.62, and 0.25, and p-value = 0.19, 0.59, and 0.20, respectively). Finally, regarding the quantile analyses of the coordinate components and the planimetric and plano-altimetric differences, the smallest characterize the GNSS–CTN pairs for the differences. The range of variability of the planimetric components was one-fifth of the range of variability of the altimetric component.
It needs to be remarked that this work aimed to analyze the congruence of the PF positions obtained with different methods (GE, CTN, MC, and GNSS), not to evaluate the position accuracies. Most of the analyses indicate that the highest congruencies seem to characterize the pairs GNSS–CTN.
The rapid advances in the GNSS technology affected surveyors’ profession and facilitated the use of satellite-based positioning systems, especially with the advent of the NRTK correction.
Indeed, GNSS surveying has advantages, such as not requiring surveying points seeing each other, besides being a fast positioning method. Although NRTK correction could be not always available, GNSS fixed solutions could be affected by high-voltage transmission lines, and reflecting surfaces, such as metal roofing, big vehicles, and large water surface, in surveying areas may cause multipath error [59]. However, the GNSS surveying scheme requires auxiliary measurements. Indeed, when GNSS receivers cannot be placed on the cadastral mark, a lateral offset method or forward intersection needs to be employed.
The future development of cartographic maps, and in particular both those developed by AE in Web Map Service (WMS) standard and those updated by Google Earth, would allow completing the analysis carried out in this study. The AE, in the context of the project for the implementation of the European Directive INSPIRE (INfrastructure for SPatial InfoRmation in Europe), makes the cadastral cartography available for consultation by public administrations, enterprises, professionals, and citizens, through interoperability services based on the latest international standards. The consultation service is realized according to the WMS standard and allows one to navigate many cadastral map contents and visualize them integrated with other spatial data, directly through GIS software or specific user applications.
In addition, in view of the forthcoming upgrades of GNSS receivers to the quadri-constellations [60], namely, BeiDou (BDS), Galileo, Glonass, and GPS, these instruments will allow for improving the accuracy of the coordinate positioning, given the larger number of satellites used and more uniform distribution of the dilution of the precision of the satellites.
Author Contributions
Conceptualization of the manuscript idea: G.D. and A.M.; methodology and software: A.M. and G.D.; writing—original draft preparation, G.D. and A.M.; review and editing, A.M. and G.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pregeo, L. Pregeo GPS Altimetria Proposta di Aggiornamento. Available online: https://swdownload2.agenziaentrate.gov.it/pub/pregeo/Guida-Pregeo.pdf (accessed on 6 July 2022).
- Agenzia delle Entrate Interrogazione Schede Monografiche Punti Fiduciali. Available online: https://www1.agenziaentrate.gov.it/servizi/Monografie/ricerca.php (accessed on 6 July 2022).
- Circolare, n. 3 del 16/10/2009—Agenzia del Territorio—Direzione Centrale Cartografia, Catasto e Pubblicita Immobiliare. Available online: https://def.finanze.it/DocTribFrontend/getPrassiDetail.do?id=%7B398FD334-5069-45C0-ADBB-986BDD4D0426%7D (accessed on 4 August 2022).
- Document Library|INSPIRE. Available online: https://inspire.ec.europa.eu/docs (accessed on 3 August 2022).
- Istituto Geografico Militare—Direzione Geodetica. Codici EPSG in Uso in Italia—IGM E-Commerce Site. Available online: https://www.igmi.org/it/descrizione-prodotti/elementi-geodetici-1/EPSG_Italia (accessed on 4 August 2022).
- Hope, S.; Gordini, C.; Kealy, A. Positional Accuracy Improvement: Lessons Learned from Regional Victoria, Australia. Surv. Rev. 2008, 40, 29–42. [Google Scholar] [CrossRef]
- Tong, X.; Shi, W.; Liu, D. Introducing Scale Parameters for Adjusting Area Objects in GIS Based on Least Squares and Variance Component Estimation. Int. J. Geogr. Inf. Sci. 2009, 23, 1413–1432. [Google Scholar] [CrossRef]
- Janssen, V.; Grinter, T.; Roberts, C. Can RTK GPS Be Used to Improve Cadastral Infrastructure? Eng. J. 2011, 15, 43–54. [Google Scholar] [CrossRef] [Green Version]
- Dabove, P. The Usability of GNSS Mass-Market Receivers for Cadastral Surveys Considering RTK and NRTK Techniques. Geod. Geodyn. 2019, 10, 282–289. [Google Scholar] [CrossRef]
- Cina, A.; Manzino, A.M.; Manzino, G. Recovery of Cadastral Boundaries with GNSS Equipment. Surv. Rev. 2016, 48, 338–346. [Google Scholar] [CrossRef] [Green Version]
- Charoenkalunyuta, T.; Satirapod, C.; Keitniyomrung, V.; Yomwan, P. Performance of Network-Based RTK GNSS for the Cadastral Survey in Thailand. Int. J. Geoinform. 2019, 15, 13–19. [Google Scholar]
- Housarová, E. Testing RPAS for cadastre purposes. In Proceedings of the 15th International Multidisciplinary Scientific Geoconference SGEM 2015, Albena, Bulgaria, 18–24 June 2015. [Google Scholar]
- Yuwono, B.D.; Suprayogi, A.; Azeriansyah, R.; Nukita, D. UAV Photogrammetry Implementation Based on GNSS CORS UDIP to Enhance Cadastral Surveying and Monitoring Urban Development (Case Study: Ngresep Semarang). IOP Conf. Ser. Earth Environ. Sci. 2018, 165, 012031. [Google Scholar] [CrossRef]
- Bramanto, B.; Gumilar, I.; Taufik, M.; Hermawan, I. Long-Range Single Baseline RTK GNSS Positioning for Land Cadastral Survey Mapping. E3S Web Conf. 2019, 94, 01022. [Google Scholar] [CrossRef]
- Gill, J.; Shariff, N.S.; Omar, K.M.; Din, A.H.M.; Amin, Z.M. A Review on legal traceability of GNSS measurements in the malaysian cadastral practice. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Kuala Lumpur, Malaysia, 3–5 October 2016; Volume XLII-4-W1, pp. 191–197. [Google Scholar]
- Erenoglu, R.C. A Comprehensive Evaluation of GNSS- and CORS-Based Positioning and Terrestrial Surveying for Cadastral Surveys. Surv. Rev. 2017, 49, 28–38. [Google Scholar] [CrossRef]
- Lauterbach, R.; Timo de Vries, W. Beyond Accuracy: Evaluating Alternative Measurement Methods in Context of Flexible Land Tenure System in Namibia. Surv. Rev. 2022, 54, 281–289. [Google Scholar] [CrossRef]
- Melnikov, A.; Poddubsky, A.; Aleshin, M.; Kalyadina, A. The Study of Possibility of Using Web Service Csrs-Ppp for Processing the Results of GNSS Observations by Precise Point Positioning Method for Geodetic Support of Cadastral Works. Int. Multidiscip. Sci. GeoConf. 2020, 20, 131–138. [Google Scholar]
- Beinat, A.; Crosilla, F. Generalised Procrustes Algorithms for the Conformal Updating of a Cadastral Map. ZFV Z. Geodasie Geoinf. Landmanag. 2003, 128, 341–348. [Google Scholar]
- Agenzia del Territorio. Istruzioni GPS e Altimetria. Available online: https://www.geolive.org/normativa/tutte-le-circolari-riguardanti-pregeo/2003/istruzioni-gps-e-altimetria-1161/ (accessed on 3 August 2022).
- Pullar, D.; Donaldson, S. Accuracy Issues for Spatial Update of Digital Cadastral Maps. ISPRS Int. J. Geo-Inf. 2022, 11, 221. [Google Scholar] [CrossRef]
- Dardanelli, G.; Lo Brutto, M.; Pipitone, C. GNSS Cors Network of the University of Palermo: Design and First Analysis of Data. Geogr. Tech. 2020, 15, 43–69. [Google Scholar] [CrossRef]
- Maseroli, R. Evoluzione del Sistema Geodetico di Riferimento in Italia: La RDN2. Boll. Assoc. Ital. Cartogr. 2015, 153, 19–44. [Google Scholar] [CrossRef]
- Kenyeres, A.; Bellet, J.G.; Bruyninx, C.; Caporali, A.; de Doncker, F.; Droscak, B.; Duret, A.; Franke, P.; Georgiev, I.; Bingley, R.; et al. Regional Integration of Long-Term National Dense GNSS Network Solutions. GPS Solut. 2019, 23, 122. [Google Scholar] [CrossRef] [Green Version]
- Dardanelli, G.; Maltese, A.; Pipitone, C.; Pisciotta, A.; Lo Brutto, M. Nrtk, Ppp or Static, That Is the Question. Testing Different Positioning Solutions for Gnss Survey. Remote Sens. 2021, 13, 1406. [Google Scholar] [CrossRef]
- Dardanelli, G.; Pipitone, C. The Effects of Cors Network Geometry and Differential Nrtk Corrections on Gnss Solutions. Geogr. Tech. 2021, 16, 56–69. [Google Scholar] [CrossRef]
- Timár, G.; Baiocchi, V.; Lelo, K. Geodetic Datums of the Italian Cadastral Systems. Geogr. Tech. 2011, 6, 82–90. [Google Scholar]
- Baiocchi, V.; Deligios, M.; Giannone, F.; Timar, G. Reconstruction of historical geodetic systems for Their implementation in reprojection algorithms. In Proceedings of the 2nd International Conference of Geomatics and Restoration, Milan, Italy, 8–10 May 2019; Volume 42, pp. 127–131. [Google Scholar]
- Burša, M. The theory for the determination of the non-parallelism of the minor axis of the reference ellipsoid and the inertial polar axis of the Earth, and the planes of the initial astronomic and geodetic meridians from observations of artificial Earth satellites. Stud. Geophys Geod. 1962, 6, 209–214. [Google Scholar] [CrossRef]
- Deakin, R. A Note on the Bursa-Wolf and Molodensky-Badekas Transformations. Sch. Math. Geospat. Sci. RMIT Univ. 2006, 1, 21. [Google Scholar]
- Molodenskiy, M.S.; Eremeyev, V.F.; Yurkina, M.I. Methods for Studying the External Gravitational Field and the Figure of the Earth. Trudy TSNIIGAiK 1960, 131, 250–251. [Google Scholar]
- Molnár, G.; Timár, G. A Legjobb Vízszintes Illeszkedést Biztosító Molodensky-Paraméterek Meghatározása Azonos Pontok Adatai Alapján. Geodézia Kartográfia 2004, 56, 9–13. [Google Scholar]
- Antongiovanni, R.; Ghetti, G. Problemi Riguardanti La Correlazione Fra i Vari Sistemi Locali Catastali, Fra Loro e Con Il Sistema Di GaussBoaga, Risolti Con l’ausilio Del Personal Computer. Riv. Del Catasto Dei Serv. Tec. Erariali 1985, 2, 79–98. [Google Scholar]
- Leick, A. GPS Satellite Surveying; John Wiley and Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- VERTO2K and VERTO3K SOFTWARE. Available online: https://www.igmi.org/en/descrizione-prodotti/elementi-geodetici-1/software-verto-2k-3k?set_language=en (accessed on 2 August 2022).
- Agenzia del Territorio. Disposizioni Operative in Materia di Fornitura Delle Mappe Catastali d’impianto per le Attività di Acquisizione in Formato Digitale. Available online: https://www.geolive.org/normativa/procedure-operative/2008/scansione-mappe-originali-di-impianto-disposizione-operativa-39391-27mag2008-309/ (accessed on 4 August 2022).
- Regione Siciliana. Assessorato Territorio e Ambiente Dipartimento Urbanistica Area 2 Interdipartimentale Servizi Informativi Territoriali e Cartografia Nodo Regionale S.I.T.R. Geoportale Regione Siciliana—Infrastruttura Dati Territoriali—S.I.T.R. Available online: https://www.sitr.regione.sicilia.it/geoportale/it/Home/GeoViewer (accessed on 6 July 2022).
- Google LLC. Google Earth. Available online: https://www.google.com/intl/it/earth/ (accessed on 6 July 2022).
- Grossner, K.; Clarke, K. Is Google Earth, “Digital Earth?”—Defining a vision. In Proceedings of the Fifth International Symposium on Digital Earth, Berkeley, CA, USA, 5 June 2007. [Google Scholar]
- Goodchild, M.F. Cartographic Futures on A Digital Earth. Cartogr. Perspect. 2000, 3–11. [Google Scholar] [CrossRef]
- Pulighe, G.; Baiocchi, V.; Lupia, F. Horizontal Accuracy Assessment of Very High Resolution Google Earth Images in the City of Rome, Italy. Int. J. Digit. Earth 2016, 9, 342–362. [Google Scholar] [CrossRef]
- Potere, D. Horizontal Positional Accuracy of Google Earth’s High-Resolution Imagery Archive. Sensors 2008, 8, 7973–7981. [Google Scholar] [CrossRef]
- Zomrawi, N.; Ahmed, G.; Eldin, M. Positional Accuracy Testing of Google Earth. Int. J. Multidiscip. Sci. Eng. 2013, 4, 6–9. [Google Scholar]
- Guo, J.; Tu, H.J.; Li, H.; Zhao, Y.; Zhou, J. Horizontal Accuracy Assessment of Google Earth Data Overtypical Regions of Australia Using Worldview. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2021, XLIII-B3-2021, 763–768. [Google Scholar] [CrossRef]
- Farah, A.; Algarni, D. Positional Accuracy Assessment of Google Earth in Riyadh. Artif. Satell. 2014, 49, 101–106. [Google Scholar] [CrossRef] [Green Version]
- Adam, S.M.; Heeto, A.F. The Use of Semi-Automated Method for Assessing the Horizontal Positional Accuracy of Google Earth Imagery. Acad. J. Nawroz Univ. 2018, 7, 173. [Google Scholar] [CrossRef]
- Mardia, K.V. Measures of Multivariate Skewness and Kurtosis with Applications. Biometrika 1970, 57, 519–530. [Google Scholar] [CrossRef]
- Royston, J.P. An Extension of Shapiro and Wilk’s W Test for Normality to Large Samples. J. R. Stat. Soc. Ser. C Appl. Stat. 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Royston, J.P. Some Techniques for Assessing Multivarate Normality Based on the Shapiro-Wilk W. J. R. Stat. Society. Ser. C Appl. Stat. 1983, 32, 121–133. [Google Scholar] [CrossRef]
- Royston, J.P. Remark ASR 63: A Remark on AS 181. The W Test for Normality. J. R. Stat. Soc. Ser. C Appl. Stat. 1986, 35, 232–234. [Google Scholar] [CrossRef]
- Royston, P. Approximating the Shapiro-Wilk W-Test for Non-Normality. Stat. Comput. 1992, 2, 117–119. [Google Scholar] [CrossRef]
- Doornik, J.A.; Hansen, H. An Omnibus Test for Univariate and Multivariate Normality. Oxf. Bull. Econ. Stat. 2008, 70, 927–939. [Google Scholar] [CrossRef]
- Semantic Scholar. An Analysis of Variance Test for Normality (Complete Samp 1 Es) t. Available online: https://www.semanticscholar.org/paper/An-analysis-of-variance-test-for-normality- (accessed on 27 June 2022).
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- D’Agostino, R.B. Transformation to Normality of the Null Distribution of g 1. Biometrika 1970, 57, 679. [Google Scholar] [CrossRef]
- D’Agostino, R.; Pearson, E.S. Tests for Departure from Normality. Empirical Results for the Distributions of b 2 and √b 1. Biometrika 1973, 60, 613. [Google Scholar] [CrossRef]
- Dekking, F.M.; Kraaikamp, C.; Lopuhaä, H.P.; Meester, L.E. A Modern Introduction to Probability and Statistics; Springer Texts in Statistics; Springer: London, UK, 2005; ISBN 978-1-85233-896-1. [Google Scholar]
- Amirrudin, M.; Md Din, A.H.; Zulkifli, N.A.; Che Amat, A.; Hamden, M. Assessment of The Accuracy and Precision of Myrtknet Real-Time Services. J. Teknol. 2020, 83, 93–103. [Google Scholar] [CrossRef]
- Alkan, R.M.; Murat Ozulu, I.; İlçi, V.; Engin Tombuş, F.; Şahin, M. Usability of GNSS Technique for Cadastral Surveying. In Cadastre: Geo-Information Innovations in Land Administration; Yomralioglu, T., McLaughlin, J., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 77–91. ISBN 978-3-319-51216-7. [Google Scholar]
- Jin, S.; Wang, Q.; Dardanelli, G. A Review on Multi-GNSS for Earth Observation and Emerging Applications. Remote Sens. 2022, 14, 3930. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).