Abstract
Satellite-based gross primary production (GPP) estimation has uncertainties due to shadow fraction caused by the geometric relationship between the complex forest structure and the Sun. The virtual forests allow shadow fraction estimation without 3D measurements, but require optimal structural parameters. In this study, we developed the reflectance simulator (Canopy-level Shadow and Reflectance Simulator, CSRS) that considers tree shadows and the method to determine the optimal canopy shape for shadow fraction estimation. The target forest is any tropical evergreen forest which accounts for 58% of tropical forests. Firstly, we analyzed the effects of canopy shape on the reflectance simulation based on virtual forests created with different canopy shapes. This result was checked by Tukey’s honestly significant difference (HSD) test. Secondly, the optimal canopy shape was determined by comparing the reflectance from Sentinel-2 Band 4 (red) bottom of atmosphere reflectance with those simulated from virtual forests. Finally, the shadow fraction estimated from the virtual forest was evaluated. Since the focus of this study was to derive the optimal canopy shape, unmanned aerial vehicle (UAV) structure from motion (SfM) was used to obtain the parameters other than canopy shape and to validate the estimated shadow fraction. The results showed that when the Sun zenith angle (SZA) was more than 20°, significant differences were observed among canopy shapes. The least root mean square error (RMSE) for reflectance simulation was 0.385 from the canopy shape of a half ellipsoid. Moreover, the half ellipsoid also showed the smallest RMSE in estimating shadow fraction (0.032), which indicated the reliability and applicability of CSRS. This study is the first attempt to determine the optimal canopy shape for estimating shadow fraction and is expected to improve the accuracy of GPP estimation in the future.
1. Introduction
Tropical forests account for 45% of the world’s forests [1] and 34% of global ground gross primary production (GPP) [2]. Tropical evergreen forests are some of the most important tropical forests, and are the majority of them, up to 58% [3]. Due to cloud contamination and the complicated three-dimensional (3D) structure of forests, it is difficult to estimate the GPP using remote sensing with high accuracy in such forests. Recently, geostationary satellites such as HIMAWARI and GOES [4,5] have provided opportunities to acquire cloud-free images. However, uncertainties caused by the complicated forest structures remain. In particular, the shadow fraction is a major determinant of leaf surface conductance, which in turn affects the net photosynthetic rate and therefore, light use efficiency (LUE) and GPP of the forest [6,7]. Hilker et al. (2008) [8] showed that the inclusion of shadow fraction calculated from the digital surface model (DSM) in the LUE parameters increased the variance of the LUE by 5–16% compared to existing models driven by climate variables alone. Their study emphasized the importance of including shadow fraction caused by forest structure in LUE modeling, but limited measurements made it difficult to apply on a larger scale.
One of the methods to estimate the shadow fraction without 3D measurement is to use virtual forests. An advantage of using virtual forests is the estimation of diurnal shadows. A virtual forest is often used to develop an equation relating the physical quantity of the forest to the reflectance observed by the satellite sensor. Since the shadow fraction is closely related to the forest roughness [9], the virtual forest should be composed of tree models at level 2—which consider geometric characteristics such as canopy shape, crown width and crown depth—or higher according to the level of tree (LOT) [10]. Currently, there is an increasing number of globally available datasets on forest structure, such as tree height (TH) [11,12,13] and tree density [14]. Despite canopy shape also being an important parameter that determines forest surface roughness [15], it is estimated by researcher’s experience or assigned by a forest category defined by the International Geosphere-Biosphere Programme (IGBP). Typically, cones and ellipsoids are used for coniferous forests and broadleaf forests to represent canopy shapes, respectively, [16,17,18]. However, the canopy shapes for tropical rainforests with various tree species are uncertain, depending on the experience of different researchers. Therefore, it is necessary to determine the optimal canopy shape for virtual forests to estimate the shadow fraction. Moreover, in some satellite-based products, such as clumping index (CI), it has also been pointed out that we should correctly assign the canopy shape because the product is sensitive to the shadow fraction [19,20].
The shadow fraction generated by the forest surface significantly alters the reflectance observed in the bidirectional reflectance distribution function (BRDF) [21,22]. This implies that the closer the shadow fraction estimated from the virtual forest is to one from the actual forest, the closer the reflectance simulated from the virtual forest is to that observed by the satellite. Therefore, it is expected that the shadow fraction of the actual forest can be estimated by using a virtual forest with the least reflectance simulation error among the virtual forests with different structural parameters. The reflectance simulation model must account for the shadows of the trees. The objective of this study was to develop a reflectance simulator (Canopy-level Shadow and Reflectance Simulator; CSRS), and to find the optimal canopy shape for estimating the shadow fraction using the reflectance observed by satellite sensors as a constraint.
Several challenges were already known of for reflectance simulation approaches [23]. The first is the accuracy of structural parameters other than canopy shape. In this study, parameters such as crown coverage (CC) and TH were obtained by unmanned aerial vehicle (UAV) structure from motion (SfM). The second is using absolute reflectance as a constraint condition. If a parameter of CSRS, such as spectral reflectance of leaves, differs from the actual one, the error will be large, even if other parameters are accurate. Therefore, relative reflectance is used in this study (the ratio of absolute reflectance in two seasons). In case the phenological change is less, as in tropical rainforests [24], it is assumed that the change in reflectance observed by the satellite in the two seasons is affected by shadow due to canopy shape and Sun zenith angle (SZA). The size of the virtual forest should consider the spatial resolution of satellite sensors. If the target sensor is MODIS with a spatial resolution of 500 m, it may result in a heterogeneous forest structure within a pixel. This means the parameter setting is complicated (e.g., cylinder 30% and ellipsoid 70%). Therefore, in this study, Sentinel-2 satellite, which has a high spatial resolution (10–20 m) and is freely available, was selected as the target. We assumed that the forest within one pixel of Sentinel-2 is composed of a single canopy shape. The main objectives of this study using CSRS were: (1) to analyze the effects of canopy shape on simulating reflectance, (2) to obtain the optimal canopy shapes of virtual forests by reflectance simulation, and (3) to evaluate the performance of the optimal canopy shape on shadow fraction estimation.
2. Methodology
2.1. Study Area
The tropical rainforest in this study is located in Yangon Technological University (N, E), Myanmar, as displayed in Figure 1. The size of the study area is 400 m × 200 m. The study area is flat, being without mountains or other high buildings, and has a tropical monsoon climate [25]. This forest is composed of several tree species, not one.
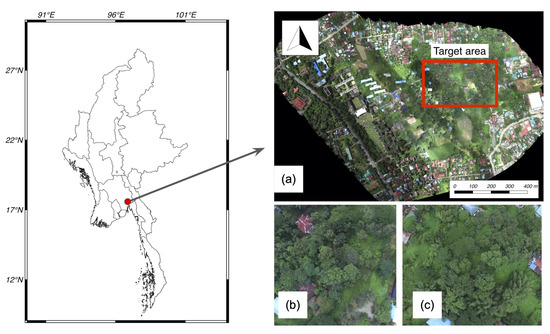
Figure 1.
Location of the study area: (a) Overall target forest (red rectangular shows the target area of 400 m × 200 m). (b,c) Photographs taken by UAV (30 September 2018).
2.2. Sentinel-2 Image
The Bottom Of Atmosphere (BOA) reflectance provided by the Level-2 product from Sentinel-2 was used as a constraint to use when determining the optimal canopy shape for estimating shadow fraction. The red to near infrared (NIR) band is sensitive to illumination conditions [26]. The NIR band is more affected by multiple scattering than the red band, and CSRS does not consider multiple scattering. Therefore, in this study, the reflectance of Band 4 (red, center wavelength of 665 nm, spatial resolution of 10 m) of Sentinel-2 was simulated. The images used to calculate the relative reflectance were determined after investigating the SZA, which causes significant differences in reflectance due to canopy shape.
Figure 2 shows the satellite overpass times for Sentinel-2A and B in the target region for 2019, and the SZA and Sun Azimuth Angle (SAA) at the time of satellite overpass. Satellite images were obtained using Google Earth engine, and metadata were referenced to plot the time of overpass, SZA and SAA. Sentinel-2A and Sentinel-2B acquired 38 and 37 images, respectively.
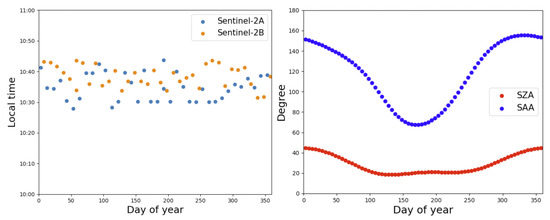
Figure 2.
Sentinel-2A/B local overpass time in 2019 (left) and Sun zenith angle and Sun azimuth angle during the time of Sentinel-2A/B overpass in the target area (right).
2.3. Research Flow
The overall flowchart of this study is shown in Figure 3. First, several virtual forests were created in step 1. Parameters other than canopy shape (e.g., TH and CC) were obtained from point clouds acquired by UAV-SfM. The canopy shapes used were cylinder, ellipsoid, half ellipsoid, and inverted half ellipsoid, as shown in Figure 4. The tree model parameters TH, canopy length (CL), canopy radius (CR) and diameter at breast height (DBH) were also referenced to the UAV-SfM results. We used Phantom 4 for UAV observation and flight condition, as shown in Table 1. Details on the parameters used for the virtual forests can be found in Section 2.5. In Step 2, CSRS was used to simulate the reflectance of each virtual forest under several SZA conditions. The aim of the step 2 was to analyze the effect of canopy shape on simulated reflectance and to determine the SZA to be employed when finding the optimal canopy shape in the next step. Therefore, the analysis in step 2 could not be performed using a specific satellite image. Then, we used the , , , and SZAs in this step based on the SZAs checked in Section 2.2 for satellite overpasses over a one-year period. For the SAA, we assumed that the effect of the SAA was less and set it to because of the symmetrical canopy shape. The description of CSRS is in Section 2.4, and the detail simulation conditions are described in Section 2.5. To investigate the significant difference between each simulated reflectance, we applied Tukey’s honestly significant difference (HSD) test. After that, in step 3, the optimal canopy shape for estimating the shadow fraction was determined. We determined the optimal canopy shape by minimizing the discrepancy between the simulated reflectance from the virtual forest and the reflectance observed by satellite sensor. Based on the results of step 2, Sentinel-2 images were selected that satisfy the SZA, which causes significant differences among canopy shapes in reflectance. Finally, the shadow fractions calculated from virtual forests were compared with those calculated from the 3D model acquired by UAV-SfM in target forest.

Figure 3.
Overall flowchart of this study.
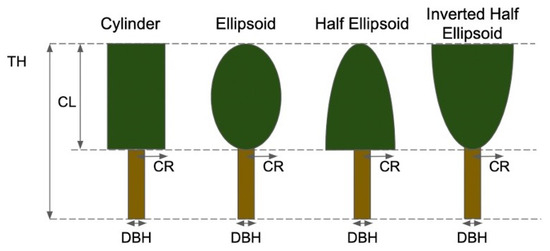
Figure 4.
Canopy shapes used for the virtual forest. The canopy structures are tree height (TH), canopy length (CL), canopy radius (CR) and diameter at breast height (DBH).

Table 1.
Specifications of the UAV and flight conditions.
2.4. Description of Canopy-Level Shadow and Reflectance Simulator
Various simulation models have been developed to understand the relationships between the reflectance which the satellite sensor observes and forest structures (e.g., the Discrete Anisotropic Radiative Transfer Model (DART) [27], Forest Light Environmental Simulator (FLiES) [28], and Radiosity–Graphics combined Method (RGM) [29]). While the accuracy of simulated reflectance obtained from those simulators is high, it is necessary to provide parameters obtained through field measurements. The simulator required in this study considers the shadow fraction caused by canopy shapes of the virtual forest. Then, we focused on the simulation model which uses shadows caused by trees as the shielding ratios of direct and diffuse solar irradiance reaching the forest developed by Fujiwara and Takeuchi (2021) [23]. Therefore, we developed CSRS (https://github.com/Takumi-Fuji6936/CSRS.git, accessed on 29 June 2022), which incorporates that simulation model into a virtual forest. CSRS has the following three advantages. (1) The canopy shape can be freely changed as long as it is geometrically representable, (2) compared to existing simulators, CSRS requires fewer parameters, and (3) the irradiance reaching the virtual forest at an arbitrary point in time can be calculated at the voxel level by considering the shadows of the trees.
The scale of the virtual forest was 50 m × 50 m, as shown in Figure 5. Individual trees in the virtual forest were represented by voxel models with a size of 0.5 m. After the virtual forest’s creation, Cast Shadow (CS) and Self Cast Shadow (SCS), which correspond to the shielding ratios of direct and diffuse solar irradiance, were calculated for each voxel. The details on the calculation methods of CS and SCS can be found in Fujiwara and Takeuchi [30]. Reflectance was then calculated for each voxel according to Equations (1)–(3). Since the lateral boundaries of the forest scene were not taken into account, voxels within a central 40 m × 40 m area were used for computing reflectance. With a target pixel size of 10 m, 16 pixels could be obtained from a single forest scene. In this study, three virtual forest scenes were created by changing the tree positions randomly, so 48 pixels of reflectance were calculated per canopy shape.
where () is radiance from a voxel considering and (W/m/sr/m); is the wavelength; () is direct horizontal irradiance (W/m/m); () is diffuse horizontal irradiance (W/m/m); () is spectral reflectance of the over- and understory; () is radiance which the sensor observes (W/m/sr/m); () is the spectral response function of the target sensor; () is reflectance observed by the satellite.
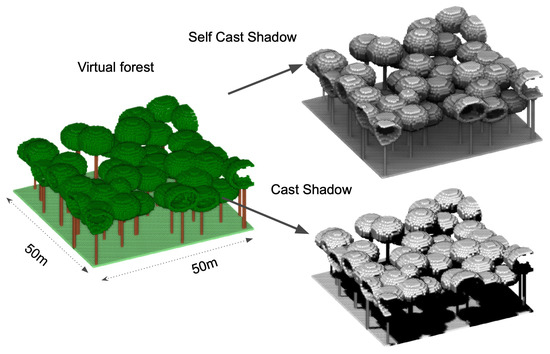
Figure 5.
Schematic illustration of the virtual forest scene.
2.5. Forest Scene and Parameters
Table 2 shows the parameter list of CSRS in reflectance simulation. Slope, TH, CC, CR, CL and DBH were obtained from the UAV-SfM [23]. Four patterns of virtual forests were created, along with four different canopy shapes. The Simple Model of the Atmospheric Radiative Transfer of Sunshine (SMARTS) code, version 2.9.5. [31], was employed to calculate the direct and diffuse irradiance. The spectral reflectance data of overstory and understory were selected among tree species which are found in Southeast Asia from ECOSTRESS Spectral Library (version 1.0) (https://speclib.jpl.nasa.gov, accessed on 15 May 2022). Reflectance data of Prosopis articulata from tropical South Asia were used for overstory reflectance, and data from a grass species (Avena fatua) were used for forest floor reflectance. The wavelength interval was 1 nm. SZA was changed from to in a increment, and SAA was set to .

Table 2.
Characteristics of the forest scenes and optical parameters used in the simulation.
2.6. Performance Assessment of Estimated Reflectance and Shadow Fraction
The assessment of error using relative reflectance was evaluated by root mean square error (RMSE) of the reflectance for the two seasons obtained from Sentinel-2 and CSRS, respectively, as shown in Equation (4). Based on the results of step 2, images for the two seasons were selected.
To evaluate the shadow fraction estimated by CSRS, we compared it with one calculated from the voxel model based on the point cloud data obtained by UAV-SfM. The shadow fraction was calculated under solar geometry conditions at 8:00, 10:00, 12:00, 14:00 and 16:00 on UAV observation date (30 September 2018). The corresponding solar geometry is listed in Table 3. In addition, we calculated the RMSE (Equation (5)) to evaluate the performance of the simulated shadow fraction from the virtual forest.
where is the RMSE of relative reflectance between Sentinel-2 and simulation; (season ) is average reflectance from Sentinel-2 at season ; (season ) is the simulated reflectance at season .
where is the RMSE between shadow fraction calculated from the 3D model obtained from UAV-SfM and simulation.

Table 3.
Solar geometric conditions for estimating shadow fraction.
3. Results
3.1. Reflectance Simulation under Several SZA
Firstly, the effect of SZA was investigated on each canopy shape. Figure 6 plots the relative changes in reflectance at 20°, 30°, and 40° SZA for each canopy shape, based on reflectance at 10° SZA. For cylinders and inverted half ellipsoids, relative reflectance decreased to 0.9 when SZA increased from 10° to 20°; however, when SZA increased from 20° to 40°, the values were almost 0.9. For ellipsoid, relative reflectance decreased to 0.8 when SZA increased from 10° to 20°, but even when SZA increased from 20° to 40°, the mean values did not change. For the half ellipsoid, relative reflectance decreased to 0.8 when SZA increased from 10° to 20°, and when SZA increased 20° to 40°, the values decreased to 0.7.
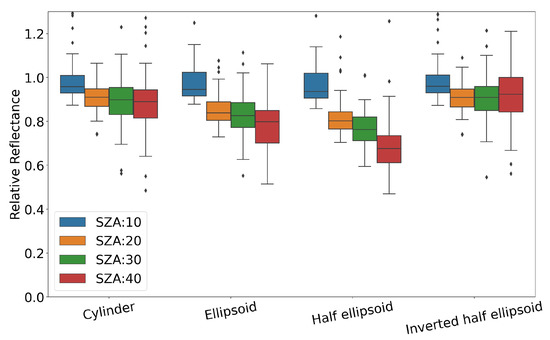
Figure 6.
Relative reflectance simulated at SZA from 10° to 40° for each tree canopy shape. Base reflectance is mean reflectance at SZA 10° for each canopy shape.
Secondly, the effect of canopy shape on the same SZA was investigated. Figure 7 shows the reflectance simulation results for the same SZA with different canopy shapes. As shown in Figure 7, when SZA is 10° to, the simulated reflectances of the four canopy geometries are almost the same. When SZA is greater than 20° to, the cylinder and the inverted half ellipsoid have almost the same reflectance and higher reflectance than the other two. It also shows that the ellipsoid is higher in reflectance than the half ellipsoid. Table 4 shows the results of multiple comparisons by Tukey’s HSD test on the results. The p value was set to 0.05. No significant difference in reflectance obtained from each canopy shape was observed when SZA was 10° to, but when SZA was greater than 10° to, the differences in reflectance among canopy shapes became larger. However, as mentioned above, no significant difference was observed between the canopy shapes of the cylinder and the inverted half ellipsoid.
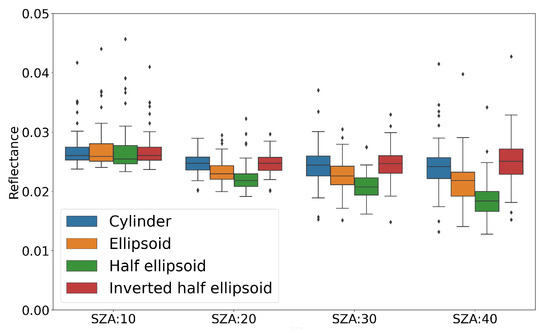
Figure 7.
Reflectance simulation results for the same SZA with different canopy shapes. X-axis is SZA and y-axis is reflectance.

Table 4.
Multiple comparisons using Tukey’s HSD test for reflectance simulation results for different canopy shapes in each SZA (C: cylinder, E: ellipsoid, HE: half ellipsoid and IHE: inverted half ellipsoid). p value is 0.05.
3.2. Determination of Optimal Canopy Shape and Comparison of Shadow Fraction
Based on the results in Section 3.1, Sentinel-2 images from the two seasons with SZA close to 20° and 40°, shown in Table 5, were employed in the simulations. Due to the availability of Sentinel-2 BOA products beginning at the end of 2019 in the target area and cloud contamination, images in 2019 and 2020 were used. The relative reflectance was calculated using the average of the reflectance for each of Season 1 and Season 2. Note that because non-forest pixels, such as those for buildings, exist in the target forest, as shown in Figure 1, 40 forest pixels were sampled visually.

Table 5.
Date of Sentinel-2 image acquisition and Sun geometry conditions (Sun azimuth angle (SAA) and Sun zenith angle (SZA)).
Table 6 shows the RMSE of the Sentinel-2 Band 4 reflectance simulated and the simulated shadow fraction. The shadow fraction calculated from the voxel model based on the point cloud acquired by UAV-SfM was used for the comparison of shadow fractions. The canopy shape that had the lowest RMSE in both reflectance and shadow simulations was the half ellipsoid. The use of a canopy shape with a large error in the reflectance simulation also resulted in a larger error in the shadow fraction. The shadow fraction simulation shows that the RMSE differs by about 10% between canopy shapes with rounded (ellipsoid and half ellipsoid) and flat (cylinder and inverted half ellipsoid) tops.

Table 6.
RMSE of Sentinel-2 Band 4 reflectance simulation and shadow simulation in each canopy shape (C: cylinder, E: ellipsoid, HE: half ellipsoid and IHE: inverted half ellipsoid).
4. Discussion
4.1. The Effect of Canopy Shape on Reflectance Simulation
Considering the potential role of canopy shape in estimating reflectance and shadow fraction, it is crucial to quantify its effects, and therefore improve the simulation. The optimal canopy shape was determined by comparing the simulated reflectance with satellite-based reflectance, which enabled estimating the canopy shape without field measurements. This was the first study to conduct an analysis of canopy shape in a reflectance simulation. Based on the results of the analysis, we could choose the SZA when the canopy shape had the most significant effect on the reflectance simulation, namely, the SZA of 40°. At 40° SZA, the reflectance simulation varied distinctly with different canopy shapes and could therefore be used to determine the optimal combination. In addition, this method is flexible and can be applied to various forests by adjusting the parameters. The slope is also in the parameters, so forests in mountainous areas can also be represented.
The results in Table 6 showed that the optimal canopy shape that had the least RMSE (0.385) in the reflectance simulation also had the lowest RMSE (0.032) in the shadow fraction estimation. Additionally, canopy shapes with larger RMSE in the reflectance simulation had larger RMSE in the shadow simulation. These findings emphasize that the results of reflectance simulations using CSRS are effective for estimating the shadow fraction. Therefore, it is possible to determine the optimal canopy shape by simulating the reflectance using a virtual forest, and then applying it in estimating the shadow fraction.
Furthermore, relative reflectance calculated based on the images from two seasons was adopted instead of using absolute reflectance. In absolute reflectance, if the spectral reflectance of each overstory or understory given to the CSRS differs from the actual one, the error becomes larger. With relative reflectance, on the other hand, the effects of canopy shape and SZA are larger than those effects; this helped us with obtaining optimal canopy shape. Although the UAV-SfM results were used to determine parameters other than canopy shape in this study, satellite-based forest structure products or allometric equations for representative tree species contribute to not using field measurements. To extend the method greatly, it will be necessary to simulate various forest structures and create look-up tables for Sentinel-2 reflectance and canopy shape. This will enable estimation of shadow fraction at arbitrary locations, which is expected to further improve the accuracy of GPP estimation in the future. In addition, a trait-based approach using remote sensing data has recently been developed [32]. This approach is limited in coverage because the forest structure is obtained by the Airborne Laser Scanner, but it is expected that the method could be extended to a wider area by combining it with CSRS.
4.2. Limitations and Uncertainties of Reflectance Simulation
Despite the encouraging results of the proposed method in this study, there are still some limitations that should be addressed. Firstly, forest phenology could affect the reflectance simulation and shadow fraction estimation. In this study, we assumed that the phenology of tropical rainforest would not experience much change. Figure 8 shows the time series of Normalized Difference Vegetation Index (NDVI) in the target area using Sentinel-2 images between January 2019 and December 2020. The NDVI values were calculated from the same 40 pixels described in Section 3.2. As shown in Figure 8, the average of the NDVI shows a minimum in April at 0.7 and a maximum in October at 0.85, indicating that it fluctuates by about 0.15 throughout the year. Although NDVI is affected by many other environmental factors, such as shadows [33] and the water content of leaves [34], there is still a slight change in the phenology. Consequently, the use of relative reflectance could be affected by phenology, making it difficult to apply this method to forests with noticeable phenological variation. Secondly, there is uncertainty in the creation of virtual forests. Allometric equations were used to create the virtual forest, and growth of the canopy was assumed to be orthotropic. However, canopy shyness is an important factor for canopy closure [35,36,37]. Therefore, there may be differences between the actual forested landscape and the virtual forest.
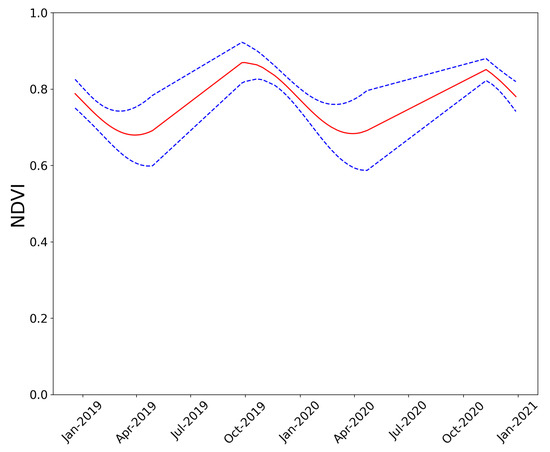
Figure 8.
Time series of NDVI in 2019 and 2020. The red line represents the mean value (50th percentile), the upper blue dashed line represents the 84th percentile and the lower blue dashed line the 16th percentile.
4.3. Future Work
The proposed method can be expected to be applicable to evergreen broadleaf forests (EBF) with little phenological variation. Although EBF accounts for 48% of the world’s forests [38], this study applied the proposed method to these forests with limited conditions. Characteristics of forests where the method is difficult to apply are having prominent tall trees, such as those found in natural forests, and sparsity of trees. The heights of trees in the virtual forests were assumed to follow a normal distribution, but the probability of generating a tree with a prominent height is low. In addition, since the CC was set to 80%, the reflectance of the canopy (leaves) had a large influence on the reflectance simulation. In sparse forests, on the other hand, the soil and forest floor have a greater influence. Therefore, it is necessary to further validate the effectiveness of CSRS in various forests.
Although only Sentinel-2 was targeted in this study, it is expected that the method could be applied to Landsat as well. It is recommended that the number of available satellite images increase, especially in areas where tropical rainforests are located, because the images are contaminated by clouds. However, when targeting satellite imagery coarser than the spatial resolution of Sentinel-2 and Landsat sensors, e.g., MODIS, there may be multiple canopy shapes within a pixel. It is necessary to simulate a virtual forest with multiple canopy shapes within a pixel.
Furthermore, boreal forest is second only to tropical forest in terms of the proportion of forest area, at 27.3% [1]. Moreover, it is very sensitive to the effects of climate change, and therefore, the GPP of boreal forest should be estimated with high accuracy. However, the canopy shape of boreal forest is asymmetrical, which is called tropism. Kobayashi et al. (2010) [16] suggested that the diversity of canopy shape, such as asymmetry, should be considered when creating virtual forests for boreal forests. Therefore, it is important to improve the CSRS by considering the asymmetric canopy shape, which could be more responsive to real forests and contribute to the shadow fraction estimation.
5. Conclusions
In conclusion, in this study, we analyzed the effect of canopy shape on simulating reflectance and estimated the optimal canopy shape using CSRS in the tropical rainforest—both firsts. The effect of canopy shape was negligible when SZA was 10°, but it increased with the increase in SZA. It is worth noting that the cylinders with flat canopy tops and inverted half ellipsoids showed similar reflectance. The reflectance of the half ellipsoid was lower than that of the ellipsoid, indicating the influence of shadows caused by the rounded lower part of the canopy. To determine the optimal canopy shape, we compared the reflectance of Sentinel-2 with the reflectance simulated from a virtual forest and found that the half ellipsoid performed the best, having the lowest RMSE, and this canopy shape showed the best results when estimating the shadow fraction. To improve the accuracy of the estimation in the future, it will be necessary to reduce the uncertainty caused by phenology, simulation models and virtual forest creation.
Author Contributions
Conceptualization, T.F. and W.T.; methodology, T.F. and W.T.; software, T.F.; validation, T.F.; formal analysis, T.F.; investigation, W.T.; resources, W.T.; data curation, T.F. and W.T.; writing—original draft preparation, T.F.; writing—review and editing, W.T.; visualization, T.F.; supervision, W.T.; project administration, W.T.; funding acquisition, W.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The simulation code of CSRS is available from https://github.com/Takumi-Fuji6936/CSRS.git (accessed on 29 June 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- FAO. Assessment, Global Forest Resources 2020. Available online: https://www.fao.org/3/CA8753EN/CA8753EN.pdf (accessed on 10 November 2021).
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hengl, T.; Walsh, M.G.; Sanderman, J.; Wheeler, I.; Harrison, S.P.; Prentice, I.C. Global mapping of potential natural vegetation: An assessment of machine learning algorithms for estimating land potential. PeerJ 2018, 6, e5457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miura, T.; Nagai, S.; Takeuchi, M.; Ichii, K.; Yoshioka, H. Improved Characterisation of Vegetation and Land Surface Seasonal Dynamics in Central Japan with Himawari-8 Hypertemporal Data. Sci. Rep. 2019, 9, 15692. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, H.; Wang, W.; Dungan, J.L.; Li, S.; Michaelis, A.R.; Takenaka, H.; Higuchi, A.; Myneni, R.B.; Nemani, R.R. New generation geostationary satellite observations support seasonality in greenness of the Amazon evergreen forests. Nat. Commun. 2021, 12, 684. [Google Scholar] [CrossRef] [PubMed]
- Brooks, J.R.; Flanagan, L.B.; Varney, G.T.; Ehleringer, J.R. Vertical gradients in photosynthetic gas exchange characteristics and refixation of respired CO2 within boreal forest canopies. Tree Physiol. 1997, 17, 1–12. [Google Scholar] [CrossRef]
- Ellsworth, D.S.; Reich, P.B. Canopy structure and vertical patterns of photosynthesis and related leaf traits in a deciduous forest. Oecologia 1993, 96, 169–178. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Schwalm, C.R.; Jassal, R.P.S.; Black, T.A.; Krishnan, P. Effects of mutual shading of tree crowns on prediction of photosynthetic light-use efficiency in a coastal Douglas-fir forest. Tree Physiol. 2008, 28, 825–834. [Google Scholar] [CrossRef]
- Kane, V.R.; Gillespie, A.R.; McGaughey, R.; Lutz, J.A.; Ceder, K.; Franklin, J.F. Interpretation and topographic compensation of conifer canopy self-shadowing. Remote Sens. Environ. 2008, 112, 3820–3832. [Google Scholar] [CrossRef]
- Chen, M. Comparison of 3D Tree Parameters. Master’s Thesis, Wageningen University and Research Centre, Wageningen, The Netherlands, 2013. [Google Scholar]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface Lidar Remote Sensing of Basal Area and Biomass in Deciduous Forests of Eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116, 4021. [Google Scholar] [CrossRef] [Green Version]
- Crowther, T.W.; Glick, H.B.; Covey, K.R.; Bettigole, C.; Maynard, D.S.; Thomas, S.M.; Smith, J.R.; Hintler, G.; Duguid, M.C.; Amatulli, G.; et al. Mapping tree density at a global scale. Nature 2015, 525, 201–205. [Google Scholar] [CrossRef] [PubMed]
- Nelson, R. Modeling forest canopy heights: The effects of canopy shape. Remote Sens. Environ. 1997, 60, 327–334. [Google Scholar] [CrossRef]
- Kobayashi, H.; Delbart, N.; Suzuki, R.; Kushida, K. A satellite-based method for monitoring seasonality in the overstory leaf area index of Siberian larch forest. J. Geophys. Res. Biogeosci. 2010, 115, 1002. [Google Scholar] [CrossRef] [Green Version]
- Ligot, G.; Ameztegui, A.; Courbaud, B.; Coll, L.; Kneeshaw, D. Tree light capture and spatial variability of understory light increase with species mixing and tree size heterogeneity. Can. J. For. Res. 2016, 46, 968–977. [Google Scholar] [CrossRef] [Green Version]
- Pisek, J.; Chen, J.M. Mapping forest background reflectivity over North America with Multi-angle Imaging SpectroRadiometer (MISR) data. Remote Sens. Environ. 2009, 113, 2412–2423. [Google Scholar] [CrossRef]
- Asner, G.P.; Braswell, B.H.; Schimel, D.S.; Wessman, C.A. Ecological Research Needs from Multiangle Remote Sensing Data. Remote Sens. Environ. 1998, 63, 155–165. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Global clumping index map derived from the MODIS BRDF product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. Four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Hasegawa, K.; Izumi, T.; Matsuyama, H.; Kajiwara, K.; Honda, Y. Seasonal change of bidirectional reflectance distribution function in mature Japanese larch forests and their phenology at the foot of Mt. Yatsugatake, central Japan. Remote Sens. Environ. 2018, 209, 524–539. [Google Scholar] [CrossRef]
- Fujiwara, T.; Takeuchi, W. Estimation of optimal crown coverage and canopy shape for shadow estimation on tropical moist broadleaf forest. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 5, 211–217. [Google Scholar] [CrossRef]
- Hmimina, G.; Dufrêne, E.; Pontailler, J.Y.; Delpierre, N.; Aubinet, M.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; Granier, A.; et al. Evaluation of the potential of MODIS satellite data to predict vegetation phenology in different biomes: An investigation using ground-based NDVI measurements. Remote Sens. Environ. 2013, 132, 145–158. [Google Scholar] [CrossRef]
- Myanmar Information Management Unit. Koppen–Geiger Climate Zones of Myanmar (1986–2010). Available online: https://themimu.info/sites/themimu.info/files/documents/Map_Koppen–Geiger_Climate_Zones_of_Myanmar_1986-2010_MIMU1548v01_17Jan2018_A4.pdf (accessed on 10 January 2021).
- Xu, N.; Tian, J.; Tian, Q.; Xu, K.; Tang, S. Analysis of Vegetation Red Edge with Different Illuminated/Shaded Canopy Proportions and to Construct Normalized Difference Canopy Shadow Index. Remote Sens. 2019, 11, 1192. [Google Scholar] [CrossRef] [Green Version]
- Gastellu-Etchegorry, J.P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling radiative transfer in heterogeneous 3-D vegetation canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, H.; Iwabuchi, H. A coupled 1-D atmosphere and 3-D canopy radiative transfer model for canopy reflectance, light environment, and photosynthesis simulation in a heterogeneous landscape. Remote Sens. Environ. 2008, 112, 173–185. [Google Scholar] [CrossRef]
- Qin, W.; Gerstl, S.A. 3-D Scene Modeling of Semidesert Vegetation Cover and its Radiation Regime. Remote Sens. Environ. 2000, 74, 145–162. [Google Scholar] [CrossRef]
- Fujiwara, T.; Takeuchi, W. Simulation of Sentinel-2 Bottom of Atmosphere Reflectance Using Shadow Parameters on a Deciduous Forest in Thailand. ISPRS Int. J. Geo-Inf. 2020, 9, 582. [Google Scholar] [CrossRef]
- Gueymard, C.A. Parameterized transmittance model for direct beam and circumsolar spectral irradiance. Sol. Energy 2001, 71, 325–346. [Google Scholar] [CrossRef]
- Wieczynski, D.J.; Díaz, S.; Durán, S.M.; Fyllas, N.M.; Salinas, N.; Martin, R.E.; Shenkin, A.; Silman, M.R.; Asner, G.P.; Bentley, L.P.; et al. Improving landscape-scale productivity estimates by integrating trait-based models and remotely-sensed foliar-trait and canopy-structural data. Ecography 2022, 2022, e06078. [Google Scholar] [CrossRef]
- Ma, X.; Huete, A.; Tran, N.N.; Bi, J.; Gao, S.; Zeng, Y. Sun-Angle Effects on Remote-Sensing Phenology Observed and Modelled Using Himawari-8. Remote Sens. 2020, 12, 1339. [Google Scholar] [CrossRef] [Green Version]
- Seelig, H.; Hoehn, A.; Stodieck, L.S.; Klaus, D.M.; Adams, W.W., III; Emery, W.J. The assessment of leaf water content using leaf reflectance ratios in the visible, near-, and short-wave-infrared. Int. J. Remote Sens. 2008, 29, 3701–3713. [Google Scholar] [CrossRef]
- Purves, D.W.; Lichstein, J.W.; Pacala, S.W. Crown Plasticity and Competition for Canopy Space: A New Spatially Implicit Model Parameterized for 250 North American Tree Species. PLoS ONE 2007, 2, e870. [Google Scholar] [CrossRef] [PubMed]
- Van Der Zee, J.; Lau, A.; Shenkin, A. Understanding crown shyness from a 3-D perspective. Ann. Bot. 2021, 128, 725–736. [Google Scholar] [CrossRef] [PubMed]
- Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Spatially explicit characterization of boreal forest gap dynamics using multi-temporal lidar data. Remote Sens. Environ. 2008, 112, 2326–2340. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens. 2010, 21, 1303–1330. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).