A Spatial–Spectral Joint Attention Network for Change Detection in Multispectral Imagery
Abstract
:1. Introduction
- (1)
- A spatial–spectral attention network is proposed to extract more discriminative spatial–spectral features, which can capture the spatial key changed areas by the spatial-attention module and explore the separable bands of materials through the spectral-attention module.
- (2)
- A novel objective function is developed to better distinguish the differences of the learned spatial–spectral features, which simultaneously calculate the similarity of learned spatial–spectral features from the spectrum amplitude and angle perspectives.
- (3)
- Comprehensive experiments in three benchmark datasets indicate that the proposed SJAN can achieve superior performance compared to other state-of-the-art change-detectionmethods.
2. Materials and Methods
2.1. Literature Review
2.1.1. Change Detection
2.1.2. Attention Mechanism
2.2. Method
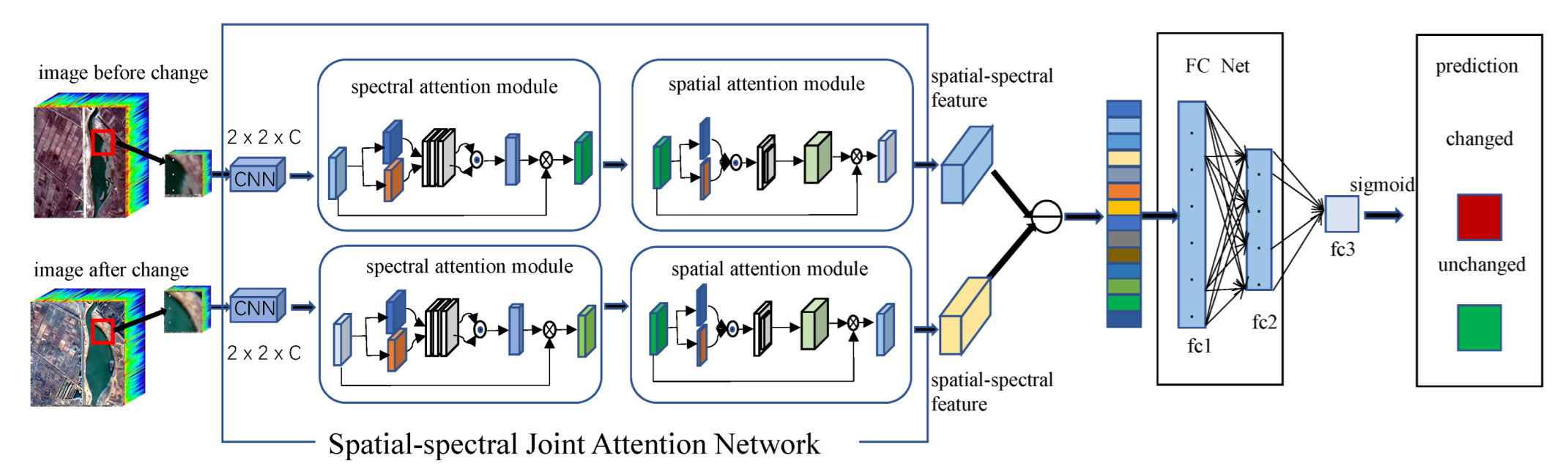
2.2.1. Network Architecture
2.2.2. Spatial-Attention Module
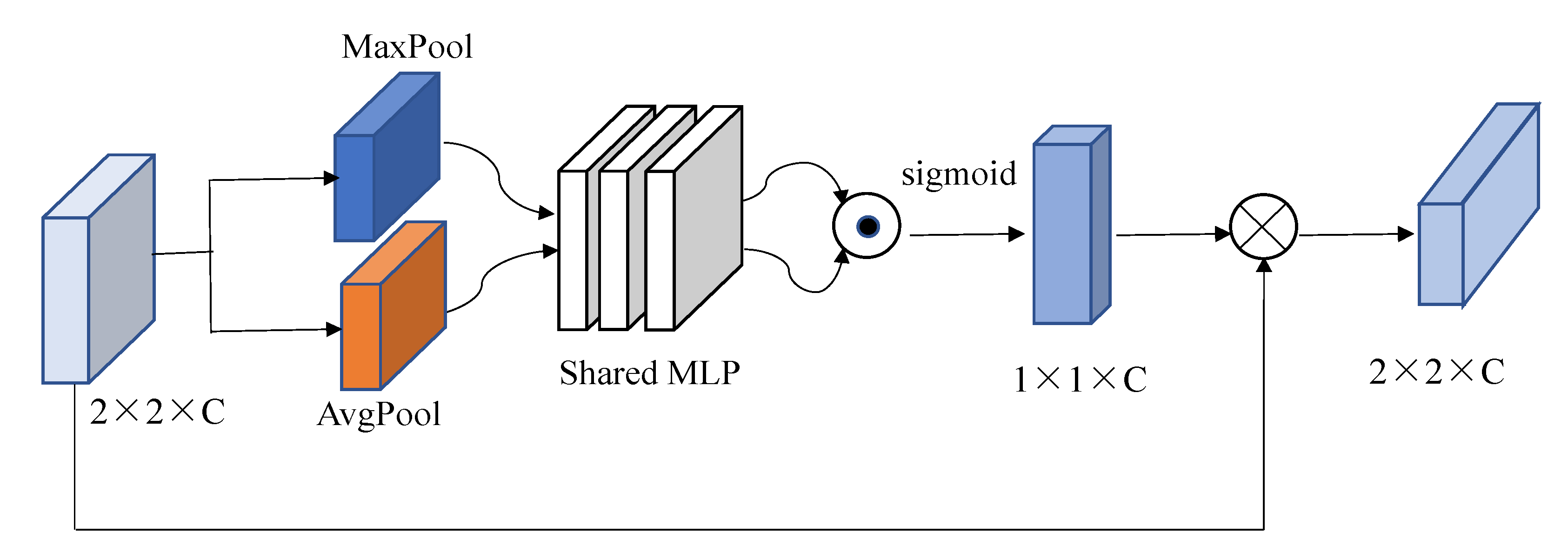
2.2.3. Spectral-Attention Module
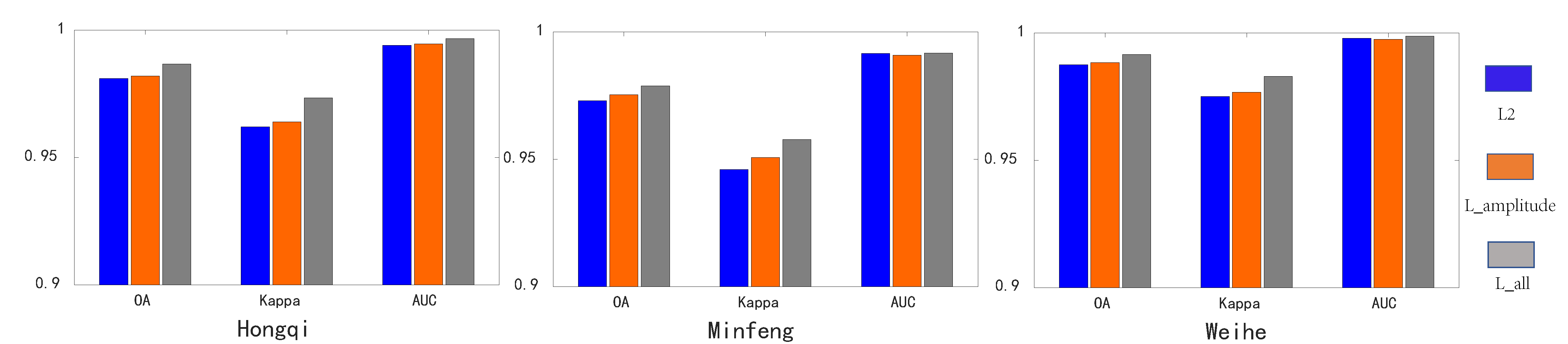
2.3. Loss Function
2.4. Training Process
| Algorithm 1 Framework of SJAN. |
| Input: |
|
|
| Output: |
|
3. Results
3.1. Datasets
3.2. Evaluation Criteria
3.3. Competitors
- (1)
- CVA [31] is a typically unsupervised change-detection method. Difference operations are performed on the images from two temporal images to identify the changed areas.
- (2)
- IRMAD [34] assigns larger weights to the pixels that have not changed, and after several iterations, the weights of the pixel points are compared with the threshold value to determine whether they have changed. IR-MAD is better than MAD in identifying significant changes, and this method is widely used in multivariate change detection.
- (3)
- SCCN [37] is a symmetric network, which includes a convolutional layer and several coupling layers. The input images are connected to each side of the network and are transformed into a feature space. The distances of the feature pairs are calculated to generate the difference map.
- (4)
- SSJLN [40] considers both spectral and spatial information and deeply explores the implicit information of the fused features. SSJLN is very good at improving change-detection performance.
- (5)
- STA [27] designs a new CD based on the self-attention module to simulate a spatial–temporal relationship. The self-attention module can calculate the attention weights between any two pixels at different times and locations, which can generate more discriminative features.
- (6)
- DSAMNet [52] includes a CBAM-integrated metric module that learns a change map directly through the feature extractor and an auxiliary deep-supervision module that generates change maps with more spatial information.
3.4. Performance Analysis
4. Discussion
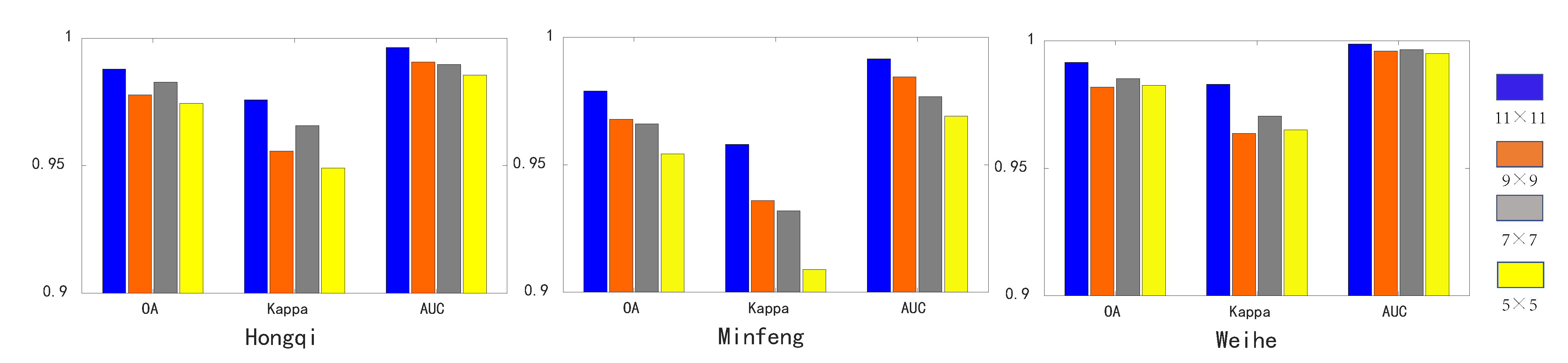
4.1. Parameter Settings
Effect of Patch
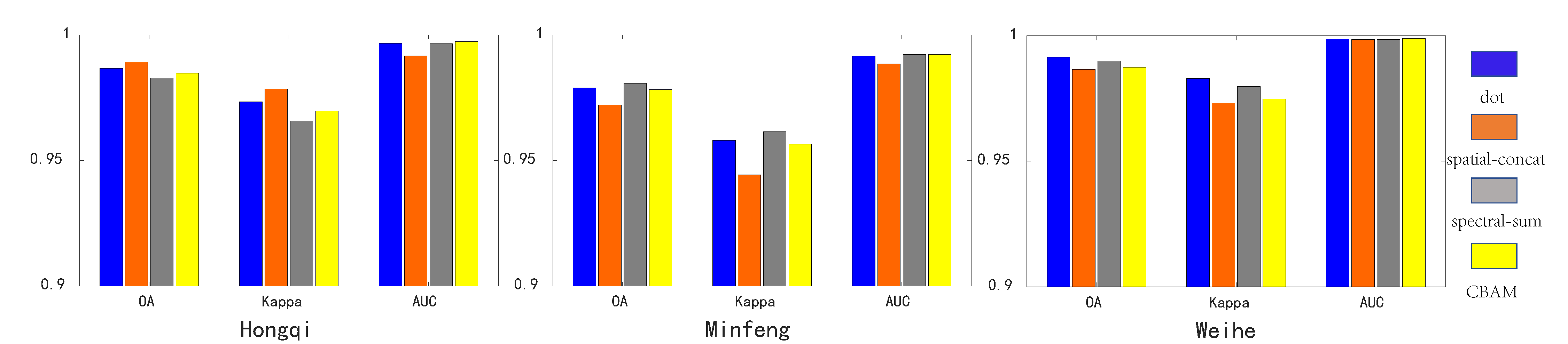
4.2. Comparison with CBAM
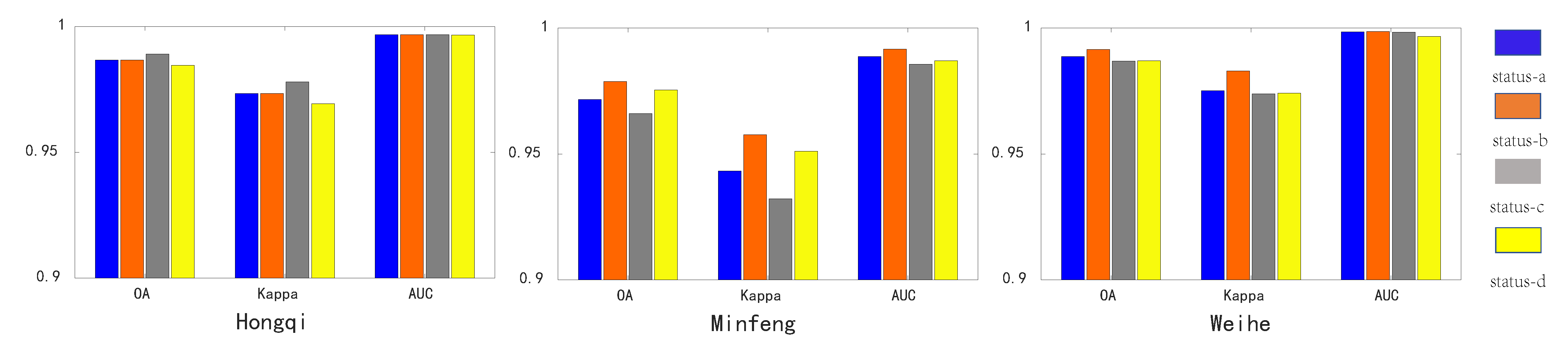
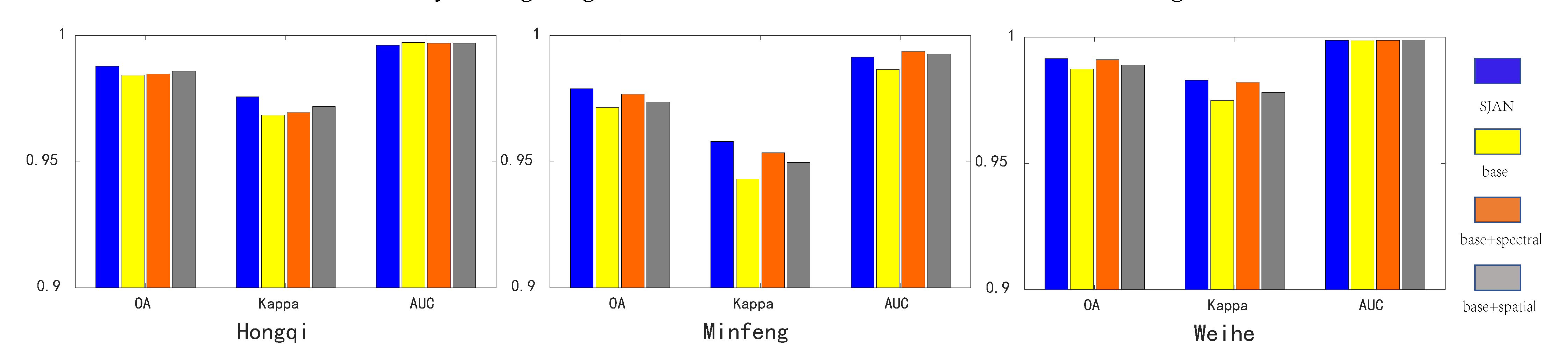
4.3. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Haque, M.A.; Shishir, S.; Mazumder, A.; Iqbal, M. Change detection of Jamuna River and its impact on the local settlements. Phys. Geogr. 2022, 1–21. [Google Scholar] [CrossRef]
- Pasang, S.; Norbu, R.; Timsina, S.; Wangchuk, T.; Kubíček, P. Normalized difference vegetation index analysis of forest cover change detection in Paro Dzongkhag, Bhutan. In Computers in Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2022; pp. 417–425. [Google Scholar]
- Hajarian, M.H.; Atarchi, S.; Hamzeh, S. Monitoring seasonal changes of Meighan wetland using SAR, thermal and optical remote sensing data. Phys. Geogr. Res. Q. 2021, 53, 365–380. [Google Scholar]
- Hasanlou, M.; Seydi, S.T. Use of multispectral and hyperspectral satellite imagery for monitoring waterbodies and wetlands. In Southern Iraq’s Marshes; Springer: Berlin/Heidelberg, Germany, 2021; pp. 155–181. [Google Scholar]
- Guo, R.; Xiao, P.; Zhang, X.; Liu, H. Updating land cover map based on change detection of high-resolution remote sensing images. J. Appl. Remote. Sens. 2021, 15, 044507. [Google Scholar] [CrossRef]
- Di Francesco, S.; Casadei, S.; Di Mella, I.; Giannone, F. The Role of Small Reservoirs in a Water Scarcity Scenario: A Computational Approach. Water Resour. Manag. 2022, 36, 875–889. [Google Scholar] [CrossRef]
- Li, J.; Peng, B.; Wei, Y.; Ye, H. Accurate extraction of surface water in complex environment based on Google Earth Engine and Sentinel-2. PLoS ONE 2021, 16, e0253209. [Google Scholar] [CrossRef]
- Lynch, P.; Blesius, L.; Hines, E. Classification of urban area using multispectral indices for urban planning. Remote Sens. 2020, 12, 2503. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, B.; Song, Y. Urban land-use mapping using a deep convolutional neural network with high spatial resolution multispectral remote sensing imagery. Remote Sens. Environ. 2018, 214, 73–86. [Google Scholar] [CrossRef]
- Yang, C.; Zhao, S. Urban vertical profiles of three most urbanized Chinese cities and the spatial coupling with horizontal urban expansion. Land Use Policy 2022, 113, 105919. [Google Scholar] [CrossRef]
- Aamir, M.; Ali, T.; Irfan, M.; Shaf, A.; Azam, M.Z.; Glowacz, A.; Brumercik, F.; Glowacz, W.; Alqhtani, S.; Rahman, S. Natural disasters intensity analysis and classification based on multispectral images using multi-layered deep convolutional neural network. Sensors 2021, 21, 2648. [Google Scholar] [CrossRef]
- Jun, L.; Shao-qing, L.; Yan-rong, L.; Rong-rong, Q.; Tao-ran, Z.; Qiang, Y.; Ling-tong, D. Evaluation and Modifying of Multispectral Drought Severity Index. Spectrosc. Spectr. Anal. 2020, 40, 3522. [Google Scholar]
- Peng, B.; Meng, Z.; Huang, Q.; Wang, C. Patch similarity convolutional neural network for urban flood extent mapping using bi-temporal satellite multispectral imagery. Remote Sens. 2019, 11, 2492. [Google Scholar] [CrossRef] [Green Version]
- Afaq, Y.; Manocha, A. Analysis on change detection techniques for remote sensing applications: A review. Ecol. Inform. 2021, 63, 101310. [Google Scholar] [CrossRef]
- Gong, M.; Zhan, T.; Zhang, P.; Miao, Q. Superpixel-based difference representation learning for change detection in multispectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2658–2673. [Google Scholar] [CrossRef]
- Geng, J.; Wang, H.; Fan, J.; Ma, X. Change detection of SAR images based on supervised contractive autoencoders and fuzzy clustering. In Proceedings of the 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP), Shanghai, China, 18–21 May 2017; pp. 1–3. [Google Scholar]
- Su, L.; Gong, M.; Zhang, P.; Zhang, M.; Liu, J.; Yang, H. Deep learning and mapping based ternary change detection for information unbalanced images. Pattern Recognit. 2017, 66, 213–228. [Google Scholar] [CrossRef]
- Gao, F.; Dong, J.; Li, B.; Xu, Q. Automatic change detection in synthetic aperture radar images based on PCANet. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1792–1796. [Google Scholar] [CrossRef]
- Zhan, T.; Song, B.; Sun, L.; Jia, X.; Wan, M.; Yang, G.; Wu, Z. TDSSC: A Three-Directions Spectral–Spatial Convolution Neural Network for Hyperspectral Image Change Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 377–388. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, G.; Yuan, Y. A novel unsupervised change detection approach based on spectral transformation for multispectral images. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 51–55. [Google Scholar]
- Liu, Y.; Pang, C.; Zhan, Z.; Zhang, X.; Yang, X. Building change detection for remote sensing images using a dual-task constrained deep siamese convolutional network model. IEEE Geosci. Remote Sens. Lett. 2020, 18, 811–815. [Google Scholar] [CrossRef]
- Zhan, T.; Gong, M.; Jiang, X.; Zhang, M. Unsupervised scale-driven change detection with deep spatial–spectral features for VHR images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5653–5665. [Google Scholar] [CrossRef]
- Liu, G.; Yuan, Y.; Zhang, Y.; Dong, Y.; Li, X. Style transformation-based spatial–spectral feature learning for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2020, 60, 5401515. [Google Scholar] [CrossRef]
- Lei, T.; Wang, J.; Ning, H.; Wang, X.; Xue, D.; Wang, Q.; Nandi, A.K. Difference Enhancement and Spatial–Spectral Nonlocal Network for Change Detection in VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Wang, D.; Chen, X.; Jiang, M.; Du, S.; Xu, B.; Wang, J. ADS-Net: An Attention-Based deeply supervised network for remote sensing image change detection. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102348. [Google Scholar]
- Chen, J.; Yuan, Z.; Peng, J.; Chen, L.; Huang, H.; Zhu, J.; Liu, Y.; Li, H. DASNet: Dual attentive fully convolutional siamese networks for change detection in high-resolution satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1194–1206. [Google Scholar] [CrossRef]
- Chen, H.; Shi, Z. A spatial–temporal attention-based method and a new dataset for remote sensing image change detection. Remote Sens. 2020, 12, 1662. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, D.; Li, P.; Lv, P. Change detection of remote sensing images based on attention mechanism. Comput. Intell. Neurosci. 2020, 2020, 6430627. [Google Scholar] [CrossRef]
- Ma, W.; Zhao, J.; Zhu, H.; Shen, J.; Jiao, L.; Wu, Y.; Hou, B. A spatial-channel collaborative attention network for enhancement of multiresolution classification. Remote Sens. 2020, 13, 106. [Google Scholar] [CrossRef]
- Chen, S.; Yang, K.; Stiefelhagen, R. DR-TANet: Dynamic Receptive Temporal Attention Network for Street Scene Change Detection. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021. [Google Scholar]
- Bovolo, F.; Bruzzone, L. A theoretical framework for unsupervised change detection based on change vector analysis in the polar domain. IEEE Trans. Geosci. Remote Sens. 2006, 45, 218–236. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Wang, K.; Deng, Y.; Qi, G. PCA-based land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate alteration detection (MAD) and MAF postprocessing in multispectral, bitemporal image data: New approaches to change detection studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Canty, M.J.; Nielsen, A.A. Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted MAD transformation. Remote Sens. Environ. 2008, 112, 1025–1036. [Google Scholar] [CrossRef] [Green Version]
- Radhika, K.; Varadarajan, S. A neural network based classification of satellite images for change detection applications. Cogent Eng. 2018, 5, 1484587. [Google Scholar] [CrossRef]
- Vignesh, T.; Thyagharajan, K.; Murugan, D.; Sakthivel, M.; Pushparaj, S. A novel multiple unsupervised algorithm for land use/land cover classification. Indian J. Sci. Technol. 2016, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A deep convolutional coupling network for change detection based on heterogeneous optical and radar images. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 545–559. [Google Scholar] [CrossRef]
- Zhan, Y.; Fu, K.; Yan, M.; Sun, X.; Wang, H.; Qiu, X. Change detection based on deep siamese convolutional network for optical aerial images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1845–1849. [Google Scholar] [CrossRef]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning spectral–spatial–temporal features via a recurrent convolutional neural network for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 57, 924–935. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Lu, X. The Spectral-Spatial Joint Learning for Change Detection in Multispectral Imagery. Remote Sensing 2019, 11, 240. [Google Scholar] [CrossRef] [Green Version]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 3–6. [Google Scholar]
- Ramachandran, P.; Parmar, N.; Vaswani, A.; Bello, I.; Levskaya, A.; Shlens, J. Stand-alone self-attention in vision models. Adv. Neural Inf. Process. Syst. 2019, 32, 3–5. [Google Scholar]
- Cai, W.; Liu, B.; Wei, Z.; Li, M.; Kan, J. TARDB-Net: Triple-attention guided residual dense and BiLSTM networks for hyperspectral image classification. Multimed. Tools Appl. 2021, 80, 11291–11312. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.I. Feedback attention-based dense CNN for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Shi, C.; Liao, D.; Zhang, T.; Wang, L. Hyperspectral Image Classification Based on 3D Coordination Attention Mechanism Network. Remote Sens. 2022, 14, 608. [Google Scholar] [CrossRef]
- Peng, C.; Tian, T.; Chen, C.; Guo, X.; Ma, J. Bilateral attention decoder: A lightweight decoder for real-time semantic segmentation. Neural Netw. 2021, 137, 188–199. [Google Scholar] [CrossRef]
- Fu, J.; Zheng, H.; Mei, T. Look closer to see better: Recurrent attention convolutional neural network for fine-grained image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4438–4446. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Misra, D.; Nalamada, T.; Arasanipalai, A.U.; Hou, Q. Rotate to attend: Convolutional triplet attention module. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 3139–3148. [Google Scholar]
- Rahman, F.; Vasu, B.; Van Cor, J.; Kerekes, J.; Savakis, A. Siamese network with multi-level features for patch-based change detection in satellite imagery. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; pp. 958–962. [Google Scholar]
- Shi, Q.; Liu, M.; Li, S.; Liu, X.; Wang, F.; Zhang, L. A deeply supervised attention metric-based network and an open aerial image dataset for remote sensing change detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]







| Module | Layer Names | Input Dim. | Output Dim. | KS | S |
|---|---|---|---|---|---|
| inital feature extraction (CNN) | conv1 | 1 | |||
| conv2 | 1 | ||||
| pool1 | 1 | ||||
| conv3 | 2 | ||||
| conv4 | 1 | ||||
| pool2 | 2 | ||||
| spectral attention | spectral-attention | - | - | ||
| spatial attention | spatial-attention | - | - | ||
| flatten | 512 | - | - | ||
| discrimination | dense1 | 512 | 256 | - | - |
| dense2 | 256 | 128 | - | - | |
| dense3 | 128 | 1 | - | - |
| Method | Number of Parameters | Cost Time/s | ||
|---|---|---|---|---|
| Hongqi | Minfeng | Weihe | ||
| SCCN | 7736 | 37 | 35 | 36 |
| SSJLN | 71,042 | 54 | 31 | 59 |
| STA | 277,828 | 545 | 461 | 500 |
| DSAMNet | 16,955,200 | 3000 | 2505 | 1533 |
| SJAN | 276,892 | 483 | 403 | 491 |
| Data | Metric | CVA | IRMAD | SCCN | SSJLN | STA | DSAMNet | Ours |
|---|---|---|---|---|---|---|---|---|
| hongqi | OA | 0.8239 | 0.9419 | 0.9569 | 0.9746 | 0.9670 | 0.9602 | 0.9772 |
| Kappa | 0.3928 | 0.6902 | 0.7609 | 0.8490 | 0.8318 | 0.7737 | 0.8775 | |
| AUC | 0.8089 | 0.8627 | 0.8893 | 0.9889 | 0.9763 | 0.9243 | 0.9770 | |
| minfeng | OA | 0.6961 | 0.8376 | 0.9435 | 0.9494 | 0.9379 | 0.9002 | 0.9596 |
| Kappa | 0.1698 | 0.5221 | 0.6093 | 0.6506 | 0.6826 | 0.5048 | 0.7715 | |
| AUC | 0.6434 | 0.7411 | 0.7856 | 0.9705 | 0.9644 | 0.8787 | 0.9741 | |
| weihe | OA | 0.7953 | 0.9603 | 0.8260 | 0.9854 | 0.9772 | 0.9194 | 0.9889 |
| Kappa | 0.5318 | 0.8790 | 0.6149 | 0.9618 | 0.9411 | 0.7690 | 0.9708 | |
| AUC | 0.7474 | 0.8438 | 0.8502 | 0.9821 | 0.9803 | 0.8959 | 0.9845 |
| Results | Datasets | ||
|---|---|---|---|
| Hongqi | Minfeng | Weihe | |
| OA | |||
| Kappa | |||
| AUC | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhang, Q.; Liu, S.; Pan, X.; Lu, X. A Spatial–Spectral Joint Attention Network for Change Detection in Multispectral Imagery. Remote Sens. 2022, 14, 3394. https://doi.org/10.3390/rs14143394
Zhang W, Zhang Q, Liu S, Pan X, Lu X. A Spatial–Spectral Joint Attention Network for Change Detection in Multispectral Imagery. Remote Sensing. 2022; 14(14):3394. https://doi.org/10.3390/rs14143394
Chicago/Turabian StyleZhang, Wuxia, Qinyu Zhang, Shuo Liu, Xiaoying Pan, and Xiaoqiang Lu. 2022. "A Spatial–Spectral Joint Attention Network for Change Detection in Multispectral Imagery" Remote Sensing 14, no. 14: 3394. https://doi.org/10.3390/rs14143394
APA StyleZhang, W., Zhang, Q., Liu, S., Pan, X., & Lu, X. (2022). A Spatial–Spectral Joint Attention Network for Change Detection in Multispectral Imagery. Remote Sensing, 14(14), 3394. https://doi.org/10.3390/rs14143394






