Column-Spatial Correction Network for Remote Sensing Image Destriping

Abstract

The stripe noise in the multispectral remote sensing images, possibly resulting from the instrument instability, slit contamination, and light interference, significantly degrades the imaging quality and impairs high-level visual tasks. The local consistency of homogeneous region in striped images is damaged because of the different gains and offsets of adjacent sensors regarding the same ground object, which leads to the structural characteristics of stripe noise. This can be characterized by the increased differences between columns in the remote sensing image. Therefore, the destriping can be viewed as a process of improving the local consistency of homogeneous region and the global uniformity of whole image. In recent years, convolutional neural network (CNN)-based models have been introduced to destriping tasks, and have achieved advanced results, relying on their powerful representation ability. Therefore, to effectively leverage both CNNs and the structural characteristics of stripe noise, we propose a multi-scaled column-spatial correction network (CSCNet) for remote sensing image destriping, in which the local structural characteristic of stripe noise and the global contextual information of the image are both explored at multiple feature scales. More specifically, the column-based correction module (CCM) and spatial-based correction module (SCM) were designed to improve the local consistency and global uniformity from the perspectives of column correction and full image correction, respectively. Moreover, a feature fusion module based on the channel attention mechanism was created to obtain discriminative features derived from different modules and scales. We compared the proposed model against both traditional and deep learning methods on simulated and real remote sensing images. The promising results indicate that CSCNet effectively removes image stripes and outperforms state-of-the-art methods in terms of qualitative and quantitative assessments.

1. Introduction

Remote sensing technology aims to achieve the long-distance information detection in a non-contact way. The multispectral remote sensing images of different ground objects are received by sensors and further processed and analyzed to realize the detection and identification of earth resources and geographical environments. However, there often exist various kinds of stripe noise in different remote sensing imaging systems given their unique image acquisition modes. The stripe noise not only reduces the visibility of images [1,2], but also adversely affects their interpretations and applications, such as classification [3,4], endmember extraction [5,6,7], unmixing [8,9], segmentation [10], target detection [11,12], etc. Therefore, the destriping is a necessary step of remote sensing image processing.

In the remote sensing image, the digital numbers (DNs) of pixels on the same column often derive from the same detector pixel. Therefore, the DNs of homogeneous region generally come from several adjacent detectors, which tend to maintain the local consistency of these regions. However, different detector pixels sometimes output different DNs for the same object irradiance due to various factors, such as optical system, detector pixel response, readout circuit, and electronic systems, making images contain the vertically distributed stripe noises. Therefore, the destriping, which aims to reduce the differences between adjacent columns caused by the stripe noise, plays a crucial role in improving the uniformity of the whole image.

In the past few decades, various methods dedicated to remote sensing image destriping have been proposed to mitigate the impact of stripe noise on image quality. The existing methods can be grouped into four categories according to the principle of stripe removal, namely, statistical-based, filtering-based, optimization-based, and deep learning-based methods, each of which possesses unique advantages and limitations. The statistical-based methods assume that the signal acquired by each pixel in the detector shares the same statistical distribution, such as histogram matching [13,14] and moment matching (MM) [15,16]. The statistical information of each column is matched to the same reference, e.g., the information of the whole image. According to the noise characteristics in the spatial and transformed domains, filtering-based methods remove the stripe by designing the appropriate filter [17,18]. Differently from them, optimization-based methods estimate the clean image from its striped counterpart by optimizing the designed object function, which usually contains the fidelity and constraint terms. The fidelity term is adopted to retain the original image structure. The constraint term is formulated from the smoothness of clean image and the characteristics of image spectrum or noise components, such as the total variation (TV) [19,20], low-rank property [21,22], or sparsity [23,24]. For example, Chang et al. [19] introduced an anisotropic spectral-spatial total variation (ASSTV) model for multispectral remote sensing image destriping. Subsequently, a low-rank-based single-image decomposition model (LRSID) was proposed to separate the original image from the stripe component [25].

Among above traditional destriping methods, it is proven that effectively exploring the structural characteristics of the stripe play a crucial role in the process of destriping. For example, statistical-based methods assume the image scene is evenly distributed, and baseline objects within each column of pixels in the scanning direction have the similar radiation distribution, among which, the histogram matching [13,14] and moment matching [15,16] are representative methods. They remove the stripe noise by adjusting the statistical information of each column, including the histogram or mean and standard deviation. Alternatively, the TV model [19] is usually adopted in the optimization-based destriping methods. The conventional TV model enhances the smoothness of images from both horizontal and vertical directions for the general denoising task. Given that the stripe noise does not damage the vertical structure information of an image, optimization-based methods consider limiting the smoothness along the horizontal direction to adjust the TV model to be more suitable for destriping.

Recently, deep learning-based methods rely on the advanced capability of convolutional neural networks (CNNs) to remove the various noises of images [26,27]. Zhang et al. [28] presented the spatial-spectral gradient network (SSGN) for removing the mixed noise using the gradient feature in hyperspectral images. Xiao et al. [29] developed the infrared cloud image stripe removal network (ICSRN) with a local-global combination structure. These methods mainly utilize the global contextual information to improve the uniformity of the whole image, yet the significance of the structural characteristics is often neglected [29,30]. To effectively leverage both CNNs and the structural characteristics of stripe noise, we propose a multi-scaled column-spatial correction network (CSCNet) for remote sensing image destriping, in which the local structural characteristic of stripe noise and the global contextual information of image are both explored at multiple feature scales. More specifically, we designed a column-based correction module (CCM) to capture the local feature, which enables the network to pay more attention to eliminating the differences between columns caused by the stripe noise. For the global feature, the spatial attention mechanism is adopted in the spatial-based correction module (SCM) to further improve the image’s uniformity. In addition, we utilize a feature fusion module (FFM) based on the channel attention mechanism to fuse features obtained from different correction modules and scales. Overall, our main contributions are summarized as follows:

(1)

Based on the structural characteristics of stripe, we propose a multi-scaled column-spatial correction network (CSCNet), aiming at improving the local consistency of homogeneous region and the global uniformity of whole image. The proposed CSCNet can effectively remove different kinds of stripe noise, including non-periodic, periodic, and wide stripe.

(2)

A column-based correction module is proposed to reduce the differences between columns caused by stripe noise. To the best of our knowledge, this was one of the first attempts to explore the column-based correction strategy in deep neural network-based models for destriping according to the structural characteristics of the stripe.

(3)

The proposed method has been evaluated on both simulated and real remote sensing images with promising results. Compared to existing methods, our CSCNet has achieved superior qualitative and quantitative assessments.

The remainder of this paper is organized as follows. In Section 2, existing methods for remote sensing image destriping are introduced. The proposed CSCNet and the related details are described in Section 3. The simulated and experimental results with real data are presented in Section 4. Finally, our conclusions are summarized in Section 5.

2. Related Work

In recent decades, various methods dedicated to remote sensing image destriping have been proposed. The existing methods can be coarsely grouped into four categories, i.e., statistical-based, filtering-based, optimization-based, and deep learning-based methods.

2.1. Statistical-Based Methods

Statistical-based methods focus on the statistical properties of DNs for each detector and assume a linear relationship between the response values of detector pixels and the input radiance. They assume the scene is evenly distributed in the remote sensing image, and that each column of data in the scanning direction has a similar radiation distribution. The most common methods, including histogram matching [13,14] and moment matching (MM) [15,16], mainly consist of two steps: allocating the reference and statistical matching. The histogram matching adopts the histogram as a clean reference and adjusts the histogram of each detector by referring to the reference. Similarly, MM assumes that the mean and standard deviation of all detectors are approximately equal. These statistics of each detector are rectified to those reference values based on the entire image for stripe removal. The statistics-based methods manage to obtain satisfactory destriping results when scenes are simple and homogeneous. However, the distribution of ground objects is rather complex in practice, and the statistical information originated from each detector often dramatically changes. Therefore, the assumption of distribution similarity cannot always holds, resulting in poor destriping results in those complex scenes.

2.2. Filtering-Based Methods

Filtering-based methods aim at processing the stripe in the spatial and transformed domains. Among early works, Crippe et al. [31] proposed a simple spatial filtering routine to remove the stripe. Fourier transform [32] and Wavelet decomposition [33] are the typical domain transform filters. Following the assumption of stripe noise with strong periodicity characteristics, Fourier transform-based methods aim at suppressing the specific frequencies caused by stripe to separate useful signals from a striped image by designing an appropriate filter in the transformed domain. Nevertheless, since signals and the noise are mixed together, useful signals are often compromised during the stripe removal. In particular, when the input radiance changes abruptly, ringing artifacts appear in the destriping results [34]. To sum up, Fourier transform methods are efficient to implement, yet the assumption for the periodicity of stripe limits the effectiveness of stripe removal. Moreover, wavelet decomposition is also applied to remove the stripe noise under the consideration of scaling directional properties [35]. It is worth noting that the selection of wavelet transform function plays a crucial role in the destriping process.

2.3. Optimization-Based Methods

Optimization-based methods treat the destriping as an ill-posed inverse problem and mainly include two types of methods, i.e., variation-based and low-rank-based methods. The former one obtains the desired destriping results by optimizing the variation model with priors. A destrping framework based on maximum a posterior (MAP) was firstly presented by Shen et al. [36], in which the Huber–Markov-based variation model is used as the prior likelihood probability density function. They treat the stripe as the isotropic noise, which lacks the consideration of the anisotropic property of the stripe. Consequently, unidirectional variation models were proposed which focus on the directional characteristic of the stripe. They constrain the image smoothness in the cross-stripe direction and retain the information in the along-stripe direction [19,20,23]. The aforementioned models are dedicated to estimate the image prior. On the contrary, since the stripe noise possesses significant directional features compared to the clean component, alternative methods choose to focus on utilizing the stripe prior [17,20]. The low-rank-based methods consider that the data, such as images, abundance matrices, and stripe noises, possess the low-rank characteristic; thus, they adopt the low-rank restriction during the estimation of desired results. According to the form of data processing, they can be divided into matrix-based [1,25] and tensor-based [37,38] methods. The matrix-based methods take the advantage of spectral coherence by lexicographically ordering the 3D cubic into a 2D matrix [39]. Though promising results have been demonstrated, matricization techniques preliminarily vectorize all image bands, which inevitably causes the loss of the spectral–spatial structural correlation of the image cube. Therefore, the subsequent tensor-based methods were proposed to make up for this drawback. However, the tensor-based methods are relatively inefficient given the large data size and the high computation complexity.

2.4. Deep Learning-Based Methods

Various assumptions or handcrafted priors have been designed in previous methods for the image and stripe components to promote the improvement of destriping. However, these assumptions and priors are often inconsistent with realistic scenarios, leading to the weak generalization ability of such methods. Most recently, deep convolutional neural network-based methods have been proposed to remove the stripe noise for remote sensing images [29,30,39]. The plain neural network-based methods utilize the strong learning capacity of CNN to output a clean image from a striped one [29,30]. Subsequently, residual learning is introduced into networks to obtain the stripe noise [39,40]. Moreover, the additional information, such as the horizontal and vertical gradient features of the image, are used to assist the model in learning discriminative features [28]. Zhang et al. [28] presented the spatial-spectral gradient network (SSGN) to remove mixed noises, including Gaussian and stripe noise. A two-stream wavelet enhanced U-net (TSWEU) model was presented by Chang et al. [39] to learn the relationship between the clean image and stripe noise, and the wavelet is adopted to extract the multiscale information of global contextual feature with a larger receptive field. Compared to traditional methods, deep learning-based methods have achieved a superior destriping effect, relying on the strong ability of feature learning; however, these methods neglect the special structural characteristic of the stripe.

3. Methodology

3.1. Overall Framework

We propose a column-spatial correction network (CSCNet) for remote sensing image destriping, which leverages the global image uniformity and the local difference between columns. The flowchart of the proposed method is shown in Figure 1. CSCNet learns an end-to-end mapping between the striped image and its clean counterpart. Considering that the striped remote sensing image retains the structural information in the vertical direction, both the striped image and its vertical gradient are used as inputs in CSCNet. First of all, we feed the original striped image and its vertical gradient to a $3\times 3$ convolutional layer. Then, the extracted feature passes through the middle part of the network composed of the multiple multi-scaled column-spatial correction module (MCSCM) based on a residual design. Finally, a $3\times 3$ convolutional layer followed by a residual connection to the original striped image are used to generate the destriping result. Except in downsampling and upsampling, the padding operation is utilized to keep the spatial sizes of features in all correction modules the same. The Charbonnier loss is adopted to optimize the proposed network [41]:

$$\mathcal{L}(\hat{\mathbf{I}},{\mathbf{I}}^{*})=\sqrt{{∥\hat{\mathbf{I}}-{\mathbf{I}}^{*}∥}^2+{\epsilon }^2},$$

(1)

where Î and I* d-truth (clean image), respectively. $\epsilon$ is a constant.

3.2. Multi-Scaled Column-Spatial Correction Module

As the basic unit of the network, the structure of MCSCM is shown in Figure 1, which is a multi-scaled residual structure and is mainly composed of a column-spatial correction module (CSCM) and a feature fusion module (FFM). CSCM is responsible for enhancing uniformity from the global and local perspectives, and FFM is utilized to fuse features derived from different correction modules. Firstly, we generate multi-scaled features by downsampling. These features are then fed to CSCM for the correction at different scale branches; subsequently, the generated smaller scale features are upsampled and gradually fused with larger scale features by FFM. Finally, the fused feature passes through a $3\times 3$ convolutional layer followed by a residual connection to the input feature as the final prediction. To improve the readability, we give the details of the CSCM and FFM first, and then introduce their multi-scale extensions.

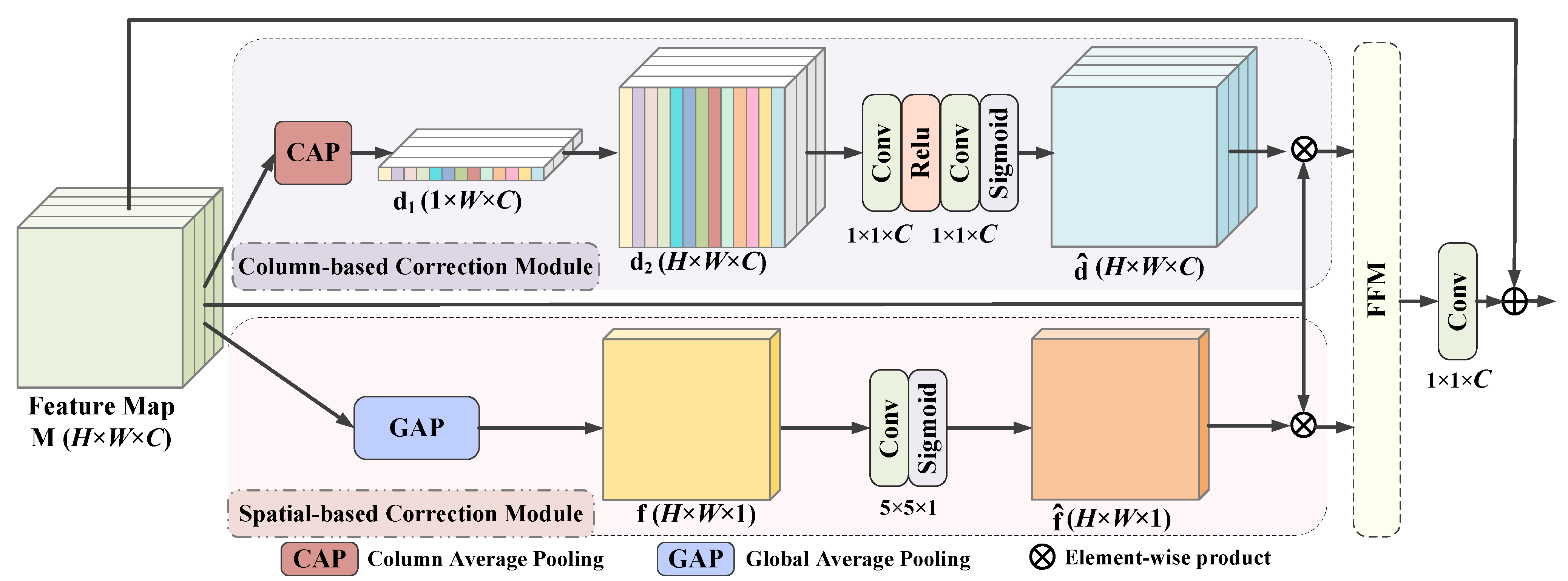
3.3. Column-Spatial Correction Module

The structure of the CSCM is shown in Figure 2. Since the destriping can be viewed as reducing the differences between columns caused by stripe noise, we intuitively designed two correction modules from the perspectives of reducing local differences and improving global uniformity, denoted column-based and spatial-based correction modules (CCM and SCM), respectively. The two modules generate correction coefficient maps to correct input features, and the corrected features are further fused as the results of CSCM.

3.3.1. Column-Based Correction Module

The column-based correction module (CCM) is designed to reduce the local differences based on the column; i.e., features in the same convolutional column should be allocated with similar correction coefficients. As illustrated in the upper part of Figure 2, the CCM first performs the column average pooling on each channel of input feature $\mathbf{M}\in {\mathbb{R}}^{H\times W\times C}$, which calculates the average values column-wise. The yielded feature ${\mathbf{d}}_1\in {\mathbb{R}}^{1\times W\times C}$ is then copied along the column direction H times as ${\mathbf{d}}_2\in {\mathbb{R}}^{H\times W\times C}$ with the same size as the input feature. The copied feature is fed to two $1\times 1$ convolutional layers sequentially, which are followed by relu and sigmoid activation, respectively, to form the column correction maps $\hat{\mathbf{d}}\in {\mathbb{R}}^{H\times W\times C}$. We reduce the local differences by employing an element-wise product between the correction coefficient maps $\hat{\mathbf{d}}$ and the input feature $\mathbf{M}$.

3.3.2. Spatial-Based Correction Module

Differently from CCM, the spatial-based correction module (SCM) focuses on utilizing the global feature to improve the image uniformity. As illustrated in the lower part of Figure 2, the input feature $\mathbf{M}\in {\mathbb{R}}^{H\times W\times C}$ first passes through the global average pooling (GAP) layer along the channel dimension. Then we generate the spatial correction map $\hat{\mathbf{f}}\in {\mathbb{R}}^{H\times W\times 1}$ by feeding the pooled $\mathbf{f}\in {\mathbb{R}}^{H\times W\times 1}$ to one convolutional layer followed by the sigmoid gating. To extract the spatial information in a larger range, the $5\times 5$ convolutional kernel is used to increase the receptive field in SCM. Similarly to CCM, the output feature with the high uniformity is obtained by rescaling $\mathbf{M}$ with the coefficient map $\hat{\mathbf{f}}$.

3.4. Feature Fusion Module

Based on the proposed network structure, features derived from different modules and scales need to be aggregated for generating discriminative representations. The details of multi-scale extension will be elaborated in the next section. Therefore, we carry out a fusion process based on the channel attention mechanism to enhance the feature selectively and remove the possible redundancy, denoted the feature fusion module (FFM).

As shown in Figure 3, the FFM receives input features ${\mathbf{F}}_1\in {\mathbb{R}}^{H\times W\times C}$ and ${\mathbf{F}}_2\in {\mathbb{R}}^{H\times W\times C}$ from different scales or correction modules, i.e., SCMs and CCMs. These features are firstly combined by the element-wise sum as: $\mathbf{F}={\mathbf{F}}_1+{\mathbf{F}}_2$. We apply the global average pooling on the spatial dimension of $\mathbf{F}\in {\mathbb{R}}^{H\times W\times C}$ to compute the channel-wise statistics $\mathbf{w}\in {\mathbb{R}}^{1\times 1\times C}$. The vector $\mathbf{w}$ is then passed through a $1\times 1$ convolutional layer and a sigmoid activation layer to generate fusion weights $\hat{\mathbf{w}}\in {\mathbb{R}}^{1\times 1\times C}$. FFM strengthens the important features and suppresses the less significant ones based on learned weights. Therefore, we conduct a soft selection to fuse input features ${\mathbf{F}}_1$ and ${\mathbf{F}}_2$, which are allocated with the weights $\hat{\mathbf{w}}$ and (1$-\hat{\mathbf{w}}$), respectively. Finally, the sum of two weighted features formulates the output of FFM. The feature fusion procedure can be summarized as:

$$\mathbf{U}=\hat{\mathbf{w}}\otimes {\mathbf{F}}_{\mathbf{1}}+(1-\hat{\mathbf{w}})\otimes {\mathbf{F}}_2,$$

(2)

where $\mathbf{U}$ is the fusion result and ⊗ represents the element-wise product.

3.5. Multi-Scale Extension

To collect multi-scaled spatial information, as illustrated in Figure 1, the proposed column-spatial correction modules (CSCMs) are constructed at three different scale branches; the convolution with a padding operation in the correction modules projects features with the same spatial size in different branches. First of all, the input is downsampled to three scales, including original, one-half, and one-quarter size, which are denoted ${\mathbf{B}}_1$, ${\mathbf{B}}_2$, and ${\mathbf{B}}_3$, respectively. We then apply the CSCM twice in each branch. Moreover, to enhance complementary advantages between high and low resolutions, the information is exchanged across parallel streams after the first CSCM. More specifically, by downsampling or upsampling, the outputs of the first CSCM (denoted ${\mathit{f}}_{11}$, ${\mathit{f}}_{21}$, and ${\mathit{f}}_{31}$, respectively) are resized to the same scale as other two branches. We then add features derived from three branches and feed the result to the second CSCM in each branch. For example, the input of second CSCM is ${\mathbf{B}}_2$, which is the sum of the downsampling of ${\mathit{f}}_{11}$ and ${\mathit{f}}_{12}$, and the upsampling of ${\mathit{f}}_{13}$. Finally, corrected features derived from three branches (denoted ${\mathit{f}}_{12}$, ${\mathit{f}}_{22}$, and ${\mathit{f}}_{32}$, respectively) are fused using the proposed fusion module FFM. We fuse two low-resolution representations ${\mathit{f}}_{22}$ and ${\mathit{f}}_{32}$ first; then, the fused feature and high-resolution feature ${\mathit{f}}_{12}$ are passed through FFM to obtain the final output with the same size as the input.

To align the spatial sizes of features from different scales, we employ the anti-aliasing downsampling [42] and a $1\times 1$ convolutional layer to downsample the features, where the anti-aliasing downsampling can improve the shift-equivariance of proposed model. Moreover, the bilinear interpolation, followed by a $1\times 1$ convolutional layer, is used to upsample the features. The $1\times 1$ convolutional layers are utilized to adjust the number of feature channels. The size of each feature is reduced by half for each downsampling, and the number of channels is doubled; i.e., we set the channel number of original scale branches to 64, and the other two branches are 128 and 256, respectively. The change in feature size during upsampling is the opposite to that in downsampling.

3.6. Training Details

The number of multi-scaled column-spatial correction modules in the proposed model is four. The relative analysis and discussion are given in Section 4.4. To speed up the training, we cropped image patches of the size $80\times 80$ from the University of Houston dataset. These training samples were then expanded to 10,000 through the rotation. The training data were normalized to [0, 1]; the learning rate and epoch were set to 0.0001 and 200, respectively. The learning rate was reduced by half every 50 epochs. We set the batch size to 120, and the ADAM optimizer was adopted to minimize the total loss.

4. Experimental Results and Analysis

In this section, we compare our proposed CSCNet against eight classic destriping methods, namely, MM [15], ASSTV [19], LRSID [25], that of reference [43], PADMM [44], ICSRN [29], SSGN [28], and TSWEU [39] on multiple datasets. Both simulated and real images with the size of $256\times 256$ are tested, and we present the visualization analysis of the destriping effect of all methods. Moreover, we also give the quantitative analysis of the model’s performance. The quantitative evaluation includes the peak signal-to-noise ratio (PSNR), structural similarity (SSIM), mean relative deviation (MRD), and non-uniformity of images.

4.1. Simulated Image Destriping

4.1.1. Simulated Data Preparation

We collected four remote sensing images as simulated datasets for fair comparisons, including Washington DC Mall, HYDICE Urban, Pavia University, and Salinas, which are denoted DC, Urban, PaviaU, and Salinas in the following section. By referring to [39], two ways of adding stripes were investigated, namely, adding noise to the entire image and a part of the image. The former consists of non-periodicity and periodicity stripes, whereas the latter adds stripes to certain rows and columns, respectively. The additive noise was utilized to generate the periodical stripe, and the others were mixed noise. The additive and mixed noise can be, respectively, formulated as: $V_{l,j}^{\prime }\left(\phi \right)=v_{l,j}\left(\phi \right)+C_{l,j}$ and $V_{l,j}^{\prime }\left(\phi \right)=A_{l,j}\times v_{l,j}\left(\phi \right)+C_{l,j}$, where $v_{l,j}\left(\phi \right)$ stands for the pixel located in the l-th row and j-th column. To simulate the vertical characteristics of stripe noise, $A_{l,j}$ and $C_{l,j}$ are the multiplicative and additive noise values and $A_{l,j}$ and $C_{l,j}$ are random values, but the same columns share the same $A_{l,j}$ and $C_{l,j}$. The University of Houston dataset was employed to generate the simulated data for training. For fair comparisons, by referring to their original implementations, data-driven models were retrained with the same set of training data and followed the same testing protocol as the proposed model. The details of simulated data are described as follows.

Entire Image: In order to generate test images with the non-periodic stripe, we added the multiplicative and additive noise to each column of the original DC image. For the periodic stripe, we added noise to columns with a certain number of intervals on the Urban image. The non-periodically and periodically degraded images are shown in Figure 4b and Figure 5b, respectively. Figure 4c–j and Figure 5c–j show the correction results of all compared algorithms.

A Part of Image: In practice, the stripe noise often exists in some rows and columns of the image due to the instability of the remote sensing imaging system. In order to simulate the stripe noise more realistically, we randomly selected a number of columns and rows to add stripes to the PaviaU and Salinas images, respectively, where the selected rows are successive. Two degraded images are shown in Figure 6b and Figure 7b, respectively. We provide the corrected images of eight methods in Figure 6c–j and Figure 7c–j.

4.1.2. Evaluation

As shown in Figure 4, Figure 5, Figure 6 and Figure 7, the visualization of destriping results on simulated images indicates that CSCNet achieves the overall best performance for stripe noise removal. More specifically, for the comparisons against statistical-based methods, the complex ground target distribution led to the failure of MM, as shown in Figure 4c, Figure 5c, Figure 6c and Figure 7c, whereas in Figure 4c, the brightness of some areas on the original image was changed after correction. In particular, in Figure 7c, MM not only failed to remove the stripe noise existing in the part rows of the image, but also changed the structural information of the original image, causing additional noise. This is due to the assumption of statistic-based methods, i.e., the mean value and standard deviation of each column are approximately equal, not always being able to hold in real images.

From the destriping results of optimization-based methods, since the total variation (TV) model is employed in ASSTV to increase the smoothness between columns, the destriping performance was somewhat satisfactory. For example, we observe that ASSTV achieved relatively decent performance on the simulated images from Figure 4d, Figure 5d, Figure 6d and Figure 7d. However, as for LRSID, the destriping with the additive low-rank constraint was less satisfactory, including the residual stripes in Figure 4e, Figure 6e, and Figure 7e. Both the method of [43] and PADMM generated promising destriping results on the degraded image with periodical stripe noise (Figure 5f,g); the residual stripe still appeared in the restored images when dealing with the severe noise (Figure 4f,g). In addition, from Figure 7f,g), the method of [43] and PADMM cannot handle the situation of the stripe existing in the rows.

As for the deep learning-based methods, SSGN had relatively better results for images with lighter stripes compared to traditional methods, which can be observed in Figure 6i. However, as shown in Figure 4h, Figure 5h, Figure 6h and Figure 7h and Figure 4i, Figure 5i and Figure 7i, the severe stripes were not fully removed. Compared to these models, relying on the proposed CCM and SCM, our CSCNet is much more effective for various stripes by reducing the local difference between columns and improving the global uniformity of the whole image.

PSNR and SSIM: To quantitatively evaluate the destriping effect of the aforementioned methods, PSNR and SSIM were used to measure the corrected image. The corresponding results are shown in

Table 1. PSNR and SSIM of the simulated image destriping results.

Image	Index	MM	ASSTV	LRSID	Ref. [43]	PADMM	ICSRN	SSGN	CSCNet
DC	PSNR	26.31	17.75	23.32	23.82	23.81	23.59	24.23	28.98
	SSIM	0.89	0.90	0.90	0.81	0.81	0.77	0.82	0.90
Urban	PSNR	32.86	23.71	32.87	29.40	29.49	29.21	28.05	34.43
	SSIM	0.96	0.97	0.94	0.95	0.96	0.94	0.94	0.96
PaviaU	PSNR	28.48	29.40	35.55	28.94	29.14	28.92	31.34	36.56
	SSIM	0.95	0.98	0.98	0.97	0.98	0.96	0.98	0.99
Salinas	PSNR	22.06	27.43	26.85	30.73	30.71	31.24	34.55	35.54
	SSIM	0.82	0.97	0.94	0.96	0.95	0.97	0.98	0.98

. The quantitative assessments listed in Table 1 show that the CSCNet achieved the highest PSNR values of all methods on the four simulated images. As for SSIM, our method was only 0.01 lower than ASSTV on the Urban data, which obtained the best results on other simulated images. The results of PSNR and SSIM validate that the proposed CSCNet obtained the overall best performance concerning stripe removal and structural information preservation.

To validate the effectiveness of methods impacted by different noise intensities, we added four types of additive noise to the Urban dataset and provide the relative evaluation indicators for comparisons, including PSNR and SSIM. The results are listed in

Table 2. PSNR and SSIM of the urban images with different stripe noise intensities.

Intensity	Index	MM	ASSTV	LRSID	Ref. [43]	PADMM	ICSRN	SSGN	CSCNet
(−50, 50)	PSNR	27.86	39.53	46.29	44.68	47.48	45.92	39.14	51.63
	SSIM	0.9391	0.9883	0.9940	0.9916	0.9977	0.9963	0.9809	0.9989
(−100, −50) (50, 100)	PSNR	27.80	37.48	41.94	39.57	39.97	43.16	38.97	50.12
	SSIM	0.9365	0.9844	0.9922	0.9859	0.9925	0.9935	0.9816	0.9987
(−200, −100) (100, 200)	PSNR	27.23	34.38	37.04	34.48	34.35	39.45	36.54	46.29
	SSIM	0.9243	0.9749	0.9835	0.9731	0.9806	0.9898	0.98	0.9973
(−300, −200) (200, 300)	PSNR	26.12	32.18	33.03	30.71	30.54	40.04	36.62	46.56
	SSIM	0.9074	0.9628	0.9708	0.9568	0.9656	0.9900	0.9747	0.9972

. In Table 2, we can observe that CSCNet achieved the best results among PSNR and SSIM with different stripe noise intensities. As the noise intensity increased, the effectiveness of all methods experienced certain decreases. It can be observed that the traditional methods are more susceptible to the noise intensity, which can generate the relative advanced destriping results with low-intensity noise, though the effect is limited when handling the high-intensity noise. Compared to other methods, CSCNet possesses powerful generalization ability to deal with different stripe noise intensities.

4.2. Real Image Destriping

4.2.1. Real Data

Apart from the simulated images, we also evaluated the destriping effects of different methods on five real images to investigate their practicability. The two hyperspectral remote sensing images produced by the full spectrum airborne hyperspectral imager (FAHI), including the near-infrared (VNIR) and shortwave-infrared (SWIR) images, were utilized to test the destriping performances of nine methods. FAHI is the Chinese next-generation pushbroom hyperspectral image instrument [45], and the main parameters are listed in

Table 3. Main FAHI parameters (VNIR; SWIR; CCD; and MCT).

Item	VNIR	SWIR
Spectral range ($\mathsf{\mu }$m)	0.4–0.95	0.95–2.5
FOV (∘)	14.7	14.7
Detector/array size	CCD/1024 × 256	MCT/512 × 512
Spectral resolution (nm)	2.34	3
Band numbers	64	512

. Other test images were the public CHRIS images, including CHRIS_AM and CHRIS_UK, and Terra MODIS. The correction results are shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

4.2.2. Evaluation

In particular, the destriping results on real images, including the correction results of continuous, discontinuous, thin, and wide stripes, demonstrate the practicality and generalization capacity of the proposed model. Consistently with the results on the simulated data, the classical MM is unsuitable when the ground target distribution between columns changes drastically, as shown in Figure 9b, Figure 10b and Figure 11b. The original image structure was often damaged to a certain degree after the correction.

The optimization-based methods, including ASSTV and LRSID, achieved relatively good correction results for thin stripes; see Figure 9c and Figure 11c, and Figure 9d, relying on the adopted TV model. However, the results in Figure 8c,d indicate that the wide stripe cannot be fully removed. Similarly, in Figure 10c,d, we can also observe that the destriping is rather unstable. In Figure 12c,d and Figure 13c,d, we can see that they affect the original image information after the destriping. For the method of [43], it can be observed from Figure 8e and Figure 11e that this method can remove simple stripe noise (Figure 9e and Figure 11e), and the destriping performance was poor when the noise distribution was complicated (Figure 8e and Figure 10e). PADMM possessed a stronger ability for stripe removal; however, it generally causes over-smoothness, losing the detailed information of original image after destriping (Figure 9f, Figure 12f and Figure 13f).

As shown in Figure 8h, Figure 10h, and Figure 11h, the destriping effects of deep learning-based methods on real images are similar to observations on simulated images. SSGN is more suitable for images with lighter stripes; however, from Figure 8g, Figure 9g, Figure 10g and Figure 11g, and Figure 9h and Figure 12h, it can be observed that the stripe noise remained after the destriping with ICSRN and SSGN. As we can see from the visualization results, TSWEU achieved relatively satisfactory performance except on the VNIR image with the residual stripes. In Figure 13, the detailed structures demonstrate that CSCNet achieved the balance between the stripe removal and original information preservation. Overall, the promising performance on various kinds of simulated and real images indicates the effectiveness of CSCNet on stripe removal.

MRD: The destriping methods should retain the original image information to the greatest extent while removing the stripe. Therefore, the MRD was adopted to measure the distortion of the original image after the different correction methods. It is defined as [34]:

$$\begin{array}{c}\hfill MRD=\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^n\frac{\left|y(i,j)-x(i,j)\right|}{x(i,j)},\end{array}$$

(3)

where $x(i,j)$ and $y(i,j)$ stand for the pixel value in positions $(i,j)$ of the original image and the corrected image, respectively. m and n are the numbers of rows and columns in the image, respectively. According to the definition, the average relative difference in images before and after destriping is calculated by MRD. The lower the MRD values are, the greater the ability of the method to preserve the image’s original information. The MRD results concerning nine methods on the five real remote sensing images are shown in

Table 4. MRD of real images’ destriping results.

Method	VNIR	SWIR	CHRIS_AM	CHRIS_UK	Terra MODIS
MM	0.0781	0.1042	0.0155	0.1145	0.1179
ASSTV	0.0445	0.0981	0.0404	0.0528	0.0436
LRSID	0.0464	0.0793	0.0567	0.0172	0.0418
Ref. [43]	0.0182	0.1153	0.0396	0.0533	0.0093
PADMM	0.1526	0.1758	0.0622	0.6424	0.0201
ICSRN	0.0100	0.0586	0.0070	0.0131	0.0754
SSGN	0.0235	0.0614	0.0085	0.0177	0.0077
TSWEU	0.1049	0.2142	0.0630	0.1432	0.0758
CSCNet	0.0112	0.0713	0.0082	0.0163	0.0196

. The lower MRD represents that the image distortion caused by the correction is relatively slighter. Since the destriping changes the information of original striped image, especially in the case of severe stripe noise, it is natural that the corrected image with residual stripe noise often has a lower MRD. Therefore, it is reasonable that the radiation quality of corrected image needs to be improved first before considering reducing the image distortion; i.e., the MRD comparison is meaningful only when compared methods can effectively remove the stripe noise. It was observed that stripes were not fully removed by ICSRN, resulting in the lowest MRD values on all images. A similar case also existed for the corrected result of SSGN on the SWIR image. In Terra MODIS image, our MRD was only about 0.01 larger than the method of [43] with the effective stripe removal. Therefore, CSCNet had a lower MRD on five real images, indicating that the distortion of useful information caused by our model is minimal, which verifies that the proposed model is more balanced between removing the stripe and preserving the detail information.

4.3. Image Uniformity

It is expected that the stripe removal will improve the uniformity of images. Therefore, the comparisons of image non-uniformity could be used to quantitatively validate the destriping ability of algorithms. The lower value of non-uniformity indicates the improvement of image uniformity, which can be calculated as [46]:

$$\begin{array}{c}\hfill U=\frac{1}{\overline{S}}\times \sqrt{\frac{{\sum }_{i=1}^{N_s}{(S_i-\overline{S})}^2}{N_s}}=\frac{{\sigma }_i}{\overline{S}}.\end{array}$$

(4)

where U represents the image non-uniformity, $\overline{S}$ is the mean value of DNs, $N_s$ is the sample number, $S_i$ is the DN of pixel i, and ${\sigma }_i$ stands for the standard deviation of pixel i. Two uniform regions with the size of $20\times 60$ marked by red boxes in Figure 14 were selected from SWIR images. The calculated results of nine methods are shown in

Table 5. Image non-uniformity using nine methods.

Method	MM	ASSTV	LRSID	Ref. [43]	PADMM	ICSRN	SSGN	TSWEU	CSCNet
Region1	0.0556	0.0561	0.0556	0.0787	0.0611	0.0535	0.0514	0.0919	0.0548
Region2	0.0411	0.0232	0.0219	0.0271	0.0350	0.0221	0.0211	0.0181	0.0206

. Based on the evaluation results of non-uniformity improvement, it can be seen in Table 5 that corrected images obtained by CSCNet had lower non-uniformity. It is worth noting that even though the U value of CSCNet is comparable with those of ICSRN and SSGN in region 1, the clear residual stripes remained in the corrected images of ICSRN and SSGN. Therefore, compared to other methods, CSCNet is slightly larger than TSWEU in region 2. Overall, CSCNet improved the image uniformity and smoothness significantly, while achieving advanced destriping results simultaneously, compared to other methods.

4.4. Ablation Study

CCM and SCM: This section verifies the effectiveness of different modules in CSCNet, including CCM and SCM. The SCM was removed in CSCNet to evaluate the capacity of CCM, and vice visa. In Figure 15a, we can observe that the SCM can remove parts of noise by improving the global uniformity of image, but residual stripes remain in the image. Compared to the SCM, the destriping effect is significantly promoted by CCM, as shown in Figure 15b. In particular, in Figure 15b,c, it can be seen that both CCM and CSCNet effectively removed stripes on the SWIR image, which further demonstrates the effectiveness of CCM, that is, focusing on improving the local consistency of homogeneous regions. Relying on SCM and CCM, CSCNet achieved the best performance, as shown in Figure 15c.

The Number of MCSCM: CSCNet consists of multiple multi-scale column-spatial correction modules (MCSCMs). To evaluate the impact of the number of MCSCMs on the destriping performance, we investigated different numbers of MCSCM: 1, 2, 4, and 6. The corresponding PSNR comparisons are shown in Figure 16, and the corrected CHRIS_AM images for band 6 are given in Figure 17. In Figure 16, we can observe that the learning capacity of CSCNet on the training set was promoted with more MCSCMs: the PSNR values for 4 and 6 MCSCMs are both above 36. As shown in Figure 17, CSCNet with 4 and 6 MCSCMs demonstrated similar performance; thus, we selected four MCSCMs in the final CSCNet based on its correction performance, learning capacity, and network complexity.

Multi-scale extension: Moreover, we also evaluated the effectiveness of multi-scale extension. The proposed network without two downsampling branches was utilized for fair comparisons. PSNR during the training is shown in Figure 18, and the correction results of VNIR images for band 64 are shown in Figure 19. It can be observed from PSNR curves that the multi-scale structure significantly promotes the learning ability. Correspondingly, the proposed CSCNet achievd a better destriping effect on the VNIR image, demonstrating that multi-scale branches and the information exchanging among different resolutions effectively improved the stripe noise removal performance.

4.5. Model Complexity Analysis

We have conducted thorough analysis regarding the balance between the effectiveness and efficiency of the destriping models. Specifically, we list the network parameters and flops of four deep learning-based methods in

Table 6. Network parameters and flops of five deep learning-based models.

Method	ICSRN	SSGN	TSWEU	Lite-CSCNet	CSCNet
Parameters (M)	0.8	0.2	3.2	3.1	6.2
Flops (G)	54	11	103	90	175

. Since final CSCNet consists of multiple (four) multi-scaled column-spatial correction modules (MCSCM) in its final version and the parameters and flops naturally increase as the number of MCSCMs raises, we also constructed a light version of CSCNet (denoted Lite-CSCNet) to demonstrate the relationship between the network complexity and effectiveness. The Lite-CSCNet contains two MCSCM. The destriping results of all compared models on CHRIS_AM are shown in Figure 20.

In addition, we also report the inference time for every method on the CHRIS_AM image in Table 6 to evaluate the time complexity of our method. The traditional methods, including MM, ASSTV, LRSID, the method of [43], and PADMM, ran on the MATLAB 2016a platform with an Intel i5-10210U CPU at 1.6 GHz and with 8 GB memory; the deep learning methods, including ICSRN, SSGN, and CSCNet were conducted with pytorch 1.1.0 framework on the workstation with an Intel i7-8700k CPU at 3.8 GHz and with 128 GB memory and NVIDIA GTX1080Ti GPU. The results of TSWEU were obtained on the same workstation with the MATLAB 2016a, Matconvnet framework.

From Table 6, we can observe that ICSRN and SSGN are lightweight models given their simple network architectures, and the parameters and flops of Lite-CSCNet are comparable to those of TSWEU. The final CSCNet was superior compared to other models. In

Table 7. Inference time (in seconds) of every method on the CHRIS_AM image (for one band).

Method	MM	ASSTV	LRSID	Ref. [43]	PADMM	ICSRN	SSGN	TSWEU	Lite-CSCNet	CSCNet
Time	0.01	9.93	44.47	6.31	3.99	0.26	0.07	0.45	0.35	0.61

, it can be observed that the inference speed of MM was the fastest among all traditional methods relying on its simplest implementation, whereas it generated poor destriping performance with the complicated noise distribution, as expected. Compared to traditional methods, deep learning methods process images with much faster speeds. Among the four deep learning methods, although the running time of final CSCNet was not dominant due to its network design, its destriping performance was much better than those of other methods.

It is unreasonable to solely focus on the complexity of models without appropriate consideration of the destriping performance. Therefore, we display the destriping results of five deep learning-based models on the CHRIS_AM image for band 1 in Figure 20. As we can observe that the lightweight models cannot effectively remove the stripe noise. On the other hand, TSWEU and Lite-CSCNet manage to achieve certain improvements against these light models. Though the complexity of CSCNet is the highest, it effectively handles diverse noise distributions. Additionally, it is worth noting that the complexity of CSCNet matches that of the popular modern CNN-based vision models, and the inference speed is acceptable for real applications, as addressed before.

Moreover, since each part of CSCNet, including CCM, SCM, and FFM, is well motivated and was designed by referring to the characteristics of stripe noise, to further validate the improvements made by the proposed model do not come from the increase in the parameters, we conducted extensive ablation studies and parameter analysis to prove the effectiveness of each proposed module (Section 4.4). In summary, by leveraging both effectiveness and efficiency, we selected the current version of CSCNet as our final model.

5. Conclusions

In this paper, we proposed the multi-scaled column-spatial correction network (CSCNet) for remote sensing image destriping. We design the column-based and spatial-based correction modules (CCM and SCM) to focus on reducing the local differences between columns and improving the global uniformity of image, respectively. Moreover, we presented a channel attention-based feature fusion module to facilitate learning representative features from different modules and scales. Extensive experiments were conducted on several simulated and real remote sensing image datasets to verify the effectiveness of the proposed model. The advanced visual and qualitative assessment results indicate that the CSCNet is effective for various types of stripe noise and outperforms state-of-the-art methods. Moreover, CSCNet achieved an adequate balance between improving the uniformity and preserving the original structural information. The supervised deep learning methods often require paired training data, in which the simulated image is commonly generated by manually adding the stripe noise on the clean image according to the degradation model. Since the physical degradation procedure of the stripe is rather complex, the simplified additive or multiplicative model cannot well handle all kinds of stripes in practice. Therefore, the destriping performance of CSCNet is somewhat limited, when dealing with the extremely complex stripe noise distribution. To address the above issue, self-supervised or semi-supervised learning could be leveraged to further improve the generalization capability of the destriping model as our future work.