Abstract
In this paper, a diverse-region hyperspectral image classification (DRHy) method is proposed by considering both irregularly local pixels and globally contextual connections between pixels. Specifically, the proposed method is operated on non-Euclidean graphs, which are constructed by superpixel segmentation methods for diverse regions to cluster irregularly local-region pixels. In addition, the dimensionality reduction method is employed to alleviate the curse of dimensionality problem with a lower computational burden, generating more representative data with the input graph features. In this context, it then constructs a superpixelwise Chebyshev polynomial graph convolution network (ChebyNet) to aggregate global-region superpixels. Benefiting from different superpixel numbers of segmentations, we construct different graph structures, and multiple classification results are obtained, which brings more opportunities to represent the hyperspectral data correctly. Then, all the diverse-region results are further fused by a majority voting technique to improve the final performance. Finally, numerical experiments on two benchmark datasets are provided to demonstrate the superiority of the proposed DRHy-ChebyNet method to the other state-of-the-art methods.
1. Introduction
1.1. Background
In past decades, the hyperspectral image (HSI) has attracted considerable attention all over the world due to its unique ability, compared with other sensor data, to provide hundreds of contiguous spectral bands, which are helpful to recognize the terrain covers, such as grass, road, building. With the increasing number of hyperspectral sensors and the exploded big data of HSI datasets, the HSI classification problem rapidly became a hot topic in remote sensing [1,2,3,4,5,6,7].
Many approaches have been proposed for the HSI classification problem for the past decades. Most studies focused on classifying the land-cover categories in a high-resolution hyperspectral image. In the beginning, several conventional pattern recognition methods, such as k-nearest neighbor [8], support vector machine [9], Bayesian-based methods [10], and kernel-based methods [11], were proposed to classify the HSI land covers by leveraging the abundant spectral information. Furthermore, the extreme learning machine [12] and the sparse coding methods [13] were developed to improve the classification performance.
It is difficult to accurately recognize the land covers solely with the spectral information, especially for cases with few known samples. In this context, many researchers have focused on the extra spatial information of an HSI image since the spatially neighboring pixels commonly have strong correlations in a local region. Multiple spectral–spatial classification methods have been leveraged to combine both spatial and spectral features. In [14], a Markov random field (MRF) model was employed for sufficient spatial information, which realized impressive performance. It optimized the maximum of a posterior with the spatial information as a prior. Furthermore, the morphological profile based methods [15,16] have been widely employed to effectively integrate useful spectral–spatial features.
1.2. Previous Methods
However, how to accurately extract useful spectral–spatial information depends on the researchers’ professional experience, which is empirical and thus requires being tested manually. In recent years, due to the intrinsically strong representation ability, deep-learning techniques [17,18,19,20,21,22,23,24] have been extensively employed among all applications of the remote sensing area, especially for the HSI classification problem. These deep-learning methods have greatly improved HSI classifiers automatically via high-level features extracted through deep neural networks.
In the past five or six years, hundreds of deep-learning attempts were made, and they can be classified in several categories. The autoencoders (AEs) are easy to implement and demonstrated to be an effective tool: in [25], a stacked AE was employed for HSI classification by extracting high-level features. In order to reduce the computational burden of the stacked AE, a segmented stacked AE was built to separate features into smaller segments [26].
Next, a segmented stacked AE was developed for a spectral–spatial HSI classification problem by involving the mutual information (MI) and morphological profiles [27]. Then, the deep belief network (DBN) was addressed as a stack of unsupervised networks for the HSI classification. Three DBNs were constructed to extract spectral, spatial, and spectral–spatial features from HSI data hierarchically [28]. In [29], the restricted Boltzmann machine (RBM) was employed with a greedy learning algorithm as an optimizer. A group belief network (GBN) was proposed to consider the grouped spectral–spatial features by modifying the bottom layer of each RBM [30].
However, both AE and DBM models are restricted by the same requirement, i.e., one-dimensional (1-D) input data. The recurrent neural network (RNN) models have been exploited to combine each HSI pixel in a band-to-band mode and to perform a similarity check between temporary data and spectral bands. Both the long short-term memory (LSTM) and the gated recurrent unit (GRU) were first employed for HSI classification in [31].
In recent years, one of the most popular techniques for HSI classification was the convolutional neural network (CNN), which typically achieves state-of-the-art performance for almost all kinds of computer vision tasks [32,33,34,35]. In [36], a five-layer 1-D CNN was proposed to classify HSIs via the spectral information. Similar to previous analysis, spectral information is not sufficient for accurate classification; hence, the spatial domain should also be considered in CNN models. In [37], a multi-dimensional CNN model was developed to automatically extract hierarchical spectral–spatial features. Several 3-D CNN models were built to extract deep spectral–spatial features directly from raw HSI data [38,39].
Furthermore, a pixel-pair CNN model was proposed to combine any two pixels as pixel pairs and learn their deep discriminative representations for the HSI classification [40]. Although the existing CNN approaches outperformed other models to some extent, several intrinsic defections were revealed during the previous experiments. For example, the conventional CNN models only consider a square neighboring region to extract the spatial features, failing to capture the geometric margins or construct the connection with the other pixels in the whole HSI. In addition, the CNN methods require a long training time for deep networks with millions of parameters.
To relieve the computational burden and improve the contextual connections in spatial domain, an effective way is to change the pixel-based deep-learning method to an superpixel-based method. A superpixel in an HSI is a local cluster of similar land-cover pixels, and it contains the spatial and margin connections among these pixels. In these years, multiple superpixel-based methods were proposed to extract the spectral–spatial features via segmentation methods [41,42,43,44]. In [45,46], the superpixel methods were mainly used to generate homogeneous region before constructing a graph on superpixels, realizing robust classification results.
In order to combine the advantages of superpixel-based and CNN-based methods, the graph convolutional framework is the solution for HSI classification tasks. The graph convolutional framework can be simply interpreted as the convolution operation on a graph [47], which is able to aggregate node neighbors among the global HSI pixels. The convolution on graph is actually a weighting function over the neighboring nodes of each node. Then, both the node features and connections of nodes are fully represented in the hidden layers by convolutions on graph. Therefore, the graph convolutional framework can not only learn the local boundary of each superpixel landcover but also aggregate the globally contextual connections of similar superpixels.
Some pioneer researchers have proposed a few graph convolution works for HSI classification [48,49]. In [50], a spectral–spatial graph convolutional network (SGCN) was proposed for semisupervised HSI classification. It used the second-order neighborhood to approximate the graphical convolution operation and realized good performance. However, directly using the existing GCN work for HSI classification did not achieve the desired expectation.
In [51], a multi-scale dynamic graph convolutional network (GCN) was proposed to combine the classification results with different numbers of neighbors and to dynamically change the graph adjacency for different layers. However, the dynamic scheme did not change the node representations but modified their adjacency connections. Furthermore, deeper GCN may suffer from over-smooth problem, and second-layer GCN has been demonstrated to be a good choice for the Cora dataset; however, five-layer GCN is the opposite [52,53]. The adjacency can be updated only twice for a two-layer GCN, and its improvement is limited based on the same graph structure.
The direct use of GCN on the superpixels may face certain problems. For extracting spatial features, the basic superpixel segmentation idea is dependent on the spectral signatures of each pixel. Although the same-category pixels have similar spectral characteristics, one specific segmentation may not be always correct. This is because one pixel of the HSI dataset may actually contain two or more categories of land covers [54,55,56], especially for the low spatial resolution of HSI data.
The constructed GCN model based on this superpixel segmentation would not be guaranteed accurate for representing the spatial features. Then, for extracting spectral features, although the rich spectra can provide quite useful information for data analysis, the high dimensionality of HSI data may lead to the curse of dimensionality problem [57]. It would deteriorate the potential of GCN for representing the true spectral information of each category.
1.3. Proposed Method
Motivated by the aforementioned concerns of the existing GCN-based and superpixel-based methods, we propose a novel graph convolution framework based on the diverse-region hyperspectral data (DRHy) for the semisupervised HSI classification task. Instead of a fixed input graph for GCN, we employ the superpixel-based segmentation method, such as the entropy rate superpixel (ERS) method [58], to segment the whole spatial scene into relatively homogenous regions with different numbers of superpixels.
Furthermore, to avoid the Hugh phenomenon and extract intrinsic low-dimensional features simultaneously, we employ the principal component analysis (PCA) in each homogenous superpixel region, which is inspired by the method in [59]. It is equivalent to a smoothing preprocessing, which helps to aggregate the locally homogenous region pixels and also relieve the total computational burden.
In addition, in order to further improve the representative ability of the low-dimensional data, we concatenate both the intensity and the energy of the low-dimensional data as the new feature. After all previous processing, the input graph can be built by using the aggregated features as nodes and constructing their connections. In this context, different graphs encode different spectral–spatial information and indicate different connections among all the nodes (homogenous superpixel regions). Therefore, we reproduce the above steps to generate diverse superpixel regions and then construct diverse graphs based on these superpixels.
Next, we individually train the corresponding second-layer graph convolutional networks for different input graphs to aggregate and smooth similar superpixels. In this paper, we employ the Chebyshev polynomial graph convolution network (ChebyNet) [60], for the diverse-region hyperspectral image classification, which is termed as the proposed DRHy-ChebyNet algorithm. Then, we back-project the learned superpixel classification result to the original pixels for evaluating the performance. As a result, the final classification results are obtained via the majority voting decision fusion strategy. More specific steps and tricks are analyzed in detail in the following sections.
The main contributions of this paper can be summarized as follows: first, the usage of graph convolution can extend the spatial information connection from the local region to the whole spatial domain, which is helpful for sufficiently learning spatial features; second, the constructed graphs based on segmented superpixel of HSI data provide diverse spatial-spectral information, which is critical to extract the intrinsic spectral–spatial features for classification; and third, the majority voting fusion technique is helpful to yield a more persuasive result, especially when the label information is limited.
The rest contents of this paper are organized as follows: Section 2 reviews the preliminary works and introduces the motivations of the proposed DRHy-ChebyNet method; Section 3 shows the detailed steps of the proposed method with sufficient analysis; and Section 4 provides multiple experiments on the public datasets to demonstrate the effectiveness of the proposed method.
2. Method
In this section, we review several preliminary works of graph convolutional techniques and introduce the motivation of the proposed method for HSI classification.
2.1. Preliminary Works of Graph Convolution Techniques
As we know, deep-learning techniques, such as CNN, RNN, AE, and DBN, have been proved to effectively reveal hidden features of Euclidean data. When facing the tasks for handling non-Euclidean data, the above deep-learning methods may be restricted. Recently, there has been increasing interest in extending deep-learning approaches from Euclidean data to irregular graph data. The generalizations of some common operations on the Euclidean data have developed rapidly for the past few years. In particular, a graph convolution can be generalized from a 2-D convolution by taking the weighted average of one node’s adjacent neighbors, which yields the convolutional graph neural networks (ConvGNNs).
ConvGNNs are grouped into two categories, spectral-based and spatial-based methods. Spatial-based methods define graph convolutions by information propagation and it propagates node information along edges. Furthermore, they resemble the form of traditional convolution operation on Euclidean data [61]. Spectral-based methods interpret the convolution operation as noise removal from the perspective of graph signal processing [62]. The spectral convolutional neural network (Spectral CNN) was proposed to define the graph convolution in spectral domain with the help of a graph Fourier transform [63].
However, this requires the eigendecomposition of the Laplacian matrix, which brings a heavy computational burden. Furthermore, any perturbation to a graph results in a change of eigenvectors and eigenvalues. Then, in [60], a Chebyshev spectral CNN (ChebyNet) approximates the spectral filter by Chebyshev polynomials of the diagonal matrix of eigenvalues. It defines the spectral filters in spatial domain and can extract local features without considering the graph size. Then, a GCN was proposed by Kipf and Welling [47] as a first-order approximation of the ChebyNet, further decreasing the computational complexity. The GCN can be considered to bridge the gap between spectral-based and spatial-based approaches.
2.2. Motivations of the Proposed DRHy Method
A few GCN-based methods, such as the SGCN [50] and the MDGCN [51], were proposed for semisupervised HSI classification, and both approaches have their own advantages and limitations for implementing. The SGCN approach used the second-order polynomials to approximate the graphical convolution operation and realized good performance. However, to directly use the existing GCN work for HSI classification does not achieve the best expectation.
In [51], a multi-scale dynamic graph convolutional network was proposed to combine the classification results with different numbers of neighbors and to dynamically change the graph adjacency for different layers. However, the dynamic scheme actually does not change the node representations but modify their adjacency connections. Furthermore, it is noted that deeper GCN may suffer from over-smooth problem. In [52,53], they prefer the two-layer GCN rather than the five-layer GCN for the Cora dataset. The adjacency can be updated only once for a two-layer GCN, so its improvement is limited. Based on the aforementioned problems, here are several motivations that inspire us for the proposed method:
First, spectral information is critical to determine the classification accuracy and it should be carefully preprocessed. In previous studies, it has been demonstrated that the high dimensionality of HSI data leads to the curse of dimensionality problem, which will reduce the generalization capability of classifiers and surely increase the computational complexity. Hence, in this paper, we perform the dimensionality reduction method, such as the PCA method, to improve the efficiency and the performance.
Second, spatial information should be carefully considered, including both globally and locally spatial information. It is easy to verify that locally spatial information helps cluster the similar pixels since local homogenous pixels commonly belong to the same land cover. Herein, globally spatial information indicates the connections between any spatial region in the whole HSI data, which can be used for the aggregations of homogenous neighbors that locate far away from each other. Due to limited receptive field of each layer, the CNN-based methods require deep networks to cover a large receptive field.
Hence, in this paper, we first employ the superpixel-based segmentation methods to cluster the pixels of homogenous regions, and then leverage GCN-based schemes to further aggregate all similar superpixels and to learn their intrinsic connections and representations. Note that the final performance depends mainly on the input graph, which is determined by the superpixel-based segmentation method. To alleviate this dependency, we re-segment diverse superpixels for constructing different input graphs to get the classification results. Then, we fuse these results via majority voting to improve the robustness. More details please refer to Section 2.3.4.
2.3. Proposed DRHy Method
In this section, a specific method is proposed to extract the features of diverse-region hyperspectral data by using the ChebyNet, which is termed as DRHy-ChebyNet. The proposed DRHy method is concatenated in four steps: (a) superpixel segmentation and dimensionality reduction, (b) graph construction, (c) graph convolution and pixel backprojection, and (d) diverse region scheme. The illustration of the proposed method is shown in Figure 1. The details of the above steps are introduced as follows.
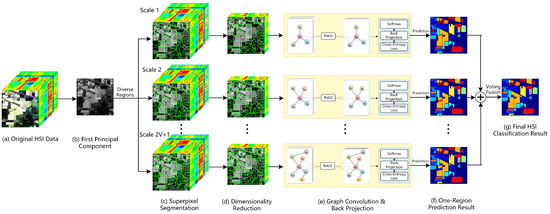
Figure 1.
Illustration of the proposed DRHy-ChebyNet method.
2.3.1. Superpixel Segmentation and Dimensionality Reduction
Graph-based segmentation approaches have been widely employed in superpixel segmentation [59]. However, it commonly has heavy computational burden for implementation. In this paper, we first employ the PCA to extract the first principal component by solving the following problem [64]
where is the reshaped HSI data (from a 3-D image to a 2-D matrix), the superscript is the transpose operation, B is the number of spectrum bands, T is the total number of pixels, is the first principal direction, and is the first principal component. After reshaping the first principal component to its original size, then we employ the ERS approach to segment the pixels into superpixels. The ERS segmentation is an undirected graph-based clustering algorithm. Given an input image with the preset number of superpixels, a graph can be constructed based on the input image. We divide the whole graph into smaller connected subgraphs by solving the following optimization problem
where denotes the trace operation, is the edge of a graph , is the subset of , is the hyperparameter, and and are the entropy rate and balance term, respectively. A greedy algorithm was proposed in [59] to solve the above problem efficiently.
Suppose that there are S superpixel regions in total, and each region corresponds to a small irregular HSI cube , where and. Then, we reshape the cube to a 2-D matrix, , where is the number of pixels in the s-th superpixel region, and each column of denotes the spectrum vector of one pixel. In this context, we consider a linear dimensionality reduction approach, such as PCA, which projects the signal onto a low-dimensional space in a linear way. The basic idea of the PCA structure can be formulated as
where is the identity matrix, denotes the principal directions, denotes the principal components, i.e., the low-dimensional data. The principal components can be considered as the cluster indicators that gather the same cluster of data linearly in the low-dimensional domain, i.e., the PCA provides an embedding for the data lying on a linear manifold. The problem in Equation (2) can be easily solved via singular value decomposition (SVD). Then, the matrix is reshaped to the original size of the cube, and each pixel corresponds to its original location.
PCA works well in many previous studies as a preprocessing tool to extract more representative features and reduce the dimensionality. In [65], the PCA algorithm can increase the spectral separability of pixels. Furthermore, in [59], they proved that PCA on superpixels was better than PCA on the entire data cube. Therefore, we follow this useful scheme before constructing the graph.
2.3.2. Graph Construction
After superpixel segmentation and dimensionality reduction, multiple small superpixel regions are obtained with d principal components left in the spectral domain. As analyzed before, the construction of the graph is critical to the final performance. To explore the local and global connections on a graph, the key idea is to obtain the node features and build their edges. First, the mean spectral signature of each superpixel region is calculated as the standard feature of this region, which is termed as . According to the analysis in [43], an extra energy feature of the same superpixel region can be generated as , where ⊙ denotes the Hadamard product. Both the mean and the energy signatures can be combined to characterize the s-th superpixel, and then the new feature is
Then, the weight of each pixels in the s-th superpixel region can be measured by its “distance” to the corresponding feature in this region, which can be calculated as
where the subscript denotes the element at the k-th row and s-th column, and is the hyperparameter, which is empirically set to 0.2 [51]. Note that this is the weight between any pixel and the corresponding feature in one superpixel, and thus it does not construct a graph. Furthermore, the entire weight matrix of all the pixels in the HSI data is
Through this preprocessing, we have the weight of every pixel in the HSI data. Then, each superpixel can be regarded as one node of the constructed graph, and its node feature can be defined by the normalized weighted sum of all the pixels, that is,
Then, the input graph nodes can be confirmed to represent all the superpixel regions with their corresponding features. As analyzed in [43], superpixel regions reflect the spatial distributions of local regions and the distance metrics, which represent the similarity of the superpixels, should be well designed. Any two similar superpixels should be guaranteed a large adjacency value, while those discrepant superpixels should output a relatively lower adjacency value. Then, their adjacency matrices can be constructed as
where denotes the norm and denotes the set of neighbor nodes. Until now, the input graph is built with node features and weight adjacency . The distance between pixel, and the standard feature is useful to measure its contribution to the input. Furthermore, it can be also regarded as a preprocessed filter for aggregating the similar pixels.
2.3.3. Spectral-Based Graph Convolution Framework and Pixel Backprojection
The implementation of spectral-based graph convolution framework is defined in the Fourier domain by computing the eigendecomposition of the graph Laplacian. It can also be formulated as the multiplication of a signal with a filter parameterized by
where is the eigenvector matrix of the normalized graph Laplacian . Here, is the diagonal eigenvalue matrix of , and is the degree matrix, which is defined as . This operation results in potentially intense computations and non-spatially localized filters.
In [47], it was suggested that can be approximated by a truncated expansion in terms of Chebyshev polynomials up to K-th order. Then, the operation can be reformulated as
with . Herein, is the largest value of , is now a vector of Chebyshev coefficients. The Chebyshev polynomials are defined as with and . Due to the K-th order approximation in the Laplacian, the filters defined by ChebyNet are K-localized in space, which means filters can extract local features independently to the graph size. Hence, we only need to perform the eigendecomposition of the Laplacian once, and this relieves the computational burden.
Then, by considering the feature maps in multiple graph convolution layers, the graph convolution processing of the ChebyNet can be formulated as
Next, the final learned features for all superpixels regions should be back-projected to the pixel level. In this context, we employ the aforementioned weighted matrix to allocate the contribution of each pixel to the final features. It can be formulated in a simply linear way by a matrix multiplication, that is,
The softmax activation function, defined as with , is applied row-wise. For the semi-supervised multi-class classification, we then evaluate the cross-entropy error over all labeled samples:
where is the set of pixel indices that have labels and is the label matrix. The weight matrices of neural networks are trained by gradient descent. We perform batch gradient descent using the full dataset for every training iteration.
2.3.4. Diverse-Region Scheme
The graph convolution can be regarded as a low-pass filter in frequency domain on graph [52]. Therefore, the output representations are corresponding to the initial input graph, which depends on the superpixel segmentation methods. If the superpixel segmentation results are not accurate, the final classification performance would be degraded.
As it is easy to imagine, if we segment few superpixels, the segmentation results may contain several classes of land covers, which requires further segmentation. However, if we segment too many superpixels, then the features obtained from the over-segmented regions may become less distinctive, and it is even harder to infer the true class labels. According to the analysis in [59], there is no single region size that is able to adequately characterize the spatial information of HSIs. Therefore, we propose a diverse-region scheme to provide diverse input graphs and to improve the final performance by combing all the output representations of different graphs.
Suppose that we segment the HSI data with kinds of scales, which correspond to input graphs. Similar to the segmentation scheme in [59], the number of superpixels of the v-th scale is
where is the basic segmentation number. Specifically, we fuse the final predictions of different graphs via the majority voting decision as follows
where denotes the class label of the n-th pixel, is the confidence that class c is predicted for the n-th pixel, and is the indicator function. Herein, indicates the weighted confidence scores of the v-th segmentation, which was previously calculated via the distance between the pixel and the standard point. Figure 1 illustrates all the steps of the proposed DRHy method for HSI classification and the pseudo code is listed in Algorithm 1.
| Algorithm 1 Proposed DRHy Method. | |
| Input: The HSI data, true labels of the labeled data, and locations of the labeled and unlabeled data | |
| 1: | Perform PCA on the HSI data to obtain the first principal component by solving Equation (1); |
| 2: | for to V do |
| 3: | Employ ERS approach on the first principal component to segment superpixel regions by solving Equation (2); |
| 4: | Reshape the corresponding s-th superpixel cube of the original HSI data into a 2-D matrix ; |
| 5: | Use linear dimensionality reduction approach to extract main features by solving Equation (3); |
| 6: | Construct the graph according to the data matrix of each superpixel region via Equations (4)–(8); |
| 7: | for to Epoch Number do |
| 8: | Calculate the graph convolution via Equation (11); |
| 9: | Back-project to the pixel level via Equation (12); |
| 10: | Optimize the network parameters driven by the loss function in Equation (13); |
| 11: | ; |
| 12: | end for |
| 13: | ; |
| 14: | end for |
| 15: | Predict labels and take the majority voting to fuse the results of all the superpixel segmentaions via Equation (15); |
| Output: The predicted labels. | |
3. Experimental Results
In this section, numerous experiments are provided to demonstrate the effectiveness of the proposed DRHy methods. Specifically, we compare both proposed methods with other state-of-the-art methods, including the GCN-based and CNN-based methods, on several public datasets. Three common metrics, the overall accuracy (OA), average accuracy (AA), and kappa coefficient, are used to quantitatively measure the classification performance. Furthermore, we tested the influence of the labeled sample number on the final result, and the computational times are further given for a comparison.
3.1. Datasets
In this section, two public datasets (https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes, accessed on 17 June 2022) are used to evaluate the performance of the state-of-the-art methods and the proposed methods.
(1) Indian Pines Dataset: It was recorded by the airborne visible/Infrared Imaging Spectrometer (AVIRIS) sensor in June 1992. The dataset has pixels in spatial domain and 220 spectral bands covering 0.4–2.45 m spectrum. In this paper, 20 low signal-to-noise ratio (SNR) bands are removed, and a total of 200 bands are used for classification. It contains 16 different land covers in total, and 10,249 pixels are labeled as the ground truth. The numbers of labeled and unlabeled samples are listed in Table 1 and the Indian Pines dataset is illustrated in Figure 2.

Table 1.
Numbers of labeled and unlabeled samples for Indian Pine Dataset.

Figure 2.
Indian Pines dataset. (a) Pseudo-color image. (b) Ground truth.
(2) University of Pavia Dataset: It was collected by the ROSIS sensor under the HySens project managed by the German Aerospace Agency in 2001. It contains a spatial coverage of pixels with 115 spectral bands, 12 of which are removed due to their low SNRs. It has a spectral coverage from 0.43 to 0.86 m and a spatial resolution of 1.3 m. Herein, 42,776 labeled pixels of nine classes are used as the ground truth. The numbers of labeled and unlabeled samples are listed in Table 2, and the University of Pavia dataset is illustrated in Figure 3.

Table 2.
Numbers of labeled and unlabeled samples for the University of Pavia Dataset.

Figure 3.
University of Pavia dataset. (a) RGB image. (b) Ground truth.
3.2. Classification Results and Discussion
In this subsection, in order to compare the proposed DRHy methods with the other state-of-the-art methods, we use the same training data and the test data for all the methods by using the same random seeds. In this context, three GCN-based methods, including the traditional GCN method, the method, and the MDGCN method, and three CNN-based methods, i.e., the spectral–spatial residual network (SSRN) method, the fast dense spectral–spatial convolutional network (FDSSC) method, and the diverse-region CNN (DR-CNN) method, are tested as a comparison. The mentioned methods include the recent graph convolution frameworks, two representative recent works by using 3D CNN scheme, and one representative research, which employs the diverse-region scheme.
To generate the training data and testing data, we randomly labeled 30 samples of the classes that have plenty of samples and the half samples of the classes that do not have enough samples. Furthermore, 90 percent of the labeled samples are used to learn the potential representation and the rest of them are used as the validation set to tune the model parameters. The exact numbers of labeled data and unlabeled data of the Indian Pines Dataset and the University of Pavia Dataset are listed in Table 1 and Table 2, respectively. The classification results of both datasets are analyzed in detail as follows:
(1) Indian Pines Dataset
Before illustrating the results, the experimental settings are introduced first. For the proposed methods, we segment 50, 71, 100, 141, and 200 superpixel regions for constructing different input graphs and then fuse their results at the end. The dimensions are reduced to 30 for all superpixel cube. Furthermore, as analyzed in Section 2.3.3, we use two-layer graph convolutional networks for both proposed methods with 64 hidden units. For the DRHy-ChebyNet method, the same learning rate is set to 0.05 with 2000 epochs. All the adjacency matrices for different graphs are truncated with the threshold 0.9.
The classification maps of the proposed methods and the other five GCN- and CNN-based methods are compared with the ground truth in Figure 4. Their quantitative results are listed in Table 3, and the best scores are marked in bold. As can be seen, although the 3D CNN methods extract deep spectral–spatial features directly from raw HSIs, they rely highly on the number of labeled data and the deep depth of convolutional networks for learning globally contextual representations. In another words, all CNN-based methods realized good performance; however, their performance is likely restricted by the few labeled samples.
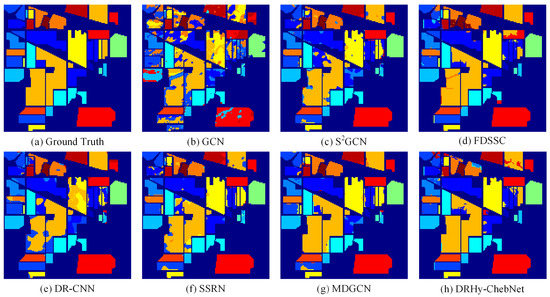
Figure 4.
Classification results of different methods on the Indian Pines dataset. (a) Ground truth. (b) GCN. (c) SGCN. (d) FDSSC. (e) DR-CNN. (f) SSRN. (g) MDGCN. (h) The proposed DRHy-ChebyNet method.

Table 3.
Classification results of different methods on the Indian Pines dataset.
In addition, the traditional GCN method performs well for the natural language processing (NLP) dataset, such as the Cora dataset [47]; however, it may not be suitable for HSI classification problem without any modifications. The SGCN method, as a successful improvement of the traditional GCN method, considers the local connections between pixel nodes, achieving good performance.
However, it lacks of constructing the global connections with the other nodes, which are outside the local regions. The MDGCN has better performance compared with the SGCN for the full consideration of dynamic graph update and multi-scale neighborhoods of node connections. However, it uses only one kind of graph constructions with updated neighborhood connections. Then, its final performance depends on the original construction of the graph. Furthermore, due to the shallow GCN framework leveraged in the experiments, the number of updates is limited.
Among all the listed methods, the proposed method achieved excellent performance in terms of the three quantitative metrics. In particular, we used a truncation operation on the adjacency matrix for cutting off the non-correlated edges, i.e., the edges with small similarity weights. This truncation is similar with the dynamic label propagation (DLP) [43], which has a faster convergence and robust performance. Furthermore, based on our test, the ChebyNet framework has more robust performance for HSI classification problem. However, it should be noted that the proposed method wrongly recognize the large regions of “Soybean-mintill” class (Orange part) into the “Corn-notill” (Dark blue part) in the center of the scene. Essentially, these two classes of land covers are quite similar in spectral domain. Hence, it is difficult to distinguish them and not to mention the limited number of labeled data.
(2) University of Pavia Dataset
The University of Pavia dataset has more samples than the Indian Pines dataset does. There are 42,776 labeled pixels in total. We segment the whole scene into 30, 42, 60, 85, and 120 superpixel regions for this case. The dimension is reduced to 30 for all superpixel cube. The other parameters are the same as those in the above subsection. In [51], it mentioned that the GCN and SGCN are not scalable to this large dataset because the adjacency matrix can be dense with 42,776 times 42,776 pixels or nodes in total. That requires a terrible memory indeed. However, SGCN restricts the adjacency in a local region and the truncation can be further applied for constructing the edge weights by abandoning the small weights. Then, the final adjacency matrix would be a sparse matrix and can be saved in a low-dimensional dense matrix. Then, both the GCN and SGCN are scalable for the University of Pavia dataset.
The classification maps of all the methods are illustrated in Figure 5 and their quantitative results are listed in Table 4. Similar to the results of Indian Pines Dataset, the GCN method still performs not good enough and the SGCN method is also restricted by the lack of globally contextual representations.
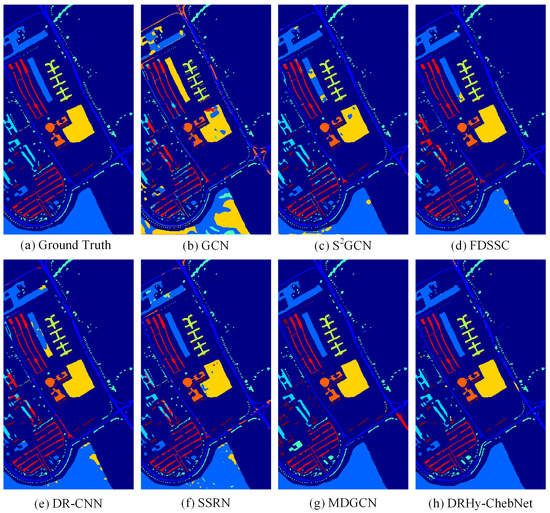
Figure 5.
Classification results of different methods on the University of Pavia dataset. (a) Ground truth. (b) GCN. (c) SGCN. (d) FDSSC. (e) DR-CNN. (f) SSRN. (g) MDGCN. (h) The proposed DRHy-ChebyNet method.

Table 4.
Classification results of different methods on the University of Pavia dataset.
Thus, there are multiple prominent misclassifications that can be easily visualized in a glance. Regarding to the two 3D CNN methods, they perform even better for the University of Pavia dataset than they did for the Indian Pines dataset. Based on the analysis in the original reference [39], the overall accuracy can achieve 99.61% if it has enough training data. Thus, we believe that it is the limitation of few samples that makes it perform not as well as the expectation. For the MDGCN method, it shows a smooth visualization by aggregating multi-scale neighbors and realizes high classification accuracy, especially for accurately classifying the orange Bare Soil region in the center compared with the other aforementioned methods.
In this context, the proposed method had the best performance among all the methods by fully considering the locally and globally connections among all pixels and using the majority voting to fuse the results of different input graphs. The input graph was constructed based on the superpixel segmentation methods, which determined the upper bound of the representative ability. Even though the MDGCN updated the adjacency dynamically and also fused different numbers of neighbor adjacencies, the performance was still restricted by the representative ability of a single graph.
Based on the final classification results, we demonstrate that the modification of input graphs was more effective than the modification of the adjacencies of one fixed graph for the HSI classification problem. Benefiting from the superpixel segmentation method, the scale of the input graph was small, and thus the computational burden of the ChebyNet was indeed acceptable. However, if the input graph is quite large, then we would prefer to choose the trade-off between high accuracy and high efficiency.
4. Discussion
4.1. Discussion of the Proposed Method for One Region
In this section, we evaluate the importance of the diverse-region fusion scheme. Herein, we take five different segmentation scales, i.e., v is selected from the set . The case that corresponds to the basic number of segmentations and we choose for Indian Pines and for University of Pavia. Table 5 and Table 6 list the OA, AA, and Kappa coefficients on the Indian Pines dataset and the University of Pavia dataset under the same configuration as the above subsections. For the Indian Pines dataset, the accuracy of one single region reaches the best when , while the accuracy is the best for the ‘’ region for the University of Pavia dataset. As can be seen, the final fusion technique has significant improvement on the classification accuracy.

Table 5.
Classification performance for different superpixels on the Indian Pines dataset.

Table 6.
Classification performance for different superpixels on the University of Pavia dataset.
4.2. Discussion of the Different Labeled Data
In this subsection, in order to evaluate the robust performance of the proposed methods on few labeled samples, we test all the GCN-based methods, i.e., the traditional GCN method, the S2GCN method, the MDGCN method, and the proposed methods, on different number of labeled samples for the Indian Pines dataset. Three classes of the Indian Pines dataset (“Alfalfa”, “Grass-pasture-mowed”, and “Oats”) have small amount of samples; hence, the final performance is highly dependent on the number of labeled samples. We randomly select 5, 10, 15, 20, 25, and 30 samples per class, following the same selection rule mentioned in Section 4.2. For the small number of labeled samples, we do not segment too many superpixel regions.
Then, the final classification results in terms of three quantitative metrics versus different numbers of labeled samples are shown in Figure 6 and Figure 7 for the two data, respectively. The superpixel-based methods can gather the local pixels before classifications, and the graph convolution can further aggregate global pixels, which reduces the reliance on the number of samples. If there is at least one labeled sample falling into every superpixel region, then this labeled sample is helpful to classify all the pixels in one superpixel region. However, in the worst case, there are too few labeled samples, and thus we cannot guarantee that each superpixel contains one labeled sample. This increases the difficulty of classifications.
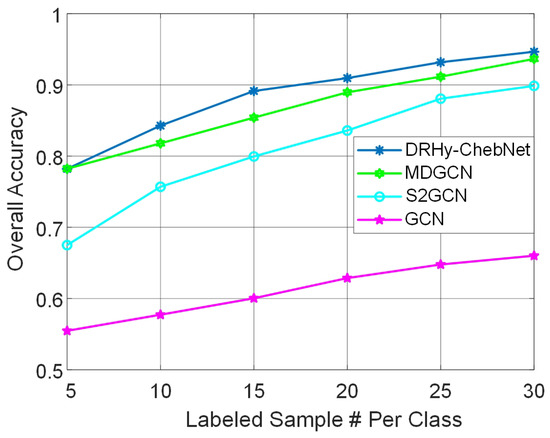
Figure 6.
Overall accuracies of the GCN-based methods versus different numbers of labeled samples on the Indian Pines dataset.
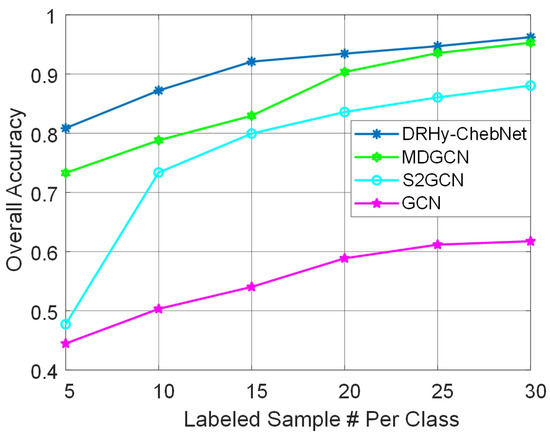
Figure 7.
Overall accuracies of GCN-based methods versus different numbers of labeled samples on the University of Pavia dataset.
As can be seen, the proposed DRHy-ChebyNet had the best performance for all numbers of labeled data except for the worst case, i.e., when the number of labeled samples was down to 5, where it had comparable performance with the MDGCN. When the number of labeled samples per class grew to 10, the proposed method had a giant step of improvement, realizing good classification accuracy. The GCN and method do not use the superpixel to cluster local pixels, and thus their performance is not as good as the other superpixel-based methods when lacking labeled samples.
4.3. Discussion of Running Time
The CNN-based methods are supervised learning methods, which require large computational time to train the models, while all the GCN-based methods are semi-supervised learning methods. Therefore, it would be fair to compare the running times of only GCN-based methods. The running times of all GCN-based methods for the Indian Pines dataset and University of Pavia dataset are listed in Table 7.

Table 7.
Running times of training and testing processes of the semi-supervised learning methods.
All the simulations were conducted on a portable workstation with a 2.6-GHz CPU and 64 GB memory. More importantly, we used a Quadro T2000 GPU for accelerating computations. Essentially, the ChebyNet requires a heavier training burden for each epoch than the GCN does. However, as can be seen, the proposed DRHy-ChebyNet is more efficient than the other methods since it requires less training epochs to realize the optimum.
Empirically, 2000 epochs are enough for the DRHy-ChebyNet, while GCN-based methods need about 4000 epochs. In this context, both the traditional GCN method and the method are pixelwise methods, and thus their training times are clearly much larger than any other superpixel methods. Regarding to the testing times, all methods are comparable, and the GCN and methods are more efficient.
5. Conclusions
In this paper, we proposed a graph convolution framework based on diverse-region segmentation for the HSI classification problem, which is named the DRHy method. Specifically, we fully considered several concerns of previous studies as follows:
First, the superpixel segmentation method was leveraged to cluster the pixels in local irregular regions. Second, the principal component analysis (PCA) method was employed to relieve the curse of dimensionality problem and to improve the representation ability of spectral information. Third, we constructed graphs based on the superpixels and employed ChebyNet to aggregate similar superpixel regions and to efficiently classify each pixel via semi-classification scheme. Fourth, diverse regions were used to construct diverse graphs for reproducing different classification results, which were fused to vote for the final classification performance.
Compared with previous state-of-the-art methods, the proposed method considered the locally clustered spatial regions, globally contextual connections between similar pixels, and dimensionality reduction for better spectral representations, realizing excellent performance even with only a few labeled samples. Furthermore, as a benefit from the superpixel framework, the proposed methods are quite efficient compared with the traditional GCN methods that are based on a tremendous number of pixels. In the future, we would like to explore deeper GCN features of the HSIs and to construct an end-to-end model without superpixel preprocessing.
Author Contributions
Conceptualization, Y.H.; methodology, Y.H.; software, Y.H. and X.Z.; validation, Y.H., B.X. and J.L.; formal analysis: Y.H., J.K. and S.T.; investigation, Y.H. and Z.C.; resources: Y.H. and W.H.; data curation, Y.H., X.Z. and B.X.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H., X.Z., B.X., J.L., J.K., S.T., Z.C. and W.H.; visualization, Y.H., J.K. and S.T.; supervision, Y.H. and W.H.; project administration, Y.H. and W.H.; funding acquisition, Y.H., J.L., J.K., S.T. and Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China under Grant 61901112, 62001062, 62101371 and 61971329, in part by Jiangsu Province Science Foundation under Grant BK20190330 and BK20210707, in part by the state Key Laboratory of Geo-Information Engineering under Grant SKLGIE2020-M-3-1, and in part by the Government-Business-University-Research Cooperation foundation between Wuhu and Xidian under Grant XWYCXY-012021002-HT.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fang, L.; Liu, G.; Li, S.; Ghamisi, P.; Benediktsson, I. Hyperspectral image classification with squeeze multibias network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1291–1301. [Google Scholar] [CrossRef]
- Li, J.; Zhao, X.; Li, Y.; Du, Q.; Xi, B.; Hu, J. Classification of hyperspectral imagery using a new fully convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 292–296. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Xi, B.; Li, J.; Li, Y.; Song, R.; Xiao, Y.; Shi, Y.; Du, Q. Multi-Direction Networks with Attentional Spectral Prior for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Xi, B.; Li, J.; Li, Y.; Song, R.; Sun, W.; Du, Q. Multiscale Context-Aware Ensemble Deep KELM for Efficient Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5114–5130. [Google Scholar] [CrossRef]
- Kang, J.; Wang, Z.; Zhu, R.; Xia, J.; Sun, X.; Fernandez-Beltran, R.; Plaza, A. DisOptNet: Distilling Semantic Knowledge From Optical Images for Weather-Independent Building Segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Kang, J.; Wang, Z.; Zhu, R.; Sun, X.; Fernandez-Beltran, R.; Plaza, A. PiCoCo: Pixelwise Contrast and Consistency Learning for Semisupervised Building Footprint Segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10548–10559. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.; Tian, J. Local manifold learning-based k-nearest neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- He, Z.; Shen, Y.; Zhang, M.; Wang, Q.; Wang, Y.; Yu, R. Spectral–spatial hyperspectral image classification via SVM and superpixel segmentation. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Montevideo, Uruguay, 12–15 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 422–427. [Google Scholar]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Li, J.; Plaza, A. Active learning with convolutional neural networks for hyperspectral image classification using a new bayesian approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6440–6461. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gomez-Chova, L.; Munoz-Mari, J.; Vila-Frances, J.; Calpe-Maravilla, J. Composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local binary patterns and extreme learning machine for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Wang, Y.; Loe, K.; Tan, T.; Wu, J. A dynamic hidden markov random field model for foreground and shadow segmentation. In Proceedings of the WACV, Breckenridge, CO, USA, 5–7 January 2005; pp. 474–480. [Google Scholar]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using svms and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef] [Green Version]
- Song, B.; Li, J.; Dalla Mura, M.; Li, P.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A.; Chanussot, J. Remotely sensed image classification using sparse representations of morphological attribute profiles. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5122–5136. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Fu, W.; Fang, L. Multiscale Superpixel-Based Sparse Representation for Hyperspectral Image Classification. Remote Sens. 2017, 9, 139. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A Fast Dense Spectral–Spatial Convolution Network Framework for Hyperspectral Images Classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Peng, J.; Sun, W. Spatial–Spectral Squeeze-and-Excitation Residual Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 884. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhang, L.; Du, B. Spectral-Spatial Hyperspectral Image Classification with Superpixel Pattern and Extreme Learning Machine. Remote Sens. 2019, 11, 1983. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.K.; Zhang, X.; Huang, X. Hyperspectral image classification with deep learning models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Zheng, J.; Zhao, H.; Qing, C.; Yang, Z.; Du, P.; Marshall, S. Novel segmented stacked autoencoder for effective dimensionality reduction and feature extraction in hyperspectral imaging. Neurocomputing 2016, 185, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Paul, S.; Kumar, D. Spectral spatial classification of hyperspectral data with mutual information basd segmented stacked autoencoder approach. ISPRS J. Photogramm. Remote Sens. 2018, 138, 265–280. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Ob. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Tan, K.; Wu, F.; Du, Q.; Du, P.; Chen, Y. A parallel gaussian-bernoulli restricted boltzmann machine for mining area classification with hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obser. Remote Sens. 2019, 12, 627–636. [Google Scholar] [CrossRef]
- Zhou, X.; Li, S.; Tang, F.; Qin, K.; Hu, S.; Liu, S. Deep learning with grouped features for spatial spectral classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 97–101. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Kwon, H. Going deeper with contextual CNN for hyperspectral image classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Ma, X.; Jie, G.; Wang, H. Hyperspectral image classification via contextual deep learning. EURASIP J. Image Video Process. 2015, 2015, 20. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral–spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L. Efficient superpixel-level multitask joint sparse representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5338–5351. [Google Scholar]
- Zhang, G.; Jia, X.; Hu, J. Superpixel-based graphical model for remote sensing image mapping. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5861–5871. [Google Scholar] [CrossRef]
- Jia, S.; Deng, X.; Zhu, J.; Xu, M.; Zhou, J.; Jia, X. Collaborative representation-based multiscale superpixel fusion for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7770–7784. [Google Scholar] [CrossRef]
- Mei, J.; Wang, Y.; Zhang, L.; Zhang, B.; Liu, S.; Zhu, P.; Ren, Y. PSASL: Pixel-level and superpixel-level aware subspace learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4278–4293. [Google Scholar] [CrossRef]
- Cui, B.; Xie, X.; Ma, X.; Ren, G.; Ma, Y. Superpixel-based extended random walker for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3233–3243. [Google Scholar] [CrossRef]
- Sellars, P.; Aviles-Rivero, A.; Schonlieb, C. Superpixel contracted graph-based learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4180–4193. [Google Scholar] [CrossRef] [Green Version]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Xi, B.; Li, J.; Li, Y.; Song, R.; Xiao, Y.; Du, Q.; Chanussot, J. Semisupervised Cross-scale Graph Prototypical Network for Hyperspectral Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xi, B.; Li, J.; Song, R.; Xiao, Y.; Chanussot, J. SGML: A Symmetric Graph Metric Learning Framework for Efficient Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 609–622. [Google Scholar] [CrossRef]
- Qin, A.; Shang, Z.; Tian, J.; Wang, Y.; Zhang, T.; Tang, Y. Spectral–spatial graph convolutional networks for semisupervised hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 16, 241–245. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multi-scale dynamic graph convolutional network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3162–3177. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Han, Z.; Wu, X. Deeper insights into graph convolutional networks for semisupervised learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.; Jegelka, S. Representation learning on graphs with jumping knowledge networks. arXiv 2018, arXiv:1806.03536. [Google Scholar]
- Drumetz, L.; Meyer, T.; Chanussot, J.; Bertozzi, A.; Jutten, C. Hyperspectral image unmixing with endmemb bundles and group sparsity inducing mixed norms. IEEE Trans. Image Process. 2019, 28, 3435–3450. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Wu, C.; Plaza, A. Regional clustering-based spatial preprocessing for hyperspectral unmixing. Remote Sens. Environ. 2018, 204, 333–346. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Li, S.; Plaza, A. Generalized morphological component analysis for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2817–2832. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.-Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the CVPR, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery. IEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef] [Green Version]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the 2016 NIPS, Barcelona, Spain, 5–10 December 2016; pp. 3844–3852. [Google Scholar]
- Micheli, A. Neural network for graphs: A contextual constructive approach. IEEE Trans. Neural Netw. 2009, 20, 498–511. [Google Scholar] [CrossRef]
- Shuman, D.; Narang, S.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Sandryhaila, A.; Moura, J. Discrete signal processing on graphs. IEEE Trans. Signal Process. 2013, 61, 1644–1656. [Google Scholar] [CrossRef] [Green Version]
- Shlens, J. A tutorial on principal component analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar]
- Li, S.; Hao, Q.; Kang, X.; Benediktsson, J. Gaussian pyramid based multiscale feature fusion for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 3312–3324. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).