MSAC-Net: 3D Multi-Scale Attention Convolutional Network for Multi-Spectral Imagery Pansharpening
Abstract
:1. Introduction
- Designs a 3D CNN to probe the spectral correlation of adjacent band images, thus reducing the spectral distortion in MS pansharpening;
- Uses a deep supervision mechanism that utilizes multi-scale spatial information to solve the spatial detail missing problem;
- Applies the AG mechanism instead of the skip connection in U-Net structure and presents experiments demonstrating its advantages in MS pansharpening.
2. Related Work
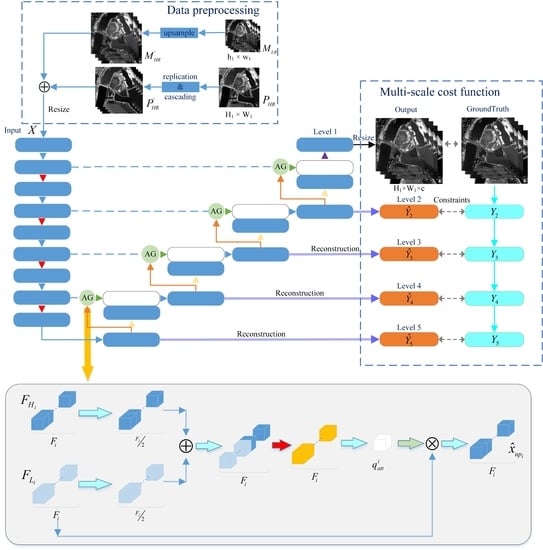
3. Method
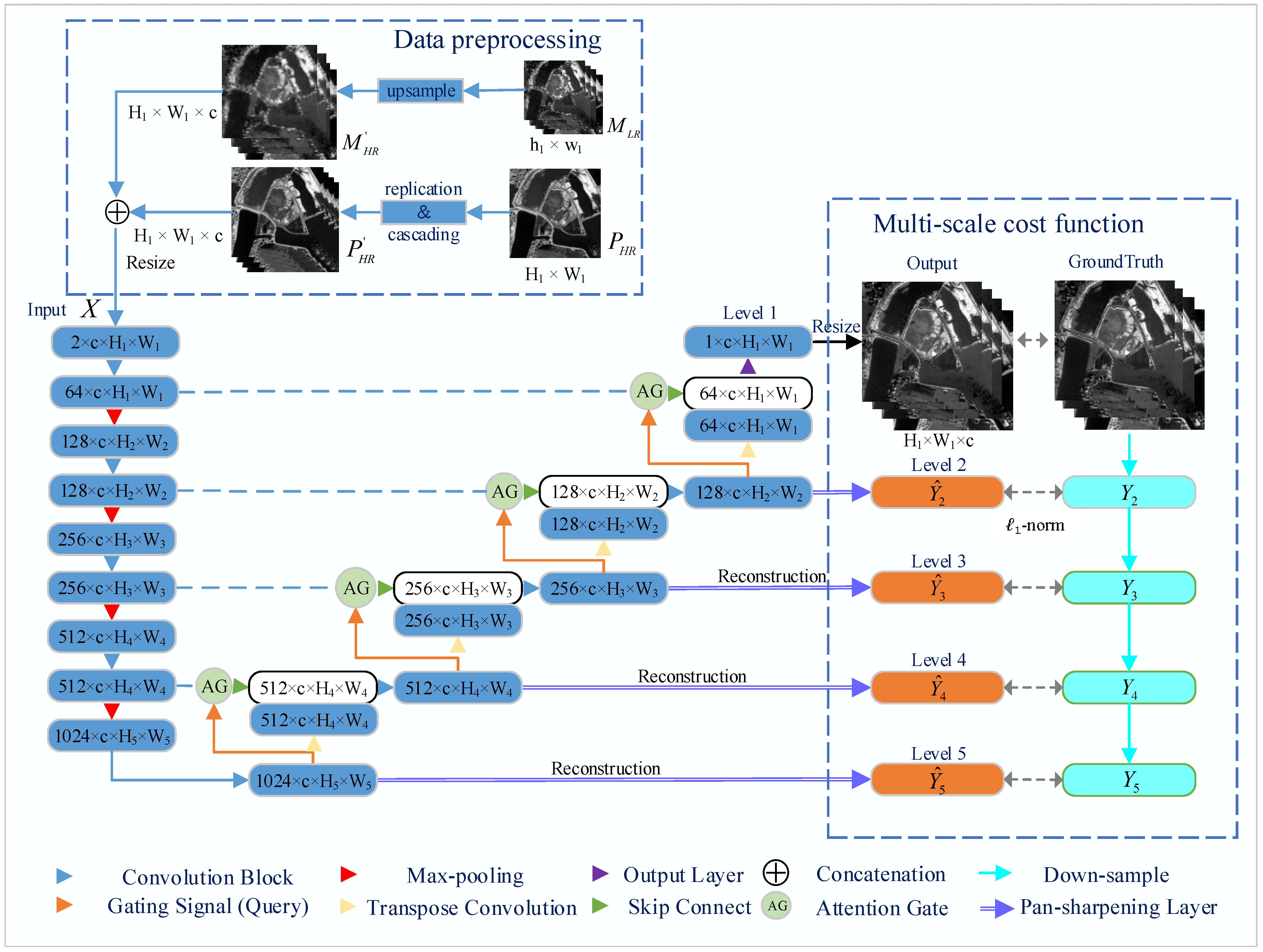
3.1. The MSAC-Net’s Structure
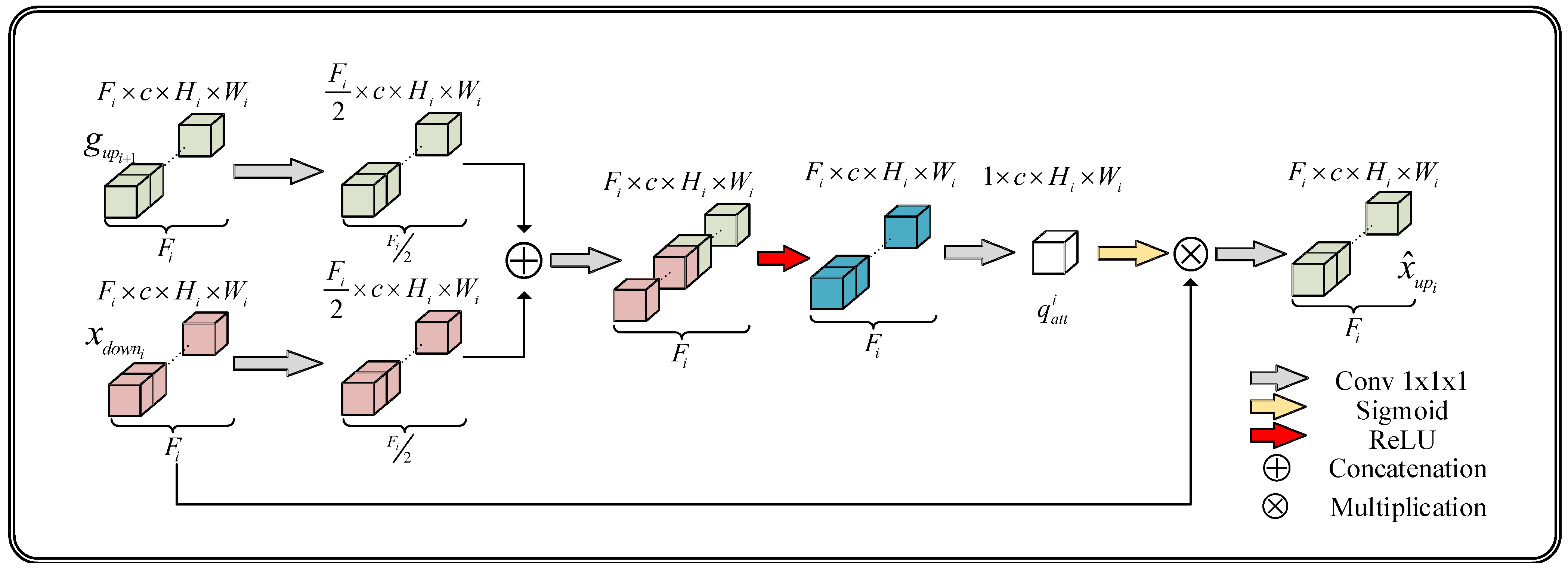
3.2. The Attention Gate (AG) Module
3.3. Pansharpening Layer and Multi-Scale Cost Function
4. Results
4.1. Experimental Setup
4.1.1. Datasets & Parameter Settings
- (1)
- The original HR-PAN and LR-MS images were down-sampled with a factor of 4;
- (2)
- The down-sampled HR-PAN was used as the input PAN, and the down-sampled LR-MS was used as the input LR-MS;
- (3)
- The original LR-MS was used as ground truth in the simulation experiment.
4.1.2. Compared Methods
4.1.3. Performance Metrics
- (1)
- The correlation coefficient (CC) [53]: CC reflects the similarity of spectral features between the fused image and the ground truth. CC, with 1 being the best attainable value. CC can be expressed as follows:
- (2)
- Peak signal-to-noise ratio (PSNR) [54]: PSNR is an objective measure of the information contained in an image. A larger value demonstrates that there is less distortion between the two images. PSNR can be expressed as follows:
- (3)
- Spectral angle mapper (SAM) [55]: SAM calculates the overall spectral distortion between the fused image and the ground truth. , with 0 being the best attainable value, is defined as follows:
- (4)
- Root mean square error (RMSE) [56]: RMSE measures the deviation between the fused image and the ground truth. , with 0 being the best attainable value, is defined as follows:
- (5)
- Erreur relative globale adimensionnelle de synthèse (ERGAS) [57]: ERGAS represents the difference between the fused image and the ground truth. , with 0 being the best attainable value, can be expressed as follows:
- (6)
- Structural similarity index measurement (SSIM) [54]: SSIM measures the similarity between the fusion image and the ground truth image. , with 1 being the best attainable value, is defined as follows:
- (7)
- Quality without reference (QNR) [58]: As a non-reference evaluation indicator, QNR compares the brightness, contrast and local correlation of the fused image with the original image. , with 1 being the best attainable value, is defined as follows:where usually and the spatial distortion index and the spectral distortion index are based on universal image quality index (Q) [59]. Furthermore, , with 0 being the best attainable value. Q is defined as:thus, and are defined as:
4.2. The Influences of Multi-Scale Fusion and Attention Gate Mechanism
4.2.1. The Influence of the Pansharpening Layer
4.2.2. The Influence of the AG Module
4.2.3. The Influence of Different Structures
4.3. Comparison of 2D and 3D Convolutional Networks
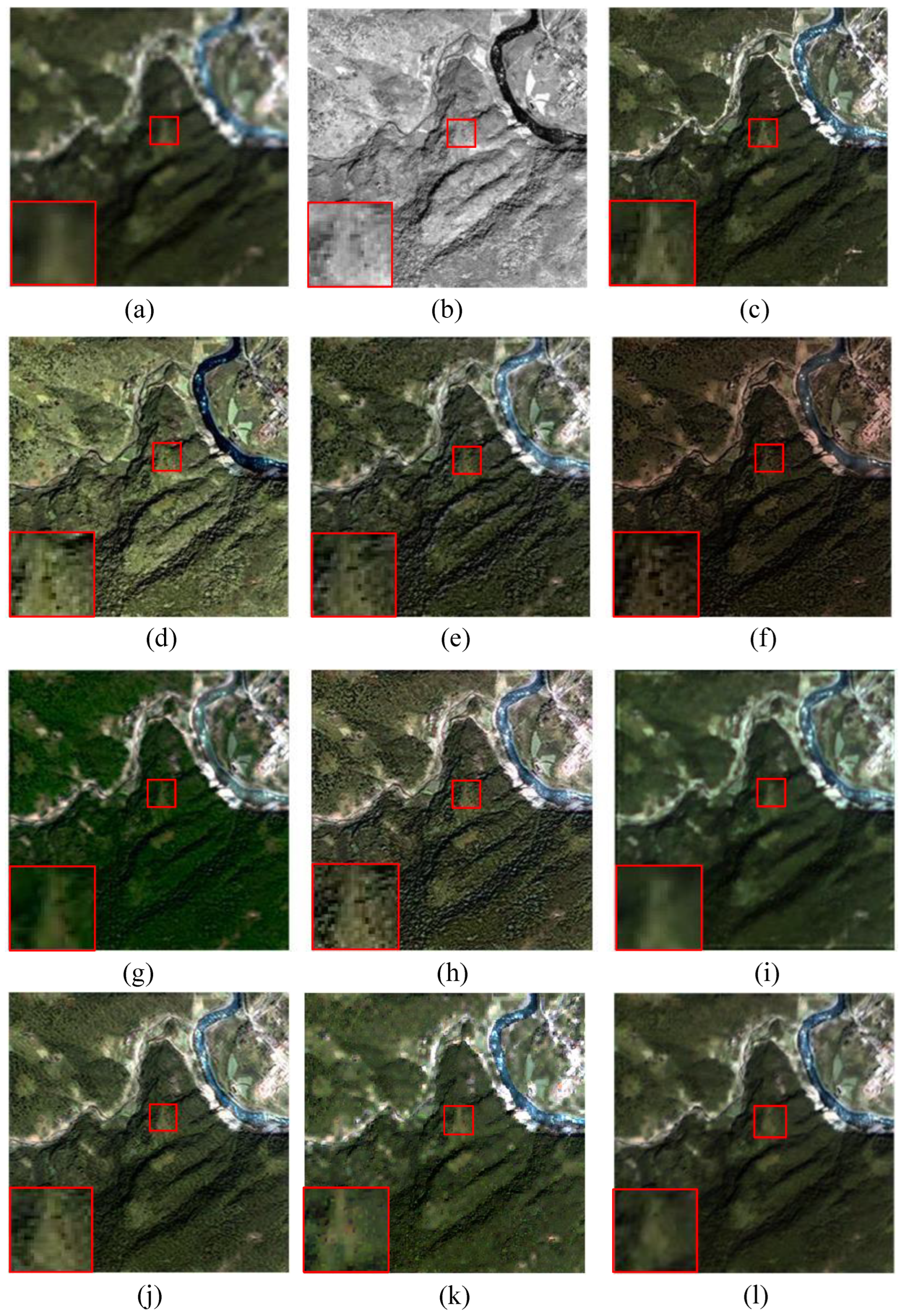
4.4. Comparison with the State-of-the-Art Methods
4.4.1. Experiments on the Simulated Dataset
4.4.2. Experiments on the Real Dataset
5. Discussion
5.1. The Effect of Convolution Times
5.2. The Effect of Multi-Scale Information Weight
5.3. The Effect of Network Depth
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MS | Multi-spectral |
| PAN | Panchromatic |
| HR | High resolution |
| LR | Low resolution |
| CNN | Convolutional neural network |
| PNN | Pansharpening neural network |
| MSDCNN | Multi-scale and multi-depth CNN |
| AG | Attention gate |
| GS | Gram–Schmidt |
| CC | Correlation coefficient |
| PSNR | Peak signal-to-noise ratio |
| SAM | Spectral angle mapper |
| RMSE | Root mean square error |
| ERGAS | Erreur relative globale adimensionnelle de synthèse |
| SSIM | Structural similarity index measurement |
| QNR | Quality without reference |
| Q | Image quality index |
References
- Liu, Y.; Li, Q.; Yuan, Y.; Du, Q.; Wang, Q. ABNet: Adaptive Balanced Network for Multi-scale Object Detection in Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5614914. [Google Scholar] [CrossRef]
- Zhang, W.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Jorgenson, M.T.; Kent, K. Transferability of the deep learning mask R-CNN model for automated mapping of ice-wedge polygons in high-resolution satellite and UAV images. Remote Sens. 2020, 12, 1085. [Google Scholar] [CrossRef] [Green Version]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Daanen, R.; Griffin, C.G.; Kent, K.; Jones, M.K.W. Understanding the synergies of deep learning and data fusion of multi-spectral and panchromatic high resolution commercial satellite imagery for automated ice-wedge polygon detection. ISPRS J. Photogramm. Remote Sens. 2020, 170, 174–191. [Google Scholar] [CrossRef]
- Tan, K.; Ma, W.; Chen, L.; Wang, H.; Du, Q.; Du, P.; Yan, B.; Liu, R.; Li, H. Estimating the distribution trend of soil heavy metals in mining area from HyMap airborne hyperspectral imagery based on ensemble learning. J. Hazard. Mater. 2021, 401, 123288. [Google Scholar] [CrossRef]
- Tan, K.; Jin, X.; Plaza, A.; Wang, X.; Xiao, L.; Du, P. Automatic change detection in high-resolution remote sensing images by using a multiple classifier system and spectral–spatial features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3439–3451. [Google Scholar] [CrossRef]
- Tan, K.; Zhang, Y.; Du, Q.; Du, P.; Jin, X.; Li, J. Change Detection based on Stacked Generalization System with Segmentation Constraint. Photogramm. Eng. Remote Sens. 2018, 84, 733–741. [Google Scholar] [CrossRef]
- Lei, J.; Gu, Y.; Xie, W.; Li, Y.; Du, Q. Boundary Extraction Constrained Siamese Network for Remote Sensing Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5621613. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2007, 46, 228–236. [Google Scholar] [CrossRef]
- Khan, M.M.; Chanussot, J.; Condat, L.; Montanvert, A. Indusion: Fusion of multispectral and panchromatic images using the induction scaling technique. IEEE Geosci. Remote Sens. Lett. 2008, 5, 98–102. [Google Scholar] [CrossRef] [Green Version]
- Ranchin, T.; Aiazzi, B.; Alparone, L.; Baronti, S.; Wald, L. Image fusion—The ARSIS concept and some successful implementation schemes. ISPRS J. Photogramm. Remote Sens. 2003, 58, 4–18. [Google Scholar] [CrossRef] [Green Version]
- Palsson, F.; Ulfarsson, M.O.; Sveinsson, J.R. Model-based reduced-rank pansharpening. IEEE Geosci. Remote Sens. Lett. 2019, 17, 656–660. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Ai, N.; Peng, J.; Li, X. Pansharpening based on details injection model and online sparse dictionary learning. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 1939–1944. [Google Scholar]
- Peng, J.; Liu, L.; Wang, J.; Zhang, E.; Zhu, X.; Zhang, Y.; Feng, J.; Jiao, L. PSMD-Net: A Novel Pan-Sharpening Method Based on a Multiscale Dense Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4957–4971. [Google Scholar] [CrossRef]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. In Fundamental Papers in Wavelet Theory; Princeton University Press: Princeton, NJ, USA, 2009; pp. 494–513. [Google Scholar]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A multiscale and multidepth convolutional neural network for remote sensing imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Wang, J.; Zhang, E.; Li, B.; Zhu, X.; Zhang, Y.; Peng, J. Shallow–deep convolutional network and spectral-discrimination-based detail injection for multispectral imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1772–1783. [Google Scholar] [CrossRef]
- Jiang, H.; Peng, M.; Zhong, Y.; Xie, H.; Hao, Z.; Lin, J.; Ma, X.; Hu, X. A Survey on Deep Learning-Based Change Detection from High-Resolution Remote Sensing Images. Remote Sens. 2022, 14, 1552. [Google Scholar] [CrossRef]
- Jin, Z.R.; Zhuo, Y.W.; Zhang, T.J.; Jin, X.X.; Jing, S.; Deng, L.J. Remote Sensing Pansharpening by Full-Depth Feature Fusion. Remote Sens. 2022, 14, 466. [Google Scholar] [CrossRef]
- Zhou, M.; Fu, X.; Huang, J.; Zhao, F.; Liu, A.; Wang, R. Effective Pan-Sharpening with Transformer and Invertible Neural Network. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5406815. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, J. GTP-PNet: A residual learning network based on gradient transformation prior for pansharpening. ISPRS J. Photogramm. Remote Sens. 2021, 172, 223–239. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Mei, S.; Ji, J.; Geng, Y.; Zhang, Z.; Li, X.; Du, Q. Unsupervised spatial–spectral feature learning by 3D convolutional autoencoder for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6808–6820. [Google Scholar] [CrossRef]
- Wang, L.; Bi, T.; Shi, Y. A Frequency-Separated 3D-CNN for Hyperspectral Image Super-Resolution. IEEE Access 2020, 8, 86367–86379. [Google Scholar] [CrossRef]
- Shi, C.; Liao, D.; Zhang, T.; Wang, L. Hyperspectral Image Classification Based on 3D Coordination Attention Mechanism Network. Remote Sens. 2022, 14, 608. [Google Scholar] [CrossRef]
- Mei, S.; Yuan, X.; Ji, J.; Zhang, Y.; Wan, S.; Du, Q. Hyperspectral image spatial super-resolution via 3D full convolutional neural network. Remote Sens. 2017, 9, 1139. [Google Scholar] [CrossRef] [Green Version]
- Mnih, V.; Heess, N.; Graves, A.; Kavukcuoglu, K. Recurrent models of visual attention. arXiv 2014, arXiv:1406.6247. [Google Scholar]
- Mei, X.; Pan, E.; Ma, Y.; Dai, X.; Huang, J.; Fan, F.; Du, Q.; Zheng, H.; Ma, J. Spectral-spatial attention networks for hyperspectral image classification. Remote Sens. 2019, 11, 963. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Zheng, H.; Mei, T. Look closer to see better: Recurrent attention convolutional neural network for fine-grained image recognition. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4438–4446. [Google Scholar]
- Wang, F.; Jiang, M.; Qian, C.; Yang, S.; Li, C.; Zhang, H.; Wang, X.; Tang, X. Residual attention network for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3156–3164. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin, Germany, 2015; pp. 234–241. [Google Scholar]
- Guo, Y.; Chen, J.; Wang, J.; Chen, Q.; Cao, J.; Deng, Z.; Xu, Y.; Tan, M. Closed-loop matters: Dual regression networks for single image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5407–5416. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention u-net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Wang, Y.; Peng, Y.; Liu, X.; Li, W.; Alexandropoulos, G.C.; Yu, J.; Ge, D.; Xiang, W. DDU-Net: Dual-Decoder-U-Net for Road Extraction Using High-Resolution Remote Sensing Images. arXiv 2022, arXiv:2201.06750. [Google Scholar]
- Banerjee, S.; Lyu, J.; Huang, Z.; Leung, F.H.; Lee, T.; Yang, D.; Su, S.; Zheng, Y.; Ling, S.H. Ultrasound spine image segmentation using multi-scale feature fusion skip-inception U-Net (SIU-Net). Biocybern. Biomed. Eng. 2022, 42, 341–361. [Google Scholar] [CrossRef]
- Khalel, A.; Tasar, O.; Charpiat, G.; Tarabalka, Y. Multi-task deep learning for satellite image pansharpening and segmentation. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 4869–4872. [Google Scholar]
- Ni, Y.; Xie, Z.; Zheng, D.; Yang, Y.; Wang, W. Two-stage multitask U-Net construction for pulmonary nodule segmentation and malignancy risk prediction. Quant. Imaging Med. Surg. 2022, 12, 292. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Berlin, Germany, 2018; pp. 3–11. [Google Scholar]
- Rundo, L.; Han, C.; Nagano, Y.; Zhang, J.; Hataya, R.; Militello, C.; Tangherloni, A.; Nobile, M.S.; Ferretti, C.; Besozzi, D.; et al. USE-Net: Incorporating Squeeze-and-Excitation blocks into U-Net for prostate zonal segmentation of multi-institutional MRI datasets. Neurocomputing 2019, 365, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Y.; Kong, J.; Zhang, H. U-Net: A Smart Application with Multidimensional Attention Network for Remote Sensing Images. Sci. Program. 2022, 2022, 1603273. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, Y.; Wu, Z.; Wei, Z. Hyperspectral and multispectral image fusion based on deep attention network. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar]
- Wei zhou, W.; Guo wu, Y.; Hao, W. A multi-focus image fusion method based on nested U-Net. In Proceedings of the 2021 the 5th International Conference on Video and Image Processing, Hayward, CA, USA, 22–25 December 2021; pp. 69–75. [Google Scholar]
- Xiao, J.; Li, J.; Yuan, Q.; Zhang, L. A Dual-UNet with Multistage Details Injection for Hyperspectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5515313. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the Summaries 3rd Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; Volume 1, pp. 147–149. [Google Scholar]
- Yang, Y.; Wan, W.; Huang, S.; Lin, P.; Que, Y. A novel pan-sharpening framework based on matting model and multiscale transform. Remote Sens. 2017, 9, 391. [Google Scholar] [CrossRef] [Green Version]
- Wald, L. Data Fusion: Definitions and Architectures: Fusion of Images of Different Spatial Resolutions; Presses des MINES: Paris, France, 2002. [Google Scholar]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Sun, W.; Ren, K.; Meng, X.; Yang, G.; Xiao, C.; Peng, J.; Huang, J. MLR-DBPFN: A Multi-scale Low Rank Deep Back Projection Fusion Network for Anti-noise Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522914. [Google Scholar] [CrossRef]










| Module | Input Size | Layer (Filter Size) or Method | Filters | Output Size |
|---|---|---|---|---|
| Down | 64 | |||
| − | ||||
| Down | 128 | |||
| − | ||||
| Down | 256 | |||
| − | ||||
| Down | 512 | |||
| − | ||||
| Down | 1024 | |||
| 512 | ||||
| Up | 512 | |||
| 256 | ||||
| Up | 256 | |||
| 128 | ||||
| Up | 128 | |||
| 64 | ||||
| Up | 64 | |||
| Output | 1 | |||
| Reconstruction | 1 | |||
| AG | ||||
| − | ||||
| 1 | ||||
| ⊗ | − | |||
| Satellite | Pan | Blue | Green | Red | NIR | Resolution (PAN/MS) |
|---|---|---|---|---|---|---|
| IKONOS | 450–900 | 450–530 | 520–610 | 640–720 | 760–860 | 1 m/4 m |
| QuickBird | 450–900 | 450–520 | 520–600 | 630–690 | 760–900 | 0.7 m/2.8 m |
| Learning Rate | Weight Decay | Momentum | Batch Size | Iteration |
|---|---|---|---|---|
| 0.01 | 10 | 0.9 | 16 |
| Symbol | Means | Symbol | Means |
|---|---|---|---|
| Input image | X | Ground Truth | |
| Sample means of | Sample means of X | ||
| A pixel in | x | A pixel in X | |
| N | Number of pixels | M | Number of band |
| Mean square error | L | Gray level | |
| Brightness parameter | Contrast parameter | ||
| Structural parameter | Infinitely small constant | ||
| Variances of | Variances of X | ||
| Covariance of and X | Positive integer | ||
| d | PAN image spatial resolution/MS image spatial resolution | ||
| Structures | CC | PSNR | SAM | ERGAS | RMSE | SSIM |
|---|---|---|---|---|---|---|
| U-Net | 0.8959 | 21.5200 | 5.1670 | 7.8263 | 0.0839 | 0.6525 |
| U-Net + AG | 0.8949 | 21.5247 | 5.2721 | 7.8407 | 0.0839 | 0.6543 |
| U-Net + scale | 0.8955 | 21.5754 | 4.8187 | 7.6403 | 0.0837 | 0.6624 |
| Our | 0.8968 | 21.6184 | 4.4281 | 7.4303 | 0.0830 | 0.6755 |
| Kernel | CC | PSNR | SAM | ERGAS | RMSE | SSIM |
|---|---|---|---|---|---|---|
| 2D | 0.8660 | 19.5025 | 5.4445 | 6.1638 | 0.1059 | 0.6628 |
| 3D | 0.8870 | 20.2168 | 5.1269 | 5.7446 | 0.0975 | 0.7107 |
| Methods | CC | PSNR | SAM | ERGAS | RMSE | SSIM |
|---|---|---|---|---|---|---|
| GS | 0.5320 | 14.3940 | 5.7520 | 20.5527 | 0.1948 | 0.2964 |
| Indusion | 0.8330 | 19.9235 | 6.2750 | 11.3609 | 0.1004 | 0.4136 |
| SR | 0.8206 | 18.8363 | 12.2147 | 15.6579 | 0.1398 | 0.4513 |
| PNN | 0.8952 | 17.7485 | 24.1477 | 12.2516 | 0.0965 | 0.5553 |
| PanNet | 0.8514 | 18.7474 | 6.8293 | 12.6693 | 0.1128 | 0.3931 |
| MSDCNN | 0.9063 | 21.0595 | 5.6025 | 9.8053 | 0.0758 | 0.5728 |
| MIPSM | 0.9070 | 21.0746 | 4.4221 | 9.7840 | 0.0896 | 0.5855 |
| GTP-PNet | 0.9096 | 23.4467 | 6.0760 | 8.1888 | 0.0763 | 0.6020 |
| MSAC-Net | 0.8968 | 21.6184 | 4.4281 | 7.4303 | 0.0830 | 0.6755 |
| Motheds | CC | PSNR | SAM | ERGAS | RMSE | SSIM |
|---|---|---|---|---|---|---|
| GS | 0.8866 | 19.6392 | 2.9178 | 9.5928 | 0.1031 | 0.6973 |
| Indusion | 0.9178 | 21.6106 | 2.6969 | 7.5648 | 0.0822 | 0.7116 |
| SR | 0.9115 | 18.3991 | 3.5598 | 10.7052 | 0.1179 | 0.5897 |
| PNN | 0.9297 | 21.5744 | 5.7713 | 7.2483 | 0.0778 | 0.7398 |
| PanNet | 0.9141 | 21.0793 | 3.8142 | 8.0859 | 0.0883 | 0.7010 |
| MSDCNN | 0.9269 | 21.9366 | 3.8053 | 7.2514 | 0.0794 | 0.7330 |
| MIPSM | 0.9403 | 22.7724 | 4.3359 | 6.6432 | 0.0724 | 0.7300 |
| GTP-PNet | 0.9311 | 21.9180 | 7.9021 | 7.8661 | 0.0962 | 0.7109 |
| MSAC-Net | 0.9515 | 23.0800 | 5.3120 | 6.2297 | 0.0701 | 0.7966 |
| Methods | QNR | ||
|---|---|---|---|
| GS | 0.2479 | 0.7366 | 0.0588 |
| Indusion | 0.6785 | 0.3150 | 0.0096 |
| SR | 0.5923 | 0.3934 | 0.0236 |
| PNN | 0.7443 | 0.1579 | 0.1162 |
| PanNet | 0.9251 | 0.0679 | 0.0075 |
| MSDCNN | 0.8016 | 0.1493 | 0.0577 |
| MIPSM | 0.9502 | 0.0267 | 0.0237 |
| GTP-PNet | 0.9494 | 0.0203 | 0.0309 |
| MSAC-Net | 0.9529 | 0.0194 | 0.0282 |
| Methods | QNR | ||
|---|---|---|---|
| GS | 0.3689 | 0.4446 | 0.3358 |
| Indusion | 0.6622 | 0.1870 | 0.1854 |
| SR | 0.7468 | 0.2250 | 0.0364 |
| PNN | 0.7139 | 0.1329 | 0.1767 |
| PanNet | 0.7925 | 0.0469 | 0.1685 |
| MSDCNN | 0.7184 | 0.2098 | 0.0908 |
| MIPSM | 0.8816 | 0.0420 | 0.0797 |
| GTP-PNet | 0.8065 | 0.0141 | 0.1820 |
| MSAC-Net | 0.9546 | 0.0267 | 0.0192 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Fu, Y.; Wang, J.; Liu, L.; Yu, K.; Peng, J. MSAC-Net: 3D Multi-Scale Attention Convolutional Network for Multi-Spectral Imagery Pansharpening. Remote Sens. 2022, 14, 2761. https://doi.org/10.3390/rs14122761
Zhang E, Fu Y, Wang J, Liu L, Yu K, Peng J. MSAC-Net: 3D Multi-Scale Attention Convolutional Network for Multi-Spectral Imagery Pansharpening. Remote Sensing. 2022; 14(12):2761. https://doi.org/10.3390/rs14122761
Chicago/Turabian StyleZhang, Erlei, Yihao Fu, Jun Wang, Lu Liu, Kai Yu, and Jinye Peng. 2022. "MSAC-Net: 3D Multi-Scale Attention Convolutional Network for Multi-Spectral Imagery Pansharpening" Remote Sensing 14, no. 12: 2761. https://doi.org/10.3390/rs14122761
APA StyleZhang, E., Fu, Y., Wang, J., Liu, L., Yu, K., & Peng, J. (2022). MSAC-Net: 3D Multi-Scale Attention Convolutional Network for Multi-Spectral Imagery Pansharpening. Remote Sensing, 14(12), 2761. https://doi.org/10.3390/rs14122761