Shipborne GNSS-Determined Sea Surface Heights Using Geoid Model and Realistic Dynamic Topography
Abstract
1. Introduction
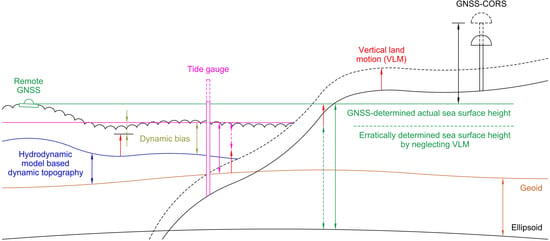
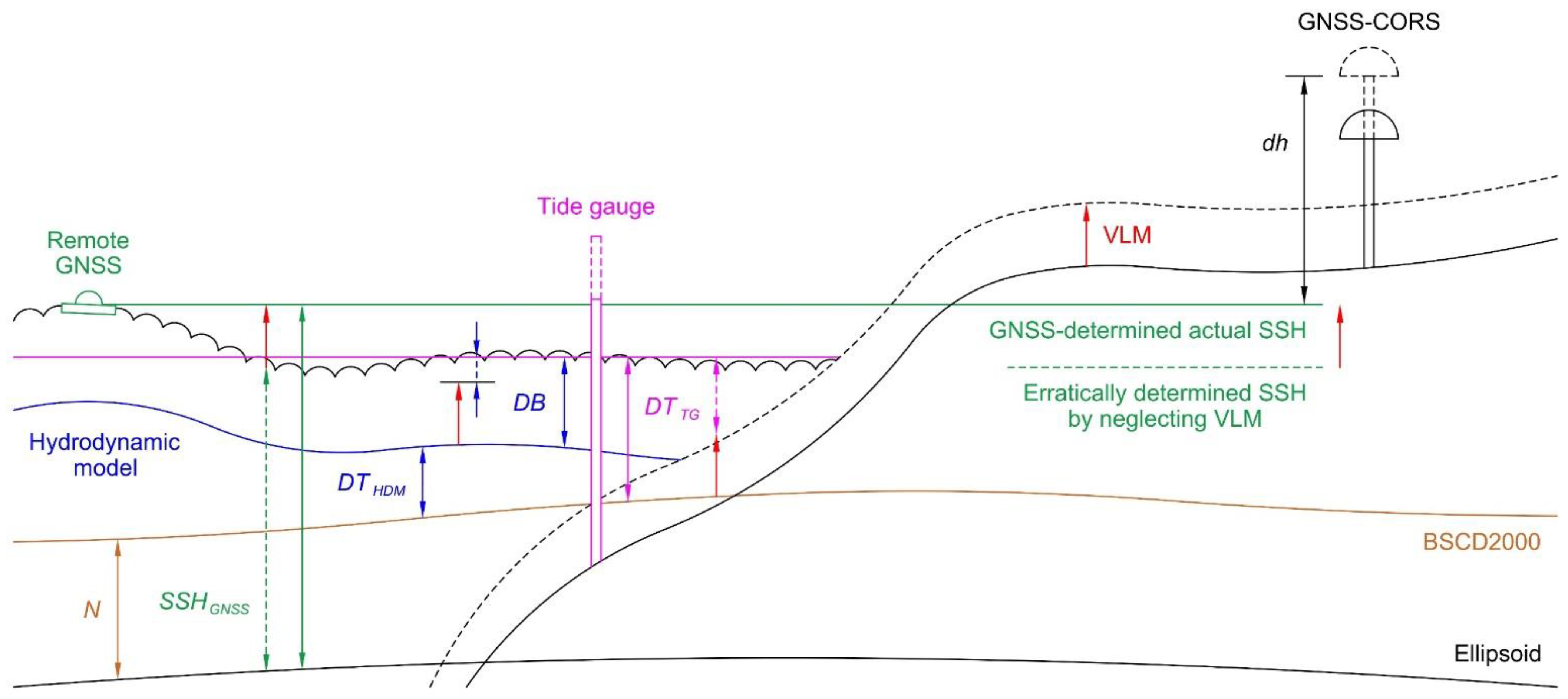
2. Theoretical Principles
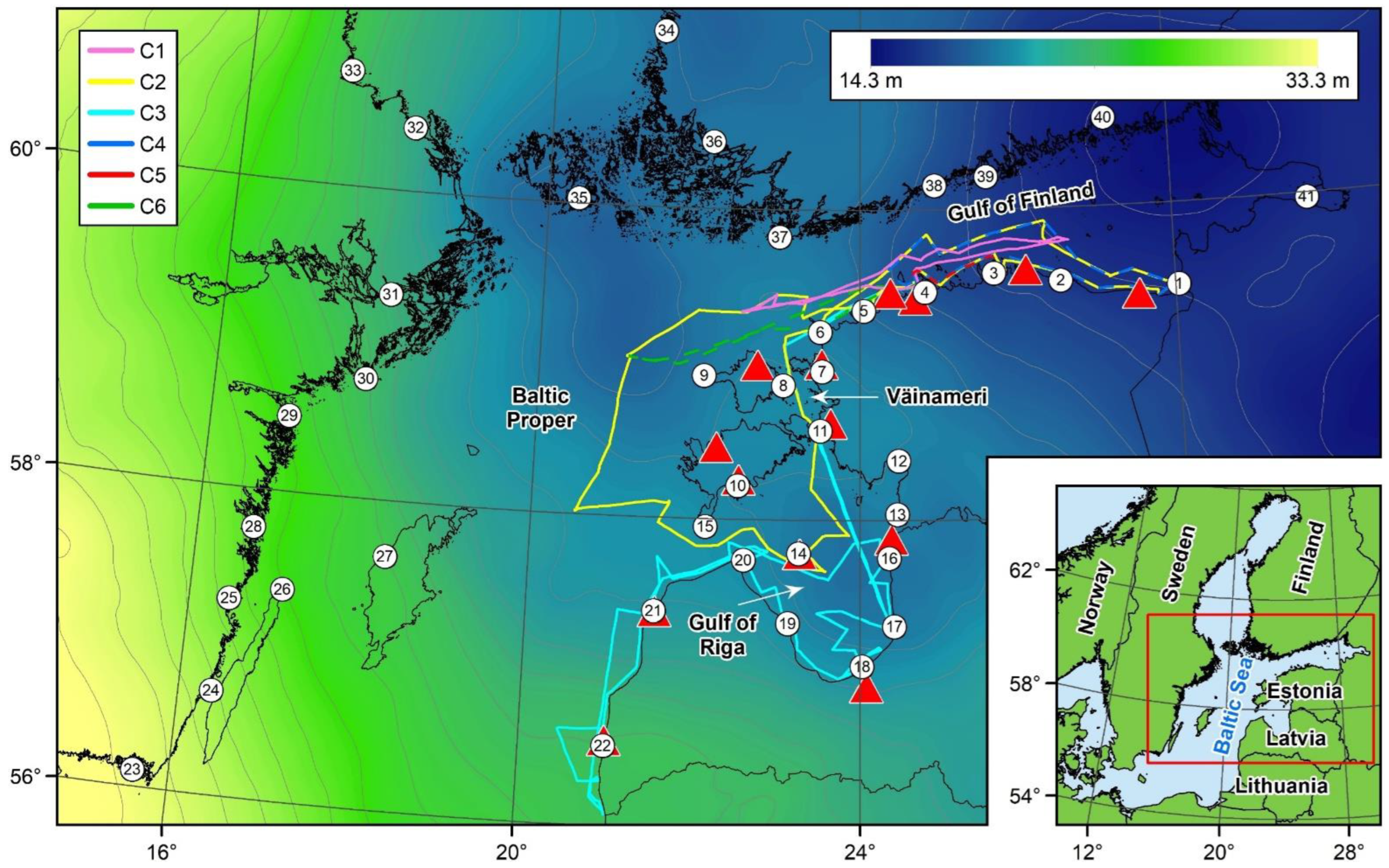
3. Shipborne GNSS Surveys, Data, and Other Used Information
Hydrodynamic Model and Tide Gauge Data
4. Derivation of Offshore Dynamic Topography
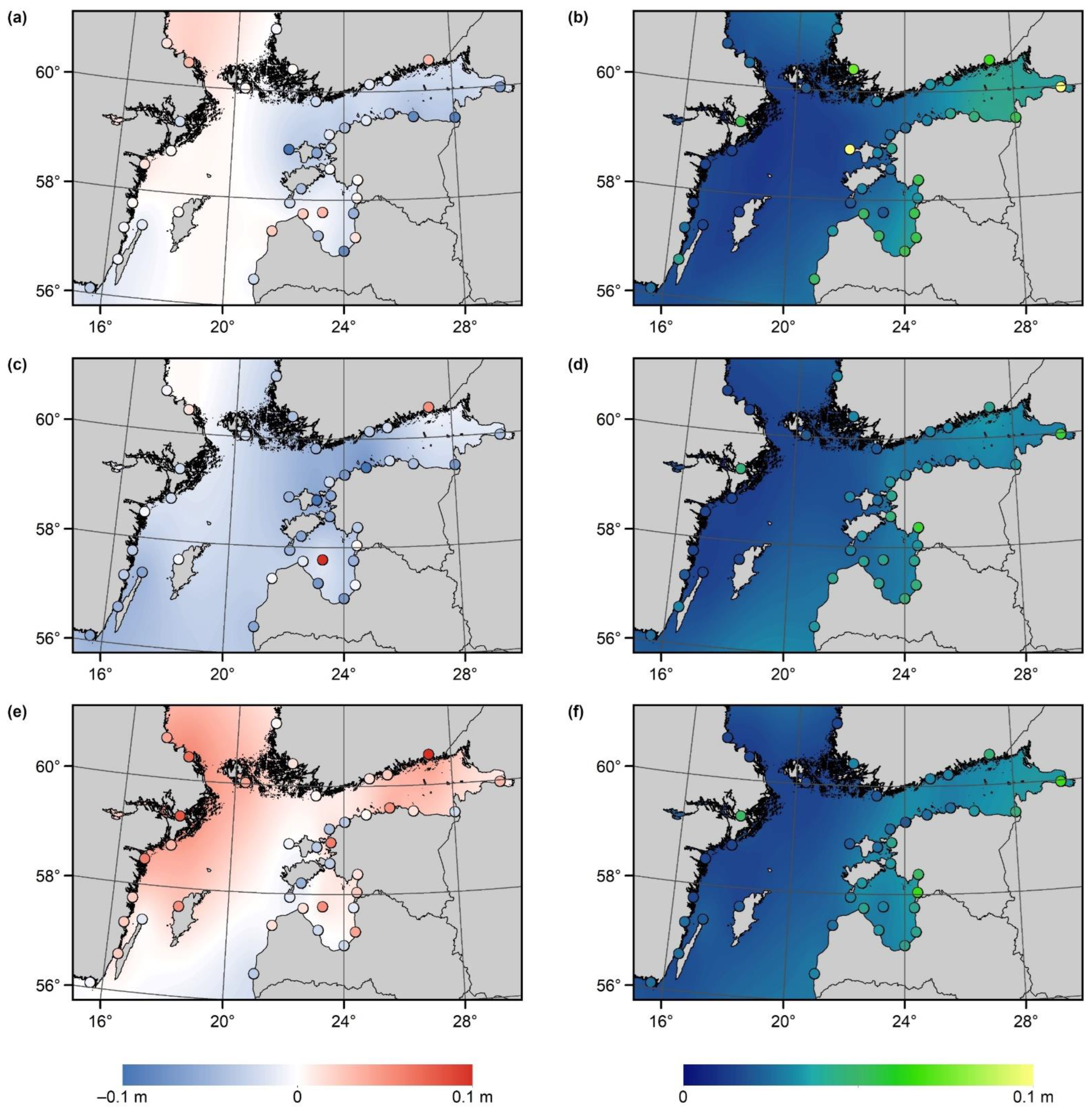
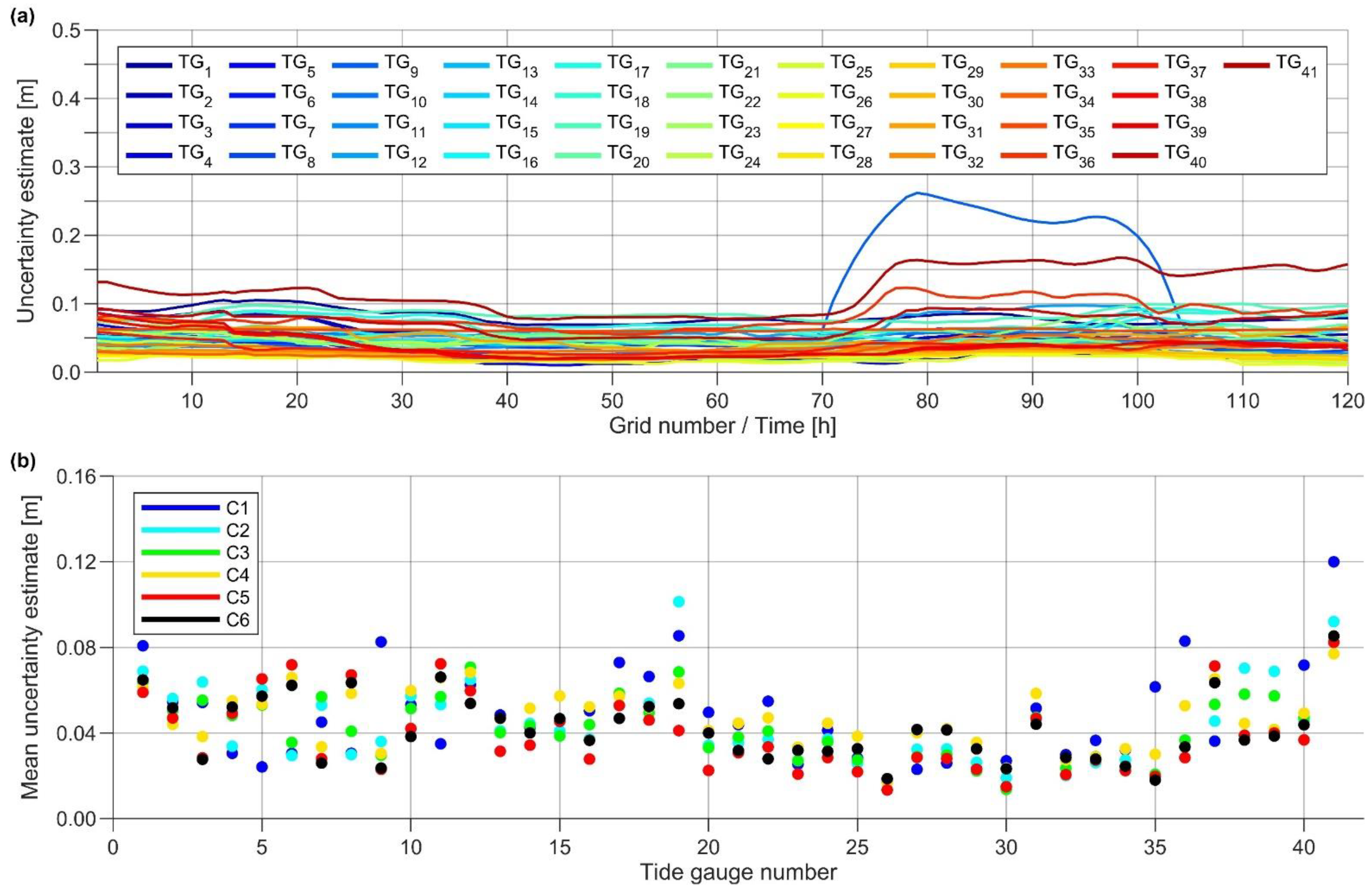
4.1. Estimation of Dynamic Bias Uncertainties at the Tide Gauge Locations
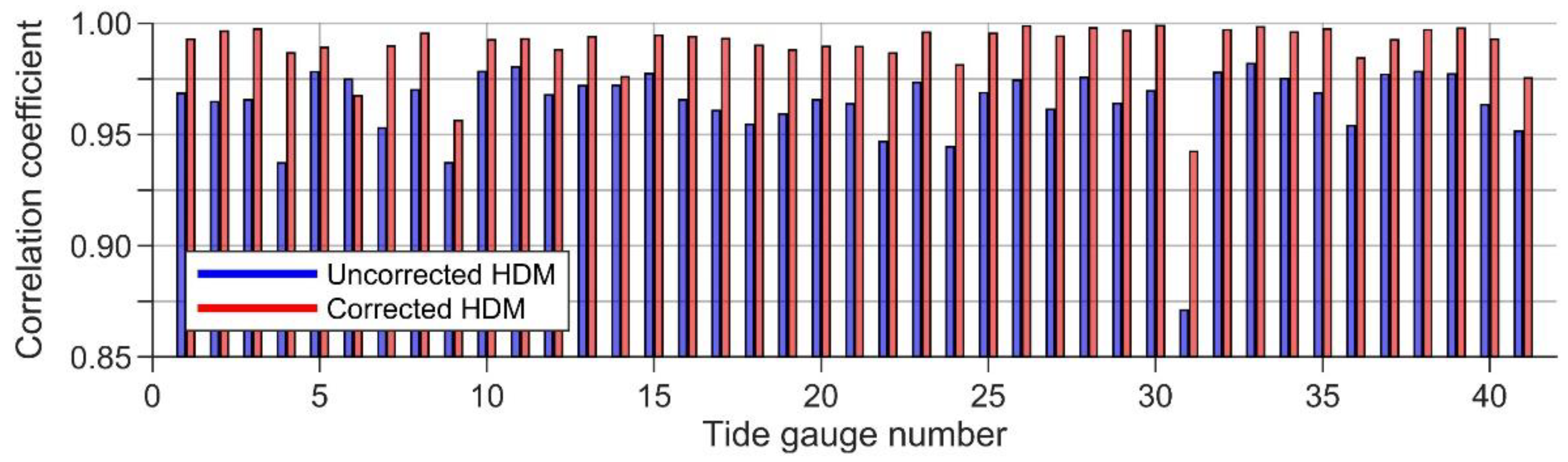
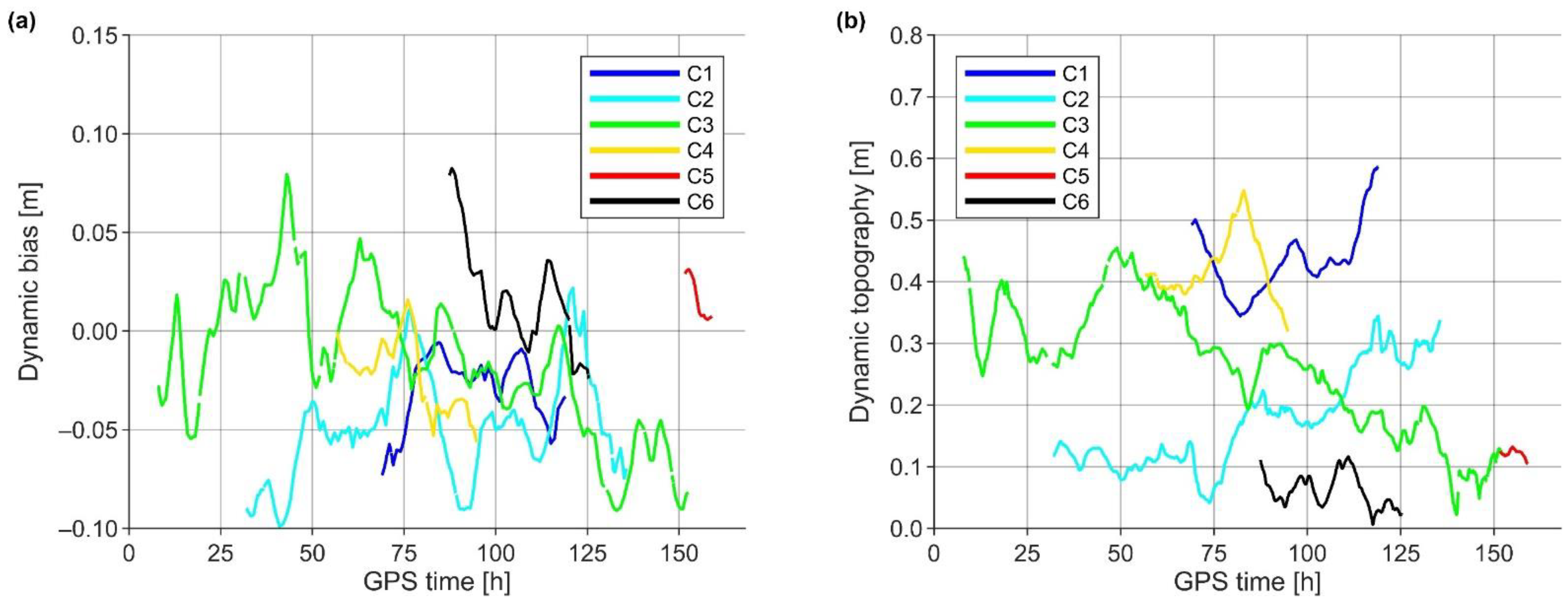
4.2. Correction of Hydrodynamic Model Based Dynamic Topography
5. Derivation and Validation of Shipborne GNSS-Based Sea Surface Heights
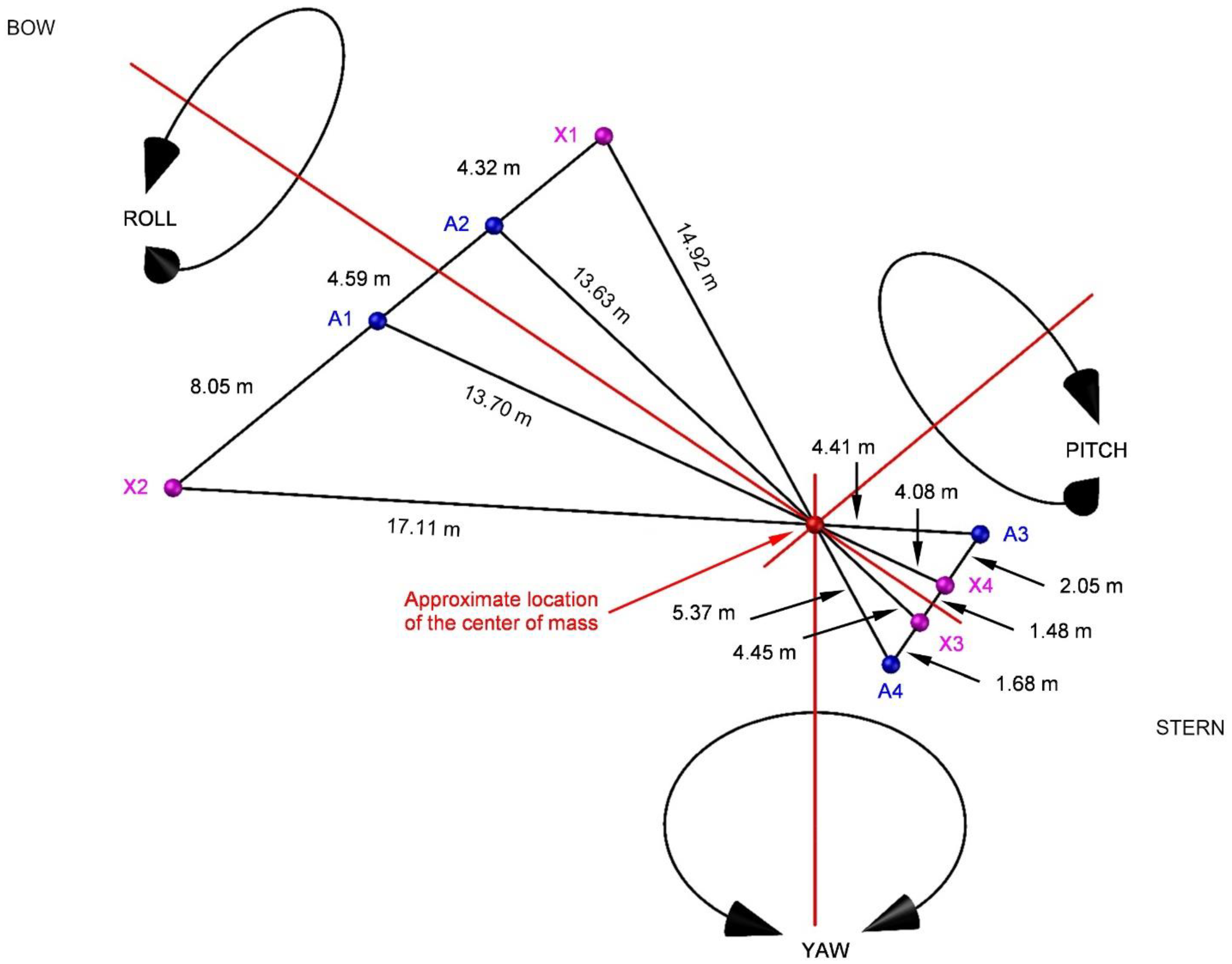
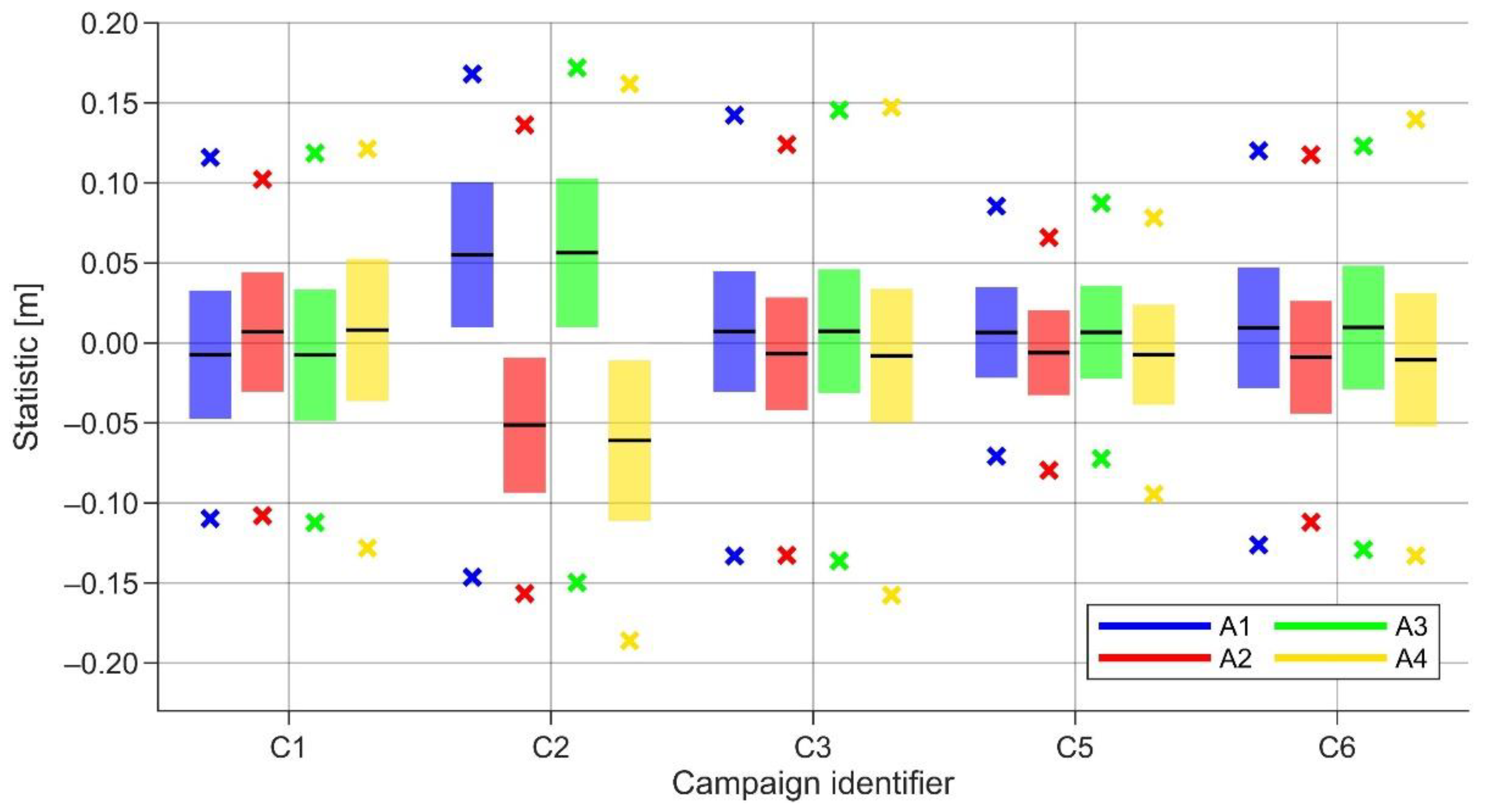
5.1. Reducing the Effects of Vessel’s High-Frequency Attitude Changes
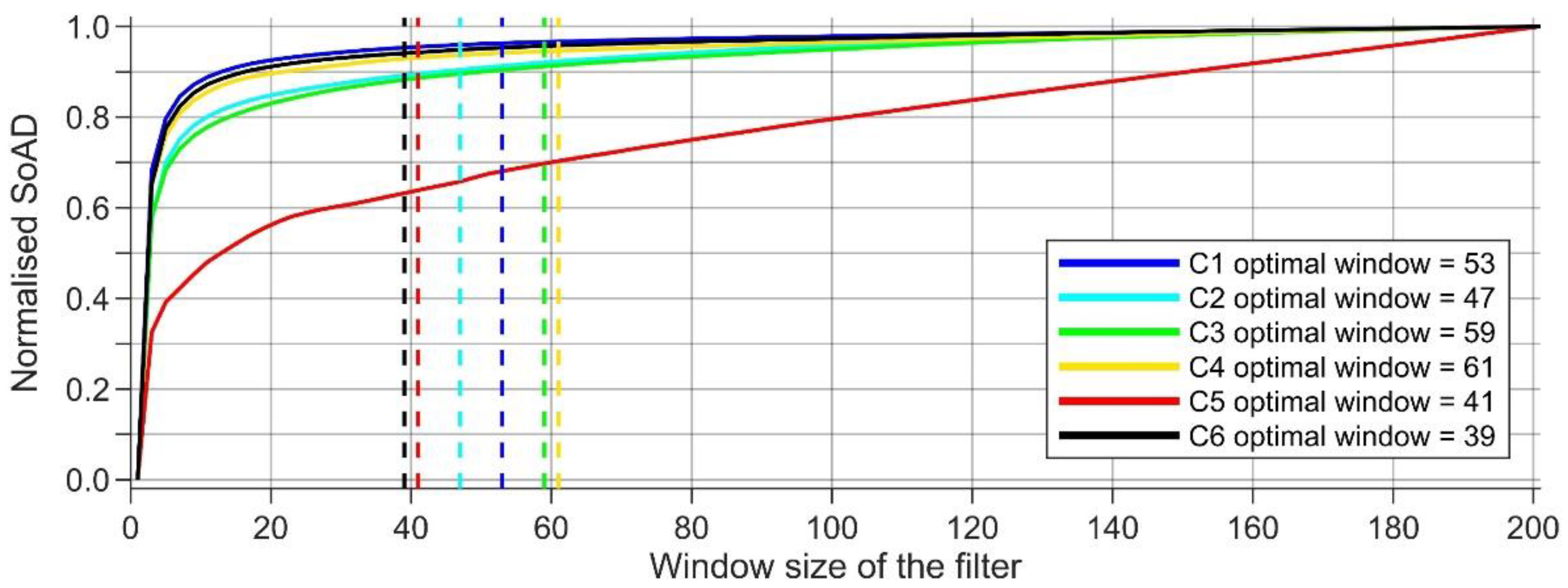
5.2. Reducing the Effects of Sea State Conditions
Low-Pass Filtering Results
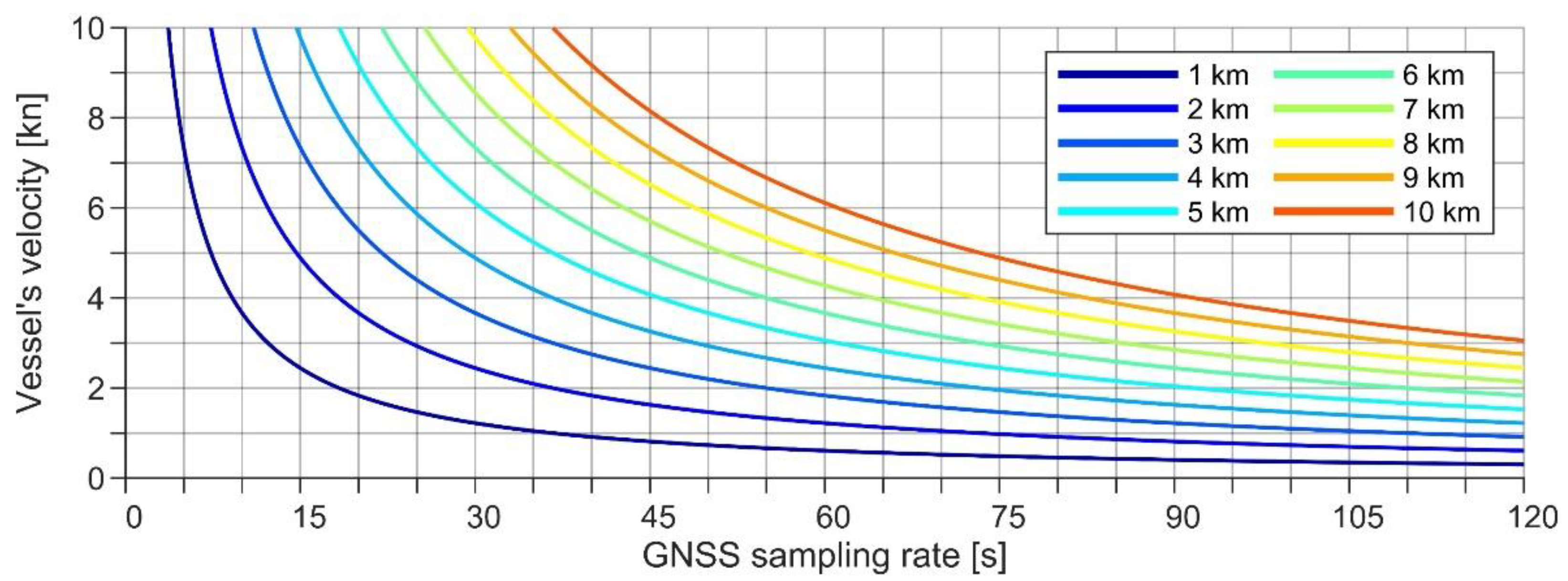
5.3. Vessel Sailing-Related Corrections
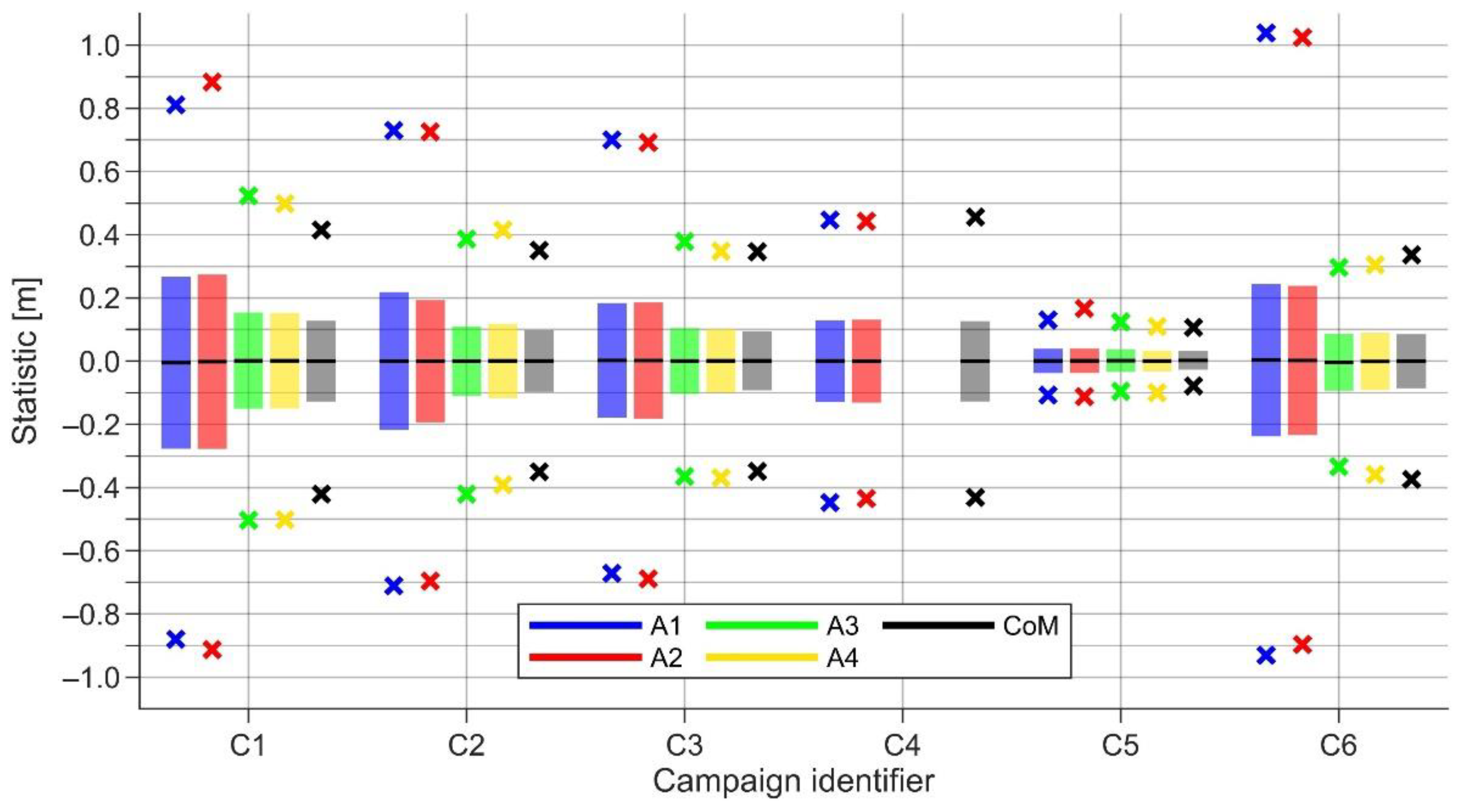
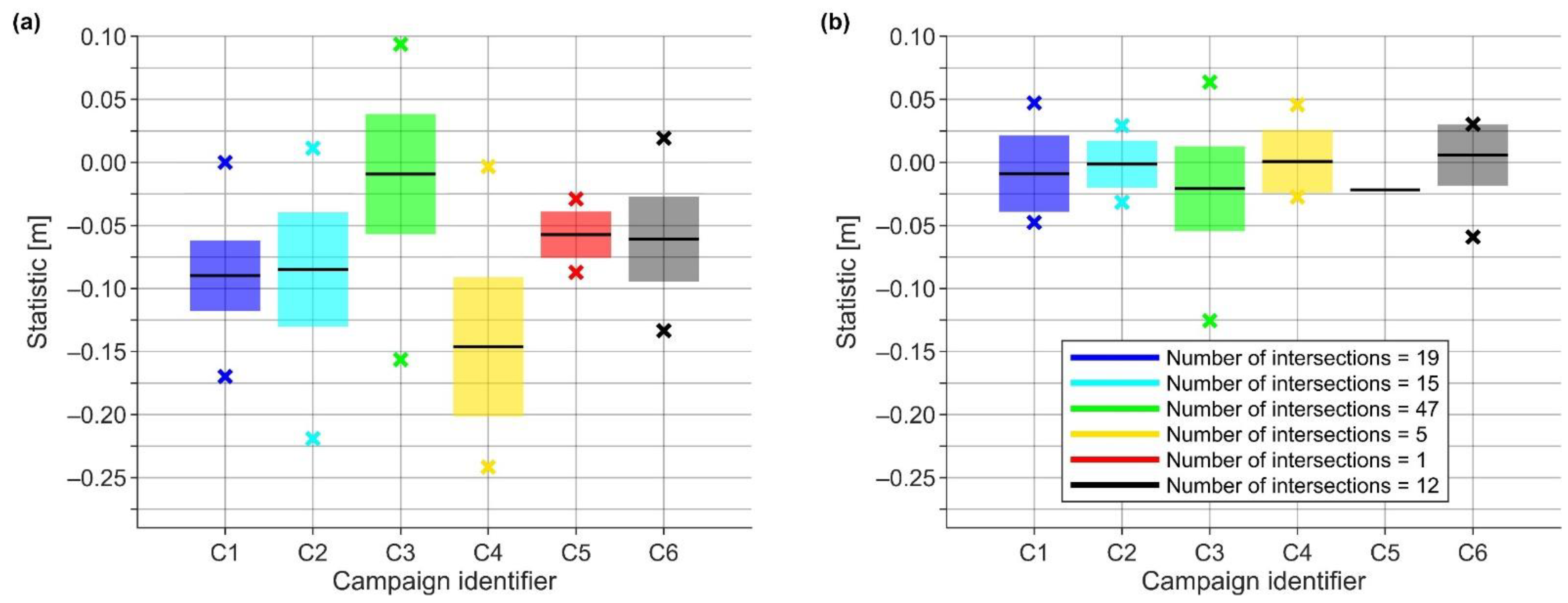
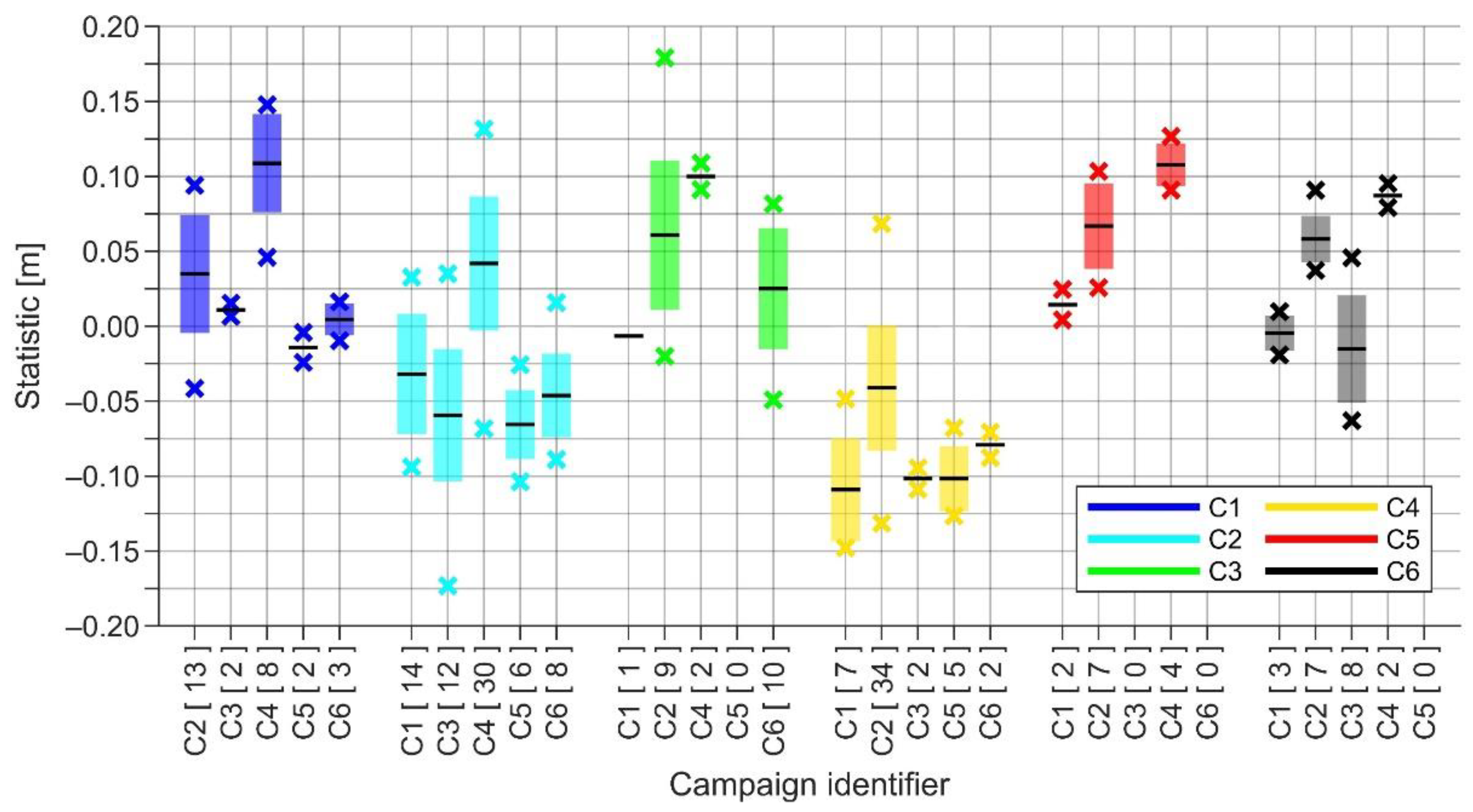
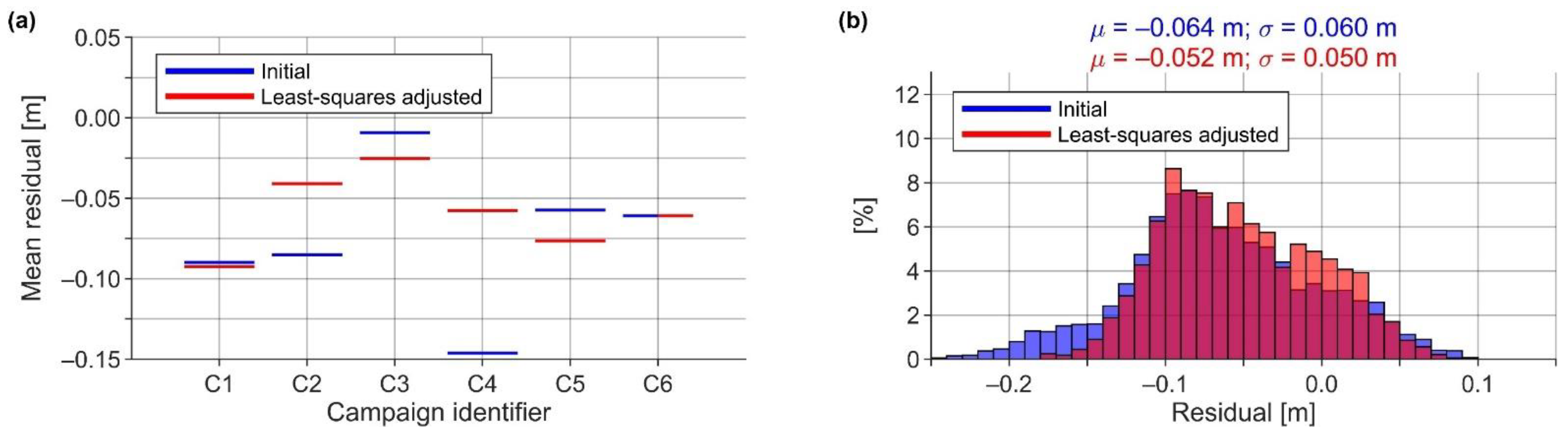
5.4. Validation and Least-Squares Adjustment of the Results
5.4.1. The Final Data Processing Results
6. Discussion
6.1. Dynamic Bias Prediction Method
6.2. Data Filtering Approach
6.3. Choice of a Geoid Model
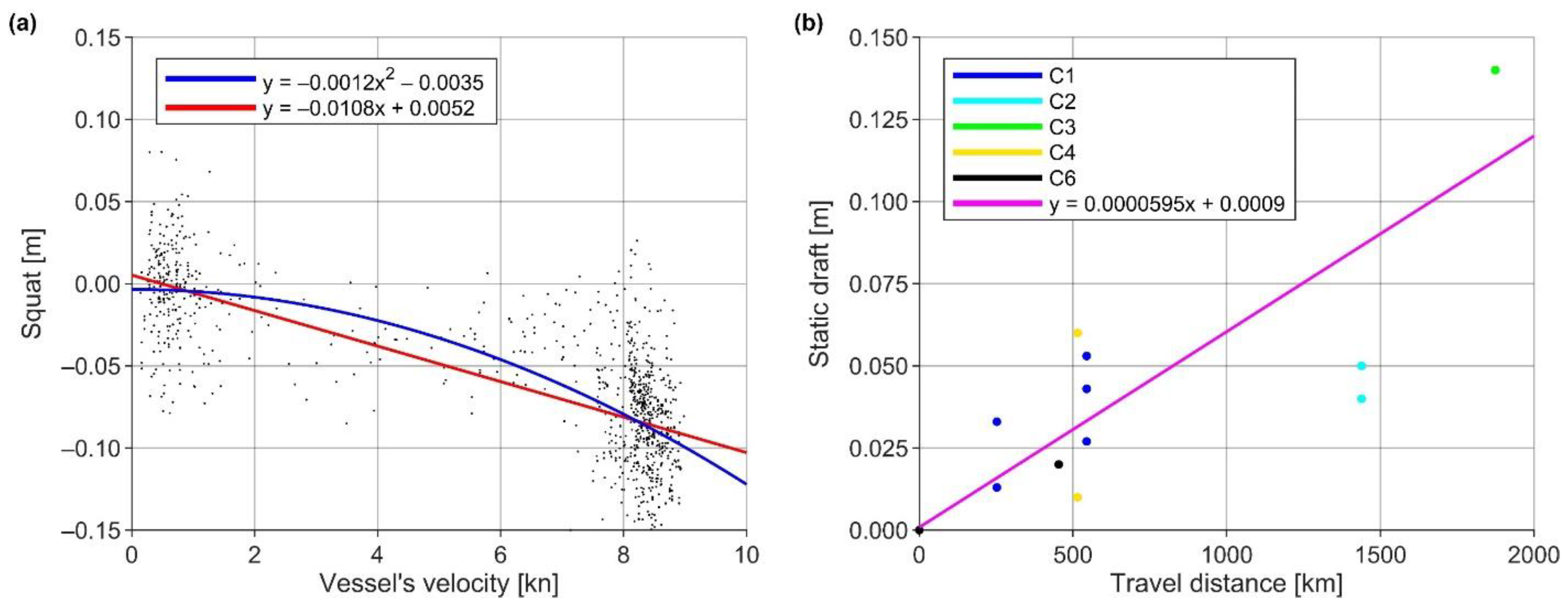
6.4. Squat Estimation Function
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Visser, H.; Dangendorf, S.; Petersen, A.C. A review of trend models applied to sea level data with reference to the “acceleration-deceleration debate”. J. Geophys. Res. Ocean. 2015, 120, 3873–3895. [Google Scholar] [CrossRef]
- Breili, K.; Simpson, M.J.R.; Nilsen, J.E.Ø. Observed sea-level changes along the Norwegian coast. J. Mar. Sci. Eng. 2017, 5, 29. [Google Scholar] [CrossRef]
- Madsen, K.S.; Høyer, J.L.; Suursaar, Ü.; She, J.; Knudsen, P. Sea level trends and variability of the Baltic Sea from 2D statistical reconstruction and altimetry. Front. Earth Sci. 2019, 7, 243. [Google Scholar] [CrossRef]
- Vu, P.L.; Frappart, F.; Darrozes, J.; Marieu, V.; Blarel, F.; Ramillien, G.; Bonnefond, P.; Birol, F. Multi-satellite altimeter validation along the French Atlantic coast in the southern Bay of Biscay from ERS-2 to SARAL. Remote Sens. 2018, 10, 93. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J.; Wang, C. Sentinel-3A SRAL global statistical assessment and cross-calibration with Jason-3. Remote Sens. 2019, 11, 1573. [Google Scholar] [CrossRef]
- Liibusk, A.; Kall, T.; Rikka, S.; Uiboupin, R.; Suursaar, Ü.; Tseng, K.-H. Validation of Copernicus sea level altimetry products in the Baltic Sea and Estonian lakes. Remote Sens. 2020, 12, 4062. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring sea level in the coastal zone with satellite altimetry and tide gauges. Surv. Geophys. 2017, 38, 33–57. [Google Scholar] [CrossRef]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Fu, L.-L.; Picot, N.; Raynal, M.; Roinard, H. Satellite altimetry measurements of sea level in the coastal zone. Surv. Geophys. 2019, 40, 1319–1349. [Google Scholar] [CrossRef]
- Bouin, M.-N.; Ballu, V.; Calmant, S.; Boré, J.-M.; Folcher, E.; Ammann, J. A kinematic GPS methodology for sea surface mapping, Vanuatu. J. Geod. 2009, 83, 1203. [Google Scholar] [CrossRef]
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Validation of marine geoid models by utilizing hydrodynamic model and shipborne GNSS profiles. Mar. Geod. 2020, 43, 134–162. [Google Scholar] [CrossRef]
- Saari, T.; Bilker-Koivula, M.; Koivula, H.; Nordman, M.; Häkli, P.; Lahtinen, S. Validating geoid models with marine GNSS measurements, sea surface models, and additional gravity observations in the Gulf of Finland. Mar. Geod. 2021, 44, 196–214. [Google Scholar] [CrossRef]
- Gruno, A.; Liibusk, A.; Ellmann, A.; Oja, T.; Vain, A.; Jürgenson, H. Determining sea surface heights using small footprint airborne laser scanning. In Proceedings of the Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2013, Dresden, Germany, 23–26 September 2013. [Google Scholar] [CrossRef]
- Zlinszky, A.; Timár, G.; Weber, R.; Székely, B.; Briese, C.; Ressl, C.; Pfeifer, N. Observation of a local gravity potential isosurface by airborne lidar of Lake Balaton, Hungary. Solid Earth 2014, 5, 355–369. [Google Scholar] [CrossRef]
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Applications of airborne laser scanning for determining marine geoid and surface waves properties. Eur. J. Remote Sens. 2021, 54, 557–567. [Google Scholar] [CrossRef]
- Xu, X.-Y.; Xu, K.; Shen, H.; Liu, Y.-L.; Liu, H.-G. Sea surface height and significant wave height calibration methodology by a GNSS buoy campaign for HY-2A altimeter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5252–5261. [Google Scholar] [CrossRef]
- Zhou, B.; Watson, C.; Legresy, B.; King, M.A.; Beardsley, J.; Deane, A. GNSS/INS-equipped buoys for altimetry validation: Lessons learnt and new directions from the Bass Strait validation facility. Remote Sens. 2020, 12, 3001. [Google Scholar] [CrossRef]
- Penna, N.T.; Morales Maqueda, M.A.; Martin, I.; Guo, J.; Foden, P.R. Sea surface height measurement using a GNSS wave glider. Geophys. Res. Lett. 2018, 45, 5609–5616. [Google Scholar] [CrossRef]
- Chupin, C.; Ballu, V.; Testut, L.; Tranchant, Y.-T.; Calzas, M.; Poirier, E.; Coulombier, T.; Laurain, O.; Bonnefond, P.; Team FOAM Project. Mapping sea surface height using new concepts of kinematic GNSS instruments. Remote Sens. 2020, 12, 2656. [Google Scholar] [CrossRef]
- Rocken, C.; Johnson, J.; Van Hove, T.; Iwabuchi, T. Atmospheric water vapor and geoid measurements in the open ocean with GPS. Geophys. Res. Lett. 2005, 32, L12813. [Google Scholar] [CrossRef]
- Jürgenson, H.; Liibusk, A.; Ellmann, A. Geoid profiles in the Baltic Sea determined using GPS and sea level surface. Geod. Cartogr. 2008, 34, 109–115. [Google Scholar] [CrossRef]
- Ince, E.S.; Förste, C.; Barthelmes, F.; Pflug, H.; Li, M.; Kaminskis, J.; Neumayer, K.-H.; Michalak, G. Gravity measurements along commercial ferry lines in the Baltic Sea and their use for geodetic purposes. Mar. Geod. 2020, 43, 573–602. [Google Scholar] [CrossRef]
- Liibusk, A.; Varbla, S.; Ellmann, A.; Vahter, K.; Uiboupin, R.; Delpeche-Ellmann, N. Shipborne GNSS acquisition of sea surface heights in the Baltic Sea. J. Geod. Sci. 2022, in print. [CrossRef]
- Varbla, S.; Ellmann, A.; Märdla, S.; Gruno, A. Assessment of marine geoid models by ship-borne GNSS profiles. Geod. Cartogr. 2017, 43, 41–49. [Google Scholar] [CrossRef]
- Schwabe, J.; Ågren, J.; Liebsch, G.; Westfeld, P.; Hammarklint, T.; Mononen, J.; Andersen, O.B. The Baltic Sea Chart Datum 2000 (BSCD2000)—Implementation of a common reference level in the Baltic Sea. Int. Hydrogr. Rev. 2020, 23, 63–83. [Google Scholar]
- Varbla, S.; Ågren, J.; Ellmann, A.; Poutanen, M. Treatment of tide gauge time series and marine GNSS measurements for vertical land motion with relevance to the implementation of the Baltic Sea Chart Datum 2000. Remote Sens. 2022, 14, 920. [Google Scholar] [CrossRef]
- Suursaar, Ü.; Kall, T. Decomposition of relative sea level variations at tide gauges using results from four Estonian precise levelings and uplift models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1966–1974. [Google Scholar] [CrossRef]
- Kollo, K.; Ellmann, A. Geodetic reconciliation of tide gauge network in Estonia. Geophysica 2019, 54, 27–38. [Google Scholar]
- Lagemaa, P.; Elken, J.; Kõuts, T. Operational sea level forecasting in Estonia. Est. J. Eng. 2011, 17, 301–331. [Google Scholar] [CrossRef]
- Jahanmard, V.; Delpeche-Ellmann, N.; Ellmann, A. Realistic dynamic topography through coupling geoid and hydrodynamic models of the Baltic Sea. Cont. Shelf Res. 2021, 222, 104421. [Google Scholar] [CrossRef]
- Slobbe, D.C.; Verlaan, M.; Klees, R.; Gerritsen, H. Obtaining instantaneous water levels relative to a geoid with a 2D storm surge model. Cont. Shelf Res. 2013, 52, 172–189. [Google Scholar] [CrossRef]
- Nordman, M.; Kuokkanen, J.; Bilker-Koivula, M.; Koivula, H.; Häkli, P.; Lahtinen, S. Geoid validation on the Baltic Sea using ship-borne GNSS data. Mar. Geod. 2018, 41, 457–476. [Google Scholar] [CrossRef]
- Roggenbuck, O.; Reinking, J. Sea surface heights retrieval from ship-based measurements assisted by GNSS signal reflections. Mar. Geod. 2019, 42, 1–24. [Google Scholar] [CrossRef]
- Metsar, J.; Kollo, K.; Ellmann, A. Modernization of the Estonian national GNSS reference station network. Geod. Cartogr. 2018, 44, 55–62. [Google Scholar] [CrossRef][Green Version]
- Balodis, J.; Morozova, K.; Reiniks, M.; Normand, M. Normal heights for GNSS reference station antennas. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Riga, Latvia, 27–29 September 2017. [Google Scholar] [CrossRef]
- Vestøl, O.; Ågren, J.; Steffen, H.; Kierulf, H.; Tarasov, L. NKG2016LU: A new land uplift model for Fennoscandia and the Baltic region. J. Geod. 2019, 93, 1759–1779. [Google Scholar] [CrossRef]
- Roggenbuck, O.; Reinking, J.; Härting, A. Oceanwide precise determination of sea surface height from in-situ measurements on cargo ships. Mar. Geod. 2014, 37, 77–96. [Google Scholar] [CrossRef]
- Shih, H.-C.; Yeh, T.-K.; Du, Y.; He, K. Accuracy assessment of sea surface height measurement obtained from shipborne PPP positioning. J. Surv. Eng. 2021, 147, 04021022. [Google Scholar] [CrossRef]
- Natural Resources Canada. Precise Point Positioning. Available online: https://webapp.geod.nrcan.gc.ca/geod/tools-outils/ppp.php (accessed on 28 February 2022).
- Ågren, J.; Strykowski, G.; Bilker-Koivula, M.; Omang, O.; Märdla, S.; Forsberg, R.; Ellmann, A.; Oja, T.; Liepins, I.; Parseliunas, E.; et al. The NKG2015 gravimetric geoid model for the Nordic-Baltic region. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems 2016, Thessaloniki, Greece, 19–23 September 2016. [Google Scholar] [CrossRef]
- Poutanen, M.; Vermeer, M.; Mäkinen, J. The permanent tide in GPS positioning. J. Geod. 1996, 70, 499–504. [Google Scholar] [CrossRef]
- Ihde, J.; Mäkinen, J.; Sacher, M. Conventions for the Definition and Realization of a European Vertical Reference System (EVRS); Version 5.2; Federal Agency for Cartography and Geodesy (BKG): Frankfurt, Germany, 2019.
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Utilizing airborne laser scanning and geoid model for near-coast improvements in sea surface height and marine dynamics. J. Coast. Res. 2020, 95, 1339–1343. [Google Scholar] [CrossRef]
- Hordoir, R.; Axell, L.; Höglund, A.; Dieterich, C.; Fransner, F.; Gröger, M.; Liu, Y.; Pemberton, P.; Schimanke, S.; Andersson, H.; et al. Nemo-Nordic 1.0: A NEMO-based ocean model for the Baltic and North seas—Research and operational applications. Geosci. Model Dev. 2019, 12, 363–386. [Google Scholar] [CrossRef]
- Kärnä, T.; Ljungemyr, P.; Falahat, S.; Ringgaard, I.; Axell, L.; Korabel, V.; Murawski, J.; Maljutenko, I.; Lindenthal, A.; JanDT-Scheelke, S.; et al. Nemo-Nordic 2.0: Operational marine forecast model for the Baltic Sea. Geosci. Model Dev. 2021, 14, 5731–5749. [Google Scholar] [CrossRef]
- LVĢMC Hydrological Data Search (in Latvian). Available online: https://www.meteo.lv/hidrologija-datu-meklesana/?nid=466 (accessed on 28 February 2021).
- SMHI Oceanographic Observations. Available online: https://www.smhi.se/data/oceanografi/ladda-ner-oceanografiska-observationer/#param=sealevelrh2000,stations=all (accessed on 28 February 2021).
- FMI Observations. Available online: https://en.ilmatieteenlaitos.fi/download-observations#!/ (accessed on 28 February 2021).
- EMODnet Data Explorer. Available online: http://www.emodnet-physics.eu/Map/DefaultMap.aspx (accessed on 28 February 2021).
- LVĢMC Observation Network (in Latvian). Available online: https://www.meteo.lv/hidrologijas-staciju-karte/?nid=465 (accessed on 28 February 2021).
- Theoretical Mean Water and Geodetical Height Systems in Finland. Available online: https://en.ilmatieteenlaitos.fi/theoretical-mean-sea-level (accessed on 28 February 2021).
- EVRS Height Datum Relations. Available online: https://evrs.bkg.bund.de/Subsites/EVRS/EN/Projects/HeightDatumRel/height-datum-rel.html (accessed on 28 February 2021).
- Lan, W.-H.; Kuo, C.-Y.; Kao, H.-C.; Lin, L.-C.; Shum, C.K.; Tseng, K.-H.; Chang, J.-C. Impact of geophysical and datum corrections on absolute sea-level trends from tide gauges around Taiwan, 1993–2015. Water 2017, 9, 480. [Google Scholar] [CrossRef]
- Denys, P.H.; Beavan, R.J.; Hannah, J.; Pearson, C.F.; Palmer, N.; Denham, M.; Hreinsdottir, S. Sea level rise in New Zealand: The effect of vertical land motion on century-long tide gauge records in a tectonically active region. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018055. [Google Scholar] [CrossRef]
- Moritz, H. Advanced Physical Geodesy; Wichmann: Karlsruhe, Germany, 1980. [Google Scholar]
- Kasper, J.F. A second-order Markov gravity anomaly model. J. Geophys. Res. 1971, 76, 7844–7849. [Google Scholar] [CrossRef]
- Barrass, C.B. Ship Design and Performance for Masters and Mates; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Ellmann, A.; Märdla, S.; Oja, T. The 5 mm geoid model for Estonia computed by the least squares modified Stokes’s formula. Surv. Rev. 2020, 52, 352–372. [Google Scholar] [CrossRef]

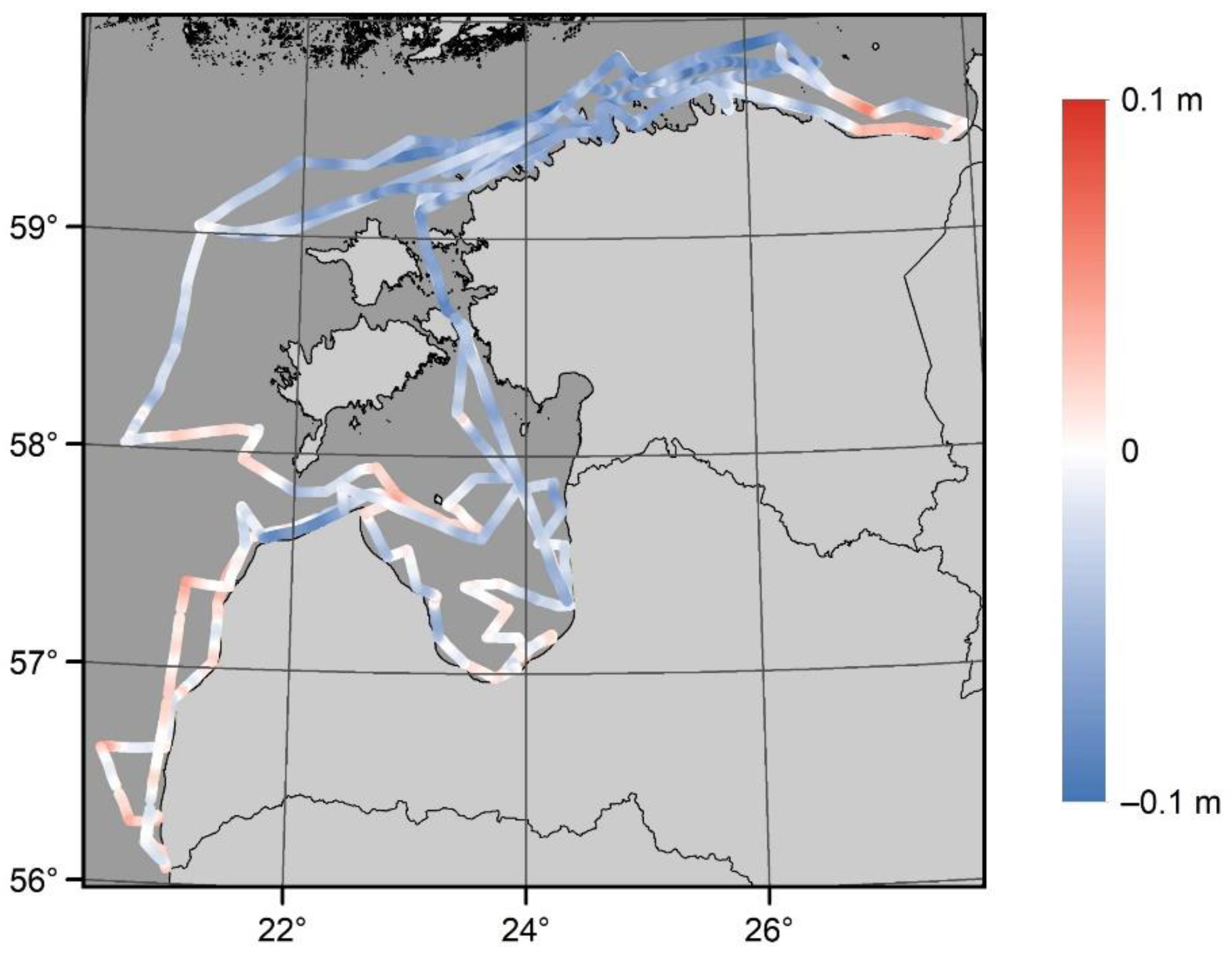


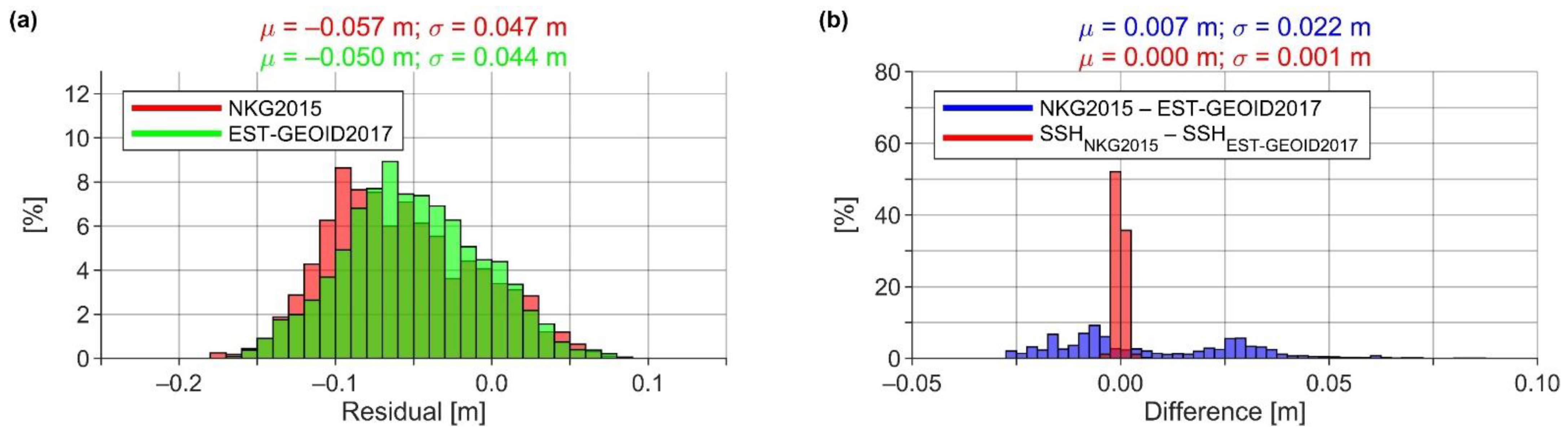
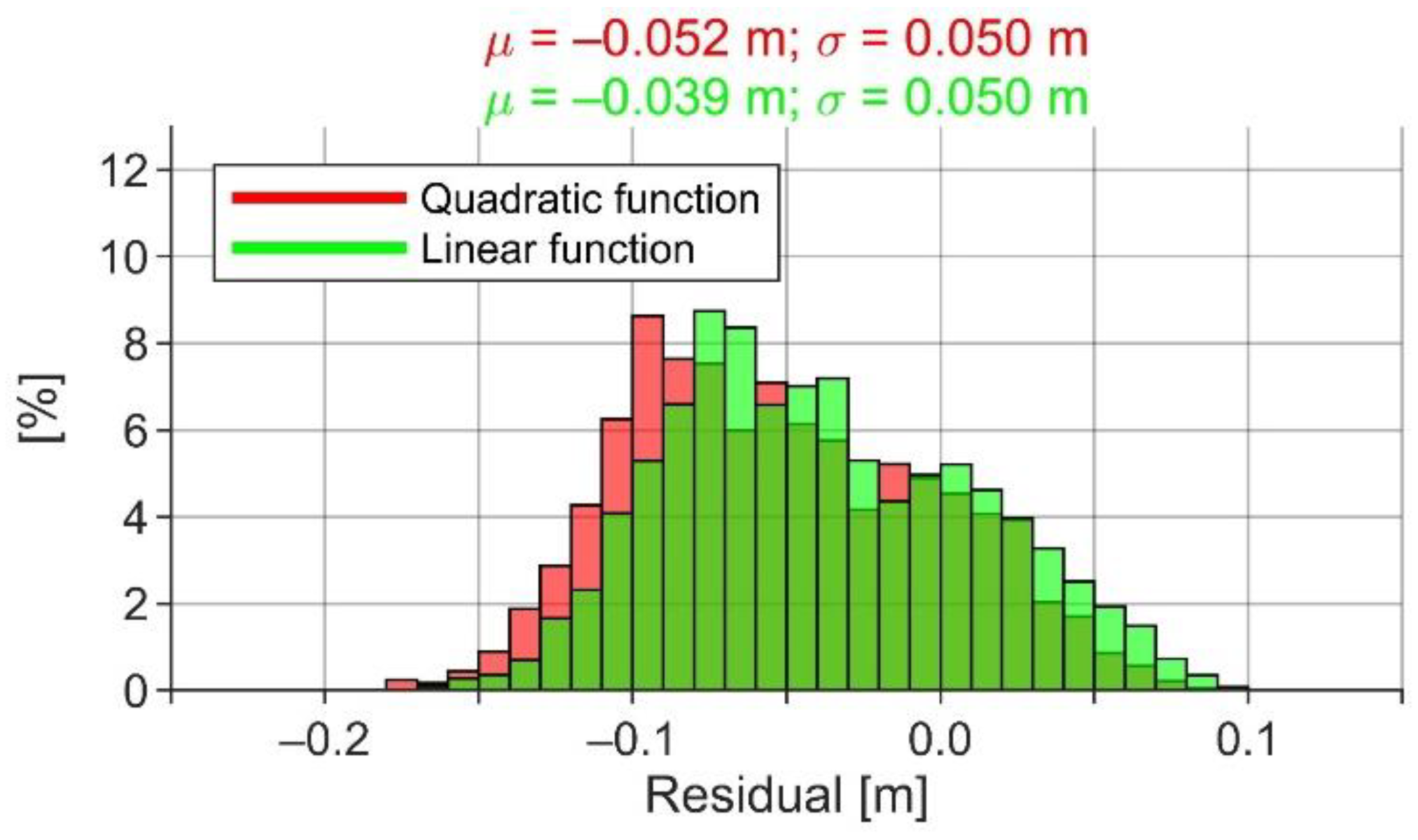
| Campaign Identifier | Month (GPS Week) | Duration of a Campaign (h) | Route Length of a Campaign (km) | Number of HDM Grids/DT Computation Duration (h) | Number of Computed SSH Data Points | Temporal Resolution of SSH (s) |
|---|---|---|---|---|---|---|
| C1 | April (2152) | 52 | 544 | 120 | 11,908 | 15 |
| C2 | July (2168) | 106 | 1439 | 168 | 12,253 | 30 |
| C3 | August (2169) | 146 | 1874 | 192 | 16,222 | 30 |
| C4 | August (2172) | 40 | 515 | 96 | 4390 | 30 |
| C5 | September (2174) | 9 | 98 | 96 | 832 | 30 |
| C6 | September (2175) | 40 | 454 | 120 | 4449 | 30 |
| Index/Coefficient | Solution | Solution | Solution | Solution |
|---|---|---|---|---|
| 3 | 4 | 1 | 2 | |
| 4 | 3 | 2 | 1 | |
| 3 | 3 | 1 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varbla, S.; Liibusk, A.; Ellmann, A. Shipborne GNSS-Determined Sea Surface Heights Using Geoid Model and Realistic Dynamic Topography. Remote Sens. 2022, 14, 2368. https://doi.org/10.3390/rs14102368
Varbla S, Liibusk A, Ellmann A. Shipborne GNSS-Determined Sea Surface Heights Using Geoid Model and Realistic Dynamic Topography. Remote Sensing. 2022; 14(10):2368. https://doi.org/10.3390/rs14102368
Chicago/Turabian StyleVarbla, Sander, Aive Liibusk, and Artu Ellmann. 2022. "Shipborne GNSS-Determined Sea Surface Heights Using Geoid Model and Realistic Dynamic Topography" Remote Sensing 14, no. 10: 2368. https://doi.org/10.3390/rs14102368
APA StyleVarbla, S., Liibusk, A., & Ellmann, A. (2022). Shipborne GNSS-Determined Sea Surface Heights Using Geoid Model and Realistic Dynamic Topography. Remote Sensing, 14(10), 2368. https://doi.org/10.3390/rs14102368