Abstract
Galileo satellites can broadcast signals on five frequencies, namely E1, E5A, E5B, E5 (A+B), and E6. The multi-frequency integration has become an emerging trend in Global Navigation Satellite System (GNSS) data processing. This study focused on the precise time transfer based on Galileo five-frequency uncombined precise point positioning (PPP), including the performance comparison of PPP time transfer with a priori and a posteriori weighting strategies, with different inter-frequency bias (IFB) dynamic models, and with the precise satellite products from different analysis centers, as well as the contribution of multi-frequency observations for time transfer. Compared with the a priori weighting strategy, the short-term frequency stability of time transfer adopting the Helmert variance component estimation method can be improved by 28.9–37.6% when the average time is shorter than 100 s. The effect of IFB dynamic models on Galileo five-frequency PPP time transfer is not obvious. When employing the post-processed precise satellite products from seven analysis centers, the accuracy of time transfer can be better than 0.1 ns, while an accuracy of 0.253 ns can be obtained in the real-time mode. At an average time of approximately 10,000 s, the post-processed time transfer with Galileo five-frequency PPP can provide a frequency stability of 3.283 × 10−14 to 3.459 × 10−14, while that in real-time mode can be 3.541 × 10−14. Compared with dual-frequency PPP results, the contribution of multi-frequency combination to the accuracy and frequency stability of time transfer is not significant, but multi-frequency PPP can achieve more reliable time transfer results when the signal quality is poor.
1. Introduction
Global Navigation Satellite System (GNSS) is one of the main tools for precise time transfer. In comparison with traditional tools, GNSS time transfer has the advantages of low cost, small size, all-weather availability, and easy maintenance. Since 1980, many researchers have focused on the GNSS technology for time transfer, and several typical technologies have been proposed, including common view (CV), all-in view (AV), two-way satellite time and frequency transfer (TWSTFT), and carrier phase (CP) methods [1]. The basic idea, advantage, and disadvantage of the four GNSS time transfer methods are listed in Table 1. The CP method, which is also called the precise point positioning (PPP) method, combines the advantages of the other three methods. The short-term frequency stability of PPP time transfer is higher than that of TWSTFT method [2]. Currently, PPP has become the primary method to maintain the International Atomic Time (TAI) by Bureau International des Poids et Mesures (BIPM) and to keep the time synchronization by time laboratories in various countries [3,4].

Table 1.
Basic idea, advantage, and disadvantage of four typical GNSS time transfer technologies.
For a long period, the PPP time transfer technology mainly relied on GPS. The frequency stability of GPS PPP time transfer with ambiguity resolution (AR) could reach a level of 1 × 10−16 and sub−10−16 at an average time of five days and seven days, respectively [5,6]. In recent years, with the overall deployment of Multi-GNSS Experiment (MGEX) stations, the PPP time transfer based on GLONASS-only, Galileo-only, BDS-only, and multi-GNSS integrated measurements has been a research focus. Ge et al. [7] investigated the effects of three different inter-frequency bias (IFB)-handling strategies on the time transfer performance with GLONASS-only dual-frequency PPP, and the results indicated that the standard deviation (STD) statistics of the differences between receiver clock estimates derived from GLONASS-only and GPS-only PPP could be 0.2 ns when estimating IFB for each GLONASS satellite. Xu et al. [8] evaluated the contribution of Galileo PPP AR on the frequency stability of time transfer. The results indicated that the ambiguity-fixed solutions had slightly reduced short-term stability compared with that of the ambiguity-float solutions, but the long-term stability of the ambiguity-fixed solutions was significantly improved. Zhang et al. [9] compared the time transfer performance of GPS-only, Galileo-only, BDS-2-only, and GPS/Galileo/BDS-2 combined dual-frequency PPP, and it was indicated that the STD statistics of the short time link could be 0.059, 0.116, 0.089, and 0.055 ns for the four different constellation combination cases, respectively. Ge et al. [10,11] further jointly used the single- or dual-frequency observations from GPS, GLONASS, Galileo, and BDS-2 satellites to carry out the time transfer. The four-system integrated PPP could improve the frequency stability of time links by 9.61% and 20.3% for single- and dual-frequency cases over GPS-only PPP, respectively. Lyu et al. [12] analyzed the time transfer accuracy of GPS/GLONASS/Galileo/BDS-2 combined PPP with fixed ambiguities for GPS, and it was proved that the STD statistics of the time link were decreased by 38.1% over GPS-only ambiguity-float PPP.
As most of the modernized GNSS satellites start to broadcast multi-frequency signals, many researchers investigated the time transfer performance of multi-frequency combined PPP. Tu et al. [13] proved that the BDS-2 triple-frequency uncombined (UC) PPP model could be applied to the time transfer, and the obtained accuracy and frequency stability of time links were comparable to those of the traditional dual-frequency ionospheric-free (IF) model. With the use of BDS-3 observations, Su and Jin [14] derived similar conclusions. Zhang et al. [15] rigorously evaluated the time transfer performance of five Galileo four-frequency IF combined models. The average STD statistics of time link differences between four-frequency and triple-frequency PPP models, and between four-frequency and dual-frequency PPP models could be 0.041 ns, but they exhibited consistency in terms of frequency stability of time links. Ge et al. [16] compared the time transfer performance of Galileo and BDS-3 four-frequency PPP. The results indicated that the frequency stability of Galileo time transfer results was slightly better than that of BDS-3, and both the accuracy and frequency stability of them were comparable to those of the corresponding dual-frequency PPP model.
According to the above research status, the precise time transfer with multi-frequency PPP has attracted an increasing attention from the GNSS community, but most of the existing studies were confined to triple- or four-frequency observations. Actually, Galileo satellites can provide signals on five frequencies, namely E1, E5A, E5B, E5 (A+B), and E6, and BDS-3 satellites can transmit five open-service signals, namely B1I, B3I, B1C, B2a, and B2b. The current multi-frequency PPP time transfer models need to be extended so as to incorporate the five-frequency observations. Most importantly, the existing studies did not carefully consider the differences of multi-frequency observations. Taking Galileo five-frequency observations as an example, the signals on different frequencies differ in data quality, anti-jamming capability, hardware delay, and measurement noises because they employ different modulation modes. The E1 signal is modulated using Composite Binary Offset Carrier (CBOC) modulation, while the Alternative Binary Offset Carrier (AltBOC) modulation is used for the E5 signal (E5A/E5B/E5 (A+B)) [17,18,19]. Thus, the precision of observations differs among different frequencies. Most of the existing studies lost sight of this and set the same variances for the measurements on all the frequencies, which is obviously unreasonable.
This study focused on the precise time transfer based on the Galileo five-frequency UC PPP, including the effects of weighting strategies and IFB dynamic models as well as the contribution of multi-frequency combination. In addition, there are seven analysis centers (ACs) in support of post-processed or real-time Galileo precise satellite products at present. The systematic biases contained in the precise satellite products differ among different ACs, as they employ different strategies and models during precise orbit determination and precise clock estimation. These biases will be partially absorbed by the receiver clock parameters during PPP data processing, and thus affect the time transfer performance. Therefore, we also compared the time transfer performance of Galileo five-frequency UC PPP with the precise products from different ACs. In Section 2, the Galileo five-frequency UC PPP model for time transfer is first described, and then the Helmert variance component estimation method in Kalman filter is introduced. Subsequently, Section 3 presents the results, including the accuracy and frequency stability of time transfer derived from two different weighting strategies, three different IFB dynamic models, eight different precise satellite products, and four different inter-frequency combination cases. Next, the discussion is conducted in Section 4. Finally, we summarize the main points and the conclusions in Section 5.
2. Methods
2.1. Galileo Five-Frequency Uncombined PPP Model for Time Transfer
The single-frequency code and carrier phase observations from a Galileo receiver can be described below:
with where refers to the Galileo E1, E5A, E5B, E6, and E5 (A+B) frequency when it is equal to 1, 2, 3, 4, and 5, respectively, is the measured pseudorange, is the measured carrier phase, is the geometric range, is the receiver clock offset, is the satellite clock offset, is the ionospheric path delay on the E1 frequency, is the ionospheric delay factor, is the carrier frequency, is the tropospheric path delay, is the phase ambiguity, and are the receiver- and satellite-dependent code hardware delay, respectively, and and refer to the phase-specific hardware delay at the receiver and satellite, respectively. The four hardware delay terms are considered to be stable within a short period of time, for example, a day.
In precise clock estimation (PCE), the common clock is usually assumed for both code and carrier phase observation equations, but the code hardware delay is ignored. Consequently, the satellite clock parameters will absorb the time-invariant satellite code hardware delay. The current Galileo satellite clocks, which are computed with E1/E5A IF combined code and carrier phase observations, can be expressed as:
with and .
When the PCE is carried out based on different observations, the estimated satellite clocks will be different. The satellite clock estimates are frequency dependent due to the frequency-dependent code hardware delays lumped into them. Thus, the current E1/E5A IF satellite clocks provided by the international GNSS service (IGS) cannot be directly applied to the Galileo multi-frequency PPP processing. The E1/E5A IF satellite clocks can be converted into the desired satellite clocks for the UC observables on a specific frequency by combining them with the differential code biases (DCBs), that is:
with
where , , and denote the DCBs between E1 and E5A, between E1 and E5B, between E1 and E6, and between E1 and E5 (A+B), respectively, and , , , and denote the satellite clocks on a single frequency, namely the E1, E5A, E5B, E6, and E5 (A+B) UC satellite clocks, respectively. The four sets of DCB products have been provided by the Chinese Academy of Sciences (CAS) [20]. As shown in Equation (3), in addition to the frequency-independent physical clock error of the satellite (i.e., ), the UC satellite clocks only contain the single-frequency satellite code hardware delays on the corresponding frequency. As such, the satellite code hardware delays in the UC code observation equation (see Equation (1)) can be removed by applying these UC satellite clocks.
The ionospheric delay in the UC-based PPP model is taken as unknown parameter. As both the hardware delay and ionospheric delay are frequency dependent, only their combination rather than the separated term is unbiasedly estimable because of rank deficiency. Due to the perfect correlation between the receiver code hardware delay and ionospheric delay for the dual-frequency PPP with E1 and E5A UC observations, we usually estimate them as a lumped term in the dual-frequency UC model. As to the Galileo five-frequency UC PPP, the ionospheric delay estimate cannot completely absorb the effect of receiver code hardware delay on the E5B, E6, and E5 (A+B) frequencies. Therefore, three additional IFB parameters need to be respectively introduced into the E5B, E6, and E5 (A+B) code observation equations. Regarding the tropospheric delays, we usually employ an a priori model to correct the dry parts, while the wet parts are estimated as unknowns from the observations. After applying the E1, E5A, E5B, E6, and E5 (A+B) UC satellite clocks as well as the satellite orbits, the linearized observation model for Galileo five-frequency UC PPP can be given below:
with
where and are the observed-minus-computed (OMC) code and carrier phase observables, respectively, is the unit vector in the direction from the receiver to the satellite, is the three-dimensional (3D) receiver positions, is the receiver clock estimates, which are a lumped term of frequency-independent receiver physical clocks and receiver code hardware delays on E1 and E5A frequencies combined within the E1/E5A IF combination, is the slant ionospheric delay estimate on the E1 frequency, which is not the real ionospheric delay because of the lumped receiver code hardware delays on E1 and E5A frequencies, is the wet mapping function, is the tropospheric zenith wet delay (ZWD), , , and are the receiver IFBs on the E5B, E6, and E5 (A+B) frequencies, respectively, all of which are a linear combination of receiver code hardware delays on E1 and E5A frequencies as well as those on a third frequency (E5B, E6, or E5 (A+B)), and is the phase ambiguity estimates, which are non-integers because of the integrated code and phase hardware delays of the satellite and receiver.
The parameters which need estimation for Galileo five-frequency UC PPP include the receiver 3D coordinates, receiver clocks, slant ionospheric delays on the E1 frequency, ZWD, receiver IFBs on the E5B, E6, and E5 (A+B) frequencies, and E1, E5A, E5B, E6, and E5 (A+B) UC float ambiguities, that is:
where is the state vector for the Galileo five-frequency UC PPP.
To optimize the time transfer performance with Galileo five-frequency UC PPP, the proper stochastic models should also be determined. Following Satirapod and Luansang [21], the satellite elevations with a mapping form of trigonometric function or exponential function can be used to quantify the precision of satellite observations. The elevation-dependent weighting scheme with a Sine mapping function was adopted in this study. It was assumed that the observations in the E1, E5A, E5B, E6, and E5 (A+B) carriers are uncorrelated. In addition, they have the same a priori noises. The covariance matrix of UC code and phase observations can be computed as:
with and where both and are constants, which are set to 0.3 m for code observations and 0.003 m for phase observations, respectively, and is the satellite elevation angle. For the Galileo five-frequency UC PPP model, the covariance matrix is a diagonal matrix.
Based on the established observation model and stochastic model, the Kalman filter is employed to estimate the unknown parameters (state vector) by the following equation:
where and are the predicted state vector and its covariance matrix at epoch k, respectively, and and are the corresponding filtering results. and are the observation vector and its covariance matrix, respectively, is the unit matrix, is the design matrix, and is the Kalman gain matrix.
2.2. Helmert Variance Component Estimation Method for Kalman Filter
Obviously, the a priori weighting method (see Equation (8)) is not rigorous. In the Helmert variance component estimation (HVCE) method, the a posteriori observation residuals are used to determine the variance components of various observations so that the influence of different types of GNSS observations on the solutions can be effectively balanced [22,23]. In this study, based on the a priori weighting method, the HVCE method was further introduced into the Galileo five-frequency UC PPP data processing to determine the reasonable variances of observations on different frequencies.
Considering that the noise level is different between code and carrier phase observations as well as among the observations on different frequencies, the code and carrier phase observations on five frequencies are grouped into ten types to conduct the HVCE. To obtain the reliable HVCE time transfer solutions, there must be enough observations for each type and the difference of the number of observations among the ten types should not be significant. Based on this classification principle, the residuals and covariance matrix of various observations after carrying out the Kalman filter can be expressed as:
where and denote the code and phase observations on the frequency for all visible satellites, respectively, and are the corresponding covariance matrix, , , and denote the observation vector, observation residual error vector, and design matrix, respectively, and denotes the estimated parameters with Kalman filter. As the HVCE method requires iterative processing, to omit the complex matrix operation and improve the calculation efficiency, the simplified HVCE calculation formula is used to estimate the variance components of all types of observations [24], that is:
with
where and denote the variance components of code and phase observations on the frequency, respectively, and denote the corresponding number of observations, and denotes the covariance matrix of the predicted state vector.
Based on the obtained variance components, the variances of observations can be re-computed as:
where the subscripts and denote the times of iterations, and is an arbitrary constant, which is usually taken as one of the estimated variance components.
Figure 1 presents the flow chart of the HVCE method for Kalman filter. The computation procedure of the HVCE method includes the following steps:
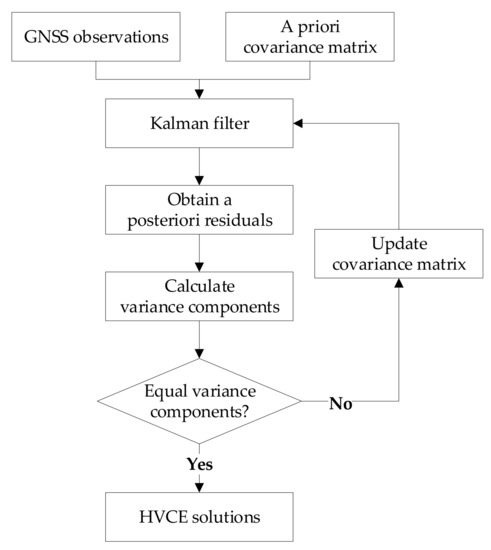
Figure 1.
Flow chart of the HVCE method for Kalman filter.
Step 1: Obtain the state vector and observation residual error vector by performing Kalman filter with a priori covariance matrix at an epoch.
Step 2: Calculate the variance components of all types of observations based on Equation (12).
Step 3: Update the covariance matrix of observations based on Equation (14), and then rerun the Kalman filter to obtain a posteriori residuals once more.
Step 4: Repeat Step 2 and Step 3 until the difference of the maximum value and minimum value among the derived variance components of ten types of observations is smaller than 0.001, namely .
3. Results
3.1. Datasets and Processing Strategies
To assess the time transfer performance of the Galileo five-frequency UC PPP model, the datasets from a week on day of year (DOY) 248 to 254, 2021, collected at 18 MGEX stations were used for static data processing. The sampling interval was 30 s, and the cut-off elevation angle was set to 10°. Following Prochniewicz and Grzymala [17], both the code and phase multipath errors (including measurement noises) of Galileo significantly increased with decreasing elevation angles when the elevation angles were lower than 20°. After considering a compromise between signal quality and satellite availability (note that there were only 24 operational Galileo satellites during the analysis period), the widely used threshold of 10° was taken as the cut-off elevation here. The geographical distribution of 18 MGEX tracking stations is shown in Figure 2. All stations were equipped with high-performance hydrogen clocks and could support the Galileo five-frequency observations. The BRUX station operated by a time laboratory at the Royal Observatory of Belgium was chosen as the central node for the time transfer, and a total of 17 time links were designed. Considering that the accuracy of the post-processed receiver clock offset products provided by IGS can reach 75 ps, they were taken as the reference values when evaluating the accuracy of time transfer results. Since the PPP time transfer technology has a significant advantage in short-term (shorter than one day) frequency stability, the data processing was carried out day-by-day. To analyze the effects of different precise products on PPP time transfer, eight precise satellite products in support of the Galileo system, which are identified by “COD”, “GBM”, “WUM”, “SHA”, “IAC”, “ESA”, “GRG”, and “CNT”, over the analysis period were collected. It should be noted that the Galileo precise satellite products were not provided by “SHA” on DOY 250, 2021. These precise products were generated by the analysis centers Center for Orbit Determination in Europe (CODE), GeoForschungsZentrum Potsdam (GFZ), Wuhan University (WHU), Shanghai Observatory (SHAO), Information and Analysis Center (IAC), European Space Agency (ESA), and Centre National d’Etudes Spatiales (CNES), and their information is detailed in Table 2. It is worth noting that CNES provides two sets of precise products, namely “GRG” and “CNT”, among which “GRG” is the post-processed precise products, and “CNT” is the real-time precise products retrieved based on real-time data stream CLK93 and broadcast ephemeris.
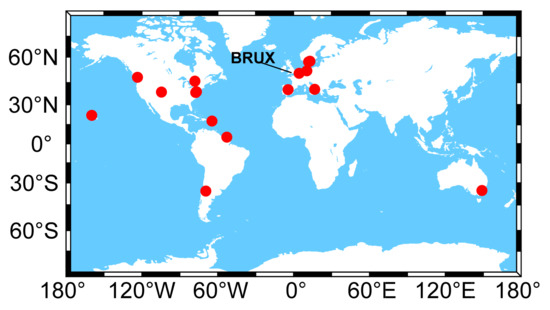
Figure 2.
Geographical distribution of 18 MGEX tracking stations.

Table 2.
Galileo precise satellite products from different ACs.
The sufficient visible satellites and the smaller time dilution of precision (TDOP) values are beneficial for the high-accuracy time transfer. As of the end of 2021, the Galileo constellation had a total of 24 operational satellites, including three in-orbit validation (IOV) satellites and 21 Full Operational Capability (FOC) satellites [25]. Figure 3 and Figure 4 provide the geographical distribution of the average number of visible satellites and average TDOP values for Galileo over the entire analysis period, respectively. There are seven visible Galileo satellites (on average) in areas spanning the latitudes 15°N to 55°N and 15°S to 55°S, while the satellite numbers are slightly increased to eight (on average) in other areas. Due to the evenly distributed visible satellites, the change of average TDOP values on a global scale is not significant, with a varying range of 1.1 to 1.4. Therefore, the current number of Galileo satellites is sufficient and the TDOP value is satisfactory, which can meet the requirements of PPP time transfer.
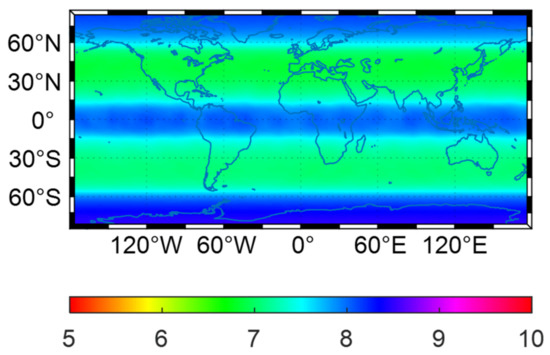
Figure 3.
Average number of visible satellites for Galileo during DOY 248–254 of 2021.
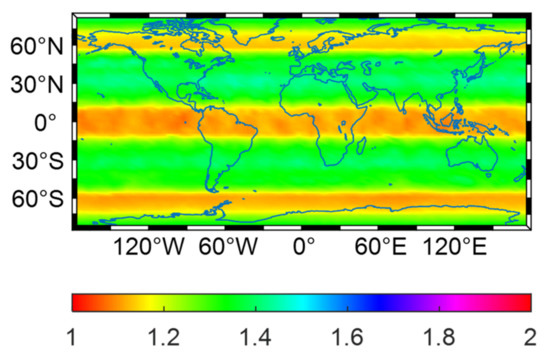
Figure 4.
Average TDOP values for Galileo during DOY 248–254 of 2021.
3.2. Time Transfer Results with HVCE Method
Four time links (i.e., the difference of receiver clock estimates at two different stations) between BRUX and KOKB, between BRUX and ONSA, between BRUX and SPT0, and between BRUX and PTBB on DOY 251, 2021, were selected to compare the time transfer performance of the Galileo five-frequency PPP with a priori weighting method and the HVCE a posterior weighting method, and the results are illustrated in Figure 5. The post-processed precise products “GBM” were used for PPP processing. It can be seen that the estimates of time links showed a significant difference between the two different weighting schemes in the first 8 h. After the filter fully converged, the corresponding difference of the time link results was not obvious. Most importantly, compared with the a priori weighting method, the time links of the HVCE method converged faster. The results indicate that the adjustment of weights of observations with HVCE method is helpful to the filter convergence, and thus is expected to improve the accuracy of PPP time transfer within the first several hours.
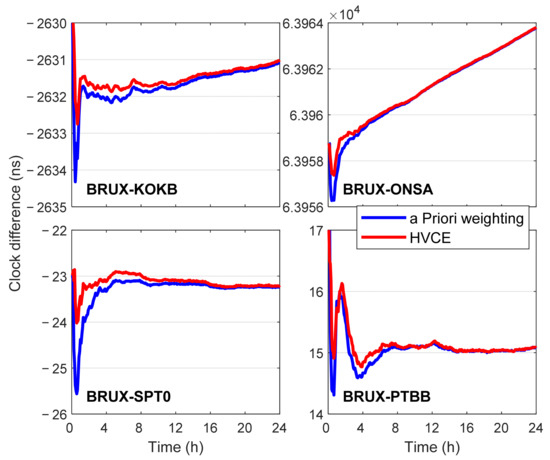
Figure 5.
Four time links generated by Galileo five-frequency PPP with the a priori weighting method and HVCE method on DOY 251, 2021.
The frequency stability, which can be expressed by Modified Allan Deviation (MDEV), is an important index to evaluate the time transfer performance. Figure 6 displays the MDEV of four time links with two different weighting schemes on DOY 251, 2021, and Table 3 lists the MDEV values at several specific average times. It is clearly seen that the frequency stability of the HVCE scheme was better than that of the a priori weighting scheme for all the four time links, especially for the short-term frequency stability. Based on the average results over the four time links, the HVCE scheme can improve the frequency stability by 28.9%–37.6% when the average time is shorter than 100 s (including 30, 60, and 90 s). With the increasing average time, the corresponding improvement rate of HVCE scheme decreased. When the average time fell between 1000 and 10,000 s, the frequency stability of the HVCE scheme was even slightly lower than that of the a priori weighting scheme sometimes for the time links between BRUX and KOKB, between BRUX and SPT0, and between BRUX and PTBB. For the long-term (with an average time longer than 10,000 s) frequency stability, the HVCE scheme outperformed the a priori weighting scheme, but the difference between them was confined to a level of 10−16 to 10−15. With the increment of average time, the number of samples for MDEV calculation was continuously reduced, which may have resulted in the increasing MDEV errors [26]. In addition, the difference of time link results between the HVCE scheme and a priori weighting scheme was not significant after the filter converged. Thus, the frequency stability at an average time longer than 1000 s seems to be at a similar level for the two different weighting schemes. The results indicate that the HVCE scheme can also be beneficial to improve the short-term frequency stability of time transfer compared with the a priori weighting scheme.
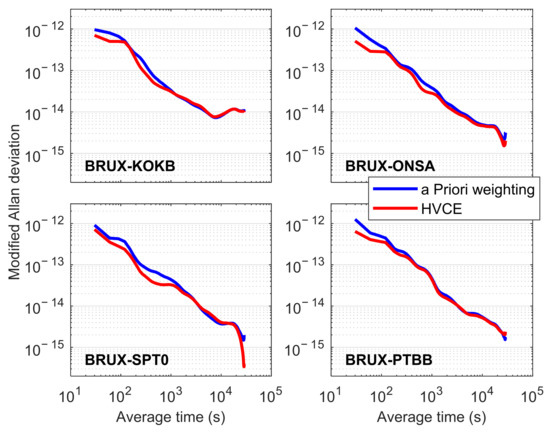
Figure 6.
MDEV of four time links with the a priori weighting method and HVCE method on DOY 251, 2021.

Table 3.
MDEV values at several specific average times of four time links with the a priori weighting method and HVCE method on DOY 251, 2021.
3.3. Time Transfer Results with Different IFB Dynamic Models
There are three IFB parameters in the Galileo five-frequency UC PPP observation model, and thus a reasonable IFB dynamic model should be taken to ensure the reliability of the receiver clock offsets estimated through Kalman filter. The post-processed precise products “GBM” are used for analysis. To investigate the time correlation of IFB parameters among the epochs, the IFBs are modeled as constants, random walk process, and white noise process for comparison to conduct the time transfer with Galileo five-frequency PPP. If IFBs are very stable and will not change over time, they should be estimated as constants. In the case of IFBs with a high time correlation, they should be estimated as random walk process. If the IFBs are independent among different epochs, they should be estimated as white noise process. Figure 7 illustrates the time series of receiver clock offset estimates with three different IFB dynamic models at BRUX and SPT0 stations on DOY 248, 2021. It can be seen that the receiver clock estimates were consistent for the three IFB dynamic models (with a maximum difference smaller than 0.01 ns). With the use of receiver clock estimates at the two stations, a time link can be generated. We can also obtain the corresponding time link using the IGS final products. Taking the time link derived from IGS final products as references, the epoch-wise time transfer errors are shown in Figure 8. The effects of different time datums are eliminated by subtracting the average value. The time transfer errors with a varying range of 0.25 ns (excluding the results within the first several minutes) were also consistent for the three IFB dynamic models (with a maximum difference smaller than 0.01 ns). The STD statistics can be used to assess the time transfer accuracy. The STD values of time link differences were 0.041 ns for all the three IFB dynamic models (excluding the results within the first four hours at a converging stage). To investigate the frequency stability, Figure 9 further provides the MDEV results of the time link BRUX-SPT0. Similarly, both the short-term and long-term frequency stability were basically consistent for the three IFB dynamic models. When the IFBs were modeled as constants, random walk process, and white noise process, the frequency stability at an average time of 90 s was 2.777 × 10−13, 2.778 × 10−13, and 2.769 × 10−13, respectively, while the corresponding stability at an average time of 9990 s was 4.066 × 10−15, 4.064 × 10−15, and 4.050 × 10−15, respectively. Therefore, the effects of IFB dynamic models on the precise time transfer with Galileo five-frequency UC PPP were marginal. For simplicity, the random walk process was employed for IFB estimation in the following data processing.
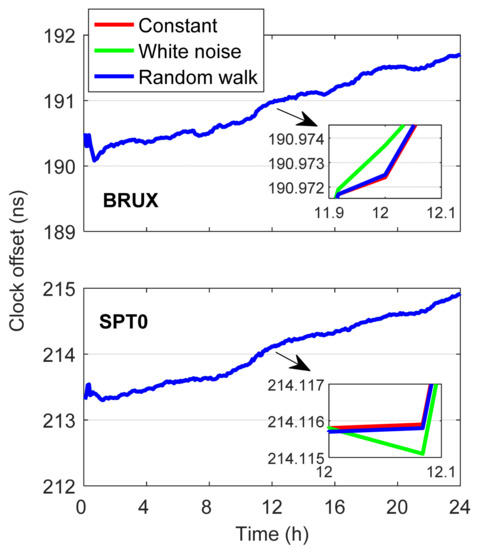
Figure 7.
Receiver clock offset estimates with three different IFB dynamic models at BRUX and SPT0 stations on DOY 248, 2021.
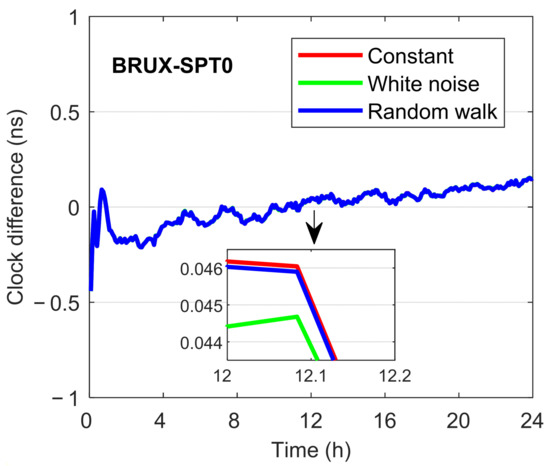
Figure 8.
Differences of the time link BRUX-SPT0 between three sets of estimates and IGS final products on DOY 248, 2021.
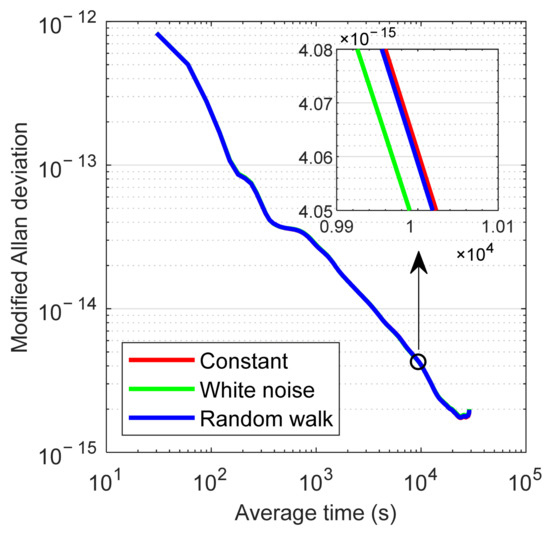
Figure 9.
MDEV of the time link BRUX-SPT0 with three different IFB dynamic models on DOY 248, 2021.
3.4. Time Transfer Results with Precise Products from Different Analysis Centers
In order to evaluate the time transfer performance of different precise products, the Galileo five-frequency PPP processing with eight different precise products was carried out at 18 selected MGEX stations to generate 17 time links. Figure 10 illustrates the time transfer results of three time links BRUX-SPT0, BRUX-KOKB, and BRUX-USN7 on DOY 248, 2021. The time links of seven post-processed precise products were consistent with each other, which indicates that all the post-processed precise products in support of Galileo can be used for time transfer. The time transfer results of the real-time product “CNT” were significantly different from those of the post-processed ones, especially for the time link BRUX-USN7, in which the maximum differences could reach 0.5 ns. Figure 11 shows the differences of the time links between Galileo five-frequency PPP estimates with different precise products and IGS final products on DOY 248, 2021, and Table 4 provides the corresponding STD statistics. To ensure that only the fully converged results are involved in the analysis, the results in the first four hours were excluded. After removing the effects of different time datums, the time transfer accuracy of post-processed products (usually better than 0.2 ns) was significantly higher than that of real-time products (usually better than 0.6 ns). According to the average STDs over the three time links, the product “GRG” achieved the highest time transfer accuracy with a statistic of 0.072 ns, while that of the product “IAC” was the worst among the post-processed products, which was 0.099 ns. As to the real-time product “CNT”, the time transfer accuracy degraded to only 0.253 ns.
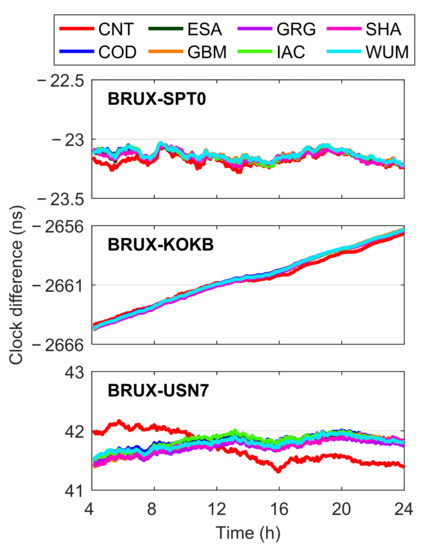
Figure 10.
Three time links generated by Galileo five-frequency PPP using precise products from different ACs on DOY 248, 2021.
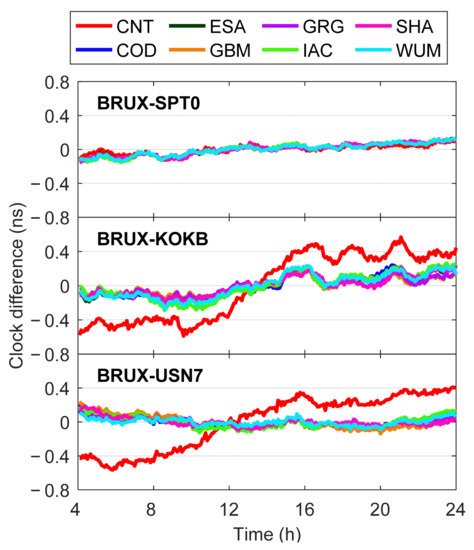
Figure 11.
Differences of the time links between Galileo five-frequency PPP estimates with different precise products and IGS final products on DOY 248, 2021.

Table 4.
STD values of differences of the time links between PPP estimates and IGS final products on DOY 248, 2021.
The frequency stability of time transfer with various precise products was further analyzed. Figure 12 illustrates the MDEV of the time link BRUX-KOKB derived with eight different precise products on DOY 248, 2021. In terms of the short-term frequency stability, the MDEV of post-processed product “SHA” was 5.802 × 10−13 at an average time of 90 s, while that of real-time product “CNT” was 4.844 × 10−13, which is better than the post-processed product “SHA” but slightly worse than the other six post-processed products. This may be because the sampling interval of “SHA” precise satellite clock product was as long as 5 min, which is much longer than that for other post-processed products (30 s) and real-time products (5 s). When employing the product “SHA” for PPP processing, the interpolation errors of satellite clock offsets will be larger. Due to the difference in accuracy between real-time products and post-processed products, the frequency stability of “CNT” results gradually deteriorated with the increase of average time, while that of “SHA” results became close to other post-processed products. In terms of the long-term frequency stability (e.g., at an average time of 10,000 s), the “CNT” results were obviously worse than those of the seven post-processed products.
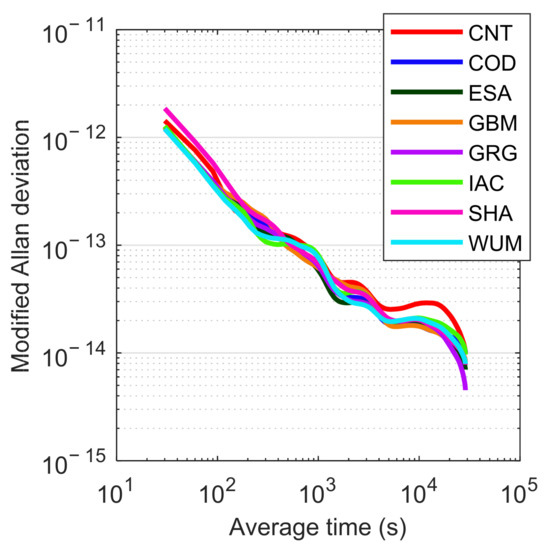
Figure 12.
MDEV of the time link BRUX-KOKB derived with eight different precise products on DOY 248, 2021.
Figure 13 exhibits the mean MDEV values for 17 time links derived from Galileo five-frequency PPP with eight different precise products over a week from DOY 248 to 254, 2021. For simplicity, the numbers of 102, 103, and 104 in the figure refer to the average time of 90, 990, and 9990 s, respectively. When the average time was less than 1000 s, the frequency stability of “SHA” post-processed results was significantly lower than that of other precise products for most of the cases, even in comparison with “CNT” real-time results, while that of “CNT” results was slightly worse than the other six post-processed products. In contrast, regarding the long-term frequency stability, the results of real-time product “CNT” were slightly worse than those of all the seven post-processed products. Table 5 further lists the mean MDEV values over all the time links with eight different precise products at an average time of 90, 990, and 9990 s. When the average time was 90 s, the average MDEV of “SHA” post-processed results was 8.539 × 10−13, which is much larger than that of other precise products, while that of “CNT” real-time results was 6.648 × 10−13. Except for the above two products, the difference of frequency stability among the other six post-processed precise products was confined to 1.4 × 10−14. The average MDEV of “COD” results was the smallest with a value of 6.125 × 10−13, while that of “ESA” results was the largest, which was 6.257 × 10−13. When the average time was 990 s, there was still a big gap between “SHA” and other precise products in terms of MDEV statistics. When the average time was further increased to 9990 s, the frequency stability of “ESA”, “GBM”, and “GRG” results was slightly better than that of the other four post-processed precise products, which was smaller than 3.301 × 10−14, while the frequency stability of real-time product “CNT” was the worst, with an average MDEV of 3.541 × 10−14.
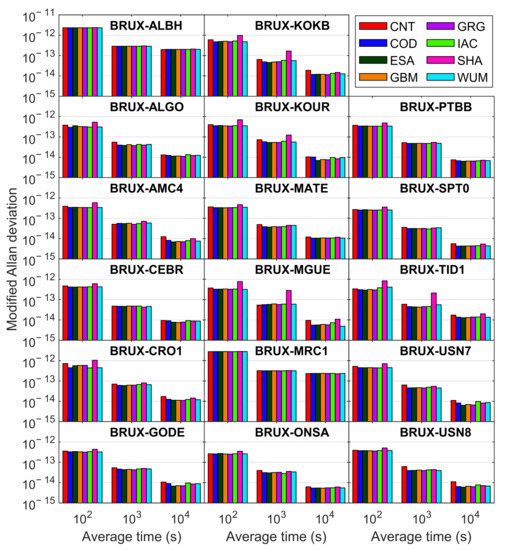
Figure 13.
Mean MDEV values for 17 time links derived from Galileo five-frequency PPP with eight different precise products over a week from DOY 248 to 254, 2021.

Table 5.
Mean MDEV values over all the time links with eight different precise products at an average time of 90, 990, and 9990 s.
According to the above analysis, in terms of time transfer accuracy, the results of real-time product “CNT” showed a worse performance compared with those of post-processed products, while the corresponding accuracy difference among the seven post-processed products was not obvious. As to frequency stability, both the short-term and long-term performance of “CNT” real-time results were slightly worse than those of the post-processed products (except for “SHA”). Due to the lower sampling rate of satellite clock offset products, the “SHA” post-processed results had poor short-term frequency stability but satisfied long-term frequency stability. The short-term frequency stability of “COD”, “GRG”, and “WUM” products was slightly better than that of other post-processed products, while the “ESA”, “GBM”, and “GRG” products slightly outperformed other post-processed products in terms of the long-term frequency stability. Therefore, when the Galileo five-frequency PPP is used for short-term or long-term time transfer, these precise products can be given priority.
3.5. Time Transfer Results with Galileo Dual-, Triple-, Four- and Five-Frequency UC PPP
To investigate the contribution of Galileo multi-frequency observations to PPP time transfer, the E1/E5A dual-frequency (UC-2), E1/E5A/E5B triple-frequency (UC-3), E1/E5A/E5B/E6 four-frequency (UC-4), and E1/E5A/E5B/E6/E5 (A+B) five-frequency (UC-5) integration were employed to conduct the Galileo UC PPP time transfer. The post-processed precise product “GBM” was used for data processing. Figure 14 illustrates three time links (BRUX-SPT0, BRUX-KOKB, and BRUX-USN7) derived from Galileo dual-, triple-, four-, and five-frequency UC PPP solutions on DOY 248, 2021. To ensure that only the fully converged results were involved in the analysis, the results in the first four hours were excluded. It was seen that there was no significant difference in the time transfer results among the four different frequency combination cases. Figure 15 shows the differences of the time links between Galileo UC PPP estimates and IGS final products on DOY 248, 2021, and Table 6 provides the corresponding STD statistics. The joint use of more frequencies did not obviously improve the accuracy of time transfer compared with the results of dual-frequency UC PPP. Figure 16 presents the MDEV of the time link BRUX-KOKB. It was indicated that there was still no significant difference in the frequency stability of time transfer among the four different frequency combination cases.
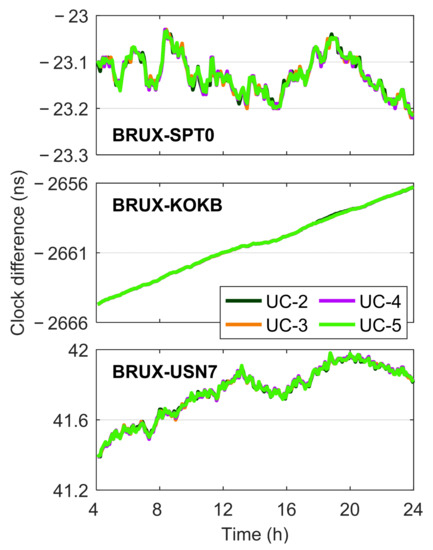
Figure 14.
Three time links derived from Galileo dual-, triple-, four-, and five-frequency UC PPP solutions on DOY 248, 2021.
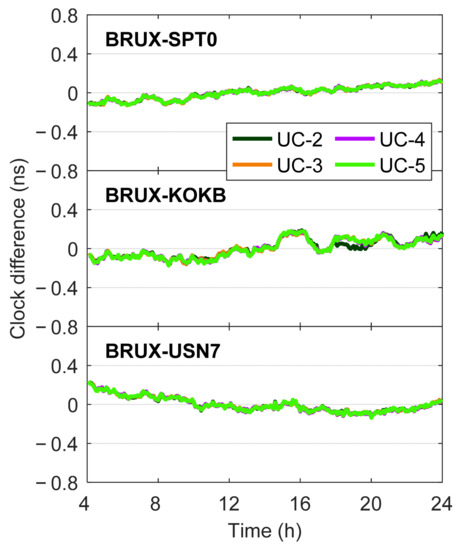
Figure 15.
Differences of the time links between Galileo UC PPP estimates with four different multi-frequency combinations and IGS final products on DOY 248, 2021.

Table 6.
STD value of differences of the time links between Galileo UC PPP estimates and IGS final products on DOY 248, 2021.
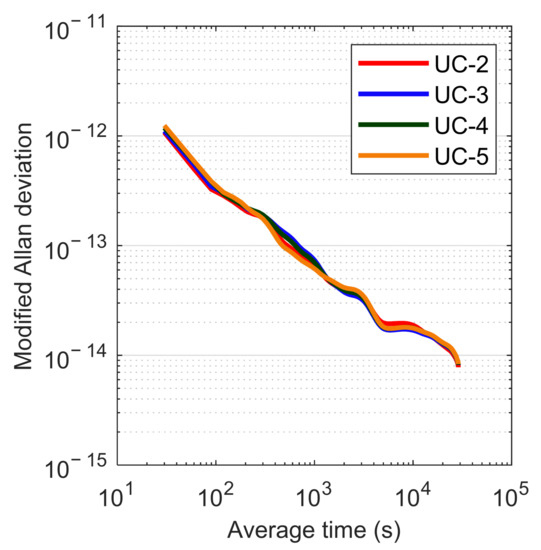
Figure 16.
MDEV of the time link BRUX-KOKB derived from Galileo dual-, triple-, four-, and five-frequency UC PPP on DOY 248, 2021.
Figure 17 shows the mean MDEV values for 17 time links generated with Galileo dual-, triple-, four-, and five-frequency UC PPP over a week from DOY 248 to 254, 2021. Except for the time link BRUX-MRC1, the results of dual-, triple-, four-, and five-frequency cases showed consistent levels in terms of MDEV values. Table 7 further lists the mean MDEV values over 16 time links (except for BRUX-MRC1) for different frequency integration cases at an average time of 90, 990, and 9990 s. In terms of short-term frequency stability (90 s), the UC-5 case slightly outperformed other multi-frequency cases, with a statistic of 4.885 × 10−13, while those of other three cases varied within the range of 4.944 × 10−13 to 4.983 × 10−13. Regarding the long-term frequency stability (9990 s), there was no significant difference among the four different frequency combination cases, all of which were close to 2.03 × 10−14.
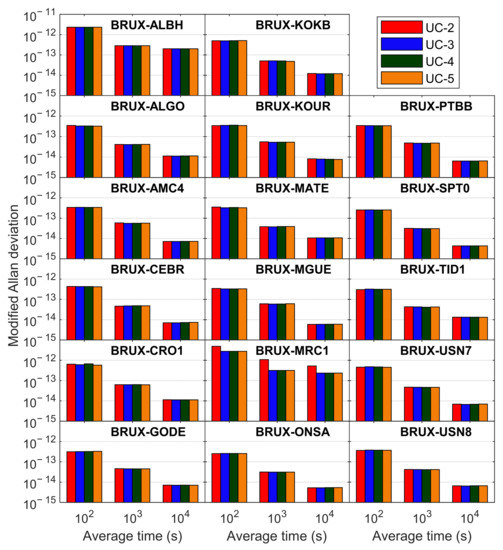
Figure 17.
Mean MDEV values for 17 time links generated with Galileo dual-, triple-, four-, and five-frequency UC PPP over a week from DOY 248 to 254, 2021.

Table 7.
Mean MDEV values over 16 time links (except for BRUX-MRC1) generated with Galileo dual-, triple-, four-, and five-frequency UC PPP at an average time of 90, 990, and 9990 s.
For the time link BRUX-MRC1, the MDEV results of time transfer with UC-2 were dramatically worse than those of the cases employing more frequencies. It was found that there was a significant difference between the dual-frequency PPP solutions and other multi-frequency PPP solutions on DOY 249, 2021. Figure 18 shows the MDEV of the time link BRUX-MRC1 derived from Galileo dual-, triple-, four-, and five-frequency UC PPP on DOY 249, 2021. It was seen that the MDEV results of UC-3, UC-4, and UC-5 were consistent, but far different from those of UC-2. The reason for this phenomenon is that the quality of observations at station MRC1 on DOY 249, 2021 was poor, with frequent cycle slips and loss of lock of satellite signals on the E1 and E5A frequencies. This leads to the unreliable time transfer results of dual-frequency PPP, and the frequency stability at an average time of 90 and 9990 s was only 2.092 × 10−11 and 2.160 × 10−12, respectively. By contrast, the corresponding frequency stability reached approximately 6.06 × 10−12 and 1.14 × 10−13 for other multi-frequency cases, which was much better than that of dual-frequency PPP.
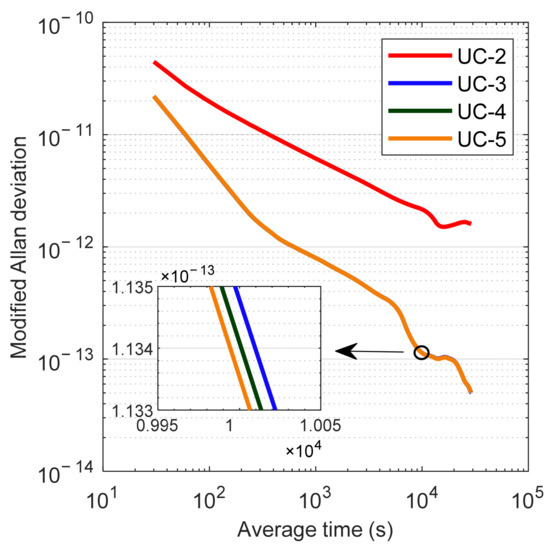
Figure 18.
MDEV of the time link BRUX-MRC1 derived from Galileo dual-, triple-, four-, and five-frequency UC PPP on DOY 249, 2021.
4. Discussion
The obtained results indicated that both the accuracy and frequency stability of time transfer were at a similar level for the dual-frequency and multi-frequency PPP under an open sky environment, namely under the observing conditions with no signal blockage around the receiver. However, in the constrained visibility environments (poor signal quality), the time transfer results of multi-frequency PPP were more reliable. This is because the multi-frequency observations can be regarded as the repeated measurement for the geometric range between the receiver and the satellite, and there is a strong correlation among them. When the observation conditions were ideal, the observations on all frequencies were of high quality, and the benefits from the repeated measurement were limited. Thus, the time transfer results of multi-frequency and dual-frequency PPP were almost the same. When the signal quality degrades due to various interference (surrounding the stations), the joint use of more available observations is beneficial to the cycle slip detection and data quality control, and thus the negative effects of cycle slips and gross errors on the PPP processing can be effectively weakened. Therefore, the time transfer results of multi-frequency PPP are expected to be much better than those of dual-frequency PPP in harsh environments.
5. Conclusions
Based on 18 MGEX stations equipped with high-performance hydrogen clocks, we rigorously investigated the precise time transfer with Galileo five-frequency UC PPP, including the effects of different weighting strategies (a priori method and a posterior method), of different IFB dynamic models (white noise process, random walk process and constants), and of precise products from different ACs, as well as the contribution of multi-frequency integration. After employing the HVCE a posterior weighting method, the accuracy of time transfer in the first several hours was significantly improved, and the short-term frequency stability (at an average time shorter than 100 s) could be improved by 28.9%–37.6%. The IFB dynamic models had little influence on time transfer results. The time transfer accuracy of Galileo five-frequency UC PPP with the real-time product “CNT” was 0.253 ns, while that of all the seven post-processed products was better than 0.1 ns. In terms of the short-term frequency stability, the PPP time transfer with the post-processed product “SHA” showed the worst performance, with the MDEV of 8.539 × 10−13 at an average time of 90 s, which was even worse than that of the real-time product “CNT” (6.648 × 10−13), while that of other post-processed products ranged from 6.125 × 10−13 to 6.257 × 10−13. The PPP time transfer with the real-time product “CNT” achieved the worst long-term frequency stability, with the MDEV of 3.541 × 10−14 at an average time of 9990 s, which was inferior to the post-processed products (3.283 × 10−14 to 3.459 × 10−14). Usually, the time transfer results of multi-frequency PPP and dual-frequency PPP are basically consistent in terms of accuracy and frequency stability. When the signal quality becomes poor (e.g., in harsh environments), the time transfer results of multi-frequency PPP are more reliable because of the higher redundancy of observations.
Author Contributions
Conceptualization, L.P.; methodology, L.P.; software, Z.Z.; validation, Z.Z.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Z.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, L.P.; visualization, Z.Z.; supervision, L.P.; project administration, L.P.; funding acquisition, L.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Key Laboratory of Geo-Information Engineering (Grant No. SKLGIE2019–Z–1–1), National Natural Science Foundation of China (Grant No. 41904030), and Natural Science Foundation of Hunan Province, China (Grant No. 2020JJ5706).
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found from MGEX.
Acknowledgments
The contribution of data from MGEX is appreciated.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ouyang, M.; Li, J.; Li, W.; Ge, Y.; Zhu, X.; Chen, Z.; Dai, Z. Research on Time and Frequency Transfer during PPP Convergence with Parameters Correlation Comparison. Measurement 2021, 173, 108597. [Google Scholar] [CrossRef]
- Jiang, Z.; Petit, G. Combination of TWSTFT and GNSS for Accurate UTC Time Transfer. Metrologia 2009, 46, 305–314. [Google Scholar] [CrossRef]
- Defraigne, P.; Aerts, W.; Pottiaux, E. Monitoring of UTC(k)’s Using PPP and IGS Real-Time Products. GPS Solut. 2015, 19, 165–172. [Google Scholar] [CrossRef]
- Petit, G.; Jiang, Z. Precise Point Positioning for TAI Computation. Int. J. Navig. Obs. 2008, 2008, 562878. [Google Scholar] [CrossRef]
- Petit, G. Sub-10–16 Accuracy GNSS Frequency Transfer with IPPP. GPS Solut. 2021, 25, 22. [Google Scholar] [CrossRef]
- Petit, G.; Kanj, A.; Loyer, S.; Delporte, J.; Mercier, F.; Perosanz, F. 1 × 10−16 Frequency Transfer by GPS PPP with Integer Ambiguity Resolution. Metrologia 2015, 52, 301–309. [Google Scholar] [CrossRef]
- Ge, Y.; Qin, W.; Cao, X.; Zhou, F.; Wang, S.; Yang, X. Consideration of GLONASS Inter-Frequency Code Biases in Precise Point Positioning (PPP) International Time Transfer. Appl. Sci. 2018, 8, 1254. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Shen, W.; Cai, C.; Li, L.; Wang, L.; Ning, A.; Shen, Z. Comparison and Evaluation of Carrier Phase PPP and Single Difference Time Transfer with Multi-GNSS Ambiguity Resolution. GPS Solut. 2022, 26, 58. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Zhang, R.; Gao, Y.; Cai, H. Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations. Remote Sens. 2018, 10, 324. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Zhou, F.; Dai, P.; Qin, W.; Wang, S.; Yang, X. Precise Point Positioning Time Transfer with Multi-GNSS Single-Frequency Observations. Measurement 2019, 146, 628–642. [Google Scholar] [CrossRef]
- Ge, Y.; Dai, P.; Qin, W.; Yang, X.; Zhou, F.; Wang, S.; Zhao, X. Performance of Multi-GNSS Precise Point Positioning Time and Frequency Transfer with Clock Modeling. Remote Sens. 2019, 11, 347. [Google Scholar] [CrossRef] [Green Version]
- Lyu, D.; Zeng, F.; Ouyang, X. Time Transfer Algorithm Using Multi-GNSS PPP with Ambiguity Resolution. Chin. Astron. Astrophys. 2020, 44, 371–382. [Google Scholar]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and Performance Analysis of Precise Time Transfer Based on BDS Triple-Frequency Un-Combined Observations. J. Geod. 2019, 93, 837–847. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Triple-Frequency Carrier Phase Precise Time and Frequency Transfer Models for BDS-3. GPS Solut. 2019, 23, 86. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Gao, Y.; Zhang, R.; Han, J. Performance of Galileo Precise Time and Frequency Transfer Models Using Quad-Frequency Carrier Phase Observations. GPS Solut. 2020, 24, 40. [Google Scholar] [CrossRef]
- Ge, Y.; Cao, X.; Shen, F.; Yang, X.; Wang, S. BDS-3/Galileo Time and Frequency Transfer with Quad-Frequency Precise Point Positioning. Remote Sens. 2021, 13, 2704. [Google Scholar] [CrossRef]
- Prochniewicz, D.; Grzymala, M. Analysis of the Impact of Multipath on Galileo System Measurements. Remote Sens. 2021, 13, 2295. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Liu, G.; Xie, W.; Guo, F.; Yuan, Y.; Zhang, K.; Feng, G. The Phase and Code Biases of Galileo and BDS-3 BOC Signals: Effect on Ambiguity Resolution and Precise Positioning. J. Geod. 2020, 94, 9. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Galileo Status: Orbits, Clocks, and Positioning. GPS Solut. 2017, 21, 319–331. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of Differential Code Biases with Multi-GNSS Observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Satirapod, C.; Luansang, M. Comparing Stochastic Models Used in GPS Precise Point Positioning Technique. Surv. Rev. 2008, 40, 188–194. [Google Scholar] [CrossRef]
- Gao, Z.; Shen, W.; Zhang, H.; Ge, M.; Niu, X. Application of Helmert Variance Component Based Adaptive Kalman Filter in Multi-GNSS PPP/INS Tightly Coupled Integration. Remote Sens. 2016, 8, 553. [Google Scholar] [CrossRef]
- Li, M.; Nie, W.; Xu, T.; Rovira-Garcia, A.; Fang, Z.; Xu, G. Helmert Variance Component Estimation for Multi-GNSS Relative Positioning. Sensors 2020, 20, 669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Xu, T.; Song, L. Robust Estimation of Variance Components with Application in Global Positioning System Network Adjustment. J. Surv. Eng. 2005, 131, 107–112. [Google Scholar] [CrossRef]
- European Global Navigation Satellite Systems Agency. The Current Constellation of the Galileo. Available online: https://www.gsc-europa.eu/system-service-status/constellation-information (accessed on 20 April 2022).
- Zhang, P.; Tu, R.; Gao, Y.; Zhang, R.; Liu, N. Improving the Performance of Multi-GNSS Time and Frequency Transfer Using Robust Helmert Variance Component Estimation. Sensors 2018, 18, 2878. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).