Analysis of Two Convective Storms Using Polarimetric X-Band Radar and Satellite Data
Abstract
1. Introduction
2. Data
2.1. Milešovka Meteorological Observatory
2.2. FURUNO X-Band Weather Radar and Its Data
- R [mm/h]: Rainfall intensity.
- Zh [dBZ]: Reflectivity intensity factor of horizontal polarization wave.
- Zh_corr [dBZ]: Attenuation corrected Zh of the horizontal polarity data.
- V [m/s]: Doppler velocity.
- Zdr [dB]: Differential reflectivity.
- Zdr_corr [dB]: Corrected differential reflectivity.
- Kdp [deg/km]: Specific differential phase.
- Φdp [deg]: Differential Phase Shift (cross polarization).
- Rhohv: Co-polar correlation coefficient.
- W [m/s]: Doppler velocity spectrum width.
- (i).
- Dry snow or ice cannot be identified within the ML;
- (ii).
- Below the ML, only rain, graupel, and hail can be detected;
- (iii).
- Wet snow cannot occur above the ML;
- (iv).
- If there is dry snow above the ML, then there should be wet snow in the ML;
- (v).
- If hail occurs below the ML with no connection to hail above the ML, then the classification is changed to rain. Specifically, this rule tests whether graupel/hail occurs at (i, j), where i is the horizontal coordinate and j the vertical coordinate (oriented upward). If it does, then graupel/hail must occur at at least one point (I − 1, j + 1), (i, j + 1), and (i + 1, j + 1) as well.
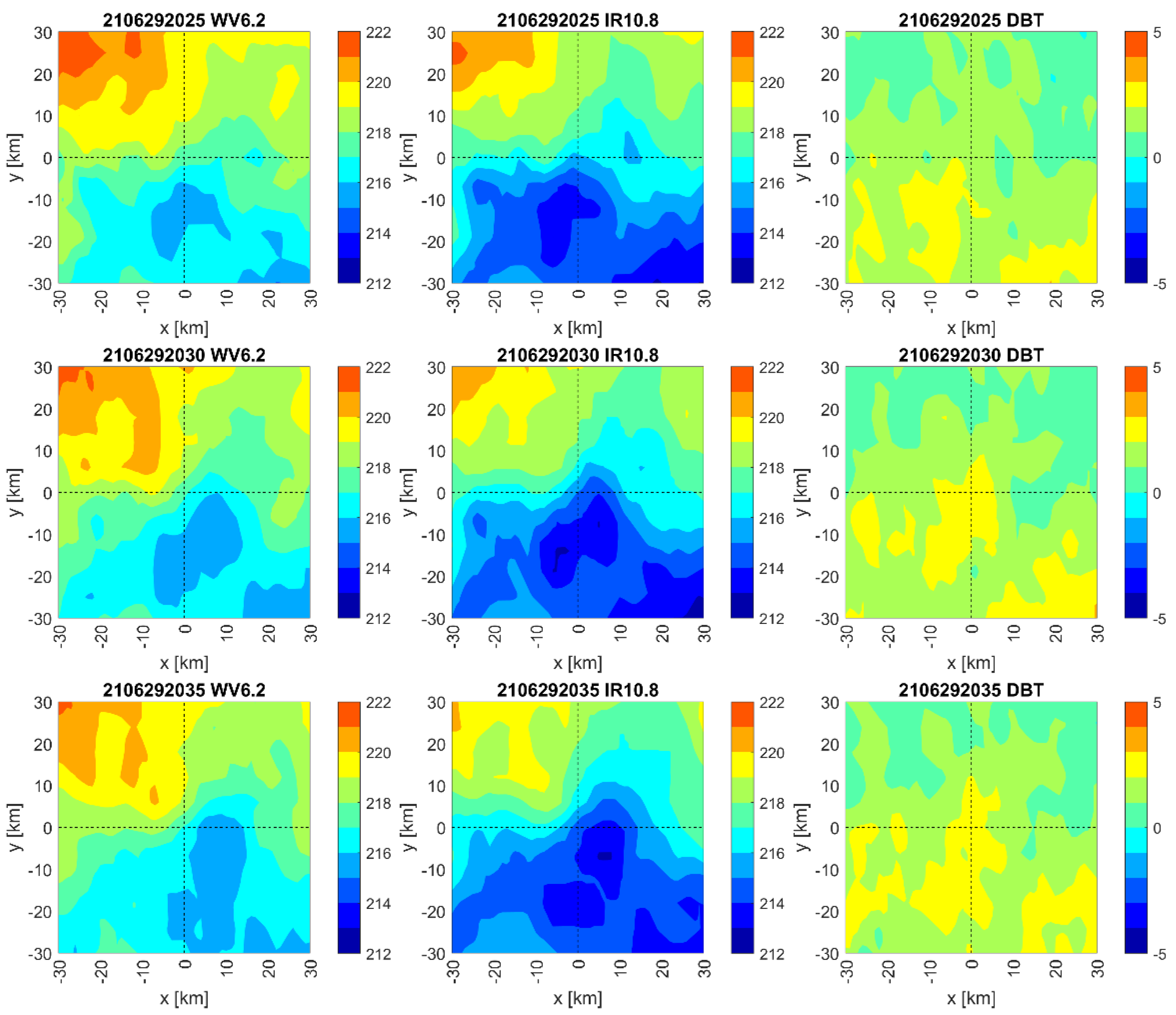
2.3. Satellite Data Meteosat Second Generation
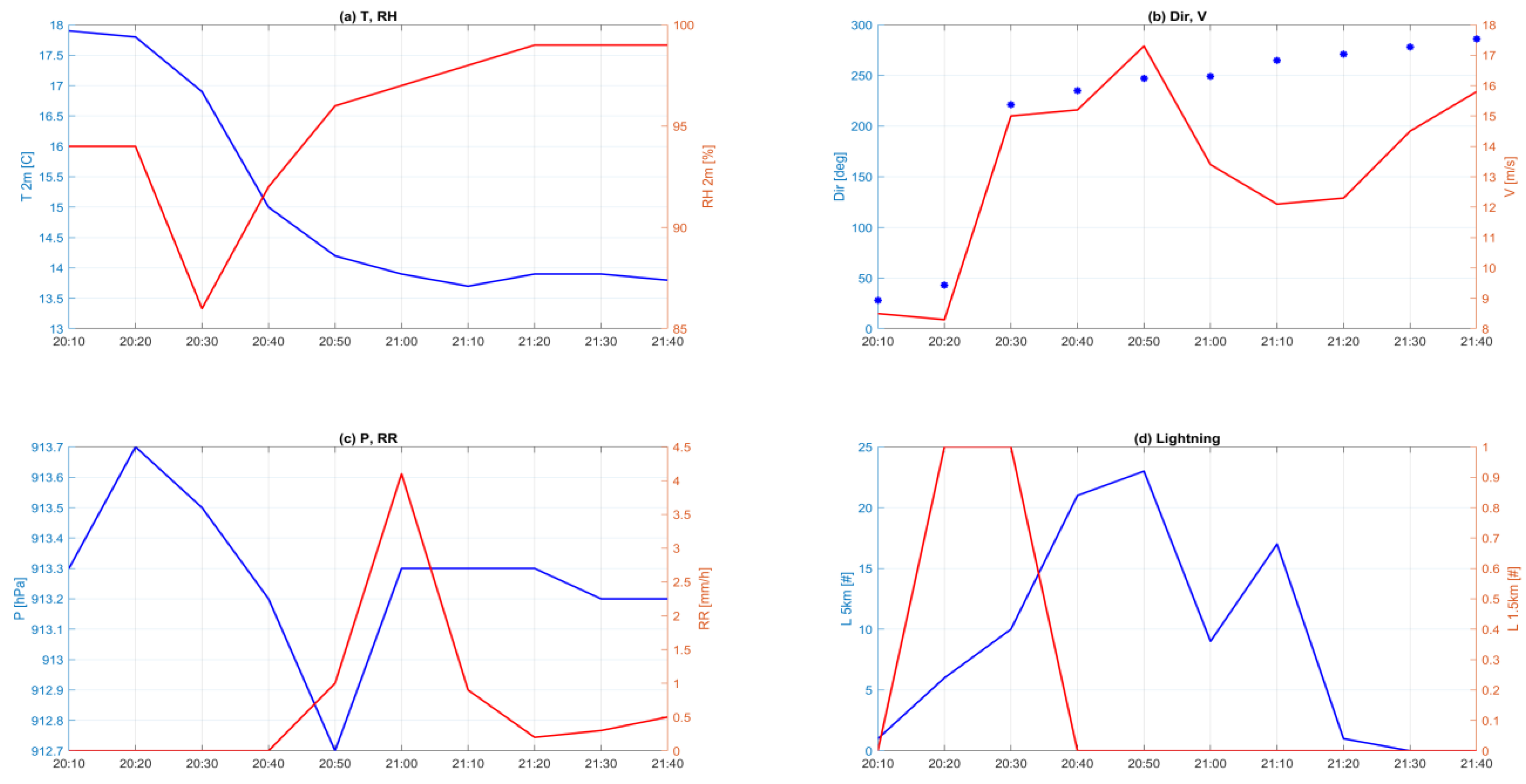
2.4. Lightning Data and Other Complementary Data
3. Results
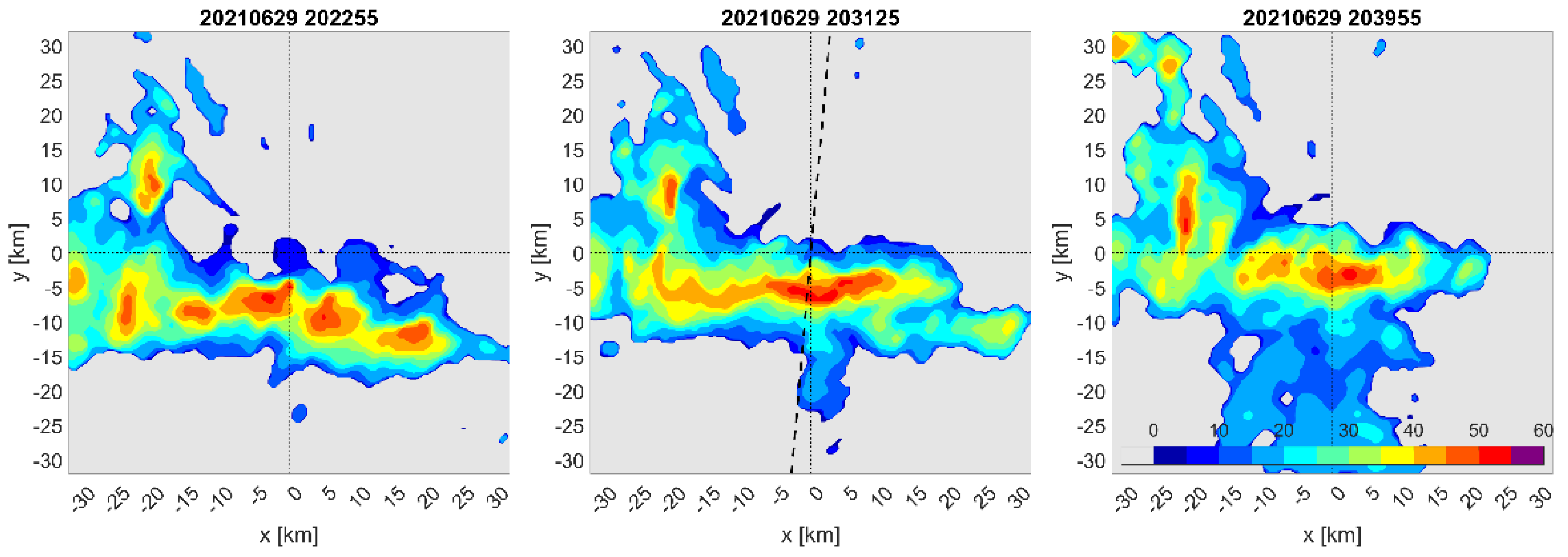
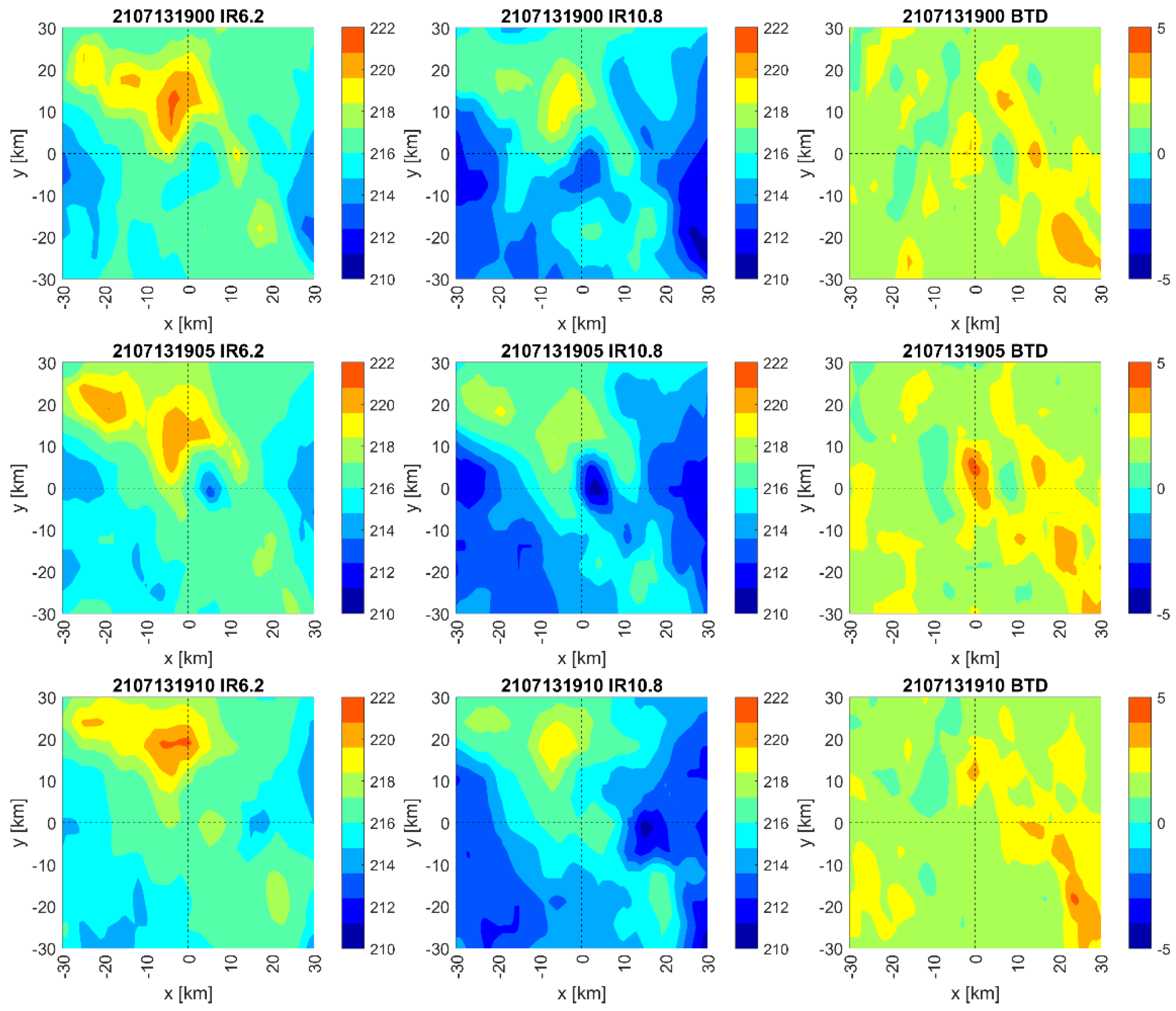
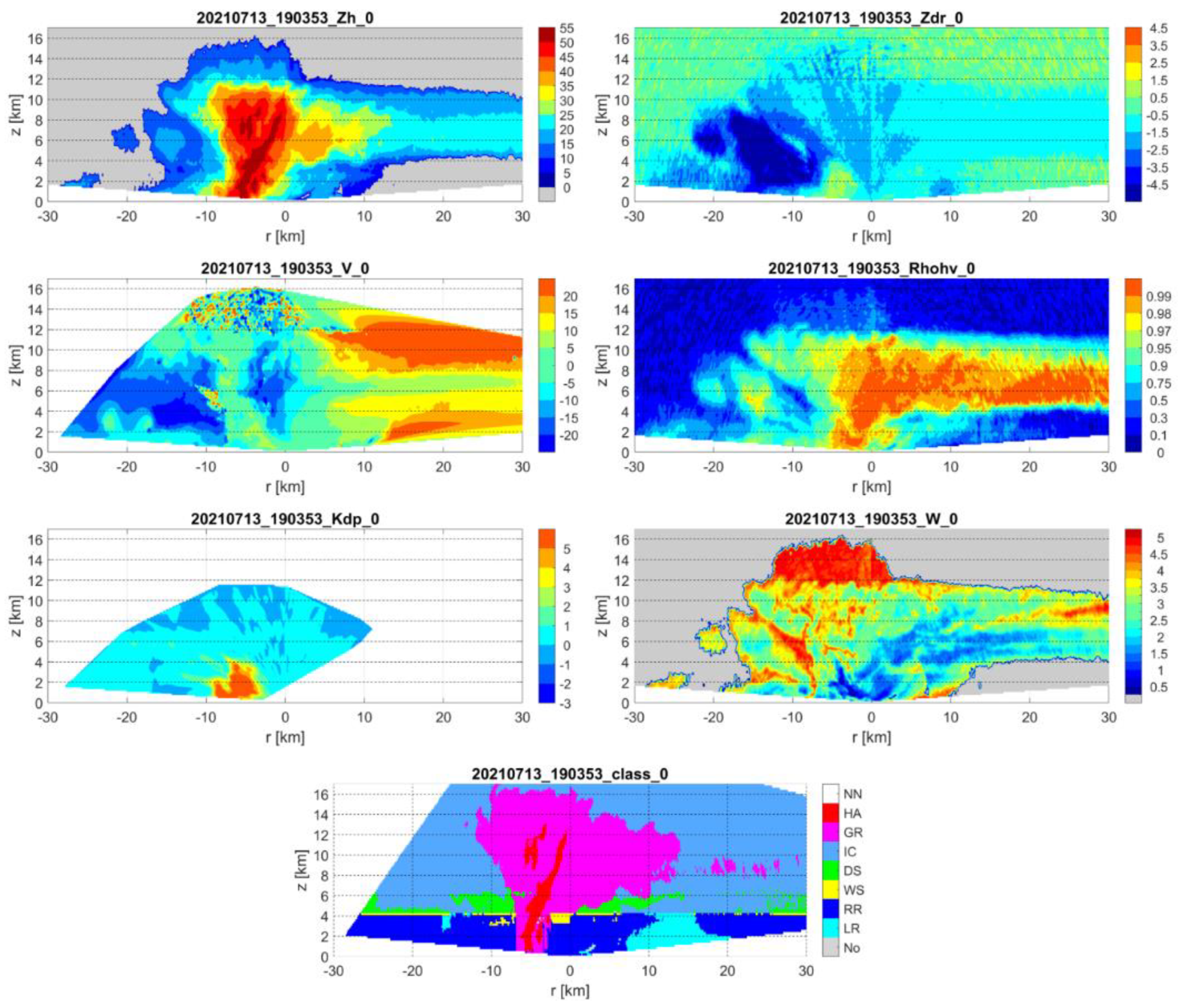
3.1. 29 June 2021
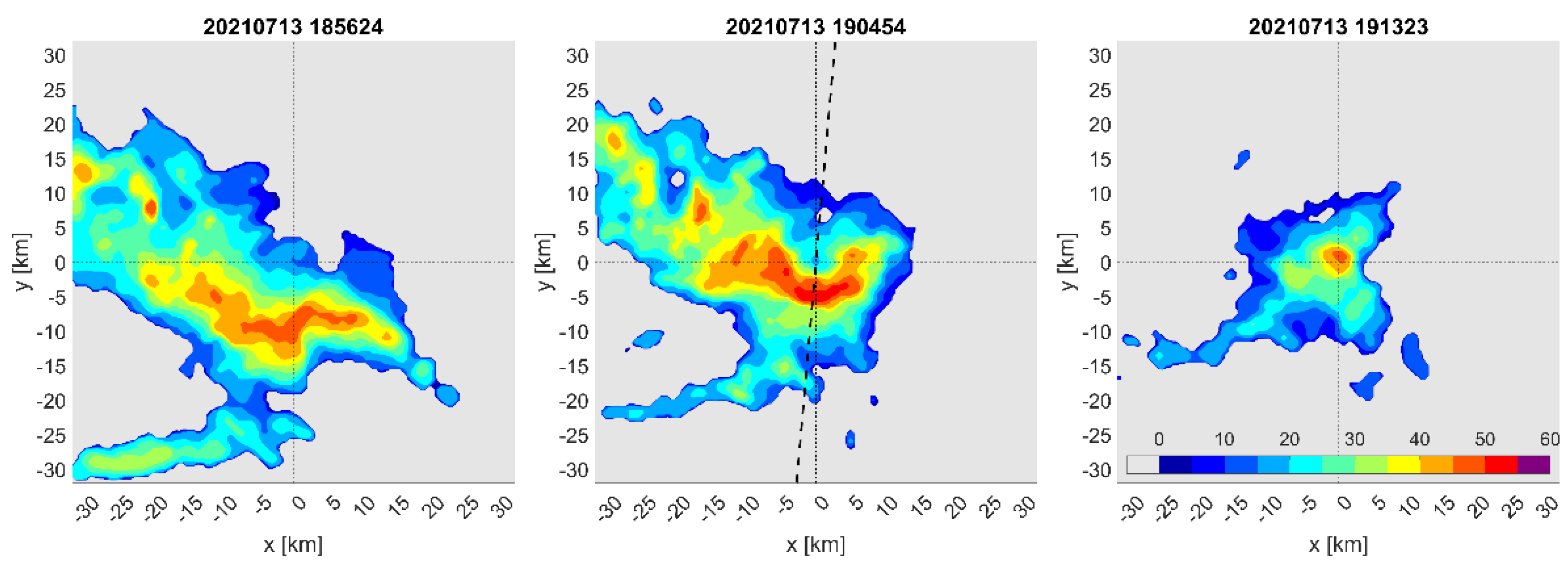
3.2. 13 July 2021
4. Discussion
5. Conclusions
- The attenuation of X-band radar measurements is noticeable in PPI scans and partly in RHI scans. The attenuation is visible even when the attenuation correction is applied to Zh and Zdr. Attenuation is also visible in Rhohv, where the correction has not yet been applied. The results show that the attenuation correction should be considered;
- Although the radar measurements are contaminated by attenuation, they give information about the cloud structure. However, the measurements should be interpreted with caution;
- Radial velocity measurements indicate a strongly turbulent character of the flow in the upper part of the plume. This is particularly evident in the extreme storm of 13 July 2021;
- Radar measurements of the upper part of the cloud cover are consistent with the data measured by the Meteosat Second Generation satellite;
- The hydrometeor classification algorithm that we call XCLASS, developed by modifying a previously published procedure, to a large extent removes the shortcomings of the original algorithm and, subjectively, gives more acceptable results;
- Analysis of two convective storms showed several erroneous measurements occurring near and above the radar. This problem is being addressed; however, it does not affect the results and the use of radar data for convective cloud research.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. We Present here all Parameter Values Needed for the Application of XCLASS Algorithm
| Hydrometeor | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| Rain | −4 | −0.5 | 50 | 50 |
| Wet snow | −5 | −2.0 | 4 | 7 |
| Dry snow | −15 | −10.0 | 0 | 3 |
| Ice | −75 | −70.0 | −10 | −3 |
| Graupel/Hail | −90 | −20.0 | 20 | 40 |
| Zh [dBZ] | R1 | R2 | W1 | W2 | S1 | S2 | I1 | I2 | H1 | H2 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0–2.5 | −0.66 | 0.22 | - | - | - | - | - | - | - | - |
| 2.5–5 | −0.66 | 0.22 | - | - | - | - | −0.44 | 0.66 | - | - |
| 5–7.5 | −0.66 | 0.22 | - | - | - | - | −0.66 | 0.66 | - | - |
| 7.5–10 | −0.66 | 0.22 | - | - | - | - | −0.66 | 0.66 | - | - |
| 10–12.5 | −0.66 | 0.22 | - | - | - | - | −0.66 | 0.66 | - | - |
| 12.5–15 | −0.66 | 0.22 | - | - | - | - | −0.66 | 0.66 | - | - |
| 15–17.5 | −0.66 | 0.22 | - | - | 0.22 | 0.22 | −0.66 | 0.66 | - | - |
| 17.5–20 | −0.66 | 0.22 | - | - | −0.22 | 0.66 | −0.66 | 0.66 | - | - |
| 20–22.5 | −0.66 | 0.22 | 0.88 | 1.10 | −0.44 | 0.88 | −0.44 | 0.66 | - | - |
| 22.5–25 | −0.66 | 0.22 | 0.22 | 1.32 | −0.44 | 0.44 | −0.44 | 0.44 | - | - |
| 25–27.5 | −0.66 | 0.22 | 0.22 | 1.32 | −0.44 | 0.88 | - | - | - | - |
| 27.5–30 | −0.66 | 0.22 | 0.22 | 1.32 | −0.44 | 0.88 | - | - | - | - |
| 30–32.5 | −0.44 | 0.22 | 0.22 | 1.32 | −0.44 | 0.88 | - | - | - | - |
| 32.5–35 | −0.44 | 0.44 | 0.22 | 1.32 | −0.44 | 0.88 | - | - | - | - |
| 35–37.5 | −0.44 | 0.44 | 0.22 | 1.32 | −0.44 | 0.88 | - | - | - | - |
| 37.5–40 | −0.44 | 0.44 | 0.22 | 1.32 | −0.44 | 0.88 | - | - | - | - |
| 40–42.5 | −0.44 | 0.44 | 0.22 | 1.32 | −0.44 | 0.88 | - | - | - | - |
| 42.5–45 | −0.44 | 0.66 | 0.22 | 1.32 | −0.22 | 0.66 | - | - | - | - |
| 45–47.5 | −0.22 | 0.88 | 0.22 | 1.32 | - | - | - | - | - | - |
| 47.5–50 | 0.00 | 1.32 | 0.44 | 1.32 | - | - | - | - | −0.66 | 2.86 |
| 50–52.5 | 0.44 | 2.20 | - | - | - | - | - | - | −0.66 | 3.08 |
| 52.5–55 | 1.32 | 3.30 | - | - | - | - | - | - | −0.66 | 3.30 |
| 55–57.5 | 3.08 | 5.28 | - | - | - | - | - | - | −0.66 | 3.52 |
| 57.5–60 | 4.62 | 5.28 | - | - | - | - | - | - | −0.66 | 3.74 |
| 60–62.5 | - | - | - | - | - | - | - | - | −0.66 | 3.74 |
| 62.5–65 | - | - | - | - | - | - | - | - | −0.66 | 3.96 |
| 65–67.5 | - | - | - | - | - | - | - | - | −0.66 | 4.18 |
| 67.5–70 | - | - | - | - | - | - | - | - | −0.66 | 4.40 |
| 70–99 | - | - | - | - | - | - | - | - | −0.66 | 4.62 |
| Zh [dBZ] | R1 | R2 | W1 | W2 | S1 | S2 | I1 | I2 | H1 | H2 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0–2.5 | 0.97 | 1.00 | - | - | - | - | - | - | - | - |
| 2.5–5 | 0.97 | 1.00 | - | - | - | - | - | - | - | - |
| 5–7.5 | 0.97 | 1.00 | - | - | - | - | 0.92 | 0.99 | - | - |
| 7.5–10 | 0.97 | 1.00 | - | - | - | - | 0.92 | 0.99 | - | - |
| 10–12.5 | 0.97 | 1.00 | - | - | - | - | 0.92 | 0.99 | - | - |
| 12.5–15 | 0.97 | 1.00 | - | - | - | - | 0.92 | 0.99 | - | - |
| 15–17.5 | 0.97 | 1.00 | - | - | 0.96 | 0.97 | 0.92 | 0.99 | - | - |
| 17.5–20 | 0.97 | 1.00 | - | - | 0.93 | 0.99 | 0.92 | 0.99 | - | - |
| 20–22.5 | 0.97 | 1.00 | 0.89 | 0.92 | 0.92 | 0.99 | 0.93 | 0.99 | - | - |
| 22.5–25 | 0.97 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | 0.94 | 0.98 | - | - |
| 25–27.5 | 0.97 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | - | - | - | - |
| 27.5–30 | 0.96 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | - | - | - | - |
| 30–32.5 | 0.96 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | - | - | - | - |
| 32.5–35 | 0.95 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | - | - | - | - |
| 35–37.5 | 0.95 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | - | - | - | - |
| 37.5–40 | 0.95 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | - | - | - | - |
| 40–42.5 | 0.95 | 1.00 | 0.86 | 0.96 | 0.92 | 0.99 | - | - | - | - |
| 42.5–45 | 0.95 | 1.00 | 0.86 | 0.96 | 0.93 | 0.99 | - | - | - | - |
| 45–47.5 | 0.95 | 1.00 | 0.86 | 0.96 | - | - | - | - | - | - |
| 47.5–50 | 0.94 | 1.00 | 0.88 | 0.95 | - | - | - | - | 0.80 | 1.00 |
| 50–52.5 | 0.94 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 52.5–55 | 0.94 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 55–57.5 | 0.94 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 57.5–60 | 0.94 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 60–62.5 | 0.94 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 62.5–65 | 0.94 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 65–67.5 | 0.95 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 67.5–70 | 0.96 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| 70–99 | 0.96 | 1.00 | - | - | - | - | - | - | 0.80 | 1.00 |
| Zh [dBZ] | R1 | R2 | W1 | W2 | S1 | S2 | I1 | I2 | H1 | H2 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0–2.5 | −0.72 | 0.83 | - | - | - | - | - | - | - | - |
| 2.5–5 | −0.72 | 0.83 | - | - | - | - | −0.1 | 0.83 | - | - |
| 5–7.5 | −0.72 | 0.83 | - | - | - | - | −0.1 | 0.83 | - | - |
| 7.5–10 | −0.72 | 0.83 | - | - | - | - | −0.1 | 0.83 | - | - |
| 10–12.5 | −0.72 | 0.83 | - | - | - | - | −0.1 | 0.83 | - | - |
| 12.5–15 | −0.72 | 0.83 | - | - | - | - | −0.1 | 0.83 | - | - |
| 15–17.5 | −0.72 | 0.83 | - | - | 0.21 | 0.21 | −0.1 | 0.83 | - | - |
| 17.5–20 | −0.72 | 1.14 | - | - | −0.41 | 0.52 | −1.34 | 0.52 | - | - |
| 20–22.5 | −0.72 | 1.14 | 1.14 | 2.38 | −0.41 | 0.83 | −1.03 | 0.52 | - | - |
| 22.5–25 | −0.72 | 1.14 | −0.41 | 3 | −0.41 | 0.83 | −1.03 | 0.21 | - | - |
| 25–27.5 | −0.72 | 1.14 | −0.41 | 3 | −0.41 | 0.83 | - | - | - | - |
| 27.5–30 | −0.41 | 1.14 | −0.41 | 3 | −0.41 | 0.83 | - | - | - | - |
| 30–32.5 | −0.41 | 1.45 | −0.41 | 3 | −0.41 | 0.83 | - | - | - | - |
| 32.5–35 | −0.41 | 1.45 | −0.41 | 3 | −0.41 | 0.83 | - | - | - | - |
| 35–37.5 | −0.1 | 1.45 | −0.41 | 3 | −0.41 | 0.83 | - | - | - | - |
| 37.5–40 | −0.1 | 1.76 | −0.41 | 3 | −0.41 | 0.83 | - | - | - | - |
| 40–42.5 | 0.21 | 1.76 | −0.41 | 3 | −0.41 | 0.83 | - | - | - | - |
| 42.5–45 | 0.21 | 2.07 | −0.41 | 3 | −0.41 | 0.52 | - | - | - | - |
| 45–47.5 | 0.52 | 2.07 | −0.1 | 3 | - | - | - | - | - | - |
| 47.5–50 | 0.52 | 2.38 | 0.21 | 2.69 | - | - | - | - | −0.41 | 3 |
| 50–52.5 | 0.83 | 2.69 | - | - | - | - | - | - | −0.41 | 3 |
| 52.5–55 | 1.14 | 2.69 | - | - | - | - | - | - | −0.41 | 3 |
| 55–57.5 | 1.14 | 3 | - | - | - | - | - | - | −0.41 | 3 |
| 57.5–60 | 1.45 | 3 | - | - | - | - | - | - | −0.41 | 3 |
| 60–62.5 | 1.45 | 3 | - | - | - | - | - | - | −0.41 | 2.69 |
| 62.5–65 | 1.76 | 3.31 | - | - | - | - | - | - | −0.41 | 2.38 |
| 65–67.5 | 2.07 | 3.31 | - | - | - | - | - | - | −0.41 | 2.38 |
| 67.5–70 | 2.38 | 3.31 | - | - | - | - | - | - | −0.41 | 2.38 |
| 70–99 | 2.69 | 3.31 | - | - | - | - | - | - | −0.41 | 2.38 |
References
- Brázdil, R.; Chroma, K.; Púčik, T.; Černoch, Z.; Dobrovolný, P.; Dolák, L.; Kotyza, O.; Řezníčková, L.; Taszarek, M. The climatology of significant tornadoes in the Czech Republic. Atmosphere 2020, 11, 689. [Google Scholar] [CrossRef]
- Kašpar, M.; Müller, M.; Kakos, V.; Řezáčová, D.; Sokol, Z. Severe storm in Bavaria, the Czech Republic and Poland on 12–13 July 1984: A statistic- and model-based analysis. Atmos. Res. 2009, 93, 99–110. [Google Scholar] [CrossRef]
- Sokol, Z.; Zacharov, P.; Skripniková, K. Simulation of the storm on 15 August, 2010, using a high resolution COSMO NWP model. Atmos. Res. 2014, 137, 100–111. [Google Scholar] [CrossRef]
- Salek, M.; Brezkova, L.; Novak, P. The use of radar in hydrological modeling in the Czech Republic—Case studies of flash floods. Nat. Hazards Earth Syst. Sci. 2006, 6, 229–236. [Google Scholar] [CrossRef]
- Bliznak, V.; Sokol, Z.; Zacharov, P. Nowcasting of deep convective clouds and heavy precipitation: Comparison study between NWP model simulation and extrapolation. Atmos. Res. 2017, 184, 24–34. [Google Scholar] [CrossRef]
- Orville, R.E.; Maier, M.W.; Mosher, F.R.; Wylie, D.P.; Rust, W.D. The simultaneous display in a severe storm of lightning ground strike locations onto satellite images and radar reflectivity patterns. Bull. Am. Meteorol. Soc. 1981, 62, 1421. [Google Scholar]
- Putsay, M.; Szenyán, I.; Simon, A. Case study of mesoscale convective systems over Hungary on 29 June 2006 with satellite, radar and lightning data. Atmos. Res. 2009, 93, 82–92. [Google Scholar] [CrossRef]
- Matthee, R.; Mecikalski, J.R.; Carey, L.D.; Bitzer, P.M. Quantitative differences between lightning and nonlightning convective Rainfall. Mon. Weather Rev. 2014, 142, 3651–3665. [Google Scholar] [CrossRef]
- Hu, J.; Rosenfeld, D.; Ryzkov, A.; Zhang, P. Synergetic Use of the WSR-88D radars, GOES-R satellites, and lightning networks to study microphysical characteristics of hurricanes. J. Appl. Meteorol. Climatol. 2020, 59, 1051–1068. [Google Scholar] [CrossRef]
- Mulholland, J.P.; Nesbitt, S.W.; Trapp, R.J.; Rasmussen, K.L.; Salio, P.V. Convective storm life cycle and environments near the Sierras de Cordoba, Argentina. Mon. Weather Rev. 2018, 146, 2541–2557. [Google Scholar] [CrossRef]
- Murillo, E.M.; Homeyer, C.R. Severe Hail fall and hailstorm detection using remote sensing observations. J. Appl. Meteorol. Climatol. 2019, 52, 947–970. [Google Scholar] [CrossRef] [PubMed]
- Sandmæl, T.N.; Homeyer, C.R.; Bedka, K.M.; Apke, J.M.; Mecikalski, J.R.; Khlopenkov, K. Evaluating the ability of remote sensing observations to identify significantly severe and potentially tornadic storms. J. Appl. Meteorol. Climatol. 2019, 52, 2569–2590. [Google Scholar] [CrossRef] [PubMed]
- Jones, T.A.; Stensrud, D.; Wicker, L.; Minnis, P.; Palikonda, R. Simultaneous radar and satellite data storm-scale assimilation using an ensemble kalman filter approach for 24 May 2011. Mon. Weather Rev. 2015, 143, 165–194. [Google Scholar] [CrossRef]
- Khan, M.D.; Rabbani, G.; Das, S.; Panda, S.K.; Kabir, A.; Mallik, M.A.K. Physical and dynamical characteristics of thunderstorms over bangladesh based on radar, satellite, upper-air observations, and WRF model simulations. Pure Appl. Geophys. 2021, 178, 3747–3767. [Google Scholar] [CrossRef]
- Manzato, A.; Davolio, S.; Miglietta, M.M.; Puciloa, A.; Setvak, M. 12 September 2012: A supercell outbreak in NE Italy? Atmos. Res. 2015, 153, 98–118. [Google Scholar] [CrossRef]
- Sokol, Z.; Minářová, J.; Novák, P. Classification of hydrometeors using measurements of the Ka-band cloud radar installed at the Milešovka Mountain (Central Europe). Remote Sens. 2018, 10, 1674. [Google Scholar] [CrossRef]
- Sokol, Z.; Popová, J. Differences in cloud radar phase and power in co and cross-channel—indicator of lightning. Remote Sens. 2021, 13, 503. [Google Scholar] [CrossRef]
- Ośródka, K.; Jan Szturc, J. Improvement in algorithms for quality control of weather radar data (RADVOL-QC System). Atmos. Meas. Tech. 2022, 15, 261–277. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Zrnić, D.S. Radar Polarimetry for Weather Observations; Springer: Berlin/Heidelberg, Germany, 2019; Volume 486. [Google Scholar]
- Maesaka, T.; Maki, M.; Iwanami, K.; Tsuchiya, S.; Kieda, K.; Hoshi, A. Operational rainfall estimation by X-band MP radar network in Mlit, Japan. In Proceedings of the 35th Conference on Radar Meteorology, Pittsburgh, PA, USA, 26–30 September 2011; p. 11. [Google Scholar]
- Al-Sakka, H.; Boumahmoud, A.A.; Fradon, B.; Frazier, S.J.; Tabary, P. A new fuzzy logic hydrometeor classification scheme applied to the french X-, C-, and S-band polarimetric radars. J. Appl. Meteorol. Climatol. 2013, 52, 2328–2344. [Google Scholar] [CrossRef]
- Geotis, S.G. Some radar measurements of hailstorms. J. Appl. Meteorol. Climatol. 1963, 2, 270–275. [Google Scholar] [CrossRef][Green Version]
- Schmetz, J.; Tjemkes, S.A.; Gube, M.; Van de Berg, L. Monitoring deep convection and convective overshooting with METEOSAT. Adv. Space Res. 1997, 19, 433–441. [Google Scholar] [CrossRef]
- Setvak, M.; Lindsey, D.T.; Novak, P.; Wang, P.K.; Radova, M.; Kerkmann, J.; Grasso, L.; Su, S.H.; Rabin, R.M.; St’astka, J.; et al. Satellite-observed cold-ring-shaped features atop deep convective clouds. Atmos. Res. 2010, 97, 80–96. [Google Scholar] [CrossRef]
- Bedka, K.M.; Wang, C.; Rogers, R.; Carey, L.D.; Feltz, W.; Kanak, J. Examining deep convective cloud evolution using total lightning, WSR-88D, and GOES-14 super rapid scan datasets. Weather Forecast. 2015, 30, 571–590. [Google Scholar] [CrossRef]
- Bližňák, V.; Sokol, Z. The exploitation of Meteosat Second Generation data for convective storms over the Czech Republic. Atmos. Res. 2012, 103, 60–69. [Google Scholar] [CrossRef]
- Blids, Der Blitz Informationsdienst Von Siemens. Available online: https://new.siemens.com/global/de/produkte/services/blids.html (accessed on 3 August 2021).
- Lane, T.P.; Sharman, R.D.; Clark, T.L.; Hsu, H.-M. An Investigation of turbulence generation mechanisms above deep convection. J. Atmos. Sci. 2003, 60, 1297–1321. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Antenna Polarization | Dual polarimetric (Vertical and Horizontal) Simultaneous transmission/receiving |
| Operating Frequency | 9.4 GHz band |
| Pulse Width | 0.5–50 us |
| Pulse Repetition Frequency (PRF) | 2000 Hz max. |
| Beam Width | 2.7° (both horizontal and vertical beams) |
| Peak Output Power | 100 W (both horizontal and vertical beams) |
| Vertical Scan Angle | −2° to 182° (adjustable) |
| Horizontal Scan Angle | 360°(continuous) |
| Antenna Rotation Speed | 0.5–10 rpm (adjustable) |
| Observation Range | 70 km max |
| Scan Modes | PPI, Volume Scan, Sector PPI, Sector RHI |
| Doppler Speed | From ±40 m/s in |
| Operating Temperature | −10 to +50 °C (Start-up), −25 to +50 °C (In operation) |
| Maximum Wind Survival Speed | 90 m/s |
| Sensitivity-reflectivity | Typ. 22 dBZ@50 km @Q0N 50 µs 2 MHz (SNR = 4 dB) |
| Gain | ≥33.0 dBi |
| Transmitter Type | Solid state |
| Antenna Polarization | Dual polarimetric (Vertical and Horizontal) Simultaneous transmission/receiving |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobotová, G.; Sokol, Z.; Popová, J.; Fišer, O.; Zacharov, P. Analysis of Two Convective Storms Using Polarimetric X-Band Radar and Satellite Data. Remote Sens. 2022, 14, 2294. https://doi.org/10.3390/rs14102294
Bobotová G, Sokol Z, Popová J, Fišer O, Zacharov P. Analysis of Two Convective Storms Using Polarimetric X-Band Radar and Satellite Data. Remote Sensing. 2022; 14(10):2294. https://doi.org/10.3390/rs14102294
Chicago/Turabian StyleBobotová, Gabriela, Zbyněk Sokol, Jana Popová, Ondřej Fišer, and Petr Zacharov. 2022. "Analysis of Two Convective Storms Using Polarimetric X-Band Radar and Satellite Data" Remote Sensing 14, no. 10: 2294. https://doi.org/10.3390/rs14102294
APA StyleBobotová, G., Sokol, Z., Popová, J., Fišer, O., & Zacharov, P. (2022). Analysis of Two Convective Storms Using Polarimetric X-Band Radar and Satellite Data. Remote Sensing, 14(10), 2294. https://doi.org/10.3390/rs14102294







