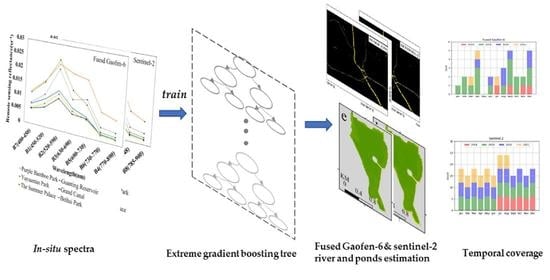
Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Study Area
2.1.2. Field Measurements
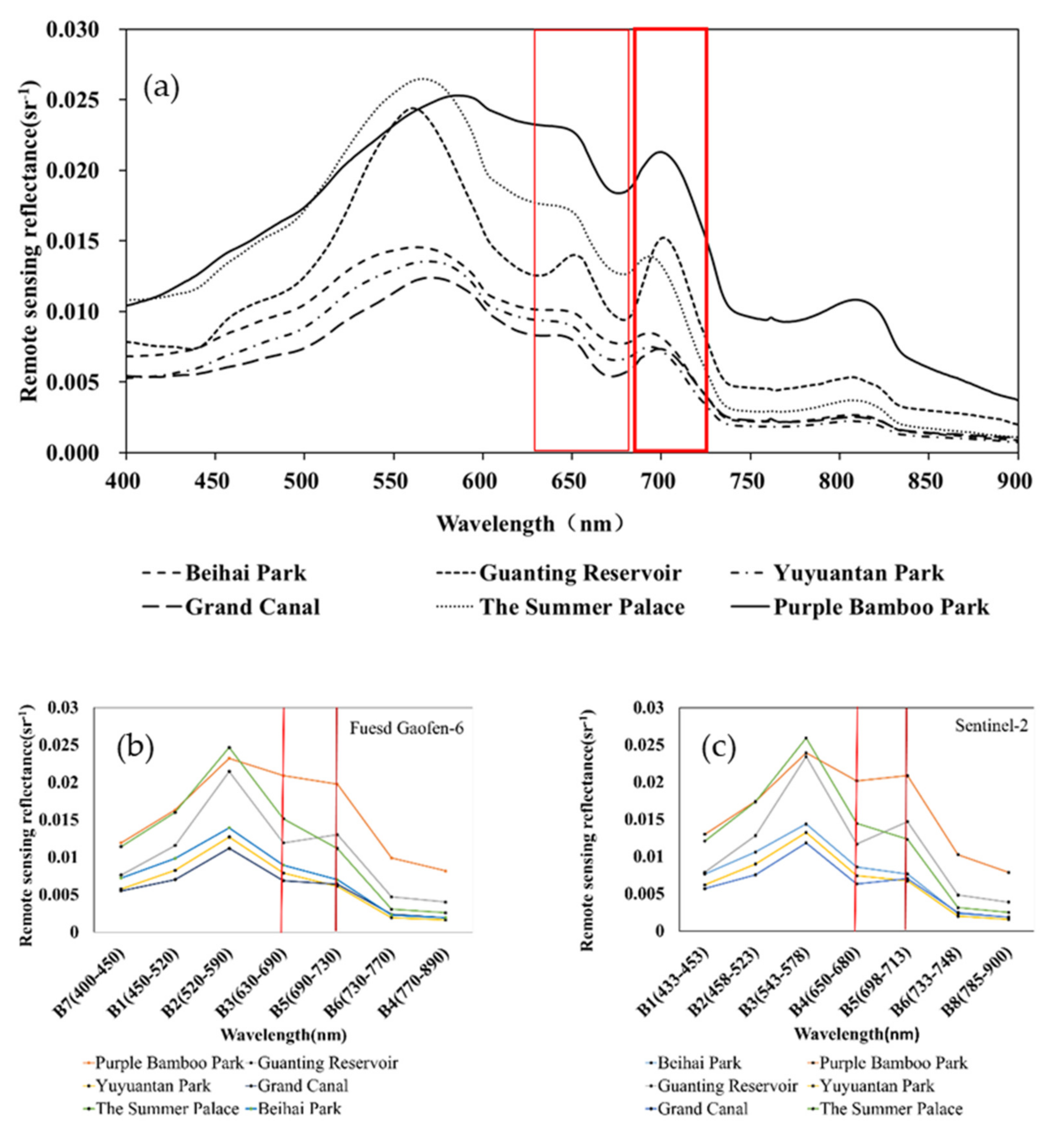
2.1.3. Radiometric Measurements
2.1.4. Bands Spectral Simulation
2.1.5. Chlorophyll-a Concentrations Measurement
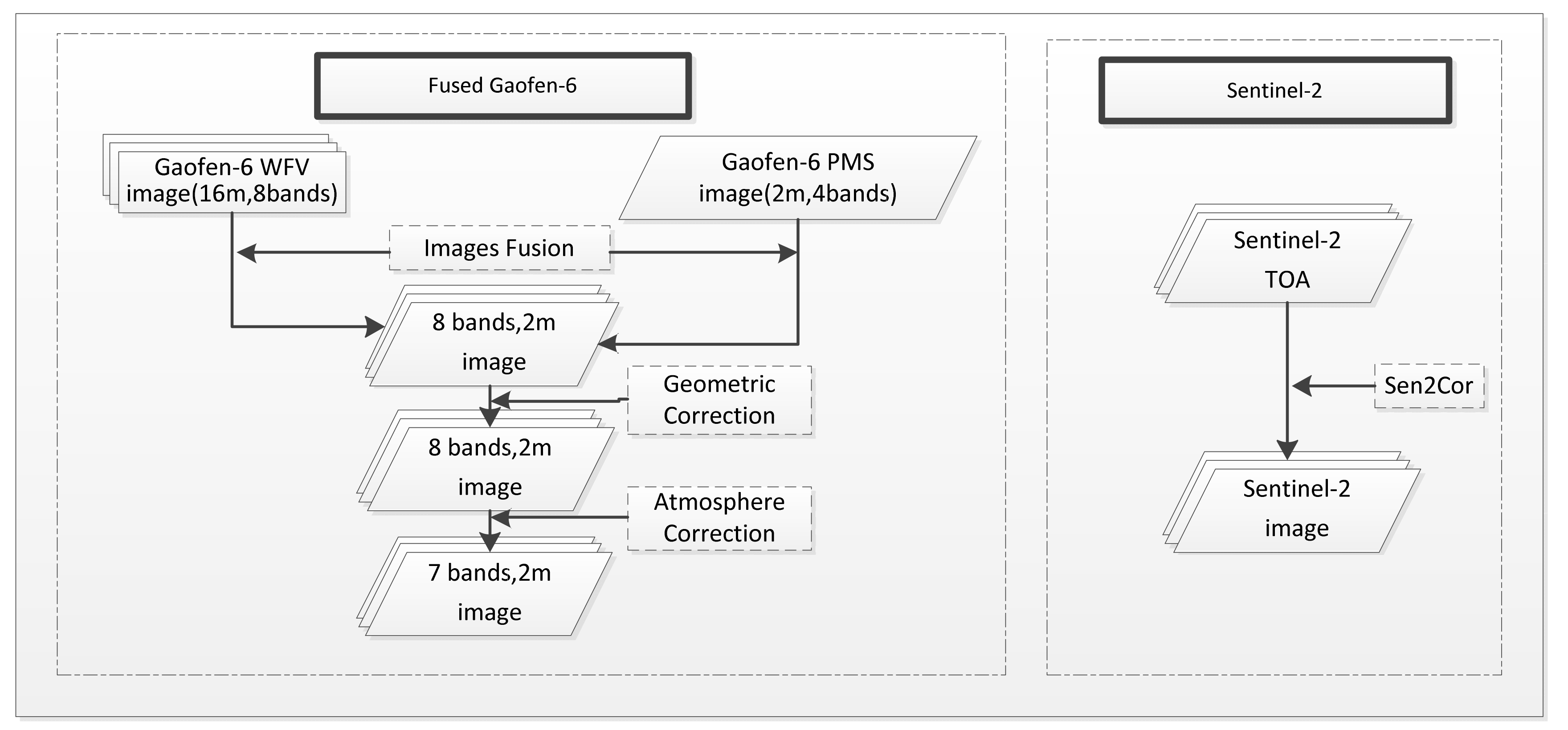
2.2. Remote Sensing Materials
2.2.1. Fused Gaofen-6 Remote Sensing Materials
2.2.2. Sentinel-2 Remote Sensing Materials
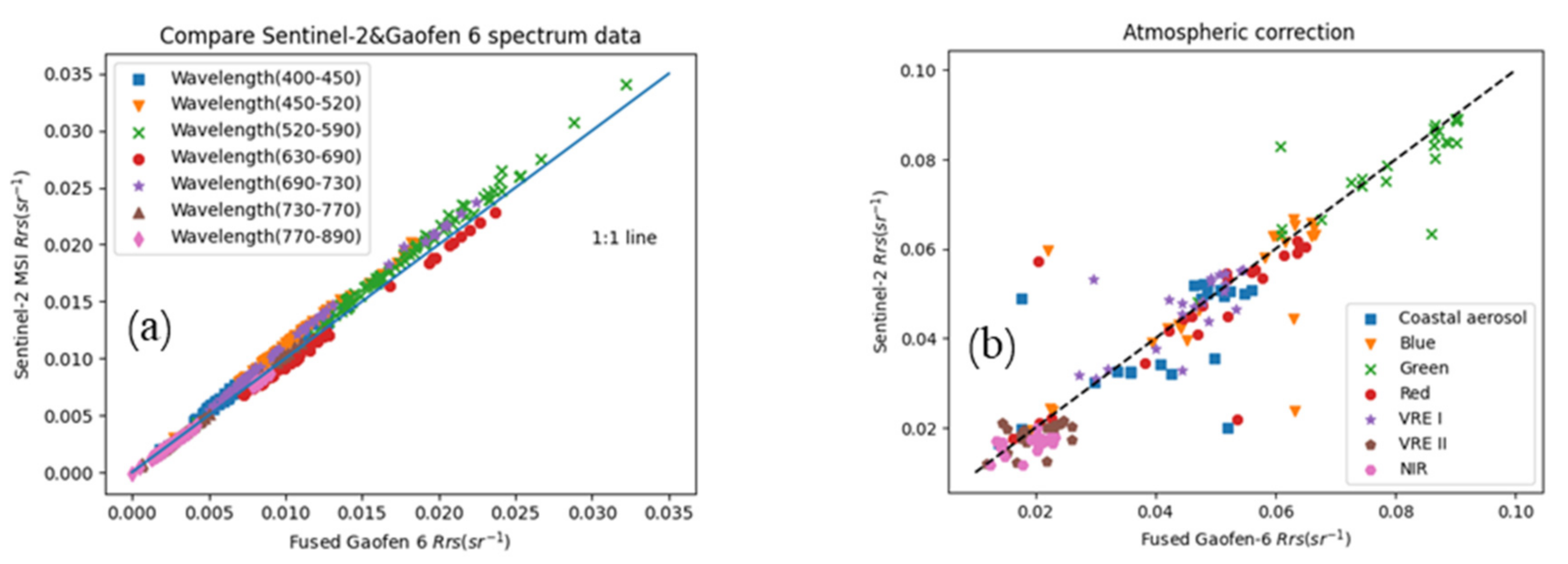
2.3. Accuracy Evaluation
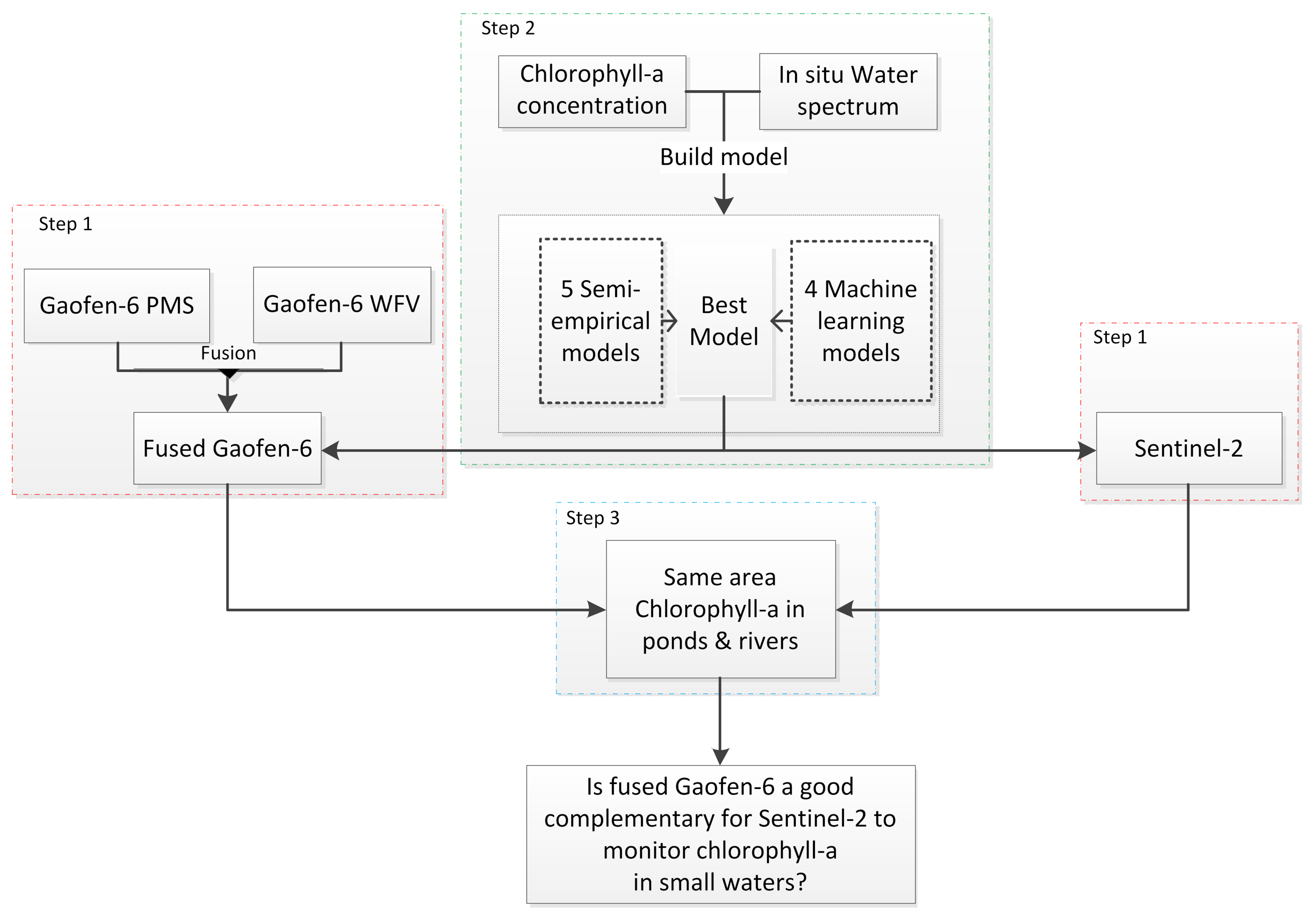
2.4. Methods
3. Results
3.1. Semi-Empirical Model
3.1.1. Fused Gaofen-6 Semi-Empirical Model
3.1.2. Sentinel-2 Semi-Empirical Model
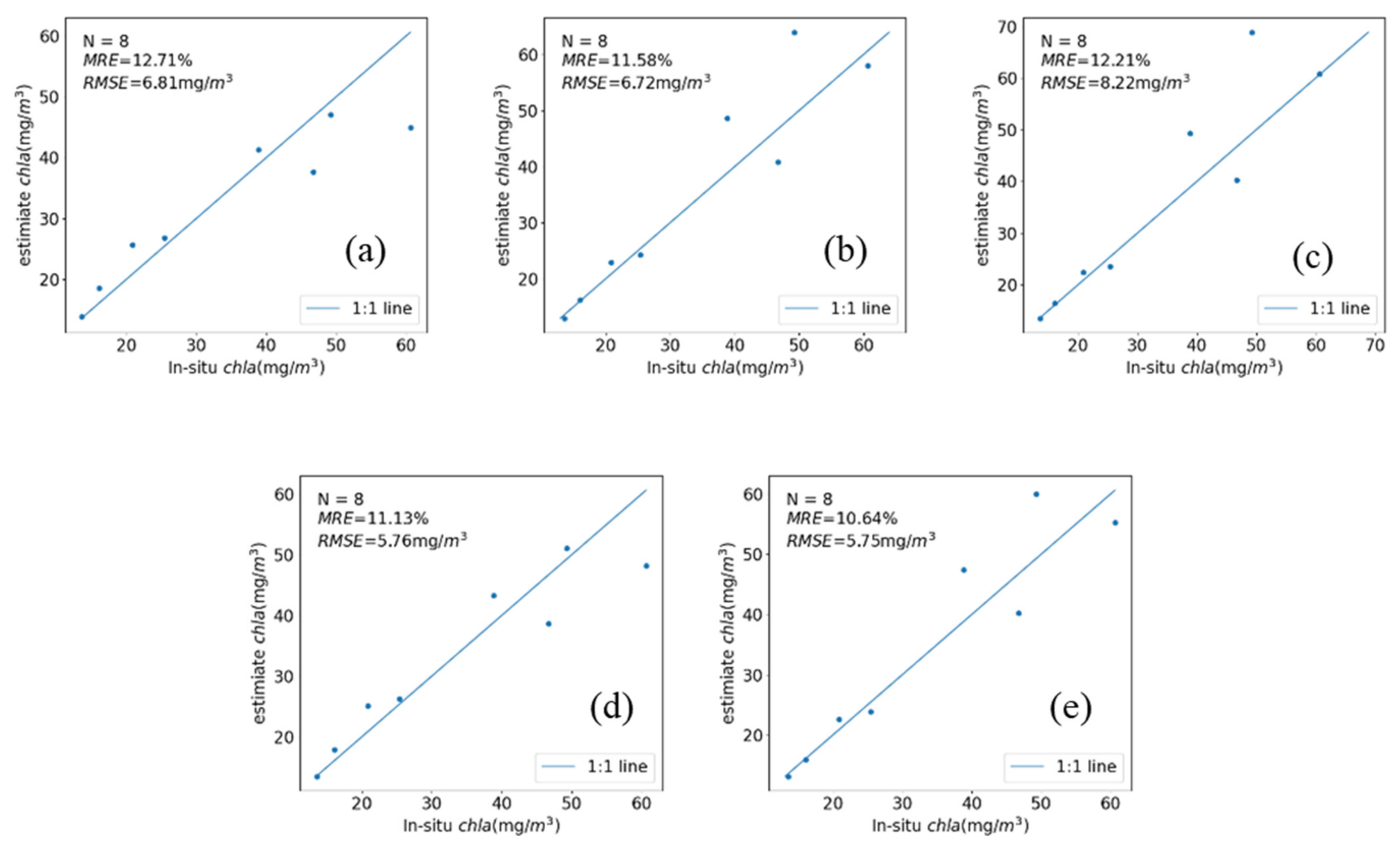
3.2. Machine Learning Model
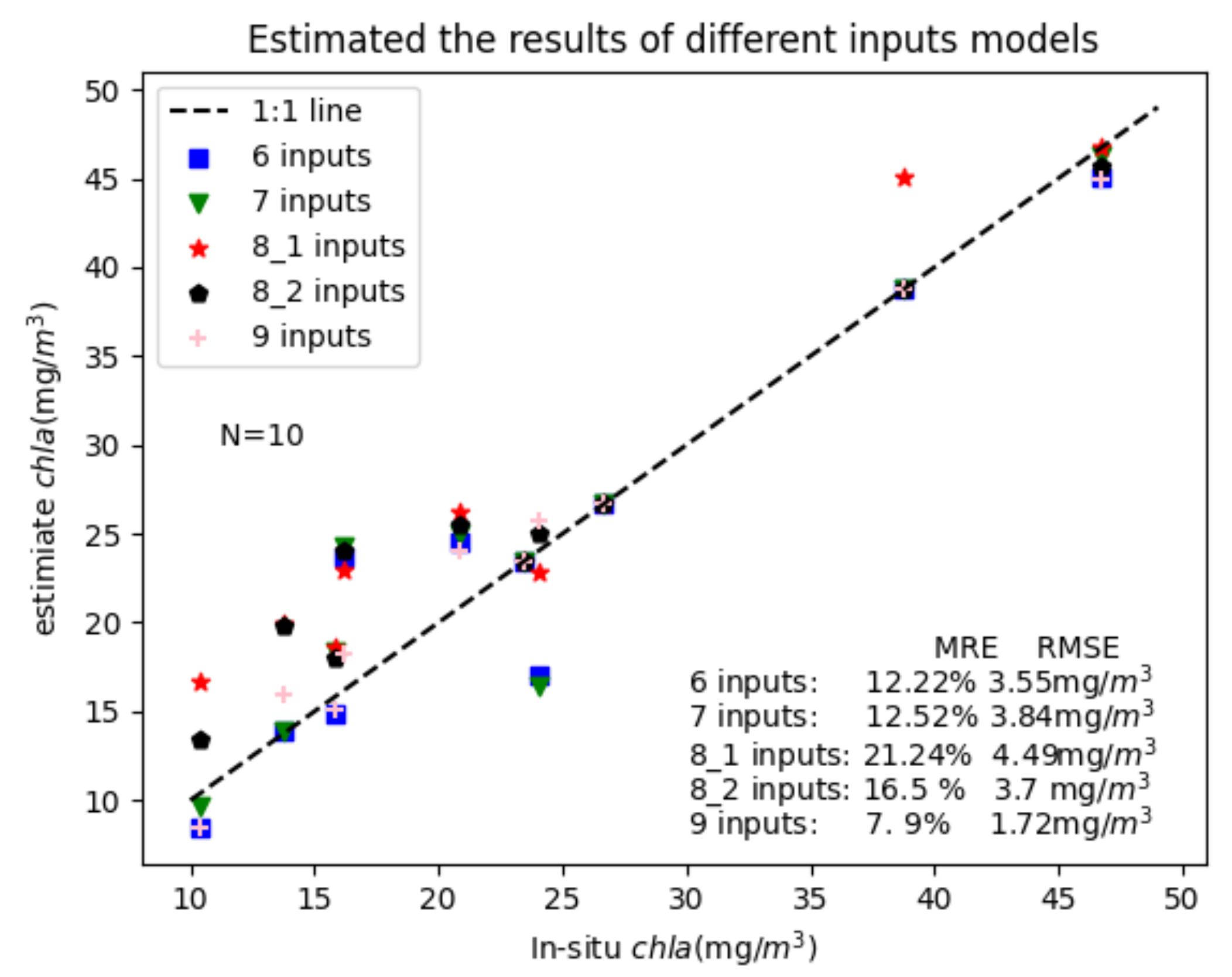
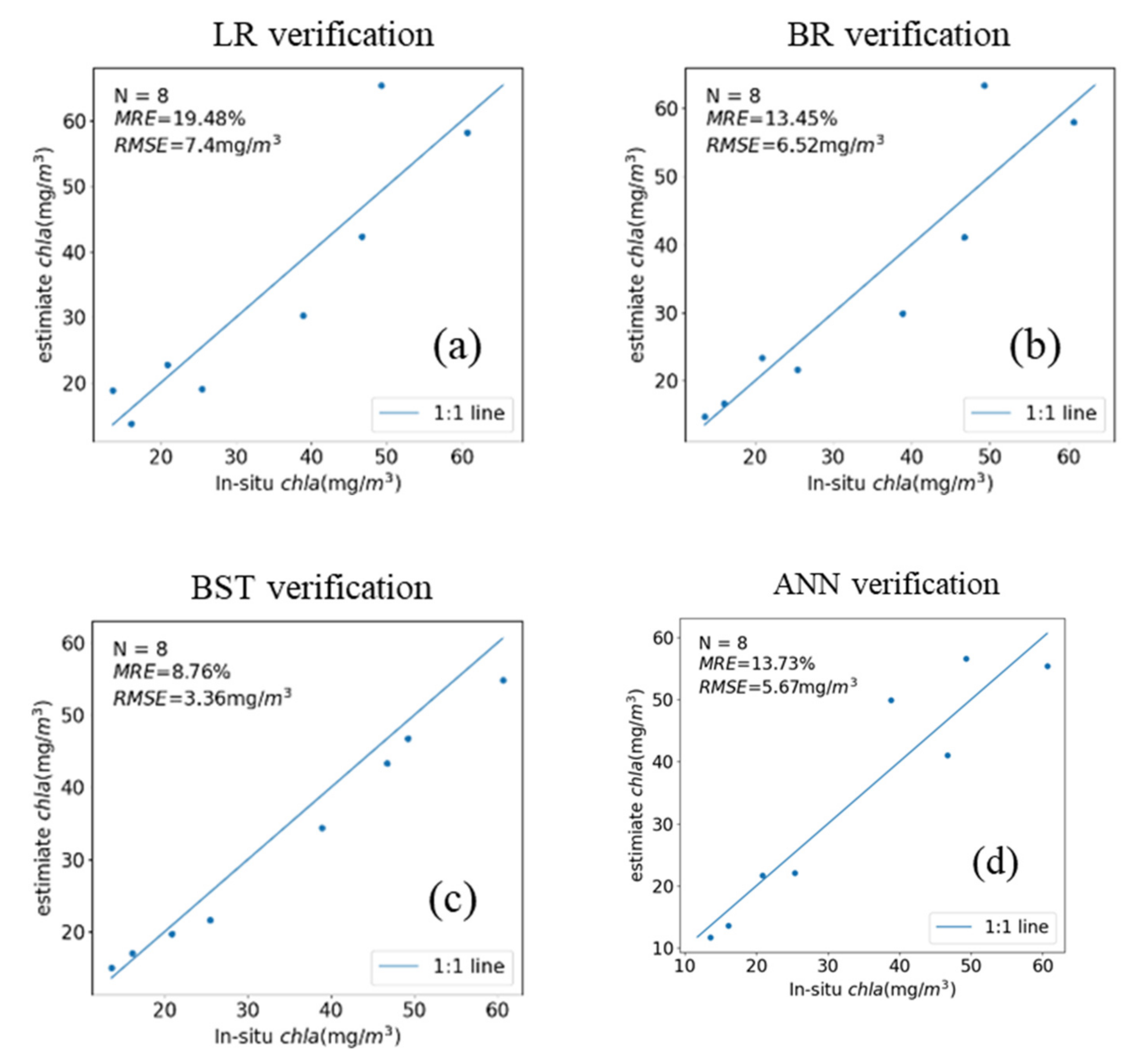
3.2.1. Fused Gaofen-6 Machine Learning Model
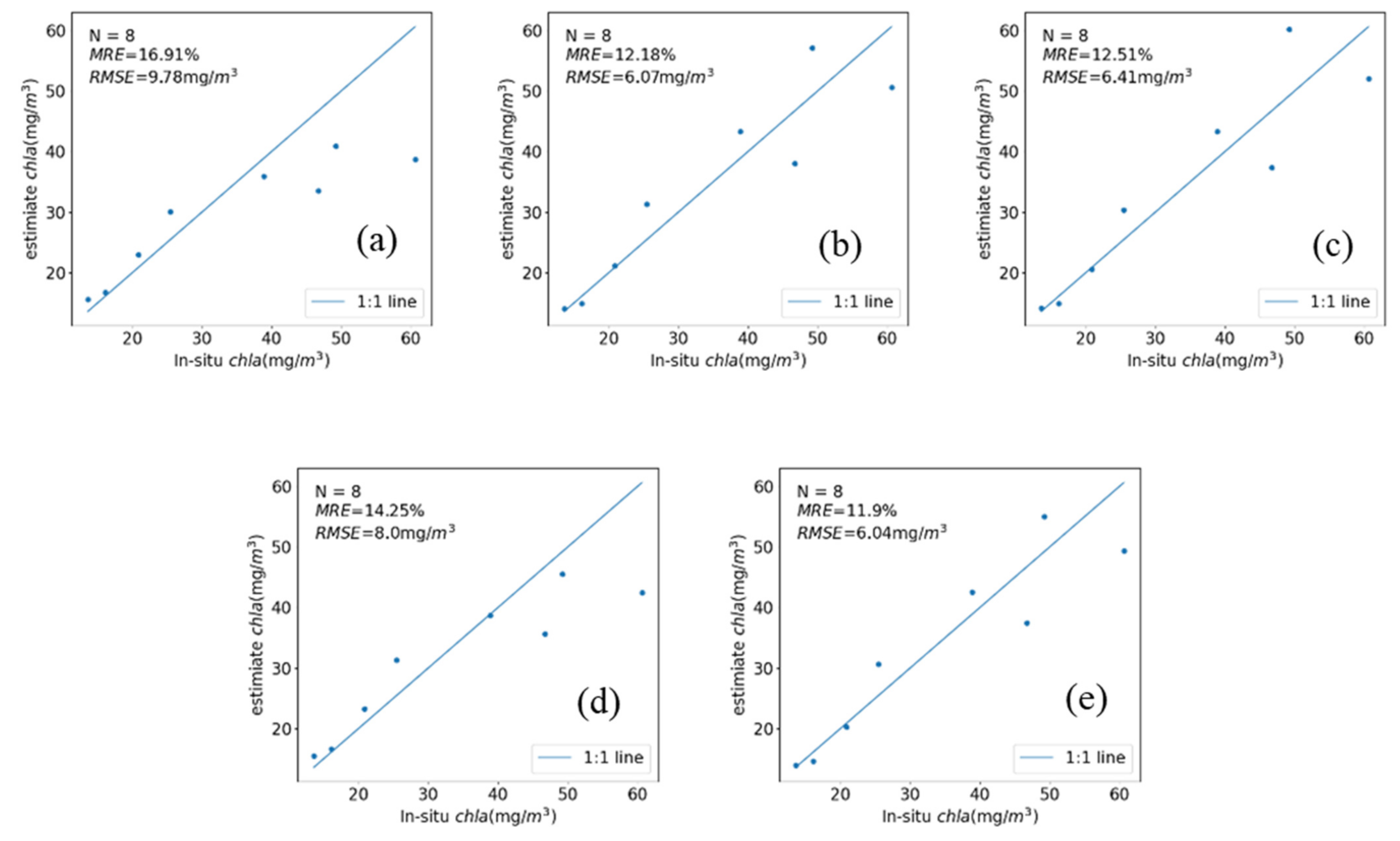
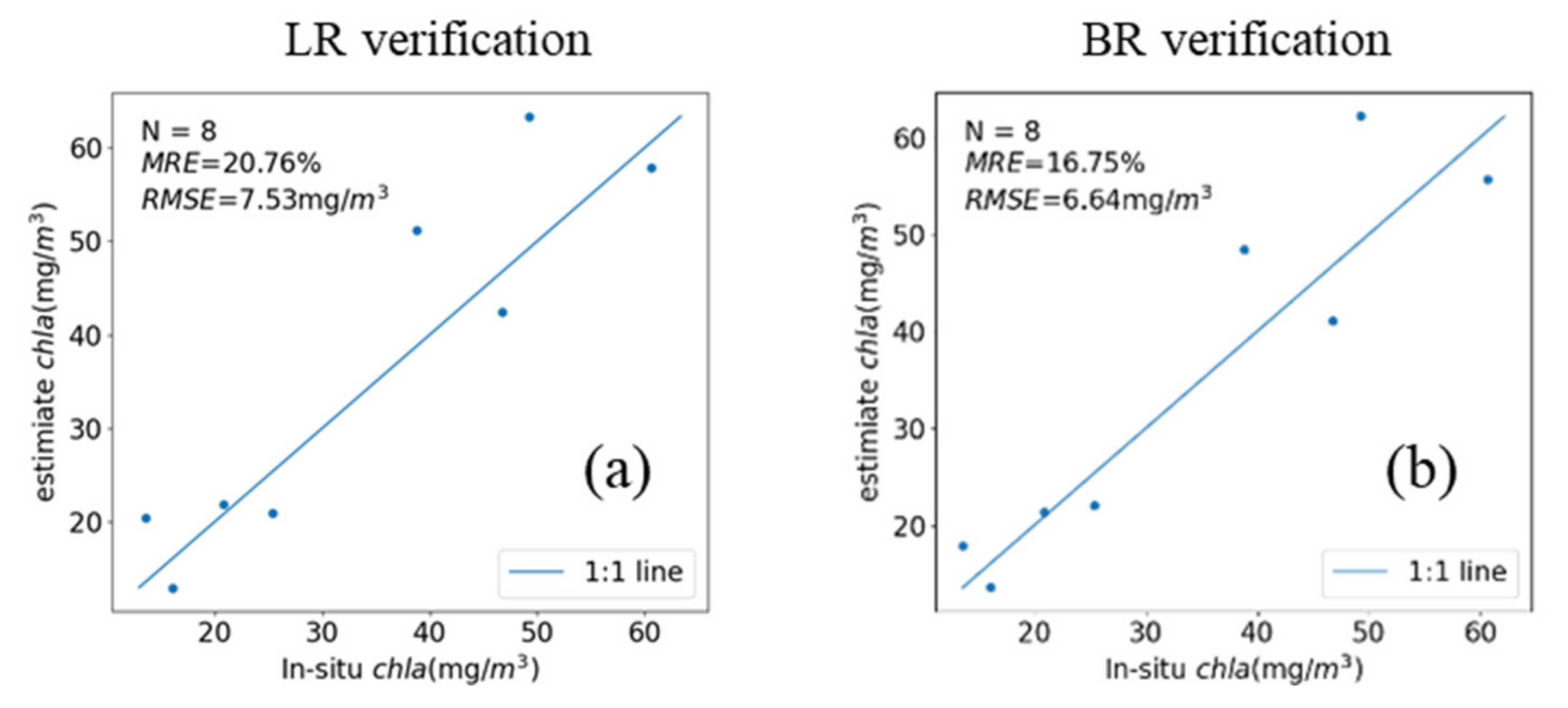
3.2.2. Sentinel-2 Machine Learning Model
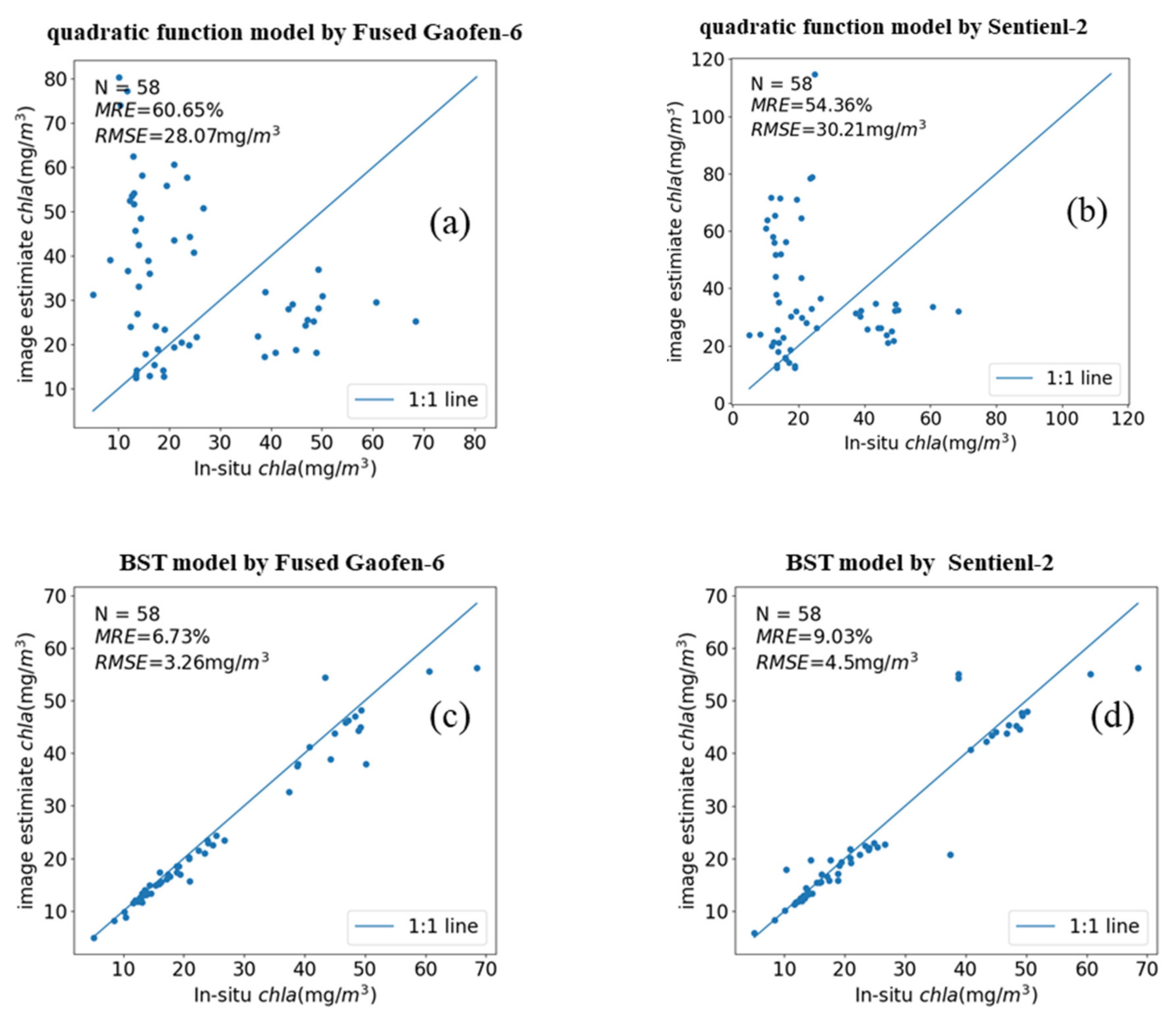
3.3. Comparison of Semi-Empirical Model and Machine Learning Model
4. Discussion
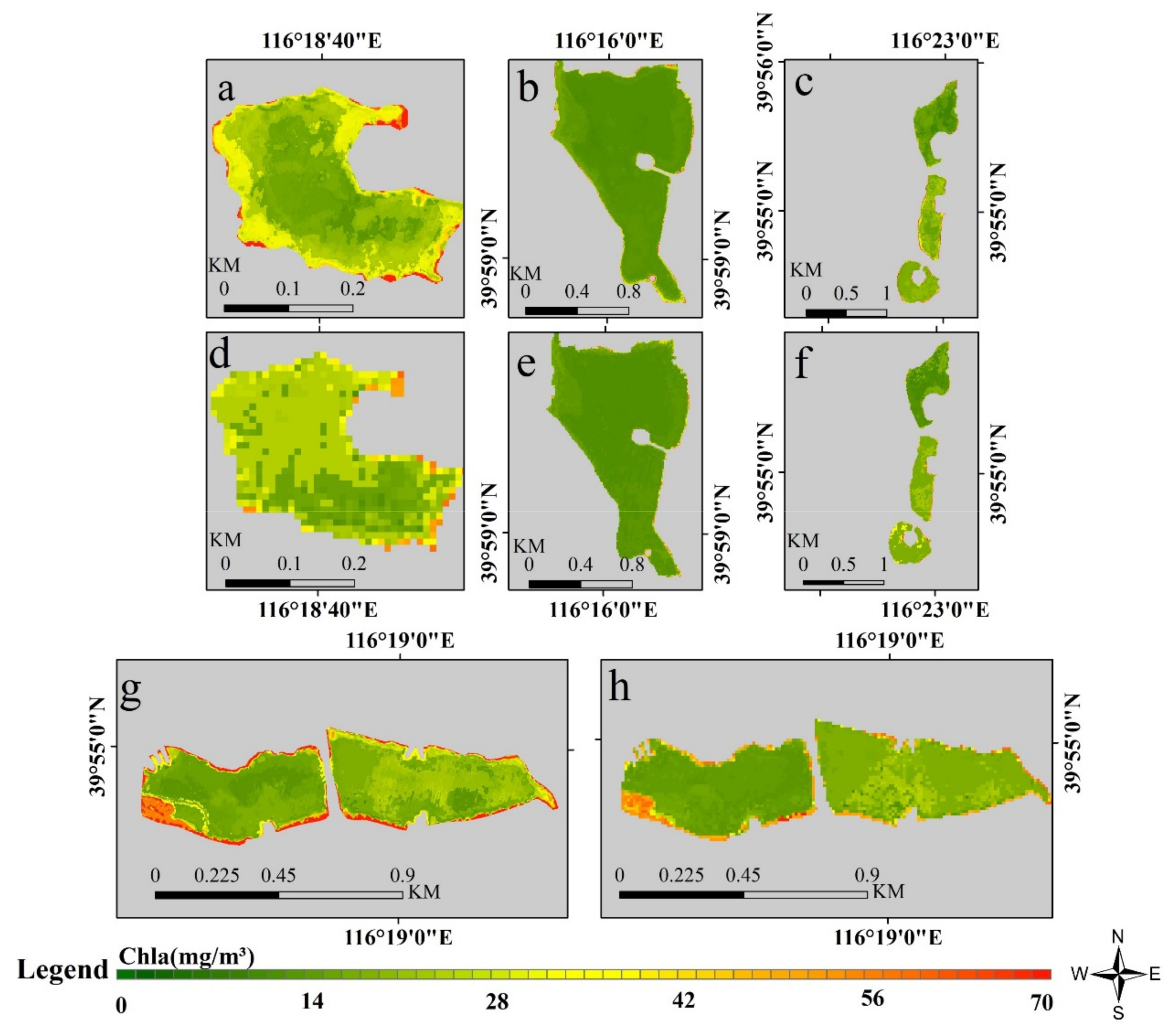
4.1. Comparison of Chla Estimation in Ponds
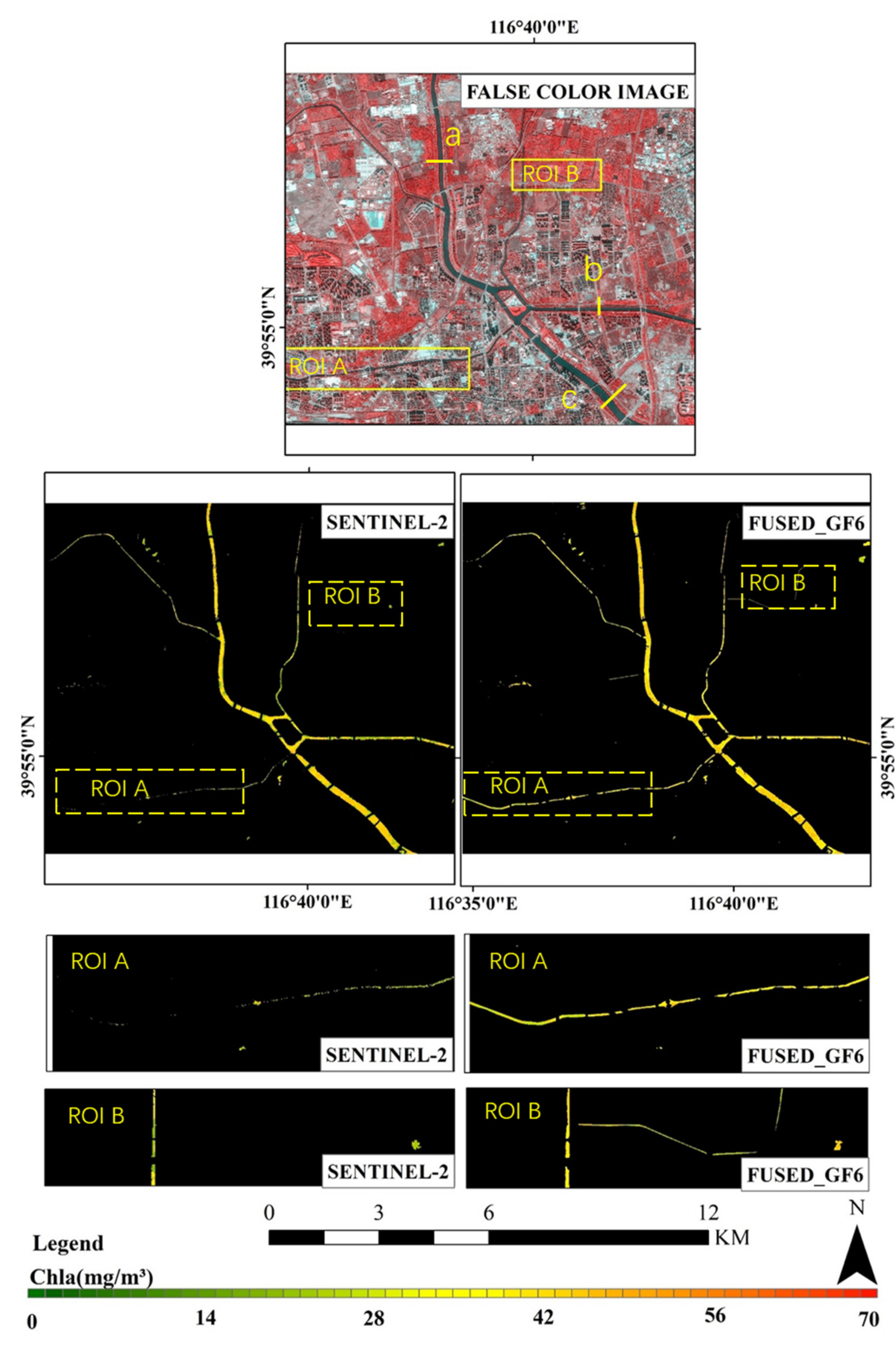
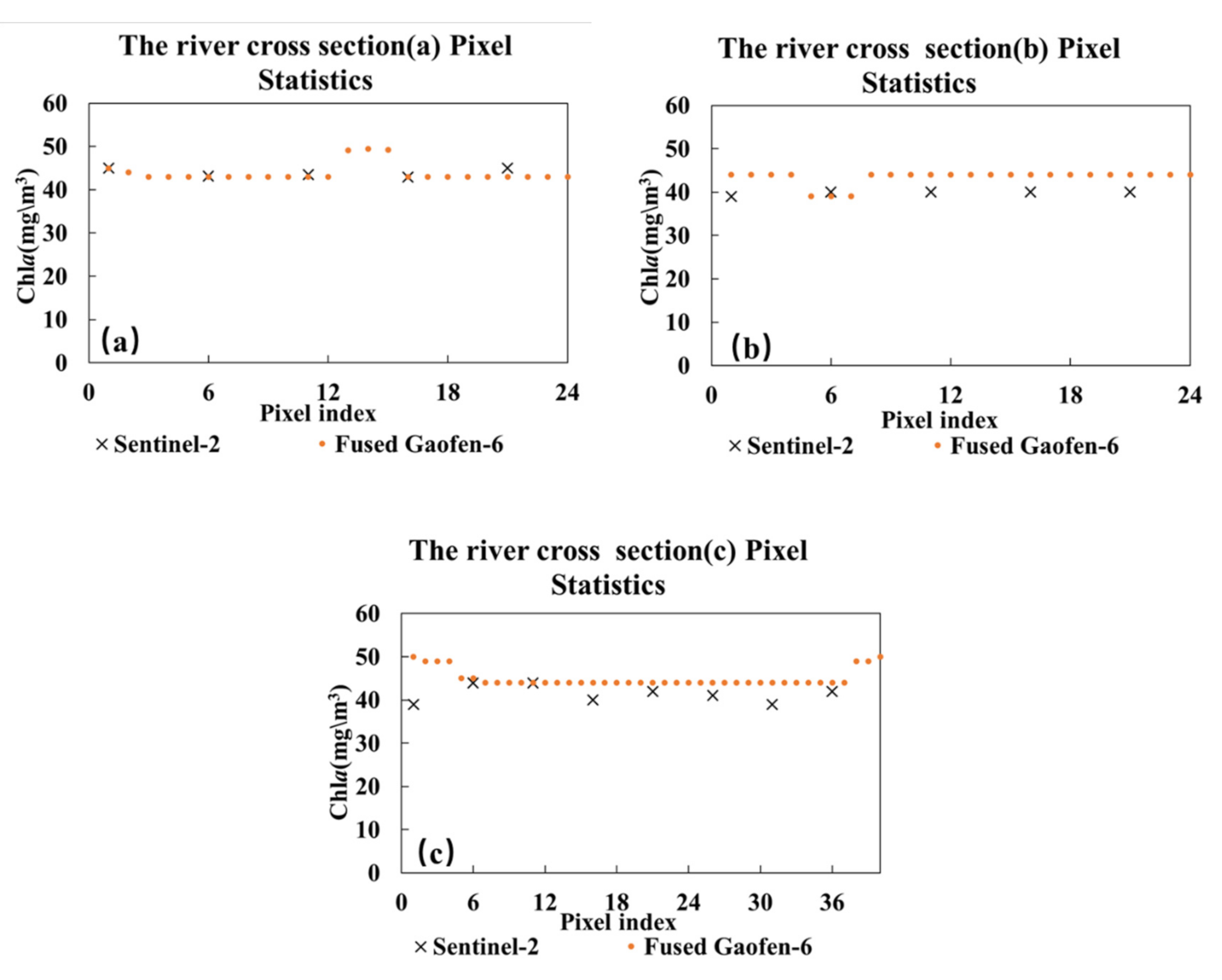
4.2. Comparison of Chla Estimation in the Rivers
4.3. Fused Gaofen-6 and Sentinel-2 Monitoring Frequency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm | Variable (x) | Formula | R2 | RMSE (mg/m3) | MRE |
|---|---|---|---|---|---|
| NDCI [58] | (Rrs (705) − Rrs (665)) /(Rrs (705) + Rrs (665)) | Chla = 745.08x2 + 159.37x + 20.354 | 0.87 | 7.13 | 11.17 |
| 3BDA [59] | (1/Rrs (665) − 1/Rrs (705)) × Rrs (740) | Chla = 743.73x2 + 225.02x + 20.517 | 0.88 | 7.84 | 11.89 |
| YA10 [60] | (Rrs−1 (665) − Rrs−1 (705)) /(Rrs−1 (754) − Rrs−1 (705)) | Chla = 262.04x2 + 144.71x + 20.405 | 0.86 | 7.67 | 11.79 |
| This study | Rrs (705)/Rrs (665) | Chla = 126.45x2 − 178.9x + 72.976 | 0.88 | 7.79 | 12.21 |
| Algorithm | Variable (x) | Formula | R2 | RMSE (mg/m3) | MRE |
|---|---|---|---|---|---|
| NDCI [58] | (Rrs (705) − Rrs (665)) /(Rrs (705) + Rrs (665)) | Chla = 1051.1x2 + 323.98x + 38.229 | 0.74 | 6.30 | 13.11 |
| 3BDA [59] | (1/Rrs (665) − 1/Rrs (705)) × Rrs (740) | Chla = 2040.4x2 + 474.61x + 37.772 | 0.78 | 7.28 | 11.39 |
| YA10 [60] | (Rrs−1 (665) − Rrs−1 (705)) /(Rrs−1 (754) − Rrs−1 (705)) | Chla = 864.57x2 + 307.18x + 37.22 | 0.78 | 7.96 | 13.62 |
| This study | Rrs (705)/Rrs (665) | Chla = 304.42x2 − 435.6x + 169.14 | 0.78 | 6.88 | 13.64 |
| Algorithm | R2 | RMSE (mg/m3) | MRE |
|---|---|---|---|
| LR | 0.92 | 4.72 | 19.33 |
| BR | 0.92 | 4.72 | 19.33 |
| BST | 0.91 | 4.55 | 12.56 |
| ANN | 0.92 | 3.38 | 16.67 |
| Algorithm | R2 | RMSE (mg/m3) | MRE |
|---|---|---|---|
| LR | 0.96 | 2.31 | 11.56 |
| BR | 0.95 | 3.83 | 11.14 |
| BST | 0.95 | 3.32 | 10.90 |
| ANN | 0.96 | 3.05 | 10.82 |
References
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
- Conkright, M.E.; Gregg, W.W. Comparison of global chlorophyll climatologies: In situ, CZCS, Blended in situ-CZCS and SeaWiFS. Int. J. Remote Sens. 2003, 24, 969–991. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Saprygin, V.; Povazhnyi, V. Operational MERIS-based NIR-red algorithms for estimating chlorophyll-a concentrations in coastal waters—The Azov Sea case study. Remote Sens. Environ. 2012, 121, 118–124. [Google Scholar] [CrossRef]
- Augusto-Silva, P.B.; Ogashawara, I.; Barbosa, C.C.F.; De Carvalho, L.A.S.; Jorge, D.S.F.; Fornari, C.I.; Stech, J.L. Analysis of MERIS reflectance algorithms for estimating chlorophyll-a concentration in a Brazilian reservoir. Remote Sens. 2014, 6, 11689–11707. [Google Scholar] [CrossRef]
- Ogashawara, I.; Alcântara, E.; Curtarelli, M.; Adami, M.; Nascimento, R.; Souza, A.; Stech, J.; Kampel, M. Performance analysis of MODIS 500-m spatial resolution products for estimating chlorophyll-a concentrations in oligo- to meso-trophic waters case study: Itumbiara Reservoir, Brazil. Remote Sens. 2014, 6, 1634–1653. [Google Scholar] [CrossRef]
- Li, J.; Gao, M.; Feng, L.; Zhao, H.; Shen, Q.; Zhang, F.; Wang, S.; Zhang, B. Estimation of chlorophyll-a concentrations in a highly turbid eutrophic lake using a classification-based MODIS land-band algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3769–3783. [Google Scholar] [CrossRef]
- Li, J.; Yin, Z.; Lu, Z.; Ye, Y.; Zhang, F.; Shen, Q.; Zhang, B. Regional vicarious calibration of the SWIR-based atmospheric correction approach for MODIS-Aqua measurements of highly turbid inland water. Remote Sens. 2019, 11, 1670. [Google Scholar] [CrossRef]
- Wang, M.H.; Son, S. VIIRS-derived chlorophyll-a using the ocean color index method. Remote Sens. Environ. 2016, 182, 141–149. [Google Scholar] [CrossRef]
- Kim, W.; Moon, J.E.; Park, Y.J.; Ishizaka, J. Evaluation of chlorophyll retrievals from Geostationary Ocean Color Imager (GOCI) for the North-East Asian Region. Remote Sens. Environ. 2016, 184, 482–495. [Google Scholar] [CrossRef]
- Werther, M.; Spyrakos, E.; Simis, S.G.H.; Odermatt, D.; Stelzer, K.; Krawczyk, H.; Berlage, O.; Hunter, P.; Tyler, A. Meta-classification of remote sensing reflectance to estimate trophic status of inland and nearshore waters. ISPRS J. Photogramm. Remote Sens. 2021, 176, 109–126. [Google Scholar] [CrossRef]
- Kravitz, J.; Matthews, M.; Bernard, S.; Griffith, D. Application of Sentinel 3 OLCI for chl-a retrieval over small inland water targets: Successes and challenges. Remote Sens. Environ. 2020, 237, 111562. [Google Scholar] [CrossRef]
- Hori, M. Near-daily monitoring of surface temperature and channel width of the six largest Arctic rivers from space using GCOM-C/SGLI. Remote Sens. Environ. 2021, 263, 112538. [Google Scholar] [CrossRef]
- Xu, Y.; He, X.; Bai, Y.; Wang, D.; Zhu, Q.; Ding, X. Evaluation of Remote-Sensing Reflectance Products from Multiple Ocean Color Missions in Highly Turbid Water (Hangzhou Bay). Remote Sens. 2021, 13, 4267. [Google Scholar] [CrossRef]
- Hori, M.; Murakami, H.; Miyazaki, R.; Honda, Y.; Nasahara, K.; Kajiwara, K.; Nakajima, T.Y.; Irie, H.; Toratani, M.; Hirawake, T.; et al. GCOM-C Data Validation Plan for Land, Atmosphere, Ocean, and Cryosphere. Trans. Jpn. Soc. Aeronaut. Spaceences Aerosp. Technol. Jpn. 2018, 16, 218–223. [Google Scholar] [CrossRef][Green Version]
- Ilori, C.; Pahlevan, N.; Knudby, A. Analyzing performances of different atmospheric correction techniques for Landsat 8: Application for coastal remote sensing. Remote Sens. 2019, 11, 469. [Google Scholar] [CrossRef]
- Kuhn, C.; de Matos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef]
- Pu, F.; Ding, C.; Chao, Z.; Yu, Y.; Xu, X. Water-quality classification of inland lakes using Landsat8 images by convolutional neural networks. Remote Sens. 2019, 11, 1674. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Estimating chlorophyll-a of inland water bodies in Greece based on Landsat data. Remote Sens. 2020, 12, 2087. [Google Scholar] [CrossRef]
- Ogashawara, I.; Jechow, A.; Kiel, C.; Kohnert, K.; Berger, S.A.; Wollrab, S. Performance of the Landsat 8 provisional aquatic reflectance product for inland waters. Remote Sens. 2020, 12, 2410. [Google Scholar] [CrossRef]
- Somasundaram, D.; Zhang, F.; Ediriweera, S.; Wang, S.; Yin, Z.; Li, J.; Zhang, B. Patterns, trends and drivers of water transparency in Sri Lanka using Landsat 8 observations and Google Earth Engine. Remote Sens. 2021, 13, 2193. [Google Scholar] [CrossRef]
- Asim, M.; Brekke, C.; Mahmood, A.; Eltoft, T.; Reigstad, M. Improving chlorophyll-a estimation from Sentinel-2 (MSI) in the Barents Sea using machine learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5529–5549. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L.; Gege, P. Inter-comparison of methods for chlorophyll-a retrieval: Sentinel-2 time-series analysis in Italian lakes. Remote Sens. 2021, 13, 2381. [Google Scholar] [CrossRef]
- Ogashawara, I.; Kiel, C.; Jechow, A.; Kohnert, K.; Ruhtz, T.; Grossart, H.-P.; Hölker, F.; Nejstgaard, J.C.; Berger, S.A.; Wollrab, S. The use of Sentinel-2 for chlorophyll-a spatial dynamics assessment: A comparative study on different lakes in northern Germany. Remote Sens. 2021, 13, 1542. [Google Scholar] [CrossRef]
- Perrone, M.; Scalici, M.; Conti, L.; Moravec, D.; Kropáček, J.; Sighicelli, M.; Lecce, F.; Malavasi, M. Water mixing conditions influence Sentinel-2 monitoring of chlorophyll content in monomictic lakes. Remote Sens. 2021, 13, 2699. [Google Scholar] [CrossRef]
- Sent, G.; Biguino, B.; Favareto, L.; Cruz, J.; Sá, C.; Dogliotti, A.I.; Palma, C.; Brotas, V.; Brito, A.C. Deriving water quality parameters using Sentinel-2 imagery: A case study in the Sado Estuary, Portugal. Remote Sens. 2021, 13, 1043. [Google Scholar] [CrossRef]
- Zhai, Z.K.; Lu, S.L.; Wang, P.; Wang, C.; Tang, H.L.; Liu, D.Y.; Han, Q.Y.; Guo, J.; Liu, X.H.; Wei, T.L. Ocean chlorophyll-a retrieval using GF1-WFV data-a case study of the central Bohai Sea. In Proceedings of the 2nd International Conference on Advances in Civil and Ecological Engineering Research (ACEER), Beijing, China, 20–23 October 2020. [Google Scholar]
- Cao, Y.; Ye, Y.; Zhao, H.; Jiang, Y.; Wang, H.; Shang, Y.; Wang, J. Remote sensing of water quality based on HJ-1A HSI imagery with modified discrete binary particle swarm optimization-partial least squares (MDBPSO-PLS) in inland waters: A case in Weishan Lake. Ecol. Inform. 2018, 44, 21–32. [Google Scholar] [CrossRef]
- Wang, X.; Gong, Z.; Pu, R. Estimation of chlorophyll a content in inland turbidity waters using WorldView-2 imagery: A case study of the Guanting Reservoir, Beijing, China. Environ. Monit. Assess. 2018, 190, 620. [Google Scholar] [CrossRef]
- Zhao, L.; Qi, J.; Ren, Z.; Zhu, J. Shallow water bathymetry retrieving of optical remote sensing combined with SVM bottom classification. In Proceedings of the 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 3–5 July 2020; pp. 530–534. [Google Scholar]
- Rotta, L.H.; Alcântara, E.H.; Watanabe, F.S.; Rodrigues, T.W.; Imai, N.N. Atmospheric correction assessment of SPOT-6 image and its influence on models to estimate water column transparency in tropical reservoir. Remote Sens. Appl. Soc. Environ. 2016, 4, 158–166. [Google Scholar] [CrossRef]
- Mansaray, A.S.; Dzialowski, A.R.; Martin, M.E.; Wagner, K.L.; Gholizadeh, H.; Stoodley, S.H. Comparing PlanetScope to Landsat-8 and Sentinel-2 for Sensing Water Quality in Reservoirs in Agricultural Watersheds. Remote Sens. 2021, 13, 1847. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Konik, M.; Kowalczuk, P.; Zabłocka, M.; Makarewicz, A.; Meler, J.; Zdun, A.; Darecki, M. Empirical relationships between remote-sensing reflectance and selected inherent optical properties in Nordic Sea surface waters for the MODIS and OLCI ocean colour sensors. Remote Sens. 2020, 12, 2774. [Google Scholar] [CrossRef]
- Zhang, R.; Zheng, Z.; Liu, G.; Du, C.; Du, C.; Lei, S.; Xu, Y.; Xu, J.; Mu, M.; Bi, S.; et al. Simulation and assessment of the capabilities of Orbita Hyperspectral (OHS) imagery for remotely monitoring chlorophyll-a in eutrophic plateau lakes. Remote Sens. 2021, 13, 2821. [Google Scholar] [CrossRef]
- Gitelson, A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Serenko, V. A semi-analytical model for remote estimation of chlorophyll-a in turbid productive waters: Calibration and Validation. Int. J. Adv. Comput. Res. 2008, 2008, GC41A-0696. [Google Scholar]
- Jorge, D.S.F.; Loisel, H.; Jamet, C.; Dessailly, D.; Demaria, J.; Bricaud, A.; Maritorena, S.; Zhang, X.; Antoine, D.; Kutser, T.; et al. A three-step semi analytical algorithm (3SAA) for estimating inherent optical properties over oceanic, coastal, and inland waters from remote sensing reflectance. Remote Sens. Environ. 2021, 263, 112537. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: Experimental results. Appl. Opt. 2005, 44, 411–422. [Google Scholar]
- Botha, E.J.; Anstee, J.M.; Sagar, S.; Lehmann, E.; Medeiros, T.A.G. Classification of Australian waterbodies across a wide range of optical water types. Remote Sens. 2020, 12, 3018. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Shen, Q.; Zhang, B.; Tian, L.; Ye, H.; Wang, S.; Lu, Z. A soft-classification-based chlorophyll-a estimation method using MERIS data in the highly turbid and eutrophic Taihu Lake. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 138–149. [Google Scholar] [CrossRef]
- Zhu, S.; Mao, J. A machine learning approach for estimating the trophic state of urban waters based on remote sensing and environmental factors. Remote Sens. 2021, 13, 2498. [Google Scholar] [CrossRef]
- Xie, F.; Tao, Z.; Zhou, X.; Lv, T.; Wang, J.; Li, R. A prediction model of water in situ data change under the influence of environmental variables in remote sensing validation. Remote Sens. 2020, 13, 70. [Google Scholar] [CrossRef]
- Watanabe, F.S.Y.; Miyoshi, G.T.; Rodrigues, T.W.P.; Bernardo, N.M.R.; Rotta, L.H.S.; Alcântara, E.; Imai, N.N. Inland water’s trophic status classification based on machine learning and remote sensing data. Remote Sens. Appl. Soc. Environ. 2020, 19, 100326. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Li, N. Machine learning algorithms for chromophoric dissolved organic matter (CDOM) estimation based on Landsat 8 images. Remote Sens. 2021, 13, 3560. [Google Scholar] [CrossRef]
- Su, H.; Lu, X.; Chen, Z.; Zhang, H.; Lu, W.; Wu, W. Estimating coastal chlorophyll-a concentration from time-series OLCI data based on machine learning. Remote Sens. 2021, 13, 576. [Google Scholar] [CrossRef]
- Li, T.; Zhu, B.; Cao, F.; Sun, H.; He, X.; Liu, M.; Gong, F.; Bai, Y. Monitoring changes in the transparency of the largest reservoir in eastern China in the past decade, 2013–2020. Remote Sens. 2021, 13, 2570. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.; Ho, H.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.; Pun, L. Comparison of machine learning algorithms for retrieval of water quality indicators in case-II waters: A case study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- Awad, M. Sea water chlorophyll-a estimation using hyperspectral images and supervised artificial neural network. Ecol. Inform. 2014, 24, 60–68. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Tang, J.; Guo, T.; Wang, X.; Wang, X.; Song, Q.J.J.o.R.S. The methods of water spectra measurement and analysis I: Above-water method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar]
- Shi, K.; Zhang, Y.; Zhou, Y.; Liu, X.; Zhu, G.; Qin, B.; Gao, G.J.R. Long-term MODIS observations of cyanobacterial dynamics in Lake Taihu: Responses to nutrient enrichment and meteorological factors. Sci. Rep. 2017, 7, 40326. [Google Scholar] [CrossRef]
- Chen, F. Pixel-Pixel Knife High Partial Satellite Processing Software. Available online: https://www.zybuluo.com/novachen/note/426294 (accessed on 16 May 2021).
- Long, T.; Jiao, W.; He, G.; Zhang, Z. A Fast and reliable matching method for automated georeferencing of remotely sensed imagery. Remote Sens. 2016, 8, 56. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A. Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted MAD transformation. Remote Sens. Environ. 2008, 112, 1025–1036. [Google Scholar] [CrossRef]
- Lanaras, C.; Bioucas-Dias, J.; Galliani, S.; Baltsavias, E.; Schindler, K. Super-resolution of Sentinel-2 images: Learning a globally applicable deep neural network. ISPRS J. Photogramm. 2018, 146, 305–319. [Google Scholar] [CrossRef]
- Gao, B. NDWI-A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of chl-a concentration in turbid productive waters—return to a simple two-band NIR-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- Yang, W.; Matsushita, B.; Chen, J.; Fukushima, B.; Ma, R. An enhanced three-band index for estimating chlorophyll-a in turbid case-II waters: Case studies of Lake Kasumigaura, Japan, and Lake Dianchi, China. IEEE Geosci. Remote Sens. Lett. 2010, 7, 655–659. [Google Scholar] [CrossRef]
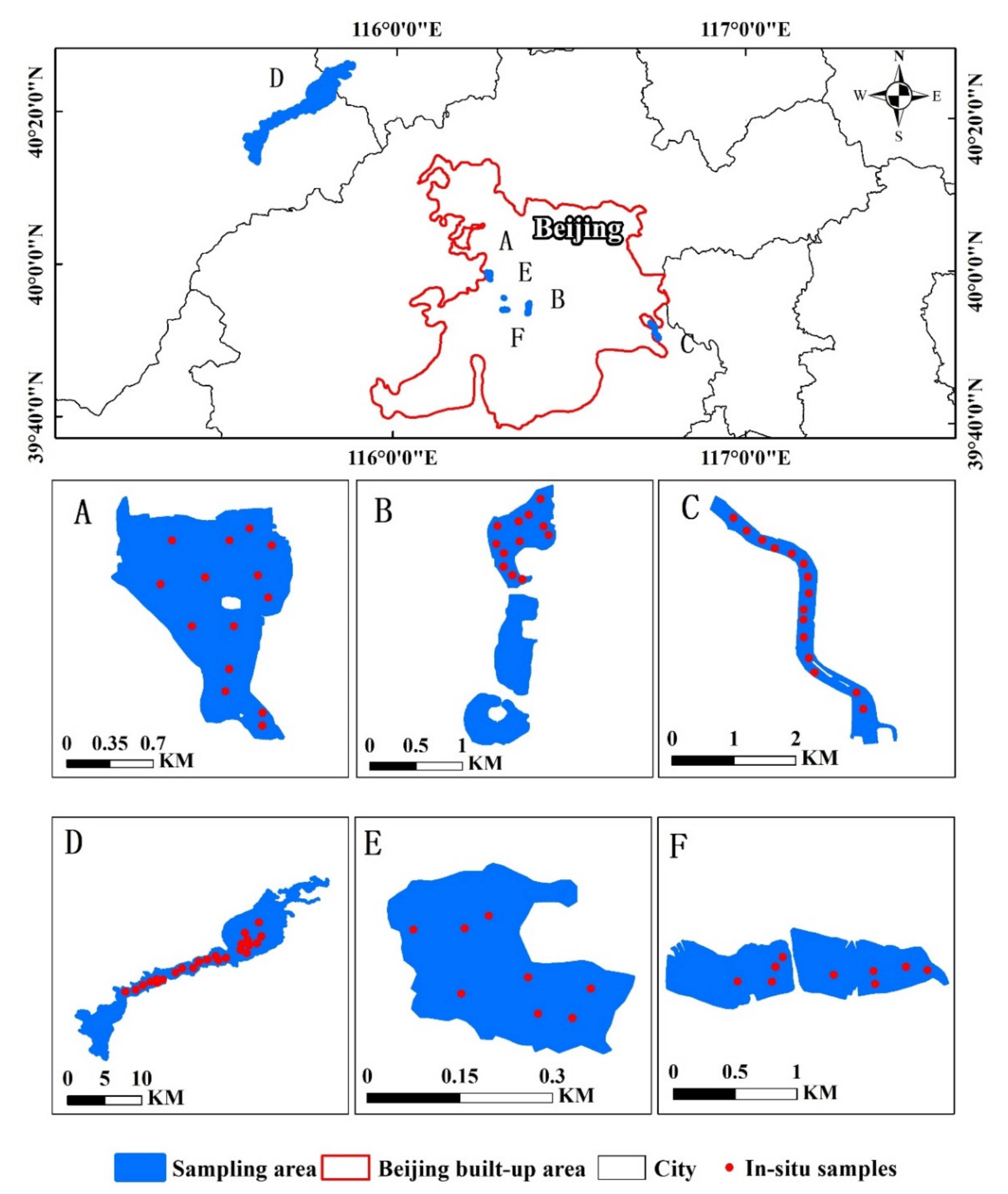


| Field Experiment Data | In Situ Location | In Situ Numbers | Symbols in Figure 2 |
|---|---|---|---|
| 8 September 2016 | Guanting Reservoir | 24 | d |
| 21 August 2019 | Yuyuantan Park | 9 | f |
| 16 September 2019 | Summer Palace | 14 | a |
| 18 September 2019 | Beihai Park | 12 | b |
| 15 October 2019 | Grand Canal | 15 | c |
| 25 October 2019 | Purple Bamboo Park | 8 | e |
| Sensor | Data | ID | Spatial Resolution (m) |
|---|---|---|---|
| Gaofen-6 PMS | 18 September 2019 | 1119925935 | 2 |
| Gaofen-6 PMS | 18 September 2019 | 1119925944 | 2 |
| Gaofen-6 WFV | 18 September 2019 | 1119926317 | 16 |
| Gaofen-6 PMS | 25 October 2019 | 1119938225 | 2 |
| Gaofen-6 PMS | 25 October 2019 | 1119938263 | 2 |
| Gaofen-6 WFV | 25 October 2019 | 1119938347 | 16 |
| Sentinel-2 | 25 October 2019 | - | 10 |
| Fused Gaofen-6 | Sentinel-2 MSI | |||||
|---|---|---|---|---|---|---|
| Bands Name | Band Index | Wavelength (nm) | Resolution (m) | Band Index | Wavelength (nm) | Resolution (m) |
| Blue | B1 | 450–520 | 2 | B2 | 458–523 | 10 |
| Green | B2 | 520–590 | 2 | B3 | 543–578 | 10 |
| Red | B3 | 630–690 | 2 | B4 | 650–680 | 10 |
| NIR | B4 | 770–890 | 2 | B8 | 785–900 | 10 |
| Red-Edge I | B5 | 690–730 | 2 | B5 | 698–713 | 20 |
| Red-Edge II | B6 | 730–770 | 2 | B6 | 733–748 | 20 |
| Coastal aerosol | B7 | 400–450 | 2 | B1 | 433–453 | 60 |
| Yellow | B8 | 590–630 | 2 | None | ||
| Model Form | Formula |
|---|---|
| Linear model | Chla = a × x +b |
| Exponential model | Chla = a × exp (b × x) + c |
| Logarithmic model | Chla = a × power (x, b) + c |
| Power function model | Chla = a × log(x) + b |
| Quadratic function model | Chla = a × x2 + b × x + c |
| Model Form | Formula |
|---|---|
| Linear model | Chla = −65.788453 × x + 99.5654 |
| Exponential model | Chla = 1485.8 × exp(−3.65197 × x) |
| Logarithmic model | Chla = 37.9778 × power (x, 4.0432) |
| Power function model | Chla = −83.5964 × log(x) + 35.9646 |
| Quadratic function model | Chla = 186.537 × x2 − 511.3751 × x + 362.781 |
| Model Form | Formula |
|---|---|
| Linear model | Chla = −83.028 × x + 107.0218 |
| Exponential model | Chla = 1139.618 × exp (−3.98529 × x) |
| Logarithmic model | Chla = 20.76 × power (x, 3.6926) |
| Power function model | Chla = −85.2146 × log(x) + 23.37083 |
| Quadratic function model | Chla = 119.624 × x2 − 485.476 × x + 306.563 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Shen, Q.; Yao, Y.; Li, J.; Chen, F.; Wang, R.; Xu, W.; Gao, Z.; Wang, L.; Zhou, Y. Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors. Remote Sens. 2022, 14, 229. https://doi.org/10.3390/rs14010229
Shi J, Shen Q, Yao Y, Li J, Chen F, Wang R, Xu W, Gao Z, Wang L, Zhou Y. Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors. Remote Sensing. 2022; 14(1):229. https://doi.org/10.3390/rs14010229
Chicago/Turabian StyleShi, Jiarui, Qian Shen, Yue Yao, Junsheng Li, Fu Chen, Ru Wang, Wenting Xu, Zuoyan Gao, Libing Wang, and Yuting Zhou. 2022. "Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors" Remote Sensing 14, no. 1: 229. https://doi.org/10.3390/rs14010229
APA StyleShi, J., Shen, Q., Yao, Y., Li, J., Chen, F., Wang, R., Xu, W., Gao, Z., Wang, L., & Zhou, Y. (2022). Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors. Remote Sensing, 14(1), 229. https://doi.org/10.3390/rs14010229