UAV-Based LiDAR Scanning for Individual Tree Detection and Height Measurement in Young Forest Permanent Trials
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. LiDAR Data Collection and Pre-Processing
2.3. Field Data and Photointerpretation
2.4. Individual Tree Detection Algorithms
2.5. Accuracy Evaluation
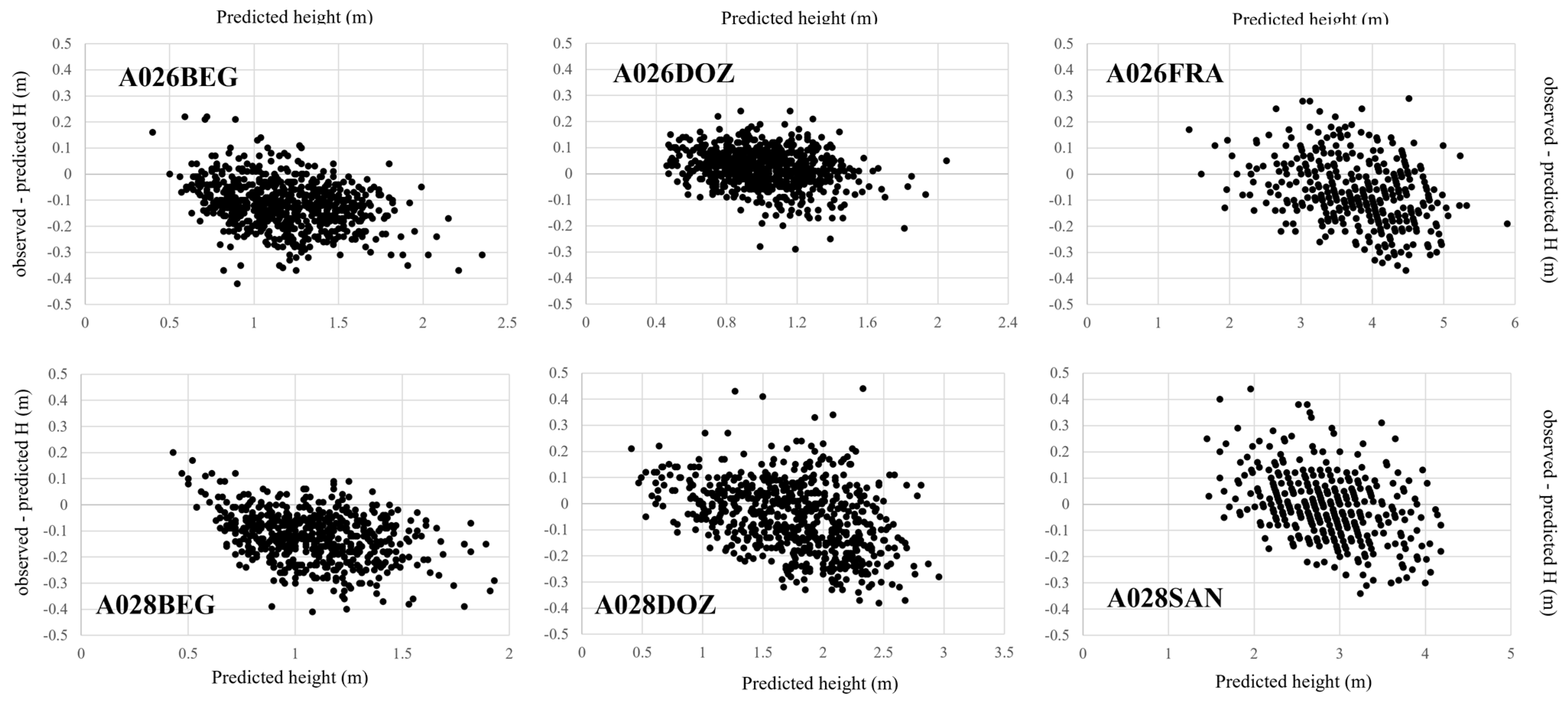
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Bolte, A.; Ammer, C.; Löf, M.; Nabuurs, G.-J.; Schall, P.; Spathelf, P. Adaptive Forest Management: A Prerequisite for Sustainable Forestry in the Face of Climate Change; Springer: Dordrecht, The Netherlands, 2010; pp. 115–139. ISBN 978-90-481-3300-0. [Google Scholar]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994; ISBN 978-0-85198-913-6. [Google Scholar]
- Wimberly, M.C.; Bare, B.B. Distance-Dependent and Distance-Independent Models of Douglas-Fir and Western Hemlock Basal Area Growth Following Silvicultural Treatment. For. Ecol. Manag. 1996, 89, 1–11. [Google Scholar] [CrossRef]
- Brandtberg, T. Automatic Individual Tree Based Analysis of High Spatial Resolution Aerial Images on Naturally Regenerated Boreal Forests. Can. J. For. Res. 1999, 29, 1464–1478. [Google Scholar] [CrossRef]
- Wang, L.; Gong, P.; Biging, G.S. Individual Tree-Crown Delineation and Treetop Detection in High-Spatial-Resolution Aerial Imagery. Photogramm. Eng. Remote Sens. 2004, 70, 351–357. [Google Scholar] [CrossRef]
- Brandtberg, T.; Walter, F. Automated Delineation of Individual Tree Crowns in High Spatial Resolution Aerial Images by Multiple-Scale Analysis. Mach. Vis. Appl. 1998, 11, 64–73. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A Review of Methods for Automatic Individual Tree-Crown Detection and Delineation from Passive Remote Sensing. Int. J. Remote Sens. 2011, 32, 4725–4747. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar Detection of Individual Tree Size in Tropical Forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Gomes, M.F.; Maillard, P.; Deng, H. Individual Tree Crown Detection in Sub-Meter Satellite Imagery Using Marked Point Processes and a Geometrical-Optical Model. Remote Sens. Environ. 2018, 211, 184–195. [Google Scholar] [CrossRef]
- Kansanen, K.; Vauhkonen, J.; Lähivaara, T.; Seppänen, A.; Maltamo, M.; Mehtätalo, L. Estimating Forest Stand Density and Structure Using Bayesian Individual Tree Detection, Stochastic Geometry, and Distribution Matching. ISPRS J. Photogramm. Remote Sens. 2019, 152, 66–78. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å. Identifying Species of Individual Trees Using Airborne Laser Scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Baltsavias, E.; Gruen, A.; Eisenbeiss, H.; Zhang, L.; Waser, L.T. High-quality Image Matching and Automated Generation of 3D Tree Models. Int. J. Remote Sens. 2008, 29, 1243–1259. [Google Scholar] [CrossRef]
- Waser, L.T.; Baltsavias, E.; Ecker, K.; Eisenbeiss, H.; Ginzler, C.; Küchler, M.; Thee, P.; Zhang, L. High-resolution Digital Surface Models (DSMs) for Modelling Fractional Shrub/Tree Cover in a Mire Environment. Int. J. Remote. Sens. 2008, 29, 1261–1276. [Google Scholar] [CrossRef]
- Hudak, A.T.; Haren, A.T.; Crookston, N.L.; Liebermann, R.J.; Ohmann, J.L. Imputing Forest Structure Attributes from Stand Inventory and Remotely Sensed Data in Western Oregon, USA. For. Sci. 2014, 60, 253–269. [Google Scholar] [CrossRef]
- Hansen, E.; Gobakken, T.; Bollandsås, O.; Zahabu, E.; Næsset, E. Modeling Aboveground Biomass in Dense Tropical Submontane Rainforest Using Airborne Laser Scanner Data. Remote Sens. 2015, 7, 788–807. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Karjalainen, M.; Nurminen, K.; Karila, K.; Vastaranta, M.; Kankare, V.; Kaartinen, H.; Holopainen, M.; Honkavaara, E.; et al. Comparison of Laser and Stereo Optical, SAR and InSAR Point Clouds from Air- and Space-Borne Sources in the Retrieval of Forest Inventory Attributes. Remote Sens. 2015, 7, 15933–15954. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Mišurec, J.; Kopačková, V.; Mielke, C.; Rogass, C. Assessment of Red-Edge Position Extraction Techniques: A Case Study for Norway Spruce Forests Using HyMap and Simulated Sentinel-2 Data. Forests 2016, 7, 226. [Google Scholar] [CrossRef]
- Zhang, Z.; Kazakova, A.; Moskal, L.; Styers, D. Object-Based Tree Species Classification in Urban Ecosystems Using LiDAR and Hyperspectral Data. Forests 2016, 7, 122. [Google Scholar] [CrossRef]
- St-Onge, B.; Vega, C.; Fournier, R.A.; Hu, Y. Mapping Canopy Height Using a Combination of Digital Stereo-photogrammetry and Lidar. Int. J. Remote Sens. 2008, 29, 3343–3364. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local Maximum Filtering for the Extraction of Tree Locations and Basal Area from High Spatial Resolution Imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, P. Accuracy of Airborne Lidar-Derived Elevation. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Silva, C.A.; Valbuena, R.; Pinagé, E.R.; Mohan, M.; de Almeida, D.R.A.; North Broadbent, E.; Jaafar, W.S.W.M.; de Almeida Papa, D.; Cardil, A.; Klauberg, C. ForestGapR: An r Package for Forest Gap Analysis from Canopy Height Models. Methods Ecol. Evol. 2019, 10, 1347–1356. [Google Scholar] [CrossRef]
- Picos, J.; Bastos, G.; Míguez, D.; Alonso, L.; Armesto, J. Individual Tree Detection in a Eucalyptus Plantation Using Unmanned Aerial Vehicle (UAV)-LiDAR. Remote Sens. 2020, 12, 885. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Cosenza, D.N.; Rodriguez, L.C.E.; Silva, M.; Tomé, M.; Díaz-Varela, R.A.; González-Ferreiro, E. Comparison of ALS- and UAV(SfM)-Derived High-Density Point Clouds for Individual Tree Detection in Eucalyptus Plantations. Int. J. Remote Sens. 2018, 39, 5211–5235. [Google Scholar] [CrossRef]
- Mohan, M.; Mendonça, B.A.F.; de Silva, C.A.; Klauberg, C.; de Saboya Ribeiro, A.S.; Araújo, E.J.G.; de Monte, M.A.; Cardil, A. Optimizing Individual Tree Detection Accuracy and Measuring Forest Uniformity in Coconut (Cocos nucifera L.) Plantations Using Airborne Laser Scanning. Ecol. Model. 2019, 409, 108736. [Google Scholar] [CrossRef]
- Hartley, R.J.L.; Leonardo, E.M.; Massam, P.; Watt, M.S.; Estarija, H.J.; Wright, L.; Melia, N.; Pearse, G.D. An Assessment of High-Density UAV Point Clouds for the Measurement of Young Forestry Trials. Remote Sens. 2020, 12, 4039. [Google Scholar] [CrossRef]
- Hao, Z.; Lin, L.; Post, C.; Yusen, J.; Li, M.; Wei, N.; Yu, K.; Liu, J. Assessing Tree Height and Density of a Young Forest Using a Consumer Unmanned Aerial Vehicle (UAV). New For. 2021, 52, 843–862. [Google Scholar] [CrossRef]
- Li, Y.; Hess, C.; von Wehrden, H.; Härdtle, W.; von Oheimb, G. Assessing Tree Dendrometrics in Young Regenerating Plantations Using Terrestrial Laser Scanning. Ann. For. Sci. 2014, 71, 453–462. [Google Scholar] [CrossRef]
- Zaforemska, A.; Xiao, W.; Gaulton, R. Individual tree detection from UAV LIDAR dta in a mixed species woodland. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 657–663. [Google Scholar] [CrossRef]
- Mohan, M.; Leite, R.V.; Broadbent, E.N.; Jaafar, W.S.W.M.; Srinivasan, S.; Bajaj, S.; Corte, A.P.D.; Amaral, C.H.; do Gopan, G.; Saad, S.N.M.; et al. Individual Tree Detection Using UAV-Lidar and UAV-SfM Data: A Tutorial for Beginners. Open Geosci. 2021, 13, 1028–1039. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned Aerial Systems for Photogrammetry and Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry Applications of UAVs in Europe: A Review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A Low-Cost Multi-Sensoral Mobile Mapping System and Its Feasibility for Tree Measurements. ISPRS J. Photogramm. Remote Sens. 2010, 65, 514–522. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Valbuena-Rabadán, M.-Á.; Santamaría-Peña, J.; Sanz-Adán, F. Estimation of Diameter and Height of Individual Trees for Pinus sylvestris L. Based on the Individualising of Crowns Using Airborne LiDAR and the National Forestry Inventory Data. For. Syst. 2016, 25, 046. [Google Scholar] [CrossRef]
- Korpela, I.; Anttila, P.; Pitkänen, J. The Performance of a Local Maxima Method for Detecting Individual Tree Tops in Aerial Photographs. Int. J. Remote Sens. 2006, 27, 1159–1175. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating Tree Detection and Segmentation Routines on Very High Resolution UAV LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Mohan, M.; Silva, C.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.; Dia, M. Individual Tree Detection from Unmanned Aerial Vehicle (UAV) Derived Canopy Height Model in an Open Canopy Mixed Conifer Forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Solberg, S.; Naesset, E.; Bollandsas, O.M. Single Tree Segmentation Using Airborne Laser Scanner Data in a Structurally Heterogeneous Spruce Forest. Photogramm. Eng. Remote Sens. 2006, 72, 1369–1378. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric Mapping of Forest Carbon Density from Airborne Laser Scanning and Hyperspectral Data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating Individual Trees in a Savanna Woodland Using Small Footprint Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Gupta, S.; Weinacker, H.; Koch, B. Comparative Analysis of Clustering-Based Approaches for 3-D Single Tree Detection Using Airborne Fullwave Lidar Data. Remote Sens. 2010, 2, 968–989. [Google Scholar] [CrossRef]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L.; Tomé, M.; Soares, P. 3-D Mapping of a Multi-Layered Mediterranean Forest Using ALS Data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- Lindberg, E.; Eysn, L.; Hollaus, M.; Holmgren, J.; Pfeifer, N. Delineation of Tree Crowns and Tree Species Classification From Full-Waveform Airborne Laser Scanning Data Using 3-D Ellipsoidal Clustering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3174–3181. [Google Scholar] [CrossRef]
- Xiao, W.; Xu, S.; Elberink, S.O.; Vosselman, G. Individual Tree Crown Modeling and Change Detection From Airborne Lidar Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3467–3477. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Mehtätalo, L.; Maltamo, M. Comparing Individual Tree Detection and the Area-Based Statistical Approach for the Retrieval of Forest Stand Characteristics Using Airborne Laser Scanning in Scots Pine Stands. Can. J. For. Res. 2011, 41, 583–598. [Google Scholar] [CrossRef]
- Goerndt, M.E.; Monleon, V.J.; Temesgen, H. Relating Forest Attributes with Area- and Tree-Based Light Detection and Ranging Metrics for Western Oregon. West. J. Appl. For. 2010, 25, 105–111. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.-P. Generalizing Predictive Models of Forest Inventory Attributes Using an Area-Based Approach with Airborne LiDAR Data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Z.; Tang, Y.; Qu, Y. Individual Tree Crown Detection from High Spatial Resolution Imagery Using a Revised Local Maximum Filtering. Remote Sens. Environ. 2021, 258, 112397. [Google Scholar] [CrossRef]
- Santos, A.A.; dos Marcato Junior, J.; Araújo, M.S.; Di Martini, D.R.; Tetila, E.C.; Siqueira, H.L.; Aoki, C.; Eltner, A.; Matsubara, E.T.; Pistori, H.; et al. Assessment of CNN-Based Methods for Individual Tree Detection on Images Captured by RGB Cameras Attached to UAVs. Sensors 2019, 19, 3595. [Google Scholar] [CrossRef] [PubMed]
- Zucon, A.R.S.; Hawkes, B.; Lemos, C.; Batistuzzo, G.Z.B.; Hakamada, R.; Pontes, G.R.; de Freitas, T.U.; de Bazani, J.H.; Alvares, C.A.; Junior, J.C.A.; et al. Use of Unmanned Aerial Vehicle Images as a Tool to Evaluate Stand Uniformity in Clonal Eucalyptus Plantations. In Proceedings of the Anais XVII Simpósio Brasileiro de Sensoriamento Remoto—SBSR, João Pessoa, PB, Brasil, 25–29 April 2015; INPE. [Google Scholar]
- Hakamada, R.E.; Stape, J.L.; Lemos, C.C.Z.; de Almeida, A.E.A.; Silva, L.F. Uniformidade entre árvore durante uma rotaçao como a productividade em Eucalyptus clonais. CERNE 2015, 21, 465–472. [Google Scholar] [CrossRef][Green Version]
- Hentz, Â.M.K.; Silva, C.A.; Dalla Corte, A.P.; Netto, S.P.; Strager, M.P.; Klauberg, C. Estimating Forest Uniformity in Eucalyptus Spp. and Pinus taeda L. Stands Using Field Measurements and Structure from Motion Point Clouds Generated from Unmanned Aerial Vehicle (UAV) Data Collection. For. Syst. 2018, 27, e005. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Caspersen, J.P.; Béland, M.; Thomas, S.C.; Achim, A. Removing Bias from LiDAR-Based Estimates of Canopy Height: Accounting for the Effects of Pulse Density and Footprint Size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Hyyppä, J.; Inkinen, M. Detecting and Estimating Attributes for Single Trees Using Laser Scanner. Photogramm. J. Finl. 1999, 16, 27–42. [Google Scholar]
- Hyyppä, J.; Hyyppä, H.; Litkey, P.; Yu, X.; Haggrén, H.; Rönnholm, P.; Pyysalo, U.; Pitkänen, J.; Maltamo, M. Algorithms and Methods of Airborne Laser Scanning for Forest Measurements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 82–89. [Google Scholar]
- Hyyppä, E.; Yu, X.; Kaartinen, H.; Hakala, T.; Kukko, A.; Vastaranta, M.; Hyyppä, J. Comparison of Backpack, Handheld, Under-Canopy UAV, and Above-Canopy UAV Laser Scanning for Field Reference Data Collection in Boreal Forests. Remote Sens. 2020, 12, 3327. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating Plot-Level Tree Heights with Lidar: Local Filtering with a Canopy-Height Based Variable Window Size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Persson, Å.; Holmgren, J.; Söderman, U. Detecting and Measuring Individual Trees Using an Airborne LIDAR. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined High-Density Lidar and Multispectral Imagery for Individual Tree Crown Analysis. Can. J. Remote. Sens. 2003, 29, 633–649. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree Height Quantification Using Very High Resolution Imagery Acquired from an Unmanned Aerial Vehicle (UAV) and Automatic 3D Photo-Reconstruction Methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Merino, A.; Balboa, M.A.; Rodríguez Soalleiro, R.; González, J.G.Á. Nutrient Exports under Different Harvesting Regimes in Fast-Growing Forest Plantations in Southern Europe. For. Ecol. Manag. 2005, 207, 325–339. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LiDAR Data Analysis and Visualization; Version 3.01; US Department of Agriculture, Forest Service, Pacific Northwest Research Station, University of Washington: Seattle, WA, USA, 2012.
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Plowright, A.; Plowright, M.A. R Package ‘ForestTools.’ CRAN. 2018. Available online: https://github.com/andrew-plowright/ForestTools (accessed on 21 December 2021).
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of Individual Longleaf Pine (Pinus palustris Mill.) Tree Attributes from Field and LiDAR Data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest: Using Lidar and Multispectral Data Fusion with Local Filtering and Variable Window Size for Estimating Tree Height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Meyer, F.; Beucher, S. Morphological Segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and F-Score, with Implication for Evaluation. In Proceedings of the Advances in Information Retrieval, Santiago de Compostela, Spain, 21–23 March 2005; Losada, D.E., Fernández-Luna, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond Accuracy, F-Score and ROC: A Family of Discriminant Measures for Performance Evaluation. In Proceedings of the AI 2006: Advances in Artificial Intelligence, Hobart, Australia, 4–8 December 2006; Sattar, A., Kang, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1015–1021. [Google Scholar]
- Kwak, D.-A.; Lee, W.-K.; Lee, J.-H.; Biging, G.S.; Gong, P. Detection of Individual Trees and Estimation of Tree Height Using LiDAR Data. J. For. Res. 2007, 12, 425–434. [Google Scholar] [CrossRef]
- Vasilescu, M.M. Standard Error of Tree Height Using Vertex III. Bulletin of the Transilvania University of Brasov. For. Wood Ind. Agric. Food Eng. Ser. II 2013, 6, 75. [Google Scholar]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is Field-Measured Tree Height as Reliable as Believed—A Comparison Study of Tree Height Estimates from Field Measurement, Airborne Laser Scanning and Terrestrial Laser Scanning in a Boreal Forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Wu, D.; Johansen, K.; Phinn, S.; Robson, A.; Tu, Y.-H. Inter-Comparison of Remote Sensing Platforms for Height Estimation of Mango and Avocado Tree Crowns. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102091. [Google Scholar] [CrossRef]
- Burt, A.; Disney, M.; Raumonen, P.; Armston, J.; Calders, K.; Lewis, P. Rapid Characterisation of Forest Structure from TLS and 3D Modelling; IEEE: Piscataway, NJ, USA, 2013; pp. 3387–3390. [Google Scholar]
- Erfanifard, Y.; Stereńczak, K.; Kraszewski, B.; Kamińska, A. Development of a Robust Canopy Height Model Derived from ALS Point Clouds for Predicting Individual Crown Attributes at the Species Level. Int. J. Remote Sens. 2018, 39, 9206–9227. [Google Scholar] [CrossRef]
- Paris, C.; Kelbe, D.; Van Aardt, J.; Bruzzone, L. A Novel Automatic Method for the Fusion of ALS and TLS LiDAR Data for Robust Assessment of Tree Crown Structure. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3679–3693. [Google Scholar] [CrossRef]
- Dai, W.; Yang, B.; Liang, X.; Dong, Z.; Huang, R.; Wang, Y.; Li, W. Automated Fusion of Forest Airborne and Terrestrial Point Clouds through Canopy Density Analysis. ISPRS J. Photogramm. Remote Sens. 2019, 156, 94–107. [Google Scholar] [CrossRef]
- Jiménez-Brenes, F.M.; López-Granados, F.; de Castro, A.I.; Torres-Sánchez, J.; Serrano, N.; Peña, J.M. Quantifying Pruning Impacts on Olive Tree Architecture and Annual Canopy Growth by Using UAV-Based 3D Modelling. Plant Methods 2017, 13, 55. [Google Scholar] [CrossRef] [PubMed]
- Johansen, K.; Raharjo, T.; McCabe, M.F. Using Multi-Spectral UAV Imagery to Extract Tree Crop Structural Properties and Assess Pruning Effects. Remote Sens. 2018, 10, 854. [Google Scholar] [CrossRef]
- Di Gennaro, S.F.; Nati, C.; Dainelli, R.; Pastonchi, L.; Berton, A.; Toscano, P.; Matese, A. An Automatic UAV Based Segmentation Approach for Pruning Biomass Estimation in Irregularly Spaced Chestnut Orchards. Forests 2020, 11, 308. [Google Scholar] [CrossRef]
- Muth, C.C.; Bazzaz, F.A. Tree Canopy Displacement and Neighborhood Interactions. Can. J. For. Res. 2003, 33, 1323–1330. [Google Scholar] [CrossRef]
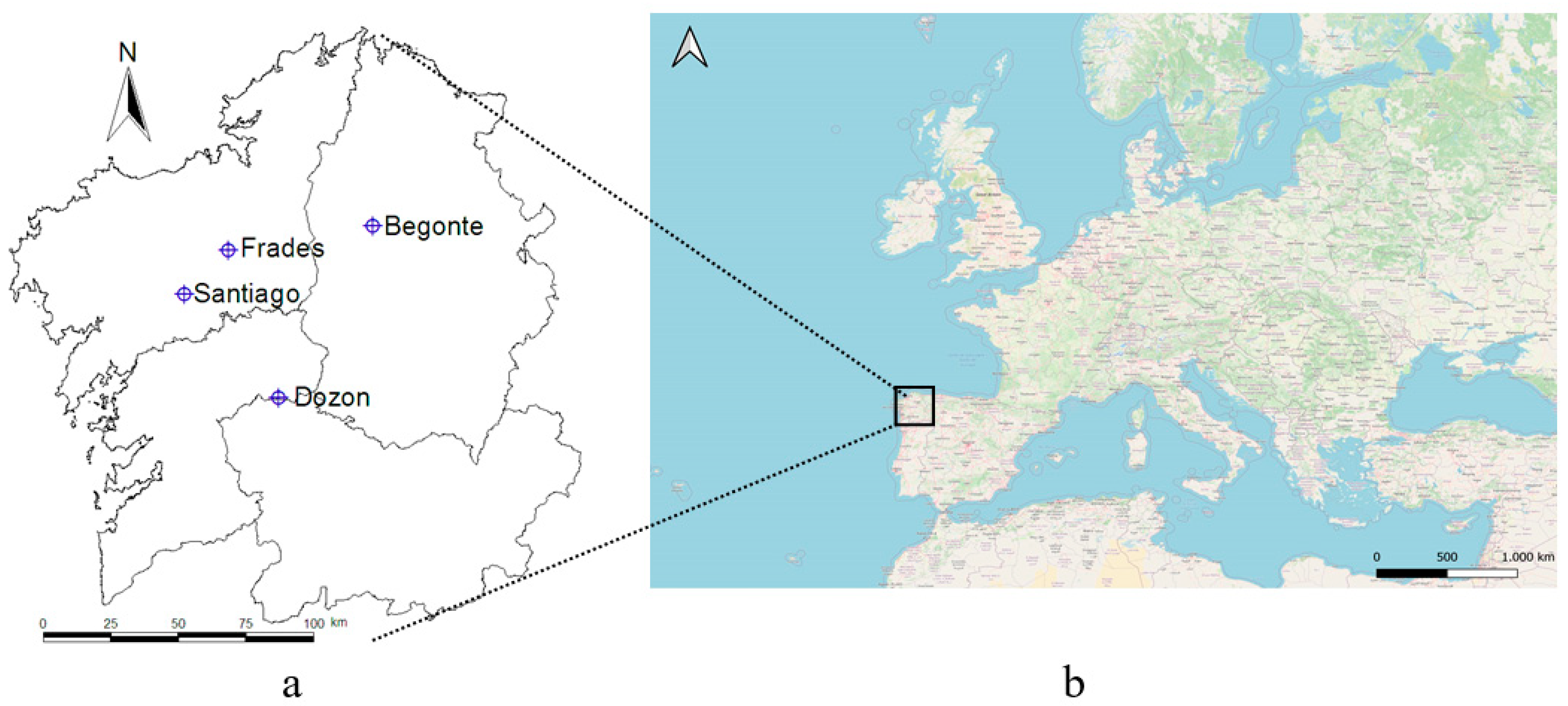
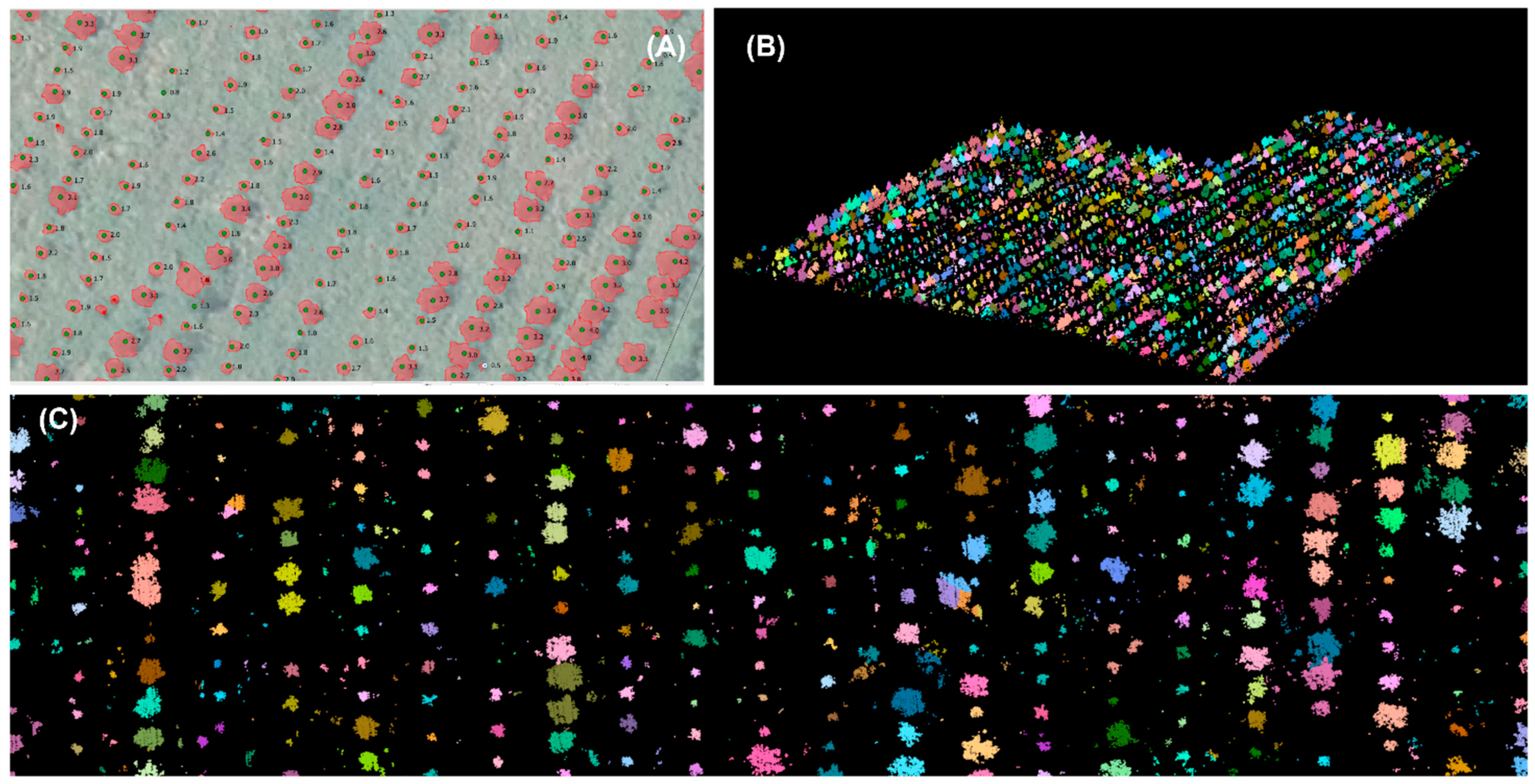

| Site | UTM Coordinates (X-Y) | Elevation (m) | Plantation (yr) | Species |
|---|---|---|---|---|
| Frades (FRA) | 556799-4766773 | 375 | 2016 | A026 |
| Santiago (SAN) | 540550-4750580 | 325 | 2017 | A028 |
| Dozon (DOZ) | 575255-4712433 | 770 | 2017, 2018 | A028, A026 |
| Begonte (BEG) | 609842-4775917 | 400 | 2019 | A026, A028 |
| Plot | N | Mean H (m) | Min H (m) | Max H (m) |
|---|---|---|---|---|
| A026BEG | 871 | 0.95 | 0.24 | 2.04 |
| A028BEG | 777 | 0.87 | 0.15 | 1.75 |
| A026DOZ | 776 | 1.03 | 0.36 | 2.10 |
| A028DOZ | 676 | 1.68 | 0.35 | 2.88 |
| A026FRA * | 420 | 3.70 | 1.60 | 5.70 |
| A028SAN * | 950 | 2.85 | 1.50 | 4.10 |
| RE (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Plot | ForestTools (CHM) | rLiDAR (CHM) | lidR (CHM) | lidR (Point-Cloud) | ||||||
| 0.1 | 0.25 | 0.5 | 0.1 | 0.25 | 0.5 | 0.1 | 0.25 | 0.5 | * | |
| A026BEG | −18.1 | −31.5 | −51.0 | −26.7 | −36.4 | −52.4 | −10.7 | −23.2 | −39.6 | −21.5 |
| A028BEG | −17.4 | −29.0 | −47.4 | −24.7 | −33.2 | −48.8 | −11.6 | −21.4 | −38.4 | −23.8 |
| A026DOZ | −7.0 | −14.6 | −31.4 | −9.5 | −16.0 | −33.6 | −3.5 | −8.5 | −26.4 | −10.4 |
| A028DOZ | −0.6 | −8.5 | −24.0 | −2.8 | −9.3 | −26.7 | −0.9 | −4.5 | −25.0 | −5.5 |
| A026FRA | −1.3 | −9.9 | −41.2 | −7.4 | −8.0 | −19.8 | 1.8 | 8.4 | −9.2 | 4.8 |
| A028SAN | −0.2 | −10.2 | −42.5 | −18.2 | −20.9 | −37.5 | −1.7 | −11.9 | −34.8 | −0.2 |
| RE (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean RE (%) | ForestTools (CHM) | rLiDAR (CHM) | lidR (CHM) | lidR (Point-Cloud) | ||||||
| 0.1 | 0.25 | 0.5 | 0.1 | 0.25 | 0.5 | 0.1 | 0.25 | 0.5 | * | |
| all Sites | −7.4 | −17.3 | −39.6 | −14.9 | −20.6 | −36.5 | −4.4 | −10.2 | −28.9 | −9.4 |
| Pinus pinaster | −8.8 | −18.7 | −41.2 | −14.5 | −20.2 | −35.3 | −4.1 | −7.8 | −25.1 | −9.1 |
| Pinus radiata | −6.1 | −15.9 | −38.0 | −15.2 | −21.1 | −37.7 | −4.7 | −12.6 | −32.7 | −9.8 |
| Plot | H(m) | r | p | F | RE (%) |
|---|---|---|---|---|---|
| A026BEG | 0.95 | 0.885 | 0.999 | 0.939 | −10.7 |
| A028BEG | 0.87 | 0.894 | 0.969 | 0.930 | −11.6 |
| A026DOZ | 1.03 | 0.948 | 0.999 | 0.973 | −3.5 |
| A028DOZ | 1.68 | 0.966 | 0.998 | 0.981 | −0.9 |
| A026FRA | 3.70 | 0.998 | 0.993 | 0.995 | 1.8 |
| A028SAN | 2.85 | 0.982 | 0.997 | 0.990 | −1.7 |
| Smoothed CHM (m) | Non-Smoothed CHM (m) | Point Cloud (m) | ||||
|---|---|---|---|---|---|---|
| Plot | BE | RMSE | BE | RMSE | BE | RMSE |
| A026BEG | 0.271 | 0.302 | 0.178 | 0.205 | −0.109 | 0.143 |
| A028BEG | 0.214 | 0.242 | 0.123 | 0.175 | 0.019 | 0.081 |
| A026DOZ | 0.245 | 0.279 | 0.112 | 0.159 | −0.047 | 0.121 |
| A028DOZ | 0.257 | 0.279 | 0.133 | 0.163 | −0.101 | 0.138 |
| A026FRA | 0.253 | 0.290 | 0.143 | 0.143 | −0.058 | 0.151 |
| A028SAN | 0.267 | 0.335 | 0.143 | 0.194 | 0.012 | 0.189 |
| all sites | 0.251 | 0.288 | 0.139 | 0.173 | −0.047 | 0.137 |
| Pinus pinaster | 0.243 | 0.274 | 0.138 | 0.180 | −0.046 | 0.115 |
| Pinus radiata | 0.259 | 0.301 | 0.139 | 0.166 | −0.049 | 0.160 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Puerta, F.; Gómez-García, E.; Martín-García, S.; Pérez-Rodríguez, F.; Prada, E. UAV-Based LiDAR Scanning for Individual Tree Detection and Height Measurement in Young Forest Permanent Trials. Remote Sens. 2022, 14, 170. https://doi.org/10.3390/rs14010170
Rodríguez-Puerta F, Gómez-García E, Martín-García S, Pérez-Rodríguez F, Prada E. UAV-Based LiDAR Scanning for Individual Tree Detection and Height Measurement in Young Forest Permanent Trials. Remote Sensing. 2022; 14(1):170. https://doi.org/10.3390/rs14010170
Chicago/Turabian StyleRodríguez-Puerta, Francisco, Esteban Gómez-García, Saray Martín-García, Fernando Pérez-Rodríguez, and Eva Prada. 2022. "UAV-Based LiDAR Scanning for Individual Tree Detection and Height Measurement in Young Forest Permanent Trials" Remote Sensing 14, no. 1: 170. https://doi.org/10.3390/rs14010170
APA StyleRodríguez-Puerta, F., Gómez-García, E., Martín-García, S., Pérez-Rodríguez, F., & Prada, E. (2022). UAV-Based LiDAR Scanning for Individual Tree Detection and Height Measurement in Young Forest Permanent Trials. Remote Sensing, 14(1), 170. https://doi.org/10.3390/rs14010170










