Fast Bayesian Compressed Sensing Algorithm via Relevance Vector Machine for LASAR 3D Imaging

Abstract

Because of the three-dimensional (3D) imaging scene’s sparsity, compressed sensing (CS) algorithms can be used for linear array synthetic aperture radar (LASAR) 3D sparse imaging. CS algorithms usually achieve high-quality sparse imaging at the expense of computational efficiency. To solve this problem, a fast Bayesian compressed sensing algorithm via relevance vector machine (FBCS–RVM) is proposed in this paper. The proposed method calculates the maximum marginal likelihood function under the framework of the RVM to obtain the optimal hyper-parameters; the scattering units corresponding to the non-zero optimal hyper-parameters are extracted as the target-areas in the imaging scene. Then, based on the target-areas, we simplify the measurement matrix and conduct sparse imaging. In addition, under low signal to noise ratio (SNR), low sampling rate, or high sparsity, the target-areas cannot always be extracted accurately, which probably contain several elements whose scattering coefficients are too small and closer to 0 compared to other elements. Those elements probably make the diagonal matrix singular and irreversible; the scattering coefficients cannot be estimated correctly. To solve this problem, the inverse matrix of the singular matrix is replaced with the generalized inverse matrix obtained by the truncated singular value decomposition (TSVD) algorithm to estimate the scattering coefficients correctly. Based on the rank of the singular matrix, those elements with small scattering coefficients are extracted and eliminated to obtain more accurate target-areas. Both simulation and experimental results show that the proposed method can improve the computational efficiency and imaging quality of LASAR 3D imaging compared with the state-of-the-art CS-based methods.

1. Introduction

Synthetic aperture radar (SAR) is a radar imaging technology and has been applied in different fields such as ocean surface monitoring [1], target identification and classification [2,3], resource exploration [4], and natural calamity monitoring [5] successfully because of its all-day and all-weather working capabilities. Traditional SAR images only reflect the two-dimensional (2D) information of targets while usually lose targets’ information in the height direction; they cannot reflect the three-dimensional (3D) structure of targets. This disadvantage limits the application of SAR seriously, and how to obtain targets’ 3D imaging results is an important research area in SAR imaging fields.

In recent years, scholars have obtained targets’ 3D information successfully under different SAR modes such as the tomography SAR (TomoSAR) [6], curvilinear SAR (CurSAR) [7], and linear array SAR (LASAR) [8,9]. The TomoSAR obtains the third-dimension imaging resolution by synthesizing the parallel baselines into a virtual aperture along the elevation direction [6]. The CurSAR usually synthesizes a curved array by controlling the moving trajectory of a single antenna; it combines the pulse compression technology to obtain the 3D imaging resolution [7]. The moving trajectories of both TomoSAR and CurSAR are strictly limited to achieve high-quality imaging, which limits their applications seriously [8]. In addition, the LASAR synthesizes the 2D equivalent array by the moving of linear array; it obtains the 3D imaging results of the imaging scene by combining the pulse compression technology. Compared with both TomoSAR and CurSAR, the LASAR has a better antenna phase center (APC) control accuracy and a flexible moving trajectory [8,9]. Therefore, the LASAR is studied for 3D imaging in this paper.

When performing the LASAR 3D imaging by the matched filter (MF) [10] algorithms, the array imaging resolution of LASAR is limited by the length of the linear array [11]. To realize high-quality imaging, the LASAR must satisfy the following two requirements:

• The spacing between adjacent elements in the linear array must satisfy the Nyquist sampling theorem to avoid the grating lobes [12].
• The echo signals of the whole linear array must be adopted to avoid the sidelobes interference as much as possible.

The above two requirements make the number of elements in the linear array very huge; the realization of the LASAR in the real hardware system is very complex and costly.

Compressed sensing (CS) algorithms [13,14,15,16] can recover the original sparse signals by using random sampling signals; they have been introduced into LASAR imaging successfully according to the sparsity of the LASAR imaging scene. When performing LASAR sparse imaging by different CS algorithms (e.g., the orthogonal matching pursuit (OMP) [17], the Bayesian compressed sensing (BCS) [18], the sparsity Bayesian recovery via iterative minimum (SBRIM) [19], and the iterative shrinkage thresholding (ISTA) [20] algorithm); those algorithms improve the array imaging resolution of LASAR. The linear array is usually replaced with the random sampling array to reduce the array elements used for sparse imaging.

Those CS algorithms must set several parameters (e.g., the sparsity of the imaging scene, the hyper-parameters in the BCS algorithms, the iteration stepsize in the ISTA algorithm) manually before conducting sparse imaging. Once the preset parameters are set inappropriately; CS algorithms probably suffer from the sidelobe interferences seriously and even cannot estimate the scattering coefficients correctly. Their computational complexity probably increase significantly. Those preset parameters cannot always meet the requirement of high-quality sparse imaging under different LASAR data; they need to be debugged repeatedly. Since the preset parameters usually do not need to be re-debugged under different LASAR data, the SBRIM algorithm obtains imaging results with relatively high quality among CS algorithms. However, its computational complexity is very huge because of the high-dimensional matrix operations (e.g., the matrix-inversion); the hardware system must have very strong computational power to complete the high-dimensional matrix operations. This disadvantage limits the applications of the SBRIM algorithm in 3D sparse imaging seriously. Therefore, we need to study how to improve the computational efficiency of the SBRIM algorithm under the premise of ensuring imaging quality.

Due to the strong sparsity of the 3D imaging scene, the target-areas usually only occupy a small part of the whole imaging scene. The measurement matrix in sparse imaging usually contains a large number of elements which are not related to the targets. Therefore, the computational efficiency of sparse imaging can be improved effectively by simplifying the measurement matrix. In our previous research, the fast sparse recovery algorithm via resolution approximation (FSRARA) [21] improves the computational efficiency of sparse imaging successfully through simplifying the measurement matrix according to the target-areas in the imaging scene. However, once the 3D preliminary imaging results are not obtained correctly, the FSRARA cannot extract the target-areas accurately and estimate the scattering coefficients correctly. Its imaging quality and computational efficiency decrease significantly. Therefore, we need to study a new fast CS algorithm for LASAR 3D imaging.

In this paper, we propose a fast Bayesian compressed sensing (FBCS–RVM) algorithm via relevance vector machine to achieve LASAR 3D sparse imaging with high efficiency and quality. Under the framework of the relevance vector machine (RVM) [22], every scattering unit in the imaging scene is given an independent hyper-parameter to measure its scattering coefficient’s estimation accuracy. The optimal hyper-parameters are obtained successfully by calculating the maximum marginal likelihood function, and the scattering units corresponding to the non-zero elements in the optimal hyper-parameters are extracted as the target-areas. Then, the target-areas are used as the prior information to simplify the measurement matrix and conduct sparse imaging. Under several imaging conditions (e.g., low signal to noise ratio (SNR) [23], low sampling rate, or high sparsity of the imaging scene), the target-areas cannot be always extracted accurately. They probably contain several elements whose scattering coefficients are too small or closer to 0 compared to other elements. Those elements make the diagonal matrix (which is calculated by the measurement matrix and the preliminary estimation values of the scattering coefficients; it is used to obtain the optimal scattering coefficients) singular and irreversible; the scattering coefficients cannot be estimated correctly. To solve this problem, the inverse matrix of the singular matrix is replaced with the generalized inverse matrix obtained by the truncated singular value decomposition (TSVD) [24] algorithm to correctly estimate the scattering coefficients. These elements with small scattering coefficients are extracted and eliminated to obtain more accurate target-areas. The main contributions of this paper are summarized as the following content:

1.

The FBCS–RVM algorithm is proposed to achieve LASAR 3D sparse imaging with high imaging quality and computational efficiency.

2.

The FBCS–RVM algorithm extracts scattering units corresponding to the non-zero optimal hyper-parameters in the RVM as the target-areas in the imaging scene.

3.

The FBCS–RVM algorithm correctly estimates the scattering coefficients and obtains more accurate target-areas through eliminating the elements with small scattering coefficients in the target-areas by the TSVD algorithm.

The remaining sections are arranged as: the sparse imaging model of LASAR is given in Section 2. The basic principles of the FBCS–RVM algorithm are introduced in Section 3. Section 4 conducts the simulation and experimental results to illustrate the effectiveness and evaluate the performance of the FBCS–RVM algorithm. Section 5 and Section 6 give the discussions and conclusions of this paper, respectively.

2. The Sparse Imaging Model of LASAR

According to Figure 1, the linear array is located in the CT direction. LASAR obtains a 2D equivalent array by moving along the AT direction under a constant speed, and it obtains the 3D imaging results after combining the range compression technology. When conducting LASAR 3D imaging, the 3D imaging scene is usually considered as composed of discrete scattering units. After performing range compression on the original echo signals, according to the range information of the sampling points in the range domain, the 3D imaging scene is divided into $N_R$ equidistant planar 2D imaging scene along the range direction. Every equidistant planar 2D imaging scene is divided into M discrete scattering units with uniform spacing, where $N_R$ is the number of sampling points in the range domain.

Figure 1. The geometric model of LASAR. The x, y, and z-axes represent the along-track (AT), cross-track (CT) direction, and height direction, respectively.

Set the LASAR to transmit the linear frequency modulation (LFM) signal [25]. After range compression, the lth APC’s echo signal in the nth equidistant plane is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathit{s}}_r(n,l)=\sum _{m=1}^M{\alpha }_{n_m}{\chi }_R(r_n-R_{n,l,m})\exp \{-j2k{R}_{n,l,m}\}\end{array}\end{array}$$

(1)

where $n=1,\cdots ,N_R$, $l=1,\cdots ,{\mathit{N}}_A$, and $m=1,\cdots ,\mathit{M}$. ${\mathit{N}}_A$ denotes the total number of APCs in the 2D equivalent array. $\mathit{r}$ represents the range domain. $\mathit{k}$ represents the wave-number of LASAR. $R_{n,l,m}={\parallel {\mathit{Q}}_l-{\mathit{P}}_{n_m}\parallel }_2$ is the distance between ${\mathit{Q}}_l$ and ${\mathit{P}}_{n_m}$. $Q_l=({\mathit{x}}_{\mathit{l}},{\mathit{y}}_{\mathit{l}},{\mathit{z}}_{\mathit{l}})$ is the 3D coordinate of the lth APC in the 2D equivalent array. ${\alpha }_{n_m}$ and $P_{n_m}=({\mathit{x}}_{{\mathit{n}}_{\mathit{m}}},{\mathit{y}}_{{\mathit{n}}_{\mathit{m}}},{\mathit{z}}_{{\mathit{n}}_{\mathit{m}}})$ represent the scattering coefficient and 3D coordinate of the mth scattering unit in the nth equidistant plane. ${\chi }_R(.)$ represents the ambiguity function in the range direction.

Set ${\psi }_n(m,l)={\chi }_R(r_n-R_{n,l,m})\exp (-j2k{R}_{n,l,m})$ to represent the delay phase between ${\mathit{P}}_{n_m}$ and ${\mathit{Q}}_l$; the echo signal ${\mathit{s}}_r(n,l)$ can be decomposed as:

$$\begin{array}{c}\hfill {\mathit{s}}_r(n,l)={\psi }_n{\left(l\right)}^T{\mathbf{\alpha }}_n\end{array}$$

(2)

where ${\psi }_n\left(l\right)=\mathrm{Vec}\left[{\psi }_n(m,l)\right]\in {\mathbb{C}}^{M\times 1}$. ${\mathbf{\alpha }}_n=\mathrm{Vec}\left[{\alpha }_{n_m}\right]\in {\mathbb{C}}^{M\times 1}$. $m=1,\cdots ,M$. $\mathrm{Vec}[.]$ is the vectorized symbol. ${\mathbf{\alpha }}_n$ is the nth equidistant planar scattering coefficients.

When considering all APCs in the 2D equivalent array, the linear representation model of the nth equidistant planar echo signal is defined as:

$$\begin{array}{c}\hfill s_n={\mathsf{\Theta }}_n{\mathbf{\alpha }}_n+\mathbf{\xi }\end{array}$$

(3)

where $s_n=\mathrm{Vec}[s_r(n,l),l=1,\cdots ,{\mathit{N}}_A]\in {\mathbb{C}}^{N_A\times 1}$ represents the echo signal of the nth equidistant plane after range compression. ${\mathsf{\Theta }}_n=\mathrm{Vec}{[{\psi }_n(m,l),l=1,\cdots ,{\mathit{N}}_A,m=1,\cdots ,\mathit{M}]}^T\in {\mathbb{C}}^{N_A\times M}$ represents the measurement matrix corresponding to $s_n$ and is composed of the phase delay between the APCs in the 2D array and the scattering units in the imaging scene. $\mathbf{\xi }$ is the signal noise in $s_n$.

Therefore, based on the CS theory, sparse imaging on the nth equidistant planar imaging scene is translated into getting the optimal value of the scattering coefficients ${\mathbf{\alpha }}_n$ by solving the $L_1$ norm optimization problem in Equation (4). In addition, the 3D imaging results are obtained by combining all equidistant planar 2D imaging results according to their information in the range direction:

$$\begin{array}{c}\hfill {\widehat{\mathbf{\alpha }}}_n=arg\underset{{\mathbf{\alpha }}_n}{min}{∥{\mathbf{\alpha }}_n∥}_1\mathrm{s}.\mathrm{t}{∥s_n-{\mathsf{\Theta }}_n{\mathbf{\alpha }}_n∥}_2^{}\le \epsilon \end{array}$$

(4)

where $\epsilon$ is the termination threshold of the signal noise.

However, when performing LASAR sparse imaging by CS algorithms, the parameters (e.g., the termination threshold $\epsilon$ or the sparsity of the imaging scene) should be debugged carefully and repeatably in most cases; this usually produces extensive computational complexity. In addition, the high-dimensional matrix operations in the several CS algorithms (e.g., the BCS and SBRIM algorithm) make their computational complexity huge. The huge computational complexity requires very strong computational power on the hardware system. Since the measurement matrix ${\mathsf{\Theta }}_n$ in Equation (3) is corresponding to all scattering units in the imaging scene, ${\mathsf{\Theta }}_n$ usually contains lots of elements that are not related to the targets because of the sparsity of the imaging scene. Therefore, we propose the FBCS–RVM algorithm to improve the computational efficiency of sparse imaging, which can extract the target-areas in the imaging scene and simplify the measurement matrix and its corresponding matrix operations.

3. FBCS–RVM

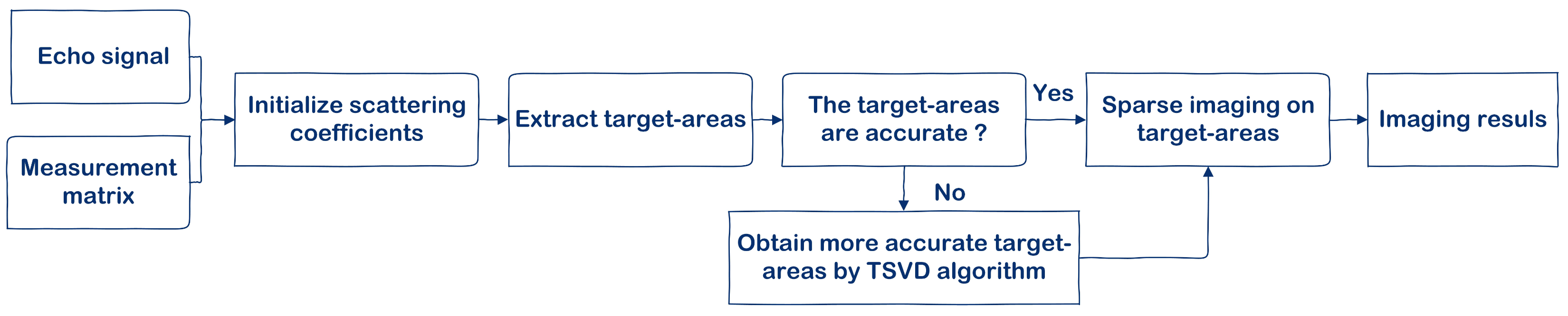
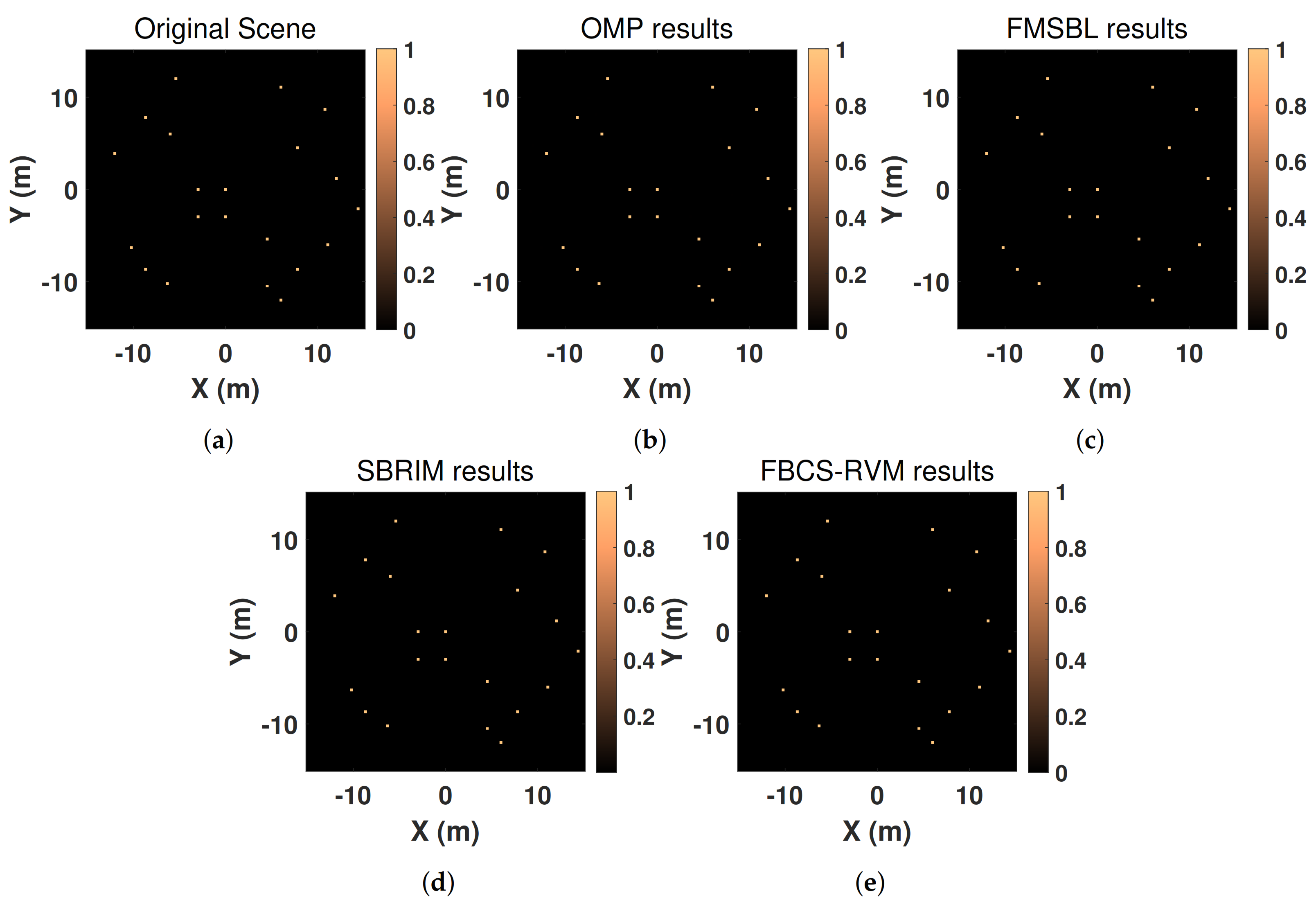
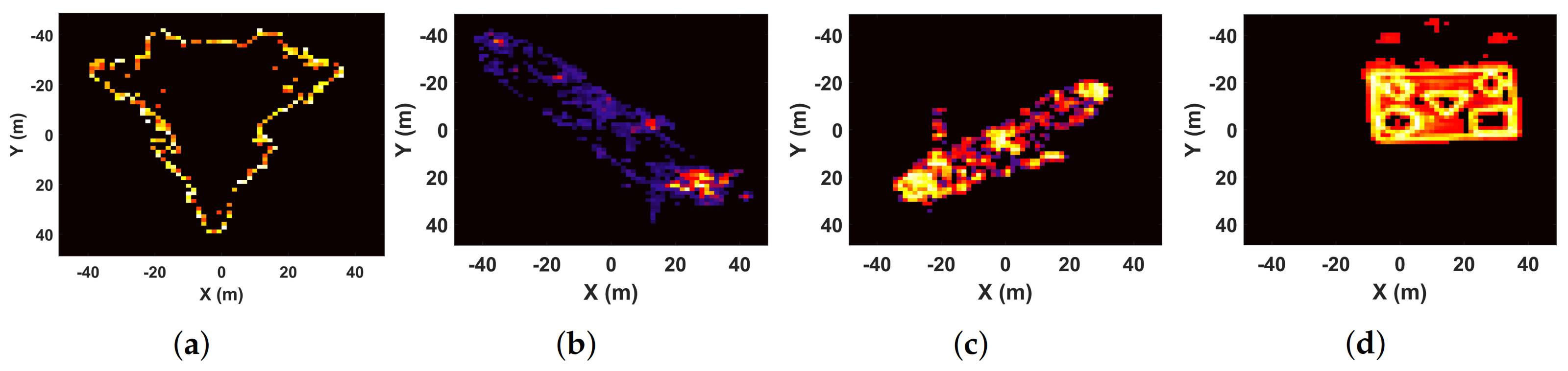
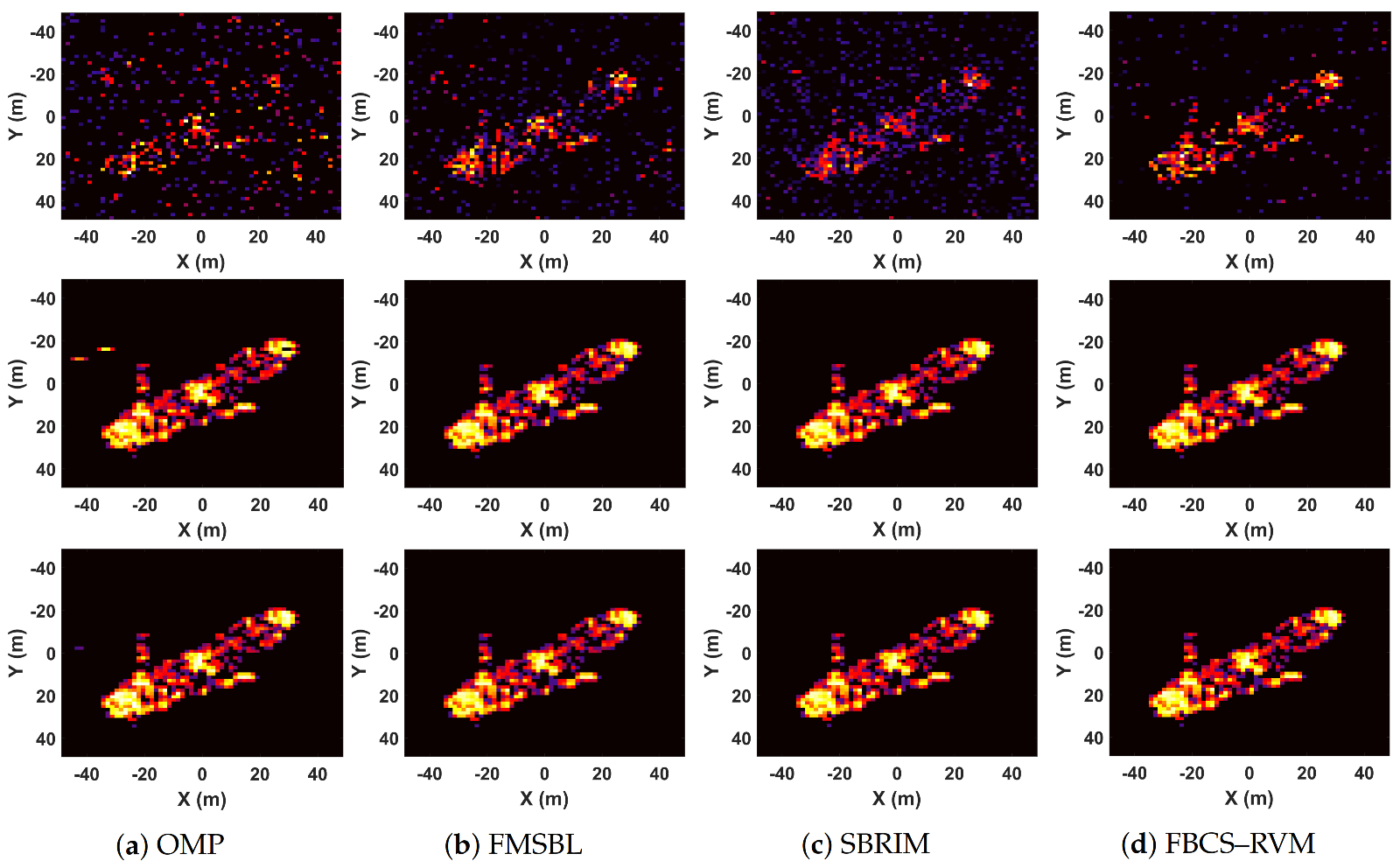
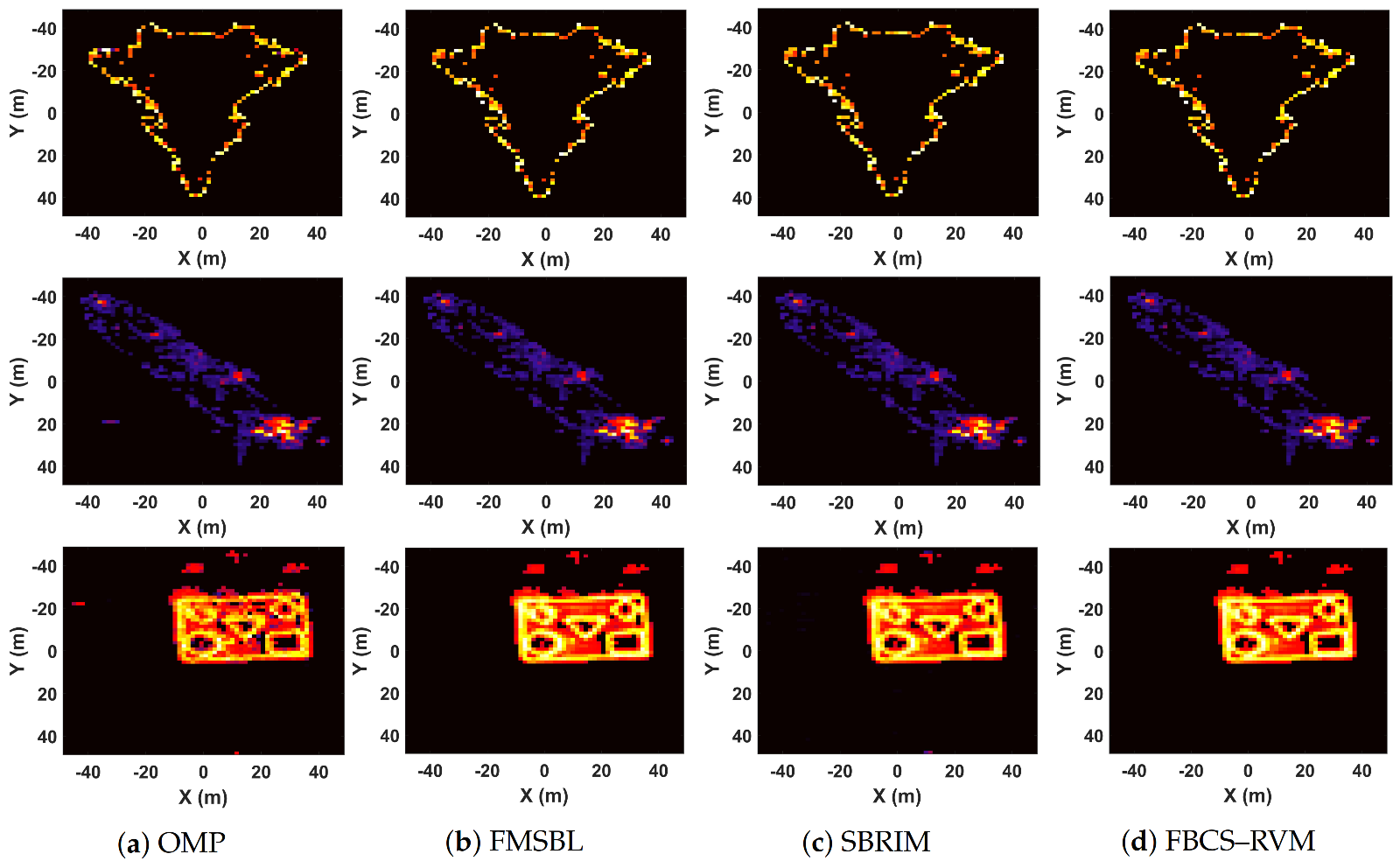
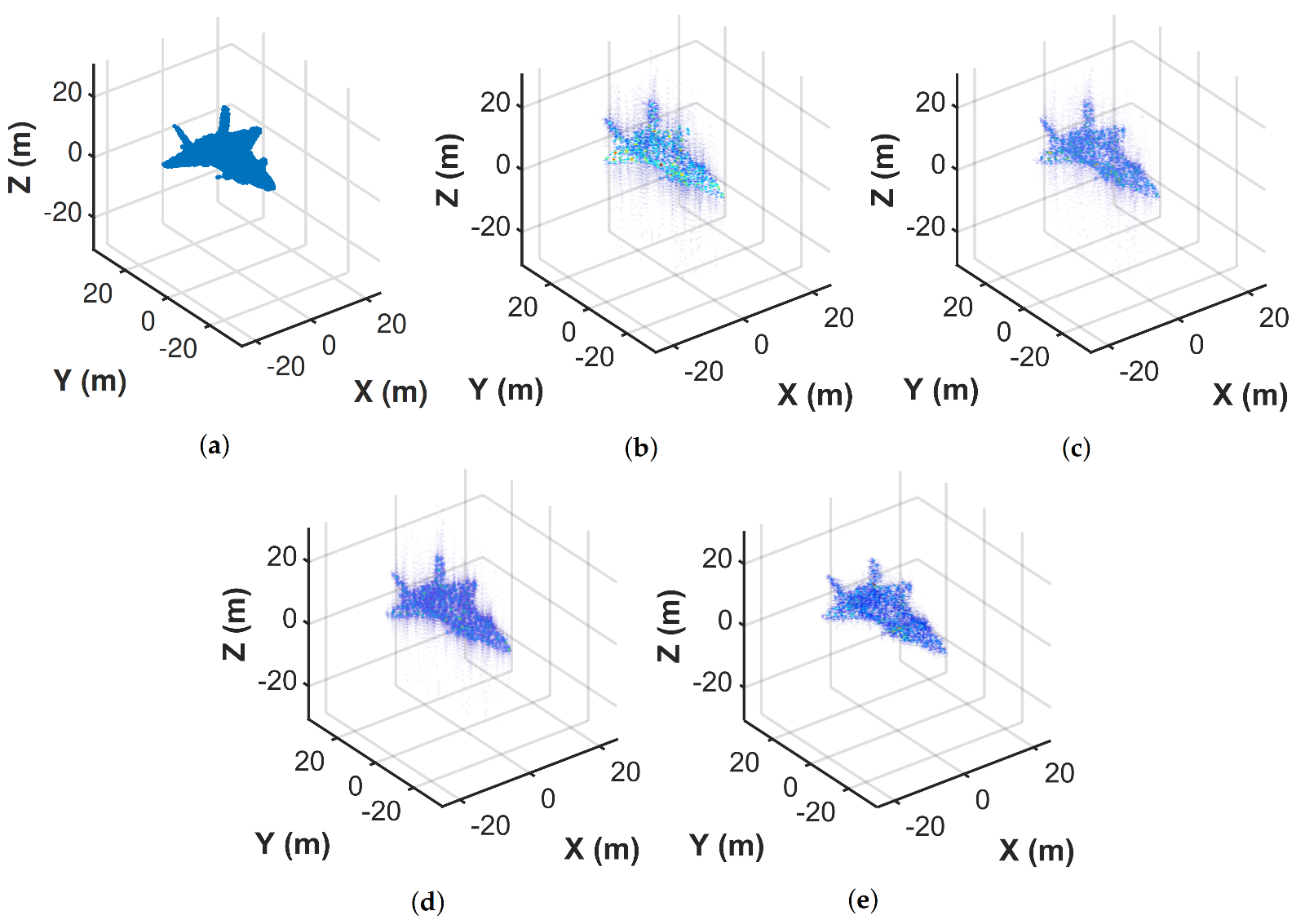
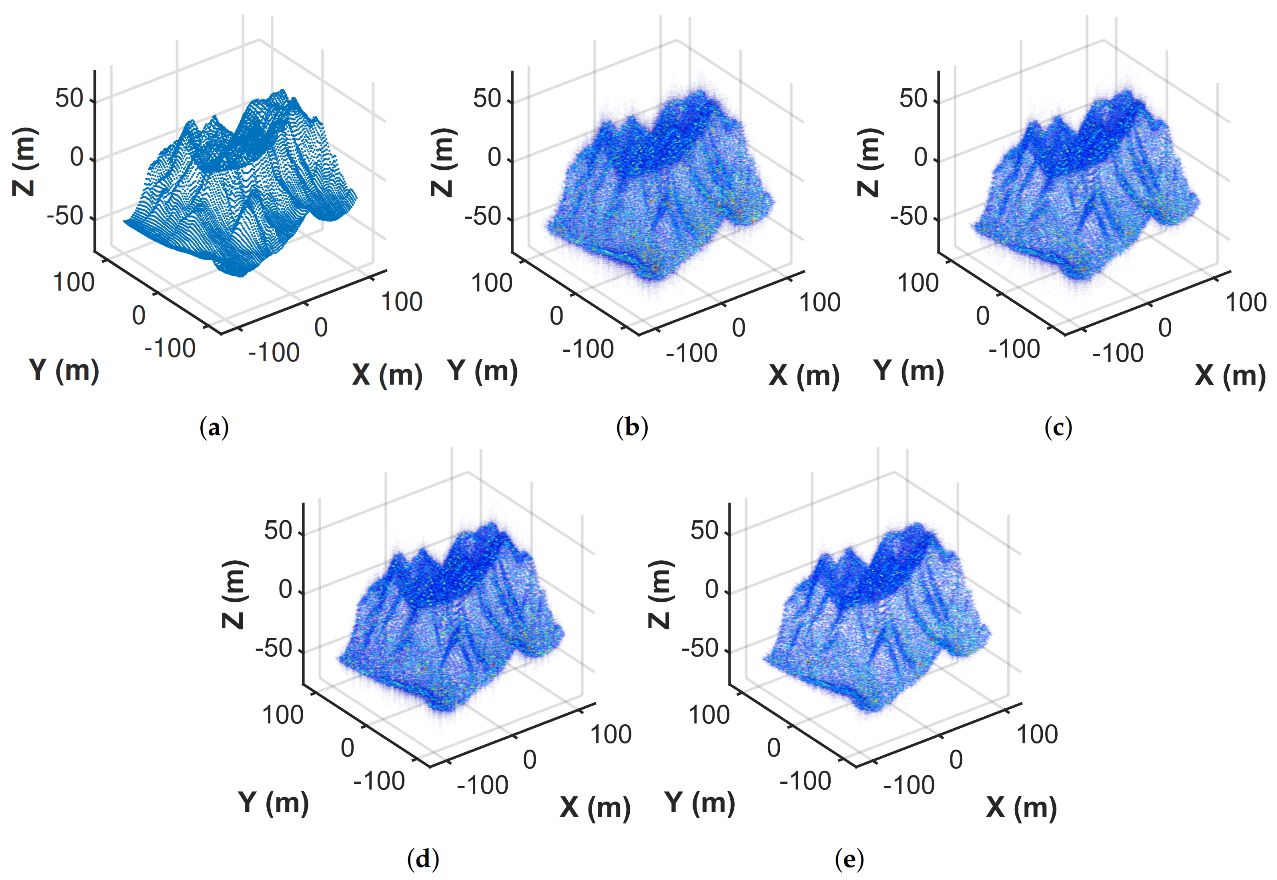
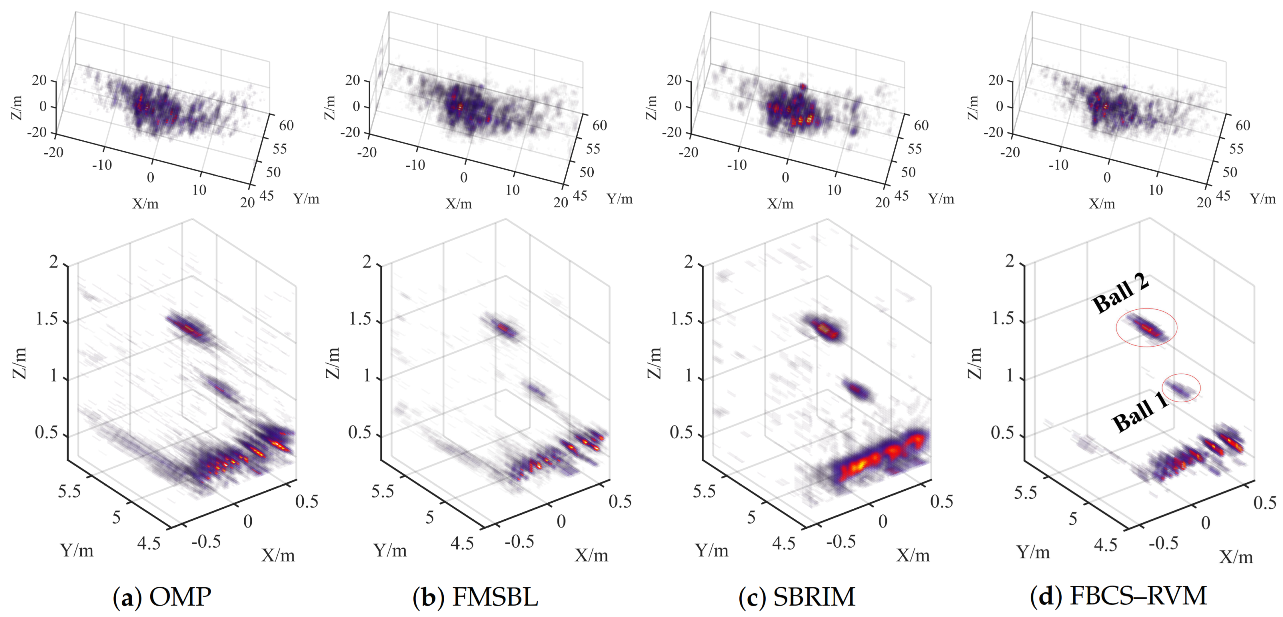
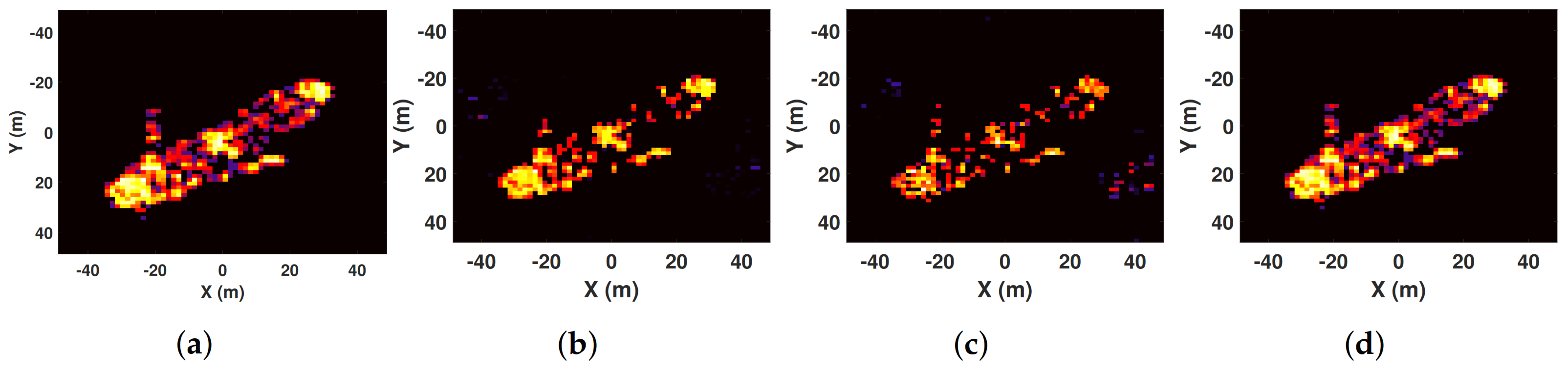
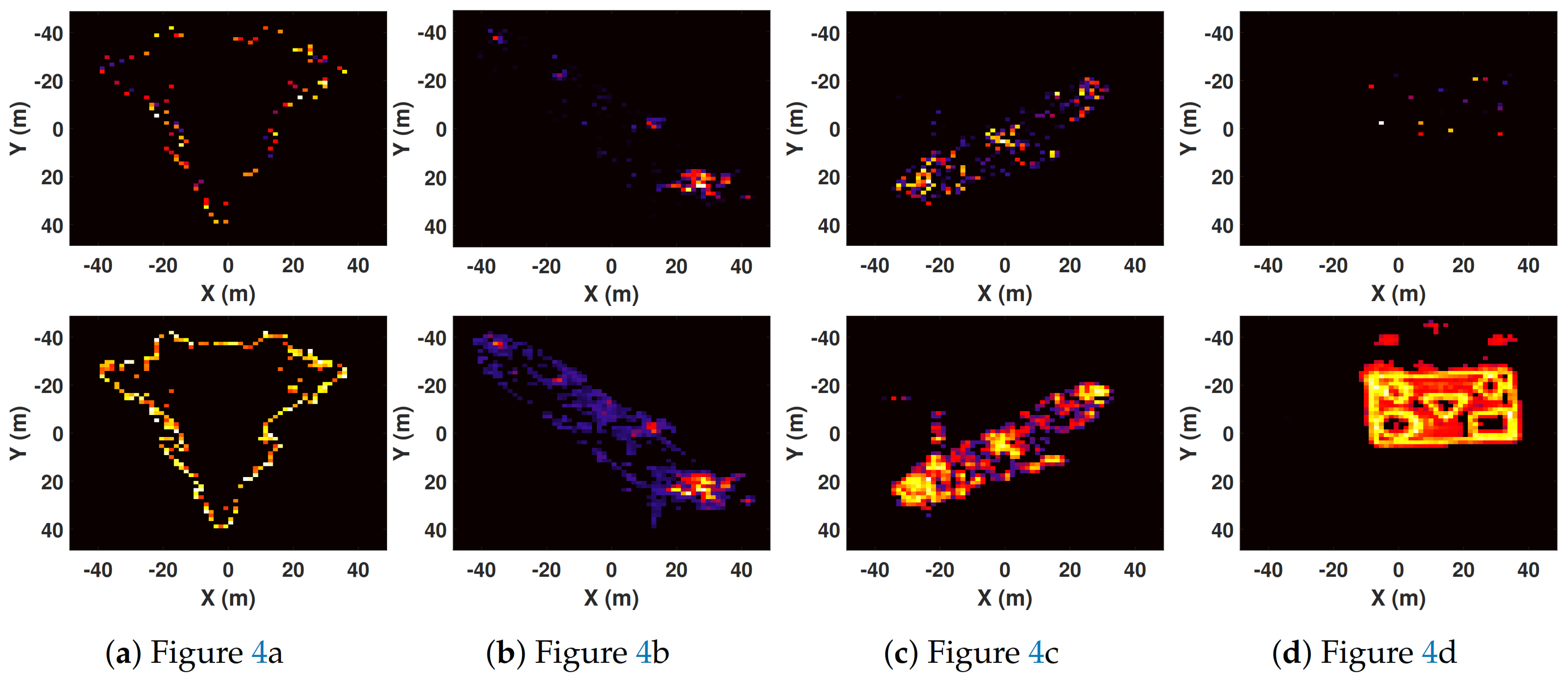
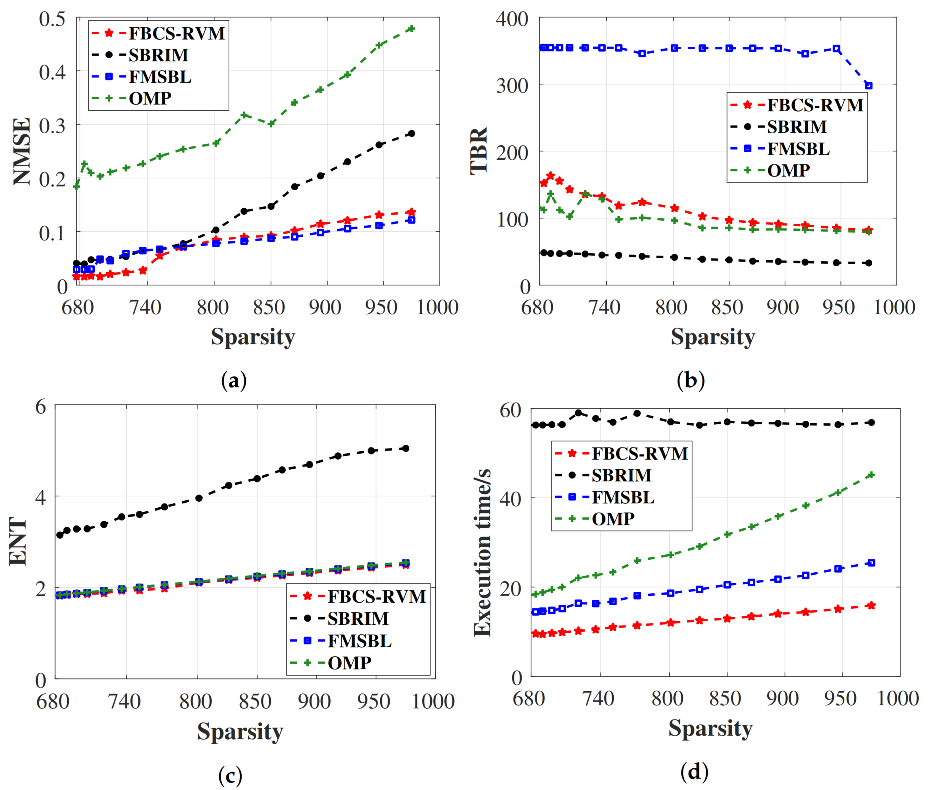
In this section, the FBCS–RVM algorithm is proposed to achieve sparse imaging with high quality and efficiency, which mainly includes two parts: extracting the target-areas and sparse imaging on the target-areas. Firstly, based on the sparsity of the 3D imaging scene, we treat extracting the target-areas as the classification of targets and background in the imaging scene. Inspired by the relevance vector machine (RVM) [22], we obtain the target-areas successfully by calculating the maximum marginal likelihood function in the RVM to classify the scattering units. Secondly, we use the target-areas as the prior information to simplify the measurement matrix and achieve sparse imaging with high efficiency. However, when the target-areas contain several elements whose scattering coefficients are too small or closer to zero compared to other elements, the diagonal matrix in sparse imaging becomes singular and the scattering coefficients cannot be correctly estimated. Then, we introduce the truncated singular value decomposition (TSVD) algorithm [24] to correctly estimate scattering coefficients and eliminate the elements with too small scattering coefficients in the target-areas.

According to Section 2, the 3D sparse imaging has been translated into 2D sparse imaging on every equidistant planar 2D imaging scene. We choose 2D sparse imaging on the nth equidistant planar 2D imaging scene as an example to introduce the basic steps of the FBCS–RVM algorithm in the following section. In addition, its flowchart is shown in Figure 2.

Figure 2. The flowchart of the FBCS–RVM algorithm.

3.1. Extract the Target-Areas in the Imaging Scene

In this subsection, we classify the scattering units to extract the target-areas by calculating the maximum marginal likelihood function in the RVM. In addition, the maximum marginal likelihood function is obtained by calculating its maximum value corresponding to every scattering unit to improve the computational efficiency. The basic steps of extracting the target-areas are introduced in the following content.

Step 1: Obtain the real-valued echo signal and measurement matrix.

Since the RVM only can deal with real-valued data and both the echo signal $s_n$ and measurement matrix ${\mathsf{\Theta }}_n$ are complex-valued data, both $s_n$ and ${\mathbf{\alpha }}_n$ are represented equivalently by their real and imaginary parts before classifying the scattering units. The real-valued echo signal $s_{n_r}\in {\mathbb{C}}^{2N_A\times 1}$ and scattering coefficients ${\mathbf{\alpha }}_{n_r}\in {\mathbb{C}}^{2M\times 1}$ are obtained by Equation (5):

$$\begin{array}{c}\hfill s_{n_r}=\left\{\begin{array}{c}\mathrm{Re}\left(s_r(n,l)\right)\\ \mathrm{Im}\left(s_r(n,l)\right)\end{array}\right\}{\mathbf{\alpha }}_{n_r}=\left\{\begin{array}{c}\mathrm{Re}\left({\mathbf{\alpha }}_{n_m}\right)\\ \mathrm{Im}\left({\mathbf{\alpha }}_{n_m}\right)\end{array}\right\}\end{array}$$

(5)

where $l=1,\cdots ,N_A$ and $m=1,\cdots ,M$. $\mathrm{Re}(·)$ and $\mathrm{Im}(·)$ are the real and imaginary parts of the complex-valued data, respectively. Based on the equivalent representation of complex-valued echo signal and scattering coefficients in Equation (5), the echo signals’ linear representation model in Equation (3) is equivalently represented as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill s_{n_r}={\mathsf{\Theta }}_{n_r}{\mathbf{\alpha }}_{n_r}+{\mathbf{\xi }}_r\end{array}\end{array}$$

(6)

where ${\mathbf{\xi }}_r$ is the signal noise in $s_{n_r}$. ${\mathsf{\Theta }}_{n_r}$ is the real-valued measurement matrix and shown in Equation (7):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathsf{\Theta }}_{n_r}=\left\{\begin{array}{cc}\mathrm{Re}\left({\mathsf{\Theta }}_n(m,l)\right)& -\mathrm{Im}\left({\mathsf{\Theta }}_n(m,l)\right)\\ \mathrm{Im}\left({\mathsf{\Theta }}_n(m,l)\right)& \mathrm{Re}\left({\mathsf{\Theta }}_n(m,l)\right)\end{array}\right\}\end{array}\end{array}$$

(7)

Step 2: Initialize the basic parameters: the nth equidistant planar scattering coefficients ${\widehat{\mathbf{\alpha }}}_{n_r}^0$ and their corresponding hyper-parameters ${\lambda }_n^0$.

Based on Equation (6) and the matched filter (MF) algorithm, the initial scattering coefficients ${\widehat{\mathbf{\alpha }}}_{n_r}^0$ of the nth equidistant planar imaging scene are obtained by Equation (8):

$$\begin{array}{c}\hfill {\widehat{\mathbf{\alpha }}}_{n_r}^0=\{{\widehat{\alpha }}_{n_{r_m}}^0={\displaystyle \frac{{∥{\varphi }_{r_m}^T{s}_{n_r}∥}^2}{{\left(\sum {\varphi }_{r_m}^2\right)}^T}},1\le m\le 2M\}\end{array}$$

(8)

where ${\varphi }_{r_m}$ is the mth column vector in ${\mathsf{\Theta }}_{n_r}$. M is the total number of the scattering units in the nth equidistant plane. Then, the independent hyper-parameters are introduced to evaluate the estimation accuracy and initialized by ${\lambda }_n^0=\{{\lambda }_{n_m}^0=0,1\le m\le 2M\}$.

Step 3: Select the maximum element in ${\widehat{\mathbf{\alpha }}}_{n_r}^0$ as the initial target-areas.

To ensure the extraction of the scattering unit where targets as the initial target-areas exist, the scattering unit corresponding to the maximum element in ${\widehat{\mathbf{\alpha }}}_{n_r}^0$ is considered as the initial target-areas ${\mathit{G}}_{n_r}^0$, which is the global maximum element and unique in the nth equidistant planar 2D imaging scene; it is also the local maximum value in the 3D imaging scene. Its serial number in the imaging scene is $I{d}_0$. Its hyper-parameter ${\lambda }_{n_{I{d}_0}}^0$ is calculated by Equation (9) to avoid full-zero hyper-parameters ${\lambda }_n^0$:

$$\begin{array}{c}\hfill {\lambda }_{n_{I{d}_0}}^0={\displaystyle \frac{{∥{\varphi }_{r_0}{s}_{n_r}∥}^2}{\max \left({\widehat{\mathbf{\alpha }}}_{n_r}^0\right)-{\beta }_0}}\end{array}$$

(9)

where ${\varphi }_{r_0}={\mathsf{\Theta }}_{n_r}\left(:,I{d}_0\right)$. ${\beta }_0$ is the variance of the signal noise in $s_{n_r}$.

Step 4: Calculate the optimal hyper-parameters to extract the target-areas.

We calculate the maximum marginal likelihood function in the RVM [26] after several iterations to obtain the optimal hyper-parameters; the scattering units corresponding to the non-zero optimal hyper-parameters are extracted as the target-areas. In the tth iteration, the marginal likelihood function $L\left({\lambda }_n^t\right)$ is shown in Equation (10) and related to the echo signal, measurement matrix, and hyper-parameter’ estimation value:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill L\left({\lambda }_n^t\right)& =-{\displaystyle \frac{1}{2}}\left[2Mlog2\pi +log|{\mathit{C}}_t|+s_{n_r}^T{\mathit{C}}_t^{-1}{s}_{n_r}\right]\hfill \end{array}\end{array}$$

(10)

where ${\mathit{C}}_t=\beta \mathit{I}+{\mathsf{\Theta }}_{n_r}{\left({\Lambda }_{\lambda }^t\right)}^{-1}{\mathsf{\Theta }}_{n_r}^T\in {\mathbb{C}}^{2N_A\times 2N_A}$. $\mathit{I}$ is the identity matrix. $\beta$ is the variance of signal noise in $s_{n_r}$. ${\Lambda }_{\lambda }^t=\mathrm{diag}({\lambda }_{n_i}^t,i=1,\cdots ,2M)$ and ${\lambda }_n^t=\{{\lambda }_{n_i}^t,i=1,\cdots ,2M\}$ are the diagonal matrix and vector of the hyper-parameters in the tth iteration, respectively.

If we calculate the maximum $L\left({\lambda }_n^t\right)$ directly, the computational complexity is huge because of the matrix operations on ${\mathit{C}}_t$. To solve this problem, $L\left({\lambda }_n^t\right)$ is decomposed into two parts corresponding to one and other hyper-parameters, respectively. The maximum $L\left({\lambda }_n^t\right)$ can be obtained by calculating its maximum value corresponding to every hyper-parameter. For example, when only considering the ith hyper-parameter ${\lambda }_{n_i}^t$, $L\left({\lambda }_n^t\right)$ is decomposed as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L\left({\lambda }_n^t\right)=L\left({\lambda }_{n_{-i}}^t\right)+l\left({\lambda }_{n_i}^t\right)\end{array}\end{array}$$

(11)

where $l\left({\lambda }_{n_i}^t\right)$ is the marginal likelihood function corresponding to ${\lambda }_{n_i}^t$ and shown in Equation (12) (its detailed derivation is shown in Appendix A). $L\left({\lambda }_{n_{-i}}^t\right)$ is the marginal likelihood function corresponding to other hyper-parameters. The maximum value of $l\left({\lambda }_{n_i}^t\right)$ is obtained by calculating its derivative with Equation (13) to estimate ${\lambda }_{n_i}^t$:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill l\left({\lambda }_{n_i}^t\right)={\displaystyle \frac{1}{2}}[log|{\lambda }_{n_i}^t|-log|{\lambda }_{n_i}^t+f_i^t|+{\displaystyle \frac{{\left(q_i^t\right)}^2}{{\lambda }_{n_i}^t+f_i^t}}]\end{array}\end{array}$$

(12)

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial l\left({\lambda }_{n_i}^t\right)}{\partial {\lambda }_{n_i}^t}}={\displaystyle \frac{{\left(f_i^t\right)}^2-\left({\lambda }_{n_i}^t\right)({\left(q_i^t\right)}^2-f_i^t)}{{\lambda }_{n_i}^t{({\lambda }_{n_i}^t+f_i^t)}^2}}\end{array}$$

(13)

where $f_i^t={\varphi }_{r_i}^T{\mathit{C}}_{t_{-i}}^{-1}{\varphi }_{r_i}$ and $q_i^t={\varphi }_{r_i}^T{\mathit{C}}_{t_{-i}}^{-1}{s}_{n_r}$ are calculated by Equation (14) (Their derivation is shown in Appendix B):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathrm{If}i\in {\mathbf{G}}_{n_r}^{t-1}{f}_i^t={\displaystyle \frac{{\lambda }_{n_i}^{t-1}{F}_i^{t-1}}{{\lambda }_{n_i}^{t-1}-F_i^{t-1}}}{q}_i^t={\displaystyle \frac{{\lambda }_{n_i}^{t-1}{Q}_i^{t-1}}{{\lambda }_{n_i}^{t-1}-F_i^{t-1}}}\\ \mathrm{Else}{f}_i^t=F_i^{t-1}{q}_i^t=Q_i^{t-1}\end{array}\right.\end{array}$$

(14)

where $F_i^{t-1}={\varphi }_{r_i}^T{\mathit{C}}_{t-1}^{-1}{\varphi }_{r_i}$ and $Q_i^{t-1}={\varphi }_{r_i}^T{\mathit{C}}_{t-1}^{-1}{s}_{n_r}$; ${\lambda }_{n_i}^{t-1}$ is the estimation value of the ith hyper-parameter after $t-1$ iterations.

When $f_i^t$ and $q_i^t$ satisfy ${\left(q_i^t\right)}^2-f_i^t\le 0$, $l\left({\lambda }_{n_i}^t\right)$ increases gradually, and a maximum value corresponding to ${\lambda }_{n_i}^t$ does not exist. Under this case, ${\lambda }_{n_i}^t$ is set as 0, its corresponding scattering unit does not belong to the target-areas. Otherwise, $l\left({\lambda }_{n_i}^t\right)$ has a maximum value when ${\displaystyle \frac{\partial l\left({\lambda }_{n_i}^t\right)}{\partial {\lambda }_{n_i}^t}}=0$; the estimation value of ${\lambda }_{n_i}^t$ is ${\lambda }_{n_i}^t={\displaystyle \frac{{\left(f_i^t\right)}^2}{{\left(q_i^t\right)}^2-f_i^t}}$; its corresponding scattering unit is classified into the target-areas. Similarly, the hyper-parameters ${\lambda }_n^t=\{{\lambda }_{n_i}^t,1\le i\le 2M\}$ and their marginal likelihood function’s increase $E^t=\{e_i^t=l\left({\lambda }_{n_i}^t\right)-l\left({\lambda }_{n_i}^{t-1}\right),1\le i\le 2M\}$ are updated by Equation (15):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathrm{If}{\left(q_i^t\right)}^2-f_i^t>0{\lambda }_{n_i}^t={\displaystyle \frac{{\left(f_i^t\right)}^2}{{\left(q_i^t\right)}^2-f_i^t}}{e}_i^t=\frac{{\left(Q_i^{t-1}\right)}^2-F_i^{t-1}}{F_i^{t-1}}+log\left(\frac{F_i^{t-1}}{{\left(Q_i^{t-1}\right)}^2}\right)\\ \mathrm{Else}{\lambda }_{n_i}^t=0e_i^t=\frac{{\left(Q_i^{t-1}\right)}^2}{F_i^{t-1}-{\lambda }_{n_i}^{t-1}}+log\left(\frac{{\lambda }_{n_i}^{t-1}}{F_i^{t-1}-{\lambda }_{n_i}^{t-1}}\right)\end{array}\right.\end{array}$$

(15)

If $E^t$ satisfies ${\displaystyle \frac{∥max\left(E^t\right)-max\left(E^{t-1}\right)∥}{∥max\left(E^t\right)-max\left(E^0\right)∥}}<{\epsilon }_e$, the marginal likelihood function $L\left({\lambda }_n^t\right)$ reaches the preset estimation accuracy. ${\lambda }_n^t$ is considered as the optimal hyper-parameters, where ${\epsilon }_e$ is the iteration termination threshold. Under this case, the iteration will be terminated, and the final target-areas are obtained and recorded as ${\mathit{G}}_{n_r}={\mathit{G}}_{n_r}^{t-1}$. Otherwise, the scattering unit corresponding to the maximum element in $E^t$ is extracted and recorded as $I{d}_t$. Based on the hyper-parameter ${\lambda }_{I{d}_t}^{t-1}$, $f_{I{d}_t}^t$ and $q_{I{d}_t}^t$, the $I{d}_t$ scattering unit is judged whether it belongs to the target-areas.

When ${\left(q_{I{d}_t}^t\right)}^2-f_{I{d}_t}^t>0$, the marginal likelihood function corresponding to the $I{d}_t$ scattering unit has a maximum value; the $I{d}_t$ scattering unit is added into the target-areas. Otherwise, when ${\left(q_{I{d}_t}^t\right)}^2-f_{I{d}_t}^t\le 0$ and ${\lambda }_{I{d}_t}^{t-1}>0$, the $I{d}_t$ scattering unit is divided into the target-areas ${\mathit{G}}_{n_r}^{t-1}$ in the previous iterations; its corresponding marginal likelihood function does not have a maximum value after the current iteration. The $I{d}_t$ scattering unit must be deleted from the target-areas. Therefore, the target-areas are updated by Equation (16). Meanwhile, the calculation formula of ${\lambda }_{I{d}_t}^t$ is shown in Equation (16):   

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathrm{If}{\left(q_i^t\right)}^2-f_i^t>0{\mathit{G}}_{n_r}^t={\mathit{G}}_{n_r}^{t-1}\cup I{d}_t{\lambda }_{I{d}_t}^t={\displaystyle \frac{{\left(f_{I{d}_t}^t\right)}^2}{{\left(q_{I{d}_t}^t\right)}^2-f_{I{d}_t}^t}}\\ \mathrm{If}{\left(q_{I{d}_t}^t\right)}^2-f_{I{d}_t}^t\le 0,{\lambda }_{I{d}_t}^{t-1}>0{\mathit{G}}_{n_r}^t={\mathit{G}}_{n_r}^{t-1}/\phantom{{\mathit{G}}_n^{t-1}I{d}_t}I{d}_t{\lambda }_{I{d}_t}^t=0\end{array}\right.\end{array}$$

(16)

where ∪ and / are the add element and delete element operation, respectively. In addition, $F_i^t$ and $Q_i^t$ are updated by Equation (17); we continue iterations to obtain the optimal hyper-parameters:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{F}_i^t={\varphi }_{r_i}^T{\mathit{C}}_t^{-1}{\varphi }_{r_i}={\displaystyle \frac{{\varphi }_{r_i}^T{\varphi }_{r_i}}{{\beta }_0}}-{\displaystyle \frac{{\varphi }_{r_i}^T{\mathsf{\Phi }}_t{\Sigma }_n^{t-1}{\mathsf{\Phi }}_t^T{\varphi }_{r_i}}{{\beta }_0^2}}\\ Q_i^t={\varphi }_{r_i}^T{\mathit{C}}_t^{-1}{s}_{n_r}={\displaystyle \frac{{\varphi }_{r_i}^T{s}_{n_r}}{{\beta }_0}}-{\displaystyle \frac{{\varphi }_{r_i}^T{\mathsf{\Phi }}_t{\Sigma }_n^{t-1}{\mathsf{\Phi }}_t^T{s}_{n_r}}{{\beta }_0^2}}\end{array}\right.\end{array}$$

(17)

where ${\mathsf{\Phi }}_t=\{{\varphi }_{r_{I{d}_1}},\cdots ,{\varphi }_{r_{I{d}_t}}\}$ represents the column vectors corresponding to ${\mathit{G}}_{n_r}^t$. ${\Sigma }_n^{t-1}$ is the estimation variance of the scattering coefficients.

Step 5: Calculate the complex-valued target-areas ${\mathit{G}}_n$ by Equation (18).

Since the target-areas ${\mathit{G}}_{n_r}$ are corresponding to the real-valued scattering coefficients ${\mathbf{\alpha }}_{n_r}$, ${\mathit{G}}_{n_r}$ cannot be used as the prior information to simplify the measurement matrix and conduct sparse imaging. Because one element in the complex-valued scattering coefficients ${\mathbf{\alpha }}_n$ is related to two adjacent elements in ${\mathbf{\alpha }}_{n_r}$ (e.g., the $2m-1$ and $2m$ element in ${\mathbf{\alpha }}_{n_r}$ are the real and imaginary part of the m element in ${\mathbf{\alpha }}_n$, respectively); the target-areas ${\mathit{G}}_n$ corresponding to ${\mathbf{\alpha }}_n$ are obtained by Equation (18):

$$\begin{array}{c}\hfill {\mathit{G}}_n=\{w_r=round\left(\frac{{\mathit{G}}_{n_r}\left(r\right)+1}{2}\right),1\le r\le N_n\}\end{array}$$

(18)

where $N_n$ is the total number of elements in the target-areas ${\mathit{G}}_n$, and $w_r$ is the serial number of the rth element in the target-areas ${\mathit{G}}_n$ in the imaging scene.

In addition, the main steps of obtaining ${\mathit{G}}_n$ are summarized in Algorithm 1.

Algorithm 1 Extract the target-areas.

Input: Echo signal $s_n$, measurement matrix ${\mathsf{\Theta }}_n$, ${\epsilon }_e$     Step 1: Obtain the real-valued echo signal and measurement matrix by Equations (5) and (6), respectively.     Step 2: Initialize the nth equidistant planar scattering coefficients ${\widehat{\mathbf{\alpha }}}_{n_r}^0$ by Equation (9);     Step 3: Select the maximum element in ${\widehat{\mathbf{\alpha }}}_{n_r}^0$ as the initial target-areas: ${\mathit{G}}_n^0=I{d}_0$;     Calculate its hyper-parameter ${\lambda }_{n_{I{d}_0}}^0$ by Equation (9);     Step 4: Calculate the optimal hyper-parameters to extract the target-areas.     Calculate the hyper-parameters ${\lambda }_n^t$ and the marginal likelihood function’s increase $E^t$ by Equation (15).     if ${\displaystyle \frac{∥max\left(E^t\right)-max\left(E^{t-1}\right)∥}{∥max\left(E^t\right)-max\left(E^0\right)∥}}>{\epsilon }_e$ then         Continue iteration, update the target-areas ${\mathit{G}}_{n_r}^t$ and ${\lambda }_{I{d}_t}^t$ by Equation (16);         Update $F_i^t$ and $Q_i^t$ by Equation (17)         $t=t+1$;     else         Terminate iteration;     end if     Step 5: Calculate the complex-valued target-areas ${\mathit{G}}_n$ by Equation (18). Output: the target-areas ${\mathit{G}}_n$.

3.2. Sparse Imaging According to the Target-Areas

To achieve sparse imaging with high-efficiency, the key is to avoid or simplify the high-dimensional matrix-operations corresponding to the measurement matrix. In this subsection, we use the target-areas as the prior information to simplify the measurement matrix and scattering coefficients firstly. Then, we estimate the target-areas’ scattering coefficients with the simplified measurement matrix to obtain imaging results with high quality and efficiency.

However, when the target-areas probably contain several elements whose scattering coefficients are too small compared to other elements. Those elements with too small scattering coefficients probably lead to the diagonal matrix become singular and irreversible; the scattering coefficients cannot be estimated correctly because of the singular matrix. To solve this problem, the truncated singular value decomposition (TSVD) [24] algorithm is introduced to eliminate the elements with too small scattering coefficients and estimate the scattering coefficients correctly. The detailed steps of sparse imaging on the target-areas are introduced as the following content.

Step 1: Simplify the scattering coefficients and measurement matrix.

Since the target-areas ${\mathit{G}}_n$ contain part scattering units and the column vectors in the measurement matrix ${\mathsf{\Theta }}_n$ are corresponding to the scattering units one to one (e.g., the mth column vector is corresponding to the mth scattering unit), we extract the scattering coefficients and measurement matrix’s column vectors corresponding to ${\mathit{G}}_n$ based on the serial numbers of the scattering units in ${\mathit{G}}_n$. The target-areas’ scattering coefficients ${\mathbf{\alpha }}_w\in {\mathbb{C}}^{N_n\times 1}$ and measurement matrix ${\mathsf{\Theta }}_w\in {\mathbb{C}}^{N_A\times N_n}$ are shown in:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathbf{\alpha }}_w=\{{\alpha }_{w_1},\cdots ,{\alpha }_{w_r},\cdots ,{\alpha }_{w_{N_n}}\}\\ {\mathsf{\Theta }}_w=\{{\varphi }_{w_1},\cdots ,{\varphi }_{w_r},\cdots ,{\varphi }_{w_{N_n}}\}\end{array}\right.\end{array}$$

(19)

where ${\varphi }_{w_r}=\left[{\mathsf{\Theta }}_n(1,w_r),\cdots ,{\mathsf{\Theta }}_n(N_A,w_r)\right]$ is the column vector in ${\mathsf{\Theta }}_n$ related to the r element in the target-areas ${\mathit{G}}_n$. ${\mathit{N}}_A$ denotes the total number of APCs in the 2D array.

The linear representation model of the nth equidistant planar echo signal $s_n$ is translated into $s_n={\mathsf{\Theta }}_w{\mathbf{\alpha }}_w+\mathbf{\xi }$, where $\mathbf{\xi }$ is the signal noise in $s_n$ and obeys the Gaussian distribution. Therefore, sparse imaging on the target-areas is translated into getting the optimal estimation value of ${\widehat{\mathbf{\alpha }}}_w$. In addition, ${\widehat{\mathbf{\alpha }}}_w$ is initialized by ${\widehat{\mathbf{\alpha }}}_w^0={\displaystyle \frac{{\mathsf{\Theta }}_w^H{s}_n}{N_A}}$ to eliminate the false targets or sidelobes caused by the signal noise preliminarily.

Step 2: Estimate the target-areas’ scattering coefficients.

Since the target-areas’ measurement matrix ${\mathsf{\Theta }}_w$ and scattering coefficients ${\widehat{\mathbf{\alpha }}}_w$ are simplified effectively, the optimal target-areas’ scattering coefficients ${\widehat{\mathbf{\alpha }}}_w$ are obtained by calculating the minimum cost function in the SBRIM algorithm [19] after several iterations. In the tth iteration, the cost function is shown in Equation (20):

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill J({\widehat{\mathbf{\alpha }}}_w^{\left(t\right)},{\widehat{\beta }}^{\left(t\right)})\triangleq & N_A\ln {\widehat{\beta }}^{\left(t\right)}+{\displaystyle \frac{\parallel s_n-{\mathsf{\Theta }}_w{\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}{\parallel }_2^2}{{\widehat{\beta }}^{\left(t\right)}}}+\lambda \sum _{r=1}^{N_n}{({|{\widehat{\alpha }}_{w_r}^{\left(t\right)}|}^2+\eta )}^{{\displaystyle \frac{p}{2}}}\hfill \end{array}\end{array}$$

(20)

where $\lambda >0$. $\eta >0$. $0<p\le 1$. $N_n$ is the total number of elements in the target-areas ${\mathit{G}}_n$.

The estimation values of ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ and ${\widehat{\beta }}^{\left(t\right)}$ are obtained by calculating the partial derivative of the cost function $J({\widehat{\mathbf{\alpha }}}_w^{\left(t\right)},{\widehat{\beta }}^{\left(t\right)})$ with respect to ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ and ${\widehat{\beta }}^{\left(t\right),}$ respectively. As a result, ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ and ${\widehat{\beta }}^{\left(t\right)}$ are updated by Equation (21):

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}={\mathsf{\Theta }}_{{\Lambda }_t}^{-1}{\mathsf{\Theta }}_w^H{s}_n\hfill \\ & {\widehat{\beta }}^{\left(t\right)}={\displaystyle \frac{\parallel s_n-{\mathsf{\Theta }}_w{\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}{\parallel }_2^2}{N_A}}\hfill \end{array}\right.\end{array}$$

(21)

where ${\mathsf{\Theta }}_{{\Lambda }_t}=\mathrm{diag}\{{\mathsf{\Theta }}_{{\Lambda }_t}(w_r,w_r),1\le r\le N_n\}$ is the diagonal matrix in the tth iteration and defined as:

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_{{\Lambda }_t}(w_r,w_r)={\varphi }_{w_r}^H{\varphi }_{w_r}+\lambda {\widehat{\beta }}^{(t-1)}{\displaystyle \frac{p}{2}}{({\left|{\widehat{\alpha }}_{w_r}^{(t-1)}\right|}^2+\eta )}^{{\displaystyle \frac{p}{2}}-1}\end{array}$$

(22)

where ${\varphi }_{w_r}$ is the rth column vector in ${\mathsf{\Theta }}_w$. ${\widehat{\alpha }}_{w_r}^{(t-1)}$ is the rth element in the estimation value of ${\widehat{\mathbf{\alpha }}}_w$ after $t-1$ iterations.

However, when conducting sparse imaging under low sampling rate, low SNR, or high sparsity, several false targets in the initial scattering coefficients ${\widehat{\mathbf{\alpha }}}_{n_r}^0$ usually exist, which correspond to the hyper-parameters and their corresponding estimation errors according to Equations (14)∼(17). Those false targets probably are classified into the target-areas erroneously or lead to the iterations in extracting the target-areas terminating earlier. Those two cases above will result in the target-areas losing partial targets’ information or suffering due to the false targets.

Once the target-areas ${\mathit{G}}_n$ have several elements whose scattering coefficients are too small or closer to zero compared to the other elements, the diagonal matrix ${\mathsf{\Theta }}_{{\Lambda }_t}$ is singular and irreversible because of the elements with scattering coefficients that are too small; we cannot estimate ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ correctly by Equation (21). To eliminate the elements with a scattering coefficient that is too small in ${\mathit{G}}_n$, the truncated singular value decomposition (TSVD) algorithm is introduced in this subsection.

Firstly, the singular matrix ${\mathsf{\Theta }}_{{\Lambda }_t}$ is decomposed as Equation (23) by the singular value decomposition (SVD) [27] method:

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_{{\Lambda }_t}={\mathit{U}}_n^t{\mathbf{\sigma }}_n^t{{\mathit{V}}_n^t}^T=\sum _{i=1}^{N_n}{u}_{n_i}^t{\sigma }_{n_i}^t{\left(v_{n_i}^t\right)}^T\end{array}$$

(23)

where ${\mathit{U}}_n^t=\left[u_{n_1}^t,\cdots ,u_{n_{N_n}}^t\right]\in {\mathbb{C}}^{N_n\times N_n}$ and ${\mathit{V}}_n^t=\left[v_{n_1}^t,\cdots ,v_{n_{N_n}}^t\right]\in {\mathbb{C}}^{N_n\times N_n}$ are formed by the singular vectors of ${\mathsf{\Theta }}_{{\Lambda }_t}$. ${\mathbf{\sigma }}_n^t=\mathrm{diag}({\sigma }_{n_i}^t,i=1,\cdots ,N_n)\in {\mathbb{C}}^{N_n\times N_n}$; ${\sigma }_{n_i}^t$ is the ith singular value of ${\mathsf{\Theta }}_{{\Lambda }_t}$ and satisfies ${\sigma }_{n_1}^t>{\sigma }_{n_2}^t>\cdots >{\sigma }_{n_{N_n}}^t$.

Once ${\mathsf{\Theta }}_{{\Lambda }_t}$ is singular and irreversible, ${\mathbf{\sigma }}_n^t$ contains $N_n-K$ elements which are too small compared to other elements, where $K=rank\left({\mathsf{\Theta }}_{{\Lambda }_t}\right)$ is the rank of ${\mathsf{\Theta }}_{{\Lambda }_t}$ [28]. To eliminate the small singular values, the generalized inverse matrix ${\mathsf{\Theta }}_G^t\in {\mathbb{C}}^{N_n\times N_n}$ is obtained by ${\mathsf{\Theta }}_G^t={\displaystyle \sum _{i=1}^K}{\displaystyle \frac{v_{n_i}^t{\left(u_{n_i}^t\right)}^T}{{\sigma }_{n_i}^t}}$. Then, the inverse matrix of ${\mathsf{\Theta }}_{{\Lambda }_t}$ is replaced with the generalized inverse matrix ${\mathsf{\Theta }}_G^t$ to estimate the ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ correctly:

$$\begin{array}{c}\hfill {\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}={\mathsf{\Theta }}_G^t{\mathsf{\Theta }}_w^H{s}_n\end{array}$$

(24)

Since the elements with the small scattering coefficients still exist in the target-areas ${\mathit{G}}_n$, we extract the elements in ${\mathit{G}}_n$ corresponding to the largest K elements in ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ as the new target-areas by Equation (25) to eliminate those elements:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \mathrm{If}{\widehat{\alpha }}_{w_r}^{\left(t\right)}<{\widehat{\alpha }}_{w_0}^{\left(t\right)}{w}_r\notin {\mathit{G}}_n\hfill \\ & \mathrm{If}{\widehat{\alpha }}_{w_r}^{\left(t\right)}\ge {\widehat{\alpha }}_{w_0}^{\left(t\right)}{w}_r\in {\mathit{G}}_n\hfill \end{array}\right.\end{array}$$

(25)

where ${\widehat{\alpha }}_{w_0}^{\left(t\right)}$ is the $K^{th}$ largest element in ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$.

Step 3: Determine whether to continue iteration.

If ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ and current iteration t satisfy ${\displaystyle \frac{{\parallel {\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}-{\widehat{\mathbf{\alpha }}}_w^{(t-1)}\parallel }_2}{{\parallel {\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}\parallel }_2}}\ge {\epsilon }_0$ and $t\le I_S$. This indicates that ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ does not meet the preset estimation accuracy; the current iteration is smaller than the preset maximum iterations; then, continue the iteration, where ${\epsilon }_0$ represents the iteration termination threshold; and $I_S$ represents the total number of iterations. Otherwise, the iterations will be ended; ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ is considered as the optimal target-areas scattering coefficients.

The nth equidistant planar 2D imaging results ${\mathbf{\alpha }}_n=\{{\alpha }_n\left(m\right),m=1,\cdots ,M\}$ are obtained by Equation (26). The main steps of sparse imaging on the target-areas are shown in Algorithm 2. In addition, the 3D imaging results $\mathbf{\alpha }=\{{\mathbf{\alpha }}_n,n=1,\cdots ,N_R\}$ are obtained by combining all equidistant planar imaging results:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \mathrm{If}m\notin {\mathit{G}}_n{\alpha }_n\left(m\right)=0\hfill \\ & \mathrm{If}m\in {\mathit{G}}_n{\alpha }_n\left(m\right)={\widehat{\alpha }}_{w_m}^{\left(t\right)}\hfill \end{array}\right.\end{array}$$

(26)

where M is the total number of scattering units in the imaging scene.

Algorithm 2 Sparse imaging on the target-areas.

Input: Echo signals $s_n$; measurement matrix ${\mathsf{\Theta }}_n$; target-areas ${\mathit{G}}_n$; the total number of the iterations $I_S$; the termination threshold ${\epsilon }_0$;     Step 1: Simplify the measurement matrix and scattering coefficients by Equation (19).     Step 2: Estimate the target-areas’ scattering coefficients ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$;     if    $K<N_n$ then         Calculate ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ by Equation (24);         Obtain more accurate target-areas ${\mathit{G}}_n$ by Equation (25).     else   $K=N_n$         Calculate ${\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}$ by Equation (21).     end if     Calculate the noise variance ${\widehat{\beta }}^{\left(t\right)}$ by Equation (21).     Step 3: Determine whether to continue iteration;     if $1\le t\le I_S$ and ${\displaystyle \frac{{\parallel {\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}-{\widehat{\mathbf{\alpha }}}_w^{(t-1)}\parallel }_2}{{\parallel {\widehat{\mathbf{\alpha }}}_w^{\left(t\right)}\parallel }_2}}<{\epsilon }_0$ then         Continue iteration: $t=t+1$ and return to Step 2.     else         End iteration.         Obtain the nth equidistant planar imaging results ${\mathbf{\alpha }}_n^{\left(t\right)}$ by Equation (26).     end if Output: The 2D imaging results: ${\mathbf{\alpha }}_n$.

3.3. Computational Complexity of the FBCS–RVM Algorithm

In this subsection, we analyze the computational complexity of the FBCS–RVM algorithm. According to Section 3.1 and Section 3.2, the computational complexity of the FBCS–RVM algorithm is mainly generated by two parts: extracting the target-areas and sparse imaging on the target-areas.

(1):

The computational complexity of extracting the target-areas is ${\displaystyle \sum _{n=1}^{N_R}}\vartheta \left(4I_n{N}_{A}M\right)$, which is mainly generated by Equation (17); where $\vartheta \left(1\right)$ is the unit computational complexity; $I_n$ is the total number of iterations in extracting the target-areas; $N_A$ represents the total number of APCs in the 2D equivalent array; M is the total number of the scattering units in the 2D imaging scene.

(2):

The computational complexity of sparse imaging on the target-areas is ${\displaystyle \sum _{n=1}^{N_R}\sum _{n=1}^{I_S}}\vartheta \left(N_A{N}_n^2\right)$, which is mainly generated in ${\widehat{\mathbf{\alpha }}}_w$ by Equation (21) or (24), where $N_n$ is the total number of elements in the target-areas; $I_S$ is the total iterations in sparse imaging.

Hence, the total computational complexity of LASAR 3D imaging by the FBCS–RVM algorithm is ${\displaystyle \sum _{n=1}^{N_R}}\vartheta \left(4I_n{N}_{A}M\right)+{\displaystyle \sum _{n=1}^{N_R}\sum _{t=1}^{I_S}}\vartheta \left(N_A{N}_n^2\right)$.

According to the Introduction, CS algorithms must set several parameters manually before conducting sparse imaging. Most CS algorithms (e.g., the OMP and BCS algorithms) are influenced by the preset parameters greatly; their computational complexity significantly increases once the preset parameters are set inaccurately. However, the computational complexity of both SBRIM and FBCS–RVM algorithm are not affected by the preset parameters. Therefore, we only give the comparison results of the computational complexity between the SBRIM and FBCS–RVM algorithm in Table 1.

Table 1. The computational complexity of the SBRIM and FBCS–RVM algorithm.

Algorithm	Computational Complexity
SBRIM	$\vartheta \left(N_R{I}_S{N}_A{M}^2\right)$
FBCS–RVM	${\displaystyle \sum _{n=1}^{N_R}}\vartheta \left(4I_n{N}_{A}M\right)+{\displaystyle \sum _{n=1}^{N_R}\sum _{t=1}^{I_S}}\vartheta \left(N_A{N}_n^2\right)$

Since the target-areas usually occupy a small part of the imaging scene, M, $I_n$, and $N_n$ satisfy $N_n\le I_n<M$. The computational complexities of the SBRIM and FBCS–RVM algorithm satisfy ${\displaystyle \sum _{n=1}^{N_R}}(4N_A{I}_{n}M+{\displaystyle \sum _{t=1}^{I_S}}{N}_A{N}_n^2)<N_R{I}_S{N}_A{M}^2$. The FBCS–RVM algorithm improves the computational efficiency effectively compared to the SBRIM algorithm.

4. Results on Simulation and Experimental Data

To verify the effectiveness of the FBCS–RVM algorithm, the simulation results are used to quantitatively analyze the imaging quality and estimation accuracy of the FBCS–RVM algorithm under known targets’ information (such as the scattering coefficients and geometric distribution) firstly. Secondly, the experimental results are used to certify the effectiveness of the FBCS–RVM algorithm in the real LASAR data.

In addition, the OMP [17], fast marginalized sparse Bayesian learning (FMSBL) [29,30], and SBRIM [21] algorithms are used as the comparison algorithms to evaluate the performance of the FBCS–RVM algorithm better. The normalized mean square error (NMSE) [31,32] measures the scattering coefficients’ estimation accuracy; the smaller NMSE indicates that the estimation results of the scattering coefficients are more accurate. The target background contrast (TBR) [33] and image entropy (ENT) [34] are used to quantitatively evaluate the imaging quality. TBR reflects the targets’ characteristics in the imaging results; targets can be identified from the imaging results more easily under larger TBR. ENT quantifies the focus quality of the imaging results; targets are focused better under smaller ENT. Therefore, the larger TBR and smaller ENT indicate higher imaging quality. The running time speed-up ratio (RTSR) [21] and execution time (ExT) are used to evaluate the computational efficiency. The higher RTSR indicates that the improvement of the computational efficiency is larger between the FBCS–RVM and the comparison algorithm. Both simulation and experimental experiments are carried out on the computer with Intel Core i9 10,900K CPU at 3.70 GHz, Nvidia GeForce RTX 2060 Super with 8 GB memory, and 32 GB computer memory space.

4.1. Compared with the Comparison Algorithms

4.1.1. Results on the 2D Point-Target Simulation Data

Since the 3D sparse imaging has been translated into the sparse imaging on every equidistant planar 2D imaging scene, the point-target simulations on one equidistant planar 2D imaging scene are conducted firstly to illustrate the effectiveness of the FBCS–RVM algorithm quickly and evaluate its performance accurately. The main parameters and the original scene of the point-target simulations are shown in Table 2 and Figure 3a, respectively. After getting the appropriate preset parameters, the imaging results of the OMP, FMSBL, SBRIM, and FBCS–RVM algorithms are shown in Figure 3b–e.

Table 2. The basic parameters of the 2D point-target simulations.

Parameters	Value
Center frequency/GHz	30
Signal bandwidth/MHz	150
Platform height /m	1000
The size of the 2D array/m	4 × 4
Total number of APCs	1600
Total number of scattering units	101× 101
Spacing between adjacent scattering unit/m	0.3 m

Figure 3. The original scene and imaging results of point–target simulations. (a) Original scene; (b) OMP; (c) FMSBL; (d) SBRIM; (e) FBCS–RVM.

According to Figure 3b–e, the same as the comparison methods under correct preset parameters, the FBCS–RVM algorithm can estimate the scattering coefficients accurately and obtain high-quality imaging results. To evaluate the performance of the above four algorithms in more detail, we have conducted point-target simulations under different sampling rates and SNR [23]. The Monte Carlo experiments of the above algorithms are all set hundreds of times to evaluate their performance more accurately. Table 3 and Table 4 give the evaluation results under different sampling rates and SNR, respectively.

Table 3. The evaluation results under different sampling rates.

Sampling Rate	Standards	OMP	FMSBL	SBRIM	FBCS–RVM
20%	NMSE	0.3884	0.0102	0.0063	0.0035
	TBR	78.0341	312.9847	103.6925	313.0533
	ENT	0.1495	0.0244	0.0343	0.0238
	ExT/s	0.4645	0.4084	84.1898	0.8922
	RTSR	0.5206	0.4578	94.3654	1
40%	NMSE	0.0326	0.0051	0.0029	0.0024
	TBR	85.9777	313.0286	114.8554	313.0587
	ENT	0.1250	0.0233	0.0236	0.0232
	ExT/s	0.8680	0.6106	90.6742	0.9839
	RTSR	0.8822	0.6207	92.1619	1
60%	NMSE	0.0093	0.0034	0.0026	0.0019
	TBR	88.3392	313.0428	118.3356	313.0610
	ENT	0.1205	0.0232	0.0255	0.0232
	ExT/s	1.3479	0.8379	102.7153	1.0381
	RTSR	1.2984	0.8072	98.9465	1
80%	NMSE	0.0066	0.0026	0.0019	0.0017
	TBR	89.8987	313.0514	120.3862	313.0625
	ENT	0.1118	0.0232	0.0232	0.0231
	ExT/s	1.8296	1.1590	118.8683	1.1151
	RTSR	1.6407	1.0394	106.5902	1
100%	NMSE	0.0057	0.0021	0.0016	0.0015
	TBR	91.0592	313.0541	121.5146	313.0634
	ENT	0.0923	0.0230	0.0232	0.0230
	ExT/s	2.2521	1.6765	131.0763	1.1934
	RTSR	1.8896	1.4048	109.8315	1

Table 4. The evaluation results under different SNR.

SNR	Standards	OMP	FMSBL	SBRIM	FBCS–RVM
0	NMSE	1.4546	1.2445	0.6486	0.4202
	TBR	70.1586	65.3756	45.0455	61.9777
	ENT	0.4355	0.6267	0.7383	0.1245
	ExT/s	2.4882	68.6281	100.2196	3.7812
	RTSR	0.6581	16.3911	27.8272	1
10	NMSE	0.4229	0.2132	0.2290	0.0911
	TBR	44.6720	58.4351	61.8170	76.7137
	ENT	0.3944	0.3366	0.3611	0.0836
	ExT/s	2.4847	15.5745	100.0990	2.3617
	RTSR	1.0521	6.5945	46.2305	1
20	NMSE	0.1328	0.0393	0.0669	0.0216
	TBR	60.1341	75.5671	76.4821	228.0255
	ENT	0.3461	0.1611	0.1664	0.0592
	ExT/s	2.4923	3.2620	99.6250	1.2129
	RTSR	2.0548	2.6877	82.1351	1
30	NMSE	0.0415	0.0081	0.0201	0.0067
	TBR	70.2377	93.5478	88.6350	313.0359
	ENT	0.2950	0.0252	0.0819	0.0252
	ExT/s	2.4900	1.5547	99.5041	1.1929
	RTSR	2.0873	1.2956	83.4110	1
40	NMSE	0.0133	0.0041	0.0074	0.0018
	TBR	80.1339	312.0601	97.4627	313.0600
	ENT	0.2020	0.0232	0.0449	0.0232
	ExT/s	2.4902	0.7551	99.7141	1.1836
	RTSR	2.1004	0.6380	84.1035	1

From Table 3, we can get the following conclusions:

• The NMSE of the FBCS–RVM algorithm is the minimum among those four algorithms; it is smaller than 0.01 under the 20% sampling rate. This shows that the FBCS–RVM algorithm achieves high-quality sparse imaging; its scattering coefficients’ estimation accuracy is higher than the other three algorithms.
• The FBCS–RVM algorithm obtains the maximum TBR and minimum ENT among the above four algorithms. This indicates that the FBCS–RVM algorithm obtains imaging results with the strongest and best-focused targets; it improves the imaging quality compared to the other three algorithms.
• The execution time of the FBCS–RVM algorithm belongs to 0.8∼1.2 s, and it achieves high-efficiency sparse imaging. Its computational efficiency is improved by two orders of magnitude compared to the SBRIM algorithm at most, and it is the same level as the OMP and the FMSBL algorithms.

According to Table 4, we can get the following conclusions:

• The NMSE of the FBCS–RVM algorithm is the minimum among those four algorithms. This proves that the FBCS–RVM algorithm estimates the scattering coefficients more accurately than the other three algorithms.
• The FBCS–RVM algorithm obtains the maximum TBR and minimum ENT among the above four algorithms. Except when the SNR is 0 dB, both the OMP and FMSBL algorithms obtain slightly larger TBR because of the strong false targets. Therefore, the FBCS–RVM algorithm suppresses the signal noise better and improves the imaging quality compared to the other three algorithms.
• The execution time of the FBCS–RVM algorithm belongs to 1∼4 s and is the minimum among those four algorithms. Except for the two cases, the OMP and FMSBL algorithms obtain slightly smaller execution time under the 0 dB and 40 dB SNR, respectively. The computational efficiency of the FBCS–RVM algorithm is improved 27∼84 times compared to the SBRIM algorithm; it achieves sparse imaging with high efficiency.

4.1.2. Results on the 2D Complex-Target Simulation Data

To evaluate the performance of the FBCS–RVM algorithm under the complex imaging scene, the 2D complex-target simulations are conducted in this subsection. The main parameters and the original scene of the 2D complex-target simulation are shown in Table 5 and Figure 4, respectively.

Table 5. The basic parameters of the complex-target simulations.

Parameters	Value
Center frequency/GHz	30
Signal bandwidth/MHz	150
Platform height /m	3000
The size of the 2D array/m	10 × 15
Traditional array imaging resolution/m	1.5 × 1
Total number of APCs	4096
Total number of scattering units	64 × 64
Spacing between adjacent scattering unit/m	1.5 m

Figure 4. The original scene of the complex–target simulations. (a) airplane model under 210 sparsity; (b) ship model under 495 sparsity; (c) ship model under 515 sparsity; (d) complex–target model under 677 sparsity.

Figure 4 shows four complex-targets with different sparsity and density. Figure 5 gives the imaging results of Figure 4c obtained by the OMP, FMSBL, SBRIM, and FBCS–RVM algorithms under different sampling rates (e.g., 20%, 35%, and 50%).

Figure 5. The imaging results of targets in Figure 4c under different sampling rates; first row: 20% sampling rate, second row: 35% sampling rate, third row: 50% sampling rate.

According to Figure 5, those four algorithms cannot estimate the scattering coefficients correctly under the 20% sampling rate. They lose the targets’ information and suffer from the false targets seriously. The OMP algorithm still suffers from some false targets under the 35% and 50% sampling rate because of its preset sparsity. Meanwhile, the other three algorithms can eliminate the false targets better; they obtain higher imaging quality. To quantitatively evaluate the performance of the above four algorithms, the evaluation results under different sampling rates are shown in Table 6.

Table 6. The evaluation results under different sampling rates.

Sampling Rate	Standards	OMP	FMSBL	SBRIM	FBCS–RVM
35%	NMSE	0.1860	0.0343	0.0180	0.0081
	TBR	64.8529	356.5519	86.1030	347.7633
	ENT	1.5965	1.4042	1.4499	1.3975
	ExT/s	9.9206	7.9548	50.0197	4.1410
50%	NMSE	0.1229	0.0191	0.0070	0.0059
	TBR	67.5803	356.6352	92.5163	356.7727
	ENT	1.5795	1.3999	1.4261	1.3951
	ExT/s	13.4775	10.1920	59.2569	5.0914
75%	NMSE	0.0488	0.0118	0.0050	0.0045
	TBR	70.9421	356.6923	100.2144	356.7769
	ENT	1.5746	1.3982	1.4082	1.3951
	ExT/s	19.1810	11.8886	68.7381	7.0756
100%	NMSE	0.0049	0.0087	0.0042	0.0038
	TBR	73.3827	356.7177	115.6553	356.7790
	ENT	1.5587	1.3959	1.3972	1.3940
	ExT/s	25.7976	16.3656	82.4328	9.6135

From Table 6, we can get the conclusions as follows:

• The NMSE of the FBCS–RVM algorithm is the minimum among those four algorithms under different sampling rates. This indicates that its scattering coefficients’ estimation accuracy is higher than the other three algorithms.
• The FBCS–RVM algorithm obtains the minimum ENT and the maximum TBR among the above four algorithms—except, under the 35% sampling rate, the FMSBL algorithm obtains the slightly higher TBR. Therefore, the FBCS–RVM algorithm improves the imaging quality compared to the other three algorithms.
• The execution time of the FBCS–RVM algorithm is the minimum among the above four algorithms under all sampling rates; its computational efficiency is higher than the other three algorithms.

To evaluate the performance of the FBCS–RVM algorithm under different sparsity, we have conducted sparse imaging on the four targets in Figure 4 in this subsection. Moreover, the imaging results of the complex-target in Figure 4a,b,d under 50% sampling rate are shown in Figure 6.

Figure 6. The imaging results of targets in Figure 4a,b,d. first row: Figure 4a, second row: Figure 4b, third row: Figure 4d.

According to Figure 6, the imaging results of the OMP algorithm contain several false targets and lose partial targets’ information, while the FMSBL, SBRIM, and FBCS–RVM algorithms eliminate the false targets better and obtain imaging results with higher imaging quality. Table 7 shows the evaluation results under different sparsity to evaluate the performance of the above four algorithms better.

Table 7. The evaluation results under different sparsity.

Sparsity	Standards	OMP	FMSBL	SBRIM	FBCS–RVM
210	NMSE	0.1719	0.0065	0.0131	0.0039
	TBR	80.6241	358.1459	94.6461	358.1873
	ENT	0.7115	0.6127	0.6383	0.6122
	ExT/s	2.2293	4.0253	51.5601	2.1532
	RTSR	1.0353	1.8695	23.9458	1
495	NMSE	0.0454	0.0254	0.0075	0.0062
	TBR	67.2429	356.6358	53.6697	356.7732
	ENT	1.4737	1.3122	1.3052	1.3050
	ExT/s	13.8548	9.4727	52.3047	4.6349
	RTSR	2.9892	2.0438	11.2631	1
515	NMSE	0.1229	0.0191	0.0070	0.0059
	TBR	67.5803	356.6352	92.5163	356.7727
	ENT	1.5795	1.3999	1.4261	1.3951
	ExT/s	13.4775	10.1920	59.2569	5.0914
	RTSR	2.6431	1.9171	10.8217	1
677	NMSE	0.1716	0.0245	0.0340	0.0136
	TBR	65.4404	354.6187	88.7377	253.3289
	ENT	2.0640	1.8092	1.8432	1.8043
	ExT/s	17.0740	13.6286	53.3612	8.2566
	RTSR	2.0671	1.6506	6.4629	1

According to Table 7, we can obtain the following conclusions:

• The NMSE of the FBCS–RVM algorithm is smaller than 0.05 and is the minimum among the above four algorithms. This shows that the FBCS–RVM estimates the scattering coefficients more accurately than the other three algorithms, which achieves high-quality sparse imaging.
• The FBCS–RVM algorithm obtains the maximum TBR and minimum ENT among those four algorithms. Except under the 677 sparsity, the FMSBL algorithm obtains the maximum TBR. Therefore, the FBCS–RVM algorithm obtains the imaging results with the strongest and best-focused targets, and its imaging quality is higher than the other three algorithms.
• The FBCS–RVM algorithm obtains the minimum execution time among those four algorithms; its computational efficiency is higher than the other three algorithms.

4.1.3. Results on the 3D Simulation Data

Since the 3D sparse imaging results are obtained by conducting 2D sparse imaging on every equidistant plane with the fixed preset parameters, we conduct 3D sparse imaging to analyze the stability of the FBCS–RVM algorithm under different imaging scenes with the fixed preset parameters better. The main parameters of the 3D simulations are shown in Table 8. The original scene of the 3D simulations is shown in Figure 7 and Figure 8a, respectively.

Table 8. The main parameters of 3D simulations.

Parameters	Airplane	Mountain
Center frequency/GHz	37.5	37.5
Signal bandwidth/GHz	0.8	0.3
Platform height /m	1000	3000
Size of the 2D array/m	3 × 3	3 × 3
Number of sampling points in range domain	512	512
Number of APCs in the 2D array	4096	16,384
The sampling rate of echo signal	50%	50%
The size of the 2D imaging scene/m	50 × 70	250 × 250
The number of scattering units in the 2D imaging scene	101 × 101	101 × 101

Figure 7. The original scene and 3D imaging results of the airplane model; (a) original scene; (b) OMP; (c) FMSBL; (d) SBRIM; (e) FBCS–RVM;

Figure 8. The original scene and imaging results of the mountain model. (a) original scene; (b) OMP; (c) FMSBL; (d) SBRIM; (e) FBCS–RVM.

Firstly, the airplane model in Figure 7a is used for 3D sparse imaging to certify the effectiveness of the FBCS–RVM algorithm under the 3D imaging scene; the 3D imaging results of the airplane model obtained by the OMP, FMSBL, SBRIM, and FBCS–RVM algorithms are given in Figure 7b–e.

According to Figure 7, because the preset sparsity in the OMP algorithm cannot meet the requirement of every equidistant planar high-quality sparse imaging, the OMP algorithm suffers from sidelobes and loses the partial targets’ information. Its imaging quality is lower than the other three algorithms. Similarly, both FMSBL and SBRIM algorithms suffer from sidelobes to some extent because of their fixed preset parameters and measurement matrices corresponding to the whole imaging scene. The FBCS–RVM algorithm uses the target-areas as the prior information to simplify the measurement matrix and conduct sparse imaging; its measurement matrix indicates the targets’ characteristics better. As a result, the FBCS–RVM algorithm eliminates the sidelobes better and improves the imaging quality compared to the other three algorithms.

To analyze the performance of the FBCS–RVM algorithm under larger imaging scenes, we conduct 3D sparse imaging on the mountain model shown in Figure 8a. The 3D imaging results obtained by the OMP, FMSBL, SBRIM, and FBCS–RVM algorithms are shown in Figure 8b–e.

According to Figure 8, because of the fixed preset parameters and the measurement matrix corresponding to the whole imaging scene, the OMP, FMSBL, and SBRIM algorithms suffer from the sidelobe interferences to some extent. The FBCS–RVM algorithm suppresses the sidelobes better than the other three algorithms by using the target-areas as the prior information to simplify the measurement matrix and conduct sparse imaging. Since both airplane and mountain models are composed of several discrete scattering points, which are not accurately located in the 3D scattering units, their 3D original scattering coefficients are hardly predefined accurately. The NMSE is not used as the evaluation standard of the 3D imaging results. Table 9 gives the evaluation results of Figure 7 and Figure 8 to evaluate their performance of the above four algorithms in 3D sparse imaging quantitatively.

Table 9. The evaluation results under different targets.

Target	Standards	OMP	FMSBL	SBRIM	FBCS–RVM
Airplane	TBR	65.3520	63.9603	59.3230	68.9073
	ENT	0.1924	0.1998	0.3998	0.0615
	ExT/s	2628.89	3525.32	53347.14	848.20
	RTSR	3.0095	4.1570	62.8955	1
Mountain	TBR	45.6039	43.8738	37.1098	49.3453
	ENT	0.7645	0.9574	1.4492	0.4036
	ExT/s	60530.26	220966.74	223913.66	18547.83
	RTSR	3.2636	11.9139	12.0727	1

According to Table 9, we can know that the FBCS–RVM algorithm obtains the 3D imaging results with the minimum ENT, execution time, and maximum TBR among the above four algorithms. Therefore, the computational efficiency and imaging quality of the FBCS–RVM algorithm are higher than the other three algorithms.

Therefore, according to the 2D and 3D simulation results, the FBCS–RVM algorithm achieves sparse imaging with high-quality and efficiency. It improves the imaging quality, stability, and computational efficiency compared to the OMP, SBRIM, and FMSBL algorithms successfully.

4.1.4. Results on Experimental Data

To fully certify the effectiveness of the FBCS–RVM algorithm in the real data, the experimental data obtained by two ground equivalent LASAR (GDLASAR) [32,35] systems with different aperture lengths and moving trajectories are used for 3D sparse imaging in this subsection. The main parameters of the two GDLASAR systems are listed in Table 10. The above two systems and their experimental scene are shown in Figure 9.

Table 10. The parameters of two GDLASAR systems.

Parameters	System 1	System 2
Center frequency /GHz	9.62	10
Signal bandwidth /GHz	0.08	2
Size of the 2D array/m	1.25 × 1.25	1.5 × 1.3
Number of sampling points in range domain	500	801
Number of APCs in the 2D array	8928	8394
Size of 2D imaging scene/m	40× 70	5 × 5
Number of scattering units in the 2D imaging scene	101 × 101	101 × 101

Figure 9. (a) System; (b) experimental scene; first row: wall experiment, second row: Two balls experiment.

To improve the computational efficiency of 3D sparse imaging on the experimental data, the targets’ echo signals are extracted firstly by their locations in the experimental scene. Moreover, the 3D imaging results of the OMP, FMSBL, SBRIM, and FBCS–RVM algorithms are shown in Figure 10.

Figure 10. The 3D imaging results by the OMP, FMSBL, SBRIM, and FBCS–RVM algorithms. first row: wall experiment, second row: two balls experiment.

According to Figure 10, the above four algorithms can achieve 3D sparse imaging on both experimental data. Because of the inevitable signal noise in the experimental data, the OMP, FMSBL, and SBRIM algorithms suffer from the sidelobe interferences to some extent. Since the FBCS–RVM algorithm uses the target-areas to simplify the measurement matrix and conduct sparse imaging, it eliminates the sidelobe interferences more effectively and improves imaging quality compared to the other three algorithms. To evaluate the performance of those four algorithms on the experimental data, Table 11 and Table 12 show the evaluation results under different sampling rates.

Table 11. The evaluation results of wall experiment.

Sampling Rate	Standards	OMP	FMSBL	SBRIM	FBCS–RVM
12.5%	TBR	27.8904	25.8961	30.3913	31.8609
	ENT	1.8007	1.8691	2.0098	1.4276
	ExT/s	244.7976	913.0925	15,523.19	148.4204
	RTSR	1.6525	6.1639	104.7912	1
25%	TBR	29.9577	27.7150	31.5723	33.0056
	ENT	1.5790	1.7417	1.9560	1.3140
	ExT/s	467.4062	1358.39	21,076.94	301.6024
	RTSR	1.5499	4.5043	69.8898	1
50%	TBR	31.1948	28.8495	32.9698	34.1467
	ENT	1.4733	1.5387	1.8587	1.2026
	ExT/s	950.8605	1950.28	32,152.46	587.49
	RTSR	1.6185	3.3196	54.7279	1
75%	TBR	31.7079	29.1247	33.1911	34.4093
	ENT	1.4184	1.5000	1.8037	1.1544
	ExT/s	1364.31	2623.59	42,886.93	834.57
	RTSR	1.6347	3.1436	51.3877	1
100%	TBR	31.8951	25.8961	33.2413	34.3879
	ENT	1.4021	1.5150	1.7713	1.1752
	ExT/s	1827.54	3876.47	53,749.08	1038.27
	RTSR	1.7602	3.7336	51.7677	1

Table 12. The evaluation results of the two balls experiment.

Sampling Rate	Standards	OMP	FMSBL	SBRIM	FBCS–RVM
12.5%	TBR	45.3686	57.9804	31.3033	59.1770
	ENT	1.8858	0.6891	3.7257	0.6068
	ExT/s	137.1024	285.7793	11,718.08	55.0775
	RTSR	2.4893	5.1887	212.7652	1
25%	TBR	47.2367	59.1535	33.8888	60.6803
	ENT	1.6312	0.5383	3.2330	0.4548
	ExT/s	257.5522	569.6074	15,654.62	84.1086
	RTSR	3.0621	6.7659	186.1239	1
50%	TBR	48.1008	60.2373	36.2445	61.5205
	ENT	1.4724	0.4749	2.8011	0.3666
	ExT/s	495.9828	1175.66	23,527.45	125.8026
	RTSR	3.9425	9.3453	187.0188	1
75%	TBR	48.5975	60.5376	37.4526	61.9171
	ENT	1.3887	0.4846	2.6097	0.3449
	ExT/s	769.3935	1872.83	31,422.70	175.1862
	RTSR	4.3919	10.6905	179.3674	1
100%	TBR	48.5673	61.1714	38.0847	62.8071
	ENT	1.3939	0.4783	2.5305	0.3320
	ExT/s	1060.19	2361.45	39,405.99	301.1206
	RTSR	3.5208	7.8442	130.8645	1

According to Table 11 and Table 12, we can get the following conclusions:

• In both pieces of experimental data, the FBCS–RVM algorithm obtains imaging results with the maximum TBR, minimum ENT, and execution time among those four algorithms. Therefore, its imaging quality and computational efficiency are higher than the other three algorithms.
• The RTSR between the FBCS–RVM algorithm and the other three algorithms in the two balls experiment is larger than the wall experiment. This indicates that the computational efficiency’s improvement of the FBCS–RVM algorithm is higher when the sparsity of the imaging scene is smaller.

4.2. Ablation Study

According to Section 3.1 and Section 3.2, the FBCS–RVM algorithm contains two key steps: extracting the target-areas under the framework of RVM and eliminating the elements with small scattering coefficients in the target-areas by the TSVD algorithm. Therefore, we verify the effectiveness of the above two steps in the following subsections.

4.2.1. Ablation Study on Extracting the Target-Areas under the Framework of RVM

To verify the effectiveness of extracting the target-areas under the framework of RVM, both fuzzy c-means (FCM) [36] and k-means algorithms [37] are used to extract the target-areas while the other steps of the FBCS–RVM algorithm remain unchanged. Figure 11 lists the imaging results of the complex-targets in Figure 4c obtained by the FCM, K-means, and the FBCS–RVM algorithm. Table 13 gives the evaluation results of the above three algorithms to evaluate their performance more clearly and accurately.

Figure 11. The original scene and imaging results of Figure 4c. (a) original scene; (b) the imaging results corresponding to the FCM algorithm; (c) the imaging results corresponding to the K–Means algorithm; (d) the imaging results of the FBCS–RVM algorithm.

Table 13. The evaluation results of Figure 11.

Methods	NMSE	TBR	ENT	ExT/s
FCM	0.2432	60.3040	1.0713	1.7540
K-Means	0.7264	111.0213	0.8455	3.9616
FBCS–RVM	0.0060	247.0184	1.3961	5.9264

According to Figure 11 and Table 13, we can get the following conclusions:

• Both FCM and K-Means algorithms cannot extract the target-areas accurately and lose partial targets’ information, and we cannot achieve high-quality sparse imaging with the above two algorithms.
• The FBCS–RVM algorithm obtains the minimum NMSE, maximum TBR, and execution time among those three algorithms; its NMSE is smaller than 0.01. This indicates that the FBCS–RVM algorithm extracts the target-areas more accurately than the FCM and K-Means algorithm; it achieves high-quality sparse imaging.

4.2.2. Ablation Study on the TSVD Algorithm

In the subsection, when the diagonal matrix is singular due to the elements with too small scattering coefficients in the target-areas, we obtain two comparative imaging results to verify the effectiveness of the TSVD algorithm in eliminating those elements. Figure 12 lists the imaging results of the FBCS–RVM algorithm and without the TSVD algorithm. Table 14 gives the evaluation results of the above two imaging results to certify the effectiveness of the TSVD algorithm better.

Figure 12. The imaging results of the complex–target in Figure 4. First row: imaging results without the TSVD algorithm, second row: imaging results of the FBCS–RVM algorithm.

Table 14. The evaluation results of Figure 12.

	TSVD	NMSE	TBR	ENT	ExT/s
Figure 12a	×	2.2746$\times {10}^{12}$	348.4178	0.6053	3.0735
	✓	0.0053	356.6006	0.6116	3.0740
Figure 12b	×	2.8868× ${10}^5$	84.7975	1.2917	5.7222
	✓	0.0061	82.9849	1.3050	5.9755
Figure 12c	×	9.9908× ${10}^{28}$	347.4051	1.3722	5.0965
	✓	0.0088	351.4521	1.3958	5.1139
Figure 12d	×	4.7497$\times {10}^{31}$	346.5817	1.7125	8.7975
	✓	0.0159	317.3393	1.8043	8.8991

According to Figure 12 and Table 14, we can get the following conclusions:

• Without the TSVD algorithm, the scattering coefficients cannot be estimated correctly under the singular diagonal matrix, and the imaging results lose too much of the targets’ effective information. After eliminating the elements with the small scattering coefficients by the TSVD algorithm, we can obtain the correct imaging results.
• The execution time of the FBCS–RVM algorithm is slightly larger than without the TSVD algorithm. This indicates that the computational efficiency of the FBCS–RVM algorithm decreases slightly due to the TSVD algorithm.

5. Discussion

In this section, we use the complex-targets in Figure 4d as the initial target-areas and increase the sparsity of imaging scene gradually to analyze the application scenes of the FBCS–RVM algorithm; the total number of scattering units in the whole imaging scene is fixed and set as 4096. The evaluation results of the OMP, FMSBL, SBRIM, and FBCS–RVM algorithms under increasing sparsity with fixed total scattering units are shown in Figure 13.

Figure 13. The evaluation results under increasing sparsity with fixed total scattering units. (a) NMSE; (b) TBR; (c) ENT; (d) execution time.

According to Figure 13, we can get the following conclusions:

• Computational efficiency: The FBCS–RVM algorithm obtains the minimum execution time among the above four algorithms; its computational efficiency is higher than the other three algorithms.
• Imaging quality: When the sparsity is smaller than 800, the FBCS–RVM algorithm obtains the minimum NMSE among the above four algorithms; its imaging quality is higher than the other three algorithms. Otherwise, its NMSE is slightly smaller than the FMSBL algorithm when the sparsity is higher than 800, which indicates that targets occupy more than 20% of the whole imaging scene. Its imaging quality is slightly lower than the FMSBL algorithm.

In addition, similarly to most CS algorithms, when conducting 3D sparse imaging with large scale remote sensing data by the FBCS–RVM algorithm, the measurement matrix usually becomes huge because of the large imaging scene. The huge measurement matrix and its matrix operations lead to the FBCS–RVM algorithm hardly achieving 3D sparse imaging with high-efficiency on the large scale remote sensing data. Therefore, the main limitations of the FBCS–RVM algorithm are summarized as the following content:

• The FBCS–RVM algorithm probably loses partial targets’ information under high sparsity; it cannot achieve high-quality sparse imaging.
• The FBCS–RVM algorithm cannot always achieve high-efficiency 3D sparse imaging under large scale remote sensing data.

6. Conclusions

In this paper, we propose the FBCS–RVM algorithm to achieve LASAR 3D sparse imaging with high quality and efficiency. Firstly, after calculating the maximum marginal likelihood function under the framework of the relevance vector machine (RVM), the scattering units corresponding to the non-zero optimal hyper-parameters are extracted as the target-areas in the imaging scene. Then, we use the target-areas as the prior information to simplify the measurement matrix and conduct sparse imaging. In addition, when the target-areas contain several elements whose scattering coefficients are too small or closer to 0 compared to other elements, the diagonal matrix becomes singular and irreversible. Its inverse matrix is replaced with the generalized inverse matrix obtained by the TSVD algorithm to estimate the scattering coefficients correctly; the elements with small scattering coefficients are extracted and deleted from the target-areas successfully according to the rank of the singular diagonal matrix. By taking the target-areas as the prior information for sparse imaging, the FBCS–RVM simplifies the matrix operations corresponding to the measurement matrix successfully. As a result, it improves the computational efficiency and decreases the requirements from the hardware system effectively. Both simulation and experimental results illustrate that the FBCS–RVM algorithm achieves sparse imaging with high quality and efficiency successfully. It improves the computational efficiency and imaging quality compared to the other three comparison algorithms (the OMP, FMSBL, and SBRIM algorithms). Especially in the computational efficiency, the FBCS–RVM algorithm can be 100 times higher than the SBRIM algorithm, 10 times higher than the FMSBL algorithm, and 4 times higher than the OMP algorithm.

Since CS algorithms can obtain higher imaging quality under under-sampling than traditional remote sensing imaging algorithms and the FBCS–RVM algorithm improves the computational efficiency compared to most CS algorithms, the FBCS–RVM algorithm has great application prospects in 3D digital elevation models and urban area imaging.

Our future work is as follows:

• Study the target-areas extraction methods based on the convolution neural network for the high sparsity imaging scene with higher accuracy and efficiency.
• Achieve 3D sparse imaging in the large scale remote sensing applications by simplifying the measurement matrix by dividing the original imaging scene into several smaller imaging scenes.