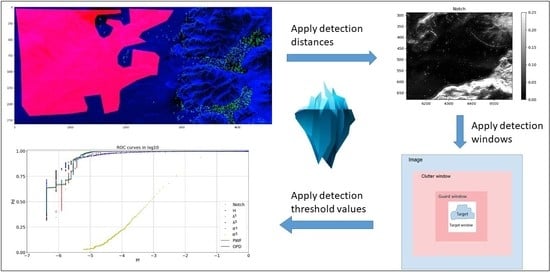
Comparison of Target Detectors to Identify Icebergs in Quad-Polarimetric L-Band Synthetic Aperture Radar Data
Abstract
1. Introduction
Polarimetry
2. Detectors
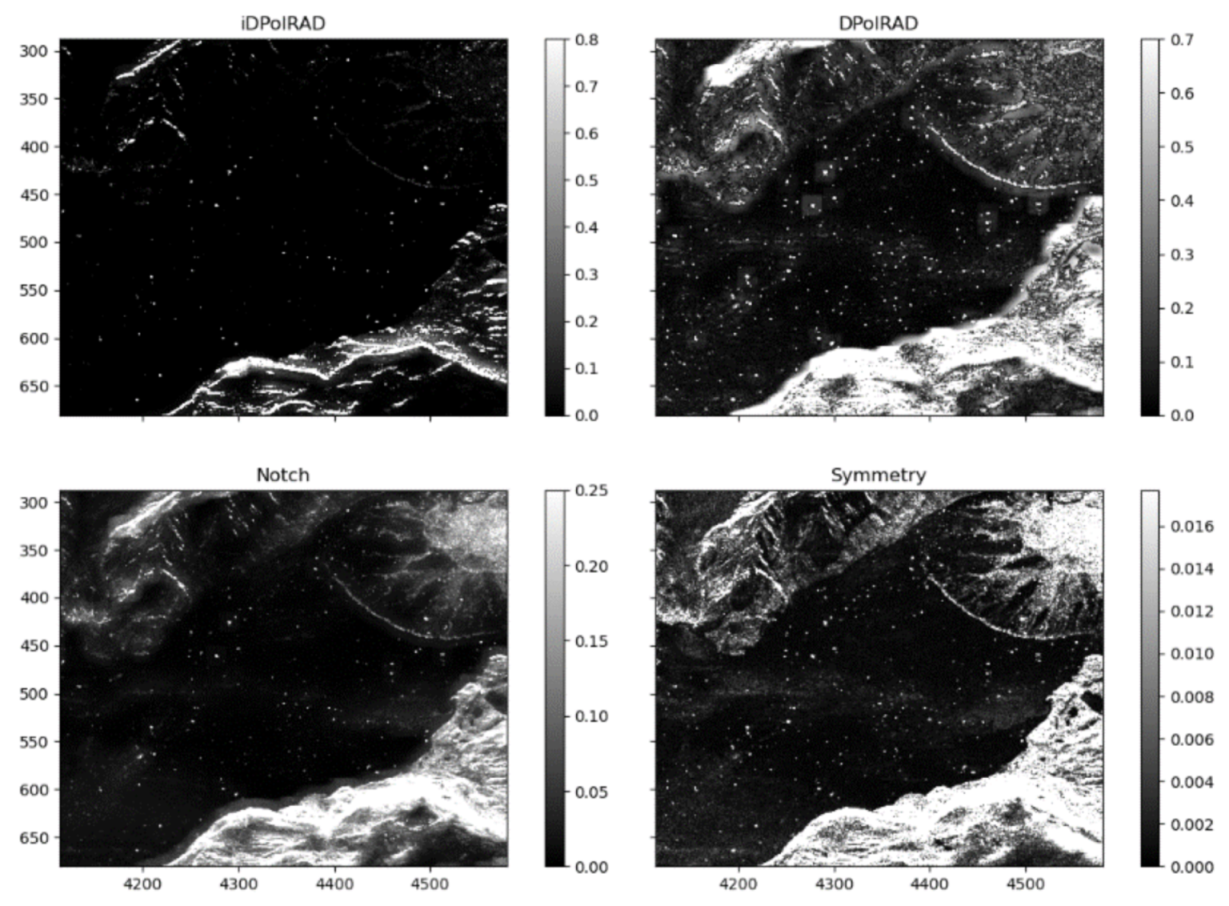
2.1. The IDPolRAD and the DPolRAD
2.2. The Polarimetric Notch Filter
2.3. The Polarimetric Match Filter
2.4. The Reflection Symmetry Detector
2.5. Optimal Polarimetric Detector
2.6. The Polarimetric Whitening Filter
3. Dataset
4. Methods
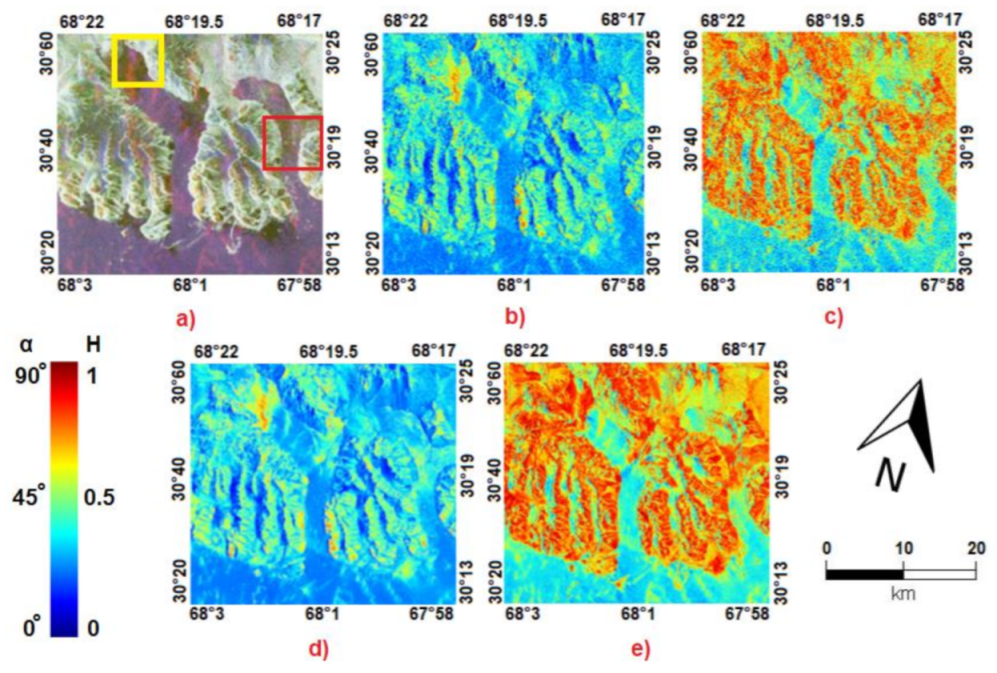
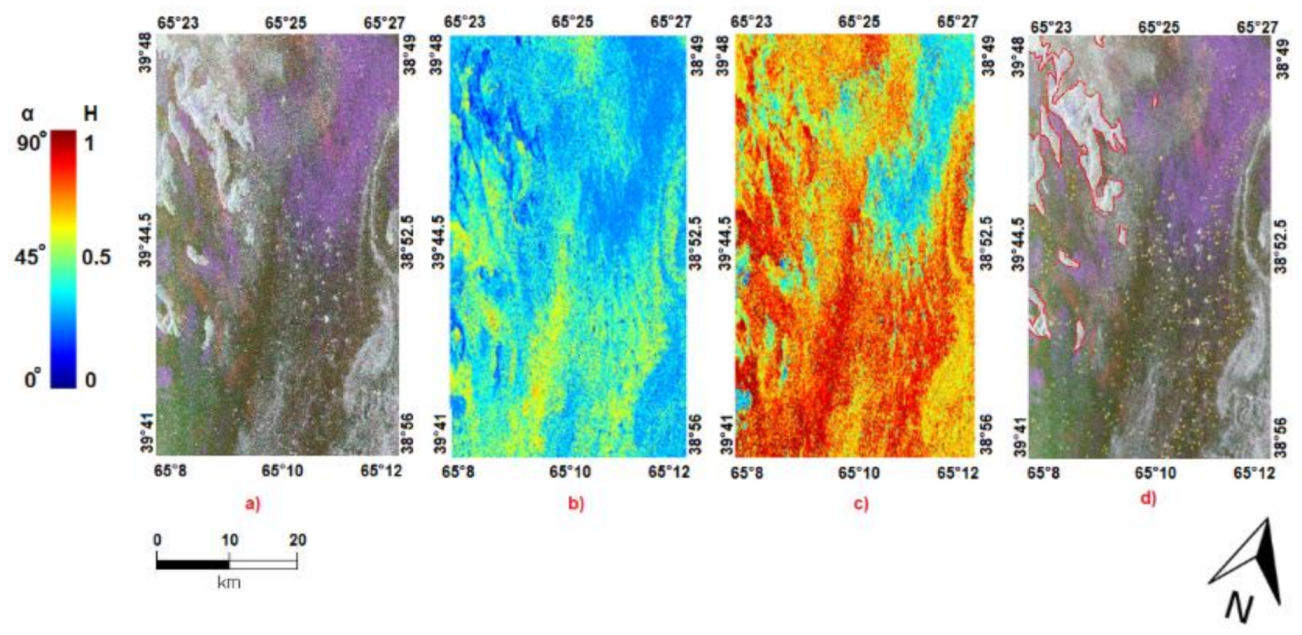
4.1. Preliminary Image Analysis
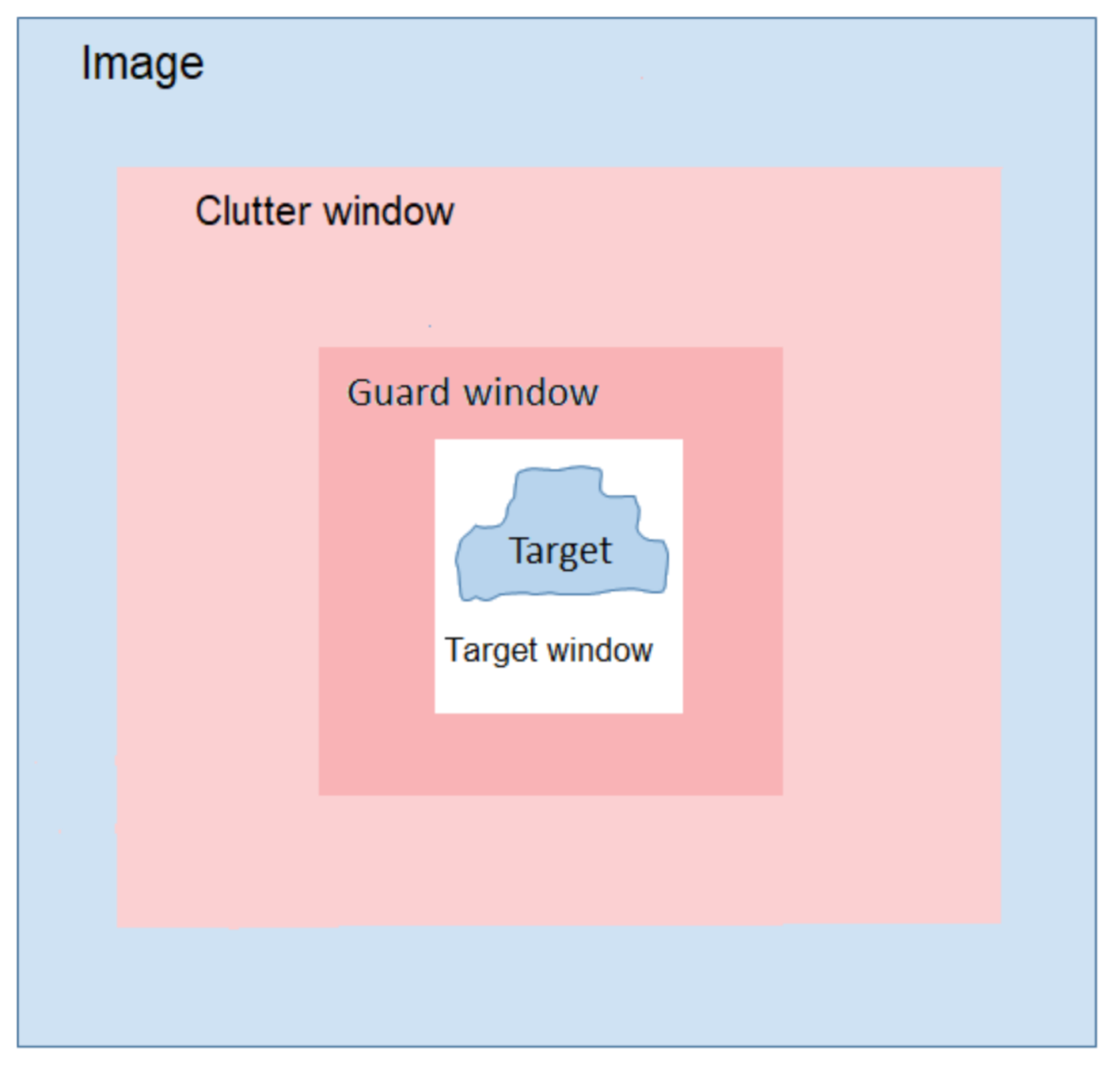
4.2. Identifying Targets and Clutter
4.3. Preliminary Detection Comparison
Detection Distances
5. Results
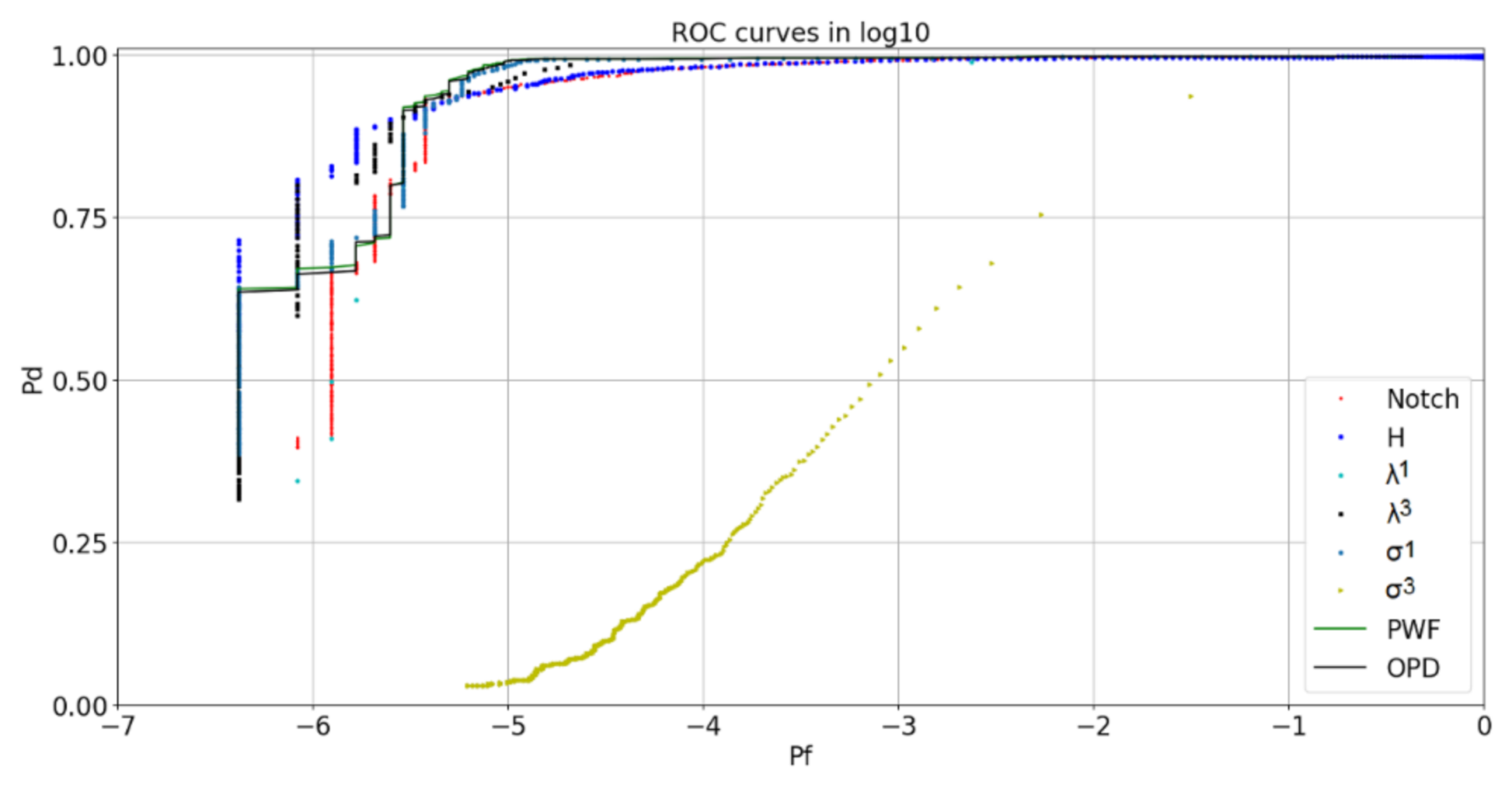
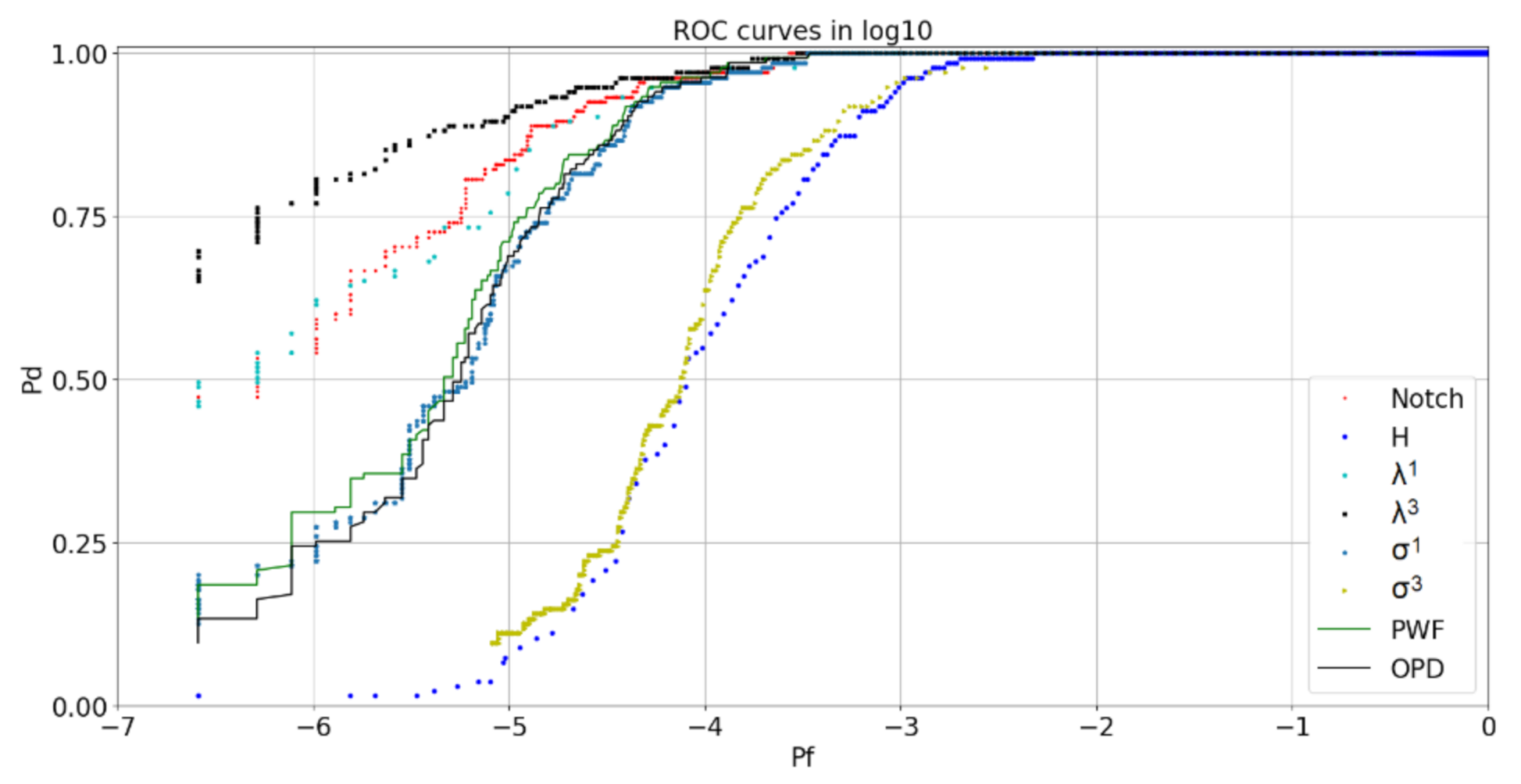
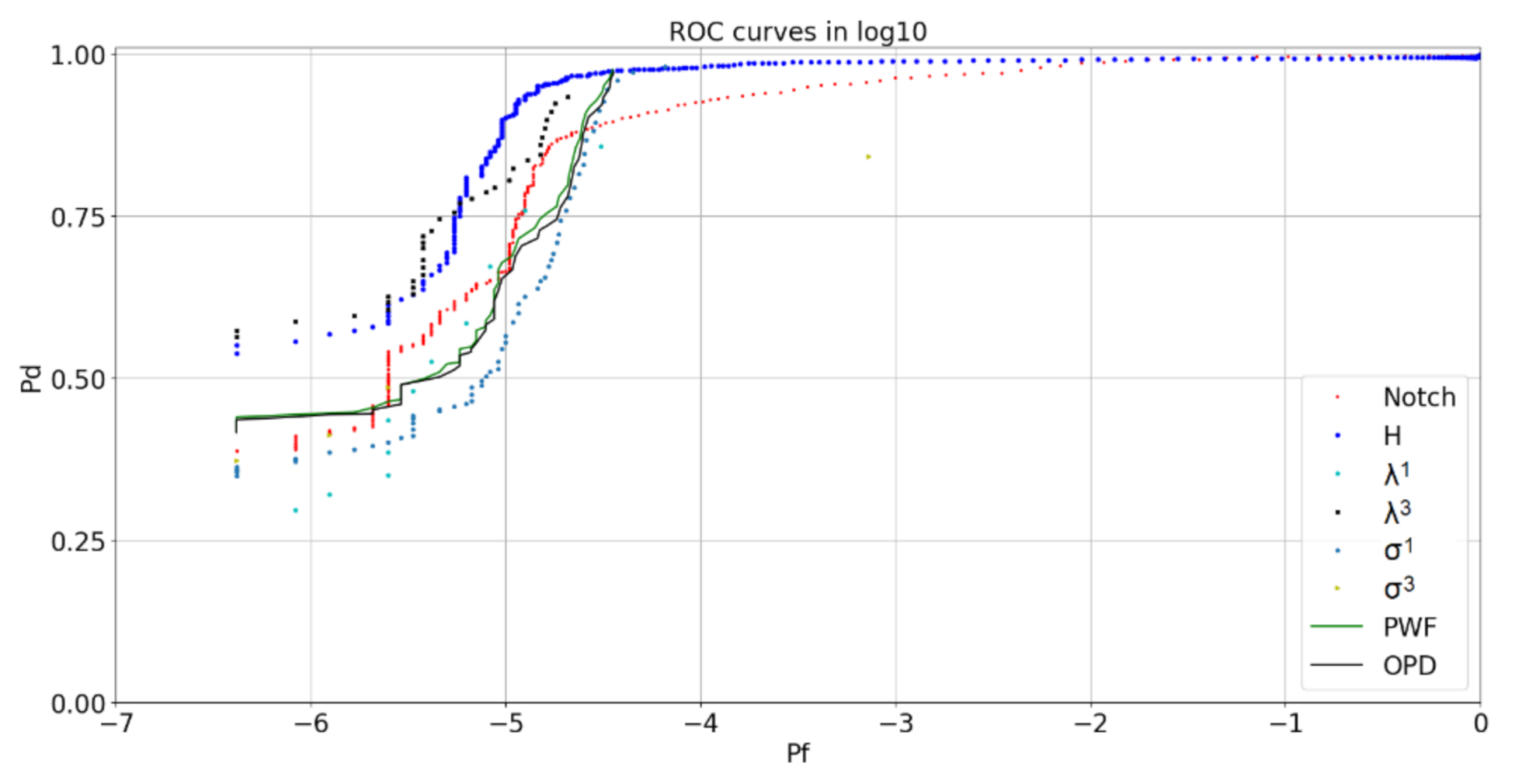
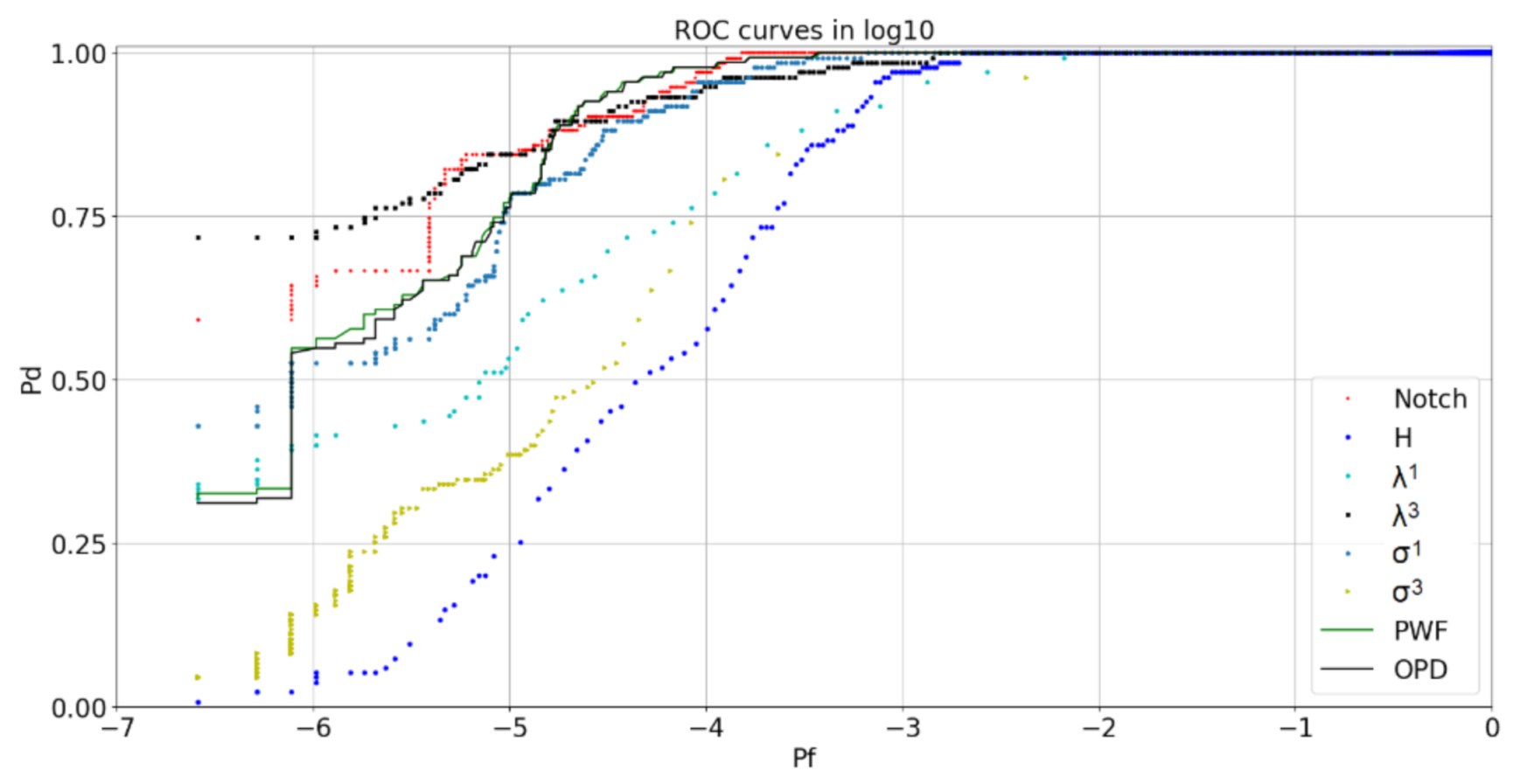
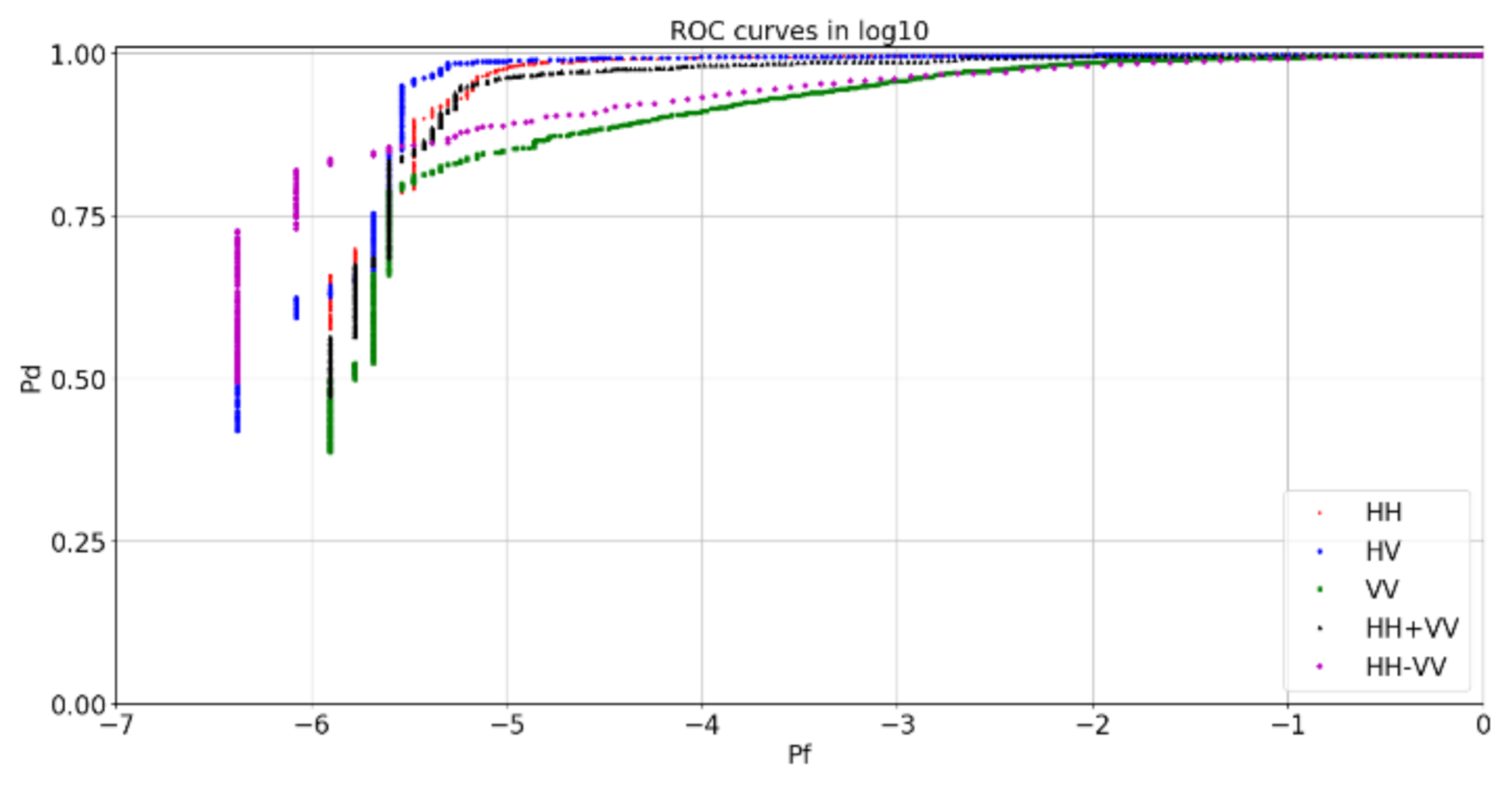
5.1. Quad-Polarimetric ROC Curves
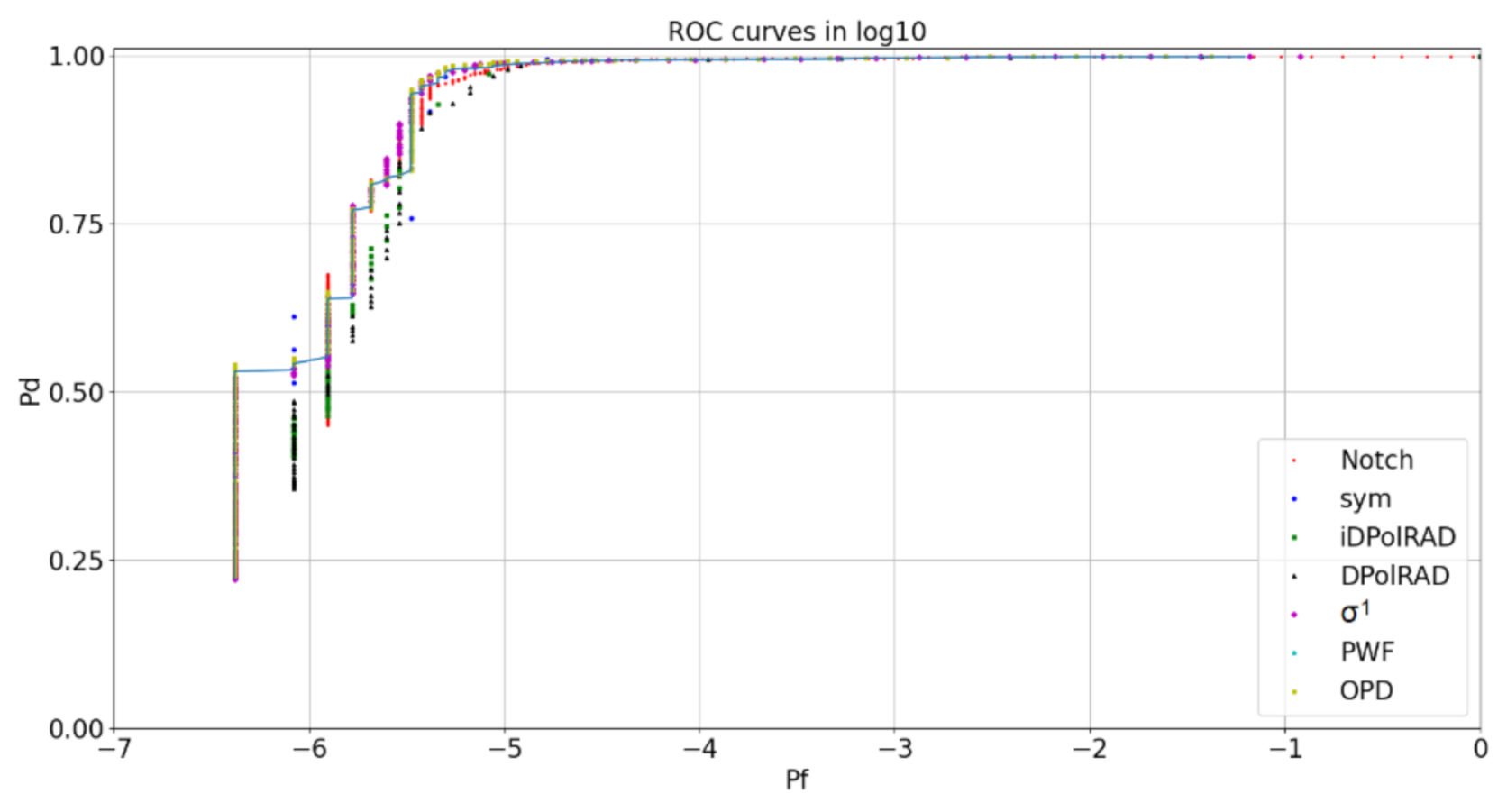
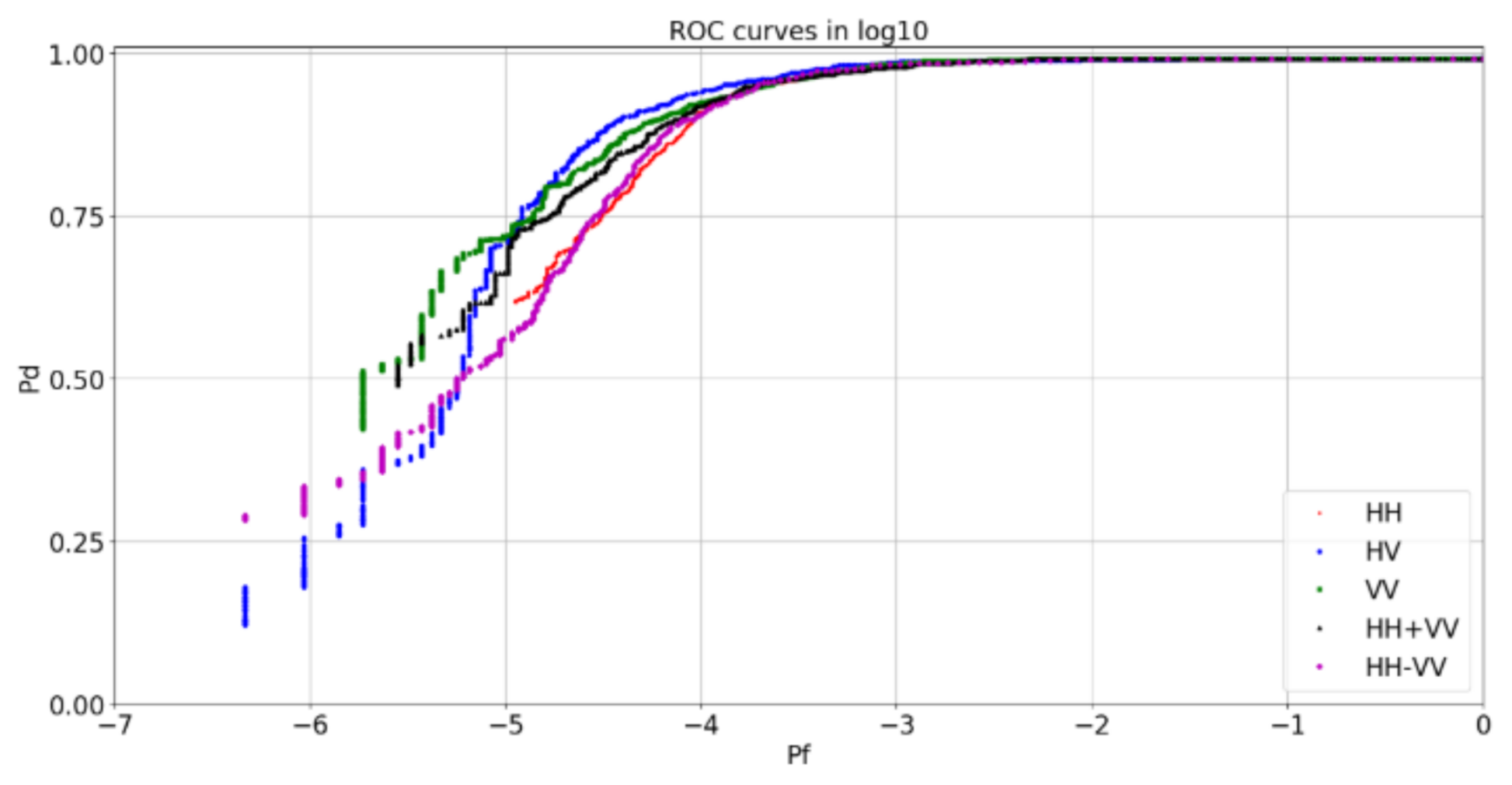
5.2. Dual-Polarimetric ROC Curves
5.3. Intensities ROC Curves
5.4. Best Detectors
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hanna, E.; Mernild, S.H.; Cappelen, J.; Steffen, K. Recent warming in Greenland in a long-term instrumental (1881–2012) climatic context: I. Evaluation of surface air temperature records. Environ. Res. Lett. 2012, 7, 045404. [Google Scholar] [CrossRef]
- Akbari, V.; Brekke, C. Iceberg detection in open water and sea ice using C-band radar polarimetry. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2298–2301. [Google Scholar]
- Bigg, G.R. Icebergs: Their Science and Links to Global Change; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Frost, A.; Ressel, R.; Lehner, S. Automated iceberg detection using high-resolution X-band SAR images. Can. J. Remote Sens. 2016, 42, 354–366. [Google Scholar] [CrossRef]
- Wesche, C.; Dierking, W. Estimating iceberg paths using a wind-driven drift model. Cold Reg. Sci. Technol. 2016, 125, 31–39. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Heiselberg, H. Ship-iceberg classification in SAR and multispectral satellite images with neural networks. Remote Sens. 2020, 12, 2353. [Google Scholar] [CrossRef]
- Lopez-Lopez, L.; Parmiggiani, F.; Moctezuma-Flores, M.; Guerrieri, L. SAR image observations of the A-68 iceberg drift. Cryosphere Discuss. 2020, 1–16. [Google Scholar]
- Heiselberg, H. Ship-iceberg detection & classification in sentinel-1 SAR images. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 235–241. [Google Scholar]
- Powell, R.; Domack, G.W. Modern glaciomarine environments. In Modern and Past Glacial Environments; Elsevier: Amsterdam, The Netherlands, 2002; pp. 361–389. [Google Scholar]
- Wadhams, P.; Woodwort-Lynas, C. Icebergs; Butterworth-Heinemann Limited: Oxford, UK, 2004. [Google Scholar]
- Akbari, V.; Brekke, C.; Doulgeris, A.P.; Storvold, R.; Sivertsen, A.H. Quad-polarimetric SAR for detection and characterization of icebergs. In Proceedings of the ESA Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Marino, A.; Dierking, W.; Wesche, C. A depolarization ratio anomaly detector to identify icebergs in sea ice using dual-polarization SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5602–5615. [Google Scholar] [CrossRef]
- Marino, A. A notch filter for ship detection with polarimetric SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1219–1232. [Google Scholar] [CrossRef]
- Novak, L.M.; Sechtin, M.B.; Cardullo, M.J. Studies of target detection algorithms that use polarimetric radar data. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 150–165. [Google Scholar] [CrossRef]
- Nunziata, F.; Migliaccio, M.; Brown, C.E. A physically-based approach to observe man-made metallic objects in dual-polarized SAR data. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3007–3010. [Google Scholar]
- Chaney, R.; Bud, M.; Novak, L. On the performance of polarimetric target detection algorithms. IEEE Aerosp. Electron. Syst. Mag. 1990, 5, 10–15. [Google Scholar] [CrossRef]
- Novak, L.M.; Burl, M.C. Optimal speckle reduction in polarimetric SAR imagery. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 293–305. [Google Scholar] [CrossRef]
- Soldal, I.H.; Dierking, W.; Korosov, A.; Marino, A. Automatic Detection of Small Icebergs in Fast Ice Using Satellite Wide-Swath SAR Images. Remote Sens. 2019, 11, 806. [Google Scholar] [CrossRef]
- Crisp, D.J. The State-of-the-Art in Ship Detection in Synthetic Aperture Radar Imagery; DSTO-RR-0272; Defence Science And Technology Organisation Edinburgh: Edinburgh, Australia, 2004. [Google Scholar]
- Dierking, W.; Wesche, C. C-band radar polarimetry—Useful for detection of icebergs in sea ice? IEEE Trans. Geosci. Remote Sens. 2013, 52, 25–37. [Google Scholar] [CrossRef]
- Bailey, J.; Marino, A. Quad-Polarimetric Multi-Scale Analysis of Icebergs in ALOS-2 SAR Data: A Comparison between Icebergs in West and East Greenland. Remote Sens. 2020, 12, 1864. [Google Scholar] [CrossRef]
- Jagdhuber, T.; Stockamp, J.; Hajnsek, I.; Ludwig, R. Identification of soil freezing and thawing states using SAR polarimetry at C-band. Remote Sens. 2014, 6, 2008–2023. [Google Scholar] [CrossRef]
- Park, S.-E. Variations of microwave scattering properties by seasonal freeze/thaw transition in the permafrost active layer observed by ALOS PALSAR polarimetric data. Remote Sens. 2015, 7, 17135–17148. [Google Scholar] [CrossRef]
- Muhuri, A.; Manickam, S.; Bhattacharya, A. Scattering mechanism based snow cover mapping using RADARSAT-2 C-Band polarimetric SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3213–3224. [Google Scholar] [CrossRef]
- Touzi, R. Target scattering decomposition in terms of roll-invariant target parameters. IEEE Trans. Geosci. Remote Sens. 2006, 45, 73–84. [Google Scholar] [CrossRef]
- Willis, C.; Macklin, J.; Partington, K.; Teleki, K.; Rees, W.; Williams, R. Iceberg detection using ERS-1 synthetic aperture radar. Int. J. Remote Sens. 1996, 17, 1777–1795. [Google Scholar] [CrossRef]
- Wesche, C.; Dierking, W. Iceberg signatures and detection in SAR images in two test regions of the Weddell Sea, Antarctica. J. Glaciol. 2012, 58, 325–339. [Google Scholar] [CrossRef]
- Gladstone, R.; Bigg, G. Satellite tracking of icebergs in the Weddell Sea. Antarct. Sci. 2002, 14, 278–287. [Google Scholar] [CrossRef]
- Collares, L.L.; Mata, M.M.; Kerr, R.; Arigony-Neto, J.; Barbat, M.M. Iceberg drift and ocean circulation in the northwestern Weddell Sea, Antarctica. Deep Sea Res. Part II Top. Stud. Oceanogr. 2018, 149, 10–24. [Google Scholar] [CrossRef]
- Yamaguchi, Y. Polarimetric SAR Imaging: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Akbari, V.; Doulgeris, A.P.; Eltoft, T. Non-Gaussian clustering of SAR images for glacier change detection. In Proceedings of the ESA Living Planet Symposium, Bergen, Norway, 28 June–2 July 2010. [Google Scholar]
- Lee, J.-S.; Jurkevich, L.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Rev. 1994, 8, 313–340. [Google Scholar] [CrossRef]
- Chen, J.Y.; Reed, I.S. A detection algorithm for optical targets in clutter. IEEE Trans. Aerosp. Electron. Syst. 1987, 1, 46–59. [Google Scholar] [CrossRef]
- Liu, G.; Huang, S.; Torre, A.; Rubertone, F. The multilook polarimetric whitening filter (MPWF) for intensity speckle reduction in polarimetric SAR images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1016–1020. [Google Scholar]
- Lopes, A.; Séry, F. Optimal speckle reduction for the product model in multilook polarimetric SAR imagery and the Wishart distribution. IEEE Trans. Geosci. Remote Sens. 1997, 35, 632–647. [Google Scholar] [CrossRef]
- Khan, S.; Guida, R. On fractional moments of multilook polarimetric whitening filter for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3502–3512. [Google Scholar] [CrossRef]
- Akbari, V.; Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T. A change detector for polarimetric SAR data based on the relaxed Wishart distribution. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3806–3809. [Google Scholar]
- Galland, F.; Nicolas, J.-M.; Sportouche, H.; Roche, M.; Tupin, F.; Réfrégier, P. Unsupervised synthetic aperture radar image segmentation using Fisher distributions. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2966–2972. [Google Scholar] [CrossRef]
- Bjørk, A.A.; Kruse, L.; Michaelsen, P. Brief communication: Getting Greenland’s glaciers right–a new data set of all official Greenlandic glacier names. Cryosphere 2015, 9, 2215–2218. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
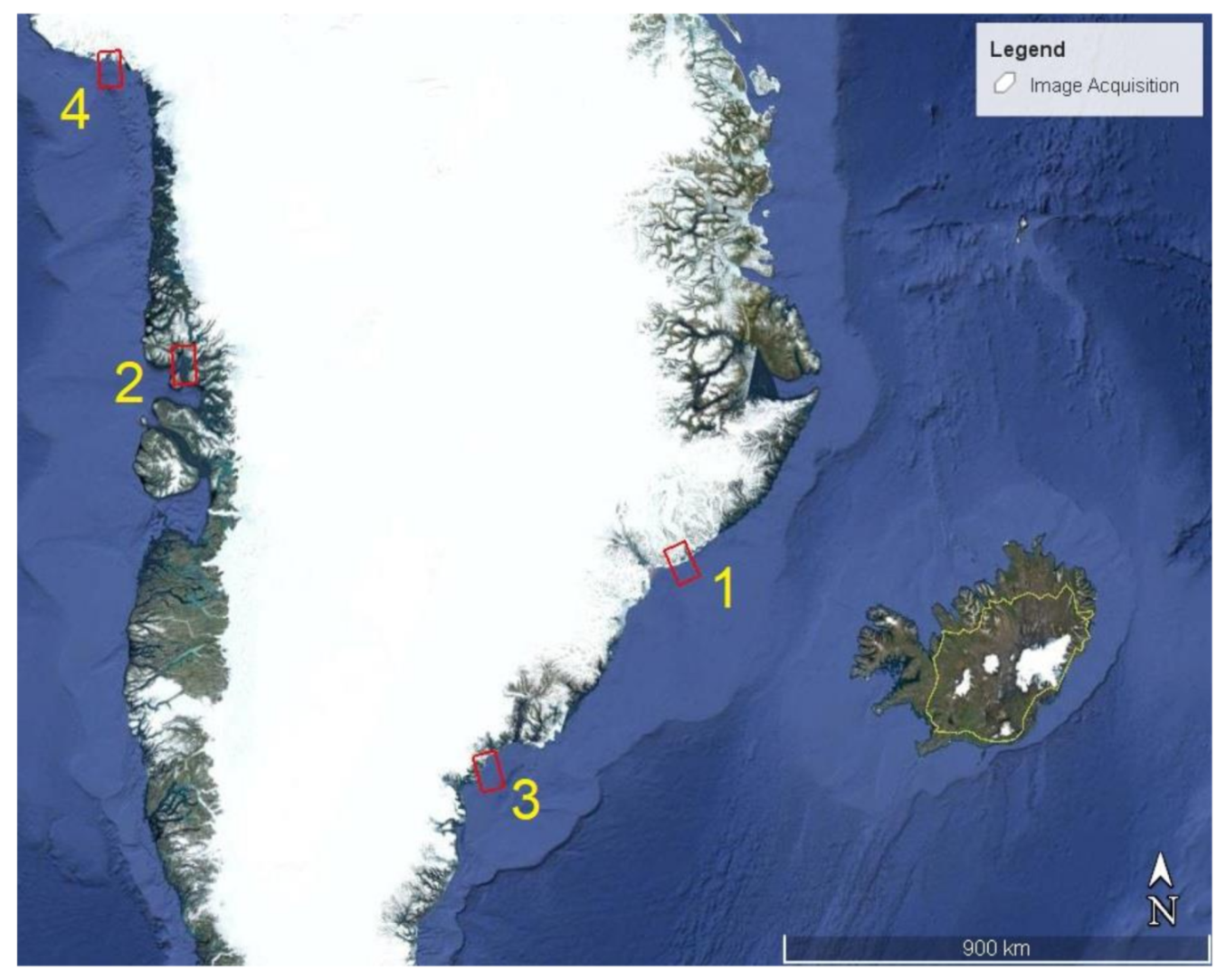


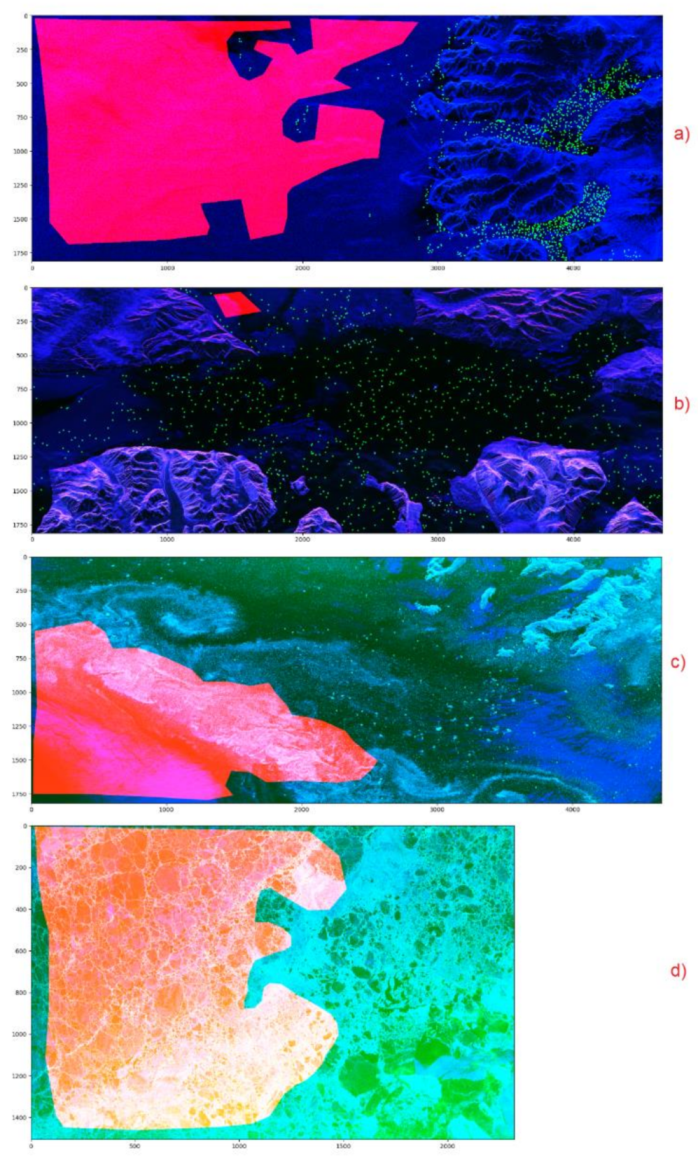





| ID | Location | Lat/Lon (DMS) | Resolution (m) | Incidence Angle Range (°) | Date/Time |
|---|---|---|---|---|---|
| (1) ALOS2066231 360-150815 | Blosseville Coast | 68°02′13.2″ N 30°19′58.8″ W | 4.3 × 5.1 | 37, 39, 41.5 | 15 August 2015 01:26 |
| (2) ALOS2064761 430-150805 | Nuugaatsiaq | 71°25′26.4″ N 53°26′52.8″ W | 4.3 × 5.1 | 37, 39, 41.5 | 5 August 2015 02:48 |
| (3) ALOS2064461 300-150803 | Isortoq | 65°07′08.4″ N 39°13′37.2″ W | 4.3 × 5.1 | 37, 39, 41.5 | 3 August 2015 02:07 |
| (4) ALOS2191031 530-171206 | Savissivik | 75°52′19.2″ N 62°10′48″ W | 4.3 × 5.1 | 29, 31, 33.6 | 6 December 2017 02:52 |
| λ1 | λ3 | H | PNF | σ1 | σ3 | PWF | OPD | |
|---|---|---|---|---|---|---|---|---|
| PF = 16 | 0.345 | 0.800 | 0.809 | 0.412 | 0.668 | 0.671 | 0.663 | |
| PF = 15 | 0.799 | 0.944 | 0.948 | 0.950 | 0.983 | 0.034 | 0.990 | 0.990 |
| PF = 14 | N/A | 0.986 | 0.982 | 0.986 | 0.994 | 0.218 | 0.995 | 0.994 |
| λ1 | λ3 | H | PNF | σ1 | σ3 | PWF | OPD | |
|---|---|---|---|---|---|---|---|---|
| PF = 16 | 0.570 | 0.770 | 0.015 | 0.541 | 0.222 | 0.296 | 0.244 | |
| PF = 15 | 0.785 | 0.904 | 0.074 | 0.837 | 0.674 | 0.111 | 0.711 | 0.689 |
| PF = 14 | 0.970 | 0.970 | 0.548 | 0.970 | 0.956 | 0.615 | 0.963 | 0.963 |
| iD | D | PNF | σ1 | Sym | PWF | OPD | |
|---|---|---|---|---|---|---|---|
| PF = 1−6 | 0.462 | 0.487 | 0.451 | 0.535 | 0.612 | 0.551 | 0.542 |
| PF = 1−5 | 0.972 | 0.970 | 0.978 | 0.988 | 0.969 | 0.990 | 0.985 |
| PF = 1−4 | 0.993 | 0.994 | 0.993 | 0.994 | 0.994 | 0.993 |
| iD | D | PNF | σ1 | Sym | PWF | OPD | |
|---|---|---|---|---|---|---|---|
| PF=1−6 | 0.593 | 0.593 | 0.556 | 0.385 | 0.363 | 0.370 | 0.313 |
| PF=1−5 | 0.837 | 0.874 | 0.793 | 0.808 | 0.867 | 0.815 | 0.800 |
| PF=1−4 | 0.963 | 0.963 | 0.963 | 0.970 | 0.970 | 0.978 | 0.978 |
| HV | HH | VV | HH + VV | HH-VV | |
|---|---|---|---|---|---|
| PF = 1−6 | 0.624 | 0.782 | 0.822 | ||
| PF=1−5 | 0.989 | 0.977 | 0.851 | 0.962 | 0.890 |
| PF=1−4 | 0.995 | 0.993 | 0.911 | 0.982 | 0.930 |
| HV | HH | VV | HH + VV | HH − VV | |
|---|---|---|---|---|---|
| PF = 1−6 | 0.255 | 0.334 | |||
| PF = 1−5 | 0.706 | 0.719 | 0.663 | 0.561 | |
| PF = 1−4 | 0.940 | 0.910 | 0.926 | 0.920 | 0.905 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bailey, J.; Marino, A.; Akbari, V. Comparison of Target Detectors to Identify Icebergs in Quad-Polarimetric L-Band Synthetic Aperture Radar Data. Remote Sens. 2021, 13, 1753. https://doi.org/10.3390/rs13091753
Bailey J, Marino A, Akbari V. Comparison of Target Detectors to Identify Icebergs in Quad-Polarimetric L-Band Synthetic Aperture Radar Data. Remote Sensing. 2021; 13(9):1753. https://doi.org/10.3390/rs13091753
Chicago/Turabian StyleBailey, Johnson, Armando Marino, and Vahid Akbari. 2021. "Comparison of Target Detectors to Identify Icebergs in Quad-Polarimetric L-Band Synthetic Aperture Radar Data" Remote Sensing 13, no. 9: 1753. https://doi.org/10.3390/rs13091753
APA StyleBailey, J., Marino, A., & Akbari, V. (2021). Comparison of Target Detectors to Identify Icebergs in Quad-Polarimetric L-Band Synthetic Aperture Radar Data. Remote Sensing, 13(9), 1753. https://doi.org/10.3390/rs13091753