Spatial-Temporal Distribution of the Freeze–Thaw Cycle of the Largest Lake (Qinghai Lake) in China Based on Machine Learning and MODIS from 2000 to 2020
Abstract
1. Introduction
2. Data
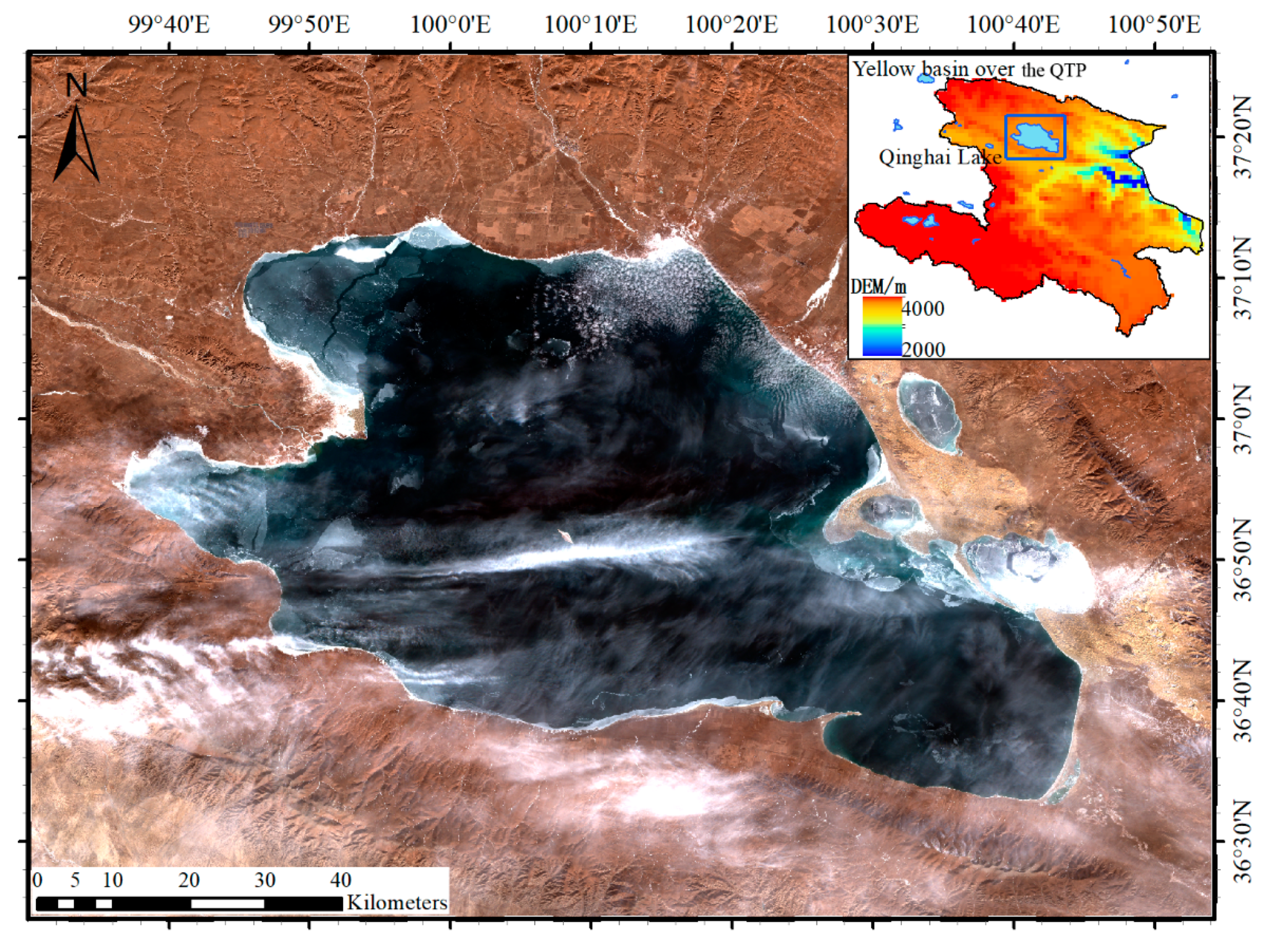
2.1. Study Area
2.2. MODIS Surface Reflectance
2.3. Sentinel-2 Surface Reflectance
2.4. JRC GSW
2.5. ERA5 Daily Aggregates
3. Methodology
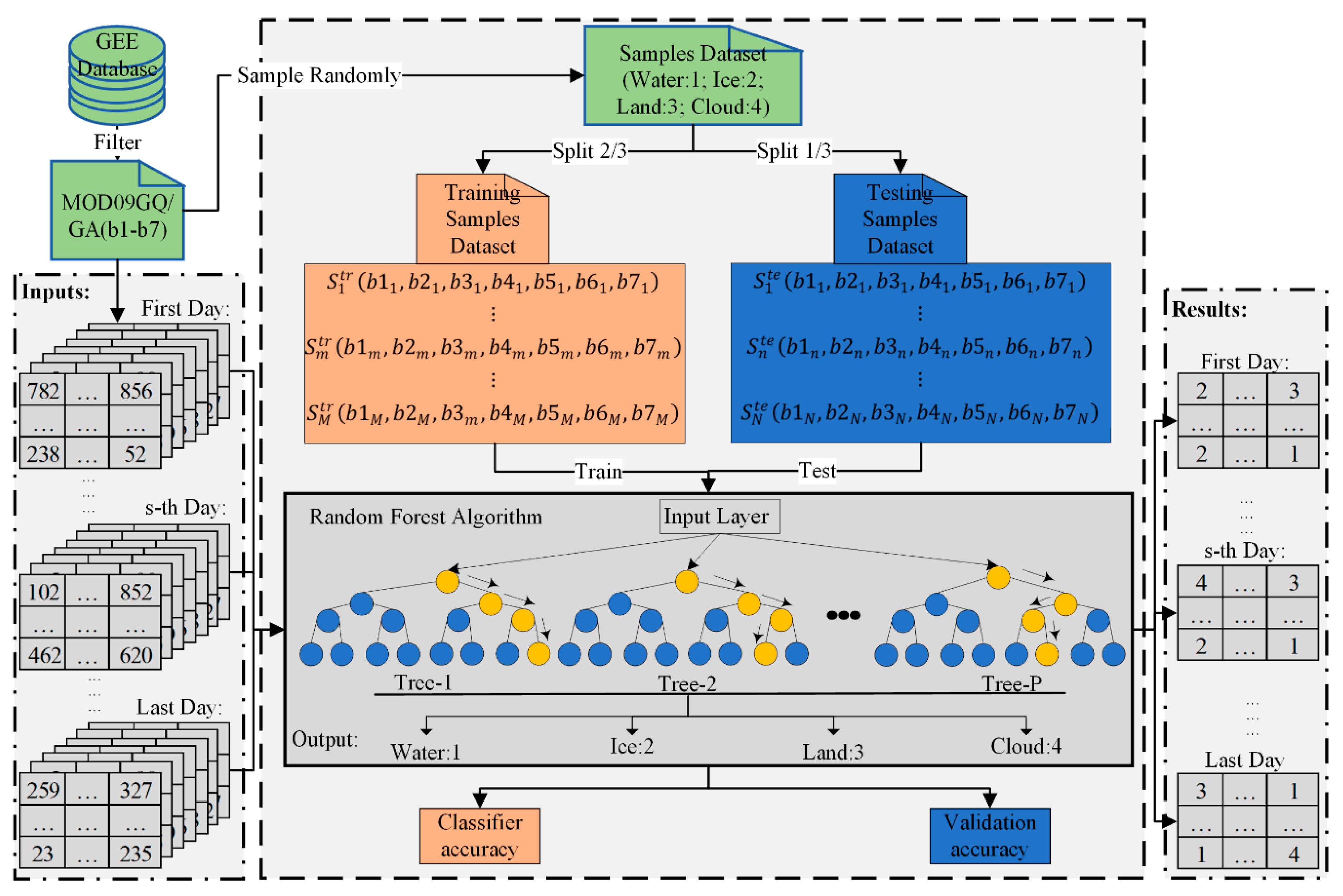
3.1. RF Classification
3.1.1. Training and Testing Dataset
3.1.2. Model Training and Validation
3.2. Cloud Gap-Filling
3.3. Methods Evaluation Approaches
3.4. Definition of Lake Phenology
4. Results
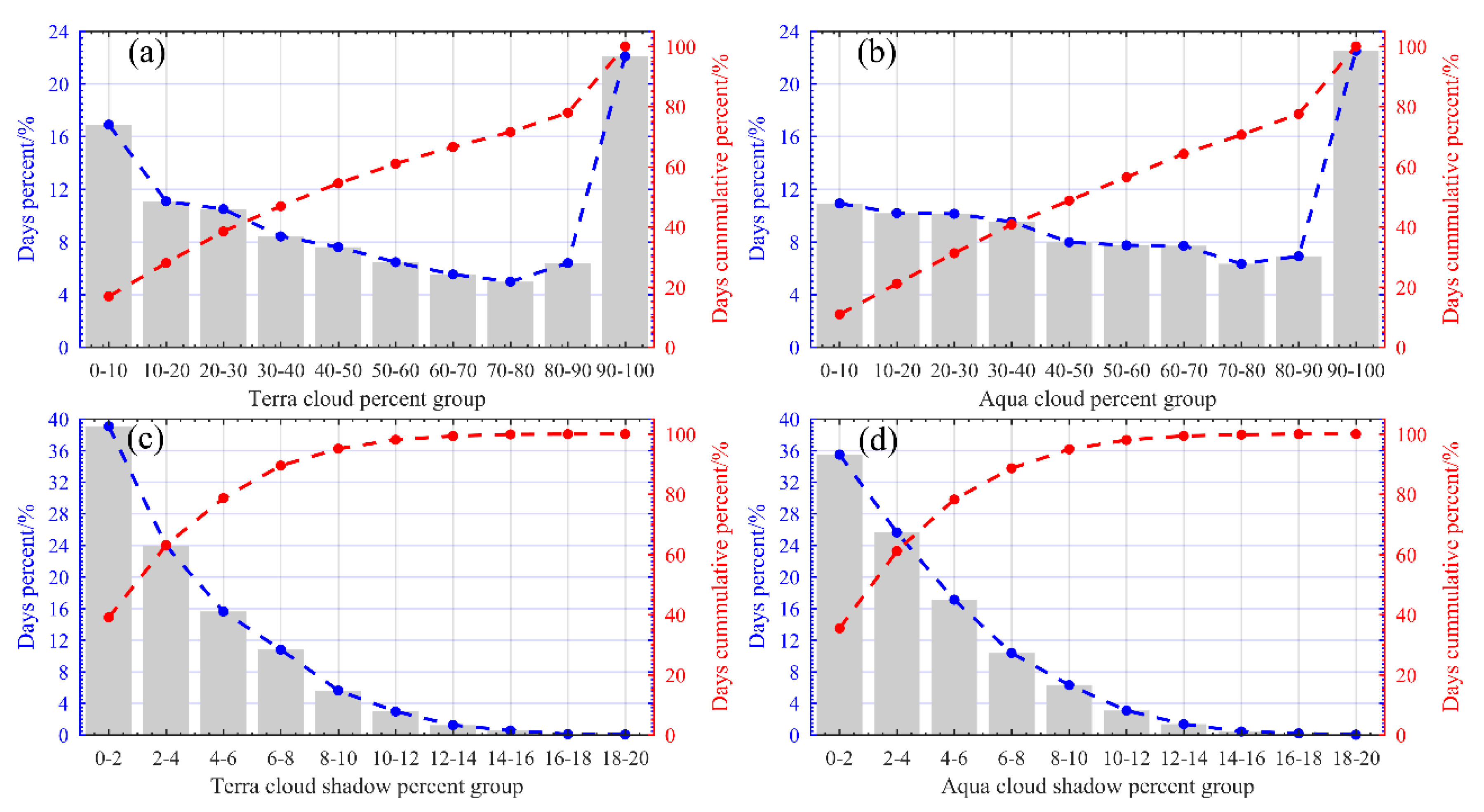
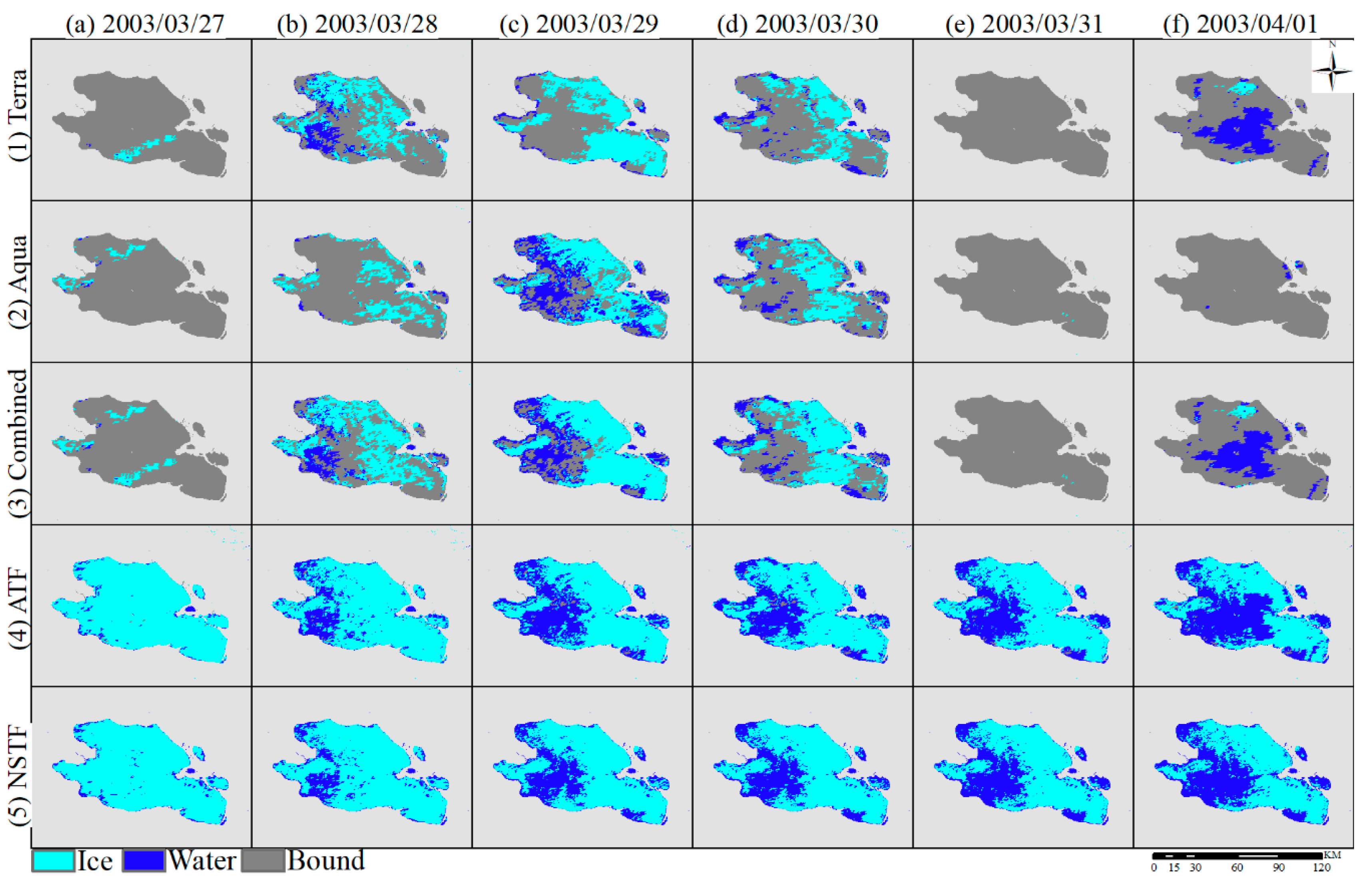
4.1. Cloud Removal from MODIS Images
4.2. Extraction of Water and Ice by RF Algorithm
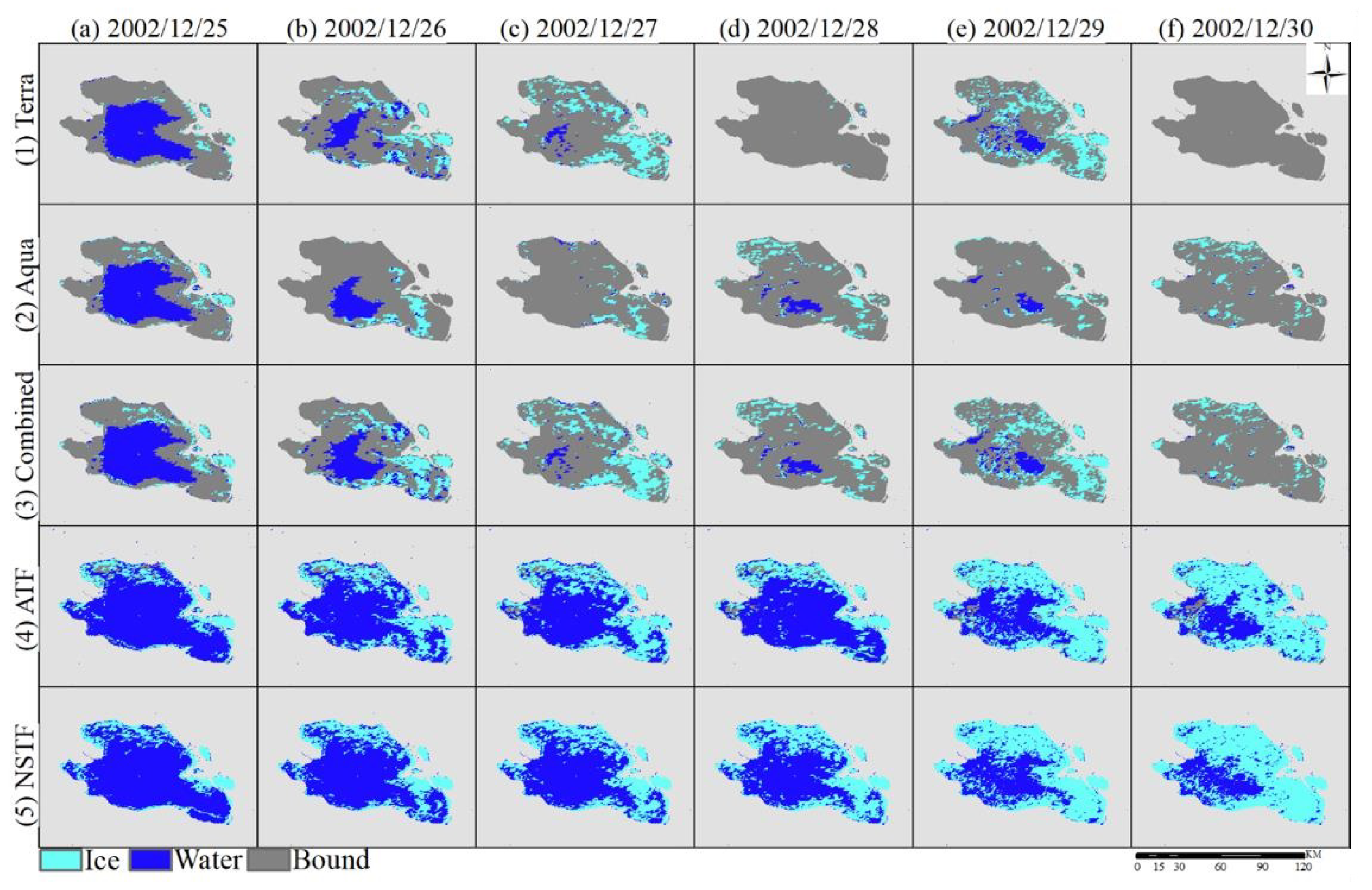
4.3. Reconstruction of Water and Ice by Cloud Gap-Filling
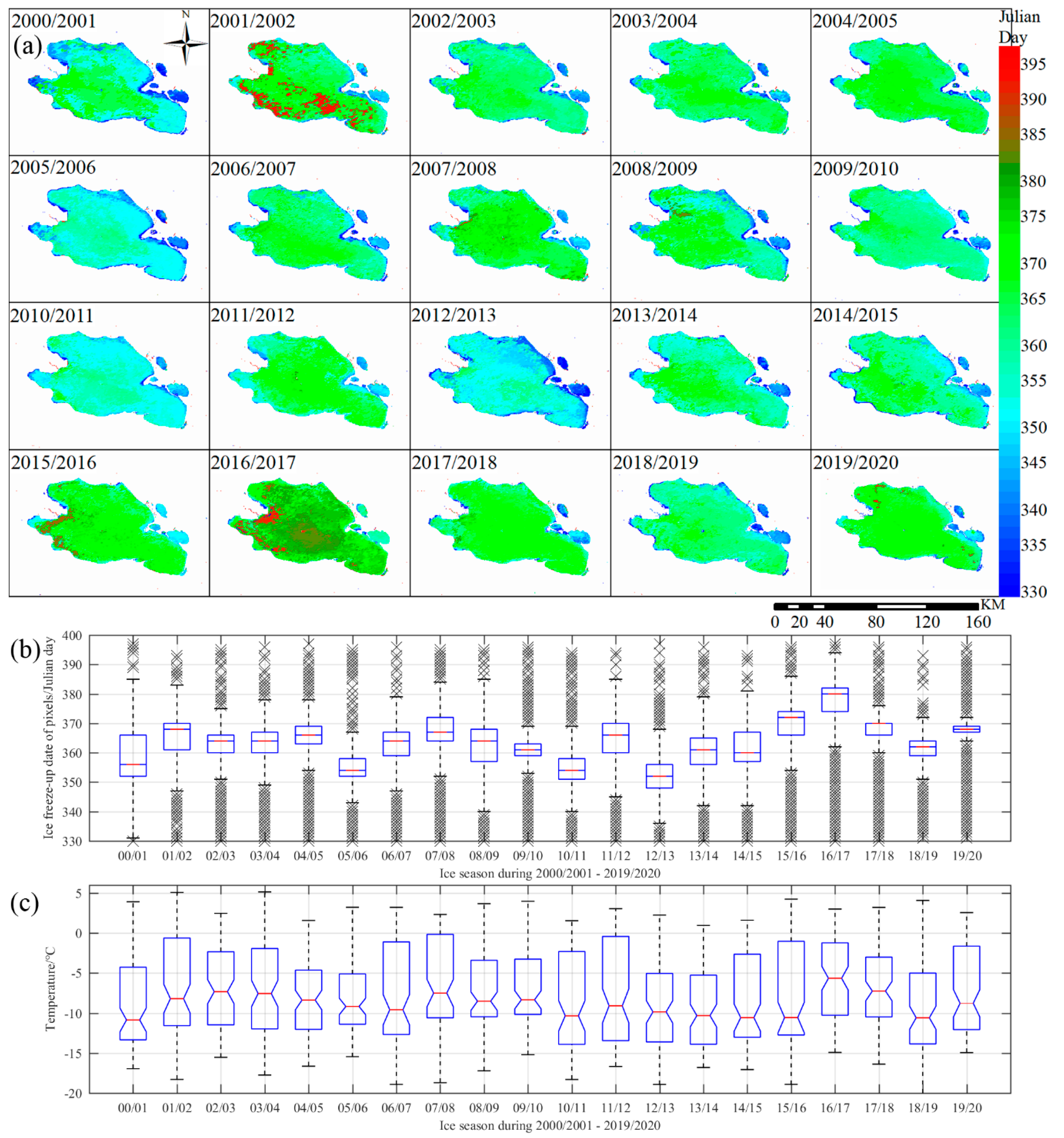
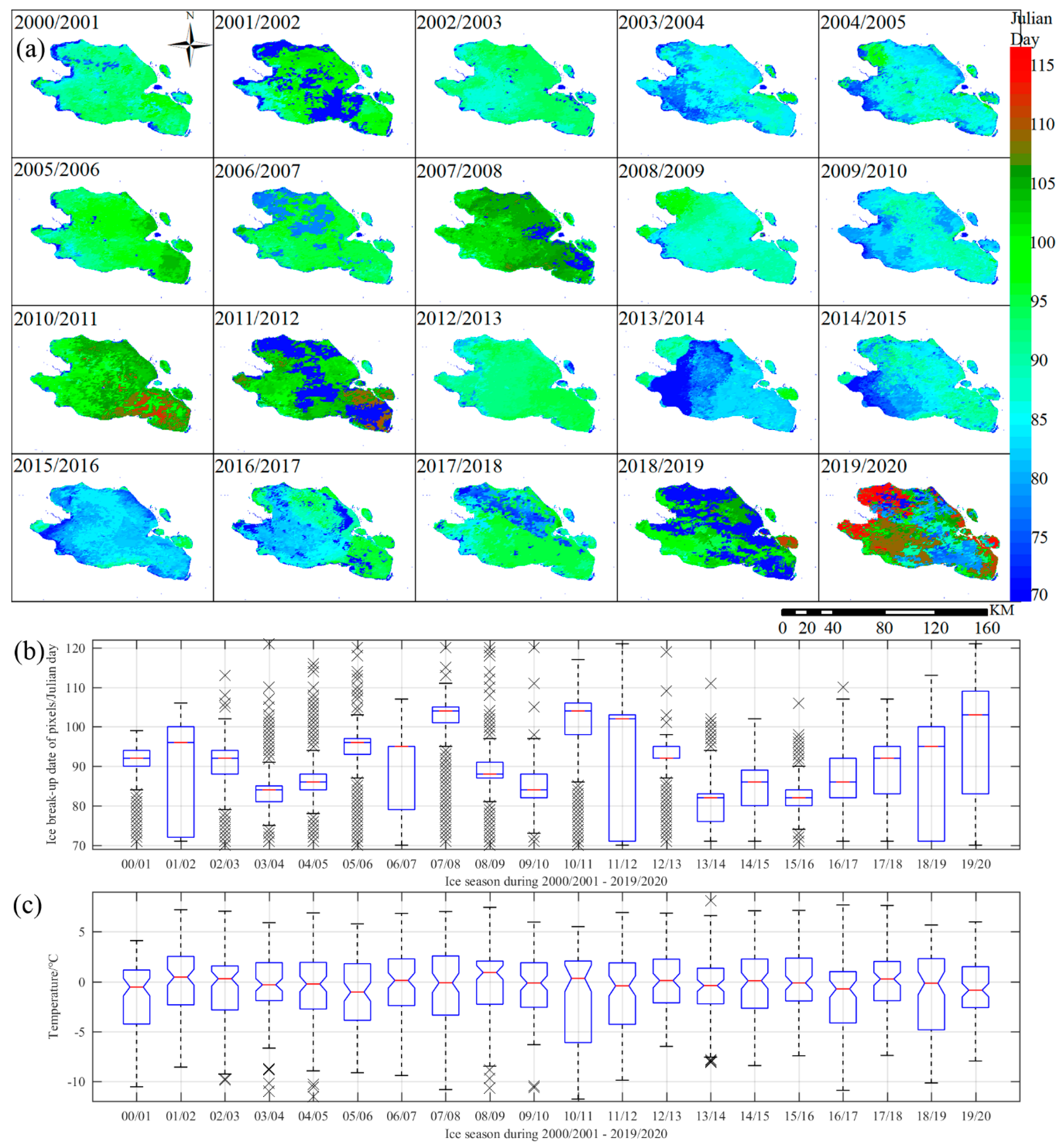
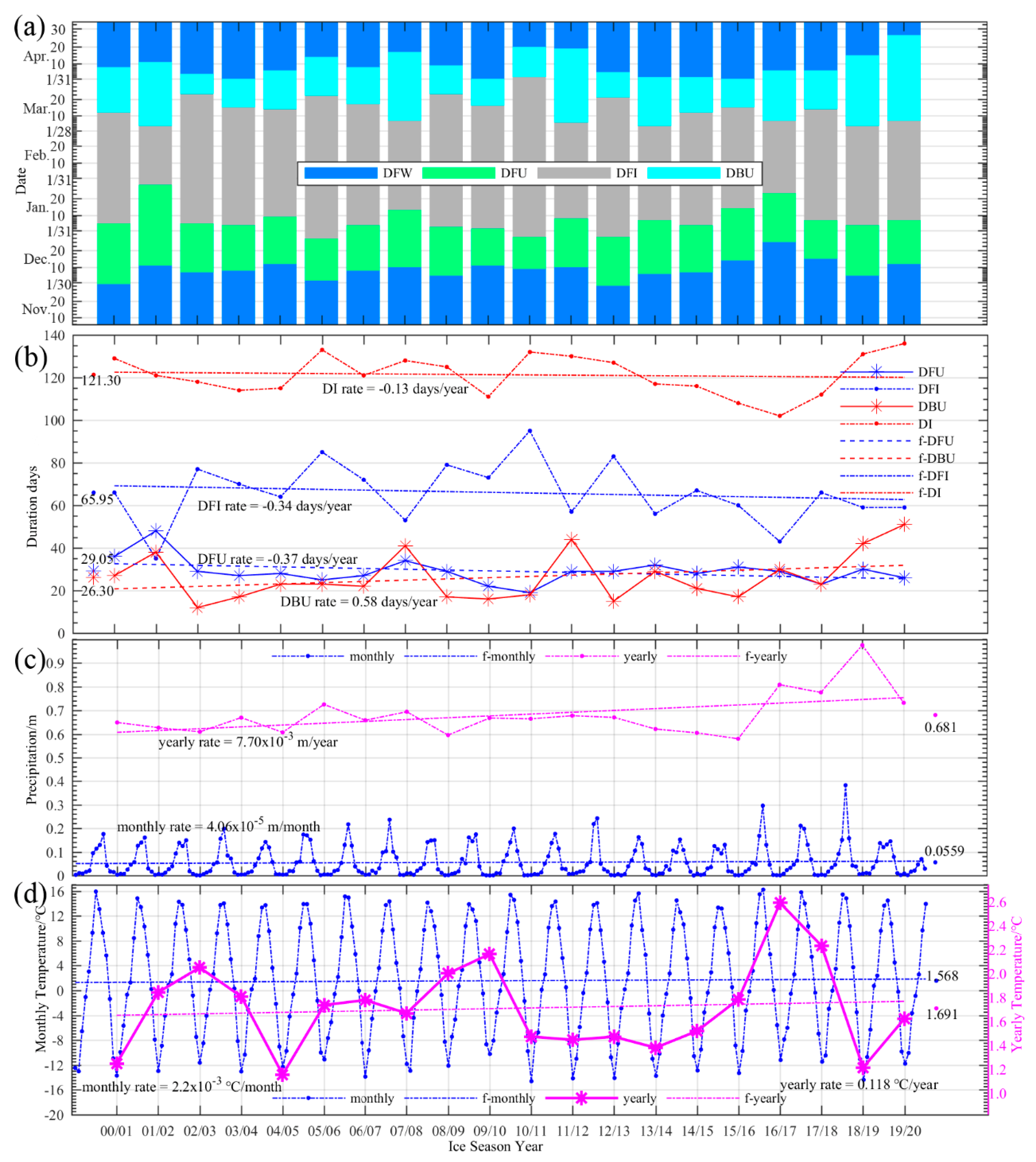
4.4. Annual Spatial Dynamics of Freeze-Up and Break-Up Dates
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Woolway, R.I.; Merchant, C.J. Intralake Heterogeneity of Thermal Responses to Climate Change: A Study of Large Northern Hemisphere Lakes. J. Geophys. Res. Atmos. 2018, 123, 3087–3098. [Google Scholar] [CrossRef]
- Latifovic, R.; Pouliot, D. Analysis of climate change impacts on lake ice phenology in Canada using the historical satellite data record. Remote Sens. Environ. 2007, 106, 492–507. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Zhang, K.; Zhu, F. Lakes’ state and abundance across the Tibetan Plateau. Chin. Sci. Bull. 2014, 59, 3010–3021. [Google Scholar] [CrossRef]
- Kang, S.; Xu, Y.; You, Q.; Flügel, W.-A.; Pepin, N.; Yao, T. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 015101. [Google Scholar] [CrossRef]
- Brown, L.C.; Duguay, C.R. The response and role of ice cover in lake-climate interactions. Prog. Phys. Geogr. Earth Environ. 2010, 34, 671–704. [Google Scholar] [CrossRef]
- Rouse, W.R.; Oswald, C.J.; Binyamin, J.; Spence, C.; Schertzer, W.M.; Blanken, P.D.; Bussières, N.; Duguay, C.R. The Role of Northern Lakes in a Regional Energy Balance. J. Hydrometeorol. 2005, 6, 291. [Google Scholar] [CrossRef]
- Ke, C.-Q.; Tao, A.-Q.; Jin, X. Variability in the ice phenology of Nam Co Lake in central Tibet from scanning multichannel microwave radiometer and special sensor microwave/imager: 1978 to 2013. J. Appl. Remote Sens. 2013, 7, 073477. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R. Monitoring the frozen duration of Qinghai Lake using satellite passive microwave remote sensing low frequency data. Chin. Sci. Bull. 2009, 54, 2294–2299. [Google Scholar] [CrossRef]
- Gou, P.; Ye, Q.; Che, T.; Feng, Q.; Ding, B.; Lin, C.; Zong, J. Lake ice phenology of Nam Co, Central Tibetan Plateau, China, derived from multiple MODIS data products. J. Great Lakes Res. 2017, 43, 989–998. [Google Scholar] [CrossRef]
- Higgins, S.N.; Desjardins, C.; Drouin, H.; Hrenchuk, L.; van der Sanden, J.J. The role of climate and lake size in regulating the ice phenology of boreal lakes. J. Geophys. Res. Biogeosci. 2021. [Google Scholar] [CrossRef]
- Xie, P.; Qiu, Y.; Wang, X.; Shi, L.; Liang, W. Lake Ice Phenology Extraction using Machine Learning Methodology. Iop Conf. Ser. Earth Environ. Sci. 2020, 502, 012034. [Google Scholar] [CrossRef]
- Wu, Y.; Duguay, C.R.; Xu, L. Assessment of machine learning classifiers for global lake ice cover mapping from MODIS TOA reflectance data. Remote Sens. Environ. 2021, 253, 112206. [Google Scholar] [CrossRef]
- Dirscherl, M.; Dietz, A.J.; Kneisel, C.; Kuenzer, C. Automated Mapping of Antarctic Supraglacial Lakes Using a Machine Learning Approach. Remote Sens. 2020, 12, 1203. [Google Scholar] [CrossRef]
- Kling, G.; Hayhoe, K.; Johnson, L.; Magnuson, J.; Polassky, S.; Robinson, S.; Shuter, B.; Wander, M.; Wubbles, D.; Zak, D. Confronting Climate Change in the Great Lakes Region: Impacts on Our Communities and Ecosystems; Ecological Society of America: Washington, DC, USA, 2003. [Google Scholar]
- Chaouch, N.; Temimi, M.; Romanov, P.; Cabrera, R.; McKillop, G.; Khanbilvardi, R. An automated algorithm for river ice monitoring over the Susquehanna River using the MODIS data. Hydrol. Process. 2014, 28, 62–73. [Google Scholar] [CrossRef]
- Gafurov, A.; Bárdossy, A. Cloud removal methodology from MODIS snow cover product. Hydrol. Earth Syst. Sci. 2009, 13, 1361–1373. [Google Scholar] [CrossRef]
- López-Burgos, V.; Gupta, H.V.; Clark, M. Reducing cloud obscuration of MODIS snow cover area products by combining spatio-temporal techniques with a probability of snow approach. Hydrol. Earth Syst. Sci. 2013, 17, 1809–1823. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. Isprs J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Han, W.; Huang, C.; Duan, H.; Gu, J.; Hou, J. Lake Phenology of Freeze-Thaw Cycles Using Random Forest: A Case Study of Qinghai Lake. Remote Sens. 2020, 12, 4098. [Google Scholar] [CrossRef]
- Guoqing, Z. Dataset of river basins map over the TP (2016). Natl. Tibet. Plateau Data Cent. 2019. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased mass over the Tibetan Plateau: From lakes or glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Han, W.; Huang, C.; Wang, Y.; Gu, J. Study on the Area Variation of Qinghai Lake Based on Long-Term Landsat 5/8 Multi-Band Remote Sensing Imagery. Adv. Earth Sci. 2019, 34, 346–355. [Google Scholar] [CrossRef]
- Li, X.-Y.; Xu, H.-Y.; Sun, Y.-L.; Zhang, D.-S.; Yang, Z.-P. Lake-Level Change and Water Balance Analysis at Lake Qinghai, West China during Recent Decades. Water Resour. Manag. 2007, 21, 1505–1516. [Google Scholar] [CrossRef]
- Ding, Z.; Lu, R.; Lyu, Z.; Liu, X. Geochemical characteristics of Holocene aeolian deposits east of Qinghai Lake, China, and their paleoclimatic implications. Sci. Total Environ. 2019, 692, 917–929. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Zhang, W.; Wang, X.H.; Sun, J.; Feng, X.; Sun, Y. Increasing Water Levels of Global Lakes Between 2003 and 2009. IEEE Geosci. Remote Sens. Lett. 2020, 17, 187–191. [Google Scholar] [CrossRef]
- Cai, Y.; Ke, C.-Q.; Duan, Z. Monitoring ice variations in Qinghai Lake from 1979 to 2016 using passive microwave remote sensing data. Sci. Total Environ. 2017, 607–608, 120–131. [Google Scholar] [CrossRef]
- Vermote, E.F.; Roger, J.C.; Ray, J.P. MODIS Surface Reflectance User’s Guide. 2015; p. 35. [Google Scholar]
- Kharbouche, S.; Muller, J.-P.; Gatebe, K.C.; Scanlon, T.; Banks, C.A. Assessment of Satellite-Derived Surface Reflectances by NASA’s CAR Airborne Radiometer over Railroad Valley Playa. Remote Sens. 2017, 9, 562. [Google Scholar] [CrossRef]
- Gonzalez, L.; Bréon, F.-M.; Caillault, K.; Briottet, X. A sub km resolution global database of surface reflectance and emissivity based on 10-years of MODIS data. Isprs J. Photogramm. Remote Sens. 2016, 122, 222–235. [Google Scholar] [CrossRef]
- Vuolo, F.; Żółtak, M.; Pipitone, C.; Zappa, L.; Wenng, H.; Immitzer, M.; Weiss, M.; Baret, F.; Atzberger, C. Data Service Platform for Sentinel-2 Surface Reflectance and Value-Added Products: System Use and Examples. Remote Sens. 2016, 8, 938. [Google Scholar] [CrossRef]
- Sentinel, E. User Handbook. ESA Standard Document 64.
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Busker, T.; de Roo, A.; Gelati, E.; Schwatke, C.; Adamovic, M.; Bisselink, B.; Pekel, J.-F.; Cottam, A. A global lake and reservoir volume analysis using a surface water dataset and satellite altimetry. Hydrol. Earth Syst. Sci. 2019, 23, 669–690. [Google Scholar] [CrossRef]
- Service, C.C.C. ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate, Copernicus Climate Change Service Climate Data Store (CDS). 2017. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Segal, M.R. Machine learning benchmarks and random forest regression. 2004. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255. [Google Scholar] [CrossRef]
- Sun, J.; Zhong, G.; Huang, K.; Dong, J. Banzhaf random forests: Cooperative game theory based random forests with consistency. Neural Netw. 2018, 106, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Guan, H.; Li, J.; Chapman, M.; Deng, F.; Ji, Z.; Yang, X. Integration of orthoimagery and lidar data for object-based urban thematic mapping using random forests. Int. J. Remote Sens. 2013, 34, 5166–5186. [Google Scholar] [CrossRef]
- Sukhija, S.; Krishnan, N.C.; Singh, G. Supervised heterogeneous domain adaptation via random forests. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 2039–2045. [Google Scholar]
- Topouzelis, K.; Psyllos, A. Oil spill feature selection and classification using decision tree forest on SAR image data. Isprs J. Photogramm. Remote Sens. 2012, 68, 135–143. [Google Scholar] [CrossRef]
- Zhou, Y.; Qiu, G. Random forest for label ranking. Expert Syst. Appl. 2018, 112, 99–109. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Ménard, C.B.; Luojus, K.; Lemmetyinen, J.; Pulliainen, J. Evaluation of snow products over the Tibetan Plateau. Hydrol. Process. 2015, 29, 3247–3260. [Google Scholar] [CrossRef]
- Dariane, A.B.; Khoramian, A.; Santi, E. Investigating spatiotemporal snow cover variability via cloud-free MODIS snow cover product in Central Alborz Region. Remote Sens. Environ. 2017, 202, 152–165. [Google Scholar] [CrossRef]
- Huang, X.; Deng, J.; Wang, W.; Feng, Q.; Liang, T. Impact of climate and elevation on snow cover using integrated remote sensing snow products in Tibetan Plateau. Remote Sens. Environ. 2017, 190, 274–288. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. Spatio-temporal combination of MODIS images – potential for snow cover mapping. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Paudel, K.P.; Andersen, P. Monitoring snow cover variability in an agropastoral area in the Trans Himalayan region of Nepal using MODIS data with improved cloud removal methodology. Remote Sens. Environ. 2011, 115, 1234–1246. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Liang, T.; Huang, X. Comparison and validation of MODIS standard and new combination of Terra and Aqua snow cover products in northern Xinjiang, China. Hydrol. Process. 2009, 23, 419–429. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Yao, T.; Xue, C. Integrated assessment on multi-temporal and multi-sensor combinations for reducing cloud obscuration of MODIS snow cover products of the Pacific Northwest USA. Remote Sens. Environ. 2010, 114, 1662–1675. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ramesh, S.; Kannan, S.; Baskar, S. Application of modified NSGA-II algorithm to multi-objective reactive power planning. Appl. Soft Comput. 2012, 12, 741–753. [Google Scholar] [CrossRef]
- Hou, J.; Huang, C.; Zhang, Y.; Guo, J.; Gu, J. Gap-Filling of MODIS Fractional Snow Cover Products via Non-Local Spatio-Temporal Filtering Based on Machine Learning Techniques. Remote Sens. 2019, 11, 90. [Google Scholar] [CrossRef]
- Stehman, S. Estimating the kappa coefficient and its variance under stratified random sampling. Photogramm. Eng. Remote Sens. 1996, 62, 401–407. [Google Scholar]
- Livingstone, D.M. Break-up dates of alpine lakes as proxy data for local and regional mean surface air temperatures. Clim. Chang. 1997, 37, 407–439. [Google Scholar] [CrossRef]
- Franssen, H.J.H.; Scherrer, S.C. Freezing of lakes on the Swiss plateau in the period 1901–2006. Int. J. Climatol. 2008, 28, 421–433. [Google Scholar] [CrossRef]
- Johnson, M.; Eicken, H. Estimating Arctic sea-ice freeze-up and break-up from the satellite record: A comparison of different approaches in the Chukchi and Beaufort Seas. Elem Sci Anth 2016, 4. [Google Scholar] [CrossRef]
- Marszelewski, W.; Skowron, R. Ice cover as an indicator of winter air temperature changes: Case study of the Polish Lowland lakes. Hydrol. Sci. J. 2006, 51, 336–349. [Google Scholar] [CrossRef]
- Ghanbari, R.N.; Bravo, H.R.; Magnuson, J.J.; Hyzer, W.G.; Benson, B.J. Coherence between lake ice cover, local climate and teleconnections (Lake Mendota, Wisconsin). J. Hydrol. 2009, 374, 282–293. [Google Scholar] [CrossRef]
- Dibike, Y.; Prowse, T.; Saloranta, T.; Ahmed, R. Response of Northern Hemisphere lake-ice cover and lake-water thermal structure patterns to a changing climate. Hydrol. Process. 2011, 25, 2942–2953. [Google Scholar] [CrossRef]
- Duguay, C.R.; Prowse, T.D.; Bonsal, B.R.; Brown, R.D.; Lacroix, M.P.; Ménard, P. Recent trends in Canadian lake ice cover. Hydrol. Process. 2006, 20, 781–801. [Google Scholar] [CrossRef]
- Ma, R.; Duan, H.; Hu, C.; Feng, X.; Li, A.; Ju, W.; Jiang, J.; Yang, G. A half-century of changes in China’s lakes: Global warming or human influence? Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Clausius–Clapeyron equation and saturation vapour pressure: Simple theory reconciled with practice. Eur. J. Phys. 2012, 33, 295. [Google Scholar] [CrossRef]
- Ali, H.; Fowler, H.J.; Mishra, V. Global observational evidence of strong linkage between dew point temperature and precipitation extremes. Geophys. Res. Lett. 2018, 45, 12,320–312,330. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Rybski, D.; Zschiegner, S.A.; Braun, P.; Koscielny-Bunde, E.; Livina, V.; Havlin, S.; Bunde, A. Multifractality of river runoff and precipitation: Comparison of fluctuation analysis and wavelet methods. Phys. A: Stat. Mech. Its Appl. 2003, 330, 240–245. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rybski, D.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of precipitation and river runoff records. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. Stochastic synthesis approximating any process dependence and distribution. Stoch. Environ. Res. Risk Assess. 2018, 32, 1493–1515. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Dimitriadis, P.; Lombardo, F.; Stevens, S. From fractals to stochastics: Seeking theoretical consistency in analysis of geophysical data. In Advances in Nonlinear Geosciences; Springer: Berlin/Heidelberg, Germany, 2018; pp. 237–278. [Google Scholar]



| Predicted | Row Total | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | … | q | |||
| Actual | 1 | N11 | N12 | … | N1q | a1 |
| 2 | N21 | N22 | … | N2q | a2 | |
| … | … | … | Nij… | … | ai… | |
| q | Nq1 | Nq2 | … | Nqq | aq | |
| Column Total | b1 | b2 | bj… | bq | N | |
| Predicted | Producer Accuracy/% | |||||
|---|---|---|---|---|---|---|
| Water | Ice | Land | Cloud | |||
| Actual | Water | 1538 | 7 | 0 | 0 | 99.55 |
| Ice | 1 | 909 | 0 | 1 | 99.78 | |
| Land | 1 | 0 | 1872 | 2 | 99.84 | |
| Cloud | 0 | 2 | 1 | 780 | 99.62 | |
| Overall accuracy: 99.71 | ||||||
| Kappa coefficient: 99.59 | ||||||
| Predicted | Producer Accuracy/% | |||||
|---|---|---|---|---|---|---|
| Water | Ice | Land | Cloud | |||
| Actual | Water | 776 | 18 | 3 | 1 | 97.24 |
| Ice | 3 | 491 | 0 | 16 | 96.27 | |
| Land | 4 | 4 | 960 | 7 | 98.46 | |
| Cloud | 1 | 9 | 2 | 367 | 96.83 | |
| Overall accuracy: 97.45 | ||||||
| Kappa coefficient: 96.45 | ||||||
| Predicted | Producer Accuracy/% | |||
|---|---|---|---|---|
| Water | Ice | |||
| Actual | Water | 1969 | 30 | 98.50 |
| Ice | 9 | 369 | 97.62 | |
| Overall accuracy: 98.36 | ||||
| Kappa coefficient: 94.00 | ||||
| Predicted | Producer Accuracy/% | |||
|---|---|---|---|---|
| Water | Ice | |||
| Actual | Water | 1978 | 204 | 90.65 |
| Ice | 16 | 760 | 97.94 | |
| Overall accuracy: 92.56 | ||||
| Kappa coefficient: 82.17 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Huang, C.; Gu, J.; Hou, J.; Zhang, Y. Spatial-Temporal Distribution of the Freeze–Thaw Cycle of the Largest Lake (Qinghai Lake) in China Based on Machine Learning and MODIS from 2000 to 2020. Remote Sens. 2021, 13, 1695. https://doi.org/10.3390/rs13091695
Han W, Huang C, Gu J, Hou J, Zhang Y. Spatial-Temporal Distribution of the Freeze–Thaw Cycle of the Largest Lake (Qinghai Lake) in China Based on Machine Learning and MODIS from 2000 to 2020. Remote Sensing. 2021; 13(9):1695. https://doi.org/10.3390/rs13091695
Chicago/Turabian StyleHan, Weixiao, Chunlin Huang, Juan Gu, Jinliang Hou, and Ying Zhang. 2021. "Spatial-Temporal Distribution of the Freeze–Thaw Cycle of the Largest Lake (Qinghai Lake) in China Based on Machine Learning and MODIS from 2000 to 2020" Remote Sensing 13, no. 9: 1695. https://doi.org/10.3390/rs13091695
APA StyleHan, W., Huang, C., Gu, J., Hou, J., & Zhang, Y. (2021). Spatial-Temporal Distribution of the Freeze–Thaw Cycle of the Largest Lake (Qinghai Lake) in China Based on Machine Learning and MODIS from 2000 to 2020. Remote Sensing, 13(9), 1695. https://doi.org/10.3390/rs13091695








