Hyperspectral Data Simulation (Sentinel-2 to AVIRIS-NG) for Improved Wildfire Fuel Mapping, Boreal Alaska
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
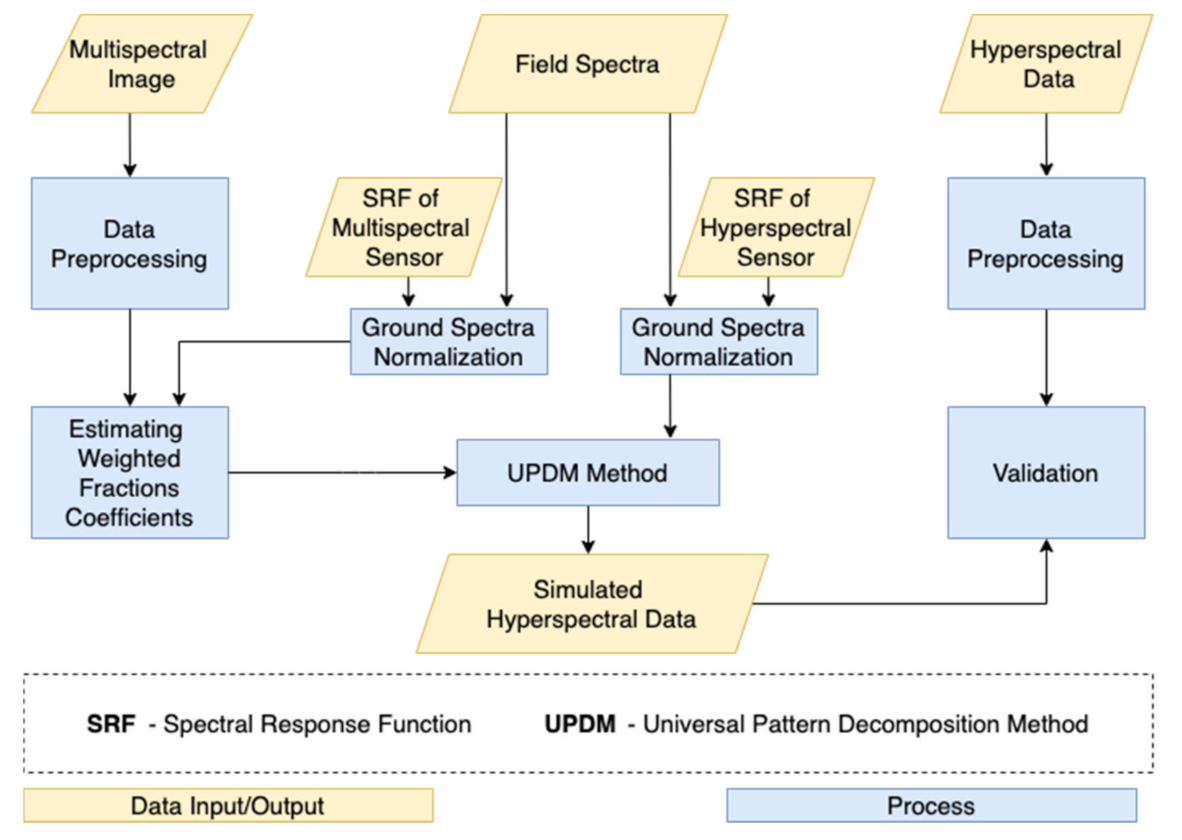
2.2. Processing Workflow
2.3. Field Data Collection
2.4. Remote Sensing Data Preprocessing
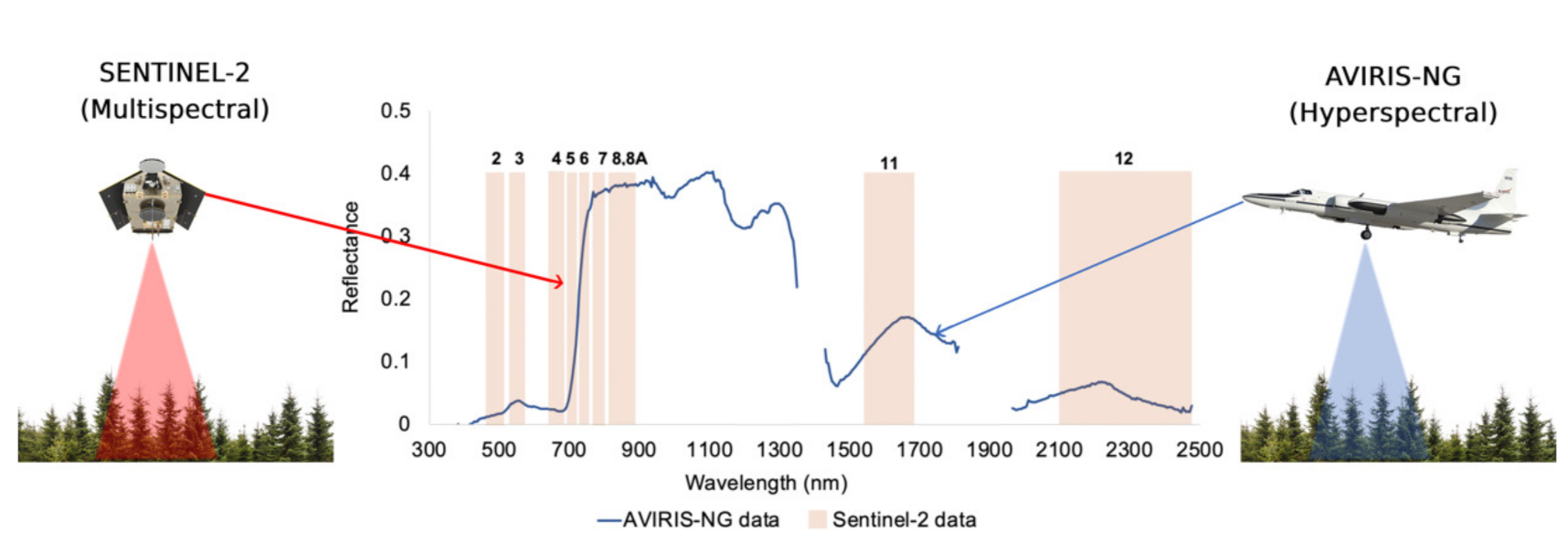
2.4.1. Multispectral Data Preprocessing
2.4.2. Hyperspectral Data Preprocessing
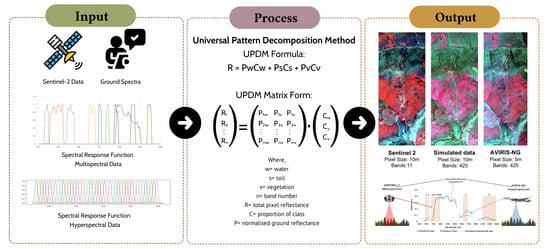
2.5. Hyperspectral Simulation
2.5.1. Ground Spectra Normalization
2.5.2. Calculation of Weighted Fractional Coefficients
2.5.3. Hyperspectral Data Simulation
2.6. Validation
2.6.1. Visual and Statistical Analysis
2.6.2. Classification
2.7. Fuel Type Classification
3. Results
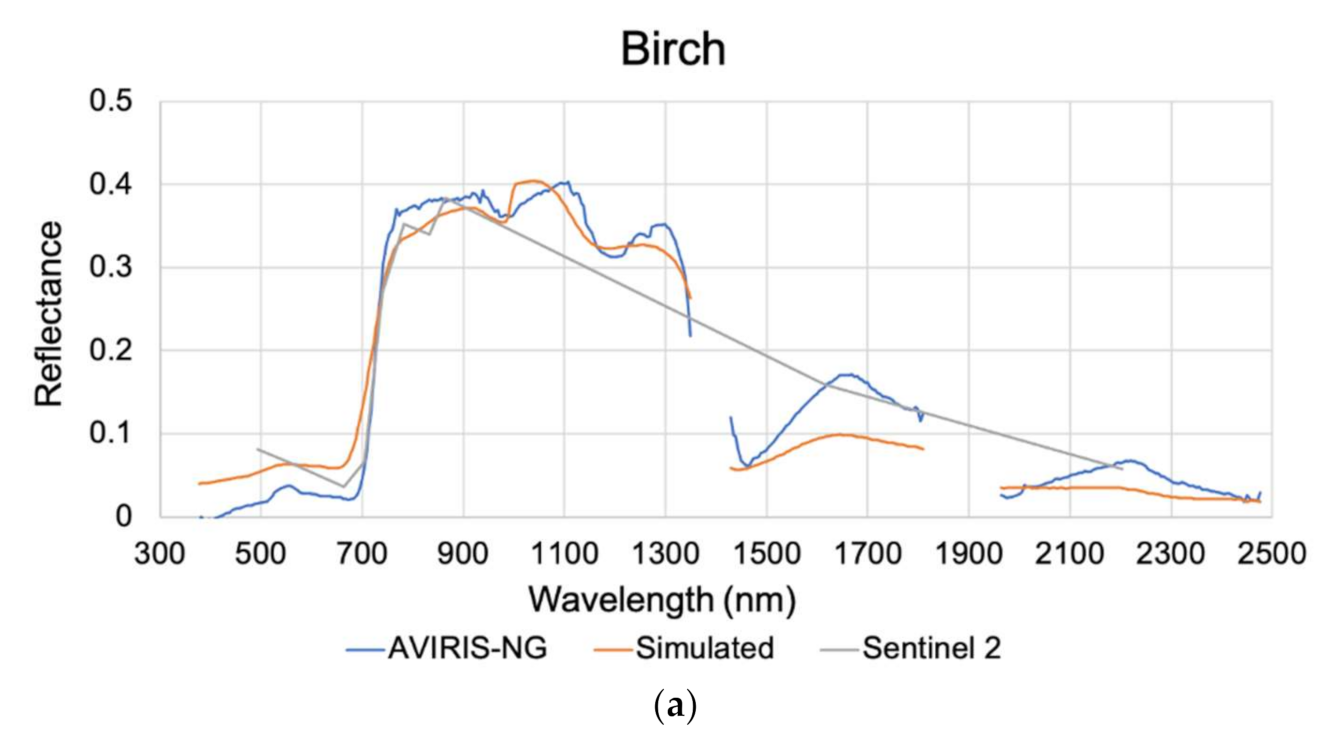
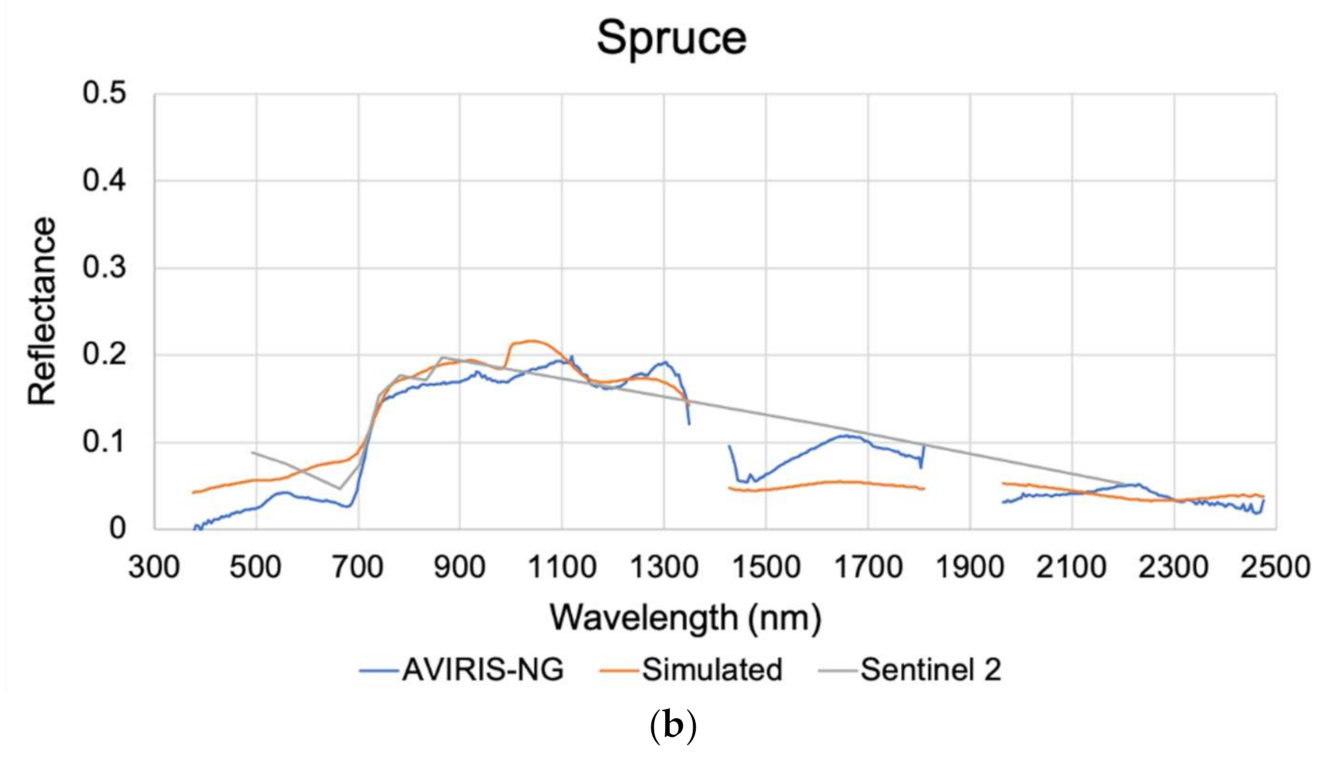
3.1. Spectral Profile Comparison
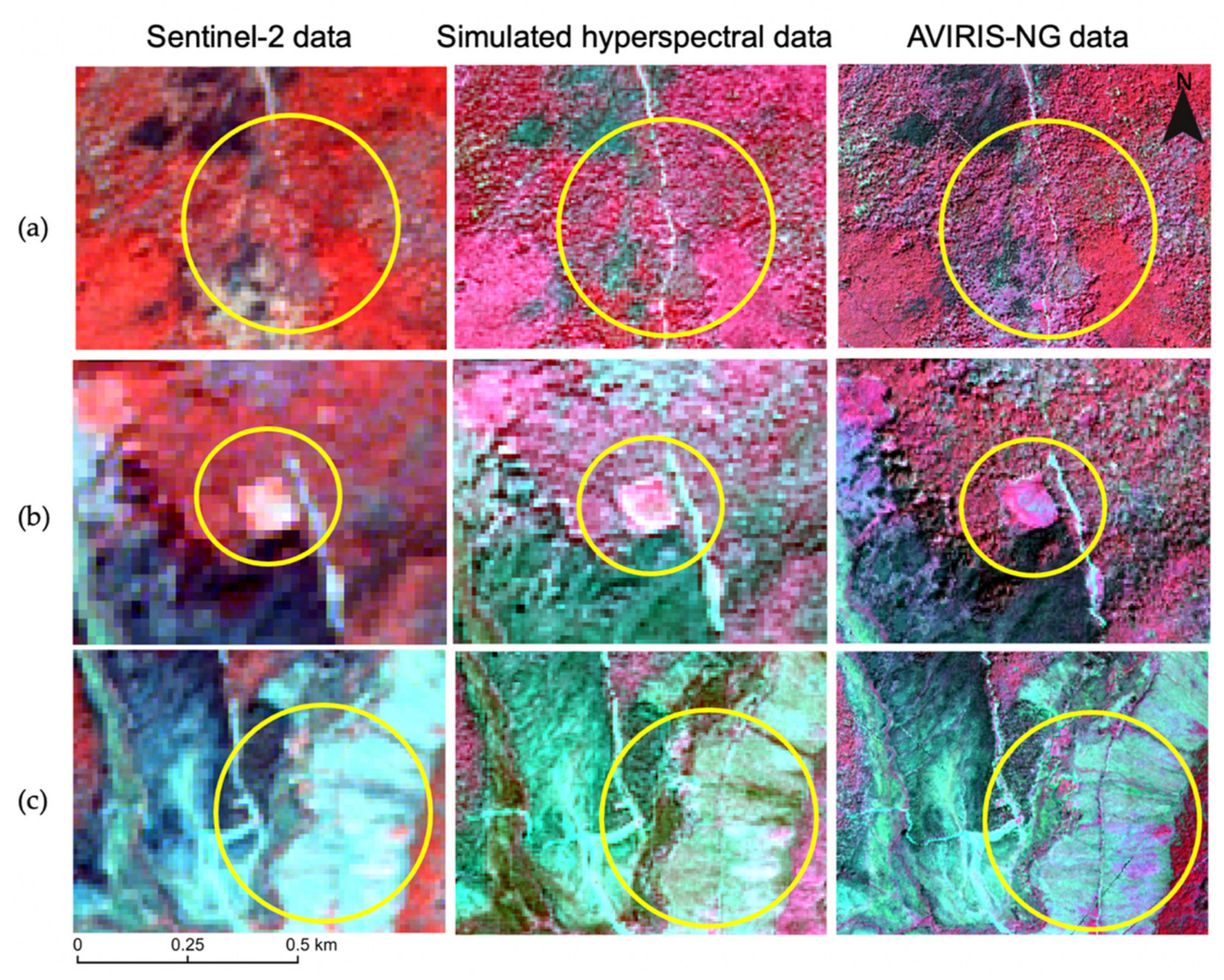
3.2. Visual Interpretation
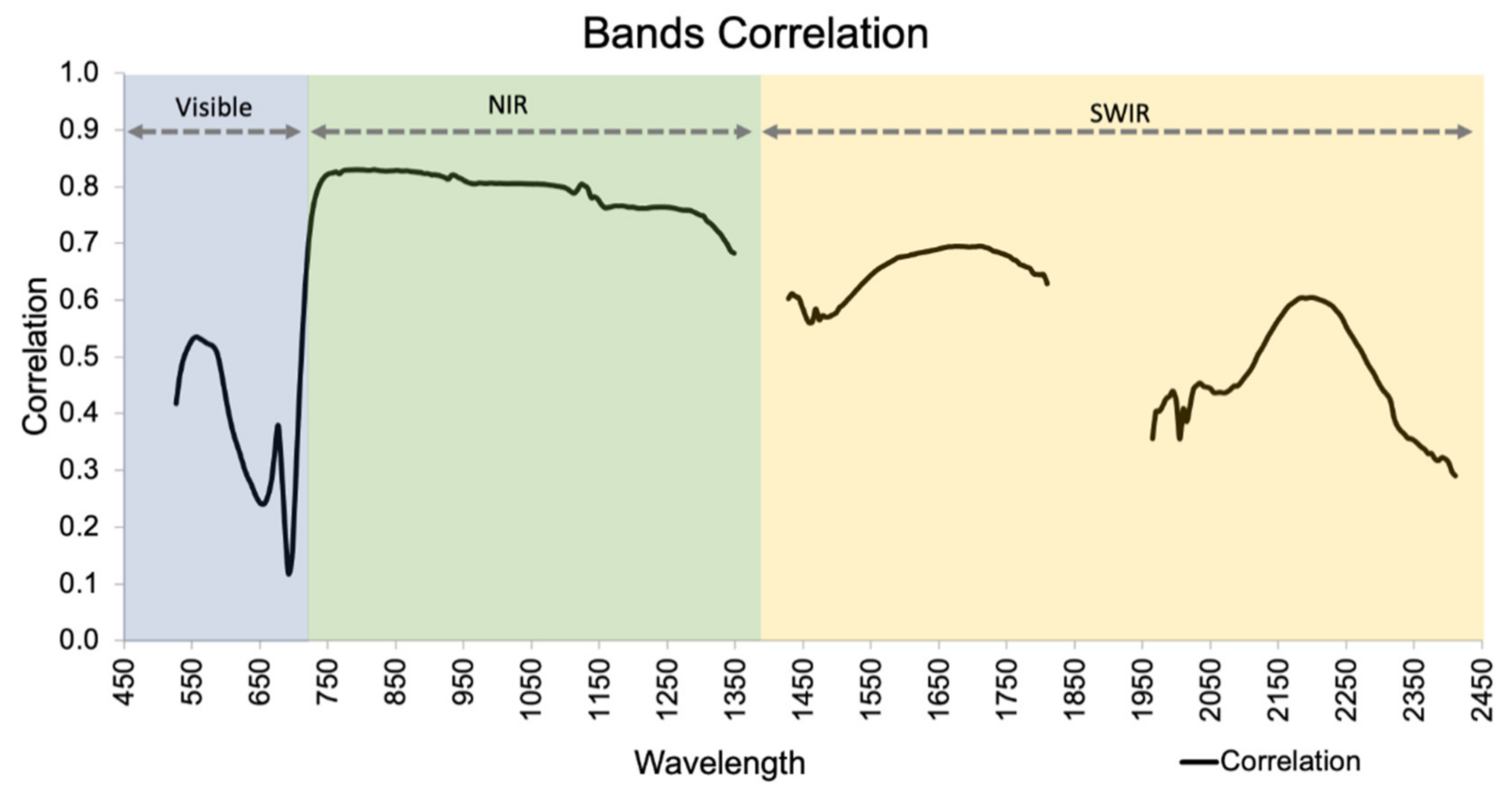
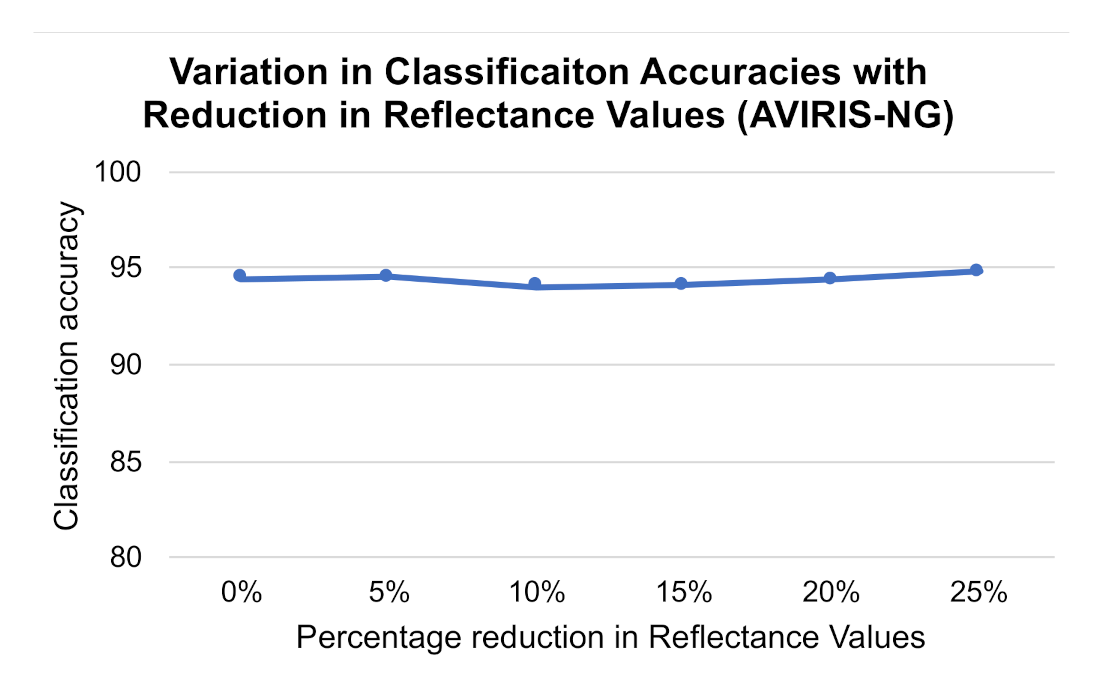
3.3. Statistical Analysis
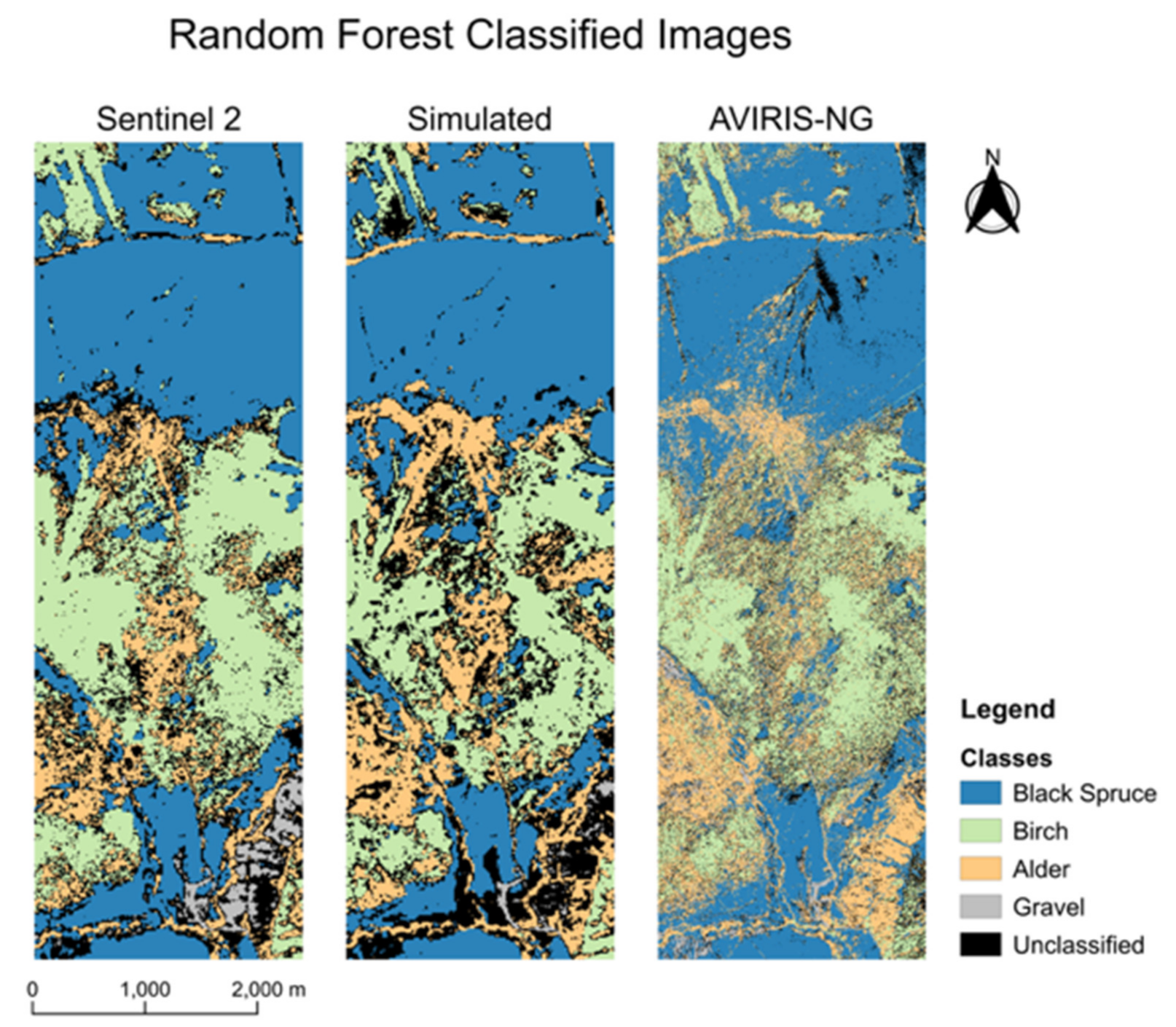
3.4. Image Classification
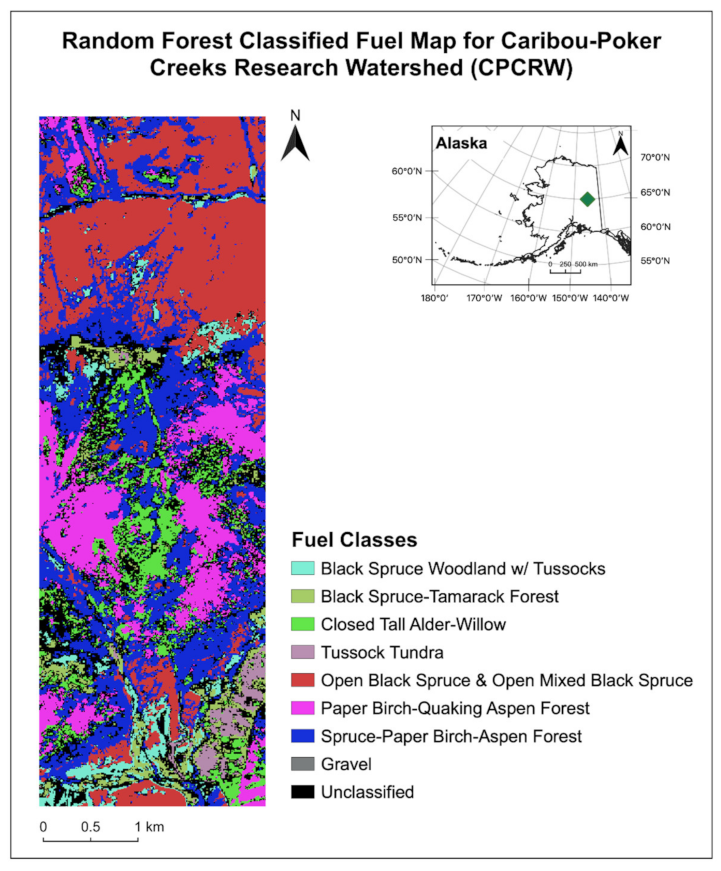
3.5. Fuel Map
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Leblon, B.; San-Miguel-Ayanz, J.; Bourgeau-Chavez, L.; Kong, M. Remote Sensing of Wildfires. In Land Surface Remote Sensing: Environment and Risks; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 55–95. ISBN 9780081012659. [Google Scholar] [CrossRef]
- NASA Earth Observatory Fires Raged in the Amazon Again in 2020. Available online: https://earthobservatory.nasa.gov/images/147946/fires-raged-in-the-amazon-again-in-2020 (accessed on 8 April 2021).
- The Climate Reality Project Global Wildfires by the Numbers|Climate Reality. Available online: https://www.climaterealityproject.org/blog/global-wildfires-numbers (accessed on 8 April 2021).
- CAL FIRE 2020 Fire Season|Welcome to CAL FIRE. Available online: https://www.fire.ca.gov/incidents/2020/ (accessed on 21 April 2021).
- FS-R10-FHP. Forest Health Conditions in Alaska 2019. A Forest Health Protection Report; Publication R10-PR-45; U.S. Forest Service: Anchorage, AK, USA, 2019; 68p. [Google Scholar]
- Box, J.E.; Colgan, W.T.; Christensen, T.R.; Schmidt, N.M.; Lund, M.; Parmentier, F.J.W.; Brown, R.; Bhatt, U.S.; Euskirchen, E.S.; Romanovsky, V.E.; et al. Key indicators of Arctic climate change: 1971–2017. Environ. Res. Lett. 2019, 14, 045010. [Google Scholar] [CrossRef]
- Thoman, R.; Walsh, J.; Eicken, H.; Hartig, L.; Mccammon, M.; Bauer, N.; Carlo, N.; Rupp, S.; Buxbaum, T.; Bhatt, U.; et al. Alaska’s Changing Environment: Documenting Alaska’s Physical and Biological Changes through Observations; Review; University of Alaska Fairbanks: Fairbanks, AK, USA, 2019. [Google Scholar]
- Alaska Department of Natural Resources Division of Forestry. Alaska 2019 Fire Numbers; Alaska Department of Natural Resources Division of Forestry: Anchorage, AK, USA, 2019. [Google Scholar]
- Chuvieco, E.; Kasischke, E.S. Remote sensing information for fire management and fire effects assessment. J. Geophys. Res. Biogeosci. 2007, 112. [Google Scholar] [CrossRef]
- Ziel, R. Alaska’s Fire Environment: Not an Average Place—International Association of Wildland Fire. Available online: https://www.iawfonline.org/article/alaskas-fire-environment-not-an-average-place/ (accessed on 7 February 2021).
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Burai, P.; Deák, B.; Valkó, O.; Tomor, T.; Burai, P.; Deák, B.; Valkó, O.; Tomor, T. Classification of Herbaceous Vegetation Using Airborne Hyperspectral Imagery. Remote Sens. 2015, 7, 2046–2066. [Google Scholar] [CrossRef]
- Smith, C.W.; Panda, S.K.; Bhatt, U.S.; Meyer, F.J. Improved Boreal Forest Wildfire Fuel Type Mapping in Interior Alaska using AVIRIS-NG Hyperspectral data. Remote Sens. 2021, 13, 897. [Google Scholar] [CrossRef]
- Baldeck, C.A.; Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E.; Kellner, J.R.; Wright, S.J. Operational Tree Species Mapping in a Diverse Tropical Forest with Airborne Imaging Spectroscopy. PLoS ONE 2015, 10, e0118403. [Google Scholar] [CrossRef]
- Landfire: Existing Vegetation Type. Available online: http://www.landfire.gov (accessed on 10 February 2021).
- Rollins, M. Landfire: A nationally consistent vegetation, wildland fire, and fuel assessment. Int. J. Wildl. Fire 2009, 18, 235–249. [Google Scholar] [CrossRef]
- DeVelice, R.L. Accuracy of the LANDFIRE Alaska Existing Vegetation Map over the Chugach National Forest. 2012. Available online: https://landfire.cr.usgs.gov/documents/LANDFIRE_ak_110evt_accuracy_summary_013012.pdf (accessed on 26 April 2021).
- Roberts, D.A.; Smith, M.O.; Adams, J.B.; Roberts, D.A. Green Vegetation, Nonphotosynthetic Vegetation, and Soils in AVIRIS Data. Remote Sens. Environ. 1993, 44, 255–269. [Google Scholar] [CrossRef]
- Roberts, D.A.; Ustin, S.L.; Ogunjemiyo, S.; Greenberg, J.; Bobrowski, S.Z.; Chen, J.; Hinckley, T.M. Spectral and structural measures of northwest forest vegetation at leaf to landscape scales. Ecosystems 2004, 7, 545–562. [Google Scholar] [CrossRef]
- Smith, C.W.; Panda, S.K.; Bhatt, U.S.; Meyer, F.J.; Haan, R.W. Improved Vegetation and Wildfire Fuel Type Mapping Using NASA AVIRIS-NG Hyperspectral Data, Interior AK. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1307–1310. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R.O. Mapping Chaparral in the Santa Monica Mountains Using Multiple Endmember Spectral Mixture Models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Zhang, C. Combining hyperspectral and lidar data for vegetation mapping in the Florida everglades. Photogramm. Eng. Remote Sens. 2014, 80, 733–743. [Google Scholar] [CrossRef]
- Singh, P.; Srivastava, P.K.; Malhi, R.K.M.; Chaudhary, S.K.; Verrelst, J.; Bhattacharya, B.K.; Raghubanshi, A.S. Denoising AVIRIS-NG data for generation of new chlorophyll indices. IEEE Sens. J. 2020, 21, 6982–6989. [Google Scholar] [CrossRef]
- Salas, E.A.L.; Subburayalu, S.K.; Slater, B.; Zhao, K.; Bhattacharya, B.; Tripathy, R.; Das, A.; Nigam, R.; Dave, R.; Parekh, P. Mapping crop types in fragmented arable landscapes using AVIRIS-NG imagery and limited field data. Int. J. Image Data Fusion 2020, 11, 33–56. [Google Scholar] [CrossRef]
- Hati, J.P.; Goswami, S.; Samanta, S.; Pramanick, N.; Majumdar, S.D.; Chaube, N.R.; Misra, A.; Hazra, S. Estimation of vegetation stress in the mangrove forest using AVIRIS-NG airborne hyperspectral data. Model. Earth Syst. Environ. 2020, 1–13. [Google Scholar] [CrossRef]
- Ahmad, S.; Pandey, A.C.; Kumar, A.; Lele, N.V. Potential of hyperspectral AVIRIS-NG data for vegetation characterization, species spectral separability, and mapping. Appl. Geomat. 2021, 1–12. [Google Scholar] [CrossRef]
- Badola, A.; Padalia, H.; Belgiu, M.; Prabhakar, M.; Verma, A. Mapping Tree Species Richness of Tropical Forest Using Airborne Hyperspectral Remote Sensing. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2019. [Google Scholar]
- Varshney, P.K.; Arora, M.K. Advanced Image Processing Techniques for Remotely Sensed Hyperspectral Data; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.; Zhang, X.; Zhang, B.; Tong, Q. Simulation of EO-1 Hyperion Data from ALI Multispectral Data Based on the Spectral Reconstruction Approach. Sensors 2009, 9, 3090–3108. [Google Scholar] [CrossRef]
- Tiwari, V.; Kumar, V.; Pandey, K.; Ranade, R.; Agrawal, S. Simulation of the hyperspectral data using Multispectral data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Institute of Electrical and Electronics Engineers Inc., Beijing, China, 10–15 July 2016; Volume 2016, pp. 6157–6160. [Google Scholar] [CrossRef]
- Zhang, L.; Fujiwara, N.; Furumi, S.; Muramatsu, K.; Daigo, M.; Zhang, L. Assessment of the universal pattern decomposition method using MODIS and ETM data. Int. J. Remote Sens. 2007, 28, 125–142. [Google Scholar] [CrossRef]
- Townsend, P.A.; Foster, J.R. Comparison of EO-1 Hyperion to AVIRIS for mapping forest composition in the Appalachian Mountains, USA. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, ON, Canada, 24–28 June 2002; Volume 2, pp. 793–795. [Google Scholar] [CrossRef]
- USGS USGS EROS Archive—Earth Observing One (EO-1)—Hyperion. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-earth-observing-one-eo-1-hyperion?qt-science_center_objects=0#qt-science_center_objects (accessed on 11 April 2021).
- Grabska, E.; Hostert, P.; Pflugmacher, D.; Ostapowicz, K. Forest Stand Species Mapping Using the Sentinel-2 Time Series. Remote Sens. 2019, 11, 1197. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- ESA Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/dhus/#/home (accessed on 23 November 2020).
- NEON Caribou-Poker Creeks Research Watershed NEON|NSF NEON|Open Data to Understand our Ecosystems. Available online: https://www.neonscience.org/field-sites/bona (accessed on 3 March 2021).
- QGIS Development Team. QGIS Geographic Information System; Version 3.14; Open Source Geospatial Foundation: Beaverton, OR, USA, 2020. [Google Scholar]
- Gao, B.C.; Heidebrecht, K.H.; Goetz, A.F.H. Derivation of scaled surface reflectances from AVIRIS data. Remote Sens. Environ. 1993, 44, 165–178. [Google Scholar] [CrossRef]
- NASA JPL AVIRIS-NG Data Portal. Available online: https://avirisng.jpl.nasa.gov/dataportal/ (accessed on 17 February 2021).
- Exelis Visual Information Solutions Version 5.3; Exelis Visual Information Solutions Inc.: Boulder, CO, USA, 2010.
- Harris Geospatial Solutions Preprocessing AVIRIS Data Tutorial. Available online: http://enviidl.com/help/Subsystems/envi/Content/Tutorials/Tools/PreprocessAVIRIS.htm (accessed on 17 November 2020).
- Kim, D.S.; Pyeon, M.W. Aggregation of hyperion hyperspectral bands to ALI and ETM+ bands using spectral response information and the weighted sum method. Int. J. Digit. Content Technol. Appl. 2012, 6, 189–199. [Google Scholar] [CrossRef]
- European Space Agency Sentinel-2 Spectral Response Functions (S2-SRF)—Sentinel-2 MSI Document Library—User Guides—Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi/document-library/-/asset_publisher/Wk0TKajiISaR/content/sentinel-2a-spectral-responses (accessed on 23 November 2020).
- Zhang, L.; Furumi, S.; Muramatsu, K.; Fujiwara, N.; Daigo, M.; Zhang, L. Sensor-independent analysis method for hyperspectral data based on the pattern decomposition method. Int. J. Remote Sens. 2006, 27, 4899–4910. [Google Scholar] [CrossRef]
- Python Core Team. Python; A Dynamic, Open Source Programming Language; Python Software Foundation: Wilmington, DE, USA, 2015. [Google Scholar]
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 445, pp. 51–56. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with {NumPy}. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- GDAL/OGR contributors {GDAL/OGR} Geospatial Data Abstraction Software Library 2021. Available online: https://gdal.org/ (accessed on 26 April 2021).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in {P}ython. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Douzas, G.; Bacao, F.; Fonseca, J.; Khudinyan, M. Imbalanced Learning in Land Cover Classification: Improving Minority Classes’ Prediction Accuracy Using the Geometric SMOTE Algorithm. Remote Sens. 2019, 11, 3040. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Barnes, J.; Peter Butteri, N.; Robert DeVelice, F.; Kato Howard, U.; Jennifer Hrobak, B.; Rachel Loehman, N.; Nathan Lojewski, U.; Charley Martin, C.; Eric Miller, L.; Bobette Rowe, B.; et al. Fuel Model Guide to Alaska Vegetation; Alaska Wildland Fire Coordinating Group, Fire Modeling and Analysis Committee: Fairbanks, AK, USA, 2018. [Google Scholar]
- NASA JPL AVIRIS-Next Generation. Available online: https://avirisng.jpl.nasa.gov/platform.html (accessed on 24 November 2020).
- König, M.; Hieronymi, M.; Oppelt, N. Application of Sentinel-2 MSI in Arctic Research: Evaluating the Performance of Atmospheric Correction Approaches Over Arctic Sea Ice. Front. Earth Sci. 2019, 7, 22. [Google Scholar] [CrossRef]


| Bands | Wavelength (nm) | Remarks |
|---|---|---|
| 1–30 | 376.85–522.09985 | Noise due to atmospheric scattering and poor sensor radiometric calibration |
| 196–210 | 1353.55–1423.67 | Water vapor absorption bands |
| 288–317 | 1814.35–1959.60 | Water vapor absorption bands |
| 408–425 | 2415.39–2500.00 | Noise due to poor radiometric calibration and strong water vapor and methane absorption |
| Class | Number of Pixels |
|---|---|
| Spruce | 1847 |
| Birch | 426 |
| Alder | 302 |
| Gravel | 129 |
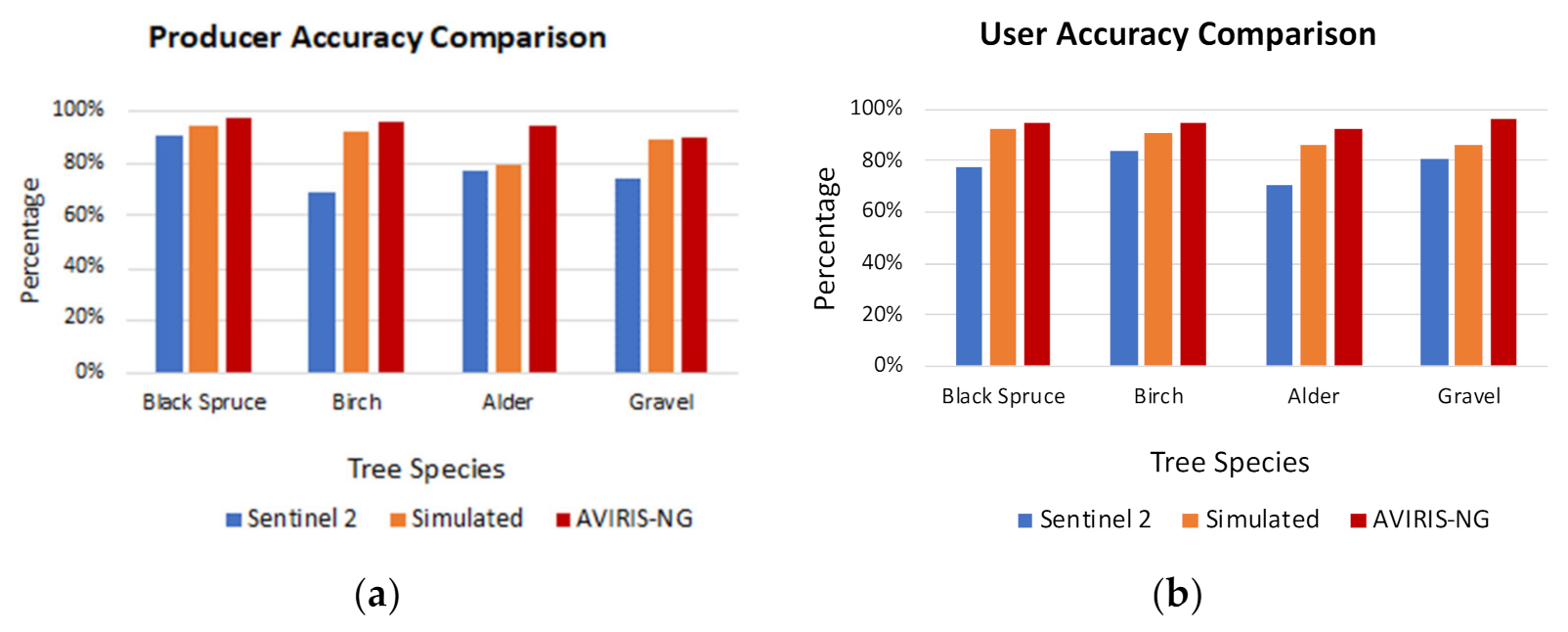
| Sentinel-2 Classification Confusion Matrix (Test Data) | |||||||
| Reference Data | Total | Producer Accuracy(%) | |||||
| Black Spruce | Birch | Alder | Gravel | ||||
| Map Data | Black Spruce | 642 | 33 | 9 | 22 | 706 | 90.9% |
| Birch | 0 | 488 | 218 | 0 | 706 | 69.1% | |
| Alder | 0 | 61 | 543 | 102 | 706 | 76.9% | |
| Gravel | 183 | 0 | 0 | 523 | 706 | 74.1% | |
| Total | 825 | 582 | 770 | 647 | 2824 | ||
| User Accuracy (%) | 77.8% | 83.8% | 70.5% | 80.8% | |||
| Simulated Hyperspectral Classification Confusion Matrix (Test Data) | |||||||
| Reference Data | Total | Producer Accuracy | |||||
| Black Spruce | Birch | Alder | Gravel | ||||
| Map Data | Black Spruce | 666 | 0 | 40 | 0 | 706 | 94.3% |
| Birch | 53 | 653 | 0 | 0 | 706 | 92.5% | |
| Alder | 0 | 42 | 563 | 101 | 706 | 79.7% | |
| Gravel | 0 | 21 | 53 | 632 | 706 | 89.5% | |
| Total | 719 | 716 | 656 | 733 | 2824 | ||
| User Accuracy (%) | 92.6% | 91.2% | 85.8% | 86.2% | |||
| AVIRIS-NG Classification Confusion Matrix (Test Data) | |||||||
| Reference Data | Total | Producer Accuracy | |||||
| Black Spruce | Birch | Alder | Gravel | ||||
| Map Data | Black Spruce | 688 | 0 | 17 | 1 | 706 | 97.5% |
| Birch | 0 | 679 | 5 | 22 | 706 | 96.2% | |
| Alder | 0 | 39 | 667 | 0 | 706 | 94.5% | |
| Gravel | 38 | 0 | 37 | 631 | 706 | 89.4% | |
| Total | 726 | 718 | 726 | 654 | 2824 | ||
| User Accuracy (%) | 94.8% | 94.6% | 91.9% | 96.5% | |||
| Data | Overall Accuracy |
|---|---|
| Sentinel-2 | 77.8% |
| Simulated hyperspectral data | 89.0% |
| AVIRIS-NG data | 94.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badola, A.; Panda, S.K.; Roberts, D.A.; Waigl, C.F.; Bhatt, U.S.; Smith, C.W.; Jandt, R.R. Hyperspectral Data Simulation (Sentinel-2 to AVIRIS-NG) for Improved Wildfire Fuel Mapping, Boreal Alaska. Remote Sens. 2021, 13, 1693. https://doi.org/10.3390/rs13091693
Badola A, Panda SK, Roberts DA, Waigl CF, Bhatt US, Smith CW, Jandt RR. Hyperspectral Data Simulation (Sentinel-2 to AVIRIS-NG) for Improved Wildfire Fuel Mapping, Boreal Alaska. Remote Sensing. 2021; 13(9):1693. https://doi.org/10.3390/rs13091693
Chicago/Turabian StyleBadola, Anushree, Santosh K. Panda, Dar A. Roberts, Christine F. Waigl, Uma S. Bhatt, Christopher W. Smith, and Randi R. Jandt. 2021. "Hyperspectral Data Simulation (Sentinel-2 to AVIRIS-NG) for Improved Wildfire Fuel Mapping, Boreal Alaska" Remote Sensing 13, no. 9: 1693. https://doi.org/10.3390/rs13091693
APA StyleBadola, A., Panda, S. K., Roberts, D. A., Waigl, C. F., Bhatt, U. S., Smith, C. W., & Jandt, R. R. (2021). Hyperspectral Data Simulation (Sentinel-2 to AVIRIS-NG) for Improved Wildfire Fuel Mapping, Boreal Alaska. Remote Sensing, 13(9), 1693. https://doi.org/10.3390/rs13091693