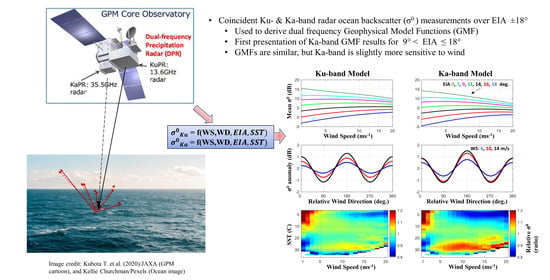
Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data
Abstract
1. Introduction
2. Materials and Methods
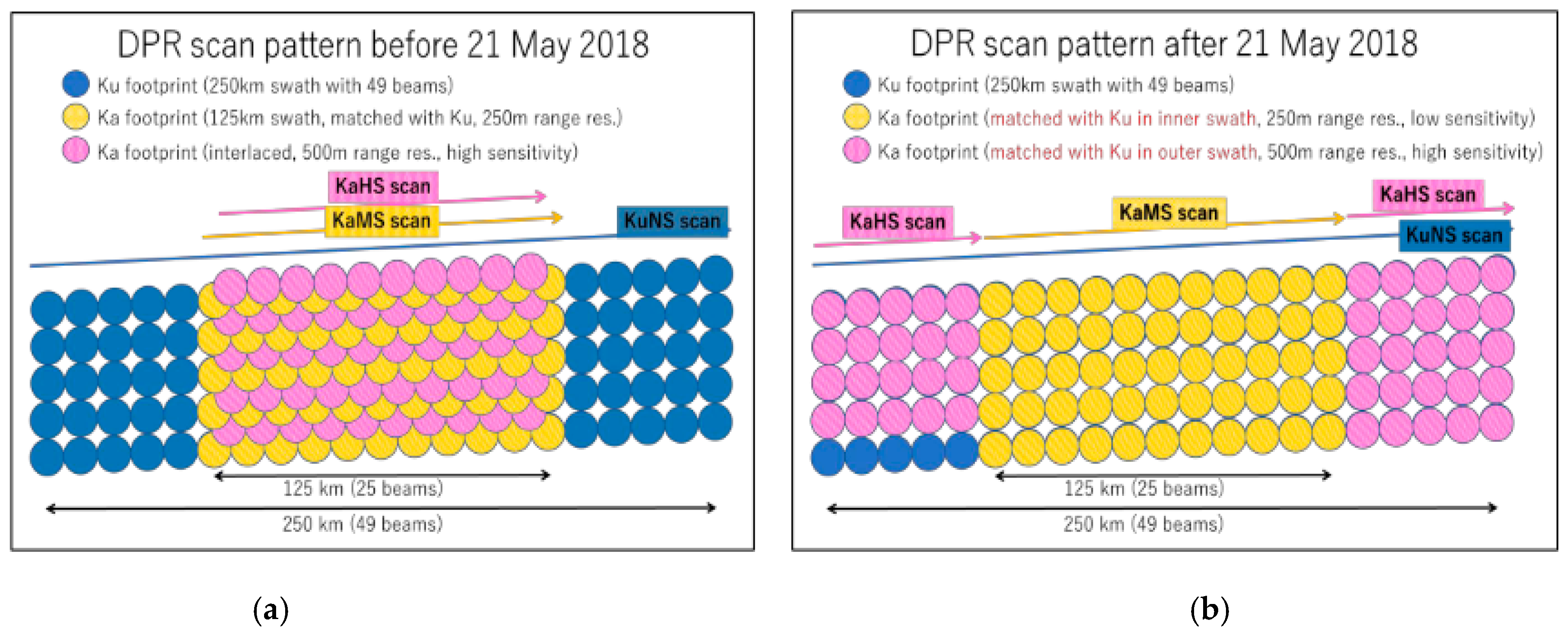
2.1. GPM Dual-Frequency Precipitation Radar (DPR)
2.2. GPM Microwave Imager (GMI)
2.3. Collocation and Quality Control
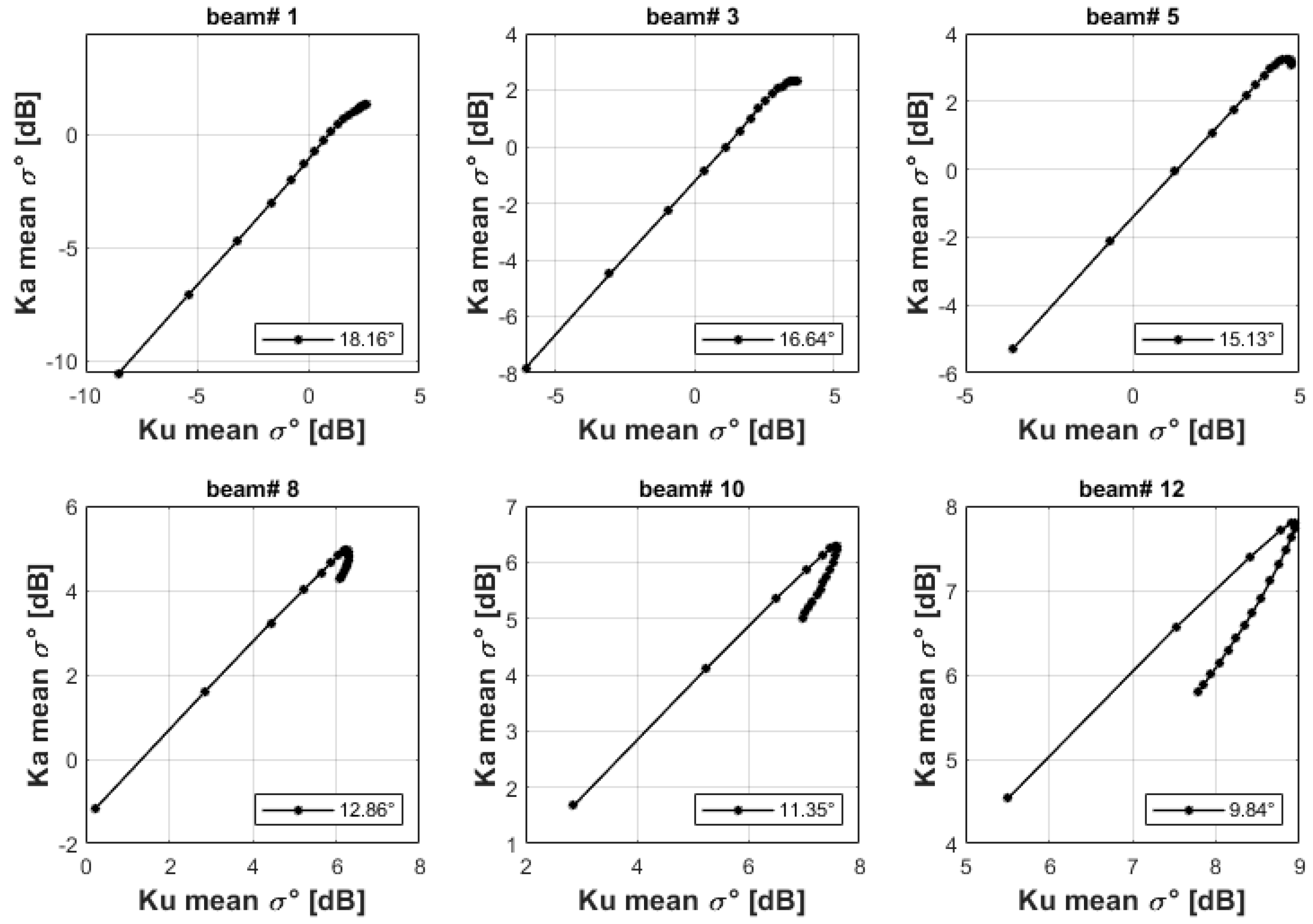
3. Geophysical Model Function for the Ocean Ku and Ka-Band PR Backscatter
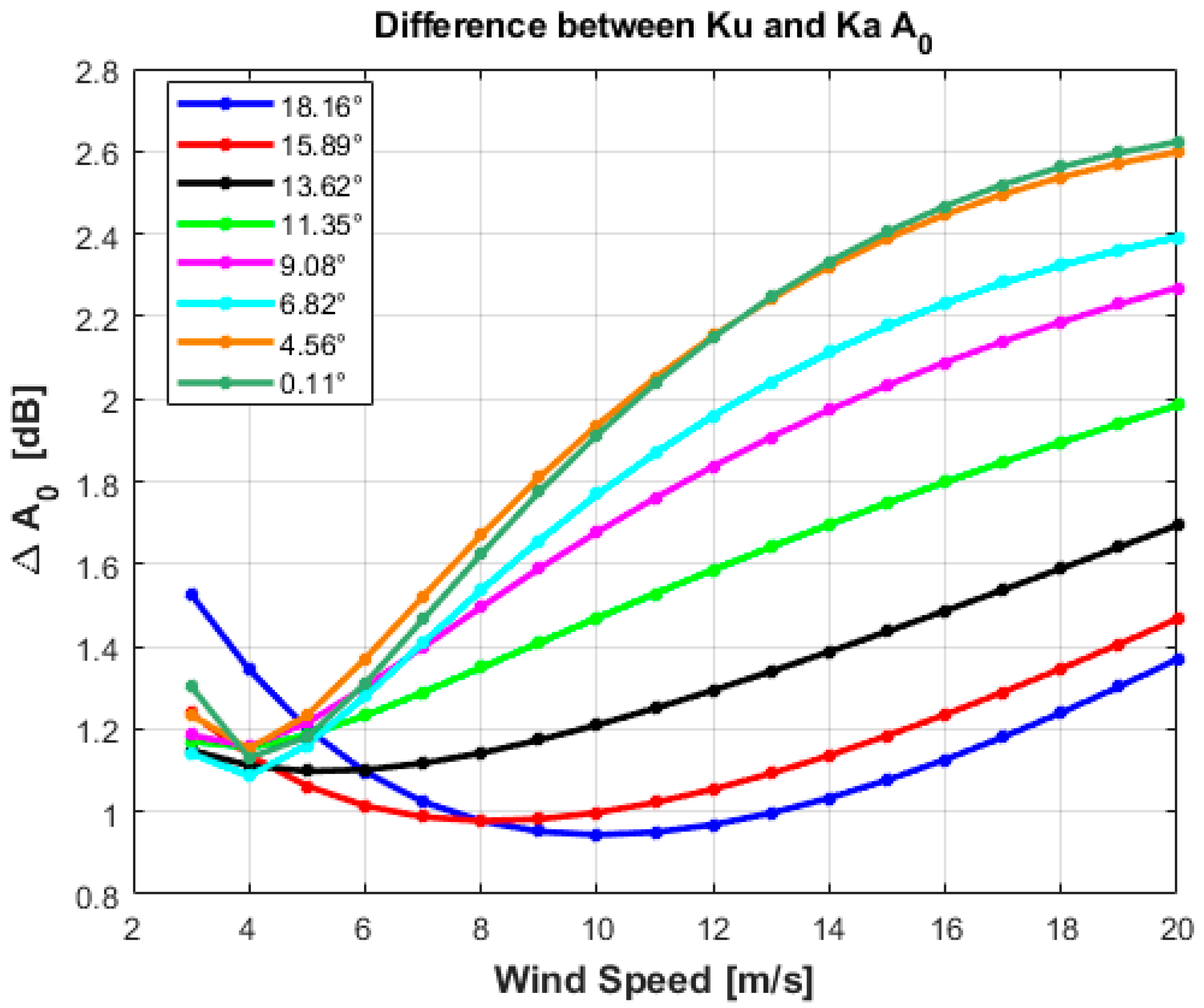
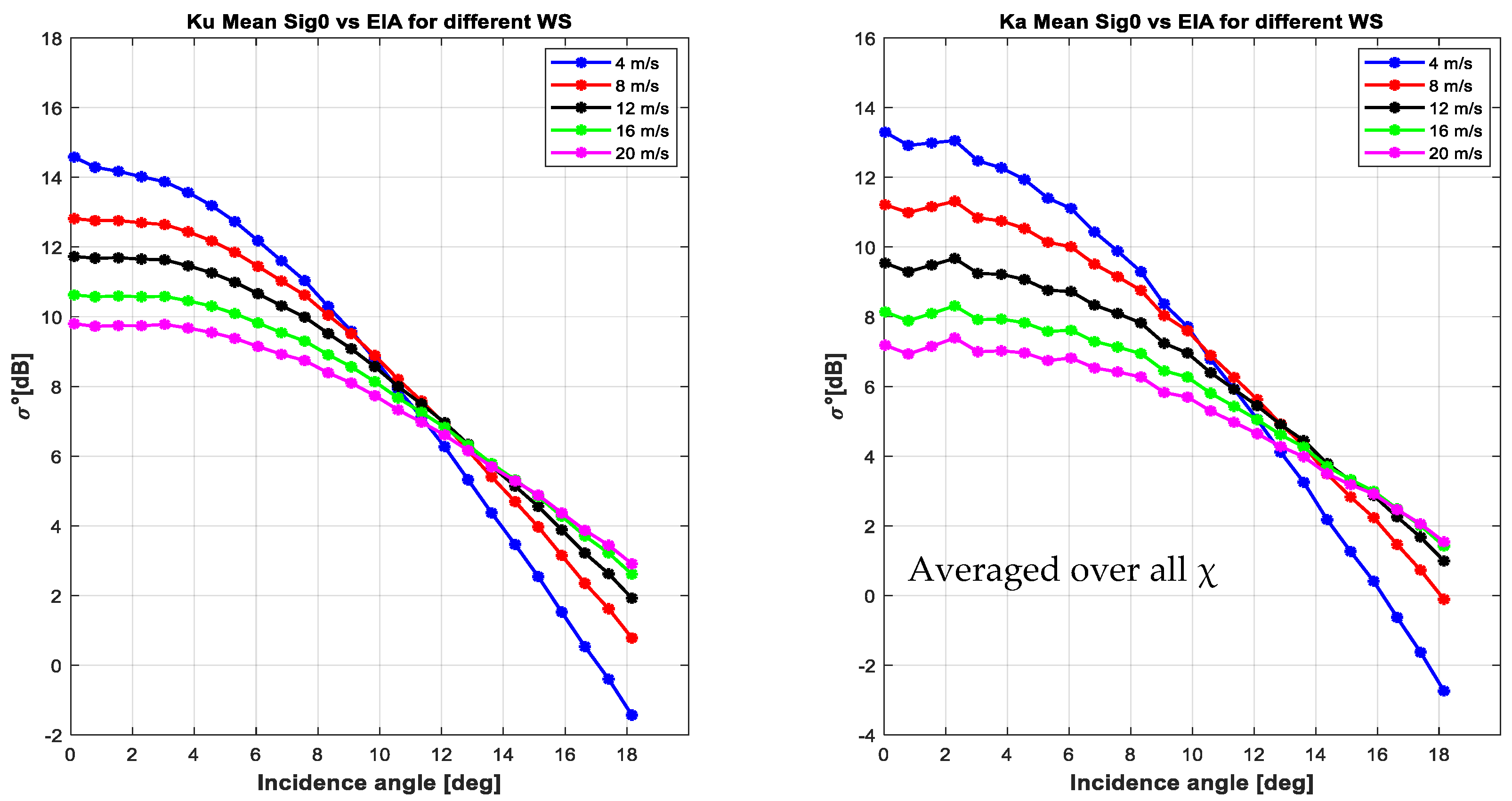
3.1. Isotropic Ku and Ka-Band Model Function at Low Incidence Angles
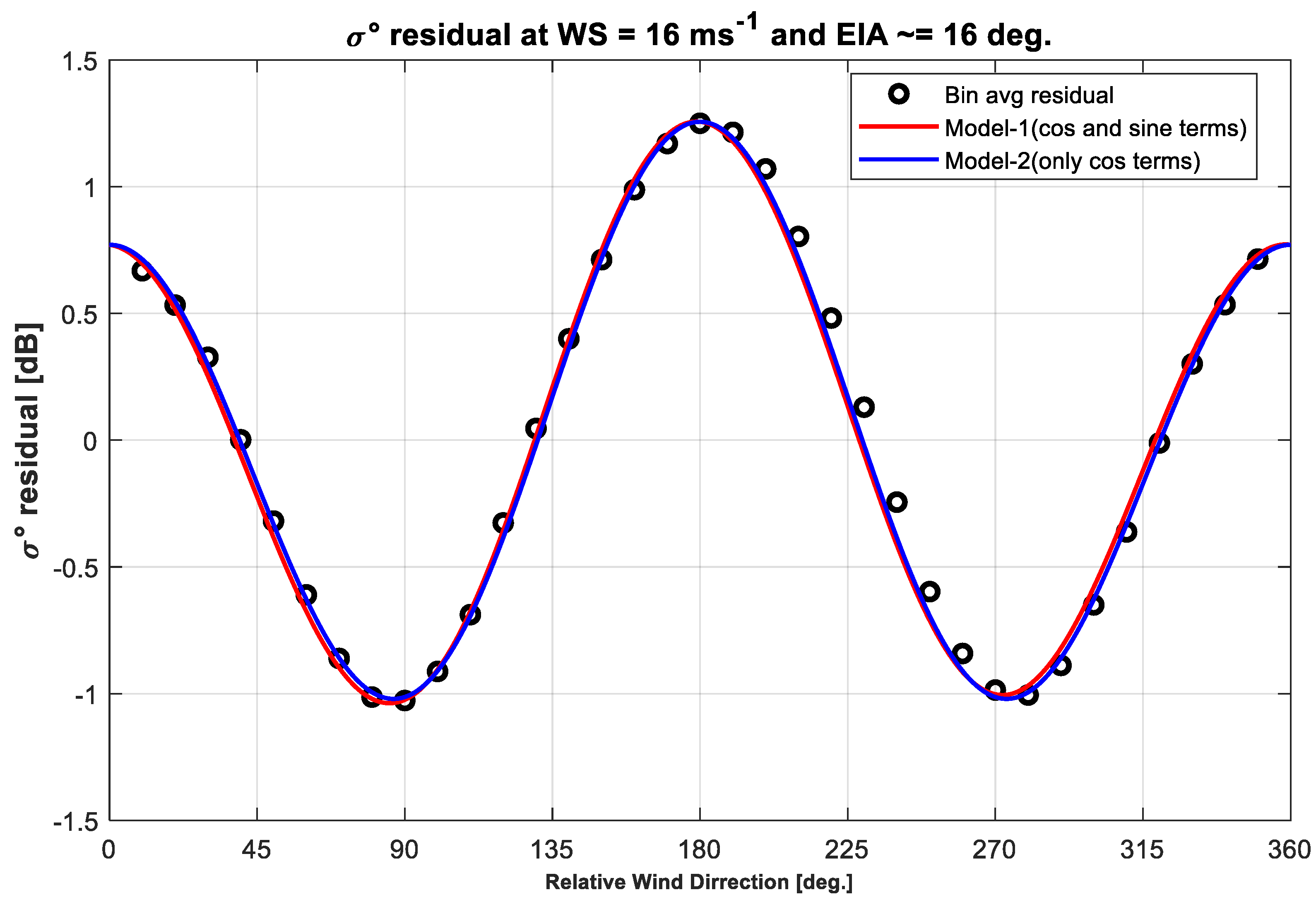
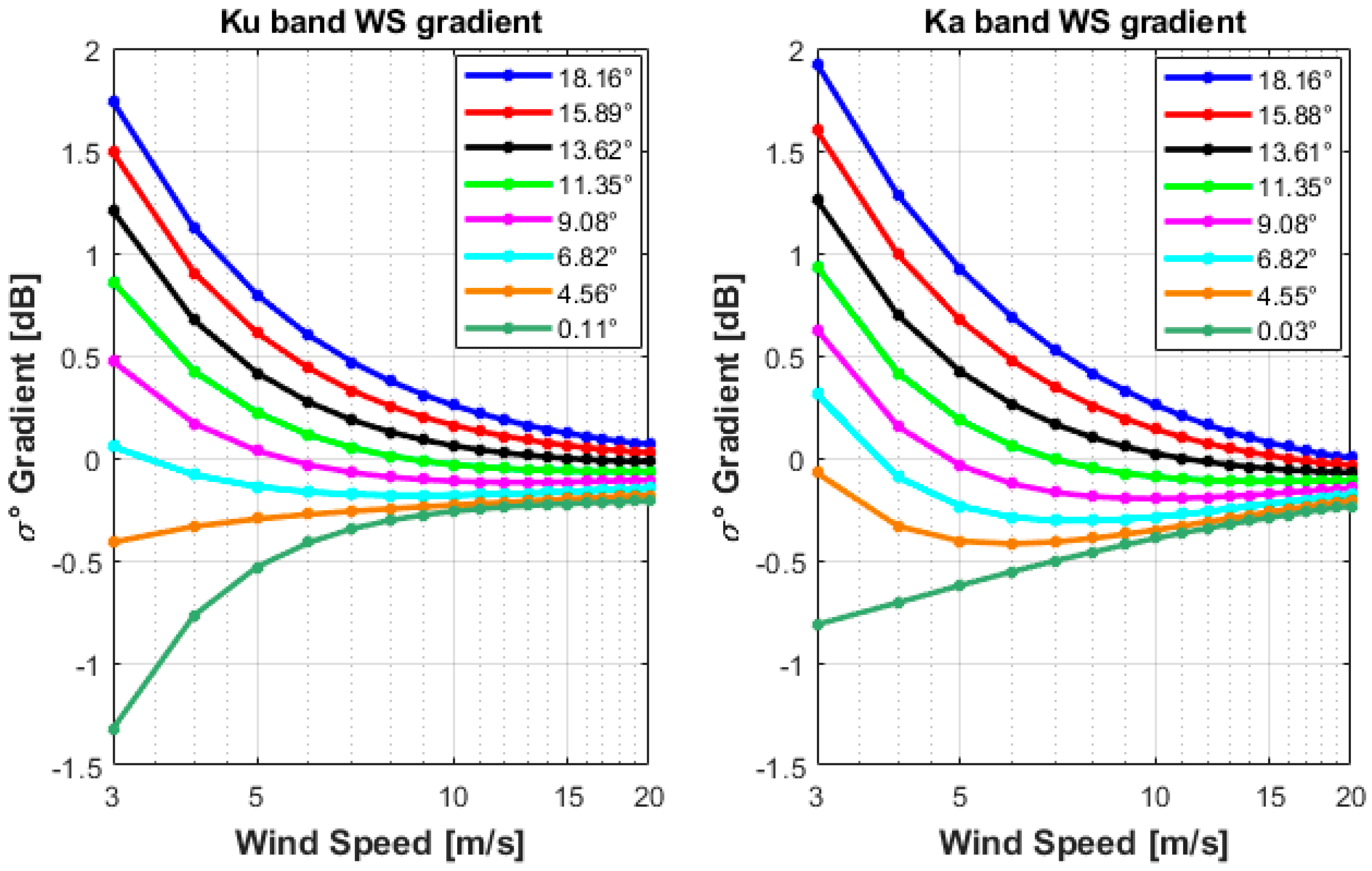
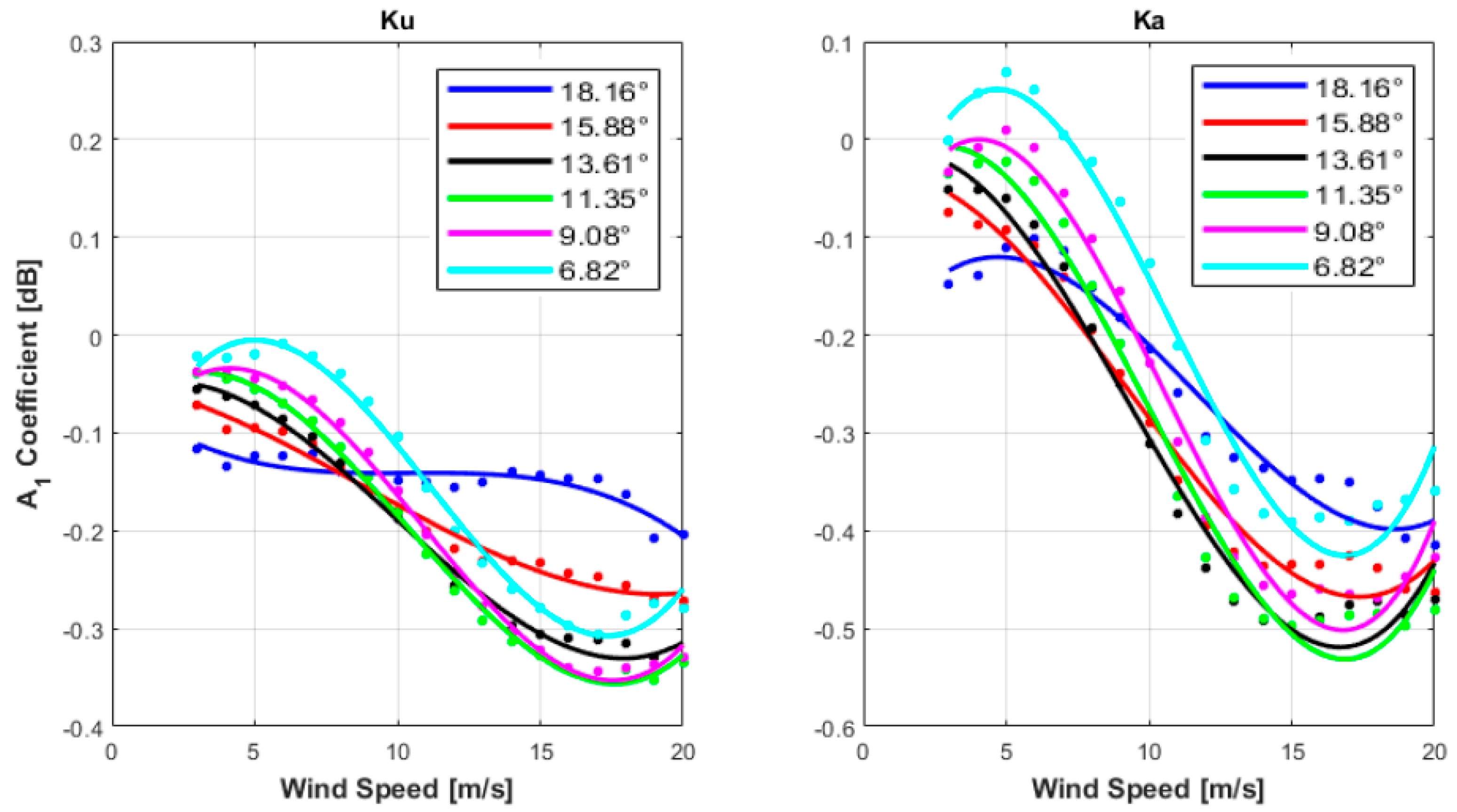
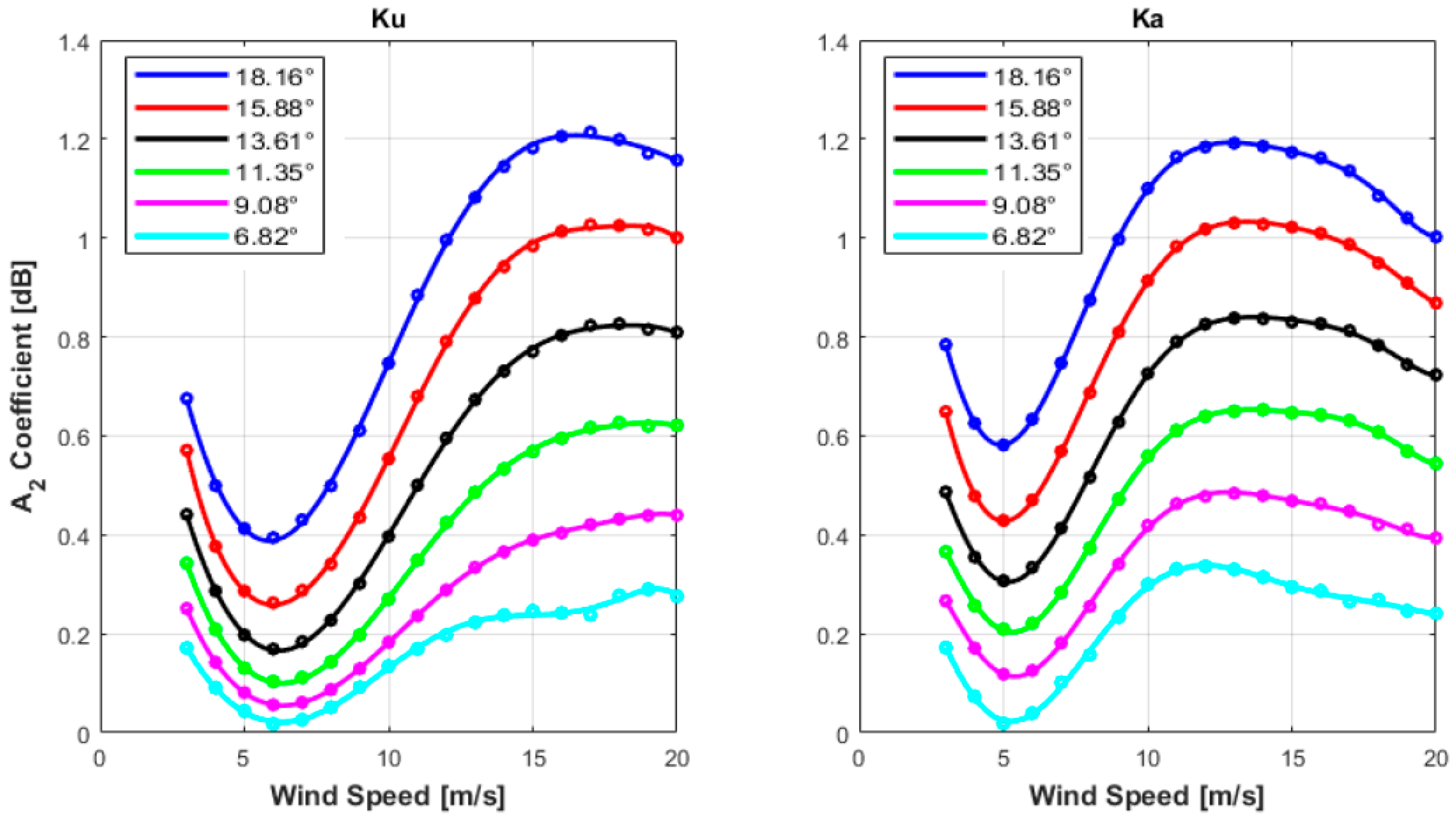
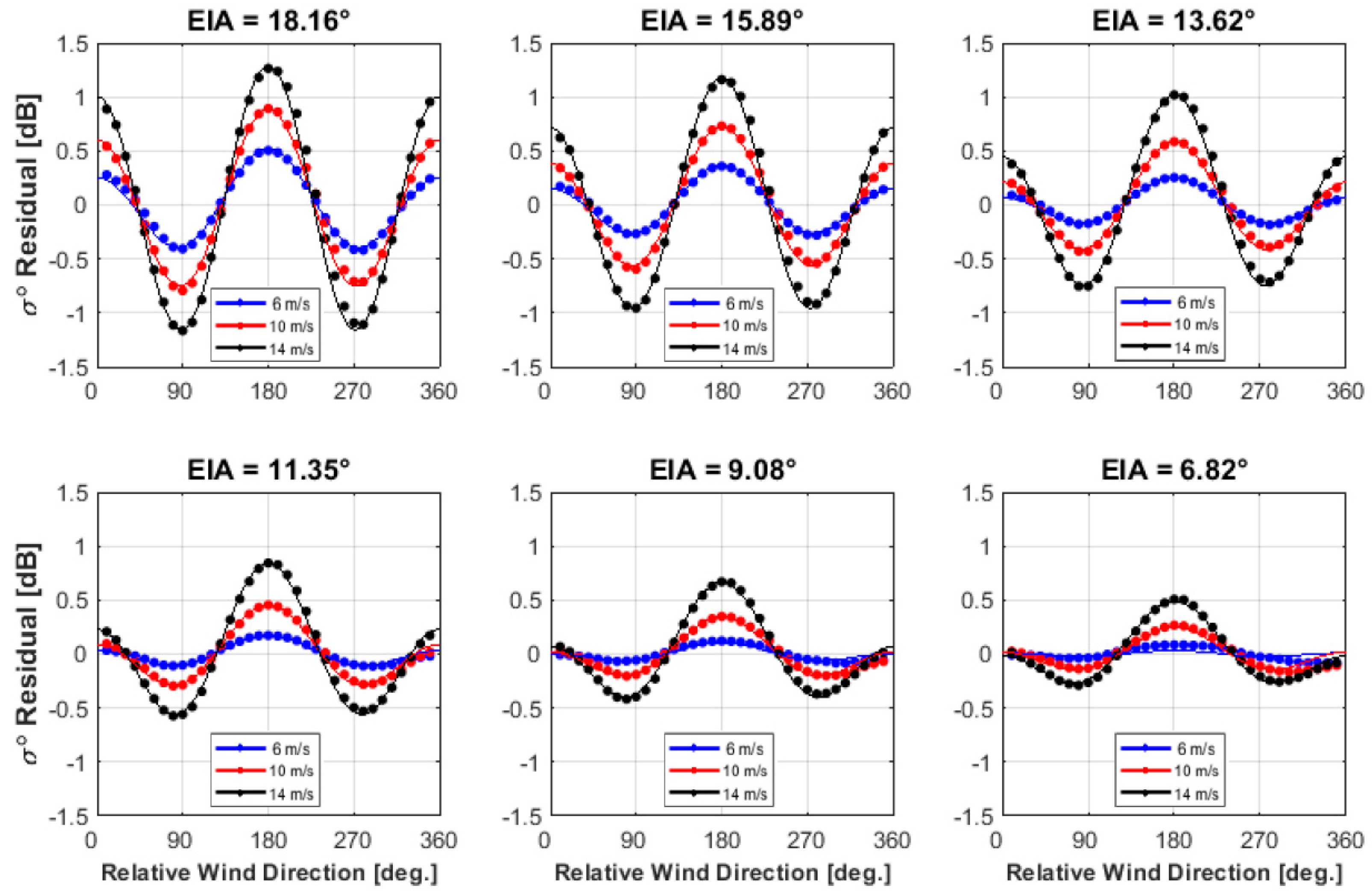
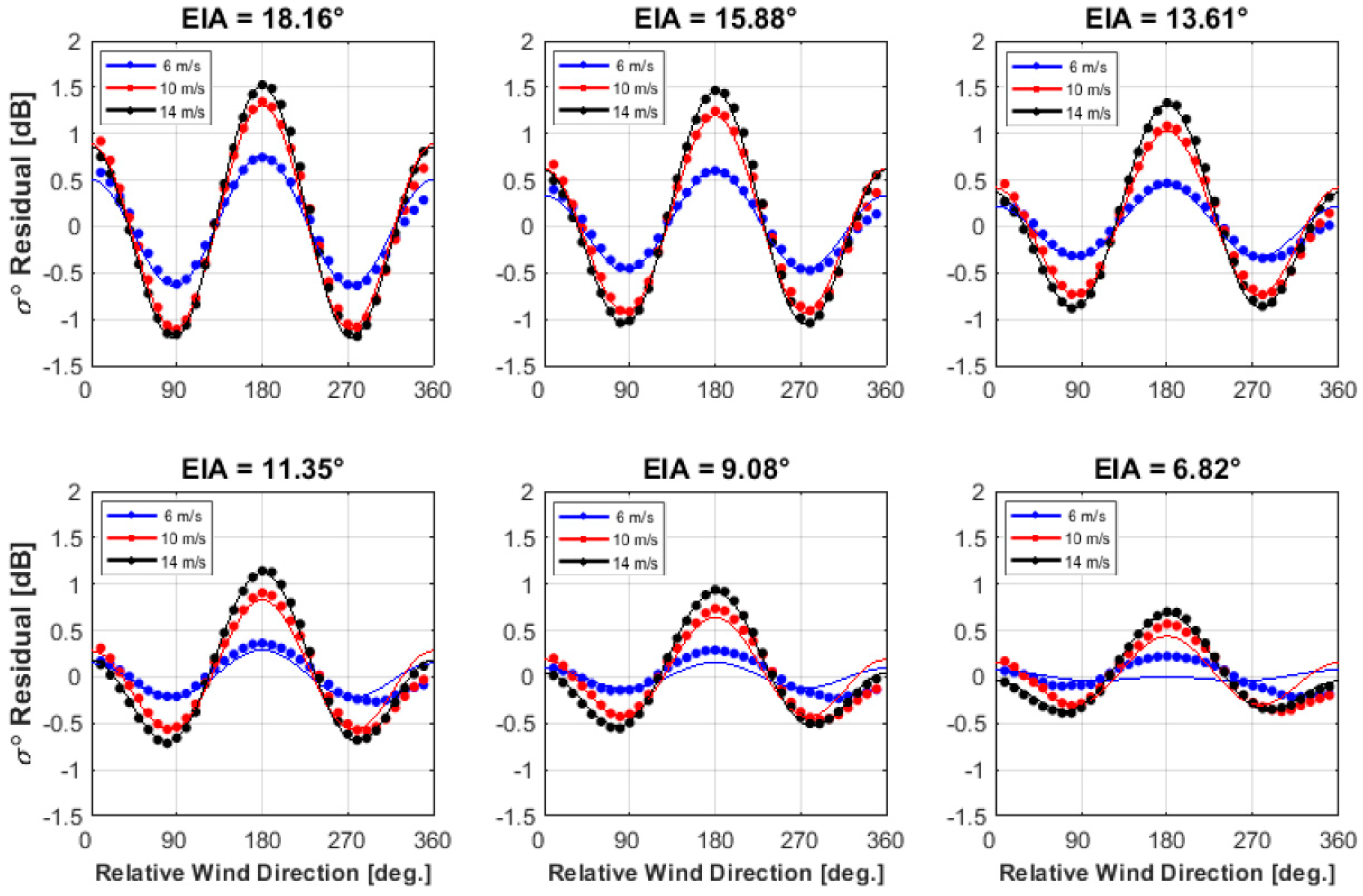
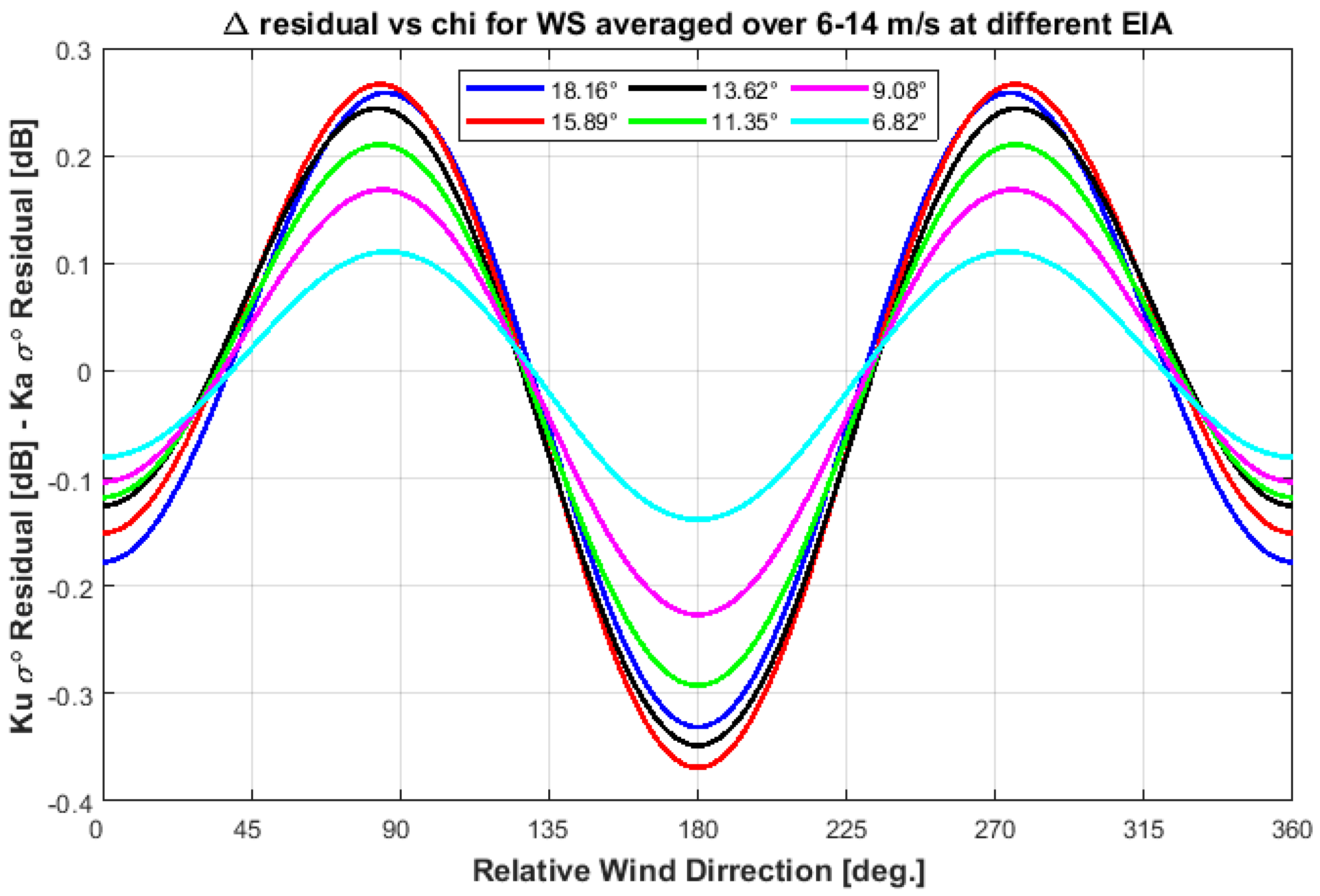
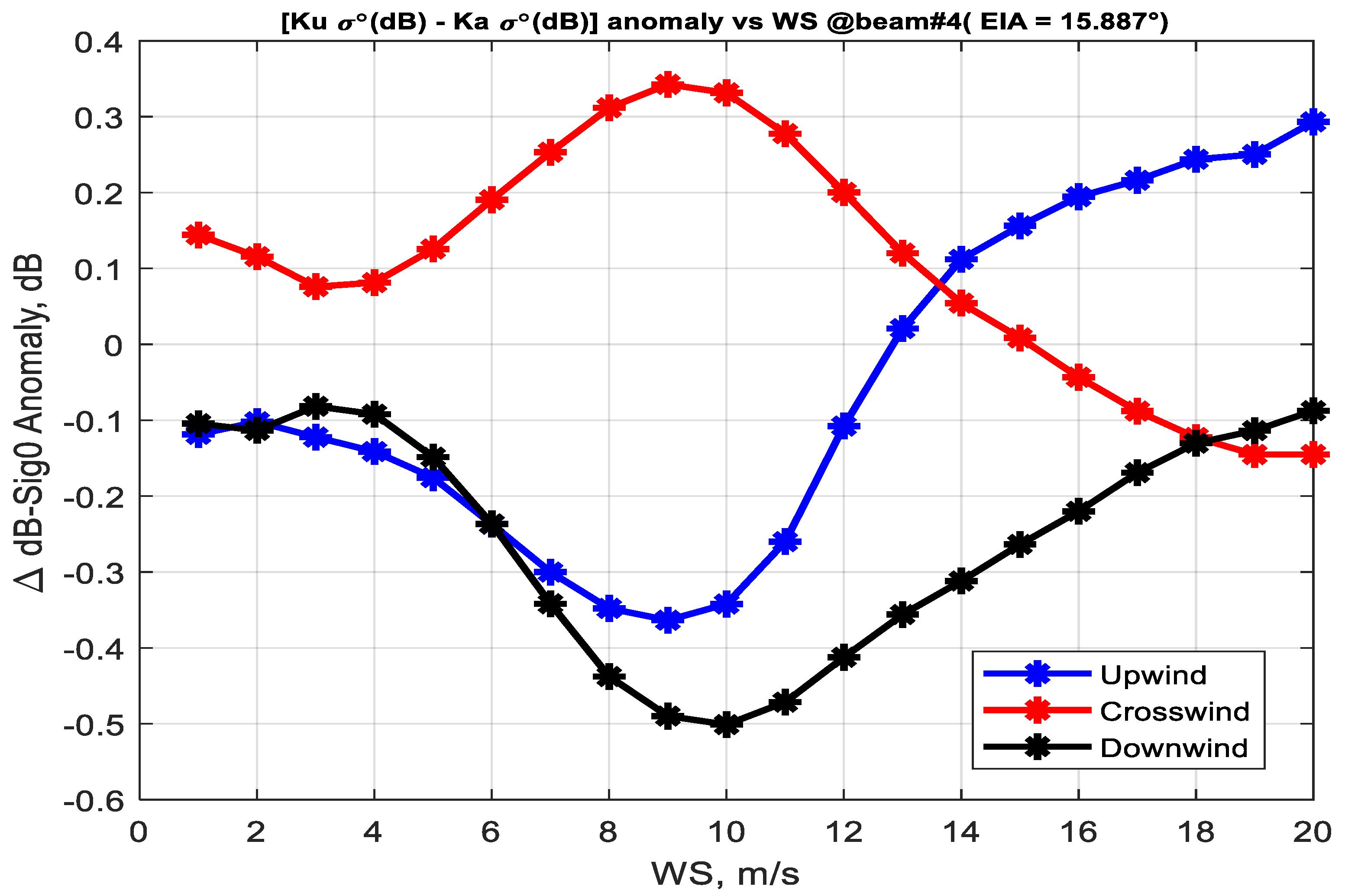
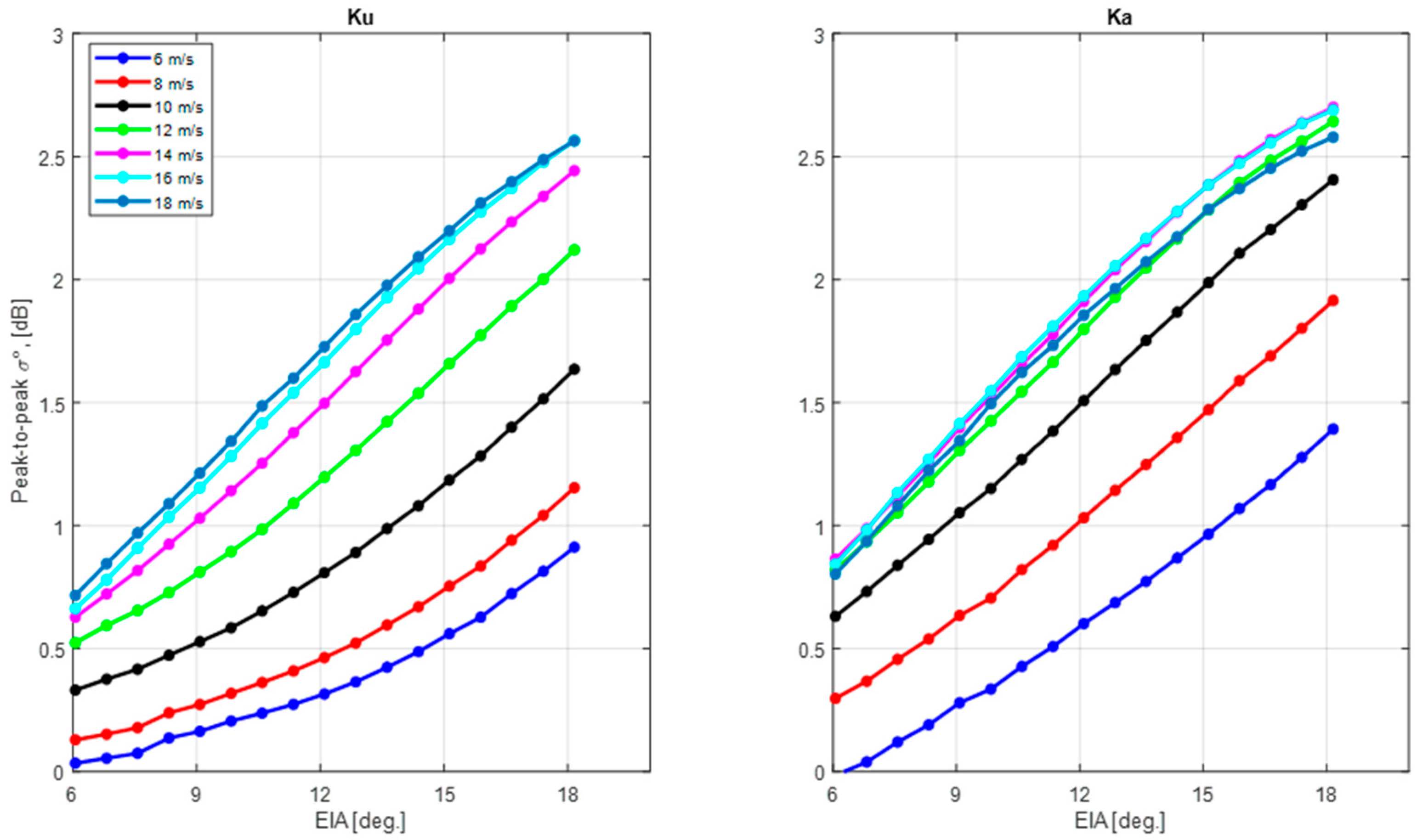
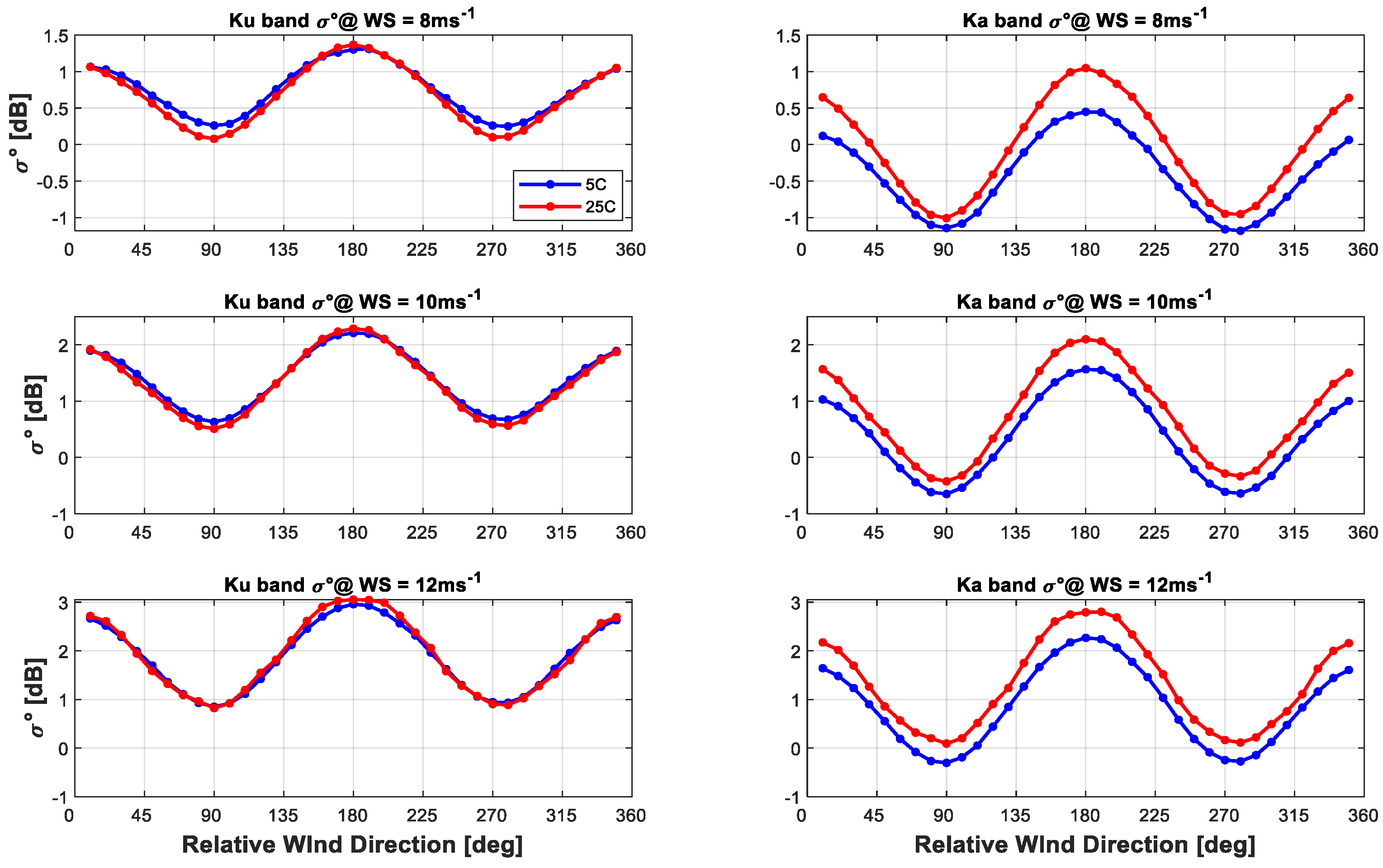
3.2. σ0 Azimuthal Anisotropy
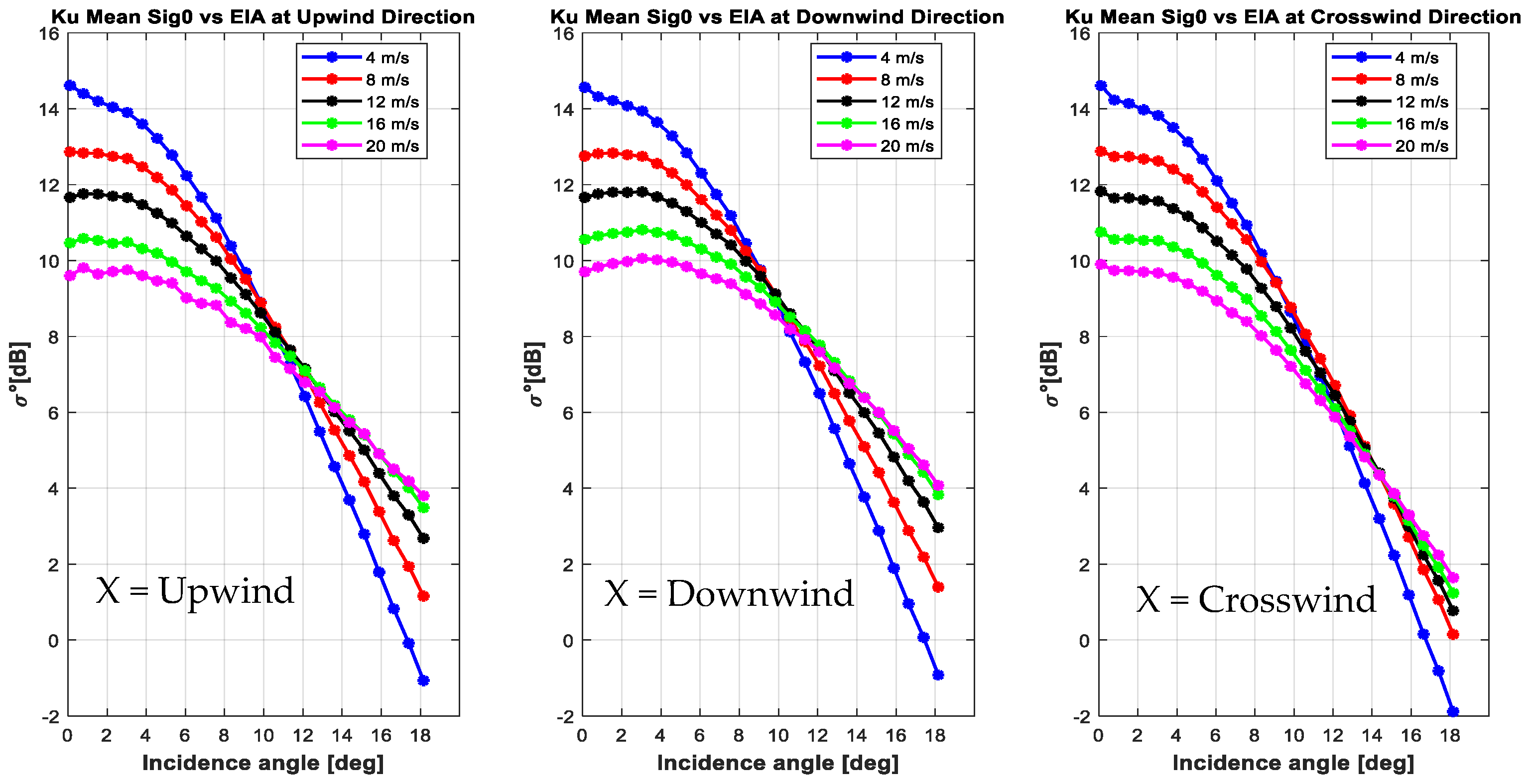
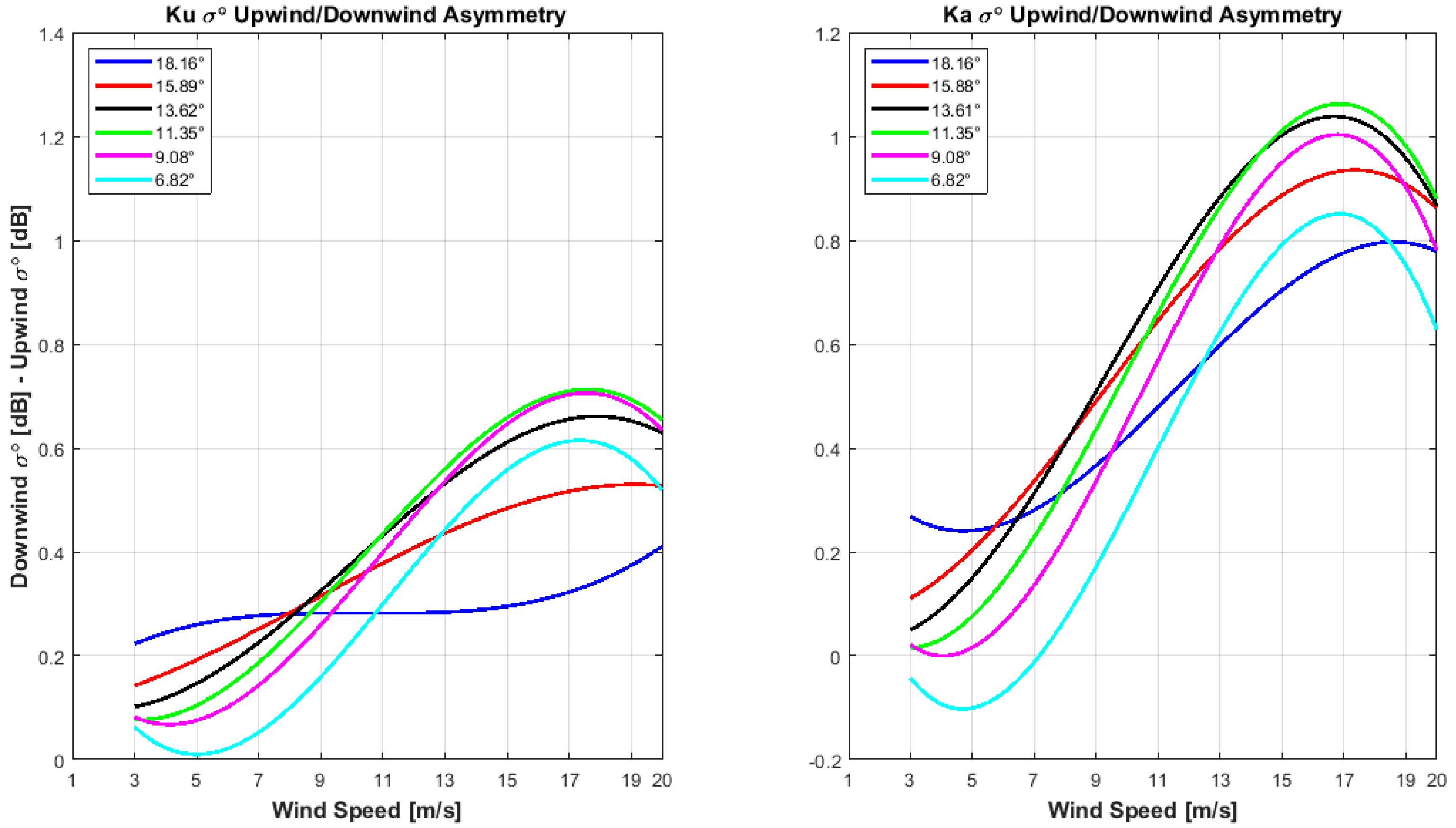
3.2.1. Upwind and Downwind Asymmetry of σ0
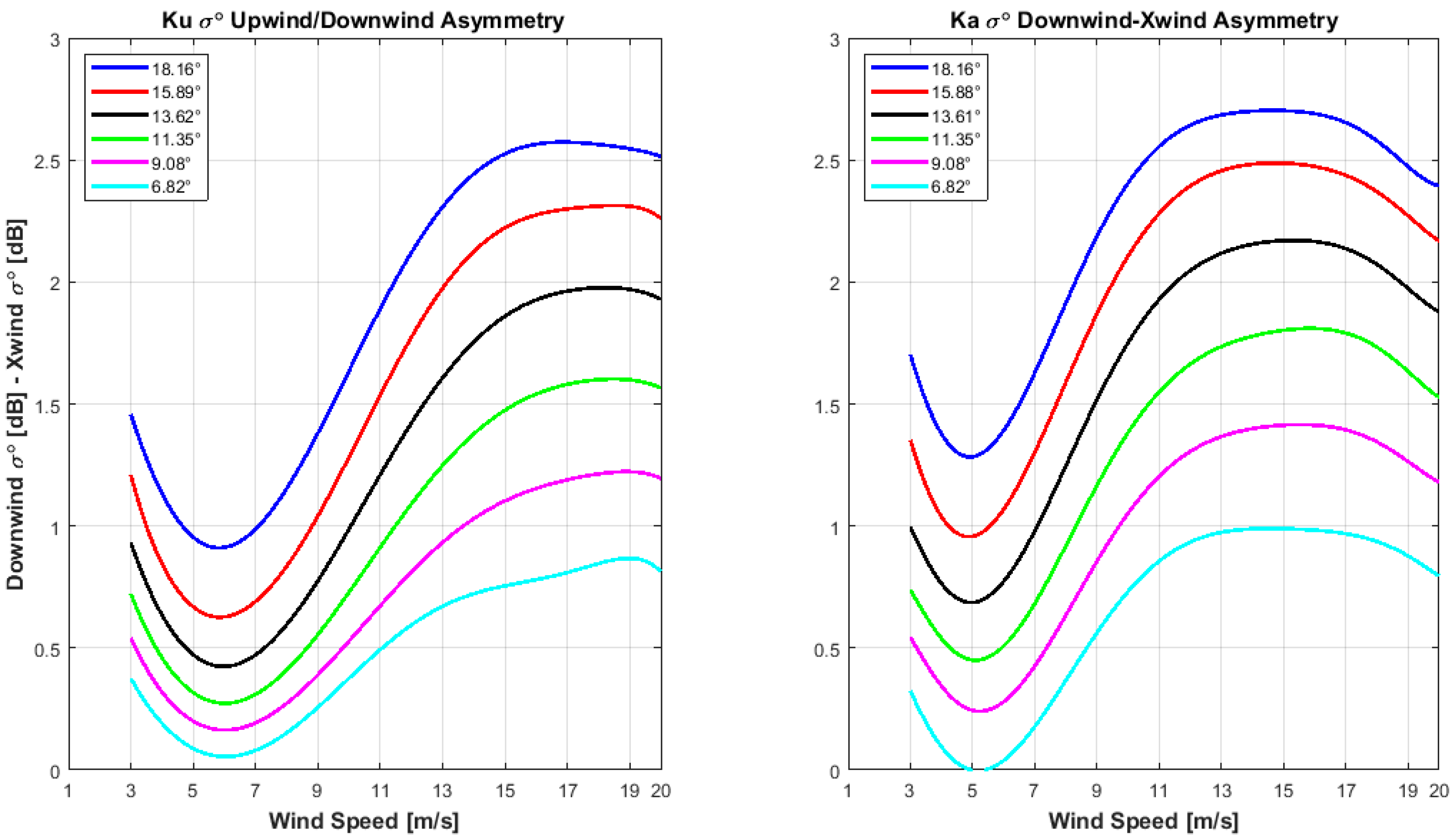
3.2.2. Downwind and Crosswind Anisotropy of σ0
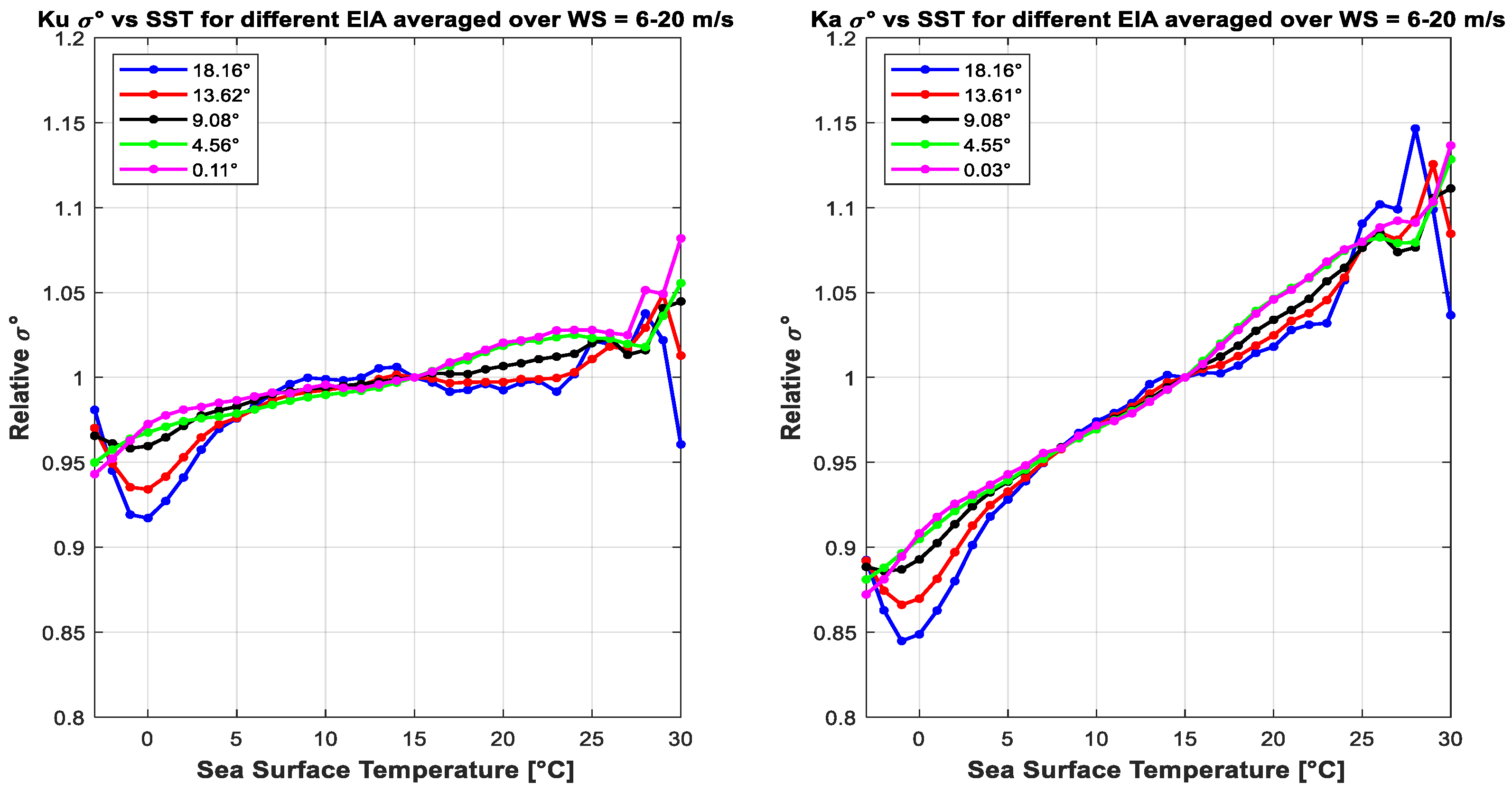
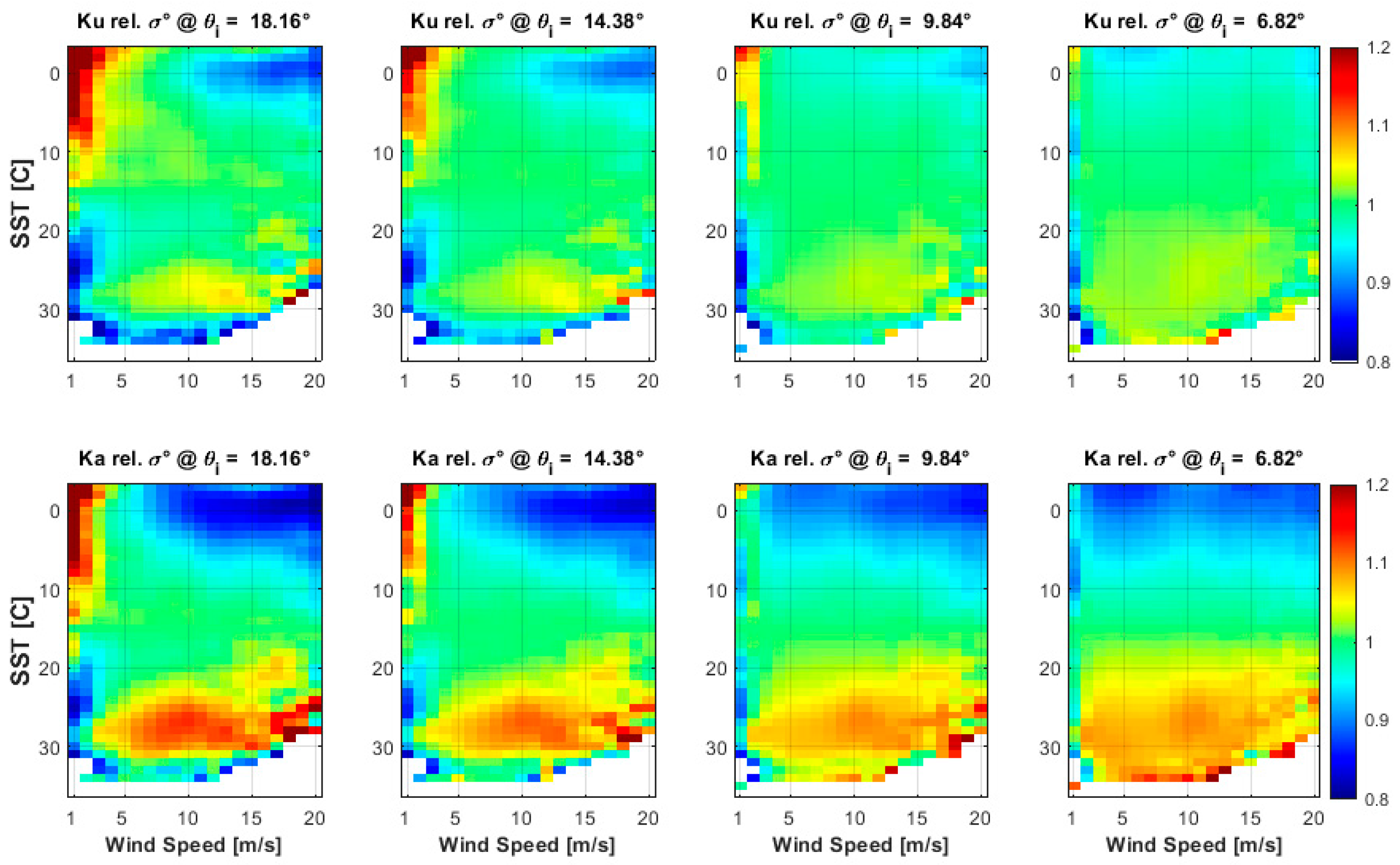
3.3. SST Dependency of σ0
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Beam No | Ku | Ka | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EIA | EIA | |||||||||
| 1 | 18.16 | 0.23 | −5.69 | 16.54 | −9.71 | 18.16 | −2.92 | 0.01 | 14.62 | −11.28 |
| 2 | 17.41 | 0.70 | −6.96 | 16.95 | −8.53 | 17.40 | −2.25 | −1.64 | 15.01 | −9.92 |
| 3 | 16.64 | 1.01 | −7.82 | 16.97 | −7.35 | 16.64 | −1.63 | −3.14 | 15.25 | −8.62 |
| 4 | 15.89 | 1.15 | −8.21 | 16.60 | −5.99 | 15.88 | −1.08 | −4.46 | 15.32 | −7.23 |
| 5 | 15.13 | 1.41 | −8.95 | 16.51 | −4.68 | 15.13 | −0.51 | −5.81 | 15.41 | −6.03 |
| 6 | 14.38 | 1.69 | −9.69 | 16.40 | −3.45 | 14.37 | 0.09 | −7.26 | 15.60 | −4.79 |
| 7 | 13.62 | 1.78 | −9.92 | 15.85 | −2.12 | 13.61 | 0.69 | −8.70 | 15.79 | −3.40 |
| 8 | 12.86 | 1.73 | −9.72 | 14.89 | −0.63 | 12.86 | 1.20 | −9.92 | 15.83 | −2.20 |
| 9 | 12.10 | 1.84 | −10.02 | 14.42 | 0.72 | 12.10 | 1.73 | −11.21 | 15.93 | −0.92 |
| 10 | 11.35 | 1.72 | −9.64 | 13.33 | 2.14 | 11.35 | 2.21 | −12.39 | 15.98 | 0.28 |
| 11 | 10.59 | 1.57 | −9.12 | 12.12 | 3.55 | 10.59 | 2.67 | −13.50 | 16.01 | 1.45 |
| 12 | 9.84 | 1.31 | −8.34 | 10.70 | 5.07 | 9.84 | 3.04 | −14.37 | 15.86 | 2.74 |
| 13 | 9.08 | 1.07 | −7.55 | 9.27 | 6.51 | 9.08 | 3.46 | −15.43 | 15.90 | 3.70 |
| 14 | 8.33 | 0.62 | −6.23 | 7.41 | 7.98 | 8.33 | 3.83 | −16.29 | 15.77 | 4.97 |
| 15 | 7.57 | 0.33 | −5.25 | 5.81 | 9.42 | 7.57 | 4.03 | −16.69 | 15.27 | 5.98 |
| 16 | 6.82 | −0.11 | −3.92 | 3.97 | 10.72 | 6.82 | 4.25 | −17.09 | 14.80 | 6.94 |
| 17 | 6.06 | −0.66 | −2.23 | 1.82 | 12.11 | 6.06 | 4.14 | −16.61 | 13.61 | 8.19 |
| 18 | 5.31 | −1.32 | −0.18 | −0.66 | 13.57 | 5.31 | 3.95 | −15.86 | 12.19 | 9.13 |
| 19 | 4.56 | −2.07 | 2.12 | −3.33 | 14.98 | 4.55 | 3.64 | −14.78 | 10.55 | 10.35 |
| 20 | 3.80 | −2.66 | 3.97 | −5.54 | 16.16 | 3.80 | 3.36 | −13.77 | 9.04 | 11.31 |
| 21 | 3.04 | −3.31 | 5.96 | −7.79 | 17.25 | 3.04 | 3.12 | −12.93 | 7.77 | 12.03 |
| 22 | 2.29 | −4.01 | 8.06 | −10.05 | 18.14 | 2.29 | 2.79 | −11.82 | 6.32 | 13.15 |
| 23 | 1.54 | −4.73 | 10.28 | −12.42 | 19.06 | 1.54 | 2.37 | −10.45 | 4.68 | 13.66 |
| 24 | 0.79 | −5.31 | 12.25 | −14.66 | 19.89 | 0.78 | 2.00 | −9.22 | 3.22 | 14.08 |
| 25 | 0.11 | −6.73 | 17.07 | −19.93 | 21.84 | 0.03 | 0.35 | −4.06 | −1.96 | 16.00 |
| Beam No | Ku | Ka | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EIA | EIA | |||||||||
| 1 | 18.16 | −0.0001 | 0.0023 | −0.0243 | −0.0576 | 18.16 | 0.0002 | −0.0072 | 0.0545 | −0.2377 |
| 2 | 17.41 | 0.0000 | 0.0011 | −0.0160 | −0.0694 | 17.4 | 0.0002 | −0.0072 | 0.0458 | −0.1950 |
| 3 | 16.64 | 0.0000 | 0.0002 | −0.0132 | −0.0550 | 16.64 | 0.0002 | −0.0062 | 0.0264 | −0.1137 |
| 4 | 15.89 | 0.0001 | −0.0013 | −0.0043 | −0.0476 | 15.88 | 0.0002 | −0.0054 | 0.0105 | −0.0432 |
| 5 | 15.13 | 0.0001 | −0.0017 | −0.0039 | −0.0363 | 15.13 | 0.0003 | −0.0071 | 0.0214 | −0.0561 |
| 6 | 14.38 | 0.0001 | −0.0029 | 0.0048 | −0.0437 | 14.37 | 0.0003 | −0.0073 | 0.0202 | −0.0352 |
| 7 | 13.62 | 0.0001 | −0.0043 | 0.0163 | −0.0650 | 13.61 | 0.0003 | −0.0085 | 0.0280 | −0.0408 |
| 8 | 12.86 | 0.0002 | −0.0047 | 0.0192 | −0.0664 | 12.86 | 0.0003 | −0.0090 | 0.0308 | −0.0351 |
| 9 | 12.1 | 0.0002 | −0.0056 | 0.0260 | −0.0751 | 12.1 | 0.0004 | −0.0103 | 0.0450 | −0.0640 |
| 10 | 11.35 | 0.0002 | −0.0066 | 0.0356 | −0.0916 | 11.35 | 0.0004 | −0.0116 | 0.0583 | −0.0891 |
| 11 | 10.59 | 0.0002 | −0.0061 | 0.0315 | −0.0780 | 10.59 | 0.0004 | −0.0134 | 0.0768 | −0.1253 |
| 12 | 9.84 | 0.0002 | −0.0068 | 0.0398 | −0.1047 | 9.84 | 0.0005 | −0.0155 | 0.0999 | −0.1827 |
| 13 | 9.08 | 0.0003 | −0.0086 | 0.0572 | −0.1425 | 9.08 | 0.0005 | −0.0152 | 0.0990 | −0.1842 |
| 14 | 8.33 | 0.0003 | −0.0088 | 0.0616 | −0.1510 | 8.33 | 0.0005 | −0.0161 | 0.1110 | −0.2023 |
| 15 | 7.57 | 0.0003 | −0.0111 | 0.0850 | −0.1987 | 7.57 | 0.0005 | −0.0152 | 0.1059 | −0.1826 |
| 16 | 6.82 | 0.0003 | −0.0108 | 0.0836 | −0.1942 | 6.82 | 0.0005 | −0.0170 | 0.1249 | −0.2141 |
| 17 | 6.06 | 0.0003 | −0.0109 | 0.0872 | −0.2043 | 6.06 | 0.0005 | −0.0165 | 0.1229 | −0.1963 |
| 18 | 5.31 | 0.0003 | −0.0105 | 0.0854 | −0.1900 | 5.31 | 0.0005 | −0.0163 | 0.1255 | −0.1987 |
| 19 | 4.56 | 0.0003 | −0.0091 | 0.0722 | −0.1562 | 4.55 | 0.0005 | −0.0148 | 0.1125 | −0.1371 |
| 20 | 3.8 | 0.0003 | −0.0079 | 0.0584 | −0.0945 | 3.8 | 0.0004 | −0.0127 | 0.0952 | −0.0876 |
| 21 | 3.04 | 0.0001 | −0.0040 | 0.0254 | −0.0119 | 3.04 | 0.0004 | −0.0131 | 0.1065 | −0.1298 |
| 22 | 2.29 | 0.0002 | −0.0087 | 0.0932 | −0.2913 | 2.29 | 0.0004 | −0.0143 | 0.1291 | −0.2344 |
| 23 | 1.54 | 0.0003 | −0.0091 | 0.0944 | −0.2678 | 1.54 | 0.0004 | −0.0148 | 0.1487 | −0.3375 |
| 24 | 0.79 | 0.0001 | −0.0053 | 0.0574 | −0.1468 | 0.78 | 0.0004 | −0.0147 | 0.1507 | −0.3238 |
| 25 | 0.11 | −0.0001 | 0.0045 | −0.0434 | 0.1710 | 0.03 | 0.0004 | −0.0141 | 0.1347 | −0.2774 |
| Beam No | EIA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 18.16 | −2.51 × 10−8 | 1.37 × 10−6 | −1.89 × 10−5 | −0.00013 | 0.00321 | 0.019326 | −0.38819 | 1.591838 |
| 2 | 17.41 | −3.03 × 10−8 | 1.88 × 10−6 | −3.86 × 10−5 | 0.000258 | −0.00098 | 0.042961 | −0.45597 | 1.628328 |
| 3 | 16.64 | −1.13 × 10−7 | 8.54 × 10−6 | −0.00026 | 0.004169 | −0.04013 | 0.263471 | −1.10123 | 2.343184 |
| 4 | 15.89 | −1.21 × 10−7 | 9.35 × 10−6 | −0.00029 | 0.004749 | −0.04628 | 0.298097 | −1.19719 | 2.406955 |
| 5 | 15.13 | −7.46 × 10−8 | 5.58 × 10−6 | −0.00017 | 0.002561 | −0.0242 | 0.169838 | −0.80344 | 1.891615 |
| 6 | 14.38 | −7.61 × 10−8 | 5.73 × 10−6 | −0.00017 | 0.002692 | −0.0255 | 0.174281 | −0.79615 | 1.810658 |
| 7 | 13.62 | −4.49 × 10−8 | 3.22 × 10−6 | −8.98 × 10−5 | 0.00127 | −0.01147 | 0.094093 | −0.54922 | 1.46773 |
| 8 | 12.86 | −5.94 × 10−8 | 4.41 × 10−6 | −0.00013 | 0.001983 | −0.01855 | 0.131392 | −0.64059 | 1.510883 |
| 9 | 12.1 | −4.93 × 10−8 | 3.60 × 10−6 | −0.0001 | 0.001547 | −0.01442 | 0.107759 | −0.56267 | 1.376621 |
| 10 | 11.35 | −3.84 × 10−8 | 2.83 × 10−6 | −8.28 × 10−5 | 0.001264 | −0.01231 | 0.097383 | −0.52466 | 1.287835 |
| 11 | 10.59 | −5.38 × 10−8 | 4.02 × 10−6 | −0.00012 | 0.001938 | −0.01902 | 0.133029 | −0.61068 | 1.328016 |
| 12 | 9.84 | −6.36 × 10−8 | 4.95 × 10−6 | −0.00016 | 0.002595 | −0.02585 | 0.170093 | −0.70143 | 1.37417 |
| 13 | 9.08 | −4.43 × 10−8 | 3.27 × 10−6 | −9.63 × 10−5 | 0.001497 | −0.01446 | 0.103187 | −0.49284 | 1.091061 |
| 14 | 8.33 | −2.86 × 10−8 | 2.02 × 10−6 | −5.61 × 10−5 | 0.000817 | −0.0079 | 0.065707 | −0.37112 | 0.906196 |
| 15 | 7.57 | −2.23 × 10−8 | 1.15 × 10−6 | −1.53 × 10−5 | −9.89E−05 | 0.00298 | −0.00386 | −0.14594 | 0.599584 |
| 16 | 6.82 | −7.29 × 10−8 | 4.99 × 10−6 | −0.00013 | 0.001829 | −0.0146 | 0.084527 | −0.36466 | 0.780318 |
| 17 | 6.06 | −8.53 × 10−8 | 6.10 × 10−6 | −0.00017 | 0.002612 | −0.02305 | 0.133651 | −0.49913 | 0.888727 |
| 18 | 5.31 | −1.31 × 10−7 | 9.80 × 10−6 | −0.0003 | 0.004725 | −0.04346 | 0.241628 | −0.77882 | 1.139603 |
| 19 | 4.56 | −2.51 × 10−7 | 1.94 × 10−5 | −0.00061 | 0.01013 | −0.09551 | 0.518007 | −1.50914 | 1.848456 |
| 20 | 3.8 | −2.91 × 10−7 | 2.16 × 10−5 | −0.00065 | 0.010106 | −0.08874 | 0.441954 | −1.16733 | 1.286324 |
| 21 | 3.04 | −4.20 × 10−7 | 3.08 × 10−5 | −0.0009 | 0.013482 | −0.10939 | 0.470893 | −0.95257 | 0.640136 |
| 22 | 2.29 | −1.11 × 10−8 | −1.13 × 10−5 | 0.000112 | −0.00337 | 0.048202 | −0.35222 | 1.258894 | −1.70139 |
| 23 | 1.54 | −3.55 × 10−7 | 2.67 × 10−5 | −0.00082 | 0.013007 | −0.11706 | 0.596926 | −1.60916 | 1.813668 |
| 24 | 0.79 | −1.29 × 10−7 | 8.34 × 10−5 | −0.0002 | 0.002153 | −0.00725 | −0.03711 | 0.326281 | −0.60025 |
| 25 | 0.11 | 2.79 × 10−7 | −2.34 × 10−5 | 0.000803 | −0.0144 | 0.144452 | −0.79752 | 2.20042 | −2.32417 |
| Beam No | EIA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 18.16 | 2.42 × 10−7 | −1.95 × 10−5 | 0.000630 | −0.010285 | 0.086533 | −0.327061 | 0.300739 | 1.182616 |
| 2 | 17.4 | 2.24 × 10−7 | −1.81 × 10−5 | 0.000584 | −0.009520 | 0.079453 | −0.290412 | 0.197955 | 1.253774 |
| 3 | 16.64 | 1.64 × 10−7 | −1.33 × 10−5 | 0.000430 | −0.006907 | 0.054482 | −0.155678 | −0.187766 | 1.661966 |
| 4 | 15.88 | 1.64 × 10−7 | −1.35 × 10−5 | 0.000440 | −0.007202 | 0.058886 | −0.190922 | −0.049940 | 1.412138 |
| 5 | 15.13 | 1.77 × 10−7 | −1.46 × 10−5 | 0.000483 | −0.008099 | 0.069775 | −0.266707 | 0.221679 | 0.986715 |
| 6 | 14.37 | 1.88 × 10−7 | −1.56 × 10−5 | 0.000520 | −0.008830 | 0.078501 | −0.327420 | 0.441136 | 0.634368 |
| 7 | 13.61 | 2.07 × 10−7 | −1.72 × 10−5 | 0.000577 | −0.009927 | 0.090532 | −0.402978 | 0.686282 | 0.284689 |
| 8 | 12.86 | 2.00 × 10−7 | −1.66 × 10−5 | 0.000560 | −0.009654 | 0.088519 | −0.398082 | 0.695758 | 0.208310 |
| 9 | 12.1 | 1.84 × 10−7 | −1.55 × 10−5 | 0.000527 | −0.009213 | 0.085757 | −0.394888 | 0.730148 | 0.078091 |
| 10 | 11.35 | 2.21 × 10−7 | −1.85 × 10−5 | 0.000628 | −0.010983 | 0.103633 | −0.497933 | 1.038398 | −0.317011 |
| 11 | 10.59 | 1.88 × 10−7 | −1.59 × 10−5 | 0.000545 | −0.009590 | 0.090552 | −0.430458 | 0.863195 | −0.171659 |
| 12 | 9.84 | 1.75 × 10−7 | −1.51 × 10−5 | 0.000530 | −0.009536 | 0.092273 | −0.453516 | 0.966268 | −0.354499 |
| 13 | 9.08 | 1.93 × 10−7 | −1.63 × 10−5 | 0.000558 | −0.009872 | 0.094156 | −0.458488 | 0.974761 | −0.398545 |
| 14 | 8.33 | 1.83 × 10−7 | −1.56 × 10−5 | 0.000540 | −0.009598 | 0.091517 | −0.442654 | 0.922165 | −0.358762 |
| 15 | 7.57 | 1.86 × 10−7 | −1.58 × 10−5 | 0.000540 | −0.009504 | 0.089661 | −0.428214 | 0.873555 | −0.330738 |
| 16 | 6.82 | 1.33 × 10−7 | −1.14 × 10−5 | 0.000390 | −0.006815 | 0.062436 | −0.274513 | 0.433755 | 0.121128 |
| 17 | 6.06 | 6.59 × 10−8 | −5.83 × 10−6 | 0.000203 | −0.003484 | 0.029146 | −0.091183 | −0.069137 | 0.611545 |
| 18 | 5.31 | −5.98 × 10−8 | 4.23 × 10−6 | −0.000126 | 0.002153 | −0.024887 | 0.192571 | −0.805417 | 1.298094 |
| 19 | 4.55 | −1.88 × 10−7 | 1.43 × 10−5 | −0.000445 | 0.007450 | −0.073550 | 0.434311 | −1.379665 | 1.725746 |
| 20 | 3.8 | −2.29 × 10−7 | 1.76 × 10−5 | −0.000545 | 0.008844 | −0.081123 | 0.420976 | −1.104958 | 1.037734 |
| 21 | 3.04 | −5.07 × 10−8 | 1.79 × 10−6 | 0.000033 | −0.002468 | 0.045852 | −0.391507 | 1.617923 | −2.622437 |
| 22 | 2.29 | −3.10 × 10−7 | 2.39 × 10−5 | −0.000747 | 0.012150 | −0.110696 | 0.558874 | −1.391901 | 1.206958 |
| 23 | 1.54 | 9.61 × 10−8 | −1.01 × 10−5 | 0.000419 | −0.008970 | 0.106483 | −0.701081 | 2.392505 | −3.269356 |
| 24 | 0.78 | −2.32 × 10−7 | 1.82 × 10−5 | −0.000592 | 0.010423 | −0.108244 | 0.664801 | −2.196144 | 2.936393 |
| 25 | 0.03 | 2.58 × 10−6 | −0.000205 | 0.006542 | −0.107272 | 0.958791 | −4.604580 | 11.119489 | −10.804452 |
Appendix B
| SST (C) | WS (m/s) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| −3 | NaN | 1.31 | 1.15 | 1.10 | 1.07 | 1.04 | 1.02 | 1.01 | 1.00 | 0.99 | 0.98 | 0.98 | 0.98 | 1.01 | 1.01 | 1.00 | 0.98 | 0.95 | 0.93 | 0.88 |
| −2 | NaN | 1.28 | 1.17 | 1.09 | 1.05 | 1.03 | 1.02 | 1.00 | 0.99 | 0.97 | 0.95 | 0.95 | 0.94 | 0.95 | 0.95 | 0.93 | 0.92 | 0.91 | 0.91 | 0.88 |
| −1 | NaN | 1.20 | 1.12 | 1.06 | 1.04 | 1.02 | 1.01 | 0.99 | 0.98 | 0.96 | 0.94 | 0.93 | 0.91 | 0.91 | 0.91 | 0.89 | 0.88 | 0.88 | 0.88 | 0.86 |
| 0 | 1.26 | 1.15 | 1.08 | 1.04 | 1.03 | 1.02 | 1.00 | 0.99 | 0.97 | 0.95 | 0.94 | 0.92 | 0.91 | 0.91 | 0.90 | 0.88 | 0.88 | 0.88 | 0.89 | 0.87 |
| 1 | 1.25 | 1.15 | 1.07 | 1.03 | 1.02 | 1.01 | 1.00 | 0.99 | 0.97 | 0.95 | 0.94 | 0.92 | 0.92 | 0.92 | 0.91 | 0.90 | 0.89 | 0.90 | 0.91 | 0.89 |
| 2 | 1.24 | 1.14 | 1.06 | 1.03 | 1.02 | 1.01 | 1.00 | 0.99 | 0.98 | 0.97 | 0.95 | 0.94 | 0.93 | 0.93 | 0.93 | 0.92 | 0.92 | 0.92 | 0.93 | 0.91 |
| 3 | 1.20 | 1.12 | 1.06 | 1.03 | 1.02 | 1.02 | 1.01 | 1.00 | 0.99 | 0.98 | 0.97 | 0.95 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.95 | 0.93 |
| 4 | 1.20 | 1.13 | 1.06 | 1.03 | 1.03 | 1.02 | 1.01 | 1.00 | 1.00 | 1.00 | 0.98 | 0.96 | 0.96 | 0.96 | 0.96 | 0.95 | 0.95 | 0.95 | 0.96 | 0.95 |
| 5 | 1.21 | 1.13 | 1.06 | 1.04 | 1.03 | 1.03 | 1.02 | 1.01 | 1.01 | 1.00 | 0.99 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.96 | 0.96 | 0.95 | 0.94 |
| 6 | 1.18 | 1.14 | 1.07 | 1.04 | 1.03 | 1.03 | 1.02 | 1.01 | 1.01 | 1.00 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.96 | 0.94 |
| 7 | 1.13 | 1.14 | 1.07 | 1.03 | 1.02 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.96 |
| 8 | 1.11 | 1.12 | 1.06 | 1.03 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.98 |
| 9 | 1.06 | 1.10 | 1.06 | 1.03 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 0.99 | 1.00 | 1.00 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 |
| 10 | 1.04 | 1.07 | 1.05 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.02 | 1.01 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 0.98 |
| 11 | 1.02 | 1.05 | 1.03 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.02 | 1.01 | 1.01 | 1.00 | 1.00 | 1.01 | 1.01 | 1.00 | 0.99 | 0.98 | 0.98 | 0.97 |
| 12 | 1.03 | 1.05 | 1.03 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.02 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 0.99 | 0.98 | 0.98 | 0.97 |
| 13 | 1.07 | 1.05 | 1.03 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 0.98 |
| 14 | 1.05 | 1.03 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 1.01 | 1.01 | 1.02 | 1.01 | 1.00 | 1.00 | 0.99 |
| 15 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 16 | 1.01 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.01 | 1.00 |
| 17 | 1.03 | 0.96 | 0.97 | 0.97 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 1.01 | 1.01 | 1.00 | 1.00 | 0.99 | 0.99 | 0.98 |
| 18 | 1.00 | 0.95 | 0.95 | 0.96 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 | 1.00 | 1.01 | 0.99 | 1.01 | 1.01 | 1.00 | 0.98 |
| 19 | 0.98 | 0.94 | 0.94 | 0.96 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 1.00 | 1.00 | 1.01 | 1.03 | 1.02 | 1.01 | 0.99 |
| 20 | 0.95 | 0.91 | 0.94 | 0.96 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 1.00 | 1.01 | 1.03 | 1.03 | 1.02 | 1.00 | 0.93 |
| 21 | 0.91 | 0.90 | 0.93 | 0.96 | 0.97 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.01 | 1.01 | 1.03 | 1.02 | 1.02 | 1.01 | 0.93 |
| 22 | 0.88 | 0.90 | 0.94 | 0.96 | 0.97 | 0.98 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 1.00 | 1.01 | 1.00 | 1.00 | 1.02 | 1.02 | 0.97 |
| 23 | 0.87 | 0.89 | 0.93 | 0.96 | 0.98 | 0.99 | 0.99 | 1.00 | 1.00 | 1.01 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 0.98 | 0.97 | 0.98 | 1.00 | 0.99 |
| 24 | 0.83 | 0.87 | 0.93 | 0.97 | 0.98 | 0.99 | 1.00 | 1.00 | 1.01 | 1.02 | 1.02 | 1.01 | 1.01 | 1.00 | 1.00 | 0.97 | 0.93 | 0.96 | 1.02 | 1.08 |
| 25 | 0.81 | 0.87 | 0.94 | 0.98 | 0.99 | 1.00 | 1.01 | 1.02 | 1.02 | 1.04 | 1.03 | 1.03 | 1.02 | 1.01 | 1.01 | 1.00 | 0.97 | 1.00 | 1.06 | 1.09 |
| 26 | 0.84 | 0.90 | 0.95 | 0.99 | 1.01 | 1.01 | 1.02 | 1.03 | 1.03 | 1.05 | 1.05 | 1.04 | 1.03 | 1.03 | 1.03 | 1.03 | 1.04 | 1.04 | 1.00 | 0.90 |
| 27 | 0.86 | 0.92 | 0.98 | 1.01 | 1.01 | 1.02 | 1.03 | 1.03 | 1.04 | 1.05 | 1.05 | 1.05 | 1.05 | 1.05 | 1.02 | 1.02 | 1.03 | 1.00 | 0.98 | 0.87 |
| 28 | 0.89 | 0.96 | 1.01 | 1.01 | 1.02 | 1.03 | 1.03 | 1.03 | 1.04 | 1.04 | 1.05 | 1.05 | 1.07 | 1.05 | 1.02 | 1.01 | 1.05 | 1.05 | 1.22 | NaN |
| 29 | 0.90 | 0.97 | 1.00 | 1.00 | 1.01 | 1.02 | 1.03 | 1.03 | 1.03 | 1.03 | 1.04 | 1.05 | 1.06 | 1.06 | 1.04 | 1.03 | 1.01 | 1.27 | NaN | NaN |
| 30 | 0.87 | 0.94 | 0.97 | 0.98 | 1.00 | 1.01 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.04 | 1.03 | 1.03 | 1.04 | 1.04 | 0.95 | NaN | NaN | NaN |
| 31 | 0.81 | 0.88 | 0.92 | 0.95 | 0.98 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 0.98 | 0.98 | 0.97 | 0.92 | 0.94 | 0.90 | 0.79 | NaN | NaN | NaN |
| 32 | 0.66 | 0.75 | 0.82 | 0.89 | 0.94 | 0.96 | 0.95 | 0.95 | 0.94 | 0.95 | 0.93 | 0.94 | 0.92 | 0.85 | 0.88 | NaN | NaN | NaN | NaN | NaN |
| 33 | 0.50 | 0.69 | 0.82 | 0.85 | 0.91 | 0.94 | 0.92 | 0.88 | 0.88 | 0.91 | 0.87 | 0.94 | 0.83 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 34 | 0.42 | 0.96 | 0.93 | 0.87 | 0.94 | 0.90 | 0.89 | 0.89 | 0.92 | 0.88 | 0.82 | 0.99 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| SST (C) | WS (m/s) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| −3 | NaN | 1.25 | 1.08 | 1.03 | 0.99 | 0.95 | 0.92 | 0.89 | 0.88 | 0.88 | 0.89 | 0.90 | 0.90 | 0.92 | 0.92 | 0.92 | 0.90 | 0.88 | 0.86 | 0.82 |
| −2 | NaN | 1.22 | 1.11 | 1.02 | 0.97 | 0.94 | 0.92 | 0.90 | 0.88 | 0.87 | 0.86 | 0.86 | 0.86 | 0.87 | 0.87 | 0.86 | 0.85 | 0.84 | 0.84 | 0.82 |
| −1 | NaN | 1.13 | 1.06 | 0.99 | 0.96 | 0.94 | 0.92 | 0.90 | 0.88 | 0.86 | 0.85 | 0.84 | 0.84 | 0.84 | 0.84 | 0.83 | 0.82 | 0.81 | 0.81 | 0.81 |
| 0 | 1.28 | 1.10 | 1.02 | 0.98 | 0.96 | 0.95 | 0.92 | 0.90 | 0.88 | 0.87 | 0.85 | 0.84 | 0.84 | 0.84 | 0.84 | 0.83 | 0.82 | 0.82 | 0.83 | 0.81 |
| 1 | 1.28 | 1.11 | 1.02 | 0.98 | 0.96 | 0.95 | 0.93 | 0.91 | 0.89 | 0.88 | 0.86 | 0.85 | 0.85 | 0.85 | 0.85 | 0.84 | 0.84 | 0.85 | 0.85 | 0.83 |
| 2 | 1.28 | 1.10 | 1.02 | 0.98 | 0.96 | 0.95 | 0.94 | 0.92 | 0.91 | 0.90 | 0.88 | 0.87 | 0.86 | 0.87 | 0.87 | 0.86 | 0.86 | 0.87 | 0.87 | 0.85 |
| 3 | 1.24 | 1.09 | 1.02 | 0.98 | 0.97 | 0.97 | 0.95 | 0.94 | 0.93 | 0.92 | 0.90 | 0.89 | 0.88 | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0.90 | 0.88 |
| 4 | 1.25 | 1.11 | 1.03 | 0.99 | 0.98 | 0.98 | 0.96 | 0.95 | 0.94 | 0.94 | 0.92 | 0.91 | 0.90 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.90 |
| 5 | 1.27 | 1.11 | 1.04 | 1.00 | 0.99 | 0.98 | 0.97 | 0.96 | 0.95 | 0.95 | 0.93 | 0.92 | 0.92 | 0.92 | 0.93 | 0.93 | 0.92 | 0.91 | 0.90 | 0.89 |
| 6 | 1.23 | 1.12 | 1.05 | 1.01 | 0.99 | 0.99 | 0.97 | 0.96 | 0.96 | 0.96 | 0.95 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.93 | 0.91 | 0.89 |
| 7 | 1.18 | 1.13 | 1.04 | 1.00 | 0.99 | 0.99 | 0.97 | 0.97 | 0.97 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.94 | 0.93 | 0.91 |
| 8 | 1.15 | 1.12 | 1.04 | 1.00 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.97 | 0.97 | 0.96 | 0.95 | 0.96 | 0.96 | 0.96 | 0.96 | 0.94 | 0.94 | 0.93 |
| 9 | 1.09 | 1.09 | 1.04 | 1.01 | 0.99 | 0.99 | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 | 0.96 | 0.96 | 0.96 | 0.97 | 0.97 | 0.96 | 0.96 | 0.96 | 0.94 |
| 10 | 1.06 | 1.06 | 1.03 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.98 | 0.97 | 0.97 | 0.97 | 0.98 | 0.98 | 0.97 | 0.96 | 0.97 | 0.94 |
| 11 | 1.05 | 1.05 | 1.03 | 1.00 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 0.99 | 0.98 | 0.98 | 0.99 | 0.99 | 0.98 | 0.97 | 0.96 | 0.95 | 0.94 |
| 12 | 1.08 | 1.05 | 1.03 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | 0.99 | 0.98 | 0.96 | 0.95 | 0.95 |
| 13 | 1.11 | 1.04 | 1.02 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 1.01 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.98 | 0.96 |
| 14 | 1.06 | 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.01 | 1.01 | 1.01 | 1.00 | 0.99 | 0.98 |
| 15 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 16 | 1.03 | 0.98 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| 17 | 1.05 | 0.96 | 0.97 | 0.98 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 1.00 | 1.02 | 1.02 | 1.02 | 1.02 | 1.01 | 1.00 | 0.99 |
| 18 | 1.04 | 0.95 | 0.95 | 0.97 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 1.00 | 1.02 | 1.02 | 1.02 | 1.04 | 1.04 | 1.01 | 0.98 |
| 19 | 1.01 | 0.93 | 0.95 | 0.97 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.01 | 1.02 | 1.04 | 1.07 | 1.06 | 1.02 | 0.99 |
| 20 | 0.97 | 0.91 | 0.95 | 0.97 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.03 | 1.04 | 1.06 | 1.07 | 1.05 | 1.02 | 0.95 |
| 21 | 0.92 | 0.90 | 0.95 | 0.98 | 0.99 | 1.00 | 1.00 | 1.01 | 1.02 | 1.02 | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.07 | 1.07 | 1.06 | 1.03 | 0.95 |
| 22 | 0.89 | 0.90 | 0.96 | 0.98 | 1.00 | 1.01 | 1.02 | 1.03 | 1.04 | 1.04 | 1.03 | 1.02 | 1.02 | 1.04 | 1.06 | 1.05 | 1.04 | 1.04 | 1.03 | 0.99 |
| 23 | 0.88 | 0.89 | 0.96 | 0.99 | 1.01 | 1.03 | 1.03 | 1.04 | 1.06 | 1.06 | 1.05 | 1.04 | 1.03 | 1.03 | 1.05 | 1.04 | 1.01 | 1.00 | 1.02 | 1.02 |
| 24 | 0.83 | 0.87 | 0.96 | 1.01 | 1.02 | 1.04 | 1.05 | 1.07 | 1.08 | 1.08 | 1.07 | 1.06 | 1.06 | 1.04 | 1.04 | 1.03 | 0.99 | 1.02 | 1.07 | 1.16 |
| 25 | 0.82 | 0.88 | 0.97 | 1.02 | 1.04 | 1.06 | 1.08 | 1.09 | 1.10 | 1.11 | 1.10 | 1.08 | 1.08 | 1.06 | 1.07 | 1.05 | 1.02 | 1.08 | 1.16 | 1.21 |
| 26 | 0.84 | 0.91 | 0.99 | 1.04 | 1.06 | 1.08 | 1.09 | 1.11 | 1.12 | 1.13 | 1.12 | 1.10 | 1.09 | 1.08 | 1.08 | 1.09 | 1.14 | 1.16 | 1.13 | 0.99 |
| 27 | 0.88 | 0.94 | 1.03 | 1.06 | 1.07 | 1.09 | 1.11 | 1.12 | 1.13 | 1.13 | 1.12 | 1.12 | 1.11 | 1.11 | 1.08 | 1.10 | 1.15 | 1.12 | 1.10 | 0.95 |
| 28 | 0.93 | 0.99 | 1.06 | 1.07 | 1.08 | 1.10 | 1.11 | 1.12 | 1.13 | 1.12 | 1.12 | 1.12 | 1.13 | 1.10 | 1.07 | 1.08 | 1.15 | 1.20 | 1.40 | 1.16 |
| 29 | 0.92 | 1.00 | 1.05 | 1.06 | 1.07 | 1.09 | 1.11 | 1.12 | 1.12 | 1.11 | 1.11 | 1.12 | 1.12 | 1.11 | 1.11 | 1.09 | 1.06 | 1.39 | NaN | NaN |
| 30 | 0.89 | 0.97 | 1.02 | 1.03 | 1.06 | 1.09 | 1.10 | 1.10 | 1.10 | 1.09 | 1.08 | 1.10 | 1.09 | 1.10 | 1.13 | 1.11 | 0.99 | NaN | NaN | NaN |
| 31 | 0.82 | 0.90 | 0.96 | 1.00 | 1.04 | 1.07 | 1.07 | 1.07 | 1.05 | 1.04 | 1.04 | 1.04 | 1.04 | 0.99 | 1.01 | 0.94 | 0.82 | NaN | NaN | NaN |
| 32 | 0.66 | 0.76 | 0.86 | 0.93 | 0.99 | 1.01 | 1.01 | 1.01 | 0.99 | 1.00 | 0.98 | 1.02 | 0.96 | 0.90 | 0.89 | NaN | NaN | NaN | NaN | NaN |
| 33 | 0.48 | 0.70 | 0.87 | 0.89 | 0.97 | 1.01 | 0.97 | 0.93 | 0.93 | 0.98 | 0.93 | 1.01 | 0.86 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 34 | 0.42 | 0.97 | 0.99 | 0.92 | 1.01 | 0.98 | 0.98 | 0.96 | 0.98 | 0.95 | 0.88 | 0.97 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
References
- Majurec, N.; Johnson, J.T.; Tanelli, S.; Durden, S.L. Comparison of Model Predictions with Measurements of Ku-and Ka-Band near-Nadir Normalized Radar Cross Sections of the Sea Surface from the Genesis and Rapid Intensification Processes Experiment. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5320–5332. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) Sensor Package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Gao, J.; Tang, G.; Hong, Y. Similarities and Improvements of GPM Dual-Frequency Precipitation Radar (DPR) upon TRMM Precipitation Radar (PR) in Global Precipitation Rate Estimation, Type Classification and Vertical Profiling. Remote Sens. 2017, 9, 1142. [Google Scholar] [CrossRef]
- Freilich, M.H.; Vanhoff, B.A. The Relationship between Winds, Surface Roughness, and Radar Backscatter at Low Incidence Angles from TRMM Precipitation Radar Measurements. J. Atmos. Ocean. Technol. 2003, 20, 549–562. [Google Scholar] [CrossRef]
- Jones, W.L.; Soisuvarn, S.; Park, J.; Adams, I.; Kasparis, T. Combined Active and Passive Microwave Sensing of Ocean Surface Wind Vector from TRMM. Ocean. ’02 MTS/IEEE 2002, 4, 1981–1986. [Google Scholar] [CrossRef]
- Soisuvarn, S.; Jones, W.L.; Kasparis, T. Combined Active and Passive Microwave Sensing of Ocean Surface Wind Vector from TRMM. Int. Geosci. Remote Sens. Symp. 2003, 2, 1257–1260. [Google Scholar] [CrossRef]
- Li, L.; Im, E.; Connor, L.N.; Chang, P.S. Retrieving Ocean Surface Wind Speed from the TRMM Precipitation Radar Measurements. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1271–1282. [Google Scholar] [CrossRef]
- Tran, N.; Chapron, B. Combined Wind Vector and Sea State Impact on Ocean Nadir-Viewing Ku- And C-Band Radar Cross-Sections. Sensors 2006, 6, 193–207. [Google Scholar] [CrossRef]
- Tran, N.; Chapron, B.; Vandemark, D. Effect of Long Waves on Ku-Band Ocean Radar Backscatter at Low Incidence Angles Using TRMM and Altimeter Data. IEEE Geosci. Remote Sens. Lett. 2007, 4, 542–546. [Google Scholar] [CrossRef]
- Chu, X.; He, Y.; Karaev, V.Y. Relationships between Ku-Band Radar Backscatter and Integrated Wind and Wave Parameters at Low Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4599–4609. [Google Scholar] [CrossRef]
- Chu, X.; He, Y.; Chen, G. Asymmetry and Anisotropy of Microwave Backscatter at Low Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4014–4024. [Google Scholar] [CrossRef]
- Tanelli, S.; Durden, S.L.; Im, E. Simultaneous Measurements of Ku- and Ka-Band Sea Surface Cross Sections by an Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2006, 3, 359–363. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, J.; Fan, C.; Meng, J. Analysis of Ku- and Ka-Band Sea Surface Backscattering Characteristics at Low-Incidence Angles Based on the GPM Dual-Frequency Precipitation Radar Measurements. Remote Sens. 2019, 11, 754. [Google Scholar] [CrossRef]
- Nouguier, F.; Mouche, A.; Rascle, N.; Chapron, B.; Vandemark, D. Analysis of Dual-Frequency Ocean Backscatter Measurements at Ku-and Ka-Bands Using Near-Nadir Incidence GPM Radar Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1310–1314. [Google Scholar] [CrossRef]
- Iguchi, T. Dual-Frequency Precipitation Radar (DPR) on the Global Precipitation Measurement (GPM) Mission’s Core Observatory. In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 1, pp. 183–192. [Google Scholar] [CrossRef]
- Wang, Z.; Stoffelen, A.; Fois, F.; Verhoef, A.; Zhao, C.; Lin, M.; Chen, G. SST Dependence of Ku-and C-Band Backscatter Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2135–2146. [Google Scholar] [CrossRef]
- Systems, R.S.; Rosa, S.; Corporation, T.A.; Angeles, L.; Systems, S.; County, B.; City, S.L. The Status of the Tropical Rainfall Measuring Mission (TRMM) after Two Years in Orbit. J. Appl. Meteorol. 2000, 39, 1965–1982. [Google Scholar]
- Wentz, F.J.; Draper, D. On-Orbit Absolute Calibration of the Global Precipitation Measurement Microwave Imager. J. Atmos. Ocean. Technol. 2016, 33, 1393–1412. [Google Scholar] [CrossRef]
- Wentz, F.J.; Meissner, T.; Scott, J.; Hilburn, K.A. Remote Sensing Systems GPM GMI Daily Environmental Suite on 0.25 Deg Grid, Version 8.2, [2019]. Remote Sensing Systems, Santa Rosa, CA, USA. Available online: www.remss.com/missions/gmi (accessed on 15 January 2021).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Tran, N.; Vandemark, D.; Ruf, C.S.; Chapron, B. The Dependence of Nadir Ocean Surface Emissivity on Wind Vector as Measured with Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2002, 40, 515–523. [Google Scholar] [CrossRef]
- Vandemark, D.; Chapron, B.; Feng, H.; Mouche, A. Sea Surface Reflectivity Variation with Ocean Temperature at Ka-Band Observed Using Near-Nadir Satellite Radar Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 510–514. [Google Scholar] [CrossRef]
- Schroeder, L.C.; Boggs, D.H.; Dome, G.; Halberstam, I.M.; Jones, W.L.; Pierson, W.J.; Wentz, F.J. The Relationship between Wind Vector and Normalized Radar Cross Section Used to Derive SEASAT-A Satellite Scatterometer Winds. J. Geophys. Res. 1982, 87, 3318. [Google Scholar] [CrossRef]
- Yueh, S.H.; Kwok, R.; Nghiem, S.V. Polarimetric Scattering and Emission Properties of Targets with Reflection Symmetry. Radio Sci. 1994, 29, 1409–1420. [Google Scholar] [CrossRef]
- Mouche, A.; Kudryavstev, V.; Hauser, D.; Caudal, G.; Chapron, B. Use of Dual Polarization Radar Measurements to Understand the Azimuth Behavior of the Sea Surface Baekscattered Signal. Int. Geosci. Remote Sens. Symp. 2006, 1867–1870. [Google Scholar] [CrossRef]
- Lin, W.; Portabella, M.; Stoffelen, A.; Verhoef, A.; Wang, Z. Validation of the NSCAT-5 Geophysical Model Function for Scatsat-1 Wind Scatterometer. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3196–3199. [Google Scholar]
- Hossan, A.; Jacob, M.; Jones, L. Ocean Vector Wind Retrievals from TRMM Using a Novel Combined Active/Passive Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5569–5579. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Vandemark, D.; Gourrion, J.; Chapron, B. Estimation of Wind Stress Using Dual-Frequency TOPEX Data. J. Geophys. Res. Ocean. 1998, 103, 25101–25108. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossan, A.; Jones, W.L. Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data. Remote Sens. 2021, 13, 1569. https://doi.org/10.3390/rs13081569
Hossan A, Jones WL. Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data. Remote Sensing. 2021; 13(8):1569. https://doi.org/10.3390/rs13081569
Chicago/Turabian StyleHossan, Alamgir, and William Linwood Jones. 2021. "Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data" Remote Sensing 13, no. 8: 1569. https://doi.org/10.3390/rs13081569
APA StyleHossan, A., & Jones, W. L. (2021). Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data. Remote Sensing, 13(8), 1569. https://doi.org/10.3390/rs13081569