Abstract
Marine oil spills are one of the most serious problems of marine environmental pollution. Hyperspectral remote sensing has been proven to be an effective tool for monitoring marine oil spills. To make full use of spectral and spatial features, this study proposes a spectral-spatial features integrated network (SSFIN) and applies it for hyperspectral detection of a marine oil spill. Specifically, 1-D and 2-D convolutional neural network (CNN) models have been employed for the extraction of the spectral and spatial features, respectively. During the stage of spatial feature extraction, three consecutive convolution layers are concatenated to achieve the fusion of multilevel spatial features. Next, the extracted spectral and spatial features are concatenated and fed to the fully connected layer so as to obtain the joint spectral-spatial features. In addition, L2 regularization is applied to the convolution layer to prevent overfitting, and dropout operation is employed to the full connection layer to improve the network performance. The effectiveness of the method proposed here has firstly been verified on the Pavia University dataset with competitive classification experimental results. Eventually, the experimental results upon oil spill datasets demonstrate the strong capacity of oil spill detection by this method, which can effectively distinguish thick oil film, thin oil film, and seawater.
1. Introduction
With the frequent activities of offshore oil exploitation and maritime transportation, the risk of marine oil spill accidents also increases. Marine oil spill pollution not only destroys the balance of the marine ecosystem, but also causes enormous economic losses to the surrounding sea countries and poses a serious threat to the health of nearby residents [1,2,3]. Therefore, it is of critical importance to rapidly acquire oil spill information for emergency decision making and accident disposal.
Remote sensing plays an important role in oil spill monitoring as one of the most effective technical means. Compared with other sensors, hyperspectral remote sensing has great potential in oil spill detection due to its high spectral and spatial capacity [4]. However, with the increase of the dimensionality of the hyperspectral image, it has some limitations, such as the data storage, high correlation among bands, and the decrease of classification accuracy and efficiency [5]. Traditional hyperspectral classification methods, such as extreme learning machine (ELM) [6], support vector machine (SVM) [7], and random forest (RF) [8], etc., operate mostly based on spectral features of hyperspectral images, which are prone to the curse of dimensionality, and it is difficult to obtain ideal detection results. For this reason, reducing the data dimension and extracting the feature information accurately are helpful to improve the classification accuracy.
Hyperspectral images have already become an important means [9,10,11] to detect marine oil spills from the sea background by virtue of its superior performance such as distinguishing fake targets [1] and identifying oil types [12]. The previous methods for oil spill detection from hyperspectral images operate mainly based on hand-crafted features. As one of the most common algorithms for oil spill detection, the spectral index family typically includes fluorescence index (FI) [13], rotation absorption index (RAI) [13], hydrogen index (HI) [14], reflection of green (RG) [15], reflection of red (RR) [15], chlorophyll (CHL) [16], water absorption feature (WAF) [17], and colored dissolved organic matter (CDOM) [18]. To quantitatively evaluate the identification ability of the above spectral indexes, index separability [19] was proposed in 2018, with comparative experimental results indicating that FI, RAI, HI, RG, and RR are more suitable for detecting oil slicks with thicknesses of more than 200 microns, while CHL, WAF, and CDOM perform better in detecting oil slicks with thicknesses less than 0.3 microns. The reason for this can be roughly summarized as the fact that the former five spectral indexes are related to the thickness of oil slicks while the latter three indexes are important spectral indices of seawater. However, the identification results of these methods are easily interfered with by various factors, such as sun glint [19] and clouds [20]. Besides, the detection capability of a single spectral index cannot be expected to be too much due to limited information involved, while a simple combination of multiple spectral indexes may give rise to feature redundancy. Thus, it is necessary considering the elaborative portfolio optimization of spectral indexes so as to enhance detection capability. There are still other approaches in the detection of oil spilling. One typical measure is spectral information divergence [21], which is defined as the similarity between the spectrums of the test images and the spectrums of each category in the standard spectrum library. Another noteworthy method for rapid spill detection is be the decision tree algorithm operating based on the minimum noise fraction transform [22]. For the traditional methods such as those mentioned above, the classification accuracy largely depends on the manual extracted features, which is generally complicated and time-consuming. Besides, each classifier also has different performances with respect to various features or feature combinations.
The deep learning method is a promising tool to extract hierarchical features. It has promoted significant developments in image classification [23], natural language processing [24], target detection [25], and other fields. Meanwhile, it has been widely applied for classification of hyperspectral images. Currently, typical deep learning models include convolutional neural network (CNN) [23], stacked auto-encoding network (SAE) [26], and deep belief network (DBN) [27]. According to the types of extracted features, deep learning networks can be roughly divided into spectral-feature, spatial-feature, and spectral-spatial-feature networks [28]. As the typical representative of spectral-feature networks, 1-D CNN was firstly utilized by Hu et al. [29] for hyperspectral image classification. Due to the lack of labeled hyperspectral data, the CNN classification framework using pixel-pair features can effectively expand the training samples [30]. In addition, the active learning, combined with a special classifier (such as SVM), can iteratively select high-quality labeled samples to train the deep learning network [31]. However, utilization of spectral information alone is prone to misclassification, as hyperspectral images are susceptible to synonyms spectrum and mixed pixels. To address this shortcoming, introducing the spatial information into classification may result in a higher accuracy [32]. The most common practice is to firstly perform PCA dimension reduction, and then extract spatial features within each pixel neighborhood by 2-D CNN [33,34]. The hyperspectral data can be typically represented in the format of a 3-D cube, containing both spatial and spectral information. Thus, classification results using the two abovementioned types of information simultaneously would be better than that using only spatial or spectral information alone. In this context, 3-D CNN is proposed for extracting the deep spectral-spatial-combined features effectively without any pre- or post-processing steps [35]. Zhong et al. [36] designed an end-to-end spectral–spatial residual network (SSRN), employing spectral residual and spatial residual blocks to explore spectral and spatial representation from hyperspectral images, in order to extract potentially discriminative features for classification. However, there are still some shortcomings 3-D CNN [37,38,39], such as incomplete noise filtering, low computational efficiency, and insufficient surface smoothness, which limit its development. In order to reduce the computation while ensuring the classification accuracy, Chen et al. [40] developed a hyperspectral image classification method using SAE to extract joint spectral–spatial features. It is worth noting that inputs of the SAE network therein are one-dimensional, which leads to insufficient expression of spatial features. Considering the advantages of convolutional neural networks in extracting spatial features, some CNN-based networks such as spectral–spatial unified network [41] and spectral–spatial attention network [42] have been proposed during recent years to simultaneously learn spectral–spatial features [43,44,45]. These networks normally consist of two or more branches for fully extracting spectral and spatial information, thereby leading to relatively preferable classification accuracy.
Recent studies indicate that deep learning can be applicable to oil spill detection from hyperspectral images, due to its capacity to automatically extract discriminative features. Specially, some of deep learning models have already achieved superior detection results compared with traditional methods [46,47]. However, research on oil spill detection based on deep learning with hyperspectral images is still in its infancy. Most deep learning models typically focus on spectral-feature networks [48] or spatial-feature networks [49] solely. The rich spectral and spatial information of hyperspectral images has not been fully exploited, thereby leading to the potentiality of deep learning not sufficiently released.
Considering the superiorities of spectral–spatial-feature networks, this paper proposed a spectral–spatial features integrated network (SSFIN) for marine oil spill detection from hyperspectral images. Specifically, 1-D CNN and 2-D CNN models have been employed for the extraction of the spectral and spatial features, respectively. Section 2 introduces the hyperspectral data employed in this study and the proposed SSFIN approach for marine oil spill detection. Section 3 is devoted to the experimental results and comparative analysis to fully verify the effectiveness of SSFIN. Discussions are conducted in Section 4, and conclusions are summarized in Section 5.
2. Data and Methodology
2.1. Remote Sensing Datasets
2.1.1. Pavia University Dataset
Firstly, the public dataset employed in this article is gathered by the Reflective Optics System Imaging Spectrometer (ROSIS) sensor during a flight campaign over the city of Pavia, northern Italy, hereinafter to be referred as Pavia University dataset. The original data cover 115 spectral bands, with a wavelength range of 0.43~0.86 mm. After removing the seriously noise-contaminated bands, there are still 103 bands left. Besides, the spatial resolution is 1.3 m, and the image size is 610 × 340. There are 42,776 reference samples with labels, which contain information of 9 classes of land covers, such as trees, asphalt, bricks, meadows, etc. False-color image and ground-truth image of Pavia University are given in Figure 1.
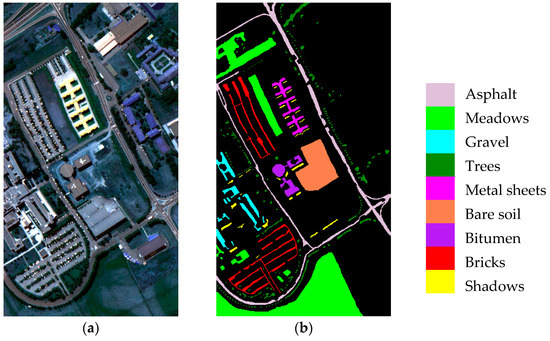
Figure 1.
Pavia University dataset. (a) False-color image and (b) ground-truth image.
2.1.2. Oil Spill Datasets
Dalian New Port is a modern deep-water oil port, located at the northeast foot of Dagu Mountain on the southern tip of Liaodong Peninsular and the southwest side of Dayao Bay on the coast of Yellow Sea. This Port covers the water area of 180 km2 and the land area of 1.57 km2. On 16 July 2010, a PetroChina pipeline caught fire and exploded near Dalian New Port, resulting in approximate 1500 tons of crude oil sent into the Yellow sea, and further, nearly 430 km2 of sea area polluted, including about 12 square kilometers of heavily contaminated area.
The experimental data obtained from the flight mission on 24 July 2010 for Dalian offshore oil spill monitoring are the airborne hyperspectral data acquired by the spectral imager sensor—AISA Eagle (made in Finland). After systematic geometric and radiometric correction, these data cover 258 spectral bands (2.4 nm, FWHM), with wavelengths ranging from 400 to 970 nm and a spatial resolution of 1.41 m. Due to the large amount of original image data, two rectangular areas are cropped out, sized 350 × 360 and 180 × 400, respectively. These two areas are named Dataset 1 and Dataset 2 accordingly. The image pixels are divided into three categories: thick oil film, thin oil film, and seawater. The false-color images and ground-truth images corresponding to the above two datasets are presented in Figure 2 and Figure 3.

Figure 2.
Oil spill dataset 1. (a) False-color image and (b) ground-truth image.
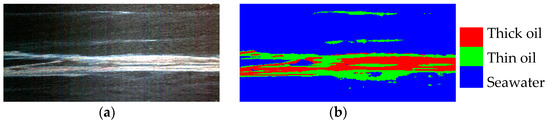
Figure 3.
Oil spill dataset 2. (a) False-color image and (b) ground-truth image.
2.2. Basic Framework of CNN
Convolutional neural network (CNN) is a multi-layer supervised learning neural network, which can simulate the process of human visual cognition [28]. In most cases, CNN is made by stacking an input layer, convolution layer, pooling layer, fully connected layer, and output layer [50]. Each layer is concatenated with the previous one, and the output of the previous layer serves as the input data for the next layer. The last output layer is essentially a classifier, which normally employs, for instance, logistic regression, softmax regression, or a support vector machine, to achieve the classification goal of input images. Weight parameters between the network layers are adjusted via backpropagation by means of the gradient descent method [51] to minimize the loss function, and the network precision is improved by repeated iterative training. The main components of CNN are the convolutional layer, the pooling layer, and the fully connected layer for achieving the function of feature extraction.
The convolutional layer is the most crucial components of the CNN architecture. Through the convolutional operation, feature extractions can be made from the target and some nonlinear relevance may get involved into the network by choosing appropriate activation function. If the lth layer is the convolution layer, then the formula for calculating the jth feature map of the lth layer is given as follows [41]:
where is the jth feature map in the (l − 1)th layer that connects to the feature map in the lth convolutional layer. is the convolutional kernel, is bias. ∗ denotes the convolutional operator. The nonlinear activation function here refers to the rectified linear unit (ReLU) [52].
Introduction of the pooling layer can effectively reduce the amount of input data and network parameters, as well as overfitting prevention to a certain extent. In addition, the pooling layer also contributes to improving the network adaptability in terms of robustness enhancement and retaining translation invariance of the features. Here we adopt the maximum pooling operation to reduce the feature maps in pooling layer.
The features obtained after convolution and pooling are normally the local features of the samples to be classified. It is generally impossible to achieve image classification by using only these local features. Therefore, these local features need to be weighed and combined together through the fully connected layer to produce the global features, and only the discriminant global features can be used as the reference basis for correct image classification.
2.3. Proposed Method
This paper proposed a novel spectral–spatial features integrated network (SSFIN) for pixel-based marine oil spill detection from hyperspectral images. The network framework mainly includes three parts: Data preprocessing, spectral and spatial features extraction, and spectral–spatial feature fusion and classification. The data preprocessing section mainly includes data normalization and dimensionality reduction via principal component analysis (PCA). The section of spectral and spatial features extraction includes two branches of CNN, utilizing information from the spectral and spatial domains, respectively. For spectral feature extraction, a spectral curve can be extracted corresponding to each pixel of the hyperspectral image, and 1-D CNN can be employed directly upon such a one-dimensional curve to further obtain the spectral features. For spatial feature extraction, the proposed 2-D CNN framework based on multi-feature fusion can be used to automatically extract spatially related high-level deep-seated features. Specifically, three consecutive convolution layers are concatenated to capture the combined multilevel spatial features. In the section of spectral–spatial feature fusion and classification, firstly, the joint spectral–spatial features are obtained by concatenating the spectral features with combined spatial features and further feeding them to the fully connected layer. Then, the classification can be achieved via the softmax classifier based on these joint features. Meanwhile, L2 regularization is applied to each convolution layer to prevent overfitting, and dropout operations are employed for the concatenated layer of spectral–spatial features and the subsequent fully connected layer to improve the classification performance. Figure 4 illustrates architecture of the proposed SSFIN method for oil detection.
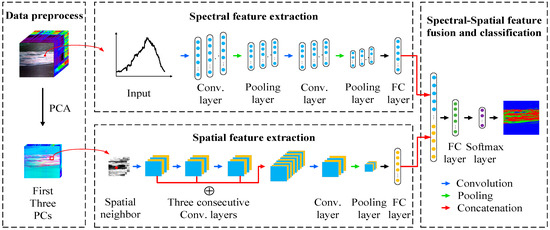
Figure 4.
Architecture of the proposed model for oil detection, where Conv. is the abbreviation of convolution and FC refers to fully connected.
The reason that 1-D CNN is adopted here to extract the spectral features is due to the full consideration of the existing difference in spectral characteristic of oil film and seawater. In 1-D CNN, the nth pixel, , is taken as the input data, followed by two convolutional operations and a maximum pooling operation. To be specific, the two convolutional layers are respectively composed of 20 and 40 convolution kernels of size 20, which are devoted to the automatic feature extraction of the input data. The two convolutional layers are followed by a pooling layer with a size of 3 pixels and a stride of 3 pixels, respectively. Output data after the second pooling layer are then stretched into a one-dimensional vector, and linked to a fully connected layer, which is the obtained spectral feature .
In this paper, 2-D CNN is employed to extract the spatial features. To reduce the redundancy of hyperspectral data, principal component analysis (PCA) is firstly utilized to reduce the dimensionality of hyperspectral oil spill data, and then a spatial neighborhood block (n is the number of central pixel) with the size of centered on each pixel was constructed and served as the input data of spatial feature extraction section. It is worth noting that three consecutive convolution layers are introduced here for feature extraction during the spatial convolution stage. Studies have indicated that a deeper structure and a small receptive field (such as a convolutional kernel with size of 3 × 3 pixels) normally yield better results [53].Therefore, the three consecutive convolution layers are composed of 40 convolution kernels with the size of 3 × 3 pixels, respectively. Meanwhile, the padding mode with default value of 0 is utilized in the convolution operation to maintain the dimensional consistency of input image and output image. To make full use of the shallow and deep features, three consecutive convolution layers are concatenated in sequence, which results in more feature channels. Therefore, channel dimension reduction can be performed by applying 1 × 1 convolution to the concatenated features so as to eliminate redundant features and reduce model parameters. To be specific, the concatenated features of 9 × 9 with 120 channels on convolution with 40 kernels of 1 × 1 would result in a size of 9 × 9 × 40. The 1 × 1 convolution acts as mathematically equivalent to the multilayer perceptron, enabling cross-channel interaction and information integration. Finally, a pooling layer with a size of 3 × 3 pixels and a stride of 3 pixels is adopted for spatial dimension reduction, and a fully connected layer is subsequently linked after the pooling layer to produce the spatial feature .
To acquire the joint spectral and spatial features, the spectral features and spatial features are merged into a vector and fed together into the fully connected layer. is given by
where and respectively represent the weight matrix and bias of the fully connected layer, denotes the concatenating operator, and is the ReLU activation function. can be deemed as the ultimate joint spectral-spatial feature linked to the softmax layer, to predict the prediction of probability distribution of each class. After completing the forward propagation as described above, the loss function is then calculated based on the predicted and true values. In this study, cross entropy [51] is employed as the loss function with its calculation formula as follows:
where N is the batch size, n denotes the number of neurons in the output layer, namely, the number of categories to be classified. y is the one-hot encoded vector of the labels, p is the predicted probability distribution given by the softmax function, and k indexes the set of classes.
Upon completing the design of the network model, the network parameters can be iteratively updated by the backpropagation (BP) algorithm. To improve the BP performance, the Adam optimizer [54] is further employed to update the parameters during the process of gradient descent. The Adam optimizer has the advantages of straightforward implementation, high computational efficiency, and low memory requirements. It uses momentum and an adaptive learning rate to accelerate the convergence rate, thereby quickly getting the predicted results. During the iterative training stage, the learning rate significantly affects the learning progress. An improper learning rate may lead to gradient dispersion or slow convergence. Besides, the ReLU activation function is applied to all convolution layers and fully connected layers. At the initial stage of network training, it is found that the training error is reduced while the verification error is high; that is, the phenomenon of overfitting appears. To prevent network overfitting and improve the generalization capability of the model, L2 regularization with a weight decay penalty of 1 × 10−4 [55,56,57] has been applied to each convolutional layer. Meanwhile, dropout operations have been adopted in the concatenated layer of spectral–spatial features and the subsequent fully connected layer [58], with the first dropout rate set to 0.25 and the second dropout rate set to 0.5. A more detailed parameter description of the designed SSFIN-based hyperspectral oil spill detection algorithm is shown in Table 1.

Table 1.
Detailed configuration of the proposed network structure.
3. Experimental Study
3.1. Data Partition
In all datasets, 10%, 10%, and 80% of the labeled data are randomly assigned to training, validation, and testing groups. The training group is used to optimize the model parameters. The validation group is built to evaluate whether the model has been sufficiently trained or over fitted, and the testing group aims to assess the performance of the trained model. To expand the training group and the verification group, the dataset is further enriched by up–down and left–right flipping. In addition, all input data of three HSI datasets are normalized by z-score standardization. Table 2, Table 3 and Table 4 list the sample numbers in the above training, validation, and testing groups.

Table 2.
Training, validation, and testing numbers in the Pavia University dataset.

Table 3.
Training, validation, and testing numbers in the dataset 1.

Table 4.
Training, validation, and testing numbers in the dataset 2.
3.2. Evaluation Metrics
In this study, the proposed architecture is evaluated according to overall accuracy (OA) [37], average accuracy (AA) [37], and Kappa coefficient [37], while the ultimate results are calculated by means of the mean and standard deviation of 10 training or testing experiments. Due to the large amount of data, this paper only refers to the precision, recall rate, and F1-score of the proposed SSFIN algorithm. Precision shows the proportion of correctly classified samples in each class. Recall rate represents the ratio between correctly classified pixels and the total pixels of each class. Concerning both of the two abovementioned indicators, the F1-score is actually the harmonic mean between precision and recall rate [59]. It is of particular importance for unbalanced classes.
Let TP, TN, FN, and FP denote the number of true positive, true negative, false negative, and false positive samples, respectively. Their formulas [59] are given as follows:
3.3. Experimental Scheme
To verify the effectiveness, the proposed algorithm has been compared with other common algorithms, which include SVM, RF, neural network (NN), and LetNet-5 [60]. In addition, the spectral feature extraction module and spatial feature extraction module of SSFIN algorithm are also verified, which are named SPE-CNN and SPA-CNN, respectively. All experiments are performed under the Python-based framework of TensorFlow and Keras. To investigate the performance difference of classification methods whether assisted by spatial information, two circumstances utilizing SVM are considered as follows. The first case is that SVM operates directly upon a hyperspectral image based on spectrum only, abbreviated as SVMHSI. Another case is that SVM operates upon a hyperspectral image together with spatial texture features generated by a gray-level co-occurrence matrix (GLCM). This classification method is named SVMHSI&GLCM hereafter. The new data of HSI&GLCM are constituted by the original hyperspectral image and GLCM-produced spatial feature layers. From each of the first three principal components by PCA, the spatial texture features can be further extracted, including mean, variance, correlation, contrast, energy, maximum probability, entropy, dissimilarity, homogeneity, and angular second moment. The type of SVM kernel function is selected as a radial basis function, and the regularization parameters are determined by 5-fold cross-validation. Random Forest operates for classification based on spectral features as well, and its parameter n_estimators is also determined by 5-fold cross-validation. To ensure the same number of test samples as SSFIN, both the experiments of SVM and Random Forest retain 20% randomly selected data for training and the rest of the data for testing. In other methods, the whole dataset is divided into the training group, validation group, and testing group by the ratio of 1:1:8. All experiments were run 10 times and the mean and standard deviation of main classification metrics were reported. The neural network model as a comparison method here consists of an input layer, two hidden layers, and an output layer. The number of neurons in the input layer is consistent to the number of bands in the original data. It has been set as 103 and 258, respectively, in regard to the number of neurons in the input layer for Pavia University and that of oil spill datasets. Both of the two hidden layers have been pre-configured by 64 neurons, and the dropout rates have been specified as 0.25 and 0.5 for the first and second hidden layers, respectively. The number of neurons in the output layer corresponds to the number of categories. For LetNet-5, the first three principal components are retained by PCA dimension reduction. Patch sizes of input images separated from the three datasets are fixed as 25 × 25, 9 × 9, and 9 × 9, respectively. Considering the neighborhood information absence at the image edges, a padding operation is employed for the convolutional layers.
3.4. Parameter Setting and Network Configuration
In the experiments, the basic learning rate and batch size are critical parameters in deep learning. Learning rate can significantly affect the training performance since inappropriate learning rate settings will lead to divergence or slow convergence. For the Pavia University dataset, the basic learning rate is set as 10−3 in accordance with other studies [61,62]. For oil spill datasets, we attempt different learning rates in our model from [10−5, 2 × 10−5, 3 × 10−5, 4 × 10−5, 5 × 10−5], and the optimal learning rate is set as 3 × 10−5 on the basis of the classification accuracy. Batch size refers to the number of training samples employed in each iteration during the training process. Its size significantly affects the speed of the model optimization by parallel processing of training samples to improve the memory utilization. Besides, the appropriate batch size would make the direction of gradient descent more accurate. In view of the size of training set and the GPU platform we used, the batch size is set as 60 for Pavia University dataset and 100 for oil spill datasets, respectively. Besides, the hyper-parameters of the Adam optimizer for these two experiments are the same as β1 = 0.9, β2 = 0.999, ε = 10−8 and the maximum iteration batch is set to be 100 epochs. For comparative classifiers, the learning rate, epoch, and batch size have been tuned elaborately to achieve their optimal classification performance. For clarity, these parameters are listed in Table 5. The experiments of this study are implemented in Keras, with an Intel i7-7700K 4.20-GHz processor with 16 GB of RAM and an NVIDIA GTX 1080Ti graphic card.

Table 5.
The learning rate, epoch, and batch size of neural network, LetNet-5, SPE-CNN, and SPA-CNN.
3.5. Experimental Results and Analysis
3.5.1. Experimental Results of Hyperspectral Classification
Table 6 reports the accuracies of all classes and the OAs, AAs, and Kappa coefficients for hyperspectral classification, and the best accuracy is shown in bold. Apparently, the proposed framework achieves the best classification performance among all considered methods in terms of OA, AA, and Kappa. From Table 6, classification accuracies of five classes reach 100% among the nine classes of land covers. This demonstrates that the proposed network has satisfactory capability of feature extraction and classification. Compared with the reference methods, this method has a smaller standard deviation, indicating that it has higher classification stability. Meanwhile, it can also be acquired from Table 6 that SPA-CNN performs better than SPE-CNN.

Table 6.
Classification results of different methods for the Pavia University dataset.
Figure 5 presents the visualization of the classification results from the optimal training model upon the dataset of Pavia University, as well as its corresponding ground truth. It can be seen from the figure that the classification map may appear as small patches instead of smoothness by using spectral features only, as it is greatly affected by noise. Instead, the addition of spatial features can significantly improve the unsmooth situations in the classification map. Meanwhile, the proposed method achieves relatively pure classification results from the perspective of visual effect in terms of the fewer misclassifications overall, which also proves the effectiveness of the algorithm.

Figure 5.
Hyperspectral image classification results of the Pavia University Dataset. (a) False-color image. (b) Ground truth. (c) RF. (d) SVMHSI. (e) SVMHSI&GLCM. (f) NN. (g) LetNet-5. (h) SPE-CNN. (i) SPA-CNN. (j) SSFIN.
3.5.2. Experimental Results of Hyperspectral Oil Spill Detection
Table 7 and Table 8 report the accuracies of all classes with the OAs, AAs, Kappa coefficients for hyperspectral oil spill detection classification. As shown in Table 7 and Table 8, the proposed method achieves the best classification results on both oil spill datasets compared with other classification methods. To be specific, experimental results of Dataset 1 show that the overall classification accuracy of SSFIN was 2.64%, 1.08%, 0.54%, 1.65%, 1.11%, 1.16%, and 0.10% higher than that of RF, SVMHSI, SVMHSI&GLCM, NN, LeNet-5, SPE-CNN, and SPA-CNN, respectively. In addition, SSFIN even achieved the highest classification accuracy and the lowest standard deviation of each category as indicated by the experimental results of Dataset 2. Although the proposed method has the best performance in the above experiments, the detection accuracy of thin oil films is still insufficient, compared with that of thick oil films. The classification results indicate that the information contained in the hyperspectral images can be fully mined by using the spectral–spatial information simultaneously, which can significantly improve the detection accuracy of oil spills, causing the classification results to have higher stability and reducing the false alarm rate. For RF and SVM classifiers, 20% of the training samples are adopted for training, and thus the accuracy of their classification results reaches a relatively high level. Especially for SVM, its OA is even higher than that of NN, Lenet-5, and SPE-CNN. It is notable that, for both oil spill datasets, the optimal detection results of SPA-CNN are more than 1% higher than that of LeNet-5 with the same training data, which proves the oil spill detection ability of the proposed multi-feature fusion spatial feature extraction algorithm.

Table 7.
Classification results of different methods for dataset 1.

Table 8.
Classification results of different methods for dataset 2.
Figure 6 and Figure 7 present the visualization of oil spill detection results from the optimal training model upon two oil spill datasets, as well as their corresponding ground truth. As shown in these figures, the method proposed here presents classification results of high purity from the perspective of visual effect. As expected, the oil spill detection results obtained by using spectral features alone, SVMHSI or SPE-CNN for instance, are more likely to be affected by noise such as sun light, resulting in misclassifications. For example, several speckled areas of seawater (blue) are misclassified as a thick oil film (red) in the lower right corner of Dataset1. After the addition of spatial information, the situation affected by noise can be greatly reduced. However, the over-smoothing phenomenon may occur, for instance the detected area at the edge of seawater (blue) within the region of the thin oil film (green) by SPA-CNN, as presented in Figure 7g. The proposed SSFIN algorithm, integrating both spectral information and spatial information, not only alleviates the occurrence of misclassification phenomenon caused by noise, but also improves the anti-noise ability and edge detection ability.
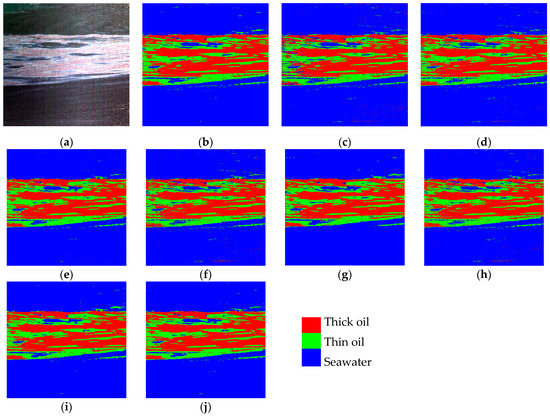
Figure 6.
Hyperspectral oil spill detection results of dataset 1. (a) False-color image. (b) Ground truth. (c) RF. (d) SVMHSI. (e) SVMHSI&GLCM. (f) NN. (g) LetNet-5. (h) SPE-CNN. (i) SPA-CNN. (j) SSFIN.
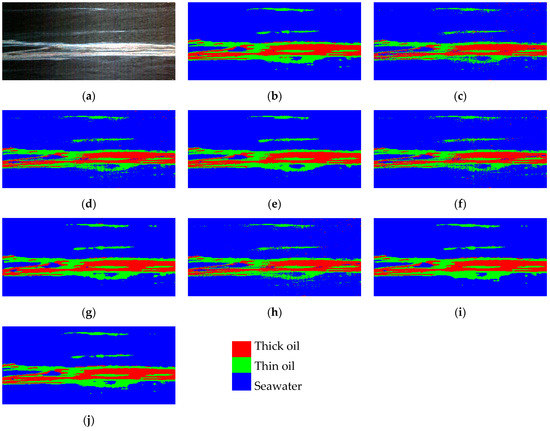
Figure 7.
Hyperspectral Oil Spill Detection Results of Dataset 2. (a) False-color image. (b) Ground truth. (c) RF. (d) SVMHSI. (e) SVMHSI&GLCM. (f) NN. (g) LetNet-5. (h) SPE-CNN. (i) SPA-CNN. (j) SSFIN.
Table 9 lists the precision, recall rate, and F1-score of each category, as well as the macro-averaged and weight-averaged quantities for the proposed model upon the oil spill datasets. As can be seen from the table, there are three indicators of the thin oil film on the low side, implying high probability of misclassification, which eventually indicates that the detection ability of the algorithm for the thin oil film needs to be further improved. Nevertheless, the superior precision, recall rate, and F1-score still indicate that the classifier is effective for hyperspectral oil spill detection.

Table 9.
The precision, recall, and F1-score for dataset 1 and dataset 2.
3.6. Analysis of Neighborhood Size
This paper has explored the impact of different neighborhood sizes on the classification results of hyperspectral oil spill detection and picks out the appropriate neighborhood size in terms of the classification accuracy. Considering the indistinct texture features of thick oil film and thin oil film, a smaller neighborhood was selected in the oil spill experiment for better distinguishing between each other. Specifically, neighborhoods of 7 × 7, 9 × 9, 11 × 11, 13 × 13, and 15 × 15 were employed in the oil spill datasets. Figure 8 and Figure 9 show the variation trend of the average classification accuracy of ten experiments under different neighborhood sizes.
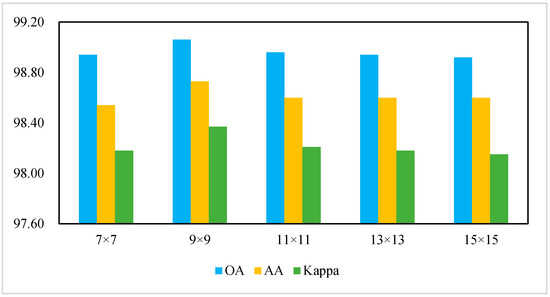
Figure 8.
Analysis of neighbor size on the classification performances of SSFIN for dataset 1 classification.
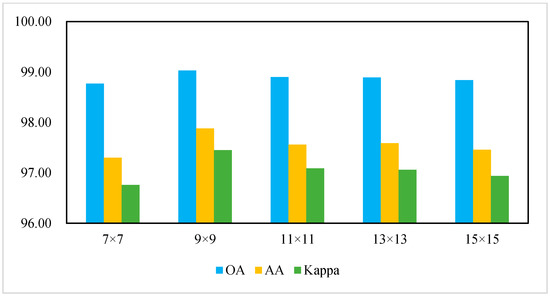
Figure 9.
Analysis of neighbor size on the classification performances of SSFIN for dataset 2 classification.
With the increase of neighborhood size, three precision evaluation indicators are firstly improved, and then become stable or decline slightly as shown in Figure 8 and Figure 9. However, generally speaking, the neighborhood size has a little effect on the classification accuracy, exhibiting a relatively stable trend. The classification accuracy reaches the highest level when the neighborhood size was 9 × 9 both for dataset 1 and dataset 2. The reason is because the proposed algorithm fully extracted the combined multilevel spatial features within the input neighborhood, thereby exerting superior classification performance without excessive addition of spatial information. Meanwhile, oversized neighborhoods usually consume more computing resources.
3.7. Time Cost
The training and testing time can be devoted to directly evaluating computational efficiency of the classification methods. To mitigate the impact of timing uncertainty, the calculating costs of different methods were recorded as the average time of ten experiments. Considering that all comparison methods are carried out on GPU except for random forest and SVM conducted on CPU, only the time costs of algorithms running on GPU are made as comparisons here, as presented in Table 10. From the table, all the algorithms can rapidly detect oil spills with less training time or testing time. It is worth noting that, in order to train the model adequately and avoid overfitting, the hyper-parameters in the compared experiments, such as epoch and batch size, may be different from that assigned in the proposed method, as listed in Table 5. However, when the hyper-parameters are consistent, taking the experiments conducted on dataset 1 and dataset 2 into consideration, the training time of SSFIN algorithm does not increase excessively compared with SPE-CNN, SPA-CNN. Although the data volume of SSFIN is the largest, it does not bring about serious computation burden. This demonstrates that the method proposed here has promising potential for rapid and accurate detection of hyperspectral oil spills.

Table 10.
Time cost of dataset 1, dataset 2, and Pavia University.
4. Discussion
Recent studies have shown that simultaneous use of spectral and spatial information can significantly improve the classification performance of hyperspectral images [36]. This point has also been confirmed by the experimental results of SPE-CNN, SPA-CNN, and SSFIN. To be specific, the spectral–spatial-feature network has the best classification effect among all the models no matter in terms of OA, AA, Kappa, or the classification accuracy of each class. Due to the influence of “same object different spectrum”, “same spectrum foreign body”, and Marine sunlight, the spectral curve contours of the oil spill, thin oil film, and thick oil film have slight differences, and the dividing line between them is not distinct enough. Using only spectral information for the classification is liable to cause misjudgment, resulting in low classification accuracy. Instead, the texture information of the oil spill and seawater exerts a significant difference and the boundary line between them is evident, judging from the oil spill RGB image. However, due to the influence of wind, wave, current, and other factors of the sea surface, thick oil films and thin oil films are often discontinuous and often mixed alternately, which affects the use of spatial information to a certain extent. Even so, it can be observed evidently from the experimental results that SPA-CNN achieves better classification accuracy than SPE-CNN. The reason can be roughly stated as follows. For SPA-CNN, vast majority of the spectral information has actually been retained by PCA in the first three principal components, whereas SPE-CNN operates only on the spectral dimension via 1D-CNN, without exploiting any spatial correlations. Nevertheless, it is worth emphasizing that the methods simultaneously employing spectral and spatial information would give better performance than that using only spatial information or spectral information, anyway.
The method proposed in this paper operates by integrating both spectral and spatial features of hyperspectral oil spill data, which can better reveal the inherent attribute information, so as to achieve high-precision detection of oil spill. Compared with other methods, this method has stronger anti-noise ability and edge detection ability, can effectively reduce the false alarm rate, and has higher oil spill detection accuracy. It is worth noting that due to the low complexity of oil spill data and the small number of categories, some models with deeper layers and more parameters are not suitable for oil spill detection, which not only increases the training burden, but also leads to low detection accuracy. The proposed model has the characteristics of fewer training parameters, strong robustness, and fast convergence, which provides a preferable classification model for remote sensing detection with difficulty in raising large amounts of samples.
In practical application, it is not clear whether deep learning is able to carry out high-precision oil spill detection under various complex sea conditions due to the complexity of the sea surface environment. There are still some shortcomings in the work of this paper. For example, the influences of solar flare on spectral curve and experimental results have not been taken into account, and the detection accuracy of thin oil film still needs to be further improved. All these topics will be future research focuses. As described previously, this paper has contributed to the feature-level fusion of images. Meanwhile, future research work can be devoted to the decision-level fusion between different models so as to further improve the accuracy and generalization performance of the model.
5. Conclusions
This study proposes a novel end-to-end deep learning network for hyperspectral detection of marine oil spill. The network consists of two branches of CNN extracting spectral and spatial features, respectively. During the stage of spatial feature extraction, the proposed method operates based on multi-feature fusion, which can extract rich target feature information by concatenating three consecutive convolution layers to simultaneously explore the shallow and deep features of the network. Further, the extracted spectral and spatial features are concatenated and fed to the fully connected layer so as to obtain the joint spectral-spatial features. Besides, to avoid over-fitting of the network, L2 regularization and dropout operation are also employed to improve the network performance. The effectiveness of the method proposed here has firstly been verified with competitive classification experimental results on the Pavia University dataset. Eventually, the experimental results of oil spill datasets demonstrate the strong capacity of oil spill detection by this method, which can effectively distinguish thick oil films, thin oil films, and seawater. This study provides a reference for the future application of deep learning in hyperspectral oil spill detection.
Author Contributions
Conceptualization, B.W., Q.S. and D.S.; methodology, B.W. and Q.S.; software, Q.S.; validation, B.W. and Q.S.; formal analysis, B.W. and D.S.; data curation, B.W. and Q.S.; writing—original draft preparation, B.W., Y.T., C.Y. and M.W.; writing—review and editing, B.W., Q.S., and Z.L.; project administration and funding acquisition, D.S., Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Key Program of Joint Fund of the National Natural Science Foundation of China and Shandong Province under Grant U1906217, in part by the Key Research and Development Program of Shandong province under Grant 2019GGX101033 and the National Key Research and Development Program of China under Grant 2017YFC1405603. Besides, this work was also supported by the National Science Foundation of China under Grant 41772350, Grant 41701513, 62071491 and Grant 61371189, and in part by the Fundamental Research Funds for the Central Universities under Grant 19CX05003A-8.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We gratefully appreciate the editor and anonymous reviewers for their efforts and constructive comments, which have greatly improved the technical quality and presentation of this study.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Leifer, I.; Lehr, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B.; et al. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef]
- Jha, M.N.; Levy, J.; Gao, Y. Advances in Remote Sensing for Oil Spill Disaster Management: State-of-the-Art Sensors Technology for Oil Spill Surveillance. Sensors 2008, 8, 236–255. [Google Scholar] [CrossRef]
- Fingas, M.; Brown, C.E. A Review of Oil Spill Remote Sensing. Sensors 2017, 18, 91. [Google Scholar] [CrossRef]
- Wettle, M.; Daniel, P.J.; Logan, G.A.; Thankappan, M. Assessing the effect of hydrocarbon oil type and thickness on a remote sensing signal: A sensitivity study based on the optical properties of two different oil types and the HYMAP and Quickbird sensors. Remote Sens. Environ. 2009, 113, 2000–2010. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, L.; Zhang, X. Three-dimensional convolutional neural network model for tree species classification using airborne hyperspectral images. Remote Sens. Environ. 2020, 247, 111938. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local Binary Patterns and Extreme Learning Machine for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Chen, T.; Lu, S. Subcategory-Aware Feature Selection and SVM Optimization for Automatic Aerial Image-Based Oil Spill Inspection. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5264–5273. [Google Scholar] [CrossRef]
- Tong, S.; Liu, X.; Chen, Q.; Zhang, Z.; Xie, G. Multi-Feature Based Ocean Oil Spill Detection for Polarimetric SAR Data Using Random Forest and the Self-Similarity Parameter. Remote Sens. 2019, 11, 451. [Google Scholar] [CrossRef]
- Chowdhury, N.U.; Sakla, A.A.; Alam, M.S. Oil spill detection in ocean environment via ultrasonic imaging and spectral fringe-adjusted joint transform correlation. Opt. Eng. 2013, 52, 3109. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Couvillion, B.R.; Holloway, J.M.; Roberts, S.A.; Ustin, S.L.; Peterson, S.H.; Khanna, S.; Piazza, S.C. Spectroscopic remote sensing of the distribution and persistence of oil from the Deepwater Horizon spill in Barataria Bay marshes. Remote Sens. Environ. 2013, 129, 210–230. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Leifer, I.; Livo, K.E.; Kokaly, R.; Hoefen, T.; Lundeen, S.; Eastwood, M.; Green, R.O.; Pearson, N.; et al. The Airborne Visible/Infrared Imaging Spectrometer(AVIRIS) Team. In A Method for Quantitative Mapping of Thick Oil Spills Using Imaging Spectroscopy; Technical Report; United States Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
- Yang, J.; Wan, J.; Ma, Y.; Zhang, J.; Hu, Y. Characterization analysis and identification of common marine oil spill types using hyperspectral remote sensing. Int. J. Remote Sens. 2020, 41, 7163–7185. [Google Scholar] [CrossRef]
- Loos, E.; Brown, L.; Borstad, G.; Mudge, T.; Alvare, M. Characterization of oil slicks at sea using remote sensing techniques. In Proceedings of the OCEANS, Yeosu, Korea, 14–19 October 2012. [Google Scholar]
- Kühn, F.; Oppermann, K.; Hoerig, B. Hydrocarbon Index–An algorithm for hyperspectral detection of hydrocarbons. Int. J. Remote Sens. 2004, 25, 2467–2473. [Google Scholar] [CrossRef]
- Sun, P. Study of prediction models for oil thickness based on spectral curve. Spectrosc. Spect. Anal. 2013, 33, 1881–1885. [Google Scholar]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll aalgorithms for oligotrophic oceans: A novel approach based on three–Band reflectance difference. J. Geophys. Res. Ocean 2012, 117. [Google Scholar] [CrossRef]
- Lu, W.; Yuan, H.; Xu, G. Modern Near Infrared Spectroscopy Analytical Technology; China Petrochemical Press: Beijing, China, 2007. [Google Scholar]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinarta, A.; Sobeka, S. Mapping lake CDOM by satellite remote sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Zhao, D.; Cheng, X.; Zhang, H.; Niu, Y.; Qi, Y.; Zhang, H. Evaluation of the Ability of Spectral Indices of Hydrocarbons and Seawater for Identifying Oil Slicks Utilizing Hyperspectral Images. Remote Sens. 2018, 10, 421. [Google Scholar] [CrossRef]
- Angelliaume, S.; Ceamanos, X.; Viallefont-Robinet, F.; Baque, R.; Deliot, P.; Miegebielle, V. Hyperspectral and Radar Airborne Imagery over Controlled Release of Oil at Sea. Sensors 2017, 17, 1772. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE T. Inform. Theory. 2000, 46, 1927–1932. [Google Scholar] [CrossRef]
- Liu, B.; Li, Y.; Chen, P.; Zhu, X. Extraction of Oil Spill Information Using Decision Tree Based Minimum Noise Fraction Transform. J. Indian Soc. Remote Sens. 2016, 44, 421–426. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent Trends in Deep Learning Based Natural Language Processing. IEEE Comput. Intell. M. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Girshick, R.B.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Li, W.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sensors 2015, 1–12. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Eom, K.B. Active Deep Learning for Classification of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 712–724. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Qin, J.; Zhang, P.; Tan, X. Deep Relation Network for Hyperspectral Image Few-Shot Classification. Remote Sens. 2020, 12, 923. [Google Scholar] [CrossRef]
- Fang, L.; Liu, Z.; Song, W. Deep Hashing Neural Networks for Hyperspectral Image Feature Extraction. IEEE Trans. Geosci. Remote Sens. Lett. 2019, 16, 1412–1416. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Seydgar, M.; Alizadeh Naeini, A.; Zhang, M.; Li, W.; Satari, M. 3-D Convolution-Recurrent Networks for Spectral-Spatial Classification of Hyperspectral Images. Remote Sens. 2019, 11, 883. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, Y.; Wang, D.; Luo, B. CSA-MSO3DCNN: Multiscale Octave 3D CNN with Channel and Spatial Attention for Hyperspectral Image Classification. Remote Sens. 2020, 12, 188. [Google Scholar] [CrossRef]
- Rao, M.; Tang, P.; Zhang, Z. A Developed Siamese CNN with 3D Adaptive Spatial-Spectral Pyramid Pooling for Hyperspectral Image Classification. Remote Sens. 2020, 12, 1964. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Du, B.; Zhang, F. Spectral–Spatial Unified Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5893–5909. [Google Scholar] [CrossRef]
- Mei, X.; Pan, E.; Ma, Y.; Dai, X.; Huang, J.; Fan, F.; Du, Q.; Zheng, H.; Ma, J. Spectral-Spatial Attention Networks for Hyperspectral Image Classification. Remote Sens. 2019, 11, 963. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Learning and Transferring Deep Joint Spectral–Spatial Features for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Feng, J.; Chen, J.; Liu, L.; Cao, X.; Zhang, X.; Jiao, L.; Yu, T. CNN-Based Multilayer Spatial–Spectral Feature Fusion and Sample Augmentation with Local and Nonlocal Constraints for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1299–1313. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, X.; Jia, X.; Ren, J.; Zhang, A.; Yao, Y.; Zhao, H. Deep Fusion of Localized Spectral Features and Multi-scale Spatial Features for Effective Classification of Hyperspectral Images. Int. J. App. Earth Obs. 2020, 91, 102157. [Google Scholar] [CrossRef]
- Liu, B.; Li, Y.; Li, G.; Liu, A. A Spectral Feature Based Convolutional Neural Network for Classification of Sea Surface Oil Spill. ISPRS Int. J. Geo Inf. 2019, 8, 160. [Google Scholar] [CrossRef]
- Zhu, X.; Li, Y.; Zhang, Q.; Liu, B. Oil Film Classification Using Deep Learning-Based Hyperspectral Remote Sensing Technology. ISPRS Int. J. Geo Inf. 2019, 8, 181. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schoenlieb, B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, L.; Xiao, C.; Qu, Y.; Zheng, K.; Marinoni, A. Hyperspectral Image Classification Based on a Shuffled Group Convolutional Neural Network with Transfer Learning. Remote Sens. 2020, 12, 1780. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Carranza-García, M.; García-Gutiérrez, J.; Riquelme, J.C. A Framework for Evaluating Land Use and Land Cover Classification Using Convolutional Neural Networks. Remote Sens. 2019, 11, 274. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Kinma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–13. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogram. Remote Sens. 2018, 145, 120–147. [Google Scholar]
- Song, D.; Zhen, Z.; Wang, B.; Li, X.; Gao, L.; Wang, N.; Xie, T.; Zhang, T. A Novel Marine Oil Spillage Identification Scheme Based on Convolution Neural Network Feature Extraction from Fully Polarimetric SAR Imagery. IEEE Access 2020, 8, 59801–59820. [Google Scholar] [CrossRef]
- Meng, Z.; Li, L.; Jiao, L.; Feng, Z.; Tang, X.; Liang, M. Fully Dense Multiscale Fusion Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 2718. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Gill, E.; Molinier, M. A new fully convolutional neural network for semantic segmentation of polarimetric SAR imagery in complex land cover ecosystem. ISPRS J. Photogram. 2019, 151, 223–236. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, J.; Zhang, L.; Tian, C.; Zhang, Y. Deep Cube-Pair Network for Hyperspectral Imagery Classification. Remote Sens. 2018, 10, 783. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3D-2D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote. Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).