Abstract
Many factors can influence the displacements of a dam, including water level variability and environmental temperatures, in addition to the dam composition. In this work, optical-based classification, thermal diachronic analysis, and a quasi-PS (Persistent Scatter) Interferometric SAR technique have been applied to determine both forcing factors and resulting displacements of the crest of the Castello dam (South Italy) over a one-year time period. The dataset includes Sentinel-1A images acquired in Interferometric Wide swath mode using the Terrain Observation with Progressive Scans SAR (TOPSAR); Landsat 8 Thermal Infrared Sensor (TIRS) thermal images, and Global Navigation Satellite System (GNSS) for interpreting the motion of the top of the dam retrieved via interferometry. Results suggest that it is possible to monitor both dam water level and temperature periodic forcing factors and resulting displacements via a synergistic use of different satellite images.
1. Introduction
The monitoring of dam displacements plays a crucial role in the detection of unsafe conditions, requiring appropriate management actions and/or counteractive measures from the early stages [1]. Indeed, the early detection of a dam instability should constitute a key component of any dam maintenance plan and could lead to structural stabilisation to prevent any initial warning from turning into a disaster [2].
Dam displacements can be due to several factors, including the consolidation of the embankment materials, the dam composition itself (including mineralogy, grain size, density of the compacted material, etc.), and forcing factors (including temperature, water level fluctuations, etc.).
Usually, concrete dams exhibit a nonlinear trend of the displacement related to thermal and hydrological loads [3], while irreversible displacements are assumed to behave linearly over time [4]. In these structures, indeed, the linear component of displacements is assumed to be the irreversible part of the displacements themselves, and the corresponding velocity is strongly connected to the stability of the structure [5] and is interpreted as the aging term. On the other hand, the oscillatory component of displacements is generally due to external seasonally varying forcing, such as thermal dilation and hydrostatic pressure (ibid.).
In this study, an earth dam is monitored since the structures of this type are the most frequent, although relatively small in size. Indeed, about 65% of the dams reported in the International Commission on Large Dams (ICOLD) World Register of [6] are earth dams, corresponding to the oldest type, followed by rock-filled dams (13%) and gravity dams (13%) (the full list of the acronyms used in the manuscript is reported in Appendix A, Table A1).
Although at the national scale of Italy, the monitoring of large dams is managed by Registro Italiano Dighe [7], a public body under the supervision of the Ministry of Infrastructure and Transport, at the regional scale (viz. Sicily), the monitoring of water reservoirs is the responsibility of the Osservatorio delle Acque office [8]. For Sicilian reservoirs, water storage data are available since 2010 with monthly frequency. However, for most of the dams, no information is available about dam deformations or displacements.
Dam structure can be monitored via traditional contact sensors (extensometers, accelerometers, tiltmeters); ground-based methods (ground-based SAR, ground-based photogrammetry, terrestrial laser scanning, robotic total stations); and global navigation satellite system (GNSS). Remotely based methods include airborne Laser Imaging Detection and Ranging (LiDAR) and space-borne InSAR. The pros and cons of these methods are summarised in [9].
More recently, Scaioni et al. [10] reviewed the available technologies for dam deformation monitoring, including geodetic and GNSS sensors for precise measurements at specific locations, remote sensors for areal deformation measurements, and integrated monitoring systems, data processing, and methods for deformation analyses.
The forcing factors include (i) reservoir water levels can be monitored in situ via traditional instruments including staff (head) gauges, water pressure measurement devices, stage encoders, ultrasonic devices, and electromagnetic gauges; (ii) the dam–reservoir system temperature can be monitored via thermo–hygrometers (air humidity and temperature) [11], noncontact infrared thermometers (target surface temperature), and fibre optic distributed temperature sensing (temperature distributions within the dam) [12].
For in situ water level observations over small reservoirs, these are discontinuously collected by several caretakers by means of staff gauges resulting in inhomogeneous time series (i.e., not accurate and subjective measures). Additionally, lack of information can occur for in situ temperature, as in situ monitoring stations require maintenance which sometimes does not follow the requested time scheduling. Regarding the dam displacements, these are rarely monitored in situ, as these activities are expensive and time demanding. In this framework, the dam structural surveillance can benefit from remote sensing techniques.
Over the last few years, it has been shown that optical satellite technologies are able to determine the variation of water level by quantifying the extent of the water surface [13,14,15]. Using the methods implemented for optical images, SAR images can also be employed to monitor the extent of the water surface [16]. Some authors [17] have quantified the water extent from COSMO-SkyMed (CSK) SAR images using an automatic classification procedure, including clumping and segmentation preprocessing. The authors highlighted that surface backscatter is influenced by local wind conditions reduced the classification performance. Indeed, the segmentation algorithm removed most of the pixels outside the reservoir even though some misclassified pixels were kept, but the subsequent clumping algorithm was not able to remove all pixels not classified as water within the water body. They concluded that the reservoir surface can be monitored accurately by discarding SAR images in which wind enhances surface roughness in relation to their intensity and direction. Despite limits related to wind conditions and surrounding morphology, SAR sensors allow also the detection of dam displacements by applying interferometric procedures [18,19,20,21,22].
Regarding temperatures, there are several sensors providing thermal data at adequate spatial resolutions, such as Landsat 8 (acquired at 100 m although resampled here to 30 m, [23]) and Sentinel 3 (SLSTR 0.75 km, suitable only for large reservoirs). For instance, applying a single-channel algorithm to Landsat 4, 5, and 8 thermal images can extend monitoring to the past (from 2018 back to 1984) to perform a lake surface temperature analysis [24].
The Landsat 8 satellite, for example, orbits the earth over the sunlit side of the earth in a sun-synchronous orbit, crossing every position on the earth’s land surface at least once every 16 days. Thermal images allow the capture at the same local time of the instantaneous brightness temperature of the water surface in clear sky conditions, allowing retrieval of any trend in surface water temperature. In the case of suddenly changing cloudiness conditions, the temperature that would characterise the water surface in absence of clouds might be estimated [25,26], thus enhancing the actual temporal resolution.
Nowadays, remote sensing SAR and thermal images are available over three decades (e.g., the Landsat 4 images from 1982 and the European Remote Sensing (ERS) satellite images from 1991), allowing the interpretation of the behaviour of any structure over long time periods.
According to [27], measuring displacements with traditional instruments (such as pendulums) are nominally more accurate than those estimated via GNSS techniques. However, the latter allows the identification of the displacements’ periodicity with denser observations. Barzaghi et al. [27] fitted an analytical model designed for describing deformations of buttress gravity dams [28] to time series of a pendulum and GNSS-estimated displacements of a dam structure, obtaining submillimetre standard deviation of residuals along the cross-crest direction (<0.88 mm for GNSS displacements, <0.37 mm for pendulum displacements).
Di Martire et al. [29] compared the displacements estimated via a Differential SAR (DInSAR) interferometry technique, the “coherent pixels” technique [30] with those recorded by a network of conventional ground-based sensors to monitor an earth dam. The authors pointed out the unique opportunity to perform extensive monitoring of the earth dam, including the embankment and the slopes surrounding the reservoir, with higher density and coverage than that provided by in situ sensors.
Recently, DInSAR and GNSS have been applied to monitor dam displacements. The deformation time series measured using GNSS techniques can reveal an uneven settlement of a dam (e.g., [31]), allowing also the analysis of the causes of deformations, including the water level change and the water–dam system temperature deemed as the main factors.
DInSAR techniques can be applied to detect subsurface anomalies including cavities due to seepage [32].
The rate of continuous nonlinear deformations of a dam over time caused by variable water levels and other forcing factors can be evaluated using a persistent scattering InSAR (PS–InSAR) technique [33]. Recently, the InSAR technique has been used for the analysis of the destabilisation process of the Mosul dam (Iraq) [34,35], using the Constellation of Small Satellites for Mediterranean Basin Observation (COSMO-SkyMed) and Sentinel-1A images. In this first study, the cumulative deformation of a dam using different SAR-sensors was mapped and two different deformation rates linked with on-site dam works were captured. In the following study, the authors took advantage of a deformation InSAR analysis together with numerical simulation modelling to shed new light on the ongoing subsidence process.
The discrimination between deformations and seasonal movements over a dam (the Plover Cove dam, Hong Kong, China) has been also discussed by [36] using PS–InSAR. This technique was originally introduced in 2001 [37]. PS–InSAR makes use of natural targets with high reflectivity over time to measure ground motions through a stack of SAR images (a review of PS–InSAR techniques is given by [38]). Some authors have shown the suitability of this method for dam monitoring [1,29,33,39]. Some limits of the PS–InSAR technique for dam monitoring are summarised in [9].
About the deformation monitoring analysis, the Small Baseline Subset (SBAS) technique based on the use of a large number of SAR acquisitions distributed with small baseline subsets can also be applied [40]. A multi-sensor full-resolution SBAS technique [41] can be used by jointly processing data acquired by compatible SAR sensors to monitor earth dams for long periods, thus showing displacements because of the consolidation process [42].
Finally, the integration of PSI and SBAS techniques allows monitoring of both linear and nonlinear ground displacements in mining structures after a collapse event occurred in the tailings of the Fundao dam in Brasil [43].
Sources of inaccuracies are both the baseline of a given interferogram, compared to the critical value [44,45], and the precision of the ephemeris (Copernicus Sentinels POD Data Hub) [46]. The baseline, indeed, controls the coherence of the interferogram, while the ephemeris accuracy, for instance, has an influence on the conversion of interferogram phases to absolute height require a relative baseline accuracy of 5 cm or even better [47].
The Castello dam was recently studied through in situ measurements, numerical models, and satellite techniques. A preliminary analysis [48] highlighted a significant correlation between water levels derived by optical remote sensing and displacements measured via the Global Navigation Satellite System (GNSS) over a short period (three months).
Thereafter, the GNSS displacements were compared with existing models implemented for concrete dams (including hydraulic models by De Sortis-Paoliani [28] and geotechnical Finite Element Method (FEM) [49]). The comparison between the modelled planimetric components of the displacements and GNSS data (over a time period of 2 years, between 2011 and 2013) appears to be satisfactory, with millimetric residuals [50]; in the same study, a comparison between the displacements measured by GNSS time series and traditional geodetic instruments (total station and spirit levelling), revealed a good agreement for both the vertical and the planimetric components. The advantage of using as reference a GNSS permanent station positioned relatively far from the dam (≈ 30 km away, at Agrigento) allowed the exclusion of any influence due to the site deformations.
More recently, the relationship between water levels and GNSS displacements measured in the midsection of the dam was analysed in [44] by processing a remote sensing dataset (including both optical and SAR images). Water levels can be indirectly determined by mapping the reservoir water surface extent using optical images [13,15,44]. Over the study area, two other approaches based on similarity indexes have also been proposed to retrieve the water levels using remote sensing datasets with different resolutions and under different conditions [45].
The present work aims to demonstrate the possibility of monitoring both the forcing factors and the resulting displacements of a dam via complementary remote sensing approaches and shows that these estimates are reliable if compared with both forcing factors and displacements measured by deploying onsite sensors.
In particular, the trustworthiness of the behaviour of the total displacements has been assessed by comparison with GNSS positioning data acquired on the crest dam during the same hydrological year. Remote sensing displacements were evaluated by employing an interferometric approach based on a quasi-PS–InSAR technique. A full graph Multi Baseline Connection (MBC) method and a nonlinear displacement trend model were selected according to [46].
2. Materials and Methods
2.1. Materials
2.1.1. Study Area
The Magazzolo reservoir (37°34′51″ N, 13°24′48″ E, World Geodetic System 1984, WGS84, European Petroleum Survey Group code: EPSG 4327) is located in Sicily (south Italy, Figure 1a). The reservoir water is used for civil purposes by a consortium of municipalities in the Province of Agrigento. Additionally, during summer, water is used for irrigation of agricultural plots in the Verdura, Magazzolo, and Platani rivers basins.
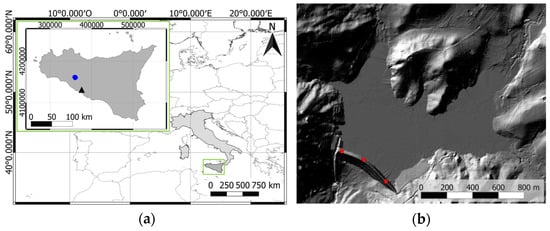
Figure 1.
The location of the study area (a) is Sicily island-Italy (dark and light grey, respectively), EPSG 4327; the upper left box reports a zoom of the island with the Agrigento permanent station (black triangle) and the Magazzolo reservoir (blue dot), EPSG 6708 and (b) hillshade of the dam–reservoir system derived from a digital surface model by setting azimuth and elevation of the incident light at 315 and 45 degrees, respectively). Superimposed the positions of the GNSS stations (red dots).
The dam (named Castello after the ruin of the castle “Castello della Pietra d’Amico” located near the left bank of the reservoir) has a semicircular shape (Figure 1b); it is built of coarse-grained homogeneous alluvium from the valley, and limestone and is covered by a sealed coat of bituminous conglomerate. The sealed coat stands on a reinforced concrete structure with a thickness of 80 cm fitted below the bulkhead in reinforced concrete. The dam, characterised by a concavity-facing valley, is 792 m long at the top, where a paved road connects the left and right sides of the dam. The two banks are characterised by different materials and different slopes. Indeed, due to the unstableness of the left side, a plate has been made with coarse-grained alluvial material, standing on a stone plinth. Thus, the left bank is characterised by a constant slope of 0.09, while on the right side, characterised by tinier material covered by spread vegetation, the values of slope span between 0.16 and 0.18. A vertical cross section of the maximum height has a trapezoidal shape, characterised by a 9 m width on the top and ≈ 214 m at the base; the valley side, covered with turf or vegetated soil, is constituted by a broken line interrupted by two quays of 2.5 m width and an elevation between 284 and 272 m a.s.l. with different slopes from the top to the bottom. Coarse-grained alluvial material is also used for the left side covering of the dam on the upstream side (Figure 1b).
2.1.2. Time Series Acquired by Devices Installed In Situ
In situ water level and air temperature measurements were supplied by the dam managing authority to support the analysis.
Water levels were measured with a staff head gauge level numbered every decimetre placed on the right bank, while air temperatures were measured via a thermo–hygrometer installed on a service area neighbouring the right bank.
A time series of GNSS displacements was measured using a permanent station (AGRI) operating 24 h a day at Agrigento (coordinates 4,131,320.31 N, 376,057.91 E; RDN2008 UTM Zone 33 N, EPSG code 6708). Although relatively far away (≈ 33 km), it was used as a base station to allow a reduction in economic costs. Similar to the setup described in [44], three receivers Geomax GPS Zenith 25 model (by GeoMax AG, Switzerland) were placed on the crest of the dam (Figure 1, panel b, red dots). Receivers were positioned on stainless steel pillars and fixed to the ground through steel plates (coordinates 4,160,249.76 N, 359,692.54 E; 4,160,208.79 N, 359,757.15 E and 4,160,159.71 N, 359,816.90 E). A power supply unit and a smartphone with an internet connection were placed in sealed boxes to transmit data in real time and continuously 24 h a day via File Transfer Protocol (FTP) using the XPAD Survey software (by GeoMax AG, Switzerland). The data transfer protocol allowed verification remotely on the correct functioning of the system. The monitoring campaign was carried out for a whole year with a 30 s postprocessing time step and hourly uploading frequency. According to the setup reported in [44], the Root-Mean-Square Errors of processed baselines are smaller than ~1.2, 2.4, and 1.0 mm (X, Y, and Z components, respectively), while the average percentage of resolved ambiguities is >90%.
2.1.3. Remote Time Series Acquisition
Remotely sensed datasets include Sentinel-1 SAR and surface temperature time series were derived by processing Landsat 8 TIR images on the Google Earth Engine environment (as discussed later on within the method section). Images acquired from the Sentinel-1 two-satellite constellations were processed to monitor both displacements and water levels; whereas Landsat 8 TIR images allowed the remote determination of the water surface temperature.
The Sentinel-1 SAR constellation is composed of Sentinel-1A (S1-A) and Sentinel-1B (S1-B) which share the same orbit plane with a 180° orbital phasing difference (near-polar sun-synchronous orbit). The so-called Interferometric Wide (IW) swath mode allows data acquisition with a 250 km swath with 5 m × 20 m ground resolution (single look) over three sub-swaths (IW1, IW2, and IW3 for increasing off-nadir angles, respectively) in the Terrain Observation with Progressive Scans SAR (TOPSAR) mode [47]. However, although S-1B was launched in April 2016, within this research, only S1-A images have been processed; thus, the SAR dataset includes 20 Sentinel TOPSAR S-1A images in Vertical transmit–Vertical receive (VV) polarisation acquired in Single Look Complex (SLC) mode in ascending, right-looking overpasses (relative orbit number 117, sub-swath IW2) (Figure 2, black box), and 17 in descending right-looking overpasses (relative orbit number 22, sub-swath IW1) (Figure 2, white box). The acquisition incidence angles were ≈ 39° and 34° for the ascending and descending images, respectively. The dataset is freely provided by the Copernicus Open Access Hub [51] (previously known as the Sentinel Scientific Data Hub). Although the dataset size is limited, the interferometric outcomes remain reliable according to Crosetto et al. [38]. Even if the use of X-band is more appropriate for datasets with limited image numerousness [52].
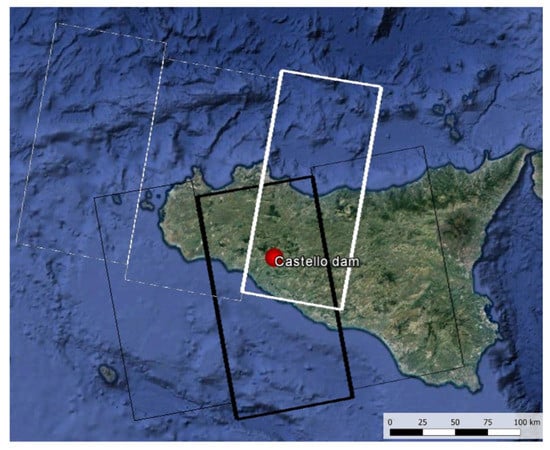
Figure 2.
The Terrain Observation with Progressive Scans SAR (TOPSAR) S-1A track over Google Earth: ascending orbit (relative orbit number 117, sub-swath IW2, thick black box) and descending orbit (relative orbit number 22, sub-swath IW1, thick white box). Other sub-swaths are represented with thin black and white lines (ascending and descending orbits, respectively). The position of the Castello dam is indicated (red dot).
Images acquired in both ascending and descending relative orbits span over a year (January 2015–January 2016) (Table 1). Most of the images were collected during the annual emptying phase of the reservoir (period 3; 17 images); during the storing phase (period 2), 10 images were available, whereas the smaller number of images were acquired during the filling phases (periods 1 and 4; three and seven images, respectively). The image acquired on 12 January 2016 was used only for the full-graph MBC method.

Table 1.
TOPSAR S-1A images.
The Land Surface Temperature (LST) time series was derived by averaging a number of points randomly distributed within the Magazzolo reservoir by processing several Landsat 8 Thermal Infrared Sensor (TIRS) images. In particular, 23 and 14 images were processed over the scene 189034 and 190034, respectively, spanning from 8 January 2015 to 26 December 2015. Just two images per month were available during the winter–spring periods from February to May 2015; three clean acquisitions per month were available in the winter period, specifically in January, November, and December; finally, four images per month were available over the Summer–Autumn periods, from June to October.
2.2. Methods
2.2.1. PS–InSAR Displacements
The dataset has been analysed using the SARProZ© software [49,53]. In the classical PS–InSAR technique, a target is required to be coherent in all interferograms generated with a star graph MBC [54]. A dam, as for many human-made structures, offers many artificial reflectors. For both ascending and descending datasets, a master image has been selected by minimizing the spatial and temporal decorrelations and is assumed as a reference for the estimation of a displacement time series of natural targets with ‘permanent’ radiometric characteristics over time. The full-graph MBC method introduces all possible connections amongst image pairs, thus using all interferograms, including those with longer temporal baseline than the ones eventually involved in the classical PS technique. The interferograms have been filtered with a Goldstein filter [55] with a fixed window size. As several interferograms were characterised by low coherence pixels, to maintain an accurate estimation of the displacements, the connections have been weighted by spatial coherence. According to [56] the temporal correlation over extra-urban areas should increase. Generally, the use of the full graph is more time demanding because it requires the analysis of n!/2(n − 2)! redundant connections (190 in this case). In addition, the size of the study area influences the processing time. In this work, the processed image is quite small (860 samples by 1120 lines), and thus, the computational time difference with the star graph is not significant. The Atmospheric Phase Screen (APS) is estimated through the inverted residuals approach [56,57], using the reflectivity map as a parameter for the sparse point selection. The method has been already applied to monitor dam via multi-temporal InSAR [39]. A threshold on the reflectivity (>1.8) excludes PS candidates falling on the reservoir surface. At the time of the data processing, external services, such as the Generic Atmospheric Correction Online Service for InSAR–GACOS [58,59,60,61,62] was not available. In this work, using the star graph MBC connections, the nonlinear displacements have been retrieved using a nonlinear model implemented [54] in the software. In this case, given the relatively few images comprising the time series (20 images for the ascending dataset and 11 images for the descending dataset), the window of the temporal filter has been set equal to three (images) [52]. In addition, weight in terms of spatial coherence (the mean interferometric coherence calculated as the average of a set of interferograms) has been applied during the processing involving the entire connections. The reference points in the ascending and descending tracks have a position almost coincident, close to the left bank of the dam in a stable area. The chosen area, indeed, does not show any kind of landslide risk according to the thematic geomorphological data [63] on the unstable areas of the Hydrogeological Plan (Piano per l’Assetto Idrogeologicom (PAI)). Dam displacements are evaluated by averaging the displacements of the selected PS points. As the direction of the retrieved displacement is only along the Line of Sight (LOS) of the sensor of the master image, the total horizontal displacement component orthogonal to the dam (DTOT) needs to be calculated [53,64] (a full list of the symbols used in the manuscript is listed in Appendix A, Table A2). Descending and ascending tracks overfly the study area on different dates; thus, it is required to interpolate the time displacements obtained using the descending tracks at the acquisition dates of the ascending tracks (as in the present case, and vice versa). Interpolated displacements then have to be composed [65,66] with those obtained by processing the other track (the descending track in this research) to obtain DTOT.
2.2.2. GNSS Displacements
In a previous study [44], it was shown that the accuracy achievable with GNSS is suitable to monitor the displacements of a dam. The same methodological scheme implemented in [44] was applied to obtain the GNSS solutions. Positions were referred to the European Terrestrial Reference System 2000 (ETRF2000) at epoch 2008. The Network Deformation Analysis (NDA) Professional software allowed applying the Saastamoinen tropospheric correction [67,68], the Klobuchar ionospheric correction [69], and the Schwiderski ocean loading correction [70]. A single baseline was used for connecting GNSS receivers with the permanent station. Double-differenced observations coming from the L5 (wide lane) and L3 (ionospheric-free) frequencies combination were used. To fix the phase ambiguity, the Least-Squares Ambiguity De-correlation Adjustment (LAMBDA) method was used [71]. In the final solution, the wide-lane observable was used to estimate the wide-lane ambiguity and then, the ionospheric-free observables to estimate the remaining narrow-lane ambiguity. All computational strategies are extensively discussed in Pipitone et al. 2018 [72]. Dam crest displacements were converted into a local reference system spatially averaged to focus the analysis to the whole dam displacements only (no to local deformations), and then, to show the tendency of the long-term displacements, a moving average was applied over a time window according to the findings of a previous study [17].
2.2.3. Water Levels
A preliminary multi-look processing [72] in the European Space Agency’s Sentinel Application Platform (SNAP) software allowed images to be processed to a 14 m ground resolution after calibrating the images by applying a terrain correction using the Shuttle Radar Topography Mission (SRTM) digital elevation model at 1 arc-second (≈30 m) spatial resolution (HGT format). Then, TOPSAR images were resampled to 28 m ground resolution, using the Pixel Aggregation method and classified. Then, the water surface extent was identified using a K-means unsupervised classification [73], using two classes and a threshold of 1% and the average distance of shoreline nodes extracted from vectorised classification images with the contour levels calculated in a GIS environment (QGIS Geographic Information System) [74]. According to Pipitone et al. [54], the contour level exhibiting the minimum distance from the classification boundary (best matching contour) allows quantification of the water level at the acquisition time.
2.2.4. Air and Water Surface Temperatures
On-site observations of the dam structure temperatures are not always available, and structure temperatures are closely related to air temperature [11]. Indeed, any change in the dam structure’s temperature is mainly affected by changes in external temperatures. External temperatures include air and water body temperatures. However, the distribution of the water temperature as a function of the depth is not constant; indeed, lakes are characterised by thermal stratification, as can be described by the thermal convection–diffusion equation [75]. Within this simplified approach, we monitor only the water surface temperature of the reservoir. Water surface temperature, TW (K), is here estimated by radiometrically processing a Landsat 8 TIRS time series. In particular, a time series of TW for the central pixel of the reservoir was retrieved by applying the Statistical Mono-Window (SMW) algorithm developed by the Climate Monitoring Satellite Application Facility (CM–SAF) [76]; in particular, the Google Earth Engine Open Source Code developed by Ermida et al. [77] was employed. Water surface temperature follows a sinusoidal behaviour, , which is a function of the yearly average of TW, (K); the yearly amplitude of TW, (K); the phase difference ≥ϕ (−); the time t, here assumed as the DOY; and the yearly angular velocity of revolution of the earth (1.7214 × 10−5 rad DOY−1). Thus, remotely sensed values were interpolated to facilitate the interpretation. Analogously, a sinusoidal curve was fitted to the measured air temperature TA (K) as well to make the interpretation easier.
2.2.5. Qualitative–Quantitative Comparisons
All of the above-mentioned variables measured via sensors installed in situ and via remote sensing were finally qualitatively and, where feasible, quantitatively compared. Firstly, in situ and remotely sensed pairs of water levels and temperatures and displacements are compared. Then, the temporal behaviour of the forcing factors and resulting displacements are analysed for both in situ and remotely sensed triplets (i.e., two forcing factors and one displacement). In particular, their behaviour is evaluated to quantify the times at which peaks and/or plateaus occur, besides analysing their range of variability.
3. Results and Discussions
In this section, the outcome of the monitoring of water levels, temperatures, and displacements through both in situ and remote sensing methods are shown; also results of the qualitative–quantitative comparison are presented.
3.1. Water Levels
During the first period (Figure 3), the water level was slightly raised until the end of January and then increased sharply to reach the maximum storage level in the last week of February (filling period). This level was kept constant until the end of May (storage period). During the third period, the reservoir was managed to satisfy the water demand, leading to a progressive almost linear decrease in the water level reaching its minimum in the middle of November (emptying period). During the fourth period, at the end of 2015, the rainy season allowed the stored water to reach a higher level than that observed at the beginning of the time series.
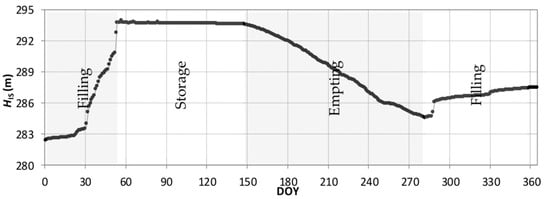
Figure 3.
Daily water levels measured in situ, HIS (m a.s.l.), from 1 January to 31 December 2015. A linear interpolation curve is superimposed–imposed (continuous line).
The water surface classification approach allowed the estimation of the water levels from remote sensing images (HRS) which show strong agreement with in situ (HIS) measurements (Figure 4). The accuracy of the procedure is confirmed by a very high coefficient of determination (r2 = 0.96, although imposing a null intercept) and a low Root-Mean-Square Error (RMSE ≈ 1.06 m). The standard deviation, σXY, between measured HIS and estimated HRS, is 3.32 m.
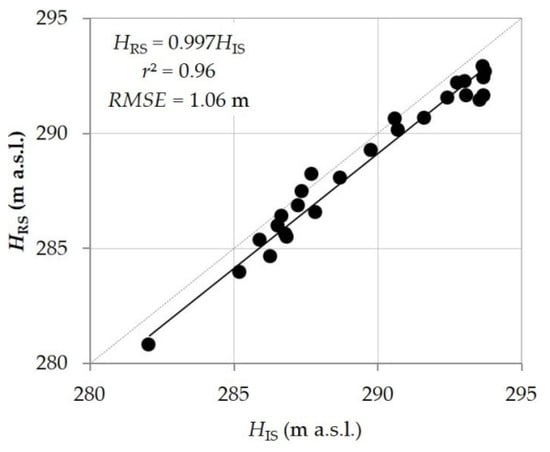
Figure 4.
Water levels measured in situ (HIS) versus levels obtained by classification (HRS) of TOPSAR ascending images.
3.2. Temperatures
3.2.1. Water Surface Temperature
The time series of water surface temperature was obtained by averaging the temperature over six points randomly distributed over the reservoir. The standard deviation was 0.42 K, on average. Since water surface temperature follows a sinusoidal behaviour [78], remotely sensed TW (black dots in Figure 5) were interpolated via a sinusoidal function (dashed line) to facilitate the interpretation of the phenomenon. A sinusoidal curve is well matched to the sparse temperature measurements (the Pearson correlation was ≈ 0.96, the Root-Mean-Square Error between measured and sine model was ≈ 1.70 K, which is coherent with the error in inferring surface temperature applying mono-window algorithms, ±2–3 K, as reported by [77]). The standard deviation, σXY, of the differences between measured and interpolated values was ≈ 1.64 K. The resulting amplitude ΔT in 2015 was 9.80 K, the average temperature was 293.16 K, and the peak (303 K) was modelled on DOY 217.
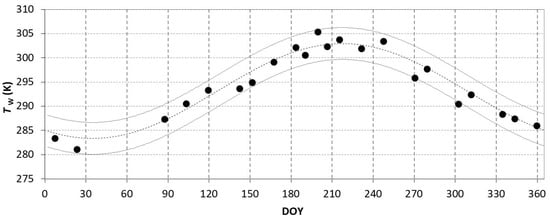
Figure 5.
The temporal behaviour of the water surface temperature, TW (K), retrieved by Landsat 8 data, using both 189-034 and 190-034 scenes. A sinusoidal interpolation curve (continuous dashed line) and a confidence band of ±2 × σXY between measured and interpolated values (dark grey lines) are reported to facilitate the interpretation of the phenomenon.
3.2.2. Air Temperature
Air temperature, TA (black dots in Figure 6), follows a similar sinusoidal behaviour. These values were interpolated to facilitate the interpretation of the phenomenon as well. The standard deviation, σXY, of the difference between measured and interpolated values was ≈ 2.12 K. The amplitude and the average temperature were 9.48 and 291.99 K, respectively. Finally, the peak (301 K) was modelled on DOY 215, which is almost exactly in phase with the water surface temperature.
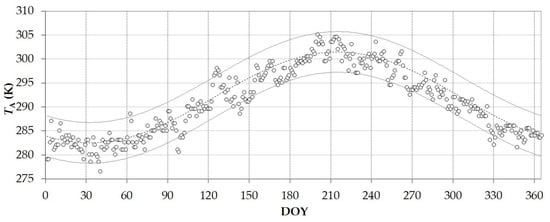
Figure 6.
The temporal behaviour of air temperature, TA (K), measured in situ. A sinusoidal interpolation curve (continuous dashed line) and a confidence band of ±2 × σXY between measured and interpolated values (dark grey lines) are reported to facilitate the interpretation of the phenomenon.
The sample covariance evaluated between the measured TA and remotely sensed TW was 47.84 K2, while the Pearson coefficient and the Root-Mean-Square Error were ≈0.95 and ≈2.28 K, respectively.
3.3. Displacements
3.3.1. PS–InSAR Displacements
Interferograms, filtered with a Goldstein filter with a fixed window size (15 × 15), were connected using the full-graph MBC method; thus, all possible connections between image pairs were considered (Figure 7). The full-graph MBC method produced both low and moderate-high coherence levels. Regarding the latter, six connections were characterised by coherences higher than 0.45, while 16 connections were characterised by coherences higher than 0.35. In order to obtain the maximum possible precision in interferometric processing, orbit parameterisation was based exclusively on the Precise Orbit Ephemerides (AUX_POEORB) provided by the Copernicus Sentinels POD Data Hub [46].
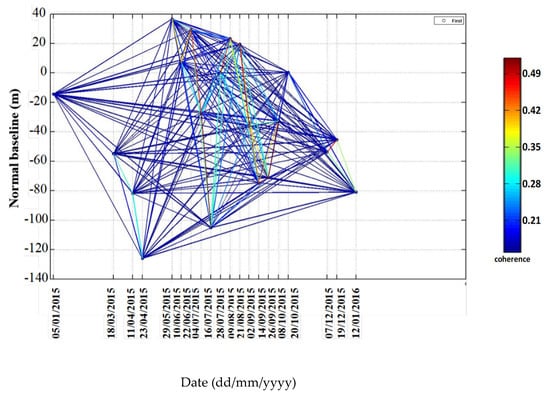
Figure 7.
Full-graph Multi-Baseline Construction (MBC) method: ascending dataset. Temporal-normal baselines are coloured using a rainbow scale according to the InSAR pair coherence.
Among connections with high coherence ~0.45, the pair 7–19 December 2015 shows the smallest normal baseline (~10 m), while the pair 22 June–16 July 2015 shows the highest normal baseline (~135 m), much smaller than the relevant critical baseline value, ~1300–1600 m, depending on descending or ascending acquisitions, respectively. However, according to Osmanoğlu et al. [79], baseline parameters were set smaller than 25% of the critical baselines. Since the acquisition of the 1 December 2016 is out of the study period, derived displacements were not compared to GNSS ones.
The interferograms of the two InSAR pairs having coherence higher than ~0.45 after applying the full-graph MBC method are shown (Figure 8, panel a). The water body pixels are characterised by low coherence, resulting in random phase differences. The x-axis represents the azimuth direction (in pixels), and the y-axis shows the range direction (in pixels).
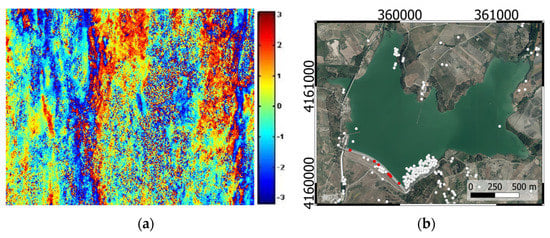
Figure 8.
Panel (a): interferogram generated (in slant geometry) using the full-graph MBC method: pair 22 June–16 July 2015, normal baseline ~135 m. The phase difference is represented between −π and +π using a rainbow colour ramp. Panel (b): High–quality Persistant Scatter (PS) obtained by processing the ascending dataset over-imposed an airborne orthophoto [80] (EPSG 6708) (red dots, selected PS on the dam to interpret the forcing–displacements phenomenon; white dots, remaining PS).
Many PS points are distributed over the dam and on the left bank with a high backscatter signal and a coherence higher than 0.7 (Figure 8, panel b). The full-graph MBC allowed them to be detected ≈ 540 PSs (displayed in red).
The objective of this research is to determine the dam displacements, not deformation, of the whole structure. PSs located over the DAM crest were then used for comparison with other data to interpret the forcing–displacements phenomenon. To this aim, displacements of selected PS over the dam have been spatially averaged to estimate a reference displacement of the dam. A one-month moving average was applied to highlight the trend of the displacement time series. The orthogonal displacements related to the water levels confirm a hysteresis-like loop during the emptying and filling periods of the dam (ibid.).
The use of the standard PS–InSAR technique (full-graph MBC method) leads to the LOS dam displacements (dLOS) reported in Figure 9. Due to the differences between the direction of the ascending and descending tracks with the direction orthogonal to the dam (43° and 23°, respectively), the relative contribution of the orbits to DTOT is greater for the ascending track than for the descending one.
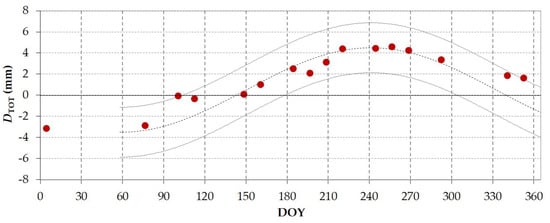
Figure 9.
The temporal behaviour (DOY in x-axis) of the horizontal total displacements orthogonal to the dam (DTOT, mm) is estimated via PS–InSAR (red dots). A sinusoidal interpolation curve (continuous dashed line) and a confidence band of ±2 × σXY between measured and interpolated values (dark grey lines) are reported to facilitate the interpretation of the phenomenon.
The temporal variability of DTOT in 2015 using a full graph MBC method (Figure 9, red dots) shows displacements increasing in the springer period to reach a platoon between DOYs 221 and 269. The standard deviation of the differences between measured and interpolated values was σXY ≈ 1.18 mm. The maximum value (≈4.5 mm) indicated by the sinusoidal fitting is on DOY 241.
3.3.2. GNSS Displacements
Daily displacements orthogonal to the dam crest were averaged by applying a one-month-long moving window, thus showing its tendency in the long term (Figure 10). After applying a temporal low pass filter, the monitored temporal range is shortened. The zero of the displacements is assumed as the first day of the time series (DOY 120). Displacements increased in the springtime period to reach a platoon between DOYs 197 and 247 (about 2.6 mm). The maximum indicated by the sinusoidal fitting is on DOY 219, which is almost in phase with air and water surface temperatures. The peak is shifted compared to that obtained via PS–InSAR (22 days), although both GNSS and PS–InSAR displacements behaviours are characterised by two plateaus that partially overlap (≈ DOYs 220–230). The standard deviation of the differences between measured and interpolated values was σXY ≈ 0.33 mm.
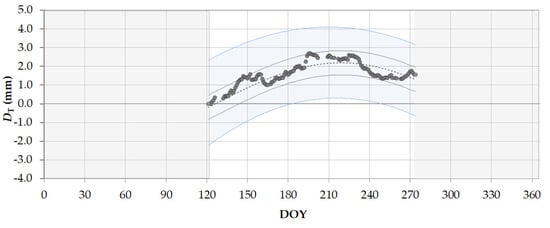
Figure 10.
The temporal behaviour (DOY in x-axis) of the horizontal total displacements orthogonal to the dam (DTOT, mm) is estimated via Global Navigation Satellite System (GNSS) (grey dots). A sinusoidal interpolation curve and confidence band of ±2 × σXY between measured and interpolated values (dark grey lines) are reported to facilitate the interpretation of the phenomenon (continuous line). The interpolation curves at the 10th and 90th percentiles of the raw data are reported (pale blue band) as a measure of its variability.
4. Conclusions
Previous work (e.g., [2,36,41]) highlighted the capability of satellite techniques for dam monitoring. This research aims to emphasise that comprehensive monitoring is achievable using satellite techniques. In particular, reliable displacements of their temporal behaviour were retrieved, in addition to the filling–emptying cycles of the water level and reservoir–dam system temperature.
The water surface extent was estimated by employing the same satellite dataset (SAR images) used for the interferometric processing. Results were estimated with very high accuracy (r2 = 0.97).
Water temperature time series was automatically retrieved by means of the Google Earth Engine platform processing all the clear sky Landsat 8 TIRS images available. Comparing time series of air temperature measured in situ and water temperatures estimated from thermal infrared remote sensing a strong agreement was shown both in terms of the range of variability (≈ 280–305 K) and phase shift (2 days).
A quasi PS–InSAR algorithm, using a full-graph MBC method and a nonlinear displacement trend model was applied to both ascending and descending SAR images. The composition of the slant displacements allowed the retrieval of the temporal evolution of total displacement orthogonal to the dam crest. The comparison with displacements measured via GNSS showed a relatively good agreement; indeed, both exhibit the same temporal behaviour, with plateaus at maximum partially overlapping (10 days).
The interpolation with a sinusoidal function for both GNSS and PS–InSAR measures allows a better description of the positive and negative displacements occurring during the filling, storage, and emptying phases.
GNSS and quasi-PS–InSAR time series exhibited comparable time behaviours. Although there was a time shift, both time series were characterised by a plateau. The plateaus were partially overlapping (≈10 days). Different MBC methods and interferometric models are planned to be tested to improve the matching between remote and in situ displacements.
However, these first outcomes suggest that a comprehensive remote sensing approach could represent a good complementary or alternative solution to monitor medium-small reservoirs, which often lack any adequate monitoring systems.
In order to confirm these preliminary results, it is necessary to plan a new in situ campaign spanning a longer time period in order to increase the number of observations while ensuring contemporaneity between the GNSS and PS–InSAR measurements. It is also necessary to evaluate the relationship of the displacements with thermal and hydrological forcing factors over a more consistent temporal time span, distinguishing between the emptying, storage, and filling periods over different years.
It is planned to complete the analysis using images acquired by the COSMO-SkyMed constellation, which have a higher spatial resolution (up to 1 m) and lower revisit time (e.g., up to 24 h using the full four satellite constellation), thus allowing more PS points to be obtained over the dam and covering the period over which GNSS measurements are currently available.
Additionally, the use of the Capella’s [81] high revisit SAR X-band 18 satellites constellation (36, once fully operational) will allow the production of interferometric images at the resolution down to 0.5 m and hourly revisit time, which looks promising.
Additionally, a higher revisit time for thermal images is expected by September 2021 with the launch of the Landsat 9 satellite-carrying onboard the Thermal Infrared Sensor 2 (TIRS-2), characterised by the same technology that was used for TIRS on Landsat 8.
Author Contributions
Conceptualisation, A.M. and C.P.; methodology, A.M., C.P., G.D., F.C., and J.-P.M.; validation, A.M., C.P., G.D., and F.C.; data curation, A.M., C.P., and G.D.; writing—review and editing, A.M., C.P., G.D., F.C., and J.-P.M.; supervision, J.-P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of meteorological data. Data were obtained from the dam management authority department and are available from the authors with the permission of the dam management authority department. Sentinel images can be found after registration at https://shihub.copernicus.eu/ (accessed on 29 March 2021). Landsat 8 TIRS data are available through the Google Earth Engine platform by requiring them at users/sofiaermida/landsat_smw_lst:modules/Landsat_LST.js. GNSS data from AGRI CORS are owned by the University of Palermo. The data from the Geomax receivers were released to the University after a scientific partnership agreement signed with the University of Palermo. GNSS data support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The software used in this work is SARProZ©, developed by D. Perissin. The authors are grateful to the developer also for his technical support. The authors would also like to thank the dam management authority for providing in situ water levels and air temperatures. The authors wish to thank the key contact people of the dam management authority department ‘Dipartimento dell’Acqua e dei Rifiuti-Assessorato Regionale all’Energia e ai Servizi di Pubblica Utilità’ of the Sicilian Regional Government. In particular, the authors would like to thank F. Greco, head of the dam during the investigation period; M. Alfonso and M. Gaglio for documentation provided; and F. Cairone, technical manager of the dam. J.-P.M. would like to acknowledge tthe support of the ESA-NRSCC DRAGON 4 programme for their support of work on InSAR.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The following acronyms (Table A1) are used in this manuscript:

Table A1.
Acronyms list.
Table A1.
Acronyms list.
| Acronym | Meaning |
|---|---|
| APS | Atmospheric Phase Screen |
| CM-SAF | Climate Monitoring Satellite Application Facility |
| CORS | Continuously Operating Reference Station |
| COSMO-SkyMed | Constellation of Small Satellites for Mediterranean basin Observation |
| DEM | Digital Elevation Model |
| DInSAR | Differential InSAR |
| DOY | Day of Year |
| EPSG | European Petroleum Survey Group |
| ESA | European Space Agency |
| ETRF | European Terrestrial Reference System |
| FEM | Finite Element Method |
| FTP | File Transfer Protocol |
| GACOS | Generic Atmospheric Correction Online Service |
| GNSS | Global Navigation Satellite System |
| ICOLD | International Commission on Large Dams |
| IGS | International GNSS Service |
| InSAR | Interferometric SAR |
| IW | Interferometric Wide |
| IW1, IW2 and IW3 | 1st, 2nd, 3rd IW sub-swath |
| LIDAR | Laser Imaging Detection and Ranging |
| LOS | Line of Sight |
| LST | Land Surface Temperature |
| MBC | Multi-Baseline Construction |
| NDA | Network Deformation Analysis |
| PS | Persistent Scatter |
| PS–InSAR | Persistent Scatter for InSAR |
| QGIS | (until 2013 known as) Quantum GIS |
| RDN2008 | National Dynamic Network, realisation epoch 2008 |
| S-1A, S-1B | Sentinel-1A and Sentinel-1B |
| SAR | Synthetic Aperture Radar |
| SARProZ | The SAR PROcessing tool by periZ |
| SBAS | Small BAseline Subset |
| SLC | Single Look Complex |
| SMW | Statistical Mono-Window |
| SNAP | Sentinel Application Platform software |
| TIRS | Thermal Infrared Sensor |
| TOPSAR | Terrain Observation with Progressive Scans SAR |
| VV | Vertical transmit-Vertical receive polarisation |
| WGS84 | World Geodetic System 1984 |
The following symbols (Table A2) are used in this manuscript:

Table A2.
Symbols list.
Table A2.
Symbols list.
| Symbol | Meaning | Unit |
|---|---|---|
| σ° | backscattering coefficient | (dB) |
| dLOS | LOS dam displacements | (mm) |
| D | horizontal displacements orthogonal to the dam measured by GNSS | (mm) |
| DTOT | total horizontal displacements orthogonal to the dam | (mm) |
| H | dam water level | (m a.s.l.) |
| HRS | H estimated from remote sensing | (m a.s.l.) |
| HIS | H measured in situ | (m a.s.l.) |
| r2 | determination coefficient | (–) |
| RMSE | Root Mean Square Error | (as the input unit) |
| TA | air temperature | (K) |
| TW | water surface temperature | (K) |
References
- Tomás, R.; Cano, M.; García-Barba, J.; Vicente, F.; Herrera, G.; Lopez-Sanchez, J.M.; Mallorquí, J.J. Monitoring an Earthfill Dam Using Differential SAR Interferometry: La Pedrera Dam, Alicante, Spain. Eng. Geol. 2013, 157, 21–32. [Google Scholar] [CrossRef]
- Al-Husseinawi, Y.; Li, Z.; Clarke, P.; Edwards, S. Evaluation of the Stability of the Darbandikhan Dam after the 12 November 2017 Mw 7.3 Sarpol-e Zahab (Iran-Iraq Border) Earthquake. Remote Sens. 2018, 10, 1426. [Google Scholar] [CrossRef]
- Mazzanti, P.; Perissin, D.; Rocca, A. Structural Health Monitoring of Dams by Advanced Satellite SAR Interferometry: Investigation of Past Processes and Future Monitoring Perspectives. In Proceedings of the 7th Internation Conference on Structural Health Monitoring of Intelligent Infrastructure, Torino, Italy, 1–3 July 2015. [Google Scholar]
- Milillo, P.; Tapete, D.; Cigna, F.; Perissin, D.; Salzer, J.; Lundgren, P.; Fielding, E.; Burgmann, R.; Biondi, F.; Milillo, G.; et al. Structural Health Monitoring of Engineered Structures Using a Space-Borne Synthetic Aperture Radar Multi-Temporal Approach: From Cultural Heritage Sites to War Zones; SPIE: Edinburgh, UK, 2016; Volume 10003. [Google Scholar]
- Milillo, P.; Perissin, D.; Salzer, J.T.; Lundgren, P.; Lacava, G.; Milillo, G.; Serio, C. Monitoring Dam Structural Health from Space: Insights from Novel InSAR Techniques and Multi-Parametric Modeling Applied to the Pertusillo Dam Basilicata, Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 221–229. [Google Scholar] [CrossRef]
- International Commission on Large Dams. Available online: https://www.icold-cigb.org/ (accessed on 29 March 2021).
- Registro Italiano Dighe—Home Page. Available online: http://dgdighe.mit.gov.it/imagemap/default.htm (accessed on 29 March 2021).
- Osservatorio Delle Acque. Available online: http://www.osservatorioacque.it/?cmd=page&id=dati_monitris_serbatoi&tpl=default (accessed on 29 March 2021).
- Sousa, J.J.; Hlaváčová, I.; Bakoň, M.; Lazecký, M.; Patrício, G.; Guimarães, P.; Ruiz, A.M.; Bastos, L.; Sousa, A.; Bento, R. Potential of Multi-Temporal InSAR Techniques for Bridges and Dams Monitoring. Procedia Technol. 2014, 16, 834–841. [Google Scholar] [CrossRef]
- Scaioni, M.; Marsella, M.; Crosetto, M.; Tornatore, V.; Wang, J. Geodetic and Remote-Sensing Sensors for Dam Deformation Monitoring. Sensors 2018, 18, 3682. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Zhao, S.; Wang, Y. Structural Health Monitoring of Concrete Dams Using Long-Term Air Temperature for Thermal Effect Simulation. Eng. Struct. 2019, 180, 642–653. [Google Scholar] [CrossRef]
- Yun, T.; Butler, K.E.; MacQuarrie, K.T.B.; Mclean, B.; Campbell, I. Seasonal Temperature Monitoring and Modelling for Seepage Reconnaissance in an Embankment Dam; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2018. [Google Scholar]
- Yue, H.; Liu, Y. Variations in the Lake Area, Water Level, and Water Volume of Hongjiannao Lake during 1986–2018 Based on Landsat and ASTER GDEM Data. Environ. Monit. Assess. 2019, 191. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Tian, J.; Su, H.; Sun, X.; Chen, S.; Xia, J. Two Improvements of an Operational Two-Layer Model for Terrestrial Surface Heat Flux Retrieval. Sensors 2008, 8, 6165–6187. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Xu, N.; Sun, J.; Wang, X.H.; Yang, F.; Li, S. Estimating Water Levels and Volumes of Lakes Dated Back to the 1980s Using Landsat Imagery and Photon-Counting Lidar Datasets. Remote Sens. Environ. 2019, 232. [Google Scholar] [CrossRef]
- Ferrentino, E.; Nunziata, F.; Buono, A.; Urciuoli, A.; Migliaccio, M. Multipolarization Time Series of Sentinel-1 SAR Imagery to Analyze Variations of Reservoirs’ Water Body. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 840–846. [Google Scholar] [CrossRef]
- Pipitone, C.; Maltese, A.; Dardanelli, G.; Lo Brutto, M.; La Loggia, G. Monitoring Water Surface and Level of a Reservoir Using Different Remote Sensing Approaches and Comparison with Dam Displacements Evaluated via GNSS. Remote Sens. 2018, 10, 71. [Google Scholar] [CrossRef]
- Droz, P.; Fumagalli, A.; Novali, F.; Young, B. Gps and Insar Technologies: A Joint Approach for the Safety of Lake Sarez. In Proceedings of the 4th Canadian Conference on Geohazards: From Causes to Management, Presse de l’Université Laval, QC, Canada, 23–24 May 2008; pp. 1–8. [Google Scholar]
- Fernandez, J.; Arjona, A.; Prieto, J.F.; Santoyo, M.A.; Seco, A.; Monells, D.; Pallero, J.L.; Prieto, E.; Luzón, F.; Mallorquí, J.J. Study of Surface Displacement Near Itoiz Reservoir, Navarra, Spain, Using an Advanced DInSAR Technique; American Geophysical Union: Washington, DC, USA, 2009. [Google Scholar]
- Grenerczy, G.; Wegmüller, U. Persistent Scatterer Interferometry Analysis of the Embankment Failure of a Red Mud Reservoir Using ENVISAT ASAR Data. Nat. Hazards 2011, 59, 1047–1053. [Google Scholar] [CrossRef]
- Wang, T.; Perissin, D.; Rocca, F.; Liao, M.-S. Three Gorges Dam Stability Monitoring with Time-Series InSAR Image Analysis. Sci. China Earth Sci. 2011, 54, 720–732. [Google Scholar] [CrossRef]
- Voege, M.; Frauenfelder, R.; Larsen, Y. Displacement Monitoring at Svartevatn Dam with Interferometric SAR. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3895–3898. [Google Scholar]
- Awada, H.; Ciraolo, G.; Maltese, A.; Provenzano, G.; Moreno Hidalgo, M.A.; Còrcoles, J.I. Assessing the Performance of a Large-Scale Irrigation System by Estimations of Actual Evapotranspiration Obtained by Landsat Satellite Images Resampled with Cubic Convolution. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 96–105. [Google Scholar] [CrossRef]
- Sharaf, N.; Fadel, A.; Bresciani, M.; Giardino, C.; Lemaire, B.J.; Slim, K.; Faour, G.; Vinçon-Leite, B. Lake Surface Temperature Retrieval from Landsat-8 and Retrospective Analysis in Karaoun Reservoir, Lebanon. J. Appl. Rem. Sens. 2019, 13, 044505. [Google Scholar] [CrossRef]
- Addesso, P.; Longo, M.; Maltese, A.; Montone, R.; Restaino, R.; Vivone, G. Robustified Smoothing for Enhancement of Thermal Image Sequences Affected by Clouds. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1076–1079. [Google Scholar]
- Addesso, P.; Longo, M.; Restaino, R.; Vivone, G. Spatio-Temporal Resolution Enhancement for Cloudy Thermal Sequences. Eur. J. Remote Sens. 2019, 52, 2–14. [Google Scholar] [CrossRef]
- Barzaghi, R.; Cazzaniga, N.E.; De Gaetani, C.I.; Pinto, L.; Tornatore, V. Estimating and Comparing Dam Deformation Using Classical and Gnss Techniques. Sensors 2018, 18, 756. [Google Scholar] [CrossRef] [PubMed]
- De Sortis, A.; Paoliani, P. Statistical Analysis and Structural Identification in Concrete Dam Monitoring. Eng. Struct. 2007, 29, 110–120. [Google Scholar] [CrossRef]
- Di Martire, D.; Iglesias, R.; Monells, D.; Centolanza, G.; Sica, S.; Ramondini, M.; Pagano, L.; Mallorquí, J.J.; Calcaterra, D. Comparison between Differential SAR Interferometry and Ground Measurements Data in the Displacement Monitoring of the Earth-Dam of Conza Della Campania (Italy). Remote Sens. Environ. 2014, 148, 58–69. [Google Scholar] [CrossRef]
- Blanco-Sánchez, P.; Mallorquí, J.J.; Duque, S.; Monells, D. The Coherent Pixels Technique (CPT): An Advanced DInSAR Technique for Nonlinear Deformation Monitoring. Pure Appl. Geophys. 2008, 165, 1167–1193. [Google Scholar] [CrossRef]
- Xiao, R.; Shi, H.; He, X.; Li, Z.; Jia, D.; Yang, Z. Deformation Monitoring of Reservoir Dams Using GNSS: An Application to South-to-North Water Diversion Project, China. IEEE Access 2019, 7, 54981–54992. [Google Scholar] [CrossRef]
- Empson, W.; Cohen, D.; Gamm, S.; Worsham, B.; Yarborough, S. Karst Investigation Program Guided by Synthetic Aperture Radar. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XXI; Neale, C.M., Maltese, A., Eds.; SPIE: Strasbourg, France, 2019; p. 42. [Google Scholar]
- Lazecký, M.; Perissin, D.; Zhiying, W.; Ling, L.; Yuxiao, Q. Observing dam’s movements with spaceborne sar interferometry. In Engineering Geology for Society and Territory—Volume 5: Urban Geology, Sustainable Planning and Landscape Exploitation; Springer: Berlin/Heidelberg, Germany, 2015; pp. 131–136. [Google Scholar]
- Milillo, P.; Porcu, M.C.; Lundgren, P.; Soccodato, F.; Salzer, J.; Fielding, E.; Burgmann, R.; Milillo, G.; Perissin, D.; Biondi, F. The Ongoing Destabilization of the Mosul Dam as Observed by Synthetic Aperture Radar Interferometry. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 6279–6282. [Google Scholar]
- Milillo, P.; Bürgmann, R.; Lundgren, P.; Salzer, J.; Perissin, D.; Fielding, E.; Biondi, F.; Milillo, G. Space Geodetic Monitoring of Engineered Structures: The Ongoing Destabilization of the Mosul Dam, Iraq. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Bakon, M.; Perissin, D.; Lazecky, M.; Papco, J. Infrastructure Non-Linear Deformation Monitoring Via Satellite Radar Interferometry. Procedia Technol. 2014, 16, 294–300. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A Review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Ruiz-Armenteros, A.M.; Lazecky, M.; Hlaváčová, I.; Bakoň, M.; Manuel Delgado, J.; Sousa, J.J.; Lamas-Fernández, F.; Marchamalo, M.; Caro-Cuenca, M.; Papco, J.; et al. Deformation Monitoring of Dam Infrastructures via Spaceborne MT-InSAR. The Case of La Viñuela (Málaga, Southern Spain). Procedia Comput. Sci. 2018, 138, 346–353. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Bonano, M.; Manunta, M.; Marsella, M.; Lanari, R. Long-Term ERS/ENVISAT Deformation Time-Series Generation at Full Spatial Resolution via the Extended SBAS Technique. Int. J. Remote Sens. 2012, 33, 4756–4783. [Google Scholar] [CrossRef]
- Corsetti, M.; Manunta, M.; Marsella, M.; Scifoni, S.; Sonnessa, A.; Ojha, C. Satellite techniques: New perspectives for the monitoring of dams. In Engineering Geology for Society and Territory—Volume 5: Urban Geology, Sustainable Planning and Landscape Exploitation; Springer: Berlin/Heidelberg, Germany, 2015; pp. 989–993. [Google Scholar]
- Mura, J.C.; Gama, F.F.; Paradella, W.R.; Negrão, P.; Carneiro, S.; de Oliveira, C.G.; Brandão, W.S. Monitoring the Vulnerability of the Dam and Dikes in Germano Iron Mining Area after the Collapse of the Tailings Dam of Fundão (Mariana-MG, Brazil) Using DInSAR Techniques with TerraSAR-X Data. Remote Sens. 2018, 10, 1507. [Google Scholar] [CrossRef]
- Li, F.K.; Goldstein, R.M. Studies of Multibaseline Spaceborne Interferometric Synthetic Aperture Radars. IEEE Trans. Geosci. Remote Sens. 1990, 28, 88–97. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in Interferometric Radar Echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Copernicus Sentinels POD Data Hub. Available online: https://scihub.copernicus.eu/gnss/#/home (accessed on 29 March 2021).
- Reigber, C.; Xia, Y.; Kaufmann, H.; Massmann, F.-H.; Timmen, L.; Bodechtel, J.; Frei, M. Fringe 96 Workshop on ERS SAR Interferometry. In Proceedings of the Fringe 96 Workshop, Zurich, Switzerland, 30 September–2 October 1996. [Google Scholar]
- Dardanelli, G.; La Loggia, G.; Perfetti, N.; Capodici, F.; Puccio, L.; Maltese, A. Monitoring Displacements of an Earthen Dam Using GNSS and Remote Sensing; SPIE: Amsterdam, The Netherlands, 2014; Volume 9239. [Google Scholar]
- Szostak-Chrzanowski, A.; Chrzanowski, A.; Massiéra, M. Use of Deformation Monitoring Results in Solving Geomechanical Problems—Case Studies. Eng. Geol. 2005, 79, 3–12. [Google Scholar] [CrossRef]
- Dardanelli, G.; Pipitone, C. Hydraulic Models and Finite Elements for Monitoring of an Earth Dam, by Using GNSS Techniques. Period. Polytech. Civ. Eng. 2016. [Google Scholar] [CrossRef]
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/dhus/#/home (accessed on 29 March 2021).
- Bovenga, F.; Wasowski, J.; Nitti, D.O.; Nutricato, R.; Chiaradia, M.T. Using COSMO/SkyMed X-Band and ENVISAT C-Band SAR Interferometry for Landslides Analysis. Remote Sens. Environ. 2012, 119, 272–285. [Google Scholar] [CrossRef]
- Perissin, Daniele Software Manual—SARPROZ©. Available online: https://www.sarproz.com/software-manual/ (accessed on 29 March 2021).
- Pipitone, C.; Maltese, A.; Dardanelli, G.G.; Capodici, F.; Lo Brutto, M.; La Loggia, G. Detection of a Reservoir Water Level Using Shape Similarity Metrics. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XIX; Neale, C.M., Maltese, A., Eds.; SPIE: Warsaw, Poland, 2017; p. 61. [Google Scholar]
- Goldstein, R.M.; Werner, C.L. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Pipitone, C.; Cigna, F.; Dardanelli, G.; La Loggia, G.; Maltese, A.; Muller, J.-P. Reservoir Monitoring Using Satellite SAR and GNSS: A Case Study in Southern Italy. EPIC Ser. Eng. 2018, 3, 1682–1691. [Google Scholar]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain Observation by Progressive Scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Generic Atmospheric Correction Online Service for InSAR (GACOS): Validation and Implications for InSAR Time Series Analysis; American Geophysical Union: Washington, DC, USA, 2018; Volume 32. [Google Scholar]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric Synthetic Aperture Radar Atmospheric Correction Using a GPS-Based Iterative Tropospheric Decomposition Model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of Real-Time Mode High-Resolution Water Vapor Fields from GPS Observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Triggered Afterslip on the Southern Hikurangi Subduction Interface Following the 2016 Kaikōura Earthquake from InSAR Time Series with Atmospheric Corrections. Remote Sens. Environ. 2020, 251, 112097. [Google Scholar] [CrossRef]
- Generic Atmospheric Correction Online Service for InSAR (GACOS). Available online: http://www.gacos.net/ (accessed on 29 March 2021).
- Piano Assetto Idrogeologico, Sistema Informativo Territoriale Regionale. Available online: https://www.sitr.regione.sicilia.it/pai-download-dati (accessed on 29 March 2021).
- Perissin, D.; Wang, Z.; Wang, T. The SARPROZ InSAR Tool for Urban Subsidence/Manmade Structure Stability Monitoring in China. In Proceedings of the ISRSE, Sidney, Australia, 10–15 April 2011; pp. 1–4. [Google Scholar]
- Eriksen, H.Ø.; Lauknes, T.R.; Larsen, Y.; Corner, G.D.; Bergh, S.G.; Dehls, J.; Kierulf, H.P. Visualizing and Interpreting Surface Displacement Patterns on Unstable Slopes Using Multi-Geometry Satellite SAR Interferometry (2D InSAR). Remote Sens. Environ. 2017, 191, 297–312. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. Resolving Three-Dimensional Surface Displacements from InSAR Measurements: A Review. Earth Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites. In The Use of Artificial Satellites for Geodesy; American Geophysical Union (AGU): Washington, DC, USA, 1972; pp. 247–251. ISBN 978-1-118-66364-6. [Google Scholar]
- Niell, A.E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Effects on GPS. In Global Positioning System: Theory and Application; Aeronautics and Astronautics: Stanford, CA, USA, 1996. [Google Scholar]
- Schwiderski, E.W. On Charting Global Ocean Tides. Rev. Geophys. 1980, 18, 243–268. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Small, D.; Schubert, A. Guide to ASAR Geocoding. ESA-ESRIN Tech. Note RSL-ASAR-GC-AD 2008, 1, 36. [Google Scholar]
- Vickers, H.; Malnes, E.; Høgda, K.-A. Long-Term Water Surface Area Monitoring and Derived Water Level Using Synthetic Aperture Radar (SAR) at Altevatn, a Medium-Sized Arctic Lake. Remote Sens. 2019, 11, 2780. [Google Scholar] [CrossRef]
- QGIS. A Free and Open Source Geographic Information System. Available online: https://qgis.org/en/site/ (accessed on 29 March 2021).
- Ji, S.; Zhu, Y.; Qiang, S.; Zeng, D. Forecast of Water Temperature in Reservoir Based on Analytical Solution. J. Hydrodyn. Ser. B 2008, 20, 507–513. [Google Scholar] [CrossRef]
- Duguay-Tetzlaff, A.; Bento, V.A.; Göttsche, F.M.; Stöckli, R.; Martins, J.P.A.; Trigo, I.; Olesen, F.; Bojanowski, J.S.; da Camara, C.; Kunz, H. Meteosat Land Surface Temperature Climate Data Record: Achievable Accuracy and Potential Uncertainties. Remote Sens. 2015, 7, 13139–13156. [Google Scholar] [CrossRef]
- Ermida, S.L.; Soares, P.; Mantas, V.; Göttsche, F.-M.; Trigo, I.F. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Piccolroaz, S. Prediction of Lake Surface Temperature Using the Air2water Model: Guidelines, Challenges, and Future Perspectives. Adv. Oceanogr. Limnol. 2016, 7, 36–50. [Google Scholar] [CrossRef]
- Osmanoğlu, B.; Sunar, F.; Wdowinski, S.; Cabral-Cano, E. Time Series Analysis of InSAR Data: Methods and Trends. ISPRS J. Photogramm. Remote Sens. 2016, 115, 90–102. [Google Scholar] [CrossRef]
- Geoportale Nazionale. Available online: http://www.pcn.minambiente.it/mattm/servizio-wms/ (accessed on 29 March 2021).
- Farquharson, G.; Woods, W.; Stringham, C.; Sankarambadi, N.; Riggi, L. The Capella Synthetic Aperture Radar Constellation. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Aachen, Germany, 4–7 June 2018; pp. 1873–1876. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).