The Surface Crack Extraction Method Based on Machine Learning of Image and Quantitative Feature Information Acquisition Method
Abstract
1. Introduction
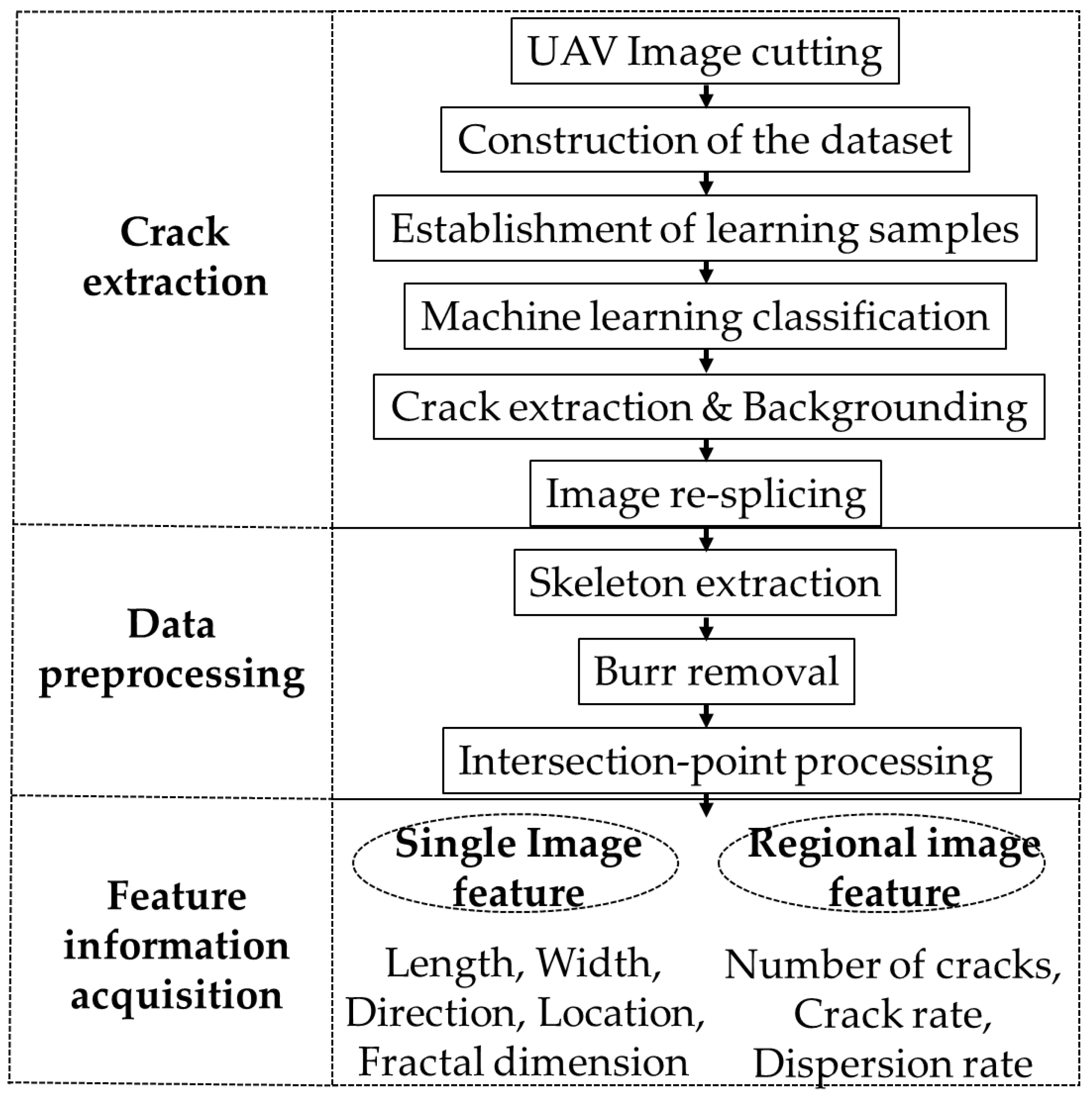
2. Materials and Methods
2.1. Data Source and Research Methods
2.1.1. Data Source
2.1.2. Research Methods
2.2. Crack Extraction Method Based on Machine Learning
2.2.1. Dataset Construction and Crack Extraction Steps
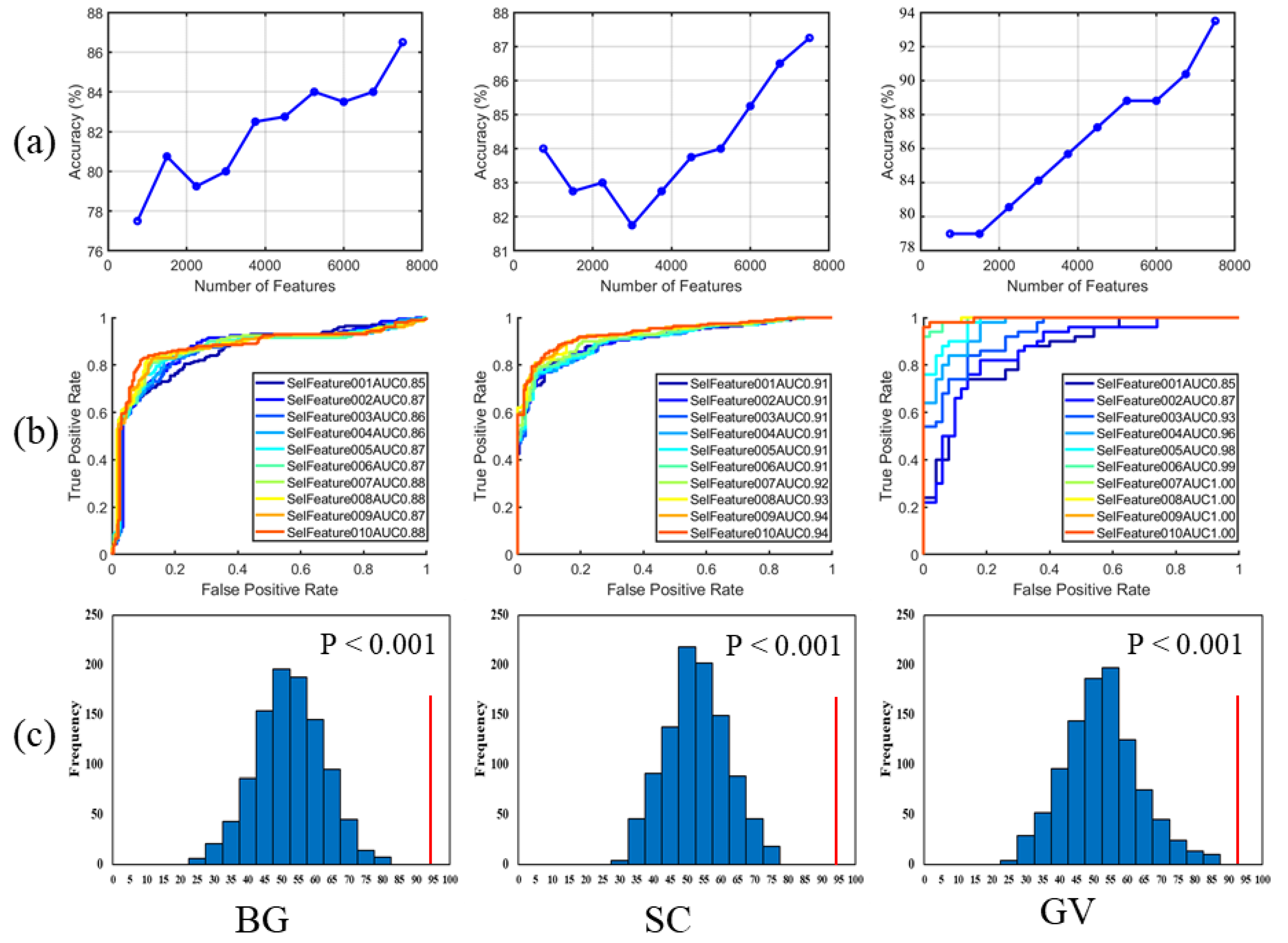
2.2.2. Leave-One-Out Cross-Validation and Permutation Test
2.3. Image Preprocessing Method
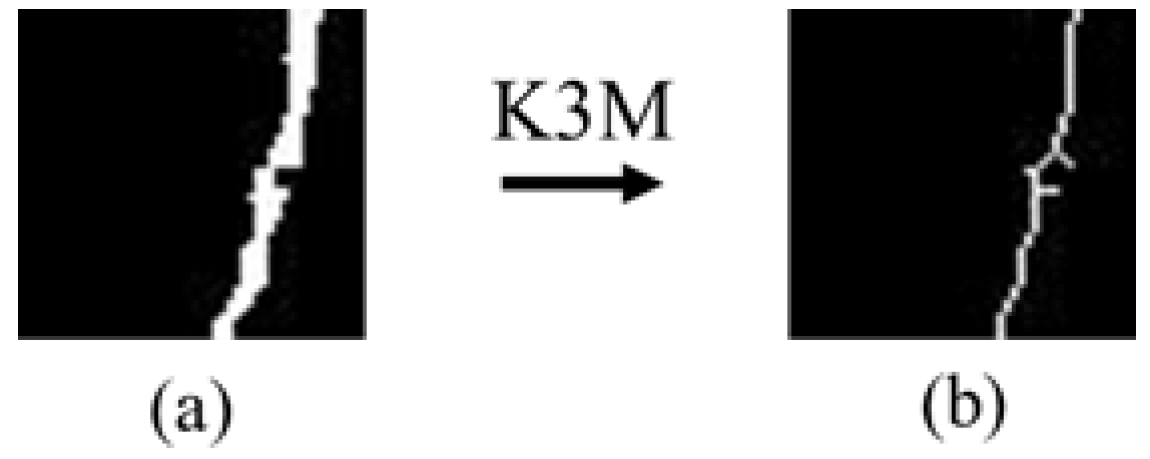
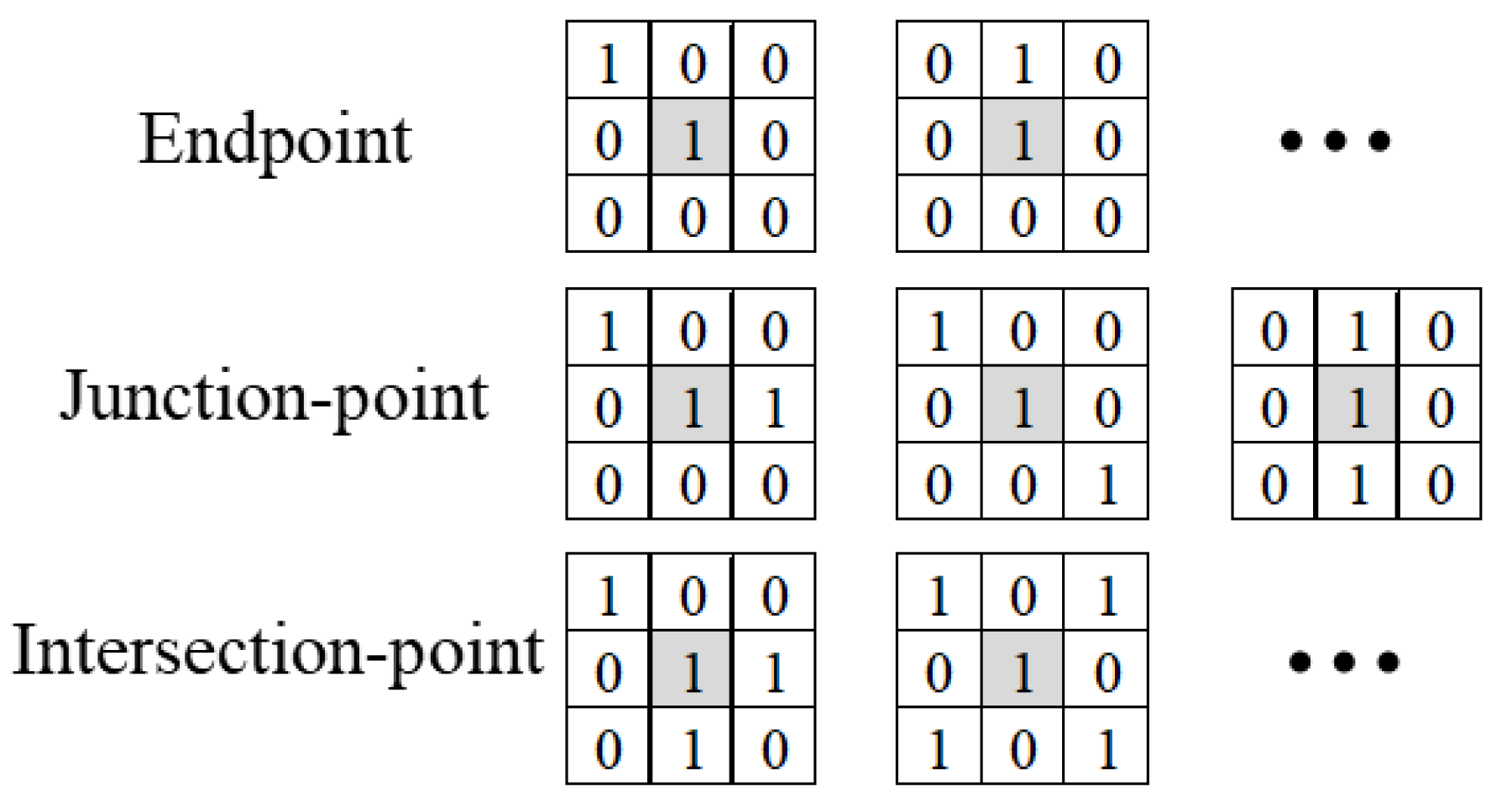
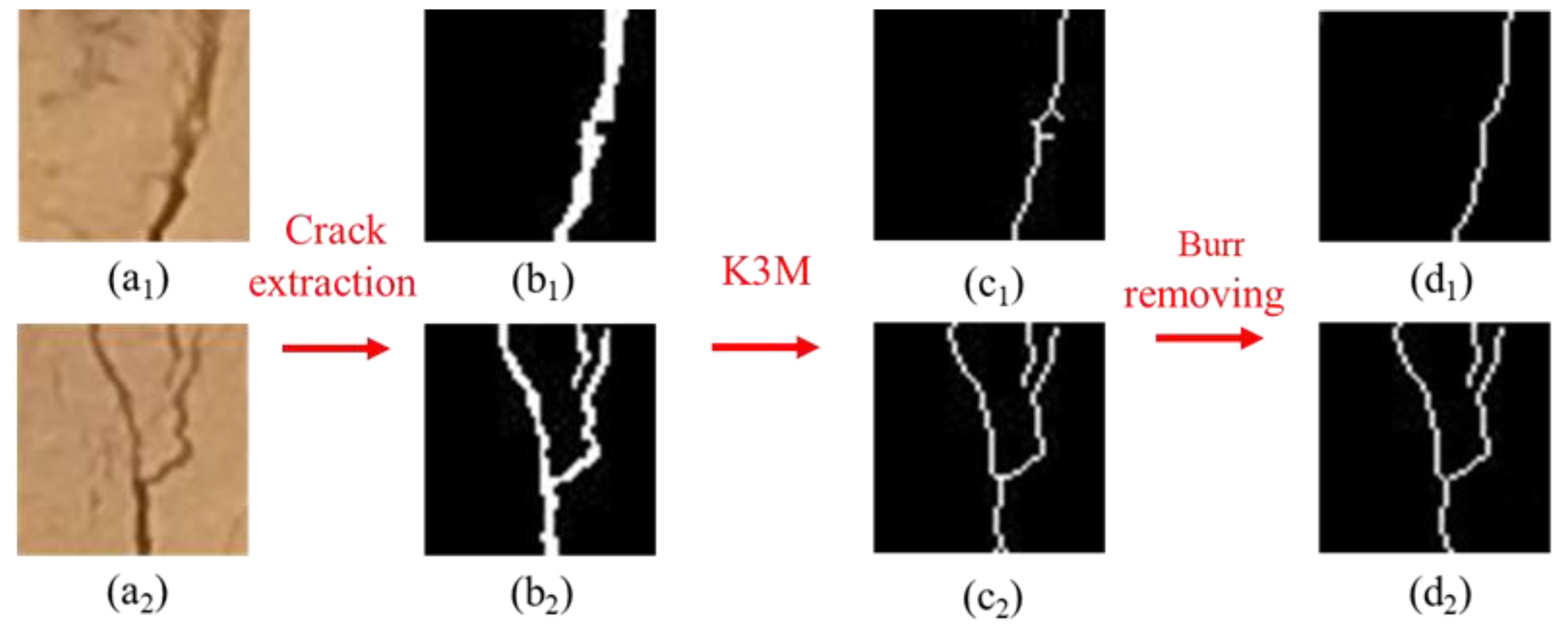
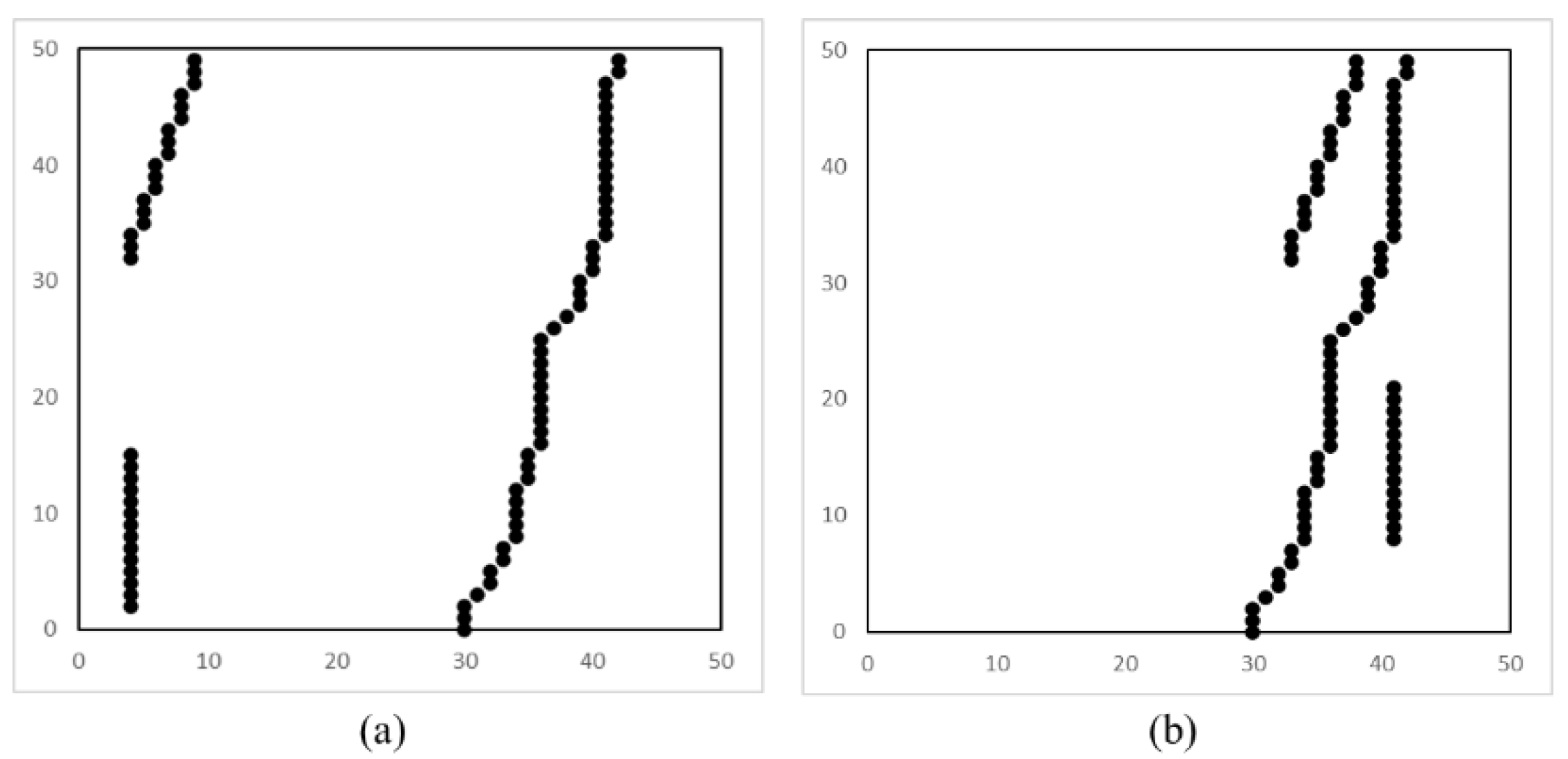
2.3.1. Skeleton Extraction
2.3.2. Burr Removal
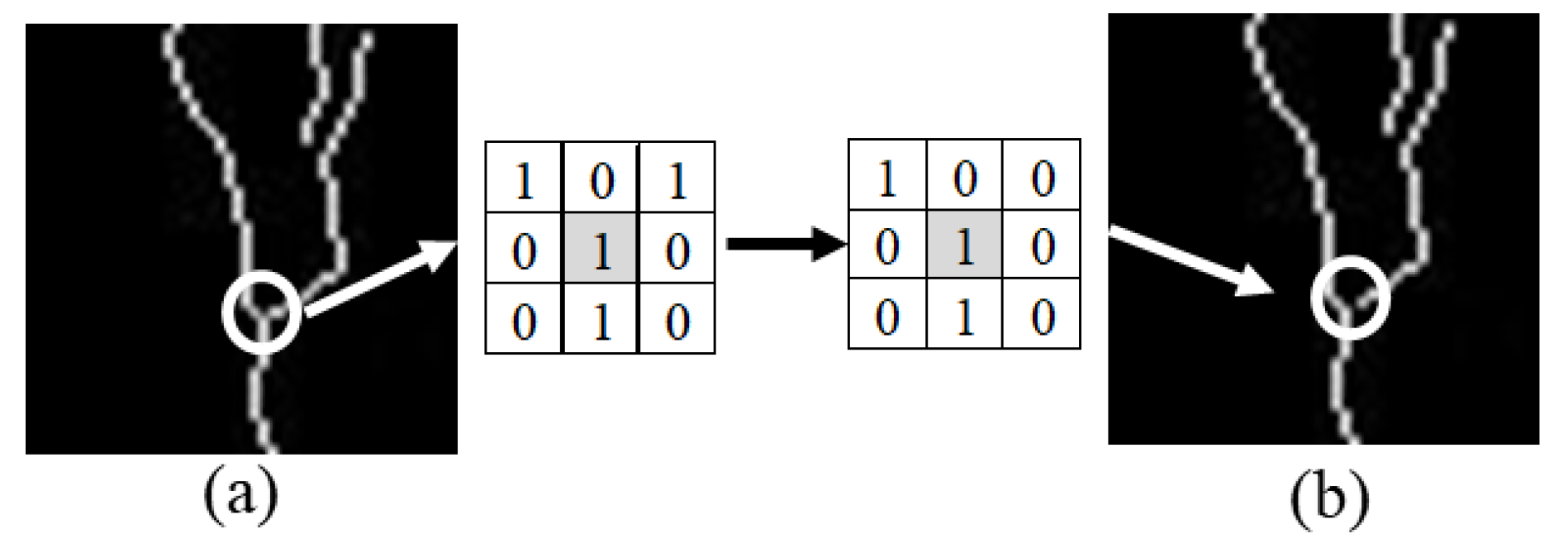
2.3.3. Intersection-Point Processing
2.4. Quantitative Acquisition Method of Crack Feature Information
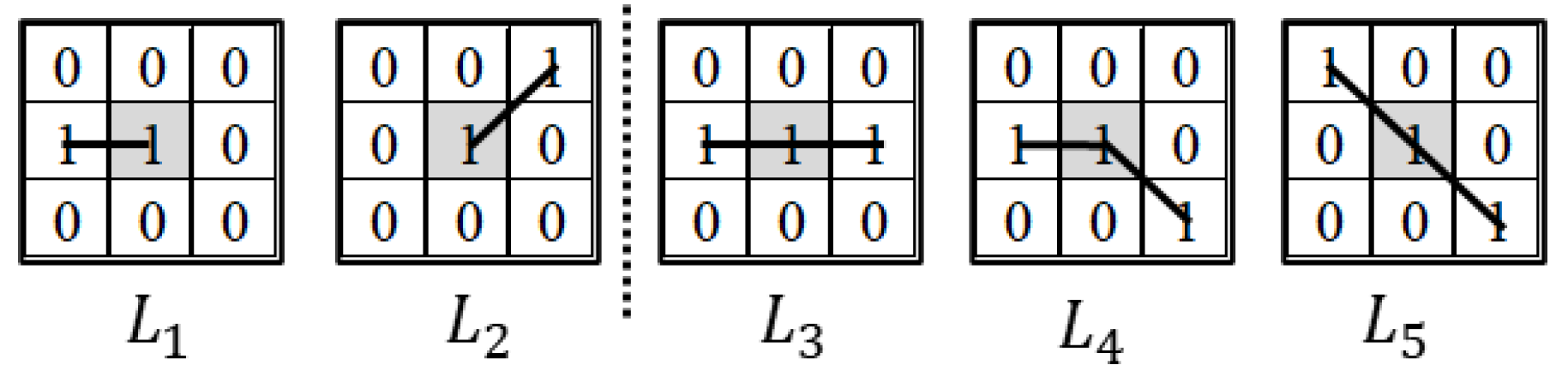
2.4.1. Crack Length
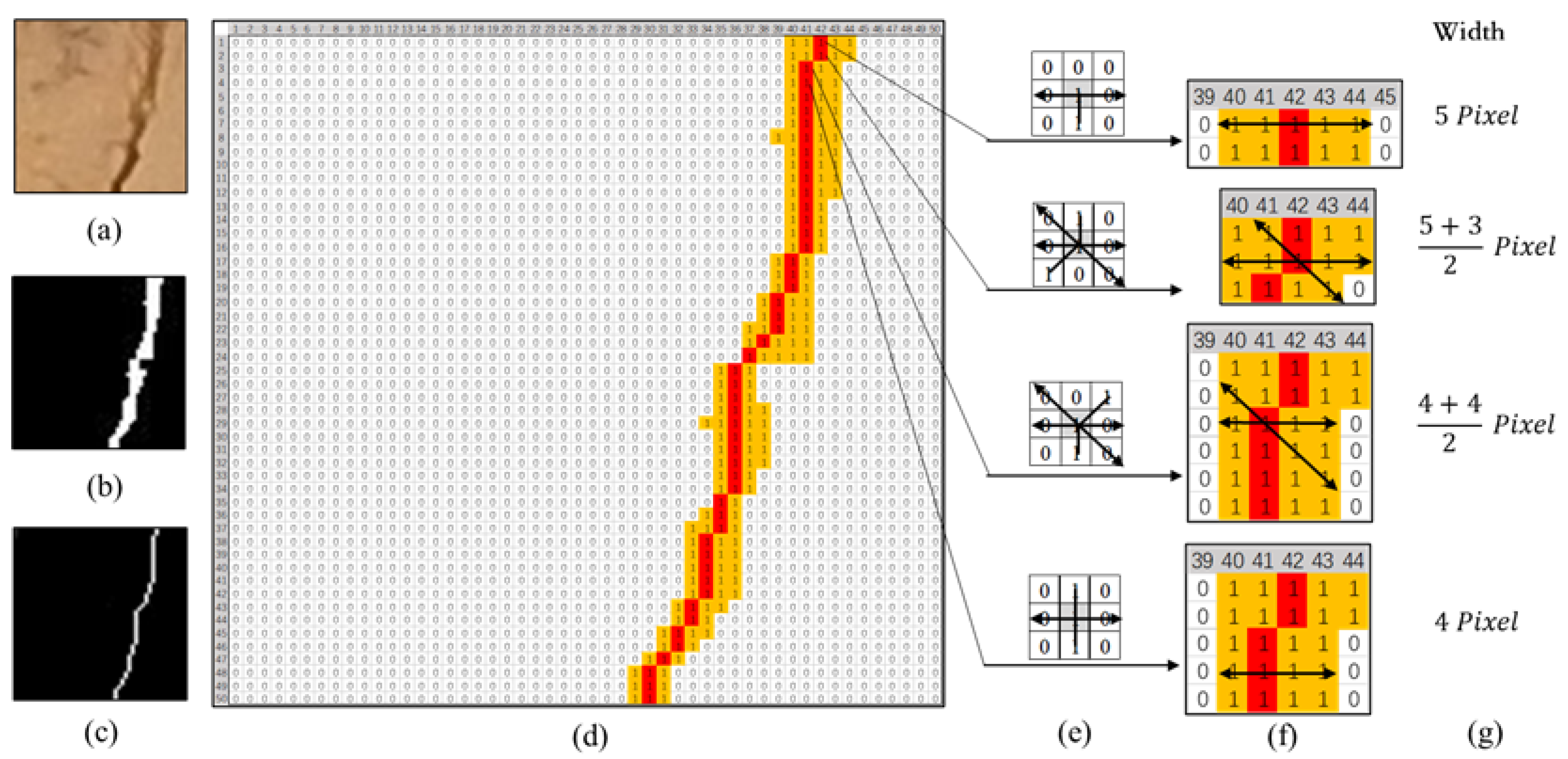
2.4.2. Crack Width
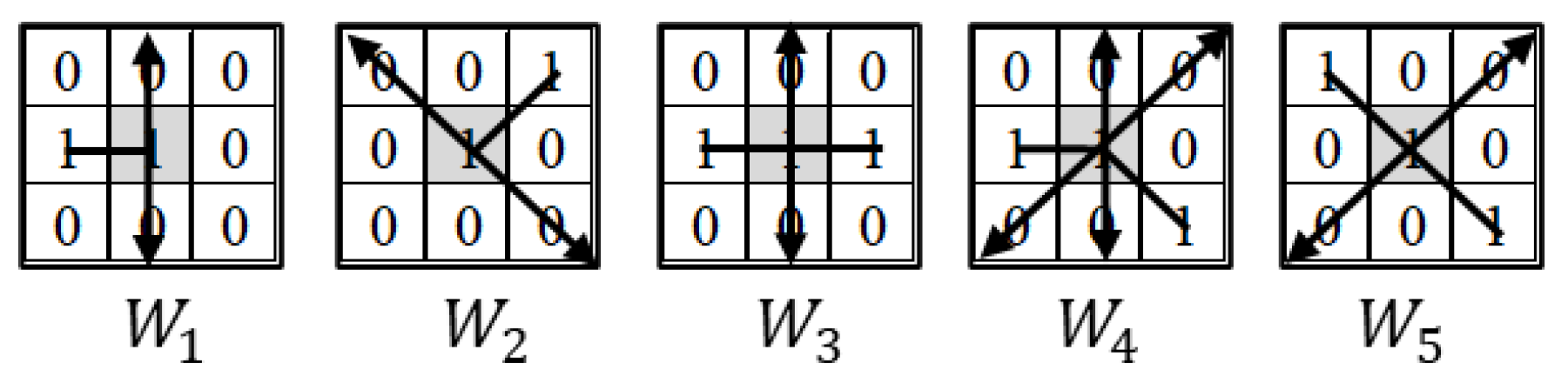
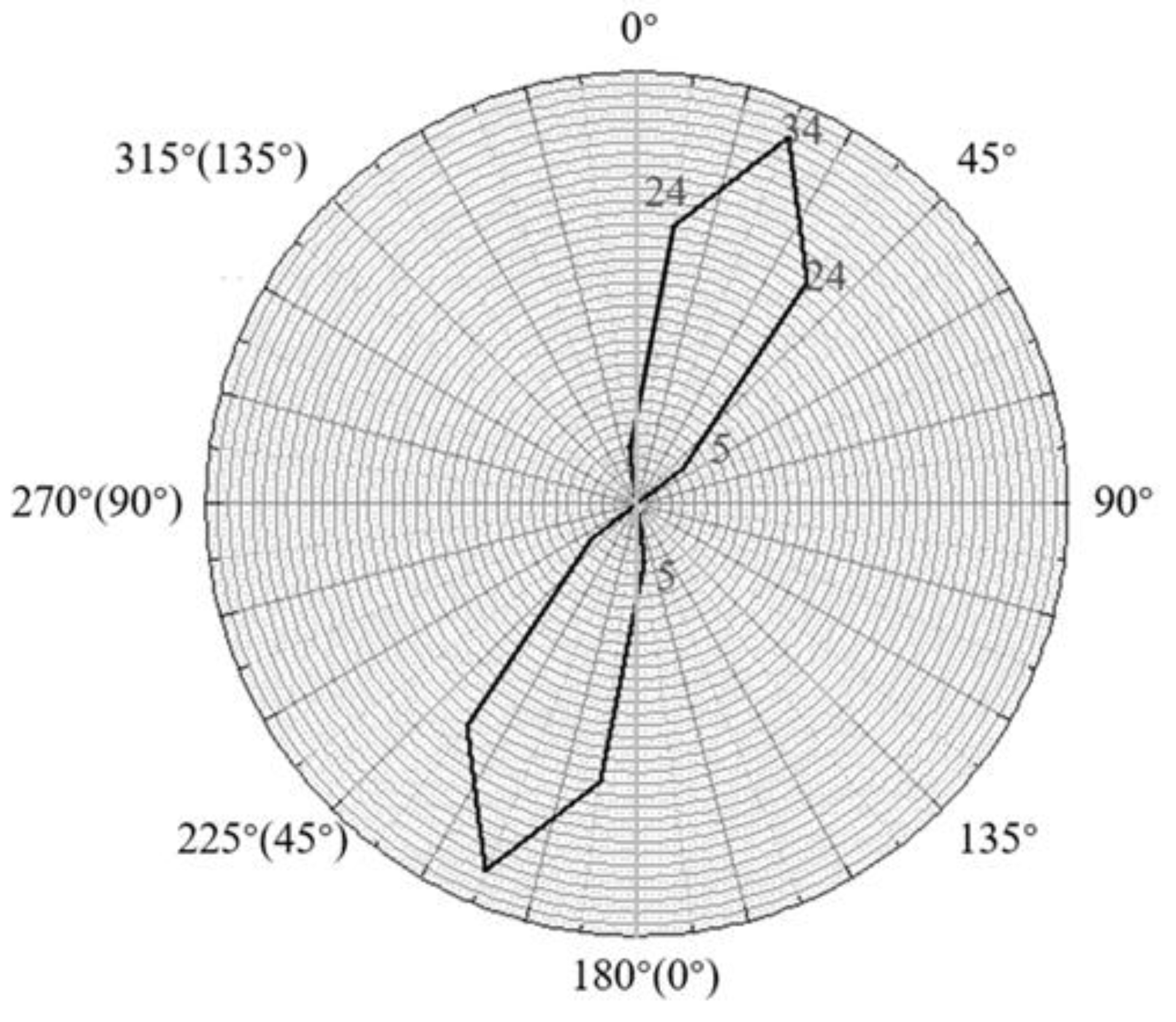
2.4.3. Crack Direction
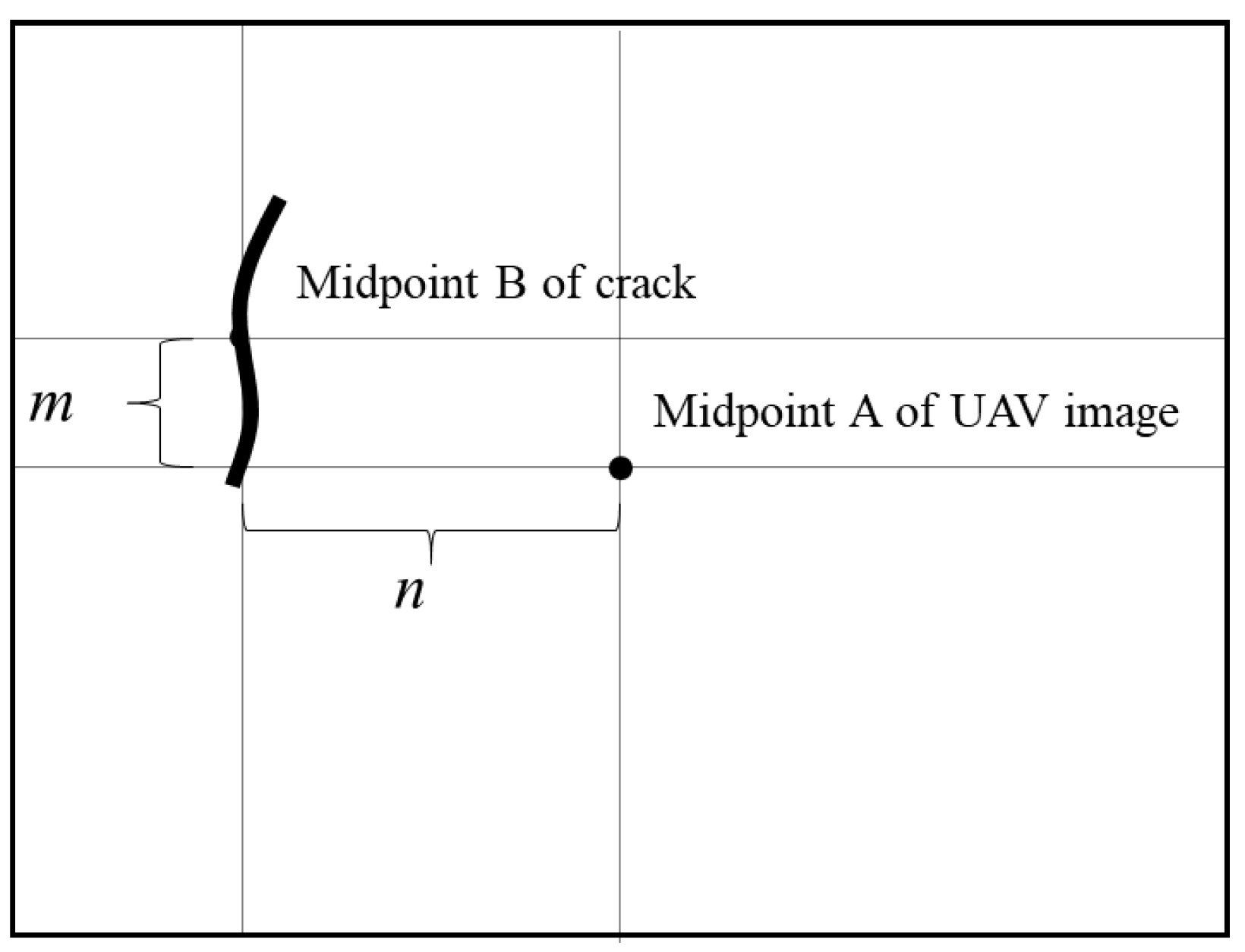
2.4.4. Crack Location
2.4.5. Crack Fractal Dimension
2.4.6. The Number of Cracks
2.4.7. Crack Rate and Dispersion Rate
3. Results and Discussion
3.1. Results of Crack Extraction
3.2. Image Preprocessing Results
3.3. Quantitative Calculation Results of Crack Feature Information
3.3.1. Single Crack Feature Calculation Results and Accuracy Verification
3.3.2. Regional Crack Feature Calculation Results
4. Conclusions
- The error in surface crack extraction from a UAV image mainly comes from complex background information such as vegetation and soil crust. Using machine learning to classify the sub-images, then to extract cracks, and to re-splice is an effective method to avoid the error. The total accuracy reached 89.50%.
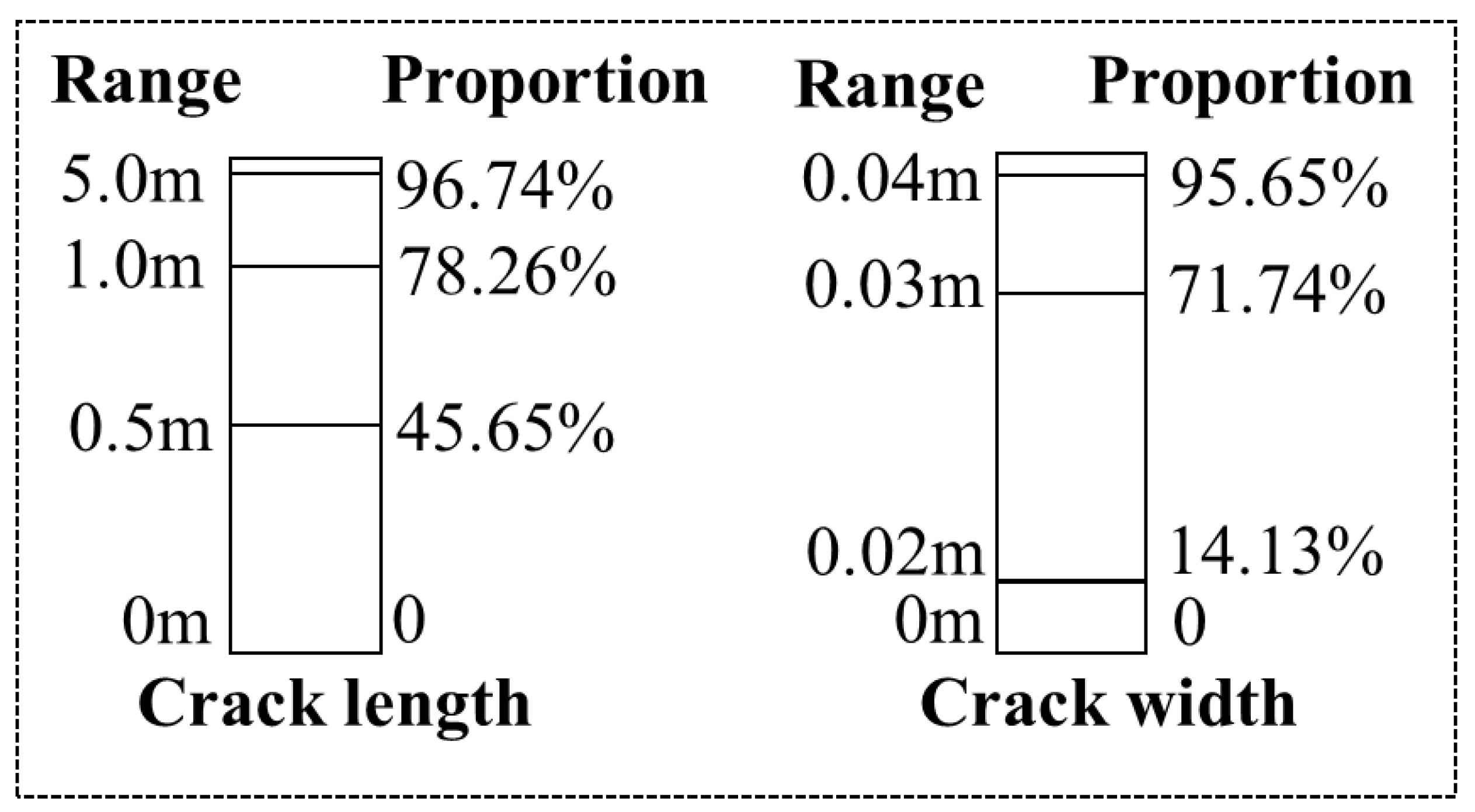
- By acquiring the single crack feature information content—crack length, width, direction, fractal dimension, and location—it can clearly describe the feature information of any crack. In this study area, the crack length is mainly within 5 m, the crack average width is mainly within 0.04 m, the crack direction is generally in the north–south direction, and the crack fractal dimension is between 1.0750 and 1.3521.
- The concept and calculation method for the dispersion rate are introduced. The crack rate is used to show the size of the crack area, and the dispersion rate is used to show the concentration or dispersion of the cracks in the area. This method more clearly and completely describes the distribution characteristics of regional cracks.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Li, S.; Cao, X.; Somerville, I.D.; Cao, H. Holocene intracontinental deformation of the northern north china plain: Evidence of tectonic ground fissures. J. Asian Earth Sci. 2016, 119, 49–64. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Z.; Kong, J.; Cheng, N.; Duan, L.; Wang, Z. Ecological impacts induced by groundwater and their thresholds in the arid areas in northwest china. Environ. Eng. Manag. J. 2013, 12, 1497–1507. [Google Scholar] [CrossRef]
- Youssef, A.M.; Sabtan, A.A.; Maerz, N.H.; Zabramawi, Y.A. Earth fissures in Wadi Najran, kingdom of Saudi Arabia. Nat. Hazards 2014, 71, 2013–2027. [Google Scholar] [CrossRef]
- Chen, Y.-G. Logistic models of fractal dimension growth of urban morphology. Fractals 2018, 26, 1850033. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.P.; Kerle, N.; Niethammer, U.; Rothmund, S. Image-based mapping of surface fissures for the investigation of landslide dynamics. Geomorphology 2013, 186, 12–27. [Google Scholar] [CrossRef]
- Ludeno, G.; Cavalagli, N.; Ubertini, F.; Soldovieri, F.; Catapano, I. On the combined use of ground penetrating radar and crack meter sensors for structural monitoring: Application to the historical consoli palace in gubbio, italy. Surv. Geophys. 2020, 41, 647–667. [Google Scholar] [CrossRef]
- Sharma, P.; Kumar, B.; Singh, D. Novel adaptive buried nonmetallic pipe crack detection algorithm for ground penetrating radar. Prog. Electromagn. Res. M 2018, 65, 79–90. [Google Scholar] [CrossRef][Green Version]
- Shruthi, R.B.V.; Kerle, N.; Jetten, V. Object-based gully feature extraction using high spatial resolution imagery. Geomorphology 2011, 134, 260–268. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, Z.; Fu, Y.; Yang, K.; Wu, Q.; Feng, Z. A New Identification Method for Surface Fissures from UAV Images Based on Machine Learning in Coal Mining Areas. Remote. Sens. 2020, 12, 1571. [Google Scholar] [CrossRef]
- Peng, J.; Qiao, J.; Leng, Y.; Wang, F.; Xue, S. Distribution and mechanism of the ground fissures in wei river basin, the origin of the silk road. Environ. Earth Sci. 2016, 75, 718. [Google Scholar] [CrossRef]
- Zheng, X.; Xiao, C. Typical applications of airborne lidar technolagy in geological investigation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 3. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. Uav for 3d mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Dhivya, R.; Prakash, R. Edge detection of satellite image using fuzzy logic. Clust. Comput. 2019, 22, 11891–11898. [Google Scholar] [CrossRef]
- Papari, G.; Petkov, N. Edge and line oriented contour detection: State of the art. Image Vis. Comput. 2011, 29, 79–103. [Google Scholar] [CrossRef]
- Verschuuren, M.; De Vylder, J.; Catrysse, H.; Robijns, J.; Philips, W.; De Vos, W.H. Accurate detection of dysmorphic nuclei using dynamic programming and supervised classification. PLoS ONE 2017, 12, e0170688. [Google Scholar] [CrossRef] [PubMed]
- Fujita, Y.; Shimada, K.; Ichihara, M.; Hamamoto, Y. A method based on machine learning using hand-crafted features for crack detection from asphalt pavement surface images. In Proceedings of the Thirteenth International Conference on Quality Control by Artificial Vision 2017, Tokyo, Japan, 14 May 2017; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10338, p. 103380I. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Nguyen, Q.-L. A novel method for asphalt pavement fissure classification based on image processing and machine learning. Eng. Comput. 2019, 35, 487–498. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Wu, B. Automatic detection of individual oil palm trees from uav images using hog features and an svm classifier. Int. J. Remote Sens. 2019, 40, 7356–7370. [Google Scholar] [CrossRef]
- Tao, P.; Yi, H.; Wei, C.; Ge, L.Y.; Xu, L. A method based on weighted F-score and SVM for feature selection. In Proceedings of the 2013 25th Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, X.; Li, Y.; Su, Q.; Liang, M. Mvpani: A toolkit with friendly graphical user interface for multivariate pattern analysis of neuroimaging data. Front. Neurosci. 2020, 14, 545. [Google Scholar] [CrossRef]
- Wang, X.; Wu, S.; Li, Q.; Wang, X. v-SVM for transient stability assessment in power systems. In Proceedings of the Autonomous Decentralized Systems. In Proceedings of the ISADS 2005, Chengdu, China, 4–8 April 2005. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, G.; Liang, D.; Yang, X.; Xu, B. An integrated skeleton extraction and pruning method for spatial recognition of maize seedlings in mgv and uav remote images. IEEE Trans. Neurosci. Remote Sens. 2018, 56, 4618–4632. [Google Scholar] [CrossRef]
- Naseri, M.; Heidari, S.; Gheibi, R.; Gong, L.H.; Sadri, A. A novel quantum binary images thinning algorithm: A quantum version of the hilditch’s algorithm. Opt. Int. J. Light Electron Opt. 2016, 131, 678–686. [Google Scholar] [CrossRef]
- Abu-Ain, W.; Abdullah, S.N.H.S.; Bataineh, B.; Abu-Ain, T.; Omar, K. Skeletonization algorithm for binary images. Procedia Technol. 2013, 11, 704–709. [Google Scholar] [CrossRef]
- Patel, R.B.; Hiran, D.; Patel, J.M. Fingerprint image thinning by applying zhang suen algorithm on enhanced fingerprint image. Int. J. Comput. Sci. Eng. 2019, 7, 1209–1214. [Google Scholar] [CrossRef]
- Saeed, K.; Tabędzki, M.; Rybnik, M.; Adamski, M. K3m: A universal algorithm for image skeletonization and a review of thinning techniques. Int. J. Appl. Math. Comput. Sci. 2010, 20, 317–335. [Google Scholar] [CrossRef]
- Qin, X.; Cai, C.; Zhou, C. An algorithm for removing burr of skeleton. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2004, 12, 28–31. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, G.; Xu, Z. Comparison of Calculation Methods-Based Image Fractal Dimension. Comput. Syst. Appl. 2011, 20, 238–241. [Google Scholar] [CrossRef]
- Chen, C.; Hu, Z. Research advances in formation mechanism of ground fissure due to coal mining subsidence in China. J. China Coal Soc. 2018, 43, 810–823. [Google Scholar] [CrossRef]
- Mao, C. Study on Fracture Distribution Characteristics of Coal Mining Collapse in Loess Hilly Area; China University of Geosciences: Beijing, China, 2018. [Google Scholar]







| Parameters | Value |
|---|---|
| Data type | Multispectral image |
| Flight date | 27 June 2019 |
| Flight height | 25 m |
| UAV model | M210RTK |
| Camera model | MS600pro |
| Focal length | 6 mm |
| Band range | 450 nm, 555 nm, 660 nm, 710 nm, 840 nm, and 940 nm |
| Ground spatial resolution (GSD) | 1.5 cm |
| Dataset | Background Information | Number of Training Sample | Number of Correct Classifications | Accuracy | AUC |
|---|---|---|---|---|---|
| BG | Bare Ground | 400 | 351 | 87.75% | 0.8802 |
| SC | Soil Crust | 400 | 349 | 87.25% | 0.9431 |
| GV | Green Vegetation | 400 | 374 | 93.50% | 0.9983 |
| Total | ALL | 1200 | 1074 | 89.50% |
| Crack | Value | Length/m | Width/m | Direction | Longitude | Latitude |
|---|---|---|---|---|---|---|
| 1 | Image | 0.359 | 0.026 | 14.0° | 110°13′41.178531″E | 39°4′44.335786″N |
| True | 0.327 | 0.022 | 15.0° | 110°13′41.193426″E | 39°4′44.342607″N | |
| Error | 9.8% | 18.2% | 1° | 0.202 m | ||
| 2 | Image | 0.296 | 0.015 | 10.7° | 110°13′40.746874″E | 39°4′43.968457″N |
| True | 0.280 | 0.013 | 12.0° | 110°13′40.787633″E | 39°4′43.985143″N | |
| Error | 5.7% | 15.4% | 1.3° | 1.446 m | ||
| 3 | Image | 0.974 | 0.038 | 40.4° | 110°13′40.771399″E | 39°4′43.251318″N |
| True | 0.925 | 0.034 | 42.0° | 110°13′40.781512″E | 39°4′43.271282″N | |
| Error | 5.3% | 11.8% | 1.6° | 0.451 m | ||
| 4 | Image | 1.079 | 0.030 | 18.2° | 110°13′41.945486″E | 39°4′43.885978″N |
| True | 1.040 | 0.027 | 20° | 110°13′41.996862″E | 39°4′43.914026″N | |
| Error | 3.8% | 11.1% | 1.8° | 2.624 m | ||
| 5 | Image | 0.525 | 0.033 | 13.1° | 110°13′41.288752″E | 39°4′43.778758″N |
| True | 0.506 | 0.030 | 16.0° | 110°13′41.338136″E | 39°4′43.806915″N | |
| Error | 3.8% | 10.0% | 2.9° | 2.487 m | ||
| Image Size/Pixel | Number of Crack/Pixels | Crack Number | Crack Rate (δ) | Dispersion Rate (σ) |
|---|---|---|---|---|
| 4000 × 3000 | 15,417 | 92 | 0.13% | 0.2128 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Hu, Z.; Yang, K.; Fu, Y.; Feng, Z.; Bai, M. The Surface Crack Extraction Method Based on Machine Learning of Image and Quantitative Feature Information Acquisition Method. Remote Sens. 2021, 13, 1534. https://doi.org/10.3390/rs13081534
Zhang F, Hu Z, Yang K, Fu Y, Feng Z, Bai M. The Surface Crack Extraction Method Based on Machine Learning of Image and Quantitative Feature Information Acquisition Method. Remote Sensing. 2021; 13(8):1534. https://doi.org/10.3390/rs13081534
Chicago/Turabian StyleZhang, Fan, Zhenqi Hu, Kun Yang, Yaokun Fu, Zewei Feng, and Mingbo Bai. 2021. "The Surface Crack Extraction Method Based on Machine Learning of Image and Quantitative Feature Information Acquisition Method" Remote Sensing 13, no. 8: 1534. https://doi.org/10.3390/rs13081534
APA StyleZhang, F., Hu, Z., Yang, K., Fu, Y., Feng, Z., & Bai, M. (2021). The Surface Crack Extraction Method Based on Machine Learning of Image and Quantitative Feature Information Acquisition Method. Remote Sensing, 13(8), 1534. https://doi.org/10.3390/rs13081534








