Abstract
Although hyperspectral images capture very detailed information about the scanned objects, their efficient analysis, transfer, and storage are still important practical challenges due to their large volume. Classifying and segmenting such imagery are the pivotal steps in virtually all applications, hence developing new techniques for these tasks is a vital research area. Here, deep learning has established the current state of the art. However, deploying large-capacity deep models on-board an Earth observation satellite poses additional technological challenges concerned with their memory footprints, energy consumption requirements, and robustness against varying-quality image data, with the last problem being under-researched. In this paper, we tackle this issue, and propose a set of simulation scenarios that reflect a range of atmospheric conditions and noise contamination that may ultimately happen on-board an imaging satellite. We verify their impact on the generalization capabilities of spectral and spectral-spatial convolutional neural networks for hyperspectral image segmentation. Our experimental analysis, coupled with various visualizations, sheds more light on the robustness of the deep models and indicate that specific noise distributions can significantly deteriorate their performance. Additionally, we show that simulating atmospheric conditions is key to obtaining the learners that generalize well over image data acquired in different imaging settings.
1. Introduction
Hyperspectral images (HSIs) capture the spectral data for each pixel, and provide very detailed characteristics of the materials within a scene. Classification and segmentation of such imagery have been attracting research attention due to their wide practical applicability in various domains including biology, medicine, environmental monitoring, and remote sensing, among others [1]. By classification, we mean assigning class labels to specific hyperspectral pixels, while by segmentation—finding the boundaries of the same-class objects in the entire input hyperspectral scene. Hence, segmentation involves classification of separate pixels in this case. The HSI classification and segmentation techniques are commonly split into conventional machine learning [2] and deep learning approaches. The former algorithms require performing the feature engineering process, in which we manually design feature extractors to capture discriminative characteristics within the hyperspectral cube. Since the number of features can easily reach hundreds, this step is often followed by feature selection to determine a much smaller subset of the most important features (there are also techniques that execute feature extraction and selection simultaneously [3]). Although there exist very powerful hand-crafted feature extraction methods, such as those based on the multiscale covariance maps that are specifically designed to improve HSI segmentation [4], alongside hyperspectral data reduction algorithms that aim at revealing better representation of the input data [5], deep learning techniques have been continuously gaining research attention, as they benefit from automated representation learning. Additionally, they are often able to uncover features that are extremely difficult (or even impossible) to design by humans [6]. Due to the large volume of hyperspectral imagery, its transfer is time-consuming and costly, so is the manual analysis of newly acquired HSIs. Therefore, deploying automated algorithms for its efficient processing on-board satellites is an important science and engineering topic, and on-board artificial intelligence—employed both in the context of hyperspectral data reduction through band selection [7,8,9] or feature extraction [10], and HSI analysis aiming at extracting the value from raw data—has a potential to speed up adoption of hyperspectral analysis in emerging use cases.
To effectively deploy machine learning HSI analysis algorithms on-board a satellite, we need to tackle not only the challenges related to the target hardware constraints, being the limited amount of available memory and computational power, but also those concerned with the acquired data [11]. The data acquisition process, and the characteristics of the captured hyperspectral imagery are dependent on various environmental and external factors, being the latitude of the satellite (alongside the target latitude), the atmospheric conditions, ground reflectance, and many more [12]. Additionally, the acquired image data can be contaminated by noise, whose source may be very different, and includes sensor’s thermal characteristics or even its failure. However, understanding (and quantifying) the impact of such noise on the deep models deployed for HSI classification and segmentation remains under-explored [13,14]. These technological difficulties hamper the wide-spread adoption of hyperspectral imaging satellite systems, and quantifying the robustness of on-board deep learning (against low-quality or contaminated data) is pivotal to successfully deploy them in practice.
1.1. Contribution
In this paper, we thoroughly investigate the robustness of deep learning HSI segmentation algorithms against various atmospheric conditions and noise distributions that may affect the test data in the target operational environment. Specifically, we analyze spectral and spectral-spatial convolutional neural networks (CNNs) which have not only been widely applied for HSI classification [6,15,16,17], but are also easy to be deployed in the target data processing units, exploiting e.g., field-programmable gate arrays (FPGAs) [11,18]. Since we are currently working on Intuition-1—a 6U-class satellite with a data processing unit enabling on-board data processing acquired via a hyperspectral instrument—we focus on our default acquisition targets in the atmospheric simulations, being urban and rural areas in Central Europe. Therefore, one of our objectives is to understand if we can skip the atmospheric correction step while preprocessing the hyperspectral image data on-board, and still maintain high-quality operation of deep models. Additionally, Intuition-1 will exploit an FPGA to execute on-board artificial intelligence, as it allows for massively parallel processing (very well-fitted to deep learning algorithms), it is energy-efficient [19], it is commonly designed to support safety-critical applications [20], and can be optimized in the context of memory usage [21]. Additionally, the satellite will be reprogrammable in the sense that it will be possible to uplink a new machine learning model, perhaps trained over an updated or new training set, while Intuition-1 is in-orbit and becomes operational. Because of these reasons—although there exist classical machine learning approaches tailored for the hyperspectral data analysis—we focus on deep learning techniques in this work. Specifically, we investigate CNNs, as they are the architectures that are currently available and heavily optimized in the available development platforms for efficient inference [22]. Overall, the contributions of this work are as follows:
- We simulate a wide range of atmospheric conditions affecting the characteristics of the resulting hyperspectral data cubes. We consider different atmospheric profiles, aerosol models, and aerosol optical thickness to precisely mimic the real acquisition settings.
- We generate Gaussian, impulsive, and Poisson noise and inject it into hyperspectral imagery. These noise distributions are exploited to simulate real noise that might be the result of hardware characteristics, failures, and much more.
- We use our simulators to preprocess the well-known benchmark hyperspectral scenes, and to quantify the robustness and generalization abilities of spectral and spectral-spatial CNNs against varying-quality data. By robustness we mean the capability of maintaining high-quality operation over data contaminated with noise or acquired in atmospheric conditions different than a training sample used for learning a model.
- We provide a battery of visualizations, and perform a thorough experimental verification to help better understand the impact of specific disturbances on the overall performance of CNNs.
1.2. Paper Structure
This paper is structured as follows. In Section 2, we review the state of the art in HSI classification and segmentation, and discuss the current approaches towards dealing with low-quality data in this context (e.g., noisy data points or noisy labels). Section 3 presents the spectral and spectral-spatial CNNs that are investigated in this work, alongside our strategies for simulating varying atmospheric conditions and for injecting noise of different distributions into the test hyperspectral data. Additionally, we discuss our technique for splitting the benchmark hyperspectral scenes into training and test subsets that ensures that there is no training-test information leakage across them. The experimental results are presented and discussed in Section 4. Finally, Section 5 concludes the paper.
2. Related Literature
The problem of segmenting HSI is often approached in a pixel-wise manner without taking into account the spatial correlations among the neighboring pixels [23]. In such cases, each individual pixel is classified independently based on its spectral signature, hence HSI segmentation consists in solving the classification task for all the pixels in the image, with each pixel treated as a point in a multi-dimensional input space of spectral coordinates. For this reason, the process of segmenting an HSI is commonly termed as HSI classification when performed in a supervised manner, even if the spatial information is exploited [24]. In many works, the HSI segmentation term is used only when considering unsupervised segmentation, thus splitting the HSI into super-pixels or larger regions of uniform properties. This is actually in contrast with the terminology adopted in the image processing community [25], where segmentation is categorized as supervised and unsupervised, while image classification is understood as assigning a label (or labels) to the entire image based on its contents. In this section, we review the state-of-the-art methods for supervised and unsupervised segmentation of HSI (Section 2.1) and we discuss the approaches towards dealing with the noisy and low-quality data (Section 2.2).
2.1. Hsi Segmentation
The first attempts to segment HSIs were based on the techniques commonly applied to classify highly-dimensional data. They encompassed the use of the k-nearest neighbor classifier [26], support vector machines (SVMs) [27], or Gaussian mixture models that presented some level of noise robustness [28]. While these techniques can be employed to classify the spectral signature of each individual pixel, sparse representation of signals helps reduce their dimensionality significantly based on a learned dictionary [29].
Sparse representation topped with machine-learned classifiers dominated the scene of hyperspectral data classification [30], before deep learning emerged with its powerful capabilities. While deep belief networks [23] and recurrent neural networks [31] were employed for elaborating improved spectral features, the use of CNNs with 3D kernels allowed for combining the spectral dimension with spatial coordinates to extract the contextual information [6,32]. The spatial-spectral techniques are characterized by intrinsic robustness against the noise [33], hence we focus on them further in this section. There were also some attempts reported to extract the spatial-spectral features without employing deep learning, for example using quaternion-based multiscale analysis [34]. While such approaches require less data for training, which is a clear advantage over deep learning, the latter remains the intensively explored mainstream direction. Recently, Okwuashi and Ndehedehe introduced a deep network combined of multiple SVMs as neurons [35]. The network classifies each pixel based on its spectral signature, while ignoring the spatial component. In fact, this is an SVM ensemble which increases the performance of individual SVMs and allows them to deal with multi-class problems [36].
Zhao and Du exploited a simple CNN composed of several convolutional layers to extract the spatial features from principal components of the spectral bands [37]. These deep features are coupled with spectral information extracted with local discriminant embedding and classified using logistic regression. Gao et al. demonstrated that both spatial and spectral information can be jointly extracted using a CNN with 3D kernels applied in the input layer [6]. The recent advancements in this field consist in proposing deeper architectures capable of extracting more informative features. This encompasses the use of densely connected CNNs [38], attention mechanisms [39], or multi-branch networks [40,41]. Additionally, many attempts are aimed at elaborating lightweight models [42] that are suitable for on-board processing. Paoletti et al. exploited the ghost module [43] that combines light convolutional layers with linear transformations that reduce the dimensionality of the input data, hence decreasing the computational cost. Their Ghostnet [44] achieves classification scores competitive to the state-of-the-art techniques at much lower computational requirements.
In their recent review, Zhou and Prasad [45] focus on the challenges concerned with the lack of labeled data which they identify as a major obstacle in deploying hyperspectral image analysis based on deep learning. Among the solutions that can help deal with limited amount of ground-truth data, are the unsupervised [46] and semi-supervised [47,48] approaches, including active learning [49]. In [50], Protopapadakis et al. utilized a very small portion of labeled examples (constituting less than 0.08% of the available data) to train their deep models. Additionally, a semi-supervised technique was used to process unlabeled data, and to estimate soft labels which are later exploited to improve the training process. The experimental study proved that this approach may not only help effectively deal with extremely limited ground-truth datasets, but also allows for obtaining the state-of-the-art performance. The possibility of exploiting unsupervised learning for segmenting HSI was tackled in our recent work [51]. We demonstrated that recurrent neural networks allow for extracting latent representation which can be topped with a simple clustering algorithm to split the HSI into regions of high similarity. Importantly, we demonstrated that this maps well onto the regions having identical ground-truth labels. Other approaches to deal with limited ground-truth labels embrace transfer learning [52,53] and data augmentation [54,55]. The latter may also include test-time data augmentation [56] that consists in generating more samples from a sample presented for classification. The classification is obtained by agglomerating the classifier’s responses for all the samples, including the original one and those that were generated. Finally, there are machine learning techniques that can be successfully learned even using very limited amounts of training data. There exist efficient tensor-based linear and nonlinear models for segmenting HSI which benefit from a low number of trainable parameters, hence require smaller training samples [57,58]. In [59], overlapping 3D tensor patches are extracted from an input HSI, and they are modelled as the summation of intrinsic spatial-spectral tensors alongside the corresponding variation tensors. Then, the intrinsic spatial-spectral tensor is decomposed into three matrices and a core tensor by the Tucker decomposition—a tensor-based dictionary learning is exploited to extract more discriminative tensor features for pixel-wise classification, which is finally performed using SVMs. Interestingly, such tensor-based techniques may be also utilized for dimensionality reduction of hyperspectral imagery [60].
The problem of limited labeled data is also reflected in the way the HSI segmentation methods are trained and evaluated. Most of the benchmarks are composed of a single image with annotated pixel-wise class labels, which means that the training data, as well as the data used for testing are extracted from the very same image. Such an approach is correct as long as there is no information leakage between the test and training samples. For the methods based on spectral features, it is sufficient to prevent the same pixel from being incorporated into the training and test set at once. However, for the methods underpinned with the spatial analysis, the whole neighborhood of the pixels in the test set must be excluded from training, which has been overlooked in many works. This problem was highlighted in our earlier paper [16] and it was also spotted by other researchers [61,62]. Overall, in many cases this leads to reporting overoptimistic quantitative scores which may not be achievable in real-life scenarios.
2.2. Dealing with Low-Quality Data
Insufficient amounts of ground-truth data limit the capabilities of investigating whether and how far the proposed techniques are robust against low quality of the data being processed. In practical scenarios, the main factors affecting the image quality are concerned with the sensor noise and atmospheric distortions [33]. There are two general ways to deal with these problems, namely to improve the data quality prior to proper HSI segmentation, or to make the segmentation techniques intrinsically robust against such distortions.
The problem of image denoising has been intensively explored over the years, with a wide range of methods proposed, including those based on deep learning [63], to deal with various types of noise that can be observed in images of manifold modality [64]. Basically, the methods elaborated for grayscale [65] images can be applied in a band-wise manner to enhance HSIs. Moreover, the techniques developed for processing color [66] or multispectral [67] images, as well as those for enhancing the volumetric data [68], can be adopted for HSI denoising. In addition to analyzing the spatial dimensions, they benefit from the correlations across the spectral bands. Similarly, the methods developed specifically for HSIs commonly operate in the spatial-spectral domain [69,70]. This can be achieved relying on tensor-based techniques [71] that were summarized in a review by Lin and Bourennane [72]. Many of the proposed methods were tailored to deal with an assumed type of noise. While this is sufficient for images with the simulated noise, taking such assumptions limits the performance in real-life scenarios. Therefore, the recently reported attempts are aimed at dealing with mixed noise that better reflects the operating conditions [73] and allows for obtaining satisfactory results for real data. Similarly as for HSI segmentation, 3D CNNs that operate in the spatial-spectral domain [74] are exploited for noise removal. In [75], Wei et al. demonstrated that their fully convolutional 3D quasi-recurrent network with residual connections is highly effective in removing simulated and real noise in HSIs.
While the existing noise reduction algorithms allow for enhancing the quality of HSIs, developing noise-robust HSI segmentation technique is also an actively researched field. Especially when CNNs are employed, there may be severe overlap between the operations executed in the convolutional layers for noise removal and HSI segmentation. This means that denoising the image before running the segmentation or classification algorithm may be suboptimal.
Among the first attempts towards noise-robust HSI data classification, was the divide-and-conquer approach reported by Prasad et al. [28]. A redundant discrete wavelet transform (RDWT) is employed to partition the highly-dimensional input space into several less-dimensional subspaces, in which the HSI data are classified independently. They demonstrated that an ensemble created out of these classifiers offers high classification scores even for low signal-to-noise ratios. Li et al. reported that the RDWT-based features can be classified using an SVM, as well as with the nearest-regularized-subspace classifier to increase the robustness against the noise [76].
Zhan et al. claimed that robustness against the noise can be achieved by splitting an HSI into super-pixels, so that each super-pixel is classified as a single entity [77]. According to the authors, this provides robustness against the noise and low data quality attributed to the atmospheric distortions, but no experimental evidence was reported in the paper. The concept of classifying the super-pixels was also explored by Huang et al., who exploited a sparse representation model to achieve robustness against the mixed noise [78]. Duan et al. proposed to employ relative total variation (commonly used for noise reduction) to extract multi-scale structural features [79].
Among the many works reported on using deep learning for HSI segmentation, just a few consider the problem of low-quality data. Recently, Li et al. proposed a capsule network that is based on maximum correntropy criterion to deal with the noise and outliers in the input HSI data [80]. Although the method obtains competitive classification scores for real-life data, it is not entirely clear whether they are indeed attributed to the claimed intrinsic noise robustness. Voulodimos et al. exploited the discrete cosine transform (DCT) to convert the HSI into the frequency domain, and these data were fed into a CNN [81]. They demonstrated that the DCT-based preprocessing allows for obtaining high robustness against the Gaussian and noise-and-pepper noise.
Importantly, not only the quality of the HSI data may be affected in real-life scenarios, but also the ground-truth labels are often incorrect which leads to elaborating suboptimal models. While the problem of noisy labels is well-known to the machine learning society, with a number of generic techniques proposed [82,83], it has also been analyzed in the context of training the classifiers with remotely-sensed data [84]. Jiang et al. proposed a label noise cleansing algorithm based on random label propagation and reported an extensive experimental study on how the noisy labels affect the classification performance [85]. Tu et al. considered several types of label noise and investigated its influence on the HSI data classification with different classifiers [86].
Overall, while the problems of atmospheric correction [87,88] (discussed in detail later in Section 3.3.1) and noise removal for HSIs have been deeply investigated in the literature, relatively little attention has been paid to verify how HSI segmentation methods behave when applied to the low-quality data. This is particularly important when the type of these distortions is unknown or changeable over time. Importantly, the robust techniques are a better choice for spaceborne platforms, as they do not require costly preprocessing.
3. Methods
In this section, we summarize the deep network architectures that are investigated in our study—they include both spectral and spectral-spatial CNNs (Section 3.1). Then, we discuss the hyperspectral datasets that are used in the experimentation, alongside our training-test splits (Section 3.2). In Section 3.3, the simulated atmospheric conditions that affect the acquired hyperspectral cubes are presented, whereas Section 3.4 focuses on the noise distributions that are injected into the test data to mimic real-life noise that may eventually happen on-board an imaging satellite.
3.1. Deep Network Architectures
To investigate the classification abilities of various CNNs, we focus on both spectral and spectral-spatial CNN architectures. In the former case, only the spectral information about a pixel is exploited to elaborate its class label while the inference, whereas spectral-spatial CNNs benefit from both spectral and spatial information captured in an input patch. In Table 1, we present the architectures of the investigated deep models—the spectral network (1D-CNN) inspired by [16], alongside two spectral-spatial CNNs (2.5D-CNN and 3D-CNN [17], with 2.5D-CNN inspired by [6]). Although both spectral-spatial models operate on hyperspectral patches, 2.5D-CNN convolutional kernels span the entire spectrum of B bands. On the other hand, we utilize small () kernels in 3D-CNN to effectively capture local features that may be manifested in specific (often tiny) parts of the spectrum [17].

Table 1.
The convolutional neural network (CNN) architectures investigated in this work. For each layer, we report its hyper-parameter values, where k stands for the number of kernels (filters), s is stride, B indicates the number of hyperspectral bands, is the size of the input patch, and c is the number of classes in the dataset. The Conv, MaxPool, and FC layers are the convolutional, max-pooling, and fully-connected ones, whereas ReLU is the rectified linear unit activation function.
3.2. Datasets and Training-Test Splits
In this work, we focus on four well-established hyperspectral images that were manually delineated and are commonly used for validating the emerging HSI segmentation techniques [16]:
- The Indian Pines (IP) hyperspectral scene ( pixels) was captured over the Indian Pines site in North-western Indiana, USA, with a spatial resolution of 20 m. It presents agriculture, forest, and natural perennial vegetation areas, and encompasses 16 classes (see the characteristics of all sets gathered in Table 2). The number of all bands was reduced to 200 (from the original 224 bands) through removing those that cover the region of water absorption. This dataset was acquired using the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor.
 Table 2. The number of samples (pixels) for each class in the investigated datasets.
Table 2. The number of samples (pixels) for each class in the investigated datasets. - The Salinas Valley (SV) hyperspectral scene ( pixels) was captured over the Salinas Valley area in California, USA, with a spatial resolution of 3.7 m. The image presents different sorts of vegetation, corresponding to 16 classes. The original set consists of 224 bands, however 20 bands were removed by the authors of SV due to either atmospheric absorption or noise contamination [16] (finally, 204 bands remained in the resulting hyperspectral cube; see http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes; last access: 25 March 2021). This dataset was acquired using the AVIRIS sensor.
- The Pavia University (PU) hyperspectral scene ( pixels) was captured over Pavia University in Lombardy, Italy, with a spatial resolution of 1.3 m. The image presents an urban scenery with nine classes, and contains 103 bands, as 12 most noisy bands (out of 115 originally acquired) were removed by the authors of this set. This dataset was acquired using the Reflective Optics System Imaging Spectrometer (ROSIS) sensor.
- The University of Houston (Houston) hyperspectral scene ( pixels) was captured over the University of Houston campus, USA, with a spatial resolution of 1 m, using an ITRES CASI 1500 hyperspectral imager. The image includes 48 bands, and presents 20 urban land-cover/land-use classes. This dataset was utilized in the 2018 IEEE GRSS Data Fusion Challenge—Fusion of Multispectral LiDAR and Hyperspectral Data [89].
Although Monte-Carlo cross-validation has been widely exploited in the literature to quantify the generalization of HSI classification and segmentation algorithms, we showed that this approach can easily lead to obtaining over-optimistic estimation of the performance of deep models [16]. It affects spectral-spatial techniques which utilize the pixel’s neighborhood information while elaborating its class label, and such neighboring pixels may fall into both training and test sub-parts of the scene, as the training and test pixels are commonly sampled from the very same image.
To tackle the problem of the training-test information leakage, we utilize the patch-based training-test splits obtained using our division technique [16]. For each scene, we elaborate separate folds—we visualize our splits for IP, SV, PU, and Houston in Figure 1, Figure 2 and Figure 3 (the training patches, containing all training pixels are rendered in yellow, and the remaining parts of the image constitute the test set ). For the Houston scene, being the most challenging one, we extract two data split versions (Version A and Version B). In Version A, the patches are of size , and they are drawn until at least samples are present in the training set (). On the other hand, in Version B, the dataset is divided into a grid ( blocks of the same size, being ), and each fold contains 20 random blocks for training. Therefore, Version A encompasses patches that are sampled more heterogeneously across the entire scene, whereas the number of training pixels is significantly larger in Version B.

Figure 1.
The false-color version of the Indian Pines (IP) scene, alongside its ground-truth manual delineation and the folds obtained using our patch-based splitting technique [16]. The training patches, containing all training pixels, are rendered in yellow, whereas all other areas constitute the test set.

Figure 2.
The false-color versions of Salinas Valley (SV) and Pavia University (PU), alongside their ground-truth manual delineations and the folds obtained using our patch-based splitting technique [16]. The training patches, containing all training pixels, are rendered in yellow, whereas all other areas constitute the test set.

Figure 3.
The color-composite version of Houston, alongside its ground-truth manual delineations and the folds obtained using our patch-based splitting technique [16]. The training patches, containing all training pixels, are rendered in yellow, whereas all other areas constitute the test set.
In Table 3, Table 4 and Table 5, we gather the number of training and test pixels for each data split. We can appreciate that the elaborated folds are not only extremely imbalanced, but they also contain classes that are either present in the test set only (with no examples in the corresponding training sample), or vice versa. Such cases, although being a real-life scenario, have to be taken into account while quantifying the performance of the machine learning algorithms learned over the corresponding training samples, as the models were not able to learn characteristics of the classes that were not captured in ’s. For more details on our approach towards calculating the classification metrics in such cases, see Section 4.1.

Table 3.
The number of pixels in each training and test set within each fold ( and , respectively) for the IP and SV scenes—we have extracted four IP and five SV folds. For each fold, we boldface the classes that are not present in , but they are captured in . Additionally, we underline those classes that are not included in , but are available in .

Table 4.
The number of pixels in each training and test set within each fold ( and , respectively) for the PU scene—we have extracted five folds. For each fold, we boldface the classes that are not present in , but they are captured in .

Table 5.
The number of pixels in each training and test set within each fold ( and , respectively) for the Houston scene—we have extracted five folds in each version (Version A and Version B). For each fold, we boldface the classes that are not present in , but they are captured in .
3.3. Hyperspectral Analysis in Varying Atmospheric Conditions
Although the atmospheric correction step is not time-consuming or computationally expensive, it is difficult to determine the atmospheric profile that should be used for this correction during the operation of a satellite. In this work, we assume that we take images of Central Europe (e.g., no tropical climate). Therefore, we should (at least) cope here with urban and rural sites with mid-latitude values, as Poland is considered our primary target. In the following sections, we summarize the atmospheric profiles (Section 3.3.1), aerosol models (Section 3.3.2), and the Aerosol Optical Thickness variants (Section 3.3.3) that were utilized to establish the atmospheric disturbance variants that reflect our on-board acquisition conditions (Section 3.3.4).
3.3.1. Atmospheric Profile
The atmospheric profile is used to represent the atmospheric gaseous absorption which takes place due to oxygen (O), ozone (O), water vapor (HO), carbon dioxide (CO), methane (CH), and nitrous oxide (NO). Four of them (O, CO, CH, and NO) are assumed constant and uniformly mixed in the atmosphere. Additionally, the HO and O concentrations depend on the time and the location of the acquisition, therefore their intensities define an atmospheric profile.
There are standard atmospheric profiles defined by water vapor and ozone concentrations in the MODTRAN6 radiative transfer algorithm (Table 6) [90]. The general recommendations are to select one of these predefined profiles based on the available water vapor information. If no water vapor information is available, then the selection should be based on the expected surface temperature. Furthermore, the Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes (FLAASH) technique exploits the rounded latitude and date of acquisition to effectively determine the atmospheric profile (Table 7) [87,91,92]. Here, we can observe that there are only three standard profiles (MLW, SAS, and MLS) used for Poland, being our default location that will be considered in the experimentation.

Table 6.
Standard atmospheric profiles available in the MODTRAN radiative transfer tool.

Table 7.
The rounded latitude and date of acquisition can be utilized to determine the atmospheric profile according to the Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes approach. The latitude of Poland, being our default coordinates, are boldfaced.
3.3.2. Aerosol Model
The aerosol model is used to represent the atmospheric scattering, which takes place due to different kinds of aerosol components: (1) dust-like, (2) water-soluble, (3) soot, (4) sea-salt, (5) mineral, (6) sulfuric acid, (7) volcanic ash, (8) meteoric, (9) sulfate, and (10) biogenic. Each type of aerosol affects scattering differently, but many useful cases could be defined with only (1–4), often called the basic components of the aerosol models. There are several inorganic ions constituting water-soluble aerosols: sodium (Na), ammonium (NH), potassium (K), magnesium (Mg), calcium (Ca), nitrate (NO), and sulphate (SO). Similarly, only three of them are usually reported in the collected data and forecasts, as these are the most relevant ones: sulphate, nitrate, and ammonium [93,94]. To handle the imaging process of Central Europe [95], we focus on rural and urban sites. The imaged area is expected to be quite vast (several dozens of kilometers in width), thus we should not consider the whole image as having exclusively only rural or only urban properties. For this reason, we create several mixed aerosol models using the rural and urban models as a baseline. Additionally, we use the continental model as it may be even more accurate for some scenes in Europe [96]. All aerosol models used in further research are summarized in Table 8.

Table 8.
Components of the investigated aerosol models in rural and urban sites of Central Europe.
3.3.3. Aerosol Optical Thickness
The Aerosol Optical Thickness (AOT) is a non-unit measure which expresses how strong is the influence of aerosols on optical phenomena [97]. The value may differ for different wavelengths, and a single value is commonly given for the 550 nm or 500 nm wavelength. Usually, the expected range for AOT is 0.1–1.2, where the values below 0.1 correspond to a totally clear sky (the best possible visibility). For Europe, most of the time AOT should be within a range of 0.1–0.3, and huge pollution above the city or a burning forest could result in values around 0.7–0.8. Importantly, this value can vary within a scene—the radiative transfer model assumes a single AOT value, being an average for a target, as we can give only one value for 550 nm. Therefore, we consider , corresponding to the clear sky, standard acquisition conditions, higher pollution, and extreme scenario, respectively.
3.3.4. The Resulting Atmospheric Disturbance Variants
In Table 9, we gather the atmospheric disturbance variants that are expected for the operational phase of Intuition-1 (note that we simulate the acquisition process that will be performed in the future; see the scan dates). The ID 0 variant does not introduce any disturbance into the original hyperspectral data, hence there is no correction—we only scale the data with the solar irradiance profile.

Table 9.
The atmospheric disturbance variants reflecting the assumed acquisition scenarios (Central Europe, urban and rural areas, with Poland being our default target).
To visualize the impact of an atmospheric disturbance variant on an image, we render an example band of the Houston scene for all variants in Figure 4. Similarly, the spectral profiles averaged for all pixels, and for all PU classes (Figure 5) indicate that the image characteristics can substantially change for different acquisition scenarios. Therefore, such cases may potentially deteriorate the classification abilities of supervised learners, if the discriminative features were capturing e.g., pixel intensities.

Figure 4.
An example part of the Houston scene with the investigated atmospheric disturbance variants applied (band 180)—the disturbances significantly affect the output image characteristics, hence may influence the performance of the classification algorithms.
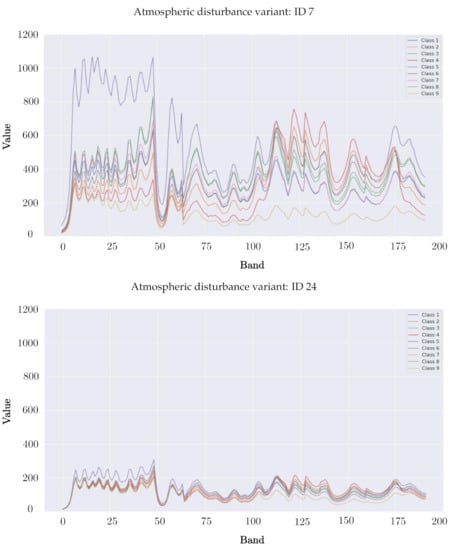
Figure 5.
The spectral profiles (averaged across all pixels, and for all classes) of the PU classes obtained for two example atmospheric disturbance variants (with IDs 7 and 24).
3.4. Hyperspectral Analysis in the Presence Of Noise
A hyperspectral cube can be represented as a three-dimensional tensor , where W and H denote its width and height, and B is the number of bands. Then, a corresponding noisy HSI () becomes:
where N is the noise signal. In this work, we consider three noise models:
- Gaussian noise—the probability density function p of a Gaussian variable x iswhere and are the mean (here, ) and variance ( is standard deviation, and in our study). This signal-independent noise models thermal and quantization disturbances [13].
- Impulsive noise (salt-and-pepper), which simulates a situation when a sensor gets saturated (it leads to obtaining “white” pixels), or when it is not able to acquire any data (“black” pixels) [98]. In this study, we draw the “white” and “black” contamination with equal probability.
- Poisson (shot) noise, with the probability density function f given as:where denotes the expected (average) value. Poisson noise is inherently related to light measurements, and can be used for modeling signal-dependent photon noise [99].
To verify the ability of coping with noisy data, we contaminate only test () subsets. Hence, we do not modify the corresponding training data, and the models are trained over non-contaminated sample. We randomly pick test pixels for contamination, where —in Figure 6, we render an example for the PU scene, and visualize all ground-truth pixels, alongside those pixels that would be contaminated by the investigated noise distributions for all values. For all affected pixels (selected randomly), we inject noise into all hyperspectral bands. A set of example spectral profiles for all classes (averaged across all pixels) in PU are gathered in Figure 7 for and . Although the shape of the spectral curves remains unchanged, we can spot visible local fluctuations, especially when the number of contaminated test pixels is large (). It is in contrast to simulating different atmospheric disturbance variants which often leads to significantly varying spectral characteristics (Figure 5).

Figure 6.
All ground-truth pixels in PU (rendered in white), alongside those pixels that would be affected by our noise contamination for all investigated values (). For simplicity, we present all pixels with ground-truth labels, not just the test pixels that would result from our patch-based data splits—in the experimental study, we contaminate test sets only.
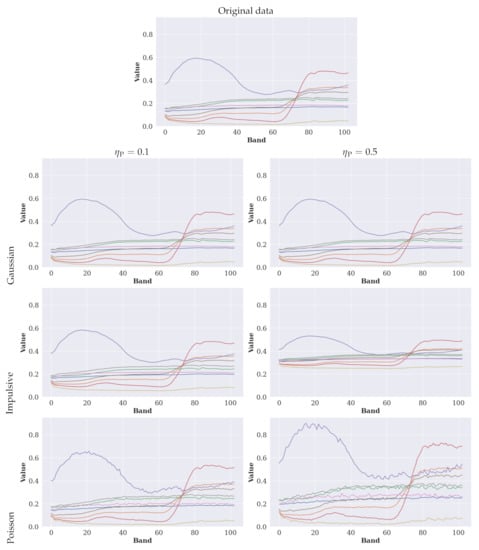
Figure 7.
The spectral profiles (averaged across all pixels) of all PU classes (for brevity, we omit the color legends in the plots—different colors present different classes) in the original data and the data contaminated with all noise distributions for and . We normalize the values to the range for readability.
4. Experimental Results and Discussion
In this section, we discuss our experimental setup (Section 4.1), and present the experimental results obtained in our two experiments. The objective of Experiment 1 (Section 4.2) was to understand the impact of varying atmospheric conditions (affecting the acquired hyperspectral cubes) on the classification abilities of deep models, whereas in Experiment 2 (Section 4.3) we investigated the influence of different noise distributions that were injected into the test data on the models.
4.1. Experimental Setup
Our deep models were implemented in Python 3.6 with Tensorflow 1.12—the implementations are available at https://github.com/ESA-PhiLab/hypernet/ (last access: 25 March 2021). The training (ADAM optimizer [100] with the learning rate of , , and ) terminated if after 15 consecutive epochs the accuracy over the validation set ( of all training pixels) did not increase.
To quantify the classification performance of the deep models, we reported the overall accuracy (OA) and the balanced accuracy (BA), where BA is the average of recall obtained on each class, and the values of the Cohen’s kappa coefficient (). This coefficient shows us how much better the classifier was than a random one which guessed the label based on the available data distribution, and it is given as , where and are the observed and expected agreement (assigned vs. correct class label), respectively, and [101]. In this paper, we will report when we refer to . As mentioned in Section 3.2, there were folds in which there were classes that were not captured within the corresponding training samples, but they were present in the test sets. Since the underlying models were unable to learn such classes from the training samples, we additionally calculated the prime metrics (OA’, BA’, and ’), for which we excluded the classes that are included in of a given fold, but were not captured in its . All the metrics reported in this paper were obtained for the test sets (unless stated otherwise), and they were averaged across all folds (for each configuration and for each fold, we ran training five times and averaged the results). Finally, although refining training sets, e.g., through selecting the best subsamples of all available training examples could enhance the abilities of supervised learners (both deep learning-powered and classical [36]), we exploited all available training examples in this work. This approach helped us focus on understanding the behavior of the CNN models in specific scenarios (different atmospheric conditions and noisy test data), when trained over the full ’s.
4.2. Experiment 1: Hyperspectral Analysis in Varying Atmospheric Conditions
The objective of this experiment was to verify if the spectral and spectral-spatial CNNs (we focus on 1D-CNN and 2.5-CNN here) are able to cope with various atmospheric conditions that may affect the resulting hyperspectral cube during its acquisition. We use the atmospheric variants discussed in Section 3.3 to radiometrically process the original datasets, and to simulate the corresponding atmospheric condition through employing the 6S model. In 6S, the corrected reflectance is [102,103]:
where , and , , and are the coefficients obtained from the model, being the inverse of the transmittance, the intrinsic atmospheric radiance, and the spherical albedo of the atmosphere, respectively, and L is the observed (original) radiance. In Figure 8, we visualize all processing steps and artifacts generated in this experiment.
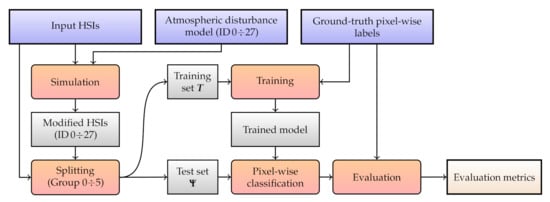
Figure 8.
A flowchart of Experiment 1. Blue rectangles indicate the input data, the red ones are the actions, and the gray ones present the artifacts, with the final outcome annotated with light gray.
The processed datasets are distributed across the folds gathered in Table 10 (these folds were independent from the folds discussed in Section 3.2)—here, we considered two additional scenarios. In (I) we randomly divided the atmospheric variants into folds, and in (II) we manually selected the most challenging atmospheric conditions, being the variants with IDs: 13, 17, 18, 21, 22, 24, and 27 (Table 9). Finally, we divided the folds into the following groups with the training and test folds over which the deep models were trained and tested, respectively (note that the training data within Group 0 contained only ID 0, being the original hyperspectral cube without any additional atmospheric profile, aerosol model or AOT applied, hence can be considered a baseline scenario):

Table 10.
The distribution of atmospheric condition variants (for details, see Table 9) across the folds.
- Group 0 (G0)—Training folds (): Variant 0, test folds (): all other variants.
- Group 1 (G1)—Training folds (): Fold 1, Fold 2, Fold 3, test folds (): Fold 4.
- Group 2 (G2)—Training folds (): Fold 1, Fold 2, Fold 4, test folds (): Fold 3.
- Group 3 (G3)—Training folds (): Fold 1, Fold 3, Fold 4, test folds (): Fold 2.
- Group 4 (G4)—Training folds (): Fold 2, Fold 3, Fold 4, test folds (): Fold 1.
- Group 5 (G5)—Training folds (): Fold 1’, Fold 2’, Fold 3’, test folds (): Fold 4’.
Since in this experiment we were interested in understanding the differences obtained using models trained and tested over differently processed samples (and not necessarily in confronting different architectures with each other), we performed Monte Carlo cross-validation for 1D-CNN (over IP, SV, PU, and Houston), and maintained the number of training pixels sampled from each variant as suggested in [6]. Note that the same pixels were sampled to a training set from each atmospheric correction variant. Hence, if a pixel with coordinates in a hyperspectral cube was selected for inclusion in , the very same pixel was picked from all atmospheric condition variants. On the other hand, we exploited our patch-based splits discussed in Section 3.2 for 2.5D-CNN (we focused on IP, SV, and PU), in order to avoid any training-test information leakage (it did not happen for spectral models [16]). Here, we did not exploit Houston for 2.5D-CNN, as its training time would become infeasible due to extremely large ’s, especially for the version B of this dataset (see the example training times for the original of such spectral-spatial models in Section 4.3). In Table 11 and Table 12, we present the average training and inference times of both models run on NVIDIA GTX 1060 (we did not impose the maximum number of training epochs, and exploited the early stopping only), together with their numbers of trainable parameters, and the floating point operations (note that the number of parameters may have varied for the very same architecture, as it was also dependent on the characteristics of the target data, as presented in Table 1). Although we were unable to confront these times across the models directly because they were trained over different data splits, we could appreciate the fact that both CNNs offered fast operation. It makes them potentially applicable in a variety of Earth observation use cases, where rapid inference is critical to ensure short response times.

Table 11.
The average training () and inference () times (both in seconds) obtained using 1D-CNN for all investigated datasets (1D-CNN has 1.2 million trainable parameters, and 50 MFLOPs in all scenarios). The metric reflects the total inference time over all test pixels.

Table 12.
The average training () and inference () times (both in seconds) obtained using 2.5D-CNN for all sets, together with the numbers of trainable parameters (#P, millions), and the floating point operations (in mega FLOPs). The metric reflects the total inference time over all test pixels.
In Figure 9 and Figure 10, we collect the results obtained over all investigated splits using 1D-CNN and 2.5-CNN, respectively. We indicate the metrics elaborated over both training and test folds (containing different atmospheric condition variants). Additionally, we present the differences between such measures—the negative values above the bars show the drop in the corresponding quality metric for the test folds, when compared with the training ones. We can observe that both models trained over Variant 0 manifested significantly worse generalization abilities over other atmospheric variants (G0). Although the drop in all metrics was observable in the pairwise comparison (training vs. test folds) for other groups, the most notable deterioration happened for the most challenging G5 group. Finally, we could appreciate that the prime metrics, being the ones that were calculated without taking into account the test classes which were not included in the corresponding training sets, were higher than the non-prime counterparts (encompassing all classes). Therefore, including such classes in test sets, and using them while calculating quality metrics, may have resulted in over-pessimistic classification performance estimations, as the underlying models were unable to learn these classes, and penalizing them for not recognizing such pixels unnecessarily decreased the measures.
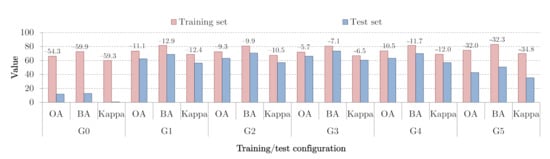
Figure 9.
The results obtained using 1D-CNN for all investigated groups in the Monte-Carlo cross-validation setting. We present the metrics obtained over both training and test sets, alongside the differences between the metrics elaborated for and .

Figure 10.
The results obtained using 2.5D-CNN for all investigated groups using our patch-based training-test data splits. We present the metrics obtained over both training and test sets, alongside the differences between the metrics elaborated for and .
Although the results indicated that the generalization abilities of the models trained over specific data samples, processed using various atmospheric conditions, may not have easily transferred to high-quality classification in the case of test imagery acquired in significantly different imaging scenario, we could observe that including such preprocessed training samples in led to notably better generalization (see the G0 groups vs. all other groups for both spectral and spectral-spatial architectures). Thus, expanding training sets with such artificially synthesized data samples (reflecting the target acquisition conditions) in the training-time augmentation step could help us obtain models successfully operating in different atmospheric conditions. This ultimately allowed us to omit (or at least reducing) the on-board atmospheric correction step while still enabling us to deliver high-quality classification. Additionally, ensembling different architectural advances into deep classification ensembles potentially brought additional improvements in the overall performance of such multi-classifier systems [104], as such models were inherently able to learn different features (e.g., spectral, spatial, or a combination of both in the case of models benefiting from 3D convolutional kernels).
4.3. Experiment 2: Hyperspectral Analysis in the Presence Of Noise
The objective of this experiment was to quantify the robustness of spectral and spectral-spatial models against various noise distributions that were injected into the test hyperspectral data. The entire processing chain is shown in Figure 11—we could observe that in this experiment, we did not contaminate the training pixels. Therefore, the CNNs (we investigated 1D-CNN, 2.5-CNN, and 3D-CNN, as gathered in Table 13) were trained over the original training samples in our patch-based data splits. Since all the deep models were trained and tested using the same validation approach, we could directly compare their performance. Table 14 presents the average training and inference times of all models (on NVIDIA Tesla T4), their numbers of trainable parameters and the floating point operations. Although all of the models classified the incoming pixels in a very short time, the spectral CNN consistently delivered the fastest operation. We could also observe that—due to the small numbers of training pixels—the training process performed over the original data converged quickly for all CNNs. It was in contrast to our previous experiment, in which the training samples were substantially extended through simulating atmospheric conditions. As before, the number of trainable parameters could vary for the very same CNN, as it depended on the characteristics of the analyzed hyperspectral data.
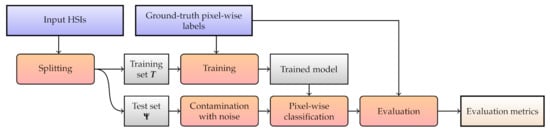
Figure 11.
A flowchart of Experiment 2. Blue rectangles indicate the input data, the red ones are the actions, and the gray ones present the artifacts, with the final outcome annotated with light gray.

Table 13.
The results obtained using all investigated deep models, and averaged across all datasets (for uncontaminated test sets), folds, and executions. We boldface the best result for each metric.

Table 14.
The average training () and inference () times (both in seconds) obtained using 1D-CNN, 2.5D-CNN, and 3D-CNN for all sets (for brevity, we refer to the A and B versions of Houston as H(A) and H(B), respectively), together with the numbers of trainable parameters of the corresponding convolutional models (#P, millions), and the floating point operations (in mega FLOPs). The metric reflects the total inference time over all test pixels.
The results averaged across all datasets, splits, and executions are presented in Table 13—here, we gather the metrics elaborated for original (uncontaminated) test sets. The best classification performance was delivered by a spectral CNN, with a visible margin in all metrics (when compared with the spectral-spatial 2.5D-CNN and 3D-CNN architectures). This was attributed to the fact that most of the training sets were fairly small in the patch-based splits (for IP, SV, PU, and the version A of Houston), hence the spectral-spatial architectures were unable to effectively learn from such . On the other hand, for the version B of Houston, 1D-CNN was outperformed by both 2.5D-CNN and 3D-CNN—we obtained the following tuples (OA’, BA’, ’) over the uncontaminated test data for 1D-CNN, 2.5D-CNN, and 3D-CNN, respectively (the best results are boldfaced): (59.85, 47.67, 47.11), (62.06, 49.11, 50.88), and (62.34, 52.08, 52.00). In order to improve the performance of spectral-spatial models in such scenarios, we could benefit from e.g., training-time data augmentation that would allow us to increase the size and representativeness of small training sets [56]. In this paper, however, we focused on investigating the models trained over original ’s (without artificially synthesized examples).
To analyze the robustness of these models against different noise distributions (Gaussian, impulsive, and Poisson), we gather the results obtained for in Table 15. We present the differences between the metrics elaborated for original (uncontaminated) and noisy test sets—the green cells present the cases in which the models were the most “robust” against the specific noise distribution (and number of affected pixels), whereas the orange cells show the highest drops in the corresponding metrics. In Table 16, we gather the results obtained for the test sets contaminated with Gaussian noise with zero mean and various standard deviations (here, and remained unchanged for different ’s). Therefore, we verified what was the impact of noise of varying intensity on the generalization of all investigated CNNs. The results showed that the more intense noise injected into ’s adversely affected the capabilities of the models—for all of them we could observe that their classification performance significantly decreased. Finally, different models are robust against different types of noise. In Table 15, we can see that 2.5D-CNN manifested the best robustness against the Poisson noise, whereas it was outperformed e.g., by 3D-CNN once the impulsive noise was present in the test data. It indicated that coupling such models together in a multi-classifier system that would be elaborating the final class label based on the class labels obtained by the base models (in this case, 2.5D-CNN and 3D-CNN) could further boost the generalization capabilities of the separate models in the target (noisy) environment. Building the deep ensembles, containing the classifiers of different architectures and potentially trained over different training samples, was thus our current research effort.

Table 15.
The differences between the values obtained for the original—uncontaminated—test sets, and the noisy ones for all classification quality metrics obtained using all deep models. The green colors indicate the smallest differences (hence the highest “robustness” against the corresponding noise distribution), whereas the orange cells highlight the largest differences.

Table 16.
The differences between the values obtained for the original—uncontaminated—test sets, and the noisy ones, obtained for the Gaussian noise with zero mean and various standard deviations () for all classification quality metrics obtained using all deep models. The green colors indicate the smallest differences (hence the highest “robustness” against the corresponding noise distribution), whereas the orange cells highlight the largest differences.
To further verify if the differences were statistically important, we executed the Friedman’s test (with post Dunn’s) over the per-class accuracies. The results indicate that injecting Gaussian, impulsive and Poisson noise into the test data deteriorates the classification ability of 1D-CNN for virtually all cases (the differences were not statistically important at only for the Gaussian distribution and ). On the other hand, both 2.5D-CNN and 3D-CNN delivered accurate classification for the Gaussian contamination (for all ’s), without any significant degradation (at ). Finally, the presence of the impulsive and Poisson noise resulted in statistically important drops in per-class accuracies for all architectures. The statistical analysis indicated that specific noise distributions may have easily affected the capabilities of the deep models trained over original ground-truth data. Thus, designing either additional regularization techniques for making CNNs robust against e.g., impulsive noise (modeling the sensor failures) or developing on-board denoising approaches should be considered important steps while deploying such machine learning algorithms in the target environment. It is worth mentioning that augmenting original training samples with simulated-noise injections has been shown as an effective way of enhancing the generalization abilities of CNNs in a statistically significant manner [56]. In this scenario, contaminated hyperspectral pixels were included in the training sets by using the training-time augmentation, hence the models were trained over ’s that encompass noisy data. Such data augmentation techniques could be easily exploited at the inference time, in order to benefit from the ensemble-like approach, in which a CNN model (trained over the original or augmented training sets) classified not only the original test pixel, but also its noise-contaminated variants. Finally, the class label was elaborated through aggregating all labels, e.g., in the voting process.
5. Conclusions
On-board deep learning, albeit becoming a well-established tool for analyzing multi- and hyperspectral image data in various fields, is still challenging to be deployed in practical Earth observation scenarios, due to numerous technological challenges related to the execution environment. In this paper, we tackled one of them, being the utilization of such techniques in varying atmospheric conditions and in the presence of noise which are inherit to the in-orbit operation. We provided a range of simulations of atmospheric conditions that were likely to be faced while imaging Central Europe urban and rural areas (with Poland being our default target location), alongside different noise simulations. These simulations were used to verify the classification abilities of spectral and spectral-spatial CNNs over hyperspectral data that may manifest different characteristics when compared to the training data (possibly acquired in different conditions), or over data contaminated with noise.
Our experimental study, performed over several hyperspectral benchmarks that were preprocessed using our simulators, revealed that synthesizing artificial training samples that resemble atmospheric variants helps significantly boost the generalization abilities of deep models, hence improve their robustness against test data acquired in different imaging circumstances. This observation may ultimately lead to mitigating the necessity of employing on-board atmospheric corrections that precede deep learning-powered analysis. On the other hand, our experiments indicated that noise contamination may be an important obstacle in delivering precise hyperspectral classification, especially if the noise is impulsive or follows the Poisson distribution. We, however, anticipate that the training-time data augmentation may greatly improve the robustness of CNNs, especially if the expected noise distributions are known in advance (e.g., thanks to the available and/or simulated sensor characteristics) [56]. We believe that the noise and atmospheric simulations should become a standard tool in testing campaigns of satellites exploiting on-board artificial intelligence, as they are key to estimating the expected robustness of deep learning techniques deployed in such extreme execution environments. Additionally, they could help us verify the machine learning algorithms before uploading them onto the operating satellites, in the case of reconfigurable missions, such as Intuition-1, that would allow us to update the analysis engine during the operational phase of the satellite.
Since capturing new ground-truth datasets is tedious, time-consuming, and costly, designing new approaches that effectively deal with limited amounts of labeled training data is a vital research area. Additionally, there are approaches, especially exploiting tensor-based techniques [57,58,59,60] and semi-supervised learning [50], that were proven highly effective and possible to train from small ’s, and could be efficiently implemented in FPGA- and GPU-based architectures. Our current research efforts are focused on understanding the robustness of CNNs against small training samples in the HSI analysis tasks [105], and will also include confronting classical machine learning and deep learning algorithms in such scenarios. We anticipate that obtaining the models that are robust against varying atmospheric conditions, noise, and limited training sets will be an important milestone towards fast adoption of on-board machine learning in a range of remote sensing and Earth observation applications.
Author Contributions
Conceptualization, J.N.; methodology, J.N.; software, M.M., M.C., L.Z., T.L., and L.T.; validation, J.N. and M.M.; investigation, J.N., M.M., M.C., L.Z., T.L., L.T., and M.K., data curation, J.N., M.M., M.C., and L.T.; writing—original draft preparation, J.N., M.C., and M.K.; visualization, J.N. and M.M.; supervision, J.N.; funding acquisition, J.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Polish National Centre for Research and Development under Grant POIR.01.01.01-00-0356/17, by the European Space Agency (the BEETLES project), and by the Silesian University of Technology grant for maintaining and developing research potential. JN was supported by the Silesian University of Technology Rector’s Research and Development Grant 02/080/RGJ20/0003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes and https://hyperspectral.ee.uh.edu/.
Acknowledgments
We thank Bertrand Le Saux (European Space Agency) for lots of fruitful discussions that helped us improve the work reported in this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AOT | Aerosol Optical Thickness |
| AVIRIS | Airborne Visible/Infrared Imaging Spectrometer |
| BA | Balanced accuracy |
| CNN | Convolutional neural network |
| FLAASH | Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes |
| HSI | Hyperspectral image |
| IP | Indian Pines |
| OA | Overall accuracy |
| PU | Pavia University |
| ROSIS | Reflective Optics System Imaging Spectrometer |
| SVM | Support vector machine |
| SV | Salinas Valley |
References
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern trends in hyperspectral image analysis: A review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Dundar, T.; Ince, T. Sparse representation-based hyperspectral image classification using multiscale superpixels and guided filter. IEEE Geosci. Remote Sens. Lett. 2018, 16, 246–250. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Du, B.; Huang, X.; Tang, Y.Y.; Tao, D. Simultaneous Spectral-Spatial Feature Selection and Extraction for Hyperspectral Images. IEEE Trans. Cybern. 2018, 48, 16–28. [Google Scholar] [CrossRef] [PubMed]
- He, N.; Paoletti, M.E.; Haut, J.M.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature Extraction With Multiscale Covariance Maps for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 755–769. [Google Scholar] [CrossRef]
- Luo, F.; Zhang, L.; Du, B.; Zhang, L. Dimensionality Reduction with Enhanced Hybrid-Graph Discriminant Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5336–5353. [Google Scholar] [CrossRef]
- Gao, Q.; Lim, S.; Jia, X. Hyperspectral Image Classification Using CNNs and Multiple Feature Learning. Remote Sens. 2018, 10, 299. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, L.; Zhang, L.; Lai, Y.M. A Dissimilarity-Weighted Sparse Self-Representation Method for Band Selection in Hyperspectral Imagery Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4374–4388. [Google Scholar] [CrossRef]
- Sun, W.; Du, Q. Hyperspectral Band Selection: A Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Ribalta Lorenzo, P.; Tulczyjew, L.; Marcinkiewicz, M.; Nalepa, J. Hyperspectral Band Selection Using Attention-Based Convolutional Neural Networks. IEEE Access 2020, 8, 42384–42403. [Google Scholar] [CrossRef]
- Wang, D.; Du, B.; Zhang, L.; Xu, Y. Adaptive Spectral–Spatial Multiscale Contextual Feature Extraction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2461–2477. [Google Scholar] [CrossRef]
- Nalepa, J.; Antoniak, M.; Myller, M.; Ribalta Lorenzo, P.; Marcinkiewicz, M. Towards resource-frugal deep convolutional neural networks for hyperspectral image segmentation. Microprocess. Microsyst. 2020, 73, 102994. [Google Scholar] [CrossRef]
- Transon, J.; D’Andrimont, R.; Maugnard, A.; Defourny, P. Survey of Hyperspectral Earth Observation Applications from Space in the Sentinel-2 Context. Remote Sens. 2018, 10, 157. [Google Scholar] [CrossRef]
- Aggarwal, H.K.; Majumdar, A. Mixed Gaussian and impulse denoising of hyperspectral images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 429–432. [Google Scholar]
- Nalepa, J.; Stanek, M. Segmenting Hyperspectral Images Using Spectral Convolutional Neural Networks in the Presence of Noise. Procroceedings of the IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 870–873. [Google Scholar]
- Acquarelli, J.; Marchiori, E.; Buydens, L.M.; Tran, T.; Van Laarhoven, T. Spectral-Spatial Classification of Hyperspectral Images. Remote Sens. 2018, 10, 1156. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Validating Hyperspectral Image Segmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1264–1268. [Google Scholar] [CrossRef]
- Nalepa, J.; Tulczyjew, L.; Myller, M.; Kawulok, M. Hyperspectral Image Classification Using Spectral-Spatial Convolutional Neural Networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 866–869. [Google Scholar]
- Lacey, G.; Taylor, G.W.; Areibi, S. Deep Learning on FPGAs: Past, Present, and Future. arXiv 2016, arXiv:cs.DC/1602.04283. [Google Scholar]
- Shawahna, A.; Sait, S.M.; El-Maleh, A. FPGA-Based Accelerators of Deep Learning Networks for Learning and Classification: A Review. IEEE Access 2019, 7, 7823–7859. [Google Scholar] [CrossRef]
- Bernardeschi, C.; Cassano, L.; Domenici, A. SRAM-Based FPGA Systems for Safety-Critical Applications: A Survey on Design Standards and Proposed Methodologies. J. Comput. Sci. Technol. 2015, 30, 373–390. [Google Scholar] [CrossRef]
- Li, R.; Huang, H.; Wang, Z.; Shao, Z.; Liao, X.; Jin, H. Optimizing Memory Performance of Xilinx FPGAs under Vitis. arXiv 2020, arXiv:cs.DC/2010.08916. [Google Scholar]
- Cosmas, K.; Kenichi, A. Utilization of FPGA for Onboard Inference of Landmark Localization in CNN-Based Spacecraft Pose Estimation. Aerospace 2020, 7, 159. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Imani, M.; Ghassemian, H. An overview on spectral and spatial information fusion for hyperspectral image classification: Current trends and challenges. Inf. Fusion 2020, 59, 59–83. [Google Scholar] [CrossRef]
- Belgiu, M.; Drǎguţ, L. Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Archibald, R.; Fann, G. Feature selection and classification of hyperspectral images with support vector machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 674–677. [Google Scholar] [CrossRef]
- Prasad, S.; Li, W.; Fowler, J.E.; Bruce, L.M. Information fusion in the redundant-wavelet-transform domain for noise-robust hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3474–3486. [Google Scholar] [CrossRef]
- Cui, M.; Prasad, S. Class-dependent sparse representation classifier for robust hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2683–2695. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral image classification with robust sparse representation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 641–645. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS Net: Band-Adaptive Spectral-Spatial Feature Learning Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5293–5301. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Zhang, L. Quaternion-based multiscale analysis for feature extraction of hyperspectral images. IEEE Trans. Signal Process. 2019, 67, 1418–1430. [Google Scholar] [CrossRef]
- Okwuashi, O.; Ndehedehe, C.E. Deep support vector machine for hyperspectral image classification. Pattern Recognit. 2020, 103, 107298. [Google Scholar] [CrossRef]
- Nalepa, J.; Kawulok, M. Selecting training sets for support vector machines: A review. Artif. Intell. Rev. 2019, 52, 857–900. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral-Spatial Feature Extraction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Li, G.; Zhang, C.; Lei, R.; Zhang, X.; Ye, Z.; Li, X. Hyperspectral remote sensing image classification using three-dimensional-squeeze-and-excitation-DenseNet (3D-SE-DenseNet). Remote Sens. Lett. 2020, 11, 195–203. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of hyperspectral image based on double-branch dual-attention mechanism network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, X.; Jia, X.; Ren, J.; Zhang, A.; Yao, Y.; Zhao, H. Deep fusion of localized spectral features and multi-scale spatial features for effective classification of hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102157. [Google Scholar] [CrossRef]
- Qu, L.; Zhu, X.; Zheng, J.; Zou, L. Triple-Attention-Based Parallel Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 324. [Google Scholar] [CrossRef]
- Li, R.; Duan, C. Litedensenet: A lightweight network for hyperspectral image classification. arXiv 2020, arXiv:2004.08112. [Google Scholar]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. Ghostnet: More features from cheap operations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1580–1589. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Pereira, N.S.; Plaza, J.; Plaza, A. Ghostnet for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2021. [Google Scholar] [CrossRef]
- Zhou, X.; Prasad, S. Advances in Deep Learning for Hyperspectral Image Analysis–Addressing Challenges Arising in Practical Imaging Scenarios. In Hyperspectral Image Analysis; Springer: Cham, Switzerland, 2020; pp. 117–140. [Google Scholar]
- Nalepa, J.; Myller, M.; Imai, Y.; Honda, K.I.; Takeda, T.; Antoniak, M. Unsupervised segmentation of hyperspectral images using 3-D convolutional autoencoders. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1948–1952. [Google Scholar] [CrossRef]
- Li, F.; Clausi, D.A.; Xu, L.; Wong, A. ST-IRGS: A Region-Based Self-Training Algorithm Applied to Hyperspectral Image Classification and Segmentation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3–16. [Google Scholar] [CrossRef]
- Protopapadakis, E.; Doulamis, A.; Doulamis, N.; Maltezos, E. Semi-supervised Fine-Tuning for Deep Learning Models in Remote Sensing Applications. In Advances in Visual Computing; Bebis, G., Yin, Z., Kim, E., Bender, J., Subr, K., Kwon, B.C., Zhao, J., Kalkofen, D., Baciu, G., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 719–730. [Google Scholar]
- Liu, H.; Cocea, M. Semi-random partitioning of data into training and test sets in granular computing context. Granul. Comput. 2017, 2, 357–386. [Google Scholar] [CrossRef]
- Protopapadakis, E.; Doulamis, A.; Doulamis, N.; Maltezos, E. Stacked Autoencoders Driven by Semi-Supervised Learning for Building Extraction from near Infrared Remote Sensing Imagery. Remote Sens. 2021, 13, 371. [Google Scholar] [CrossRef]
- Tulczyjew, L.; Kawulok, M.; Nalepa, J. Unsupervised Feature Learning Using Recurrent Neural Nets for Segmenting Hyperspectral Images. IEEE Geosci. Remote. Sens. Lett. 2020. [Google Scholar] [CrossRef]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. Lett. 2015, 13, 105–109. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Transfer learning for segmenting dimensionally reduced hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1228–1232. [Google Scholar] [CrossRef]
- Feng, J.; Chen, J.; Liu, L.; Cao, X.; Zhang, X.; Jiao, L.; Yu, T. CNN-based multilayer spatial–spectral feature fusion and sample augmentation with local and nonlocal constraints for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1299–1313. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Hyperspectral image classification using random occlusion data augmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1751–1755. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Training-and test-time data augmentation for hyperspectral image segmentation. IEEE Geosci. Remote Sens. Lett. 2020, 17, 292–296. [Google Scholar] [CrossRef]
- Makantasis, K.; Voulodimos, A.; Doulamis, A.; Doulamis, N.; Georgoulas, I. Hyperspectral Image Classification with Tensor-Based Rank-R Learning Models. In Proceedings of the IEEE International Conference on Image Processing, Taipei, Taiwan, 22–25 September 2019; pp. 3125–3148. [Google Scholar]
- Makantasis, K.; Doulamis, A.D.; Doulamis, N.D.; Nikitakis, A. Tensor-Based Classification Models for Hyperspectral Data Analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6884–6898. [Google Scholar] [CrossRef]
- Liu, F.; Wang, Q. A sparse tensor-based classification method of hyperspectral image. Signal Process. 2020, 168, 107361. [Google Scholar] [CrossRef]
- An, J.; Zhang, X.; Zhou, H.; Jiao, L. Tensor-Based Low-Rank Graph With Multimanifold Regularization for Dimensionality Reduction of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4731–4746. [Google Scholar] [CrossRef]
- Zhao, J.; Ge, Y.; Cao, X. Non-overlapping classification of hyperspectral imagery. Remote Sens. Lett. 2019, 10, 968–977. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, J.; Qian, Y.; Wen, L.; Bai, X.; Gao, Y. On the sampling strategy for evaluation of spectral-spatial methods in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 862–880. [Google Scholar] [CrossRef]
- Tian, C.; Fei, L.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.W. Deep learning on image denoising: An overview. Neural Netw. 2020, 131, 251–275. [Google Scholar] [CrossRef]
- Goyal, B.; Dogra, A.; Agrawal, S.; Sohi, B.; Sharma, A. Image denoising review: From classical to state-of-the-art approaches. Inf. Fusion 2020, 55, 220–244. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Smolka, B.; Chydzinski, A. Fast detection and impulsive noise removal in color images. Real-Time Imaging 2005, 11, 389–402. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Zhong, S. Hyper-Laplacian Regularized Unidirectional Low-Rank Tensor Recovery for Multispectral Image Denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4260–4268. [Google Scholar]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2013, 22, 119–133. [Google Scholar] [CrossRef]
- Othman, H.; Qian, S.E. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative-domain wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2006, 44, 397–408. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral image denoising employing a spectral–spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. Hyperspectral image denoising using the robust low-rank tensor recovery. JOSA A 2015, 32, 1604–1612. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.; Bourennane, S. Survey of hyperspectral image denoising methods based on tensor decompositions. EURASIP J. Adv. Signal Process. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Liao, W. HSI-DeNet: Hyperspectral image restoration via convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 667–682. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral image denoising employing a spatial–spectral deep residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1205–1218. [Google Scholar] [CrossRef]
- Wei, K.; Fu, Y.; Huang, H. 3-D Quasi-Recurrent Neural Network for Hyperspectral Image Denoising. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 363–375. [Google Scholar] [CrossRef]
- Li, W.; Liu, K.; Su, H. Wavelet-based nearest-regularized subspace for noise-robust hyperspectral image classification. J. Appl. Remote Sens. 2014, 8, 083665. [Google Scholar] [CrossRef]
- Zhan, T.; Sun, L.; Xu, Y.; Yang, G.; Zhang, Y.; Wu, Z. Hyperspectral classification via superpixel kernel learning-based low rank representation. Remote Sens. 2018, 10, 1639. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, H.; Pižurica, A. A robust sparse representation model for hyperspectral image classification. Sensors 2017, 17, 2087. [Google Scholar] [CrossRef]
- Duan, P.; Kang, X.; Li, S.; Ghamisi, P. Noise-robust hyperspectral image classification via multi-scale total variation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1948–1962. [Google Scholar] [CrossRef]
- Li, H.C.; Wang, W.Y.; Pan, L.; Li, W.; Du, Q.; Tao, R. Robust capsule network based on maximum correntropy criterion for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 738–751. [Google Scholar] [CrossRef]
- Voulodimos, A.; Fokeas, K.; Doulamis, N.; Doulamis, A.; Makantasis, K. Noise-Tolerant Hyperspectral Image Classification Using Discrete Cosine Transform and Convolutional Neural Networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 1281–1287. [Google Scholar] [CrossRef]
- Natarajan, N.; Dhillon, I.S.; Ravikumar, P.; Tewari, A. Learning with noisy labels. Proc. Neural Inf. Process. Syst. 2013, 26, 1196–1204. [Google Scholar]
- Kawulok, M.; Nalepa, J. Towards robust SVM training from weakly labeled large data sets. In Proceedings of the IAPR Asian Conference on Pattern Recognition, Kuala Lumpur, Malaysia, 3–6 November 2015; pp. 464–468. [Google Scholar]
- Mnih, V.; Hinton, G.E. Learning to label aerial images from noisy data. In Proceedings of the International Conference on Machine Learning, Edinburgh, UK, 26 June 26–1 July 2012; pp. 567–574. [Google Scholar]
- Jiang, J.; Ma, J.; Wang, Z.; Chen, C.; Liu, X. Hyperspectral image classification in the presence of noisy labels. IEEE Trans. Geosci. Remote Sens. 2018, 57, 851–865. [Google Scholar] [CrossRef]
- Tu, B.; Zhang, X.; Kang, X.; Wang, J.; Benediktsson, J.A. Spatial density peak clustering for hyperspectral image classification with noisy labels. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5085–5097. [Google Scholar] [CrossRef]
- Cooley, T.; Anderson, G.P.; Felde, G.W.; Hoke, M.L.; Ratkowski, A.J.; Chetwynd, J.H.; Gardner, J.A.; Adler-Golden, S.M.; Matthew, M.W.; Berk, A.; et al. FLAASH, a MODTRAN4-based atmospheric correction algorithm, its application and validation. Proc. IEEE Int. Geosci. Remote. Sens. Symp. 2002, 3, 1414–1418. [Google Scholar]
- Bernstein, L.S.; Jin, X.; Gregor, B.; Adler-Golden, S.M. Quick atmospheric correction code: Algorithm description and recent upgrades. Opt. Eng. 2012, 51, 111719. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, L.; Cerra, D.; Pato, M.; Carmona, E.; Prasad, S.; Yokoya, N.; Hänsch, R.; Le Saux, B. Advanced Multi-Sensor Optical Remote Sensing for Urban Land Use and Land Cover Classification: Outcome of the 2018 IEEE GRSS Data Fusion Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1709–1724. [Google Scholar] [CrossRef]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN6: A major upgrade of the MODTRAN radiative transfer code. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XX; Velez-Reyes, M., Kruse, F.A., Eds.; International Society for Optics and Photonics, SPIE: Baltimore, MD, USA, 2014; Volume 9088, pp. 113–119. [Google Scholar]
- Anderson, G.P.; Felde, G.W.; Hoke, M.L.; Ratkowski, A.J.; Cooley, T.W.; Chetwynd, J.H., Jr.; Gardner, J.A.; Adler-Golden, S.M.; Matthew, M.W.; Berk, A.; et al. MODTRAN4-based atmospheric correction algorithm: FLAASH (fast line-of-sight atmospheric analysis of spectral hypercubes). In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery VIII; Shen, S.S., Lewis, P.E., Eds.; International Society for Optics and Photonics, SPIE: Orlando, FL, USA, 2002; Volume 4725, pp. 65–71. [Google Scholar] [CrossRef]
- Felde, G.W.; Anderson, G.P.; Cooley, T.W.; Matthew, M.W.; adler-Golden, S.M.; Berk, A.; Lee, J. Analysis of Hyperion data with the FLAASH atmospheric correction algorithm. Proc. IEEE Int. Geosci. Remote. Sens. Symp. 2003, 1, 90–92. [Google Scholar]
- Wu, D.; Tie, X.; Deng, X. Chemical characterizations of soluble aerosols in southern China. Chemosphere 2006, 64, 749–757. [Google Scholar] [CrossRef]
- Zhang, T.; Cao, J.; Tie, X.; Shen, Z.; Liu, S.; Ding, H.; Han, Y.; Wang, G.; Ho, K.; Qiang, J.; et al. Water-soluble ions in atmospheric aerosols measured in Xi’an, China: Seasonal variations and sources. Atmos. Res. 2011, 102, 110–119. [Google Scholar] [CrossRef]
- American Institute of Aeronautics and Astronautics. Guide: Guide to Global Aerosol Models (GAM) (AIAA G-065-1999); American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1999. [Google Scholar] [CrossRef]
- Tirelli, C.; Curci, G.; Manzo, C.; Tuccella, P.; Bassani, C. Effect of the Aerosol Model Assumption on the Atmospheric Correction over Land: Case Studies with CHRIS/PROBA Hyperspectral Images over Benelux. Remote Sens. 2015, 7, 8391–8415. [Google Scholar] [CrossRef]
- Khan, R.; Kumar, K.R.; Zhao, T. The climatology of aerosol optical thickness and radiative effects in Southeast Asia from 18-years of ground-based observations. Environ. Pollut. 2019, 254, 113025. [Google Scholar] [CrossRef]
- Tariyal, S.; Aggarwal, H.K.; Majumdar, A. Hyperspectral impulse denoising with sparse and low-rank penalties. In Proceedings of the IEEE Workshop on Hyperspectral Imaging and Signal Processing, Tokyo, Japan, 2–5 June 2015; pp. 1–4. [Google Scholar]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise Reduction in Hyperspectral Imagery: Overview and Application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:abs/1412.6980. [Google Scholar]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Martin, J.; Eugenio, F.; Marcello, J.; Medina, A.; Bermejo, J.A.; Arbelo, M. Atmospheric correction models for high resolution WorldView-2 multispectral imagery: A case study in Canary Islands, Spain. In Remote Sensing of Clouds and the Atmosphere XVII and Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing VIII; Singh, U.N., Pappalardo, G., Kassianov, E.I., Comeron, A., Picard, R.H., Schäfer, K., Eds.; International Society for Optics and Photonics; SPIE: Edinburgh, UK, 2012; Volume 8534, pp. 153–162. [Google Scholar]
- Shang, P.; Shen, F. Atmospheric Correction of Satellite GF-1/WFV Imagery and Quantitative Estimation of Suspended Particulate Matter in the Yangtze Estuary. Sensors 2016, 16, 1997. [Google Scholar] [CrossRef]
- Kardas, A.; Kawulok, M.; Nalepa, J. On Evolutionary Classification Ensembles. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 2974–2981. [Google Scholar]
- Tulczyjew, L.; Nalepa, J. Investigating the impact of the training set size on deep learning-powered hyperspectral unmixing. Proc. IEEE Int. Geosci. Remote. Sens. Symp. 2021, 1–4, in press. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).