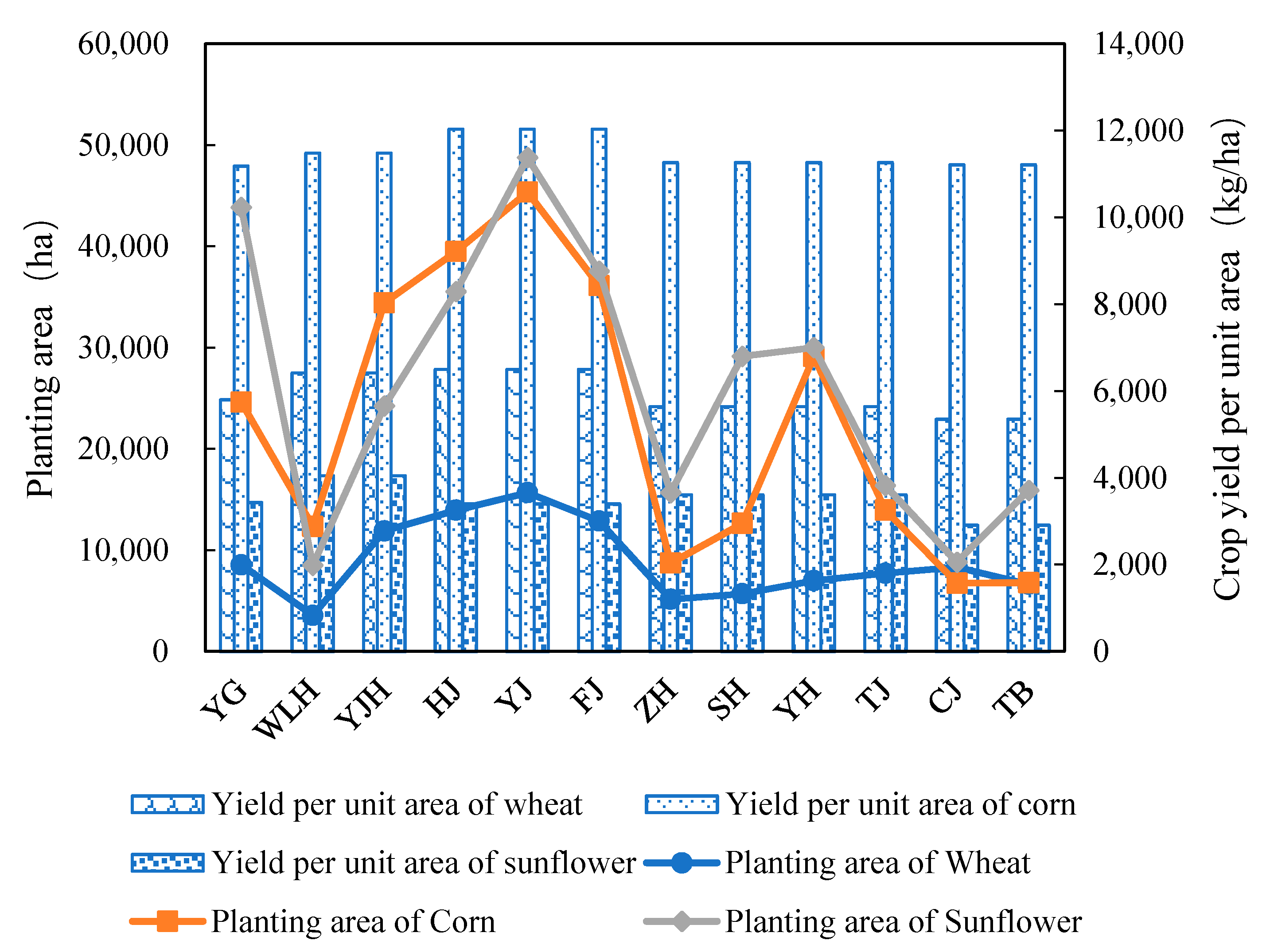
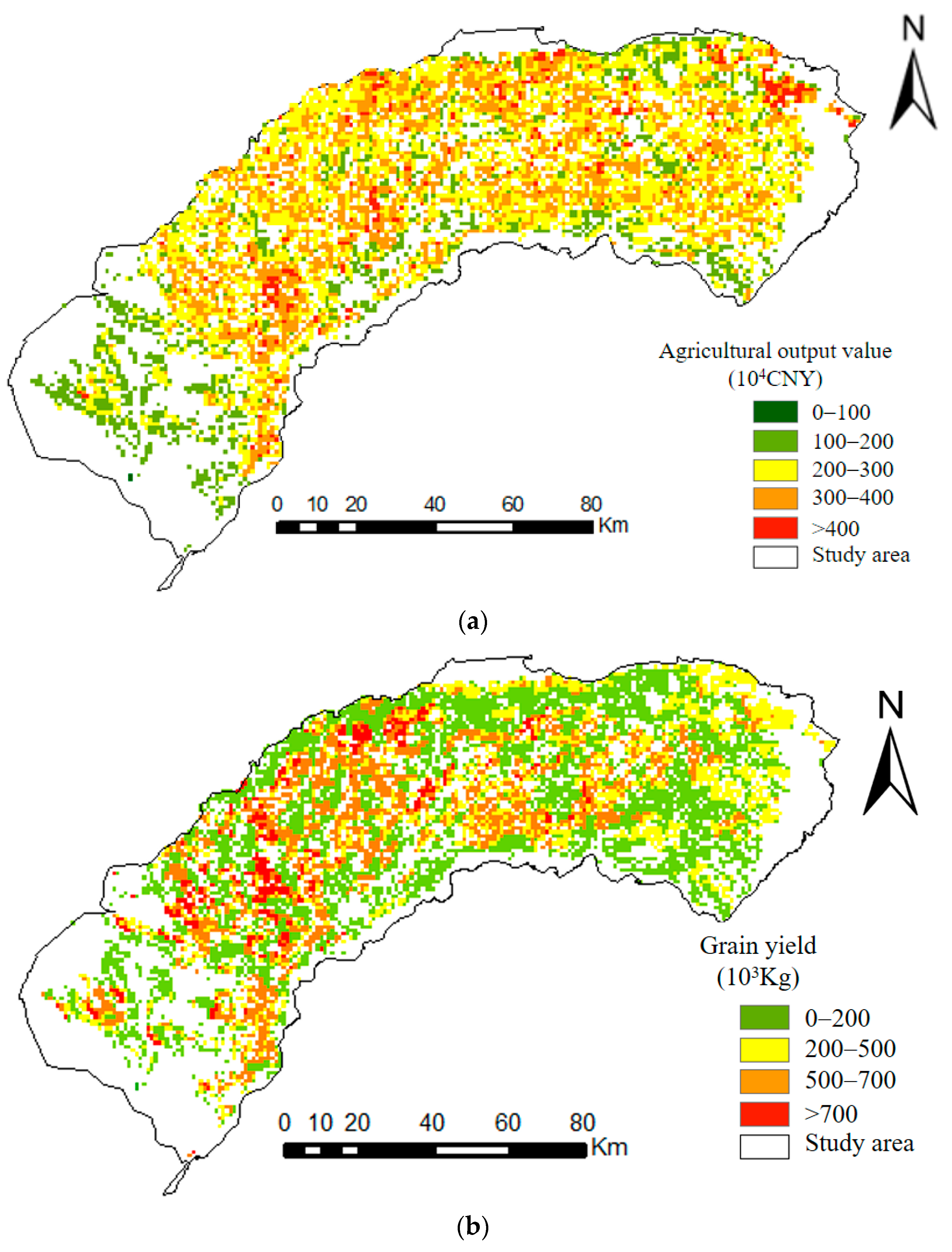
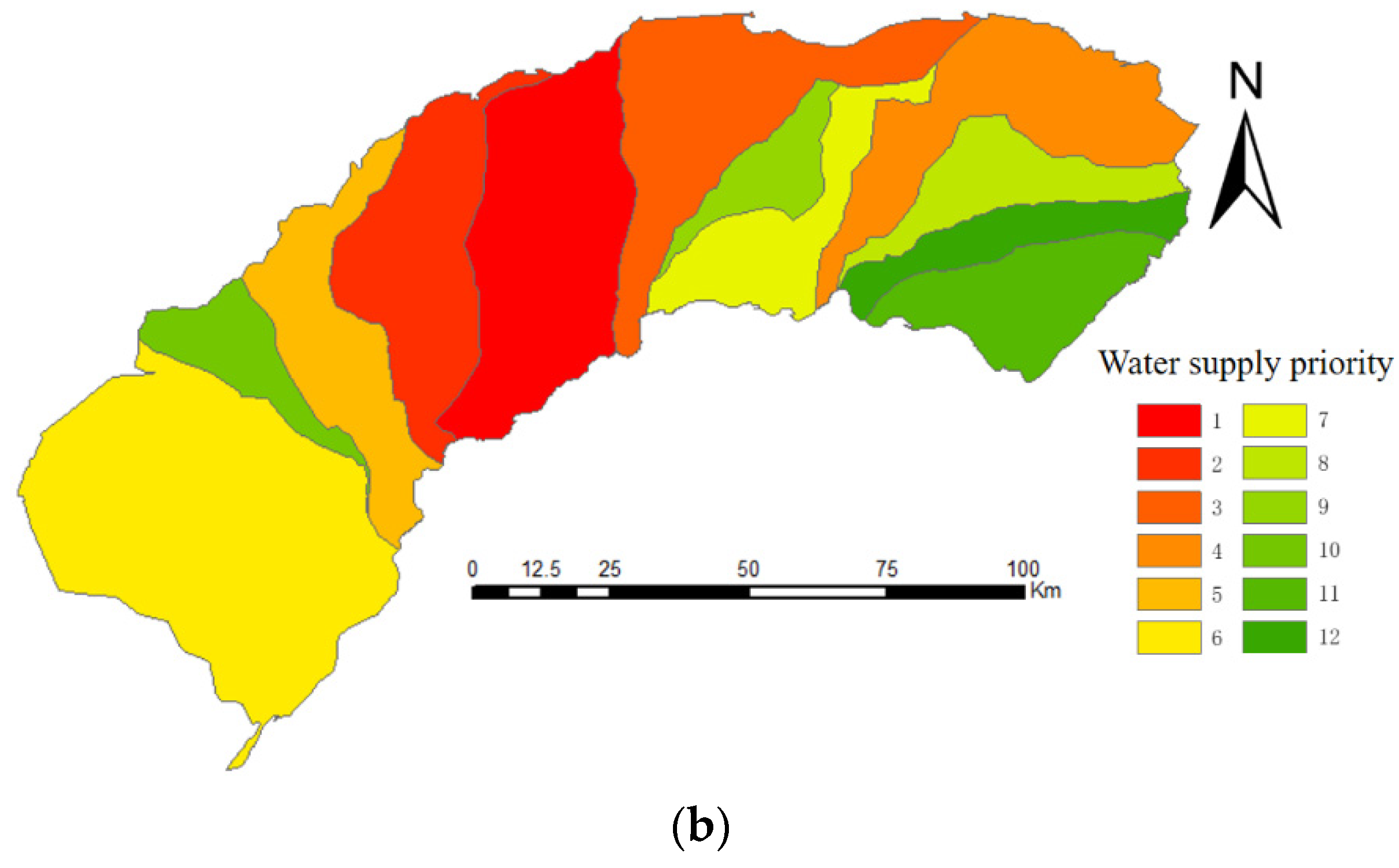
1. Introduction
Fresh water is an essential resource. It not only helps to maintain ecological health, but also promotes social development [
1]. Agriculture is the largest water use sector, accounting for approximately 70% of freshwater use globally per year [
2]. The ever-increasing food demand and decreased availability of water agriculture, calls for effective agricultural water management [
3]. Especially in arid irrigation districts, when water scarcity occurs, water managers are required to make difficult decisions about what land has higher priority and how to effectively allocate limited water resources [
4].
Priority ranking among different water users has been proven to be a useful way to help water managers identify the importance of water users [
4,
5]. A series of priority evaluation models for different water use sectors such as agriculture and industry, considering various factors such as social economy, ecological environment, and policies, have been developed [
6,
7,
8]. For example, RazaviToosi and Samani presented an assessment model including social, economic, managerial and environmental clusters to evaluate the priority of five watersheds in Iran [
9]. Gómez-Limón et al. investigated the priority of agricultural water resources allocation in different watersheds under drought conditions, and indicated that the priority can effectively improve water use efficiency [
10]. In addition, similar studies were carried out on the administrative unit and irrigation district scale. For example, Li et at. determined the water allocation priority among different cities considering different socioeconomic development levels and national or regional policies [
11]. Zhang et al. evaluated the priorities of 17 irrigation districts based on fairness, production efficiency and economic benefits, and then input them into a water resource optimization model to obtain a water resource allocation strategy [
12]. However, the priority assessment system contains many spatial variability indicators, such as population, crop yield, etc. In addition, due to the limitations of data collection, it is difficult for current studies to consider smaller scales than administrative units and irrigation areas, which ignores the spatial variability of the system.
With the development of “3S” technology (i.e., remote sensing, Global Position System, and geographic information systems), more spatial information can be collected [
13]. Some remote sensing data such as precipitation, evapotranspiration, and land use can be directly used in water resources management practices [
14,
15]. For example, remote sensing data have been utilized to evaluate the efficiency of water resources utilization, and to help optimize water resources allocation [
14,
16]. Moreover, some socioeconomic statistics can be estimated by appropriate methods and remote sensing data, which are helpful for water resources management [
17]. The spatial unit of the collection boundary for socio-economic statistics is usually the administrative unit boundary. There are several limitations in spatial analysis and interdisciplinary application, including low spatial resolution and a mismatch between administrative regions and geographical units. Compared with traditional socio-economic data, the spatialization of statistical data has the following advantages: (1) Reflecting the spatial distribution characteristics of socio-economic data within the statistical region; (2) facilitating spatial analysis through grid-based socio-economic data; and (3) breaking the limitations of administrative boundary. Liang et al. used night-time light and land use data to spatialize the GDP of a Chinese city via a linear regression model, which can provide a reference for future urban planning and social and economic development [
18]. Zhao et al. utilized different regression models to spatialize the GDP of South China and analyzed the performance of different models [
19]. Sutton used night-time light data to map urban population density distribution and analyzed the trend of urban population density in the United States [
20]. However, most relevant studies focused to gather the spatialization of GDP and population statistical data, few attempts have been made on agricultural economic statistical data, such as grain yield and agricultural output value [
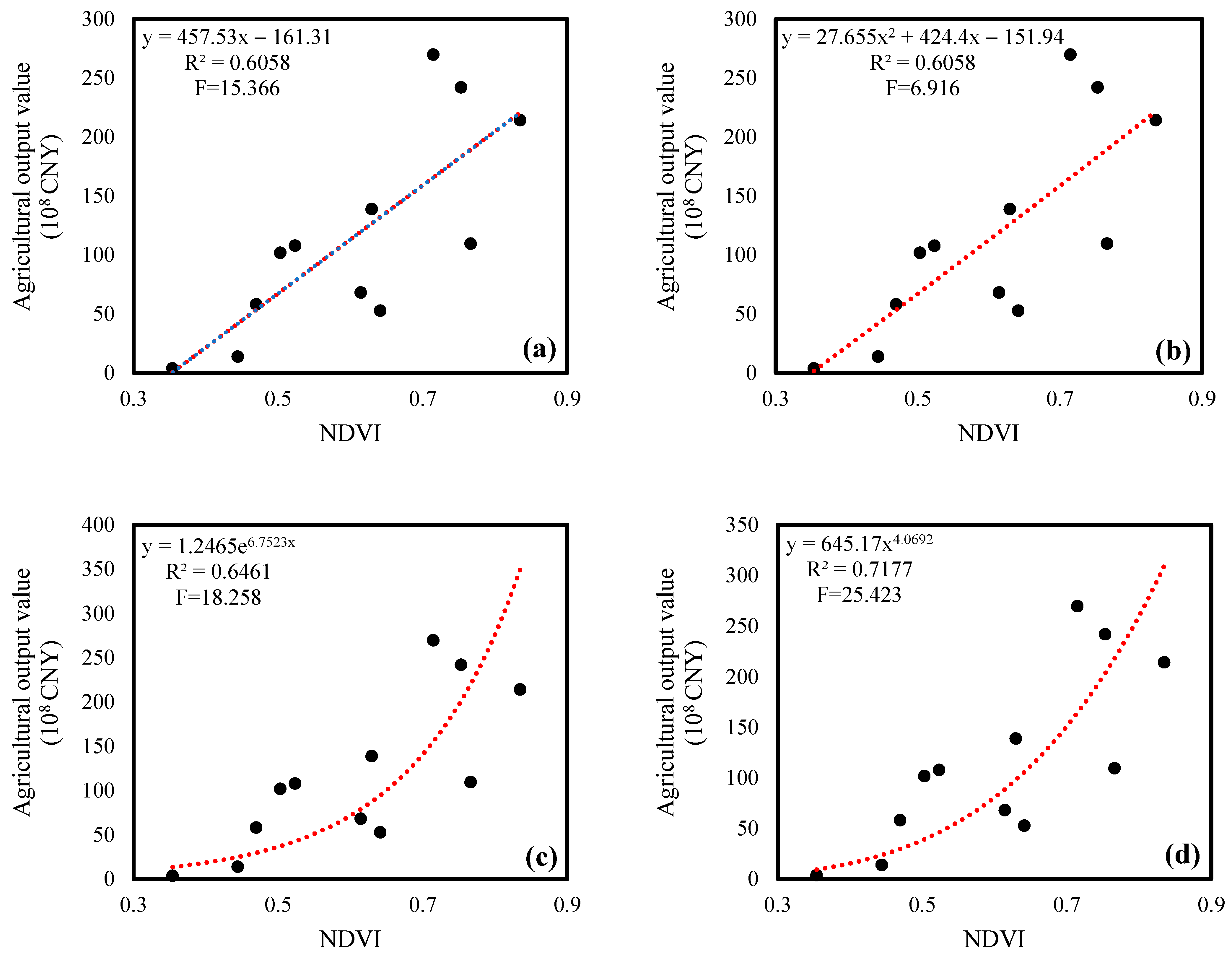
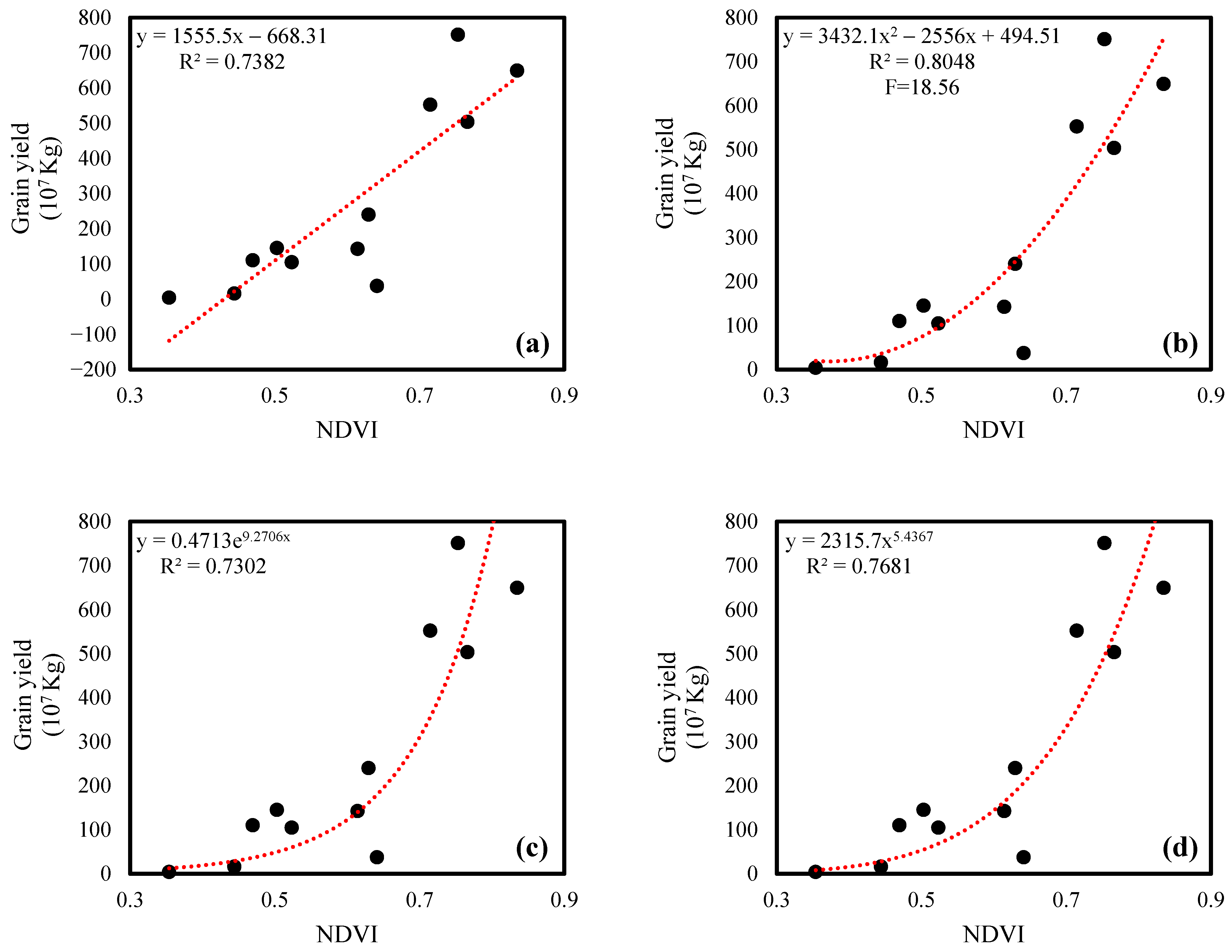
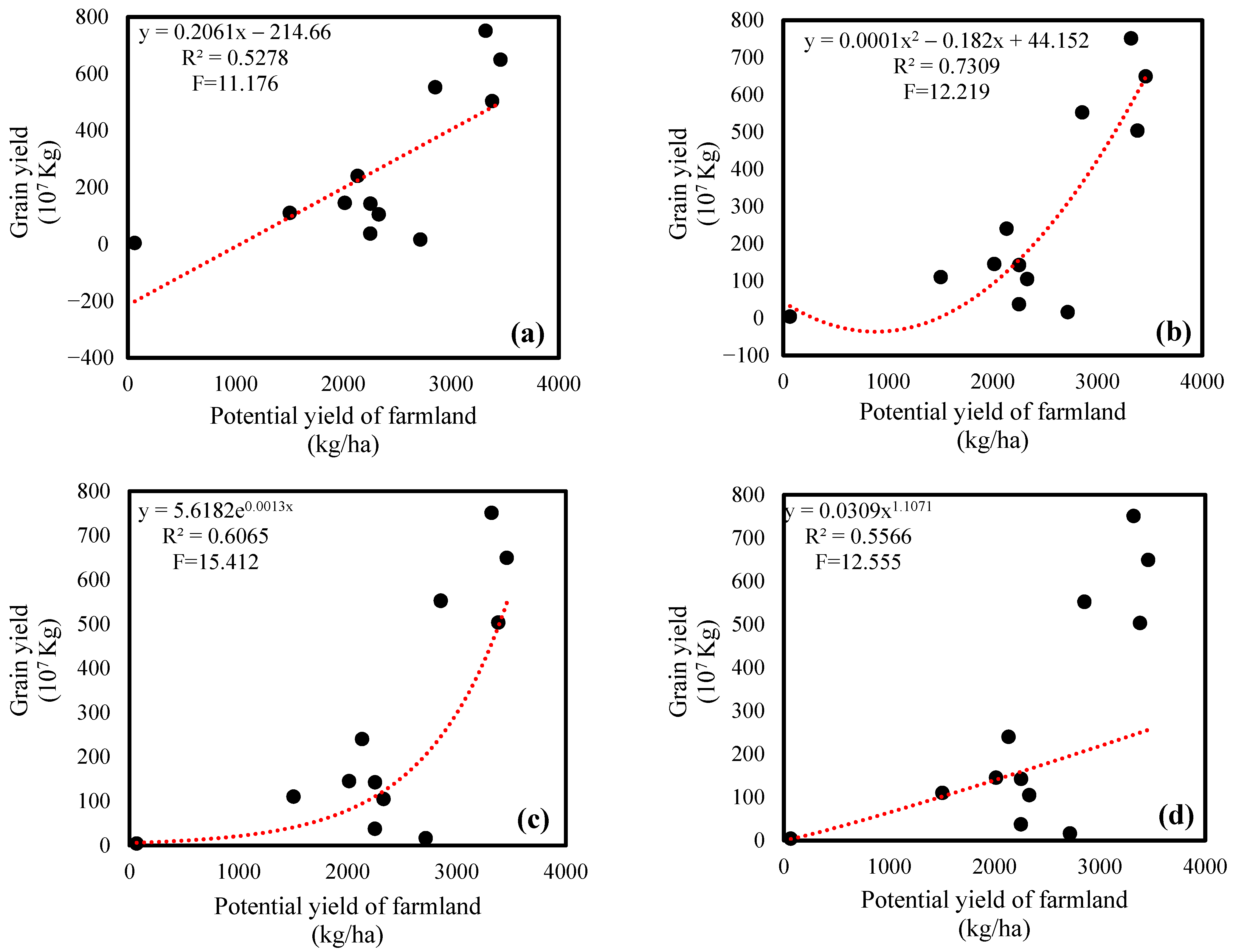
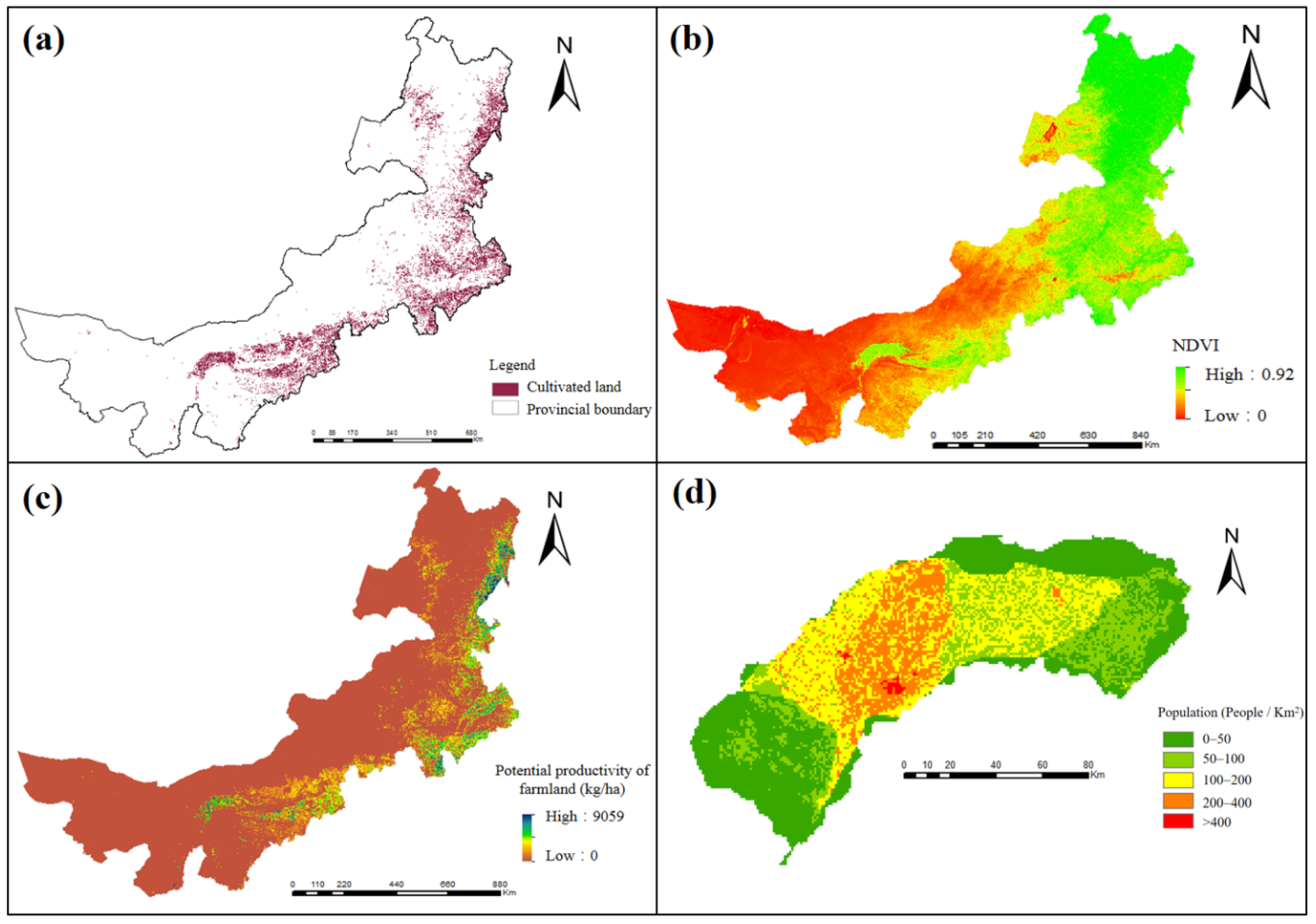
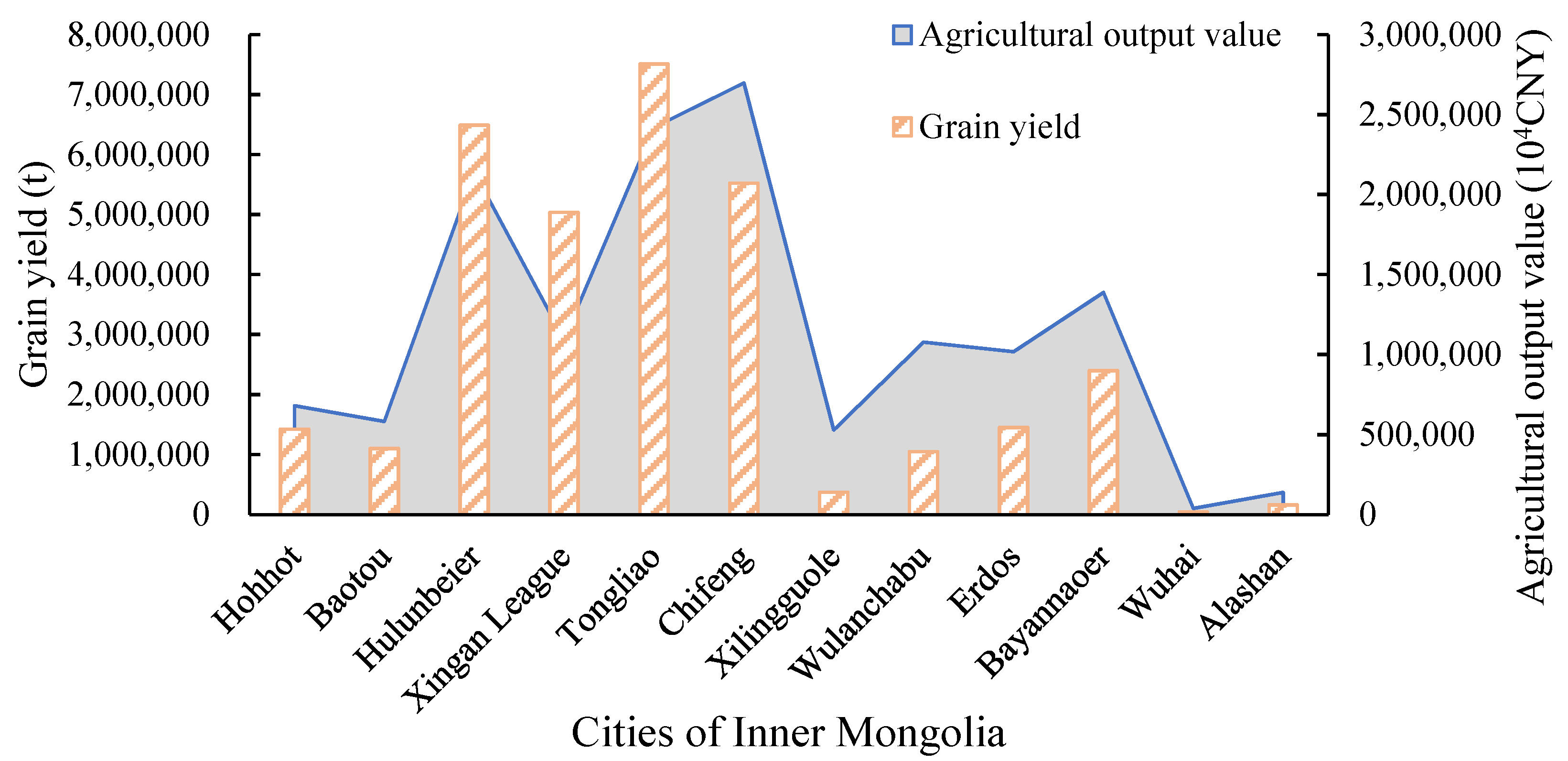
21]. Moreover, there are few reports on the application of statistical data spatialization methods in agricultural water management. Therefore, this research attempts to construct a spatialization method of agricultural output value and grain yield. After using the obtained spatialized statistical data and remote sensing data, we can ensure that the priority evaluated on a smaller scale contains more spatial information.
To formulate specific planning schemes, the priority of water users was integrated with optimization models. Generally, there are conflicting allocation objectives among different users including economic, social, and environmental impacts [
3]. Thus, multiobjective models were developed for tackling multilateral interests from decision-makers [
22,
23,
24]. In practical water-allocation problems, economic benefits, crop yield, and environmental impacts were the most common objectives, while fairness in water allocation was attracting more and more attention [
25,
26]. Zhang et al. used the Gini coefficient in water distribution to quantify the fairness among different water use sectors [
23]. Li et al. measured the fairness of water distribution by the minimum difference of water use per unit area [
3]. These indicators were presented as a function describing the absolute individual differences, such that penalties were incurred for any differences in individual distribution results (whether a customer is worse off or better off) [
27]. Through such methods, interactions between allocation individuals, such as jealousy and comparison, can be hardly considered and reflected, which may reduce the resource allocation efficiency [
28]. Envy is a measure that considers the differences in service quality between all possible pairs of customers [
29]. This fairness index, based on the jealousy value, not only considers the psychology of comparison among the allocation objects, but also effectively avoids the loss of allocation efficiency. Therefore, this indicator is applied to the allocation of limited resources to consider the envy among the allocation objects in the allocation process.
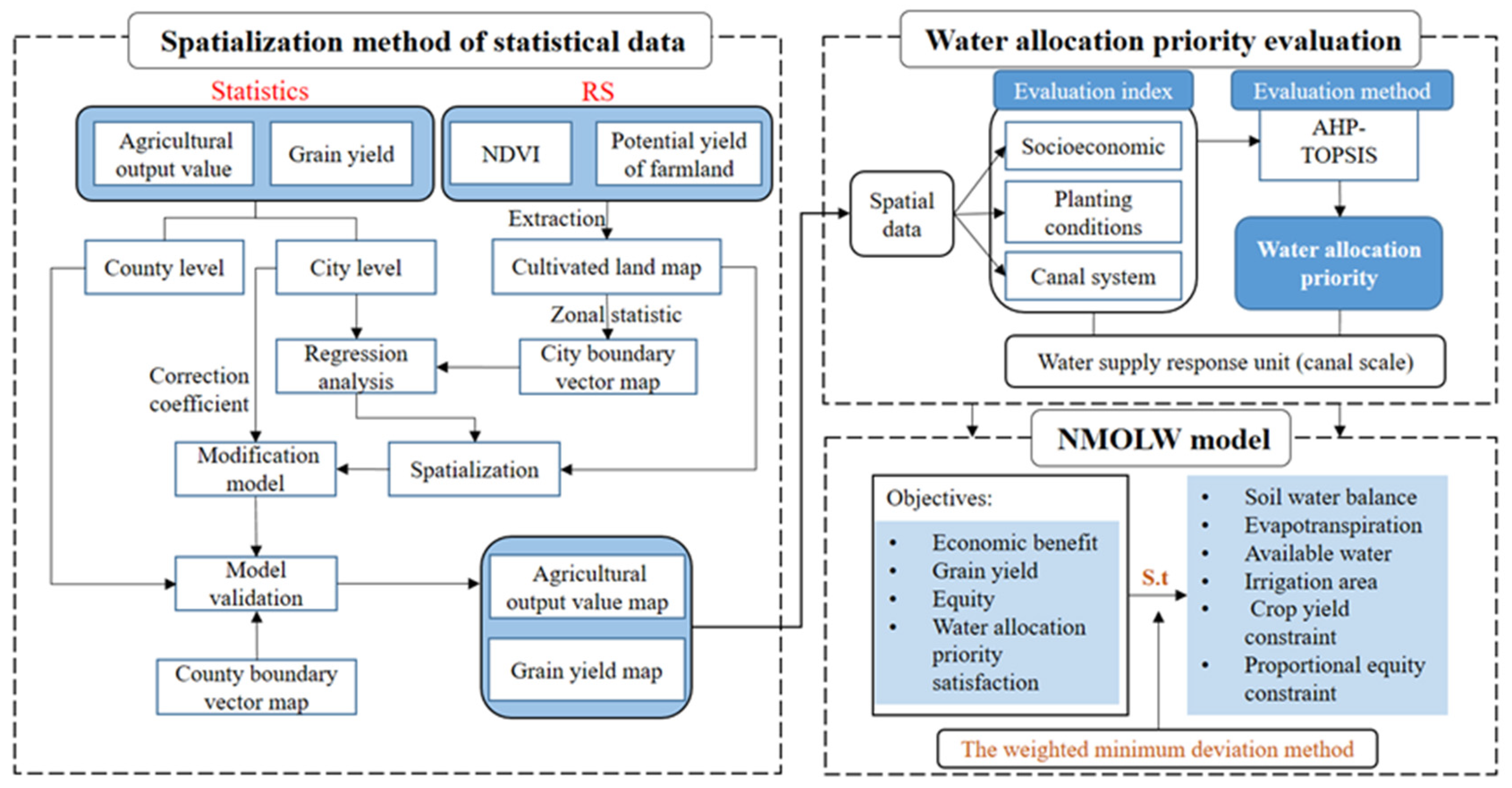
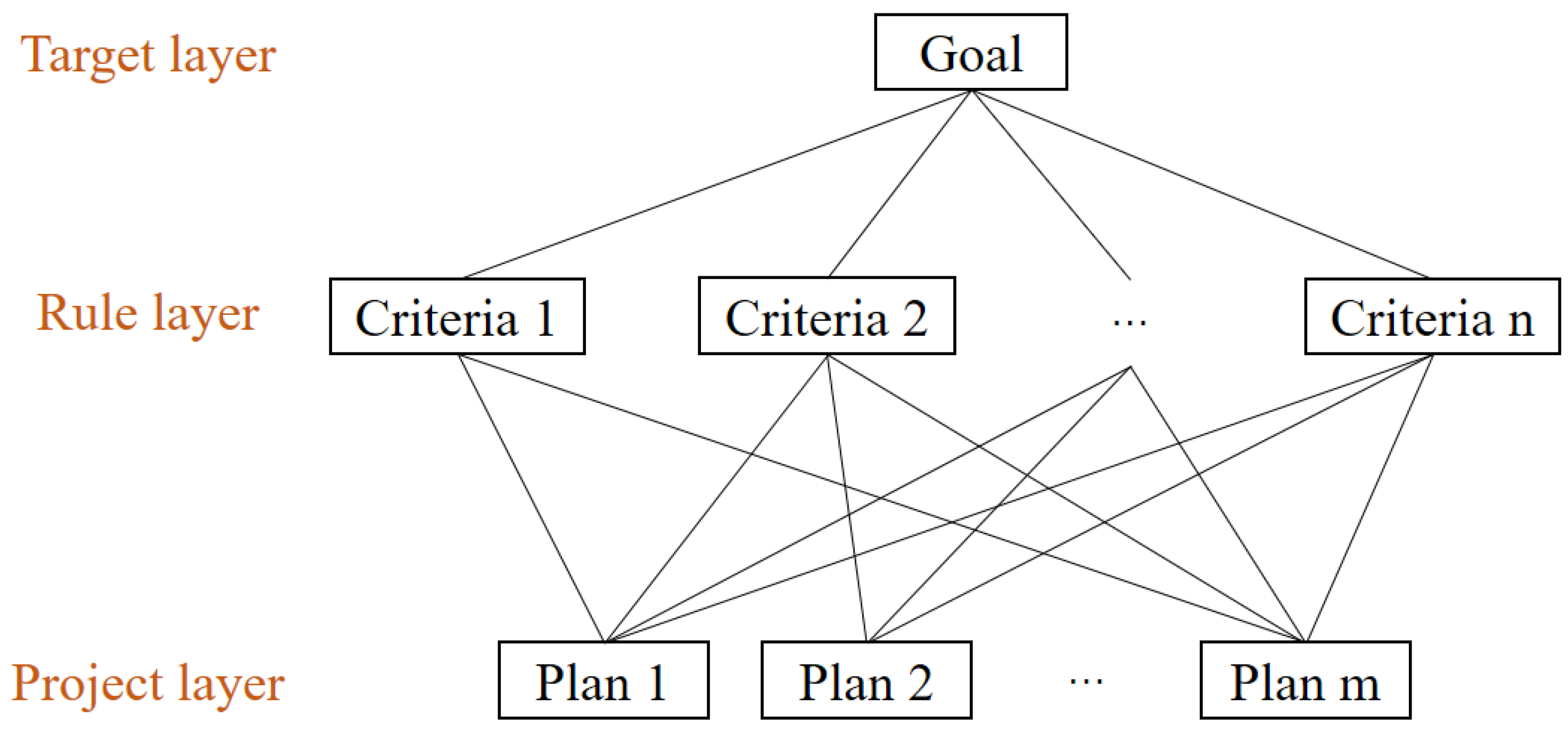
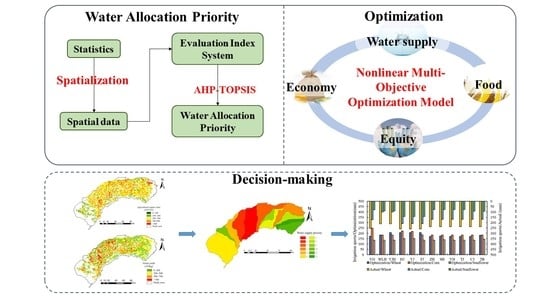
In order to effectively manage agricultural water resources, an evaluation‒optimization framework has been developed. First, a water allocation priority evaluation system is constructed, and remote sensing data is involved. After applying this evaluation model at the canal scale, both the accuracy and spatial variability can be guaranteed in the evaluation results. Then a nonlinear multi-objective optimal allocation model of agricultural land and water resources (NMOLW), considering allocation efficiency and equity, was established. The presented method improves the existing statistical data spatialization method and is applied to the constructed water allocation priority evaluation system. Then we input the priority evaluation results into the NMOLW model, and obtained the agricultural water and land resource allocation of irrigation area plan by solving the model. This can: (1) Obtain the water allocation priority through considerations of the social, economic, and environmental factors at the canal scale; (2) improve the spatialization method of agricultural output value (specifically referring to the income from the planting industry) and grain yield statistical data by introduce normalized difference vegetation index (NDVI) and remote sensing data on potential yield. Potential yield of farmland refers to the farmland production potential estimated by the GAEZ (Global Agro Ecological Zones) model, considering soil, weather, the environment, and other factors [
30]; and (3) illustrate the tradeoff between conflicting objectives, such as economic benefits, water supply priority, grain yield, and minimum envy. The method is applied to a practical case of an irrigation district in Northwest China and the optimization results can provide decision-making support for managers.
5. Conclusions
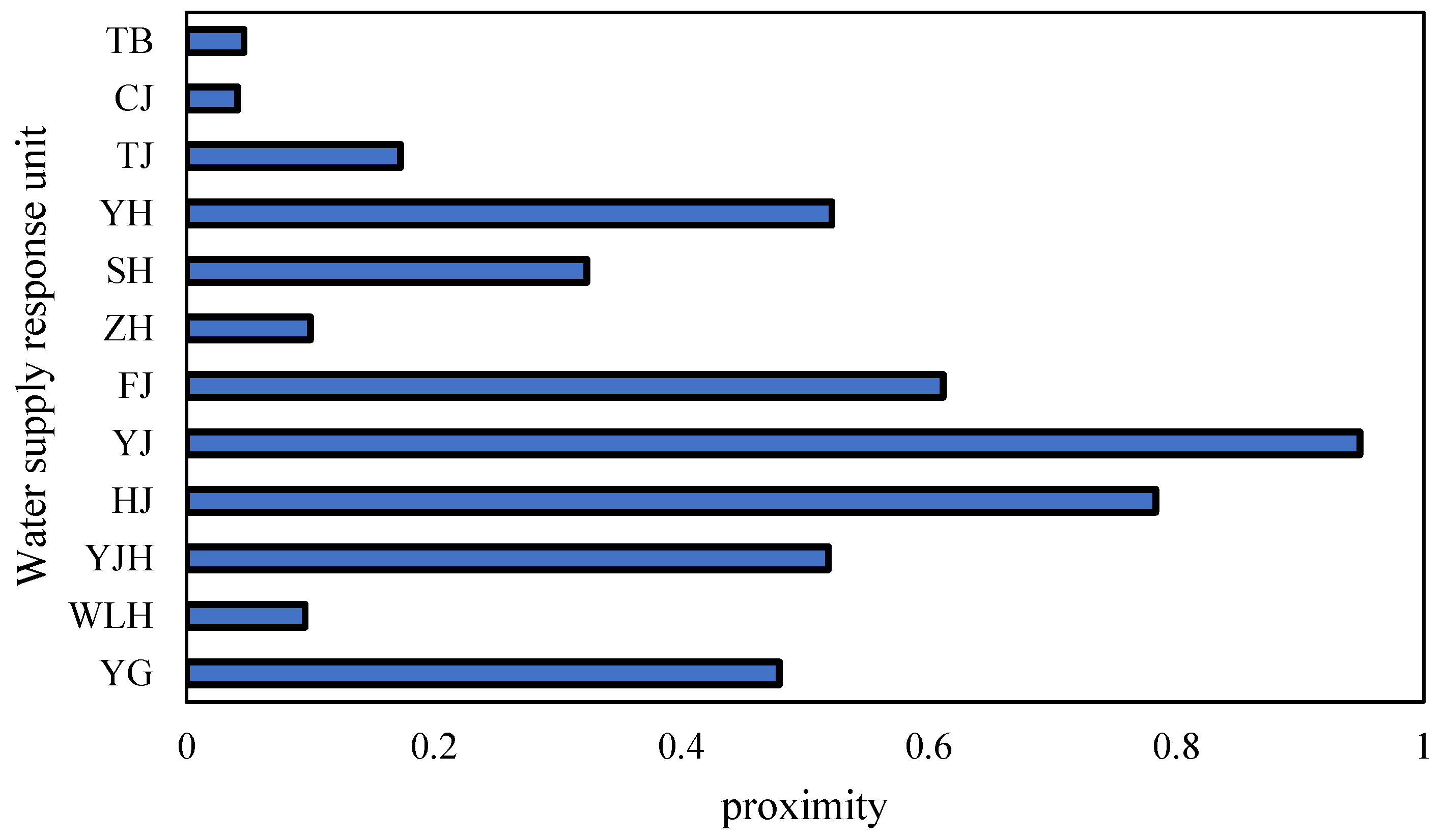
To determine the water allocation priority and manage agricultural water effectively, this study carried out the water allocation priority evaluation, and then a NMOLW model was proposed for considering fairness and efficiency. The water supply response units were divided according to the practical water supply condition of the study area. Furthermore, in order to solve the boundary conflict between the response unit and the original statistical data, a spatial method of analyzing the statistical data was introduced. This study has the following advantages:(1) Improving the spatial simulation accuracy agricultural output value and grain yield; (2) measuring the precise priorities including more spatial information; (3) fully considering the tradeoffs between allocation efficiency and equity; and (4) providing decision-making support for irrigation districts to formulate water use plans.
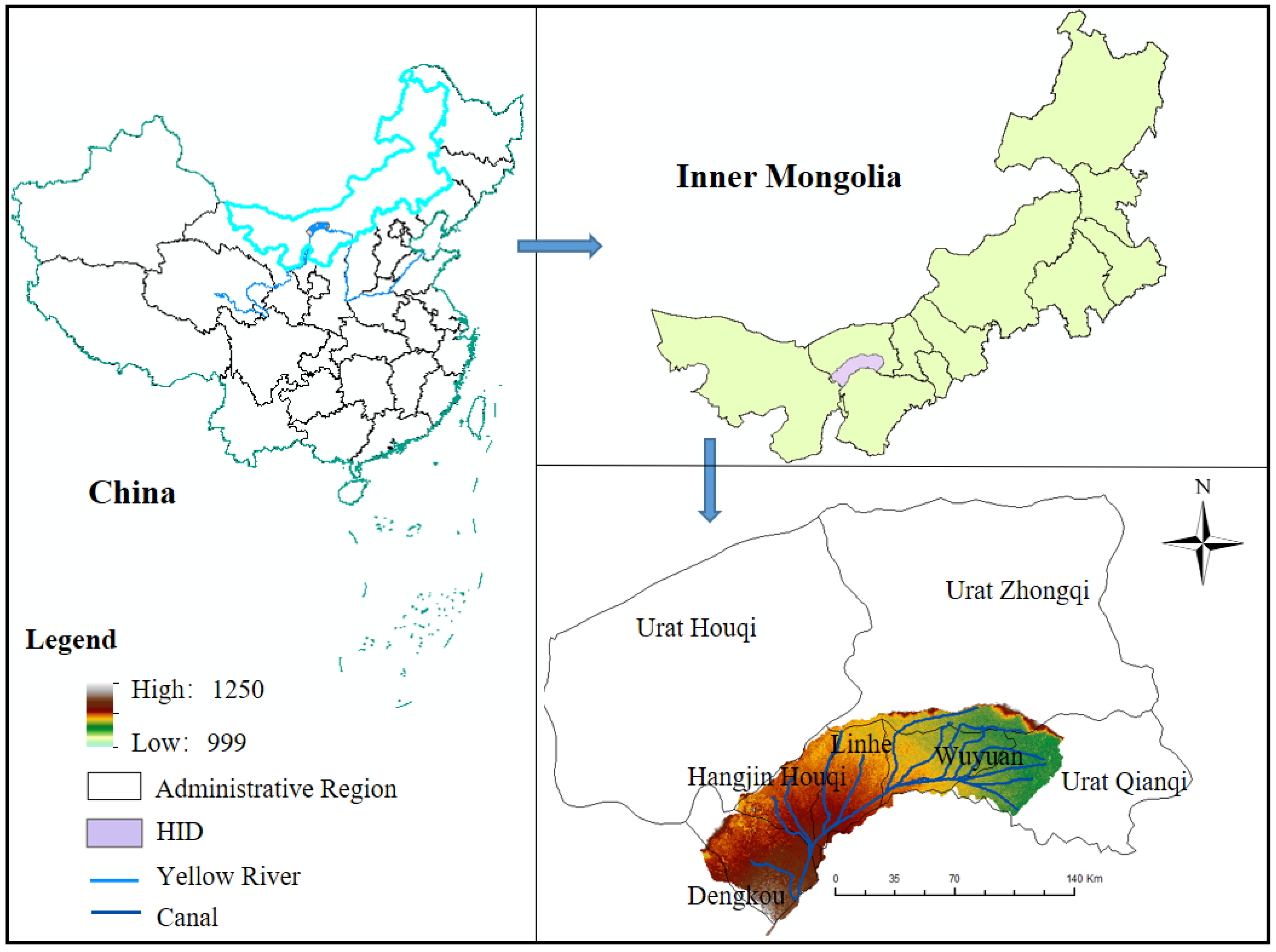
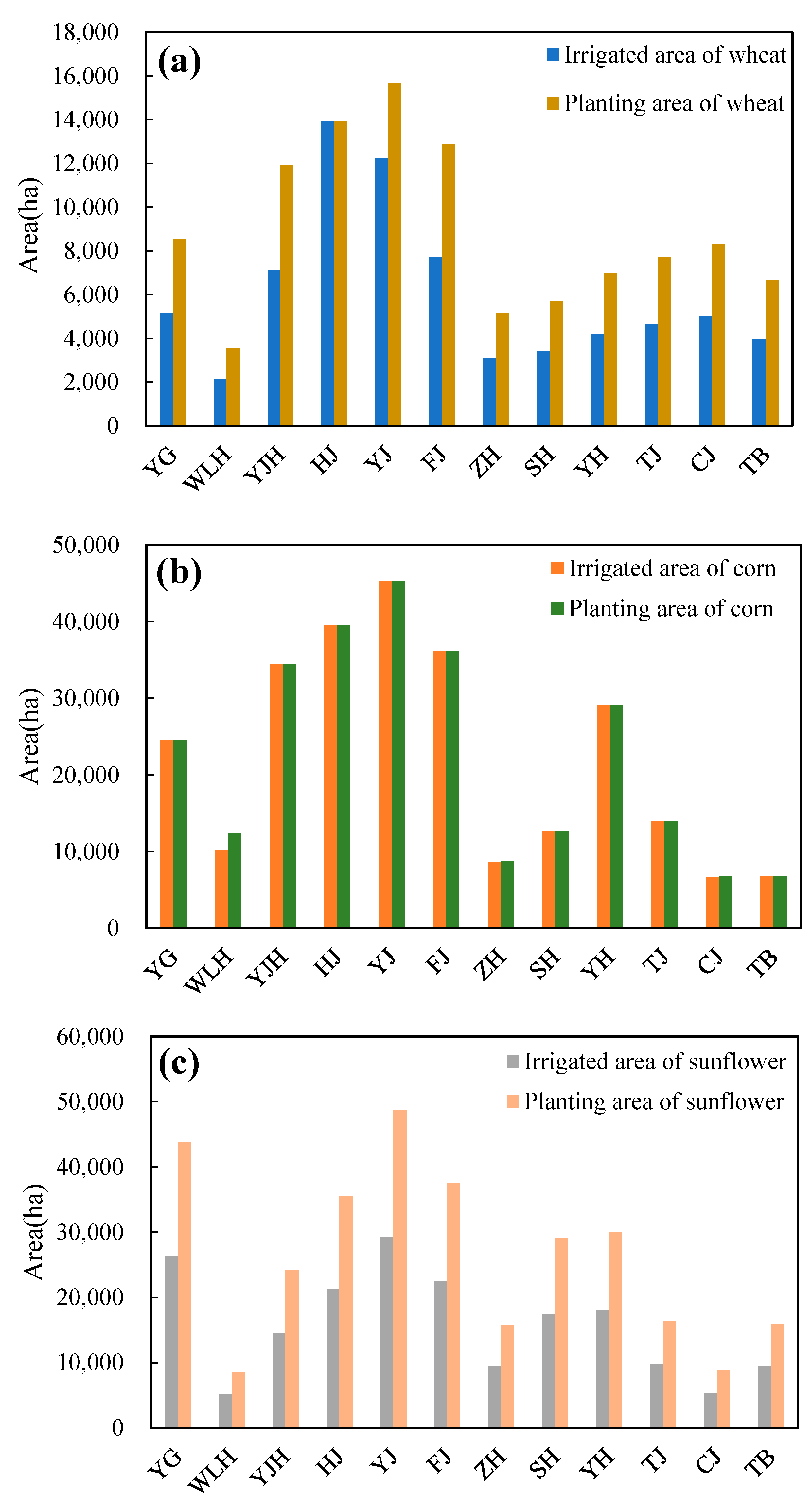
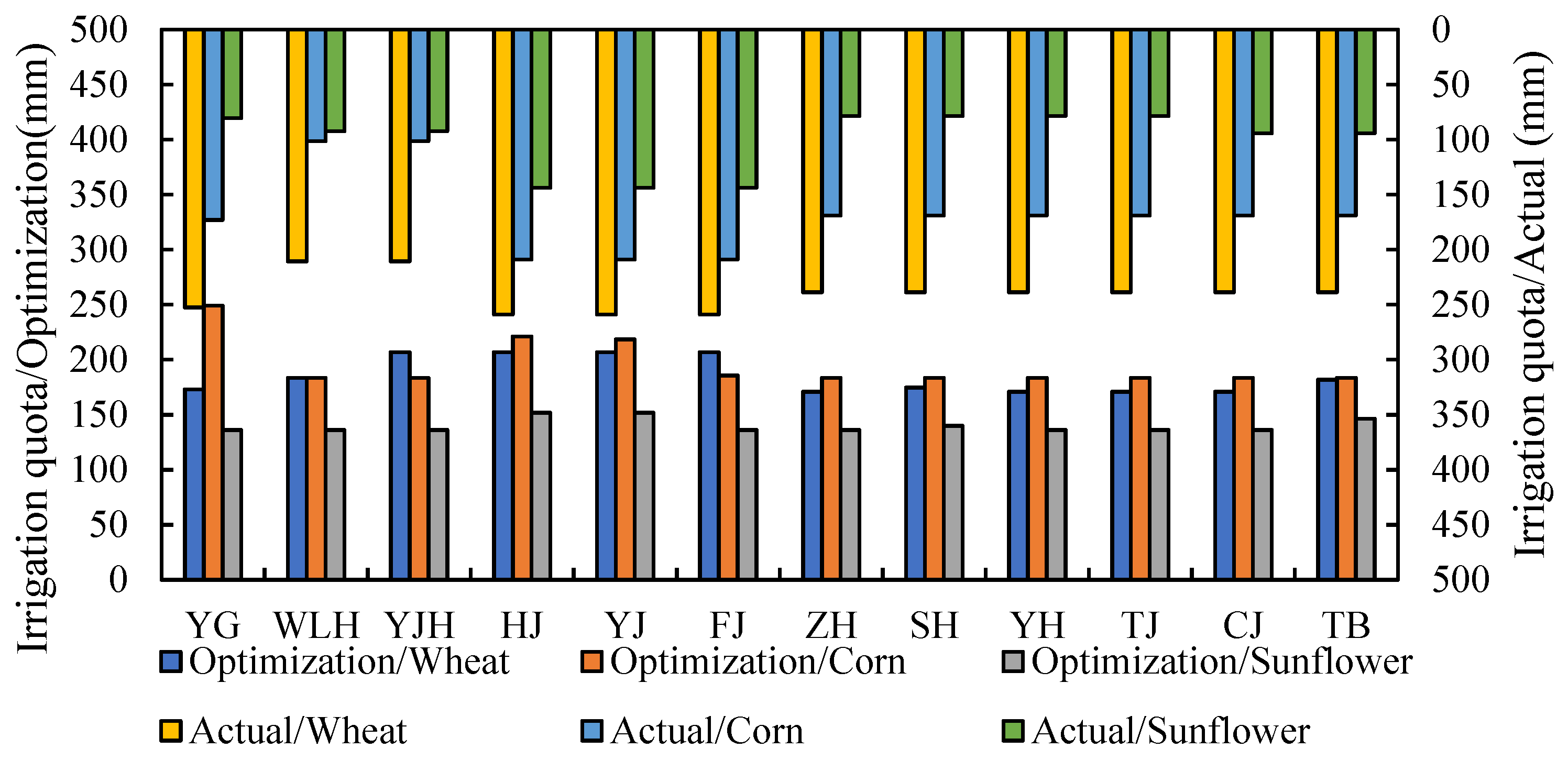
To illustrate the applicability of the proposed approach, this method has been applied to HID. The results show that: (1) the spatialization method of grain yield and agricultural production value achieved good simulation accuracy in HID; (2) we can determine the priority of water allocation at the scale of the canal system in HID; and (3) there is still room for increasing grain output in HID. The approach proposed in this study is expected to support sustainable agricultural water management in similar regions.
In fact, due to the variability of water supply response unit division and evaluating indexes, the method can be changed to suit different regions. There are many factors affecting the spatial distribution of agricultural output value and grain yield statistics, such as the detailed planting structure. These spatialization methods can be further improved.