Validation of GRACE and GRACE-FO Mascon Data for the Study of Polar Motion Excitation
Abstract
1. Introduction
2. Data and Methods
2.1. GRACE and GRACE-FO Mascon Data
| JPL RL06M v02 | CSR RL06M v01 | CSR RL06M v02 | GSFC v02.4 | |
|---|---|---|---|---|
| Abbreviation used in this study | JPL | CSR v01 | CSR v02 | GSFC |
| Mean (static) gravity field | GGM05C | GGM05C | GGM05C | GOCO-05S |
| 3rd bodies ephemerides | DE 430 | DE 430 | DE 430 | DE430 |
| AOD models | ECMWF (atmosphere) + MPIOM (ocean) | ECMWF (atmosphere) + MPIOM (ocean) | ECMWF (atmosphere) + MPIOM (ocean) | ECMWF (atmosphere) + MOG2D (ocean) |
| Ocean tides | GOT4.8 + SCEQ (Self-Consistent Equilibrium) model | GOT4.8 + SCEQ (Self-Consistent Equilibrium) model | GOT4.8 + SCEQ (Self-Consistent Equilibrium) model | GOT4.7 + SCEQ (Self-Consistent Equilibrium) model |
| Solid Earth and pole tides | IERS2010 | IERS2010 | IERS2010 | IERS2010 |
| ΔC20 replacement from SLR | TN11 [60] | TN11 [61] | TN14 [62] | TN07 [63] |
| ΔC30 replacement from SLR | − | − | TN14 [62]; for GRACE-FO only | − |
| Geocenter (degree-1 coefficients) correction | TN-13a [64] | TN-13a [64] | TN-13a [64] | [65] |
| GIA correction | ICE6G-D model [66] | ICE6G-D model [66] | ICE6G-D model [66] | ICE6G model [67] or A Geruo model [68]; in this study, we used ICE6G model |
| Correction for representation on ellipsoidal Earth | − | − | [58] | − |
| Number and shape of mascons estimated | 4551 circle cells | 40 962 (40 950 hexagons and 12 pentagons) | 40 962 (40 950 hexagons and 12 pentagons) | 41,168 squares |
| Time span for GRACE | April 2002 – June 2017 | April 2002 – June 2017 | April 2002 – June 2017 | January 2003 – July 2016 |
| Data for GRACE-FO | Yes | No | Yes | No |
| Reference | [8] | [57] | [57] | [53] |
| Data source | https://podaac-tools.jpl.nasa.gov/drive/files/GeodeticsGravity/tellus/L3/mascon (accessed on 1 July 2020) | http://www2.csr.utexas.edu/grace (accessed on 1 July 2020) | http://www2.csr.utexas.edu/grace (accessed on 1 July 2020) | https://earth.gsfc.nasa.gov/geo/data/grace-mascons (accessed on 1 July 2020) |
2.2. Land Surface Discharge Model (LSDM)
2.3. Hydrological Plus Cryospheric Signal in Observed PM Excitation
2.4. Time Series Processing
3. Results
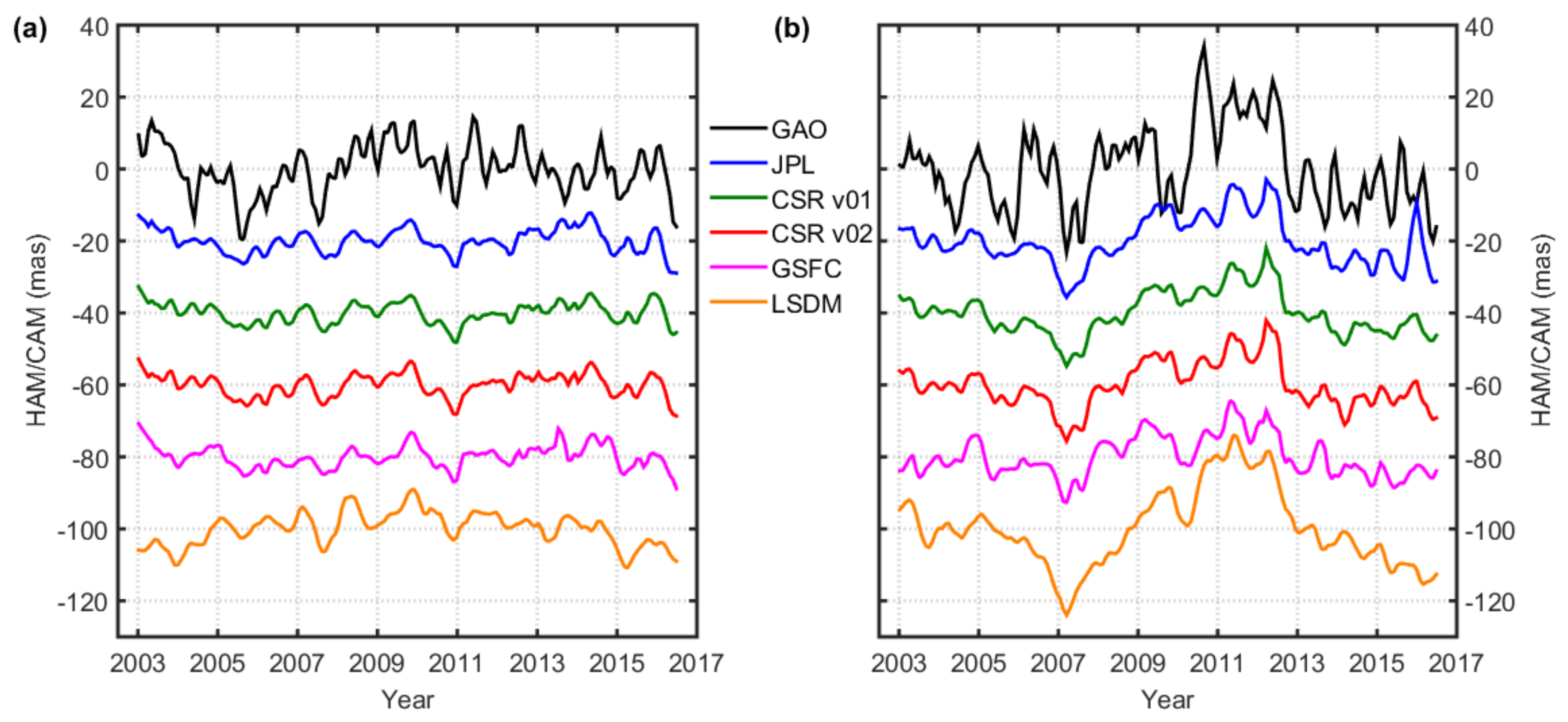
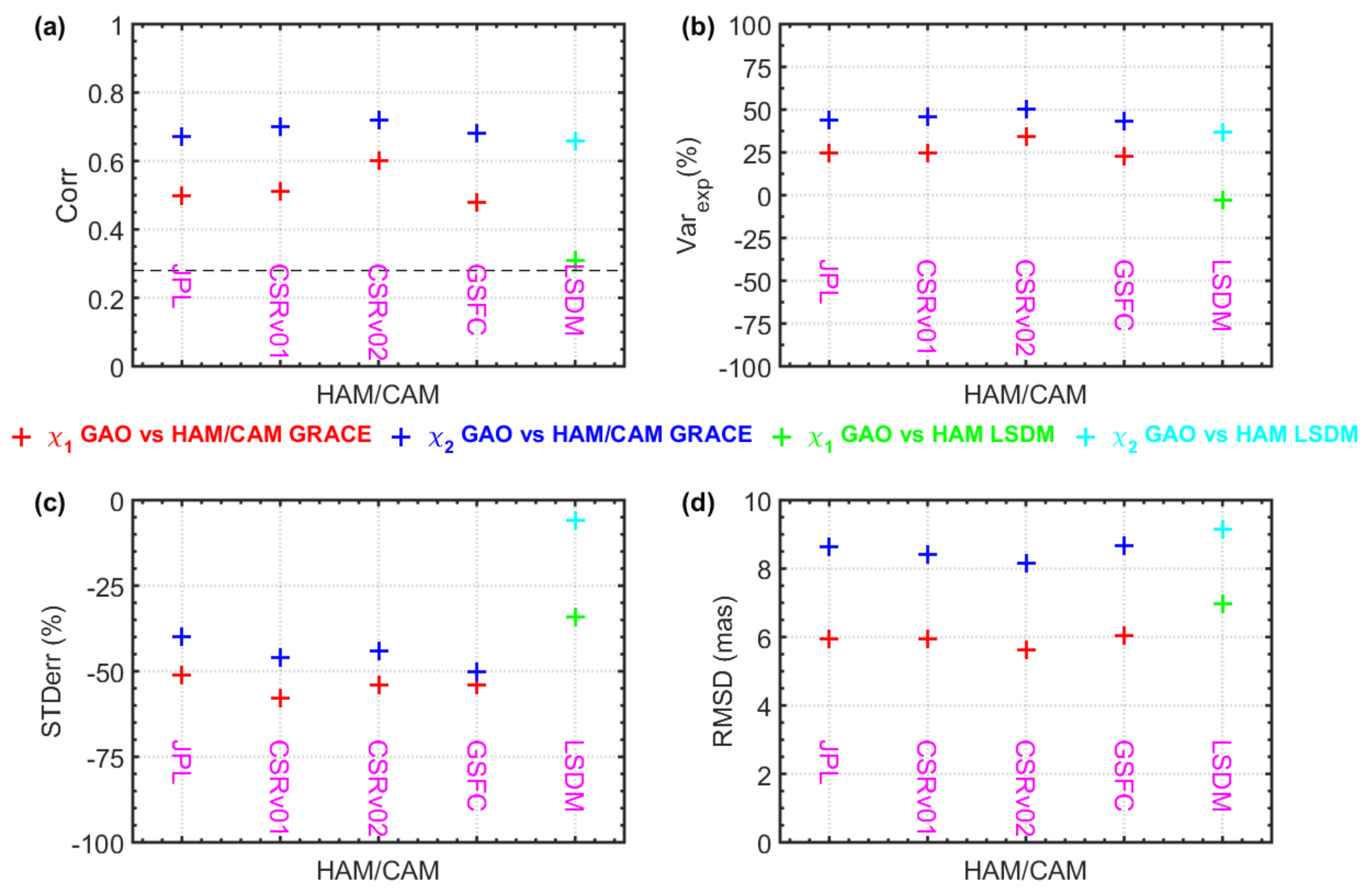
3.1. HAM/CAM Estimates from GRACE Mascon Data Provided by Different Data Centers
3.1.1. Trends
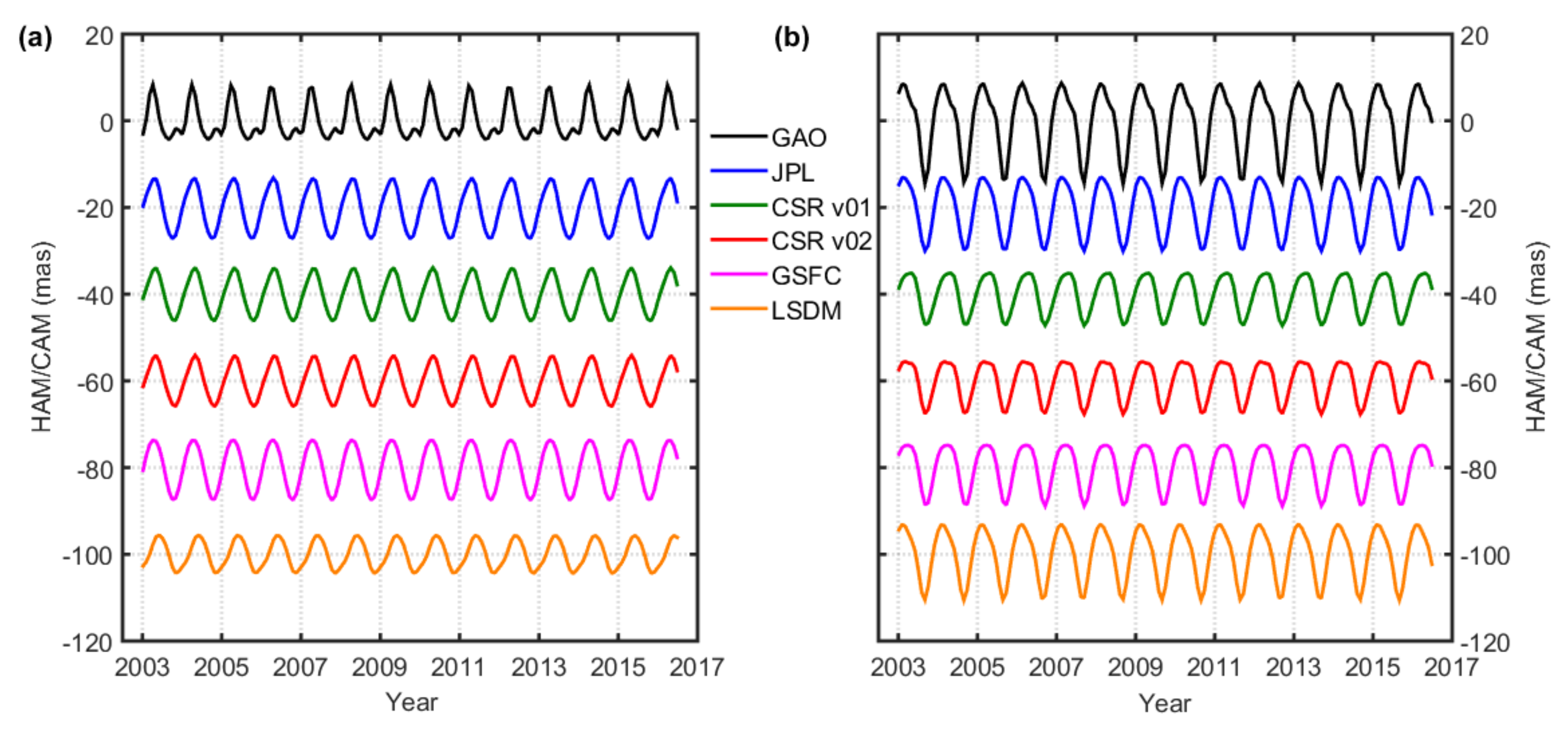
3.1.2. Overall Detrended Time Series
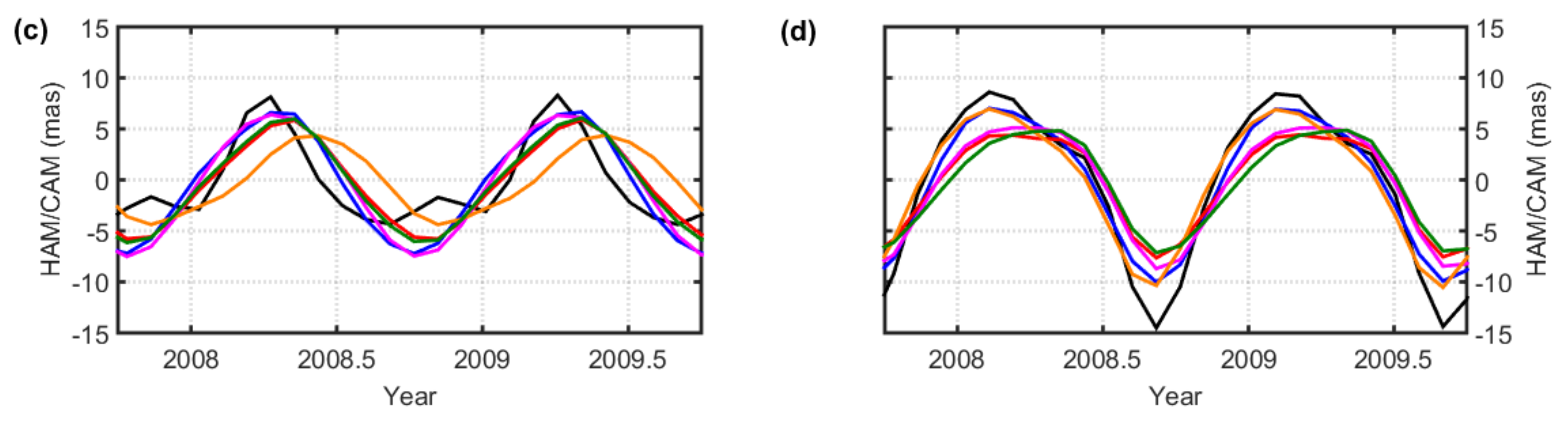
3.1.3. Seasonal Variations
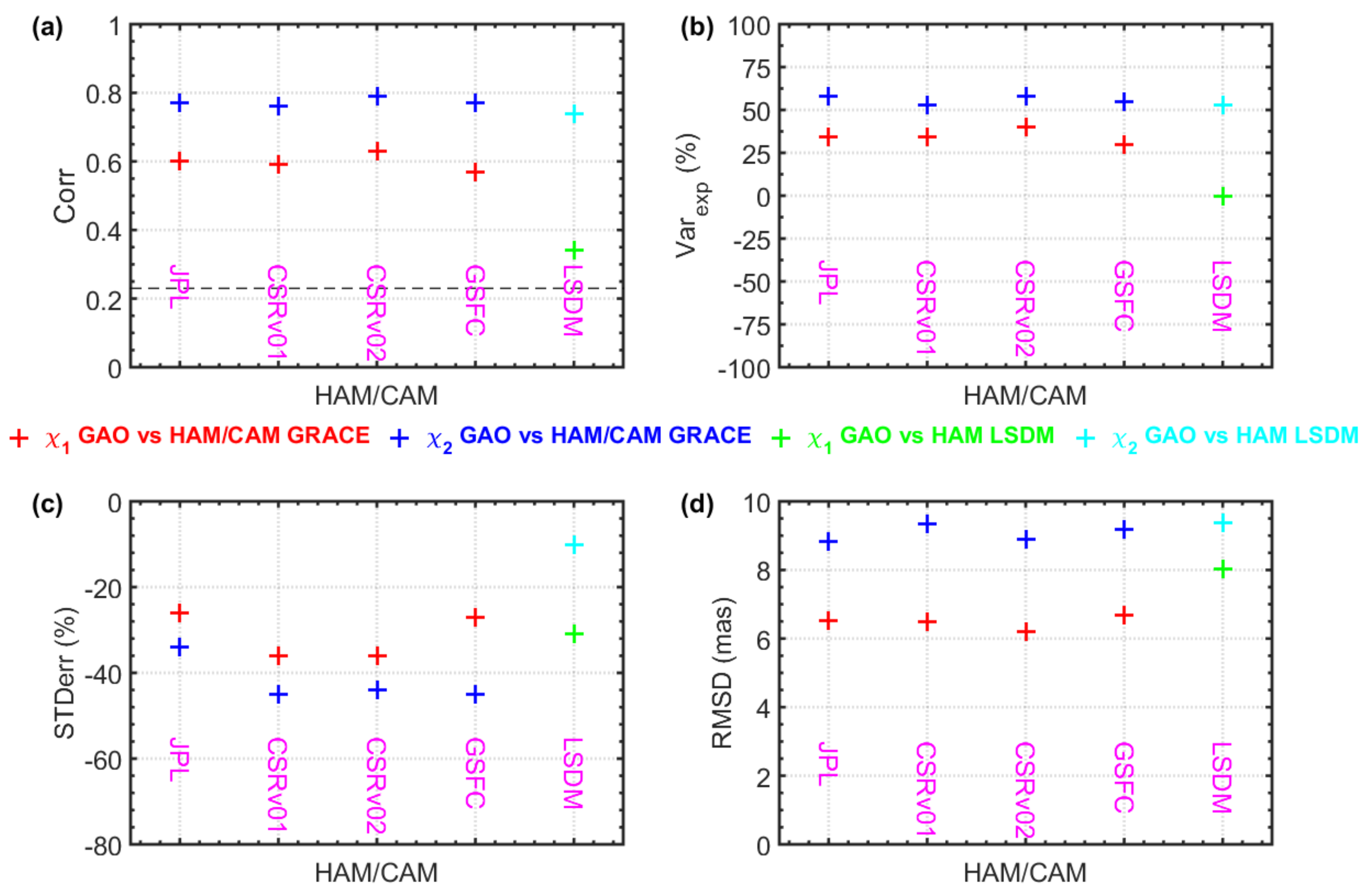
3.1.4. Non-Seasonal Variations
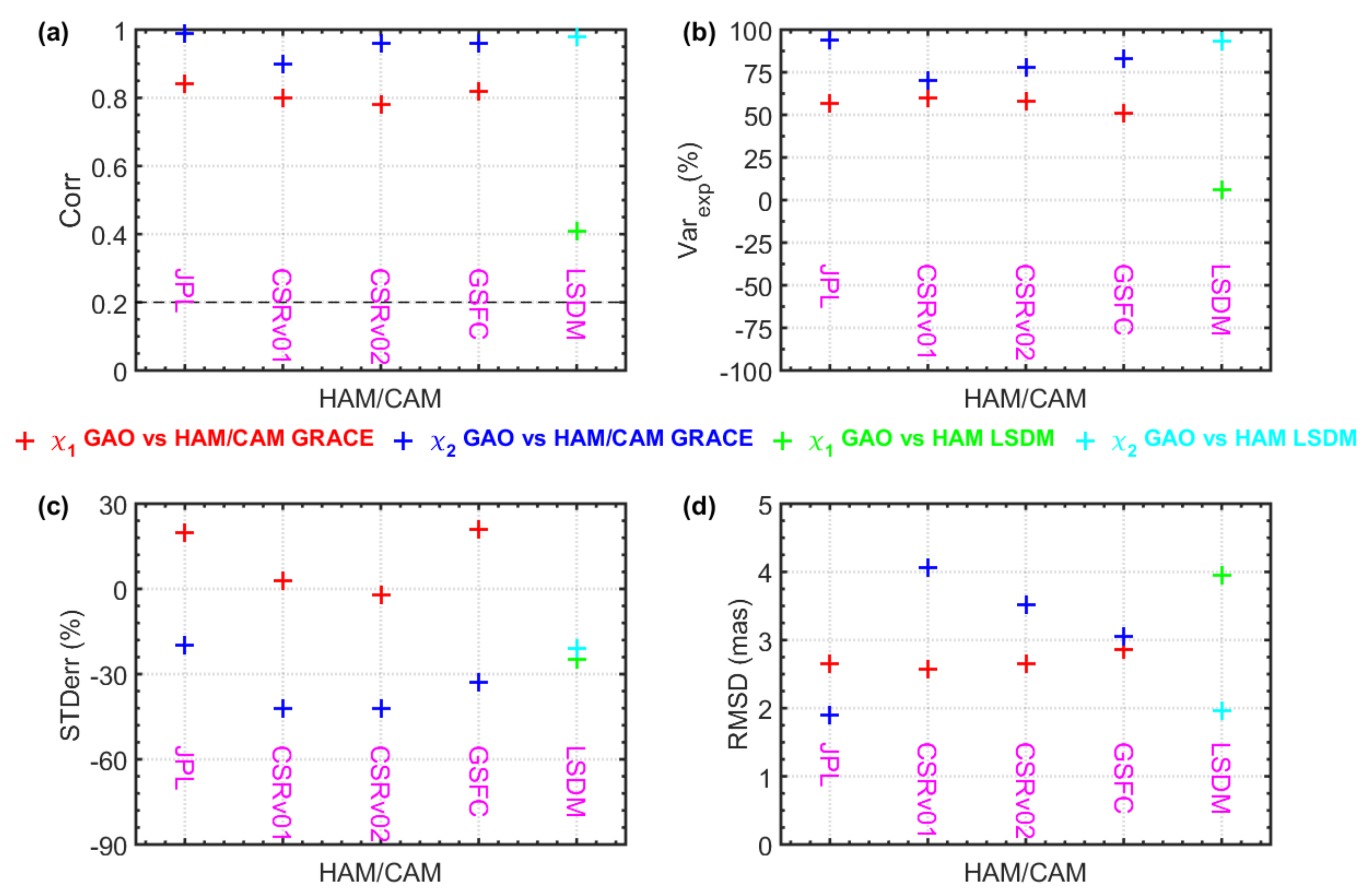
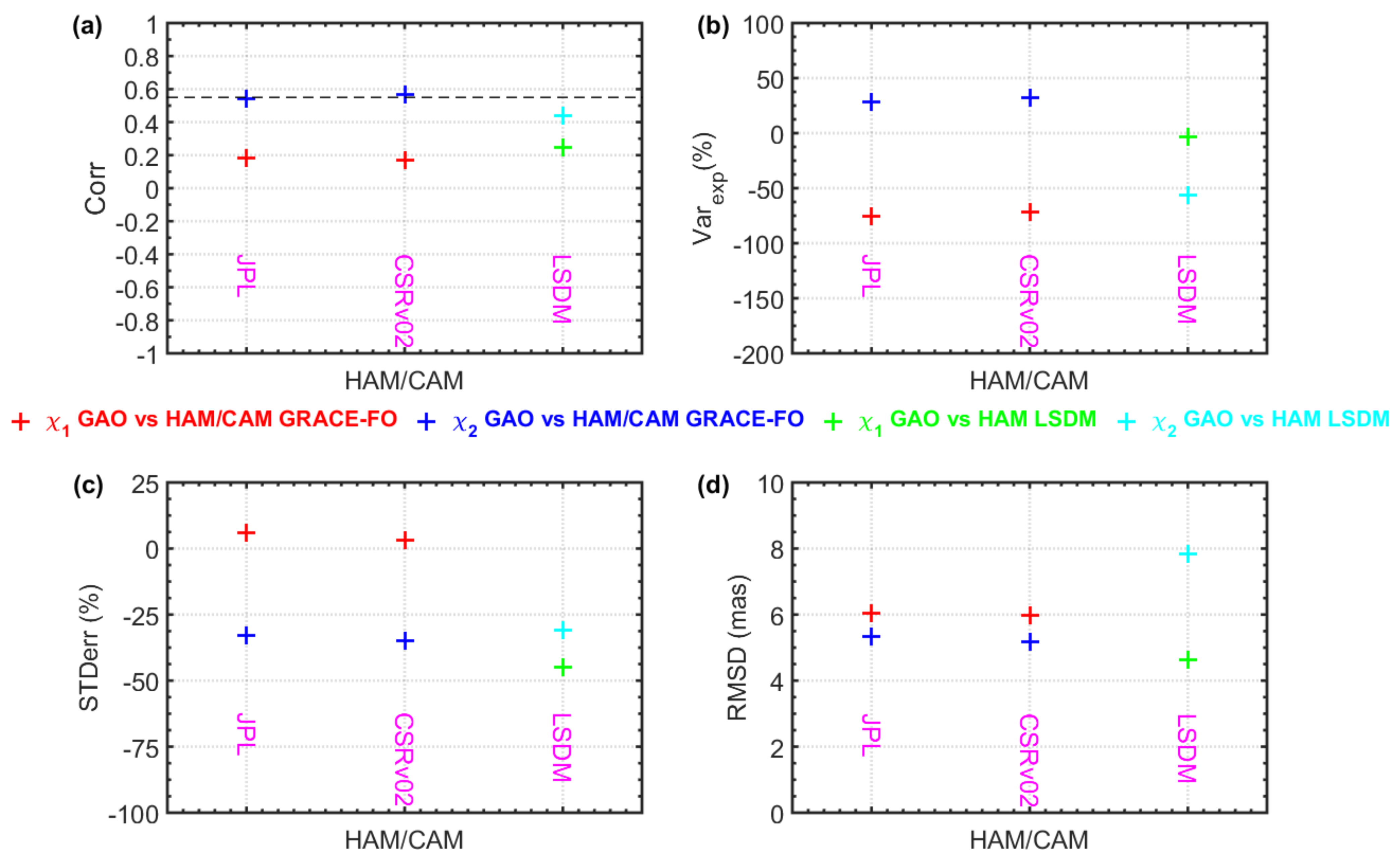
3.2. Preliminary Estimates of HAM/CAM from GRACE-FO Mascon Data
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Tapley, B.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Famiglietti, J.; Landerer, F.; Chambers, D.; Reager, J.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Wouters, B.; Bonin, J.A.; Chambers, D.P.; Riva, R.E.M.; Sasgen, I.; Wahr, J. GRACE, time-varying gravity, Earths system dynamics and climate change. Rep. Progress Phys. 2014, 77, 6801–116841. [Google Scholar] [CrossRef]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rockets 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I. Extending the global mass change data record: GRACE Follow-On instrument and science data performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Luthcke, S.B.; McCarthy, J.J.; Klosko, S.M.; Chinn, D.S.; Lemoine, F.G.; Boy, J.-P.; Sabaka, T.J. Global mass flux solutions from GRACE: A comparison of parameter estimation strategies—Mass concentrations versus Stokes coefficients. J. Geophys. Res. 2010, 115, B01403. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Swenson, S.C.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef]
- Ndehedehe, C.; Awange, J.; Agutu, N.; Kuhn, M.; Heck, B. Understanding changes in terrestrial water storage over West Africa between 2002 and 2014. Adv. Water Resour. 2016, 88, 211–230. [Google Scholar] [CrossRef]
- Shamsudduha, M.; Taylor, R.G.; Jones, D.; Longuevergne, L.; Owor, M.; Tindimugaya, C. Recent changes in terrestrial water storage in the Upper Nile Basin: An evaluation of commonly used gridded GRACE products. Hydrol. Earth System Sci. 2017, 21, 4533–4549. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Wang, L.; Chen, C.; Thomas, M.; Kaban, M.K.; Güntner, A.; Du, J. Increased water storage of Lake Qinghai during 2004–2012 from GRACE data, hydrological models, radar altimetry and in situ measurements. Geophys. J. Int. 2018, 212, 679–693. [Google Scholar] [CrossRef]
- Zhao, K.; Li, X. Estimating terrestrial water storage changes in the Tarim River Basin using GRACE data. Geophys. J. Int. 2017, 211, 1449–1460. [Google Scholar] [CrossRef]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, 2–5. [Google Scholar] [CrossRef]
- Velicogna, I.; Sutterley, T.C.; Van Den Broeke, M.R. Regional acceleration in ice mass loss from Greenland and Antarctica using GRACE time-variable gravity data. Geophys. Res. Lett. 2014, 41, 8130–8137. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Reager, J.T.; Thomas, B.F.; Famiglietti, J.S. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE- based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Chen, J.; Famigliett, J.S.; Scanlon, B.R.; Rodell, M. Groundwater Storage Changes: Present Status from GRACE Observations. Surv. Geophys. 2016, 37, 397–417. [Google Scholar] [CrossRef]
- Feng, W.; Shum, C.K.; Zhong, M.; Pan, Y. Groundwater storage changes in China from satellite gravity: An overview. Remote Sens. 2018, 10, 674. [Google Scholar] [CrossRef]
- Jin, S.; Feng, G. Large-scale variations of global groundwater from satellite gravimetry and hydrological models, 2002–2012. Glob. Planet. Chang. 2013, 106, 20–30. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Rzepecka, Z.; Birylo, M. Groundwater storage changes derived from GRACE and GLDAS on smaller river basins—A case study in Poland. Geosciences 2020, 10, 124. [Google Scholar] [CrossRef]
- Śliwińska, J.; Birylo, M.; Rzepecka, Z.; Nastula, J. Analysis of groundwater and total water storage changes in Poland using GRACE observations, in-situ data, and various assimilation and climate models. Remote Sens. 2019, 11, 2949. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49. [Google Scholar] [CrossRef] [PubMed]
- Brzeziński, A.; Nastula, J.; Kołaczek, B. Seasonal excitation of polar motion estimated from recent geophysical models and observations. J. Geodyn. 2009, 48, 235–240. [Google Scholar] [CrossRef]
- Seoane, L.; Nastula, J.; Bizouard, C.; Gambis, D. The use of gravimetric data from GRACE mission in the understanding of polar motion variations. Geophys. J. Int. 2009, 178, 614–622. [Google Scholar] [CrossRef]
- Dobslaw, H.; Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; König, R.; Flechtner, F. A new high–resolution model of non–tidal atmosphere and ocean mass variability for de–aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef]
- Barnes, R.T.H.; Hide, R.; White, A.A.; Wilson, C.A. Atmospheric Angular Momentum Fluctuations, Length-of-Day Changes and Polar Motion. Proc. Royal Soc. A Math. Phys. Eng. Sci. 1983, 387, 31–73. [Google Scholar] [CrossRef]
- Gross, R.S.; Fukumori, I.; Menemenlis, D. Atmospheric and oceanic excitation of the Earth’s wobbles during 1980–2000. J. Geophys. Res. Solid Earth. 2003, 108, 2370. [Google Scholar] [CrossRef]
- Nastula, J.; Ponte, R.M. Further evidence for oceanic excitation of polar motion. Geophys. J. Int. 1999, 139, 123–130. [Google Scholar] [CrossRef]
- Nastula, J.; Ponte, R.M.; Salstein, D.A. Regional signals in atmospheric and oceanic excitation of polar motion. In Polar Motion: Historical and Scientific Problems; Dick, S., McCarthy, D., Luzum, B., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2000; pp. 463–472. [Google Scholar]
- Nastula, J.; Ponte, R.M.; Salstein, D.A. Comparison of polar motion excitation series derived from GRACE and from analyses of geophysical fluids. Geophys. Res. Lett. 2007. [Google Scholar] [CrossRef]
- Nastula, J.; Salstein, D.A.; Kołaczek, B. Patterns of atmospheric excitation functions of polar motion from high–resolution regional sectors. J. Geophys. Res. 2009, 114, B04407. [Google Scholar] [CrossRef]
- Göttl, F.; Schmidt, M.; Seitz, F. Mass-related excitation of polar motion: An assessment of the new RL06 GRACE gravity field models. Earth Planets Space 2018, 70. [Google Scholar] [CrossRef]
- Jin, S.; Chambers, D.P.; Tapley, B.D. Hydrological and oceanic effects on polar motion from GRACE and models. J. Geophys. Res. 2010, 115, B02403. [Google Scholar] [CrossRef]
- Jin, S.; Hassan, A.A.; Feng, G.P. Assessment of terrestrial water contributions to polar motion from GRACE and hydrological models. J. Geodyn. 2012, 62, 40–48. [Google Scholar] [CrossRef]
- Meyrath, T.; van Dam, T. A comparison of interannual hydrological polar motion excitation from GRACE and geodetic observations. J. Geodyn. 2016, 99, 1–9. [Google Scholar] [CrossRef]
- Nastula, J.; Śliwińska, J. Prograde and Retrograde Terms of Gravimetric Polar Motion Excitation Estimates from the GRACE Monthly Gravity Field Models. Remote Sens. 2020, 12, 138. [Google Scholar] [CrossRef]
- Nastula, J.; Pasnicka, M.; Kolaczek, B. Comparison of the geophysical excitations of polar motion from the period 1980.0–2007.0. Acta Geophys. 2011, 59, 561–577. [Google Scholar] [CrossRef]
- Nastula, J.; Wińska, M.; Śliwińska, J.; Salstein, D. Hydrological signals in polar motion excitation—Evidence after fifteen years of the GRACE mission. J Geodyn 2019, 124, 119–132. [Google Scholar] [CrossRef]
- Seoane, L.; Nastula, J.; Bizouard, C.; Gambis, D. Hydrological excitation of polar motion derived from GRACE gravity field solutions. Int. J. Geophys. 2011. [Google Scholar] [CrossRef]
- Seoane, L.; Biancale, R.; Gambis, D. Agreement between Earth’s rotation and mass displacement as detected by GRACE. J. Geodyn. 2012, 62, 49–55. [Google Scholar] [CrossRef]
- Śliwińska, J.; Wińska, M.; Nastula, J. Terrestrial water storage variations and their effect on polar motion. Acta Geophys. 2019, 67, 17–39. [Google Scholar] [CrossRef]
- Śliwińska, J.; Nastula, J.; Dobslaw, H.; Dill, R. Evaluating Gravimetric Polar Motion Excitation Estimates from the RL06 GRACE Monthly-Mean Gravity Field Models. Remote Sens. 2020, 12, 930. [Google Scholar] [CrossRef]
- Śliwińska, J.; Wińska, M.; Nastula, J. Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data. Remote Sens. 2020, 12, 3490. [Google Scholar] [CrossRef]
- Wińska, M.; Nastula, J.; Kołaczek, B. Assessment of the global and regional land hydrosphere and its impact on the balance of the geophysical excitation function of polar motion. Acta Geophys. 2016, 64, 1–23. [Google Scholar] [CrossRef]
- Wińska, M.; Nastula, J.; Salstein, D.A. Hydrological excitation of polar motion by different variables from the GLDAS model. J. Geodesy 2017, 17, 7110. [Google Scholar] [CrossRef]
- Chen, J.L. Satellite gravimetry and mass transport in the earth system. Geodesy Geodynam. 2018, 10, 402–415. [Google Scholar] [CrossRef]
- Jing, W.; Zhao, X.; Yao, L.; Jiang, H.; Xu, J.; Yang, J.; Li, Y. Variations in terrestrial water storage in the Lancang-Mekong river basin from GRACE solutions and land surface model. J. Hydrol. 2020, 580, 124258. [Google Scholar] [CrossRef]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Luthcke, S.; Sabaka, T.; Loomis, B.; Arendt, A.; McCarthy, J.; Camp, J. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
- Schrama, E.J.O.; Wouters, B.; Rietbroek, R. A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from GRACE data. J. Geophys. Res. Solid Earth 2014, 119, 6048–6066. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J.; Liu, X. Drought evaluation using the GRACE terrestrial water storage deficit over the Yangtze River Basin, China. Sci. Total Environ. 2018, 634, 727–738. [Google Scholar] [CrossRef] [PubMed]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Ditmar, P. Conversion of time-varying Stokes coefficients into mass anomalies at the Earth’s surface considering the Earth’s oblateness. J. Geodesy 2018, 92, 1401–1412. [Google Scholar] [CrossRef]
- Save, H. CSR GRACE and GRACE-FO RL06 Mascon Solutions v02. Available online: http://www2.csr.utexas.edu/grace/RL06_mascons.html (accessed on 1 July 2020). [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 2011, 116, B01409. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geodesy 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Wiese, D.N.; Landerer, F.W.; Luthcke, S.B. Replacing GRACE/GRACE-FO with satellite laser ranging: Impacts on Antarctic Ice Sheet mass change. Geophys. Res. Lett. 2020, 47, e2019GL085488. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, 8410. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Comment on “An Assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment Model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice-age terminal deglaciation: The global ICE-6G C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Eubanks, T.M. Variations in the orientation of the Earth. In Contributions of Space Geodesy to Geodynamics: Earth Dynamics: Geodynamic Series; Smith, D.E., Turcotte, D.L., Eds.; American Geophysical Union: Washington, DC, USA, 1993; Volume 24, pp. 1–54. [Google Scholar]
- Gross, R. Theory of earth rotation variations. In VIII Hotine-Marussi Symposium on Mathematical Geodesy; Sneeuw, N., Novák, P., Crespi, M., Sansò, F., Eds.; Springer: Cham, Switzerland, 2015; Volume 142. [Google Scholar]
- Nastula, J. Polar Motion Excitation from Several Models of Land Hydrosphere. In Proceedings of the 19th EGU General Assembly, EGU2017, Vienna, Austria, 23–28 April 2017; p. 11866. Available online: https://meetingorganizer.copernicus.org/EGU2017/EGU2017-11866-1.pdf (accessed on 1 July 2020).
- Dill, R. Hydrological Model LSDM for Operational Earth Rotation and Gravity Field Variations. GFZ Scientific Technical Report STR; 08/09. Available online: https://gfzpublic.gfz-potsdam.de/pubman/faces/ViewItemFullPage.jsp?itemId=item_8770_4 (accessed on 15 January 2021).
- Dobslaw, H.; Dill, R.; Grötzsch, A.; Brzeziński, A.; Thomas, M. Seasonal polar motion excitation from numerical models of atmosphere, ocean, and continental hydrosphere. J. Geophys. Res. 2010, 115, B10406. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Fischer, N.; Haak, H.; Lohmann, K.; Marotzke, J.; Matei, D.; Mikolajewicz, U.; Notz, D.; von Storch, J.S. Characteristics of the ocean simulations in MPIOM, the ocean component of the MPI-Earth system model. J. Adv. Model. Earth Syst. 2013, 5, 422–446. [Google Scholar] [CrossRef]
- Dobslaw, H.; Dill, R. Effective Angular Momentum Functions from Earth System Modelling at GeoForschungsZentrum in Potsdam. Technical Report, Revision 1.1 (March 18, 2019), GFZ Potsdam, Germany. Available online: http://rz-vm115.gfz-potsdam.de:8080/repository (accessed on 15 January 2021).
- Brzezinski, A. Polar motion excitation by variations of the effective angular momentum function: Considerations concerning deconvolution problem. Manuscr. Geod. 1992, 17, 3–20. [Google Scholar]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geodesy 2018. [Google Scholar] [CrossRef]
- Nastula, J.; Chin, T.M.; Gross, R.; Śliwińska, J.; Wińska, M. Smoothing and predicting celestial pole offsets using a Kalman filter and smoother. J. Geodesy 2020, 94. [Google Scholar] [CrossRef]
- Bizouard, C. Elliptic polarisation of the polar motion excitation. J. Geod. 2016, 90, 179–188. [Google Scholar] [CrossRef]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes and Consequences; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Munk, W.H.; Mac Donald, G. The Rotation of the Earth; Cambridge University Press: Cambridge, UK, 1960. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, S.; Luo, J.; Ray, J.; Huang, Y.; Li, J. Global glacial isostatic adjustment constrained by GPS measurements: Spherical harmonic analyses of uplifts and geopotential variations. Remote Sens. 2020, 12, 1209. [Google Scholar] [CrossRef]
- Youm, K.; Seo, K.W.; Jeon, T.; Na, S.H.; Chen, J.; Wilson, C.R. Ice and groundwater effects on long term polar motion (1979–2010). J. Geodyn. 2017, 106, 66–73. [Google Scholar] [CrossRef]
- Güntner, A.; Stuck, J.; Werth, S.; Döll, P.; Verzano, K.; Merz, B. A global analysis of temporal and spatial variations in continental water storage. Water Resour. Res. 2007, 43, 1–19. [Google Scholar] [CrossRef]
- Adhikari, S.; Caron, L.; Steinberger, B.; Reager, J.T.; Kjeldsen, K.K.; Marzeion, B.; Larour, E.; Ivins, E.R. What drives 20th century polar motion? Earth Planet. Sci. Lett. 2018, 502, 126–132. [Google Scholar] [CrossRef]
- Adhikari, S.; Ivins, E.R. Climate-driven polar motion: 2003–2015. Sci. Adv. 2016, 2, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Carrere, L.; Lyard, F. Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing—Comparisons with observations. Geophys. Res. Lett. 2003, 30, 1275. [Google Scholar] [CrossRef]




| Trend (Mas/Year) | ||
|---|---|---|
| χ1 | χ2 | |
| GAO (without GIA removed) | +5.57 ± 0.59 | −0.72 ± 1.02 |
| GAO (with GIA removed) | +4.55 ± 0.59 | +3.88 ± 1.02 |
| JPL | +4.01 ± 0.44 | +2.04 ± 0.67 |
| CSR v01 | +3.55 ± 0.38 | +2.02 ± 0.56 |
| CSR v02 | +3.93 ± 0.38 | +2.09 ± 0.57 |
| GSFC | +0.86 ± 0.44 | +1.29 ± 0.56 |
| LSDM | +0.43 ± 0.41 | +3.39 ± 0.91 |
| Trend (Mas/Year) | ||
|---|---|---|
| χ1 | χ2 | |
| ICE6G-D | +1.02 | ‒4.60 |
| ICE6G | +0.90 | ‒4.33 |
| ICE6G ‒ ICE6G-D | ±0.12 | ±0.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Śliwińska, J.; Wińska, M.; Nastula, J. Validation of GRACE and GRACE-FO Mascon Data for the Study of Polar Motion Excitation. Remote Sens. 2021, 13, 1152. https://doi.org/10.3390/rs13061152
Śliwińska J, Wińska M, Nastula J. Validation of GRACE and GRACE-FO Mascon Data for the Study of Polar Motion Excitation. Remote Sensing. 2021; 13(6):1152. https://doi.org/10.3390/rs13061152
Chicago/Turabian StyleŚliwińska, Justyna, Małgorzata Wińska, and Jolanta Nastula. 2021. "Validation of GRACE and GRACE-FO Mascon Data for the Study of Polar Motion Excitation" Remote Sensing 13, no. 6: 1152. https://doi.org/10.3390/rs13061152
APA StyleŚliwińska, J., Wińska, M., & Nastula, J. (2021). Validation of GRACE and GRACE-FO Mascon Data for the Study of Polar Motion Excitation. Remote Sensing, 13(6), 1152. https://doi.org/10.3390/rs13061152






