Abstract
The Baihetan hydropower station is the second largest hydropower station worldwide. It began to store water in April 2021. We conducted a dense hybrid gravity and GNSS survey at 223 stations, obtained the free-air and Bouguer gravity anomalies, inversed the lithospheric density structure, and calculated the isostatic additional force (IAF) borne by lithosphere in the reservoir area. Moreover, we studied the gravity change and Coulomb stress change around the Baihetan reservoir due to impoundment. The main findings are the following. (1) Hybrid gravity and GNSS observations significantly improved the spatial resolution of the gravity field, and the maximum improvement reached up to 150 mGal. (2) A new method for risk assessment of reservoir-induced earthquakes is proposed from the perspective of lithospheric equilibrium. It was found that there is an IAF of −30 MPa at approximately 20 km upstream of the Baihetan dam, and the risk of a reservoir-induced earthquake in this area warrants attention. (3) It was found that the Coulomb stress variation on the Xiaojiang fault near Qiaojia at a depth of 10 km exceeded the threshold for inducing an earthquake (0.1 bar).
1. Introduction
The Baihetan Hydropower Station is the second largest hydropower station worldwide after the Three Gorges Project. The height of the reservoir’s dam is 289 m, the altitude of the normal storage water level is 825 m, and corresponding storage capacity is 20.6 billion m3. The Baihetan Hydropower Station is the second cascade hydropower station in the lower reaches of the Jinsha River, which is located between Ningnan County, Sichuan Province and Qiaojia County, Yunnan Province in China. It connects to the Wudongde hydropower station at the top, and Xiluodu and Xiangjiaba hydropower stations at the bottom (Figure 1). Water storage in the reservoir began in April 2021. The impoundment process of a reservoir can be regarded as a large-scale field impoundment test, which provides a rare research opportunity for studies on gravity changes and reservoir-induced earthquakes, among others.
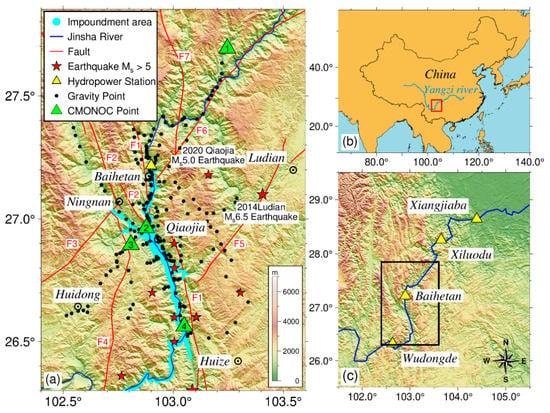
Figure 1.
Tectonic and location map of the gravity stations around Baihetan reservoir. (a) Locations of our new gravity stations (black dots). Green triangles give the gravity stations that belong to the nationwide network Crustal Movement Observation Network of China (CMONOC). Red stars indicate earthquakes (Ms > 5). Yellow triangle represents the Baihetan hydropower station. Blue area shows the reservoir. Red lines are faults. F1: Xiaojiang fault, F2: Zemuhe fault, F3: Ninghui fault, F4: Puduhe fault, F5: Zhaotong–Ludian fault, F6: Lianfeng fault, F7: Ganluo–Zhuhe fault. Colors represent terrain of the study area. (b) Location of Figure 1c in China. (c) Location of Wudongde, Baihetan, Xiluodu and Xiangjiaba hydropower stations (Yellow triangles). Blue line indicates the Jinsha River. Black box shows the location of Figure 1a.
In terms of geological structure and seismicity, the Baihetan reservoir is located on the eastern edge of the Sichuan–Yunnan rhombic block, near a high strain intensity area where the Xiaojiang, Zemuhe, and Lianfeng faults meet. The geological structure of the surrounding area is complex, and its seismic background activity is strong [1,2]. There is a possibility of an Ms 6.8–7.1 earthquake occurring around the reservoir area in the future [3]. Most of the crust at the bottom of the Baihetan reservoir shows a high-velocity anomaly, and the distribution of the wave velocity ratio is complex [2]. Historically, moderately strong earthquakes have primarily occurred in the southern segment of the Zemuhe fault, northern segment of the Xiaojiang fault, Zhaotong–Ludian fault, and Lianfeng fault (Figure 1). Currently, seismic activity is mainly distributed in the northern segment of the Zhaotong–Ludian and Xiaojiang faults [1]. The Baihetan reservoir is close to the northern section of the famous Xiaojiang fault and is distributed in parallel for a long distance (F1 in Figure 1), which is very likely to affect the activity of the fault.
The seismicity of the Baihetan reservoir area is moderate. Since 1900, four earthquakes with magnitude Ms > 6.0 have occurred near the Baihetan reservoir, including the Qiaojia Ms 6.0 earthquake in 1930, the Dongchuan Ms 6.5 earthquake in 1966, the Dongchuan Ms 6.2 earthquake in 1966 and the Ludian Ms 6.5 earthquake in 2014. In recent years, with the occurrence of the Yiliang Ms 5.7 and Ludian Ms 6.5 earthquakes in succession, the seismicity in the study area increased significantly [4]. Moreover, according to the data of the China Seismic Network Center in 2020, an Ms 3.6 earthquake and an Ms 5.0 earthquake occurred only 10 and 25 km away from the Baihetan Hydropower Station, respectively.
The faults around the Xiluodu Reservoir area, which is close to the downstream of the Baihetan reservoir, are small in scale and low in historical seismicity. A seismic network around Xiluodu Reservoir containing 35 stations was set up and observation began in September 2008, and there was no change in seismic stations before and after the reservoir impoundment. From September 2008 to June 2012, only 95 earthquakes of magnitude M 1 or above were recorded in the reservoir area, with an average of 2.06 earthquakes per month. However, during the six months from May to October 2013 after the impoundment of the Xiluodu Reservoir, there were 953 earthquakes of magnitude M 1 or above, with an average of 158 earthquakes per month [5]. Because of the complex structural conditions and huge water storage in the Baihetan reservoir, the induced seismicity is bound to be much greater than that around the Xiluodu Reservoir. In addition, the Baihetan reservoir is a reservoir with high intensity of seismic activity, high dam height, and large holding capacity. The occurrence of a strong earthquake in this region may trigger landslides and other secondary disasters, which can culminate into larger ones. Therefore, whether the impoundment process of the Baihetan reservoir will induce strong earthquakes is a major scientific problem that needs to be addressed urgently.
Reservoir-induced earthquake is a special type of seismic activity, which mainly refers to seismic activity within and around the reservoir and caused by reservoir water storage or drainage processes [6]. The impoundment of large reservoirs often induces strong earthquakes. According to incomplete statistics, reservoir earthquakes of certain intensity have occurred in more than 90 countries [7,8,9]. Among them, the impoundment of the Goina reservoir in India in 1967 induced an Ms 6.3 earthquake, the largest reservoir earthquake to have occurred to date [10,11]. After the completion of the Xinfengjiang Reservoir in 1962, the first impoundment induced an Ms 6.1 earthquake at 1.1 km downstream of the dam, which is the largest reservoir induced-earthquake in China [12]. After the impoundment of the Three Gorges, Longtan, Xiluodu, and other large reservoirs in China, regional seismicity has also increased significantly [5,6,13]. Among large and medium-sized reservoirs built worldwide, only approximately 1% of the total reservoirs have experienced earthquakes, and most of them occur in areas with low natural seismicity levels [14,15]. In contrast, for reservoirs built in areas that had experienced strong earthquakes, such as the US Grand Canyon Reservoir, the Flaming Gorge Reservoir, and the Japanese Kurobe Fourth Reservoir, micro- and weak-earthquakes increased significantly after reservoir impoundment, while medium and strong earthquakes were rare.
With the global construction of reservoirs reaching a rate of approximately 11 per year, reservoir-induced earthquake dangers and related potential disasters are increasingly attracting the attention of the international research community [12]. So far, studies on reservoir earthquakes have primarily focused on the eight following aspects [12]: (1) relationship between reservoir dam height, reservoir type, storage capacity, reservoir storage (discharge) process, and seismic activity; (2) relationship between stratigraphic media, geological structures, topography, and seismic activity; (3) correlation between fault activity and seismic activity; (4) correlation between crustal deformation and seismic activity; (5) relationship between hydrogeological environment and reservoir seismic activity; (6) relationship between crustal stress, pore water pressure, and seismic activity; (7) seismic signs and formation mechanisms of reservoir earthquakes; and (8) reservoir seismic risk assessment, monitoring, and emergency planning. To date, there have been few reports on determining the seismic risk of reservoirs based on gravity data. Considering this, we propose a new approach to assess the risk of reservoir-induced earthquakes through the Isostatic additional force (IAF) borne by the lithosphere, which can be computed using gravity and elevation data. Our aim is to assess the risk of reservoir-induced earthquakes before the formal construction of the reservoir, thereby effectively reducing earthquake disasters.
3. Bouguer and Free-Air Gravity Anomalies in Baihetan Reservoir Area
The gravity data were adjusted to four gravity stations named, respectively, Jingyang, Huloukou, Xiyao and Menggu gravity stations (green triangles with number in Figure 1a), which belong to the nationwide network “Crustal Movement Observation Network of China” [19]. Terrain corrections were performed using a topography model from the Shuttle Radar Topography Mission (SRTM) (https://www2.jpl.nasa.gov/srtm/, accessed on 5 September 2020). A finite element method was adopted to obtain terrain corrections, which used the measuring point as the center and divided the area into far, moderate, and near fields. Kane [20,21] and Nagy [19] presented calculation formulae for each field. For near-field zones (0–2 km), the data from the SRTM with a grid spacing of 1″ × 1″ were used for terrain corrections. Similarly, for moderate field zones (2–20 km), a 5″ × 5″ grid spacing was chosen, and for far-field zones (20–167 km), a 10″ × 10″ spacing was applied. These were obtained by interpolation of the digitized data from the SRTM. Such corrections can result in high accuracy and less computational effort [22]. Bouguer corrections, including elevation and middle layer corrections, were performed using topography data from GNSS surveys. The observed gravity values were then reduced to the corresponding reference ellipsoid at the observation points. Finally, the Bouguer gravity anomalies of the 223 stations were obtained by comparing the corrected results with the corresponding gravity values on the ellipsoid that can be calculated theoretically. The observation data before impoundment provide the basis for the study of environmental changes after the impoundment of the Baihetan reservoir.
The observation error of the GNSS data for ellipsoidal height is estimated to be at the semi-decimeter level, which amounts to an uncertainty of 0.3 mGal in the Bouguer gravity anomaly. The error of the gravity observation data is approximately 0.02 mGal. The reduction error of the Bouguer corrections is estimated to be approximately 0.1 mGal. After incorporating all the reductions and observation errors above, the Bouguer gravity anomaly presented in this study is estimated to have an accuracy of <0.5 mGal.
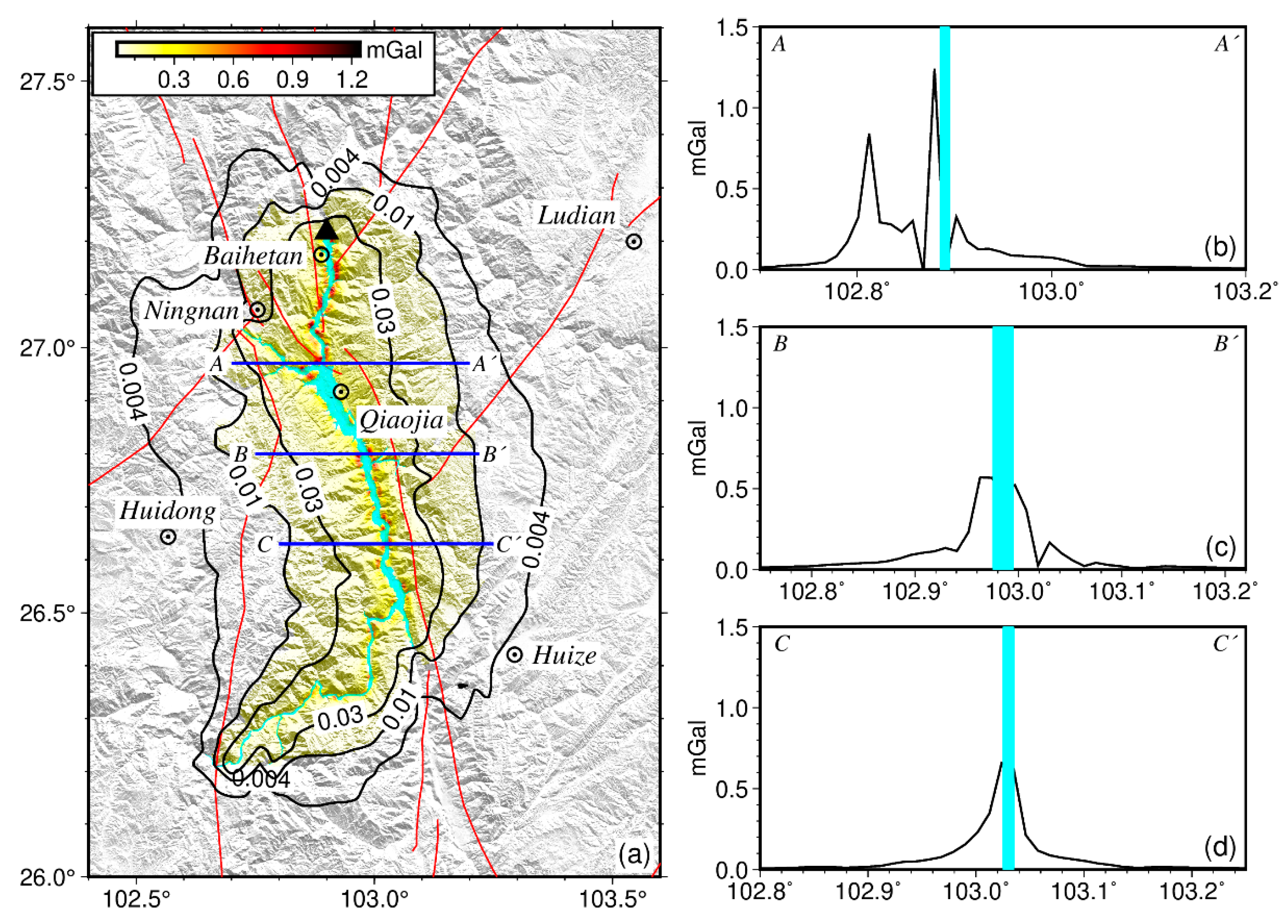
The Bouguer and free-air gravity anomaly data were interpolated using the Kriging interpolation method to obtain a spatial map. In Figure 2, only the most reliable anomalies near the observation stations (<5 km) are presented in color. The results far from the observation stations (>5 km) have lower accuracy and are presented in the contours. Figure 2a shows the free-air gravity anomalies around the Baihetan reservoir. They vary between −250 and 60 mGal in the entire study area. Along the Jinsha River, on which the Baihetan Hydropower Station is built, the free-air gravity anomalies are negative, with absolute values increasing from south to north. On the contrary, on the mountains of the two sides of the Jinsha River, the values of the free-air gravity anomalies are much smaller. Figure 2b shows the Bouguer gravity anomalies around the reservoir. Overall, the Bouguer gravity anomalies in the reservoir area vary between −300 and −200 mGal. The largest absolute values appear near the dam of the Baihetan reservoir, indicating a low-density structure nearby. Compared with the distribution of the free-air gravity anomalies (Figure 2a), the change in the Bouguer gravity anomalies is much more gentle. Overall, the consistencies of the data are sufficiently high so that the extrapolation error is not very large for Bouguer gravity anomalies. Figure 2c shows that the results come from EIGEN-6C4 gravity field model. EIGEN-6C4 is a static global combined gravity field model up to degree and order 2190 [23]. The data of first 235 degrees of the model are mainly from the observation results of GRACE and GOCE satellites, and the higher order results are from the gravity anomalies calculated by EGM2008 model and residual terrestrial terrain gravity model. For the convenience of comparison, the sampling points of EIGEN-6C4 are consistent with the actual observations in situ. Figure 2d shows the differences between the observed free-air gravity anomalies and those deduced from the EIGEN-6C4 gravity model [23] in the same area. They range between −150 and 100 mGal. The difference mainly comes from the discrepancy between the high-frequency modeled topography used to calculate the gravity anomalies of EIGEN-6C4 and the actual earth structure. This indicates that our new gravity survey improves the accuracy of the gravity anomaly fields in the reservoir area up to 150 mGal, which has significant implications for gravity measurement research in this region.
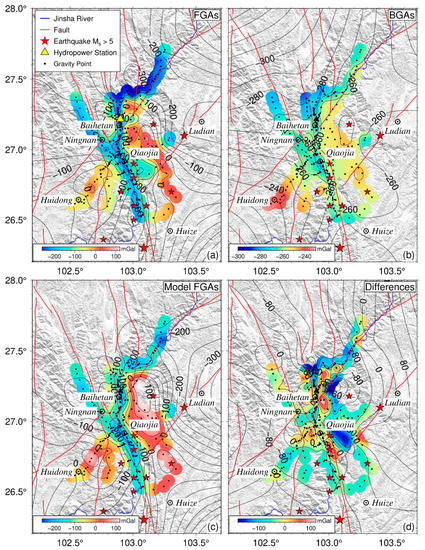
Figure 2.
Free-air and Bouguer gravity anomalies around Baihetan reservoir. (a) Observed Free-air gravity anomaly; (b) Observed Bouguer gravity anomaly; (c) Modeled Free-air gravity anomaly from EIGEN-6C4 model [23]; (d) differences between the observed and modeled free-air gravity anomalies (a–c). The results far from the observation stations (>5 km) have lower accuracy and are presented in the contours. Abbreviations are the same as those in Figure 1a.
4. Isostatic Additional Force Borne by Lithosphere Deduced from Gravity Survey
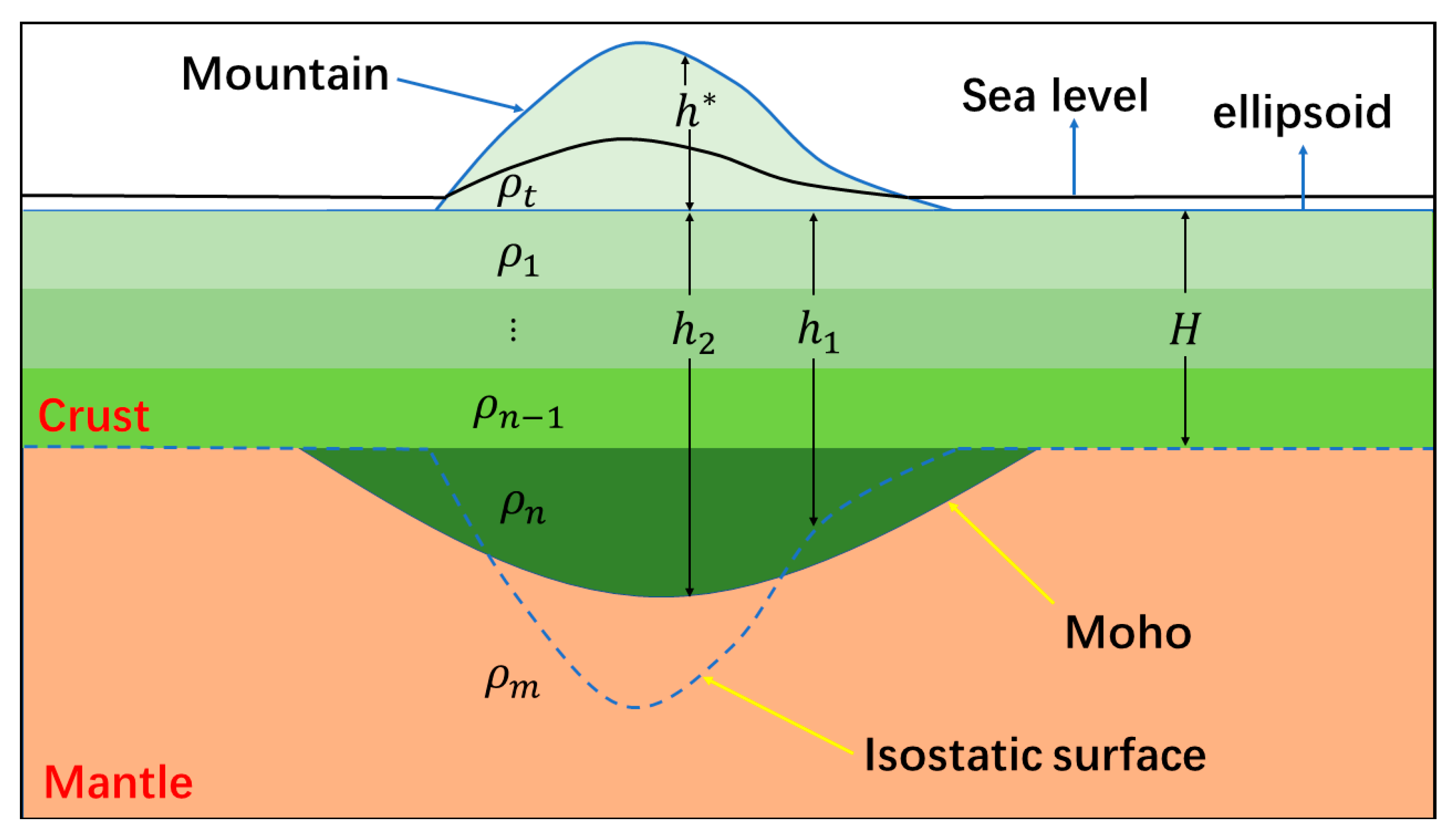
Ariy isostatic theory is a widely accepted theory. Its basic assumption is that the relatively light crust naturally floats on the relatively heavy mantle. When there are high mountains on the surface, there is a mountain root underground, and vice versa. When the earth is in fully Ariy isostatic state, the position of the Moho is called the isostatic surface (Figure 3). In this state, the crust can be decomposed into a certain number of small units, and the crust weight of each unit is completely equal to its mantle buoyancy. However, the actual earth is not always in the ideal isostatic state, so the position of the Moho of the actual earth is often different from the isostatic surface (Figure 3). In some places, the Moho is deeper than the isostatic surface. At this time, the mantle buoyancy carried by the crust is greater than the weight of the crust. In other places, the Moho is shallower than the isostatic surface, and the buoyancy of the mantle is less than the crust weight. The above two kinds of regions correspond to isostatic negative anomaly region and positive anomaly region respectively. In other words, when the crust is in an unbalanced state, the Moho of the actual earth is inconsistent with the isostatic surface, and the weight of the unit crust is different from its mantle buoyancy. The difference between mantle buoyancy and crust weight usually needs to be offset by a vertical force caused by the elastic bending of the crust [24]. Such a force is called vertical additional force (VAF for short). According to the above analysis, when the earth’s crust is in an unbalanced state, its VAF is not zero.
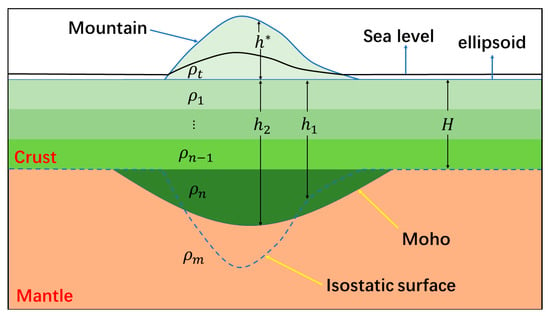
Figure 3.
Schematic diagram of the relationship between the Moho and isostatic surface.
The greater the difference between the Moho and the isostatic surface, the greater the IAF of the crust. Therefore, we can quantitatively calculate the IAF borne by crust through the residual materials (the density difference between the crust and mantle) between the Moho and the isostatic surface, which is directly related to mantle buoyancy. According to [22], the difference between the Moho and isostatic surface can be calculated using gravity and GNSS data on the Earth’s surface. Then, the IAF can be further calculated [25].
It should be noted that the IAF calculated in this study does not refer to the detailed distribution of the additional force with depth but to the total additional force borne by the entire lithosphere, that is, the vertical integration of the isostatic additional force along the entire lithosphere. This is a new expression for lithospheric equilibrium. The IAF refers to the vertical force generated by the elastic deflection of the crust. Although it may be the result of the long-term mutual movement of the crust, it represents the current state of the crust. In addition, Moho is not a boundary between solid and liquid substances, but a chemical interface. The physical properties of the materials on both sides of the Moho are significantly different. Note that it is the location of the Moho, but not the location of the boundary between the liquid and solid parts, which affects the calculation results of the above additional buoyancy and IAF.
The IAF is computable based on gravity and elevation data, according to the following procedure, which is refined from the preliminary work [24].
- The depth of the isostatic surface () is calculated according to the elevation data (Figure 3); indicates the boundary of the crust and mantle when the crust is in complete isostatic balance, under the assumption of Airy isostasy. The formula is as follows:where is the altitude of the surface observation station, is the average density of the material above the ellipsoid, is the density difference between the mantle and the crustal material, and is the average crustal thickness below ellipsoid in the area. In this study, the densities of the crust (including ) and the mantle are assumed to be 2700 and 3490 kg/m3, respectively; thus, the lower crust–mantle density difference () is approximately 649 kg/m3. In this study, the average equilibrium depth (40 km) of the continent is used.
- The depth of Moho () is calculated according to gravity and elevation data (Figure 3). The formula is as follows:where G is the gravitational constant, and is the Moho depth of the reference point, which is assumed to be completely isostatic. is the Bouguer gravity anomaly of the reference point, and is the Bouguer gravity anomaly of the observation station. At the reference point and IAF = 0. The point located on a stable plate with absolute gravity and elevation survey and not too far from the study area (<200 km for usual) is suitable to be selected as the reference point. It should be noted that the above calculation is a simplified calculation, which assumes that there is no lateral change in crustal materials, and all gravity anomalies are caused by Moho fluctuation. If we can obtain a Moho in the study area by inversion from other observations (from the receiver function method using seismic data as an example), it is better to directly use the inversed Moho to replace the calculation result of Equation (2).
- The IAF is calculated using the additional buoyancy generated by the remaining material between Moho and the isostatic surface . The additional buoyancy produced by the remaining material (the density difference between the crust and the mantle) is generally balanced by the crustal deflection; thus, in theory, the additional buoyancy and the IAF that the lithosphere bears are equal in magnitude and opposite in the direction. The formula for the IAF is as follows:where g is the gravitational acceleration. , , and are defined in Equations (1) and (2). The values of are different for different regions. The above analysis indicates that gravity and elevation data can be used to quantitatively determine the IAF.
5. Relationship between Reservoir-Induced Earthquake and Isostatic Additional Force
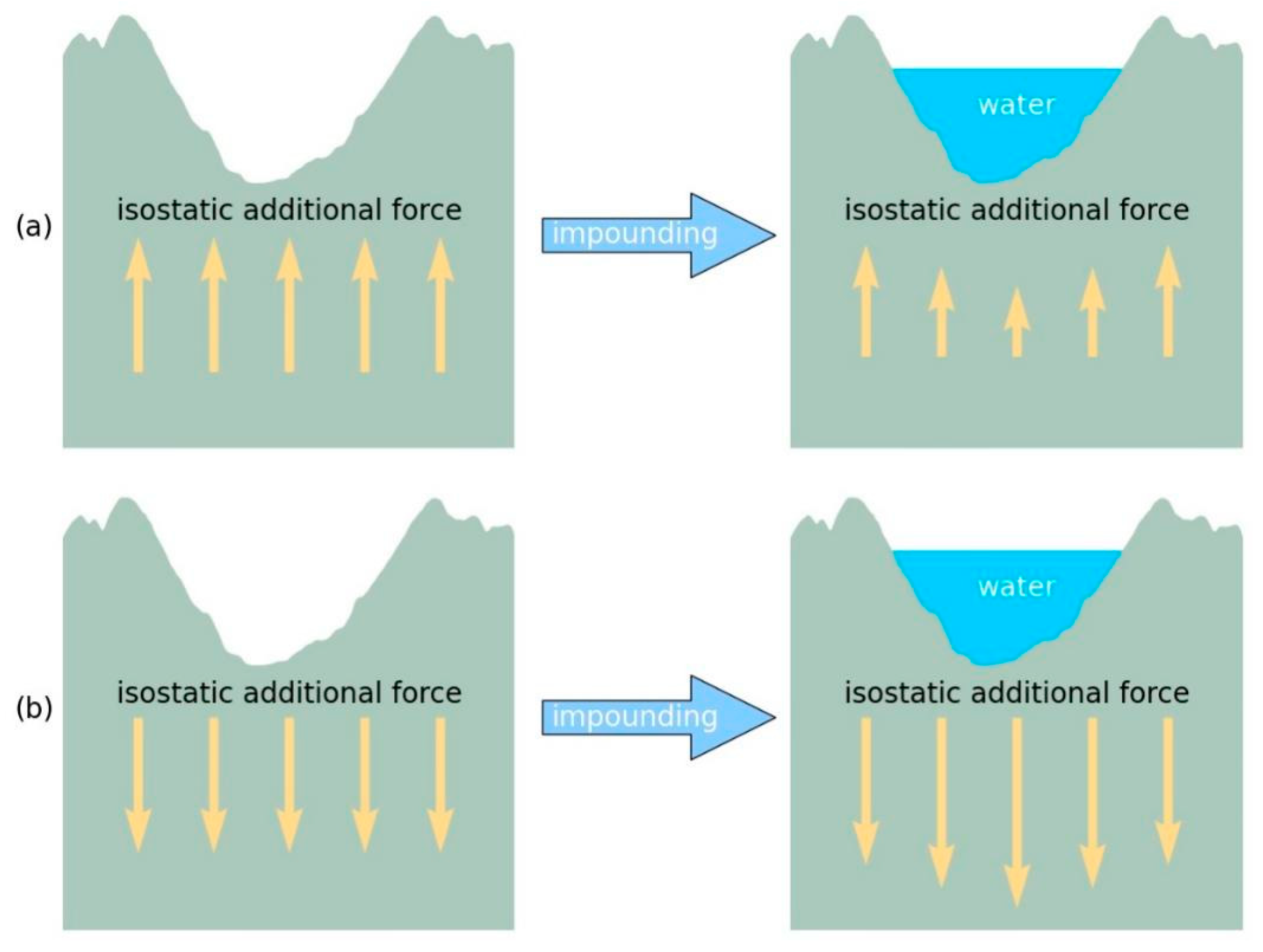
Reservoir construction can be regarded as a surface-loading problem caused by human activity, and the process of reservoir impoundment can be regarded as a downward loading effect of the water body on the surface of the lithosphere. By comparing the relationship between the surface loading caused by reservoir impoundment and the IAF carried by the current lithosphere, the loading or unloading effect of reservoir construction on the IAF can be determined. Specifically, if a reservoir is built in a river section where the IAF is upward (Figure 4a), the self-gravitation of large-scale water storage will offset some of the IAF, and form an unloading effect, which will make the lithosphere of the reach (section of a river) more balanced and thus will not induce strong earthquakes. Conversely, if a reservoir is built in a reach where the IAF is downward (Figure 4b) or in a section where the lithosphere is basically balanced, the water storage process will be accompanied by a loading effect on the IAF, which may induce strong earthquakes. Therefore, from the perspective of lithospheric equilibrium, river sections with IAF upward are suitable for large reservoir construction. The reservoir impoundment process in such areas would not easily induce a strong earthquake.
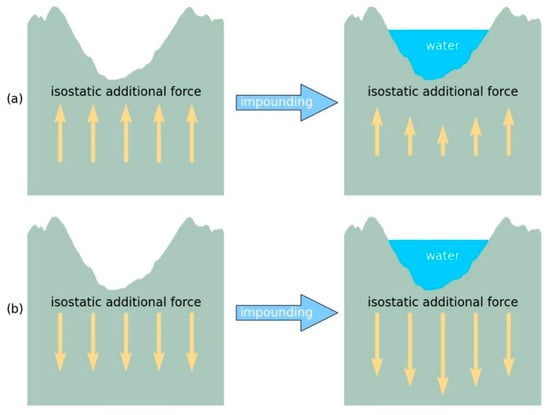
Figure 4.
Sketch section of the Isostatic additional force (IAF) borne by lithosphere before and after reservoir impoundment. (a) Process of reservoir storage is an unloading process of force when the IAF is upward; (b) loading process when the IAF is downward.
Previous studies have shown that reservoir earthquakes can generally be divided into four cases [26]: (1) there is no record of historical earthquakes before impoundment, and obvious seismicity occurs after impoundment; (2) the magnitude and frequency of earthquakes occurring after impoundment are higher than those of historical earthquakes; (3) the magnitude of earthquakes after impoundment was lower than that before impoundment; and (4) there was no obvious change in the seismic frequency and magnitude after impoundment. The first three phenomena may correspond to the three main forms of IAF. Specifically, case (1) may occur in areas where the lithosphere is generally balanced and the IAF is small. Case (2) may occur in areas where the IAF is downward, and case (3) may occur in areas where the IAF is upward. The fourth case may have been due to the small scale of the reservoir and the small influence of the water body’s own weight on the lithosphere. Thus, the distribution pattern of the IAF can readily explain the above four phenomena of reservoir-induced earthquakes.
Stability of crust depends largely on the background stresses. It is the horizontal and vertical stress setting, together with the pore-fluid pressure changes, controlling the stability and instability of the crust. Until now, the widely accepted explanation for reservoir-induced earthquakes was that the increase in fluid pressure decreases the normal stress on faults, increasing the possibility of Coulomb failure, thus increasing the likelihood of an earthquake [27,28]. The stress change on the faults due to fluid pressure is usually considered to be the dominant effect on reservoir-induced earthquakes. Compared to the effect of the fluid pressure on faults, the effect of the vertical loading (such as the weight of water in filling reservoirs) is always considered to be relatively small and therefore negligible. However, for many reservoirs, the magnitude of earthquakes after impoundment is lower than that before impoundment, which is difficult to explain using the above criterion. Wang [29] found that part of reservoirs, built in areas with strong earthquakes, such as the Grand Canyon Reservoir (United States), Flaming Gorge Reservoir (United States), Kurobe Reservoir Four (Japan), and Piave-Kardore Reservoir (Italy), all exhibit slight increases in micro and weak earthquakes after water storage, while medium and strong earthquakes are rare. This phenomenon can be well explained by the change in fault stress caused by fluid pressures and the IAF, but not by the former alone. The increase in micro and weak earthquakes after water storage should be related to reservoir water infiltration on faults, whereas few medium and strong earthquakes should be related to IAF. The above reservoirs should have been constructed in areas where the IAF was upward. The reservoir impounding process offsets some of the IAF, resulting in the weakening of strong earthquake activity.
This information indicates that the load effect of water retention has been underestimated in recent years. The change in the IAF should be considered as another factor in the seismic risk analysis of reservoir-induced earthquakes. Note that the background of IAF can be determined through gravity/GNSS observations before the impoundment of the reservoir; therefore, our method is useful in selecting the river section that is most suitable for reservoir construction and reducing the risk of induced earthquakes. The IAF calculated in this study refers to the force borne by the entire lithosphere, typically by the shallow layers. Hence, the IAF of the whole lithosphere is related to that in the region where earthquakes occur.
There is no doubt that there are many factors affecting reservoir-induced earthquakes. Reservoir dam height, reservoir type, storage capacity, reservoir storage process, strategic media, geological structures, topology, fault activity, critical deformation, hydrogeological environment, critical stress, pore water pressure and other factors may affect the occurrence of reservoir earthquakes. This paper is limited to discuss the relationship between IAF and reservoir-induced earthquake from the perspective of crustal equilibrium, which can be regarded as a useful supplement to previous work.
In summary, the current IAF can be calculated based on gravity and topographic data [24]. This physical quantity is effective for predicting reservoir-induced earthquakes. Specifically, if the gravity/GNSS joint observation is carried out along the river of the proposed reservoir, a detailed distribution pattern of the IAF can be obtained. Through the IAF, the risk of induced earthquakes after water storage in the relevant river sections can be estimated, and then the river section most suitable for reservoir construction (the river section with IAF upward) can be selected to reduce the risk of induced earthquakes.
6. Isostatic Additional Force Borne by Lithosphere along Baihetan Reservoir
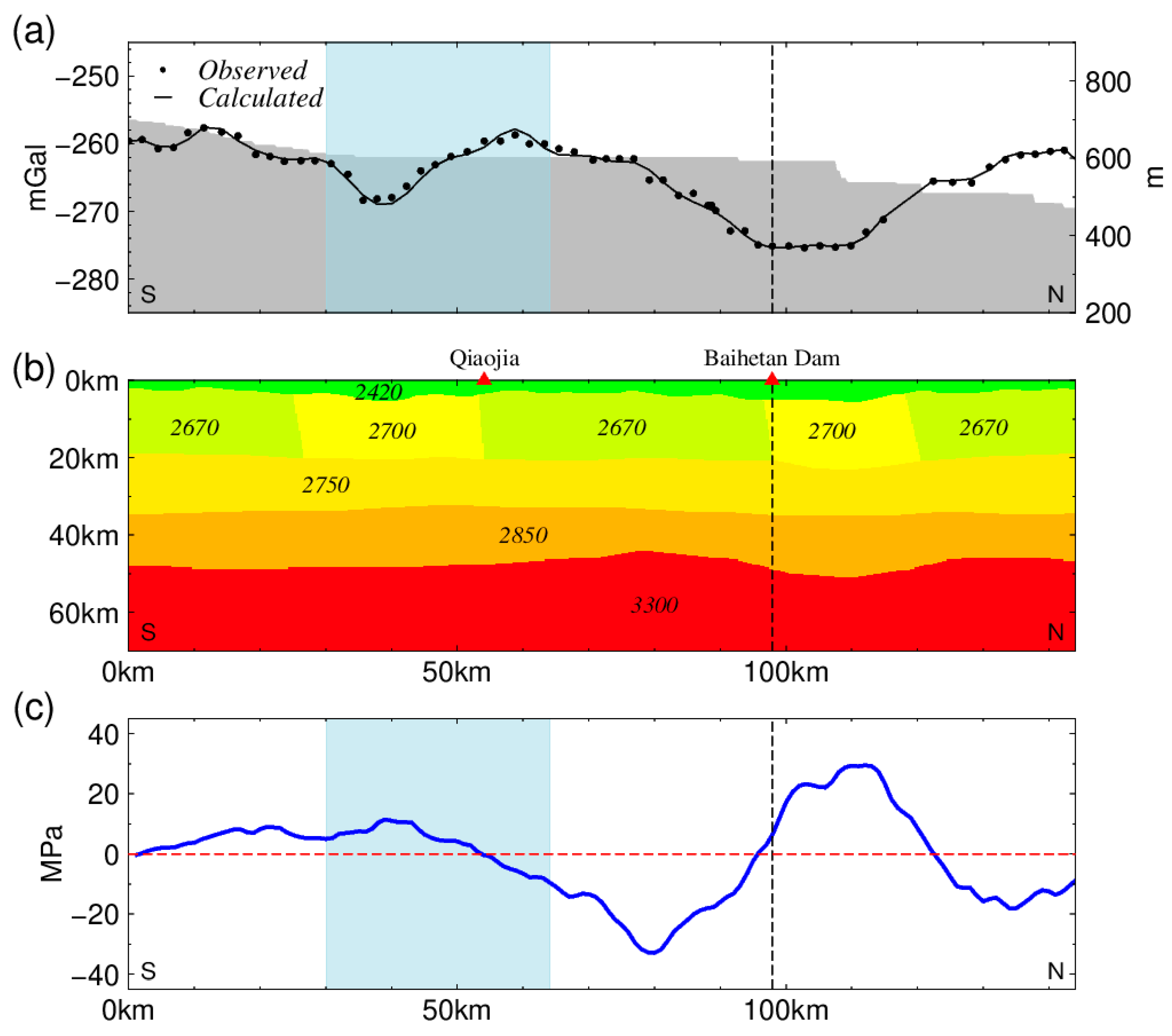
The density structures of the profiles along the Jinsha River near the Baihetan reservoir (Figure 5b) were inversed using the Bouguer gravity anomalies in Figure 2b. The data near the reservoir (<5 km) were selected to invert the density structure. Because of the ambiguity of gravity inversion, the choice of the initial model has a significant effect on the inversion results. Thus, we referred to a detailed crustal velocity structure as the initial crustal model. Such a velocity structure is obtained by direct ambient noise tomography based on the Rayleigh wave phase velocity around the reservoir [2]. Moreover, the initial Moho depths were obtained from Zheng et al. [30], which were deduced from the receiver function method using seismic data. The aim of these works is to decrease the uncertainty for the inversed density structures. The conversion relationship between the velocity and density is based on the empirical formula given by Christensen and Mooney [31]. Finally, the Gravity/Magnetic Modeling Software developed by the Northwest Geophysical Associates was used to invert the density structures along the Baihetan reservoir.
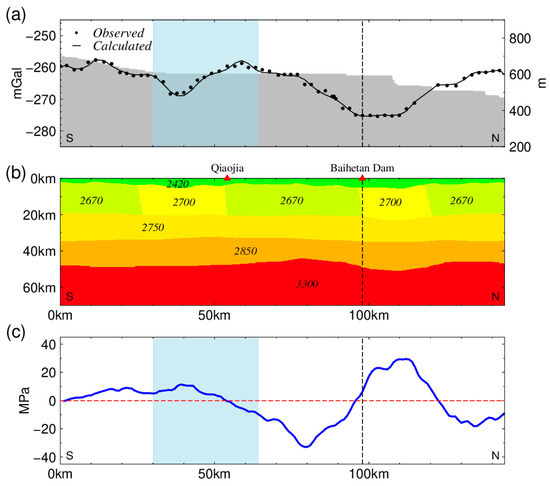
Figure 5.
Bouguer Gravity Anomaly, crustal density structure and isostatic additional force (IAF) along the Baihetan reservoir. (a) Bouguer Gravity Anomaly and the Topography. (b) Density structure. (c) IAF borne by the lithosphere. The light blue area in (a,c) indicate the main storage area where the reservoir is wide. The red dotted line denotes the zero line of IAF, and the black dotted line denotes the dam.
According to our inverted result, the densities of the upper and middle crust are approximately 2670–2750 g/m3 (yellow area in Figure 5b), and that of the lower crust is 2850 g/m3 (orange area in Figure 5b) along the reservoir. The density of the mantle was 3300 kg/m3 (red area in Figure 5b). At the top of the crust, there is a sedimentary layer with a density of approximately 2420 g/m3 (green area in Figure 5b). In addition, the lateral density changes of the upper crust can be found along the reservoir, although the changes are not very significant. Overall, there are obvious differences between the distribution of the Moho reliefs and the spatial distribution of Bouguer gravity anomalies, and the variation range of the Moho is within 10 km. The change in Moho becomes greater in the northern part of the reservoir, and the largest changes are distributed near the dam, where the Bouguer gravity anomalies change significantly.
Then, using the method presented in Section 5, we calculated the IAF along the Baihetan reservoir (Figure 5c). During our calculation, the Bouguer gravity anomalies and terrains in Figure 5a and the density structures in Figure 5b were used. The equilibrium depth was set to 40 km, which is the average value used for mainland China. As shown in Figure 5c, the dam is located on a great gradient belt of the IAF, where the IAF changes rapidly from 20 MPa in the north to −30 MPa in the south of the dam. According to She et al. [25], there is a strong correlation between the IAF gradient zone and the distribution of earthquakes. Therefore, we deem that the location of the dam is not suitable according to the distribution of the IAF. In addition, there is a significant negative anomaly of IAF at the reservoir, approximately 20 km south of the dam (Figure 5c). According to Figure 4b, the water storage process is accompanied by a loading effect on the IAF, which may induce strong earthquakes. Thus, the risk of an induced earthquake at this location needs attention. Finally, the blue area around Qiaojia City is the primary area of water storage where the reservoir is relatively wide. At such a place, the IAF is not large. In other words, the area with the largest water injection in the reservoir was not particularly large in the IAF. Such a distribution indicates a lower risk of a strong induced earthquake in the Baihetan area.
From Figure 1 and Figure 5c, we find that large earthquakes have already occurred where the IAF is small, suggesting that the other mechanisms such as horizontal stress rather than the IAF are dominant. On the other hand, smaller earthquakes have occurred in the northern area with the negative peak of the IAF (around 80 km in Figure 5c), verifying the effect of IAF on earthquakes. Such a relationship indicates that the distribution of IAF is one of many influencing factors—maybe not the most important one—that cause earthquakes. However, if the load of reservoir impoundment is considered at the same time, the distribution of IAF is of great significance to the occurrence of reservoir-induced earthquakes.
7. Theoretical Gravity Changes Accompany the Impoundment of the Baihetan Reservoir
The gravity change caused by the impoundment of the reservoir is mainly composed of two parts. One part is the gravity change caused by elastic deformation due to the load of impoundment water. The other is caused by the gravity of impoundment water itself [31]. In this section, we calculate the theoretical gravity change caused by the redistribution of water in the Baihetan reservoir after impoundment to 825 m (normal water level)—that is, the superposition effect of the two theoretical gravity changes above at each observation station.
To accurately describe the water load of the Baihetan reservoir and obtain a high-precision gravity variation field, it is necessary to rely on high-precision terrain data. The terrain data used in this study are 1 arcsec data from the Shuttle Radar Topography Mission (https://www2.jpl.nasa.gov/srtm/, accessed on 5 September 2020). The spatial resolution was approximately 30 × 30 m. Generally, a reservoir is an irregular three-dimensional water body area. To facilitate the subsequent calculation of gravity change, the water in the reservoir was divided into several layers of equal heights, and each water layer was divided into unit bodies of equal volumes. Aiming at the water storage problem of the Baihetan reservoir, the unit water body is divided into 56 × 56 × 10 m cubes. The normal water level of the Baihetan reservoir is 825 m above sea level. The corresponding reservoir area is shown in the blue area of Figure 1, and the corresponding number of unit water bodies is 543,685. The gravity change caused by the normal water level of the Baihetan reservoir can be calculated using the above terrain and water-level data.
First, the gravity change caused by elastic deformation due to the water load of the Baihetan reservoir was calculated. Reservoir impoundment is a typical load problem. In this study, Farrell’s load theory, based on the spherical earth model, was used. Farrell [32] introduced an asymptotic solution to solve the convergence problem of Green’s function and obtained the Green’s function, which can be used to deal with practical load problems. This approach is based on the preliminary reference earth model (PREM) [33]. To improve the calculation accuracy of the gravity change caused by elastic deformation, the modeled data of CRUST1.0 [34] corresponding to the research area are first extracted to replace the parameters of the PREM. Such a method has been proven by many studies to improve the accuracy of load deformation calculations [35]. Then, based on the modified earth model, the load Love number was calculated, and the load Green’s function was obtained. Finally, the elastic deformation and gravity change caused by the impoundment of the Baihetan reservoir were calculated using Green’s function combined with the water-level data of the Baihetan reservoir. The calculation points are a 0.01° × 0.01° grid. It was found that the maximum gravity change due to elastic deformation corresponding to the impounding water is 0.039 mGal on our gravity network (Figure 1), which is located on the bank of the reservoir near Qiaojia City.
Then, the gravity change caused by the gravitational action of the impounded water in the Baihetan reservoir was simulated. It is the vertical component of the gravity change caused by the impounded water at each observation station. The area along the Jinsha River around the Baihetan reservoir is mostly gorge terrain with varying elevation. Therefore, the influence of the terrain should be carefully considered when calculating gravity changes. Here, Newton’s law of universal gravitation is used to calculate the gravity change caused by each unit of water at the observation station, and the vertical component is subsequently obtained. Then, the sum is the gravity change of the total water storage at the observation point. The simulation results show that the maximum gravity change directly caused by the impoundment of the Baihetan reservoir is 1.2 mGal on our gravity network (Figure 1). In general, the gravity change caused directly by water storage itself is nearly two orders of magnitude larger than that caused by load elastic deformation. Therefore, the gravity change accompanying the impoundment of the Baihetan reservoir is mainly caused by the gravitational action of impoundment water.
The simulated results are shown in Figure 6. The corresponding water level of the reservoir was 825 m. The gravity change is primarily concentrated in the range of approximately 30 km around the impoundment area, and decays rapidly with the increase in distance from the reservoir. Within such an area, mobile gravity meters such as Burris and CG-5 can catch reliable signals of gravity changes. The theoretical gravity change is more intense in the lower reaches of the Jinsha River around Qiaojia City (Figure 6), while the gravity change in the upper reaches of the Jinsha River is relatively small. This result can be attributed to the considerable width of the reservoir around Qiaojia City, and the relatively large amount of injected water.
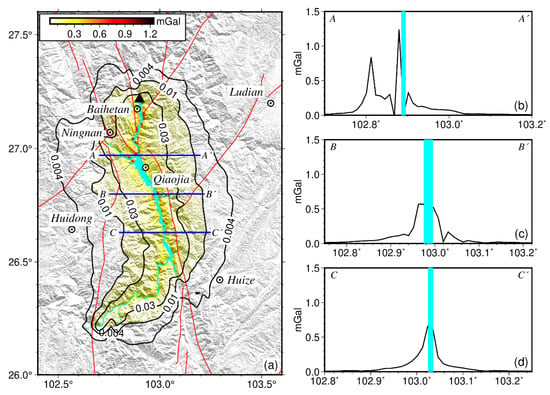
Figure 6.
Theoretical gravity changes on the Earth’s surface caused by the impoundment of Baihetan reservoir, corresponding to the water level of 825 m. (a) is the contour map of the gravity changes. Blue lines show the location of the three profiles in the right figures (b–d). Abbreviations are the same as those in Figure 1a. (b–d) shows the gravity variation of three cross sections perpendicular to the reservoir. Blue areas in right figures represent the width of the reservoir.
8. Coulomb Stress Changes on Nearby Faults Due to Baihetan Reservoir Impoundment
The impoundment of the Baihetan reservoir will not only cause a gravity change on the Earth’s surface but also a change in crustal internal stress. After the impoundment of the Baihetan reservoir, the impounded water forms a downward load on the Earth’s surface, which affects the stress field in the lithosphere and changes the Coulomb stress on the fault plane. When the change in the Coulomb stress on the fault plane within a critically stressed crust reaches the threshold (0.1 bar), there is a risk of an induced earthquake [35]. Therefore, studying Coulomb stress variation caused by the load of impounded water around the Baihetan reservoir on the main faults is essential for risk determination of induced earthquakes, and the results can serve as a reference for future studies.
Based on the discrete water of the Baihetan reservoir in Section 7, we calculated the Coulomb stress variations caused by the impoundment on the surrounding faults by using the load internal strain algorithm proposed by She et al. [35]. Similarly, we modified the crustal partition of the PREM using the CRUST1.0 model to improve the accuracy of the load Green’s function, and then calculated the Coulomb stress change at a depth of 10 km on the main fault planes caused by the impoundment of the Baihetan reservoir to improve the accuracy of the calculation results.
The correctness of the fault geometric parameters is of great significance to the reliability of the calculated Coulomb stress changes. We carefully reviewed the existing literature, particularly geological studies related to the geometric parameters of faults in the Baihetan reservoir area, to obtain data for the main faults in study area. The detailed geometric parameters of the faults, as well as the main references, are listed in Table 1.
Then, based on the layered earth model given above, the stress changes in the crust caused by the water storage in the study area were calculated using the spherical load theory [35], and the Coulomb stress changes on the main faults near the Baihetan reservoir are further obtained, including the Coulomb stress changes in the northern section of the famous Xiaojiang fault. The northern section of the Xiaojiang fault (F1 in Figure 7) is close to the Jinsha River and parallel to the Baihetan reservoir. Therefore, the stress change caused by the impoundment of the reservoir has the greatest impact on the Xiaojiang fault. Moreover, earthquakes with M ≥ 5 are mainly distributed along the Xiaojiang faults (Figure 1); thus, it is necessary to simulate the Coulomb stress variation on the fault planes and provide a possibility analysis of the triggering earthquake. The calculation formula of Coulomb stress changes is as follows:
where and are the shear and normal stress changes on the fault surface caused by the impoundment, respectively [35]; is the effective friction coefficient, which was set to 0.4 in this study [36]. An earthquake might be promoted if . Using Formula (4) and the geometric parameters of nearby faults (Table 1), the Coulomb stress variations at a depth of 10 km on the main faults in the reservoir area were calculated, considering a water level of 825 m. The results are shown in Figure 7.
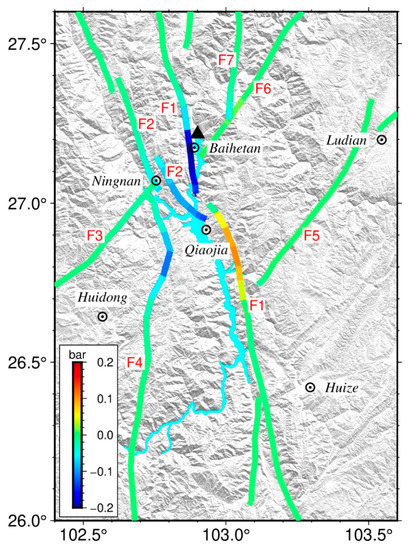
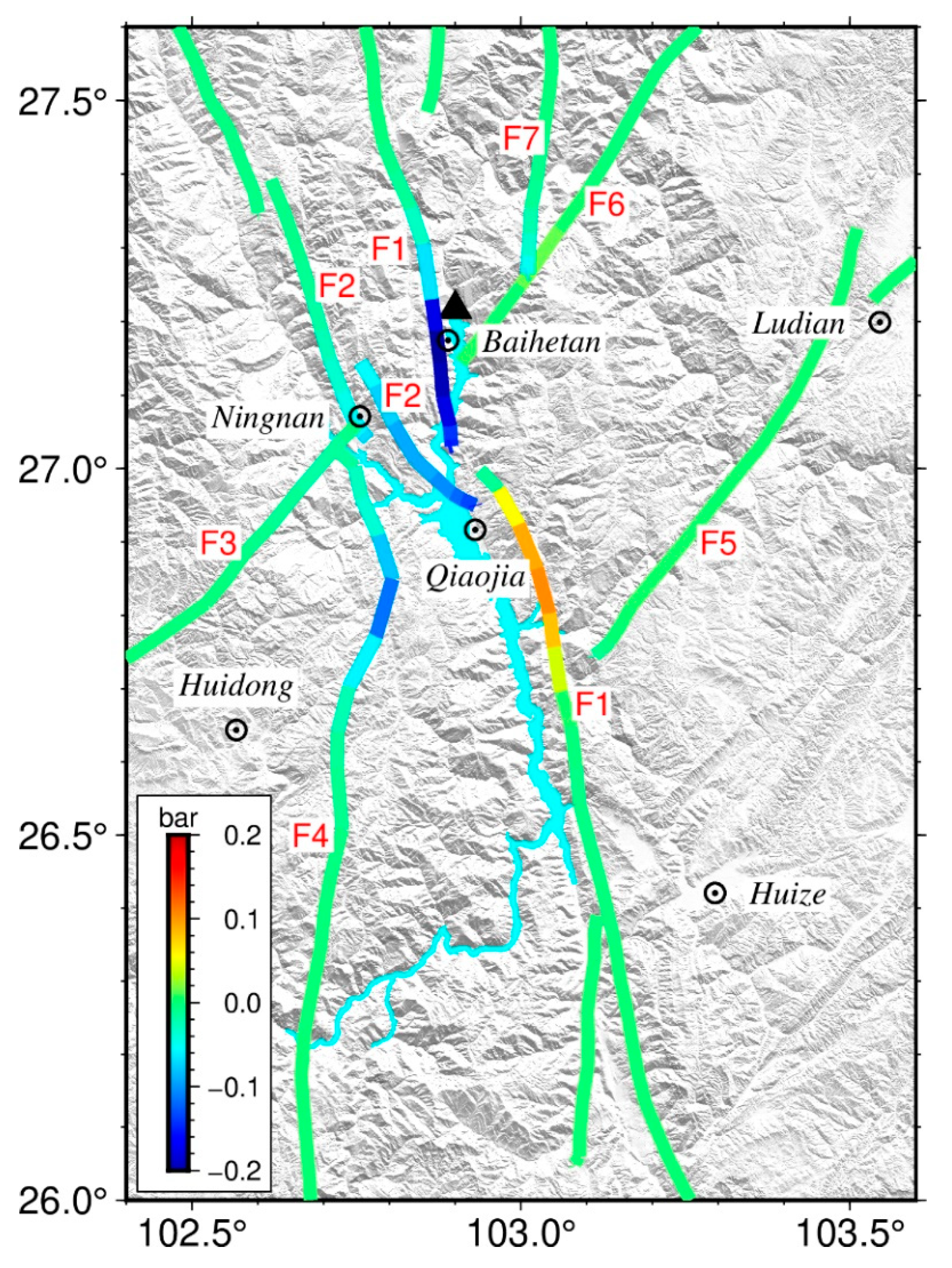
Figure 7.
Coulomb stress variation on faults at 10 km underground caused by Baihetan reservoir impoundment. Abbreviations are the same as those in Figure 1a.
Figure 7 shows the changes of Coulomb stress at 10 km underground caused by the impoundment of Baihetan reservoir on the nearby faults, among which the changes on the north section of Xiaojiang fault (F1) are the most significant. The variation in Coulomb stress is approximately −0.2 bar near the dam and about 0.1 bar in the south of Qiaojia City. The difference of Coulomb stress variation is mainly caused by the change in relative position between the reservoir and the fault. The change in Coulomb failure stress of −0.1 bar also appears in the north section of Puduhe Fault (F4). Generally speaking, the area where Coulomb stress changes violently is mainly located near Qiaojia City, which is also the area with the largest storage capacity of Baihetan reservoir (Figure 1 and Figure 7). Away from the reservoir, the variation in Coulomb stress on each fault decreases significantly. Ge et al. [37] simulated the change in the elastic stress in the crust when the reservoir was stored for 100 m. The change in Coulomb stress on the adjacent fault plane ranged from −5 to 0.5 bar, which is close to the magnitude of the calculation results in this study. When the Coulomb stress change on the fault plane reaches 0.1 bar, there is a risk of induced earthquake [36]. According to the above analysis, the Baihetan reservoir might trigger an earthquake in an area on which the Coulomb stress change is larger than the threshold. The location is near the Xiaojiang fault south of Qiaojia City. Therefore, it is necessary to pay attention to the induced earthquake in this area.
It should be noted that the above simulation did not consider the influence of pore pressure and other factors. The change in pore pressure is related to the geological and hydrological factors related to the diffusion coefficient of the pore pressure [38]. Therefore, a detailed study in the future not only needs to understand the lithologic characteristics of the area but also needs to conduct detailed observations of gravity change and groundwater level in the process of actual water storage, restrict the groundwater distribution, and obtain reasonable pore pressure so as to provide more reliable information for the risk assessment and mechanism analysis of reservoir-induced earthquakes.

Table 1.
Geometric parameters of main faults around Baihetan reservoir and the corresponding references.
Table 1.
Geometric parameters of main faults around Baihetan reservoir and the corresponding references.
| Name | Strike | Dip | Rake | References |
|---|---|---|---|---|
| Xiaojiang Fault (F1) | 347 | 80 | 170 | Wen et al., 2008; Xu et al., 2019 [39,40] |
| Zemuhe Fault (F2) | 150 | 60 | −10 | Wen et al., 2008; Xu et al., 2019 [39,40] |
| Ninghui Fault (F3) | 230 | 80 | 150 | Refer to F6 |
| Puduhe Fault (F4) | 20 | 80 | 0 | He et al., 2013; Duan and Zhao, 2019 [41,42] |
| Zhaotong Fault (F5) | 230 | 40 | 150 | Chang et al., 2014; Wen et al., 2013 [43,44] |
| Lianfeng Fault (F6) | 230 | 80 | 150 | Wen et al., 2013 [44] |
| Ganluo–Zhuhe Fault (F7) | 167 | 80 | −10 | Refer to F1 |
9. Conclusions
Strong earthquakes often occur after the impoundment of large reservoirs [10]. The Baihetan Hydropower Station is the largest under-construction hydropower station worldwide and the second largest after the Three Gorges Project. The dam is 289 m high and began to store water in April 2021. The seismic activity in the reservoir area was very strong prior to construction [1]; since 1900, four strong earthquakes of M ≥ 6 have occurred. Whether the impoundment of the Baihetan reservoir will induce strong earthquakes is an important scientific problem with significant implications for the region. In this study, the free-air and Bouguer gravity anomaly fields at 223 stations around the Baihetan reservoir were obtained using dense gravity/GNSS observations conducted at the beginning of 2021. Then, the density structure of the lithosphere in the reservoir area was inverted, following which the distributions of the isostatic additional force (IAF) borne by lithosphere were calculated. Simultaneously, the gravity and Coulomb stress changes due to the impoundment of the Baihetan reservoir were simulated to provide theoretical support for the mechanism analysis of the possible reservoir-induced earthquake.
The main findings and implications of this study are as follows:
- Thanks to our new gravity data, the accuracy of the free-air and Bouguer gravity anomalies around the Baihetan reservoir was greatly improved, with a maximum improvement of up to 150 mGal (). The observation data before impoundment provide the basis for the subsequent study of environmental change after the impoundment of the Baihetan reservoir.
- Based on gravity and elevation data, a new method for risk assessment of reservoir-induced earthquakes was proposed through a new concept of IAF borne by the lithosphere. It was found that the IAF of −30 MPa appears approximately 20 km upstream of the Baihetan dam, and the risk of reservoir-induced earthquake at such a location is worthy of attention.
- Based on the terrain and predetermined water level data, the water change before and after the impoundment of the Baihetan reservoir was simulated. The gravity changes caused by the elastic deformation due to the load of impoundment water and the gravity changes directly caused by the impoundment water were calculated. It was found that the latter is two orders of magnitude larger than the former. The gravity change caused by the storage of the Baihetan reservoir is mainly concentrated in the area within 30 km of the reservoir. The maximum theoretical gravity change on our gravity observation network reaches approximately 1.2 mGal, far exceeding the observation accuracy of current gravity instruments.
- Based on previous studies, the geometric structure models of the main faults in the Baihetan reservoir area were established, and the Coulomb stress changes caused by the impoundment of the Baihetan reservoir on the faults at 10 km underground were calculated according to the spherical earth load algorithm presented by She et al. [32]. It was found that the maximum positive Coulomb stress change was concentrated in the Xiaojiang fault near Qiaojia City, which exceeds the threshold of earthquake-trigger (0.1 bar). The maximum negative Coulomb stress variation of approximately −0.2 bar is located near the dam of the Baihetan reservoir.
- The risk area of the reservoir-induced earthquake revealed by the IAF is approximately 50 km away from that revealed by the Coulomb stress change on faults.
Author Contributions
G.F. and Y.W. proposed the idea and designed the study. Y.S. completed the calculation and mapping. G.Z. collected the gravity and GNSS data. G.F. and S.G. wrote the manuscript. T.L. prepared the fault model around the Baihetan Reservoir. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Key R&D Program of China, grant number 2018YFC1503704; the National Natural Science Foundation of China, grant number 41874003, the Project funded by China Postdoctoral Science Foundation, grant number 2020M680618; the Special Fund of the Institute of Earthquake Forecasting, China Earthquake Administration, grant number 2020IEF0708 and 2020IEF0502; the Special Fund of China Seismic Experimental Site, grant number 2019CSES0101.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
We collected gravity and GNSS data around the Baihetan Reservoir. The data can be requested by contacting the corresponding author. Terrain data is from the Shuttle Radar Topography Mission (https://www2.jpl.nasa.gov/srtm/, accessed on 5 September 2020). EIGEN-6C4 data are freely available from their providers (https://doi.org/10.5880/icgem.2015.1, accessed on 5 September 2020).
Acknowledgments
We thank the three anonymous reviewers for their conscientious review and helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, C.H.; Zhao, C.P.; Zhang, N.; Zhou, L.Q. Seismic background character in the Bahetan reservoir area. Earthquake 2018, 38, 94–108. (In Chinese) [Google Scholar]
- Zhang, N.; Zhao, C.P.; Li, C.H.; Zhou, L.Q. Velocity structure tomography of regions downstream the Jinsha River based on dense observation. Seismol. Geol. 2019, 41, 1380–1394. (In Chinese) [Google Scholar]
- Zhang, X.; Wang, Y.S. Activities of Xiaojiang fault zone in Bahetan hydropower station reservoir. J. Eng. Geol. 2017, 25, 531–540. (In Chinese) [Google Scholar]
- Xu, L.S.; Zhang, X.; Yan, C.; Li, C.L. Analysis of the Love waves for the source complexity of the Ludian Ms6.5 earthquake. Chin. J. Geophys. 2014, 57, 3006–3017. (In Chinese) [Google Scholar]
- Diao, G.L.; Wang, Y.F.; Feng, X.D.; Wang, X.S.; Feng, H.Z.; Chen, W.Z.; Li, Y.; Wang, L.B. Analysis of characteristics of focal mechanism in reservoir head region of Xiluodu reservoir after impoundment. Seismol. Geol. 2014, 36, 644–657. (In Chinese) [Google Scholar]
- Zhou, B.; Xu, S.F.; Deng, Z.H.; Sun, F.; Jiang, H.K.; Zhang, X.D.; Lu, X. Relationship between the evolution of reservoir-induced seismicity in space-time and the process of reservoir water body load-unloading and water infiltration—A case study of Zipingpu reservoir. Chin. J. Geophys. 2010, 53, 2651–2670. (In Chinese) [Google Scholar]
- Gupta, H.K. A review of recent studies of triggered earthquakes by artificial water reservoirs with special emphasis on earthquakes in Koyna, India. Earth-Sci. Rev. 2002, 58, 279–310. [Google Scholar] [CrossRef]
- McGarr, A.; Simpson, D.; Seeber, L. Case histories of induced and triggered seismicity. In International Handbook of Earthquake and Engineering Seismology, 81A; Elsevier: Amsterdam, The Netherlands, 2002; pp. 647–661. [Google Scholar]
- Wilson, M.P.; Foulger, G.R.; Gluyas, J.G.; Davies, R. HiQuake: The human-induced earthquake database. Seismol. Res. Lett. 2017, 88, 1560–1565. [Google Scholar] [CrossRef] [Green Version]
- Shashidhar, D.; Mallika, K.; Gahalaut, K.; Mahato, C.R.; Satyanarayana, V.S. A New Earthquake Sequence at Koyna–Warna, India, and Its Implication for Migration of the Reservoir Triggered Seismicity. Bull. Seismol. Soc. Am. 2019, 109, 827–831. [Google Scholar] [CrossRef]
- Foulger, G.R.; Wilson, M.P.; Gluyas, J.G.; Julian, B.R. Global review of human-induced earthquakes. Earth-Sci. Rev. 2018, 178, 438–514. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.Y.; Wu, Y.; Jang, Z.S.; Shen, C.Y.; Bo, W.J.; Qiao, X.J.; Wang, Q.L.; Li, H.; Liu, W.Y.; Tan, K.; et al. Earthquake Geodesy (in Chinese); Wuhan University Press: Wuhan, China, 2017. [Google Scholar]
- Huang, R.; Zhu, L.P.; Encarnacion, J.E.; Xu, Y.; Tang, C.C.; Luo, S.; Jiang, X. Seismic and geologic evidence of water-induced earthquakes in the Three Gorges reservoir region of China. Geophys. Res. Lett. 2018, 45, 5929–5936. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y. Reservoir induced seismicity (in Chinese); Seismological Press: Beijing, China, 1989. [Google Scholar]
- Yi, L.; Chen, Y.; Wang, G. Retrospection and prospect of the research on reservoir induced seismicity. South China J. Seismol. 2003, 23, 28–37. (In Chinese) [Google Scholar]
- Liu, D.Z.; Li, H.; Liu, S.H. A Data Processing System for Mobile Gravity Measurements—LGADJ (in Chinese); Seismological Press: Beijing, China, 1991. [Google Scholar]
- Fu, G.Y.; She, Y.W. Gravity anomalies and isostasy deduced from new dense gravimetry around the Tsangpo Gorge, Tibet. Geophys. Res. Lett. 2017, 44, 10233–10239. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Teng, J.W.; Wang, Q.S.; Hu, G.Z. Density structure and isostatic state of the crust in the Longmenshan and adjacent area. Tectonophysics 2014, 619–620, 51–57. [Google Scholar] [CrossRef]
- Liang, S.; Gan, W.; Shen, C.; Xiao, G.R.; Liu, J.; Chen, W.T.; Ding, X.G.; Zhou, D.M.; Gan, W.J. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
- Kane, M.F. A comprehensive system of terrain corrections using a digital computer. Geophysics 1962, 27, 455–462. [Google Scholar] [CrossRef]
- Nagy, D. The gravitational attraction of a right rectangular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Fu, G.Y.; Gao, S.H.; Freymueller, J.T.; Zhang, G.Q.; Zhu, Y.Q.; Yang, G.L. Bouguer gravity anomaly and isostasy at western Sichuan Basin revealed by new gravity surveys. J. Geophys. Res. 2014, 119, 3925–3938. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.; Abrikosov, O.; Lemoine, J.M.; Marty, J.C.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4-The latest combined global gravity field model including GOCE data up to degree and order 1949 of GFZ Potsdam and GRGS Toulouse. In EGU General Assembly; European Geosciences Union: Vienna, Austria, 2014. [Google Scholar]
- Gao, S.H.; She, Y.W.; Fu, G.Y. A new method for computing the vertical tectonic stress of the crust by use of hybrid gravity and GNSS data. Chin. J. Geophys. 2016, 59, 2006–2013. (In Chinese) [Google Scholar]
- She, Y.W.; Fu, G.Y.; Wang, Z.H.; Gao, Y. Vertical tectonic stress in eastern margin of Tibetan Plateau revealed by gravity and terrain data. Chin. J. Geophys. 2017, 60, 2480–2492. (In Chinese) [Google Scholar]
- Zhong, Y.; Zhou, X.; Lu, X.; Zhang, F. Application of the t test in evaluation of reservoir earthquake. South China Seismol. 2012, 32, 10–19. (In Chinese) [Google Scholar]
- Roeloffs, E.A. Fault stability changes induced beneath a reservoir with cyclic variation in water level. J. Geophys. Res. 1988, 93, 2107–2124. [Google Scholar] [CrossRef]
- Zhou, L.Q.; Zhao, C.P.; Luo, J.; Chen, Z. A detailed insight into fluid infiltration in the Three Gorges reservoir area, China from three-dimensional Vp, Vp/Vs, Qp and Qs tomography. Bull. Seismol. Soc. Am. 2018, 108, 3029–3045. [Google Scholar] [CrossRef]
- Wang, L. Influencing factors and countermeasures of reservoir induced earthquake. Henan Sci. Technol. 2013, 21, 184–185. (In Chinese) [Google Scholar]
- Zheng, C.; Ding, Z.; Song, X. Joint inversion of surface wave dispersion and receiver functions for crustal and uppermost mantle structure in Southeast Tibetan Plateau. Chin. J. Geophys. 2016, 59, 3223–3236. (In Chinese) [Google Scholar]
- Christensen, N.I.; Mooney, W.D. Seismic velocity structure and composition of the continental crust: A global view. J. Geophys. Res. 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. Space Phys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. In. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0—A 1-Degree Global Model of Earth’s Crust, Geophysical Research Abstracts, 2013, 15, Abstract EGU2013-2658. Available online: http://igppweb.ucsd.edu/~gabi/crust1.html (accessed on 5 September 2020).
- She, Y.W.; Fu, G.Y.; Liu, T. Effect of Earth Models on Coulomb Stress Change Caused by Surface Load. Pure Appl. Geophys. 2021, 178, 1235–1251. [Google Scholar] [CrossRef]
- King, G.C.P.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Ge, S.M.; Liu, M.; Lu, N.; Godt, J.W. Did the Zipingpu Reservoir trigger the 2008 Wenchuan earthquake? Geophys. Res. Lett. 2009, 36, 3–7. [Google Scholar] [CrossRef]
- Liu, Y.W.; Xu, L.Q.; Yang, D.X. Pore pressure diffusion characteristics of Longtan reservoir-induced-earthquake. Chin. J. Geophys. 2011, 54, 1028–1037. (In Chinese) [Google Scholar]
- Wen, X.Z.; Fan, J.; Yi, G.X.; Deng, Y.W.; Long, F. A seismic gap on the Anninghe fault in western Sichuan, China. Sci. China Ser. D. 2008, 51, 1375–1387. [Google Scholar] [CrossRef]
- Xu, J.; Shao, Z.G.; Liu, J.; Ji, L.Y. Coulomb stress evolution and future earthquake probability along the eastern boundary of the Sichuan-Yunnan block. Chin. J. Geophys. 2019, 62, 4189–4213. (In Chinese) [Google Scholar]
- He, Z.Q.; An, H.S.; Shen, K.; Lu, L.Y.; Hu, G.; Ye, T.L. Detection of Puduhe fault in Yuxi basin of Yunnan by seismic reflection method. Acta Seismol. Sin. 2013, 35, 836–847. [Google Scholar]
- Duan, M.Q.; Zhao, C.P. Characteristics of focal mechanisms in the downstream reservoir areas of Jinsha River. Seismol. Geol. 2019, 41, 1155–1171. (In Chinese) [Google Scholar]
- Chang, Z.F.; Zhou, R.J.; An, X.W.; Chen, Y.J.; Zhou, Q.Y.; Li, J.L. Late-quaternary activity of the Zhaotong-Ludian fault zone and its tectonic implication. Seismol. Geol. 2014, 36, 1260–1279. (In Chinese) [Google Scholar]
- Wen, X.Z.; Du, F.; Yi, G.X.; Long, F.; Fan, J.; Yang, P.X.; Xiong, R.W.; Liu, Q. Earthquake potential of the Zhaotong and Lianfeng fault zones of the eastern Sichuan-Yunnan border region. Chin. J. Geophys. 2013, 56, 3361–3372. (In Chinese) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).