Assessing Irrigation Water Use with Remote Sensing-Based Soil Water Balance at an Irrigation Scheme Level in a Semi-Arid Region of Morocco
Abstract
1. Introduction
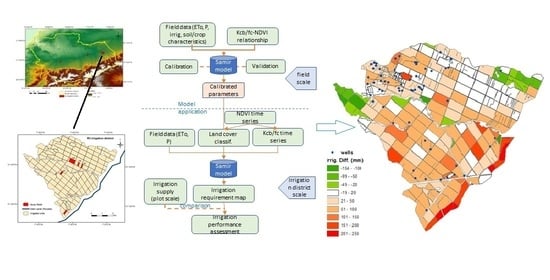
2. Materials and Methods
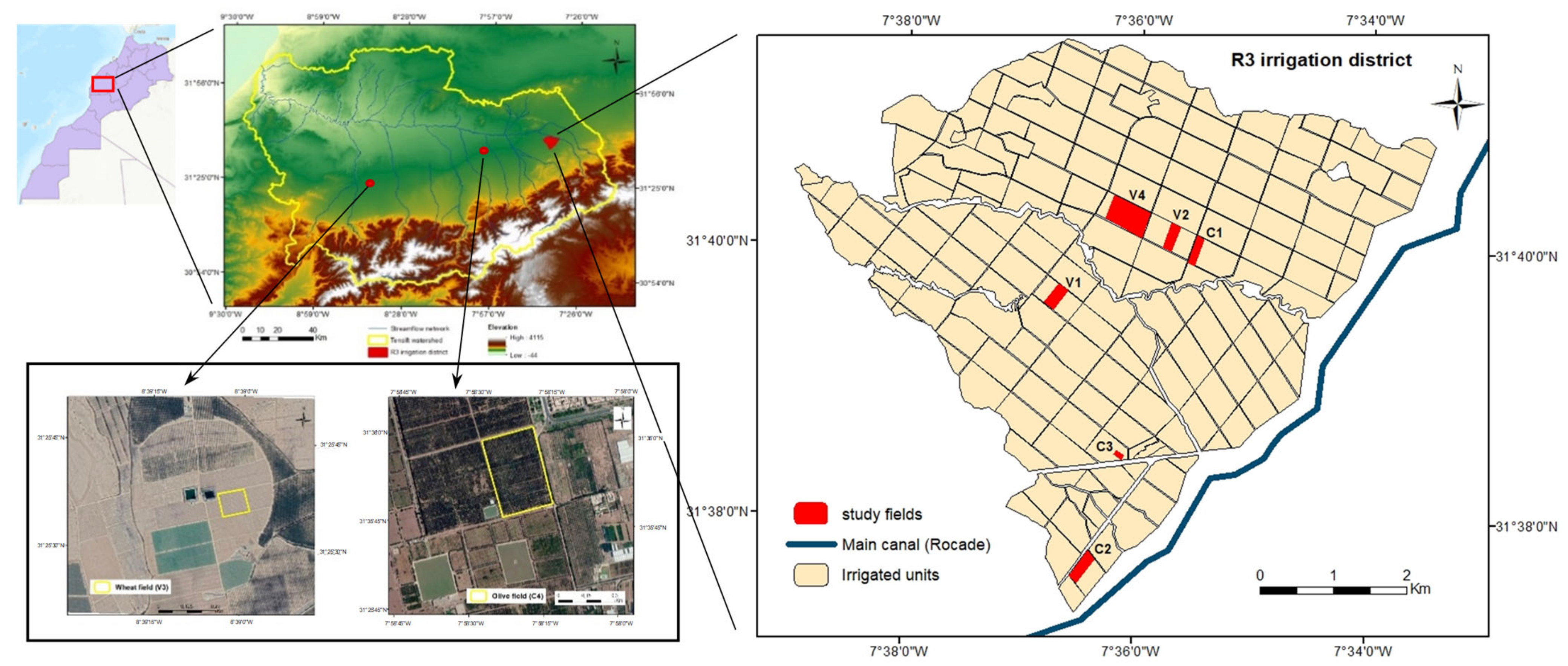
2.1. Study Area
2.2. Model Description
2.3. Experimental Data
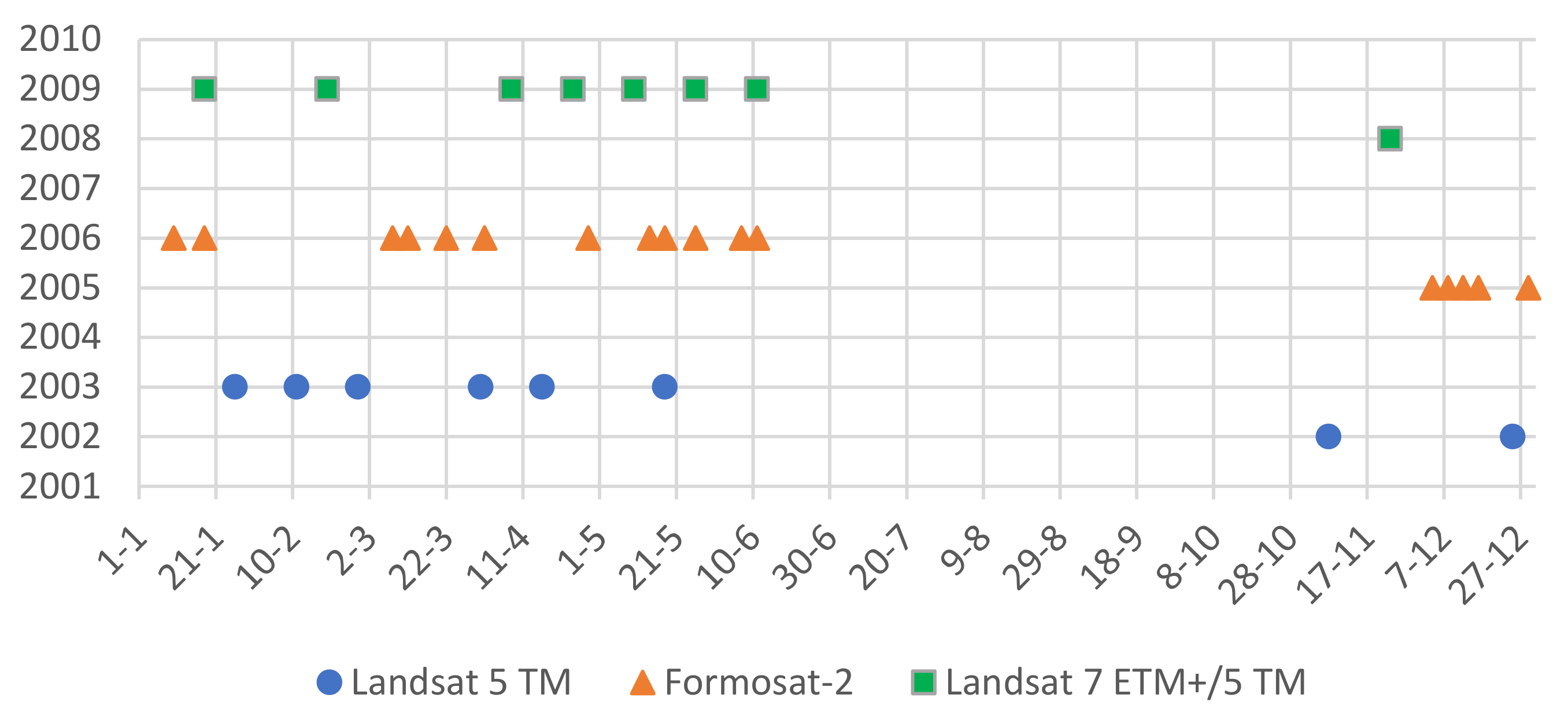
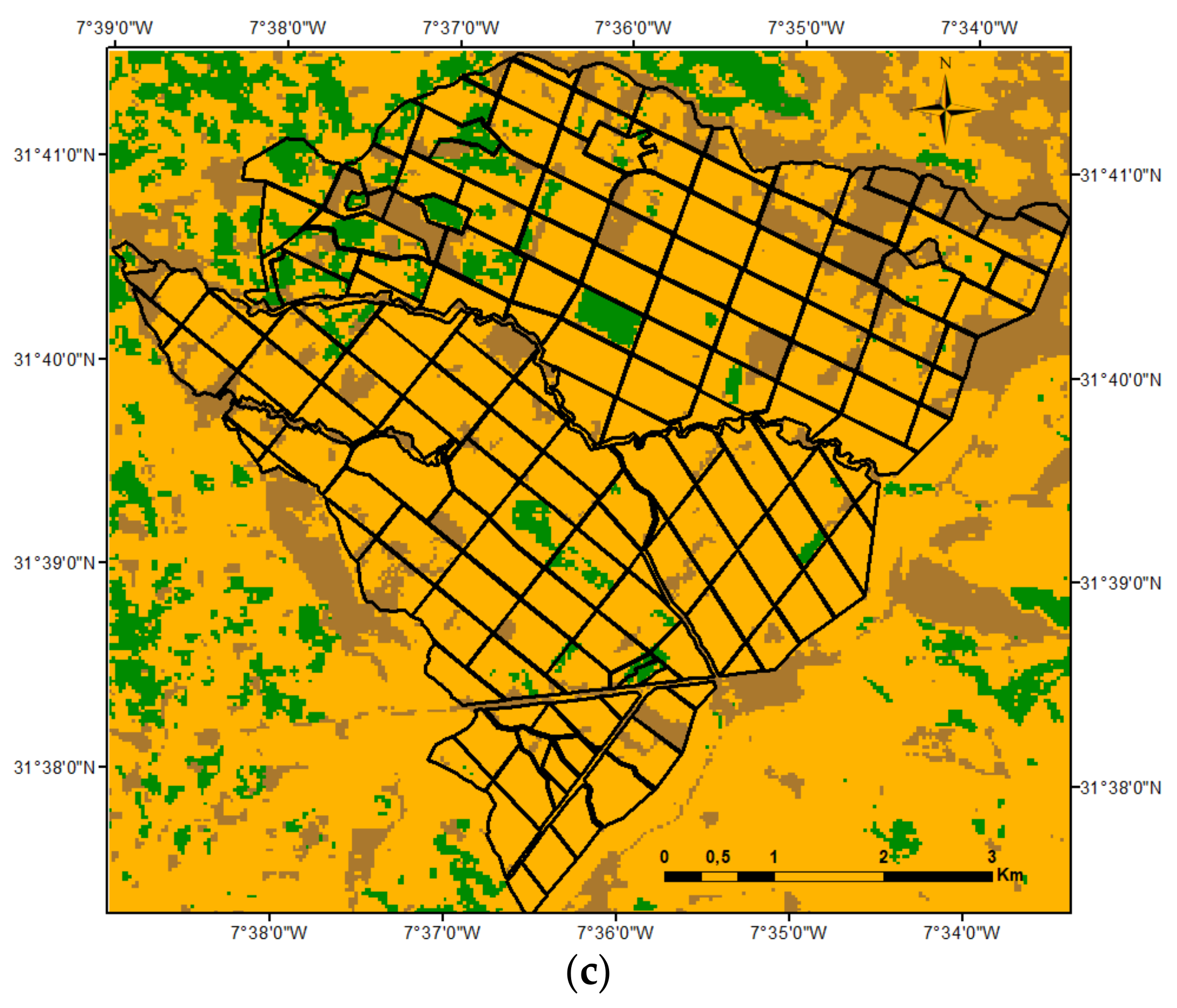
2.4. Satellite Data and Land Cover Mapping
2.5. Model Calibration and Evaluation
3. Results
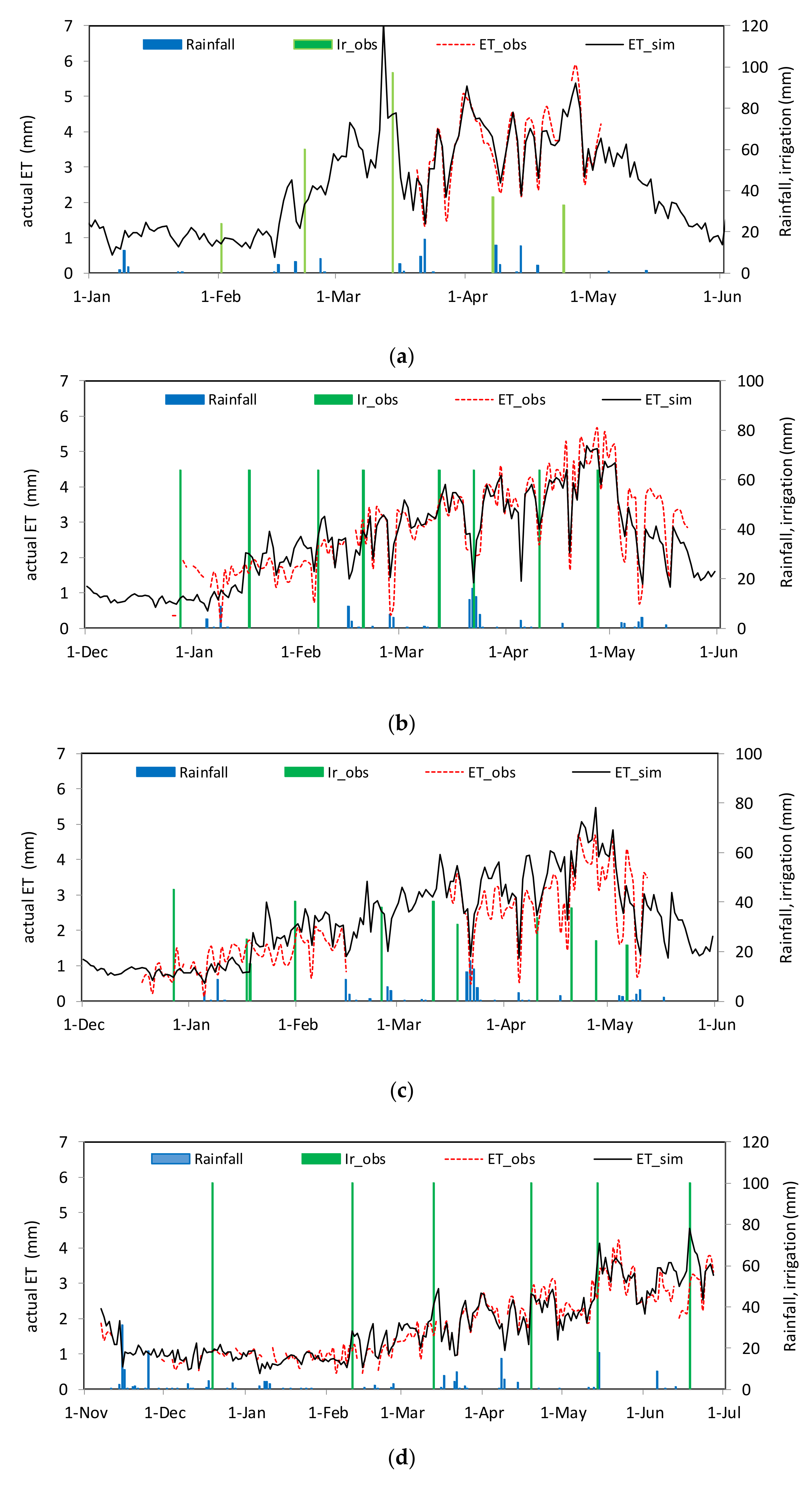
3.1. Calibration of the Model
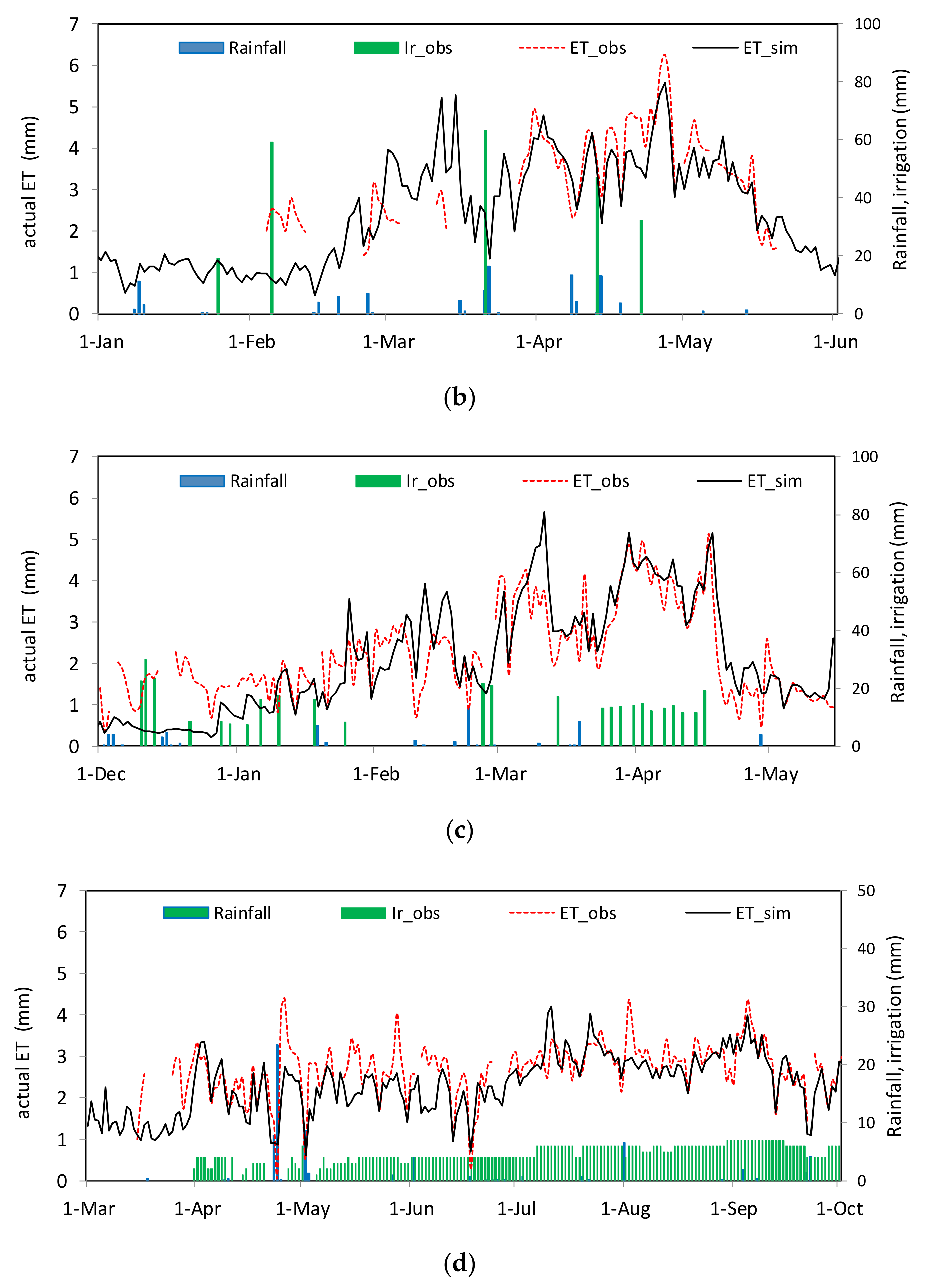
3.2. Validation of the Model
3.3. Model Application for Spatialized Estimates of RS-IWR
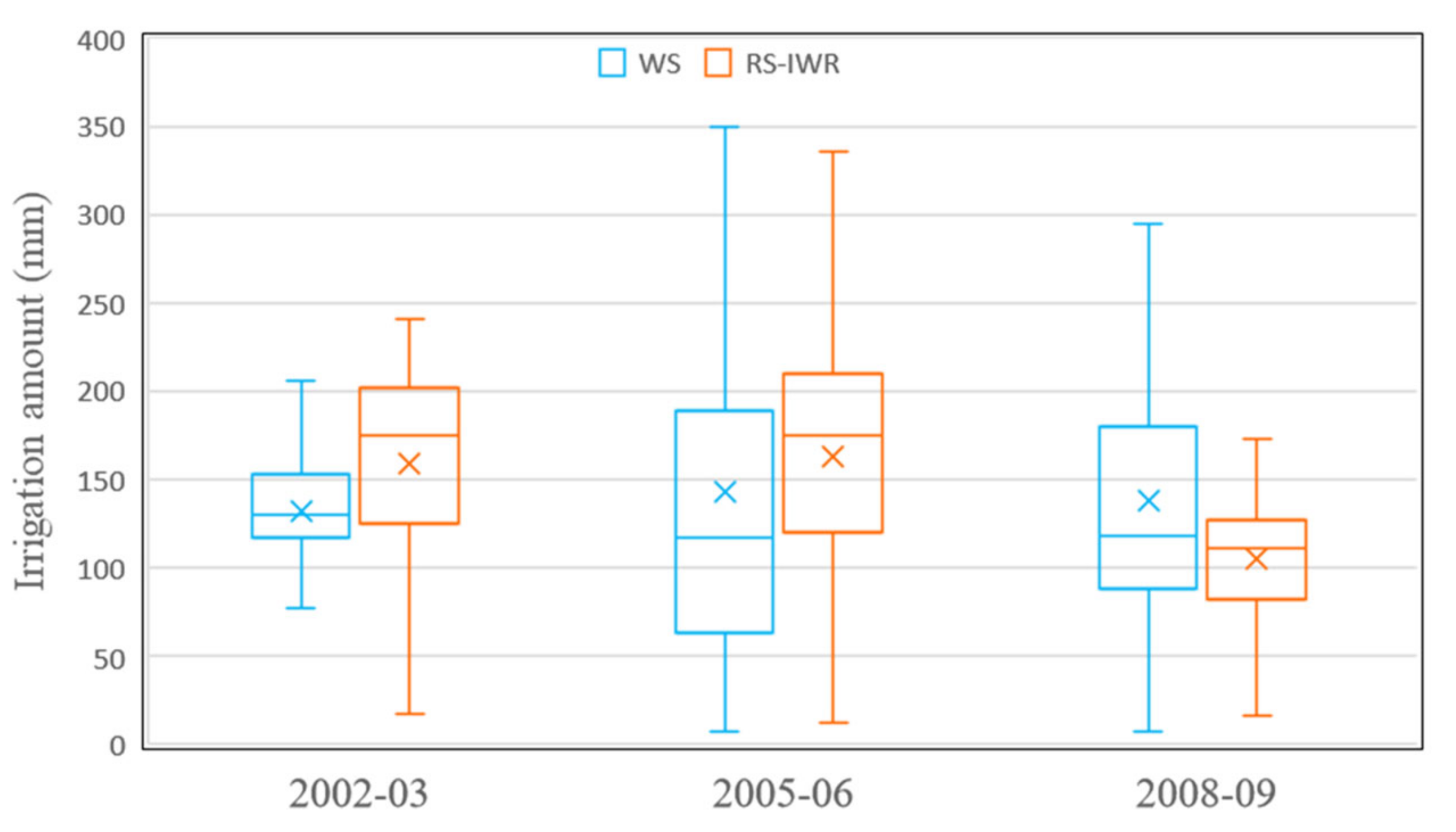
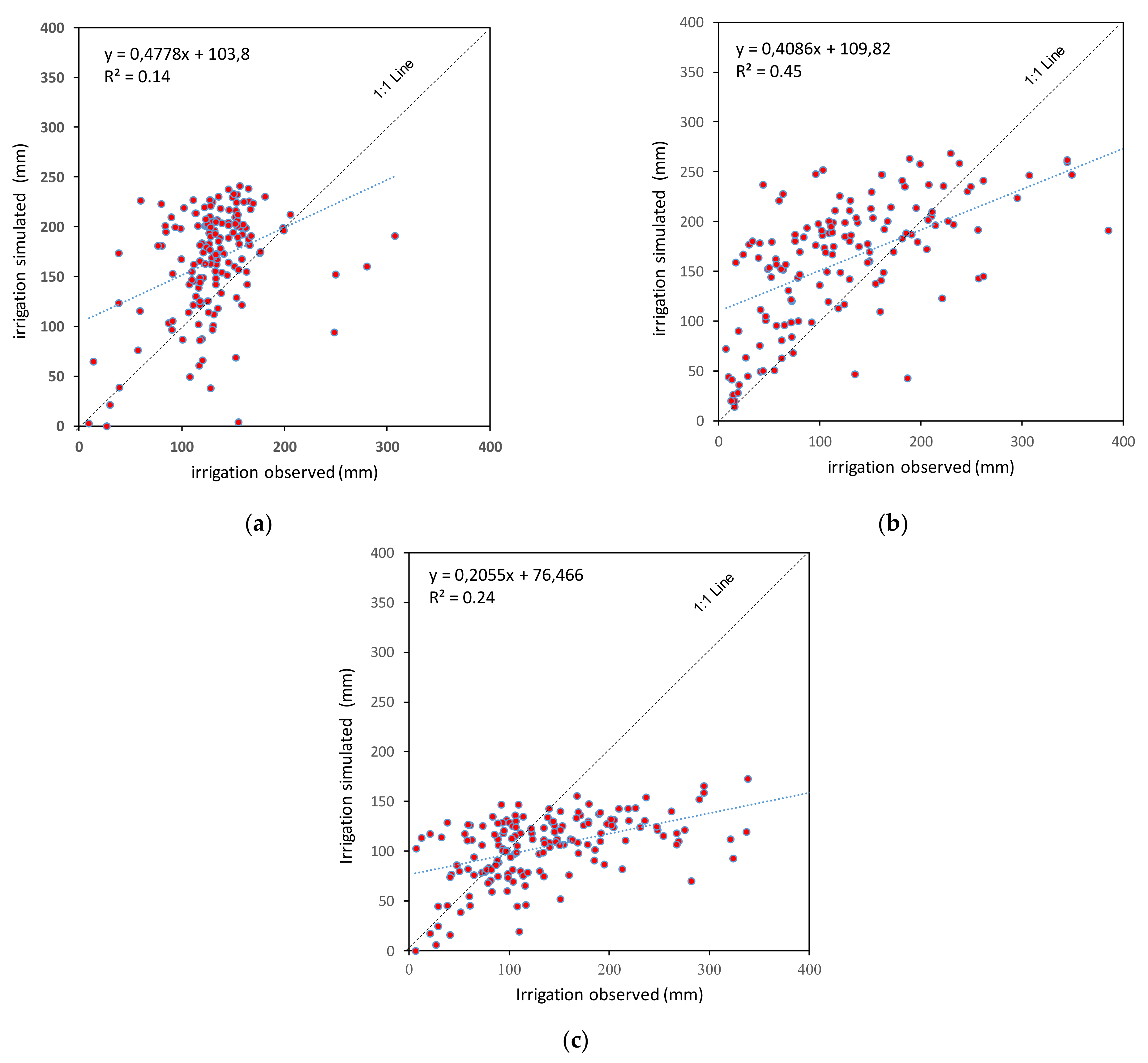
3.3.1. Analysis of Irrigation Water Practices
3.3.2. Comparison of Irrigation Water Use Anomalies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. AQUASTAT Database. 2016. Available online: http://www.fao.org/nr/water/aquastat/data (accessed on 3 November 2020).
- UN Water. Integrated Monitoring Guide for SDG 6: Targets and Global Indicators; UN Water: Geneva, Switzerland, 2016. [Google Scholar]
- Bastiaanssen, W.G.M.; Brito, R.A.L.; Bos, M.G.; Souza, R.A.; Cavalcanti, E.B.; Bakker, M.M. Low cost satellite data for monthly irrigation performance monitoring: Benchmarks from Nilo Coelho, Brazil. Irrig. Drain. Syst. 2001, 15, 53–79. [Google Scholar] [CrossRef]
- Lorite, I.J.; Mateos, L.; Fereres, E. Evaluating Irrigation Performance in a Mediterranean Environment: II. Variability among Crops and Farmers. Irrig. Sci. 2004, 23, 85–92. [Google Scholar] [CrossRef]
- Santos, C.; Lorite, I.J.; Allen, R.G.; Fereres., E. Performance Assessment of an Irrigation Scheme Using Indicators Determined with Remote Sensing Techniques. Irrig. Sci. 2010, 28, 461–477. [Google Scholar] [CrossRef]
- Taghvaeian, S.; Neale, C.M.U.; Osterberg, J.C.; Sritharan, S.I.; Watts, D.R. Remote Sensing and GIS Techniques for Assessing Irrigation Performance: Case Study in Southern California. J. Irrig. Drain. Eng. 2018, 144, 2–10. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Blatchford, M.L.; Mannaerts, C.M.; Zeng, Y.; Nouri, H.; Karimi, P. Status of accuracy in remotely sensed and in-situ agricultural water productivity estimates: A review. Remote Sens. Environ. 2019, 234, 111413. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G. Satellite-based ET mapping to assess variation in ET with timing of crop development. Agric. Water Manag. 2007, 88, 54–62. [Google Scholar] [CrossRef]
- Gowda, P.; Chavez, J.; Colaizzi, P.; Evett, S.; Howell, T.; Tolk, J. ET mapping for agricultural water management: Present status and challenges. Irrig. Sci. 2008, 26, 223–237. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.G.M. Spatial evapotranspiration, rainfall and land use data in water accounting—part 1: Review of the accuracy of the remote sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 507–532. [Google Scholar] [CrossRef]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote sensing for crop water management: From ET modelling to services for the end users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.J.; Robison, C.W. Journal of Irrigation and Drainage Engineering Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Jensen, M.E.; Wright, J.L.; Pratt, B.J. Estimating Soil Moisture Depletion from Climate, Crop and Soil Data. Trans. ASAE 1971, 14, 954–959. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop requirements. In Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Bausch, W.C.; Neale, C.M.U. Crop coefficients derived from reflected canopy radiation-a concept. Trans. ASABE 1987, 30, 703–709. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.C.B.; Kharrou, M.H.; et al. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Mateos, L. Spectral vegetation indices for benchmarking water productivity of irrigated cotton and sugar beet crops. Agric. Water Manag. 2008, 95, 48–58. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Er-Raki, S.; Rodriguez, J.C.; Garatuza-Payan, J.; Watts, C.J.; Chehbouni, A. Determination of crop evapotranspiration of table grapes in a semi-arid region of Northwest Mexico using multi-spectral vegetation index. Agric. Water Manag. 2013, 122, 12–19. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, M.C.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating evapotranspiration of an apple orchard using a remote sensing-based soil water balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef]
- Diarra, A.; Jarlan, L.; Er-Raki, S.; Le Page, M.; Aouade, G.; Tavernier, A.; Boulet, G.; Ezzahar, J.; Merlin, O.; Khabba, S. Performance of the two-source energy budget (TSEB) model for the monitoring of evapotranspiration over irrigated annual crops in North Africa. Agric. Water Manag. 2017, 193, 71–88. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J., Jr.; Barnes, E.M.; Kimball, B.A. Estimating cotton evapotranspiration crop coefficients with a multispectral vegetation index. Irrig. Sci. 2003, 22, 95–104. [Google Scholar] [CrossRef]
- Nagler, P.; Scott, R.; Westenberg, C.; Cleverly, J.; Glenn, E.; Huete, A. Evapotranspiration on western U.S. rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sens. Environ. 2005, 97, 337–351. [Google Scholar] [CrossRef]
- Katul, G.; Schieldge, J.; Hsieh, C.I. Skin temperature perturbations induced by surface layer turbulence above a grass surface. Water Resour. Res. 1998, 34, 1265–1274. [Google Scholar] [CrossRef]
- Campos, I.; Villodre, J.; Carrara, A.; Calera, A. Remote sensing-based soil water balance to estimate Mediterranean holm oak savanna (dehesa) evapotranspiration under water stress conditions. J. Hydrol. 2013, 494, 1–9. [Google Scholar] [CrossRef]
- Mateos, L.; González-Dugo, M.P.; Testi, L.; Villalobos, F.J. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. I. Method validation. Agric. Water Manag. 2013, 125, 81–91. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.; Paredes, P.; Cunha, M.; Pereira, L.S. Estimation of actual crop coefficients using remotely sensed vegetation indices and soil water balance modelled data. Remote Sens. 2015, 7, 2373–2400. [Google Scholar] [CrossRef]
- Cherif, R.; Simonneaux, V.; Rivalland, V.; Gascoin, S.; Le Page, M.; Ceschia, E. Distributed Modelling of Evapotranspiration Using High-Resolution NDVI maps Over Cropland in South-west France; General Assembly 2012, Vienna. 14.1061C; European Geosciences Union (EGU): Munich, Germany, 2012. [Google Scholar]
- Le Page, M.; Simonneaux, V.; Thomas, S.; Metral, J.; Duchemin, B.; Kharrou, H.; Cherkaoui, M.; Chehbouni, A. SAMIR A Tool for Irrigation Monitoring Using Remote Sensing for Evapotranspiration Estimate. In Technological Perspectives for Rational Use of Water Resources in the Mediterranean Region; El Moujabber, M., Mandi, L., Trisorio-Liuzzi, G., Martín, I., Rabi, A., Rodríguez, R., Eds.; CIHEAM: Bari, Italy, 2009; pp. 275–282. Available online: http://om.ciheam.org/om/pdf/a88/00801202.pdf (accessed on 13 February 2021).
- Melton, F.S.; Johnson, L.F.; Lund, C.P.; Pierce, L.L.; Michaelis, A.R.; Hiatt, S.H.; Guzman, A.; Adhikari, D.; Purdy, A.J.; Rosevelt, C.; et al. Satellite irrigation management support with the terrestrial observation and prediction system: A framework for integration of satellite and surface observations to support improvements in agricultural water resource management. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2012, 5, 1709–1721. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Escuin, S.; Cano, F.; Cifuentes, V.; Padilla, F.L.M.; Tirado, J.L.; Oyonarte, N.; Fernández, P.; Mateos, L. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. II. Application on basin scale. Agric. Water Manag. 2013, 125, 92–104. [Google Scholar] [CrossRef]
- Vuolo, F.; D’Urso, G.; De Michele, C.; Bianchi, B.; Cutting, M. Satellite-based irrigation advisory services: A common tool for different experiences from Europe to Australia. Agric. Water Manag. 2015, 147, 82–95. [Google Scholar] [CrossRef]
- Calera Belmonte, A.; Jochum, A.M.; García Cuesta, A.; Rodríguez Montoro, A.; Fuster López, P. Irrigation management from space: Towards user-friendly products. Irrig. Drain. Syst. 2005, 19, 337–353. [Google Scholar] [CrossRef]
- Moreno, R.; Arias, E.; Sánchez, J.L.; Cazorla, D.; Garrido, J.; Gonzalez-Piqueras, J. HidroMORE2: An optimized and parallel version of HidroMORE. In Proceedings of the 8th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 4–6 April 2017; pp. 1–6. [Google Scholar]
- Simonneaux, V.; Le Page, M.; Helson, D.; Metral, J.; Thomas, S.; Duchemin, B.; Cherkaoui, M.; Kharrou, H.; Berjami, B.; Chehbouni, G. Estimation spatialisée de l’évapotranspiration des cultures irriguées par télédétection: Application à la gestion de l’irrigation dans la plaine du Haouz (Marrakesh, Maroc). Sécheresse 2009, 20, 123–130. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain. Eng. ASCE 2005, 131, 2–13. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation of Natural Vegetation; NASA/GSFC, Type III, Final Report; NASA: Greenbelt, MD, USA, 1974; pp. 1–371. [Google Scholar]
- Pôças, I.; Calera, A.; Campos, I.; Cunha, M. Remote sensing for estimating and mapping single and basal crop coefficients: A review on spectral vegetation indices approaches. Agric. Water Manag. 2020, 233. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; López, M.-L.; Balbontín, C.; Calera, A. Analyzing the effect of shadow on the relationship between ground cover and vegetation indices by using spectral mixture and radiative transfer models. J. Appl. Remote Sens. 2014, 8, 083562. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.; Suyker, A.; Arkebauer, T.; Gonçalves, I. Reflectance-based crop coefficients redux: For operational evapotranspiration estimates in the age of high producing hybrid varieties. Agric. Water Manag. 2017, 187, 140–153. [Google Scholar] [CrossRef]
- Torres, E.A.; Calera, A. Bare soil evaporation under high evaporation demand: A proposed modification to the fao-56 model. Hydrol. Sci. J. 2010, 55, 303–315. [Google Scholar] [CrossRef]
- Zhang, Y.; Wegehenkel, M. Integration of MODIS data into a simple model for the spatial distributed simulation of soil water content and evapotranspiration. Remote Sens. Environ. 2006, 104, 393–408. [Google Scholar] [CrossRef]
- Devonec, E.; Barros, A.P. Exploring the transferability of a land-surface hydrology mode. J. Hydrol. 2002, 265, 258–282. [Google Scholar] [CrossRef]
- Chehbouni, A.; Escadafal, R.; Duchemin, B.; Boulet, G.; Simonneaux, V.; Dedieu, G.; Mougenot, B.; Khabba, S.; Kharrou, H.; Maisongrande, P.; et al. An Integrated Modelling and Remote Sensing Approach for Hydrological Study in Arid and Semi-arid Regions: The SUDMED Programme. Int. J. Remote Sens. 2008, 29, 5161–5181. [Google Scholar] [CrossRef]
- Jarlan, L.; Khabba, S.; Er-Raki, S.; Le Page, M.; Hanich, L. Remote Sensing of Water Resources in Semi-Arid Mediterranean Areas: The joint international laboratory TREMA. Int. J. Remote Sens. 2015, 36, 4879–4917. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Ben Abdelouahab, T. An evaporation test based on Thermal InfraRed remote-sensing to select appropriate soil hydraulic properties. J. Hydrol 2009, 376, 589–598. [Google Scholar] [CrossRef]
- Wösten, J.H.M. Pedotransfer functions to evaluate soil quality. In Soil Quality for Crop Production and Ecosystem Health; Developments in Soils Science; Gegorich, E.G., Carter, M.R., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; Volume 25, pp. 221–245. [Google Scholar]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J.; Romberger, J.S.; Papendick, R.I. Estimating generalized soil-water characteristics from texture. Soil Sci. Soc. Am. J. 1986, 50, 1031–1036. [Google Scholar] [CrossRef]
- Campbell, C.S. Soil Physics with Basic; Elsevier: New York, NY, USA, 1985; p. 149. [Google Scholar]
- Rafi, Z.; Merlin, O.; Le Dantec, V.; Khabba, S.; Mordelet, P.; Er-Raki, S.; Amazirh, A.; Olivera-Guerra, L.; Ait Hssaine, B.; Simonneaux, V.; et al. Partitioning evapotranspiration of a drip-irrigated wheat crop: Inter-comparing eddy covariance-, sap flow-, lysimeter- and FAO-based methods. Agric. For. Meteorol. 2019, 265, 310–326. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.C.B.; Er-Raki, S.; Chehbouni, A.; Boulet, G.; Bonnefond, J.M.; De Bruin, H.A.R. The use of the scintillation technique for monitoring seasonal water consumption of olive orchards in a semi-arid region. Agric. Water Manag. 2007, 89, 173–184. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G. Using the dual approach of FAO56 for partitioning ET into soil and plant components for olive orchards in a semiarid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef]
- Simonneaux, V.; Duchemin, B.; Helson, D.; Er-Raki, S.; Olioso, A.; Chehbouni, A.G. The use of high-resolution image time series for crop classiication and evapotranspiration estimate over an irrigated area in central Morocco. Int. J. Remote Sens. 2008, 29, 95–116. [Google Scholar] [CrossRef]
- Duchemin, B.; Hagolle, O.; Mougenot, B.; Benhadj, I.; Hadria, R.; Simonneaux, V.; Ezzahar, J.; Hoedjes, J.; Khabba, S.; Kharrou, M.H.; et al. Agrometeorological study of semi-arid areas: An experiment for analysing the potential of time series of FORMOSAT-2 images (Tensift-Marrakesh plain). Int. J. Remote Sens. 2008, 29, 5291–5299. [Google Scholar] [CrossRef]
- Carpintero, E.; Mateos, L.; Andreu, A.; González-Dugo, M.P. Effect of the differences in spectral response of Mediterranean tree canopies on the estimation of evapotranspiration using vegetation index-based crop coefficients. Agri. Water Manag. 2020, 238. [Google Scholar] [CrossRef]
- Toumi, J.; Er-Raki, S.; Ezzahar, J.; Khabba, S.; Jarlan, L.; Chehbouni, A. Performance assessment of AquaCrop model for estimating evapotranspiration, soil water content and grain yield of winter wheat in Tensift Al Haouz (Morocco): Application for irrigation management. Agric. Water Manag. 2016, 163, 219–235. [Google Scholar] [CrossRef]
- Er-Raki, S.; Ezzahar, J.; Merlin, O.; Amazirh, A.; Ait Hssaine, B.; Kharrou, M.H.; Khabba, S.; Chehbouni, A. Performance of the HYDRUS-1D model for water balance components assessment of irrigated winter wheat under different water managements in semi-arid region of Morocco. Agric. Water Manag. 2021, 244, 106546. [Google Scholar] [CrossRef]
- Foster, T.; Goncalves, I.Z.; Campos, I.; Neale, C.M.U.; Brozovic, N. Assessing landscape scale heterogeneity in irrigation water use with remote sensing and in-situ monitoring. Environ. Res. Lett. 2019, 14, 024004. [Google Scholar] [CrossRef]
- Kharrou, M.H.; Le Page, M.; Chehbouni, A.; Simonneaux, V.; ErRaki, S.; Simonneaux, V. Assessment of equity and adequacy of water delivery in irrigation systems using remote sensing-based indicators in semi-arid region, Morocco. Water Resour. Manag. 2013, 27, 4697–4714. [Google Scholar] [CrossRef]
- Garrido-Rubio, J.; González-Piqueras, J.; Campos, I.; Osann, A.; González-Gómez, L.; Calera, A. Remote sensing–based soil water balance for irrigation water accounting at plot and water user association management scale. Agric. Water Manag. 2020, 238, 106236. [Google Scholar] [CrossRef]



| NDVI-fc | NDVI_min | NDVI_max | fc_min | fc_max | Relation | Sources |
|---|---|---|---|---|---|---|
| Wheat/olive tree | 0.15 | 0.9 | 0 | 1 | fc = 1.33*NDVI − 0.20 | Min and Max NDVI taken in images assuming resp. bare soil and full cover |
| NDVI-Kcb | NDVI_min | NDVI_max | Kcb_min | Kcb_max | Relation | Sources |
| Wheat | 0.15 | 0.9 | 0 | 1.05 | Kcb = 1.40*NDVI − 0.21 | Kcbmax calibrated |
| olive tree | 0.15 | 0.9 | 0 | 0.76 | Kcb = 1.01*NDVI − 0.15 | Kcbmax calibrated |
| Parameter | Definition | Values | Data Source | |||
|---|---|---|---|---|---|---|
| C1 (Wheat) | C2 (Wheat) | C3 (Wheat) | C4 (Olive) | |||
| Soil Parameters: | ||||||
| θfc (m3/m3) | Volumetric water content at field capacity | 0.35 | 0.35 | 0.35 | 0.36 | ground observation |
| θwp (m3/m3) | Volumetric water content at wilting point | 0.22 | 0.22 | 0.22 | 0.22 | ground observation |
| Ze (mm) | Height of the soil evaporation layer | 125 | 125 | 125 | 125 | FAO56 |
| REW | Readily evaporable water at surface layer | 8 | 8 | 8 | 8 | calibration |
| m | correction to the coefficient of evaporation reduction | 0.58 | 0.58 | 0.58 | 0.28 | calibration |
| Zr_min (mm) | Minimum root depth | 125 | 125 | 125 | 125 | FAO56 |
| Zr_max (mm) | Maximum root depth | 700 | 700 | 700 | 950 | calibration |
| Z_tot (mm) | Total soil depth | 1450 | 1450 | 1450 | 1450 | calibration |
| p | fraction of TAW to be depleted before stress | 0.55 | 0.55 | 0.55 | 0.65 | FAO56 |
| Difer | Diffusion between surface and root layers | 16 | 16 | 16 | 0 | calibration |
| Difrd | Diffusion between deep and root layers | 8 | 8 | 8 | 7 | calibration |
| Init_RU (%) | Soil initial water content | 10 | 10 | 10 | 80 | ground observation |
| Irrigation Parameters: | ||||||
| fw | wetted fraction | 1 | 1 | 0.6 | 1 | ground observation |
| Kcb_off | Kcb threshold to stop irrigation (% of Kcbmax) | 75 | 75 | 75 | - | calibration |
| Ir_max (mm) | maximum irrigation rate | 60 | 60 | 20 | 100 | ground observation |
| Calibration Fields | Validation Fields | |||||||
|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | V1 | V2 | V3 | V4 | |
| NSE | 0.89 | 0.86 | 0.75 | 0.82 | 0.66 | 0.76 | 0.59 | 0.62 |
| RMSE (mm/day) | 0.32 | 0.46 | 0.56 | 0.37 | 0.46 | 0.54 | 0.69 | 0.54 |
| R2 | 0.91 | 0.86 | 0.50 | 0.86 | 0.67 | 0.83 | 0.80 | 0.67 |
| Pbias (%) | 0.2 | 0.02 | 16.5 | 4.2 | −1.8 | −9.9 | 0.8 | −11.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kharrou, M.H.; Simonneaux, V.; Er-Raki, S.; Le Page, M.; Khabba, S.; Chehbouni, A. Assessing Irrigation Water Use with Remote Sensing-Based Soil Water Balance at an Irrigation Scheme Level in a Semi-Arid Region of Morocco. Remote Sens. 2021, 13, 1133. https://doi.org/10.3390/rs13061133
Kharrou MH, Simonneaux V, Er-Raki S, Le Page M, Khabba S, Chehbouni A. Assessing Irrigation Water Use with Remote Sensing-Based Soil Water Balance at an Irrigation Scheme Level in a Semi-Arid Region of Morocco. Remote Sensing. 2021; 13(6):1133. https://doi.org/10.3390/rs13061133
Chicago/Turabian StyleKharrou, Mohamed Hakim, Vincent Simonneaux, Salah Er-Raki, Michel Le Page, Saïd Khabba, and Abdelghani Chehbouni. 2021. "Assessing Irrigation Water Use with Remote Sensing-Based Soil Water Balance at an Irrigation Scheme Level in a Semi-Arid Region of Morocco" Remote Sensing 13, no. 6: 1133. https://doi.org/10.3390/rs13061133
APA StyleKharrou, M. H., Simonneaux, V., Er-Raki, S., Le Page, M., Khabba, S., & Chehbouni, A. (2021). Assessing Irrigation Water Use with Remote Sensing-Based Soil Water Balance at an Irrigation Scheme Level in a Semi-Arid Region of Morocco. Remote Sensing, 13(6), 1133. https://doi.org/10.3390/rs13061133