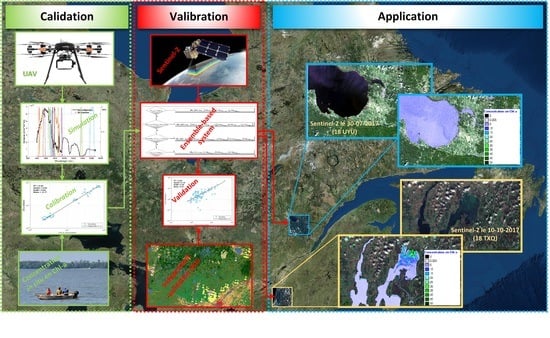
How Accurate Is an Unmanned Aerial Vehicle Data-Based Model Applied on Satellite Imagery for Chlorophyll-a Estimation in Freshwater Bodies?
Abstract
1. Introduction
2. Study Area and Materials
2.1. Study Area
2.2. Materials
3. Data Compilation and Pre-Processing
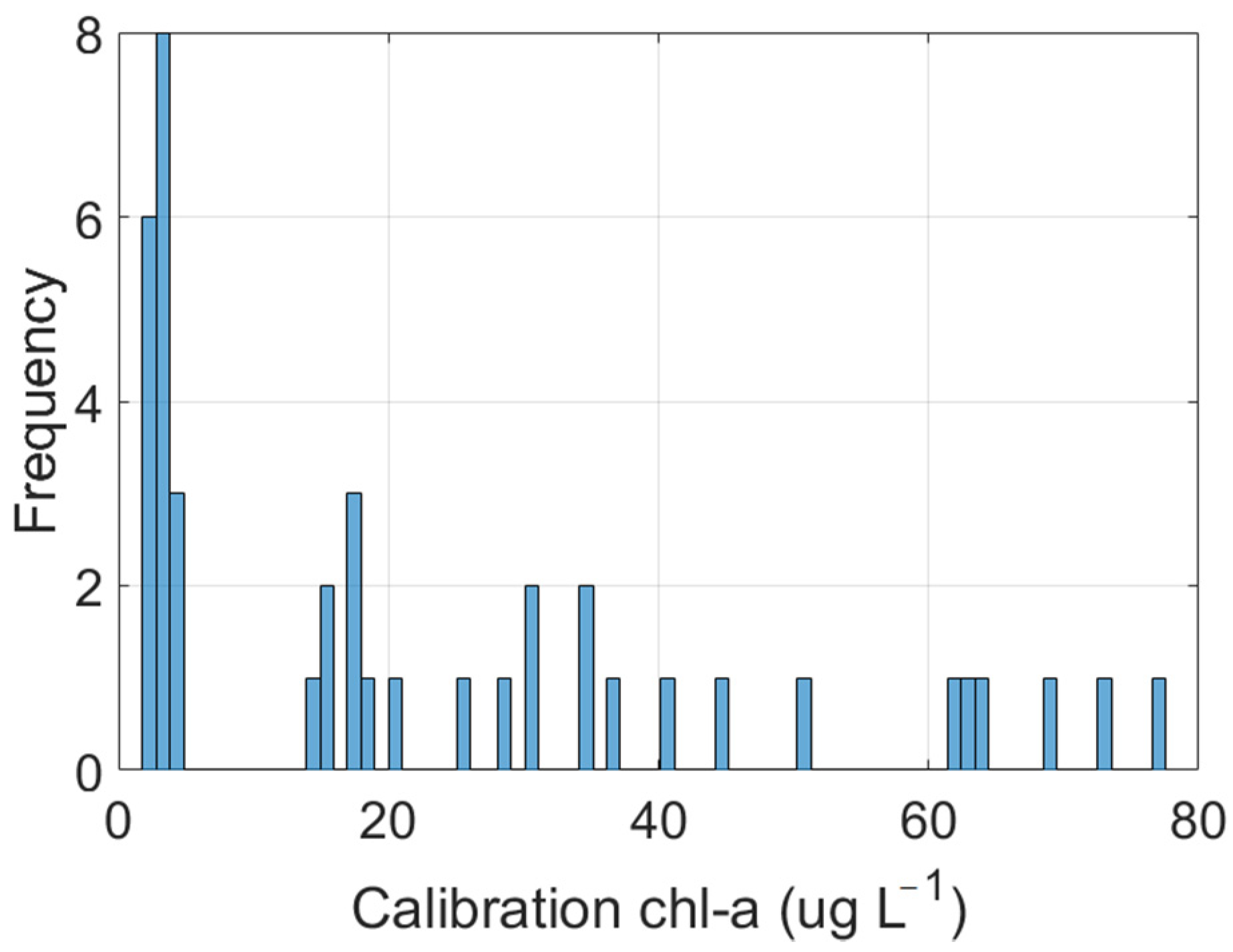
3.1. Calibration Database
3.1.1. Collection of Data from the Lake
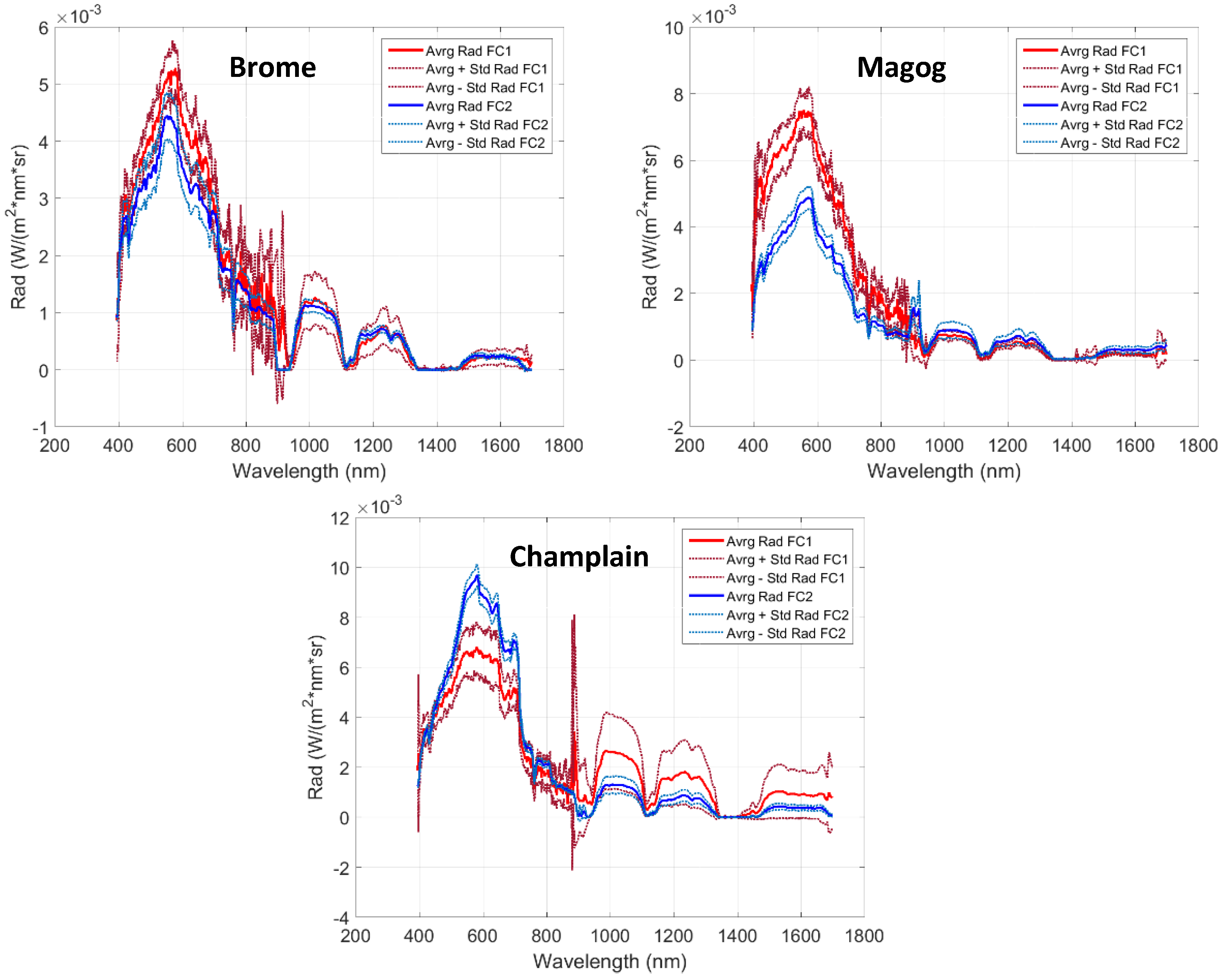
3.1.2. Hyperspectral Image Acquisition
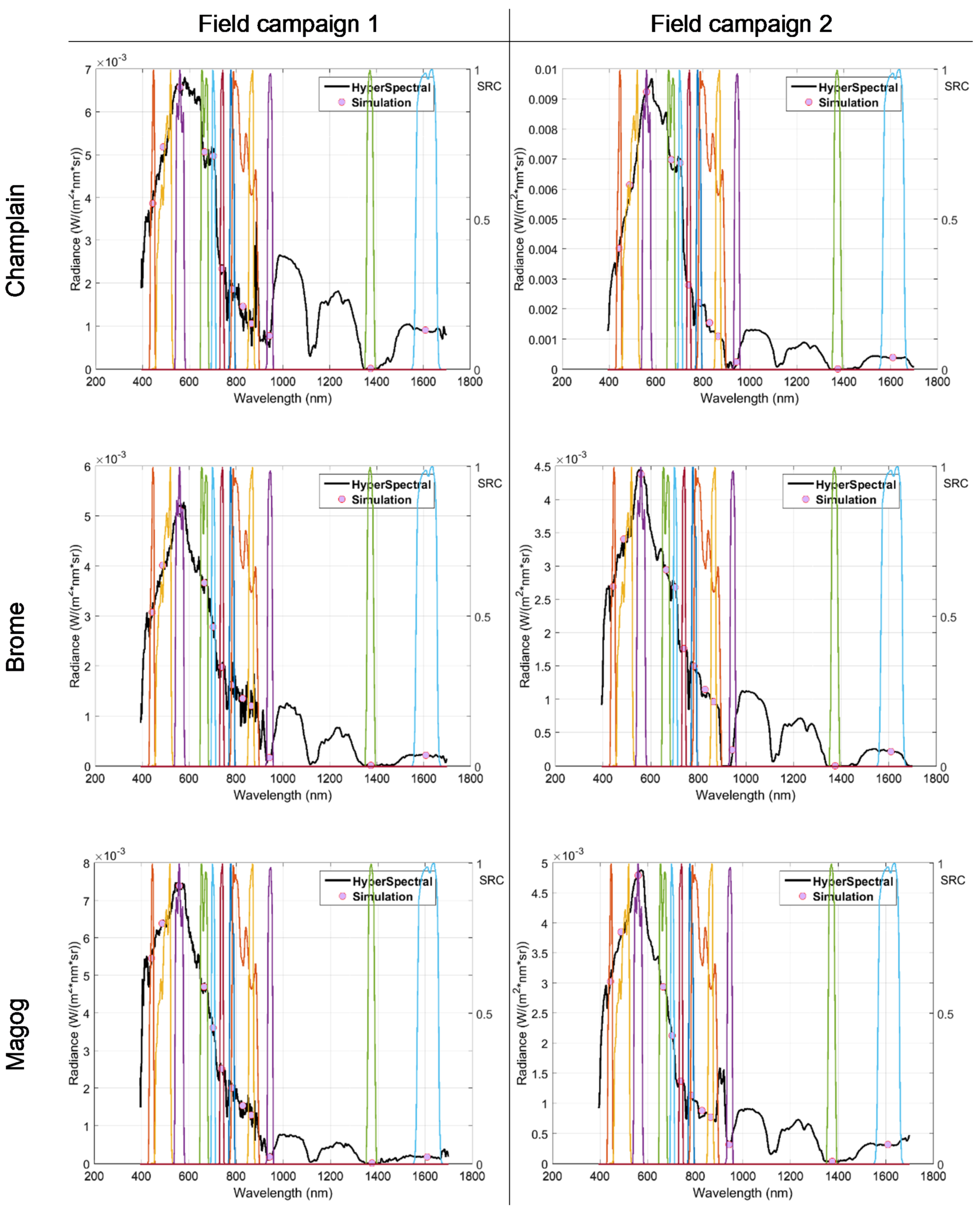
3.1.3. Sentinel-2 Bands Simulation
3.1.4. Simulated Bands Reflectance
- ➢
- Its values are usually comprised between 0 and 1;
- ➢
- It is easy to compare the reflectance from one spectral band to another;
- ➢
- It is possible to compare the reflectance directly at different times of the year or of the day, since it is already corrected for variations of earth–sun distance and solar zenith angle (https://labo.obs-mip.fr/multitemp/les-grandeurs-radiometriques-eclairement-luminance-reflectance/, accessed on 4 February 2021).
3.2. Validation Database
3.2.1. In Situ Measurements
3.2.2. Remote Sensing Data
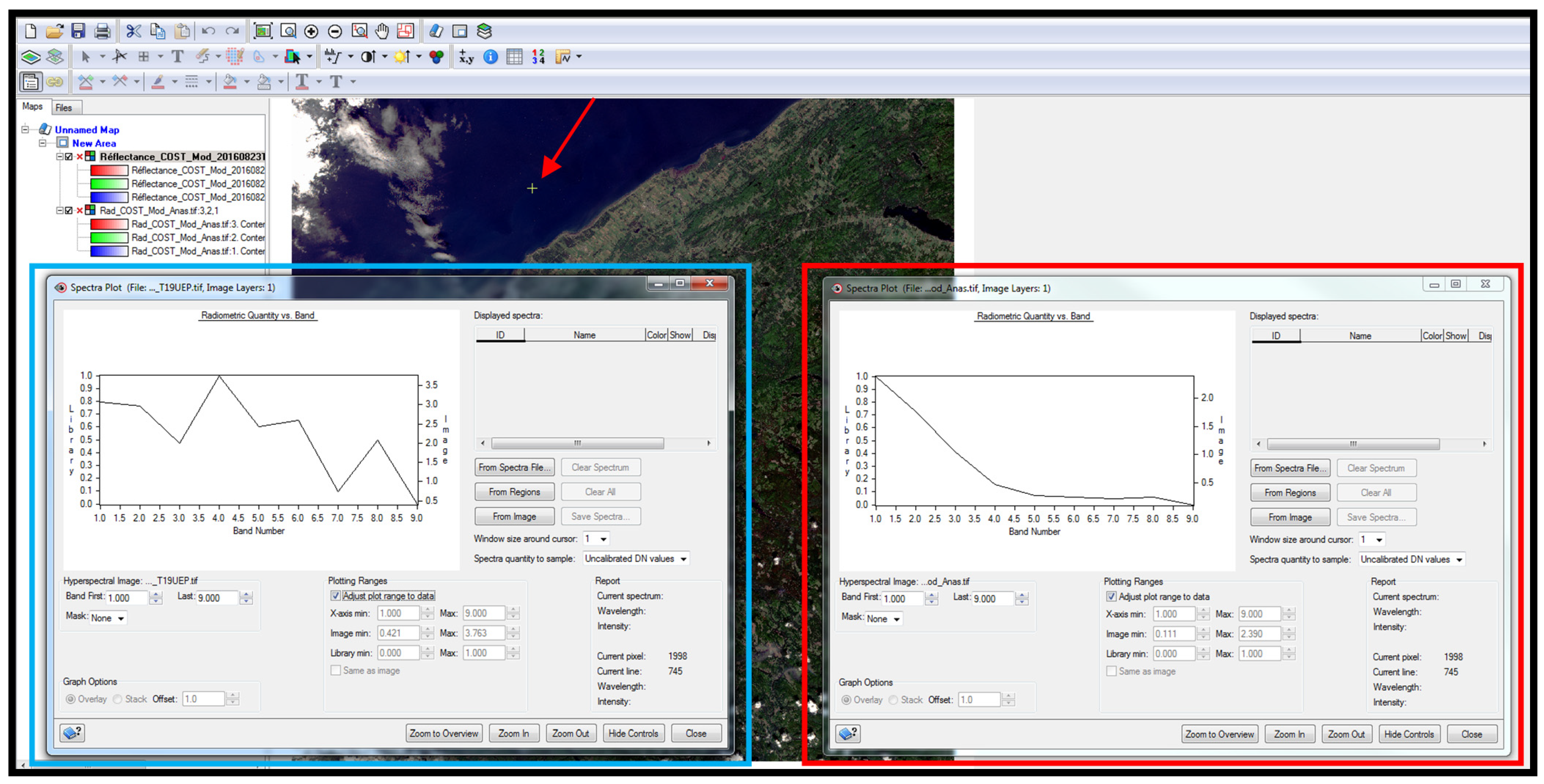
3.2.3. Atmospheric Correction of Sentinel-2 Images
4. Methodology and Statistical Evaluation Indices
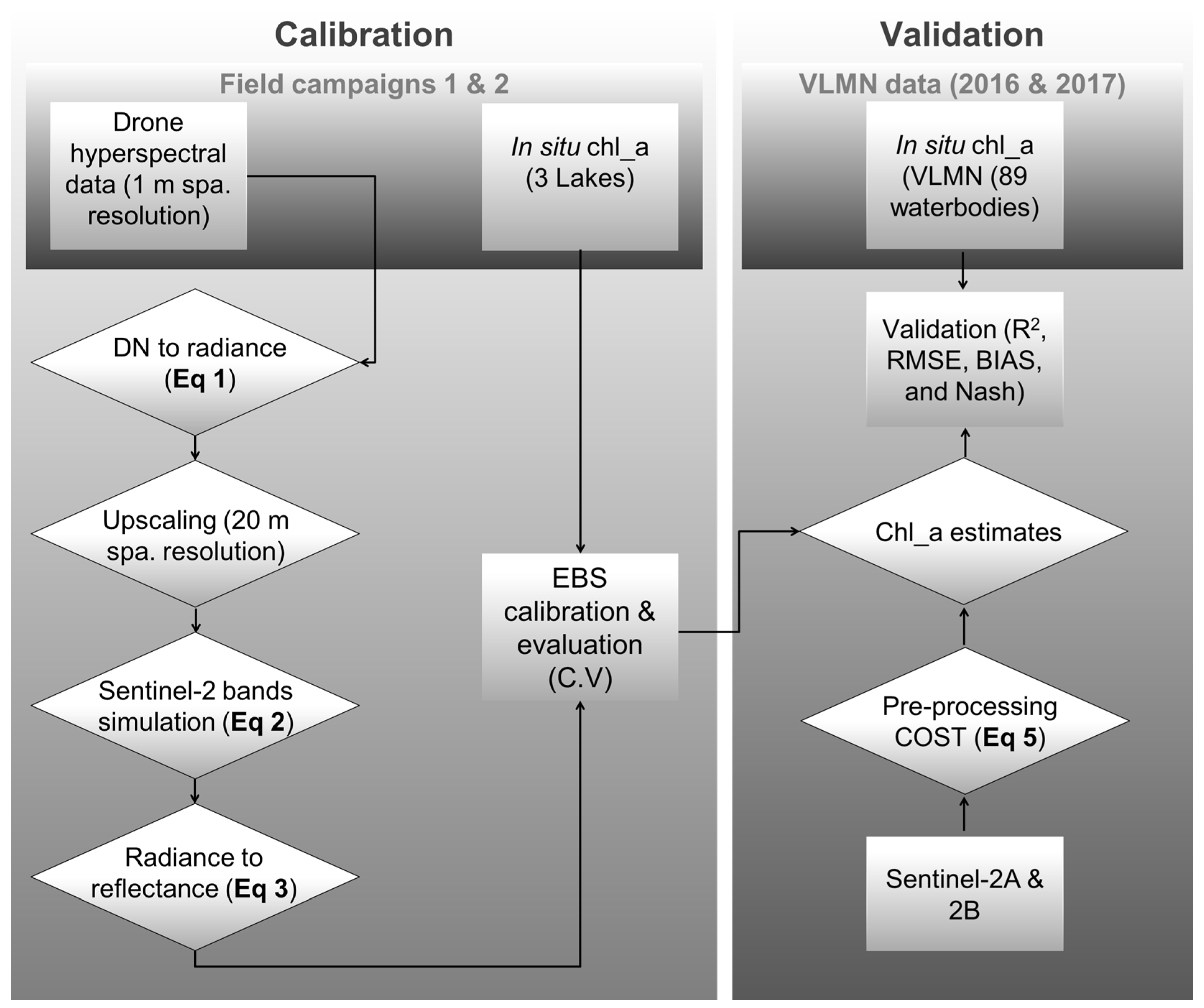
4.1. Methodological Approach
- ➢
- Geometric and radiometric (Equation (1)) corrections;
- ➢
- Upscaling to 20 m spatial resolution (equal to that of Sentinel-2);
- ➢
- Sentinel-2 spectral bands simulation (Equation (2));
- ➢
- Simulated bands reflectance computation (Equation (3)).
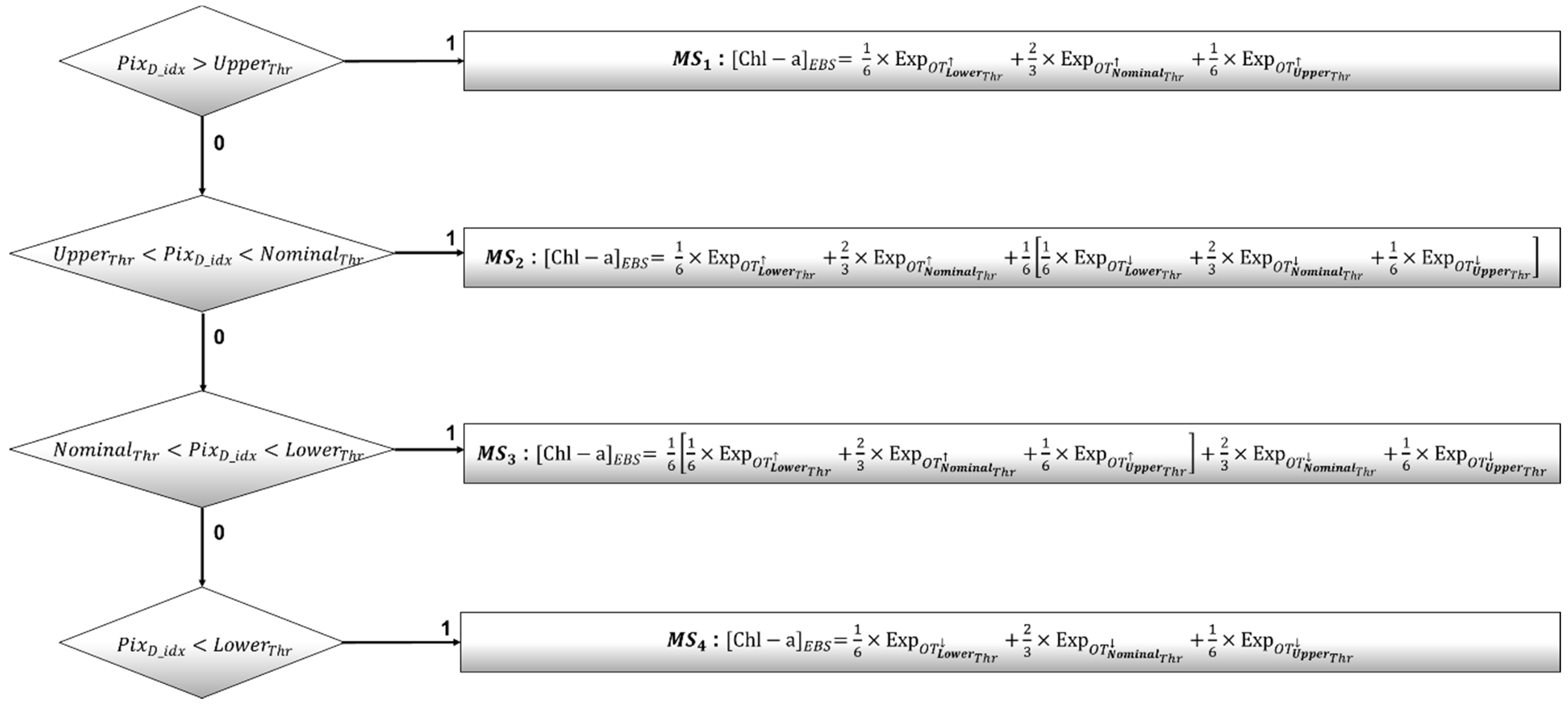
4.2. Ensemble-Based System
4.3. Statistical Indices for the Ensemble-Based System Assessment
5. Results and Discussion
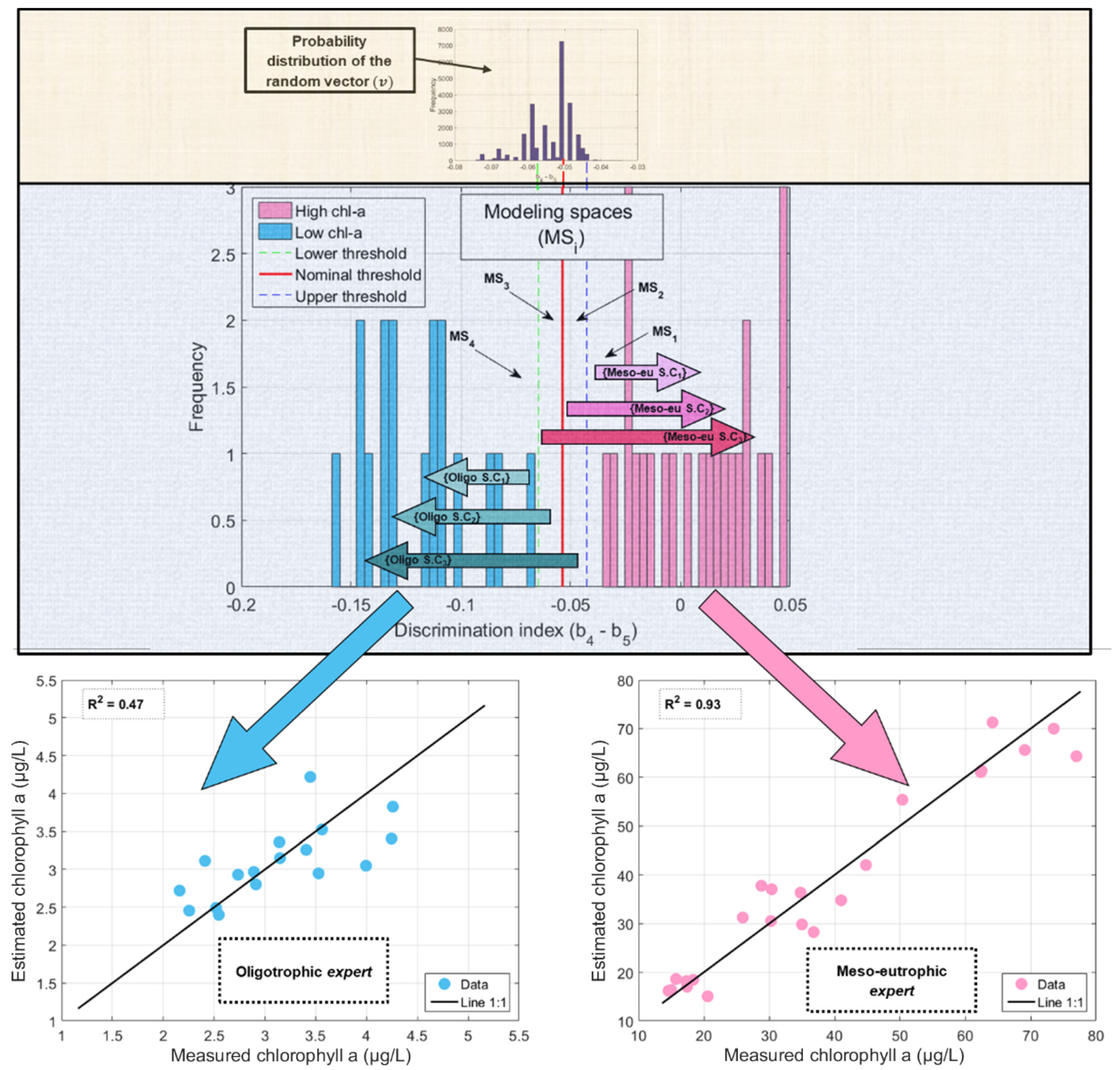
5.1. The Ensemble-Based Classifier Development
5.2. The Ensemble-Based Estimator Development
5.3. The Hybrid Ensemble-Based System for Chlorophyll-a Modeling
5.4. Calibration of the Experts
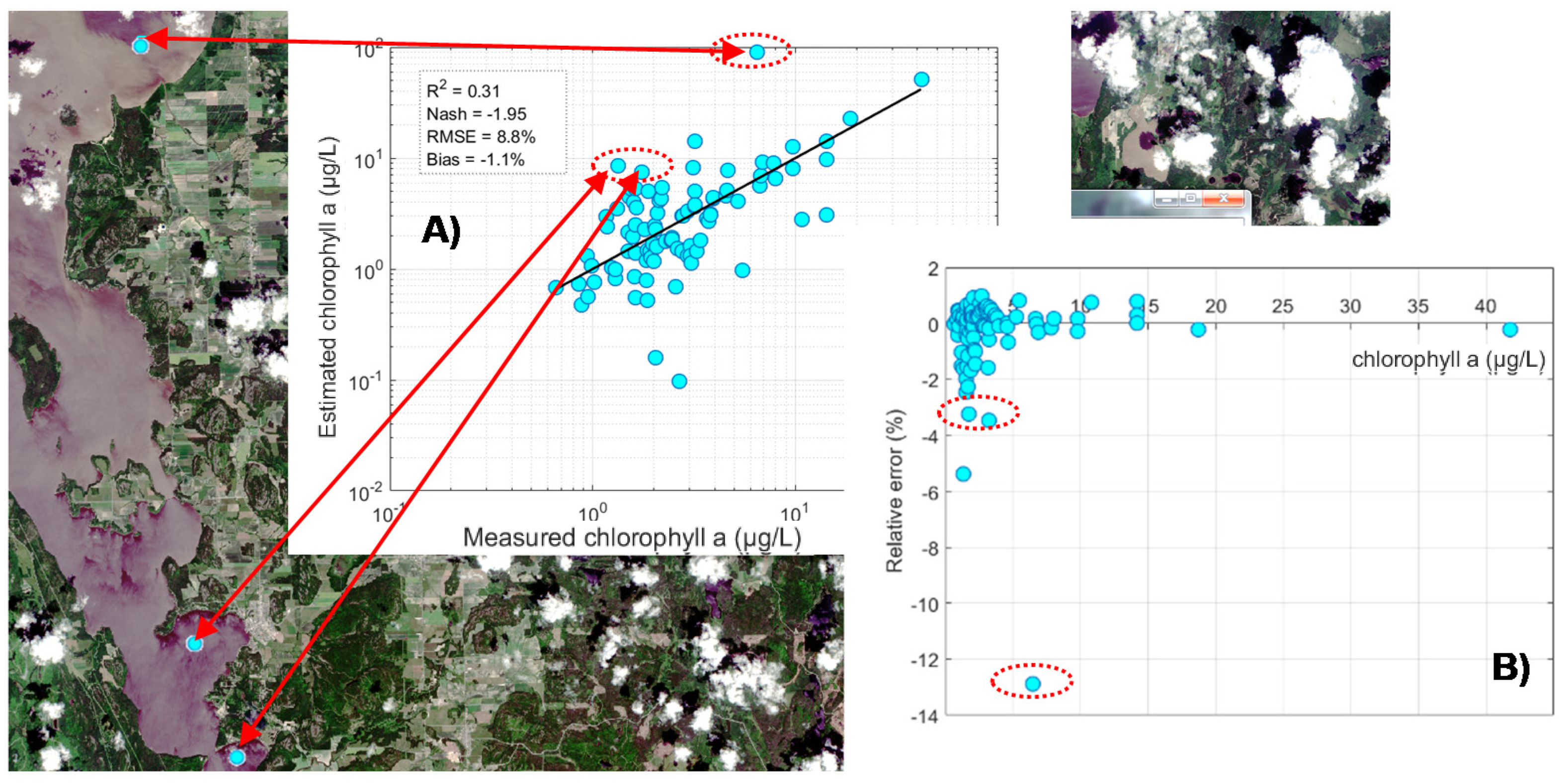
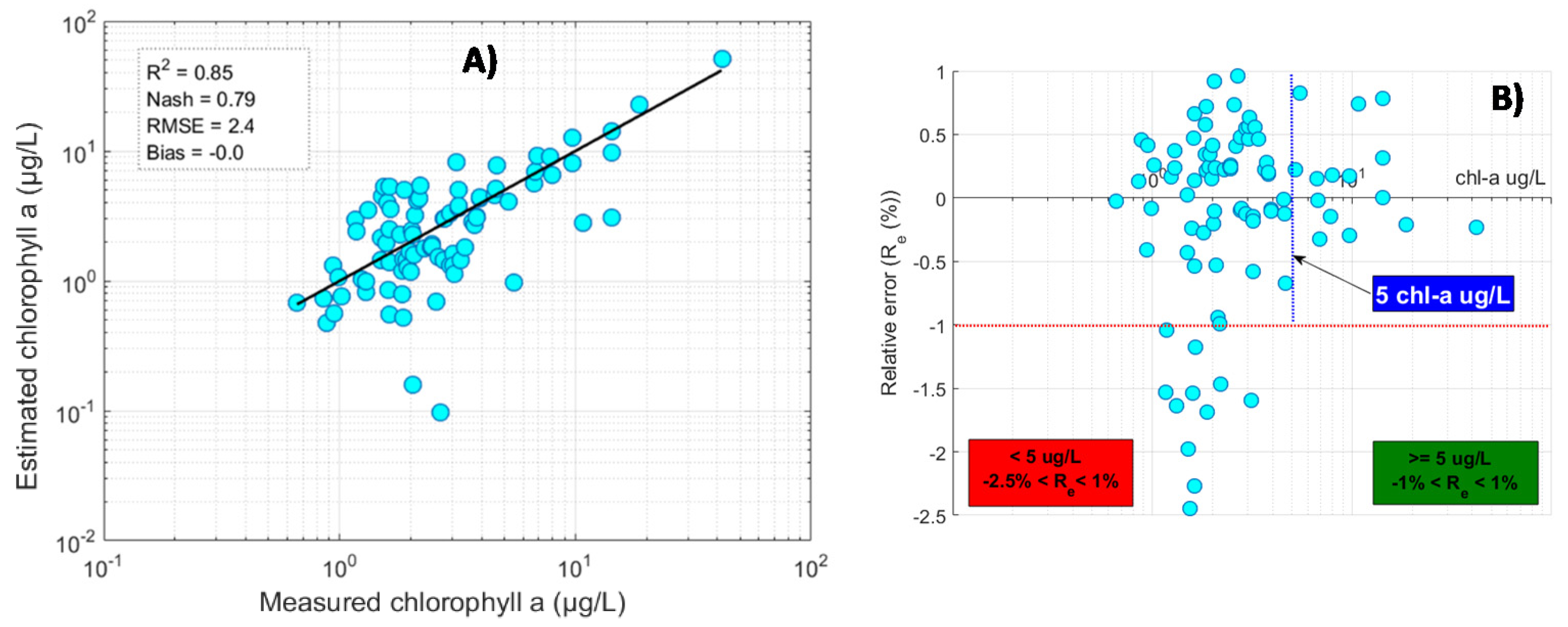
5.5. Cross-Validation: Local Evaluation
5.6. Validation with the Blind Dataset: Regional Evaluation
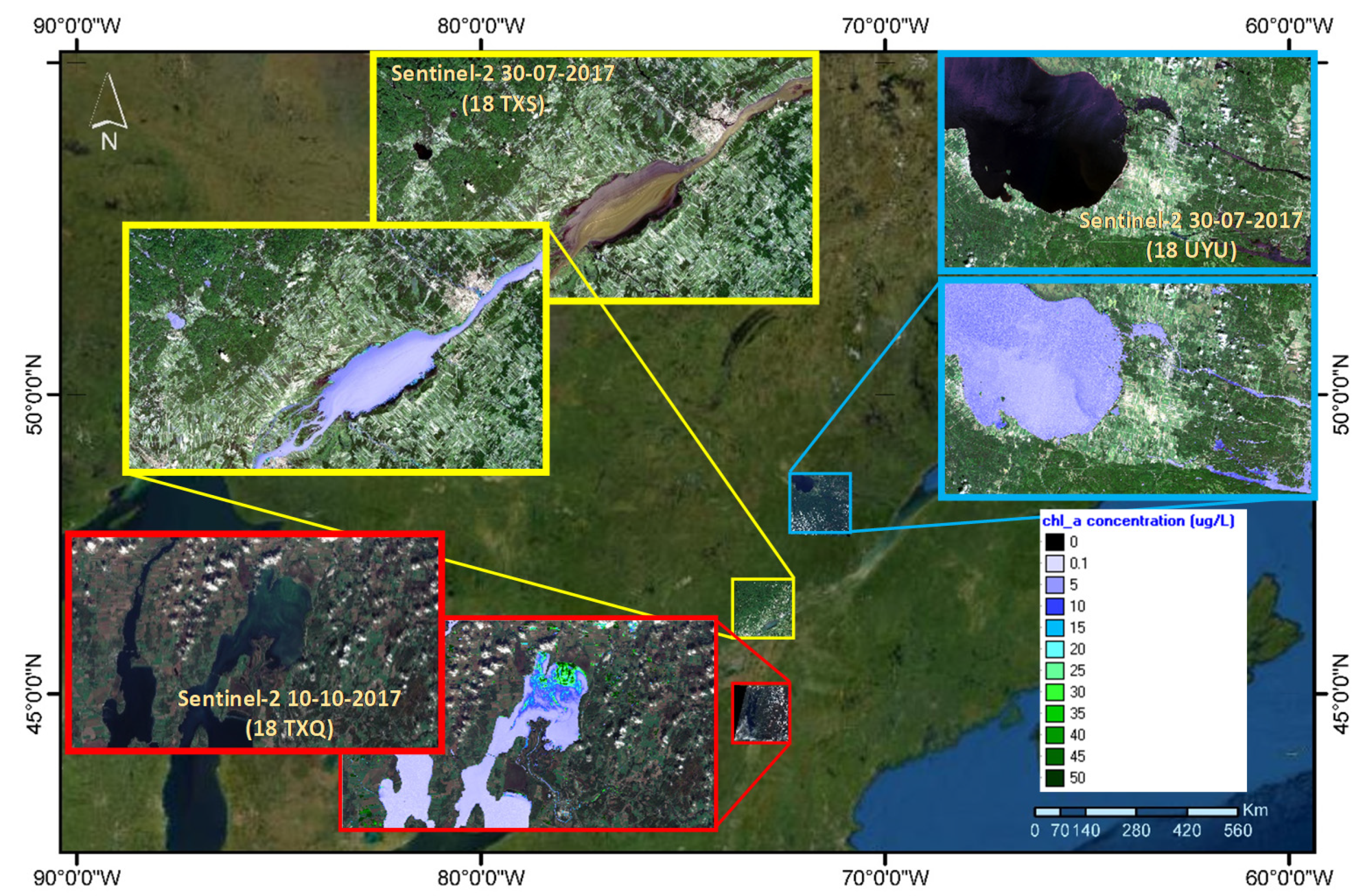
5.7. Spatial Distribution Assessment of the Ensemble-Based System
6. Challenges, Advantages, and Limitations of Chlorophyll-a Monitoring Using UAVs and Satellites Data
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Drobac, D.; Tokodi, N.; Simeunović, J.; Baltic, V.; Stanić, D.; Svircev, Z. Human exposure to cyanotoxins and their effects on health. Arch. Ind. Hyg. Toxicol. 2013, 64, 305–316. [Google Scholar] [CrossRef]
- Black, J.G.; Black, L.J. Microbiology: Principles and Explorations, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Stoermer, E.F. Phytoplankton assemblages as indicators of water quality in the laurentian great lakes. Trans. Am. Microsc. Soc. 1978, 97, 2–16. [Google Scholar] [CrossRef]
- Long, S.; Hamilton, P.B.; Yang, Y.; Ma, J.; Chobet, O.C.; Chen, C.; Dang, A.; Liu, Z.; Dong, X.; Chen, J. Multi-year succession of cyanobacteria blooms in a highland reservoir with changing nutrient status, Guizhou Province, China. J. Limnol. 2018, 77, 232–246. [Google Scholar] [CrossRef]
- Rantajärvi, E.; Olsonen, R.; Hällfors, S.; Leppänen, J.-M.; Raateoja, M. Effect of sampling frequency on detection of natural variability in phytoplankton: Unattended high-frequency measurements on board ferries in the Baltic Sea. ICES J. Mar. Sci. 1998, 55, 697–704. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Gordon, H.R.; Clark, D.K.; Brown, J.W.; Brown, O.B.; Evans, R.H.; Broenkow, W.W. Phytoplankton pigment concentrations in the Middle Atlantic Bight: Comparison of ship determinations and CZCS estimates. Appl. Opt. 1983, 22, 20–36. [Google Scholar] [CrossRef]
- Bohn, V.Y.; Carmona, F.; Rivas, R.; Lagomarsino, L.; Diovisalvi, N.; Zagarese, H.E. Development of an empirical model for chlorophyll-a and Secchi Disk Depth estimation for a Pampean shallow lake (Argentina). Egypt. J. Remote Sens. Space Sci. 2018, 21, 183–191. [Google Scholar] [CrossRef]
- Di Cicco, A.; Sammartino, M.; Marullo, S.; Santoleri, R. Regional empirical algorithms for an improved identification of phytoplankton functional types and size classes in the Mediterranean sea using satellite data. Front. Mar. Sci. 2017, 4, 126. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Robeson, S.M. Revisiting empirical ocean-colour algorithms for remote estimation of chlorophyll-a content on a global scale. Int. J. Remote Sens. 2016, 37, 2682–2705. [Google Scholar] [CrossRef]
- Watanabe, F.S.Y.; Alcântara, E.; Rodrigues, T.W.P.; Imai, N.N.; Barbosa, C.C.F.; Rotta, L. Estimation of chlorophyll-a concentration and the trophic state of the Barra Bonita hydroelectric reservoir using OLI/Landsat-8 images. Int. J. Environ. Res. Public Health 2015, 12, 10391–10417. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, J.; Zhang, Y.; Zhang, B. Comparison of different semi-empirical algorithms to estimate chlorophyll-a concentration in inland lake water. Environ. Monit. Assess. 2010, 170, 231–244. [Google Scholar] [CrossRef]
- El-Alem, A.; Chokmani, K.; Laurion, I.; El-Adlouni, S.E. Comparative Analysis of four models to estimate chlorophyll-a concentration in case-2 Waters Using moderate resolution imaging spectroradiometer (MODIS) imagery. Remote Sens. 2012, 4, 2373–2400. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Estimation of chlorophyll- a concentration in case II waters using MODIS and MERIS data—Successes and challenges. Environ. Res. Lett. 2009, 4, 045005. [Google Scholar] [CrossRef]
- El-Alem, A.; Chokmani, K.; Laurion, I.; El-Adlouni, S.E.; Raymond, S.; Ratte-Fortin, C. Ensemble-based systems to monitor algal bloom with remote sensing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7955–7971. [Google Scholar] [CrossRef]
- Ferreira, M.S.; Galo, M.D.L.B. Chlorophyll a spatial inference using artificial neural network from multispectral images and in situ measurements. An. Acad. Bras. Ciências 2013, 85, 519–532. [Google Scholar] [CrossRef][Green Version]
- Kown, Y.S.; Baek, S.H.; Lim, Y.K.; Pyo, J.; Ligaray, M.; Park, Y.; Cho, K.H.; Kwon, Y.S. Monitoring coastal chlorophyll-a concentrations in coastal areas using machine learning models. Water 2018, 10, 1020. [Google Scholar] [CrossRef]
- Aguirre-Gómez, R.; Salmerón-García, O.; Gómez-Rodríguez, G.; Peralta-Higuera, A. Use of unmanned aerial vehicles and remote sensors in urban lakes studies in Mexico. Int. J. Remote Sens. 2016, 38, 2771–2779. [Google Scholar] [CrossRef]
- Becker, R.H.; Sayers, M.; Dehm, D.; Shuchman, R.; Quintero, K.; Bosse, K.; Sawtell, R. Unmanned aerial system based spec-troradiometer for monitoring harmful algal blooms: A new paradigm in water quality monitoring. J. Great Lakes Res. 2019, 45, 444–453. [Google Scholar] [CrossRef]
- Flynn, K.F.; Chapra, S.C. Remote Sensing of submerged aquatic vegetation in a shallow non-turbid river using an unmanned aerial vehicle. Remote Sens. 2014, 6, 12815–12836. [Google Scholar] [CrossRef]
- Lyu, P.; Malang, Y.; Liu, H.H.; Lai, J.; Liu, J.; Jiang, B.; Qu, M.; Anderson, S.; Lefebvre, D.D.; Wang, Y. Autonomous cyano-bacterial harmful algal blooms monitoring using multirotor UAS. Int. J. Remote Sens. 2017, 38, 2818–2843. [Google Scholar] [CrossRef]
- Kislik, C.; Dronova, I.; Kelly, M. UAVs in support of algal bloom research: A review of current applications and future op-portunities. Drones 2018, 2, 35. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble based systems in decision making. Circuits and Systems Magazine, IEEE 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Du, P.; Xia, J.; Zhang, W.; Tan, K.; Liu, Y.; Liu, S. Multiple classifier system for remote sensing image classification: A review. Sensors 2012, 12, 4764–4792. [Google Scholar] [CrossRef] [PubMed]
- Feng, W. Investigation of Training Data Issues in Ensemble Classification Based on Margin Concept: Application to Land Cover Mapping. Ph.D. Thesis, Université Michel de Montaigne-Bordeaux III, Bordeaux, France, 2017. [Google Scholar]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Bernacchi, C.J. Hyperspectral leaf reflectance as proxy for photosynthetic capacities: An ensemble approach based on multiple machine learning algorithms. Front. Plant Sci. 2019, 10, 730. [Google Scholar] [CrossRef] [PubMed]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E.; et al. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Kadavi, P.R.; Lee, C.-W.; Lee, S. Application of ensemble-based machine learning models to landslide susceptibility mapping. Remote Sens. 2018, 10, 1252. [Google Scholar] [CrossRef]
- Lv, F.; Han, M.; Qiu, T. Remote sensing image classification based on ensemble extreme learning machine with stacked auto-encoder. IEEE Access 2017, 5, 9021–9031. [Google Scholar] [CrossRef]
- Xia, J.; Du, P.; He, X. MRF-based multiple classifier system for hyperspectral remote sensing image classification. In Proceedings of the Constructive Side-Channel Analysis and Secure Design, Paris, France, 6–8 March 2013; Springer International Publishing: Geneva, Switzerland, 2013; pp. 343–351. [Google Scholar]
- Xiaojuan, L.; Mutao, H.; Jianbao, L. Remote sensing inversion of lake water quality parameters based on ensemble modelling. E3S Web Conf. 2020. [Google Scholar] [CrossRef]
- Xu, M.; Liu, H.; Liu, Y. Multi-predictor ensemble model for river turbidity assessment using landsat 8 imagery at a regional scale. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 4758–4761. [Google Scholar]
- Peterson, K.T.; Sagan, V.; Sidike, P.; Hasenmueller, E.A.; Sloan, J.J.; Knouft, J.H. Machine learning-based ensemble prediction of water-quality variables using feature-level and decision-level fusion with proximal remote sensing. Photogramm. Eng. Remote Sens. 2019, 85, 269–280. [Google Scholar] [CrossRef]
- Blonski, S.; Glasser, G.; Russell, J.; Ryan, R.; Terrie, G.; Zanoni, V. Synthesis of Multispectral Bands from Hyperspectral Data: Validation Based on Images Acquired by AVIRIS, Hyperion, ALI, and ETM+.; NTRS—NASA Technical Reports Server: Washington, DC, USA, 2003. [Google Scholar]
- Moran, M.; Jackson, R.D.; Slater, P.N.; Teillet, P.M. Evaluation of simplified procedures for retrieval of land surface reflectance factors from satellite sensor output. Remote Sens. Environ. 1992, 41, 169–184. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. Image-based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Antal, B.; Hajdu, A. An Ensemble-Based system for microaneurysm detection and diabetic retinopathy grading. IEEE Trans. Biomed. Eng. 2012, 59, 1720–1726. [Google Scholar] [CrossRef]
- Antal, B.; Hajdu, A. An ensemble-based system for automatic screening of diabetic retinopathy. Knowl. Based Syst. 2014, 60, 20–27. [Google Scholar] [CrossRef]
- Eom, J.; Kim, S.; Zhang, B. AptaCDSS-E: A classifier ensemble-based clinical decision support system for cardiovascular disease level prediction. Expert Syst. Appl. 2008, 34, 2465–2479. [Google Scholar] [CrossRef]
- Sun, J.; Li, H. Financial distress prediction using support vector machines: Ensemble vs. individual. Appl. Soft Comput. 2012, 12, 2254–2265. [Google Scholar] [CrossRef]
- West, D.; Dellana, S.; Qian, J. Neural network ensemble strategies for financial decision applications. Comput. Oper. Res. 2005, 32, 2543–2559. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. An intelligent-agent-based fuzzy group decision making model for financial multicriteria decision support: The case of credit scoring. Eur. J. Oper. Res. 2009, 195, 942–959. [Google Scholar] [CrossRef]
- Chorus, I.; Bartram, J. Toxic Cyanobacteria in Water: A Guide to Their Public Health Consequences, Monitoring and Management; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Cairo, C.; Barbosa, C.; Lobo, F.; Novo, E.; Carlos, F.; Maciel, D.; Júnior, R.F.; Silva, E.; Curtarelli, V. Hybrid chlorophyll-a algorithm for assessing trophic states of a tropical brazilian reservoir based on msi/sentinel-2 data. Remote Sens. 2019, 12, 40. [Google Scholar] [CrossRef]
- Shi, K.; Li, Y.; Li, L.; Lu, H.; Song, K.; Liu, Z.; Xu, Y.; Li, Z. Remote chlorophyll-a estimates for inland waters based on a cluster-based classification. Sci. Total. Environ. 2013, 444, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Yang, W.; Matsushita, B.; Li, R.; Oyama, Y.; Fukushima, T. Remote Estimation of Chlorophyll-a in inland waters by a nir-red-based algorithm: Validation in Asian lakes. Remote Sens. 2014, 6, 3492–3510. [Google Scholar] [CrossRef]
- El-Alem, A.; Chokmani, K.; Laurion, I.; El-Adlouni, S.E. An ensemble based system for Chlorophyll-a estimation using MODIS imagery over Southern Quebec inland waters. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, IGARSS 2014, Quebec City, QC, Canada, 13–8 July 2014; pp. 3878–3881. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification Regression Trees; Auerbach Publications: Boca Raton, FL, USA, 2017. [Google Scholar]
- Alpak, F.O.; Vink, J.C.; Gao, G.; Mo, W. Techniques for effective simulation, optimization, and uncertainty quantification of the in-situ upgrading process. J. Unconv. Oil Gas Resour. 2013, 3–4, 1–14. [Google Scholar] [CrossRef]
- Tørvi, H.; Hertzberg, T. Estimation of uncertainty in dynamic simulation results. Comput. Chem. Eng. 1997, 21, S181–S185. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of chl-a concentration in turbid productive waters—Return to a simple two-band NIR-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- El-Alem, A.; Chokmani, K.; Laurion, I.; El-Adlouni, S.E. An adaptive model to monitor chlorophyll-a in inland waters in southern quebec using downscaled modis imagery. Remote Sens. 2014, 6, 6446–6471. [Google Scholar] [CrossRef]







| Lakes | chl_a (µg L−1) Avrg ± Std (Min − Max) | Pheo_a (µg L−1) Avrg ± Std (Min − Max) | SDD (m) Avrg ± Std (Min − Max) | DOC (µg L−1) Avrg ± Std (Min − Max) | TP (µg P/L) | TN (mg N/L) | |
|---|---|---|---|---|---|---|---|
| FC 1 | CL | 34.2 ± 4.7 (26.0 − 44.8) | 7.7 ± 0.8 (5.9 − 8.9) | 1.2 ± 0.1 (1.1 − 1.4) | 6.9 ± 1.7 (5.6 − 9.5) | 46 | 0.806 |
| BL | 3.4 ± 0.3 (2.8 − 4.3) | 1.0 ± 0.1 (0.9 − 1.2) | 4.2 ± 1.7 (1.9 − 2.2) | 3.7 ± 0.9 (3 − 4.9) | 23 | 0.409 | |
| ML | 3.4 ± 0.4 (2.8 − 4.2) | 0.7 ± 0.1 (0.6 − 0.9) | 3.6 ± 0.2 (3.2 − 4.3) | 4.4 ± 1.5 (3.4 − 7.1) | 13 | 0.330 | |
| FC 2 | CL | 61.8 ± 8.5 (38.6 − 77.0) | 19.7 ± 5.4 (11.0 − 27.5) | 0.8 ± 0.1 (0.7 − 0.9) | 4.8 ± 0.2 (4.5 − 5.2) | 66 | 0.957 |
| BL | 17.1 ± 1.3 (14.6 − 20.6) | 1.1 ± 0.5 (0.1 − 1.8) | 1.5 ± 0.1 (1.0 − 1.7) | 3.2 ± 0.1 (3.1 − 3.3) | 18 | 0.425 | |
| ML | 2.5 ± 0.2 (2.2 − 2.9) | 0.5 ± 0.2 (0.3 − 0.9) | 3.1 ± 0.2 (2.7 − 3.2) | 3.3 ± 0.1 (3.3 − 3.5) | 10 | 0.279 |
| Years | chl_a (µg L−1) Avrg ± Std (Min − Max) | Number of Samples | Number of Images | |
|---|---|---|---|---|
| VLMN | 2015 | 0 ± 0 (0 − 0) | 0 | 0 |
| 2016 | 3.4 ± 2.3 (0.9 − 10.8) | 32 | 16 | |
| 2017 | 4.4 ± 5.9 (0.7 − 41.8) | 62 | 9 | |
| Total | 4.1 ± 5.1 (0.7 − 41.8) | 94 | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Alem, A.; Chokmani, K.; Venkatesan, A.; Rachid, L.; Agili, H.; Dedieu, J.-P. How Accurate Is an Unmanned Aerial Vehicle Data-Based Model Applied on Satellite Imagery for Chlorophyll-a Estimation in Freshwater Bodies? Remote Sens. 2021, 13, 1134. https://doi.org/10.3390/rs13061134
El-Alem A, Chokmani K, Venkatesan A, Rachid L, Agili H, Dedieu J-P. How Accurate Is an Unmanned Aerial Vehicle Data-Based Model Applied on Satellite Imagery for Chlorophyll-a Estimation in Freshwater Bodies? Remote Sensing. 2021; 13(6):1134. https://doi.org/10.3390/rs13061134
Chicago/Turabian StyleEl-Alem, Anas, Karem Chokmani, Aarthi Venkatesan, Lhissou Rachid, Hachem Agili, and Jean-Pierre Dedieu. 2021. "How Accurate Is an Unmanned Aerial Vehicle Data-Based Model Applied on Satellite Imagery for Chlorophyll-a Estimation in Freshwater Bodies?" Remote Sensing 13, no. 6: 1134. https://doi.org/10.3390/rs13061134
APA StyleEl-Alem, A., Chokmani, K., Venkatesan, A., Rachid, L., Agili, H., & Dedieu, J.-P. (2021). How Accurate Is an Unmanned Aerial Vehicle Data-Based Model Applied on Satellite Imagery for Chlorophyll-a Estimation in Freshwater Bodies? Remote Sensing, 13(6), 1134. https://doi.org/10.3390/rs13061134