Beamforming of LOFAR Radio-Telescope for Passive Radiolocation Purposes
Abstract
:1. Introduction
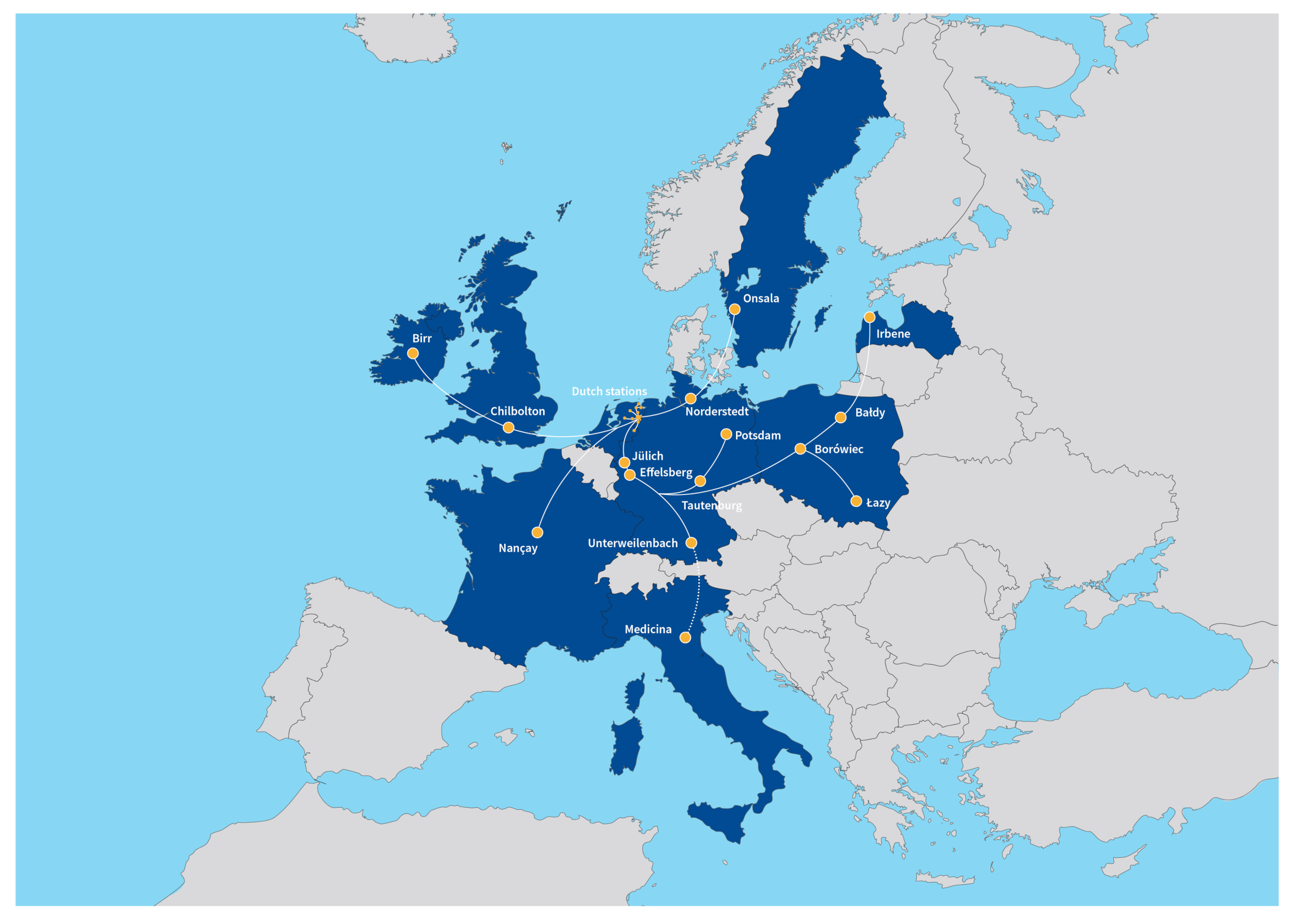
2. LOFAR Antennas as Sensors of Passive Radiolocation System
2.1. LOFAR Station Array
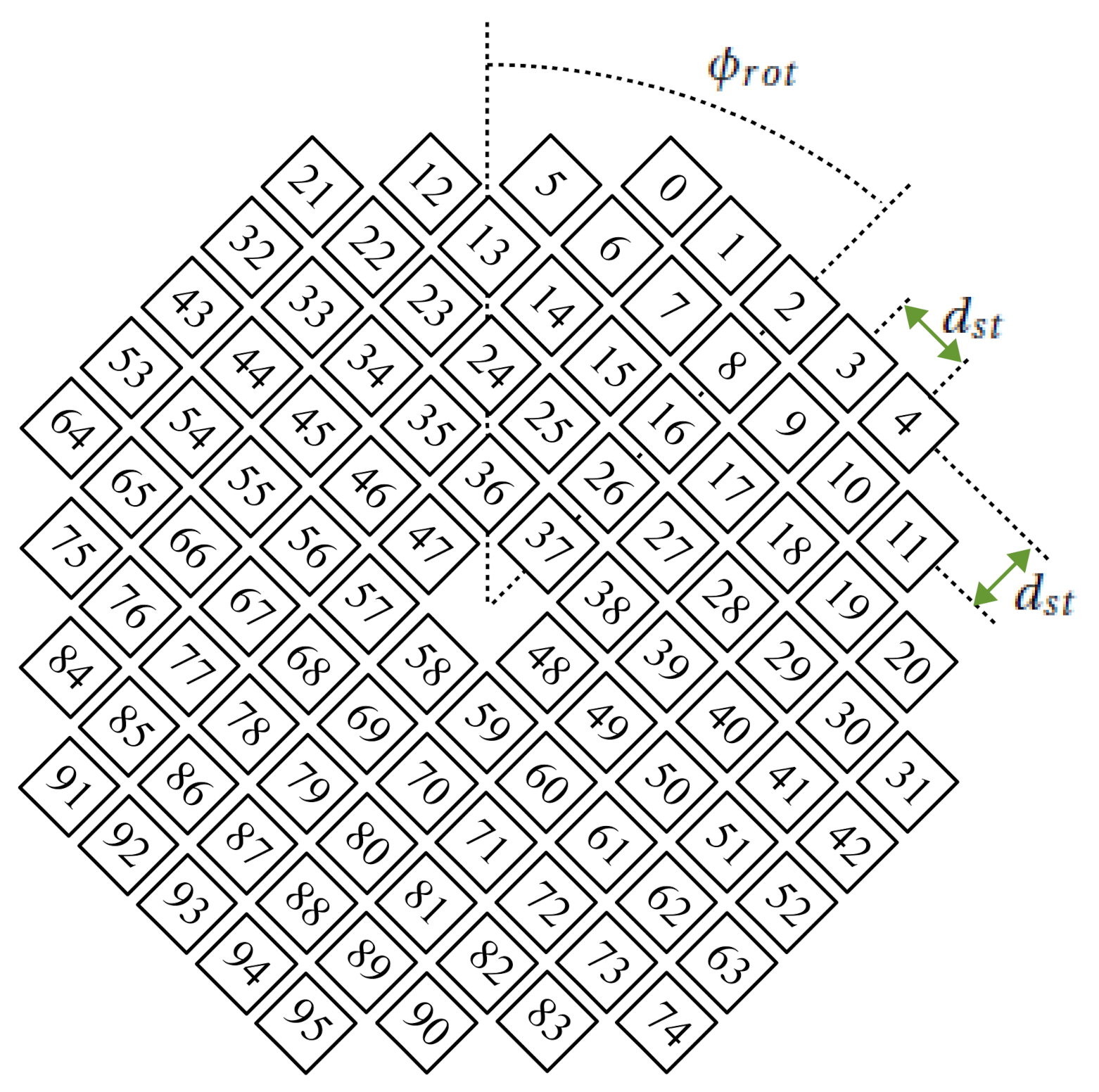
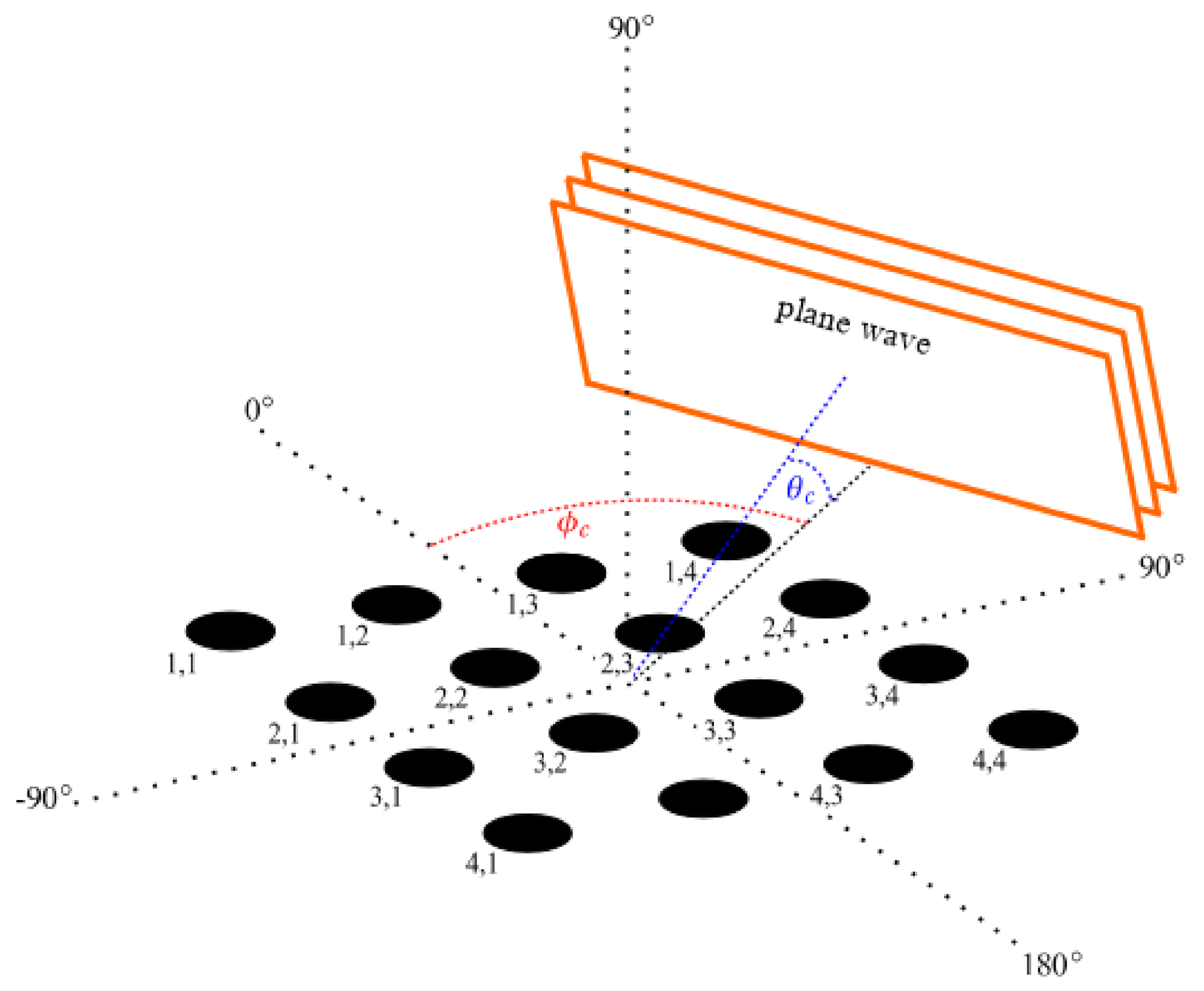
2.2. LOFAR Tile Subarray
3. Beamforming of LOFAR for Passive Coherent Location
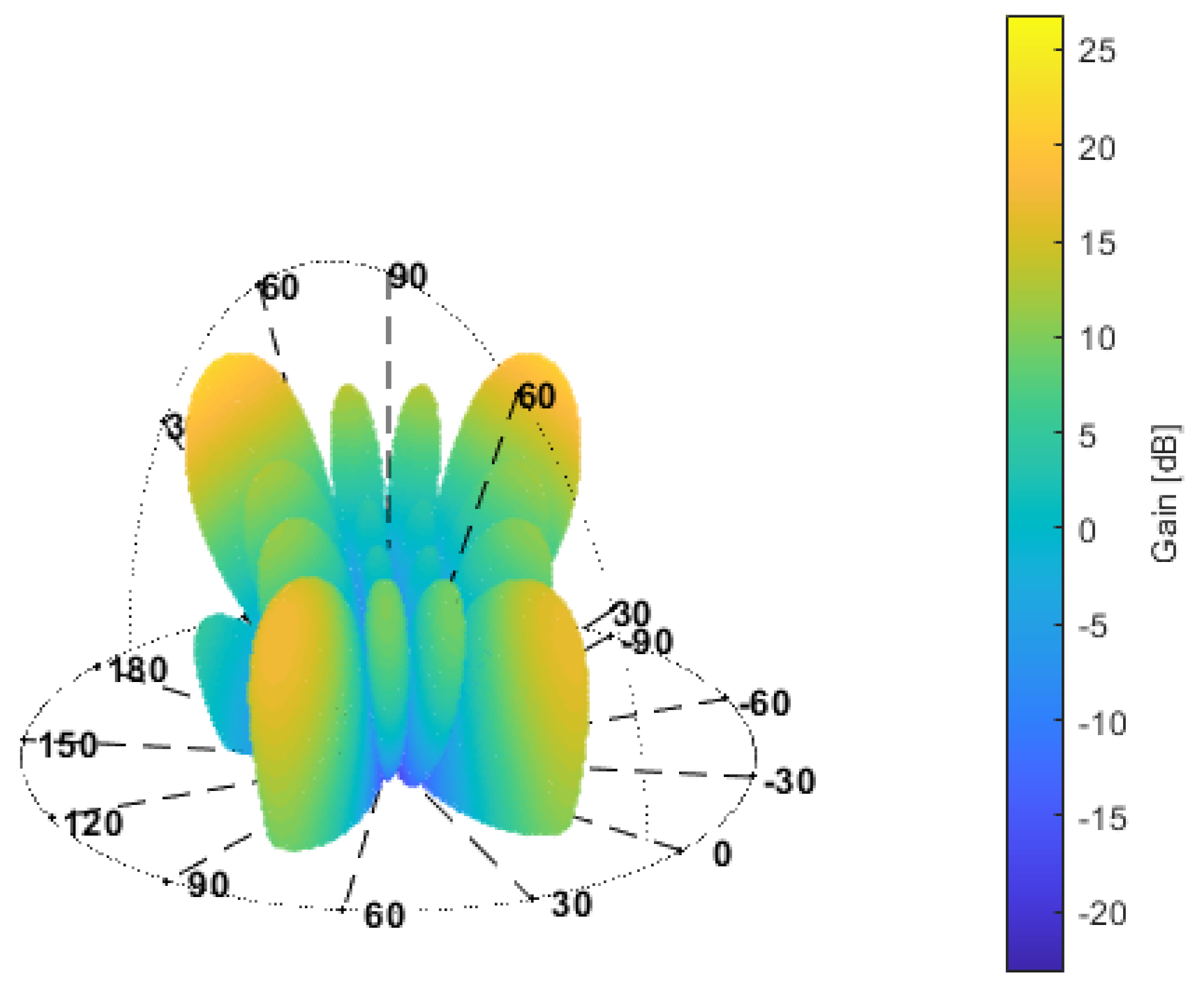
3.1. Single HBA
3.2. Single LOFAR Tile
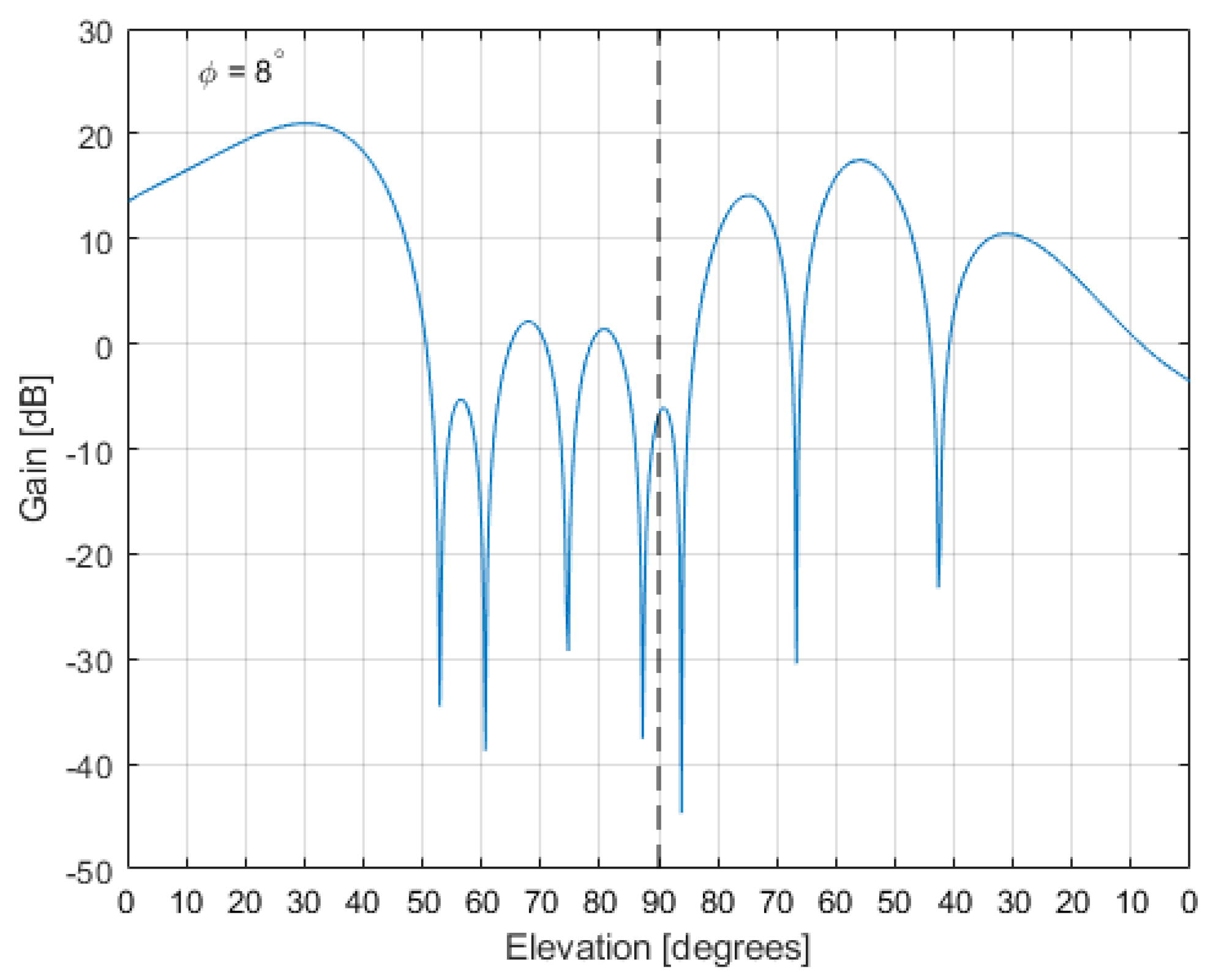
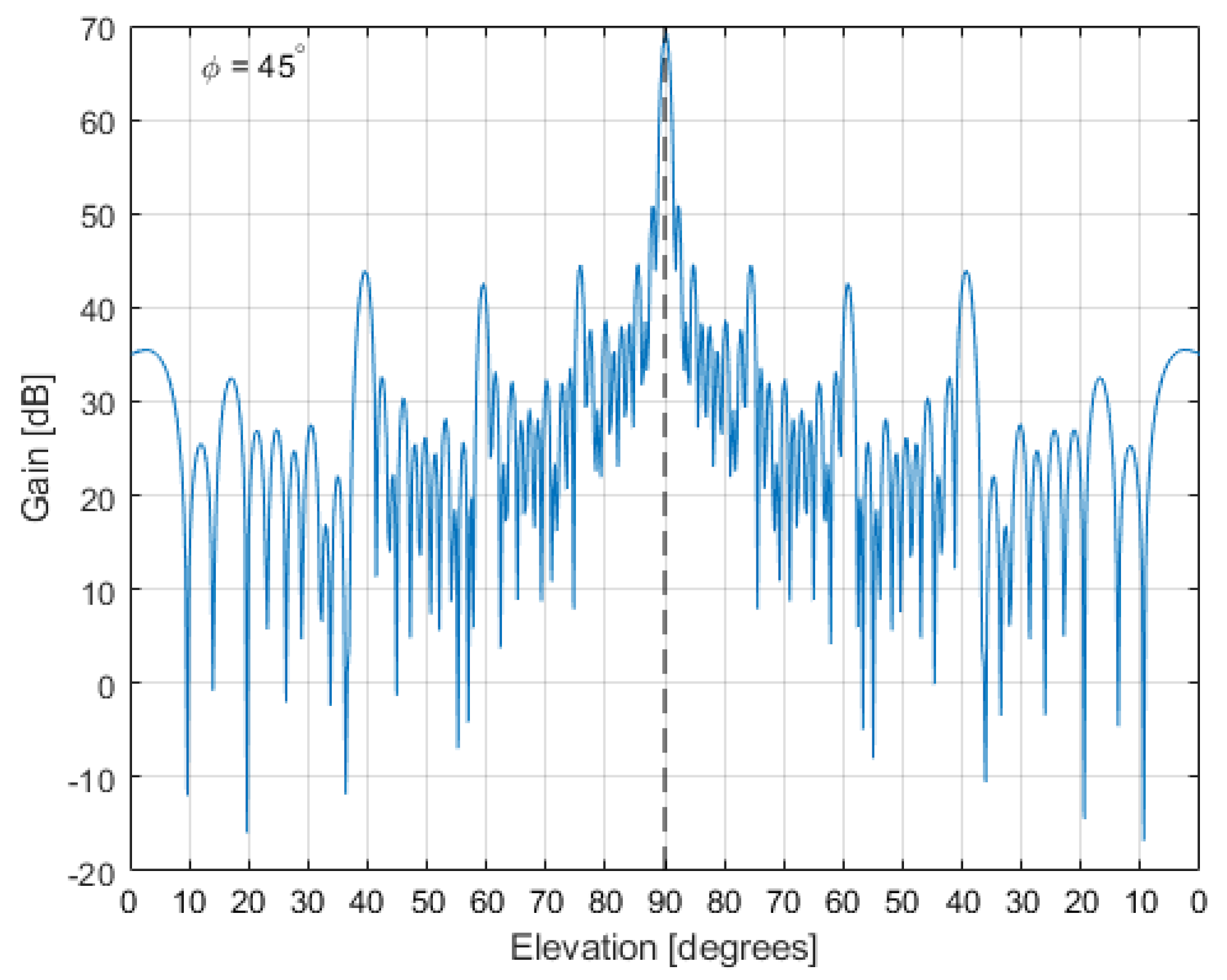
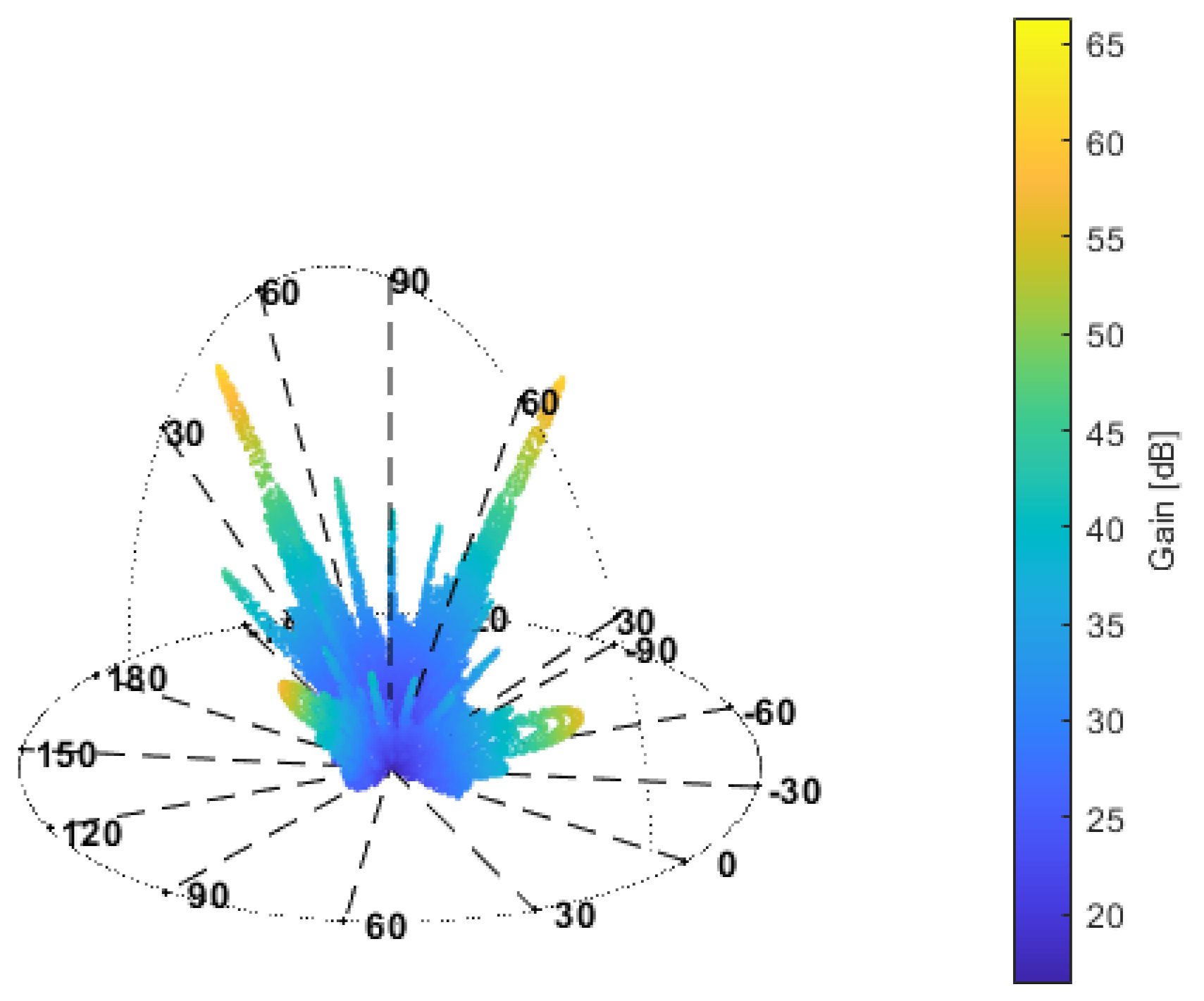
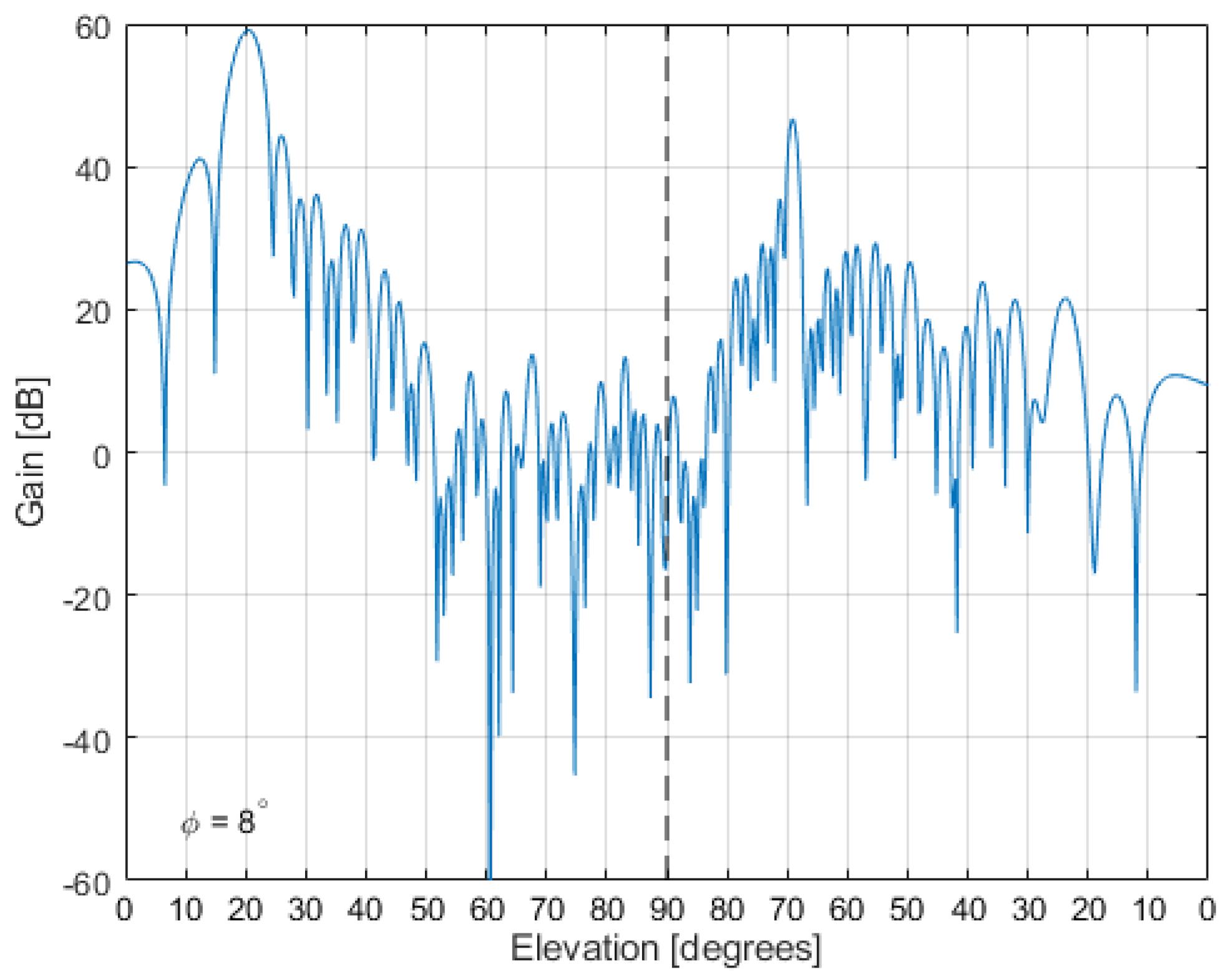
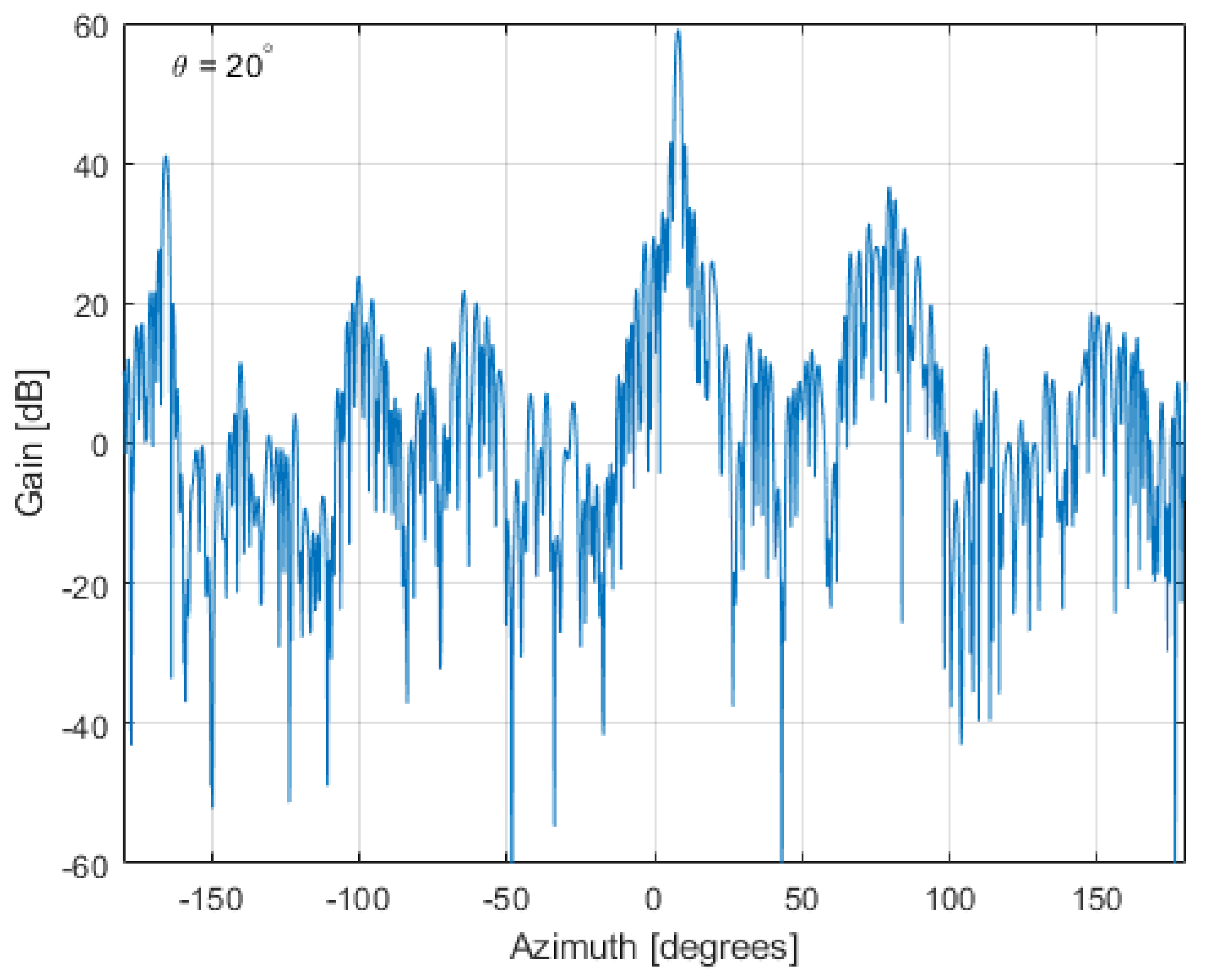
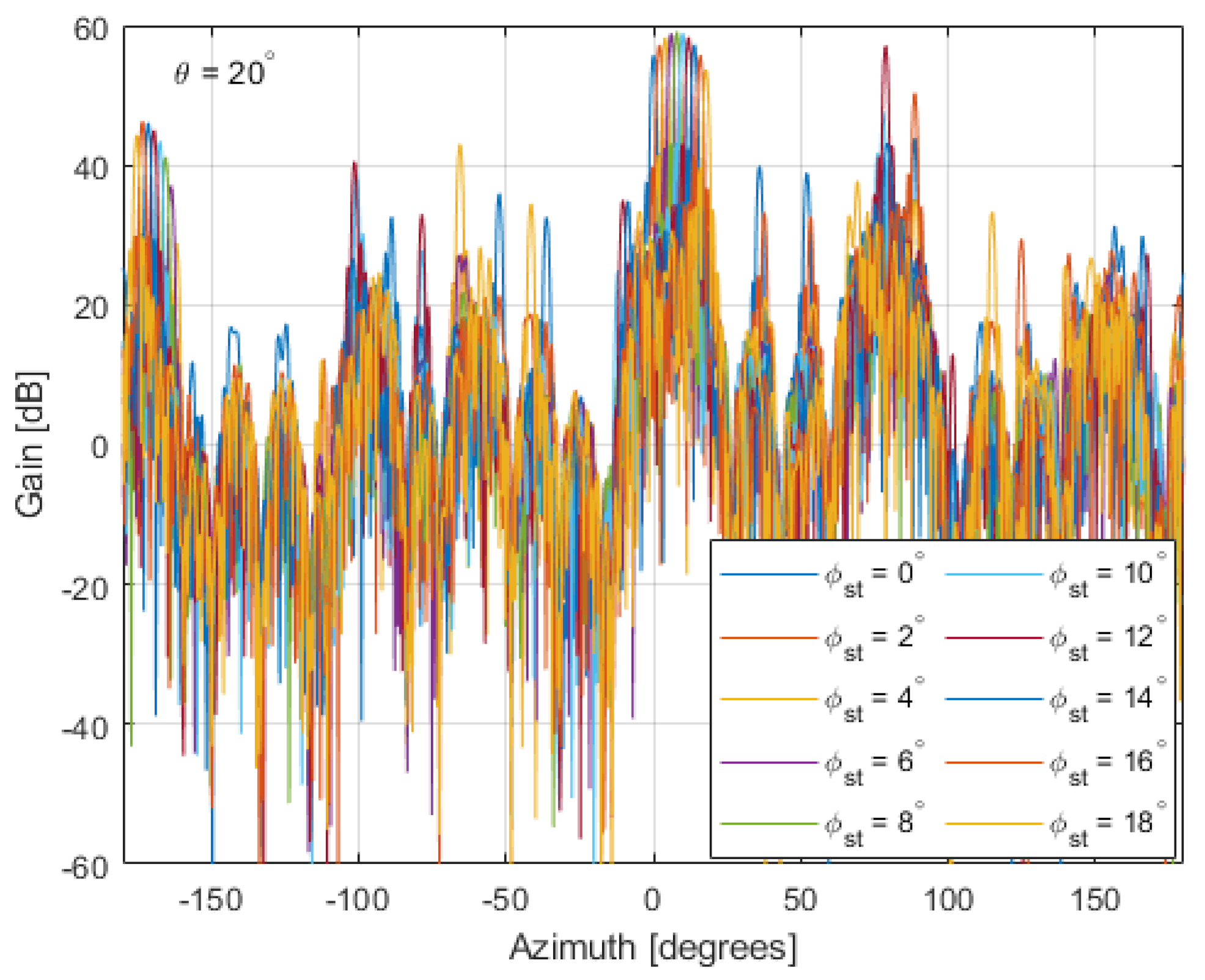
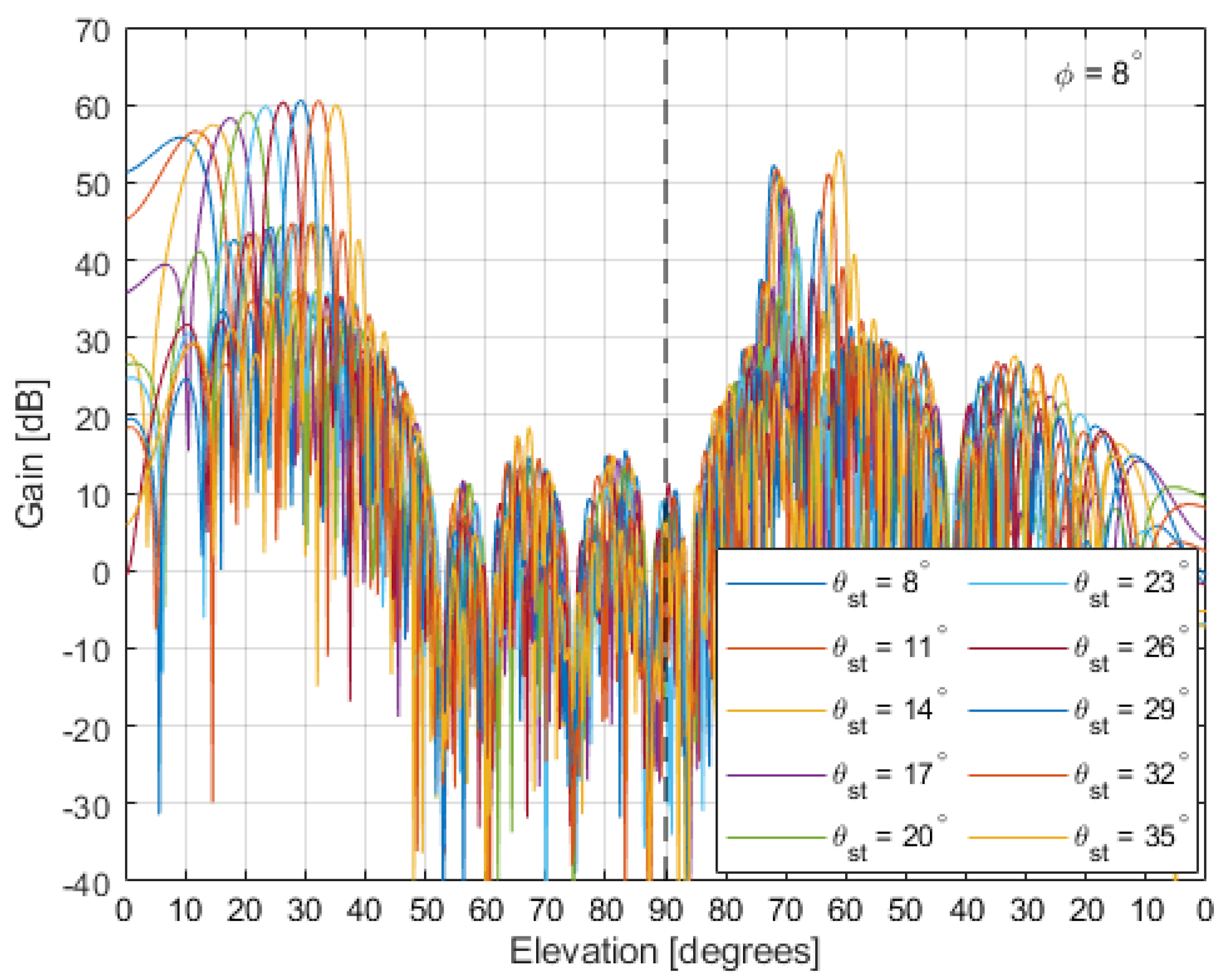
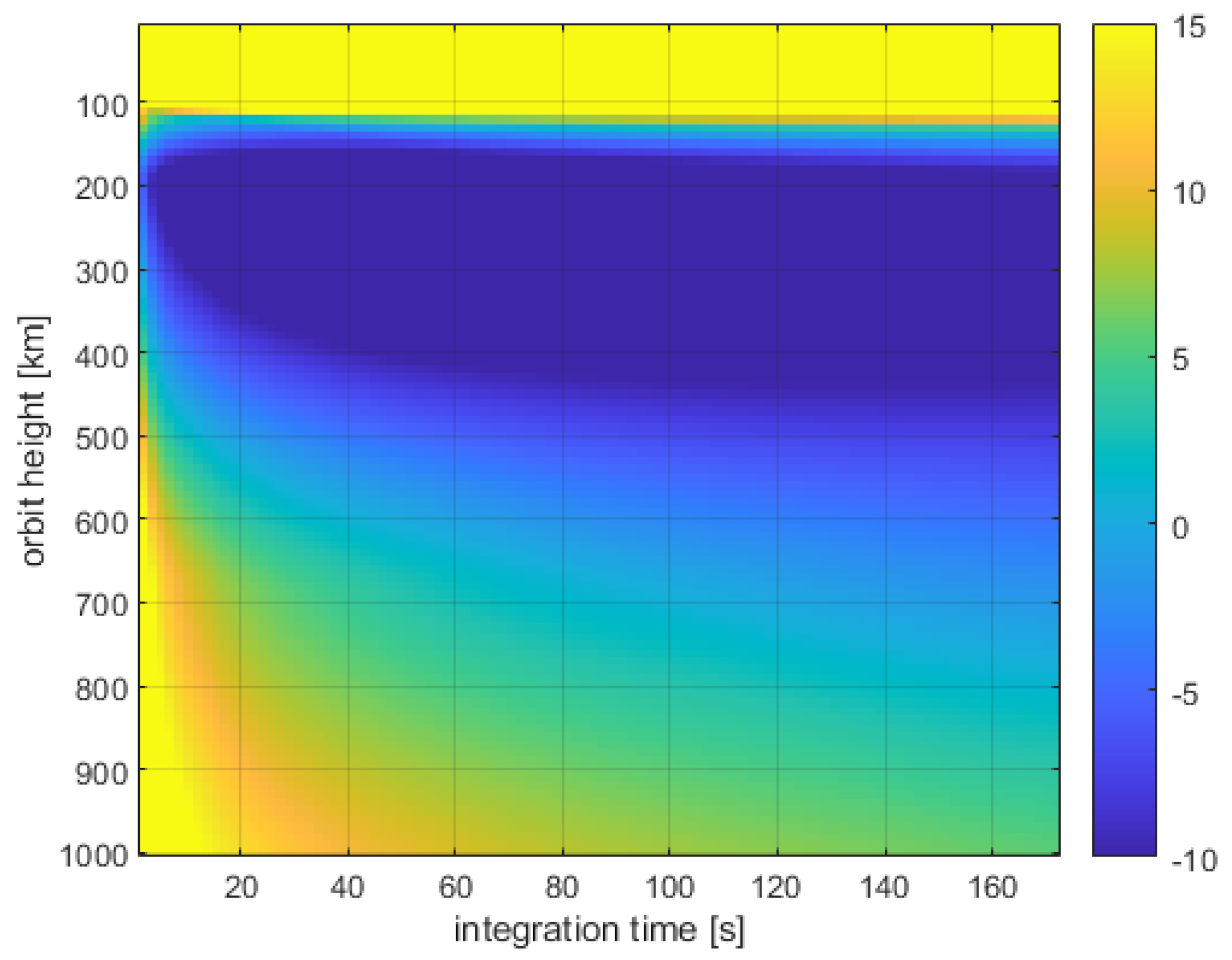
3.3. LOFAR Station
4. Experiment with Real Signals
4.1. Description of the Experiment
4.2. Results of the Experiment
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LOFAR | Low-Frequency Array for radio astronomy |
| PCL | Passive coherent location |
| ASTRON | the Netherlands Institute for Radio Astronomy |
| LBA | Low Band Antennas |
| HBA | High Band Antennas |
| DAB | Digital Audio Broadcasting |
| VHF | Very high frequency |
| DVB-T | Digital Video Broadcasting–Terrestrial |
| FM | Frequency modulation |
| SNR | Signal-to-Noise Ratio |
| CFAR | Constant False Alarm Rate |
| URA | Uniform Rectangular Array |
| LMT | Local Mean Time |
| SFN | Single Frequency Network |
| CAF | Cross-Ambiguity Function |
| CPI | Coherent Processing Time |
| TBB | Transient Buffer Board |
References
- Heald, G.; McKean, J.; Pizzo, R. Low Frequency Radio Astronomy and the LOFAR Observatory, Lectures from the Third LOFAR Data Processing School Editors; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Dąbrowski, B.P.; Krankowski, A.; Błaszkiewicz, L.; Rothkaehl, H. Prospects for solar and space weather research with polish part of the LOFAR telescope. Acta Geophys. 2016, 64, 825–840. [Google Scholar] [CrossRef]
- Droszcz, A.; Kłos, J.; Jędrzejewski, K.; Kulpa, K.; Pożoga, M. Beamforming of LOFAR radio telescope antennas used as sensors in passive radiolocation system. In Proceedings of the 2020 21st International Radar Symposium (IRS), Warsaw, Poland, 5–8 October 2020; IEEE: New York, NY, USA, 2020; pp. 323–327. [Google Scholar]
- Kłos, J.; Droszcz, A.; Jędrzejewski, K.; Kulpa, K.; Pożoga, M. On the possibility of using LOFAR radio telescope for passive radiolocation. In Proceedings of the 2020 21st International Radar Symposium (IRS), Warsaw, Poland, 5–8 October 2020; IEEE: New York, NY, USA, 2020; pp. 73–76. [Google Scholar]
- Virtanen, I.I. Station Data Cookbook. Available online: https://lofar.ie/wp-content/uploads/2018/03/station_data_cookbook_v1.2.pdf (accessed on 25 October 2020).
- Griffiths, H. Bistatic and Multistatic Radar; IEE Military Radar Seminar: Shrivenham, UK, 2004. [Google Scholar]
- Griffiths, H.; Baker, C. An Introduction to Passive Radar; Artech House radar library, Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Malanowski, M. Signal Processing for Passive Bistatic Radar; Artech House radar library, Artech House: Norwood, MA, USA, 2019. [Google Scholar]
- Richards, M.A.; Scheer, J.; Holm, W.A.; Melvin, W.L. Principles of Modern Radar; Scitech Publishing: Edison, NJ, USA, 2010. [Google Scholar]
- WorldDAB Global Summary. Available online: https://www.worlddab.org/public_document/file/916/Global_Summary_30.08.17.pdf (accessed on 25 October 2020).
- Mucci, R. A comparison of efficient beamforming algorithms. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 548–558. [Google Scholar] [CrossRef]
- Zimmerman, N. Analysis of LOFAR High Band Antenna Design. Available online: https://www.haystack.mit.edu/edu/reu/2003/files/neil/neil.pdf (accessed on 25 October 2020).
- Van Trees, H. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Malanowski, M.; Kulpa, K. Two Methods for Target Localization in Multistatic Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 572–580. [Google Scholar] [CrossRef]
- Malanowski, M.; Kulpa, K.; Suchozebrski, R. Two-stage tracking algorithm for passive radar. In Proceedings of the 2009 12th International Conference on Information Fusion, Seatle, WA, USA, 6–9 July 2009; pp. 1800–1806. [Google Scholar]
- Wielgo, M.; Rzewuski, S.; Misiurewicz, J.; Kurowska, A.; Malanowski, M. Multistatic tracking experiment with a WiFiRAD passive radar. In Proceedings of the 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 629–635. [Google Scholar]
- Cao, D.; Li, T.; Kang, P.; Liu, H.; Zhou, S.; Su, H. Single-pulse multi-beams operation of phased array radar. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar]
- Tonnaer, A. Dual axis multi-beam radars. In Proceedings of the 2013 International Conference on Radar, Adelaide, SA, Australia, 9–12 September 2013; pp. 412–416. [Google Scholar]
- Cox, P.B.; van Rossum, W.L. Analysing Multibeam, Cooperative, Ground Based Radar in a Bistatic Configuration. In Proceedings of the 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 27 April–1 May 2020; pp. 912–917. [Google Scholar]
- Malanowski, M.; Kulpa, K.S.; Samczynski, P.; Misiurewicz, J.; Kulpa, J. Long range FM-based passive radar. In Proceedings of the IET International Conference on Radar Systems (Radar 2012), Glasgow, UK, 22–25 October 2012; pp. 1–4. [Google Scholar]
- Kulpa, K.S.; Misiurewicz, J. Stretch Processing for Long Integration Time Passive Covert Radar. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Flightradar24. Available online: https://www.flightradar24.com (accessed on 21 January 2020).
- Malanowski, M.; Kulpa, K. Correction of range cell migration with FIR filter for passive radar. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; IEEE: New York, NY, USA, 2018; pp. 1123–1128. [Google Scholar]
- Kulpa, K. Adaptive clutter rejection in bi-static CW radar. In Proceedings of the 2004 International Radar Symposium, Warsaw, Poland, 17-21 May 2004; pp. 61–66. [Google Scholar]
- Malanowski, M. Comparison of adaptive methods for clutter removal in PCL radar. In Proceedings of the 2006 International Radar Symposium, Krakow, Poland, 24–26 May 2006; pp. 1–4. [Google Scholar]
- Kulpa, K. Simple sea clutter canceller for noise radar. In Proceedings of the International Radar Symposium, Krakow, Poland, 24–26 May 2006; pp. 299–302. [Google Scholar]
- Kulpa, K. The CLEAN type algorithms for radar signal processing. In Proceedings of the 2008 Microwaves, Radar and Remote Sensing Symposium, Kiev, Ukraine, 22–24 September 2008; IEEE: New York, NY, USA, 2008; pp. 152–157. [Google Scholar]
- Kulpa, K. Signal Processing in Noise Waveform Radar; Artech House radar library, Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Misiurewicz, J. Resampling methods for stretch processing in PCL radars. Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2007. Int. Soc. Opt. Photonics 2007, 6937, 693733. [Google Scholar]
- Kulpa, K.; Czekała, Z. Masking effect and its removal in PCL radar. IEE Proc. Radar Sonar Navig. 2005, 152, 174–178. [Google Scholar] [CrossRef]






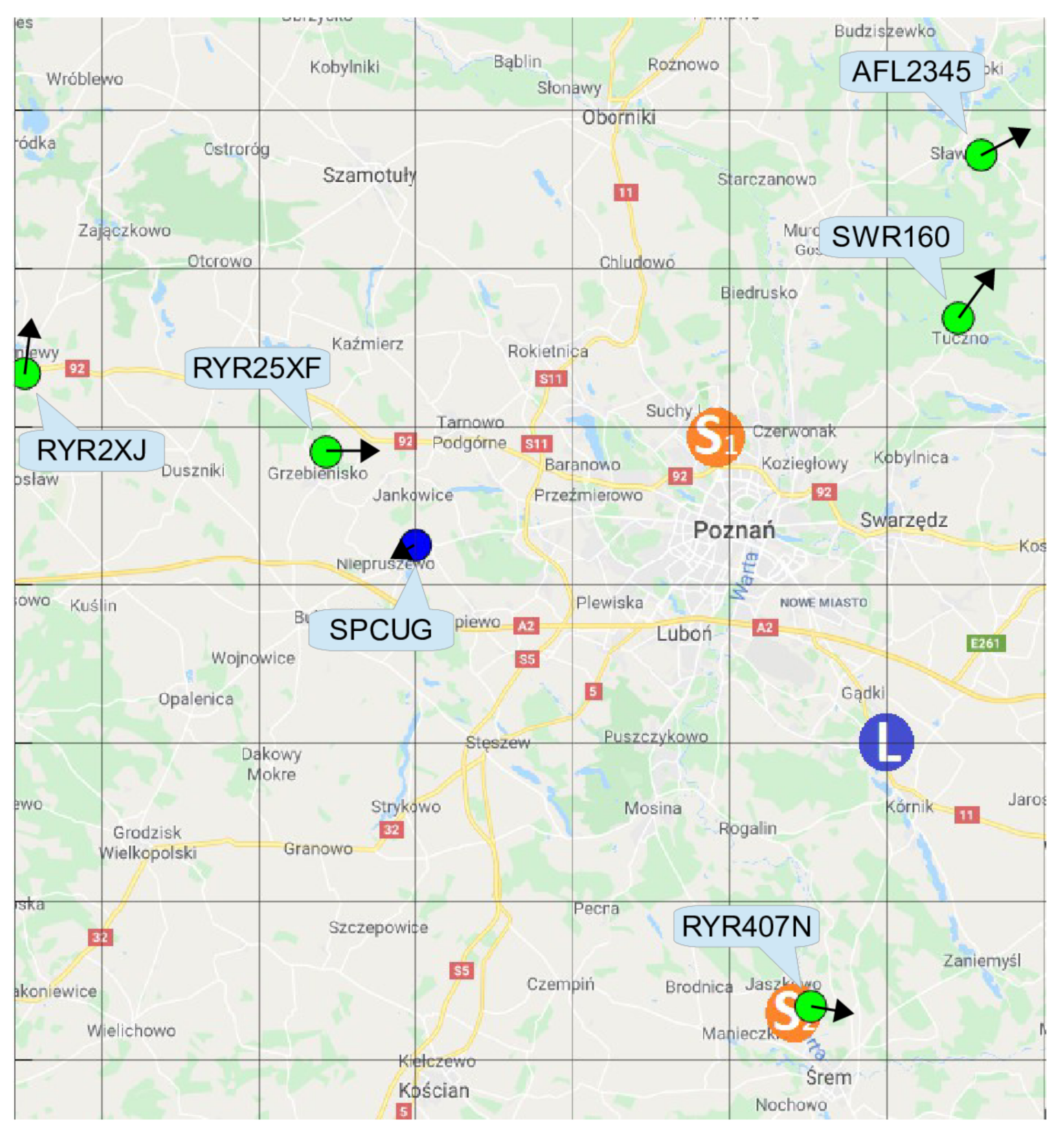
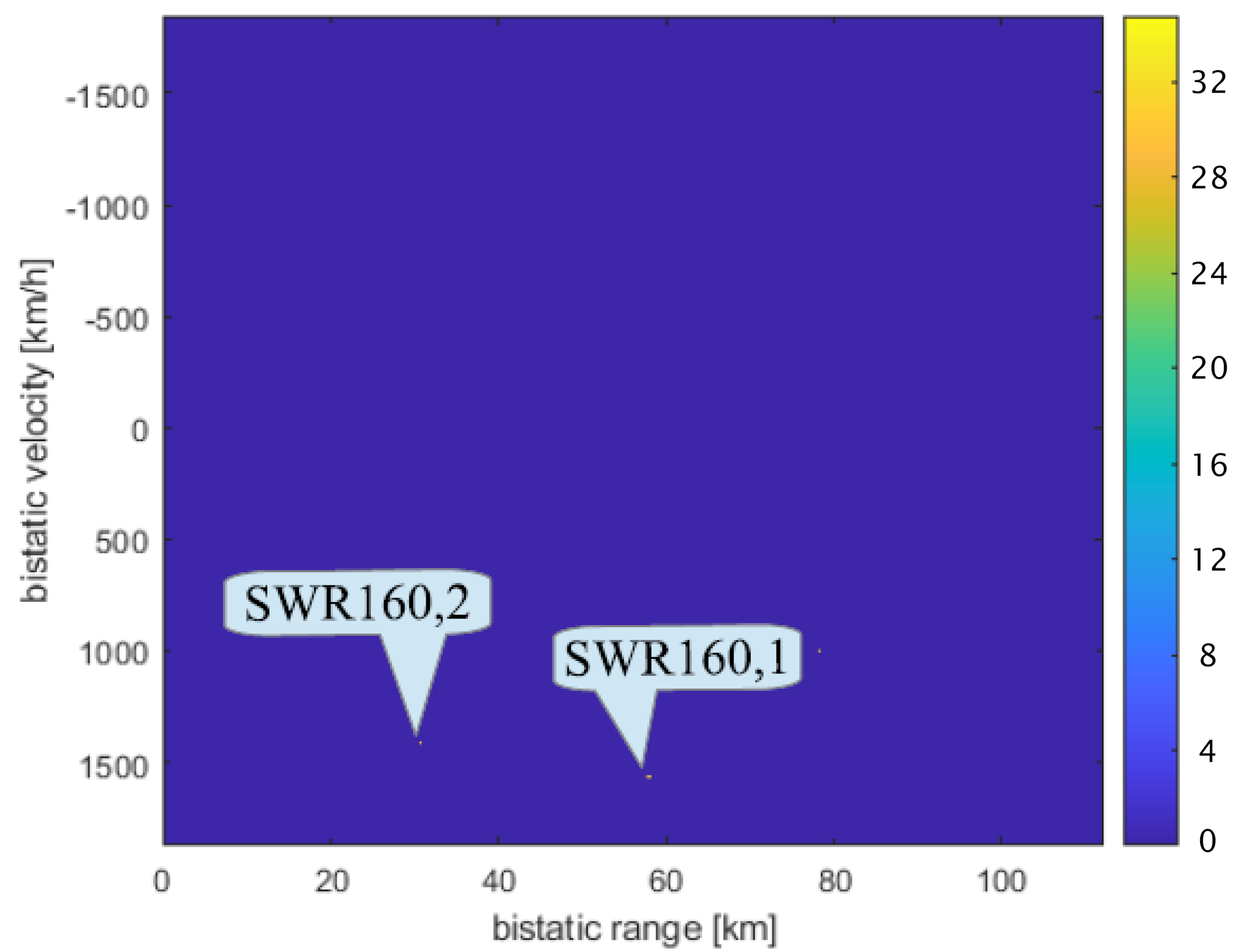
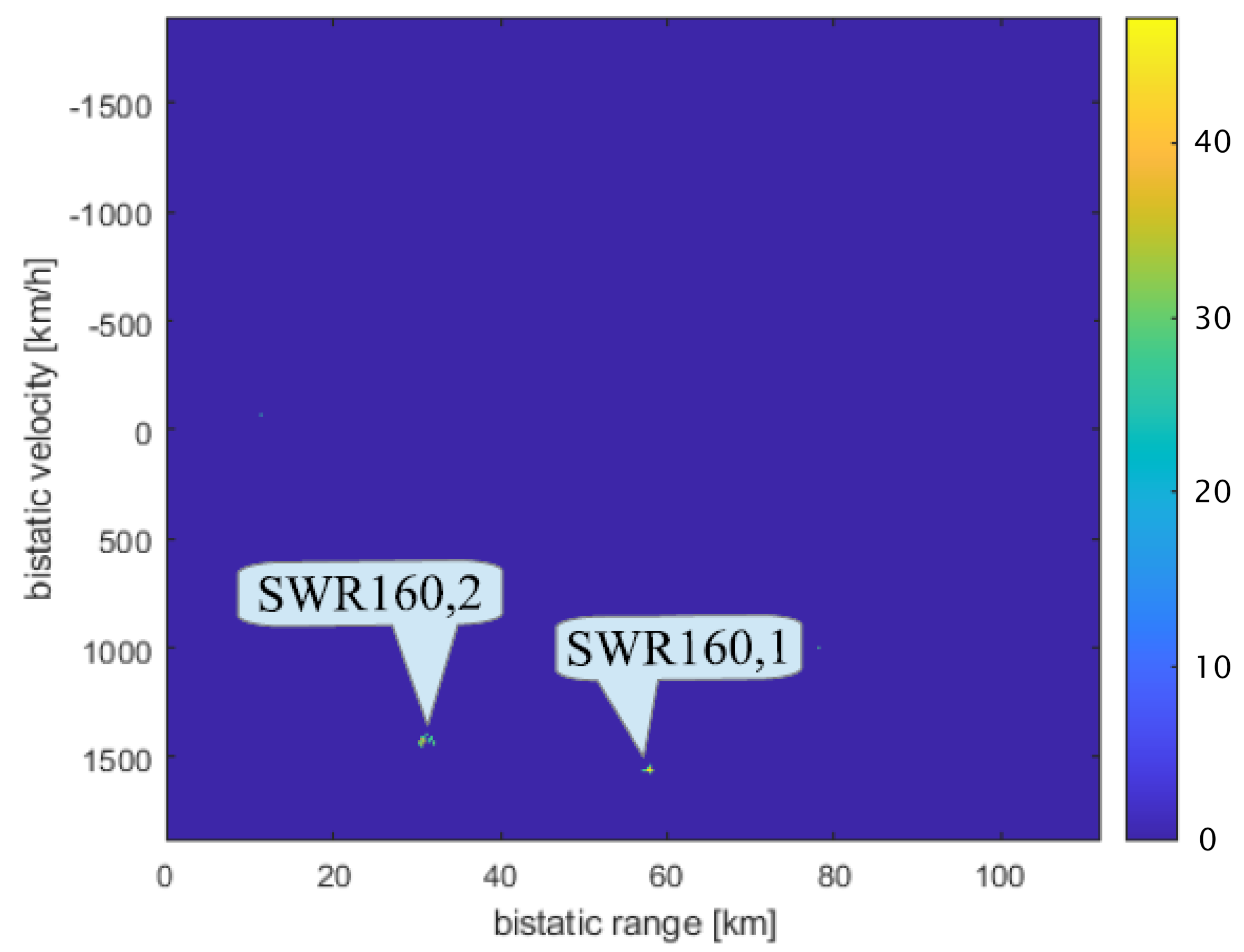
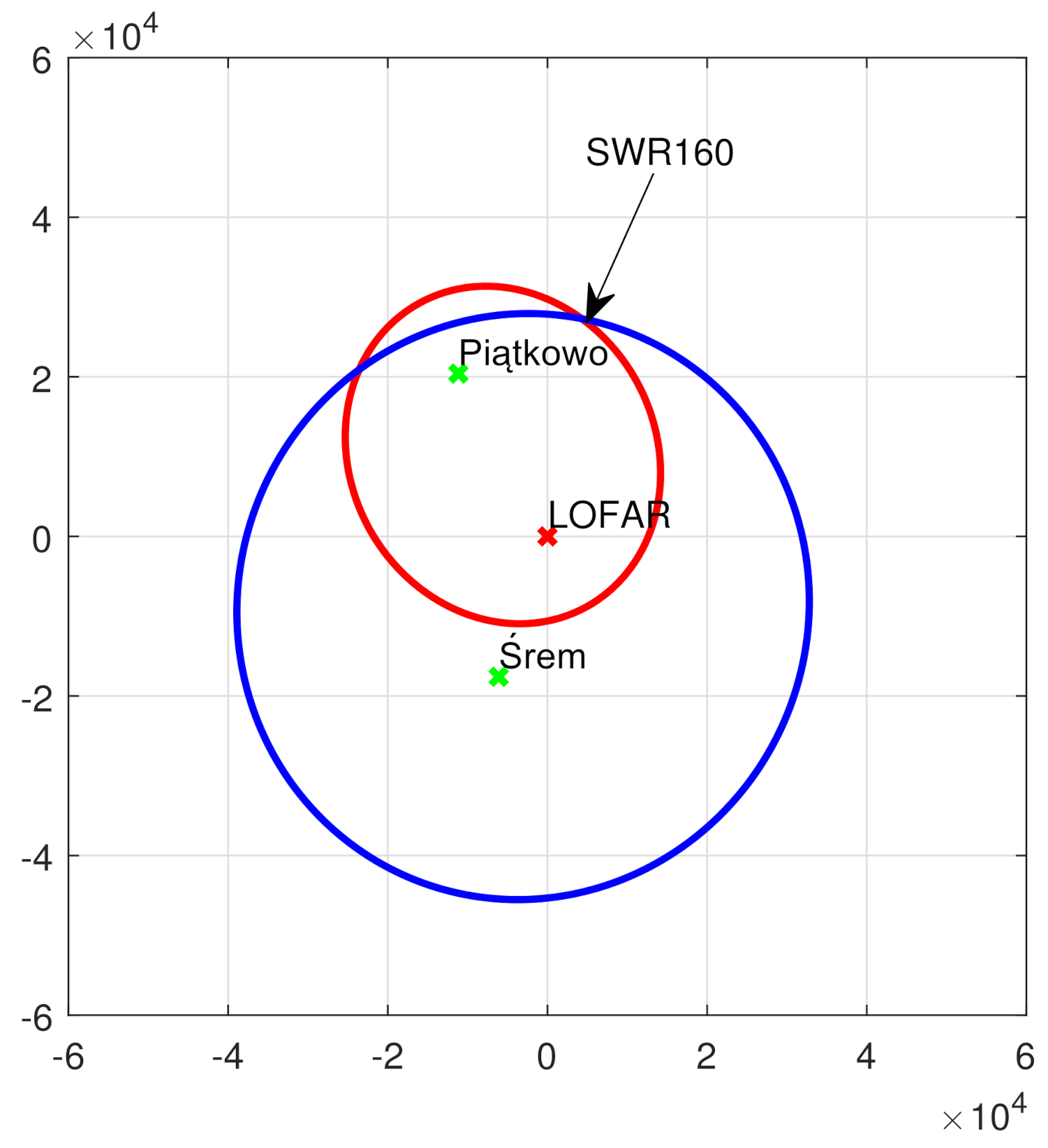
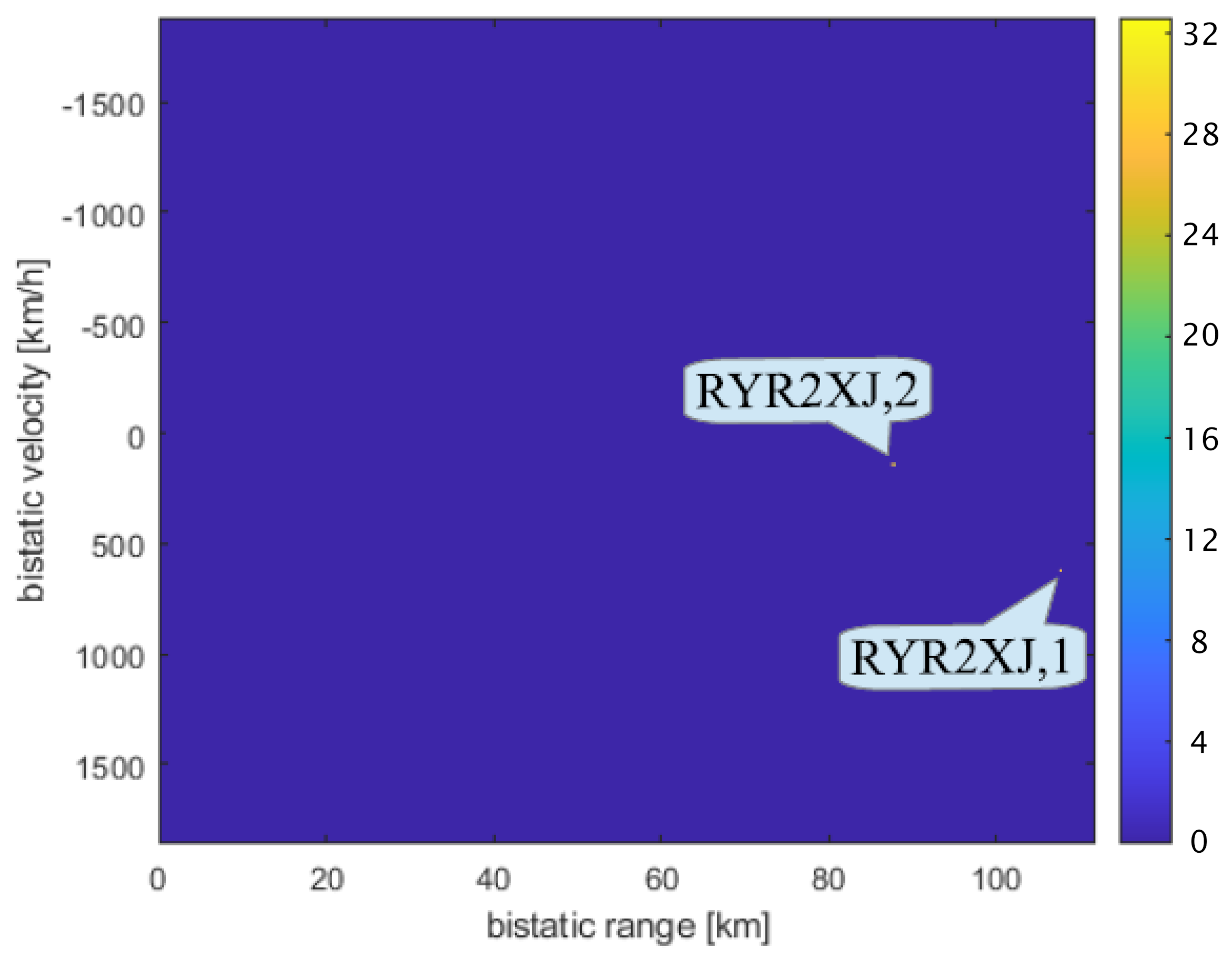
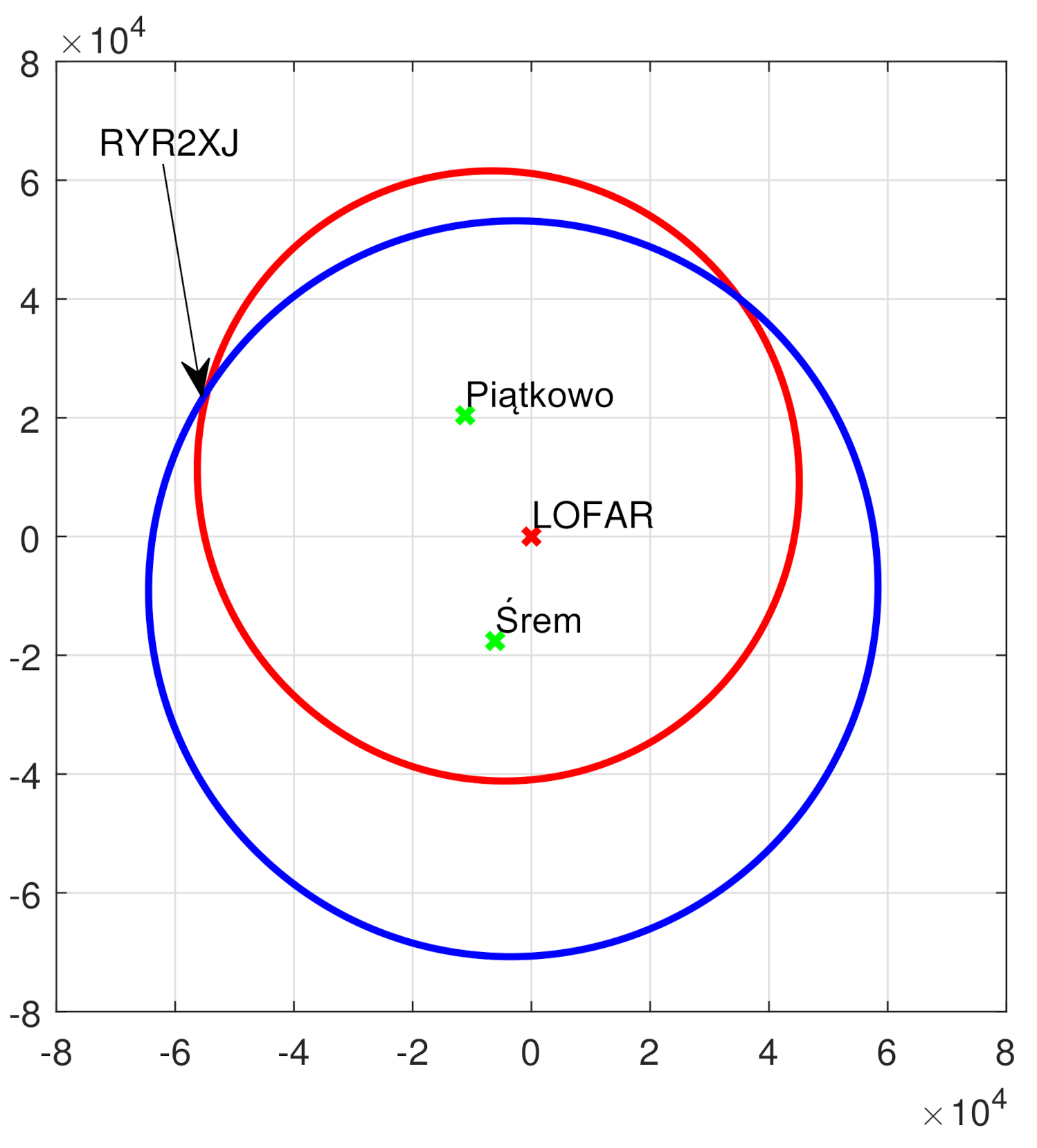
| Transmitter | [km] | [km] | [km/h] | [km/h] |
|---|---|---|---|---|
| Srem | 57.2 | 57.9 | 1565 | 1561 |
| Piatkowo | 25.5 | 25.8 | 1418 | 1423 |
| Plane | [km] | [km] | [] | [] |
|---|---|---|---|---|
| SWR160 | 27.2 | 27.6 | 8.9 | 9.7 |
| Transmitter | [km] | [km] | [km/h] | [km/h] |
|---|---|---|---|---|
| Srem | 107.2 | 107.6 | 637 | 626 |
| Piatkowo | 83.1 | 82.9 | 146 | 145 |
| Plane | [km] | [km] | [] | [] |
|---|---|---|---|---|
| RYR2XJ | 59.7 | 59.6 | −67.0 | −65.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Droszcz, A.; Jędrzejewski, K.; Kłos, J.; Kulpa, K.; Pożoga, M. Beamforming of LOFAR Radio-Telescope for Passive Radiolocation Purposes. Remote Sens. 2021, 13, 810. https://doi.org/10.3390/rs13040810
Droszcz A, Jędrzejewski K, Kłos J, Kulpa K, Pożoga M. Beamforming of LOFAR Radio-Telescope for Passive Radiolocation Purposes. Remote Sensing. 2021; 13(4):810. https://doi.org/10.3390/rs13040810
Chicago/Turabian StyleDroszcz, Aleksander, Konrad Jędrzejewski, Julia Kłos, Krzysztof Kulpa, and Mariusz Pożoga. 2021. "Beamforming of LOFAR Radio-Telescope for Passive Radiolocation Purposes" Remote Sensing 13, no. 4: 810. https://doi.org/10.3390/rs13040810
APA StyleDroszcz, A., Jędrzejewski, K., Kłos, J., Kulpa, K., & Pożoga, M. (2021). Beamforming of LOFAR Radio-Telescope for Passive Radiolocation Purposes. Remote Sensing, 13(4), 810. https://doi.org/10.3390/rs13040810








