Abstract
The electronic receivers of global navigation satellite systems (GNSSs) are implemented in various handheld electronic devices such as laptops, smartphones, and smartwatches; therefore, their dimensions are of critical importance. Achieving a GNSS terminal of a small size is difficult due to its relatively low operational frequency (L-band), which is equivalent to a wavelength of approximately 24 cm. As an efficient half-wavelength antenna is too large for compact devices, in this paper, an electrically small antenna (ESA) for GNSS terminals is presented. The antenna was miniaturized by using a dielectric block with relatively high permittivity, making some parts virtual, and optimizing its geometry. The operational frequency of the ESA is tunable by means of metallic rods of variable heights inserted into a cylindrical cavity drilled inside the dielectric block. The results confirm the feasibility of the concept and the usability of the ESA for compact GNSS terminals.
1. Introduction
The miniaturization of antennas for global navigation satellite system (GNSS) receivers is important to meeting the requirements of customers for more compact devices. If an antenna has overall dimensions (including any ground plane) of less than one-quarter of a wavelength (λ/4), it is often referred to as an electrically small antenna (ESA) [1]. The theoretical gain and bandwidth of an ESA is limited by its size [2,3,4,5]. In general, the miniaturization of an antenna leads to low radiation resistance, high input reactance, a narrow impedance bandwidth, and poor radiation efficiency. Therefore, it is somewhat difficult to design an ESA with a frequency range covering the full band of GNSS signals.
The main miniaturization techniques—antenna loading (by using high-permittivity or high-permeability materials), virtualization of some parts of the antenna (by using ground planes or short circuits), and optimization of the geometry—can be employed to design ESAs. By using at least two of the abovementioned miniaturizing techniques, one can expect better performance of ESAs. Various ESA designs employing different miniaturization techniques have been reported in the literature. For example, in [6], a monopole with a height of approximately 0.16 λ was top-loaded to cover a frequency range from 1750 to 2500 MHz, and in [7], high-permittivity materials (between 10 and 100) were investigated to shorten a rectangular dielectric resonator antenna. In [8], a short-circuited monopole antenna, which is partially similar to the design proposed in this letter, was presented. The authors noted that apart from the normal omnidirectional radiation in the plane perpendicular to the monopole antenna, some radiation was observed in a plane in the transverse direction of the antenna and parallel to the axis of the monopole. This is probably because the antenna extended in the longitudinal direction; thus, the surface current flow was more intensive in the lateral direction, which, in turn, changed the principal polarization of the antenna.
This paper is an extended version of [9], where the design of an ESA for BeiDou GNSSs is presented. The design is based on antenna loading, ground plane imaging, and optimization of the matching circuit geometry. The novel contribution of this letter in respect to [9] includes a new method of tuning to bands of different GNSSs. In addition, the operational principle and analysis of the radiation characteristic are meticulously discussed.
2. Materials and Methods
The main concept of the proposed ESA, which is shown in Figure 1, is based on antenna loading by using a dielectric block (22 × 10 × 10 mm) and utilizing a ground plane. A 7-mm-long cylindrical cavity was drilled inside the dielectric block, and a metallic rod was inserted into this cavity for frequency tuning of the ESA. The dielectric block was made of sapphire and was placed on a 30 × 30 mm ground plane. The value of the sapphire permittivity used for the simulations and optimization was measured in our laboratory and found to equal 11.2, which corresponds well with the literature [10]. The characterization of sapphire was performed by using a very precise split post-dielectric resonator technique [11]. A surface of the dielectric block adjacent to the connector was fully coated by a conductive material. This surface, together with a conductive layer placed on the top surface, formed the radiating line. The other line, named the conducting line, was also located on the top surface. An interdigital capacitor was placed between the conducting line and the radiating line and interconnected both. The interdigital capacitor was composed of 40-μm-thick parallel lines 180 μm apart, as illustrated in Figure 1. The lines alternatively connected the conducting line and the radiating line. The ESA was fed by a coaxial connector, SubMiniature version A (SMA), with a long central pin approximately 0.05 λ in length, where λ is the free-space wavelength. The length of the pin was 5 times smaller than the typical length of a quarter-wavelength monopole antenna for the L-band. The pin was connected to the conducting line on the top surface and was loaded by an interdigital capacitor. The capacitance of the interdigital capacitor has a crucial impact on antenna performance; therefore, its dimensions were optimized considering both the permittivity and dimensions of the dielectric block.
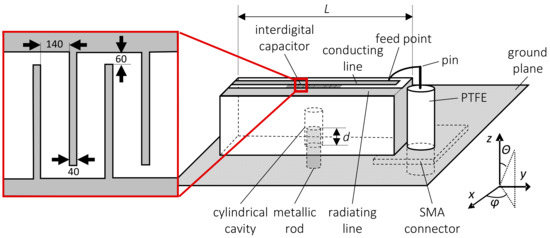
Figure 1.
Diagram of the electrically small antenna (ESA) (all dimensions in micrometers). PTFE, Polytetrafluoroethylene; SMA, SubMiniature version A.
The design of the ESA presented in this communication somewhat resembles the inverted-F antenna (IFA) and inverted-L antenna (ILA) illustrated in Figure 2a,b, respectively. However, a closer look reveals a significant difference—for both IFA and ILA, the radiation in the direction indicated by the arrows in Figure 2a,b is noticeably reduced, and the polarization of both antennas is linear and oriented toward the electric field vector E.
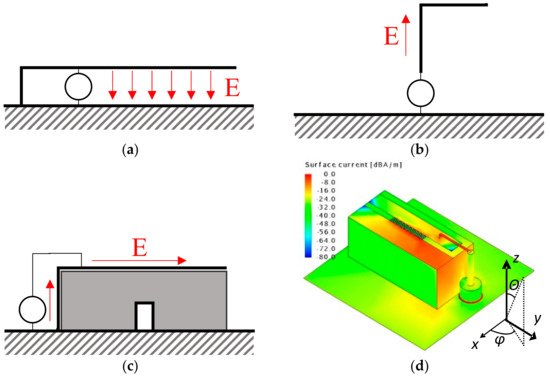
Figure 2.
Types of antennas (the orientation of the electric field vector is indicated with red arrows): (a) inverted-F antenna (IFA), (b) inverted-L antenna (ILA), and (c) the designed ESA. (d) The simulated surface currents of the designed ESA.
The ILA is a type of a top-loaded monopole. For such a structure, the surface current density is significant only in the direction that is perpendicular to the ground plane. Moreover, at the feed point of the monopole, the current density is the highest. The current distribution is almost uniform because the top-loading helps to equalize it. In the top-loaded monopole, increasing the current generates incremental radiation resistance and input impedance.
The IFA also has no longitudinal current component due to the proximity of the longitudinal part of the antenna to the ground plane. In this case, the existence of a longitudinal current is limited.
Conversely, the proposed ESA demonstrated a significant density of surface currents, not only on the parts perpendicular to the ground plane (as is the case for a monopole), but also on the parallelly oriented parts, as illustrated in Figure 2c. This is confirmed by the results of the surface current simulation shown in Figure 2d. Such a unique feature enables radiation along the z-axis.
To obtain an effective radiating structure, the currents have to add up in phase. Moreover, the impedance of the transmission line should match the input impedance of the antenna.
In our antenna, the feed “sees” a conducting line that is a fraction of a wavelength and that is connected to a radiating line with an interdigital capacitor. The radiating line consists of an open circuit on the one side of the interdigital capacitor and is connected to the ground plane on the other side according to Figure 2c. The feed location was chosen to "balance out" the capacitance and the inductance of such a structure. The inductance and capacitance canceled out one another, leaving just the radiation resistance and the resistance related to the losses. The complex reflection coefficient is shown in Figure 3. Its value is close to 1, obtained for a frequency of 1232 MHz and a 5-mm-long metallic rod inserted into the dielectric block.
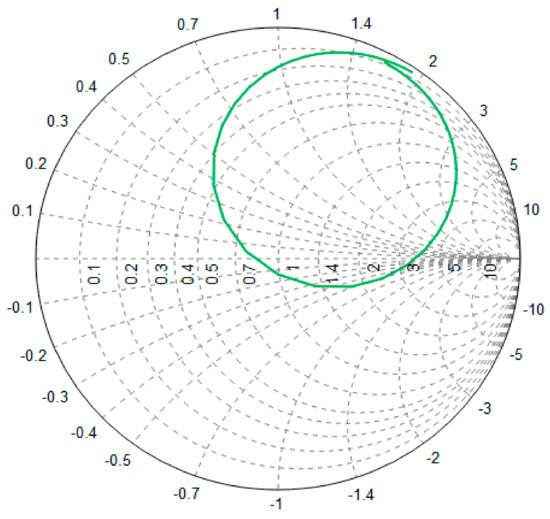
Figure 3.
Complex reflection coefficient versus frequency.
The presented ESA with a cylindrical cavity and a dielectric block length of 22 mm was also simulated for the insertion of different metallic rods. The results are presented in Figure 4. According to the results, the operational frequency of the ESA is tunable and depends on the metallic rod height. Such functionality is possible because the dielectric block was not used as a resonator, but only as an element that allows the dimensions of the radiation line to be reduced.
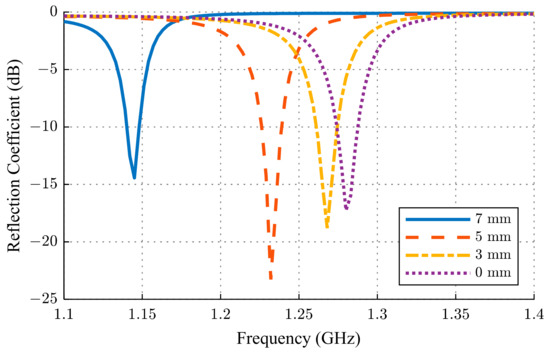
Figure 4.
Simulated reflection coefficients of the ESA for metallic rods of variable heights inserted into a cylindrical cavity drilled inside the dielectric block.
The resonant frequency of the presented ESA can be changed either by modifying the dimensions of the dielectric block or by changing the permittivity. Another method, which is proposed in this communication, is based on changing the insertion of a metallic rod into the cylindrical cavity drilled inside the dielectric block. We need to note that the size of the dielectric block has an effect on the resonant frequency; however, block sizes are chosen so as not to excite the resonant modes. To prove this, let us consider the resonant frequency of a rectangular cavity resonator, which, in a general case, could be calculated as
where n, m, and l are any integers, and b, c, and d are the dimensions of the dielectric block in the x, y, and z directions. For each value of m, n, and l, we obtained a specific type of resonance with the only difference being that one of the three indices can be equal to zero in the case of the lowest modes of the H-type (f011 = f101 = 5 GHz), and none of them can equal zero for the lowest mode of the E-type (f111 = 6.3 GHz). Assuming that the resonator is fully filled with a dielectric with a permittivity of 11.2, then the resonant frequency will be at a lower frequency. The lowest resonant frequency will be around 1.5 GHz. In our case, the dielectric block was not fully metallized, but, rather, was partially open. It should be assumed that the effective permittivity of the dielectric block will be less than the value of , and that the resonant frequency will be higher. This can also be proven by simulating the near-field distribution inside the dielectric block. Therefore, herein, the dielectric block was used only for shortening the radiator length, and its resonances were not utilized.
The design of the presented ESA was initially analyzed without the cylindrical cavity. Electromagnetic software FEKO was used to conduct a series of simulations and to find optimal dimensions for the antenna elements. The optimization revealed that the antenna resonated at 1216 MHz; hence, the corresponding free-space wavelength (λ) and the wavenumber (k) were 246.7 mm and 25.468 rad/m, respectively. These values determine the fundamental bandwidth limitation due to a reduction in the dimension. The approximate normalized bandwidth (B) for a given maximum voltage standing wave ratio (VSWR) in terms of the limit on the quality factor (QL) can be found by [12]
where
and a is the radius enclosing the antenna. Since the antenna is linearly polarized, the fundamental limit for the minimum quality factor is
A theoretical limit of the relative bandwidth for a VSWR of 2:1 can be estimated using Equation (2) as follows:
which corresponds to 28 MHz of the absolute bandwidth.
Additional simulations were performed to examine the relationship between the dielectric block length and the resonant frequency. The length of the dielectric block was changed from 21 to 22 mm, with the other dimensions remaining unchanged. In Table 1, the influence of the dielectric block length on the resonant frequency is presented. One can observe that changing the length of the dielectric block allowed us to choose the desired frequency of operation, i.e., each 0.5 mm shifted the central frequency by 25 MHz. Eventually, it was possible to easily redesign the ESA for various GNSSs, such as GPS, GLONASS, or BeiDou, only by changing the length of the dielectric block. Table 1 also shows the efficiency of radiation, which slightly decreased with the dielectric block length. The length of 22 mm was chosen for the final design.

Table 1.
Dependence of the dielectric block length on the ESA’s operational frequency and efficiency.
Figure 5 provides the far-field, 2D radiation patterns simulated at 1232 MHz in three planes (XOY, XOZ, and YOZ), which reflect the space distribution of the two field components, Eθ and Eφ. Figure 5a,b presents the radiation patterns of the ESA with and without the metallic rod. The similarity between the obtained results indicates that the influence of the metallic rod on the radiation pattern is negligible. From the presented figures, it is clear why, apart from the omnidirectional radiation in the XOY plane, some radiation can be observed in the plane in the transverse directions of the antenna (i.e., the XOZ plane). In the XOZ plane, the radiation in the perpendicular direction (z-axis) to the antenna was dominant based on the Eφ component, which is in line with the surface current direction of the designed ESA (Figure 2d).
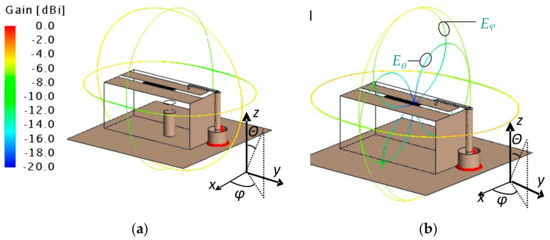
Figure 5.
Radiation patterns: (a) ESA with a metallic rod; total electric field in the XOY, XOZ, and YOZ planes; (b) ESA without a metallic rod; total electric field in the XOY and XOZ planes; Eθ and Eφ components in the XOZ plane.
Figure 6 shows the axial ratio in two planes, namely, XOZ and YOZ, where it is very clear that the presence of Eφ caused elliptical polarization in limited space. This functionality is very advantageous in navigation systems because the mutual positioning of the source and receiver is undefined and the polarization is not aligned.
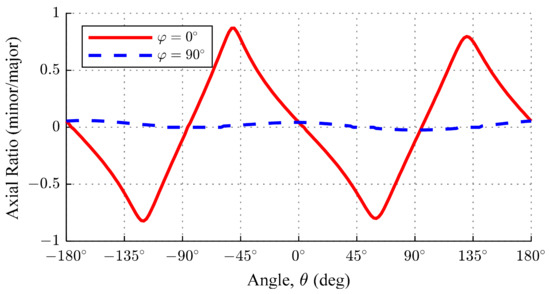
Figure 6.
Axial ratio in two planes: XOZ (red; φ = 0°) and YOZ (blue; φ = 90°).
3. Results
3.1. Measurements of the ESA
Figure 7 shows the fabricated ESA with a cylindrical cavity with a diameter of 2 mm and a length of 7 mm. The tuning rod was realized as a threaded M2 bolt, the position of which could be precisely adjusted by twisting it through a nut attached to the opening of the cavity.

Figure 7.
Photographs of the fabricated ESA: (a) Top view; (b) perspective view.
Figure 8 presents the reflection coefficient and the realized gain measured for different insertions of the tuning element (metal bolt). According to Figure 8a, the frequency of the minimum reflection coefficient shifted down with increasing insertion of the tuning element. When the metal bolt was completely removed, the empty cavity decreased the effective permittivity; hence, the operational frequency shifted up to 1.25 GHz. The results of the gain measurements presented in Figure 8b indicate that the frequency of the maximum gain followed the frequency of the minimum reflection coefficient.
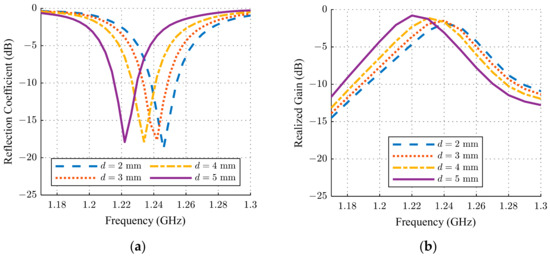
Figure 8.
Measurements of the ESA with the cavity and different metallic rod insertions: (a) Reflection coefficient; (b) realized gain.
Figure 9 presents the measured radiation patterns of the peak gain frequency. The measurements were conducted inside a 3 × 3 × 4 m fully anechoic chamber. The other frequencies near the frequency of operation were also measured, and similar radiation patterns were obtained. The maximum gain was observed in the direction almost per-pendicular to the ground plane, which is practical and useful for the reception of signals arriving from GNSS satellites. The obtained patterns are better than those of typical monopoles, which have a deep null in the direction perpendicular to the ground plane.
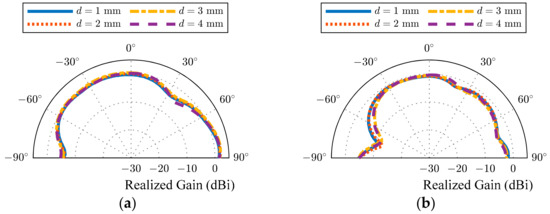
Figure 9.
Measured radiation patterns: (a) YOZ plane; (b) XOZ plane.
3.2. Measurements of the ESA Placed on a Conductive Ground Plane
In practical applications, the ESA can be mounted inside the enclosure of a smartphone or on another larger device. Such a case was examined by placing the ESA on a reflecting plate, as presented in Figure 10.

Figure 10.
The ESA mounted on a large reflecting plate.
The results of the measurements are shown in Figure 11. The resonant frequency was the same as for the ESA without the reflecting plate; however, the gain was higher by 3 dB, which improved the reception of low-power GNSS signals.
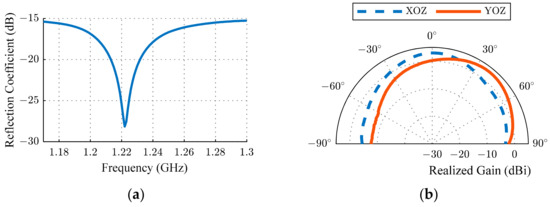
Figure 11.
Measurements of the ESA mounted on a large reflecting plane: (a) Reflection coefficient; (b) radiation pattens.
4. Discussion
The antenna presented in this paper is electrically small because the largest dimensions of the antenna equal 3 cm, which is approximately 8 times shorter than the free-space wavelength. The operational frequency of the ESA can be changed by adjusting the dielectric block length or by inserting a metallic rod into a cylindrical cavity drilled in the middle of said dielectric block. In practice, changing the metallic rod insertion depth may be used in the process of selecting the antenna for a particular navigation system. In this case, the metallic rod is mounted to a certain depth. Changing the metallic rod insertion depth can be automated for dynamic change of the operating frequency and, in turn, for a navigation system by means of, e.g., a microelectromechanical actuator. The antenna is tunable from 1225 to 1255 MHz, which covers part of the lower L-band and enables the reception of various GNSS signals. Two examples of frequency tuning to GNSS signals are listed in Table 2. The measured bandwidth of the antenna was 20 MHz for S11 < −10 dB and 32 MHz for S11 < −6 dB, which are relatively close to the fundamental limit. The radiation pattern was optimized for the reception of signals arriving from a direction perpendicular to the antenna. This is a very important characteristic compared to conventional monopole antennas, which have a null in this direction. The obtained results confirmed that the presented ESA is a good candidate for an adaptive antenna dedicated to compact GNSS receivers.

Table 2.
An example of the ESA’s tunability for different GNSSs.
5. Patents
Electrically small antenna, Polish patent (pending), P.434186; date of application: 3 June 2020.
Author Contributions
Conceptualization, Y.Y. and D.V.; methodology, C.W.; validation, Y.Y.; formal analysis, Y.Y.; investigation, G.B.; resources, V.H. and I.S.; writing—original draft preparation, Y.Y. and G.B.; writing—review and editing, Y.Y. and G.B.; visualization, G.B.; supervision, Y.Y.; project administration, J.M.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the IMAGE project that received funding from the European Union’s Horizon2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 778156. Partially supported by the Foundation for Polish Science (FNP).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Volakis, J.L. Small Antennas. In Antenna Engineering Handbook, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Hansen, R.C. Electrically Small, Superdirective, and Superconducting Antennas; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wheeler, H.A. Fundamental Limitations of Small Antennas. Proc. IRE 1947, 35, 1479–1484. [Google Scholar] [CrossRef]
- Chu, L.J. Physical Limitations of Omni-Directional Antennas. J. Appl. Phys. 1948, 19, 1163–1175. [Google Scholar]
- McLean, R.F. A re-examination of the fundamental limits on the radiation Q of electrically small antennas. IEEE Trans. Antennas Propag. 1996, 44, 672–676. [Google Scholar] [CrossRef]
- McLean, J.; Foltz, H.; Crook, G. Broadband, Robust, Low-profile Monopole Incorporating Top loading, Dielectric Loading, and a Distributed Capacitive Feed Mechanism. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Orlando, FL, USA, 11–16 July 1999; pp. 1562–1565. [Google Scholar]
- Mongia, R.K.; Ittipiboon, A. Theoretical and experimental investigations on rectangular dielectric resonator antennas. IEEE Trans. Antennas Propag. 1997, 45, 1348–1356. [Google Scholar] [CrossRef]
- Su, S.-W.; Chang, F.-S. A bent, shorted, planar monopole antenna for 2. 4 GHz WLAN applications. Microw. Opt. Technol. Lett. 2009, 51, 455–457. [Google Scholar] [CrossRef]
- Yashchyshyn, Y.; Vynnyk, D.; Haiduchok, V.; Solskii, I.; Wu, C.; Bogdan, G. Electrically Small Antenna for BeiDou Chinese Navigation Satellite System. In Proceedings of the 24th International Microwave and Radar Conference (MIKON), Warsaw, Poland, 5–8 October 2020; pp. 92–94. [Google Scholar]
- Aitken, J.E.; Ladbrooke, P.H.; Potok, M.H.N. Microwave Measurement of the Temperature Coefficient of Permittivity for Sapphir and Alumina. IEEE Trans. Microw. Theory Tech. 1975, 23, 526–529. [Google Scholar] [CrossRef]
- Krupka, J.; Clarke, R.N.; Rochard, O.C.; Gregory, A.P. Split post dielectric resonator technique for precise measurements of laminar dielectric specimens-measurement uncertainties. In Proceedings of the 13th International Conference on Microwaves, Radar and Wireless Communications (MIKON), Wroclaw, Poland, 22–24 May 2000; pp. 305–308. [Google Scholar]
- Sharma, S.K.; Nagarkoti, D.S. Meet the Challenge of Designing Electrically Small Antennas. Microwave & RF Magazine. Available online: https://www.mwrf.com/technologies/components/article/21848593/meet-the-challenge-of-designing-electrically-small-antennas (accessed on 29 November 2020).
- Teunissen, P.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer: New York, NY, USA, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).