Abstract
In this paper, multi-frequency synthetic aperture radar (SAR) data at L- and C-bands (ALOS PALSAR and Envisat/ASAR) were used to estimate forest biomass in Tuscany, in Central Italy. The ground measurements of woody volume (WV, in m3/ha), which can be considered as a proxy of forest biomass, were retrieved from the Italian National Forest Inventory (NFI). After a preliminary investigation to assess the sensitivity of backscatter at C- and L-bands to forest biomass, an approach based on an artificial neural network (ANN) was implemented. The ANN was trained using the backscattering coefficient at L-band (ALOS PALSAR, HH and HV polarization) and C-band (Envisat ASAR in HH polarization) as inputs. Spatially distributed WV values for the entire test area were derived by the integration (fusion) of a canopy height map derived from the Ice, Cloud, and Land Elevation Geoscience Laser Altimeter System (ICESat GLAS) and the NFI data, in order to build a significant ground truth dataset for the training stage. The analysis of the backscattering sensitivity to WV showed a moderate correlation at L-band and was almost negligible at C-band. Despite this, the ANN algorithm was able to exploit the synergy of SAR frequencies and polarizations, estimating WV with average Pearson’s correlation coefficient (R) = 0.96 and root mean square error (RMSE) ≃ 39 m3/ha when applied to the test dataset and average R = 0.86 and RMSE ≃ 75 m3/ha when validated on the direct measurements from the NFI. Considering the heterogeneity of the scenario (Mediterranean mixed forests in hilly landscape) and the small amount of available ground measurements with respect to the spatial variability of different plots, the obtained results can be considered satisfactory. Moreover, the successful use of WV from global maps for implementing the algorithm suggests the possibility to apply the algorithm to wider areas or even to global scales.
1. Introduction
Forest areas cover a significative percentage of the Earth’s surface and sequestrate an important amount of atmospheric carbon dioxide (CO2). Consequently, forests have a strong impact on climate change, representing one of the main sinks of atmospheric carbon. The reduction in forest biomass due to deforestation and fires (more than 3% of forest area, corresponding to 17.4 gigatonnes of forest biomass, has been lost since 1990) increased atmospheric carbon dioxide, with a strong impact (more than 10%) on all greenhouse gas emissions and, consequently, on climate change [1,2,3]. The estimation of forest biomass at the regional scale assumes, therefore, a significant importance for other environmental studies, such as bioenergy production, forest management, detection of land-use changes and assessment of carbon stocks [4].
Among forest biophysical parameters such as Leaf Area Index (LAI), net primary production (NPP) and above ground biomass (AGB) [5], which are related to the biomass quantity, AGB is a key index for the study of carbon cycle. The estimation of AGB is performed by using different approaches and techniques [6], the most accurate of which requires the harvesting of tree samples, thus being a local and destructive method that cannot be extended to a regional scale. Methods for the indirect estimation of AGB are based on specific models, focusing on allometric equations [7] or using conversion factors between the AGB and some physical attributes of the single species (e.g., canopy height and trunk diameter, wood density, canopy cover). These models are developed and calibrated by using regressions, statistical approaches, or machine learning techniques calibrated on local measured data and refer to single tree species [8]. Nevertheless, indirect techniques lack the spatial and temporal robustness of the inversion models [9], mainly due to natural spatial inhomogeneity and temporal variations of the vegetation coverage characteristics.
Remote sensing data nowadays represent the most important information source for the estimation of forest parameters, due to their significant temporal and spatial coverage [10]. For instance, gross and net primary production (GPP/NPP) [11], as well as the impact of fires on biomass [12], are commonly assessed by using the Normalized Difference Vegetation Index (NDVI) and the Enhanced Vegetation Index (EVI) that are extracted from optical remote sensing data. A recent and exhaustive review of the estimation techniques from remote sensed data can be found in [13]. In the field of optical systems, light detection and ranging (LiDAR) systems have also become progressively important due to their capability of assessing vertical structures, such as the canopy height [14,15,16], which can be successfully used to retrieve structural parameters of forests. Since the late 1990s, many studies have been proposed concerning the use of airborne LiDAR for estimating forest characteristics such as stand volume, basal area, canopy height, and tree biomass, and also in integration with other remote sensing data such as multi or hyperspectral data [17,18]. In particular, global estimates of forest canopy height have been derived from the Geoscience Laser Altimeter System (GLAS) LiDAR instrument that is aboard the NASA Ice, Cloud, and land Elevation (ICESat) satellite. The canopy heights were estimated by processing the dataset collected between October 2004 and March 2008 [19]. A new map of canopy heights at 30 m spatial resolution was made available from the ICESat heir mission, i.e., the NASA Global Ecoystem Dynamics Investigation (GEDI), which has been operating onboard the International Space Station since April 2019 [20]. The map, which is continuously updated, was obtained through the integration of the GEDI LiDAR forest structure measurements and Landsat data timeseries [21].
Unlike the optical sensors, microwave remote sensing is characterized by the independence of cloud cover and solar radiation. Microwaves’ capability to penetrate through the vegetation cover and to interact with its water content can be exploited to estimate forest biomass [22,23]. In active sensors, such as Synthetic Aperture Radar (SAR) systems, the backscatter is strongly related to the intrinsic characteristics of vegetation such as the dielectric constant of the tissues and the geometry of the forest stands, constituted by the orientation, the dimensions, and the density of trunks, leaves, and branches [22]. In general, the correlation between SAR backscatter and woody biomass is dependent on operational frequency, polarization, and incidence angle. While the backscatter at higher frequencies as C- and X-bands is mainly generated in the upper part of the crown, the contribution to total backscatter provided by soil and trunks is taken into account using longer wavelengths, such as L- and P-band [24,25,26], deeming these frequencies as the most suitable for the retrieval of forest biomass. Waiting for the ESA BIOMASS mission, which will carry on board a P-band SAR [27], the L-band SAR satellite sensors adopted for forest monitoring were the Phased Array L-band Synthetic Aperture Radar (PALSAR) installed onboard the Advanced Land Observing Satellite (ALOS), which is no longer operating [28], and its follow-on PALSAR-2 onboard ALOS-2 [29]. Both missions were conceived for environmental monitoring, including land, agricultural, and forest monitoring, natural hazard and disaster observation, and the exploration of natural resources. The revisit time for ALOS-2 is 14 days.
Further studies based on SAR data demonstrated that the correlation of backscatter to forest biomass is also dependent on forest types and, at low frequencies, on soil moisture variations [30,31]. In the specific context of Mediterranean forests, a logarithmic shape relation has been found between backscatter at L-band and woody volume (WV, expressed in m3/ha) from 200 m3/ha up to a saturation level of 400 m3/ha, whereas P-band has been found to be less affected by these saturation effects [23].
Different techniques have been proposed to estimate the AGB of vegetated areas by means of SAR data to overcome this limited range of backscatter sensitivity. Multi-polarization and multi-temporal data [32,33,34], interferometry (InSAR) [35,36,37], polarimetric SAR interferometry (PolInSAR) [38,39] and SAR tomography [40] have been used to estimate high values of forest biomass at regional and global scale [41].
Noticeably, most previous studies and several seminal papers (e.g., [42,43,44]) investigating methodologies to estimate forest biomass were focused on boreal forests, due to their significant impact on the carbon cycle. Tropical forests have also been widely considered, due to the high importance for biodiversity [45,46]. More recently, Mediterranean forests have also gained attention, mainly in the framework of forest fire impact on biomass [47,48,49]. Nevertheless, the assessment of vegetation parameters of these ecosystems is a complex task due to their marked inhomogeneity [50].
Thanks to increasing hardware and software resources, artificial neural networks (ANNs) have gained increasing attention in the analysis of complex systems, and therefore in the forest biomass estimation from SAR backscattering [51]. Multitemporal SAR-based AGB estimation by means of ANNs was presented and compared with support vector regression and multivariate linear regression in [49], where it was noted that ANNs show better results at higher AGB values. Furthermore, mixed optical-SAR ANNs based on Sentinel data were presented in [52].
Recently, the use of an ANN approach to directly estimate the WV in a Mediterranean forest contest from multifrequency SAR data was proposed in [53]. In that paper, the ANN algorithm was firstly trained using the WV derived from airborne laser scanning (ALS) data combined with data simulated by a forward electromagnetic model based on the Radiative Transfer Theory. The algorithm was thus able to merge SAR data at L- and C-bands for correctly estimating WV in diversified Mediterranean environments, showing a Pearson’s correlation coefficient (R) > 0.97 and a root mean square error (RMSE) = 28.5 m3/ha for the independent test, and R = 0.86 and RMSE ≈ 77 m3/ha for the final independent validation, the latter based on conventional measurements available in areas not included in the ALS acquisitions.
In this paper, ANN-based algorithms were developed to estimate WV in a large part of Tuscany, by spatially and temporally extending the analysis with respect to [53]. Six images of the test area from ALOS PALSAR L-band at HH and HV polarization and six from ENVISAT Advanced Synthetic Aperture Radar (ASAR) C-band at VV polarization were selected, based on minimum temporal distance: the images covered a period of about 2 years, from June 2007 to June 2009. Given the lack of spatially distributed WV measurements for the entire test area, the target data considered for training and testing the algorithm were derived from data fusion of the National Forest Inventory and a map of canopy height obtained from the ICESat GLAS satellite mission [19]. Six ANN algorithms were developed independently, considering 1% of the SAR data available at each of the six dates for training and the remaining 99% for testing the ANN. Then, a cross-fold test was performed by applying each trained ANN to the other five datasets, in order to verify the robustness and exportability of the proposed retrieval concept. Finally, the six ANN algorithms were validated on the direct WV measurements from the National Forest Inventory.
The final results, in spite of a rather scarce direct correlation between the backscattering and the target WV data (R < 0.45 at L- band and < 0.2 at C- band for all the considered dates), were revealed to be rather good, showing average R ≃ 0.96 and RMSE ≃ 39 m3/ha for the test on 99% of the WV fused map and R ≃ 0.86 and RMSE ≃ 75 m3/ha on the independent validation on National Forest Inventory data, confirming the robustness and the accuracy of the proposed algorithm.
2. Materials and Methods
2.1. Test Area Description
Tuscany is situated in Central Italy between 9° and 12° east longitude and 44° and 42° north latitude, covering more than 2,000,000 ha (Figure 1). The topography ranges from flat areas near the coastline and along the principal river valleys, to hilly and mountainous zones towards the Apennine chain. Approximately 2/3 of the area is covered by hills, 1/5 by mountains and only 1/10 by plains and valleys. From a climatic viewpoint, Tuscany is influenced by its complex orographic structure and by the direction of the prevalent air flows (from west/north-west). Thus, the climate ranges from typically Mediterranean to temperate warm or cool, according to the altitudinal and latitudinal gradients and the distance from the sea [54].
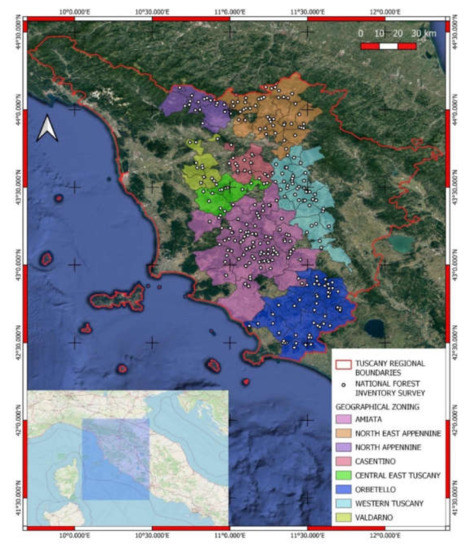
Figure 1.
Position of Tuscany (boundaries in red line) in Central Italy with the superimposition of the woody volume (WV) measurements (white dots) available for the area covered by synthetic aperture radar (SAR) images.
The high variability of ecological conditions in Tuscany results in extremely diversified vegetation types and structures. About 50% of the region is covered by forest, which makes Tuscany the most forested region in Italy. Agricultural areas cover approximately 25% of the land surface and are represented both by tree plantations (mostly olive groves and vineyards) and by cereal crops (mainly wheat and maize). The rest of the region is covered by pastures, unproductive, and urban areas.
The main forest types are dominated by Quercus cerris L., Castanea sativa Mill., Quercus pubescens Willd., Fagus sylvatica L., Quercus ilex L., Mediterranean pines, Ostrya carpinifolia Scop., Pinus nigra Arnold, Abies alba Mill., Pseudotsuga menziesii Franco, Cupressus sempervirens L. and Cupressus arizonica E. Greene.
Mediterranean forests (mostly maquis, shrubland and evergreen species) represent 25% of the total forest area and are situated mainly in the south-west of the region. Deciduous species (about 50% of the forest area) are spread partly on hilly areas (mainly deciduous oaks) and partly in higher zones (i.e., Castanea sativa Mill., Ostrya carpinifolia Scop., etc.). Mountain forests cover 15% of the area and are dominated by Fagus sylvatica L., Abies alba Mill., Pseudotsuga menziesii Franco, and Pinus nigra Arnold.
2.2. Italian National Forest Inventory (NFI) Data
Woody volume data related to the study area were derived from the Italian National Forest Inventory (NFI) [55,56]. This inventory was based on a three-phase sampling [57]: the first two phases were aimed at estimating the forest area and distribution into different classes according to qualitative attributes (e.g., property, management issues, vegetation structure and conditions, site features, etc.). The third phase was aimed at collecting quantitative measurements of trees and stand attributes by means of field surveys carried out on about 700 plots all over Tuscany region. During this last phase, which was carried out from 2003 to 2006, several forest variables (trunk diameters, canopy heights, trunk diameter increments, etc.) were collected on a plot basis.
2.3. WV Map from ICESat GLAS Mission
The sparse WV measurements derived from NFI were not sufficient for developing the algorithm, given the large amount of data required for training the ANNs. For this reason, and to keep training, testing, and validation as independent as possible, a WV map of the entire test area was obtained by merging the NFI data with a global map of canopy height derived from the ICESat GLAS acquisitions (GLAS-H) as described in [19]. The GLAS-H map contains height values of the canopy expressed in meters: for the scopes of this study, the map was clipped to match the same area covered by SAR, converted to WV and resampled up to 100 m spatial resolution by data fusion with the NFI measurements.
The map of the WV derived from GLAS-H and NFI (GLAS WV) is shown in Figure 2a, the NFI measurements are shown in Figure 2b, and the GLAS WV validation, obtained through comparison with the NFI direct measurements, is shown in the scatterplot in Figure 2c. As evident from the last figure, the overall agreement is good, with a correlation coefficient R = 0.93 and a RMSE of 58 m3/ha.
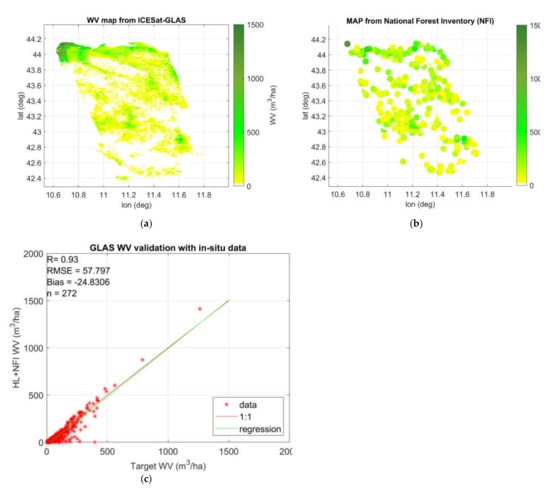
Figure 2.
(a) The WV map obtained by integrating Ice, Cloud, and Land Elevation Geoscience Laser Altimeter System (ICESat GLAS) canopy height and Italian National Forest Inventory (NFI) measurements, (b) the NFI measurements, (c) validation of the GLAS WV map obtained by comparison with ground truth measurements.
2.4. SAR Data
The considered SAR sensors are PALSAR and ASAR. PALSAR was on board the ALOS satellite that was developed by JAXA and Japan Resources Observation System Organization (JAROS). This satellite, whose repeat cycle was 46 days, was launched in 2006 into the sun-synchronous orbit and was operational until 2011.
ASAR was on board the Envisat satellite, which was operational from March 2002 until the unexpected loss of contact in April 2012. This satellite, whose repeat cycle was 30 days, was developed by European Space Agency.
The dataset of PALSAR images consists of six passes, on track 642, acquired between 2007 and 2009. Similarly, the ASAR dataset consists of six passes acquired in the same period (Table 1).

Table 1.
List of the dataset acquired over the test site (Tuscany). Legend: A/P = ALOS/PALSAR, E/A = ENVISAT/ASAR, Asc. = ascending.
Each pass is the combination of the consecutive frames: PALSAR considers frames from 840 to 870, while ASAR takes into account frames 855 and 873, in order to cover most of the Tuscan area (Figure 3). Both SAR data formats are single look complex (SLC) and are provided in the slant range coordinates (Level 1.1 for PALSAR, Image Mode Single-Look Complex for ASAR). The polarization mode is HH/HV for PALSAR and VV for ASAR, respectively.
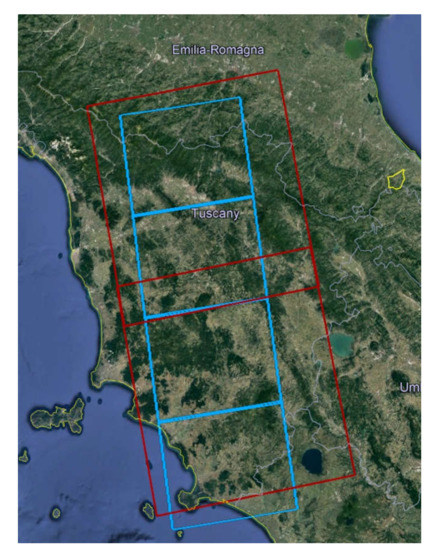
Figure 3.
PALSAR (blue) and ASAR (red) data coverage of Tuscany.
Each frame was processed in order to obtain SAR data that are radiometrically calibrated, i.e., the reflecting surface is correctly represented by the radar backscatter (σ°) of each imagery pixel. Simultaneously, the geocoding procedure was applied to carry out a precise geographic location of each pixel from the original slant range geometry. The selected projection of output images was UTM-32 North, WGS84, with 10 m pixel size. This result was achieved by using a digital elevation model at 10 m spatial resolution, provided by Tuscany Region [58] and SARscape©/ ENVI©/IDL© software. Local incidence angle images and layover and shadow masks were generated too. Each temporal pass consisted of two or more frames that were joined through a mosaicking process (Figure 3). Lastly, the mosaicked images were coregistered and collected in a single stack of images to be compared ‘pixel by pixel’.
In order to perform the sensitivity analysis described in Section 3.2, the backscattering coefficient was extracted in the areas corresponding to the biomass values of the NFI: for each WV value (Figure 2a), a mean radar backscatter value was calculated as the average value of 5 by 5 pixels window. Considering that some points were discarded since they were placed in areas affected by layover and shadow phenomena, a database of 288 points was generated. Each point contained a pair of backscattering–biomass values that allowed us to perform the sensitivity analysis.
The dataset considered for implementing and validating the algorithms was obtained by combining the six PALSAR images with the closest ASAR acquisitions, resampling and coregistering all the SAR data on the coordinates grid of the GLAS WV, at 100 m spatial resolution: the final data amount, considering the areas covered by the frames of both sensors, was of about 4 million triplets of calibrated and geocoded backscattering coefficients at the three polarizations, HH, HV, and VV, for each date.
2.5. The ANN Algorithms
ANNs were largely proven to be capable of approximating almost any kind of non-linear relationships [59,60]. For this reason, joint to the capability of easily combining multiple inputs into the retrieval scheme, their use in solving remote sensing problems increased exponentially in the last few years (e.g., [61,62,63,64,65]), thanks also to the increased computational resources of recent machines. The main limitation of ANNs is related to the training: similarly to the human brain they attempt to replicate, an ANN cannot approximate relationships it did not previously learn from the training. A training well representative of the given problem is therefore mandatory to obtain satisfactory results.
The retrieval algorithms implemented in this study were based on the feed-forward multi-layer perceptron neural networks (FF-MLPs). FF-MLPs are composed of some hidden layers with a given number of neurons, which are all interconnected with weights and biases that are iteratively adjusted during the training. In this study, the training was based on the so-called back propagation (BP) learning rule, a gradient descent algorithm that adjusts iteratively weights and biases for minimizing the mean square error (MSE) between the actual and desired output. The optimal number of neurons and hidden layers and the transfer function for the given problem were defined by the systematic search algorithm presented in [66]. The algorithm repeats training and testing for all the transfer functions available, by iteratively increasing the number of neurons and hidden layers, to select the configuration that gives the best results (highest R in the test), with the aim of preventing the overfitting and the underfitting. The “optimal” ANN resulting from the iterative search algorithm was composed of two hidden layers with 14 neurons and a transfer function of type logistic sigmoid (logsig).
Data Organization for Training and Testing the ANNs
The dataset considered for training, testing, and validating the algorithm was derived from the overall database of PALSAR and ASAR acquisitions, combined with the GLAS WV map and NFI direct measurements described in Section 2.3. In order to assess the possible effects of vegetation seasonality and rainfall on the retrieval, and to ensure the repeatability of the results, the data acquired at different dates were treated independently. Therefore, six datasets were created by co-registering the SAR data (PALSAR + ASAR) at each date with the GLAS WV map. The ANN training and test were repeated for each dataset and the test results compared. The entire process is summarized in the flowchart depicted in Figure 4.
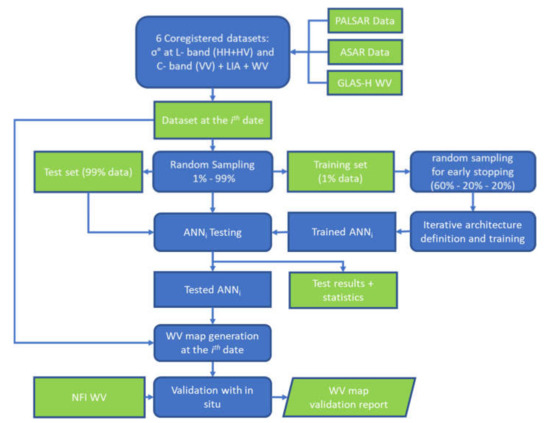
Figure 4.
Flowchart of the artificial neural network (ANN) training, testing, and validation process.
In detail, for the ith date out of the six available, a random sampling is applied to the corresponding ith dataset of SAR + WV to create the training and test subsets: their percentages are established in 1% for training and 99% for test, respectively. According to the so called “early stopping rule”, aimed at preventing the overfitting, the training set is further subsampled randomly in 60%, 20%, and 20% subsets [67]. Then, the ith ANN (ANNi) is trained by considering the σ° values at all frequencies and polarizations and the corresponding local incidence angle (LIA) as inputs, and the GLAS WV map as target. For this step, the iterative architecture definition and training described above is applied. Then, the ANNi is applied to the test set, composed of the 99% of data not included in the training process. After test, the ANNi is validated on the independent set of NFI WV data: it should be noticed that, to keep training, testing, and validation as independent as possible, both the testing and validation datasets are not directly involved in the training. Finally, the output VW map is generated. The ANNs considered in this study were developed using the Matlab Neural Network toolbox.
3. Results
3.1. Sensitivity Analysis: ALOS PALSAR vs. NFI
A sensitivity analysis was preliminarily carried out in order to check the sensitivity of backscattering coefficient at L-band to the WV and to consider the potential usefulness of an advanced algorithm for the forest biomass retrieval. The temporal trends of the backscattering coefficient at HH and HV polarizations are shown in Figure 5a,b, respectively. Different curves refer to five classes of WV obtained by averaging plots with similar biomass (the latter expressed as WV in m3/ha, i.e., 0–50, 50–100, 100–200, 200–300, and > 300 m3/ha). It can be observed that lower curves refer to lower values of biomass and the highest ones to higher values. The distance between the curves is more marked at HV polarization, which is in fact more sensitive to scattering from branches and therefore more related to WV. After an increase in backscattering values in springtime, a decrease in backscattering is observed during summer, probably due to the decrease in soil moisture. This agrees with the values of rainfall acquired at three meteorological stations located in the north, center and south of Tuscany that are reported as histograms in Figure 5a. The sensitivity to soil moisture conditions is indeed more marked at low values of biomass (green lines in Figure 5a,b).
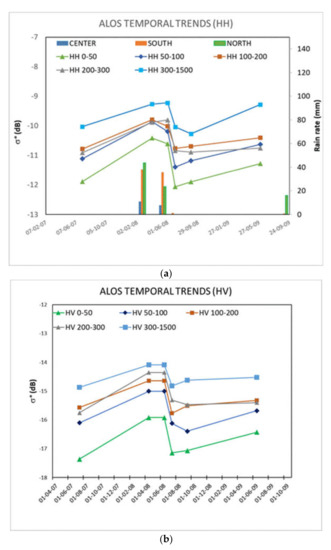
Figure 5.
Temporal trends of backscatter at L-band for different intervals of forest biomass: (a) HH polarization, (b) HV polarization. Temporal trends of rainfall acquired by meteorological stations located in north, center, and south of Tuscany are also reported in (a). Each bar represents the cumulative rainfall of the previous 7 days.
A direct comparison between backscattering coefficient at L band and the WV is reported in Figure 6a,b for the HH and the HV polarization, respectively. The sensitivity of backscatter to WV is evident, although the inhomogeneity of the different plots scattered in the entire region and characterized by different orography and species compositions. The regression curve for the HH backscatter () as a function of the WV (m3/ha) is , attaining a correlation coefficient R = 0.39. Similarly, for the HV backscatter (), the regression curve is , attaining R = 0.51.
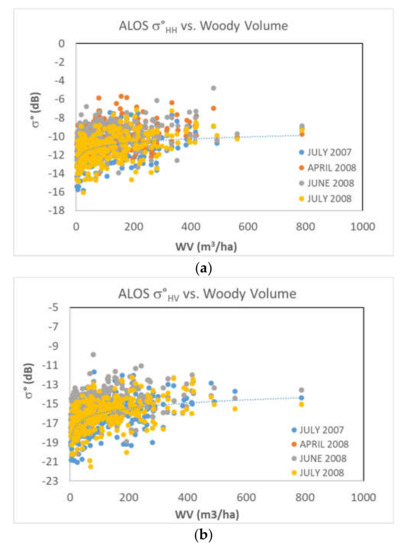
Figure 6.
Regression plots between the woody volume and the backscatter (dB) at L-band for: (a) HH polarization, (b) HV polarization.
3.2. Sensitivity Analysis: PALSAR and ASAR vs. GLAS WV Map
The sensitivity of PALSAR and ASAR to WV was also evaluated on the entire area by comparison with the GLAS WV map. The correlation coefficients obtained at each date are listed in Table 2, while the σ° behavior as a function of WV is shown in Figure 7a for PALSAR HH polarization, in Figure 7b for PALSAR HV polarization, and in Figure 7c for ASAR VV polarization. This figure refers to the acquisitions on the date 2007-07-23; however, very similar behaviors were found for the other dates.

Table 2.
Correlation coefficient values (R) between the radar backscatter (σ°) and WV for PALSAR and ASAR.
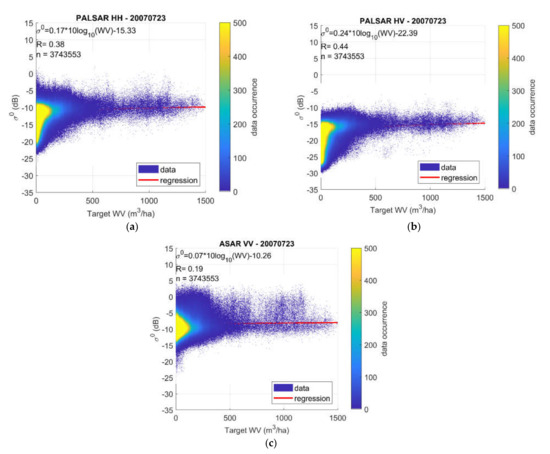
Figure 7.
Backscatter (σ°) behavior as a function of woody volume (WV): (a) PALSAR HH polarization, (b) PALSAR HV polarization, (c) ASAR VV polarization.
The R values listed in Table 2 point out some correlation of the L- band σ° to the target parameter: as expected, such correlation is slightly higher in cross-polarization than in co-polarization. Conversely, the C-band σ° was confirmed as being significantly less correlated to the WV parameter.
The sensitivities and correlations shown in Figure 7 are in line with those obtained in the previous sections by comparison with NFI. Overall, these results confirm the PALSAR and ASAR sensitivity to forest biomass reported in past studies [53], by evidencing the backscatter saturation for high WV, well demonstrated by the logarithmic relationships and more pronounced at C- than at L-band. The obtained correlations, although not negligible, were not sufficient for directly attempting the WV retrieval by simple regression algorithms. Therefore, advanced methods based on ANN were considered for implementing the WV retrieval algorithm presented in this study.
3.3. Retrieval Results
As an example, the results obtained for the date 2008-09-09 are shown in Figure 8. The figure shows: (a) the test result based on the 99% of the data not involved in the training, represented as density plot of ANN estimated vs. target WV, (b) the ANN validation on the NFI dataset, (c) the GLAS WV map considered as target, (d) the WV map generated by the ANN, and (e) the absolute error map.
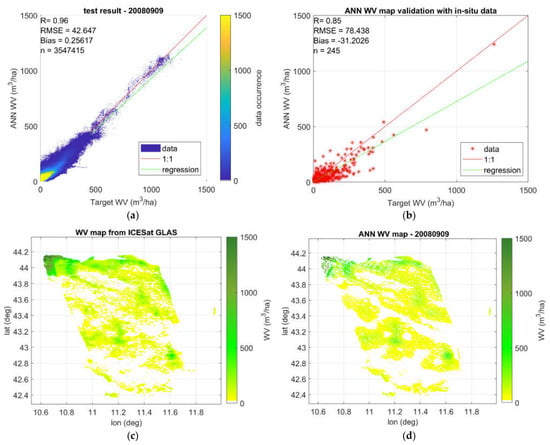
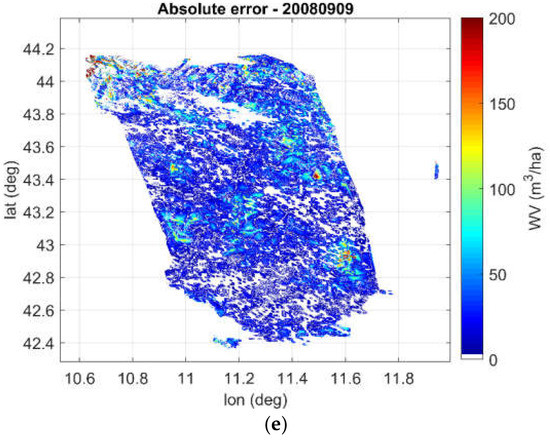
Figure 8.
Results obtained for the date 2008-09-09: (a) the test result based on the 99% of the data not involved in the training, represented as density plot of ANN estimated vs. target WV, (b) the ANN validation on the NFI dataset, (c) the GLAS WV map considered as target, (d) the WV map generated by the ANN, and (e) the absolute error map.
The results obtained for the other dates were very close each other, as pointed out by the main statistics listed in Table 3.

Table 3.
Main statistics of test and validation.
These results can be considered encouraging as they confirm and extend both spatially and temporally what was previously obtained with a similar retrieval concept [53]. In particular, although the test area was different as well as the training strategy and the WV reference data source, the correlations obtained are very similar for both testing (R = 0.96 vs. R = 0.97) and validation with direct measurements (R = 0.86).
It is worth noting that, although the driving contribution to the retrieval comes from PALSAR, some slight improvement was obtained by adding the ASAR data: in particular, another run of the algorithm by considering only PALSAR data as input gave average R ≃ 0.93 and RMSE ≃ 45 m3/ha.
3.3.1. Cross-Fold Test
To assess the exportability of the algorithm, i.e., the possibility of applying the algorithm to other datasets without repeating the training, a cross-fold test was also conducted by applying each of the six trained ANN algorithms to the SAR datasets at the other five dates. The results were more than encouraging, and each ANN was successfully applied to all datasets, by obtaining results from the 30 possible combinations (six ANNs x five dates) in line with those shown in the previous section. In particular, the average correlation coefficient was R = 0.95 for testing and R = 0.86 for validation, and the corresponding RMSE ≃ 45 and 76 m3/ha, respectively (Table 4).

Table 4.
Results of the cross-fold test and validation expressed as mean and standard deviation of R, RMSE, and bias.
4. Discussion
The study was aimed at exploiting the synergy of L- and C-band SAR observations for mapping the forest WV. Both frequencies are not the most suitable for this scope: the sensitivity of L-band SAR to forest is limited by the signal saturation arising at high WV levels, and C-band is only sensitive to the upper layer of the canopy. Better performances are expected from the P- band SAR installed onboard of the incoming ESA BIOMASS mission. However, BIOMASS has not been launched yet—the launch is indicatively planned for 2022—and BIOMASS will not acquire data on Europe, being in any case useless for studying the Mediterranean forests. Therefore, L- and C-band SAR will remain the only possibility of monitoring the WV of Mediterranean forests at high resolution with microwave sensors in the near future.
In this framework, the algorithms based on ANNs appear as a valid tool to exploit the synergy of L- and C- band for addressing the WV retrieval. Taking advantage of the dual frequency, multi-polarization observations, the algorithms were indeed able to exploit the residual sensitivity of L-band to higher WV and to take advantage of C-band for retrieving WV with good correlation and accuracy, as pointed out by the results shown in Table 3 and Figure 8. This study also attempted to assess the validity and exportability of the proposed methodology, which is one of the key problems of “data driven” approaches, i.e., approaches based exclusively on experimental and remote sensed data. In this sense, the study, although based on completely different datasets and different algorithm implementation, confirmed with similar accuracies and extended to larger areas the findings of a previous research [45]. This result is even more appealing if we consider the heterogeneity of Mediterranean forests, and it seems to suggest that the retrieval is feasible independently of the dataset (satellite/airborne LiDAR, in-situ etc.) that has been considered for representing the target parameter. Moreover, the results of cross-fold test described in Section 3.3.1 and Table 4 confirm the independence of this method from the seasonal cycle of vegetation, since each of the ANNs developed for a single date provided similar retrievals when applied to the other dates. This is particularly relevant considering that ANNs are prone to the so called “outliers”, and large errors occur if the test set contains values that are not properly represented in the training set.
In the prosecution of this research, the analysis will be spatially and temporally extended, aiming at validating the method on a larger scale as well as verifying its robustness under different environmental conditions and for various forest species. In this sense, adapting the algorithm to new datasets will be straightforward because it will simply require an ANN re-training (which on recent machines can be achieved in near real time) without changing the algorithm structure.
5. Conclusions
This study aimed at assessing the retrieval of forest woody volume (WV) by using SAR data and a machine learning approach. The investigation was conducted on the heterogeneous environment of Mediterranean forests in central Italy, using combined SAR acquisitions from ALOS PALSAR L-band and ENVISAT ASAR C-band. The results of the preliminary investigation confirmed what was expected from theory and previous studies, by pointing out some sensitivity of L-band acquisitions to WV, which was slightly more pronounced at HV polarization than HH, while the C-band, although showing some increase when biomass increases, did not reveal any significant correlation to the target parameter. The retrieval concept based on ANN confirmed its effectiveness in exploiting the synergy of the multifrequency and multi-polarization SAR data, by retrieving WV with average R = 0.96 and RMSE ≃ 39 m3/ha when applied to the test dataset and average R = 0.86 and RMSE ≃ 75 m3/ha when validated on the direct measurements from the National Forest Inventory.
Overall, this study extended the results obtained with similar retrieval approaches [53], by further demonstrating the robustness and exportability of the proposed method. The use of data derived from global maps, instead of limited ALS sampling for training the algorithm, paves the way to further extending the analysis to larger or even global scales.
Author Contributions
Conceptualization, S.P. (Simonetta Paloscia); methodology, S.P. (Simone Pettinato); software, E.S. and S.P. (Simone Pettinato); validation, E.S.; investigation, L.S.; resources, G.R. and M.C.; data curation, G.F.; writing—original draft preparation, A.L.; writing—review and editing, A.L. and M.C.; supervision, A.L. and S.P. (Simonetta Paloscia); project administration, S.P. (Simonetta Paloscia); funding acquisition, S.P. (Simonetta Paloscia). All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Japan Aerospace Exploration Agency (JAXA) through the project MIDA-OPTICAL/MICROWAVE DATA INTEGRATION FOR ESTIMATING SOIL MOISTURE AND VEGETATION BIOMASS, FY2020-21, PI#ER2GWF103.
Data Availability Statement
Publicly available datasets were analyzed in this study. These datasets do not issue any DOIs and can be openly downloaded here: (i) Italian National Inventory of Forests and Forest Carbon Sinks (INFC) at https://inventarioforestale.org/it/node/40 (accessed on 6 March 2020), (ii) Digital Elevation Model from GLAS/ICES at https://nsidc.org/data/nsidc-0305 (accessed on 6 March 2020), (iii) Tuscany Meteo data at https://www.sir.toscana.it/pluviometria-pub (accessed on 6 March 2020).
Acknowledgments
The ALOS/PALSAR images were provided under the 2nd Research Announcement on the Earth Observations Collaborative Research Agreement (non-funded) between JAXA and IFAC-CNR (PI ER2A2N062), whereas the ENVISAT/ASAR images were provided by European Space Agency and downloaded from ESA Online Catalogue.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Keenan, R.J.; Reams, G.A.; Achard, F.; de Freitas, J.V.; Grainger, A.; Lindquist, E. Dynamics of Global Forest Area: Results from the FAO Global Forest Resources Assessment 2015. For. Ecol. Manag. 2015, 352, 9–20. [Google Scholar] [CrossRef]
- Federici, S.; Tubiello, F.N.; Salvatore, M.; Jacobs, H.; Schmidhuber, J. New Estimates of CO2 Forest Emissions and Removals: 1990–2015. For. Ecol. Manag. 2015, 352, 89–98. [Google Scholar] [CrossRef]
- Waring, R.H.; Running, S.W. Forest Ecosystems: Analysis at Multiple Scales; Elsevier: Amsterdam, The Netherlands, 2010; ISBN 978-0-08-054608-7. [Google Scholar]
- Corona, P.; Chirici, G.; Marchetti, M. Forest Ecosystem Inventory and Monitoring as a Framework for Terrestrial Natural Renewable Resource Survey Programmes. Plant. Biosyst. Int. J. Deal. All Asp. Plant. Biol. 2002, 136, 69–82. [Google Scholar] [CrossRef]
- Definitional Issues Related to Reducing Emissions from Deforestation in Developing Countries. Available online: http://www.fao.org/3/j9345e/j9345e12.htm (accessed on 16 December 2020).
- Kindermann, G.; McCallum, I.; Fritz, S.; Obersteiner, M. A Global Forest Growing Stock, Biomass and Carbon Map Based on FAO Statistics. Silva. Fenn. 2008, 42. [Google Scholar] [CrossRef]
- Beaudoin, A.; Le Toan, T.; Goze, S.; Nezry, E.; Lopes, A.; Mougin, E.; Hsu, C.C.; Han, H.C.; Kong, J.A.; Shin, R.T. Retrieval of Forest Biomass from SAR Data. Int. J. Remote Sens. 1994, 15, 2777–2796. [Google Scholar] [CrossRef]
- Smith, J.E.; Heath, L.S.; Woodbury, P.B. How to Estimate Forest Carbon for Large Areas from Inventory Data. J. For. 2004, 102, 25–31. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. BioScience 2004, 54, 547. [Google Scholar] [CrossRef]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in Northern Vegetation Activity Inferred from Satellite Data of Vegetation Index during 1981 to 1999. J. Geophys. Res. Atmos. 2001, 106, 20069–20083. [Google Scholar] [CrossRef]
- Carlà, R.; Santurri, L.; Bonora, L.; Conese, C. Multitemporal Burnt Area Detection Methods Based on a Couple of Images Acquired after the Fire Event. In Proceedings of the SPIE REMOTE SENSING, Berlin, Germany, 31 August–3 September 2009; Volume 7472, p. 74720C. [Google Scholar]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote Sensing of the Terrestrial Carbon Cycle: A Review of Advances over 50 Years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Ranson, K.J.; Sun, G. Modeling Lidar Returns from Forest Canopies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2617–2626. [Google Scholar] [CrossRef]
- Bottai, L.; Arcidiaco, L.; Chiesi, M.; Maselli, F. Application of a Single-Tree Identification Algorithm to LiDAR Data for the Simulation of Stem Volume Current Annual Increment. J. Appl. Remote Sens. 2013, 7, 073699. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito-Santo, F.; Hunter, M.O.; de Oliveira, R. Estimates of Forest Canopy Height and Aboveground Biomass Using ICESat. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Nilsson, M. Estimation of Tree Heights and Stand Volume Using an Airborne Lidar System. Remote Sens. Environ. 1996, 56, 1–7. [Google Scholar] [CrossRef]
- Silva, C.A.; Klauberg, C.; Hudak, A.T.; Vierling, L.A.; Liesenberg, V.; Carvalho, S.P.E.; Rodriguez, L.C.E. A Principal Component Approach for Predicting the Stem Volume in Eucalyptus Plantations in Brazil Using Airborne LiDAR Data. Forestry 2016, 89, 422–433. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping Forest Canopy Height Globally with Spaceborne Lidar. J. Geophys. Res. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Marselis, S.M.; Abernethy, K.; Alonso, A.; Armston, J.; Baker, T.R.; Bastin, J.; Bogaert, J.; Boyd, D.S.; Boeckx, P.; Burslem, D.F.R.P.; et al. Evaluating the Potential of Full-waveform Lidar for Mapping Pan-tropical Tree Species Richness. Glob. Ecol. Biogeogr. 2020, 29, 1799–1816. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Whitt, M.W.; Dobson, M.C. Measuring the Propagation Properties of a Forest Canopy Using a Polarimetric Scatterometer. IEEE Trans. Antennas Propagat. 1990, 38, 251–258. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Paloscia, S.; Pampaloni, P.; Schiavon, G.; Sigismondi, S.; Solimini, D. The Potential of Multifrequency Polarimetric SAR in Assessing Agricultural and Arboreous Biomass. IEEE Trans. Geosci. Remote Sens. 1997, 35, 5–17. [Google Scholar] [CrossRef]
- Richards, J.; Sun, G.; Simonett, D. L-Band Radar Backscatter Modeling of Forest Stands. IEEE Trans. Geosci. Remote Sens. 1987, GE-25, 487–498. [Google Scholar] [CrossRef]
- Le Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating Forest Biomass to SAR Data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 403–411. [Google Scholar] [CrossRef]
- Hayashi, M.; Motohka, T.; Sawada, Y. Aboveground Biomass Mapping Using ALOS-2/PALSAR-2 Time-Series Images for Borneo’s Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5167–5177. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS Mission: Mapping Global Forest Biomass to Better Understand the Terrestrial Carbon Cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Rosenqvist, A.; Shimada, M.; Ito, N.; Watanabe, M. ALOS PALSAR: A Pathfinder Mission for Global-Scale Monitoring of the Environment. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3307–3316. [Google Scholar] [CrossRef]
- Rosenqvist, A.; Shimada, M.; Suzuki, S.; Ohgushi, F.; Tadono, T.; Watanabe, M.; Tsuzuku, K.; Watanabe, T.; Kamijo, S.; Aoki, E. Operational Performance of the ALOS Global Systematic Acquisition Strategy and Observation Plans for ALOS-2 PALSAR-2. Remote Sens. Environ. 2014, 155, 3–12. [Google Scholar] [CrossRef]
- Kasischke, E.S.; Tanase, M.A.; Bourgeau-Chavez, L.L.; Borr, M. Soil Moisture Limitations on Monitoring Boreal Forest Regrowth Using Spaceborne L-Band SAR Data. Remote Sens. Environ. 2011, 115, 227–232. [Google Scholar] [CrossRef]
- Ranson, K.J.; Sun, G. Effects of Environmental Conditions on Boreal Forest Classification and Biomass Estimates with SAR. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1242–1252. [Google Scholar] [CrossRef]
- Rignot, E.; Way, J.; Williams, C.; Viereck, L. Radar Estimates of Aboveground Biomass in Boreal Forests of Interior Alaska. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1117–1124. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Moghaddam, M. Estimation of Crown and Stem Water Content and Biomass of Boreal Forest Using Polarimetric SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2000, 38, 697–709. [Google Scholar] [CrossRef]
- Stelmaszczuk-Górska, M.; Urbazaev, M.; Schmullius, C.; Thiel, C. Estimation of Above-Ground Biomass over Boreal Forests on Siberia Using Updated In Situ, ALOS-2 PALSAR-2, and RADARSAT-2 Data. Remote Sens. 2018, 10, 1550. [Google Scholar] [CrossRef]
- Karila, K.; Yu, X.; Vastaranta, M.; Karjalainen, M.; Puttonen, E.; Hyyppä, J. TanDEM-X Digital Surface Models in Boreal Forest above-Ground Biomass Change Detection. ISPRS J. Photogramm. Remote Sens. 2019, 148, 174–183. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest Biomass Mapping from Lidar and Radar Synergies. Remote Sens. Environ. 2011, 115, 2906–2916. [Google Scholar] [CrossRef]
- Hajnsek, I.; Kugler, F.; Lee, S.-K.; Papathanassiou, K.P. Tropical-Forest-Parameter Estimation by Means of Pol-InSAR: The INDREX-II Campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar] [CrossRef]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing Performance of L- and P-Band Polarimetric Interferometric SAR Data in Estimating Boreal Forest Above-Ground Biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Häme, T.; Praks, J. Polarimetric ALOS PALSAR Time Series in Mapping Biomass of Boreal Forests. Remote Sens. 2017, 9, 999. [Google Scholar] [CrossRef]
- Tebaldini, S.; Rocca, F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P- and L-Bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 232–246. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O. ESA Biomass Climate Change Initiative (Biomass_cci): Global Datasets of Forest above-Ground Biomass for the Year 2017 V1; Centre for Environmental Analysis: Chilton, UK, 2019. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T.; LeToan, T.; Beaudoin, A.; Kasischke, E.S.; Christensen, N. Dependence of Radar Backscatter on Coniferous Forest Biomass. IEEE Trans. Geosci. Remote Sens. 1992, 30, 412–415. [Google Scholar] [CrossRef]
- Ranson, K.J.; Sun, G. Mapping Biomass of a Northern Forest Using Multifrequency SAR Data. IEEE Trans. Geosci. Remote Sens. 1994, 32, 388–396. [Google Scholar] [CrossRef]
- Pulliainen, J.T.; Heiska, K.; Hyyppa, J.; Hallikainen, M.T. Backscattering Properties of Boreal Forests at the C- and X-Bands. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1041–1050. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground Biomass Retrieval in Tropical Forests—The Potential of Combined X- and L-Band SAR Data Use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Neeff, T.; Dutra, L.V.; dos Santos, J.R.; da Costa Freitas, C.; Araujo, L.S. Tropical Forest Measurement by Interferometric Height Modeling and P-Band Radar Backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar] [CrossRef]
- Tanase, M.; de la Riva, J.; Santoro, M.; Pérez-Cabello, F.; Kasischke, E. Sensitivity of SAR Data to Post-Fire Forest Regrowth in Mediterranean and Boreal Forests. Remote Sens. Environ. 2011, 115, 2075–2085. [Google Scholar] [CrossRef]
- Minchella, A.; Del Frate, F.; Capogna, F.; Anselmi, S.; Manes, F. Use of Multitemporal SAR Data for Monitoring Vegetation Recovery of Mediterranean Burned Areas. Remote Sens. Environ. 2009, 113, 588–597. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Modeling Aboveground Biomass in Tropical Forests Using Multi-Frequency SAR Data—A Comparison of Methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 298–306. [Google Scholar] [CrossRef]
- Scarascia-Mugnozza, G.; Oswald, H.; Piussi, P.; Radoglou, K. Forests of the Mediterranean Region: Gaps in Knowledge and Research Needs. For. Ecol. Manag. 2000, 132, 97–109. [Google Scholar] [CrossRef]
- Bispo, P.; da, C.; Rodríguez-Veiga, P.; Zimbres, B.; do Couto de Miranda, S.; Henrique Giusti Cezare, C.; Fleming, S.; Baldacchino, F.; Louis, V.; Rains, D.; et al. Woody Aboveground Biomass Mapping of the Brazilian Savanna with a Multi-Sensor and Machine Learning Approach. Remote Sens. 2020, 12, 2685. [Google Scholar] [CrossRef]
- Alebele, Y.; Zhang, X.; Wang, W.; Yang, G.; Yao, X.; Zheng, H.; Zhu, Y.; Cao, W.; Cheng, T. Estimation of Canopy Biomass Components in Paddy Rice from Combined Optical and SAR Data Using Multi-Target Gaussian Regressor Stacking. Remote Sens. 2020, 12, 2564. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Mura, M.; Zolli, C.; Maselli, F.; Chiesi, M.; Bottai, L.; Chirici, G. The Potential of Multifrequency SAR Images for Estimating Forest Biomass in Mediterranean Areas. Remote Sens. Environ. 2017, 200, 63–73. [Google Scholar] [CrossRef]
- Rapetti, F.; Vittorini, S. Carta Climatica Della Toscana; Pacini Editore: Pisa, Italy, 1995. [Google Scholar]
- Gasparini, P.; Bertani, R.; De Natale, F.; Di Cosmo, L.; Pompei, E. Quality Control Procedures in the Italian National Forest Inventory. J. Environ. Monit. 2009, 11, 761. [Google Scholar] [CrossRef]
- Lawrence, M.; McRoberts, R.E.; Tomppo, E.; Gschwantner, T.; Gabbler, K. Comparison of National Forest Inventories. In National Forest Inventories; Tomppo, E., Gschwantner, T., Lawrence, M., McRoberts, R.E., Eds.; Springer: New York, NY, USA, 2010; ISBN 978-90-481-3232-4. [Google Scholar]
- Fattorini, L.; Marcheselli, M.; Pisani, C. A Three-Phase Sampling Strategy for Large-Scale Multiresource Forest Inventories. JABES 2006, 11, 296–316. [Google Scholar] [CrossRef]
- Regione Toscana GEOScopio. Available online: www502.regione.toscana.it/geoscopio/cartoteca.html (accessed on 6 March 2020).
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Kindermann, J.; Linden, A. Inversion of Neural Networks by Gradient Descent. Parallel Comput. 1990, 14, 277–286. [Google Scholar] [CrossRef]
- Santi, E. Neural Networks Applications for the Remote Sensing of Hydrological Parameters. In Artificial Neural Networks-Models and Applications; Garcia Rosa, J.L., Ed.; IntechOpen: London, UK, 2016; ISBN 978-953-51-2705-5. [Google Scholar]
- Baghdadi, N.; Gaultier, S.; King, C. Retrieving Surface Roughness and Soil Moisture from Synthetic Aperture Radar (SAR) Data Using Neural Networks. Can. J. Remote Sens. 2002, 28, 701–711. [Google Scholar] [CrossRef]
- Del Frate, F.; Ferrazzoli, P.; Schiavon, G. Retrieving Soil Moisture and Agricultural Variables by Microwave Radiometry Using Neural Networks. Remote Sens. Environ. 2003, 84, 174–183. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Parasuraman, K. On the Relevance of Using Artificial Neural Networks for Estimating Soil Moisture Content. J. Hydrol. 2008, 362, 1–18. [Google Scholar] [CrossRef]
- Dai, X.; Huo, Z.; Wang, H. Simulation for Response of Crop Yield to Soil Moisture and Salinity with Artificial Neural Network. Field Crop. Res. 2011, 121, 441–449. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Clarizia, M.P.; Comite, D.; Dente, L.; Guerriero, L.; Pierdicca, N.; Floury, N. Remote Sensing of Forest Biomass Using GNSS Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2351–2368. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G. Application of Artificial Neural Networks for the Soil Moisture Retrieval from Active and Passive Microwave Spaceborne Sensors. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 61–73. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).