End-to-End Super-Resolution for Remote-Sensing Images Using an Improved Multi-Scale Residual Network
Abstract
1. Introduction
- Difficulty recurring network models: most SR reconstruction models require operators to have superior training methods; meanwhile, some SR reconstruction models have many network layers, which require sophisticated hardware equipment. These characteristics make these network models difficult to recur.
- Inadequate feature utilisation: blindly increasing the number of network layers will aggravate image feature forgetting; however, using only a single up-sampling operation to increase the number of pixels in the final reconstruction stage will cause some of the LR image information to be lost.
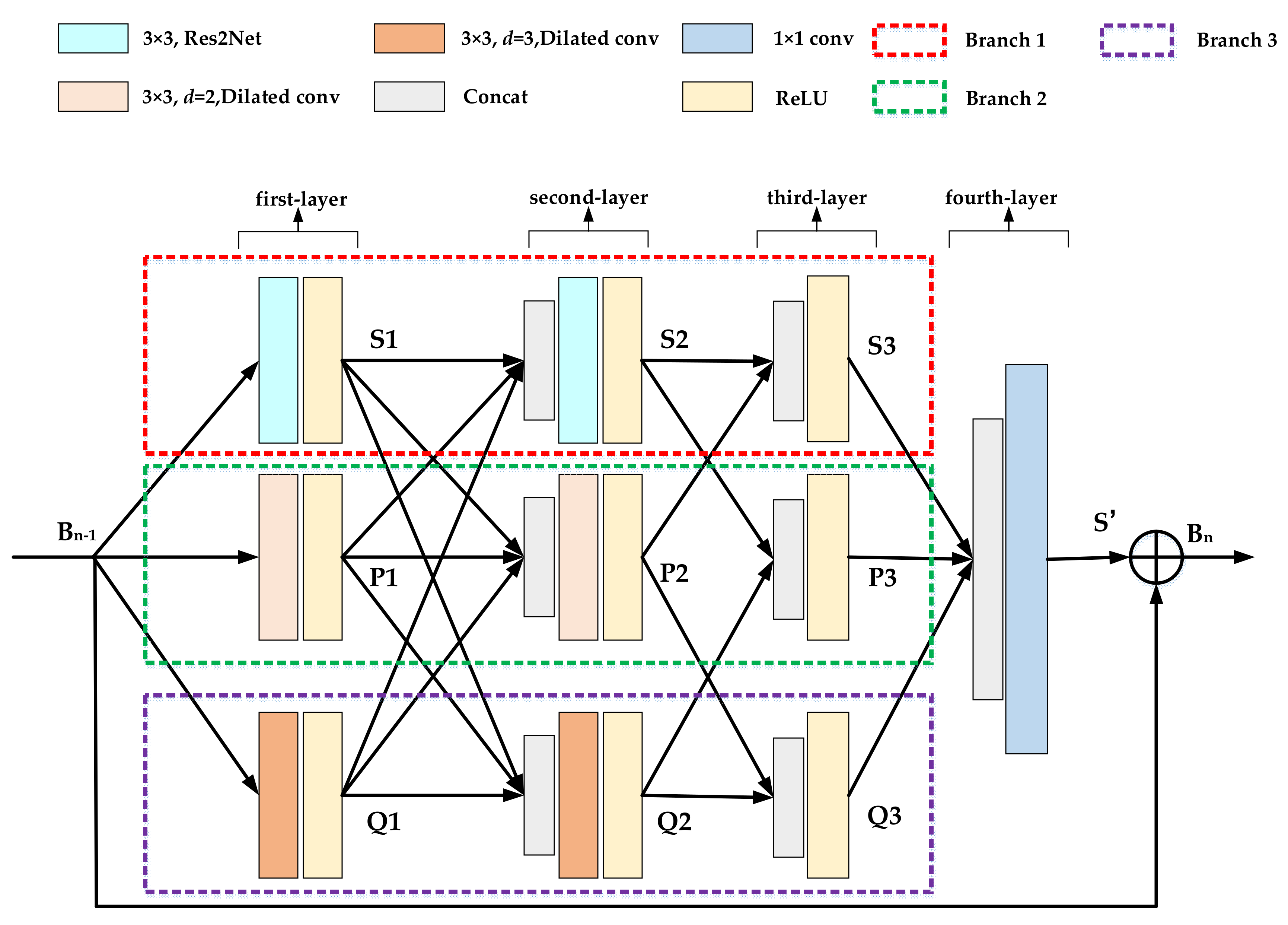
- A new MSDRB is proposed. This module expresses multi-scale features with finer granularity, increases the receptive field of each network layer, and enhances the ability to detect image features adaptively.
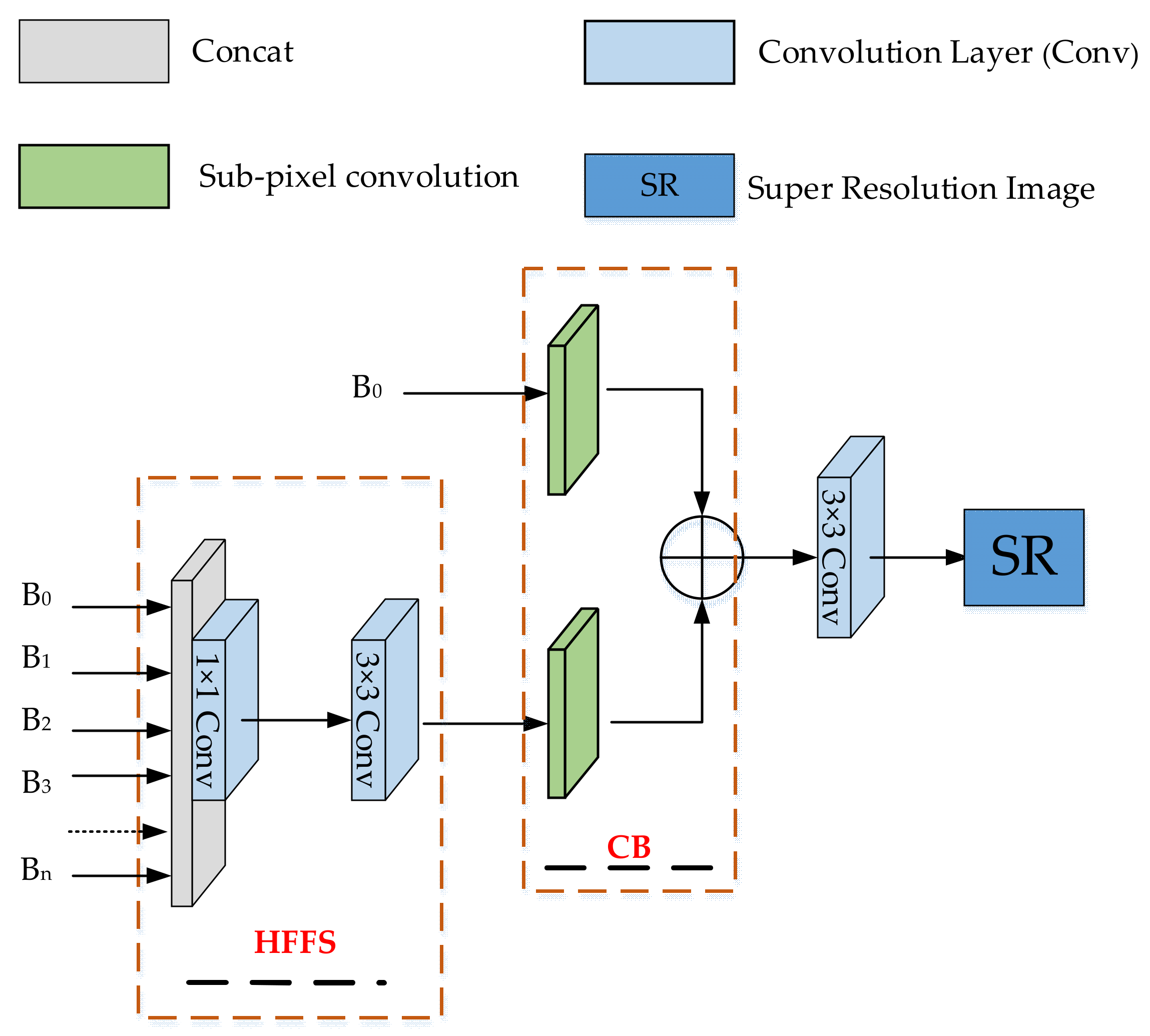
- To fuse the shallow and deep features, a new reconstruction CB is proposed. This module can fully utilise the useful information in the original LR image, prevent network instability, and improve the network robustness and image reconstruction effect.
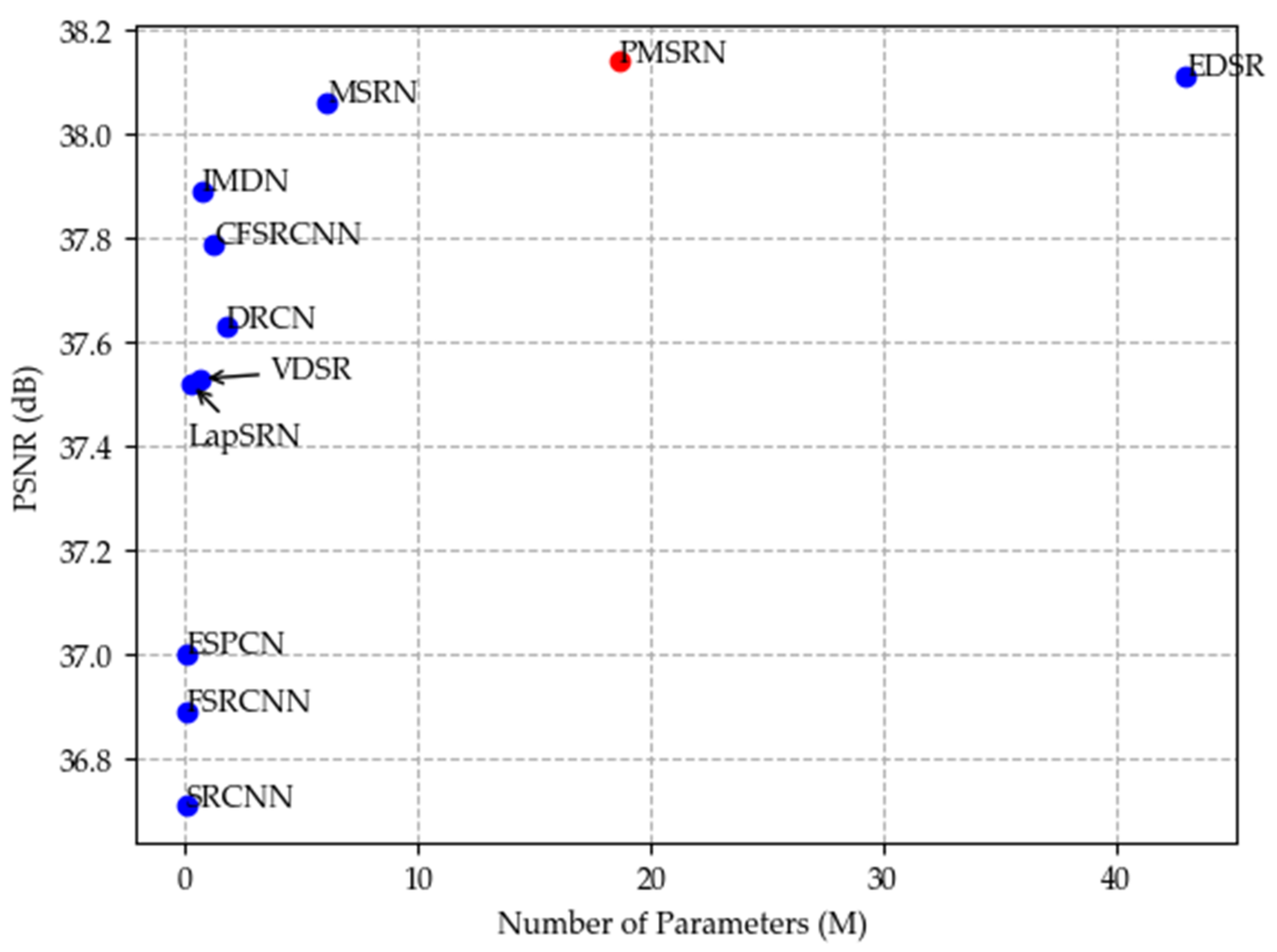
- The proposed PMSRN is easier to train than other networks, since its number of parameters is only 43.33% of that of EDSR, and the module is independent and easy to migrate to other networks for learning.
2. Materials and Methods
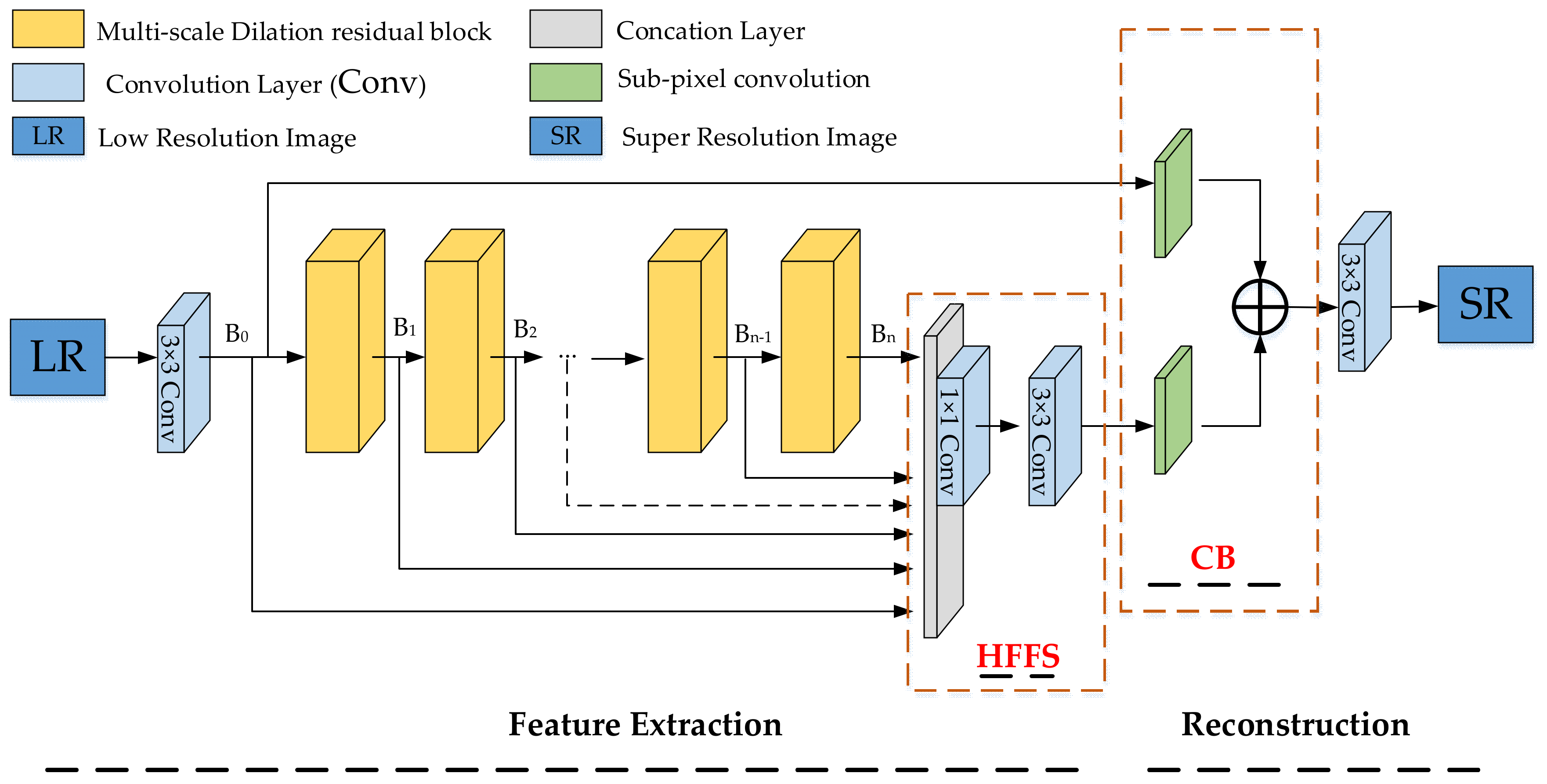
2.1. Network Architecture
- In the feature extraction, the MSDRB replaces the multi-scale residual module.
- In the reconstruction part, a CB module was added.
2.1.1. Multi-Scale Dilation Residual Block (MSDRB)
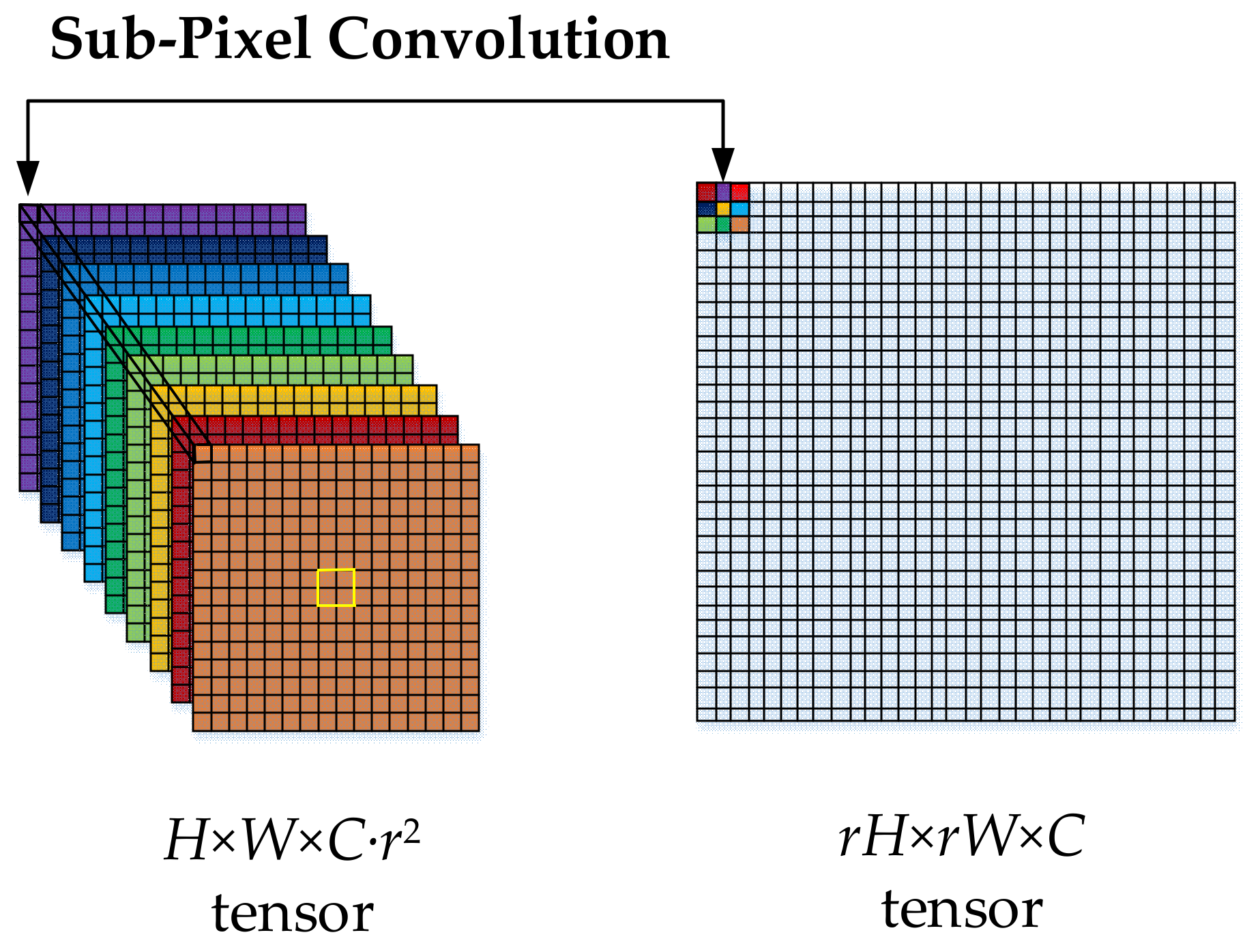
2.1.2. Complementary Block (CB) in Image Reconstruction Structure
2.2. Datasets
2.3. Experimental Environment
3. Results
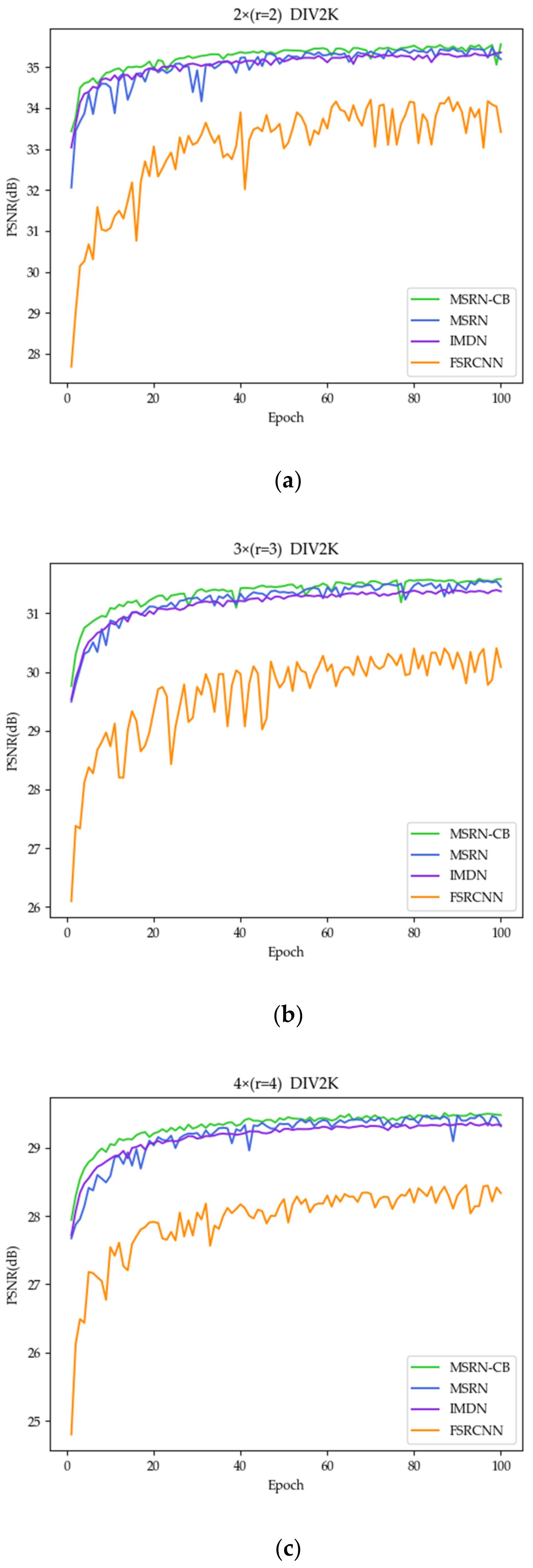
3.1. Necessity of Introducing CB and Res2Net Modules
3.1.1. Benefits of CB
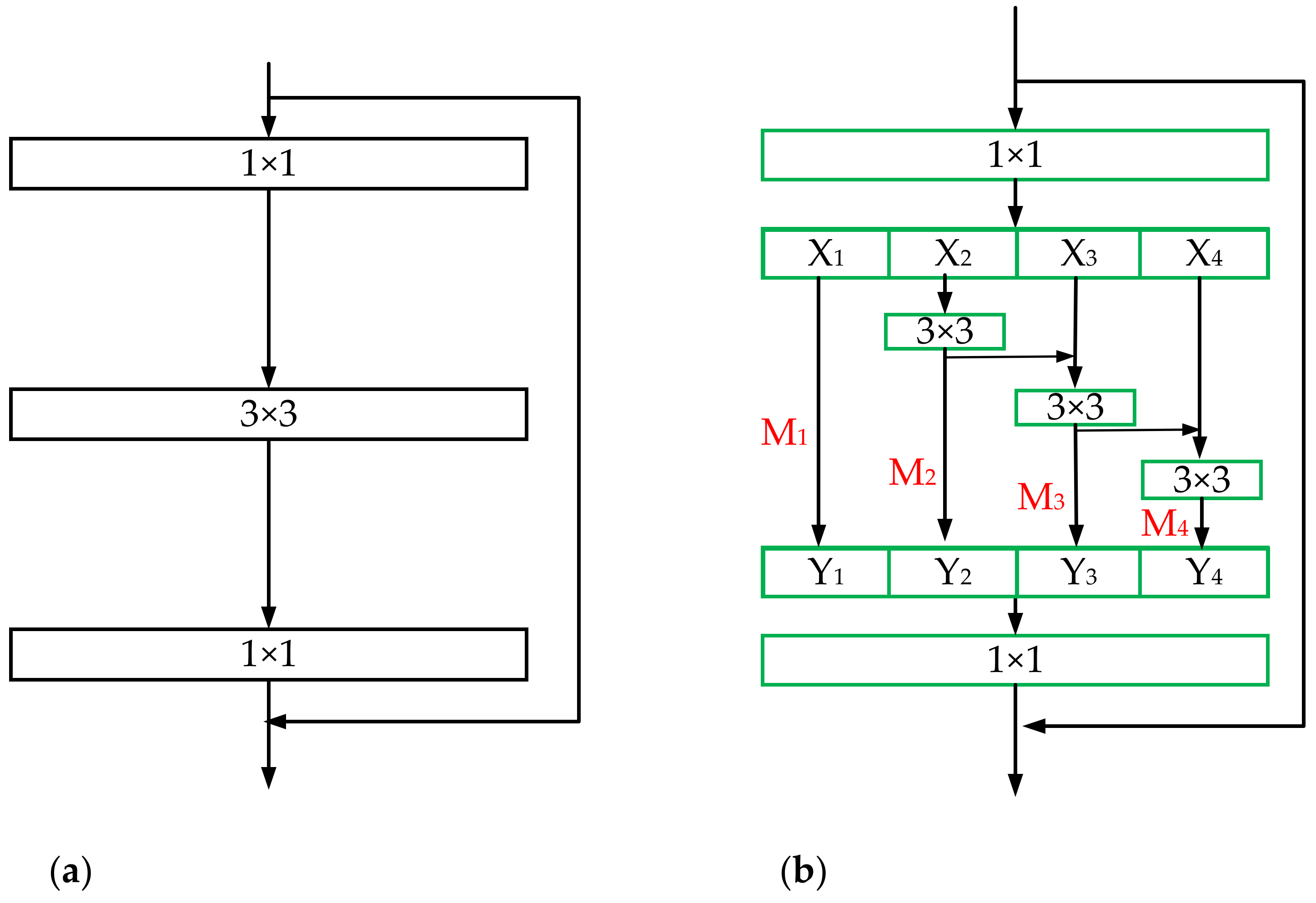
3.1.2. Benefits of Res2Net
3.2. Comparisons with State-of-the-Art Methods
3.2.1. Comparison of Evaluated Results
3.2.2. Visual Effect Comparison
3.2.3. Comparison of Network Scales
3.3. Comparison of Reconstruction Effects of Different Training Sets
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tremsin, A.S.; Siegmund, O.H.W.; Vallerga, J.V. A model of high resolution cross strip readout for photon and ion counting imaging detectors. IEEE Trans. Nucl. Sci. 2005, 52, 1755–1759. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, K.; Gan, S.; Wu, T. Structural Feature Modeling of High-Resolution Remote Sensing Images Using Directional Spatial Correlation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1727–1731. [Google Scholar] [CrossRef]
- Pashaei, M.; Starek, M.J.; Kamangir, H.; Berryhill, J. Deep Learning-Based Single Image Super-Resolution: An Investigation for Dense Scene Reconstruction with UAS Photogrammetry. Remote Sens. 2020, 12, 1757. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Q.; Bao, F.; Liu, Y.; Zhang, C. Single-Image Super-Resolution Based on Rational Fractal Interpolation. IEEE Trans. Image Process. 2018, 27, 3782–3797. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 184–199. [Google Scholar] [CrossRef]
- Brifman, A.; Romano, Y.; Elad, M. Unified Single-Image and Video Super-Resolution via Denoising Algorithms. IEEE Trans. Image Process. 2019, 28, 6063–6076. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision, ECCV 2016, Glasgow, UK, 8–16 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2016; Volume 9906, pp. 391–407. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Husz’ar, F.; Totz, J.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1874–1883. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar] [CrossRef]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Li, J.; Fang, F.; Mei, K.; Zhang, G. Multi-scale Residual Network for Image Super-Resolution. In Proceedings of the European Conference on Computer Vision (ECCV), ECCV 2018, Munich, Germany, 8–14 September 2019; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018; Volume 11212, p. 10. [Google Scholar] [CrossRef]
- Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight Image Super-Resolution with Information Multi-distillation Network. In Proceedings of the MM’19: 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; Volume 10, pp. 2024–2032. [Google Scholar] [CrossRef]
- Tian, C.; Xu, Y.; Zuo, W.; Zhang, B.; Fei, L.; Lin, C. Coarse-to-fine CNN for image super-resolution. IEEE Trans. Multimed. 2020. [Google Scholar] [CrossRef]
- Gao, S.; Cheng, M.-M.; Zhao, K.; Zhang, X.-Y.; Yang, M.-H.; Torr, P.H.S. Res2Net: A New Multi-scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Tong, N.; Lu, H.; Zhang, L.; Ruan, X. Saliency Detection with Multi-Scale Superpixels. IEEE Signal. Process. Lett. 2014, 21, 1035–1039. [Google Scholar] [CrossRef]
- Liu, C.; Sun, X.; Chen, C.; Rosin, P.L.; Yan, Y.; Jin, L. Multi-Scale Residual Hierarchical Dense Networks for Single Image Super-Resolution. IEEE Access 2019, 7, 60572–60583. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Jiang, Y.; Tian, N.; Peng, T.; Zhang, H. Retinal Vessels Segmentation Based on Dilated Multi-Scale Convolutional Neural Network. IEEE Access 2019, 7, 76342–76352. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1122–1131. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M.L. Low-complexity single image super-resolution based on nonnegative neighbor embedding. In Proceedings of the 23rd British Machine Vision Conference, Surrey, UK, 3–7 September 2012. [Google Scholar] [CrossRef]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 711–730. [Google Scholar]
- Arbeláez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar] [CrossRef]
- Matsui, Y.; Ito, K.; Aramaki, Y.; Fujimoto, A.; Ogawa, T.; Yamasaki, T.; Aizawa, K. Sketch-based Manga Retrieval using Manga109 Dataset. Multimed. Tools Appl. 2017, 76, 21811–21838. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Heidarpour, S.I.; Kim, H. Fractal Analysis and Texture Classification of High-Frequency Multiplicative Noise in SAR Sea-Ice Images Based on a Transform- Domain Image Decomposition Method. IEEE Access 2020, 8, 40198–40223. [Google Scholar] [CrossRef]









| Algorithm (Dataset) | Scale | Manga109 |
|---|---|---|
| PSNR/SSIM | ||
| FSRCNN [8] | 2× | 36.10/0.9695 |
| MSRN [15] | 2× | 38.50/0.9766 |
| MSRN-CB | 2× | 38.50/0.9769 |
| IMDN [16] | 2× | 38.47/0.9766 |
| FSRCNN [8] | 3× | 30.76/0.9188 |
| MSRN [15] | 3× | 33.51/0.9442 |
| MSRN-CB | 3× | 33.63/0.9450 |
| IMDN [16] | 3× | 33.21/0.9420 |
| FSRCNN [8] | 4× | 27.71/0.8633 |
| MSRN [15] | 4× | 30.42/0.9083 |
| MSRN-CB | 4× | 30.49/0.9088 |
| IMDN [16] | 4× | 30.19/0.9042 |
| FSRCNN [8] | 8× | 22.82/0.7048 |
| MSRN [15] | 8× | 24.40/0.7729 |
| MSRN-CB | 8× | 24.43/0.7744 |
| IMDN [16] | 8× | 24.22/0.7656 |
| Algorithm (Dataset) | Scale | Manga109 |
|---|---|---|
| PSNR/SSIM | ||
| FSRCNN [8] | 2× | 36.10/0.9695 |
| MSRN [15] | 2× | 38.50/0.9766 |
| MSRN-Res2Net | 2× | 38.68/0.9772 |
| IMDN [16] | 2× | 38.47/0.9766 |
| FSRCNN [8] | 3× | 30.76/0.9188 |
| MSRN [15] | 3× | 33.51/0.9442 |
| MSRN-Res2Net | 3× | 33.60/0.9454 |
| IMDN [16] | 3× | 33.21/0.9420 |
| FSRCNN [8] | 4× | 27.71/0.8633 |
| MSRN [15] | 4× | 30.42/0.9083 |
| MSRN-Res2Net | 4× | 30.65/0.9108 |
| IMDN [16] | 4× | 30.19/0.9042 |
| FSRCNN [8] | 8× | 22.82/0.7048 |
| MSRN [15] | 8× | 24.40/0.7729 |
| MSRN-Res2Net | 8× | 24.55/0.7790 |
| IMDN [16] | 8× | 24.22/0.7656 |
| Algorithm | Scale | Set5 | Set14 | B100 | Urban100 | Manga109 |
|---|---|---|---|---|---|---|
| PSNR/SSIM | PSNR/SSIM | PSNR/SSIM | PSNR/SSIM | PSNR/SSIM | ||
| Bicubic | 2× | 33.69/0.9284 | 30.34/0.8675 | 29.57/0.8434 | 26.88/0.8438 | 30.82/0.9332 |
| SRCNN [6] | 2× | 36.71/0.9536 | 32.32/0.9052 | 31.36/0.8880 | 29.54/0.8962 | 35.74/0.9661 |
| FSRCNN [8] | 2× | 36.89/0.9559 | 32.62/0.9085 | 31.42/0.8895 | 29.73/0.8996 | 36.10/0.9695 |
| ESPCN [9] | 2× | 37.00/0.9559 | 32.75/0.9098 | 31.51/0.8939 | 29.87/0.9065 | 36.21/0.9694 |
| VDSR [11] | 2× | 37.53/0.9583 | 33.05/0.9107 | 31.92/0.8965 | 30.79/0.9157 | 37.22/0.9729 |
| DRCN [12] | 2× | 37.63/0.9584 | 33.06/0.9108 | 31.85/0.8947 | 30.76/0.9147 | 37.63/0.9723 |
| LapSRN [13] | 2× | 37.52/0.9581 | 33.08/0.9109 | 31.80/0.8949 | 30.41/0.9112 | 37.27/0.9855 |
| EDSR [14] | 2× | 38.11/0.9601 | 33.92/0.9195 | 32.32/0.9013 | -/- | -/- |
| MSRN [15] | 2× | 38.06/0.9605 | 33.59/0.9177 | 32.19/0.8999 | 32.10/0.9285 | 38.42/0.9767 |
| IMDN [16] | 2× | 37.89/0.9602 | 33.42/0.9164 | 32.09/0.8985 | 31.84/0.9256 | 38.41/0.9766 |
| CFSRCNN [17] | 2× | 37.79/0.9591 | 33.51/0.9165 | 32.11/0.8988 | 32.07/0.9273 | -/- |
| PMSRN (our) | 2× | 38.14/0.9610 | 33.85/0.9204 | 32.27/0.9007 | 32.51/0.9317 | 38.86/0.9776 |
| Bicubic | 3× | 30.41/0.8655 | 27.64/0.7722 | 27.21/0.7344 | 24.46/0.7411 | 26.96/0.8555 |
| SRCNN [6] | 3× | 32.47/0.9067 | 29.23/0.8201 | 28.31/0.7832 | 26.25/0.8028 | 30.59/0.9107 |
| FSRCNN [8] | 3× | 33.03/0.9141 | 29.46/0.8253 | 28.47/0.7887 | 26.38/0.8065 | 30.87/0.9198 |
| ESPCN [9] | 3× | 33.02/0.9135 | 29.49/0.8271 | 28.50/0.7937 | 26.41/0.8161 | 30.79/0.9181 |
| VDSR [11] | 3× | 33.68/0.9201 | 29.86/0.8312 | 28.83/0.7966 | 27.15/0.8315 | 32.01/0.9310 |
| DRCN [12] | 3× | 33.85/0.9215 | 29.89/0.8317 | 28.81/0.7954 | 27.16/0.8311 | 32.31/0.9328 |
| LapSRN [13] | 3× | 33.82/0.9207 | 29.89/0.8304 | 28.82/0.7950 | 27.07/0.8298 | 32.21/0.9318 |
| EDSR [14] | 3× | 34.65/0.9282 | 30.52/0.8462 | 29.25/0.8093 | -/- | -/- |
| MSRN [15] | 3× | 34.45/0.9276 | 30.40/0.8431 | 29.12/0.8059 | 28.29/0.8549 | 33.62/0.9451 |
| IMDN [16] | 3× | 34.29/0.9266 | 30.23/0.8400 | 29.04/0.8037 | 28.05/0.8498 | 33.32/0.9429 |
| CFSRCNN [17] | 3× | 34.24/0.9256 | 30.27/0.8410 | 29.03/0.8035 | 28.04/0.8496 | -/- |
| PMSRN (our) | 3× | 34.66/0.9291 | 30.48/0.8456 | 29.20/0.8083 | 28.59/0.8616 | 33.92/0.9474 |
| Bicubic | 4× | 28.43/0.8022 | 26.10/0.6936 | 25.97/0.6517 | 23.14/0.6599 | 24.91/0.7826 |
| SRCNN [6] | 4× | 30.50/0.8573 | 27.62/0.7453 | 26.91/0.6994 | 24.53/0.7236 | 27.66/0.8505 |
| FSRCNN [8] | 4× | 30.74/0.8702 | 27.68/0.7580 | 26.97/0.7144 | 24.59/0.7294 | 27.87/0.8650 |
| ESPCN [9] | 4× | 30.66/0.8646 | 27.71/0.7562 | 26.98/0.7124 | 24.60/0.7360 | 27.70/0.8560 |
| VDSR [11] | 4× | 31.36/0.8796 | 28.11/0.7624 | 27.29/0.7167 | 25.18/0.7543 | 28.83/0.8809 |
| DRCN [12] | 4× | 31.56/0.8810 | 28.15/0.7627 | 27.24/0.7150 | 25.15/0.7530 | 28.98/0.8816 |
| LapSRN [13] | 4× | 31.54/0.8811 | 28.19/0.7635 | 27.32/0.7162 | 25.21/0.7564 | 29.09/0.8845 |
| EDSR [14] | 4× | 32.46/0.8968 | 28.80/0.7876 | 27.71/0.7420 | -/- | -/- |
| MSRN [15] | 4× | 32.18/0.8951 | 28.66/0.7835 | 27.61/0.7373 | 26.17/0.7887 | 30.53/0.9093 |
| IMDN [16] | 4× | 32.07/0.8933 | 28.52/0.7800 | 27.52/0.7345 | 25.99/0.7825 | 30.25/0.9052 |
| CFSRCNN [17] | 4× | 32.06/0.8920 | 28.57/0.7800 | 27.53/0.7333 | 26.03/0.7824 | -/- |
| PMSRN (our) | 4× | 32.46/0.8982 | 28.76/0.7863 | 27.69/0.7403 | 26.47/0.7982 | 30.96/0.9146 |
| Bicubic | 8× | 24.40/0.6045 | 23.19/0.5110 | 23.67/0.4808 | 20.74/0.4841 | 21.46/0.6138 |
| SRCNN [6] | 8× | 25.34/0.6471 | 23.86/0.5443 | 24.14/0.5043 | 21.29/0.5133 | 22.46/0.6606 |
| FSRCNN [8] | 8× | 25.82/0.7183 | 24.18/0.6075 | 24.32/0.5729 | 21.56/0.5613 | 22.83/0.7047 |
| ESPCN [9] | 8× | 25.75/0.6738 | 24.21/0.5109 | 24.37/0.5277 | 21.59/0.5420 | 22.83/0.6715 |
| VDSR [11] | 8× | 25.73/0.6743 | 23.20/0.5110 | 24.34/0.5169 | 21.48/0.5289 | 22.73/0.6688 |
| DRCN [12] | 8× | 25.93/0.6743 | 24.25/0.5510 | 24.49/0.5168 | 21.71/0.5289 | 23.20/0.6686 |
| LapSRN [13] | 8× | 26.15/0.7028 | 24.45/0.5792 | 24.54/0.5293 | 21.81/0.5555 | 23.39/0.7068 |
| MSRN [15] | 8× | 26.93/0.7730 | 24.86/0.6388 | 24.78/0.5959 | 22.40/0.6144 | 24.45/0.7746 |
| IMDN [16] | 8× | 26.72/0.7642 | 24.85/0.6363 | 24.74/0.5935 | 22.32/0.6096 | 24.29/0.7680 |
| PMSRN (our) | 8× | 27.07/0.7803 | 24.99/0.6439 | 24.86/0.5995 | 22.60/0.6246 | 24.80/0.7865 |
| Algorithm (Dataset) | Scale | AID-Test |
|---|---|---|
| PSNR/SSIM | ||
| MSRN(DIV2K) | 2× | 35.55/0.9403 |
| MSRN(AID) | 2× | 35.91/0.9436 |
| PMSRN(DIV2K) | 2× | 35.65/0.9413 |
| PMSRN(AID) | 2× | 36.00/0.9444 |
| MSRN(DIV2K) | 3× | 31.50/0.8634 |
| MSRN(AID) | 3× | 31.89/0.8711 |
| PMSRN(DIV2K) | 3× | 31.58/0.8656 |
| PMSRN(AID) | 3× | 32.02/0.8737 |
| MSRN(DIV2K) | 4× | 29.30/0.7917 |
| MSRN(AID) | 4× | 29.68/0.8028 |
| PMSRN(DIV2K) | 4× | 29.39/0.7950 |
| PMSRN(AID) | 4× | 29.79/0.8068 |
| MSRN(DIV2K) | 8× | 25.67/0.6299 |
| MSRN(AID) | 8× | 25.87/0.6399 |
| PMSRN(DIV2K) | 8× | 25.74/0.6342 |
| PMSRN(AID) | 8× | 25.93/0.6440 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huan, H.; Li, P.; Zou, N.; Wang, C.; Xie, Y.; Xie, Y.; Xu, D. End-to-End Super-Resolution for Remote-Sensing Images Using an Improved Multi-Scale Residual Network. Remote Sens. 2021, 13, 666. https://doi.org/10.3390/rs13040666
Huan H, Li P, Zou N, Wang C, Xie Y, Xie Y, Xu D. End-to-End Super-Resolution for Remote-Sensing Images Using an Improved Multi-Scale Residual Network. Remote Sensing. 2021; 13(4):666. https://doi.org/10.3390/rs13040666
Chicago/Turabian StyleHuan, Hai, Pengcheng Li, Nan Zou, Chao Wang, Yaqin Xie, Yong Xie, and Dongdong Xu. 2021. "End-to-End Super-Resolution for Remote-Sensing Images Using an Improved Multi-Scale Residual Network" Remote Sensing 13, no. 4: 666. https://doi.org/10.3390/rs13040666
APA StyleHuan, H., Li, P., Zou, N., Wang, C., Xie, Y., Xie, Y., & Xu, D. (2021). End-to-End Super-Resolution for Remote-Sensing Images Using an Improved Multi-Scale Residual Network. Remote Sensing, 13(4), 666. https://doi.org/10.3390/rs13040666








