Co-Seismic Inversion and Post-Seismic Deformation Mechanism Analysis of 2019 California Earthquake
Abstract
1. Introduction
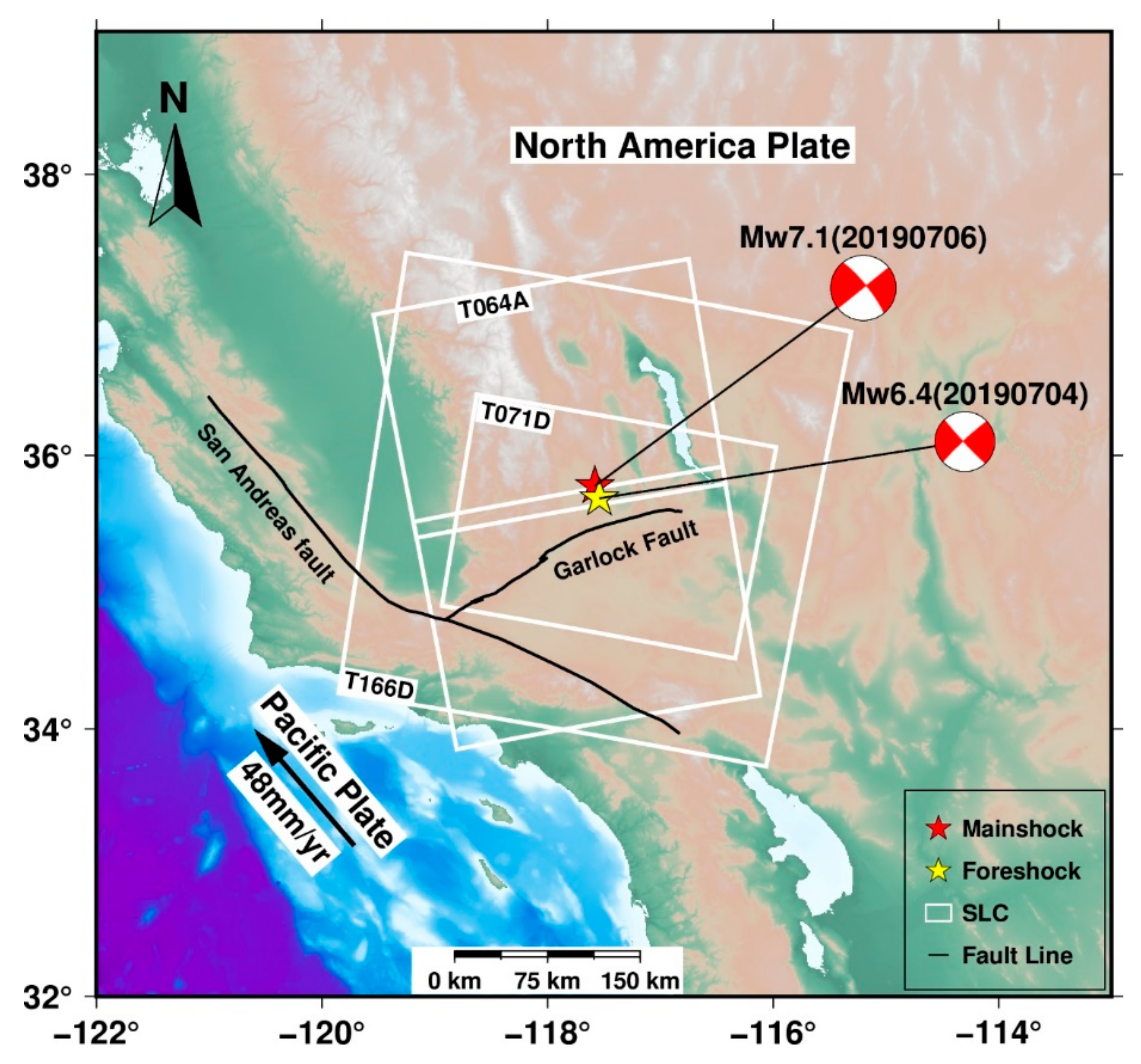
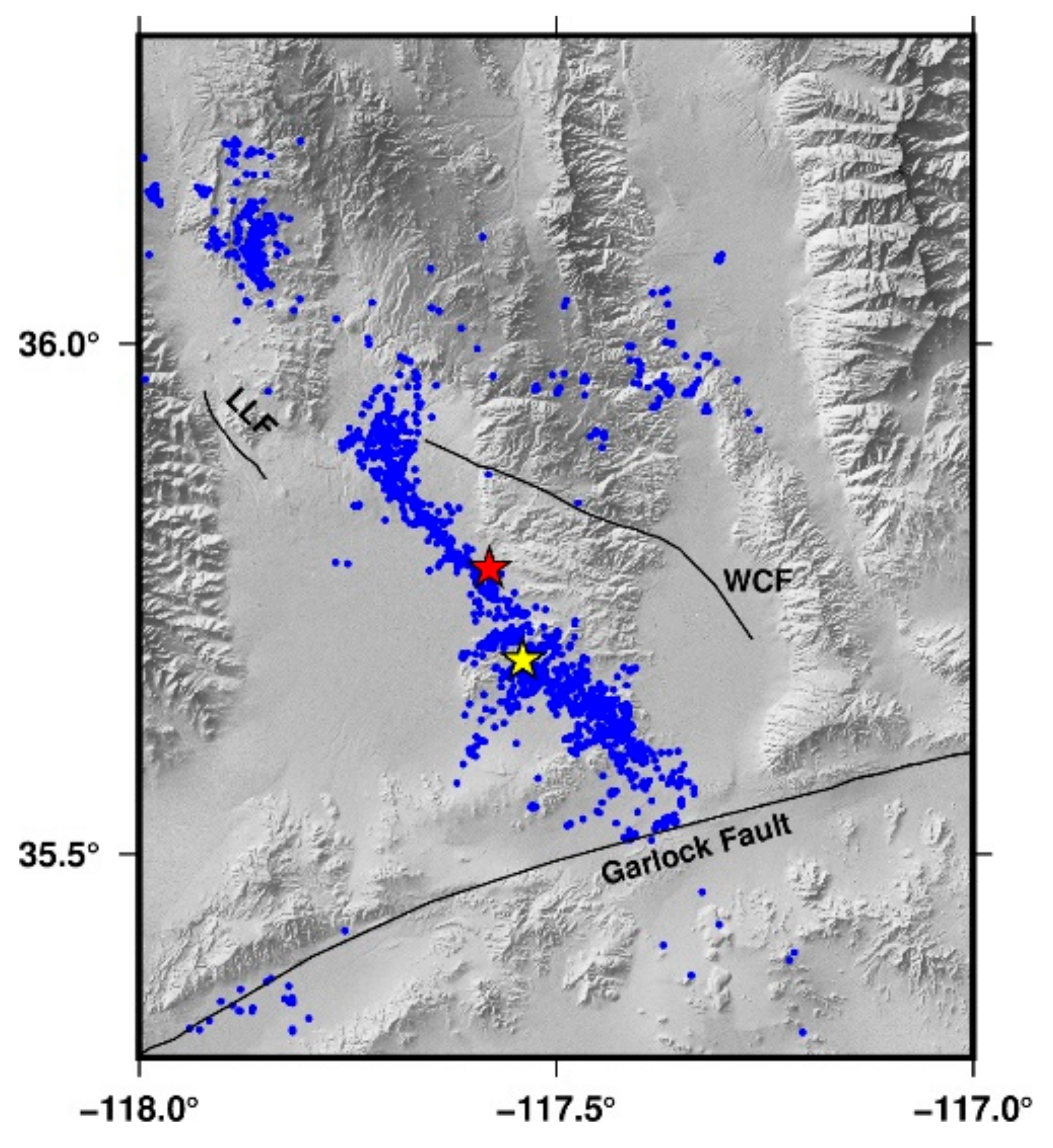
2. Geological Background
3. Materials and Methods
3.1. SAR Datasets
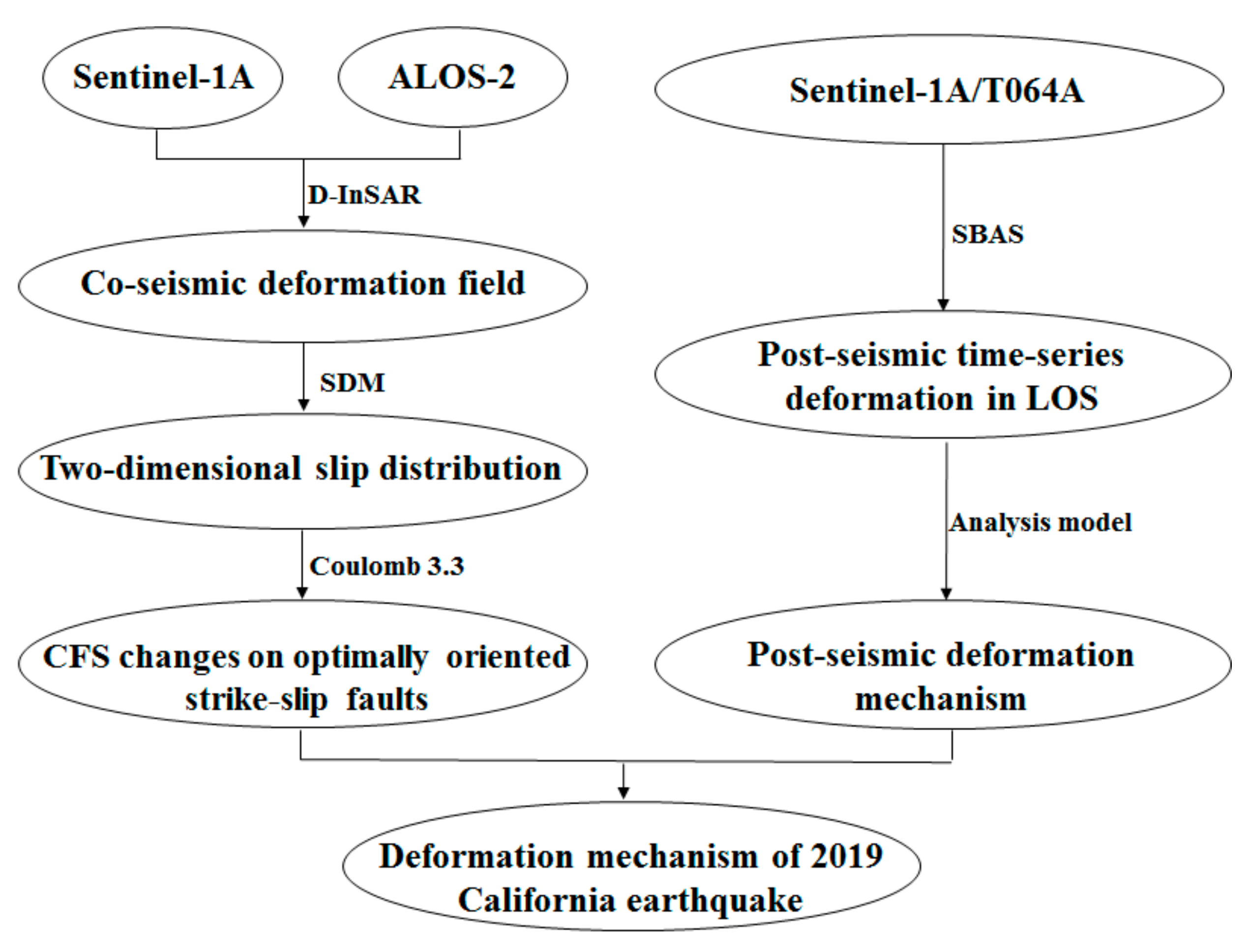
3.2. Data Processing
4. Results
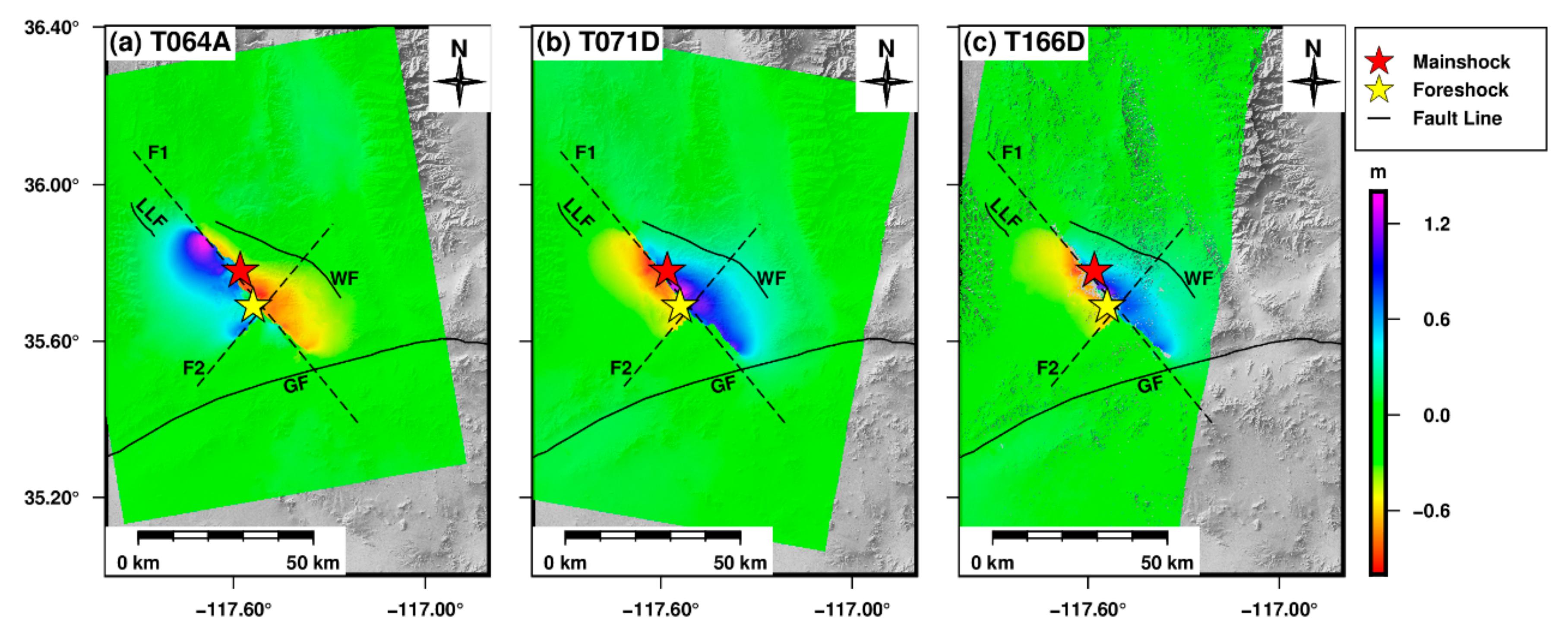
4.1. Co-Seismic Deformation Field
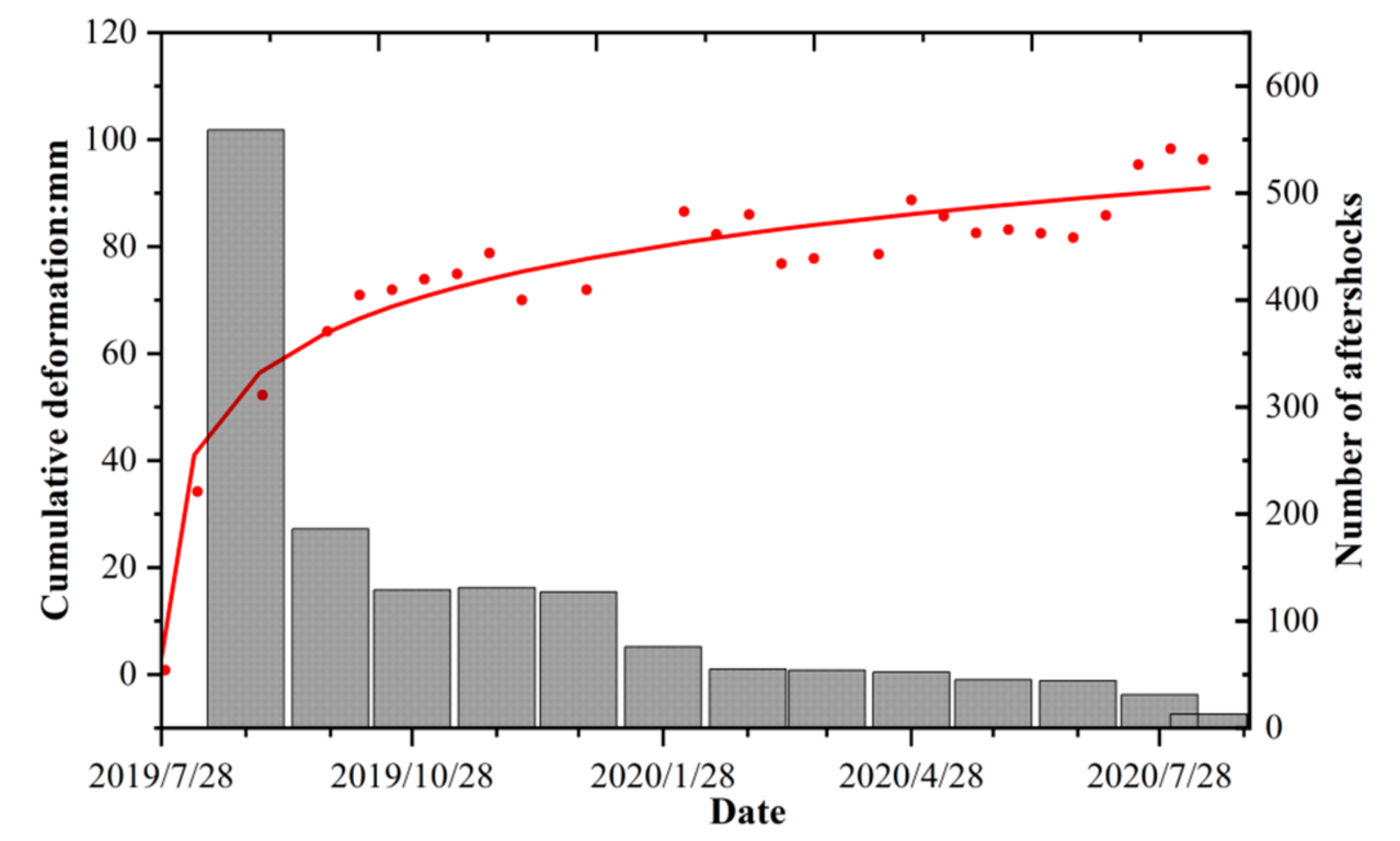
4.2. Post-Seismic Time-Series Deformation
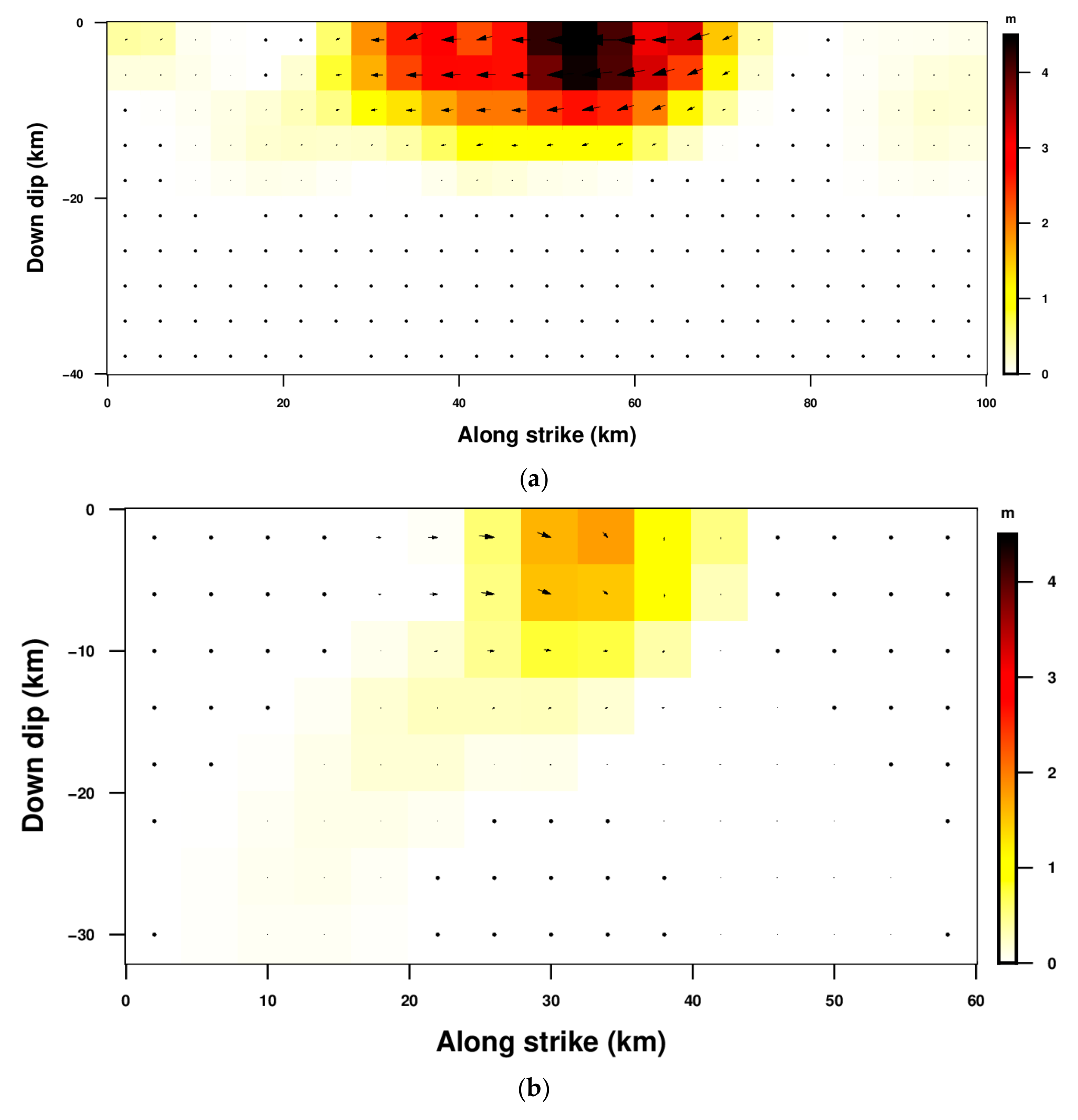
4.3. Co-Seismic Slip Distribution Inversion
5. Discussion
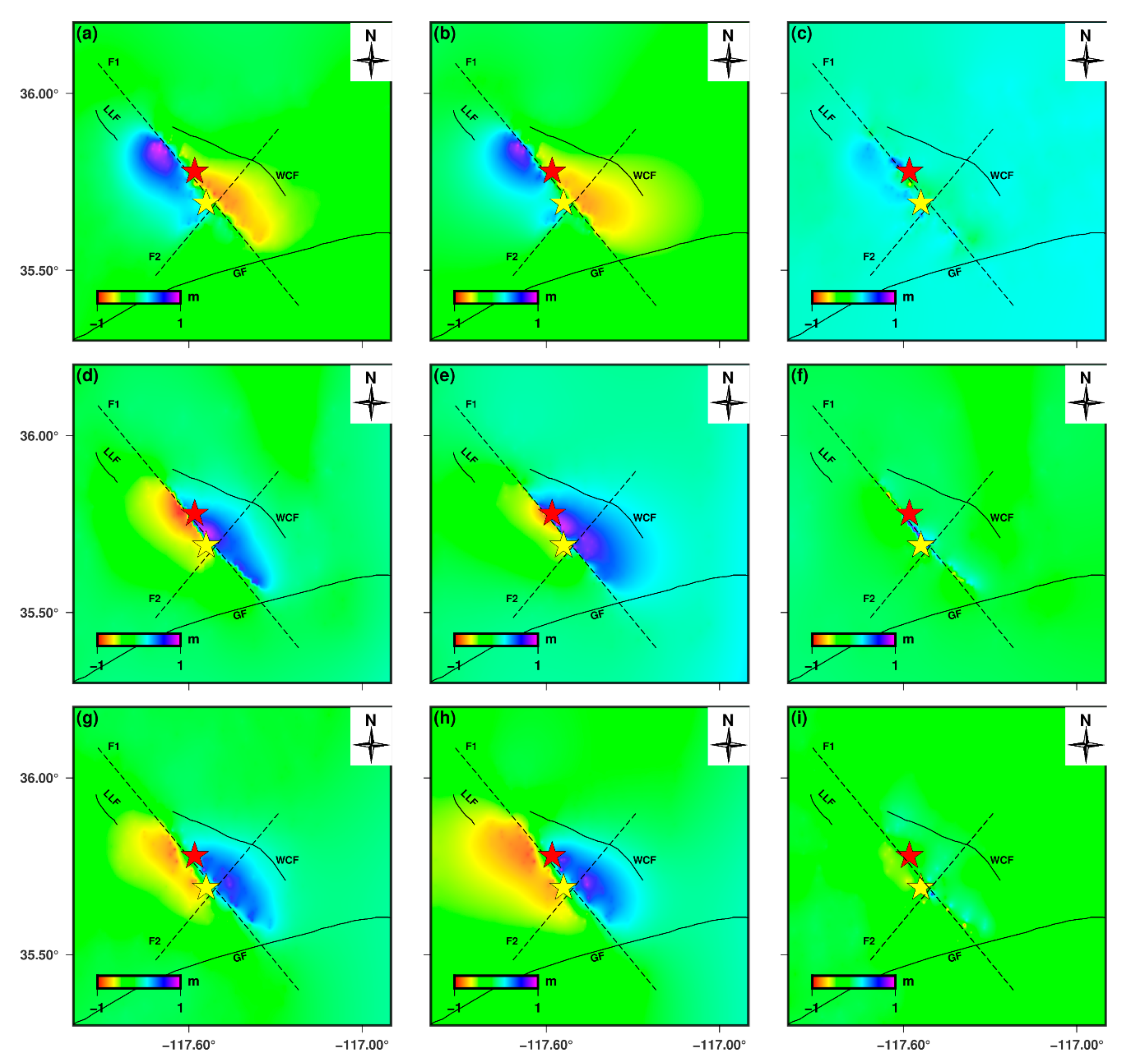
5.1. Coulomb Stress Change
5.2. Co-Seismic and Post-Earthquake Activity Mechanism
6. Conclusions
- The maximum uplift co-seismic deformation was 1.4 m in the LOS. The maximum subsidence co-seismic deformation was 1 m in the LOS. The deformation fields from the ascending and descending tracks exhibited the opposite deformation trend, which is consistent with the characteristics of a strike-slip fault. The co-seismic deformation fields demonstrated that this earthquake event was caused by the ruptures of at least two faults. Multi-faults model was used in the inversion.
- The co-seismic slip distribution inversion illustrates that F1 was dominated by a right-lateral strike-slip, the average rake was −171.83°, and the average slip was 0.4 m. F2 was dominated by a left-lateral strike-slip, the average rake was 4°, and the average slip was 0.13 m. The magnitude of this earthquake was approximately Mw 7.08. This California earthquake was a strike-slip fault event.
- The post-seismic deformation typically occurs near the epicenter. After 402 d, the post-earthquake deformation gradually tends to be stable. The post-seismic deformation mechanism of this earthquake was primarily after-slip. The calculation of the Coulomb stress change exhibits that the co-seismic moment released by the earthquake was approximately 4.24 × 1026 N × m, which is equivalent to a moment magnitude of 7.06. This finding is consistent with the co-seismic slip distribution inversion results. The maximum Coulomb stress was located near F1. However, certain aftershocks were located in negative Coulomb stress areas. Therefore, the failure process of this earthquake was complex.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Chen, G.; Tao, T.; He, P.; Ding, K.; Zou, R.; Li, J.; Wang, Q. The 2019 MW 6.4 and Mw 7.1 Ridgecrest Earthquake Sequence in Eastern California: Rupture on a Conjugate Fault Structure Revealed by GPS and InSAR Measurements. Geophys. J. Int. 2020, 221, 1651–1666. [Google Scholar] [CrossRef]
- Chen, K.; Avouac, J.-P.; Aati, S.; Milliner, C.; Zheng, F.; Shi, C. Cascading and Pulse-Like Ruptures During the 2019 Ridgecrest Earthquakes in the Eastern California Shear Zone. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
- Barnhart, W.D.; Hayes, G.P.; Gold, R.D. The July 2019 Ridgecrest, California, Earthquake Sequence: Kinematics of Slip and Stressing in Cross-Fault Ruptures. Geophys. Res. Lett. 2019, 46, 11859–11867. [Google Scholar] [CrossRef]
- Liu, C.; Lay, T.; Brodsky, E.E.; Dascher-Cousineau, K.; Xiong, X. Emily Co-seismic Rupture Process of the Large 2019 Ridgecrest Earthquakes from Joint Inversion of Geodetic and Seismological Observations. Geophys. Res. Lett. 2019, 46, 11820–11829. [Google Scholar] [CrossRef]
- Shan, X.J.; Qu, C.Y.; Song, X.G.; Zhang, G.F.; Liu, Y.H.; Guo, L.M.; Zhang, G.H.; Li, W.D. Co-seismic deformation field observation and study of Wenchuan Ms8.0 earthquake by InSAR. J. Geophys. 2009, 52, 496–504. [Google Scholar]
- Xu, C.J.; Wang, L.Y. Research progress of seismic source rupture process by joint inversion of geodesy and seismic data. J. Wuhan Univ. (Inf. Sci.) 2010, 35, 457–462. [Google Scholar]
- Wang, C.S.; Shan, X.J.; Wang, C.L.; Ding, X.L.; Zhang, G.D.; Timothy, M. Using finite element and Okada models to invert co-seismic slip of the 2008 Mw 7.2 Yutian earthquake, China, from InSAR data. J. Seismol. 2013, 17, 347–360. [Google Scholar] [CrossRef]
- Li, N.; Zhao, Q.; Sun, H. InSAR observation of the 2015 Ms 7.4 earthquake in Tajikistan and its tectonic significance. Geod. Geodyn. 2018, 38, 43–47. [Google Scholar]
- Niu, Y.F.; Wang, S.; Zhu, W.; Zhang, Q.; Lu, Z.; Zhao, C.Y.; Qu, W. The 2014 Mw 6.1 Ludian Earthquake: The Application of RADARSAT-2 SAR Interferometry and GPS for this Conjugated Ruptured Event. Remote Sens. 2019, 12, 99. [Google Scholar] [CrossRef]
- Oskin, M.; Iriondo, A. Large-Magnitude Transient Strain Accumulation on the Blackwater Fault, Eastern California Shear Zone. Geology 2004, 32, 313. [Google Scholar] [CrossRef]
- Dokka, R.K.; Travis, C.J. Role of the Eastern California Shear Zone in Accommodating Pacific-North American Plate Motion. Geophys. Res. Lett. 1990, 17, 1323–1326. [Google Scholar] [CrossRef]
- Feng, W.; Samsonov, S.; Qiu, Q.; Wang, Y.; Zhang, P.; Li, T.; Zheng, W. Orthogonal Fault Rupture and Rapid Postseismic Deformation Following 2019 Ridgecrest, California, Earthquake Sequence Revealed from Geodetic Observations. Geophys. Res. Lett. 2020, 47, e2019GL086888. [Google Scholar] [CrossRef]
- Jennifer Andrews. Searles Valley Sequence: M6.4 and M7.1, Southern California Seismic Network. Available online: http://www.scsn.org/index.php/2019/07/04/07-04-2019-searles-valley-sequence/index.html (accessed on 15 June 2020).
- Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. Gamma SAR and Interferometric Processing Software. In Proceedings of the Ers-Envisat Symposium, Gothenburg, Sweden, 15–20 October 2000. [Google Scholar]
- Goldstein, R.M.; Werner, C.L. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Eineder, M.; Hubig, M.; Milcke, B. Unwrapping Large Interferograms Using the Minimum Cost Flow Algorithm. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Seattle, WA, USA, 6–10 July 1998; IEEE Publications: New York, NY, USA, 1998; p. 1998. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface Deformation and Coherence Measurements of Kilauea Volcano, Hawaii, From SIR-C Radar Interferometry. J. Geophys. Res. 1996, 101, 23109–23125. [Google Scholar] [CrossRef]
- Yang, C.-S.; Zhang, Q.; Qu, F.-F.; Zhang, J. Obtaining an Atmospheric Delay Correction for Differential SAR Interferograms Based on Regression Analysis of the Atmospheric Delay Phase. Shanghai Land Resour. 2012, 3, 412. (In Chinese) [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A Small-Baseline Approach for Investigating Deformations on Full-Resolution Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Shan, X.J.; Qu, C.; Gong, W.Y.; Zhao, D.Z.; Zhang, Y.F.; Zhang, G.H.; Song, X.G.; Liu, Y.H.; Zhang, G.F. Co-seismic deformation field of the Jiuzhaigou Ms7.0 earthquake from Sentinel-1A InSAR data and fault slip inversion. Chin. J. Geophys. (Chin.) 2017, 60, 4527–4536. [Google Scholar] [CrossRef]
- Ji, L.Y.; Liu, C.J.; Xu, J.; Liu, L.; Long, F.; Zhang, Z.W. InSAR observation and inversion of the seismogenic fault for the 2017 Jiuzhaigou Ms 7.0 earthquake in China. Chin. J. Geophys. 2017, 60, 4069–4082. (In Chinese) [Google Scholar] [CrossRef]
- Tan, K.; Wang, Q.; Wang, X.Q.; Yang, S.; Li, J. Analysis Model and Space Time Distribution of Post-seismic Deformation. J. Geod. Geodyn. 2005, 25, 23–26. (In Chinese) [Google Scholar]
- Ji, L.; Zhu, L.; Li, N.; Wang, C.Z. Research review of fault movement based on Geodetic observation. J. Geod. Geodyn. 2017, 37, 771–776. (In Chinese) [Google Scholar]
- Freed, A.M. Afterslip (and Only Afterslip) Following the 2004 Parkfield, California, Earthquake. Geophys. Res. Lett. 2007, 34, L06312. [Google Scholar] [CrossRef]
- Barnhart, W.D.; Brengman, C.M.J.; Li, S.; Peterson, K.E. Ramp-Flat Basement Structures of the Zagros Mountains Inferred From Co-Seismic Slip and After-slip of the 2017 MW 7.3 Darbandikhan, Iran/Iraq Earthquake. Earth Planet. Sci. Lett. 2018, 49, 96–107. [Google Scholar] [CrossRef]
- Marone, C.J.; Scholtz, C.H.; Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. 1991, 96, 8441–8452. [Google Scholar] [CrossRef]
- Milliner, C.; Donnellan, A. Using Daily Observations from Planet Labs Satellite Imagery to Separate the Surface Deformation between the 4 July Mw 6.4 Foreshock and 5 July Mw 7.1 Mainshock during the 2019 Ridgecrest Earthquake Sequence. Seismol. Res. Lett. 2020, 91, 1986–1997. [Google Scholar] [CrossRef]
- Wang, R.J.; Diao, F.; Hoechner, A. SDM-A Geodetic Inversion Code Incorporating with Layered Crust Structure and Curved Fault Geometry. In Proceedings of the EGU General Assembly, Vienna, Austria, 7–12 April 2013; European Geosciences Union: Munich, Germany, 2013. [Google Scholar]
- Wang, R.J.; Parolai, S.; Ge, M.; Jin, M.; Walter, T.R.; Zschau, J. The 2011 Mw9.0 Tohoku Earthquake: Comparison of GPS and Strong-Motion Data. Bull. Seism. Soc. Am. 2013, 103, 1336–1347. [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosyst. 2005, 6, Q01007. [Google Scholar] [CrossRef]
- King, G.C.P.; Stein, R.S.; Lin, J. Static Stress changes and the Triggering of Earthquakes. Bull. Seism. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Pinar, A.; Honkura, Y.; Kuge, K. Seismic Activity Triggered by the 1999 Izmit Earthquake and Its Implications for the Assessment of Future Seismic Risk. Geophys. J. Int. 2001, 146, F1–F7. [Google Scholar] [CrossRef]
- Liu, G.P.; Fu, Z.X. The Triggering Mechanism of the Largest Aftershock (Ms = 6.3) of the. Luhuo Gr. Earthquake (Ms =7.6). Earthq. Res. China 2002, 18, 175–182. (In Chinese) [Google Scholar]
- Wan, Y.G.; Wu, Z.L.; Zhou, G.W.; Huang, J.; Qin, L.X. Research on Seismic Stress Triggering. Acta Seism. 2002, 24, 533–551. (In Chinese) [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. 2005, 110, B05S16. [Google Scholar] [CrossRef]
- Lin, J.; Stein, R.S. Stress triggering in thrust and subduction earthquakes, and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. 2004, 109, B02303. [Google Scholar] [CrossRef]
- Felzer, K.R.; Becker, T.W.; Abercrombie, R.E.; Ekström, G.; Rice, J.R. Triggering of the 1999 Mw7.1 Hector Mine earthquake by aftershocks of the 1992 Mw7.3 Landers earthquake. J. Geophys. Res. 2002, 107, 6–13. [Google Scholar]
- Steacy, S.; Marsan, D.; Nalbant, S.S.; Mccloskey, J. Sensitivity of static stress calculations to the earthquake slip distribution. Geophys. Res. 2004, 109, B04303. [Google Scholar] [CrossRef]



| Date | Longitude (°E) | Latitude (°N) | Np1 (Strike, Dip, and Rake) | Np2 (Strike, Dip, and Rake) | |
|---|---|---|---|---|---|
| USGS a | 2019.7.4 | −117.504 | 35.705 | 228/66/4 | 137/86/156 |
| 2019.7.6 | −117.599 | 35.770 | 322/81/−173 | 231/83/−9 | |
| GCMT b | 2019.7.4 | −117.54 | 35.69 | 227/86/3 | 137/87/176 |
| 2019.7.6 | −117.58 | 35.780 | 321/81/180 | 51/90/9 | |
| William D. Barnhart et al. | 7.4 | - | - | 228/66/4 | |
| 7.6 | - | - | 322/81/−173 | ||
| Li et al. | Fault 1 | - | - | 320/83/−171 | |
| Fault 2 | - | - | 225/81/− | ||
| This study | Fault 1 | - | - | 322/83/−172 | |
| Fault 2 | - | - | 225/81/4 | ||
| No. | Satellite | Orbit | Pass Direction | Master Image | Slave Image | Interval | Incidence Angle | Perpendicular Baseline |
|---|---|---|---|---|---|---|---|---|
| 1 | Sentinel-1A | T064 | Ascending | 20190704 | 20190716 | 12 | 39.2582 | −27.4 |
| 2 | Sentinel-1A | T071 | Descending | 20190704 | 20190728 | 24 | 39.2026 | −40.5 |
| 3 | ALOS-2 | T166 | Descending | 20190402 | 20190723 | 112 | 39.0301 | −496.9 |
| Orbit | Pass Direction | Incidence Angle | Heading | Number of Images | Number of Interferograms Involved in Calculation |
|---|---|---|---|---|---|
| T064A (Sentinel-1A) | Ascending | 39.2582 | −12.99 | 27 | 39 |
| Fault | Mean Rake | Mean Slip | Latitude | Longitude | Depth |
|---|---|---|---|---|---|
| F1 | −171.83 | 0.40 | 35.77 | −117.59 | 1.99 |
| F2 | 4.00 | 0.13 | 35.67 | −117.53 | 1.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wang, T.; Zhu, S.; Han, B.; Dong, J.; Zhao, C. Co-Seismic Inversion and Post-Seismic Deformation Mechanism Analysis of 2019 California Earthquake. Remote Sens. 2021, 13, 608. https://doi.org/10.3390/rs13040608
Yang C, Wang T, Zhu S, Han B, Dong J, Zhao C. Co-Seismic Inversion and Post-Seismic Deformation Mechanism Analysis of 2019 California Earthquake. Remote Sensing. 2021; 13(4):608. https://doi.org/10.3390/rs13040608
Chicago/Turabian StyleYang, Chengsheng, Ting Wang, Sainan Zhu, Bingquan Han, Jihong Dong, and Chaoying Zhao. 2021. "Co-Seismic Inversion and Post-Seismic Deformation Mechanism Analysis of 2019 California Earthquake" Remote Sensing 13, no. 4: 608. https://doi.org/10.3390/rs13040608
APA StyleYang, C., Wang, T., Zhu, S., Han, B., Dong, J., & Zhao, C. (2021). Co-Seismic Inversion and Post-Seismic Deformation Mechanism Analysis of 2019 California Earthquake. Remote Sensing, 13(4), 608. https://doi.org/10.3390/rs13040608






