3D Airborne EM Forward Modeling Based on Time-Domain Spectral Element Method
Abstract
1. Introduction
2. 3D Forward Modeling
3. Numerical Experiments
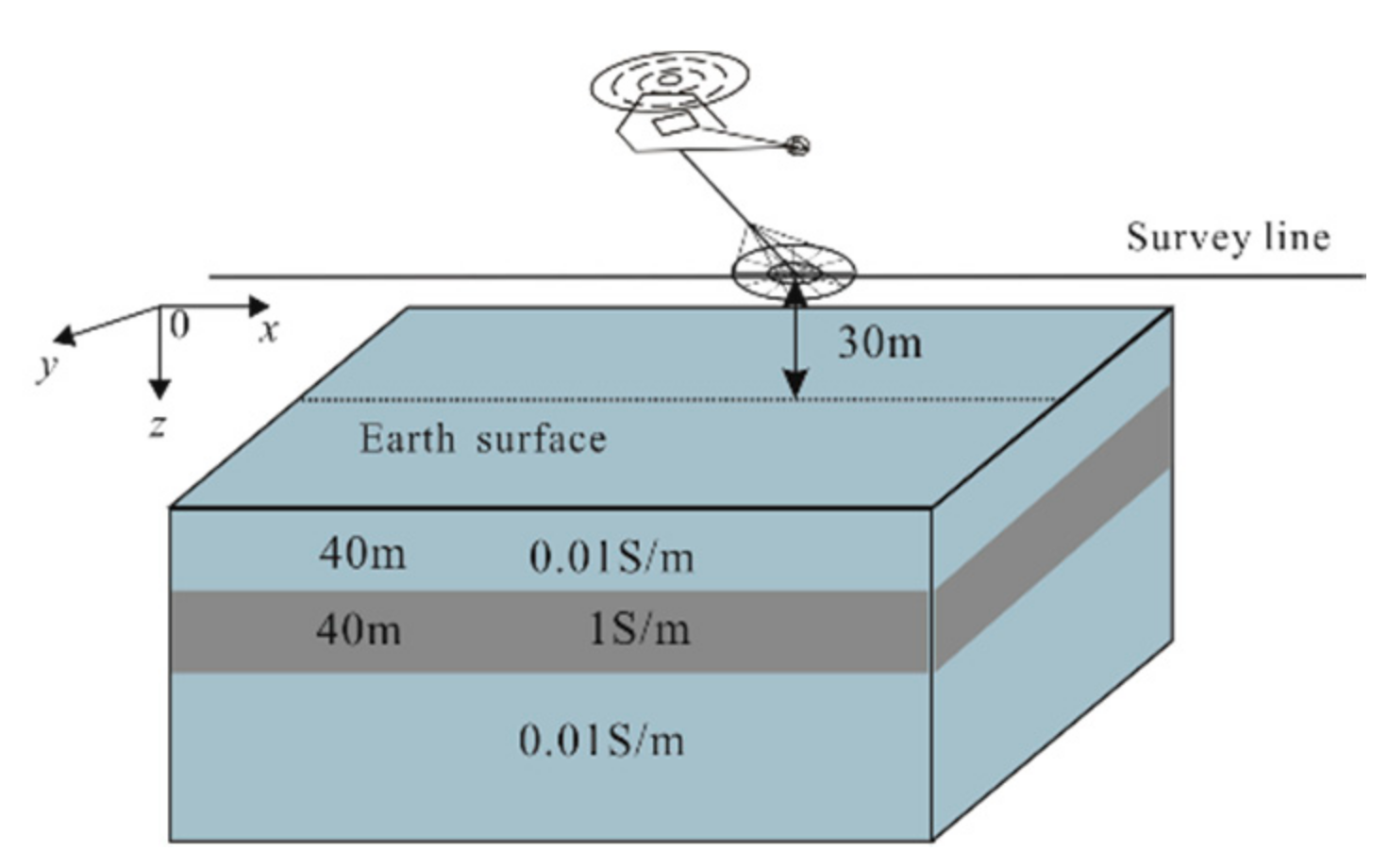
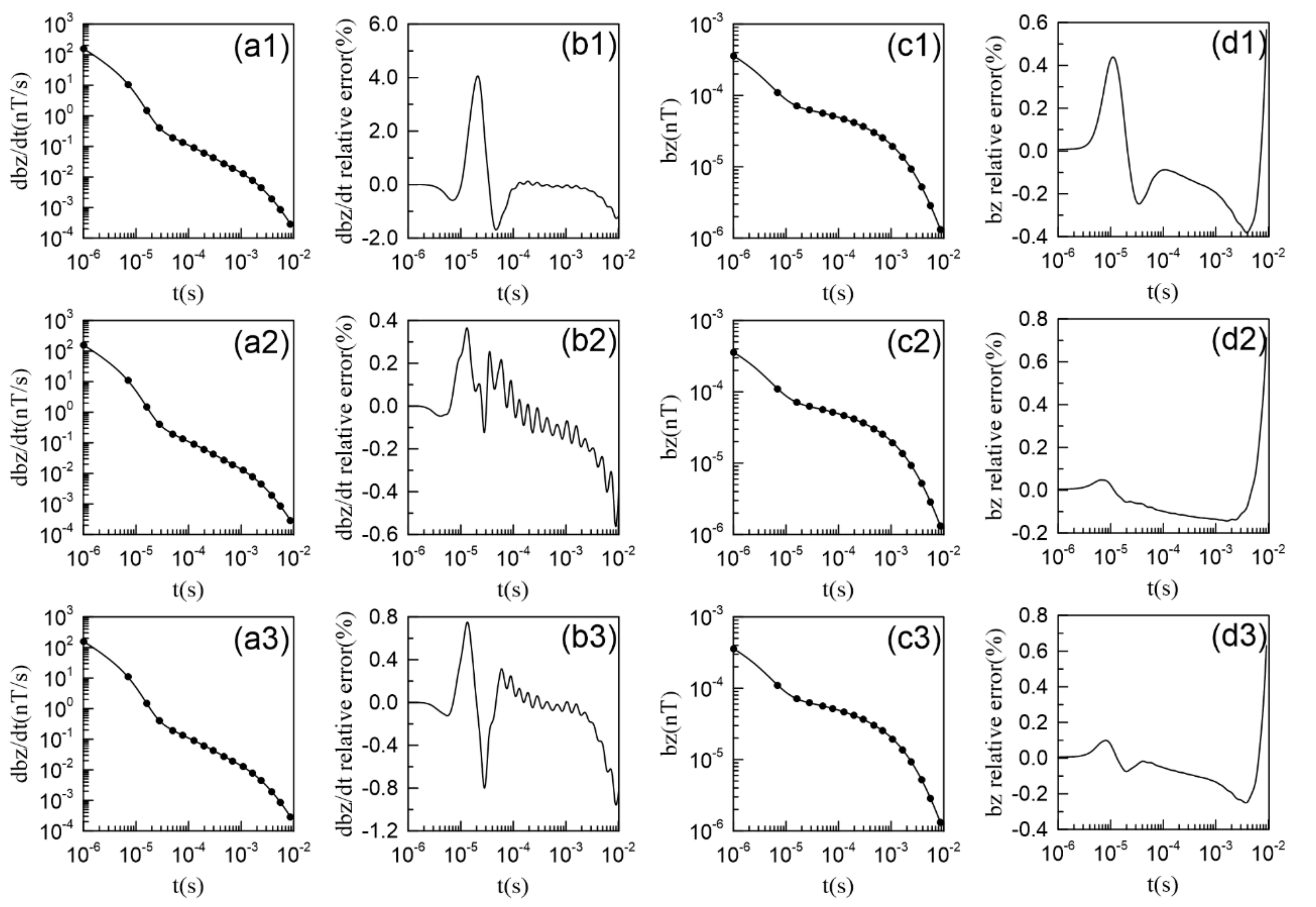
3.1. Accuracy Verification
3.2. Influence Factors of Modeling Accuracy
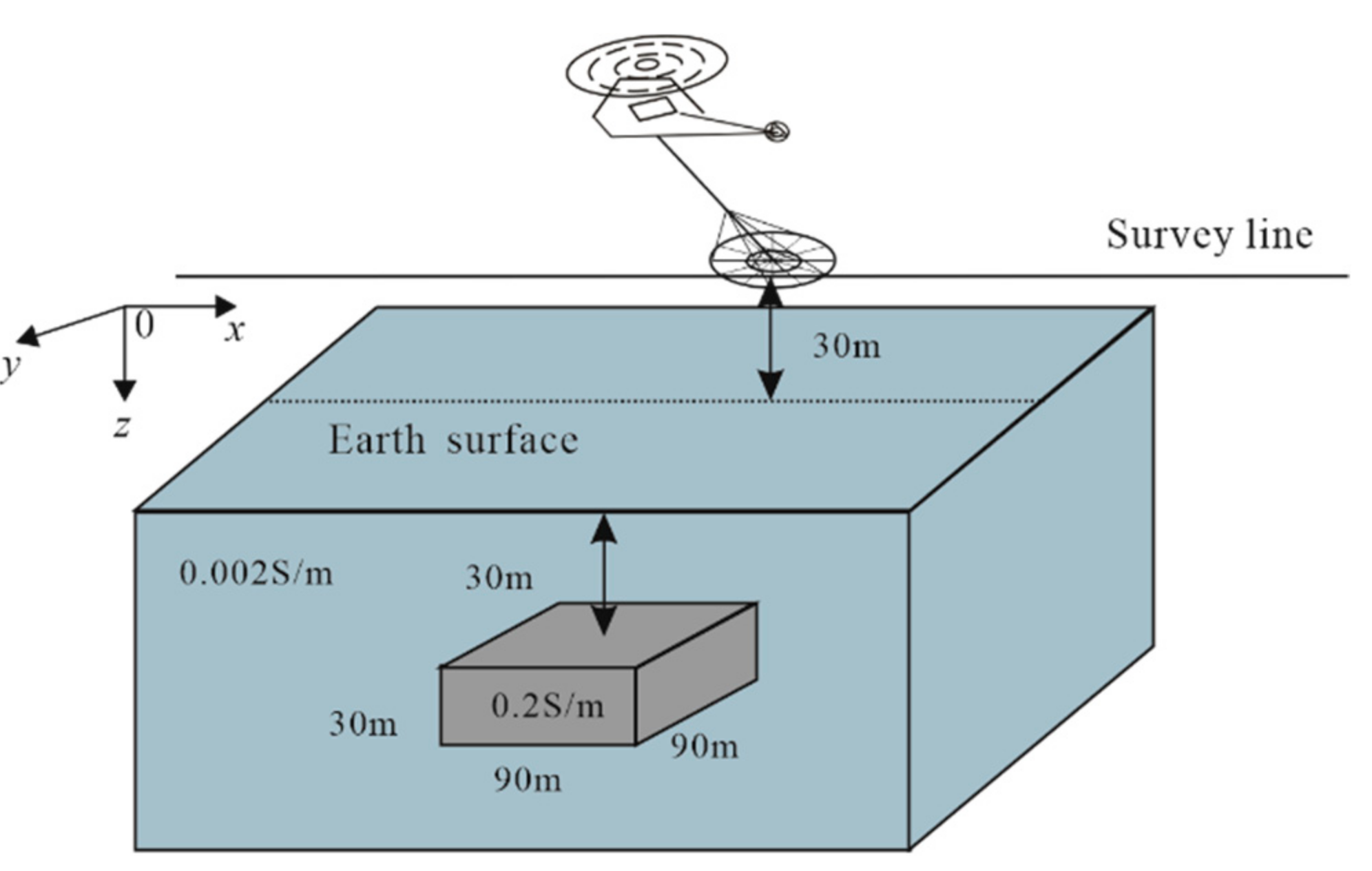
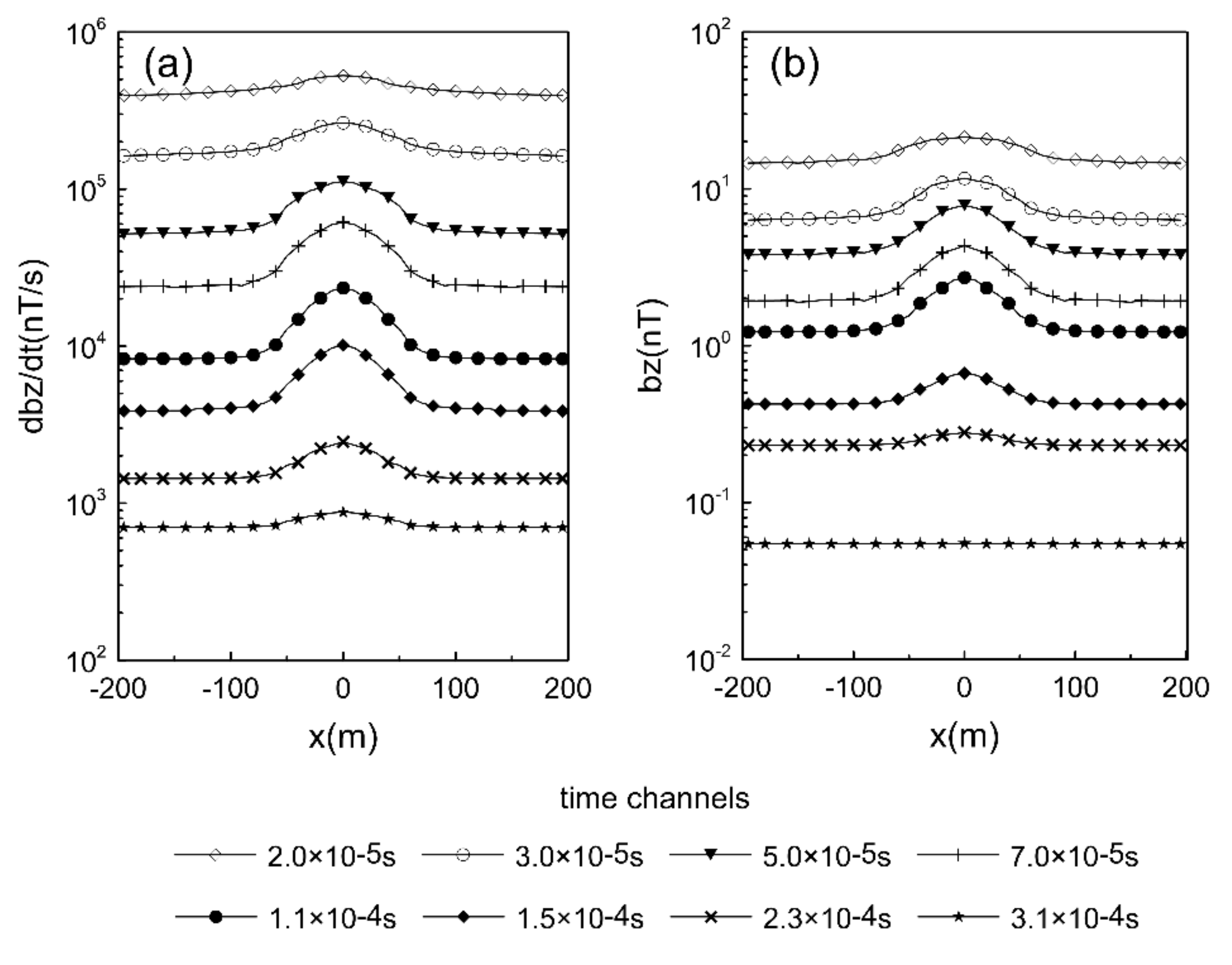
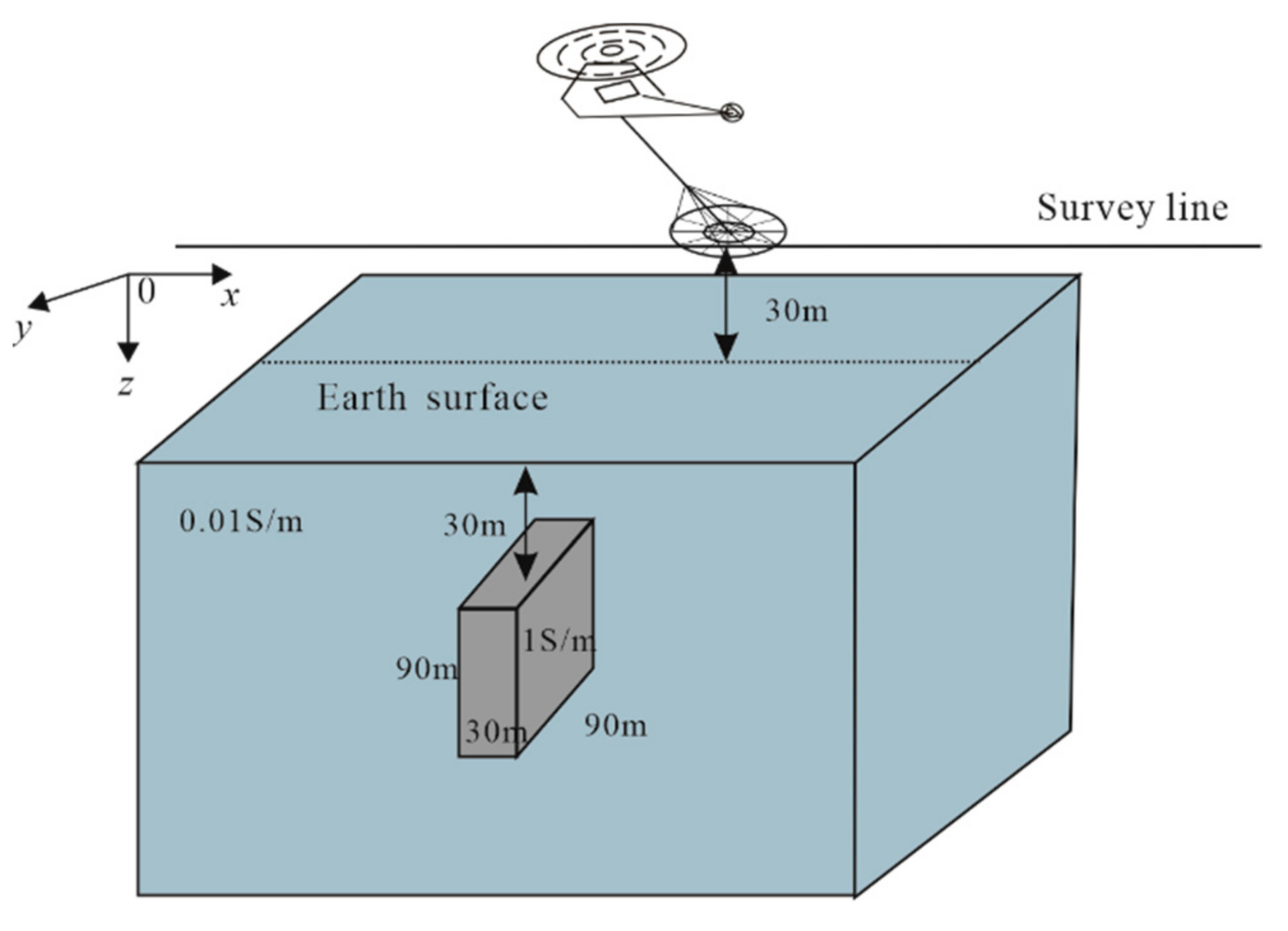
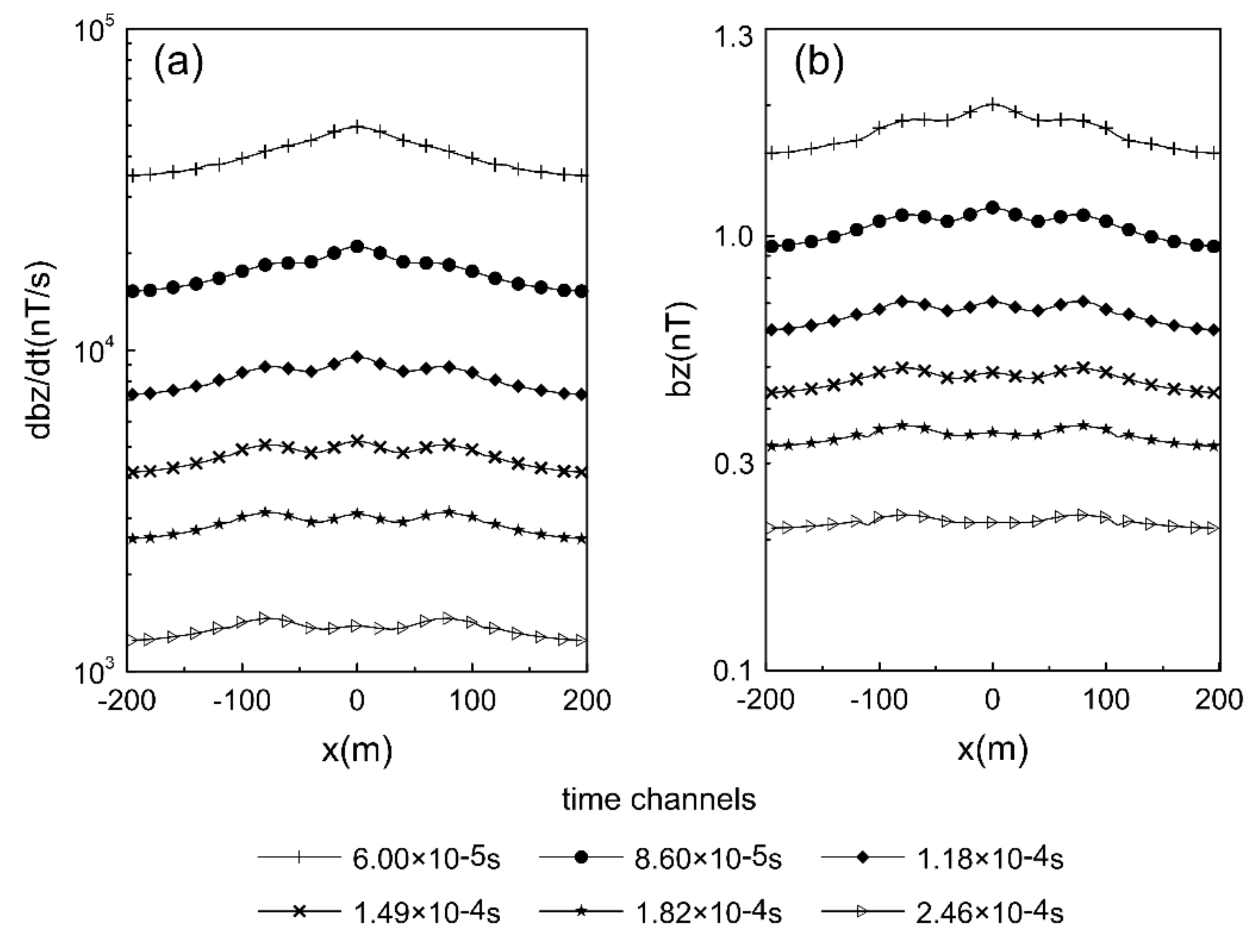
3.3. EM Responses for Typical Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Steuer, A.; Siemon, B.; Auken, E. A comparison of helicopter-borne electromagnetics in frequency- and time-domain at the Cuxhaven valley in Northern Germany. J. Appl. Geophys. 2009, 67, 194–205. [Google Scholar] [CrossRef]
- Yin, C.C. Airborne Electromagnetic Theory and Exploration Technology; Science Press: Beijing, China, 2018. [Google Scholar]
- Beamish, D. An assessment of inversion methods for AEM data applied to environmental studies. J. Appl. Geophys. 2002, 51, 75–96. [Google Scholar] [CrossRef][Green Version]
- Smith, R. Airborne electromagnetic methods: Applications to minerals, water and hydrocarbon exploration. Recorder 2010, 35, 7–10. [Google Scholar]
- Li, J.; Liu, Y.-H.; Yin, C.; Ren, X.; Su, Y. Fast imaging of time-domain airborne EM data using deep learning technology. Geophysics 2020, 85, E163–E170. [Google Scholar] [CrossRef]
- Yin, C.; Hodges, G. Simulated Annealing for Airborne EM Inversion. In Proceedings of the 69th EAGE Conference and Exhibition Incorporating SPE EUROPEC 2007, London, UK, 11–14 June 2007; European Association of Geoscientists & Engineers: Utrecht, The Netherlands. [Google Scholar]
- Hodges, G. Practical inversions for helicopter electromagnetic data. In Proceedings of the 15th Annual Symposium on the Application of Geophysics to Environmental and Engineering Problems (SAGEEP), San Antonio, TX, USA, 6–10 April 2010; Environmental & Engineering Geophysical Society: Denver, CO, USA, 2003; pp. 45–58. [Google Scholar]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Madden, T.; Mackie, R. Three-dimensional magnetotelluric modelling and inversion. Proc. IEEE 1989, 77, 318–333. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences1. Geophys. Prospect. 1995, 43, 1021–1042. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, C. 3D anisotropic modeling for airborne EM systems using finite-difference method. J. Appl. Geophys. 2014, 109, 186–194. [Google Scholar] [CrossRef]
- Tang, J.-T.; Ren, Z.-Y.; Hua, X.-R. The forward modeling and inversion in geophysical electromagnetic field. Prog. Geophys. 2007, 22, 1181–1194. [Google Scholar]
- Hohmann, G.W. Electromagnetic scattering by conductors in the earth near a line source of current. Geophysics 1971, 36, 101–131. [Google Scholar] [CrossRef]
- Peltoniemi, M.; Bärs, R.; Newman, G.A. Numerical modelling of airborne electromagnetic anomalies originating from low-conductivity 3D bodies1. Geophys. Prospect. 1996, 44, 55–69. [Google Scholar] [CrossRef]
- Cox, L.H.; Wilson, G.A.; Zhdanov, M.S. 3D inversion of airborne electromagnetic data using a moving footprint. Explor. Geophys. 2010, 41, 250–259. [Google Scholar] [CrossRef]
- Yin, C.; Lu, Y.; Liu, Y.; Zhang, B.; Qi, Y.; Cai, J. Multigrid quasi-linear approximation for three-dimensional airborne EM forward modeling. J. Jilin Univ. 2018, 48, 252–260. [Google Scholar]
- Coggon, J.H. Electromagnetic and electrical modeling by the finite element method. Geophysics 1971, 36, 132–155. [Google Scholar] [CrossRef]
- Wannamaker, P.E.; Stodt, J.A.; Rijo, L. Two-dimensional topographic responses in magnetotelluric modeled using finite ele-ments. Geophysics 1986, 51, 2131–2144. [Google Scholar] [CrossRef]
- Unsworth, M.J.; Travis, B.J.; Chave, A.D. Electromagnetic induction by a finite electric dipole source over a 2-D earth. Geophysics 1993, 58, 198–214. [Google Scholar] [CrossRef]
- Key, K.; Weiss, C. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example. Geophysics 2006, 71, G291–G299. [Google Scholar] [CrossRef]
- Ren, Z.; Tang, J. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method. Geophysics 2010, 75, H7–H17. [Google Scholar] [CrossRef]
- Ren, Z.; Kalscheuer, T.; Greenhalgh, S.; Maurer, H. A goal-oriented adaptive finite-element approach for plane wave 3D elec-tromagnetic modeling. Geophys. J. Int. 2013, 194, 700–718. [Google Scholar] [CrossRef]
- Zhang, B.; Yin, C.; Liu, Y.; Cai, J. 3D modeling on topographic effect for frequency-/time-domain airborne EM systems. Chin. J. Geophys. 2016, 59, 1506–1520. [Google Scholar]
- Yin, C.; Qi, Y.; Liu, Y.; Cai, J. 3D time-domain airborne EM forward modeling with topography. J. Appl. Geophys. 2016, 134, 11–22. [Google Scholar] [CrossRef]
- Haber, E.; Ascher, U.M. Fast Finite Volume Simulation of 3D Electromagnetic Problems with Highly Discontinuous Coefficients. SIAM J. Sci. Comput. 2001, 22, 1943–1961. [Google Scholar] [CrossRef]
- Haber, H.; Schwarzbach, C. Parallel inversion of large-scale airborne time-domain electromagnetic data with multiple OcTree meshes. Inverse Probl. 2014, 30, 055011. [Google Scholar] [CrossRef]
- Haber, E.; Ruthotto, L. A multiscale finite volume method for Maxwell’s equations at low frequencies. Geophys. J. Int. 2014, 199, 1268–1277. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. A finite-volume solution to the geophysical electromagnetic forward problem using un-structured grids. Geophysics 2014, 79, E287–E302. [Google Scholar] [CrossRef]
- Patera, A.T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Black, K. A conservative spectral element method for the approximation of compressible fluid flow. Kybern. Praha. 1999, 35, 133–146. [Google Scholar]
- Frutos, J.D.; Novo, J. A Spectral Element Method for the Navier--Stokes Equations with Improved Accuracy. Siam J. Numer. Anal. 2000, 38, 799–819. [Google Scholar] [CrossRef]
- Komatitsch, D.; Vilotte, J.P.; Vai, R.; José, M.C.C.; Sa′nchez-Sesma, F.J. The spectral element method for elastic wave equations—Application to 2-D and 3-D seismic problems. Int. J. Numer. Methods Eng. 1999, 45, 1139–1164. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation—I. Validation. Geophys. J. Int. 2002, 149, 390–412. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation-II. Three-dimensional models, oceans, rotation and self-gravitation. Geophys. J. Int. 2002, 150, 303–318. [Google Scholar] [CrossRef]
- Chaljub, E.; Komatitsch, D.; Vilotte, J.-P.; Capdeville, Y.; Valette, B.; Festa, G. Spectral-element analysis in seismology. Adv. Geophys. 2007, 48, 365–419. [Google Scholar] [CrossRef]
- Wang, T.; Li, R.; Li, X.; Zhang, M.; Long, G. Numerical spectral element modeling for seismic wave propagation in transversely isotropic medium. Prog. Geophys. 2007, 22, 778–784. [Google Scholar]
- Yin, C.; Huang, X.; Liu, Y.; Cai, J. 3-D Modeling for Airborne EM using the Spectral-element Method. J. Environ. Eng. Geophys. 2017, 22, 13–23. [Google Scholar] [CrossRef]
- Huang, X.; Yin, C.; Cao, X.-Y.; Liu, Y.-H.; Zhang, B.; Cai, J. 3D anisotropic modeling and identification for airborne EM systems based on the spectral-element method. Appl. Geophys. 2017, 14, 419–430. [Google Scholar] [CrossRef]
- Liu, L.; Yin, C.; Liu, Y.; Qiu, C.; Huang, X.; Zhang, B. Spectral element method for 3D frequency-domain marine con-trolled-source electromagnetic forward modeling. Chin. J. Geophys. 2018, 61, 756–766. [Google Scholar]
- Knight, J.H.; Raiche, A.P. Transient electromagnetic calculations using the Gaver-Stehfest inverse Laplace transform method. Geophysics 1982, 47, 47–50. [Google Scholar] [CrossRef]
- Yin, C.; Huang, W.; Ben, F. The full-time electromagnetic modeling for time-domain airborne electromagnetic systems. Chin. J. Geophys. 2003, 56, 3153–3162. [Google Scholar]
- Qiu, C.; Güttel, S.; Ren, X.; Yin, C.; Liu, Y.; Zhang, B.; Egbert, G. A block rational Krylov method for 3-D time-domain marine controlled-source electromagnetic modelling. Geophys. J. Int. 2019, 218, 100–114. [Google Scholar] [CrossRef]
- Jin, J.M. The Finite Element Method in Electromagnetics; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Ascher, U.M.; Petzold, L.R. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Comput. Methods Ordinary Differ. Equ. Differ. Algebraic Equ. 1998. [Google Scholar] [CrossRef]
- Qi, Y.-F.; Yin, C.-C.; Liu, Y.-H.; Cai, J. 3D time-domain airborne EM full-wave forward modeling based on instantaneous current pulse. Chin. J. Geophys. 2017, 60, 369–382. [Google Scholar]
- Ilić, M.M.; Notaros, B. Higher order hierarchical curved hexahedral vector finite elements for electromagnetic modeling. IEEE Trans. Microw. Theory Tech. 2003, 51, 1026–1033. [Google Scholar] [CrossRef]
- Huang, W.; Ben, F.; Yin, C. Three-dimensional anisotropic modeling for time-domain airborne electromagnetics. Appl. Geophys. 2017, 14, 431–440. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, C.; Gao, Z.; Su, Y.; Liu, Y.; Huang, X.; Ren, X.; Xiong, B. 3D Airborne EM Forward Modeling Based on Time-Domain Spectral Element Method. Remote Sens. 2021, 13, 601. https://doi.org/10.3390/rs13040601
Yin C, Gao Z, Su Y, Liu Y, Huang X, Ren X, Xiong B. 3D Airborne EM Forward Modeling Based on Time-Domain Spectral Element Method. Remote Sensing. 2021; 13(4):601. https://doi.org/10.3390/rs13040601
Chicago/Turabian StyleYin, Changchun, Zonghui Gao, Yang Su, Yunhe Liu, Xin Huang, Xiuyan Ren, and Bin Xiong. 2021. "3D Airborne EM Forward Modeling Based on Time-Domain Spectral Element Method" Remote Sensing 13, no. 4: 601. https://doi.org/10.3390/rs13040601
APA StyleYin, C., Gao, Z., Su, Y., Liu, Y., Huang, X., Ren, X., & Xiong, B. (2021). 3D Airborne EM Forward Modeling Based on Time-Domain Spectral Element Method. Remote Sensing, 13(4), 601. https://doi.org/10.3390/rs13040601





