Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Field Measurements
2.2.1. Canopy Reflectance Measurements
2.2.2. Measurement of Canopy Chlorophyll Content
2.3. ENVISAT MERIS Data
2.4. Vegetation Indices
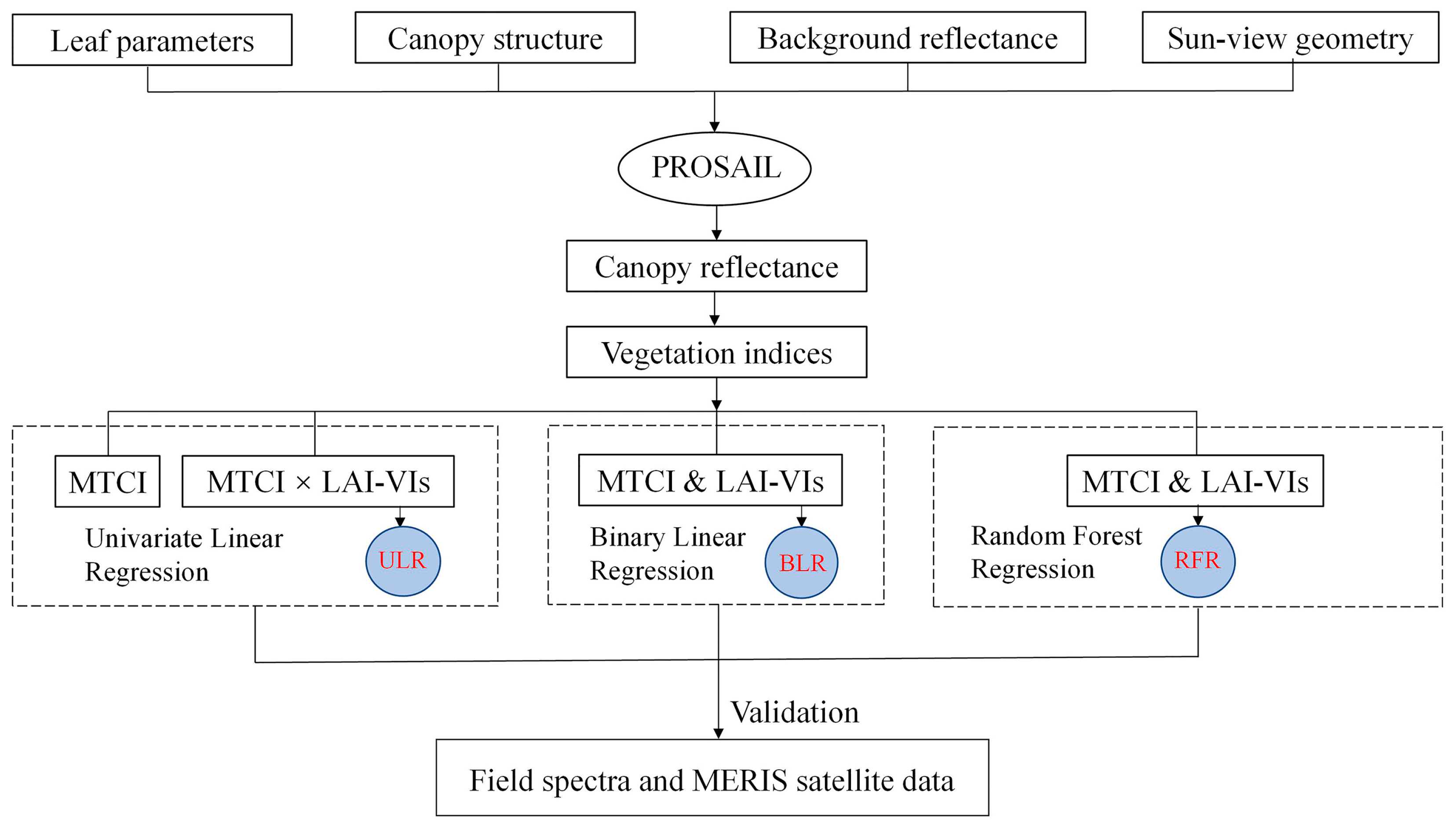
2.5. Simulation of Canopy Reflectance Using the PROSAIL-D Model
2.6. CCC Retrieval Model
2.6.1. Linear Regression Analysis
2.6.2. Implementing the Random Forest Regression Approach
3. Results
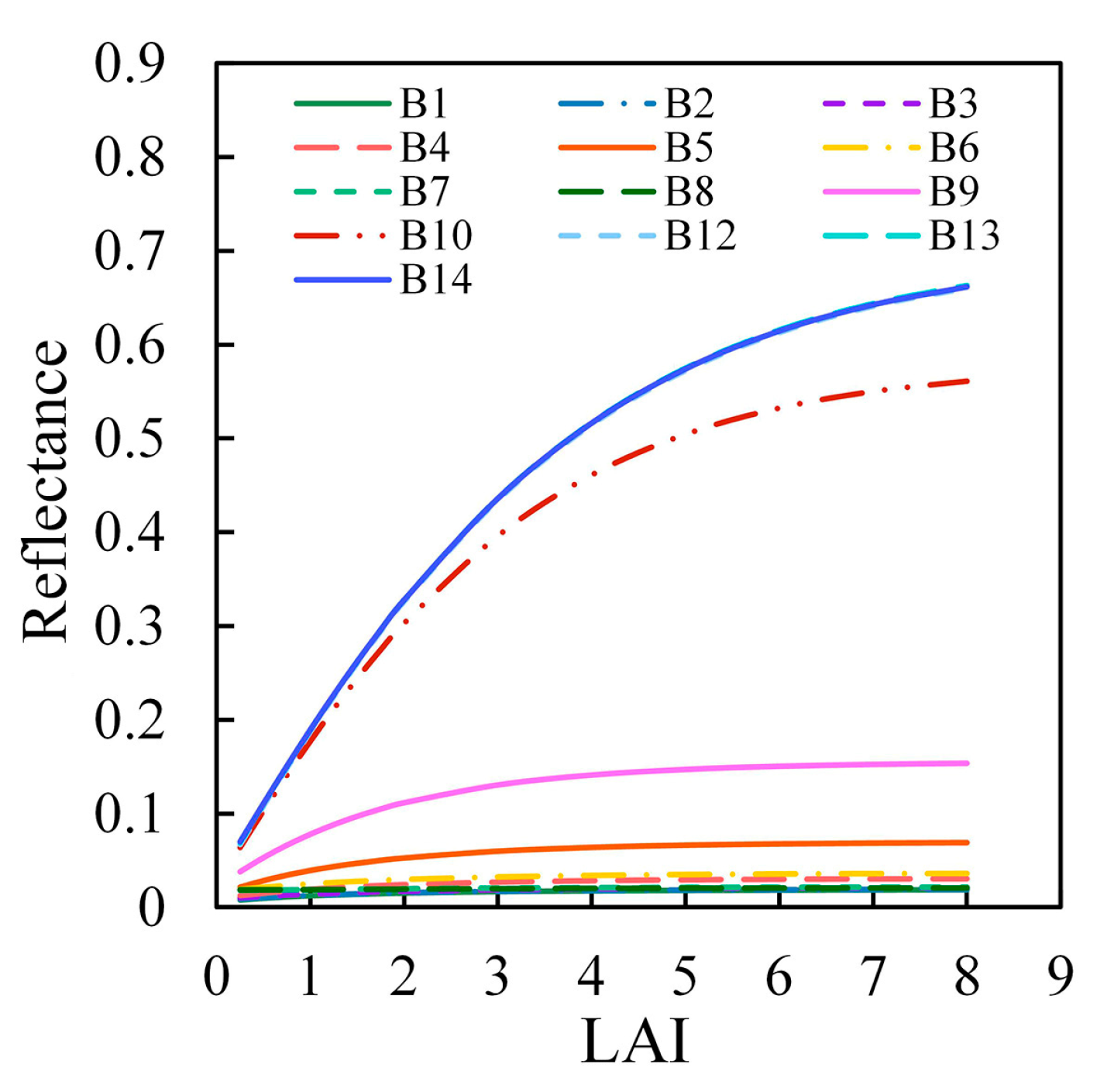
3.1. Sensitivities of Spectra and MTCI to LAI and CCC
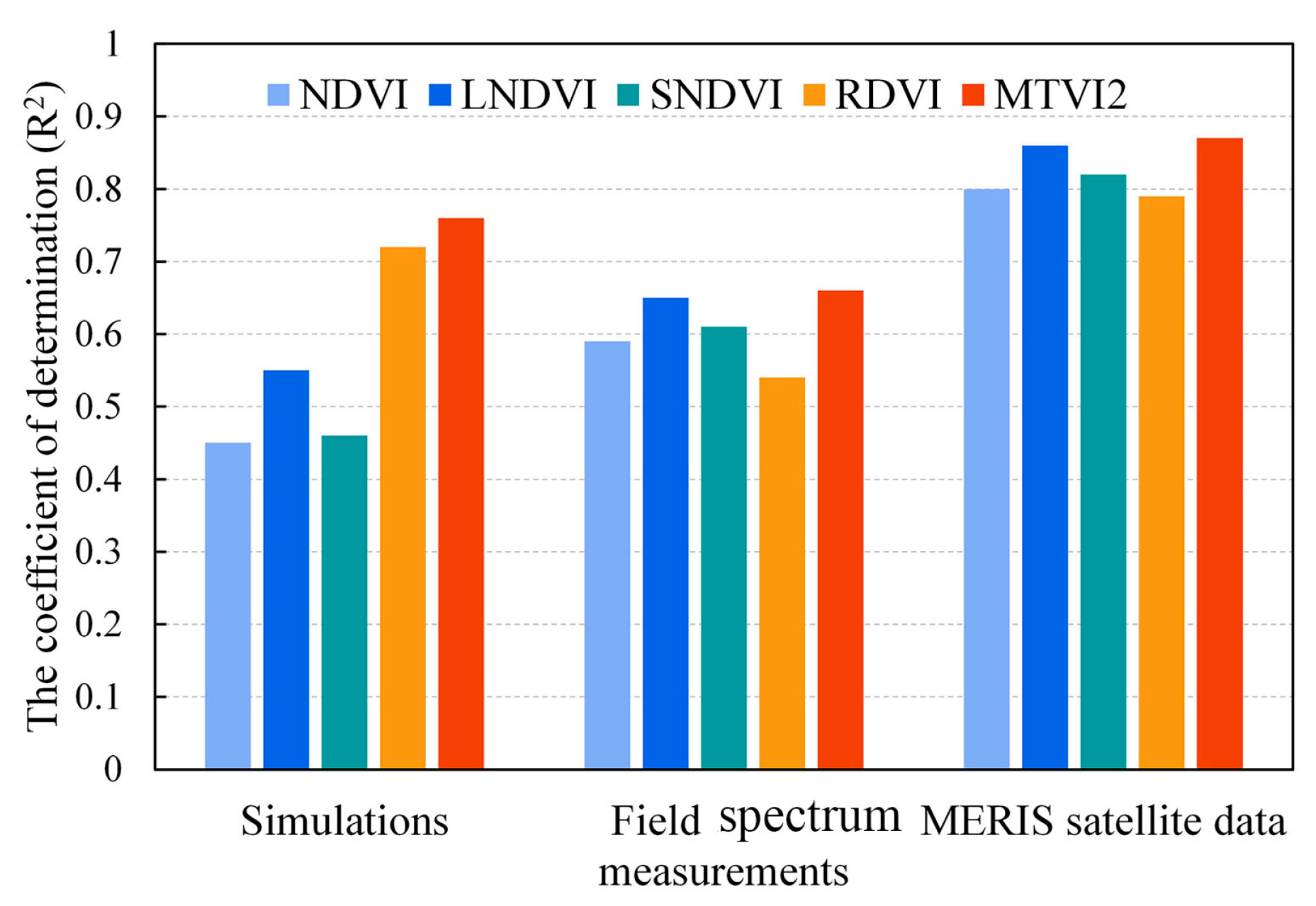
3.2. CCC Estimation Using the Simulated Dataset
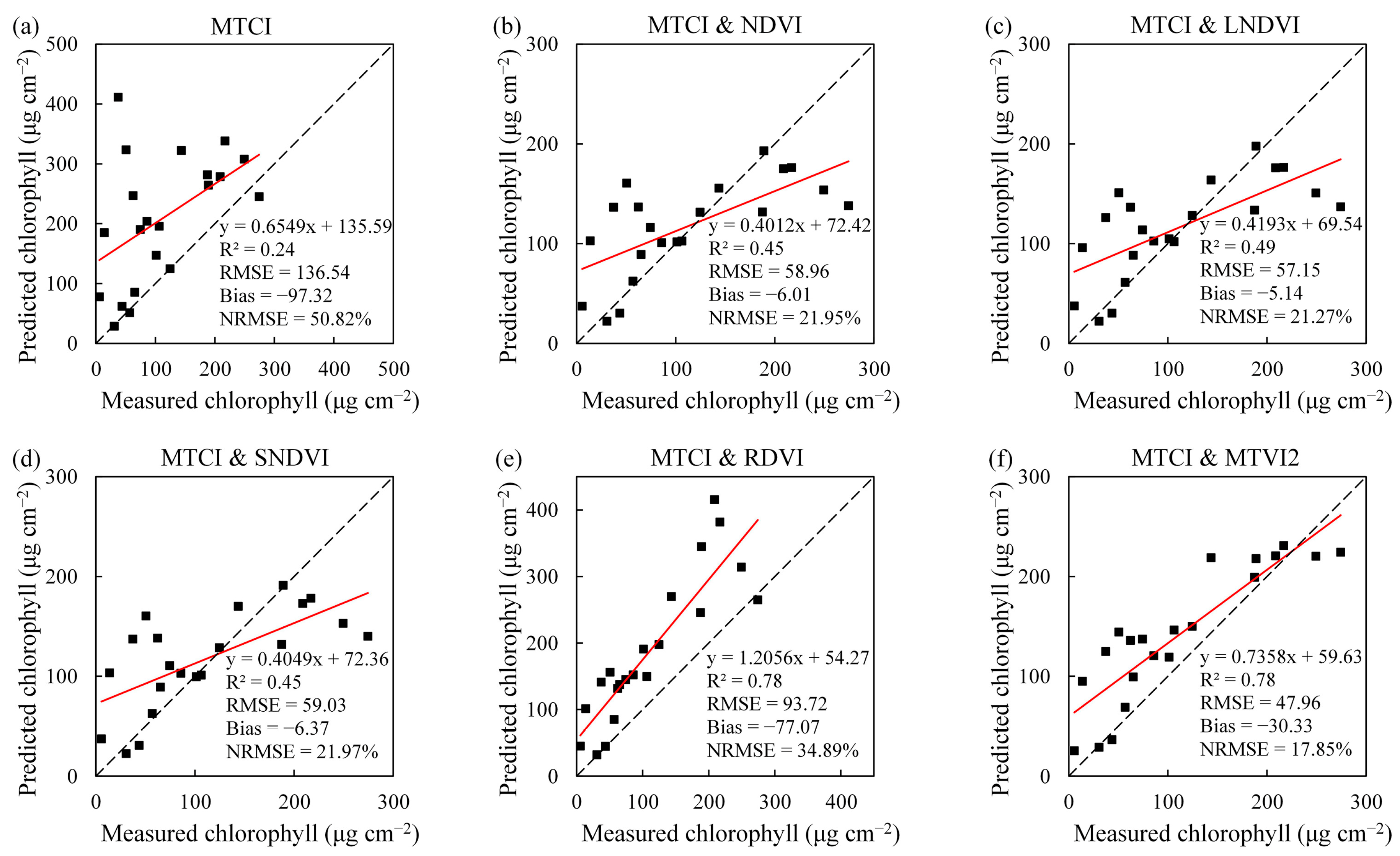
3.3. Validation of CCC Estimation Using Field Canopy Spectral Measurements
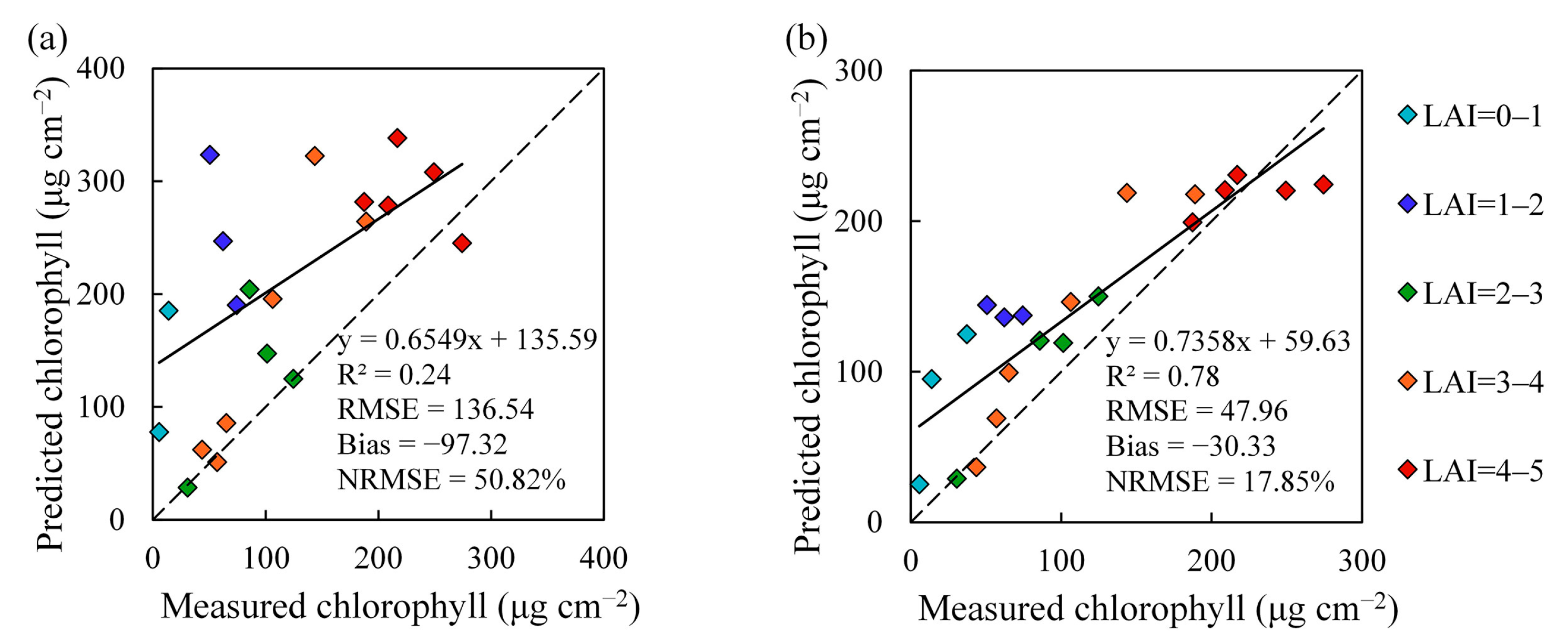
3.4. Validation of CCC Estimation from MERIS Satellite Data
4. Discussion
4.1. Role and Form of VI Combinations in CCC Estimation Models
4.2. Influence of LAI-VIs Selection of VI Combinations
4.3. Comparing the Performance of the Proposed CCC Estimation Models for Satellite Data with Variable LAIs
4.4. Limitations of Model Simulations and Validation Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gitelson, A.A.; Viña, A.; Verma, S.B.; Rundquist, D.C.; Arkebauer, T.J.; Keydan, G.; Leavitt, B.; Ciganda, V.; Burba, G.G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. JGR Atmos. 2006, 111, D08S11. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Luo, X.; Bartlett, P.; Chen, B.; Staebler, R.M. Leaf chlorophyll content as a proxy for leaf photosynthetic capacity. Glob. Chang. Biol. 2017, 23, 3513–3524. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Li, H.; Qiao, X.; Jiang, J. Using wavelet analysis of hyperspectral remote-sensing data to estimate canopy chlorophyll content of winter wheat under stripe rust stress. Int. J. Remote Sens. 2018, 39, 4059–4076. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J. Relationships between gross primary production, green LAI, and canopy chlorophyll content in maize: Implications for remote sensing of primary production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K.; Wellburn, A.R. Determinations of total carotenoids and chlorophylls a and b of leaf extracts in different solvents. Biochem. Soc. Trans. 1983, 603, 591–592. [Google Scholar] [CrossRef]
- Wu, C.; Wang, L.; Niu, Z.; Gao, S.; Wu, M. Nondestructive estimation of canopy chlorophyll content using Hyperion and Landsat/TM images. Int. J. Remote Sens. 2010, 31, 2159–2167. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Matkan, A.A.; Dashti Ahangar, A. Inversion of a radiative transfer model for estimation of rice canopy chlorophyll content using a lookup-table approach. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 1222–1230. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L. Using hyperspectral remote sensing data for retrieving canopy chlorophyll and nitrogen content. IEEE J. Sel. Top. Appl. Earth Observ. 2012, 5, 574–583. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Zhang, Y. The applicability of empirical vegetation indices for determining leaf chlorophyll content over different leaf and canopy structures. Ecol. Complex. 2014, 17, 119–130. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. IEEE J. Sel. Top. Appl. Earth Observ. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Gausman, H.W.; Allen, W.A.; Cardenas, R.; Richardson, A.J. Effects of leaf nodal position on absorption and scattering coefficients and infinite reflectance of cotton leaves, Gossypium hirsutum L. Agron. J. 1971, 63, 87–91. [Google Scholar] [CrossRef]
- Bausch, W.C. Soil background effects on reflectance-based crop coefficients for corn. Remote Sens. Environ. 1993, 46, 213–222. [Google Scholar] [CrossRef]
- Haboudane, D. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Jay, S.; Gorretta, N.; Morel, J.; Maupas, F.; Bendoula, R.; Rabatel, G.; Dutartre, D.; Comar, A.; Baret, F. Estimating leaf chlorophyll content in sugar beet canopies using millimeter-to centimeter-scale reflectance imagery. Remote Sens. Environ. 2017, 198, 173–186. [Google Scholar]
- Peng, Y.; Nguy-Robertson, A.; Arkebauer, T.; Gitelson, A.A. Assessment of canopy chlorophyll content retrieval in maize and soybean: Implications of hysteresis on the development of generic algorithms. Remote Sens. 2017, 9, 226. [Google Scholar] [CrossRef]
- Myneni, R.B.; Nemani, R.R.; Running, S.W. Estimation of global leaf area index and absorbed PAR using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation Index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar]
- Ferrara, R.M.; Fiorentino, C.; Martinelli, N.; Garofalo, P.; Rana, G. Comparison of different ground-based NDVI measurement methodologies to evaluate crop biophysical properties. Ital. J. Agron. 2010, 5, 145–154. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R. Linearization of NDVI based on its relationship with vegetation fraction. Photogramm. Eng. Remote Sens. 2010, 76, 965–975. [Google Scholar]
- Gu, Y.; Wylie, B.K.; Howard, D.M.; Phuyal, K.P.; Ji, L. NDVI saturation adjustment: A new approach for improving cropland performance estimates in the Greater Platte River Basin, USA. Ecol. Indic. 2013, 30, 1–6. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.; Gara, T.W.; O’Connor, B.; Roeoesli, C.; Heurich, M.; Paganini, M. Comparing methods for mapping canopy chlorophyll content in a mixed mountain forest using Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 87, 102037. [Google Scholar] [CrossRef]
- Broge, N.H.; Thomsen, A.G.; Andersen, P.B. Comparison of selected vegetation indices as indicators of crop status. In Proceedings of the 22nd Symposium of the European Association of Remote Sensing Laboratories, Pragua, Czech Republic, 4–5 June 2002. [Google Scholar]
- Daughtry, C.S.T.; Waltthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Kooistra, L.; Clevers, J.G.P.W. Estimating potato leaf chlorophyll content using ratio vegetation indices. Remote Sens. Lett. 2016, 7, 611–620. [Google Scholar] [CrossRef]
- Cui, B.; Zhao, Q.; Huang, W.; Song, X.; Ye, H.; Zhou, X. A new integrated vegetation index for the estimation of winter wheat leaf chlorophyll content. Remote Sens. 2019, 11, 974. [Google Scholar] [CrossRef]
- Xu, M.; Liu, R.; Chen, J.M.; Liu, Y.; Shang, R.; Ju, W.; Wu, C.; Huang, W. Retrieving leaf chlorophyll content using a matrix-based vegetation index combination approach. Remote Sens. Environ. 2019, 224, 60–73. [Google Scholar]
- Yin, C.; He, B.; Quan, X.; Liao, Z. Chlorophyll content estimation in arid grasslands from Landsat-8 OLI data. Int. J. Remote Sens. 2016, 37, 615–632. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with CHRIS/PROBA observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Land-use/cover classification in a heterogeneous coastal landscape using RapidEye imagery: Evaluating the performance of random forest and support vector machines classifiers. Int. J. Remote Sens. 2014, 35, 3440–3458. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Chen, F.; Shi, T.; Wu, G. Wavelet-based coupling of leaf and canopy reflectance spectra to improve the estimation accuracy of foliar nitrogen concentration. Agric. For. Meteorol. 2018, 248, 306–315. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Wang, L.a.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A random forest machine learning approach for the retrieval of leaf chlorophyll content in wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Huang, W.; Zhao, C. Detection of leaf and canopy EWT by calculating REWT from reflectance spectra. Int. J. Remote Sens. 2010, 31, 2681–2695. [Google Scholar] [CrossRef]
- Verma, S.B.; Dobermann, A.; Cassman, K.G.; Walters, D.T.; Knops, J.M.; Arkebauer, T.J.; Suyker, A.E.; Burba, G.G.; Amos, B.; Yang, H.; et al. Annual carbon dioxide exchange in irrigated and rainfed maize-based agroecosystems. Agric. For. Meteorol. 2005, 131, 77–96. [Google Scholar] [CrossRef]
- Rundquist, D.; Perk, R.; Leavitt, B.; Keydan, G.; Gitelson, A. Collecting spectral data over cropland vegetation using machine-positioning versus hand-positioning of the sensor. Comput. Electron. Agric. 2004, 43, 173–178. [Google Scholar] [CrossRef]
- Porra, R.J. The chequered history of the development and use of simultaneous equations for the accurate determination of chlorophylls a and b. Photosynth. Res. 2002, 73, 149–156. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Liu, L.; Huang, W.; Zhao, C.; Lu, Y. Estimation of nitrogen status in middle and bottom layers of winter wheat canopy by using ground-measured canopy reflectance. Commun. Soil Sci. Plant Anal. 2007, 36, 2289–2302. [Google Scholar] [CrossRef]
- Porra, R.J.; Thompson, W.A.; Kriedemann, P.E. Determination of accurate extinction coefficients and simultaneous equations for assaying chlorophylls a and b extracted with four different solvents: Verification of the concentration of chlorophyll standards by atomic absorption spectroscopy. Biochim. Biophys. Acta 1989, 975, 384–394. [Google Scholar] [CrossRef]
- Asrar, G.; Fuchs, M.; Kanemasu, E.T.; Hatfield, J.L. Estimating absorbed photosynthetic radiation and leaf area index from spectral reflectance in wheat. Agron. J. 1984, 76, 300. [Google Scholar] [CrossRef]
- Hobbs, T.J. The use of NOAA-AVHRR NDVI data to assess herbage production in the arid rangelands of Central Australia. Int. J. Remote Sens. 1995, 16, 1289–1302. [Google Scholar] [CrossRef]
- Chen, P.Y.; Fedosejevs, G.; Tiscareño-LóPez, M.; Arnold, J.G. Assessment of MODIS-EVI, MODIS-NDVI and VEGETATION-NDVI composite data using agricultural measurements: An example at corn fields in western Mexico. Environ. Monit. Assess. 2006, 119, 69–82. [Google Scholar] [CrossRef]
- Liu, F.; Qin, Q.; Zhan, Z. A novel dynamic stretching solution to eliminate saturation effect in NDVI and its application in drought monitoring. Chin. Geogr. Sci. 2012, 22, 683–694. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Tan, C.; Tong, L.; Ma, C.; Guo, W.; Yang, X. Extracting proper remote sensing vegetation indices obtainable from in-situ spectral measurements for evaluation of erect-type corn (Zea mays L.) leaf area index. In Proceedings of the First International Conference on Agro-geoinformatics, Shanghai, China, 2–4 August 2012. [Google Scholar]
- Rouse, J.W.; Haas, R.H., Jr.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In NASA SP-351 Third ERTS-1 Symposium; Fraden, S.C., Marcanti, E.P., Becker, M.A., Eds.; Scientific and Technical Information Office, National Aeronautics and Space Administration: Washington, DC, USA, 1974; pp. 309–317. [Google Scholar]
- Féret, J.B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Qian, X.; Liu, L. Retrieving crop leaf chlorophyll content using an improved look-up-table approach by combining multiple canopy structures and soil backgrounds. Remote Sens. 2020, 12, 2139. [Google Scholar]
- Croft, H.; Chen, J.M.; Zhang, Y.; Simic, A. Modelling leaf chlorophyll content in broadleaf and needle leaf canopies from ground, CASI, Landsat TM 5 and MERIS reflectance data. Remote Sens. Environ. 2013, 133, 128–140. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Houborg, R.; McCabe, M.F. A hybrid training approach for leaf area index estimation via Cubist and random forests machine-learning. ISPRS J. Photogramm. Remote Sens. 2018, 135, 173–188. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J.; Tallis, M.J.; Llewellyn, G.M.; Taylor, G.; Snoeij, P. Validating the MERIS Terrestrial Chlorophyll Index (MTCI) with ground chlorophyll content data at MERIS spatial resolution. Int. J. Remote Sens. 2010, 31, 5513–5532. [Google Scholar] [CrossRef]
- Alebele, Y.; Zhang, X.; Wang, W.; Yang, G.; Yao, X.; Zheng, H.; Zhu, Y.; Cao, W.; Cheng, T. Estimation of canopy biomass components in paddy rice from combined optical and SAR data using multi-target gaussian regressor stacking. Remote Sens. 2020, 12, 2564. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2000, 76, 156–172. [Google Scholar] [CrossRef]
- Broge, N.H.; Mortensen, J.V. Deriving green crop area index and canopy chlorophyll density of winter wheat from spectral reflectance data. Remote Sens. Environ. 2002, 81, 45–57. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Hornero, A.; Beck, P.S.A.; Kattenborn, T.; Kempeneers, P.; Hernandez-Clemente, R. Chlorophyll content estimation in an open-canopy conifer forest with Sentinel-2A and hyperspectral imagery in the context of forest decline. Remote Sens. Environ. 2019, 223, 320–335. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Rueda, C.A.; Ustin, S.L. Water content estimation in vegetation with MODIS reflectance data and model inversion methods. Remote Sens. Environ. 2003, 85, 109–124. [Google Scholar] [CrossRef]
- Xu, X.; Lu, J.; Zhang, N.; Yang, T.; He, J.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Inversion of rice canopy chlorophyll content and leaf area index based on coupling of radiative transfer and Bayesian network models. ISPRS J. Photogramm. Remote Sens. 2019, 150, 185–196. [Google Scholar] [CrossRef]
- Wang, S.; Yang, D.; Li, Z.; Liu, L.; Huang, C.; Zhang, L. A global sensitivity analysis of commonly used satellite-derived vegetation indices for homogeneous canopies based on model simulation and random forest learning. Remote Sens. 2019, 11, 2547. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Stisen, S. Evaluating MODIS, MERIS, and VEGETATION indices using in situ measurements in a semiarid environment. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1774–1786. [Google Scholar] [CrossRef]
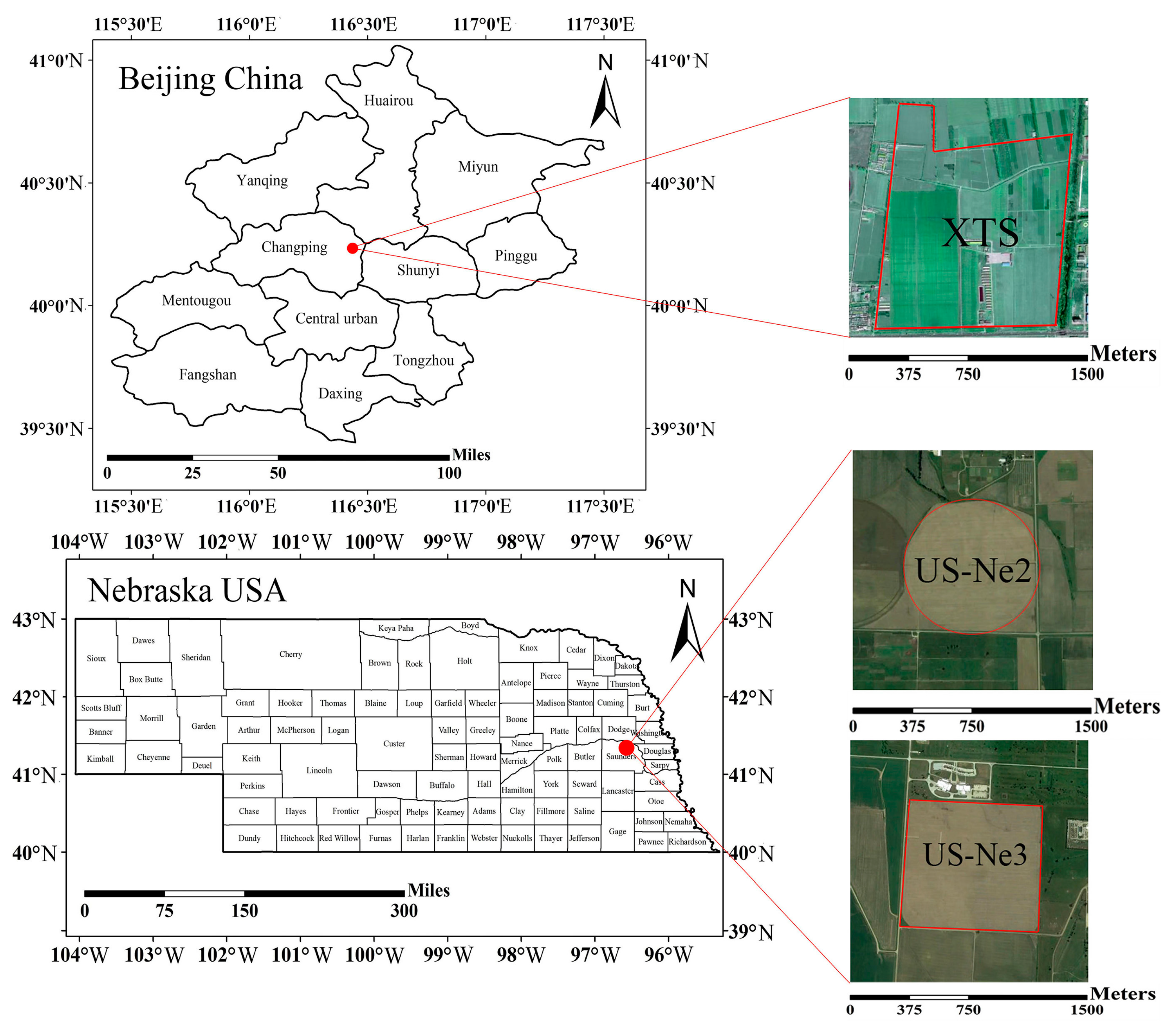


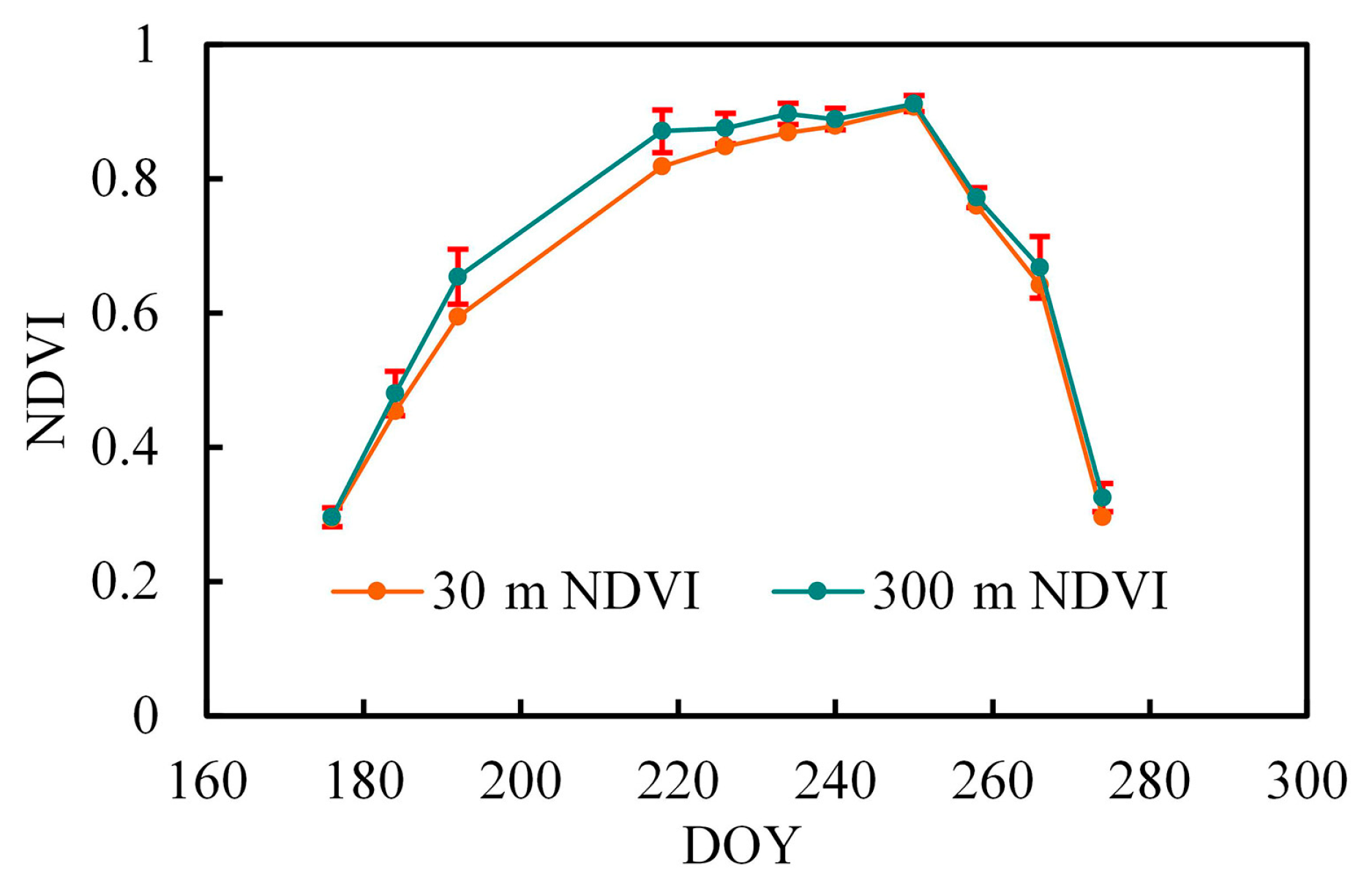
| Sites | Country | Lat/Long (°) | Crop Species | Sampling Periods | MERIS Periods |
|---|---|---|---|---|---|
| XTS | China | 40.18/116.44 | Wheat | 2 April, 10 April,18 April, 6 May, 17 May 2002 14 April, 19 May 2004 | - |
| US-Ne2 | America | 41.165/−96.47 | Soybean | 13 June–17 September 2002, 27 measurement campaigns 29 June–20 September 2004, 21 measurement campaigns | 25 June–24 September 2004 |
| US-Ne3 | America | 41.18/−96.44 | Soybean | 19 June–17 September 2002, 18 measurement campaigns | - |
| Sites | Crop Species | Year | N | Mean | Min | Max | SD | CV |
|---|---|---|---|---|---|---|---|---|
| XTS | Wheat | 2002 | 227 | 137.18 | 45.42 | 237.57 | 48.39 | 0.35 |
| 2004 | 44 | 145.57 | 73.77 | 231.13 | 38.13 | 0.26 | ||
| US-Ne2 | Soybean | 2002 | 27 | 67.83 | 3.31 | 186.33 | 48.58 | 0.72 |
| 2004 | 21 | 110.90 | 5.70 | 274.36 | 78.64 | 0.71 | ||
| US-Ne3 | Soybean | 2002 | 18 | 72.01 | 5.36 | 119.87 | 40.12 | 0.56 |
| Band | Band Center (nm) | Band Width (nm) |
|---|---|---|
| B1 | 412.5 | 10 |
| B2 | 442.5 | 10 |
| B3 | 490 | 10 |
| B4 | 510 | 10 |
| B5 | 560 | 10 |
| B6 | 620 | 10 |
| B7 | 665 | 10 |
| B8 | 681.25 | 7.5 |
| B9 | 705 | 10 |
| B10 | 753.75 | 7.5 |
| B11 | 760.625 | 3.75 |
| B12 | 775 | 15 |
| B13 | 865 | 20 |
| B14 | 885 | 10 |
| B15 | 900 | 10 |
| Index | Name | Formula | Reference |
|---|---|---|---|
| MTCI | MERIS terrestrial chlorophyll index | (B10 − B9)/(B9 − B8) | [13] |
| NDVI | Normalized difference vegetation index | (B10 − B8)/(B10 + B8) | [55] |
| LNDVI | Linearized NDVI | 1.2 (B10 − B8)/(B10 + 5 B8) | [22] |
| S–NDVI | Stretched NDVI | 4/[1 + (1.2/NDVI) 2] | [51] |
| RDVI | Renormalized difference vegetation index | (B10 − B8)/SQRT(B10 − B8) | [52] |
| MTVI2 | Modified triangular vegetation index 2 | 1.5 [1.2 (B10 − B5) − 2.5 (B8 − B5)]/ SQRT{(2 B10 + 1) 2 − [6 B10 − 5 SQRT(B8)] − 0.5} | [16] |
| Parameters | Description | Units | Range | |
|---|---|---|---|---|
| Leaf | N | Leaf structure index | - | 1.5 |
| LCC | Leaf chlorophyll content | μg cm−2 | 10~80; interval, 10 | |
| Cm | Leaf dry matter content | g cm−2 | 0.004 | |
| Cb | Leaf brown pigment content | - | 0 | |
| Cw | Equivalent water thickness | cm | 0.02 | |
| Car | Leaf carotenoid content | μg cm−2 | 25% LCC | |
| CAnt | Leaf anthocyanin content | μg cm−2 | 2 | |
| Canopy | LAI | Leaf area index | m2 m−2 | 0.25, 0.5, 0.75, 1, 1,25, 1.5 1.75, 2, 3, 4, 5, 6, 7, 8 |
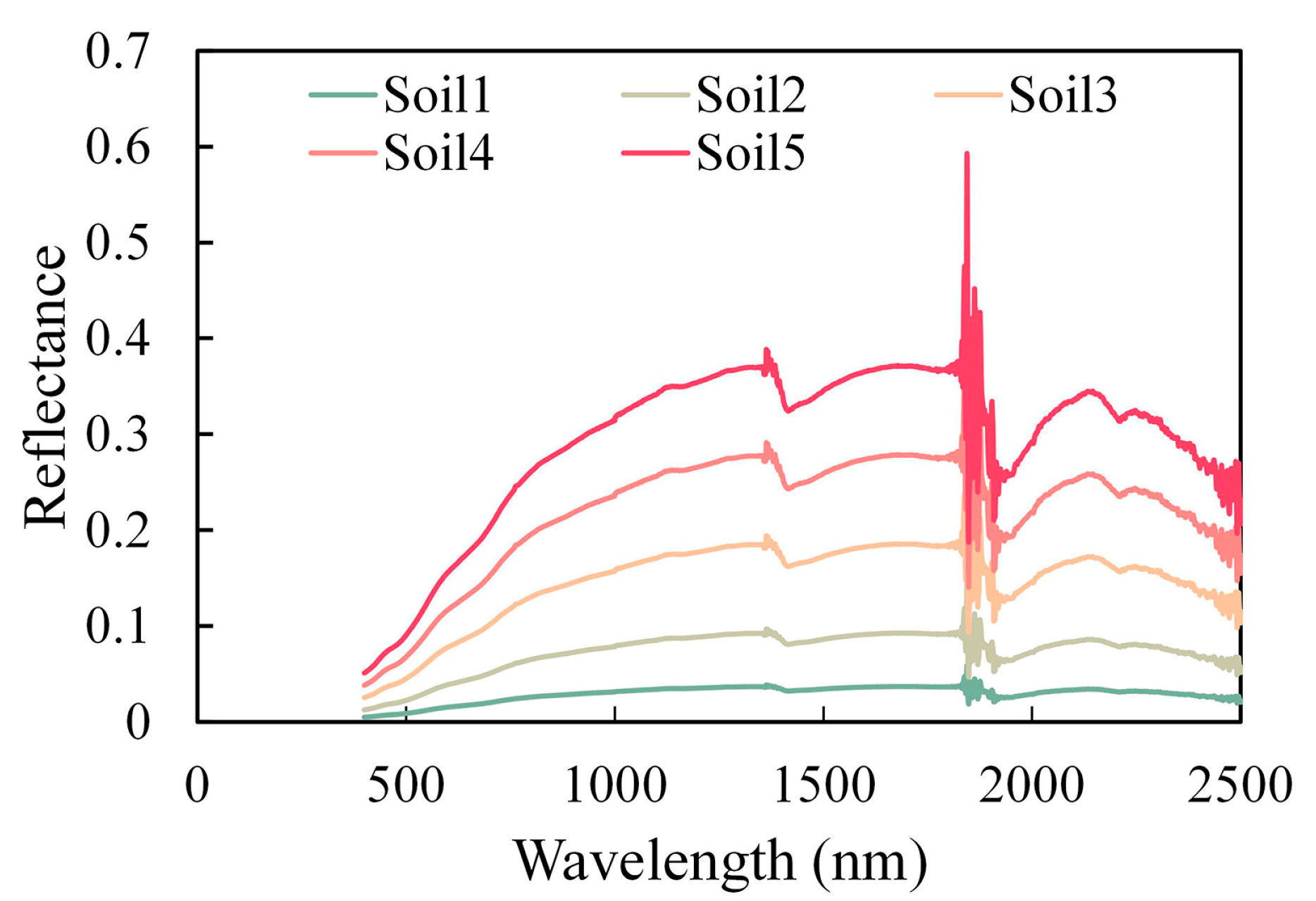
| αsoil | Soil reflectance | - | As in Figure 1 | |
| ALA | Average leaf angle | Degrees | [1, 0], [0, 1], [0, −1], [0, 0] [−0.35, −0.15] | |
| hotS | Hot spot parameter | m m−1 | 0.05 | |
| skyl | Fraction of diffuse incoming solar radiation | - | According to the solar zenith angle | |
| θs | Solar zenith angle | Degrees | 0, 10, 20, 30, 40, 50, 60 | |
| θv | View zenith angle | Degrees | 0 | |
| φ | Sun-sensor azimuth angle | Degrees | 0 |
| Name | Regression Equation | R2 |
|---|---|---|
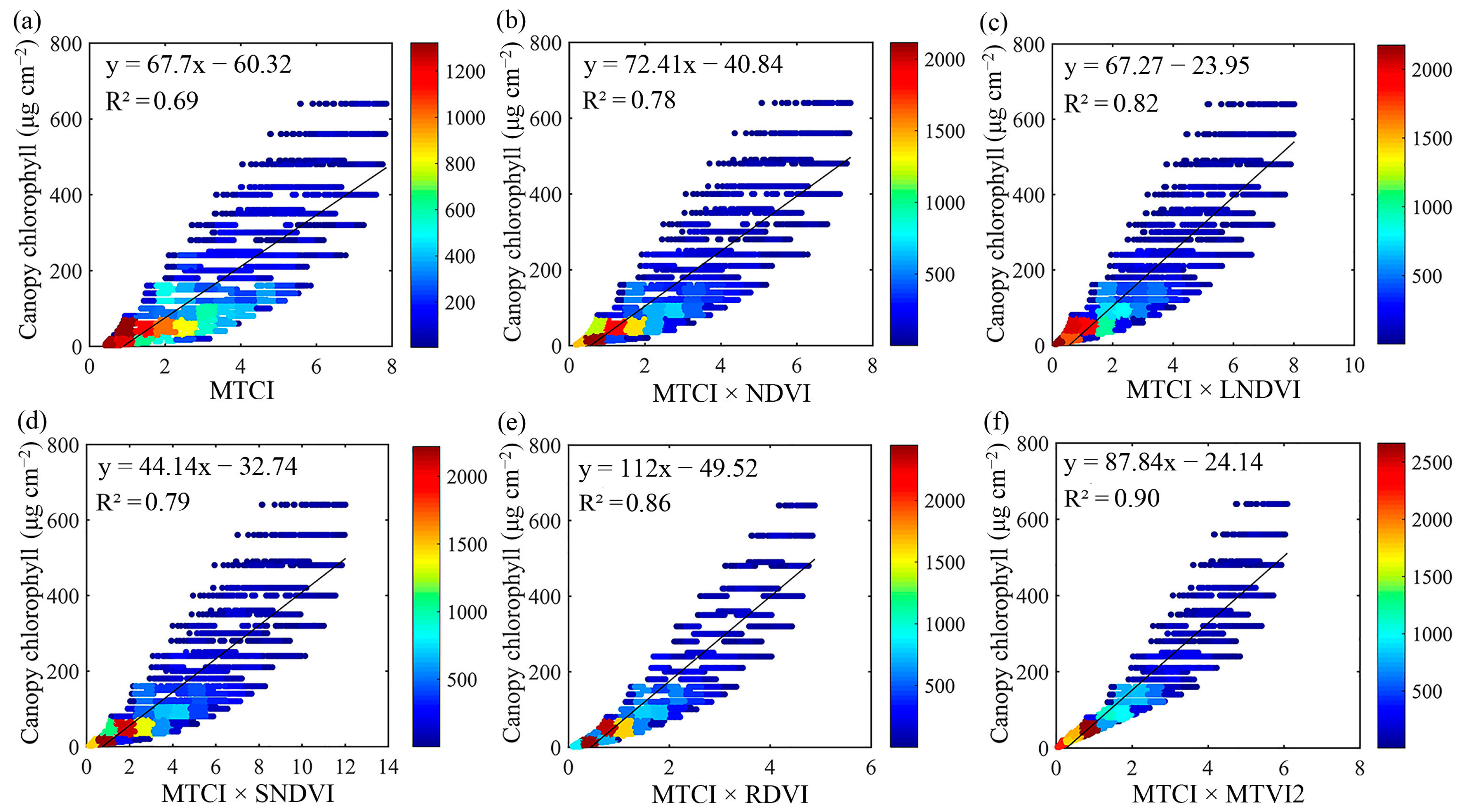
| MTCI | y = 67.7x – 60.32 | 0.69 |
| MTCI and NDVI | y = 58.1088x1 + 201.1010x2 − 191.7325 | 0.74 |
| MTCI and LNDVI | y = 53.5792x1 + 171.5196x2 − 145.0627 | 0.76 |
| MTCI and SNDVI | y = 57.9619x1 + 98.1736x2 − 151.1732 | 0.74 |
| MTCI and RDVI | y = 55.8884x1 + 209.7858x2 − 145.4328 | 0.82 |
| MTCI and MTVI2 | y = 57.8158 x1 + 381.2731x2 − 238.9448 | 0.80 |
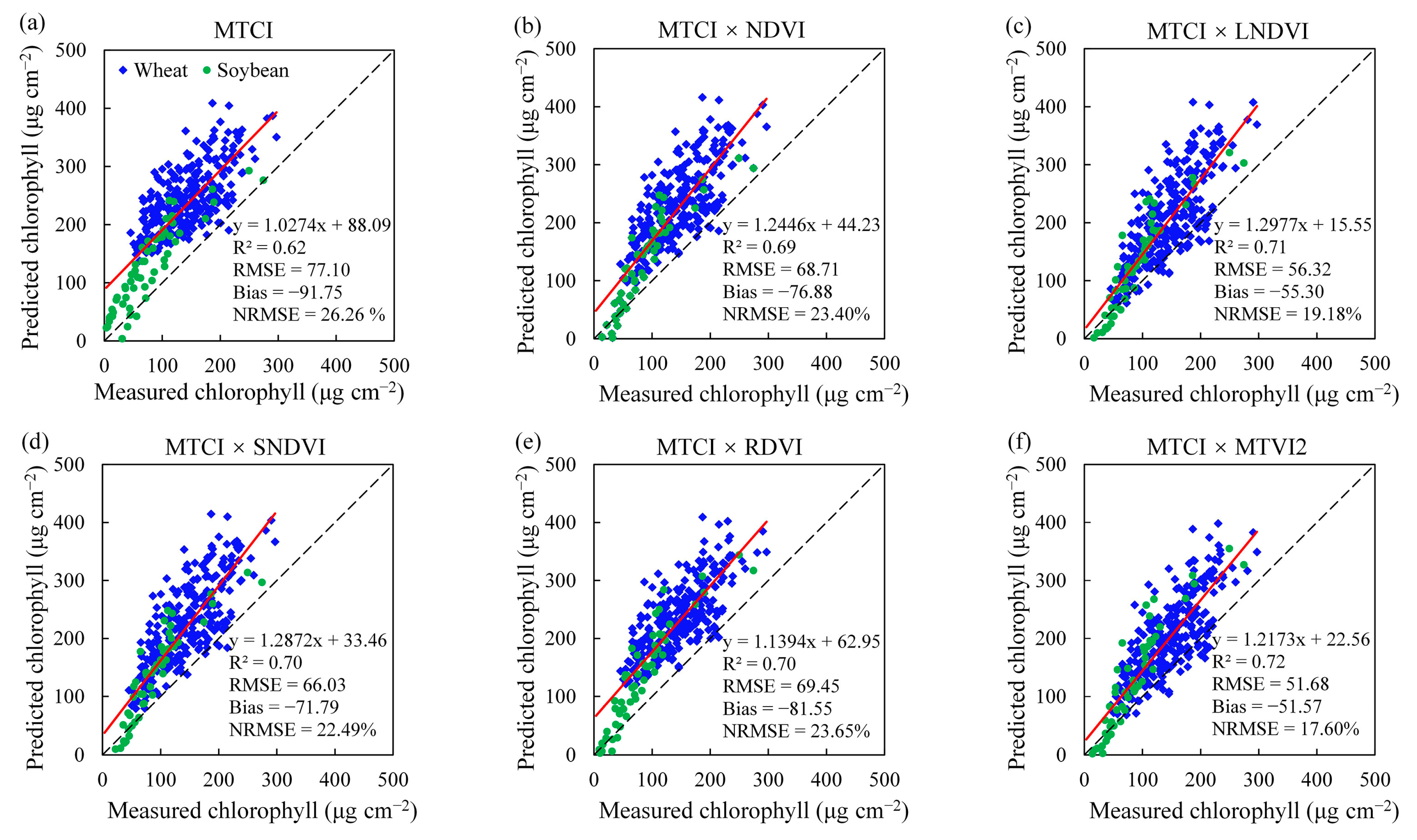
| Predictor | R2 | Predictor | R2 |
|---|---|---|---|
| MTCI | 0.69 | MTCI and SNDVI | 0.96 |
| MTCI and NDVI | 0.95 | MTCI and RDVI | 0.98 |
| MTCI and LNDVI | 0.96 | MTCI and MTVI2 | 0.99 |
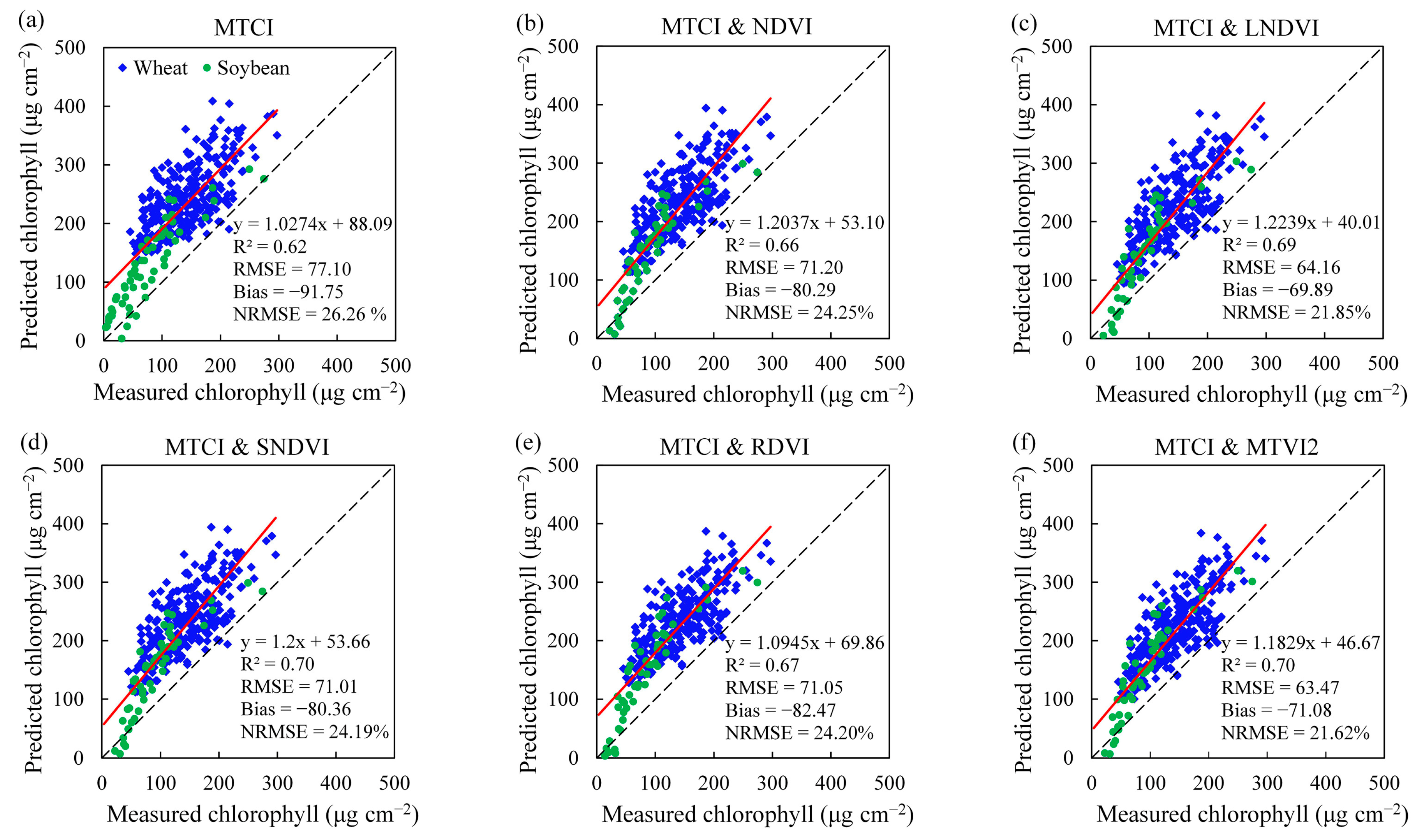
| Approaches | ULR | BLR | RFR | ||||
|---|---|---|---|---|---|---|---|
| VIs | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| MTCI | 0.24 | 136.54 | - | - | - | - | |
| MTCI and NDVI | 0.65 | 96.71 | 0.52 | 111.33 | 0.45 | 58.96 | |
| MTCI and LNDVI | 0.79 | 66.39 | 0.59 | 97.12 | 0.49 | 57.15 | |
| MTCI and SNDVI | 0.72 | 86.14 | 0.52 | 110.78 | 0.45 | 59.03 | |
| MTCI and RDVI | 0.58 | 132.50 | 0.59 | 110.76 | 0.78 | 93.72 | |
| MTCI and MTVI2 | 0.81 | 88.44 | 0.70 | 122.46 | 0.78 | 47.96 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Jiao, Q.; Qian, X.; Liu, L.; Liu, X.; Dai, H. Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations. Remote Sens. 2021, 13, 470. https://doi.org/10.3390/rs13030470
Sun Q, Jiao Q, Qian X, Liu L, Liu X, Dai H. Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations. Remote Sensing. 2021; 13(3):470. https://doi.org/10.3390/rs13030470
Chicago/Turabian StyleSun, Qi, Quanjun Jiao, Xiaojin Qian, Liangyun Liu, Xinjie Liu, and Huayang Dai. 2021. "Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations" Remote Sensing 13, no. 3: 470. https://doi.org/10.3390/rs13030470
APA StyleSun, Q., Jiao, Q., Qian, X., Liu, L., Liu, X., & Dai, H. (2021). Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations. Remote Sensing, 13(3), 470. https://doi.org/10.3390/rs13030470









