Abstract
Providing uncertainties in satellite datasets used for Earth observation can be a daunting prospect because of the many processing stages and input data required to convert raw detector counts to calibrated radiances. The Sea and Land Surface Temperature Radiometer (SLSTR) was designed to provide measurements of the Earth’s surface for operational and climate applications. In this paper the authors describe the traceability chain and derivation of uncertainty estimates for the thermal infrared channel radiometry. Starting from the instrument model, the contributing input quantities are identified to build up an uncertainty effects tree. The characterisation of each input effect is described, and uncertainty estimates provided which are used to derive the combined uncertainties as a function of scene temperature. The SLSTR Level-1 data products provide uncertainty estimates for fully random effects (noise) and systematic effects that can be mapped for each image pixel, examples of which are shown.
Keywords:
calibration; uncertainty; traceability; SLSTR; Sentinel-3; temperature; blackbody; radiometer; data processing; Earth observation; metrology 1. Introduction
Satellite datasets used for Earth observation and climate research need an indication of quality to allow users to assess the suitability of the data for their particular application [1]. At the most basic level, the quality of a measurement is defined in terms of its uncertainty and traceability to standard references. The processing of raw satellite data (Level-0 data) to radiometrically calibrated and geo-referenced data products (Level-1 data) involves a number of stages and relies on several auxiliary data files (ADFs) that contain calibration coefficients and tables used for converting digital counts to physical quantities [2]. These coefficients are derived from characterization measurements of different components of the instrument system. Furthermore, the derivation of the calibration source radiances is dependent not just on a single parameter, e.g., a temperature measurement, but other input quantities such as thermal gradients. Thus, the uncertainty of the data products is dependent on all effects contributing to the data processing. Furthermore, the uncertainty associated with a single observation in a single pixel is unlikely to be a single value but can vary with scene radiance.
The Sea and Land Surface Temperature Radiometer (SLSTR) on the Copernicus Sentinel-3 mission is an instrument designed to retrieve global sea surface temperatures (SSTs) for climate monitoring [3]. Two satellites (model A and B) provide near complete daily global coverage. SLSTR is a development of the along-track scanning radiometer series [4] and shares many of the key design features [5] needed for accurate measurement of SST, principally a conical scanning geometry to provide a 1400 km near nadir view and 750 km inclined view facing backwards towards the satellite line of sight, co-aligned spectral bands at thermal infrared (TIR) wavelengths of 3.7 µm, 10.8 µm and 12 µm for measurement of temperature, spectral bands in the visible (VIS) to short wave infrared (SWIR) for daytime cloud screening and surface classification, cryocooled detectors to minimise the noise equivalent differential temperature (NEDT), and on-board calibration systems. A more detailed description of the SLSTR instrument and the predicted design performance is described in [6,7].
The primary requirement of SLSTR is to measure sea-surface-temperatures to an uncertainty <0.3 K traceable to Système international (SI) (d’unités) [8], the uncertainties in the at-sensor brightness temperatures are required to be <0.2 K (0.1 K goal). The kelvin, the SI unit of temperature, is defined (since 2019 [9]) by the Boltzmann constant and practically realised through the International Temperature Scale of 1990, ITS-90 [10]. In principle, the radiometric calibration of a TIR instrument may be traced to SI via blackbody calibration sources whose temperatures are measured by accurate thermometers, calibrated against standard platinum resistance thermometers (S-PRTs), which in turn are calibrated against reference artefacts of the ITS-90, such as triple point cells as illustrated in Figure 1.

Figure 1.
Illustrating the traceability of the SLSTR radiometric calibration via blackbody sources to ITS-90.
Prior to launch, the SLSTR was calibrated following a full end-to-end calibration plan [11], as described in Smith et al., 2020 [12]. The pre-launch calibration activities included:
- The radiometric measurement function (calibration model) as described in Section 3.
- Detailed instrument model to predict the end-to-end performance [7].
- Characterization of the critical components of the instrument subsystems including properties of optics elements and coatings, raw detector responses [7].
- End-to-end calibration of the black-body thermometer system including thermometers, wiring harness and readout electronics [13].
- End-to-end calibration of the instrument thermometer system including thermometers, wiring harness and readout electronics [13].
- Derivation of the black-body emissivity based on measurements of the black-coatings [14].
- Spectral response calibration [15].
- Instrument level end-to-end calibration under flight representative conditions against reference blackbody sources [12].
A considerable amount of information about the instrument calibration is contained within the numerous project documents that are not easily accessible outside of the industrial consortium that developed the instrument, nor useful without understanding the context. The aim of this paper is to collate and condense this information to provide a description of the end-to-end traceability of the instrument calibration and to provide per-pixel uncertainty estimates of the Level-1 infrared radiometric data products.
2. Materials and Methods
Historically, traceability information in satellite datasets used for Earth observation has been provided inconsistently. Consequentially the performance of many sensors is poorly understood which limits the usefulness of their datasets. To address these issues, the Fidelity and Uncertainty in Climate Data Records from Earth Observation (FIDUCEO) project set out to apply metrological principles to historical satellite datasets [16]. In this paper, we have applied these principles to the SLSTR radiometric calibration of the thermal infrared channels.
The Guide to Uncertainty in Measurement (GUM [17]) describes the error in a measurement as the “result of a measurement minus a true value of the measurand” and the uncertainty in a measurement as “a parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measurand.”
The uncertainty associated with the measurement can be evaluated by analysis of all the contributing error effects. We derive the total uncertainty in the Earth scene radiance, , using the law of propagation of uncertainties given in the GUM as:
where corresponds to each input quantity to Earth scene radiance measurement equation (e.g., counts), is the sensitivity of the measurand to each input quantity and is the standard uncertainty in each input quantity which can be dependent on several effects (e.g., noise). is the error correlation coefficient between input quantities and . In this paper uncertainties are reported as standard uncertainties (i.e., at a coverage factor k = 1).
The uncertainty of some input quantities may, in some cases, be described by non-normal distributions, for example a rectangular distribution. Despite this, the resulting uncertainty of the measurand still tends towards a normal distribution, as described by the central limit theorem. The standard uncertainty for a non-normal distribution is evaluated by dividing the distribution width by a value called a divisor, as defined in the GUM. For example, the divisor for the full width of a rectangular distribution is [18].
We can restate Equation (1) in a convenient matrix form, [16] (Figure 2). In this formulation, c is the vector of the sensitivity coefficients for each input quantity, i.e., . The uncertainty matrix, , is a diagonal matrix with the standard uncertainty associated with each input quantity down the diagonal, i.e., . Finally, is the error-correlation coefficient matrix between input quantities, which has a diagonal of ones and off-diagonal elements of the error-correlation coefficient between input quantities. Together is a decomposition of error-covariance matrix of the input quantities, which provides a simple practical means of forming the error-covariance matrix.
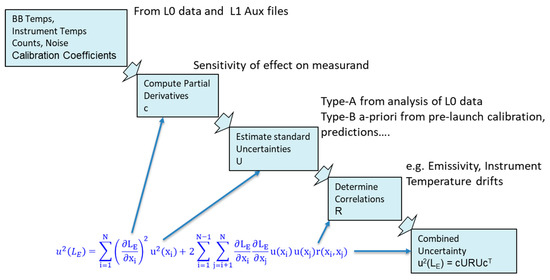
Figure 2.
Derivation of SLSTR L1 radiometric uncertainties.
By definition, the true error in the measurand cannot be known; it is, however, possible to determine how the errors are correlated along given dimensions, such as between measurements in different channels or pixels. Such information about error-correlation structures is key to enabling proper propagation of uncertainties to Level 2 products and beyond, which involves combining measurements from different channels or pixels.
Although the primary focus of this analysis is evaluation of the uncertainty for each scene radiance, an initial attempt has also been made to approximately capture some measurement error-correlation information. To achieve this, the uncertainty contributions described within are broadly divided into random and “correlated” uncertainty components. The random component of uncertainty is assumed to be fully uncorrelated between pixels and spectral bands, and here the correlated component of uncertainty is assumed to be fully correlated between pixels and spectral bands. For the correlated component of uncertainty this is, of course, a simplification as in reality, it is made up of various uncertainty contributions that may each have varying error-correlation structures. Despite this, it is thought this indicative information may be of use to some more advanced users. Future work should further investigate providing error-correlation information more accurately.
Finally, for this work, all radiometric uncertainties are expressed in kelvin in terms of brightness temperature (BT). Brightness temperature is the temperature of a perfect blackbody that has the same radiance as the Earth pixel (whose radiance comes from both surface temperature and emissivity and atmospheric radiative transfer). BT is a useful concept for translating radiance values and their uncertainties into a more intuitive quantity. The radiance uncertainty can be equated to a brightness temperature uncertainty at the measured scene temperature through the sensitivity coefficient:
3. The SLSTR Measurement Function
The level-1 products contain geo-referenced, at sensor BTs for each instrument pixel which have been derived from the raw (Level-0) detector counts as follows.
For a scene temperature , the signal measured by each channel is converted to a voltage and then digitised to counts. (in the range 0 to 16,383) may be expressed as:
where is the scaling factor of the analogue-to-digital converter (ADC), is the response of the detectors/electronics in each channel and is the offset in the detectors and electronics, is the in-band integrated spectral radiance for temperature in W m−2 sr−1 µm−1, is the total transmission of the optics at the wavelength of peak response for each spectral channel, and is the total throughput of the detectors defined by the field-of-view of the detectors. Because the detectors are cooled to approximately 86 K we can assume that the contribution from the cold focal plane assembly (FPA) and optics to the total signal can be considered to be negligible. Also, we can assume that all optical elements the main optical chain use the same high reflectivity optical coatings, and by design are approximately at the same temperature, .
The conical design of SLSTR ensures that the angle of incidence of the incident radiation is constant for all scan positions, so assuming that and remain constant around the scan the measured signal can be expressed as:
The Earth scene radiance, is assumed to a first approximation to be a linear function of Earth counts, (nonlinearity corrections are discussed below). This means the equation takes the form
Here we introduce the +0 term that explicitly represents effects, expected to have zero mean, that are not captured by the measurement function (i.e., there is an uncertainty associated with this quantity being zero). For example, possible stray light errors that are assumed to be negligible.
We derive the coefficients and using data from the two on-board SLSTR calibration blackbody sources with temperature and producing radiances, and . The detector counts when viewing these blackbody sources are and . Thus, substituting into Equation (5) we obtain:
and:
Thus Equation (5) can be rewritten as:
where:
The detector counts for the on-board blackbodies are taken as the average of all the detector counts recorded during 10 scan cycles = 10 × 8 = 80 pixels.
So, for SLSTR, the derivation of the Earth scene radiance from detector counts depends primarily on the radiances from the on-board blackbodies and the averaged blackbody counts, Table 1. The calibration scheme is not dependent on variations in the properties of the optical components, e.g., degradation or scan-dependent effects, nor on the absolute knowledge of the optical geometry. Furthermore, the calibration offset should remain constant around the scan cycle and not vary between calibration observations which is achieved by viewing the calibration sources every 600 ms to provide a continuous calibration, and at the same angle of incidence on the scan mirror as the Earth view.

Table 1.
Table of primary contributions to uncertainties in SLSTR calibration model.
The SLSTR measured Earth scene radiance is converted to brightness temperature via the Planck function as follows. For a perfect blackbody with emissivity ε = 1.0, the spectral radiance at wavelength λ emitted by a blackbody at temperature T, per unit area, per steradian, per unit wavelength is given by:
where, by definition [9]:
- -
- h is Plank’s constant = 6.626 070 15 × 10−34 J s,
- -
- c is the speed of light = 299 792 458 m s−1,
- -
- kb is Boltzmann’s constant = 1.380 649 × 10−23 J K−1.
For an instrument with a spectral response as a function of wavelength, , the integrated in-band radiance is given by:
Here the +0 term is introduced to account for errors in the interpolation of the temperature to radiance table.
In the operational Level-1 processing chain, conversion from temperature to radiance and vice versa is performed via a Look-Up-Table (LUT) using the above formulation. All calculations in the data processing are performed in radiance units and then converted to Brightness Temperature in kelvin as the final step, i.e.,:
Here the +0 term is introduced to account for errors in the inversion of the temperature to radiance table, such as interpolation errors which are considered negligible.
3.1. Non-Linearity
The equations in the previous section assume a linear response of the detector to the scene radiance. However, the detectors that are used in SLSTR have a known non-linear response caused by Auger recombination [18] that manifests as a fall of in response with increasing photon flux [19]. The response non-linearity depends on the individual detector and wavelength but can be up to 10% [12]. Following the approach described in [20], we can linearize the raw detector counts before performing the calibration using:
The correction is applied to the Earth scene counts and the blackbody signals. The non-linearity of the instrument response, was characterized during the pre-launch calibration [12] and described in Section 4.5. Here the +0 term is introduced because the non-linearity correction is an approximation and there may be residual differences between the approximation and the true non-linearity.
3.2. Blackbody Radiances
Real blackbodies are not completely black, i.e., the emissivity ε < 1.0 so the actual radiance will have a small reflected component meaning that the measured radiance during the calibration view of the blackbody is given by:
Here the +0 term is introduced to account for errors in the background term, for example due to non-uniform background.
is the radiance from the optical mechanical enclosure (OME) optics and structure corresponding to an instrument temperature . The internal structure of the OME is painted with a black-thermal coating with > 0.9, so it is possible to approximate the background radiance term using the Planck function for a temperature derived from the thermometers located within the OME structure. Therefore, the measured radiance of the blackbody becomes
By design, the blackbody apertures are larger than the optical beam of SLSTR so no correction for the source geometry is needed [6]. The contribution to the radiometric uncertainty budget from the blackbody sources is given in Table 2.

Table 2.
Table of contributions to uncertainties in blackbody radiance model.
3.3. Uncertainty Effects Tree
The uncertainty effects tree is a useful schematic representation of the sensor measurement function, and has been used previously in the FIDUCEO project [16]. The uncertainty effects tree for the SLSTR radiometric calibration is given in Figure 3. At the centre of the diagram is the measurement function for the sensor, which was given above as Equation (8) here with measurand Earth radiance, LE, and input quantities such as Earth counts, CE, and internal calibration sources radiances, LBB1 and LBB2. From this function branches spread from each input quantity, which may themselves be determined by their own measurement functions (for example here LBB1 is determined from the measured temperature TBB1 and emissivity εBB1 of the calibration target), to their uncertainty. This uncertainty can be traced back through to its impact on the measurand by the sensitivity coefficients on each branch. Finally, the effects which cause each respective uncertainty are connected to the end of each branch.
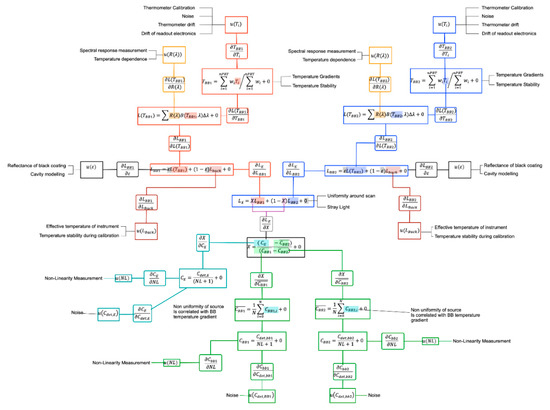
Figure 3.
SLSTR TIR Calibration uncertainty tree diagram. A full size, easier to read version of this diagram is available in Appendix A.
Note that we should also consider the extent to which the measurement function describes the true physical state of the instrument—this is accounted for this by including the term +0 at the end of each measurement function.
Each of the effects identified at the end of each of the branches should then be understood and quantified to provide:
- The uncertainty associated with the given effect.
- The sensitivity coefficient required to propagate uncertainties associated with that effect to uncertainty associated with the measurand (here Earth brightness temperature).
- The correlation structure over spatial, temporal and spectral dimensions for errors from this effect.
The following section deals with each contributing effect to the SLSTR radiometric measurement.
4. Discussion of Uncertainty Contributions
We now consider the contributing effects to the radiometric calibration budget and how these were characterized.
4.1. Radiometric Noise
Here we consider the purely random noise of the instrument detectors. At infrared wavelengths the noise performance is usually expressed as the noise equivalent temperature difference (NEDT), given by:
where is the detector noise in counts measured at a given scene temperature. Strictly speaking, there should be a +0 term to account for non-linearity but the error is negligible. The total signal noise will be a combination of the shot, detector, quantisation (digitisation) and amplifier noise sources such that:
For SLSTR, the radiometric noise is dominated by detector noise and electronics noise and is largely constant with scene signal (in counts), although channel S7 (3.7 µm) has slightly more shot noise sensitivity. Note that the exact values of these noise components cannot easily be determined individually, particularly at instrument level. For example, to measure the true dark noise of a TIR detector—the input light signal needs to be zero (or close to zero).
The radiometric noise performance was characterized at instrument level during the pre-launch calibration tests as a function of scene temperature [12], Figure 4. NEDT estimates for SLSTR-A and B derived from observations of the blackbody sources are given in Table 3.
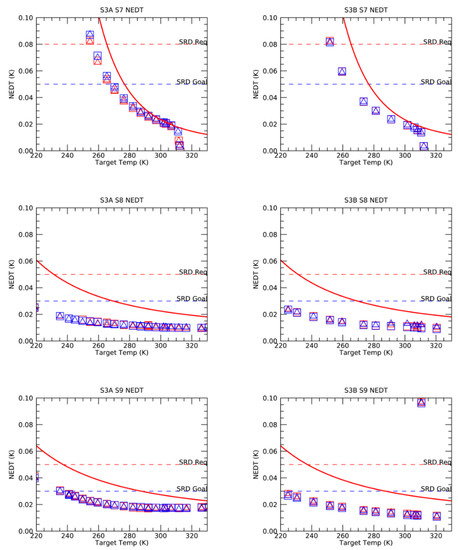
Figure 4.
SLSTR-A and B NEDT measured during pre-launch calibration tests, from [12]. The solid line is the predicted end-of-life estimate derived from the instrument model [11]. ☐ = Detector 1, Integrator 1; ☐ = Detector 1, Integrator 2; Δ = Detector 2, Integrator 1; Δ = Detector 2, Integrator 2.

Table 3.
Average on-orbit NEDT estimates (and noise in radiance) for SLSTR-A and B derived from in-flight blackbody measurements.
On orbit it is not possible to evaluate noise levels as a function of scene temperature. Instead, the radiometric noise is characterized on orbit from the radiometric signals from the two on-board blackbody sources. Noise values at other scene temperatures are derived by interpolation using the noise vs. temperature measurements acquired during the pre-launch calibration.
For the blackbody calibration source observations, the noise on the average reduces by where N is the number of pixels over which the blackbody counts, are averaged = 80 pixels. This reduction does not occur for a single Earth pixel observation.
4.2. Blackbody Temperatures
The temperatures of the SLSTR blackbody cavities are measured via precision platinum resistance thermometers embedded in the cavities. There are five thermometers (+5 redundant) in the base, and one on the cavity wall (+1 redundant). For the radiometric calibration, the thermometers mounted in the base of the cavity are the most critical. These are calibrated traceably to ITS-90 via SPRTs mounted on the cavity when the thermometry system was calibrated prior to shipment to the instrument.
There are several sources of uncertainty in the thermometry calibration that must be considered in the design, manufacture and testing of the blackbody subsystems. A detailed analysis of the uncertainty budget was performed by the then manufacturers, Advanced Battery Solutions Limited (ABSL, UK), based on the approaches adopted for the previous Advanced Along-Track Scanning Radiometer (AATSR), the Michelson Interferometer for Passive Atmospheric Sounding (MIPAS) (Envisat) and the Infrared Atmospheric Sounding Interferometer (IASI) (on Metop) [13]. The approach used the worst-case estimates for the components, in particular for the drift in the reference resistor in the instrumentation amplifier. The beginning of life (BOL) uncertainties assume a 10-year storage life, and the end of life (EOL) degradation assumes a 7.5 year mission.
The final thermometry uncertainty budget for both SLSTR models A and B is shown in Table 4 and Table 5. These are all reported here as standard uncertainties (at k = 1). At BOL, the combined uncertainty is 6.1 mK with the most significant contribution being the calibration of the thermometers and the reference SPRT that is used in the calibration. For SLSTR, the uncertainty due to the Analogue to Digital Converter (ADC) non-linearity is needed if interpolating between digital counts from the ADC. In practice, all digitiser states are calibrated so this component should be smaller.

Table 4.
SLSTR blackbody temperature measurement uncertainties at BOL from [13].

Table 5.
SLSTR temperature measurement uncertainties due to degradation effects over 7.5 year mission lifetime and EOL budget.
At EOL, the dominant effects are due to radiation and calibration drifts which gives a total EOL uncertainty of 15.5 mK.
It is not possible to design a blackbody cavity that is truly iso-thermal. Although a considerable amount of attention has been paid to the thermal design of the cavity, radiative and conductive heat-leaks within the cavity will result in small measurable temperature gradients. By design, one blackbody is unheated, and the temperature is close to the background thermal environment at 260 K. The heated BB is set to ~40 K above the thermal background and will have larger gradients because of the heater elements, and the radiative coupling between the cavity and the environment.
Table 6 shows the difference in temperature for each baseplate PRT relative to the average of the cavity base for the SLSTR-B instrument measured during on-ground calibration and on-orbit commissioning. The worst-case situation is for the heated blackbody cavity (BBC) at 302.3 K which has a max-min difference of 0.1 K. Where the BBC is unheated the max-min temperature difference is ~30 mK.

Table 6.
Temperature differences of the SLSTR-B blackbody baseplate PRTs relative to the average cavity baseplate temperature from on-ground and in-orbit for different combinations of blackbody temperatures. The thermal environment of the BBC is ~260K [18]. For SLSTR, one blackbody mounted on the +Y side of the satellite (+YBB) is normally heated and the one mounted on the opposite -Y side (-YBB) is normally unheated and floating close to ambient. The divisor is chosen as the standard deviation of a rectangular probability distribution, the distribution is bound by the upper and lower temperature readings of the blackbody.
4.3. Blackbody Emissivity
The emissivity of the SLSTR blackbody cavities was determined by combining reflectance measurements of the black coating material and a Monte-Carlo simulation to account for the cavity geometry (Table 7). The supplier, ABSL, employed their proprietary software, SMART3D, that has been previously used for the AATSR, MIPAS and IASI instruments [13]. The analysis has since been repeated by RAL Space using a more complete set of witness samples that were coated with the same black coating during the manufacture of the cavities, and the STEEP323 Monte Carlo simulation tool [21] to model the cavity emissivity [14].

Table 7.
Internal Blackbody Emissivity as Reported in [13] These values are the same for both SLSTR-A and B since it assumed that the coating and geometry are identical.
The spectral directional hemispherical reflectance from 1.5 μm to 18.5 μm of the Enhanced Deep Sky Black Enhanced samples were measured by National Institute for Standards and Technology (NIST) for SLSTR-A [NIST Certificate—685/283172-13]. For SLSTR-B, witness samples were originally measured by NIST [NIST Certificate—685/283494-13] and repeated by NPL [NPL certificate 2017030000]. Results of analysis performed by RAL showed that the emissivity derived by STEEP-323 and SMART-3D analysis agreed within the uncertainties (Figure 5).
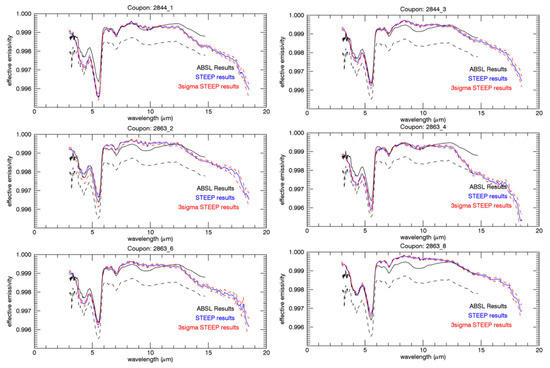
Figure 5.
Comparison of STEEP 323 and SMART3D results of the SLSTR BB Cavity geometry deduced from NIST measurements of the black-coating. The solid lines refer to the original ABSL analysis, the blue curve the analysis using the STEEP323 software.
4.4. Spectral Response
For SLSTR A and B, the spectral response functions of the channels were measured using an IFS120HR high-resolution Fourier Transform Spectrometer (FTS) [15]. This spectrometer has a spectral range of 30 cm−1 to 40,000 cm−1 (250 nm to 333 μm) with a maximum unapodized spectral resolution of 0.0015 cm−1 achieved through a combination of sources, beam splitters and detectors. Using an FTS has several advantages over a grating monochromator. Unlike a grating monochromator, the FTS has a two-dimensional aperture that is well matched to that of the instrument FPA and allows a large light throughput filling the full optical beam. Also, the input light source is un-polarised. Information is collected simultaneously over the entire spectral range of the system. This is particularly useful for SLSTR which has a spectral range from visible wavelength to thermal infrared. The spectral registration is excellent and is orders of magnitude better than can be achieved with a grating spectrometer.
Measurements were performed on the FPA sub-assembly rather than the full SLSTR instrument because the scanning geometry of the instrument would have required a complex and prohibitively expensive test setup. This was also justified because the main spectrally sensitive components of the instrument are contained in the FPA and the reflectances of the fore-optics mirrors are flat over the SLSTR bands.
The instrument spectral responses and associated systematic uncertainties for thermal infrared channels of SLSTR-A and SLSTR-B are shown in Figure 6 and Figure 7, respectively.
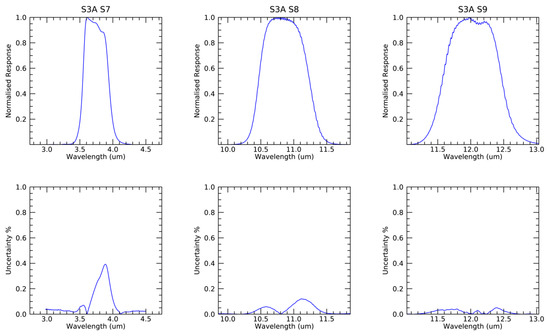
Figure 6.
SLSTR-A Spectral Response Measurements for the TIR channels at 87 K [15]. Upper plots give spectral response functions, lower plots the associated systematic uncertainties.
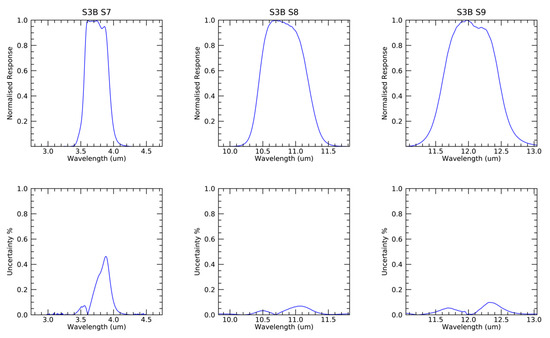
Figure 7.
SLSTR-B Spectral Response Measurements for the TIR channels at 87 K [15]. Upper plots give spectral response functions, lower plots the associated systematic uncertainties.
Uncertainties in the spectral response profile can be interpreted as having two main effects: errors in the spectral band centre and in the bandwidth, see Table 8. These effects may be correlated, where for example, a shift in the long-wavelength edge of the response will affect the band centre and the bandwidth. This is the case for the 12 µm channel (S9) where the long-wavelength edge of the response is determined by the long-wavelength cut-off of the mercury cadmium telluride (MCT) detector. Uncertainties in the spectral response will be due to the measurement process used to assess the spectral response, along with changes to the SLSTR instrument from ground-test to on-orbit such as differences in the operating temperatures of the detectors. Results from the SLSTR-A and B spectral response testing showed an uncertainty in the band centres and edge positions of <0.001 µm. Measurements at different temperatures showed a sensitivity of −0.003 µm K−1.

Table 8.
SLSTR A and SLSTR-B Band Centres, Short and Long Wavelength edges, estimated uncertainties in positions from measurements and temperature sensitivity of the band edges.
For the radiometric calibration at level 1, the main effect is on the temperature to radiance conversions. This gives a contribution to the uncertainty budget with sensitivity coefficient which varies with scene temperature as shown in Figure 8. We note that the sensitivity due to band centre errors is stronger than that for bandwidth errors.
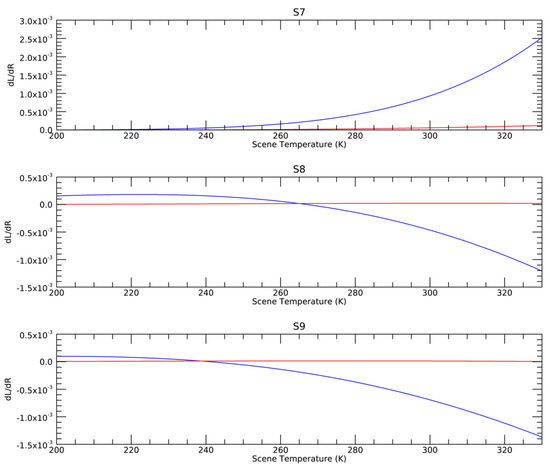
Figure 8.
Sensitivity coefficient for spectral radiance errors in Wm−2sr−1µm−1/nm due to uncertainty in spectral band-centre (blue line) and uncertainty in bandwidth (red line).
Since the same spectral response applies to the derivation of the on-board blackbody radiances from their temperatures, and to the conversion from scene radiance to brightness temperatures, we can consider the effect to be fully correlated.
We should emphasise that the effect of spectral response errors reported in this paper applies only to the calibrated BTs in the L1 product. For higher level products such as SST, the effect of spectral response errors on the retrieval process has to be considered in addition to the BT uncertainties. This is because the at sensor radiance is sensitive to the position of the spectral response in relation to the scene spectra which vary with scene type and atmospheric composition.
4.5. Non-Linearity
In Section 3.1 we introduced a correction for the non-linear response of the detectors. The response non-linearity is formally defined as the relative difference between the actual response and the linear approximation based on the calibration at two different signal levels and is defined as:
where x is the input signal and y is the measured response calibrated at two points and so that and , so that . We can adjust the non-linearity so that NL at is zero in accordance with [18]:
For SLSTR the non-linearity was characterised during the pre-launch calibration by comparing the measured detector counts against the incident scene radiance from the external blackbody calibration sources [12]. The process of determining and verifying the non-linearity correction is illustrated in Figure 9. The detector counts and scene radiance are normalised to two reference points, = 0 and = by defining the following quantities:
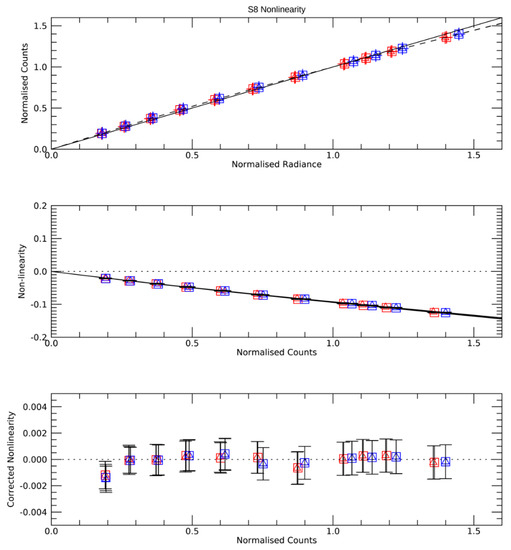
Figure 9.
Determination and verification of response non-linearity for SLSTR-B 10.8 um channel. ☐ = Detector 1, Integrator 1; ☐ = Detector 1, Integrator 2; Δ = Detector 2, Integrator 1; Δ = Detector 2, Integrator 2.
For the flight calibration = 32,768 as this is within the range of Earth scene measurements; the value is arbitrary and a different value could have been chosen provided that the same value was used for the correction. The normalisation points, and are obtained by fitting a polynomial to the measurements. Note is not necessarily zero, and could be positive or negative depending on the spectral band.
A polynomial of the form:
is fitted to the data to derive the non-linearity coefficients. We then verify the non-linearity correction by applying to using Equation (14).
Uncertainty in the non-linearity correction is mainly dependent on the external calibration sources, which in turn are mainly dependent on the temperature measurement [12]. An estimate of the uncertainty associated with the non-linearity correction (post-correction uncertainties) is ~0.2%.
Because the non-linearity is a function of the detector response, and therefore the detector counts, the effect is fully correlated between the Earth scene and blackbody signals. I.e. where the Earth scene counts are the same as the blackbody signals, the effect of non-linearity reduces to zero.
4.6. Other Effects
During the pre-launch radiometric testing of SLSTR-A and B unexpected discrepancies were observed in the brightness temperatures as measured by SLSTR-A channels S8 and S9 compared to those of the external reference source [12]. For model B, the results were significantly better for the nadir view, although they still showed some differences in the oblique view, but within the reported uncertainties. The probable cause of the effect was due to lower-than-expected performance of the black coating used in the parabolic mirror assembly (PMA) stop leading to a scan-dependent variation of the background signal. The effect was later confirmed in the oblique view by the analysis of comparisons of SLSTR-A and B data from the Sentinel-3 tandem phase [22].
An empirical correction to the calibration model was proposed to account for the stray light effect where the stray light error:
where and and then are the model parameters derived from fitting to the test results. However, the model does not fully address the actual sources of the stray light signals nor accounts for on-orbit variations in the instrument’s thermal environment. At the time of writing, the correction is yet to be fully evaluated and implemented in the L1 processing. Hence, the S8/9 oblique uncertainties reported in this paper are underestimated until a correction is applied and the uncertainty budget extended.
5. Combined Uncertainty
For the Level-1 products, uncertainties are separated between fully random noise expressed as NEDT that reduce with averaging, and uncertainties due to systematic effects in the radiometric calibration that do not reduce by averaging. To derive the combined per-pixel uncertainties we use Table 9 to derive matrices of sensitivity and correlation coefficients. For random and uncorrelated effects, the off-diagonal elements of r(i ≠ j) = 0. For all correlated effects, the off diagonal elements of r(i,j) = 1 (matrix-of-ones). Most variables are independent and therefore uncorrelated. Whilst the non-linearity and spectral response are common to the Earth scene and on-board blackbodies so will have an associated correlation.

Table 9.
Correlations of terms used in deriving individual per-pixel uncertainties in the SLSTR Level-1 BTs.
From all the effects described in the previous sections, the reported uncertainties in the component level characterizations (BB thermometers, emissivities) the instrument temperatures, and measured detector signals we derive the S7–S9 uncertainty budgets for SLSTR-A and B shown inTable 10, Figure 10 and Figure 11.

Table 10.
Breakdown of uncertainty budget expressed as BT in milli-kelvin for SLSTR IR Calibration for a reference scene temperature at 270 K. * Because the Earth scene noise (NEDT) is assumed to be purely random, it is not included in the combined radiometric uncertainty of the radiometric calibration.
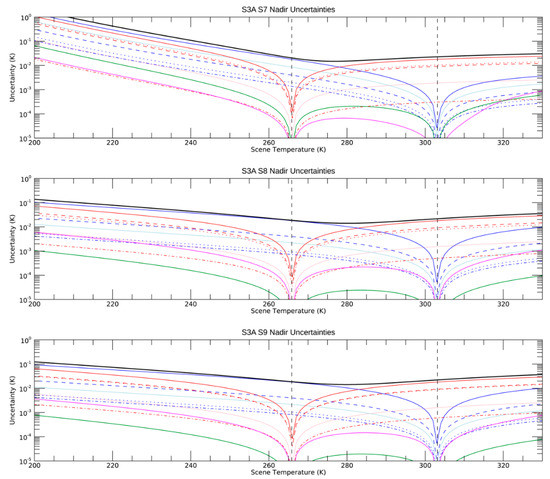
Figure 10.
SLSTR-A Thermal Infrared Uncertainty Budget for a typical orbit at 1 June 2020.
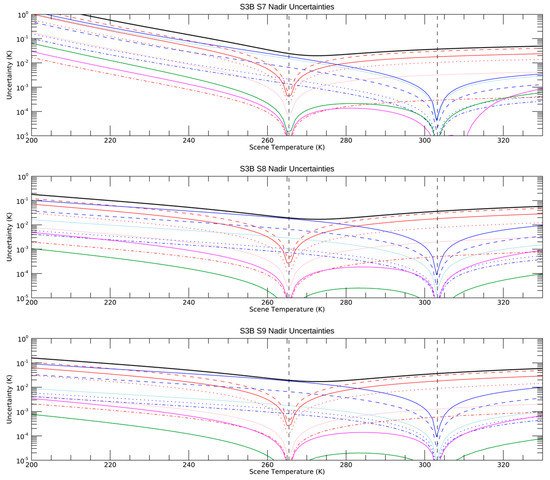
Figure 11.
SLSTR-B Thermal Infrared Uncertainty Budget for a typical orbit at 01-JUN-2020.
The uncertainty budgets in the radiometric calibration presented are for orbits on 1 June 2020 where the instruments were in their nominal flight operational configuration. The budget shows that between the temperatures of the two on-board blackbody sources at ~265 K and 302 K, the uncertainties are dominated by the blackbody temperature measurement and gradients. Other effects are small by comparison. Outside the temperature range of the on-board blackbodies, effects such as non-linearity and spectral response begin to contribute but are still smaller than the contribution from the on-board BB temperatures. We also note that the SLSTR-B uncertainties are slightly higher than for SLSTR-A because of the larger temperature gradients in the heated blackbody.
6. Discussion
Having identified the primary uncertainty effects and propagated these through the calibration model to derive uncertainty budgets in the measured brightness temperatures, we describe how to access the uncertainties and apply these to the scientific data products.
The Level-1 products [2] contain estimates of both “random uncertainties” (uncertainties associated with independent/random effects) and “correlated uncertainties” (uncertainties associated with common/correlated effects). Ideally these uncertainty components would be provided per pixel and per channel, but that was unpractical at the time of the mission development when the processing chains and product specifications were being defined. Instead, random ‘noise’ estimates are currently provided as per scan NEDTs at the two calibration source temperatures, and “correlated uncertainties” in the radiometric calibration are included in the quality annotation datasets as a table of uncertainty vs. scene temperature type-B (a-priori) estimates based on data from the pre-launch calibration test campaign [12]. The information allows per-pixel estimates to be derived by interpolating to the images as an intermediate processing step on the L1 products as follows.
Each Level-1 product comprises a set of Network Common Data Form (NetCDF) files containing images for each of the spectral channels and for each earth view. For the correlated uncertainties, the uncertainty for each image pixel corresponding to is obtained from table of uncertainties provided for each spectral channel, , using an interpolation function. i.e.,
To map the “random” NEDT values to each pixel, it is first necessary to extend the noise estimates from the two on-board BB temperatures to the full range of earth scene temperatures. Here, the pre-launch test results are used to provide reference tables of NEDT vs. Temperature for each channel [12]. These tables are scaled to flight estimates by using the NEDTs derived from the on-board BBs. Note that the scaling is performed in radiance units (W m−2 sr−1 µm−1), by using the temperature to radiance LUT described in Section 3. Mapping the NEDTs to each pixel is then performed as for the correlated uncertainties (Equation (25)).
A prototype Python tool, ‘MapnoiS3’ has been developed to perform the mapping of random and correlated uncertainties to the L1 products. The tool can process several SLSTR Level-1 products in a batch mode, and with as many channels and scan views as the user requires. The tool outputs the uncertainty estimates as separate NetCDF files following Sentinel-3 product format style. These uncertainty estimates can be propagated to level-2 and higher-level products.
Example images of uncertainties are presented in Figure 12 for typical SLSTR Level-1 products. In the examples given, we see that the uncertainties in both random and correlated increase over low temperature scenes, in particular for clouds where the BTs are below the temperature of the cold-blackbody source. For higher temperatures, particularly over land, although the random noise uncertainty decreases (consistent with Figure 4), the uncertainties in systematic effects increases as predicted by the uncertainty model (see Figure 10 and Figure 11).
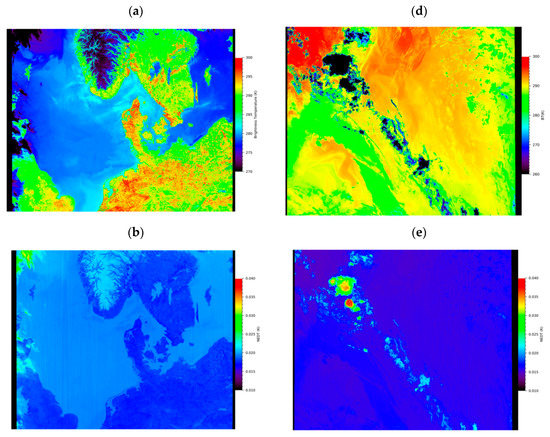
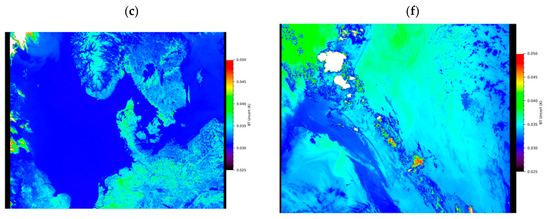
Figure 12.
Sample images showing the output of the MapnoiS3 tool for SLSTR-B 12 µm BT images for a virtually cloud free North Sea on 22 April 2020 (a–c), and off the east coast of Australia during the extreme wildfire event on 1 January 2020 (d–f). The top row (a,d) shows the measured brightness temperatures, the centre images (b,e) show the fully random noise estimates and the bottom row (c,f) show the uncertainty due to correlated (systematic) effects.
We can also use the uncertainty model to evaluate the effect of in-flight variations of the instrument behaviour. For example, the temperatures of the SLSTR instruments vary with season by ~2 °C, being warmer in northern hemisphere winter months. Applying the model to instrument detector counts and temperatures extracted from the instrument’s Level-0 science data [23] we are able to derive time series of the radiometric uncertainties, Figure 13 and Figure 14 for SLSTR-A random noise, and correlated uncertainties respectively, and Figure 15 and Figure 16 for SLSTR-B.
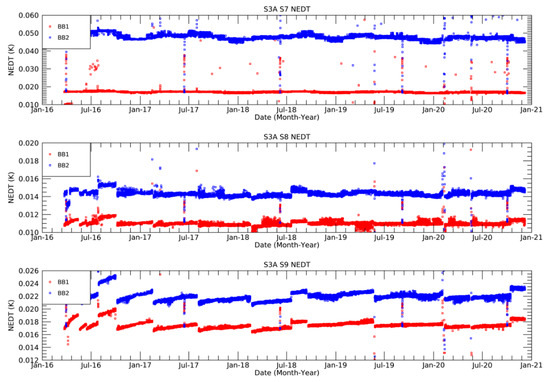
Figure 13.
Time series for the period from March 2016 to December 2020 of SLSTR-A NEDT (Fully Random Uncertainty) derived from the on-board BB targets at ~262 K (blue) and ~302 K (red).
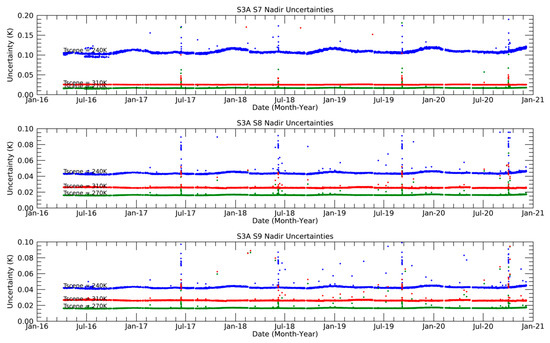
Figure 14.
Time series for the period from March 2016 to December 2020 of SLSTR-A Thermal Infrared Radiometric. Uncertainties (systematic effects) for scene temperatures of 240 K (blue), 270 K (green) and 310 K (red).
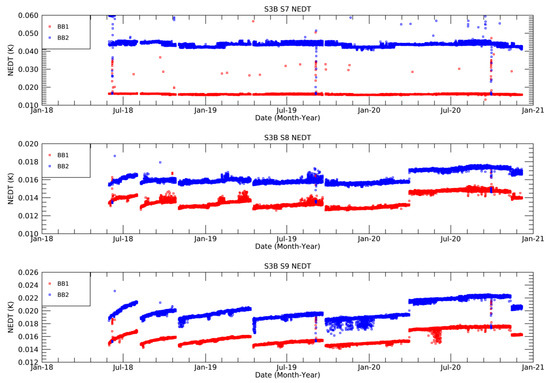
Figure 15.
Time series for the period from May 2018 to December 2020 of SLSTR-B NEDT (Fully Random Uncertainty) derived from the on-board BB targets at ~262 K (blue) and ~302 K (red).
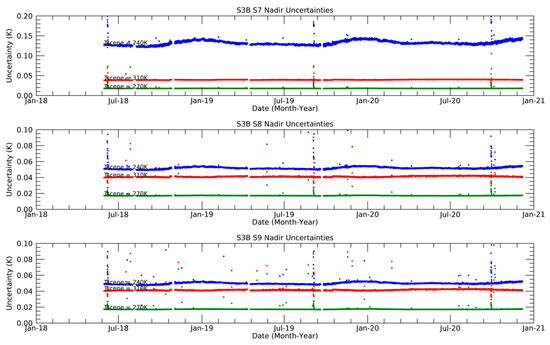
Figure 16.
Correlated Time series for the period from May 2018 to December 2020 of SLSTR-B Thermal Infrared Radiometric Uncertainties for scene temperatures of 240 K (blue), 270 K (green) and 310 K (red).
The NEDT trends measured at the on-board BB temperatures of ~262 K and ~302 K in Figure 13 and Figure 15 depend mainly on variations of the detector temperatures. This dependence is clearly seen by the discontinuities in the trend that occur before and after decontamination cycles, but also when the operating temperatures for the detector were increased slightly in June 2018 for SLSTR-A and April 2020 for SLSTR-B. The noise estimates can be extended to any scene temperature by interpolating using the noise model derived from the pre-launch results as described earlier.
Figure 14 and Figure 16 show the trends of the “correlated uncertainties” at selected temperatures at 240 K, 270 K and 310 K. In general, the uncertainties are stable over the mission lifetime. The discontinuities in the uncertainty trends correspond to periods where the detectors were switched off, or during blackbody cross-over tests. I.e., as the difference in the detector counts for the two blackbodies approaches zero, the uncertainties increase to infinity as predicted by the calibration model. Also, for scene temperatures outside the range of the on-board blackbodies, there is a more seasonal variation in the uncertainty. Again, this is predicted by the calibration model which shows a stronger sensitivity to variations in the instrument temperatures.
For most practical applications, users of SLSTR Level-1 data should consider the NEDT as fully random and the calibration uncertainty as fully correlated between spectral channels. Also, because the instrument behaviour is stable during routine operations, the uncertainties may be considered as correlated over larger scales. Note the paper reports the uncertainty of the calibration of the raw instrument detector counts to radiometric units. Uncertainties due to scene non-uniformity need to be considered as part of any subsequent data processing, for example if instrument pixels are resampled using an averaging technique.
An example of the application of the L1 uncertainties has been with comparisons of SLSTR-A and B during the tandem phase of Sentinel-3 A and B in 2018 [22]. Here the authors applied metrological principles to the comparisons of L1 data acquired during near simultaneous observations of the Earth. This analysis made use of the separate random and correlated components of uncertainty when they compared the L1 data on a 0.5 × 0.5° longitude-latitude grid. In such a binning process, the random uncertainty reduces due to the spatial averaging, whereas the correlated component of uncertainty does not. By applying the law of propagation of uncertainties, it was found that the uncertainties provided reasonable estimates for the S8 nadir channel and S7 channel in both views. The results confirmed the presence of the stray light issue for S8 and S9 oblique view as described in Section 4.5. A consistent 50 mK difference for the S9 channel was not explained by the uncertainties but is thought to be related to the temperature dependency of the spectral response.
7. Conclusions
To allow data from the Sentinel-3 SLSTR instruments to be used for scientific applications, particularly where data from multiple sensors are used, for example in climate applications, it is important that the traceability chain of the data be fully documented. This includes identification of the key sources of uncertainty, estimates of their uncertainty and their characterisation, and how these propagate through to the measurement. For this paper we have applied metrological principles to build up the uncertainty model of the SLSTR Level-1 data for the thermal infrared channels based on the pre-launch calibration and characterisation data, and the measured on-orbit performances.
The design of SLSTR is such that the primary sources of uncertainty are the radiances from the on-board calibration blackbodies which are traced to their physical temperature as measured by the precision PRTs. The calibration of these thermometers provides metrological traceability to ITS-90.
Uncertainty estimates are provided in the Level-1 data products for all spectral channels and for both Earth views in the form of fully random noise expressed as NEDT derived from the on-board sources, and uncertainties due to systematic effects. Currently the uncertainties in the radiometric calibration are based on the pre-launch test results and not computed in the current version of the level-1 processor. A future evolution of the processing chain could implement the uncertainty model to provide time varying estimates as demonstrated in Figure 13, Figure 14 and Figure 15.
Evaluating uncertainties in the Level-1 data is an on-going process, and the estimates reported are those accounted for in the data processing chain. The uncertainty budget will be revised as additional effects are assessed, such as internal stray light.
The origins of this work began during the development phase of the SLSTR instruments where preliminary uncertainty estimates were derived to assess the predicted performance with the view to demonstrate compliance to the mission requirements [6,7,8,9,10,11]. For current and future missions, it is important to start the process early, documenting the full calibration model as described in this paper and providing access to test reports in accessible forms to demonstrate traceability.
Author Contributions
Writing—original draft preparation, D.S.; writing—review and editing, S.E.H., J.M., E.R.W., M.E., T.N., D.P.; conceptualization, D.S., S.E.H. and J.M.; methodology, D.S; formal analysis, D.S.; investigation, D.S., D.P., T.N., M.E., E.P.; project administration, D.S., E.R.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded European Union’s Copernicus Programme, and managed by the European Organization for the Exploitation of Meteorological Satellites through the contract EUM/CO/18/4600002122/AOC. It has also received funding from the project MetEOC-3 (16ENV03) of the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the support of colleagues from Reading University, Eumetsat, ACRI-ST, NPL and RAL.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
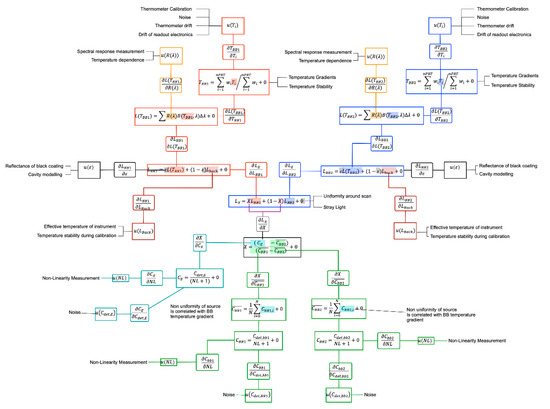
Figure A1.
Full size version of the SLSTR TIR Calibration uncertainty tree diagram.
References
- A Quality Assurance Framework for Earth Observation: Principles. 2010. Available online: http://qa4eo.org/docs/QA4EO_Principles_v4.0.pdf (accessed on 10 December 2020).
- Sentinel-3 SLSTR Technical Guide. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-slstr;jsessionid=64BD80E953E284DD446748521ABEC931.jvm1 (accessed on 19 October 2020).
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel 3 mission. Remote Sens. Environ. RSE 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Llewellyn-Jones, D.; Remedios, J.; Saunders, R. Advanced Along Track Scanning Radiometer (AATSR) Special Issue. Remote Sens. Environ. 2012, 116, 1–250. [Google Scholar] [CrossRef]
- Edwards, T.; Browning, R.; Delderfield, J.; Lee, D.J.; Lidiard, K.A.; Milborrow, R.S.; McPherson, P.H.; Peskett, S.C.; Toplis, G.M.; Taylor, H.S.; et al. The Along Track Scanning Radiometer measurement of sea-surface temperature from ERS-1. J. Br. Interplanet. Soc. 1990, 43, 160–180. [Google Scholar]
- Coppo, P.; Ricciarelli, B.; Brandani, F.; Delderfield, J.; Ferlet, M.; Mutlow, C.; Munro, G.; Nightingale, T.; Smith, D.; Bianchi, S.; et al. SLSTR: A high accuracy dual scan temperature radiometer for sea and land surface monitoring from space. J. Mod. Opt. 2010, 57, 1815–1830. [Google Scholar] [CrossRef]
- Coppo, P.; Mastrandrea, C.; Stagi, M.; Calamai, L.; Nieke, J. Sea and Land Surface Temperature Radiometer detection assembly design and performance. J. Appl. Remote Sens. 2014, 8, 084979. [Google Scholar] [CrossRef]
- Drinkwater, M.R.; Rebhan, H. Sentinel-3 Mission Requirements Document and References Therein; Sentinel-3 Project Document, EOP-SMO/1151/MD-md; ESA, ESTEC: Noordwijk, The Netherlands, 2007. [Google Scholar]
- 9th Edition of the SI Brochure. BIPM. 2019. Available online: https://www.bipm.org/utils/common/pdf/si-brochure/SI-Brochure-9-EN.pdf (accessed on 19 October 2020).
- Consultative Committee for Thermometry (CCT). The International Temperature Scale of 1990 (ITS-90); Procès-verbaux du Comité International des Poids et Mesures, 78th Meeting; International Committee for Weights and Measures (CIPM): Sèvres, France, 1989; Available online: https://www.bipm.org/utils/en/pdf/ITS-90.pdf (accessed on 19 October 2020).
- Smith, D.L.; Nightingale, T.J.; Mortimer, H.; Middleton, K.; Edeson, R.; Cox, C.V.; Mutlow, C.T.; Maddison, B.J.; Coppo, P. Calibration approach and plan for the sea and land surface temperature radiometer. J. Appl. Remote Sens. 2014, 8, 084980. [Google Scholar] [CrossRef]
- Smith, D.; Barillot, M.; Bianchi, S.; Brandani, F.; Coppo, P.; Etxaluze, M.; Frerick, J.; Kirschstein, S.; Lee, A.; Maddison, B.; et al. Sentinel-3A/B SLSTR Pre-Launch Calibration of the Thermal InfraRed Channels. Remote Sens. 2020, 12, 2510. [Google Scholar] [CrossRef]
- SLSTR BlackBody Subsystem & Temperature Acquisition Electronics Technical Budgets Report; Sentinel-3 Project Document, S3-RP-ABS-SL-0017; ESA, ESTEC: Noordwijk, Netherlands, 2012.
- Peters, D.; Etxaluze, M.; Smith, D. Report on BBS Emissivity and Sensitivity to Temperature Gradients; Sentinel-3 Project Document, S3-RP-RAL-SL-114; RAL Space: Didcot, UK, 2018. [Google Scholar]
- Nightingale, T.J.; McPheat, R.; Smith, D.L.; Mortimer, H.; Polehampton, E.; Lee, A. Sentinel-3A/B SLSTR Spectral Response Calibration. (Manuscript in Preparation). Spectral Responses and Test Reports Are Available for Download. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-slstr/instrument/measured-spectral-response-function-data (accessed on 23 June 2020).
- Mittaz, J.; Merchant, C.J.; Woolliams, E.R. Applying principles of metrology to historical Earth observations from satellites. Metrologia 2019, 56, 032002. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology, Evaluation of Measurement Data. Guide to the Expression of Uncertainty in Measurement (JCGM 100:2008). Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 30 July 2019).
- Baker, I.M.; Capocci, F.A.; Charlton, D.E.; Wotherspoon, J.T.M. Recombination in cadmium mercury telluride photodetectors. Solid State Electron. 1978, 21, 1475–1480. [Google Scholar] [CrossRef]
- Theocharous, E.; Ishii, J.; Fox, N.P. Absolute linearity measurements on HgCdTe detectors in the infrared region. Appl. Opt. 2004, 43, 4182–4188. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Vayyshenker, I.; Li, X.; Scott, T.R. Accurate Measurement of Optical Detector Nonlinearity. NCSL Workshop Symp 1994, 353–361. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/TN/nbstechnicalnote1376.pdf (accessed on 21 January 2021).
- Prokhorov, A.; Prokhorova, N.I. Application of the three-component bidirectional reflectance distribution function model to Monte Carlo calculation of spectral effective emissivities of nonisothermal blackbody cavities. Appl. Opt. 2012, 51, 8003–8012. [Google Scholar] [CrossRef] [PubMed]
- Hunt, S.E.; Mittaz, J.P.D.; Smith, D.; Polehampton, E.; Yemelyanova, R.; Woolliams, E.R.; Donlon, C. Comparison of the Sentinel-3A and B SLSTR Tandem Phase Data Using Metrological Principles. Remote Sens. 2020, 12, 2893. [Google Scholar] [CrossRef]
- Sentinel-3A and Sentinel-3B Monitoring Pages. Available online: http://gws-access.jasmin.ac.uk/public/slstr_cpa (accessed on 3 December 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).