Ancillary Data Uncertainties within the SeaDAS Uncertainty Budget for Ocean Colour Retrievals
Abstract
:1. Introduction
2. Data Description
2.1. L1 Data
2.2. NCEP Reanalysis Dataset
2.3. ERA5 Reanalysis Dataset
3. SeaDAS Uncertainty Budget
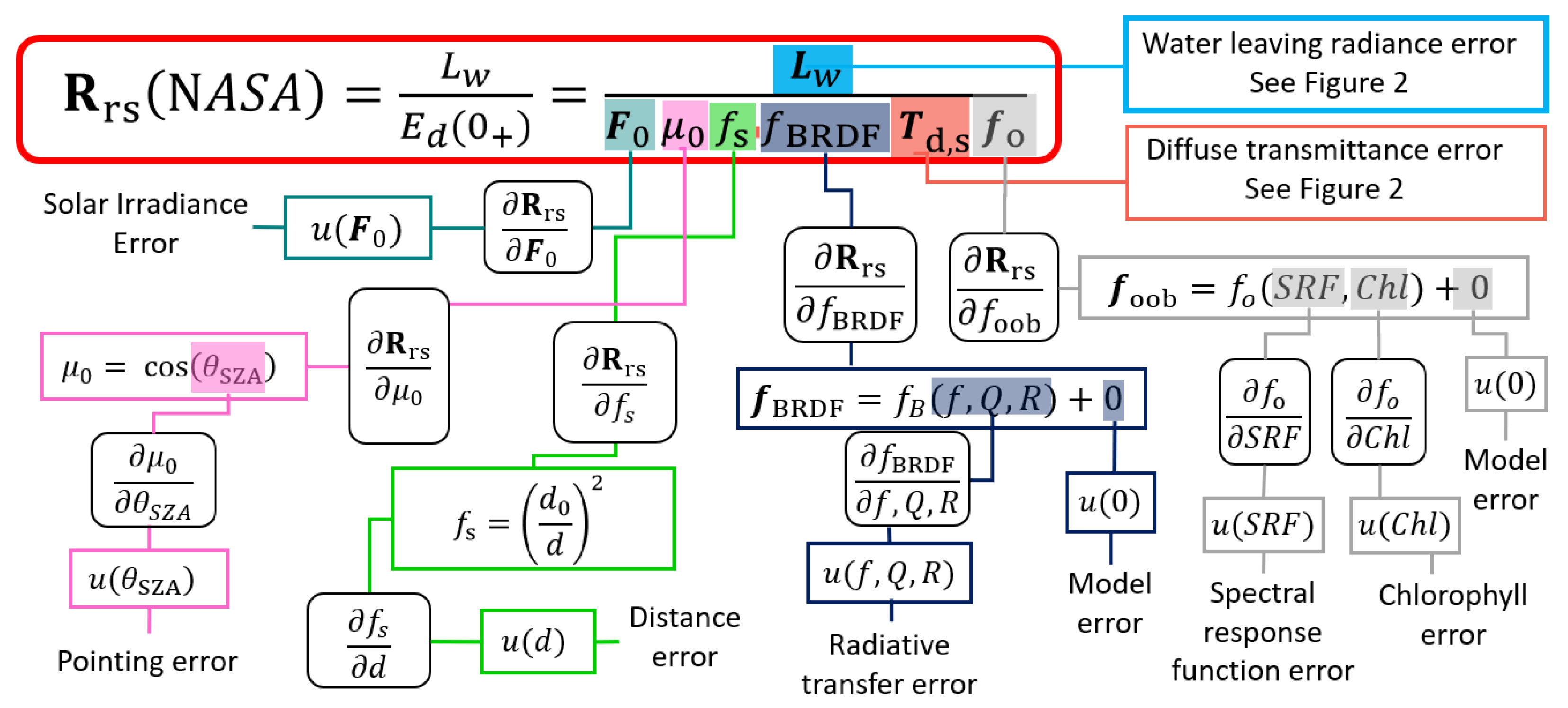
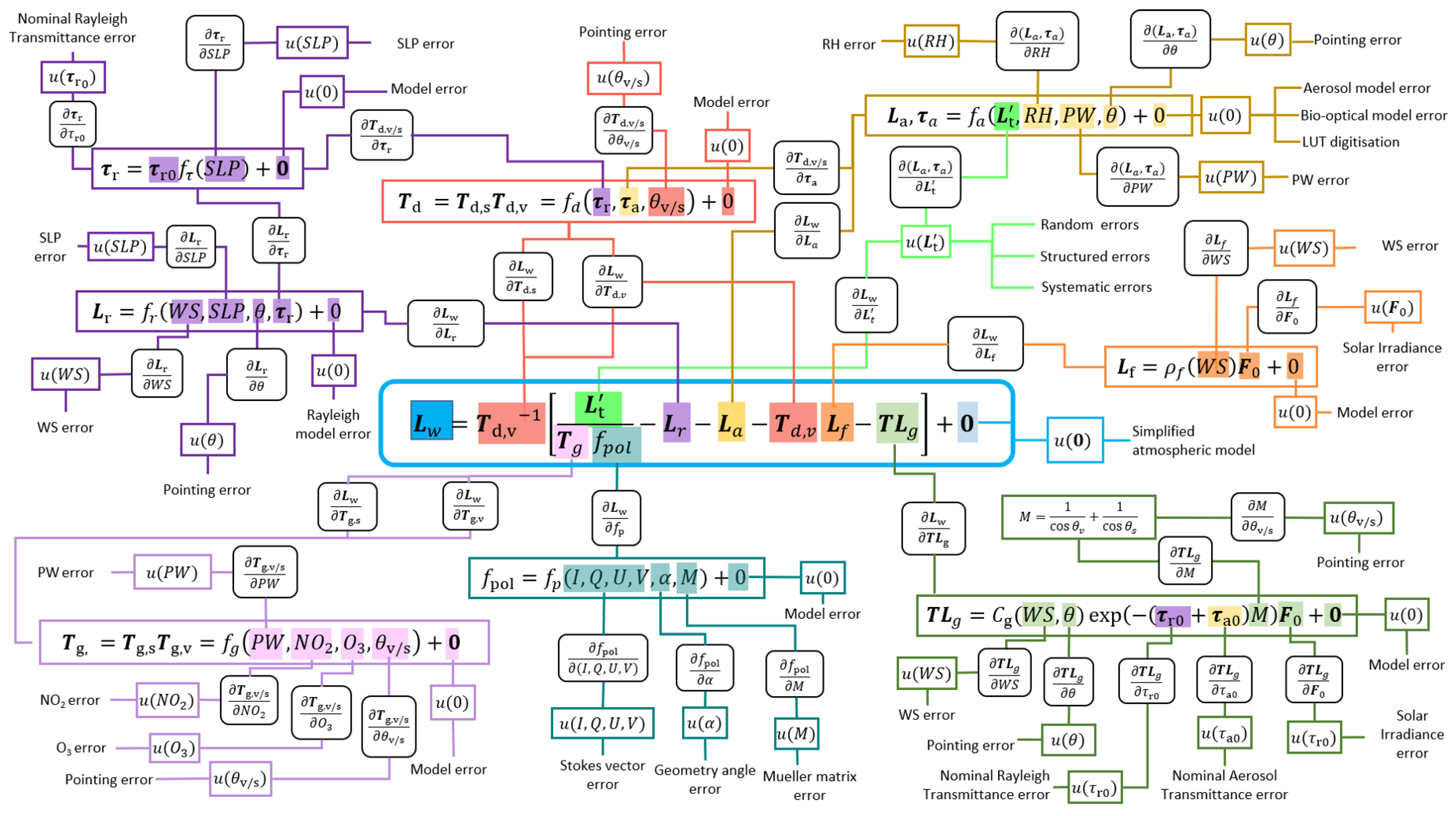
3.1. Uncertainty Tree Diagrams
3.2. Discussion of Uncertainty Contributions to Remote Sensing Reflectances
3.3. Discussion of Uncertainty Contributions to Water-Leaving Radiances
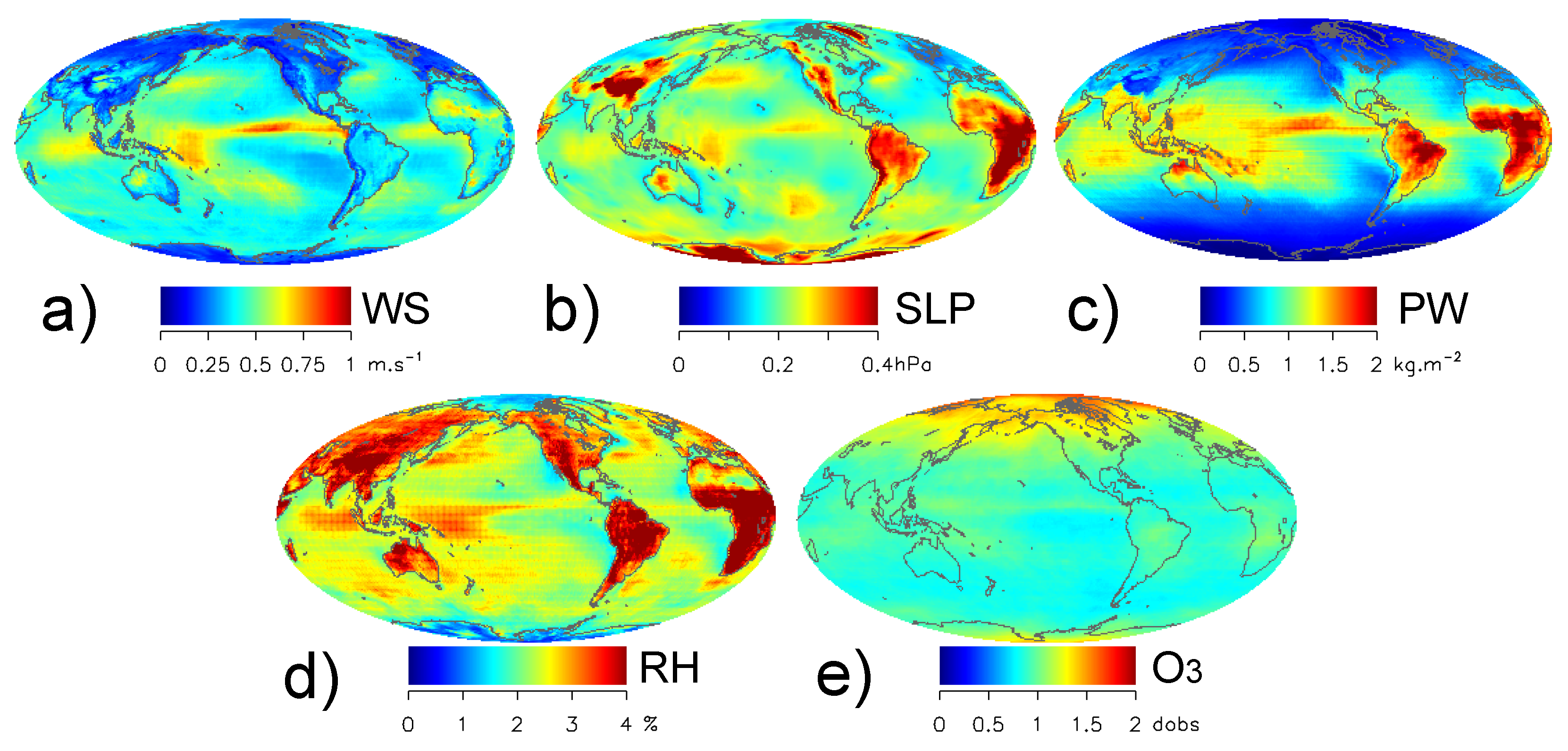
4. Global Ancillary Variables
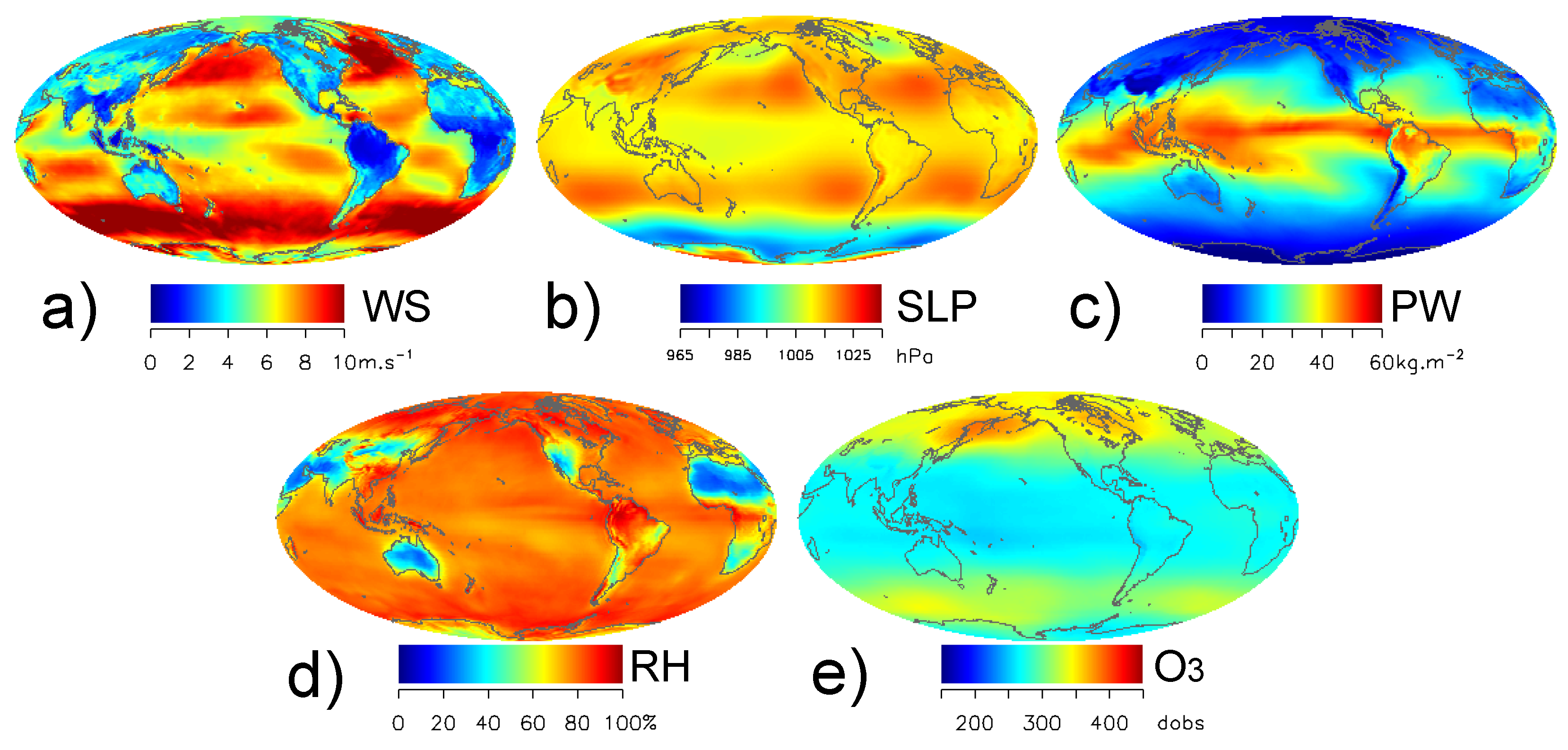
4.1. Statistics on Ancillary Variables
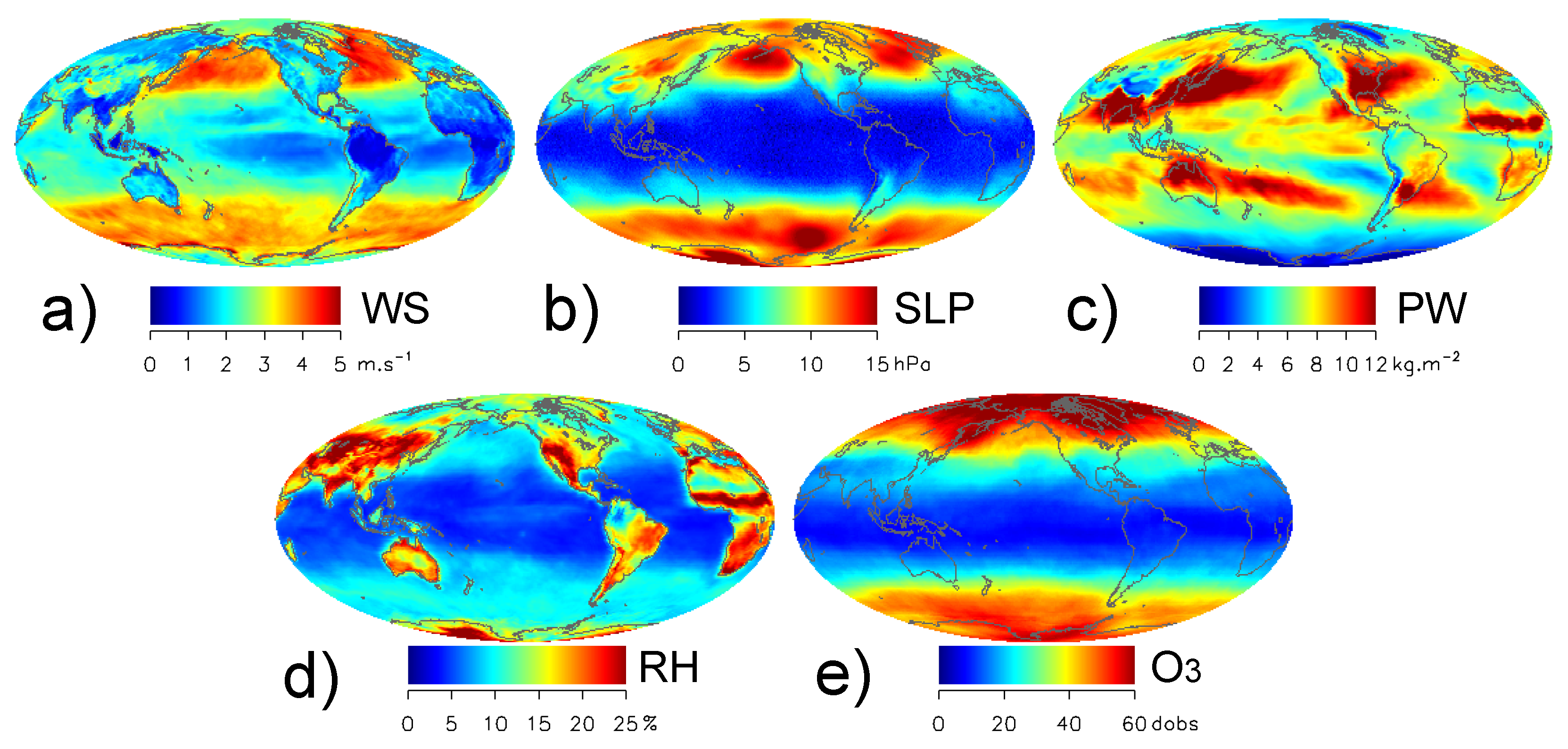
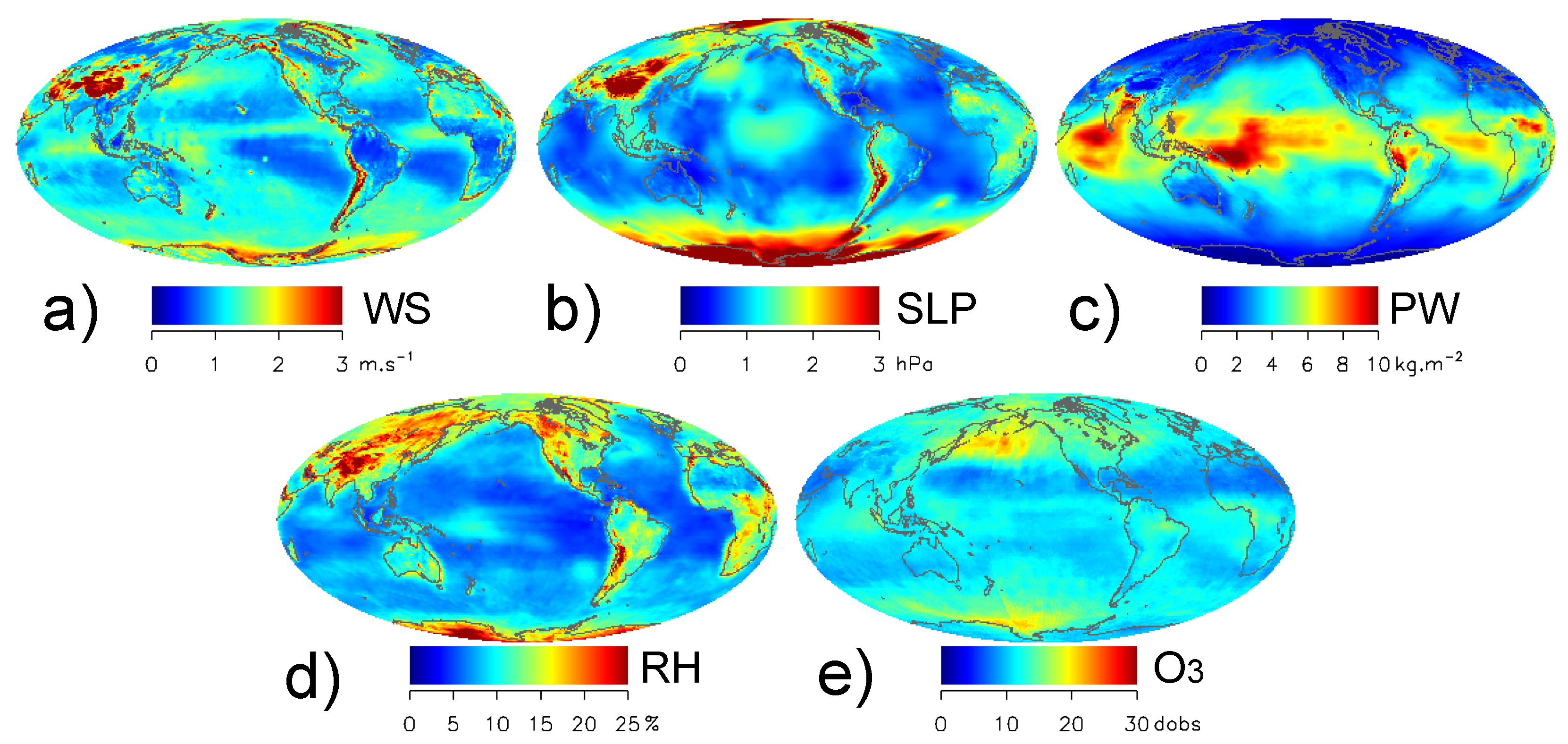
4.2. Ancillary Variables Uncertainties
5. Uncertainty Propagation Method
6. Remote Sensing Reflectance Uncertainties
6.1. Relative Uncertainty at Different Wavebands
6.2. Sensitivity to Aerosol Model Selection
6.3. Spatial Correlation between Variance in Ancillary Data and Reflectance
7. Conclusions
- The SeaDAS uncertainty budget reveals numerous sources of error. Particularly, ancillary data uncertainties enter the measurement equation through various branches and together form an important contribution to the uncertainty budget.
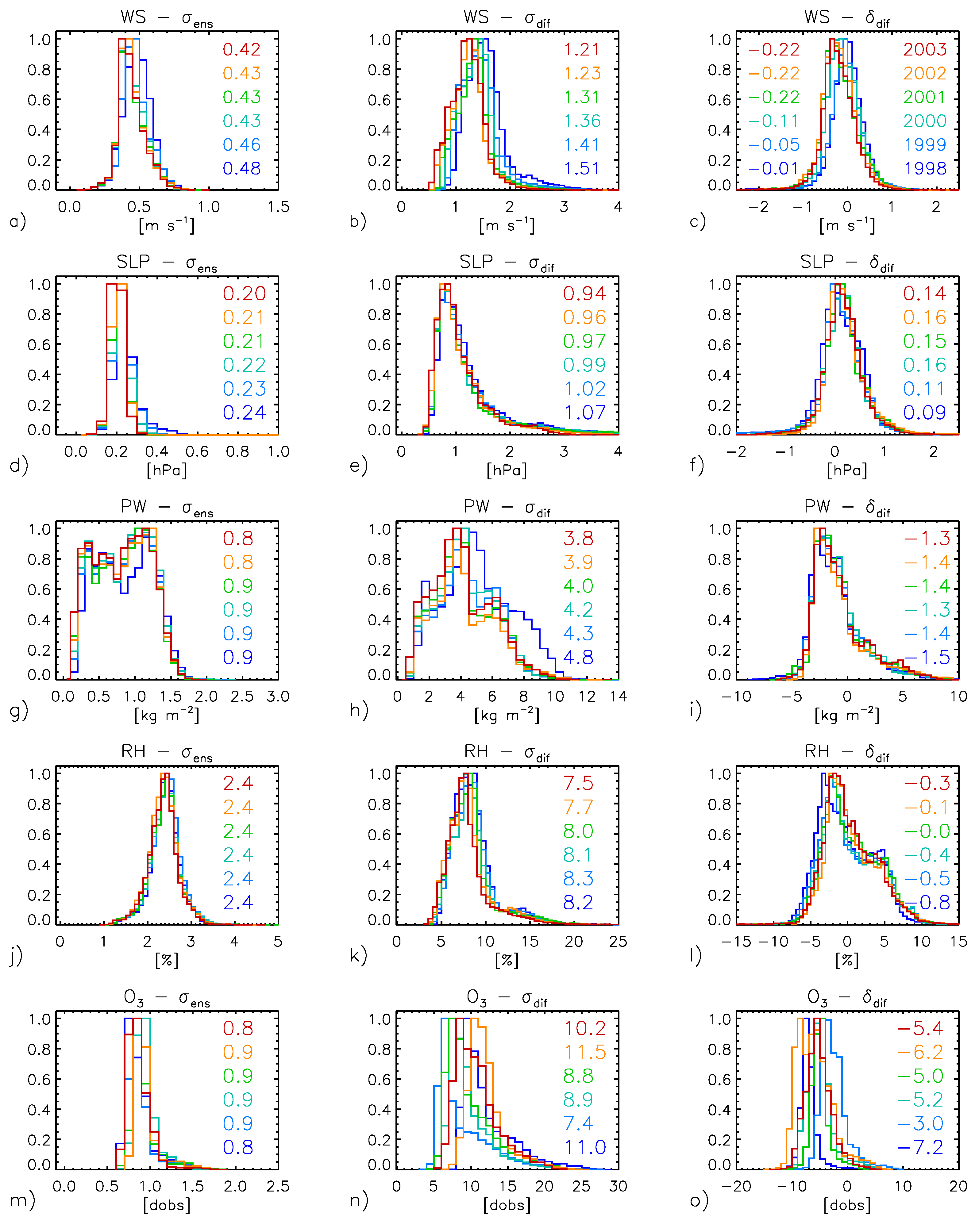
- The difference between the NCEP/TOMS and ERA5 ancillary data is larger than the variance within the ERA5 ensemble. Both the average difference between NCEP/TOMS and ERA5 and the spread within ERA5 show similar spatial patterns, with the largest values generally observed in the the mid-latitudes for surface wind speed (WS), sea level pressure (SLP), precipitable water vapour (PW), and relative humidity (RH) or the high latitudes for total ozone concentration ([]). Differences between ancillary data and within the ensemble appear to provide realistic estimates of their uncertainties in magnitude and spatial distribution, and allow sensitivity analyses on OC data processing. However, these uncertainty estimates might be slightly underestimated due to the ensemble spread not fully including systematic effects.
- WS and RH (through its interaction with aerosol model selection) were found to be the biggest contributors to the uncertainty in the atmospheric correction.
- The complex iterative aerosol model selection algorithm leads to a small fraction of pixels having significantly higher uncertainties than other pixels. This happens when the L1 radiances (of the bands used in aerosol model selection) for these pixels are near some critical transition values, which results in a different model being selected for different MC iterations.
- The uncertainties in the remote sensing reflectance due to WS and SLP typically show a strong spatial correlation with the uncertainties in WS and SLP, respectively. The other ancillary variables show no such strong correlation.
- The uncertainty in remote sensing reflectances introduced by varying RH is complex. In addition to the pixels close to the critical transition values, aerosol model selection also introduced large-scale variation in uncertainties.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GCOS. The Global Observing System for Climate: Implementation Needs; GCOS-200; WMO: Geneva, Switzerland, 2016; p. 284. [Google Scholar]
- IOCCG. Uncertainties in Ocean Colour Remote Sensing; Reports of the International Ocean Colour Coordinating Group; IOCCG: Dartmouth, ON, Canada, 2019; Volume 18. [Google Scholar] [CrossRef]
- Gordon, H.R. Removal of atmospheric effects from satellite imagery of the oceans. Appl. Opt. 1978, 17, 1631–1636. [Google Scholar] [CrossRef] [PubMed]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef] [Green Version]
- Bailey, S.; Franz, B.; Werdell, P. Estimation of near-infrared water-leaving reflectance for satellite ocean colour data processing. Opt. Exp. 2010, 18, 7521–7527. [Google Scholar] [CrossRef] [PubMed]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP/DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Steinmetz, F.; Deschamps, P.Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Exp. 2011, 19, 571–587. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Nakajima, T.; Hashimoto, M. Simultaneous retrieval of aerosol optical thickness and chlorophyll concentration from multiwavelength measurement over East China Sea. J. Geophys. Res. Atmos. 2016, 121, 14084–14101. [Google Scholar] [CrossRef]
- Frouin, R.; Pelletier, B. Bayesian methodology for inverting satellite ocean-colour data. Remote Sens. Environ. 2015, 159, 332–360. [Google Scholar] [CrossRef]
- Mittaz, J.; Merchant, C.J.; Woolliams, E.R. Applying principles of metrology to historical Earth observations from satellites. Metrologia 2019, 56, 032002. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef]
- Franz, B.; Bailey, S.; Werdell, P.; McClain, C. Sensor-independent approach to the vicarious calibration of satellite ocean colour radiometry. Appl. Opt. 2007, 46, 5068–5082. [Google Scholar] [CrossRef] [PubMed]
- Pahlevan, N.; Sarkar, S.; Franz, B.; Balasubramanian, S.; He, J. Sentinel-2 MultiSpectral Instrument (MSI) data processing for aquatic science applications: Demonstrations and validations. Remote Sens. Environ. 2017, 201, 47–56. [Google Scholar] [CrossRef]
- Hooker, S.; Esaias, W.; Feldman, G.; Gregg, W.; McClain, C. An Overview of SeaWiFS and Ocean Colour; NASA Technical Memorandum 104566; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1992; pp. 1–24.
- McPeters, R.; Bhartia, P.; Krueger, A.; Herman, J.; Wellemeyer, C.; Seftor, C.; Jaross, G.; Torres, O.; Moy, L.; Labow, G.; et al. Earth Probe Total Ozone Mapping Spectrometer (TOMS) Data Products User’s Guide; NASA Technical Publication 1998-206895; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1998; p. 64.
- Bell, B.; Hersbach, H.; Simmons, A.; Berrisford, P.; Dahlgren, P.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis: Preliminary extension to 1950. Q. J. R. Meteorol. Soc. 2021, 147, 4186–4227. [Google Scholar] [CrossRef]
- Leutbecher, M.; Lock, S.J.; Ollinaho, P.; Lang, S.T.K.; Balsamo, G.; Bechtold, P.; Bonavita, M.; Christensen, H.M.; Diamantakis, M.; Dutra, E.; et al. Stochastic representations of model uncertainties at ECMWF: State of the art and future vision. Q. J. R. Meteorol. Soc. 2017, 143, 2315–2339. [Google Scholar] [CrossRef]
- Hirahara, S.; Alonso-Balmaseda, M.; de Boisseson, E.; Hersbach, H. Sea Surface Temperature and Sea Ice Concentration for ERA5; ECMWF: Reading, UK, 2016. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1979 to present. In Copernicus Climate Change Service (C3S) Climate Data Store (CDS); ECMWF: Reading, UK, 2018. [Google Scholar] [CrossRef]
- Mobley, C.D.; Werdell, J.; Franz, B.; Ahmad, Z.; Bailey, S. Atmospheric Correction for Satellite Ocean Colour Radiometry; Technical Memorandum; NASA: Greenbelt, MD, USA, 2016.
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional reflectance of oceanic waters: Accounting for Raman emission and varying particle scattering phase function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef]
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The Solar Spectral Irradiance from 200 to 2400 nm as Measured by the SOLSPEC Spectrometer from the Atlas and Eureca Missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Voss, K.; Morel, A.; Antoine, D. Detailed validation of the bidirectional effect in various Case 1 waters for application to ocean colour imagery. Biogeosciences 2007, 4, 781–789. [Google Scholar] [CrossRef] [Green Version]
- Gleason, A.; Voss, K.; Gordon, H.; Twardowski, M.; Sullivan, J.; Trees, C.; Weideman, A.; Berthon, J.F.; Clark, D.; Lee, Z.P. Detailed validation of the bidirectional effect in various Case I and Case II waters. Opt. Exp. 2012, 20, 7630–7645. [Google Scholar] [CrossRef]
- Wang, M.; Franz, B.A.; Barnes, R.A.; McClain, C.R. Effects of spectral bandpass on SeaWiFS-retrieved near-surface optical properties of the ocean. Appl. Opt. 2001, 40, 343–348. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Z.; McClain, C.R.; Herman, J.R.; Franz, B.A.; Kwiatkowska, E.J.; Robinson, W.D.; Bucsela, E.J.; Tzortziou, M. Atmospheric correction for NO2 absorption in retrieving water-leaving reflectances from the SeaWiFS and MODIS measurements. Appl. Opt. 2007, 46, 6504–6512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barnes, B.; Eplee, R.; Schmidt, G.; Patt, F.; McClain, C. Calibration of SeaWiFS. I. Direct techniques. Appl. Opt. 2001, 40, 6682–6700. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eplee, R.E.; Meister, G.; Patt, F.S.; Franz, B.A.; McClain, C.R. Uncertainty assessment of the SeaWiFS on-orbit calibration. In Earth Observing Systems XVI; Butler, J.J., Xiong, X., Gu, X., Eds.; International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 2011; Volume 8153, pp. 93–109. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.; Hunt, S.E.; Etxaluze, M.; Peters, D.; Nightingale, T.; Mittaz, J.; Woolliams, E.R.; Polehampton, E. Traceability of the Sentinel-3 SLSTR Level-1 Infrared Radiometric Processing. Remote Sens. 2021, 13, 374. [Google Scholar] [CrossRef]
- Gordon, H.R. Atmospheric correction of ocean colour imagery in the Earth Observing System era. J. Geophys. Res. Atmos. 1997, 102, 17081–17106. [Google Scholar] [CrossRef]
- Alduchov, O.; Eskridge, R. Improved Magnus form approximation of saturation vapor pressure. J. Appl. Meteorol. 1996, 35, 601–609. [Google Scholar] [CrossRef]
- Wallcraft, A.; Kara, A.; Barron, C.; Metzger, E.; Pauley, R.; Bourass, M. Comparisons of monthly mean 10-m wind speeds from satellites and NWP products over the global ocean. J. Geophys. Res. 2009, 114, D16. [Google Scholar] [CrossRef] [Green Version]
- Chelton, D.; Freilich, M. Scatterometer-based assessment of 10-m wind analyses from the operational ECMWF and NCEP numerical weather prediction models. Mon. Weather Rev. 2005, 133, 410–429. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, A.H.; Ponte, R.M.; Forget, G.; Heimbach, P. A Comparison of Atmospheric Reanalysis Surface Products over the Ocean and Implications for Uncertainties in Air–Sea Boundary Forcing. J. Clim. 2013, 26, 153–170. [Google Scholar] [CrossRef]
- Wang, M. A refinement for the Rayleigh radiance computation with variation of the atmospheric pressure. Int. J. Remote Sens. 2005, 24, 5651–5663. [Google Scholar] [CrossRef]
- Ponte, R.M.; Dorandeu, J. Uncertainties in ECMWF Surface Pressure Fields over the Ocean in Relation to Sea Level Analysis and Modeling. J. Atmos. Ocean. Technol. 2003, 20, 301–307. [Google Scholar] [CrossRef]
- Vey, S.; Dietrich, R.; Rülke, A.; Fritsche, M.; Steigenberger, P.; Rothacher, M. Variation of precipitable water vapor within the NCEP/DOE reanalysis using global GPS observations from one decade. J. Clim. 2010, 23, 1675–1695. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z. Global water vapor variability and trend from the latest 36 year (1979 to 2014) data of ECMWF and NCEP reanalyses, radiosonde, GPS, and microwave satellite. J. Geophys. Res. 2016, 121, 11442–11462. [Google Scholar] [CrossRef]
- Wang, S.; Xu, T.; Nie, W.; Jiang, C.; Yang, Y.; Fang, Z.; Li, M.; Zhang, Z. Evaluation of precipitable water vapor from five reanalysis products with ground-based GNSS observations. Remote Sens. 2020, 12, 1817. [Google Scholar] [CrossRef]
- Ahmad, Z.; Franz, B.; McClain, C.; Kwiatkowska, E.; Werdell, P.; Shettle, E.; Holben, B. New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans. Appl. Opt. 2010, 49, 5545–5560. [Google Scholar] [CrossRef] [PubMed]
- John, V.; Soden, B. Temperature and humidity biases in global climate models and their impact on climate feedbacks. Geophys. Res. Lett. 2007, 34, L18704. [Google Scholar] [CrossRef] [Green Version]
- Vergados, P.; Mannucci, A.J.; Ao, C.O.; Jiang, J.H.; Su, H. On the comparisons of tropical relative humidity in the lower and middle troposphere among COSMIC radio occultations and MERRA and ECMWF data sets. Atmos. Meas. Tech. 2015, 8, 1789–1797. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Hubbard, K. Uncertainties of derived dewpoint temperature and relative humidity. J. Appl. Meteorol. 2003, 43, 821–825. [Google Scholar] [CrossRef]
- Lerot, C.; Van Roozendael, M.; Spurr, R.; Loyola, D.; Coldewey-Egbers, M.; Kochenova, S.; van Gent, J.; Koukouli, M.; Balis, D.; Lambert, J.C.; et al. Homogenized total ozone data records from the European sensors GOME/ERS-2, SCIAMACHY/Envisat, and GOME-2/MetOp-A. J. Geophys. Res. Atmos. 2014, 119, 1639–1662. [Google Scholar] [CrossRef]
- Garane, K.; Lerot, C.; Coldewey-Egbers, M.; Verhoelst, T.; Koukouli, M.; Zyrichidou, I.; Balis, D.; Danckaert, T.; Goutail, F.; Granville, J.; et al. Quality assessment of the ozone_cci climate research data package (release 2017)—Part 1: Ground-based validation of total ozone column data products. Atmos. Meas. Tech. 2018, 11, 1385–1402. [Google Scholar] [CrossRef] [Green Version]
- Laloyaux, P.; de Boisseson, E.; Balmaseda, M.; Bidlot, J.R.; Broennimann, S.; Buizza, R.; Dahlgren, P.; Dee, D.; Haimberger, L.; Hersbach, H.; et al. CERA-20C: A coupled reanalysis of the twentieth century. J. Adv. Model. Earth Syst. 2018, 10, 1172–1195. [Google Scholar] [CrossRef]

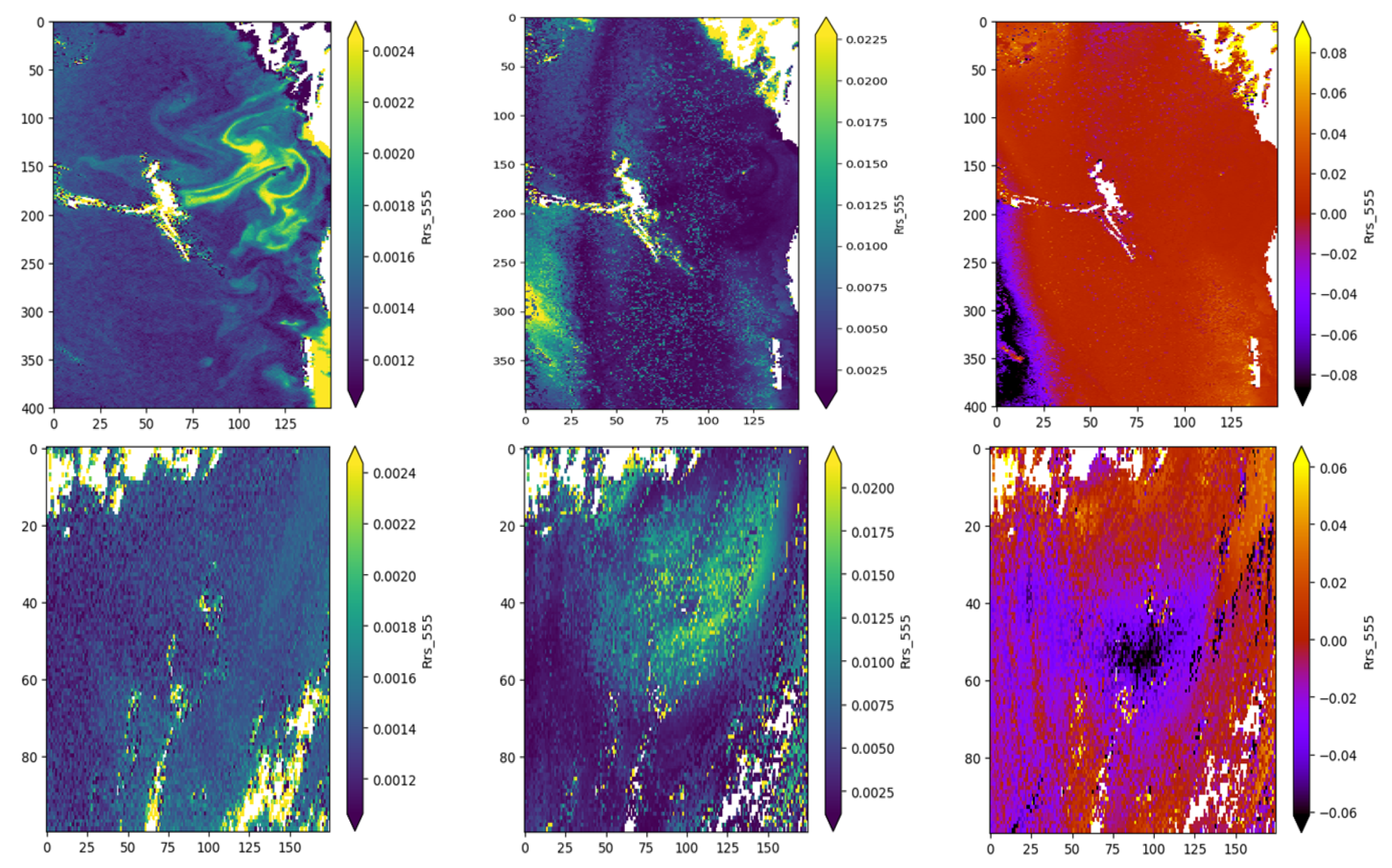


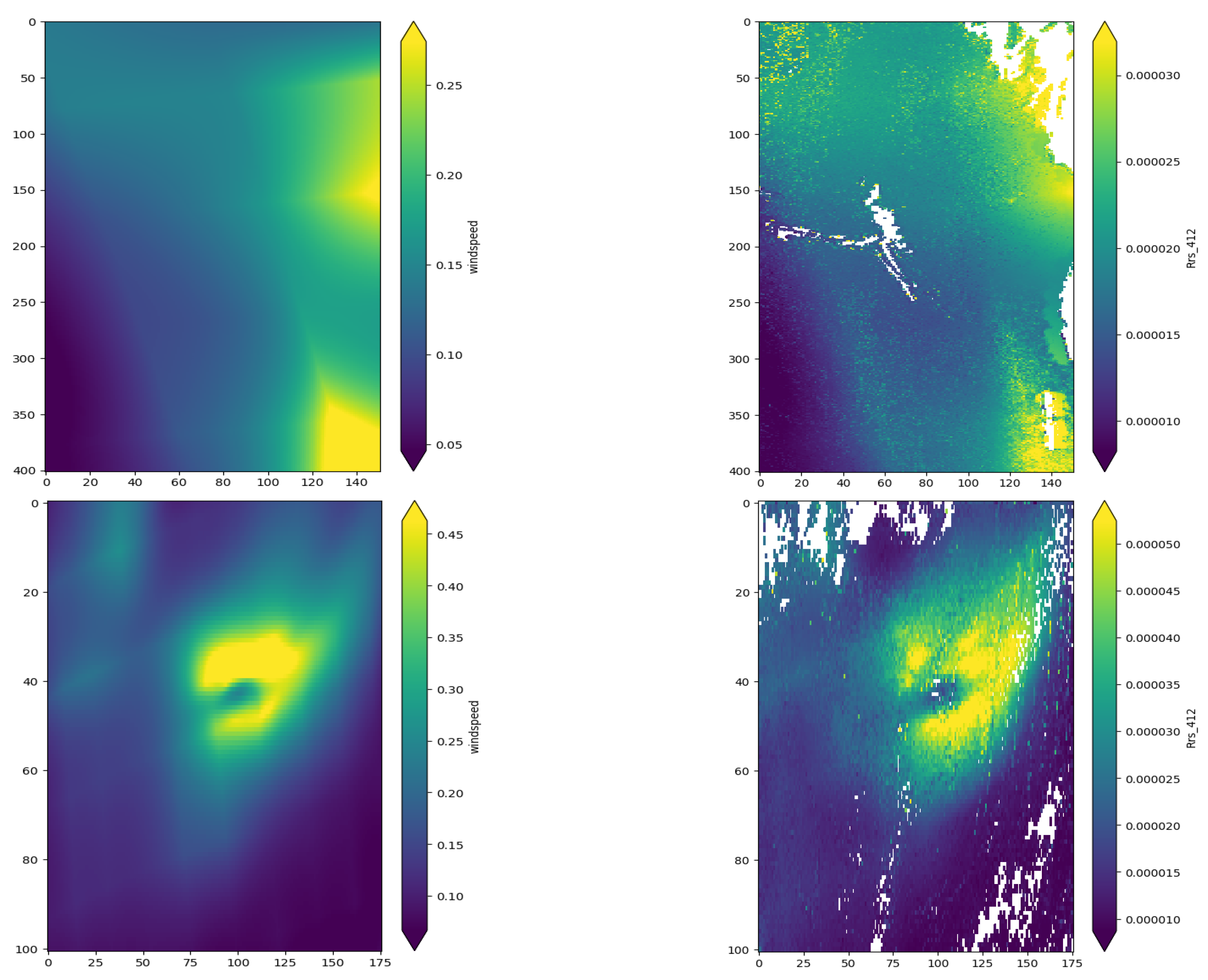
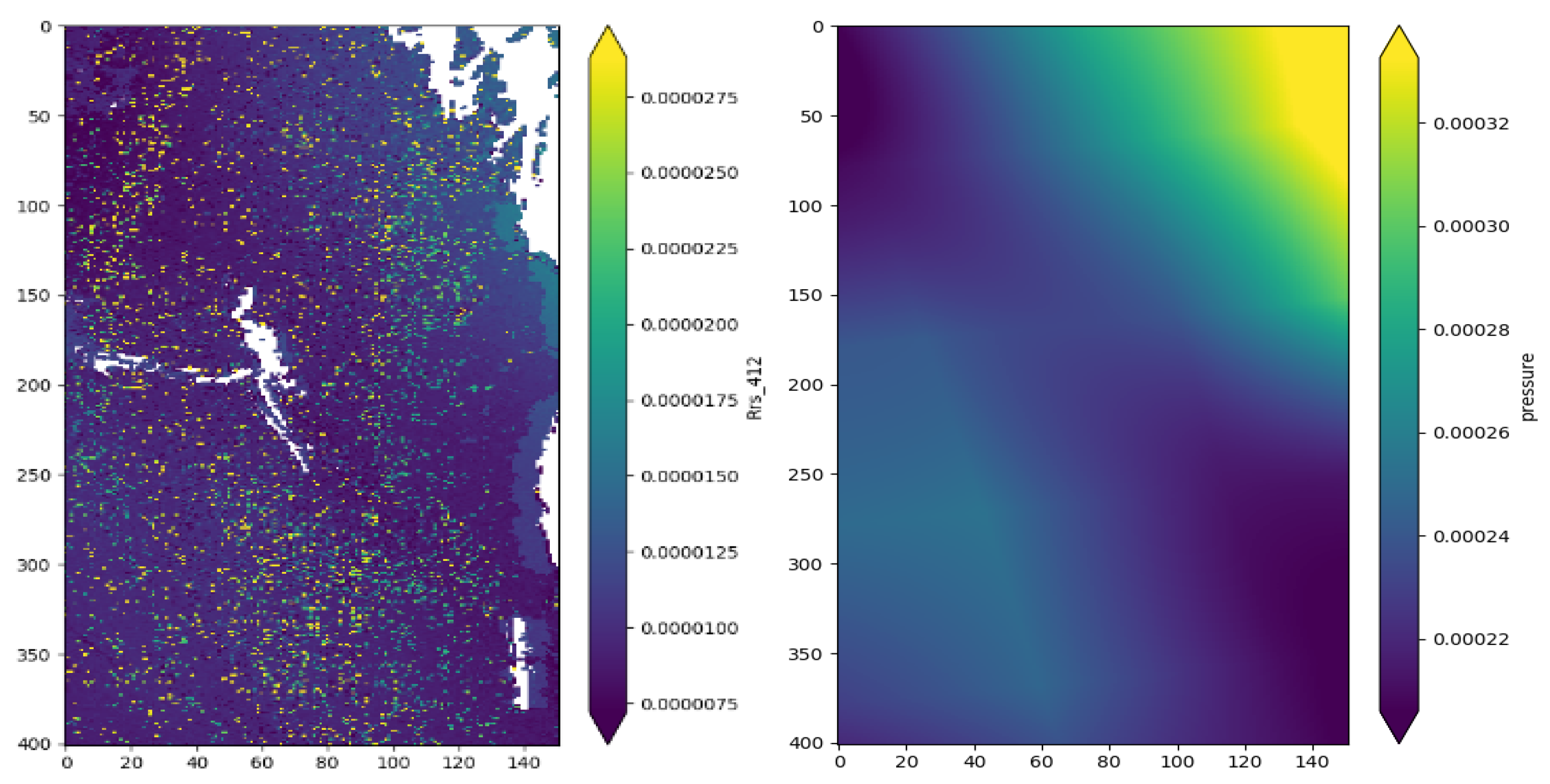
| Ancillary Variable | Australian Scene | Atlantic Scene |
|---|---|---|
| WS () | 1.5–6 | 0.5–4.5 |
| WS uncertainty () | 0.3–0.8 | 0.1–0.45 |
| SLP () | 1007–1009 | 1013–1014 |
| SLP uncertainty () | 0.22–0.32 | 0.08–0.2 |
| PW () | 23–29 | 16–40 |
| PW uncertainty () | 0.8–1.8 | 0.8–3.5 |
| RH (%) | 57.5–75 | 60–80 |
| RH uncertainty (%) | 1.25–3 | 1.5–4 |
| () | 247–252 | 242–266 |
| uncertainty () | 0.8–1.3 | 0.5–1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Vis, P.; Mélin, F.; Hunt, S.E.; Morrone, R.; Sinclair, M.; Bell, B. Ancillary Data Uncertainties within the SeaDAS Uncertainty Budget for Ocean Colour Retrievals. Remote Sens. 2022, 14, 497. https://doi.org/10.3390/rs14030497
De Vis P, Mélin F, Hunt SE, Morrone R, Sinclair M, Bell B. Ancillary Data Uncertainties within the SeaDAS Uncertainty Budget for Ocean Colour Retrievals. Remote Sensing. 2022; 14(3):497. https://doi.org/10.3390/rs14030497
Chicago/Turabian StyleDe Vis, Pieter, Frédéric Mélin, Samuel E. Hunt, Rosalinda Morrone, Morven Sinclair, and Bill Bell. 2022. "Ancillary Data Uncertainties within the SeaDAS Uncertainty Budget for Ocean Colour Retrievals" Remote Sensing 14, no. 3: 497. https://doi.org/10.3390/rs14030497
APA StyleDe Vis, P., Mélin, F., Hunt, S. E., Morrone, R., Sinclair, M., & Bell, B. (2022). Ancillary Data Uncertainties within the SeaDAS Uncertainty Budget for Ocean Colour Retrievals. Remote Sensing, 14(3), 497. https://doi.org/10.3390/rs14030497







