A Remote Sensing Image Destriping Model Based on Low-Rank and Directional Sparse Constraint
Abstract
:1. Introduction
- (a)
- Under the destriping model of image decomposition, a sparsity constraint, perpendicular to the stripes, is added to reduce the ripple effects of the output image.
- (b)
- After thoroughly analyzing the potential properties of stripe noise, we propose a regularization model combining low-rank and directional sparsity, enhancing the robustness of the stripe noise-removal model.
- (c)
- An alternate minimization scheme to the model is designed to estimate both potential priors in degraded images.
2. Degradation Model and Proposed Model
2.1. The Regularization Term and Regularization Method of the Real Image
2.2. The Regularization Term and Regularization Method of the Stripe Noise Image
3. ADMM Optimization
3.1. Image Prior Optimization Process
- (1)
- The M sub-problem can be summarized as
- (2)
- The N sub-problem can be summarized as
- (3)
- The I sub-problem can be described as
3.2. Stripe-Noise Prior Optimization Process
- (1)
- The W sub-problem can be summarized as
- (2)
- The H sub-problem can be summarized as
- (3)
- The K sub-problem can be summarized as
- (4)
- The S sub-problem can be summarized as
| Algorithm 1: The proposed destriping model |
| Input: degraded image O, parameters , , , , , and . |
| 1: Initialize. |
| 2: for k= 1: N do |
| 3: update image prior: |
| 4: solve , and via(15), (18) and (21). |
| 5: update Lagrange multiplier and by (23) and (24). |
| 6: stripe component update: |
| 7: solve , , and via(30), (33), (36) and (38) |
| 8: update Lagrange multiplier , and by (40), (41), (42) |
| 9: end for |
| Output: image I and stripe S. |
4. Simulation and the Actual Destriping Experiment
4.1. Simulation Experiment
4.2. Actual Destriping Experiment
5. Discussion
5.1. Parameter Value Determination
5.2. Result Discussion
5.3. Limitation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TV | Total Variation |
| FIR | Finite Impulse Response |
| ADMM | Alternating Direction Multiplier Method |
| PSNR | Peak Signal to Noise Ratio |
| SSIM | Structural Similarity |
| PRNU | Photo Response Non-uniformity |
| SLD | Statistical Linear Destriping |
| LRSID | Low-Rank Single-Image Decomposition |
| GSLV | Global Sparsity and Local Variational |
| TVGS | Total Variation and Group Sparse |
References
- Pan, J.J.; Chang, C.I. Destriping of Landsat MSS images by filtering techniques. Photogramm. Eng. Remote Sens. 1992, 58, 1417. [Google Scholar]
- Simpson, J.J.; Gobat, J.I.; Frouin, R. Improved destriping of GOES images using finite impulse response filters. Remote Sens. Environ. 1995, 52, 15–35. [Google Scholar] [CrossRef]
- Torres, J.; Infante, S.O. Wavelet analysis for the elimination of striping noise in satellite images. Opt. Eng. 2001, 40, 1309–1314. [Google Scholar]
- Chen, J.; Shao, Y.; Guo, H.; Wang, W.; Zhu, B. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- Chen, J.; Lin, H.; Shao, Y.; Yang, L. Oblique striping removal in remote sensing imagery based on wavelet transform. Int. J. Remote Sens. 2006, 27, 1717–1723. [Google Scholar] [CrossRef]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet—Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pal, M.K.; Porwal, A. Destriping of Hyperion images using low-pass-filter and local-brightness-normalization. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3509–3512. [Google Scholar]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Horn, B.K.; Woodham, R.J. Destriping Landsat MSS images by histogram modification. Comput. Graph. Image Process. 1979, 10, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Weinreb, M.; Xie, R.; Lienesch, J.; Crosby, D. Destriping GOES images by matching empirical distribution functions. Remote Sens. Environ. 1989, 29, 185–195. [Google Scholar] [CrossRef]
- Wegener, M. Destriping multiple sensor imagery by improved histogram matching. Int. J. Remote Sens. 1990, 11, 859–875. [Google Scholar] [CrossRef]
- Gadallah, F.; Csillag, F.; Smith, E. Destriping multisensor imagery with moment matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar] [CrossRef]
- Sun, L.; Neville, R.; Staenz, K.; White, H.P. Automatic destriping of Hyperion imagery based on spectral moment matching. Can. J. Remote Sens. 2008, 34, S68–S81. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Restoration of Aqua MODIS Band 6 Using Histogram Matching and Local Least Squares Fitting. IEEE Trans. Geosci. Remote Sens. 2009, 47, 613–627. [Google Scholar] [CrossRef]
- Carfantan, H.; Idier, J. Statistical Linear Destriping of Satellite-Based Pushbroom-Type Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1860–1871. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, W.; Zhang, H.; Zhang, L. A piece-wise approach to removing the nonlinear and irregular stripes in MODIS data. Int. J. Remote Sens. 2014, 35, 44–53. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-Based Algorithm for Destriping and Inpainting of Remotely Sensed Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward Optimal Destriping of MODIS Data Using a Unidirectional Variational Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Lu, X.; Wang, Y.; Yuan, Y. Graph-Regularized Low-Rank Representation for Destriping of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4009–4018. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, H.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral Image Restoration Using Low-Rank Matrix Recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Chang, Y.; Fang, H.; Yan, L.; Liu, H. Robust destriping method with unidirectional total variation and framelet regularization. Opt. Express 2013, 21, 23307–23323. [Google Scholar] [CrossRef]
- Yi, C.; Yan, L.; Tao, W.; Sheng, Z. Remote Sensing Image Stripe Noise Removal: From Image Decomposition Perspective. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7018–7031. [Google Scholar]
- Liu, X.; Lu, X.; Shen, H.; Yuan, Q.; Jiao, Y.; Zhang, L. Stripe Noise Separation and Removal in Remote Sensing Images by Consideration of the Global Sparsity and Local Variational Properties. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3049–3060. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.Z.; Zhao, X.L.; Deng, L.J.; Huang, J. Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint. Remote Sens. 2017, 9, 559. [Google Scholar] [CrossRef] [Green Version]
- Dou, H.X.; Huang, T.Z.; Deng, L.J.; Zhao, X.L.; Huang, J. Directional 0 Sparse Modeling for Image Stripe Noise Removal. Remote Sens. 2018, 10, 361. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.; Yan, L.; Fang, H.; Liu, H. Simultaneous Destriping and Denoising for Remote Sensing Images With Unidirectional Total Variation and Sparse Representation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1051–1055. [Google Scholar] [CrossRef]
- Yang, J.H.; Zhao, X.L.; Ma, T.H.; Chen, Y.; Huang, T.Z.; Ding, M. Remote sensing images destriping using unidirectional hybrid total variation and nonconvex low-rank regularization. J. Comput. Appl. Math. 2020, 363, 124–144. [Google Scholar] [CrossRef]
- Tikhonov, A.; Arsenin, V. Solutions of Ill-Posed Problems; Winston and Sons: Washington, DC, USA, 1977. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Qin, Z.; Goldfarb, D.; Ma, S. An Alternating Direction Method for Total Variation Denoising. Optim. Methods Softw. 2011, 30, 594–615. [Google Scholar] [CrossRef] [Green Version]
- Eckstein, J.; Bertsekas, D.P. On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 1992, 55, 293–318. [Google Scholar] [CrossRef] [Green Version]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; EcKstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 2002, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Ng, M.K.; Chan, R.H.; Tang, W.C. A Fast Algorithm for Deblurring Models with Neumann Boundary Conditions. SIAM J. Sci. Comput. 1999, 21, 851–866. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.F.; Candès, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative Thresholding for Sparse Approximations. J. Fourier Anal. Appl. 2008, 14, 629–654. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Y.; Jin, B.; Lu, X. A primal dual active set with continuation algorithm for the l(0)-regularized optimization problem. Appl. Comput. Harmon. Anal. 2015, 39, 400–426. [Google Scholar] [CrossRef]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar]






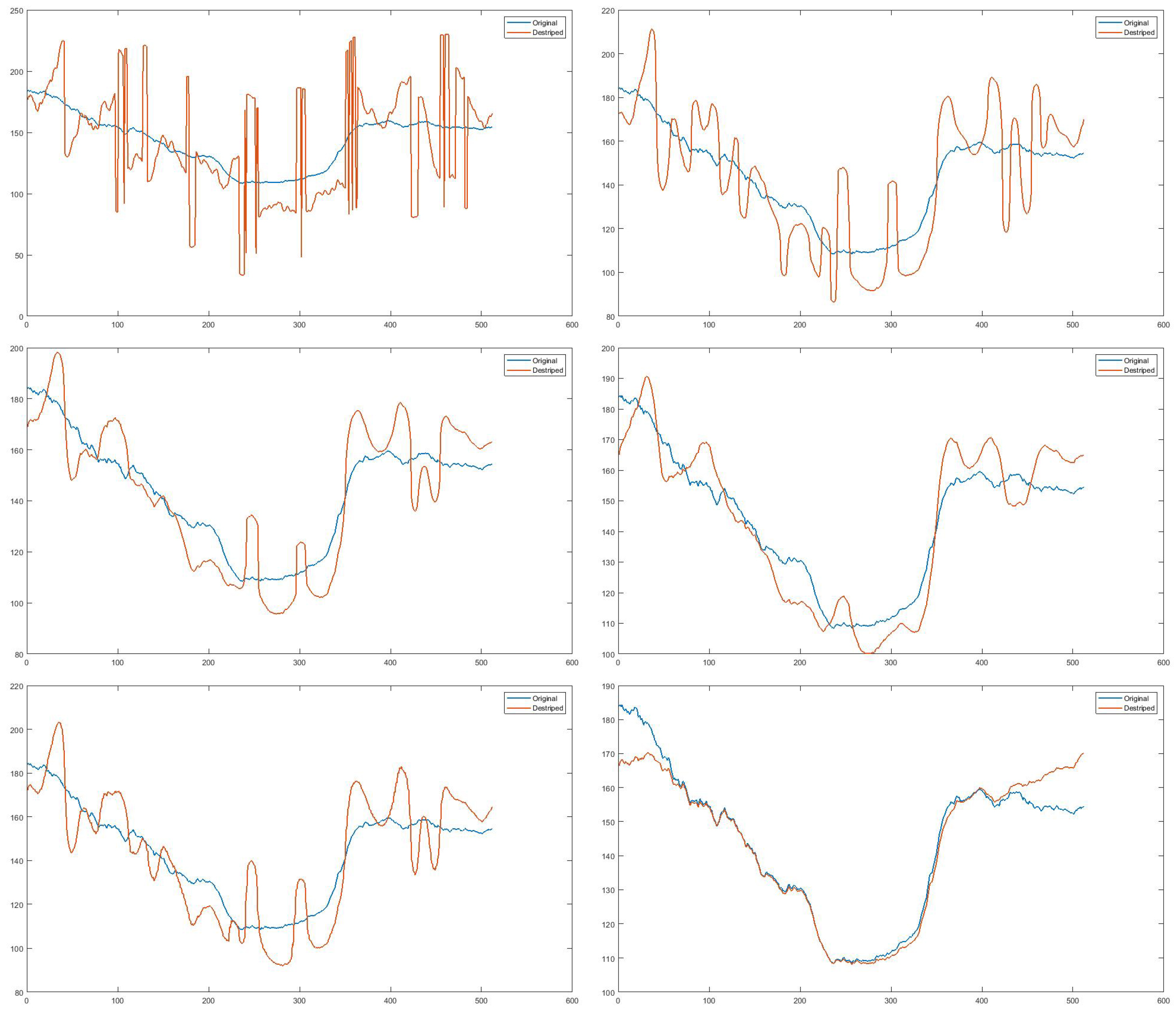






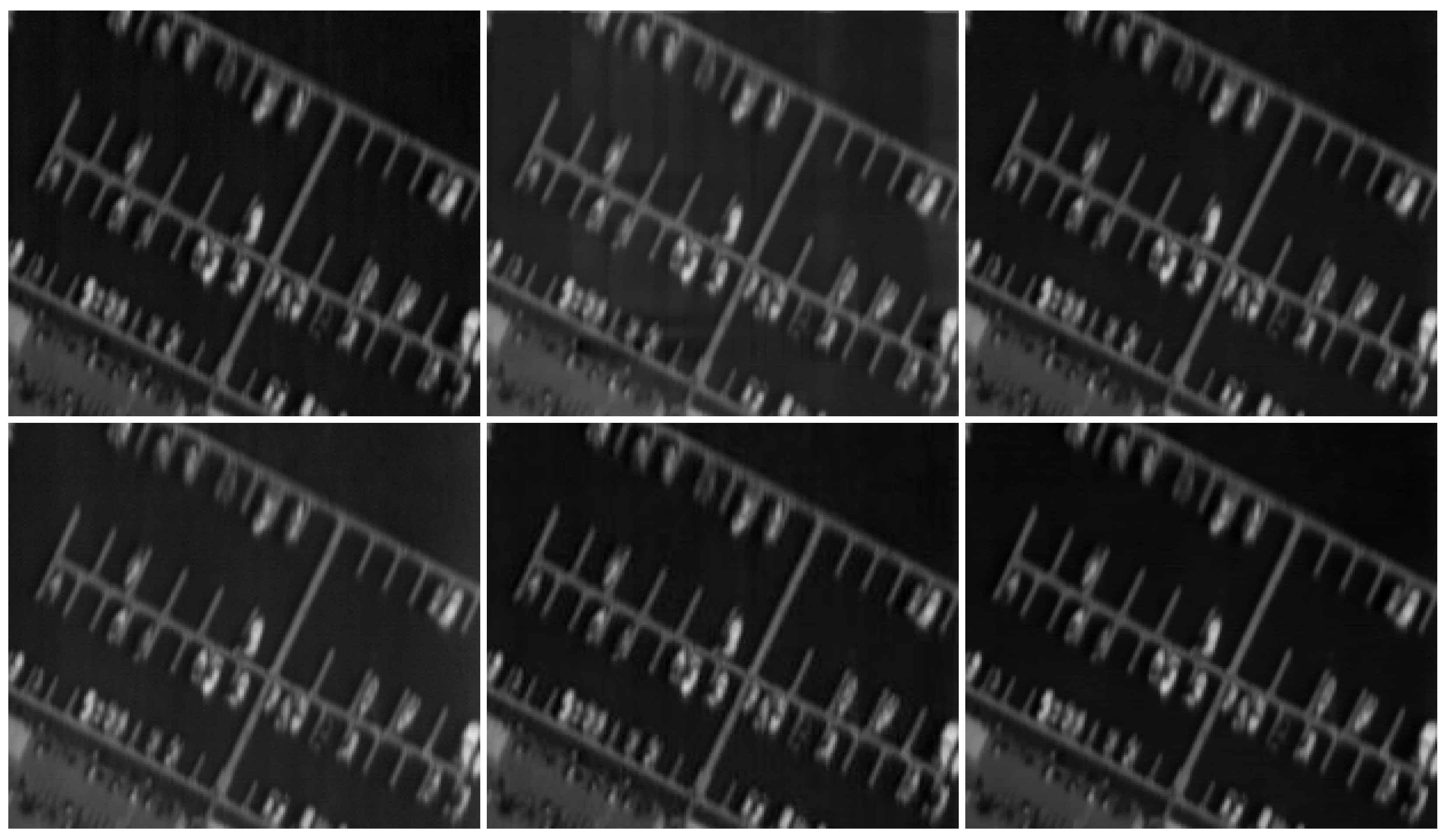
| Image | Method | r = 0.3 | r = 0.5 | r = 0.7 | r = 0.9 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | Intensity | ||||||||||||||
| 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | ||
| Hyperspectral image | SLD | 40.7623 | 40.3565 | 39.7621 | 33.1389 | 39.9614 | 38.6069 | 37.2848 | 35.9059 | 39.5197 | 37.6037 | 35.5704 | 14.6173 | 39.5197 | 37.6037 | 35.5040 | 14.6713 |
| LRSID | 35.3815 | 35.6900 | 35.7350 | 35.7470 | 35.8817 | 35.9247 | 35.9308 | 35.9474 | 35.8469 | 35.9239 | 35.9254 | 35.8749 | 35.8469 | 35.9239 | 35.9254 | 35.8749 | |
| TVGS | 39.0808 | 39.0958 | 39.0875 | 38.7651 | 38.4572 | 38.3999 | 38.4197 | 38.4480 | 37.8913 | 37.8211 | 37.7227 | 37.5384 | 37.8913 | 37.8211 | 37.7227 | 37.5384 | |
| GSLV | 35.7031 | 35.7143 | 35.7560 | 35.7098 | 35.6710 | 35.6377 | 35.6268 | 35.5980 | 35.6287 | 35.5391 | 35.4226 | 35.2289 | 35.6287 | 35.5391 | 35.4226 | 35.2289 | |
| HTVLR | 35.9175 | 32.8299 | 30.4946 | 28.6029 | 35.8070 | 32.8267 | 30.5155 | 28.6380 | 35.8323 | 32.8756 | 30.5558 | 28.6825 | 35.6965 | 32.7996 | 30.5307 | 28.6519 | |
| Proposed | 39.9943 | 39.2962 | 38.9919 | 38.8458 | 39.4150 | 38.6377 | 38.6793 | 38.9331 | 39.2052 | 38.6535 | 38.4616 | 38.1107 | 39.2052 | 38.6535 | 38.4616 | 38.1107 | |
| MODIS | SLD | 52.1371 | 51.4041 | 50.4967 | 49.5176 | 50.9999 | 48.9686 | 47.0117 | 45.2834 | 49.0407 | 47.5429 | 45.3456 | 43.4824 | 47.0761 | 44.8401 | 42.3219 | 40.3089 |
| LRSID | 39.9467 | 39.9152 | 39.9967 | 40.1257 | 40.1165 | 40.1547 | 40.1851 | 40.2119 | 40.1399 | 40.2250 | 40.3121 | 40.4414 | 39.7306 | 39.6969 | 39.6988 | 39.6793 | |
| TVGS | 47.9489 | 47.2767 | 47.0315 | 46.9728 | 48.9832 | 48.9284 | 48.7219 | 48.3933 | 47.5304 | 47.1522 | 47.2241 | 47.2893 | 44.2714 | 43.8235 | 42.9537 | 42.3731 | |
| GSLV | 40.3947 | 40.5206 | 40.7104 | 40.8861 | 41.0941 | 41.3768 | 41.6219 | 41.8463 | 40.9006 | 41.3199 | 41.8689 | 42.4452 | 40.2217 | 40.2402 | 40.4891 | 40.6818 | |
| HTVLR | 38.4765 | 34.1368 | 31.2640 | 29.0932 | 37.8805 | 33.9375 | 31.1168 | 28.9884 | 38.1052 | 33.9021 | 31.1079 | 28.9878 | 38.0341 | 33.8598 | 31.1145 | 28.9840 | |
| Proposed | 48.6227 | 46.9238 | 46.1389 | 45.9567 | 51.2011 | 50.9063 | 50.7519 | 50.6098 | 49.8948 | 49.4367 | 49.4704 | 49.7446 | 46.9948 | 44.9491 | 43.1214 | 42.8721 | |
| Image | Method | r = 0.3 | r = 0.5 | r = 0.7 | r = 0.9 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | Intensity | ||||||||||||||
| 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | ||
| Hyperspectral image | SLD | 0.9955 | 0.9946 | 0.9932 | 0.9911 | 0.9949 | 0.9926 | 0.9902 | 0.9841 | 0.9930 | 0.9876 | 0.9791 | 0.4314 | 0.9930 | 0.9876 | 0.9791 | 0.4314 |
| LRSID | 0.9918 | 0.9927 | 0.9930 | 0.9930 | 0.9939 | 0.9939 | 0.9939 | 0.9939 | 0.9934 | 0.9937 | 0.9937 | 0.9935 | 0.9934 | 0.9937 | 0.9937 | 0.9935 | |
| TVGS | 0.9964 | 0.9964 | 0.9963 | 0.9963 | 0.9960 | 0.9960 | 0.9960 | 0.9960 | 0.9953 | 0.9953 | 0.9953 | 0.9952 | 0.9953 | 0.9953 | 0.9953 | 0.9952 | |
| GSLV | 0.9910 | 0.9909 | 0.9908 | 0.9905 | 0.9910 | 0.9908 | 0.9899 | 0.9899 | 0.9908 | 0.9905 | 0.9900 | 0.9891 | 0.9908 | 0.9905 | 0.9900 | 0.9891 | |
| HTVLR | 0.9942 | 0.9917 | 0.9816 | 0.9836 | 0.9937 | 0.9911 | 0.9878 | 0.9832 | 0.9938 | 0.9914 | 0.9880 | 0.9836 | 0.9935 | 0.9912 | 0.9879 | 0.9831 | |
| Proposed | 0.9964 | 0.9964 | 0.9964 | 0.9963 | 0.9962 | 0.9962 | 0.9961 | 0.9961 | 0.9957 | 0.9956 | 0.9955 | 0.9955 | 0.9957 | 0.9956 | 0.9955 | 0.9953 | |
| MODIS | SLD | 0.9987 | 0.9982 | 0.9975 | 0.9966 | 0.9979 | 0.9959 | 0.9930 | 0.9892 | 0.9967 | 0.9926 | 0.9866 | 0.9785 | 0.9975 | 0.9949 | 0.9911 | 0.9860 |
| LRSID | 0.9983 | 0.9983 | 0.9983 | 0.9984 | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9983 | 0.9983 | 0.9983 | 0.9983 | |
| TVGS | 0.9991 | 0.9991 | 0.9991 | 0.9991 | 0.9991 | 0.9991 | 0.9991 | 0.9991 | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9989 | 0.9989 | 0.9988 | 0.9988 | |
| GSLV | 0.9982 | 0.9982 | 0.9981 | 0.9979 | 0.9982 | 0.9982 | 0.9981 | 0.9980 | 0.9982 | 0.9982 | 0.9981 | 0.9979 | 0.9981 | 0.9979 | 0.9976 | 0.9973 | |
| HTVLR | 0.9995 | 0.9989 | 0.9981 | 0.9944 | 0.9991 | 0.9982 | 0.9978 | 0.9967 | 0.9993 | 0.9987 | 0.9978 | 0.9967 | 0.9993 | 0.9986 | 0.9978 | 0.9967 | |
| Proposed | 0.9996 | 0.9996 | 0.9995 | 0.9995 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9995 | 0.9994 | 0.9993 | 0.9992 | |
| Image | Method | r = 0.3 | r = 0.5 | r = 0.7 | r = 0.9 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | Intensity | ||||||||||||||
| 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | ||
| Hyperspectral image (01) | SLD | 35.3447 | 31.7048 | 29.0013 | 26.8673 | 32.0895 | 30.1640 | 27.4199 | 20.6502 | 32.2696 | 28.0868 | 23.0584 | 14.9193 | 30.6777 | 26.3734 | 19.3105 | 10.6051 |
| LRSID | 33.8233 | 31.4653 | 29.1579 | 27.0463 | 31.5824 | 30.3996 | 27.8443 | 25.5226 | 31.8777 | 28.2986 | 25.2156 | 22.5195 | 30.7139 | 26.5208 | 23.1218 | 20.3287 | |
| TVGS | 38.7072 | 36.2829 | 33.4100 | 30.6928 | 34.2652 | 33.9721 | 31.0179 | 28.3584 | 34.0143 | 30.0883 | 26.9076 | 24.2418 | 31.5150 | 27.7069 | 24.3439 | 21.4300 | |
| GSLV | 34.6330 | 32.8944 | 30.9638 | 29.0401 | 32.6877 | 31.6578 | 29.5419 | 27.5285 | 33.4977 | 30.3310 | 27.5669 | 25.0776 | 32.8353 | 29.7059 | 26.4824 | 23.4092 | |
| HTVLR | 35.0508 | 31.2176 | 28.9420 | 28.8632 | 33.5651 | 31.4572 | 27.5688 | 26.6761 | 33.0854 | 29.2073 | 25.5829 | 22.9086 | 31.8186 | 28.4824 | 24.1032 | 20.4523 | |
| Proposed | 35.1447 | 34.5641 | 33.9571 | 33.2269 | 33.4716 | 33.6839 | 32.7429 | 31.7382 | 34.8838 | 33.6992 | 32.2696 | 30.8142 | 34.2725 | 33.5532 | 32.6933 | 31.6803 | |
| MODIS(01) | SLD | 37.3381 | 33.2820 | 30.4637 | 28.3107 | 34.3412 | 29.9283 | 26.9709 | 24.7386 | 32.2575 | 27.8777 | 24.9191 | 18.5936 | 31.9292 | 27.5246 | 24.5699 | 12.1103 |
| LRSID | 35.0517 | 32.4045 | 29.9019 | 27.7256 | 32.8137 | 29.0122 | 26.0444 | 23.6232 | 31.3061 | 26.9440 | 23.6602 | 21.0059 | 31.1085 | 26.9318 | 23.6982 | 20.9615 | |
| TVGS | 42.0600 | 38.6558 | 35.1310 | 32.1397 | 36.6404 | 31.9843 | 28.4645 | 25.7084 | 33.4679 | 28.9072 | 25.4481 | 22.6511 | 31.3206 | 27.4750 | 24.5042 | 22.0021 | |
| GSLV | 37.3673 | 34.8319 | 32.4582 | 30.3732 | 35.0774 | 31.5064 | 28.5077 | 25.9658 | 33.1705 | 30.1618 | 26.8225 | 23.9861 | 31.9486 | 28.9601 | 25.8517 | 23.2652 | |
| HTVLR | 34.7274 | 32.9110 | 29.5728 | 26.8078 | 32.2557 | 30.2083 | 28.2044 | 25.2784 | 33.0159 | 28.2989 | 25.7874 | 22.3446 | 31.8347 | 27.0853 | 23.9765 | 22.4003 | |
| Proposed | 34.3651 | 33.9262 | 33.3634 | 32.6629 | 33.2117 | 32.1403 | 31.0206 | 29.8827 | 33.7232 | 33.1588 | 32.4502 | 31.5701 | 32.3019 | 30.6507 | 29.0172 | 27.4448 | |
| Hyperspectral image (02) | SLD | 36.2916 | 31.9875 | 29.0546 | 26.8216 | 35.3499 | 31.0813 | 28.1446 | 20.0484 | 32.9993 | 28.6127 | 22.3813 | 13.4758 | 31.0791 | 26.6511 | 17.7244 | 10.3148 |
| LRSID | 35.7304 | 32.4357 | 29.7151 | 27.4146 | 35.5710 | 31.9302 | 28.9187 | 26.3609 | 33.3114 | 29.3193 | 26.1621 | 23.4309 | 31.7662 | 27.0848 | 23.5241 | 20.6438 | |
| TVGS | 43.9596 | 39.5005 | 35.1955 | 31.7593 | 42.8190 | 37.4688 | 33.1838 | 29.9043 | 35.2863 | 30.9347 | 27.7148 | 25.0720 | 32.8635 | 28.3649 | 24.7524 | 21.7456 | |
| GSLV | 38.9853 | 35.2414 | 32.2460 | 29.7611 | 38.1829 | 34.5052 | 31.5713 | 29.1273 | 35.9022 | 31.8174 | 28.6891 | 26.0784 | 36.1973 | 31.3977 | 27.3928 | 23.9869 | |
| HTVLR | 36.4678 | 33.5402 | 31.8486 | 28.3441 | 36.2421 | 32.8050 | 29.4345 | 25.6534 | 34.8462 | 29.8140 | 25.6910 | 22.6884 | 33.6814 | 28.8084 | 24.0925 | 22.1252 | |
| Proposed | 39.2506 | 37.5226 | 35.8696 | 34.3269 | 39.3499 | 38.1468 | 36.7722 | 35.3357 | 37.3850 | 35.3551 | 33.4955 | 31.8256 | 38.0805 | 36.6378 | 35.1649 | 33.6987 | |
| MODIS(02) | SLD | 37.5798 | 33.4708 | 30.6264 | 28.4564 | 33.8344 | 29.6296 | 26.7684 | 24.5903 | 32.3259 | 27.9541 | 24.1494 | 18.4432 | 32.0122 | 27.6443 | 24.2635 | 11.8774 |
| LRSID | 34.8305 | 32.1984 | 29.7625 | 27.6320 | 32.7221 | 28.9821 | 26.0387 | 23.6293 | 31.3837 | 27.0681 | 23.7680 | 21.0766 | 31.7608 | 27.4014 | 24.0023 | 21.1461 | |
| TVGS | 40.0048 | 37.1845 | 34.1550 | 31.5341 | 35.7214 | 31.5371 | 28.2808 | 25.6356 | 33.4506 | 29.0122 | 25.6242 | 22.8340 | 32.3990 | 28.2698 | 25.0687 | 22.3843 | |
| GSLV | 35.0578 | 33.2712 | 31.4417 | 29.7087 | 33.7419 | 30.8448 | 28.1933 | 25.8462 | 33.6929 | 29.2312 | 26.9986 | 24.1839 | 33.3650 | 29.6181 | 26.4697 | 23.7723 | |
| HTVLR | 36.1366 | 31.1110 | 29.7969 | 27.3224 | 34.9065 | 30.9915 | 26.9208 | 24.6307 | 33.3510 | 30.5450 | 24.1067 | 22.8506 | 32.4660 | 26.7465 | 25.0747 | 23.1931 | |
| Proposed | 31.2816 | 30.5062 | 29.8869 | 29.3222 | 31.6262 | 30.9520 | 30.2050 | 29.3541 | 30.8442 | 29.9709 | 29.1658 | 28.3991 | 31.1998 | 30.1065 | 28.8306 | 27.5111 | |
| Image | Method | r = 0.3 | r = 0.5 | r = 0.7 | r = 0.9 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | Intensity | ||||||||||||||
| 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | 30 | 50 | 70 | 90 | ||
| Hyperspectral image (01) | SLD | 0.9921 | 0.9844 | 0.9728 | 0.9570 | 0.9879 | 0.9770 | 0.9601 | 0.8346 | 0.9875 | 0.9707 | 0.9066 | 0.5559 | 0.9810 | 0.9546 | 0.8046 | 0.1775 |
| LRSID | 0.9917 | 0.9882 | 0.9813 | 0.9698 | 0.9889 | 0.9850 | 0.9747 | 0.9568 | 0.9889 | 0.9785 | 0.9563 | 0.9119 | 0.9853 | 0.9647 | 0.9254 | 0.8630 | |
| TVGS | 0.9959 | 0.9945 | 0.9917 | 0.9864 | 0.9934 | 0.9922 | 0.9879 | 0.9805 | 0.9923 | 0.9863 | 0.9745 | 0.9534 | 0.9881 | 0.9755 | 0.9487 | 0.9021 | |
| GSLV | 0.9903 | 0.9884 | 0.9852 | 0.9797 | 0.9890 | 0.9868 | 0.9827 | 0.9763 | 0.9890 | 0.9839 | 0.9751 | 0.9603 | 0.9886 | 0.9825 | 0.9677 | 0.9362 | |
| HTVLR | 0.9922 | 0.9876 | 0.9788 | 0.9772 | 0.9902 | 0.9861 | 0.9657 | 0.9649 | 0.9913 | 0.9791 | 0.9623 | 0.9294 | 0.9874 | 0.9748 | 0.9341 | 0.8770 | |
| Proposed | 0.9907 | 0.9902 | 0.9897 | 0.9890 | 0.9900 | 0.9895 | 0.9886 | 0.9874 | 0.9905 | 0.9895 | 0.9881 | 0.9860 | 0.9901 | 0.9895 | 0.9886 | 0.9875 | |
| MODIS(01) | SLD | 0.9912 | 0.9796 | 0.9634 | 0.9436 | 0.9850 | 0.9625 | 0.9322 | 0.8968 | 0.9757 | 0.9403 | 0.8955 | 0.7501 | 0.9782 | 0.9463 | 0.9043 | 0.3482 |
| LRSID | 0.9931 | 0.9851 | 0.9708 | 0.9486 | 0.9875 | 0.9643 | 0.9273 | 0.8767 | 0.9796 | 0.9382 | 0.8757 | 0.7974 | 0.9846 | 0.9509 | 0.8828 | 0.7828 | |
| TVGS | 0.9979 | 0.9958 | 0.9917 | 0.9848 | 0.9946 | 0.9856 | 0.9663 | 0.9355 | 0.9896 | 0.9685 | 0.9276 | 0.8693 | 0.9889 | 0.9712 | 0.9361 | 0.8759 | |
| GSLV | 0.9949 | 0.9925 | 0.9888 | 0.9833 | 0.9935 | 0.9870 | 0.9740 | 0.9510 | 0.9908 | 0.9792 | 0.9564 | 0.9154 | 0.9586 | 0.9821 | 0.9631 | 0.9270 | |
| HTVLR | 0.9907 | 0.9856 | 0.9694 | 0.9452 | 0.9848 | 0.9724 | 0.9508 | 0.9101 | 0.9878 | 0.9597 | 0.9254 | 0.8656 | 0.9810 | 0.9529 | 0.9065 | 0.8160 | |
| Proposed | 0.9947 | 0.9942 | 0.9936 | 0.9930 | 0.9945 | 0.9937 | 0.9926 | 0.9911 | 0.9945 | 0.9939 | 0.9931 | 0.9920 | 0.9940 | 0.9925 | 0.9902 | 0.9869 | |
| Hyperspectral image (02) | SLD | 0.9757 | 0.9401 | 0.8936 | 0.8427 | 0.9710 | 0.9330 | 0.8814 | 0.6978 | 0.9462 | 0.8703 | 0.7073 | 0.2751 | 0.9270 | 0.8403 | 0.5567 | 0.0625 |
| LRSID | 0.9804 | 0.9533 | 0.9131 | 0.8648 | 0.9818 | 0.9586 | 0.9205 | 0.8648 | 0.9596 | 0.8989 | 0.8184 | 0.7155 | 0.9455 | 0.8670 | 0.7638 | 0.6477 | |
| TVGS | 0.9949 | 0.9871 | 0.9676 | 0.9347 | 0.9943 | 0.9858 | 0.9696 | 0.9422 | 0.9710 | 0.9302 | 0.8702 | 0.7975 | 0.9536 | 0.8967 | 0.8125 | 0.7134 | |
| GSLV | 0.9874 | 0.9737 | 0.9489 | 0.9114 | 0.9855 | 0.9720 | 0.9518 | 0.9238 | 0.9736 | 0.9397 | 0.8906 | 0.8287 | 0.9756 | 0.9396 | 0.8783 | 0.7906 | |
| HTVLR | 0.9756 | 0.9632 | 0.9421 | 0.8749 | 0.9794 | 0.9477 | 0.9042 | 0.8063 | 0.9709 | 0.8986 | 0.8041 | 0.7174 | 0.9642 | 0.9113 | 0.7597 | 0.6956 | |
| Proposed | 0.9864 | 0.9828 | 0.9778 | 0.9713 | 0.9865 | 0.9835 | 0.9790 | 0.9726 | 0.9793 | 0.9697 | 0.9564 | 0.9395 | 0.9830 | 0.9771 | 0.9686 | 0.9572 | |
| MODIS(02) | SLD | 0.9732 | 0.9481 | 0.9223 | 0.8957 | 0.9568 | 0.9204 | 0.8800 | 0.8367 | 0.9489 | 0.9056 | 0.8354 | 0.6898 | 0.9508 | 0.9083 | 0.8485 | 0.3042 |
| LRSID | 0.9795 | 0.9535 | 0.9250 | 0.8941 | 0.9641 | 0.9239 | 0.8741 | 0.8132 | 0.9549 | 0.9047 | 0.8325 | 0.7407 | 0.9570 | 0.9068 | 0.8312 | 0.7263 | |
| TVGS | 0.9973 | 0.9921 | 0.9826 | 0.9639 | 0.9849 | 0.9686 | 0.9325 | 0.8879 | 0.9694 | 0.9408 | 0.8979 | 0.8341 | 0.9669 | 0.9354 | 0.8868 | 0.8148 | |
| GSLV | 0.9855 | 0.9768 | 0.9644 | 0.9466 | 0.9781 | 0.9633 | 0.9390 | 0.8997 | 0.9674 | 0.9461 | 0.9185 | 0.8754 | 0.9700 | 0.9501 | 0.9206 | 0.8705 | |
| HTVLR | 0.9779 | 0.9326 | 0.9177 | 0.8988 | 0.9740 | 0.9385 | 0.9068 | 0.8515 | 0.9607 | 0.9252 | 0.8607 | 0.8199 | 0.9552 | 0.9055 | 0.8469 | 0.7995 | |
| Proposed | 0.9740 | 0.9733 | 0.9721 | 0.9697 | 0.9750 | 0.9694 | 0.9597 | 0.9485 | 0.9645 | 0.9589 | 0.9538 | 0.9488 | 0.9625 | 0.9549 | 0.9461 | 0.9357 | |
| Method | Original | SLD | LRSID | TVGS | GSLV | HTVLR | Proposed |
|---|---|---|---|---|---|---|---|
| PRNU | 0.1039 | 0.0939 | 0.0675 | 0.0762 | 0.0795 | 0.1009 | 0.0619 |
| Original | SLD | LRSID | TVGS | GSLV | HTVLR | Proposed | |
|---|---|---|---|---|---|---|---|
| MODIS01 | 49.6308 | 48.7199 | 46.7413 | 47.4065 | 45.5546 | 48.2170 | 39.8696 |
| MODIS02 | 30.3869 | 30.1396 | 29.7943 | 30.0316 | 30.0455 | 30.1504 | 29.9884 |
| MODIS03 | 32.4919 | 32.2129 | 30.7052 | 31.2176 | 30.0831 | 32.0267 | 30.0383 |
| Our data | 42.6685 | 42.4436 | 41.9675 | 42.3616 | 42.1085 | 42.5861 | 41.3120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Qu, H.; Zheng, L.; Gao, T.; Zhang, Z. A Remote Sensing Image Destriping Model Based on Low-Rank and Directional Sparse Constraint. Remote Sens. 2021, 13, 5126. https://doi.org/10.3390/rs13245126
Wu X, Qu H, Zheng L, Gao T, Zhang Z. A Remote Sensing Image Destriping Model Based on Low-Rank and Directional Sparse Constraint. Remote Sensing. 2021; 13(24):5126. https://doi.org/10.3390/rs13245126
Chicago/Turabian StyleWu, Xiaobin, Hongsong Qu, Liangliang Zheng, Tan Gao, and Ziyu Zhang. 2021. "A Remote Sensing Image Destriping Model Based on Low-Rank and Directional Sparse Constraint" Remote Sensing 13, no. 24: 5126. https://doi.org/10.3390/rs13245126
APA StyleWu, X., Qu, H., Zheng, L., Gao, T., & Zhang, Z. (2021). A Remote Sensing Image Destriping Model Based on Low-Rank and Directional Sparse Constraint. Remote Sensing, 13(24), 5126. https://doi.org/10.3390/rs13245126






