Long-Term Lake Area Change and Its Relationship with Climate in the Endorheic Basins of the Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
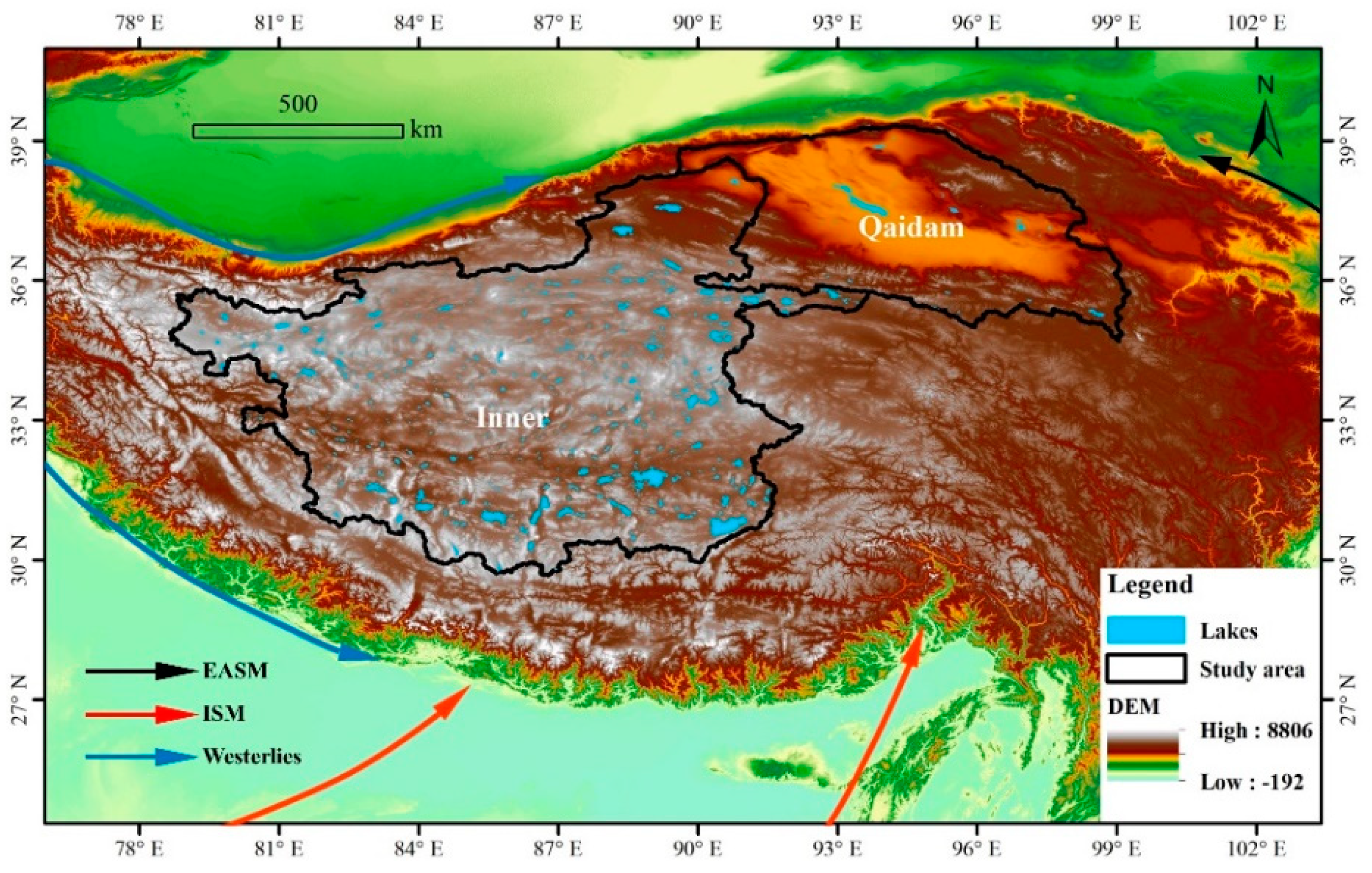
2.1. Study Area
2.2. Data
2.2.1. Surface Water Data, DEM and Landsat Imagery
2.2.2. Climate Data
2.3. Methods
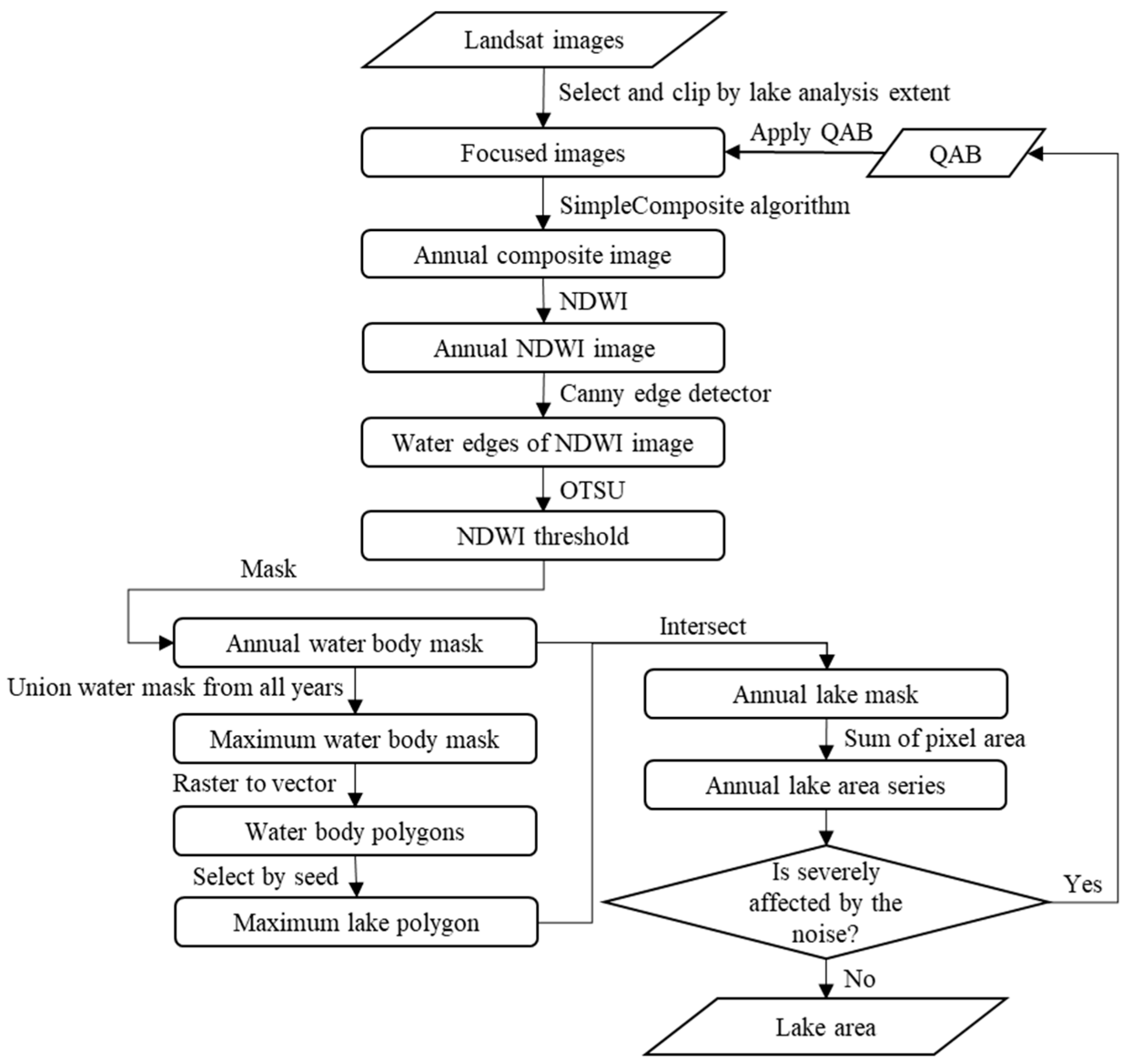
2.3.1. Calculate Annual Lake Area
2.3.2. Lake Area and Climate Relationship
3. Results
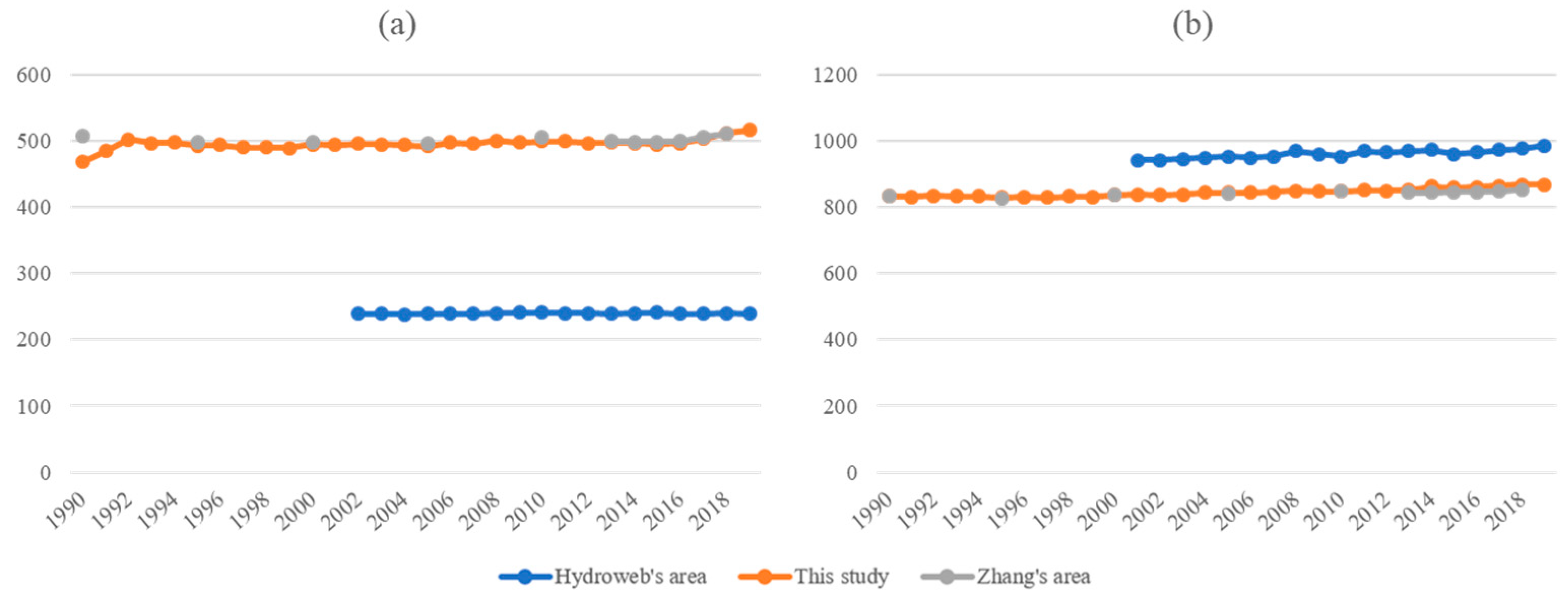
3.1. Lake Area Validation
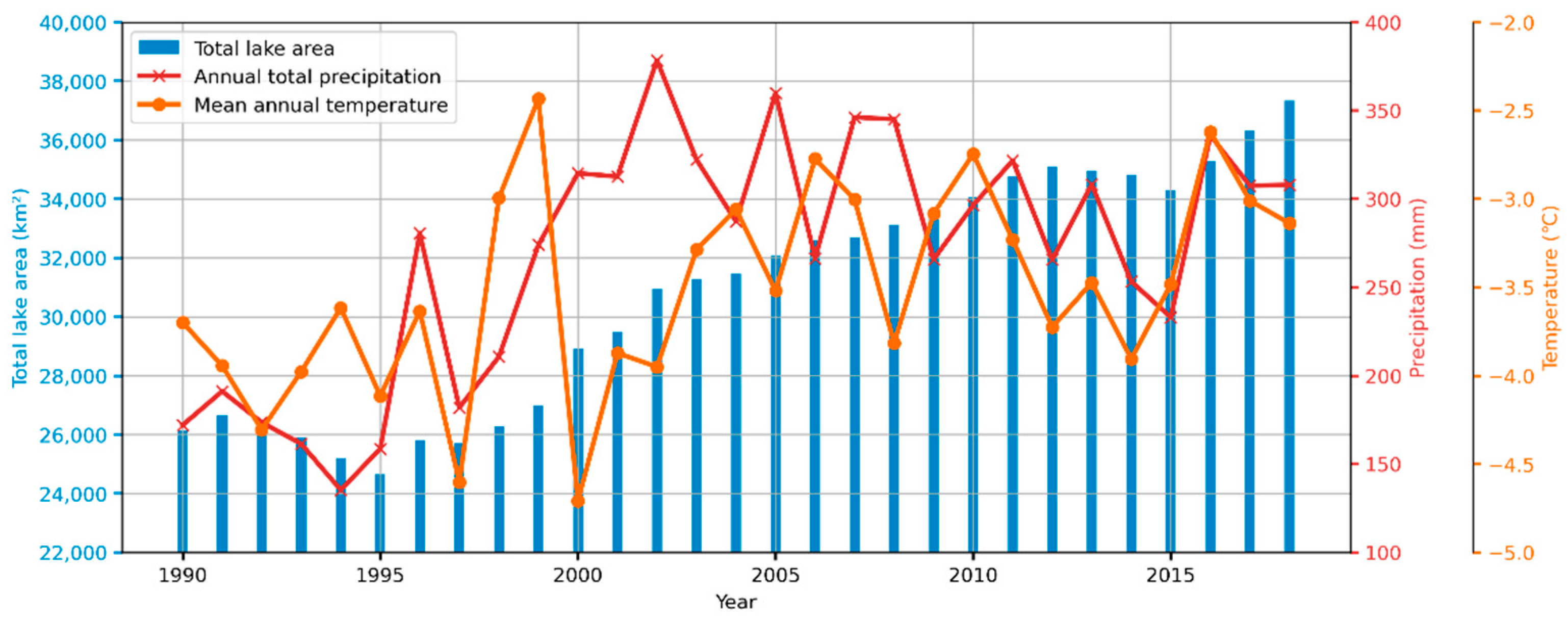
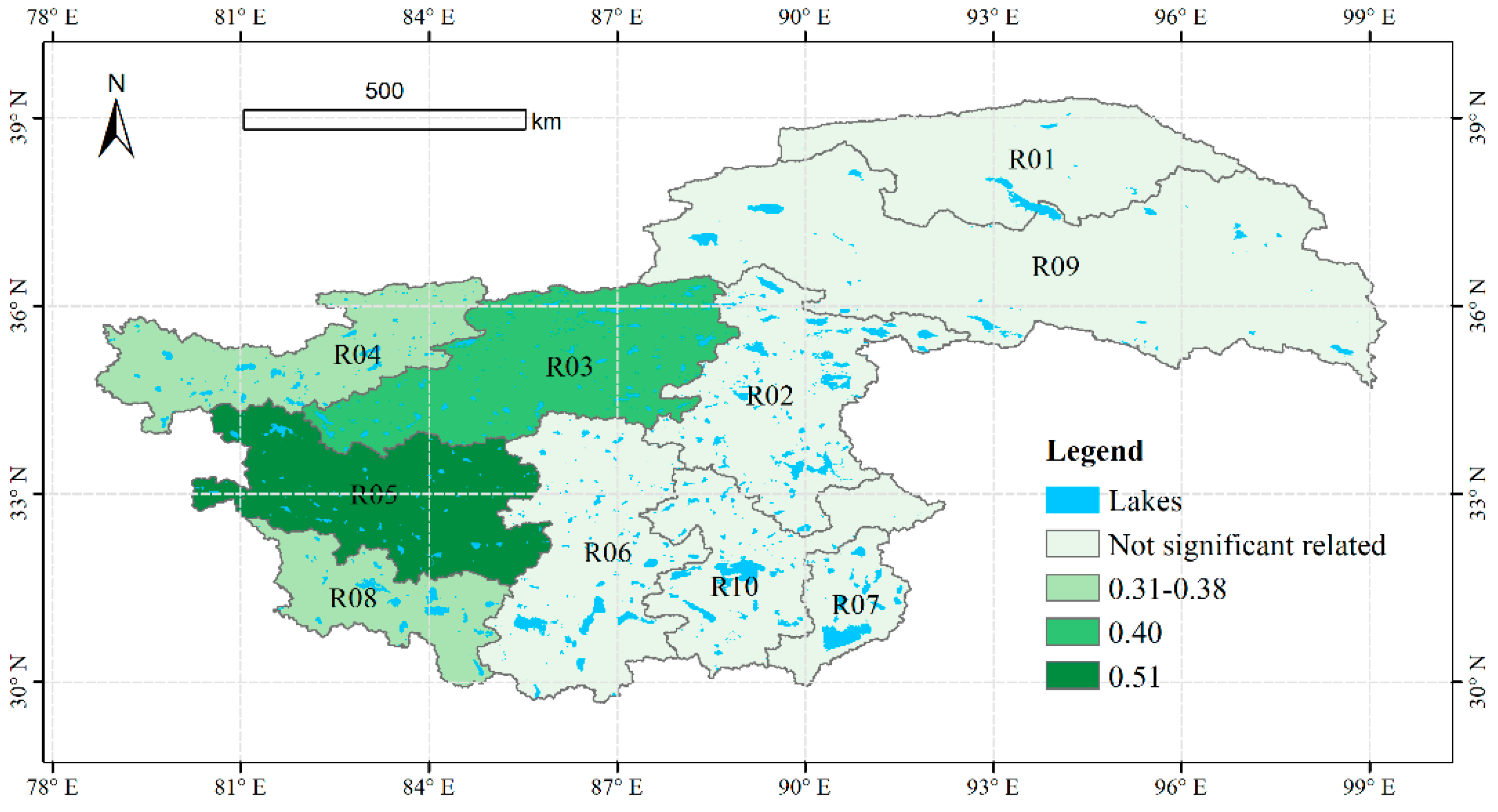
3.2. Change of Lake Area
3.3. Lake Area and Local Climate
3.4. Lake Area and Large-Scale Atmospheric Circulations
3.4.1. Impact of Regional Monsoon Systems
3.4.2. Impact of Atmospheric Circulation
3.4.3. Lake Area and the El Niño/La Niña Events
4. Discussion
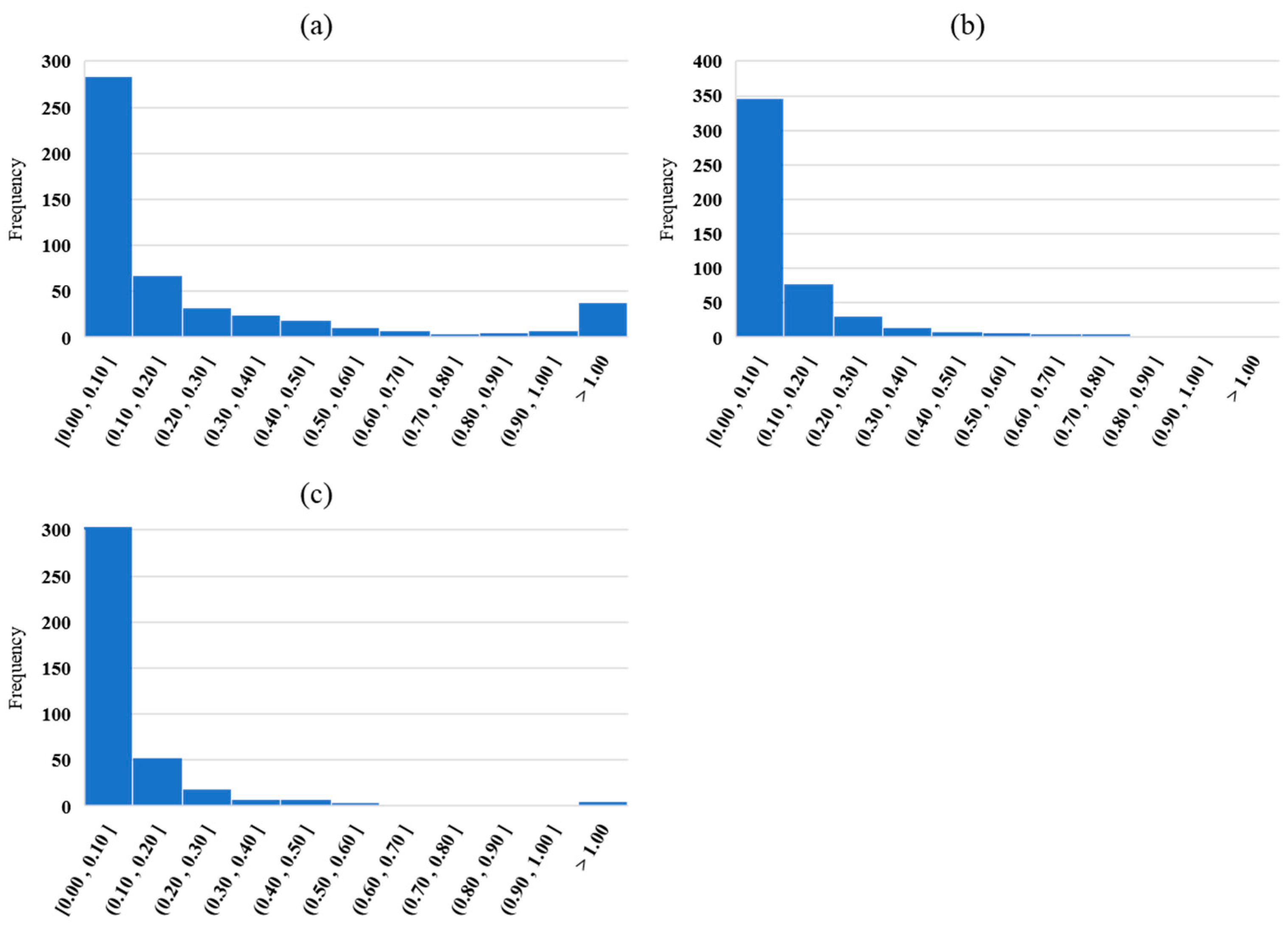
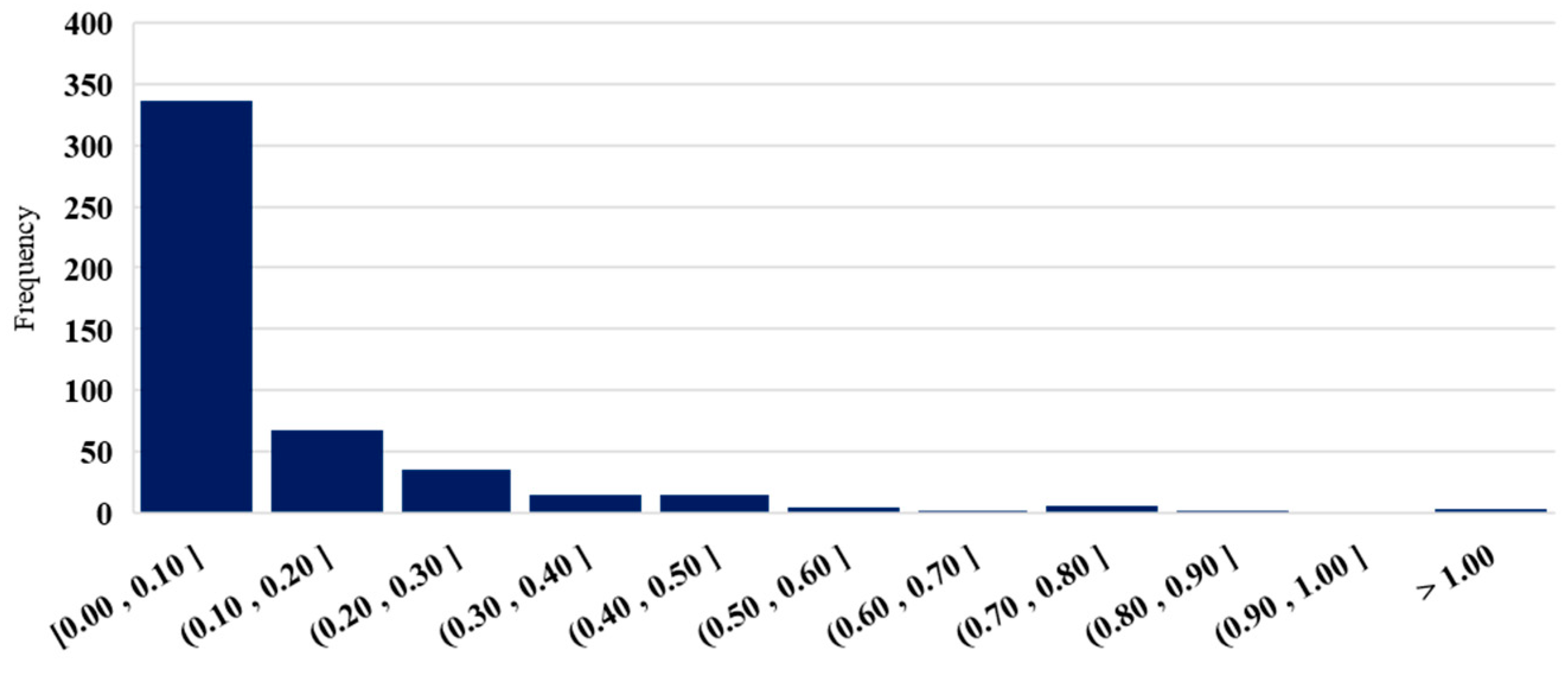
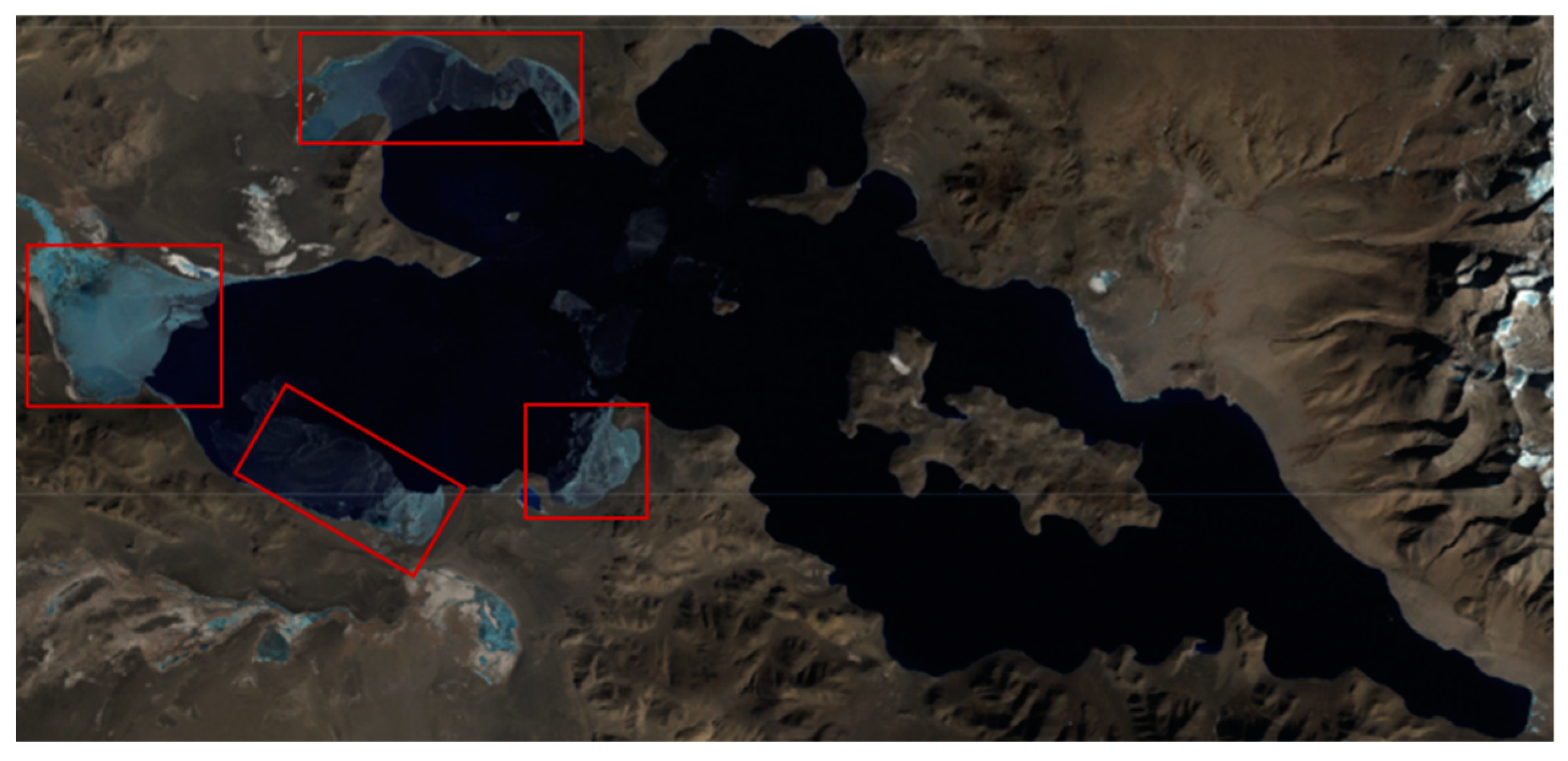
4.1. Noise on Composite Images
4.2. Canny Edge Detector Parameters
4.3. NDWI Thresholds
4.4. Lake Area Change and Climate Variables
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, C.; Huang, B.; Richards, K.; Ke, L.; Hien Phan, V. Accelerated lake expansion on the Tibetan Plateau in the 2000s: Induced by glacial melting or other processes? Water Resour. Res. 2014, 50, 3170–3186. [Google Scholar] [CrossRef] [Green Version]
- Yanai, M.; Li, C.; Song, Z. Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon. J. Meteorol. Soc. Japan. Ser. II 1992, 70, 319–351. [Google Scholar] [CrossRef] [Green Version]
- Yanai, M.; Li, C. Mechanism of Heating and the Boundary Layer over the Tibetan Plateau. Mon. Weather Rev. 1994, 122, 305. [Google Scholar] [CrossRef]
- Wang, X.; Siegert, F.; Zhou, A.-G.; Franke, J. Glacier and glacial lake changes and their relationship in the context of climate change, Central Tibetan Plateau 1972–2010. Glob. Planet Chang. 2013, 111, 246–257. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Flügel, W.-A.; Sanchez-Lorenzo, A.; Yan, Y.; Xu, Y.; Huang, J. Does a weekend effect in diurnal temperature range exist in the eastern and central Tibetan Plateau? Environ. Res. Lett 2009, 4, 045202. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, X.; Zhang, Z. Automatic Extraction of Lakes on the Qinghai-Tibet Plateau from Sentinel-1 SAR Images. In Proceedings of the 2019 SAR in Big Data Era (BIGSARDATA), Beijing, China, 5–6 August 2019; pp. 1–4. [Google Scholar]
- Wan, W.; Long, D.; Hong, Y.; Ma, Y.; Yuan, Y.; Xiao, P.; Duan, H.; Han, Z.; Gu, X. A lake data set for the Tibetan Plateau from the 1960s, 2005, and 2014. Sci. Data 2016, 3, 160039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Yao, T.; Shum, C.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Dyurgerov, M.B.; Meier, M.F. Glaciers and the Changing Earth System: A 2004 Snapshot; Institute of Arctic and Alpine Research, University of Colorado Boulder: Boulder, CO, USA, 2005; Volume 58. [Google Scholar]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Zhan, P.; Song, C.; Wang, J.; Li, W.; Ke, L.; Liu, K.; Chen, T. Recent Abnormal Hydrologic Behavior of Tibetan Lakes Observed by Multi-Mission Altimeters. Remote Sens. 2020, 12, 2986. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. A J. R. Meteorol. Soc. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Lin, C.; Yang, K.; Qin, J.; Fu, R. Observed coherent trends of surface and upper-air wind speed over China since 1960. J. Clim. 2013, 26, 2891–2903. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ren, Y.; Yin, Z.Y.; Lin, Z.; Zheng, D. Spatial and temporal variation patterns of reference evapotranspiration across the Qinghai-Tibetan Plateau during 1971–2004. J. Geophys. Res. Atmos. 2009, 114, D15105. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, Q.; Chen, D.; van der Ent, R.J.; Liu, X.; Li, W.; Haile, G.G. Moisture source changes contributed to different precipitation changes over the northern and southern Tibetan Plateau. J. Hydrometeorol. 2019, 20, 217–229. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, K.; Wang, B.; Sheng, Y.; Bird, B.W.; Zhang, G.; Tian, L. Response of inland lake dynamics over the Tibetan Plateau to climate change. Clim. Chang. 2014, 125, 281–290. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, W.; Chen, W.; Zheng, G. A robust but variable lake expansion on the Tibetan Plateau. Sci. Bull. 2019, 64, 1306–1309. [Google Scholar] [CrossRef] [Green Version]
- Liao, J.; Shen, G.; Li, Y. Lake variations in response to climate change in the Tibetan Plateau in the past 40 years. Int. J. Digit. Earth 2013, 6, 534–549. [Google Scholar] [CrossRef]
- Yang, K.; Yao, F.; Wang, J.; Luo, J.; Shen, Z.; Wang, C.; Song, C. Recent dynamics of alpine lakes on the endorheic Changtang Plateau from multi-mission satellite data. J. Hydrol. 2017, 552, 633–645. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Yang, K.; Wang, C.; Walter, B.A.; Crétaux, J.-F. Lake storage variation on the endorheic Tibetan Plateau and its attribution to climate change since the new millennium. Environ. Res. Lett 2018, 13, 064011. [Google Scholar] [CrossRef]
- Zhang, G.; Bolch, T.; Chen, W.; Crétaux, J.-F. Comprehensive estimation of lake volume changes on the Tibetan Plateau during 1976–2019 and basin-wide glacier contribution. Sci. Total Environ. 2021, 772, 145463. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Huang, B.; Ke, L. Modeling and analysis of lake water storage changes on the Tibetan Plateau using multi-mission satellite data. Remote Sens. Environ. 2013, 135, 25–35. [Google Scholar] [CrossRef]
- Ke, L.; Ding, X.; Li, W.; Qiu, B. Remote sensing of glacier change in the central Qinghai-Tibet Plateau and the relationship with changing climate. Remote Sens. 2017, 9, 114. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Zhou, T. Water vapor transport for summer precipitation over the Tibetan Plateau: Multidata set analysis. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Su, F.; Chen, D.; Tang, Q. Atmospheric water transport to the endorheic Tibetan plateau and its effect on the hydrological status in the region. J. Geophys. Res. Atmos. 2019, 124, 12864–12881. [Google Scholar] [CrossRef]
- Chang, X.; Wang, B.; Yan, Y.; Hao, Y.; Zhang, M. Characterizing effects of monsoons and climate teleconnections on precipitation in China using wavelet coherence and global coherence. Clim. Dynam. 2019, 52, 5213–5228. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Yao, T.; Masson-Delmotte, V.; Gao, J.; Yu, W.; Yang, X.; Risi, C.; Sturm, C.; Werner, M.; Zhao, H.; He, Y. A review of climatic controls on δ18O in precipitation over the Tibetan Plateau: Observations and simulations. Rev. Geophys. 2013, 51, 525–548. [Google Scholar] [CrossRef]
- Lei, Y.; Zhu, Y.; Wang, B.; Yao, T.; Yang, K.; Zhang, X.; Zhai, J.; Ma, N. Extreme lake level changes on the Tibetan Plateau associated with the 2015/2016 El Niño. Geophys. Res. Lett. 2019, 46, 5889–5898. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased mass over the Tibetan Plateau: From lakes or glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Zhang, K.; Zhu, F. Lakes’ state and abundance across the Tibetan Plateau. Chin. Sci. Bull. 2014, 59, 3010–3021. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos Trans. Am. Geophys. Union 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Yang, K.; He, J. China meteorological forcing dataset (1979–2018); National Tibetan Plateau Data Center: Beijing, China, 2018. [Google Scholar] [CrossRef]
- Sun, S.; Chen, B.; Ge, M.; Qu, J.; Che, T.; Zhang, H.; Lin, X.; Che, M.; Zhou, Z.; Guo, L. Improving soil organic carbon parameterization of land surface model for cold regions in the Northeastern Tibetan Plateau, China. Ecol. Model. 2016, 330, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Wu, R.; Lau, K. Interannual variability of the Asian summer monsoon: Contrasts between the Indian and the western North Pacific–East Asian monsoons. J. Clim. 2001, 14, 4073–4090. [Google Scholar] [CrossRef]
- Li, J.; Zeng, Q. A unified monsoon index. Geophys. Res. Lett. 2002, 29, 115-1–115-4. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental US. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef] [Green Version]
- Hurrell, J.W. Decadal trends in the North Atlantic Oscillation: Regional temperatures and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ninglian, W.; Thompson, L.; Davis, M.; Mosley-Thompson, E.; Tandong, Y.; Jianchen, P. Influence of variations in NAO and SO on air temperature over the northern Tibetan Plateau as recorded by δ18O in the Malan ice core. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Li, W.; Du, Z.; Ling, F.; Zhou, D.; Wang, H.; Gui, Y.; Sun, B.; Zhang, X. A comparison of land surface water mapping using the normalized difference water index from TM, ETM+ and ALI. Remote Sens. 2013, 5, 5530–5549. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Li, M.; Liu, Y.; Cheng, L.; Duan, Y.; Zhou, M. River delineation from remotely sensed imagery using a multi-scale classification approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4726–4737. [Google Scholar] [CrossRef]
- Donchyts, G.; Schellekens, J.; Winsemius, H.; Eisemann, E.; Van de Giesen, N. A 30 m resolution surface water mask including estimation of positional and thematic differences using landsat 8, srtm and openstreetmap: A case study in the Murray-Darling Basin, Australia. Remote Sens. 2016, 8, 386. [Google Scholar] [CrossRef] [Green Version]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; Del Rio, R.A.; Cazenave, A. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Chen, C.; Twycross, J.; Garibaldi, J.M. A new accuracy measure based on bounded relative error for time series forecasting. PLoS ONE 2017, 12, e0174202. [Google Scholar] [CrossRef] [Green Version]
- Bian, H.; Li, W.; Li, Y.; Ren, B.; Niu, Y.; Zeng, Z. Driving forces of changes in China’s wetland area from the first (1999–2001) to second (2009–2011) National Inventory of Wetland Resources. Glob. Ecol. Conserv. 2020, 21, e00867. [Google Scholar] [CrossRef]
- Pettitt, A. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Ryberg, K.R.; Hodgkins, G.A.; Dudley, R.W. Change points in annual peak streamflows: Method comparisons and historical change points in the United States. J. Hydrol. 2020, 583, 124307. [Google Scholar] [CrossRef]
- Bingyi, W. Weakening of Indian summer monsoon in recent decades. Adv. Atmos. Sci. 2005, 22, 21–29. [Google Scholar] [CrossRef]
- Sun, J.; Yang, K.; Guo, W.; Wang, Y.; He, J.; Lu, H. Why has the Inner Tibetan Plateau become wetter since the mid-1990s? J. Clim. 2020, 33, 8507–8522. [Google Scholar] [CrossRef]
- Hwang, C.; Peng, M.-F.; Ning, J.; Luo, J.; Sui, C.-H. Lake level variations in China from TOPEX/Poseidon altimetry: Data quality assessment and links to precipitation and ENSO. Geophys. J. Int. 2005, 161, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chang, J.; Xu, C.-Y.; Zhou, Y.; Wu, Y.; Chen, X.; Jiang, S.; Duan, Z. The response of lake area and vegetation cover variations to climate change over the Qinghai-Tibetan Plateau during the past 30 years. Sci. Total Environ. 2018, 635, 443–451. [Google Scholar] [CrossRef]
- Qiao, B.; Zhu, L.; Yang, R. Temporal-spatial differences in lake water storage changes and their links to climate change throughout the Tibetan Plateau. Remote Sens. Environ. 2019, 222, 232–243. [Google Scholar] [CrossRef]
- Liu, X.; Madsen, D.; Zhang, X. The Driving Forces Underlying Spatiotemporal Lake Extent Changes in the Inner Tibetan Plateau During the Holocene. Front. Earth Sci. 2021, 9, 685928. [Google Scholar]
- Zhao, Z.; Liu, F.; Zhang, Y.; Liu, L.; Qi, W. The dynamic response of lakes in the Tuohepingco Basin of the Tibetan Plateau to climate change. Environ. Earth Sci. 2017, 76, 137. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y.; Liu, L.; Liu, F.; Zhang, H. Recent changes in wetlands on the Tibetan Plateau: A review. J. Geogr. Sci. 2015, 25, 879–896. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Xu, F.; Li, X.; Xia, T.; Zhang, Y. Intensities and time-frequency variability of ENSO in the last 65 years. J. Trop. Meteorol. 2017, 33, 683–694. (In Chinese) [Google Scholar] [CrossRef]
- Li, C.; Li, X.; Liu, Y.; Pan, W. Impact of spring and summer onset type ENSO on summer precipitation in China. Clim. Environ. Res. 2016, 21, 258–268. (In Chinese) [Google Scholar]







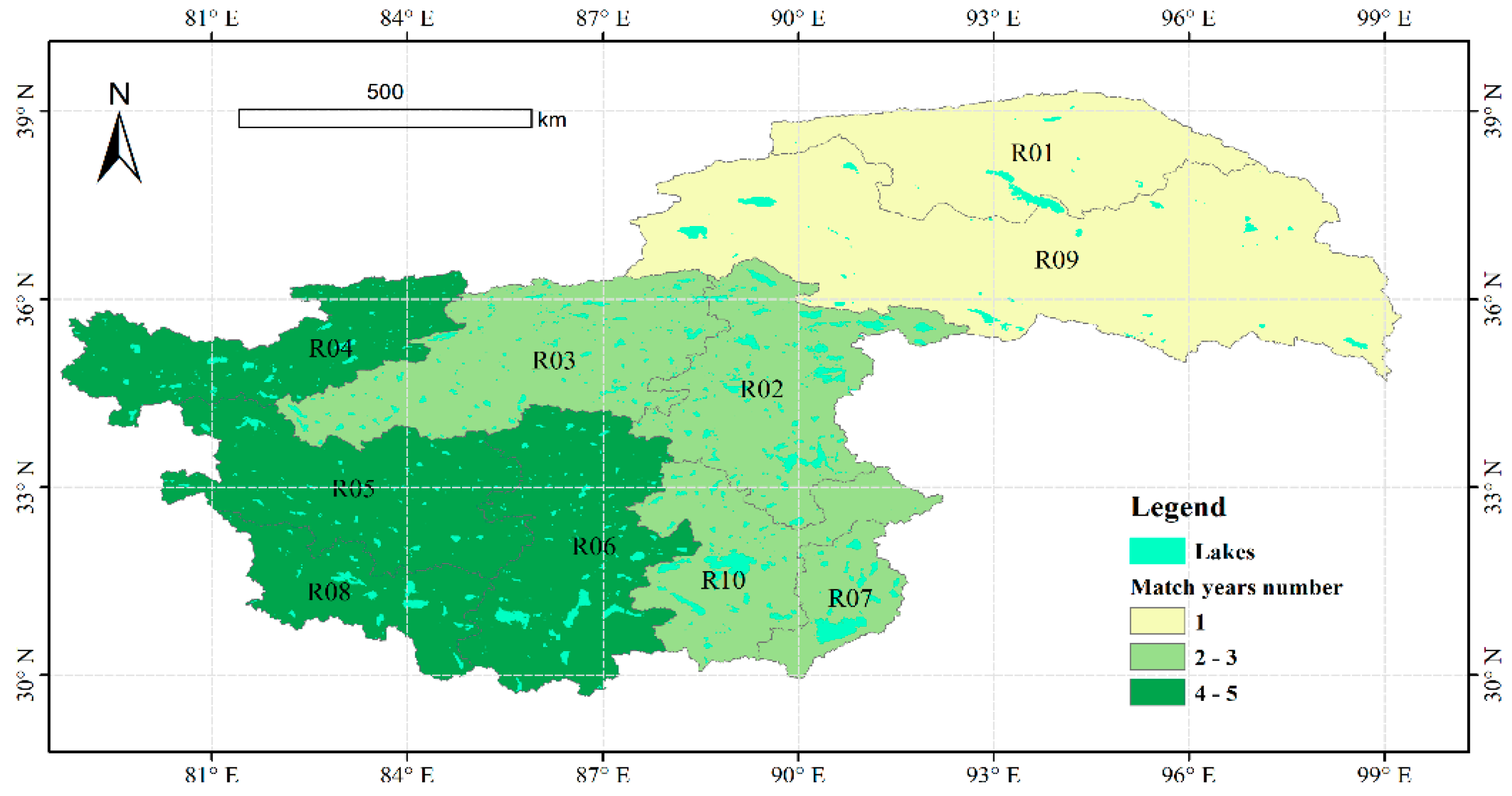
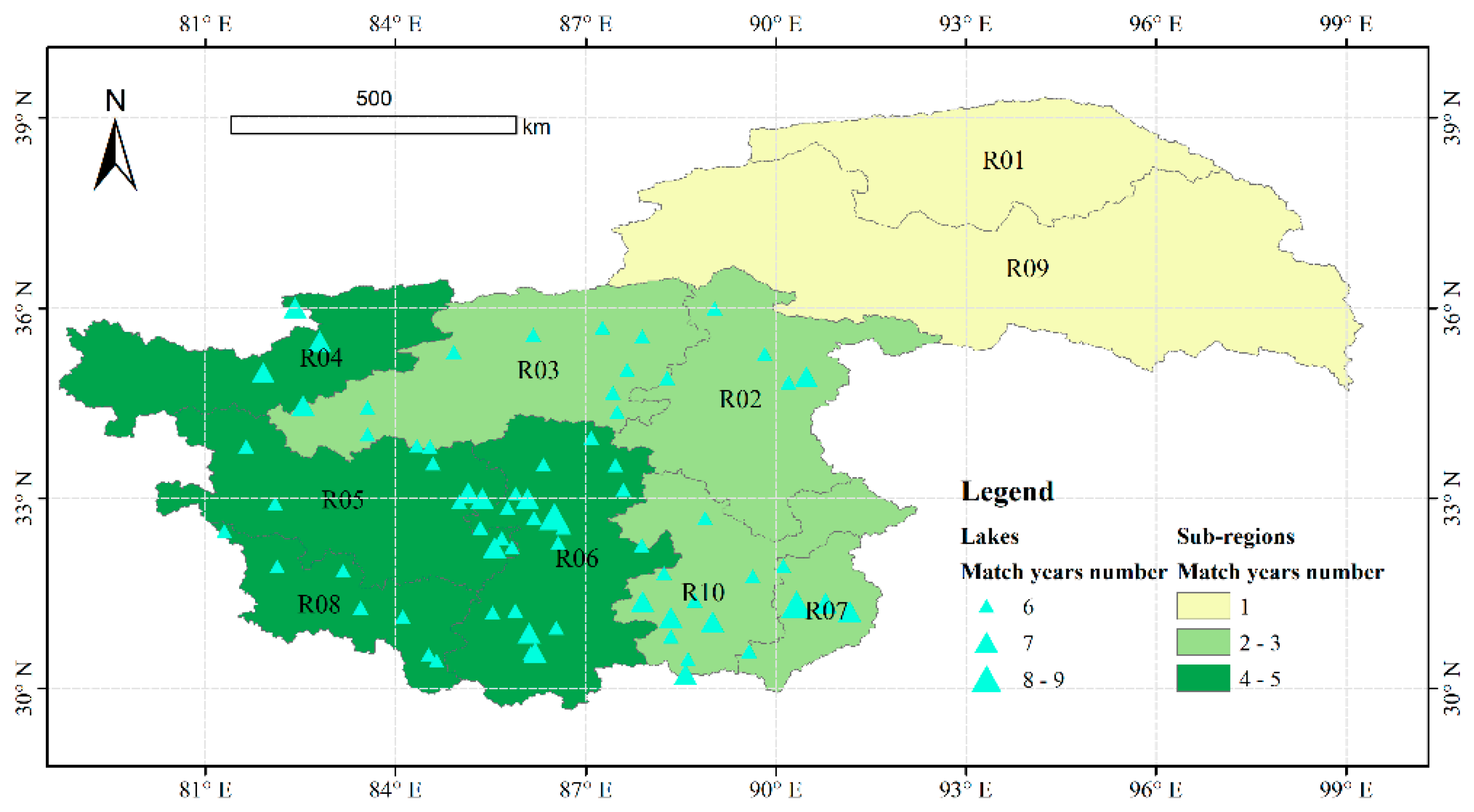



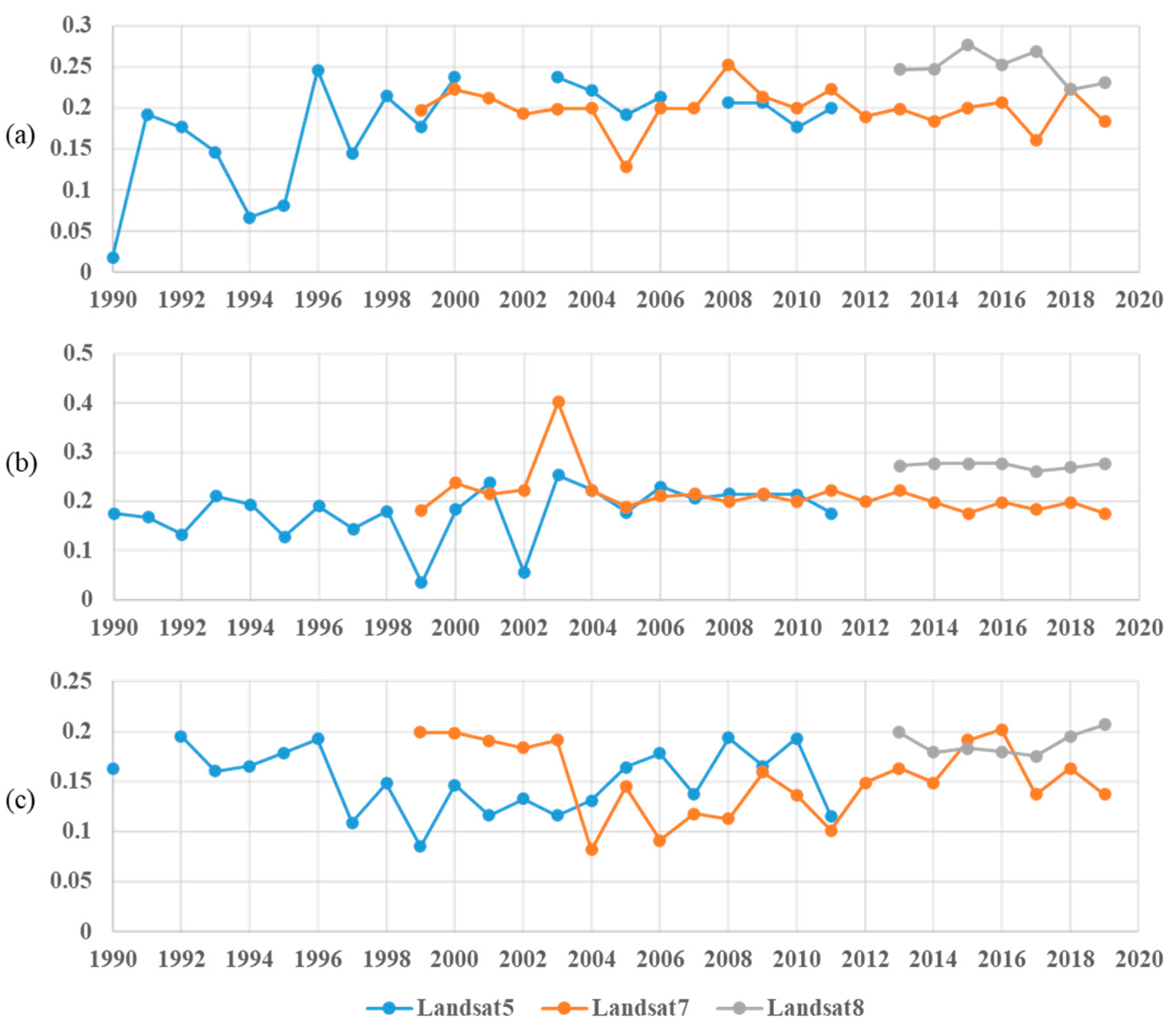
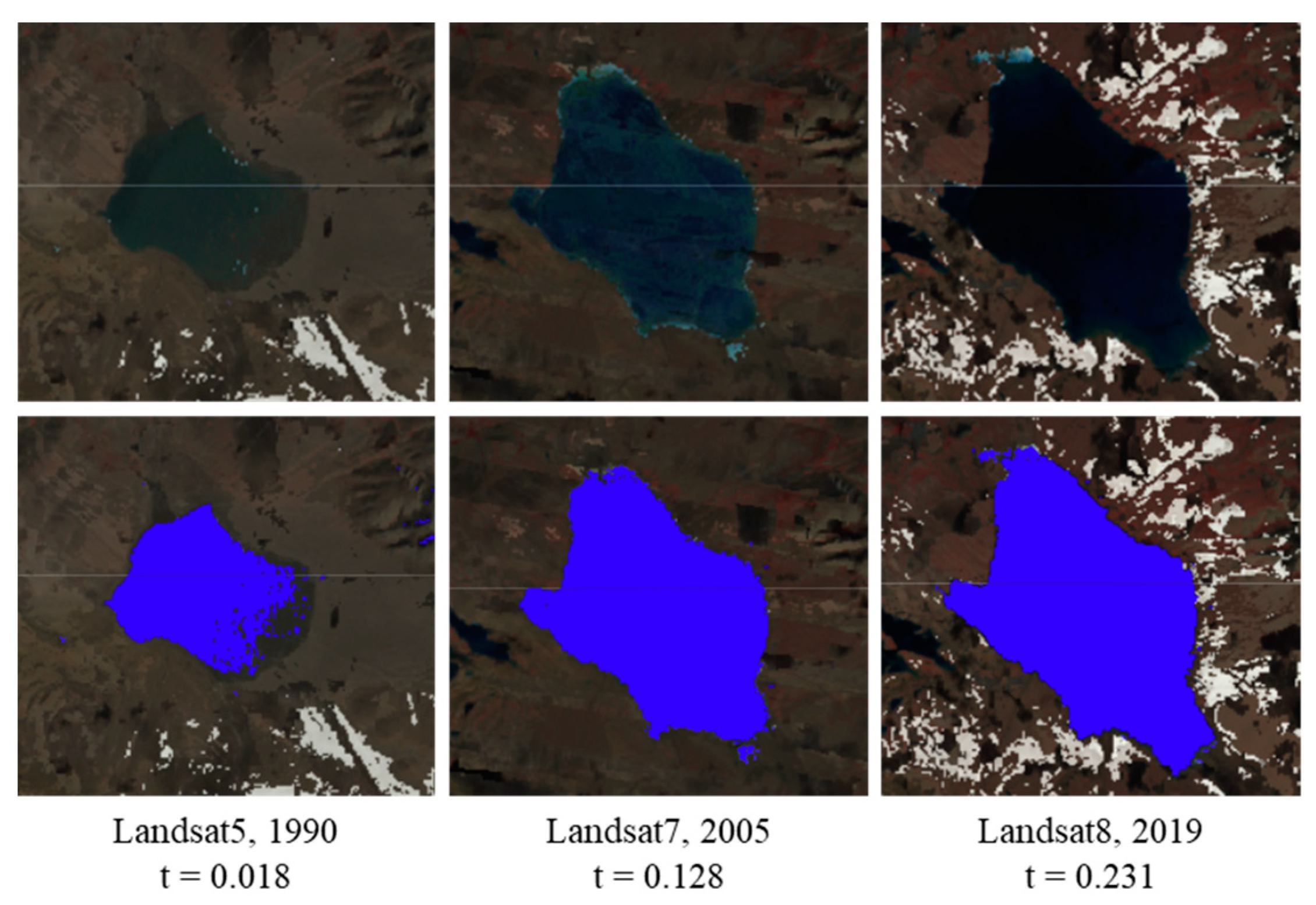

| Reference | Number of Lakes | Time Span | Study Area |
|---|---|---|---|
| Liao, Shen, and Li [19] | 328 | 1970, 1990 and 2000 | TP |
| Song, Huang, Richards et al. [24] | 312 | early 1970, 1990, 2000, 2003–2009 and 2011 | TP |
| Lei et al. [17] | 109 | 1976,1990,1999 and 2010 | TP interior |
| Yang et al. [20] | 874 | 2009 to 2014 | Changtang Plateau |
| Yao et al. [21] | 871 | 2009–2015 for 745 lakes and 2002–2015 for 126 lakes | Changtang Plateau |
| Zhang et al. [18] | 1609 | 1970, 1990, 1995, 2000, 2005, 2010, 2013–2018 | TP |
| Zhang et al. [22] | 1132 | 1976, 1990, 1995, 2000, 2005, 2010, 2015 and 2019 | TP |
| This study | 976 | Annual data for 1990–2019 | EBTP |
| Phenomenon | Years |
|---|---|
| El Niño | 1994, 1997, 2002, 2006, 2009, 2015 |
| La Niña | 1999, 2000, 2008, 2011, 2017 |
| Year | 1990 | 2000 | 2010 |
|---|---|---|---|
| Mean | 0.0815 | 0.0290 | 0.0214 |
| Standard deviation | 0.2050 | 0.0700 | 0.0622 |
| Sub-Region | Kendall Score | Increase Rate (%·year−1) | Tau | Trend |
|---|---|---|---|---|
| R01 | 259.0 | 3.47 | 0.595 * | Increasing |
| R02 | 383.0 | 1.64 | 0.880 * | Increasing |
| R03 | 373.0 | 4.01 | 0.857 * | Increasing |
| R04 | 373.0 | 1.58 | 0.857 * | Increasing |
| R05 | 343.0 | 1.49 | 0.789 * | Increasing |
| R06 | 365.0 | 0.96 | 0.839 * | Increasing |
| R07 | 261.0 | 0.35 | 0.600 * | Increasing |
| R08 | 257.0 | 0.33 | 0.591 * | Increasing |
| R09 | 337.0 | 1.65 | 0.775 * | Increasing |
| R10 | 351.0 | 1.02 | 0.807 * | Increasing |
| Region | AMO | NAO | |
|---|---|---|---|
| Lake Area | IB | 0.56 * | −0.12 |
| QB | 0.37 * | −0.21 | |
| EBTP | 0.56 * | −0.01 | |
| Temperature | IB | 0.47 * | −0.15 |
| QB | 0.66 * | −0.07 | |
| EBTP | 0.58 * | −0.07 | |
| Precipitation | IB | 0.53 * | −0.21 |
| QB | 0.58 * | −0.35 | |
| EBTP | 0.56 * | −0.23 |
| Matching Type | EBTP | IB | QB |
|---|---|---|---|
| El Niño | 1997, 2009, 2015 | 1997, 2015 | \ |
| La Niña | 2011 | 2008 | 1999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, M.; Wang, L.; She, J.; Zhu, L.; Li, X. Long-Term Lake Area Change and Its Relationship with Climate in the Endorheic Basins of the Tibetan Plateau. Remote Sens. 2021, 13, 5125. https://doi.org/10.3390/rs13245125
Wang J, Li M, Wang L, She J, Zhu L, Li X. Long-Term Lake Area Change and Its Relationship with Climate in the Endorheic Basins of the Tibetan Plateau. Remote Sensing. 2021; 13(24):5125. https://doi.org/10.3390/rs13245125
Chicago/Turabian StyleWang, Junxiao, Mengyao Li, Liuming Wang, Jiangfeng She, Liping Zhu, and Xingong Li. 2021. "Long-Term Lake Area Change and Its Relationship with Climate in the Endorheic Basins of the Tibetan Plateau" Remote Sensing 13, no. 24: 5125. https://doi.org/10.3390/rs13245125
APA StyleWang, J., Li, M., Wang, L., She, J., Zhu, L., & Li, X. (2021). Long-Term Lake Area Change and Its Relationship with Climate in the Endorheic Basins of the Tibetan Plateau. Remote Sensing, 13(24), 5125. https://doi.org/10.3390/rs13245125







